Numerical Solution of the Atmospheric Perturbations Triggered by Persistent Lithospheric Vibrations
Abstract
1. Introduction
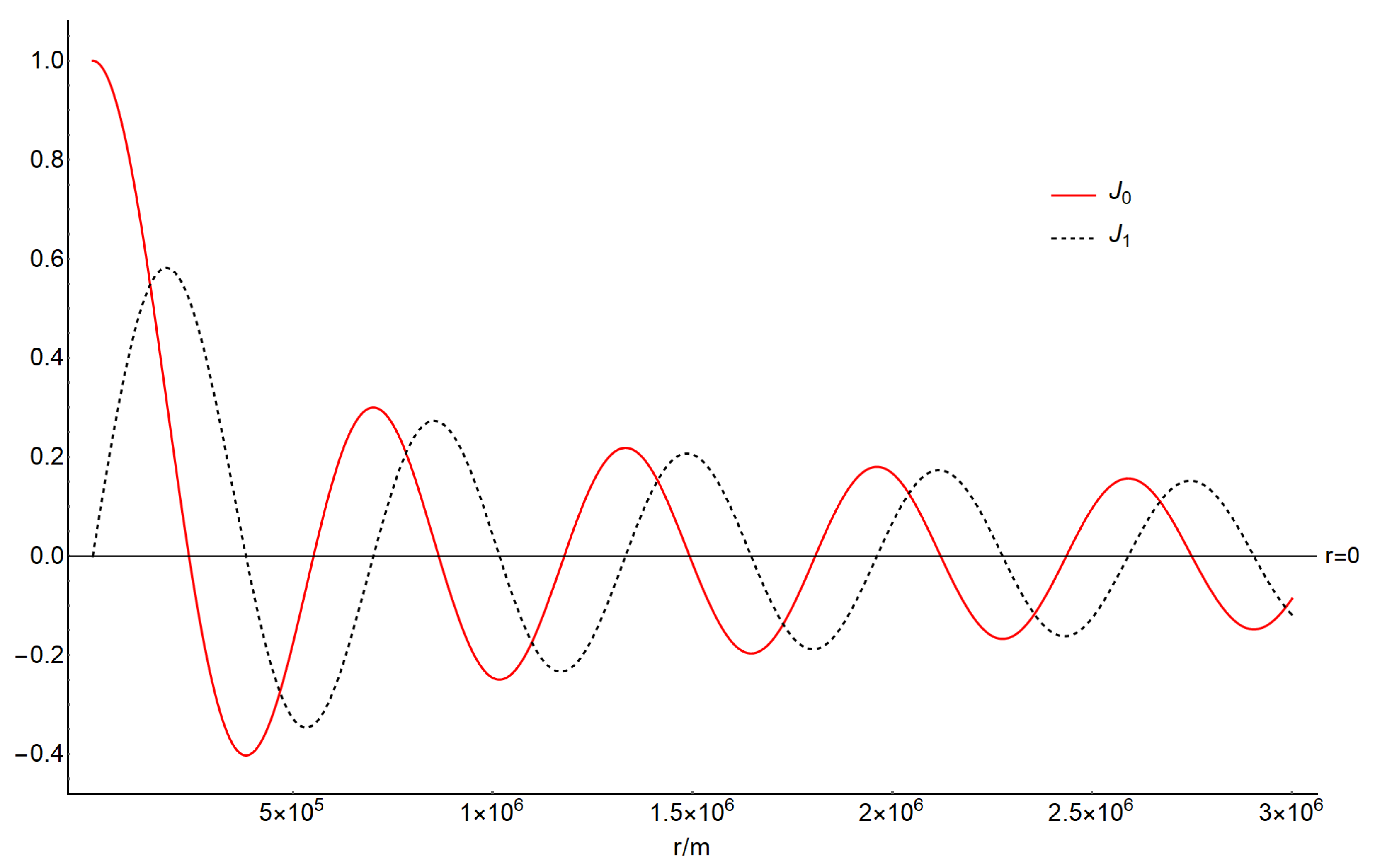
2. Perturbation Equations in the Cylindrical Symmetric Coordinates and its Numerical Solution
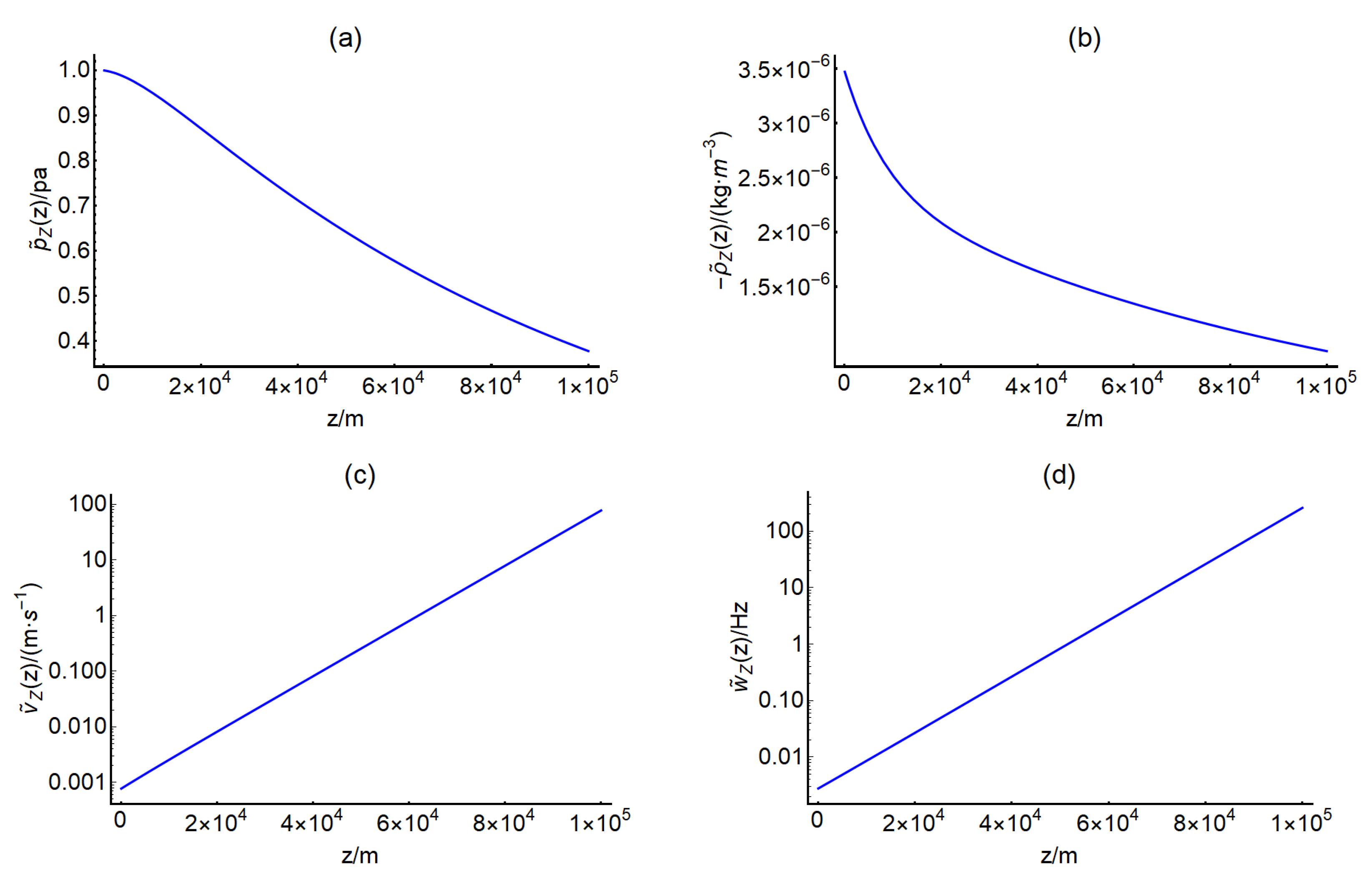
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Afraimovich, E.L.; Perevalova, N.P.; Plotnikov, A.; Uralov, A. The shock-acoustic waves generated by earthquakes. Ann. Geophys. 2001, 19, 395–409. [Google Scholar] [CrossRef]
- Artru, J.; Farges, T.; Lognonné, P. Acoustic waves generated from seismic surface waves: Propagation properties determined from Doppler sounding observations and normal-mode modelling. Geophys. J. Int. 2004, 158, 1067–1077. [Google Scholar] [CrossRef]
- Calais, E.; Bernard Minster, J.; Hofton, M.; Hedlin, M. Ionospheric signature of surface mine blasts from Global Positioning System measurements. Geophys. J. Int. 1998, 132, 191–202. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Lin, K.; Liu, J.; Wang, Y.; Gao, Y.; Zhang, D.; Xu, R.; Chen, C. The LAI Coupling Associated with the M6 Luxian Earthquake in China on 16 September 2021. Atmosphere 2021, 12, 1621. [Google Scholar] [CrossRef]
- Dautermann, T.; Calais, E.; Lognonné, P.; Mattioli, G.S. Lithosphere—Atmosphere—Ionosphere coupling after the 2003 explosive eruption of the Soufriere Hills Volcano, Montserrat. Geophys. J. Int. 2009, 179, 1537–1546. [Google Scholar] [CrossRef]
- Dautermann, T.; Calais, E.; Mattioli, G. GPS Detection, Modeling and Energy Estimation of the Ionospheric Wave following the 2003 Explosion of the Soufriere Hills Volcano, Montserrat. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 10–14 December 2007; p. V23E-08. [Google Scholar]
- Ducic, V.; Artru, J.; Lognonné, P. Ionospheric remote sensing of the Denali Earthquake Rayleigh surface waves. Geophys. Res. Lett. 2003, 30, SDE8-1. [Google Scholar] [CrossRef]
- Fitzgerald, T.J. Observations of total electron content perturbations on GPS signals caused by a ground level explosion. J. Atmos. Sol. Terr. Phys. 1997, 59, 829–834. [Google Scholar] [CrossRef]
- Hayakawa, M.; Schekotov, A.; Izutsu, J.; Yang, S.-S.; Solovieva, M.; Hobara, Y. Multi-parameter observations of seismogenic phenomena related to the Tokyo earthquake (M=5.9) on 7 October 2021. Geosciences 2022, 12, 265. [Google Scholar] [CrossRef]
- Kamiyama, M.; Sugito, M.; Kuse, M.; Schekotov, A.; Hayakawa, M. On the precursors to the 2011 Tohoku earthquake: Crustal movements and electromagnetic signatures. Geomat. Nat. Hazards Risk 2016, 7, 471–492. [Google Scholar] [CrossRef]
- Liu, J.; Chen, C.; Sun, Y.; Chen, C.; Tsai, H.; Yen, H.; Chum, J.; Lastovicka, J.; Yang, Q.; Chen, W. The vertical propagation of disturbances triggered by seismic waves of the 11 March 2011 M9. 0 Tohoku earthquake over Taiwan. Geophys. Res. Lett. 2016, 43, 1759–1765. [Google Scholar] [CrossRef]
- Occhipinti, G.; Lognonné, P.; Kherani, E.A.; Hébert, H. Three-dimensional waveform modeling of ionospheric signature induced by the 2004 Sumatra tsunami. Geophys. Res. Lett. 2006, 33, L20104. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Romanov, A.; Romanov, A.; Tsybulya, K.; Davidenko, D.; Kafatos, M.; Taylor, P. Atmosphere-ionosphere response to the M9 Tohoku earthquake revealed by multi-instrument space-borne and ground observations: Preliminary results. Earthq. Sci. 2011, 24, 557–564. [Google Scholar] [CrossRef]
- Oyama, K.-I.; Devi, M.; Ryu, K.; Chen, C.; Liu, J.; Liu, H.; Bankov, L.; Kodama, T. Modifications of the ionosphere prior to large earthquakes: Report from the Ionosphere Precursor Study Group. Geosci. Lett. 2016, 3, 6. [Google Scholar] [CrossRef]
- Parrot, M.; Tramutoli, V.; Liu, T.J.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and ionospheric coupling phenomena related to large earthquakes. Nat. Hazards Earth Syst. Sci. Discuss. 2016, 1–30. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) model–An unified concept for earthquake precursors validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- Sun, Y.-Y. GNSS brings us back on the ground from ionosphere. Geosci. Lett. 2019, 6, 14. [Google Scholar] [CrossRef]
- Hayakawa, M. The precursory signature effect of the Kobe earthquake on VLF subionospheric signals. J. Comm. Res. Lab. 1996, 43, 169–180. [Google Scholar]
- Hayakawa, M. Earthquake Prediction with Radio Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Hayakawa, M. Earthquake prediction with electromagnetic phenomena. AIP Conf. Proc. 2016, 1709, 020002. [Google Scholar]
- Pulinets, S.; Boyarchuk, K. Ionospheric Precursors of Earthquakes; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2004; p. 315. [Google Scholar]
- Sorokin, V.; Yaschenko, A.; Chmyrev, V.; Hayakawa, M. DC electric field amplification in the mid-latitude ionosphere over seismically active faults. Nat. Hazards Earth Syst. Sci. 2005, 5, 661–666. [Google Scholar] [CrossRef]
- Hayakawa, M.; Nakamura, T.; Hobara, Y.; Williams, E. Observation of sprites over the Sea of Japan and conditions for lightning-induced sprites in winter. J. Geophys. Res. Atmos. 2004, 109, A01312. [Google Scholar] [CrossRef]
- Pasko, V.; Inan, U.; Bell, T.; Taranenko, Y.N. Sprites produced by quasi-electrostatic heating and ionization in the lower ionosphere. J. Geophys. Res. Space Phys. 1997, 102, 4529–4561. [Google Scholar] [CrossRef]
- Takahashi, Y.; Miyasato, R.; Adachi, T.; Adachi, K.; Sera, M.; Uchida, A.; Fukunishi, H. Activities of sprites and elves in the winter season, Japan. J. Atmos. Sol. -Terr. Phys. 2003, 65, 551–560. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Liu, J.Y.; Lin, C.C.H.; Lin, C.Y.; Shen, M.H.; Chen, C.H.; Chen, C.H.; Chou, M.Y. Ionospheric bow wave induced by the moon shadow ship over the continent of United States on 21 August 2017. Geophys. Res. Lett. 2018, 45, 538–544. [Google Scholar] [CrossRef]
- Chou, M.Y.; Cherniak, I.; Lin, C.C.; Pedatella, N. The persistent ionospheric responses over Japan after the impact of the 2011 Tohoku earthquake. Space Weather 2020, 18, e2019SW002302. [Google Scholar] [CrossRef]
- Davies, K. Ionospheric Radio; Peregrinus: London, UK, 1990. [Google Scholar]
- De la Torre, A.; Alexander, P.; Giraldez, A. The kinetic to potential energy ratio and spectral separability from high-resolution balloon soundings near the Andes Mountains. Geophys. Res. Lett. 1999, 26, 1413–1416. [Google Scholar] [CrossRef]
- Hickey, M.P.; Schubert, G.; Walterscheid, R. Acoustic wave heating of the thermosphere. J. Geophys. Res. Space Phys. 2001, 106, 21543–21548. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Liu, J.Y.; Lin, C.Y.; Tsai, H.F.; Chang, L.C.; Chen, C.Y.; Chen, C.H. Ionospheric F2 region perturbed by the 25 April 2015 Nepal earthquake. J. Geophys. Res. Space Phys. 2016, 121, 5778–5784. [Google Scholar] [CrossRef]
- Tsuda, T.; Murayama, Y.; Nakamura, T.; Vincent, R.; Manson, A.; Meek, C.; Wilson, R. Variations of the gravity wave characteristics with height, season and latitude revealed by comparative observations. J. Atmos. Terr. Phys. 1994, 56, 555–568. [Google Scholar] [CrossRef]
- VanZandt, T. A model for gravity wave spectra observed by Doppler sounding systems. Radio Sci. 1985, 20, 1323–1330. [Google Scholar] [CrossRef]
- Yang, S.-S.; Hayakawa, M. Gravity wave activity in the stratosphere before the 2011 Tohoku earthquake as the mechanism of lithosphere-atmosphere-ionosphere coupling. Entropy 2020, 22, 110. [Google Scholar] [CrossRef]
- Piersanti, M.; Materassi, M.; Battiston, R.; Carbone, V.; Cicone, A.; Angelo, G.D.; Diego, P.; Ubertini, P. Magnetospheric–Ionospheric–Lithospheric Coupling Model. 1: Observations during the 5 August 2018 Bayan Earthquake. Remote Sens. 2020, 12, 3299. [Google Scholar] [CrossRef]
- Hines, C.O. Internal atmospheric gravity waves at ionospheric heights. Can. J. Phys. 1960, 38, 1441–1481. [Google Scholar] [CrossRef]
- Hines, C.O. The upper atmosphere in motion. Q. J. R. Meteorol. Soc. 1963, 89, 1–42. [Google Scholar] [CrossRef]
- Kasahara, Y.; Nakamura, T.; Hobara, Y.; Hayakawa, M.; Rozhnoi, A.; Solovieva, M. A statistical study on the AGW modulations in subionospheric VLF/LF propagation data and consideration of the generation mechanism of seismo-ionospheric perturbations. J. Atmos. Electr. 2010, 30, 103–112. [Google Scholar] [CrossRef]
- Korepanov, V.; Hayakawa, M.; Yampolski, Y.; Lizunov, G. AGW as a seismo-ionospheric coupling responsible agent. Phys. Chem. Earth Parts A/B/C 2009, 34, 485–495. [Google Scholar] [CrossRef]
- Miyaki, K.; Hayakawa, M.; Molchanov, O. The role of gravity waves in the lithosphere-ionosphere coupling, as revealed from the subionospheric LF propagation data. Seism. Electromagn. Lithosphere Atmos. Ionos. Coupling 2002, 229–232. [Google Scholar]
- Molchanov, O.; Hayakawa, M.; Miyaki, K. VLF/LF sounding of the lower ionosphere to study the role of atmospheric oscillations in the lithosphere-ionosphere coupling. Adv. Polar Up. Atmos. Res. 2001, 15, 146–158. [Google Scholar] [CrossRef]
- Shvets, A.; Hayakawa, M.; Molchanov, O.; Ando, Y. A study of ionospheric response to regional seismic activity by VLF radio sounding. Phys. Chem. Earth Parts A/B/C 2004, 29, 627–637. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Chen, C.-H.; Yu, T.; Wang, J.; Qiu, L.; Qi, Y.; Lin, K. Temperature response to the June 2020 solar eclipse observed by FORMOSAT-7/COSMIC2 in the Tibet sector. Terr. Atmos. Ocean. Sci. 2022, 33, 1–7. [Google Scholar] [CrossRef]
- Wang, J.; Zuo, X.; Sun, Y.Y.; Yu, T.; Wang, Y.; Qiu, L.; Mao, T.; Yan, X.; Yang, N.; Qi, Y. Multilayered sporadic-E response to the annular solar eclipse on June 21, 2020. Space Weather 2021, 19, e2020SW002643. [Google Scholar] [CrossRef]
- Sabatini, R.; Snively, J.; Bailly, C.; Hickey, M.; Garrison, J. Numerical modeling of the propagation of infrasonic acoustic waves through the turbulent field generated by the breaking of mountain gravity waves. Geophys. Res. Lett. 2019, 46, 5526–5534. [Google Scholar] [CrossRef]
- Sun, Y.Y.; Shen, M.M.; Tsai, Y.L.; Lin, C.Y.; Chou, M.Y.; Yu, T.; Lin, K.; Huang, Q.; Wang, J.; Qiu, L. Wave steepening in ionospheric total electron density due to the 21 August 2017 total solar eclipse. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028931. [Google Scholar] [CrossRef]
- Lognonné, P.; Clévédé, E.; Kanamori, H. Computation of seismograms and atmospheric oscillations by normal-mode summation for a spherical earth model with realistic atmosphere. Geophys. J. Int. 1998, 135, 388–406. [Google Scholar] [CrossRef]
- Fraser-Smith, A.C.; Bernardi, A.; McGill, P.; Ladd, M.E.; Helliwell, R.; Villard, O., Jr. Low-frequency magnetic field measurements near the epicenter of the Ms 7.1 Loma Prieta earthquake. Geophys. Res. Lett. 1990, 17, 1465–1468. [Google Scholar] [CrossRef]
- Molchanov, O.; Mazhaeva, O.; Golyavin, A.; Hayakawa, M. Observation by the Intercosmos-24 satellite of ELF-VLF electromagnetic emissions associated with earthquakes. Ann. Geophys. 1993, 11, 431–440. [Google Scholar]
- Chen, C.-H.; Yeh, T.-K.; Liu, J.-Y.; Wang, C.-H.; Wen, S.; Yen, H.-Y.; Chang, S.-H. Surface deformation and seismic rebound: Implications and applications. Surv. Geophys. 2011, 32, 291–313. [Google Scholar] [CrossRef]
- Bedford, J.R.; Moreno, M.; Deng, Z.; Oncken, O.; Schurr, B.; John, T.; Báez, J.C.; Bevis, M. Months-long thousand-kilometre-scale wobbling before great subduction earthquakes. Nature 2020, 580, 628–635. [Google Scholar] [CrossRef]
- Chen, C.-H.; Lin, L.-C.; Yeh, T.-K.; Wen, S.; Yu, H.; Yu, C.; Gao, Y.; Han, P.; Sun, Y.-Y.; Liu, J.-Y. Determination of epicenters before earthquakes utilizing far seismic and GNSS data: Insights from ground vibrations. Remote Sens. 2020, 12, 3252. [Google Scholar] [CrossRef]
- Chen, C.-H.; Tang, C.-C.; Cheng, K.-C.; Wang, C.-H.; Wen, S.; Lin, C.-H.; Wen, Y.-Y.; Meng, G.; Yeh, T.-K.; Jan, J.C. Groundwater–strain coupling before the 1999 Mw 7.6 Taiwan Chi-Chi earthquake. J. Hydrol. 2015, 524, 378–384. [Google Scholar] [CrossRef]
- Chen, C.-H.; Wen, S.; Liu, J.-Y.; Hattori, K.; Han, P.; Hobara, Y.; Wang, C.-H.; Yeh, T.-K.; Yen, H.-Y. Surface displacements in Japan before the 11 March 2011 M9. 0 Tohoku-Oki earthquake. J. Asian Earth Sci. 2014, 80, 165–171. [Google Scholar] [CrossRef]
- Han, P.; Hattori, K.; Huang, Q.; Hirooka, S.; Yoshino, C. Spatiotemporal characteristics of the geomagnetic diurnal variation anomalies prior to the 2011 Tohoku earthquake (Mw 9.0) and the possible coupling of multiple pre-earthquake phenomena. J. Asian Earth Sci. 2016, 129, 13–21. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Wen, S.; Han, P.; Lin, L.-C.; Yu, H.; Zhang, X.; Gao, Y.; Tang, C.-C.; Lin, C.-H. Spatiotemporal changes of seismicity rate during earthquakes. Nat. Hazards Earth Syst. Sci. 2020, 20, 3333–3341. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Lin, K.; Zhou, C.; Xu, R.; Qing, H.; Gao, Y.; Chen, T.; Wang, F.; Yu, H. A new instrumental array in Sichuan, China, to monitor vibrations and perturbations of the lithosphere, atmosphere, and ionosphere. Surv. Geophys. 2021, 42, 1425–1442. [Google Scholar] [CrossRef]
- Chen, C.H.; Sun, Y.Y.; Xu, R.; Lin, K.; Wang, F.; Zhang, D.; Zhou, Y.; Gao, Y.; Zhang, X.; Yu, H. Resident waves in the ionosphere before the M6. 1 Dali and M7. 3 Qinghai earthquakes of 21–22 May 2021. Earth Space Sci. 2022, 9, e2021EA002159. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Zhang, X.; Gao, Y.; Wang, F.; Lin, K.; Tang, C.C.; Huang, R.; Xu, R.; Liu, J. Resonant signals in the lithosphere–atmosphere–ionosphere coupling. Sci. Rep. 2022, 12, 14587. [Google Scholar] [CrossRef] [PubMed]
- Mikhailenko, B.; Reshetova, G. Mathematical modeling of seismic and acousto-gravitational waves in a heterogeneous earth-atmosphere model. J. Comput. Appl. Math. 2010, 234, 1678–1684. [Google Scholar] [CrossRef]
- Kherani, E.A.; Lognonné, P.; Hébert, H.; Rolland, L.; Astafyeva, E.; Occhipinti, G.; Coïsson, P.; Walwer, D.; de Paula, E.R. Modelling of the total electronic content and magnetic field anomalies generated by the 2011 Tohoku-Oki tsunami and associated acoustic-gravity waves. Geophys. J. Int. 2012, 191, 1049–1066. [Google Scholar] [CrossRef]
- Brissaud, Q.; Martin, R.; Garcia, R.F.; Komatitsch, D. Finite-difference numerical modelling of gravitoacoustic wave propagation in a windy and attenuating atmosphere. Geophys. J. Int. 2016, 206, 308–327. [Google Scholar] [CrossRef]
- Mikhailenko, B.G.; Reshetova, G.V.; Suvorov, V.D. Simulation of seismic and acoustic-gravity wave propagation in a heterogeneous “Earth-atmosphere” model. Russ. Geol. Geophys. 2006, 47, 547–556. [Google Scholar]
- Mikhailenko, B.G.; Mikhailov, A.A. Numerical modeling of seismic and acoustic-gravity waves propagation in an “Earth-Atmosphere” model in the presence of wind in the air. Numer. Anal. Appl. 2014, 7, 124–135. [Google Scholar] [CrossRef]
- Martire, L.; Brissaud, Q.; Lai, V.H.; Garcia, R.F.; Martin, R.; Krishnamoorthy, S.; Komjathy, A.; Cadu, A.; Cutts, J.A.; Jackson, J.M.; et al. Numerical Simulation of the Atmospheric Signature of Artificial and Natural Seismic Events. Geophys. Res. Lett. 2018, 45, 12085–12093. [Google Scholar] [CrossRef]
- Pavlov, V.A.; Lebedev, S.V. Nonlinear evolution of the atmosphere and ionosphere above a seismic epicenter. II. Numerical simulation. Geomagn. Aeron. 2017, 57, 602–609. [Google Scholar] [CrossRef]
- Davies, J.B.; Archambeau, C.B. Modeling of atmospheric and ionospheric disturbances from shallow seismic sources. Phys. Earth Planet. Inter. 1998, 105, 183–199. [Google Scholar] [CrossRef]
- Carbone, V.; Piersanti, M.; Materassi, M.; Battiston, R.; Lepreti, F.; Ubertini, P. A mathematical model of lithosphere–atmosphere coupling for seismic events. Sci. Rep. 2021, 11, 8682. [Google Scholar] [CrossRef] [PubMed]
- Brissaud, Q.; Martin, R.; Garcia, R.F.; Komatitsch, D. Hybrid Galerkin numerical modelling of elastodynamics and compressible Navier–Stokes couplings: Applications to seismo-gravito acoustic waves. Geophys. J. Int. 2017, 210, 1047–1069. [Google Scholar] [CrossRef]
- Gao, Y.; Li, T.; Zhou, G.; Cheng, C.-H.; Sun, Y.-y.; Zhang, X.; Liu, J.-Y.; Wen, J.; Yao, C.; Bai, X. Acoustic-gravity waves generated by a point source on the ground in a stratified atmosphere-Earth structure. Geophys. J. Int. 2022, 232, 764–787. [Google Scholar] [CrossRef]
- Lin, C.C.; Chen, C.H.; Matsumura, M.; Lin, J.T.; Kakinami, Y. Observation and simulation of the ionosphere disturbance waves triggered by rocket exhausts. J. Geophys. Res. Space Phys. 2017, 122, 8868–8882. [Google Scholar] [CrossRef]
- Matsumura, M.; Saito, A.; Iyemori, T.; Shinagawa, H.; Tsugawa, T.; Otsuka, Y.; Nishioka, M.; Chen, C. Numerical simulations of atmospheric waves excited by the 2011 off the Pacific coast of Tohoku Earthquake. Earth Planets Space 2011, 63, 885–889. [Google Scholar] [CrossRef]
- Chen, C.-H.; Zhang, X.; Sun, Y.-Y.; Wang, F.; Liu, T.-C.; Lin, C.-Y.; Gao, Y.; Lyu, J.; Jin, X.; Zhao, X. Individual Wave Propagations in Ionosphere and Troposphere Triggered by the Hunga Tonga-Hunga Ha’apai Underwater Volcano Eruption on 15 January 2022. Remote Sens. 2022, 14, 2179. [Google Scholar] [CrossRef]
- Chen, C.-H.; Sun, Y.-Y.; Zhang, X.; Wang, F.; Lin, K.; Gao, Y.; Tang, C.-C.; Lyu, J.; Huang, R.; Huang, Q. Far-field coupling and interactions in multiple geospheres after the Tonga volcano eruptions. Surv. Geophys. 2022, 44, 587–601. [Google Scholar] [CrossRef]
- Yang, S.S.; Asano, T.; Hayakawa, M. Abnormal gravity wave activity in the stratosphere prior to the 2016 Kumamoto earthquakes. J. Geophys. Res. Space Phys. 2019, 124, 1410–1425. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Chen, C.-H.; Su, X.; Wang, J.; Yu, T.; Xu, H.-R.; Liu, J.-Y. Occurrence of nighttime irregularities and their scale evolution in the ionosphere due to the solar eclipse over East Asia on 21 June 2020. J. Geophys. Res. Space Phys. 2023, 1, e2022JA030936. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Liu, H.; Miyoshi, Y.; Liu, L.; Chang, L.C. El Niño–Southern Oscillation effect on quasi-biennial oscillations of temperature diurnal tides in the mesosphere and lower thermosphere. Earth Plant Space 2018, 70, 85. [Google Scholar] [CrossRef]
- Sun, Y.-Y.; Liu, H.; Miyoshi, Y.; Chang, L.C.; Liu, L. El Niño—Southern Oscillation effect on ionospheric tidal/SPW amplitude in 2007–2015 FORMOSAT-3/COSMIC observations. Earth Plant Space 2019, 71, 35. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, K.; Mao, Z.; Xu, Z.; Dong, L.; Zhang, X.; Gao, Y.; Chen, C.-H. Numerical Solution of the Atmospheric Perturbations Triggered by Persistent Lithospheric Vibrations. Remote Sens. 2023, 15, 3336. https://doi.org/10.3390/rs15133336
Lin K, Mao Z, Xu Z, Dong L, Zhang X, Gao Y, Chen C-H. Numerical Solution of the Atmospheric Perturbations Triggered by Persistent Lithospheric Vibrations. Remote Sensing. 2023; 15(13):3336. https://doi.org/10.3390/rs15133336
Chicago/Turabian StyleLin, Kai, Zhiqiang Mao, Ziniu Xu, Lei Dong, Xuemin Zhang, Yongxin Gao, and Chieh-Hung Chen. 2023. "Numerical Solution of the Atmospheric Perturbations Triggered by Persistent Lithospheric Vibrations" Remote Sensing 15, no. 13: 3336. https://doi.org/10.3390/rs15133336
APA StyleLin, K., Mao, Z., Xu, Z., Dong, L., Zhang, X., Gao, Y., & Chen, C.-H. (2023). Numerical Solution of the Atmospheric Perturbations Triggered by Persistent Lithospheric Vibrations. Remote Sensing, 15(13), 3336. https://doi.org/10.3390/rs15133336








