Coupling Dilated Encoder–Decoder Network for Multi-Channel Airborne LiDAR Bathymetry Full-Waveform Denoising
Abstract
1. Introduction
- Based on a multi-task deep learning architecture and a centroid alignment algorithm, we propose a novel LiDAR denoising technique for multi-channel ALB systems that can improve the stability of denoising.
- The NLEB module is proposed, and the loss function is optimized to explore the impact of intra-channel autocorrelation and inter-channel structural similarity on LiDAR signal enhancement.
- We analyzed the characteristics of multi-channel ALB data and the limitations of the denoising algorithm by using measured data.
2. Related Work
2.1. Model-Based Methods
2.2. Learning-Based Methods
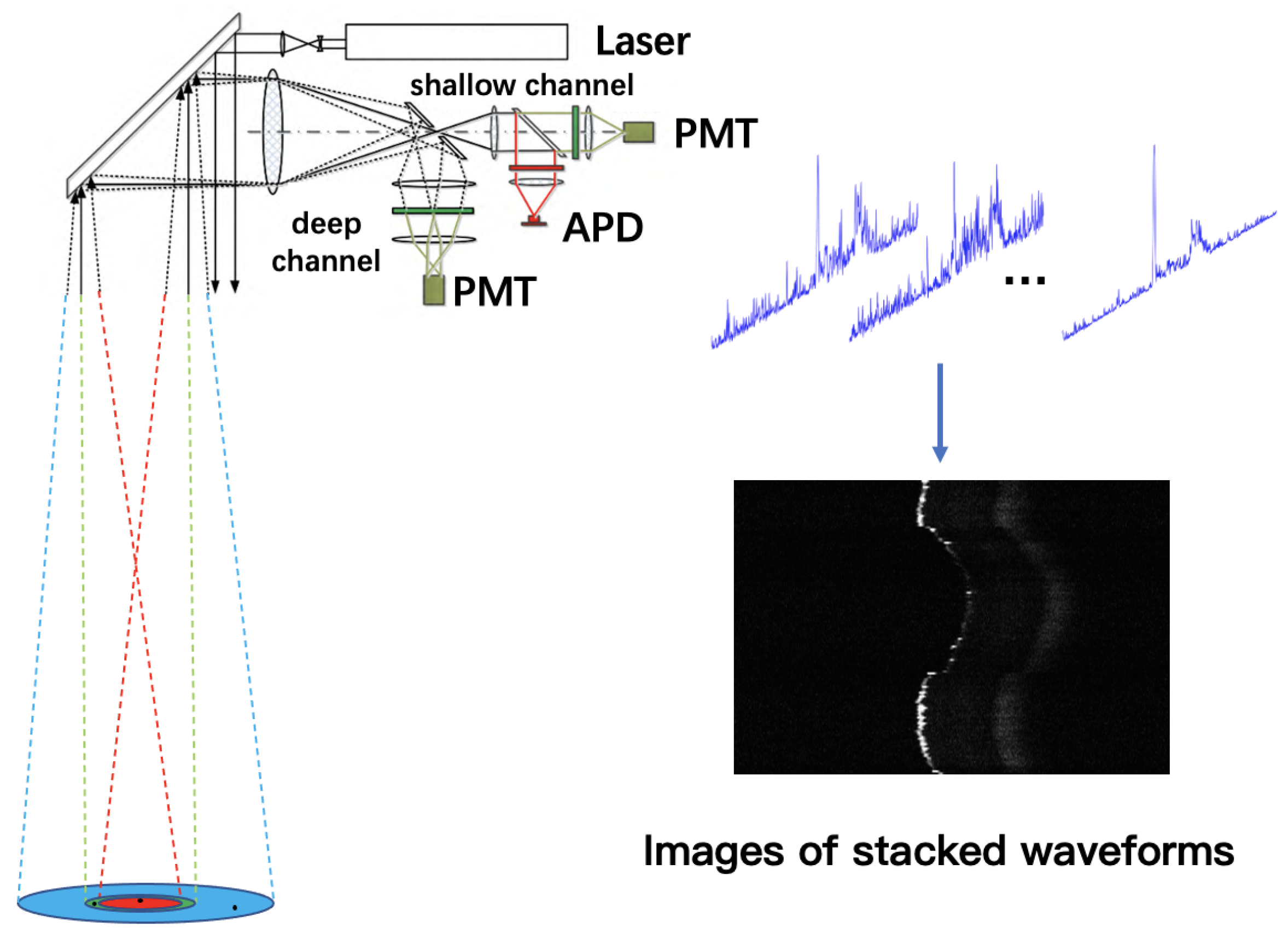
3. Materials
3.1. Analysis of ALB Data
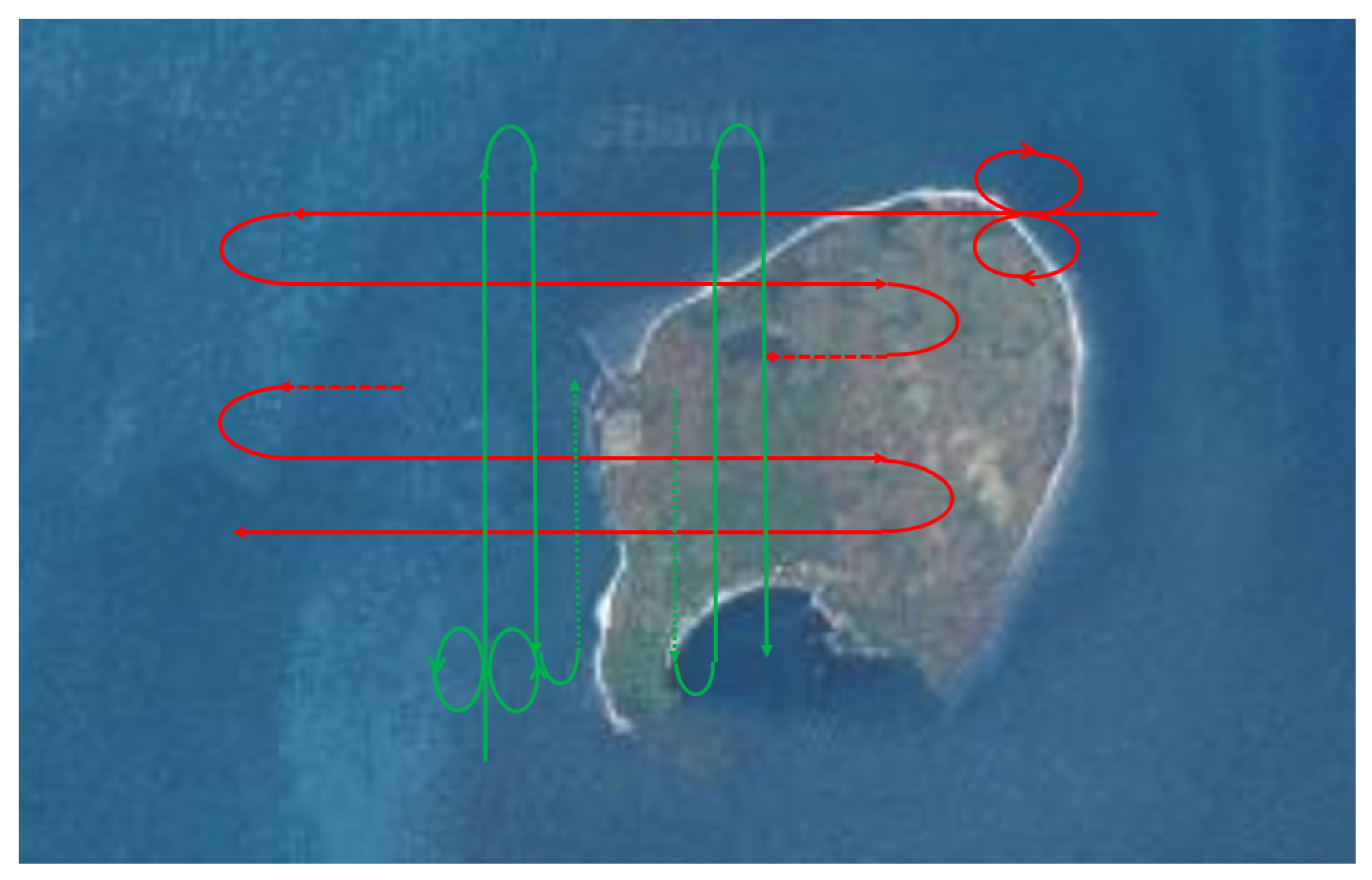
3.2. Measured Data Set
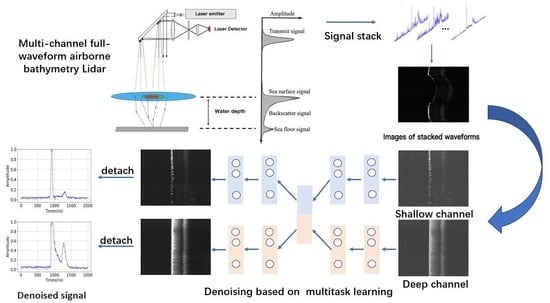
4. Proposed Method
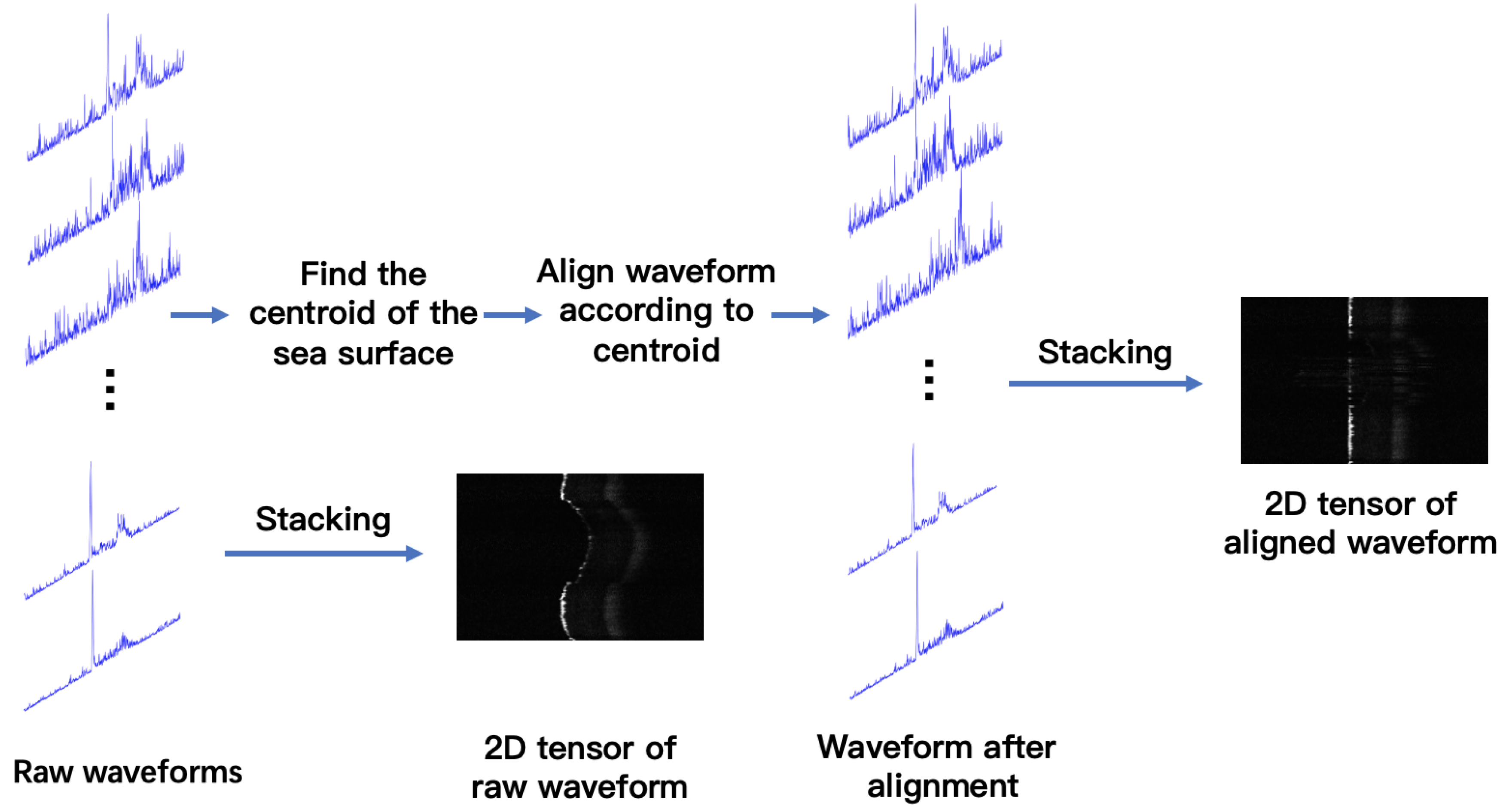
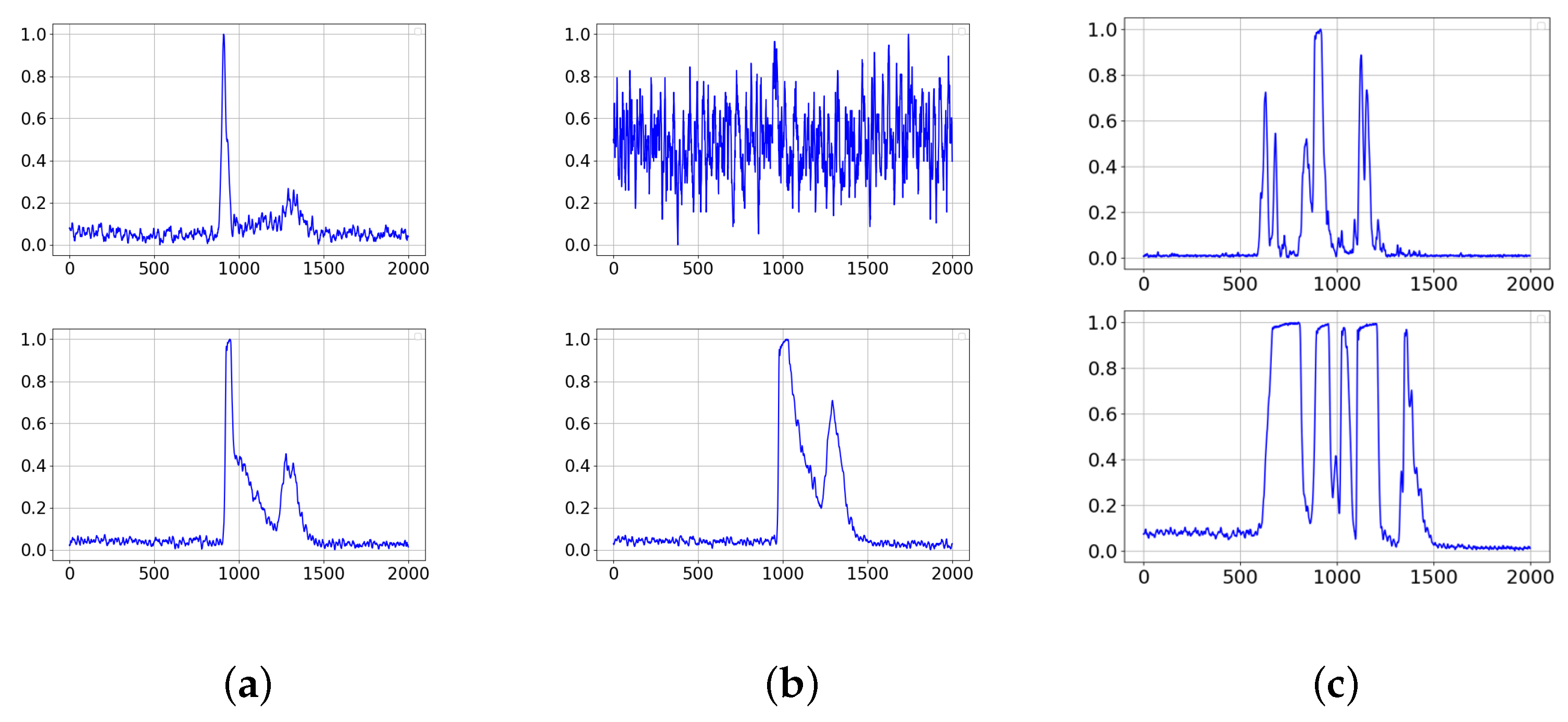
4.1. Preprocessing of Full Waveform
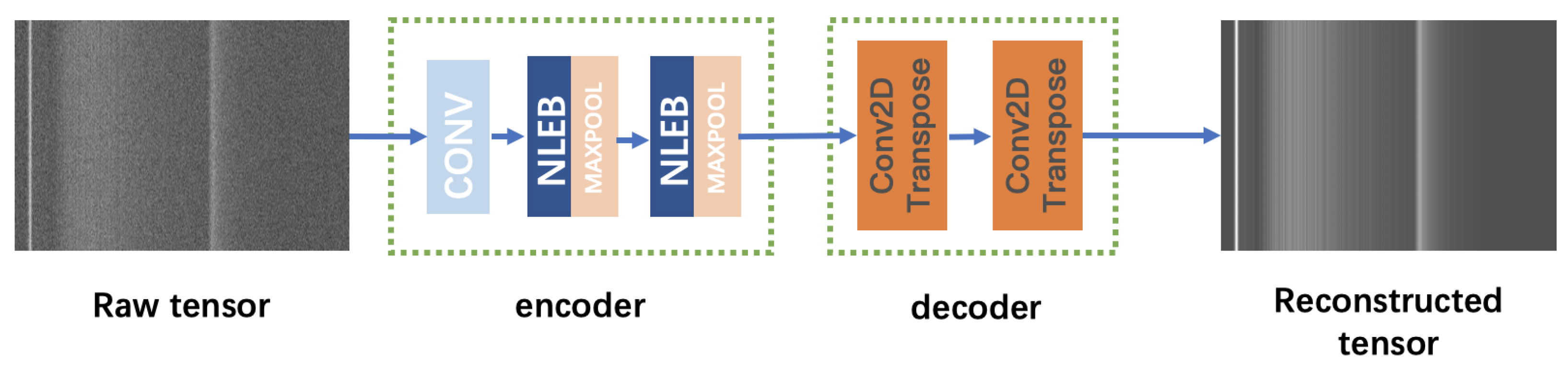
4.2. Nonlocal Encoder Block
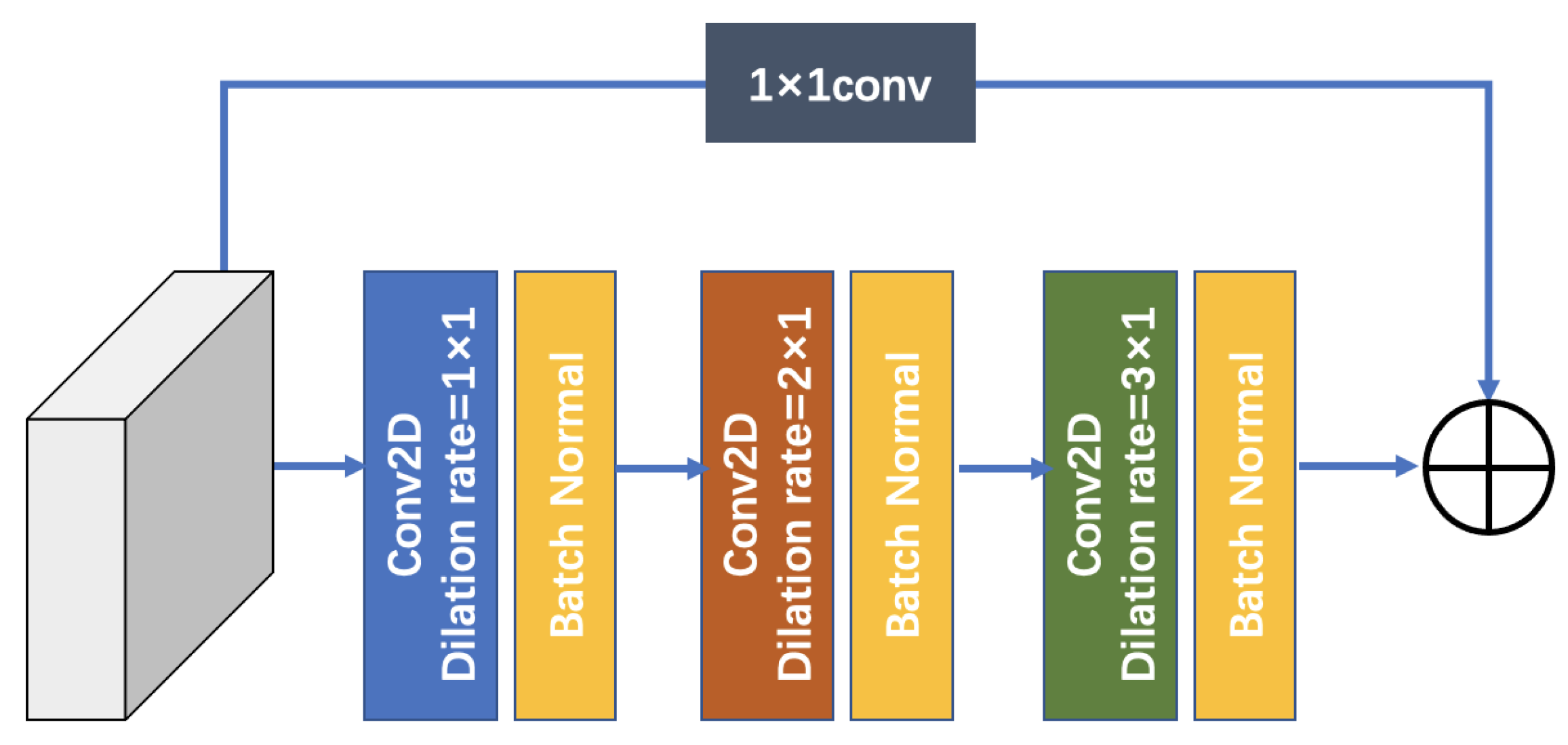
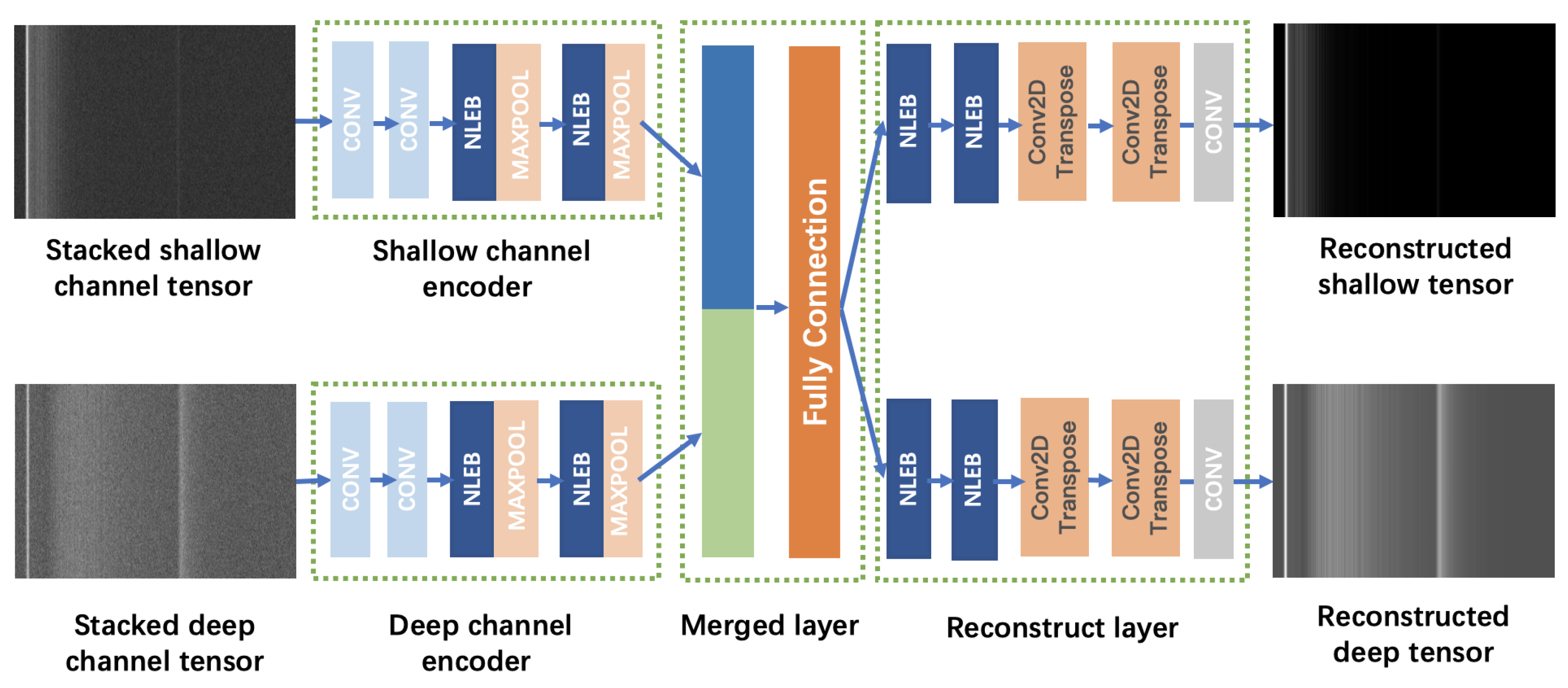
4.3. CNLD-Net Architecture
4.4. Performance Metrics
5. Experiments
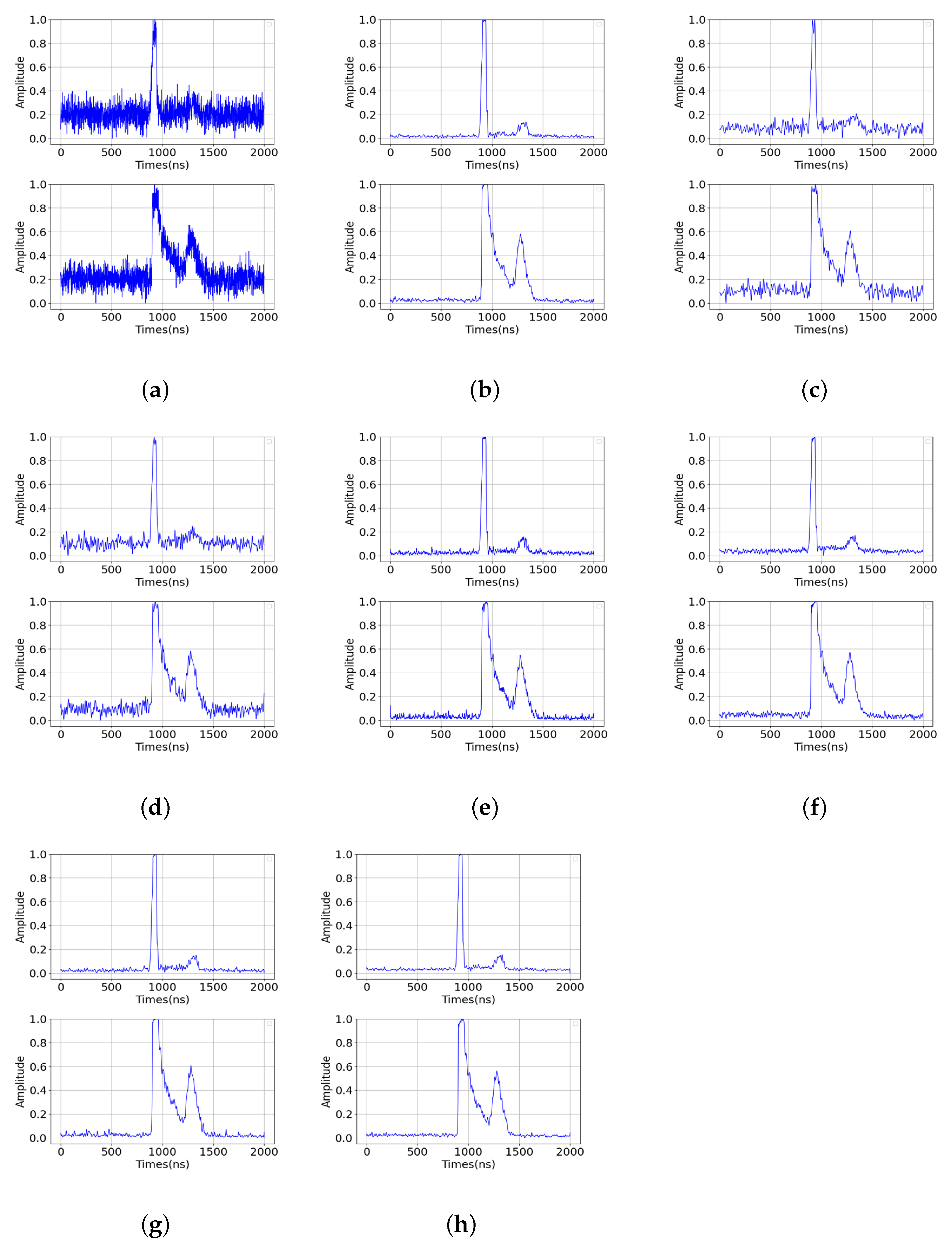
5.1. Comparison of Signal Denoising Method
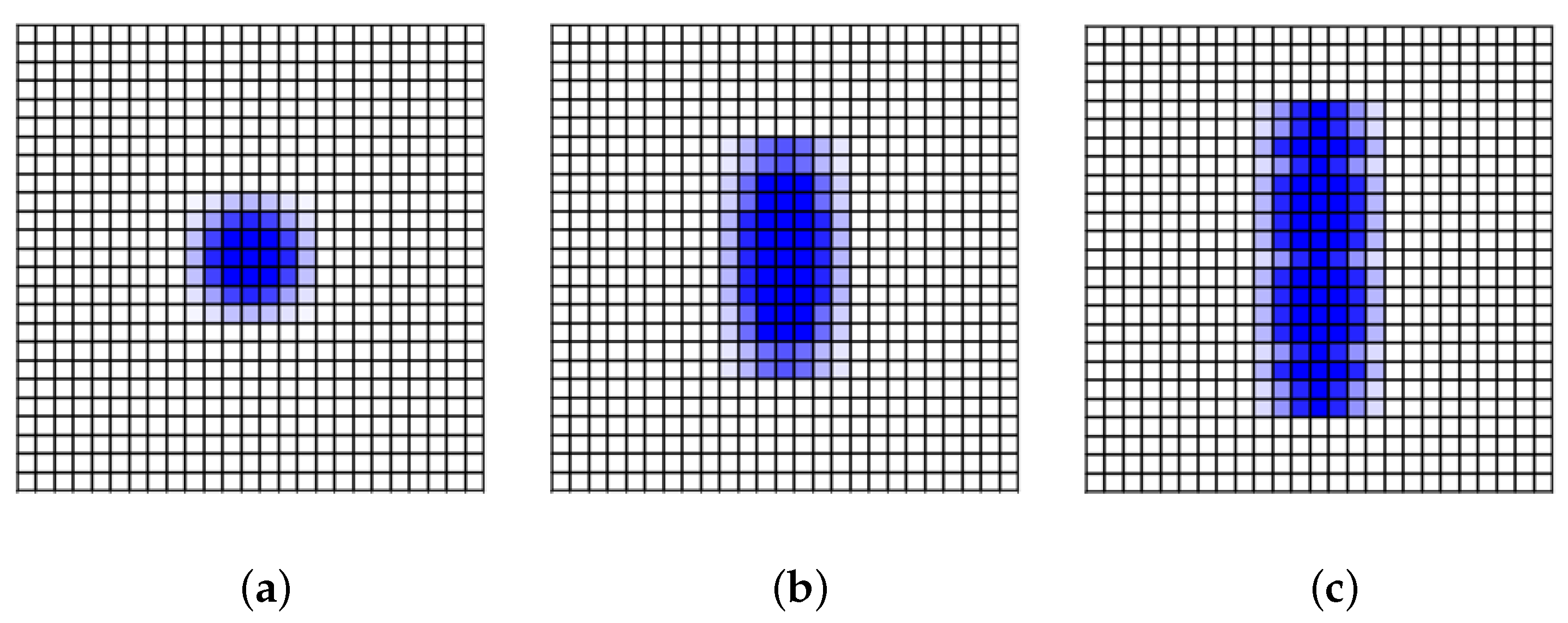
5.2. Comparison of Different Dilation Rates
5.3. Ablation Experiment
5.4. Analysis of Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Ke, J.; Lam, E.Y. Temporal Super-resolution Full Waveform LiDAR. In Proceedings of the Imaging and Applied Optics 2018 (3D, AO, AIO, COSI, DH, IS, LACSEA, LS&C, MATH, pcAOP), Orlando, FL, USA, 25–28 June 2018; Optica Publishing Group: Washington, DC, USA, 2018; p. CTh3C.1. [Google Scholar] [CrossRef]
- Balsa-Barreiro, J.; Avariento, J.; Lerma, J. Airborne light detection and ranging (LiDAR) point density analysis. Sci. Res. Essays 2012, 7, 3010–3019. [Google Scholar] [CrossRef]
- Baltsavias, E. Airborne laser scanning: Basic relations and formulas. ISPRS J. Photogramm. Remote Sens. 1999, 54, 199–214. [Google Scholar] [CrossRef]
- Hermosilla, T.; Ruiz, L.A.; Recio, J.A.; Balsa-Barreiro, J. Land-use Mapping of Valencia City Area from Aerial Images and LiDAR Data. In Proceedings of the GEOProcessing 2012: The Fourth International Conference in Advanced Geographic Information Systems, Applications and Services, Valencia, Spain, 30 January–4 February 2012. [Google Scholar]
- Huang, T.; Tao, B.; He, Y.; Hu, S.; Xu, G.; Yu, J.; Wang, C.; Chen, P. Utilization of multi-channel ocean LiDAR data to classify the types of waveform. In Proceedings of the SPIE Remote Sensing 2017, Warsaw, Poland, 11–14 September 2017; p. 61. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, X.; Hu, B.; Chen, R. A Multi-Source Convolutional Neural Network for Lidar Bathymetry Data Classification. Mar. Geod. 2022, 45, 232–250. [Google Scholar] [CrossRef]
- Chen, D.; Peethambaran, J.; Zhang, Z. A supervoxel-based vegetation classification via decomposition and modelling of full-waveform airborne laser scanning data. Int. J. Remote Sens. 2018, 39, 2937–2968. [Google Scholar] [CrossRef]
- Zhao, X.; Xia, H.; Zhao, J.; Zhou, F. Adaptive Wavelet Threshold Denoising for Bathymetric Laser Full-Waveforms With Weak Bottom Returns. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1503505. [Google Scholar] [CrossRef]
- Mader, D.; Richter, K.; Westfeld, P.; Maas, H.G. Correction to: Potential of a Non-linear Full-Waveform Stacking Technique in Airborne LiDAR Bathymetry. PFG—J. Photogramm. Remote Sens. Geoinf. Sci. 2022, 90, 495–496. [Google Scholar] [CrossRef]
- Long, S.; Zhou, G.; Wang, H.; Zhou, X.; Chen, J.; Gao, J. Denoising of Lidar Echo Signal Based on Wavelet Adaptive Threshold Method. ISPRS—Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2020, XLII-3/W10, 215–220. [Google Scholar] [CrossRef]
- Cheng, X.; Mao, J.; Li, J.; Zhao, H.; Zhou, C.; Gong, X.; Rao, Z. An EEMD-SVD-LWT algorithm for denoising a lidar signal. Measurement 2021, 168, 108405. [Google Scholar] [CrossRef]
- Zhou, G.; Long, S.; Xu, J.; Zhou, X.; Wang, C. Comparison analysis of five waveform decomposition algorithms for the airborne LiDAR echo signal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 7869–7880. [Google Scholar] [CrossRef]
- Song, Y.; Li, H.; Zhai, G.; He, Y.; Bian, S.; Zhou, W. Comparison of multichannel signal deconvolution algorithms in airborne LiDAR bathymetry based on wavelet transform. Sci. Rep. 2021, 11, 16988. [Google Scholar] [CrossRef]
- Zhang, Y. A Novel Lidar Signal Denoising Method Based on Convolutional Autoencoding Deep Learning Neural Network. Atmosphere 2021, 12, 1403. [Google Scholar]
- Gangping, L.; Ke, J. Dense and Residual Neural Networks for Full-waveform LiDAR Echo Decomposition. In Proceedings of the Imaging Systems and Applications 2021, Washington, DC, USA, 19–23 July 2021; p. IF4D.3. [Google Scholar] [CrossRef]
- Liu, G.; Ke, J.; Lam, E.Y. CNN-based Super-resolution Full-waveform LiDAR. In Proceedings of the Imaging and Applied Optics Congress, Washington, DC, USA, 22–26 June 2020; Optica Publishing Group: Washington, DC, USA, 2020; p. JW2A.29. [Google Scholar] [CrossRef]
- Bhadani, R. AutoEncoder for Interpolation. arXiv 2021, arXiv:2101.00853. [Google Scholar]
- Chen, X.; Yang, H. Full Waveform Inversion Based on Wavefield Correlation. IOP Conf. Ser. Mater. Sci. Eng. 2019, 472, 012069. [Google Scholar] [CrossRef]
- Hu, B.; Zhao, Y.; Chen, R.; Liu, Q.; Wang, P.; Zhang, Q. Denoising method for a lidar bathymetry system based on a low-rank recovery of non-local data structures. Appl. Opt. 2022, 61, 69–76. [Google Scholar] [CrossRef]
- Ma, H.; Zhou, W.; Zhang, L.; Wang, S. Decomposition of small-footprint full waveform LiDAR data based on generalized Gaussian model and grouping LM optimization. Meas. Sci. Technol. 2017, 28, 045203. [Google Scholar] [CrossRef]
- Pan, Z.; Glennie, C.; Hartzell, P.; Fernandez-Diaz, J.C.; Legleiter, C.; Overstreet, B. Performance Assessment of High Resolution Airborne Full Waveform LiDAR for Shallow River Bathymetry. Remote Sens. 2015, 7, 5133–5159. [Google Scholar] [CrossRef]
- Ding, K.; Li, Q.; Zhu, J.; Wang, C.; Guan, M.; Chen, Z.; Yang, C.; Cui, Y.; Liao, J. An Improved Quadrilateral Fitting Algorithm for the Water Column Contribution in Airborne Bathymetric Lidar Waveforms. Sensors 2018, 18, 552. [Google Scholar] [CrossRef]
- Abady, L.; Bailly, J.S.; Baghdadi, N.; Pastol, Y.; Abdallah, H. Assessment of Quadrilateral Fitting of the Water Column Contribution in Lidar Waveforms on Bathymetry Estimates. IEEE Geosci. Remote Sens. Lett. 2014, 11, 813–817. [Google Scholar] [CrossRef]
- Ma, Y.; Zhang, J.; Zhang, Z.; Zhang, J.Y. Bathymetry Retrieval Method of LiDAR Waveform Based on Multi-Gaussian Functions. J. Coast. Res. 2019, 90, 324–331. [Google Scholar] [CrossRef]
- Qi, C.; Ma, Y.; Su, D.; Yang, F.; Liu, J.; Wang, X.H. A Method to Decompose Airborne LiDAR Bathymetric Waveform in Very Shallow Waters Combining Deconvolution With Curve Fitting. IEEE Geosci. Remote Sens. Lett. 2022, 19, 7004905. [Google Scholar] [CrossRef]
- Shen, X.; Li, Q.Q.; Wu, G.; Zhu, J. Decomposition of LiDAR waveforms by B-spline-based modeling. ISPRS J. Photogramm. Remote Sens. 2017, 128, 182–191. [Google Scholar] [CrossRef]
- Wang, C.; Li, Q.; Liu, Y.; Wu, G.; Liu, P.; Ding, X. A comparison of waveform processing algorithms for single-wavelength LiDAR bathymetry. ISPRS J. Photogramm. Remote Sens. 2015, 101, 22–35. [Google Scholar] [CrossRef]
- Kogut, T.; Bakuła, K. Improvement of Full Waveform Airborne Laser Bathymetry Data Processing based on Waves of Neighborhood Points. Remote Sens. 2019, 11, 1255. [Google Scholar] [CrossRef]
- Guo, K.; Li, Q.; Wang, C.; Mao, Q.; Liu, Y.; Ouyang, Y.; Feng, Y.; Zhu, J.; Wu, A. Target Echo Detection Based on the Signal Conditional Random Field Model for Full-Waveform Airborne Laser Bathymetry. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5705421. [Google Scholar] [CrossRef]
- Xing, S.; Wang, D.; Xu, Q.; Lin, Y.; Li, P.; Jiao, L.; Zhang, X.; Liu, C. A Depth-Adaptive Waveform Decomposition Method for Airborne LiDAR Bathymetry. Sensors 2019, 19, 5065. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Yue, J.; Shi, P.; Wang, Y.; Gao, H.; Feng, B.; Liu, Z.; Li, H. A deep learning method for LiDAR bathymetry waveforms processing. In Proceedings of the 2021 International Conference on Neural Networks, Information and Communication Engineering, Qingdao, China, 27–29 August 2021; Zhang, Z., Ed.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2021; Volume 11933, p. 119331S. [Google Scholar] [CrossRef]
- Asmann, A.; Stewart, B.; Wallace, A.M. Deep Learning for LiDAR Waveforms with Multiple Returns. In Proceedings of the 2020 28th European Signal Processing Conference (EUSIPCO), Amsterdam, The Netherlands, 18–21 January 2021. [Google Scholar]
- Shanjiang, H.; Yan, H.; Bangyi, T.; Jiayong, Y.; Weibiao, C. Classification of sea and land waveforms based on deep learning for airborne laser bathymetry. Infrared Laser Eng. 2019, 48, 1113004. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Wang, Z.; Huang, G.; Shu, R. Classification of Laser Footprint Based on Random Forest in Mountainous Area Using GLAS Full-Waveform Features. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 2284–2297. [Google Scholar] [CrossRef]
- Yang, C.L.; Chen, Z.X.; Yang, C.Y. Sensor Classification Using Convolutional Neural Network by Encoding Multivariate Time Series as Two-Dimensional Colored Images. Sensors 2020, 20, 168. [Google Scholar] [CrossRef]
- Hu, B.; Zhao, Y.; He, J.; Liu, Q.; Chen, R. A Classification Method for Airborne Full-Waveform LiDAR Systems Based on a Gramian Angular Field and Convolution Neural Networks. Electronics 2022, 11, 4114. [Google Scholar] [CrossRef]
- Geng, Z.; Yan, H.; Zhang, J.; Zhu, D. Deep-Learning for Radar: A Survey. IEEE Access 2021, 9, 141800–141818. [Google Scholar] [CrossRef]
- Leng, Z.; Zhang, J.; Ma, Y.; Zhang, J. ICESat-2 Bathymetric Signal Reconstruction Method Based on a Deep Learning Model with Active dash Passive Data Fusion. Remote Sens. 2023, 15, 460. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.; Ai, T. Long-range Dependencies Learning Based on Non-Local 1D-Convolutional Neural Network for Rolling Bearing Fault Diagnosis. J. Dyn. Monit. Diagn. 2022, 1, 148–159. [Google Scholar] [CrossRef]
- Magruder, L.A.; Neuenschwander, A.L.; Marmillion, S.P. Lidar waveform stacking techniques for faint ground return extraction. J. Appl. Remote Sens. 2010, 4, 043501. [Google Scholar] [CrossRef]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local Neural Networks. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 7794–7803. [Google Scholar] [CrossRef]
- Chang, J.; Zhu, L.; Li, H.; Fan, X.; Yang, Z. Noise reduction in Lidar signal using correlation-based EMD combined with soft thresholding and roughness penalty. Opt. Commun. 2018, 407, 290–295. [Google Scholar] [CrossRef]
- Han, H.; Wang, H.; Liu, Z.; Wang, J. Intelligent vibration signal denoising method based on non-local fully convolutional neural network for rolling bearings. ISA Trans. 2022, 122, 13–23. [Google Scholar] [CrossRef] [PubMed]
- Wang, P.; Chen, P.; Yuan, Y.; Liu, D.; Huang, Z.; Hou, X.; Cottrell, G. Understanding Convolution for Semantic Segmentation. In Proceedings of the 2018 IEEE Winter Conference on Applications of Computer Vision (WACV), Lake Tahoe, NV, USA, 12–15 March 2018. [Google Scholar]



| Parameters | Parameter Indexes |
|---|---|
| Beam divergence angle | 0.2 mrad |
| Laser emission frequency | 5.5 kHz |
| Laser emission power | 17.4 W/532 nm, 18 W/1064 nm |
| Pulse energy | 3.05 mJ/532 nm, 3.5 mJ/1064 nm |
| Pulse width | 3.3 ns |
| Detection range | 500–1000 m |
| Scanning mode | Constant-angle conical scan |
| Scanning angle | ±10° |
| Scanning speed | 10 revolutions per second |
| Receiving aperture | 0.2 m |
| Detection minimum energy | 8 × 10 W |
| Maximum receiving frequency | 2 GHz |
| Module | Layer | Kernel (Size, Stride) | Dimension or Neurons |
|---|---|---|---|
| Stacked image input | ∖ | ∖ | (64,1,2000 × 100) |
| shallow encoder /deep encoder | Conv-2d | (3 × 3,2) | (64,16,1000 × 50) |
| Conv-2d | (3 × 3,2) | (64,32,500 × 25) | |
| NLEB | (64,64,500 × 25) | ||
| NLEB | (64,128,500 × 25) | ||
| Dense | 1000 | ||
| Merged layer | Concatenated | 2000 | |
| Reconstruction layer | Dense | 1,600,000 | |
| NLEB | (64,64,500 × 25) | ||
| NLEB | (64,32,500 × 25) | ||
| Conv-2d-Transpose | (3 × 3,2) | (64,32,1000 × 50) | |
| Conv-2d-Transpose | (3 × 3,2) | (64,16,2000 × 100) | |
| Conv-2d | (1 × 1,1) | (64,1,2000 × 100) | |
| Stacked image output | ∖ | ∖ | (64,1,2000 × 100) |
| Methods | 5 | 10 | 15 | 20 | Time | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | SNR | RMSE | SNR | RMSE | SNR | RMSE | SNR | ||
| AWT [10] | 0.012 | 20.55 | 0.015 | 18.62 | 0.023 | 14.95 | 0.039 | 11.51 | 0.007 s |
| EMD-STRP [42] | 0.012 | 21.03 | 0.016 | 18.55 | 0.023 | 14.96 | 0.042 | 10.59 | 0.019 s |
| CAENN [14] | 0.036 | 24.08 | 0.042 | 20.76 | 0.062 | 18.37 | 0.087 | 16.61 | 0.003 s |
| 1D-Nonlocal [43] | 0.057 | 23.94 | 0.064 | 19.84 | 0.054 | 18.42 | 0.063 | 16.91 | 0.008 s |
| MS-CNN [6] | 0.028 | 30.54 | 0.034 | 26.17 | 0.048 | 22.41 | 0.036 | 18.17 | 0.006 s |
| CNLD | 0.019 | 38.58 | 0.026 | 33.48 | 0.031 | 26.92 | 0.036 | 22.94 | 0.005 s |
| Methods | 5 | 10 | 15 | 20 | Time | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | SNR | RMSE | SNR | RMSE | SNR | RMSE | SNR | ||
| AWT [10] | 0.025 | 20.91 | 0.028 | 19.88 | 0.032 | 18.62 | 0.046 | 15.49 | 0.007 s |
| EMD-STRP [42] | 0.024 | 21.28 | 0.027 | 20.12 | 0.033 | 18.47 | 0.047 | 15.14 | 0.019 s |
| CAENN [14] | 0.052 | 32.81 | 0.054 | 30.53 | 0.057 | 28.04 | 0.064 | 22.62 | 0.003 s |
| 1D-Nonlocal [43] | 0.059 | 33.91 | 0.065 | 31.66 | 0.064 | 28.81 | 0.073 | 23.03 | 0.008 s |
| MS-CNN [6] | 0.049 | 36.82 | 0.057 | 33.48 | 0.055 | 31.62 | 0.068 | 28.18 | 0.006 s |
| CNLD | 0.027 | 40.16 | 0.045 | 37.25 | 0.052 | 33.48 | 0.062 | 29.25 | 0.005 s |
| SNR | Evaluation | Non | Dilation Rates in Spatial Direction | Dilation Rates in Both Directions | ||||
|---|---|---|---|---|---|---|---|---|
| (1,1,1) | (1,2,2) | (1,2,3) | (1,2,5) | (1,2,2) | (1,2,3) | (1,2,5) | ||
| 5 | RMSE | 0.041 | 0.035 | 0.023 | 0.022 | 0.033 | 0.029 | 0.031 |
| SNR | 37.22 | 38.68 | 39.37 | 39.32 | 38.74 | 39.28 | 39.33 | |
| 10 | RMSE | 0.047 | 0.042 | 0.036 | 0.035 | 0.043 | 0.047 | 0.049 |
| SNR | 33.66 | 34.51 | 35.36 | 35.33 | 34.92 | 35.27 | 35.32 | |
| 15 | RMSE | 0.038 | 0.040 | 0.041 | 0.043 | 0.041 | 0.046 | 0.044 |
| SNR | 28.81 | 29.76 | 30.18 | 29.86 | 29.95 | 30.19 | 30.20 | |
| 20 | RMSE | 0.043 | 0.045 | 0.048 | 0.050 | 0.046 | 0.051 | 0.049 |
| SNR | 25.47 | 25.63 | 26.09 | 25.87 | 25.94 | 26.01 | 26.02 |
| Signal | SNR_Noise | Baseline | Baseline | CNLD-Local | CNLD | ||||
|---|---|---|---|---|---|---|---|---|---|
| RMSE | SNR | RMSE | SNR | RMSE | SNR | RMSE | SNR | ||
| Shallow channel | 5 | 0.038 | 34.91 | - | - | 0.031 | 36.25 | 0.021 | 38.58 |
| 10 | 0.029 | 28.29 | - | - | 0.041 | 31.63 | 0.026 | 33.48 | |
| 15 | 0.051 | 22.71 | - | - | 0.038 | 24.65 | 0.031 | 26.92 | |
| 20 | 0.069 | 20.29 | - | - | 0.043 | 22.27 | 0.036 | 22.94 | |
| Deep channel | 5 | - | - | 0.053 | 37.65 | 0.049 | 38.19 | 0.027 | 40.16 |
| 10 | - | - | 0.075 | 34.69 | 0.054 | 35.69 | 0.045 | 37.25 | |
| 15 | - | - | 0.082 | 30.32 | 0.057 | 32.95 | 0.052 | 33.48 | |
| 20 | - | - | 0.088 | 28.37 | 0.072 | 28.56 | 0.062 | 29.25 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, B.; Zhao, Y.; Zhou, G.; He, J.; Liu, C.; Liu, Q.; Ye, M.; Li, Y. Coupling Dilated Encoder–Decoder Network for Multi-Channel Airborne LiDAR Bathymetry Full-Waveform Denoising. Remote Sens. 2023, 15, 3293. https://doi.org/10.3390/rs15133293
Hu B, Zhao Y, Zhou G, He J, Liu C, Liu Q, Ye M, Li Y. Coupling Dilated Encoder–Decoder Network for Multi-Channel Airborne LiDAR Bathymetry Full-Waveform Denoising. Remote Sensing. 2023; 15(13):3293. https://doi.org/10.3390/rs15133293
Chicago/Turabian StyleHu, Bin, Yiqiang Zhao, Guoqing Zhou, Jiaji He, Changlong Liu, Qiang Liu, Mao Ye, and Yao Li. 2023. "Coupling Dilated Encoder–Decoder Network for Multi-Channel Airborne LiDAR Bathymetry Full-Waveform Denoising" Remote Sensing 15, no. 13: 3293. https://doi.org/10.3390/rs15133293
APA StyleHu, B., Zhao, Y., Zhou, G., He, J., Liu, C., Liu, Q., Ye, M., & Li, Y. (2023). Coupling Dilated Encoder–Decoder Network for Multi-Channel Airborne LiDAR Bathymetry Full-Waveform Denoising. Remote Sensing, 15(13), 3293. https://doi.org/10.3390/rs15133293