Abstract
The monitoring of space debris is important for spacecraft such as satellites operating in orbit, but the background in star images taken by ground-based telescopes is relatively complex, including stray light caused by diffuse reflections from celestial bodies such as the Earth or Moon, interference from clouds in the atmosphere, etc. This has a serious impact on the monitoring of dim and small space debris targets. In order to solve the interference problem posed by a complex background, and improve the signal-to-noise ratio between the target and the background, in this paper, we propose a novel star image enhancement algorithm, MBS-Net, based on background suppression. Specifically, the network contains three parts, namely the background information estimation stage, multi-level U-Net cascade module, and recursive feature fusion stage. In addition, we propose a new multi-scale convolutional block, which can laterally fuse multi-scale perceptual field information, which has fewer parameters and fitting capability compared to ordinary convolution. For training, we combine simulation and real data, and use parameters obtained on the simulation data as pre-training parameters by way of parameter migration. Experiments show that the algorithm proposed in this paper achieves competitive performance in all evaluation metrics on multiple real ground-based datasets.
1. Introduction
As science and technology evolve, the aerospace industry is booming and humanity has accelerated the pace of space exploration, while a large amount of space debris is distributed in space orbit outside the Earth, which is a non-functional man-made object in Earth’s orbit, or is re-entering the atmosphere with its debris and components [1]. Debris of more than 1 cm can disable or even disintegrate an entire satellite, while a debris impact of more than 10 cm can directly destroy an entire spacecraft and produce a debris cloud [2]. Currently, a high-resolution star map based on a ground-based telescope is an important way to observe space targets. However, the astronomical optical images contain complex backgrounds of large clouds, earth light, strong undulating characteristics, as well as internal sensor noise and external impulse noise, which seriously interfere with subsequent detection. Therefore, the study of background suppression algorithms for optical detection images is of great significance and practical value.
1.1. Literature Review
Currently, image enhancement methods based on background suppression fall into two main categories, namely, traditional algorithms and deep learning algorithms based on neural networks. In traditional background suppression algorithms, most algorithms often use threshold segmentation [3] or background modeling, and then use filtering algorithms to smooth the image, such as median filtering [4], histogram stretch [5], Sigma iterative clipping [6], wavelet noise reduction [7] and other methods [8,9,10]. However, it should be noted that, unlike the general large target image processing methods, most optical star background images have complex backgrounds and strong undulating characteristics, while the usual and traditional methods are not fully applicable to images of starry backgrounds. Therefore, for the relevant characteristics of optical star detection images, researchers have also made some specific improvements. In 2012, Wang et al. [11] proposed a background clutter suppression algorithm for star images based on neighborhood filtering that can maximize the preservation of target edges, which can ensure that weak targets are not filtered out and can also keep the edges of stars and targets well, but the algorithm was only applied to noisy images that obey Gaussian distribution. In 2014, to address the problem of stray light streak noise removal, Yan et al. [12] designed a stray light streak noise correction algorithm. By measuring and deducing the spatial distribution characteristics of stray light noise in the image, the distribution characteristic model of stray light noise is established, and the sub-image adaptive algorithm is used to filter the stray light noise. And aiming at the problems of small target size, low signal-to-noise ratio and serious clutter interference in observation images, Chen et al. [13] proposed the morphological filtering of multi-structural elements in the same year to suppress the background and clutter, simultaneously enhancing the resolution and brightness of the image. In addition, in the face of a low signal-to-noise ratio of the star image and weak target, Y et al. [14] used the improved segmentation algorithm which is realized by using the shape of the object without relying on the gray threshold, it weakens the influence of the complex background and enhances the signal strength of the target. Although these algorithms have a certain background suppression effect, traditional image algorithms need to set relevant model parameters based on certain prior information. When the background and imaging mode of the data change, the prior information will also need to change. This greatly affects the universality of the algorithm, adds cumbersome operations, and limits the intelligence of the algorithm.
Compared with traditional algorithms, deep learning has been highly popular in recent years. Some methods based on CNN mainly achieve background suppression through image denoising and semantic segmentation, and then improve the signal-to-noise ratio and enhance images; these algorithm models have achieved great success [15,16,17,18,19,20,21,22,23,24,25]. Focusing on background suppression algorithms for star images or related images, there are only a few deep-learning-based image background suppression or target enhancement algorithms due to the scarcity of data and the difficulty of producing labels, but generally these algorithms achieve ideal results. Wu et al. (2019) designed a small target enhancement network using a three-layer full convolution and a one-layer deconvolution network structure to achieve the background suppression of the image [26]. Xie et al. (2020) used a hybrid Poisson–Gaussian likelihood function as the reward function for a reinforcement learning algorithm that can effectively suppress image backgrounds through a Markov decision process [27]. Zhang et al. (2021) proposed a two-stage algorithm, which used the reinforcement learning idea to realize the iterative denoising operation in the star point region [28]. Li et al. (2022) proposed a background suppression algorithm, BSC-Net (Background Suppression Convolutional Network), for astral stray light, which consists of a “background suppression part” and a “foreground preservation part”, and yields an acceptable background suppression effect on the star map [29].
In addition to these algorithms that have been applied to astronomical images, image enhancement or super-resolution algorithms in other fields also have great reference value [30,31,32,33]. They use the attention mechanism of transformers whose characteristics are highly beneficial for background modeling and global modeling. This has provided us with a lot of inspiration and is very helpful and meaningful for the study of image enhancement algorithms based on background suppression.
1.2. The Analysis of Image Characteristic
Before introducing the background-suppression-based image enhancement algorithm designed in this paper, it is important to analyze the composition of star images and their related characteristics. Firstly, optical ground-based star images are mainly taken by ground-based telescopes and space-based detection platforms, and can be divided into four components, namely, stars, space debris, noise and background [34].
At present, there are two main ways for optical observation platforms to capture star images: stellar tracking mode and space debris tracking mode, the shape of them is dotted or tailed which is affected by the exposure time and observation mode [35]. The data in the paper are taken by the ground-based telescope in the debris tracking mode in a short exposure time, the stars appear striped and the space debris is dotted in the image. In terms of gray scale, the star magnitude is stable and its imaging is bright and the space debris is smaller and its imaging brightness is unstable, while both are high-frequency information in the image. The background is relatively complex and mainly low-frequency information, consisting mostly of fluctuating stray light and clouds, of which the stray light that has a greater impact on observations is mainly ground air light and moonlight, both of which appear as local high-light or interference streaks, resulting in reduced image clarity. In addition, the noise is mainly composed of the internal noise of the system of the shooting equipment, such as shot noise and dark current noise, and the external random noise, such as impulse noise. Figure 1 shows some real images in different backgrounds and their 3D grayscale images.
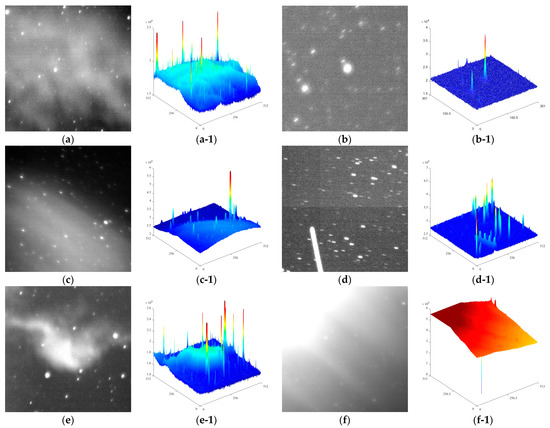
Figure 1.
Star image schematics of various backgrounds. (a) Wide cloud layer. (a-1) A 3D grayscale schematic of (a). (b) Uniform background. (b-1) A 3D grayscale schematic of (b). (c) Earth stray light. (c-1) A 3D grayscale schematic of (c). (d) Earth stray light. (d-1) A 3D grayscale schematic of (d). (e) High-speed moving objects in the field of view. (e-1) A 3D grayscale schematic of (e). (f) Moonlight background. (f-1) A 3D grayscale schematic of (f).
Here, we classify noise and undulating background as background, and classify stars and debris as targets. This is very important for our algorithm, because we do not need to distinguish stars from debris. Our purpose is to suppress noise and undulating back-ground and improve the signal-to-noise ratio of the image.
1.3. Brief Description of Work and Contribution
From the relevant research methods described above and the compositional characteristics of the images, we can clearly find that the background of star optical detection images is relatively complex, and the current deep-learning-based background suppression algorithms for star optical detection images are less studied and not widely used. However, from experimental data in recent years, we can see that the deep-learning-based background suppression algorithm generally performs well compared to traditional algorithms, with good results in suppressing complex backgrounds and noise reduction, which gives us a lot of confidence, but we also find that some issues still need special attention:
- (1)
- Firstly, most of the background suppression algorithms based on CNN directly input the whole image into the feature extraction network without relying on any prior information. This is a completely blind background suppression method. Some noise and stray light in different real images have different effects. They are very complex and randomly distributed in each local area or even all areas of the image, which will make the generalization ability of the network relatively weak. If the feature extract network can be given a background information estimation, which is used as auxiliary information to help the network understand the background noise intensity distribution of different images, the generalization ability of the network may be better.
- (2)
- Secondly, the model’s receptive field is relatively single. Many neural-network-based background suppression algorithms have a single fixed scale for their receptive field, but at many times, the background feature information is not limited to a small fixed-scale area, which makes it difficult for the network to extract accurate and discriminative feature information, resulting in a poor overall suppression effect. The full fusion of receptive domains at different scales can help the network make full use of the multi-level spatial features.
- (3)
- Thirdly, deep networks cause loss of information on weak targets. Although increasing the number of network layers can obtain high-level semantic information and a greater receptive field, which is helpful to enhance the effect, the size of small targets in the star image is often only a dozen pixels, and the fine-grained information of small targets will be lost with an increase in layers and pooling operations.
In order to alleviate these problems, and make the model better suppress stray light, undulating cloud, and retain the dim target signal to improve the contrast between the target and the background, we propose a new end-to-end image enhancement algorithm, MBS-Net, based on background suppression.
The following is the main contribution and work of this paper:
- In view of the lack of prior information on image content, and the problem of poor model fitting and generalization ability, inspired by the literature, we use multiple residual bottleneck structures to obtain a weight map which is regarded as the level estimation of background and target information [36], and adopt it as an auxiliary information to adjust the original image, so that the fitting and generalization ability of the network model is improved and the training is more stable.
- Considering the problem of a single receptive domain, we designed a U-Net cascade module with different depths and inserted a new multi-scale convolutional block into it, which has fewer parameters than the normal convolutional block. At the same time, it not only widens the width of the network, but can also obtain multi-scale background feature information at a fixed network depth. In experiments, it improves the effect of a model and converges faster.
- Recursive feature fusion: Small target information will be lost as the depth of the network deepens; so we use a strategy of recursive fusion. Specifically, we use repeated connections in the same level of the model to give the model the ability to regulate semantic information horizontally and make the semantic information learned by the model more effectively and accurately.
- For training, we combine simulated images with real images, in which the real data are the images of optical space debris detection taken by the ground-based telescope detection platform. We transfer the parameters obtained from the simulation image training as pre-training to the ground-based image training, which makes the network fit the ground-based image training better and faster.
Next, in the second chapter, we will first introduce the detailed structure, motivation and effect of each sub-module, then describe some preprocessing operations of the data set. In the third chapter, we will show and analyze our experimental results, including ablation and comparative experiments of each module, to fully verify the accuracy and effectiveness of our experiments. In the fourth chapter, we will discuss and summarize all the work and results.
2. Methods
Generally, we adopt a data-driven method with a CNN as the main algorithm architecture which is used to design an end-to-end model and learn discriminative features. The purpose is to suppress multiple types of background noise and enhance the dim target signal, thereby improving the contrast between the target and the background and providing a more favorable environment for subsequent space debris monitoring. In Section 2.1, Section 2.2, Section 2.3 and Section 2.4, we introduce the structure and function of each part in the MBS-Net in detail, and in Section 2.5, we will show the processing operation of the corresponding data set.
2.1. The Overall Architecture
It is well known that the generalization ability and learning ability of a CNN depends largely on the memory ability of the model to the data. A good and reasonable structural layout enables the network to learn the features of the target and the complex background noise relatively well, which is helpful for the algorithm to achieve the purpose of suppressing the background and enhancing the target. Compared with the traditional method, the convolution operation in the neural network is a weighted summation process. The reasonable combination of convolutions and nonlinear activation functions can be regarded as an effective filtering process.
Based on the analysis of the composition and feature attributes of the image, the main structure of the model we designed is shown in Figure 2. It consists of three parts, which are the noise background information-adjustment structure, multi-level U-Net cascade module, and recursive feature fusion structure. The overall input of the network is a single-channel image, and the size is not limited. In this experiment, the image size is uniformly cut to 512 × 512. It can be seen from Figure 1 that the input image first passes through the noise adjustment module to obtain the background information weight map, which then adjusts the input image. The adjusted single channel image is input into the feature extraction part to generate a variety of feature maps of different scales. These feature maps are finally recursively fused to obtain the predicted value, which is the image after background suppression.
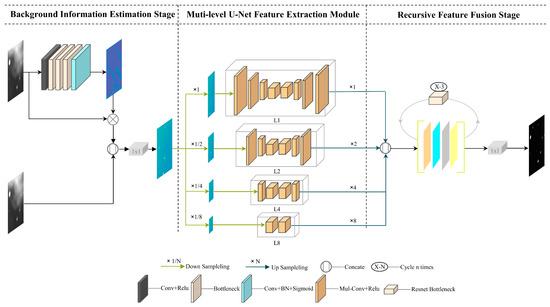
Figure 2.
Overall network of MBS-Net.
2.2. Background Information Estimation Stage
The focus of this part is to obtain the discriminative features of the relevant background from the original image, which we regard as a weight map reflecting various types of background information or an estimation of the background level. In practice, we adjust the original image by multiplication with the estimation of background, and use 1 × 1 convolution to fuse the adjusted image with the original image. Finally, the fused image is used as the input required by the second part of the feature extraction module. Its main purpose is to use the generated weight map that reflects the image content information to enrich the information available to the network so that the network can focus on learning relatively important information, rather than allowing the network to blindly extract features from extremely complex and various original images. This can help the network to accurately distinguish the background and the target, quickly adapt to the needs of suppression under different complex backgrounds, and enhance the learning ability and robustness of the model. The brief mathematical expression formula is as follows, where ƒ represents the continuous convolution operation on the upper layer, and g is the adjustment operation of 1 × 1 convolution.
In terms of specific structural design, considering the influence of network depth on the loss of weak target information and the speed of network reasoning, this part is mainly composed of five convolution layers. The two ends are ordinary 3 × 3 convolution, and the middle three layers are the bottleneck structure [37]. We compress the number of convolution channels to 1/4 of the input, and then expand to the original dimension in the bottleneck. In this way, on the one hand, the information of the small target and background can be retained on the weight map, and, on the other hand, the network is more lightweight.
2.3. Multi-Level U-Net Cascade Module
The pyramid structure has been applied in various tasks of neural networks for a long time. With its excellent multi-scale information learning ability, it has achieved good results in image restoration [38], image compression and other fields [39]. However, we find that it is rarely used in image background suppression. In the previous image enhancement algorithms based on background suppression, the scale of the network’ s extraction of image background information is mostly single. However, we know that the undulating star background may be distributed in various places of the image, and its size is not fixed. It is difficult for the network to learn more perfect background information with a single fixed acceptance domain. In addition, according to the previous research of Zhou et al. [40], in a deep network based on CNN, the actual acceptance domain of the network is much smaller than the theoretical acceptance domain. Based on these two points, it means that it is difficult for ordinary networks with a single receiving domain to extract the most effective and discriminative background information features. Therefore, drawing on the application of the pyramidal pooling structure in other image processing fields, we built a U-Net cascade module of different depths on its basis to help the network make full use of the multi-level spatial features and extract background features more fully and effectively.
Now, we introduce the specific structure of this similar pyramid multi-scale U-Net cascade module. The specific structure is shown in Figure 3. Firstly, the input of this part is the final adjusted feature map obtained in the first stage, which is sampled to different scales in a parallel way to obtain differently sized acceptance domains. Considering the small size of the target, the pooling kernel is set to 1 × 1, 2 × 2, 4 × 4, and 8 × 8, respectively, which is the average pooling. After each pooling feature, the network composed of deep encoding–decoding and skip connection is formed by U-Net [41]. Unlike the general pyramid pooling structure, we add U-Net blocks of different depths at the back of each scale. The depth of the U-Net block decreases with the size of the scale. This is because, on the one hand, a U-Net that is too deep will lose the information of dim and small space debris. We need to control the receptive field of the network within a reasonable range. On the other hand, if the model uses the same depth of U-Net, this will greatly increase the parameters and calculation of the network, and the learned information will be redundant. Therefore, taking into account the effectiveness and the size of the model, we select a suitable depth U-Net for each scale to extract feature information.
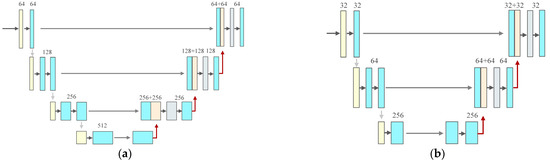
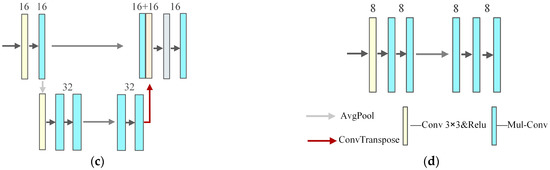
Figure 3.
U-Net structure diagrams of different depths in the background information estimation stage. (a) Network structure diagram of L1. (b) Network structure diagram of L2. (c) Network structure diagram of L4. (d) Network structure diagram of L8.
In addition, we know that the most direct way to improve the performance of deep neural networks is to expand the network model, including increasing the network depth and the number of channels per layer. However, due to the increase in computational complexity and the difficulty in producing high-quality data, there will be computational bottlenecks and overfitting. In order to alleviate this problem, inspired by reference [42], we designed a new multi-scale convolution block (MSC) based on it, which can learn receptive fields of different sizes in the same network depth and balance the depth and width of the network. Most importantly, it can make the network training effect better and the training speed faster when its parameters and calculation are less than ordinary convolution. The specific structure is shown in Figure 4, we use 1 × 1 convolution multiple times to reduce the dimension, and convert the convolutions of 5 × 5 and 7 × 7 scales into a combination of 1 × 3 and 3 × 1, or 3 × 3 convolutions. In addition, in order to reduce the number of parameters, the convolution blocks make extensive use of weight sharing mechanisms on the original basis. And the big scale convolutions are based on the small scale, which greatly reduces the computational load of the convolution blocks. Experiments have shown that our training with the designed convolutional block is faster than ordinary convolution in terms of both training fitting speed and effectiveness.
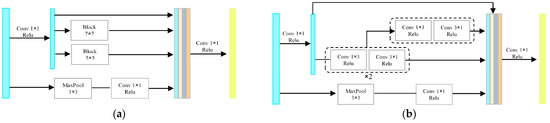
Figure 4.
(a,b) The structure of two types of multi-scale convolution block.
At the end of the module, we use bilinear interpolation to up-sample each branch to the same scale for stitching, which is used as input for the next feature fusion stage.
2.4. Recursive Feature Fusion Module
Unlike the general way of feature fusion by direct 1 × 1 convolutional compression, we think that, on the one hand, feature layers with too large of a size difference have more information variation between each other, and, on the other hand, small-scale feature layers often bring some side effects by up-sampling, such as noise amplification and blurring of the target and background, where direct fusion may not be very suitable, and a module to adjust the semantic information is needed to make the semantic information extracted by the model more accurate.
However, as mentioned above, the size of dim targets in star images is often only a few pixels to a dozen pixels. In general, the bottom layer of the network is responsible for the fine-grained learning of the image, which is extremely important for the location and representation information of the small target. The top layer is biased towards the understanding of high-level semantics. Increasing the depth of the network blindly brings about the loss of small target information, which makes the model meaningless and inconsistent with our purpose.
Therefore, considering the above problems, we adopt a recursive strategy that uses repeated connections in the same level of deep learning models. On the one hand, it can make the model adjust its semantic information horizontally, rather than continuing vertical extraction. On the other hand, the weights of repeated connections are shared, and the computational complexity of the network does not increase sharply.
2.5. Processing of Data Sets
The purpose of this paper is to provide real applications of our models, so the data used contain most of the real optical star data and a small part of the simulation data. Currently, optical stellar detection images are taken by roughly two methods, namely, ground-based or space-based optical telescopes. In this paper, the real data are taken by ground-based telescopes (please refer to Appendix A for the detailed telescope parameters). The ground-based images are relatively complex with large background fluctuations, often with local stray light and cloud cover. We know that the effect of the neural network is very dependent on the quality of the data as well as the labels; therefore, in the process of data labeling, we adopt the current industry’s more advanced methods and choose traditional image processing methods such as Top-Hat [43] and morphological filter [44] to obtain relatively clean labels. The specific processing flow can be found in the literature [29] and Figure 5 below.
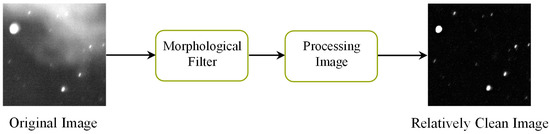
Figure 5.
The diagram of original image processing.
The experimental data are generally divided into two categories, with a total of four data sets. The first category consists of a set of simulated images with small background fluctuations, containing three parts: training set, validation set, and test set, which are 105, 10, and 10 images, respectively, with a number ratio of about 10:1:1. The simulation data are mainly based on the CCD sensor as the imaging sensor, and it is carried out by modeling the optical and motion characteristics of space debris and stars, as well as the optical imaging characteristics of the system. The location and characteristics of space debris and stars are determined by the number of TLE orbital elements [45] and the Tycho-2 catalogue [46]. The specific simulation algorithm is relatively complex and is not provided in detail, for reference, see Wang et al. [47].
The second category consists of three sets of real ground-based images with large background fluctuations and relatively complex types. In detail, in order to make our experiments more convincing and general, we randomly selected three sets of images with different sequences. Since the size of each image taken by our detection device is 4096 × 4096, which is too large for the network and the device, these images were randomly cropped to a 512 × 512 size and three datasets were made with them. They all contain a training set, a validation set, and a test set with a number ratio of 9:1:1, and the number of data in each set is specifically 90 training images, 10 validation images, and 10 test images. In addition, we would like to clarify that the training and validation data of the three sets were still randomly assigned, but in order to prevent the test set from selecting areas with relatively simple backgrounds, some of the test set data were selected from the corresponding sequence of images with relatively complex areas, such as stray light and clouds, which can be helpful to test the effect of the algorithm in the face of complex scenes. The specific training method and sequence will be introduced in Section 3.2.
3. Results
In this part, we will introduce and show the content of our experimental section in detail. Section 3.1 mainly describes the image quality evaluation criteria we used and how they were calculated. Section 3.2 introduces our training strategy and some experimental details. Section 3.3 shows our comparative experiments, and some analysis of related experimental results.
3.1. Introduction to the Evaluation Indicators
In order to verify the effectiveness of the algorithm, we evaluate both the global and the local target regions, using the currently accepted image quality evaluation metrics. The global region is evaluated in terms of the average peak signal-to-noise ratio (PSNR), structure similarity index measure (SSIM), and background suppression factor (BSF), while the local target region is evaluated in terms of the target signal-to-clutter ratio (SCR) and the average local signal-to-clutter ratio gain (SCRG). Since the real star map does not have completely clean labels and no specific target edges can be identified, we can only try to make a fair and objective evaluation. Here, it is necessary to explain and introduce the calculation methods defined in this paper.
3.1.1. Presentation of Evaluation Index for Global Area
Firstly, in terms of global region evaluation metrics, PSNR is one of the most common and widely used objective image evaluation metrics, which is based on the error between corresponding labeled pixel points, i.e., error-sensitive image quality evaluation, and it is commonly used to quantify the reconstruction quality of images and videos affected by lossy compression. In star image processing, we mainly used PSNR to quantify the degree of difference between the image and the label after background suppression, and its magnitude also reflected the algorithm’s ability to learn the image features and recover the image. The formula is as follows, where MAX is the maximum possible pixel value in the image, and we used 16-bit pixels for optical star detection images, so MAX was 65,535.
SSIM is different from MSE and PSNR in measuring absolute error. SSIM is a perceptual model, which is more in line with the intuitive feeling of the human eye. It considers the brightness, the contrast and intensity scale of the two images at the same time, and can measure the degree of distortion of the picture and the similarity of the two pictures. In this paper, considering the randomness of a single image, multiple test images are extracted to calculate their average SSIM. The calculation formula of SSIM is as follows:
where µp and µg represent the mean pixel values of the two images, respectively, δp and δg represent the pixel variances of the two images, respectively, δpg is the covariance of the pixels of the two images, and c1 and c2 and are constants.
In addition, in order to directly reflect the magnitude of background suppression, we also used the background suppression factor as one of the evaluation criteria of the algorithm model [48], which is defined as
where C is the standard deviation of the spurious waves in the whole image.
3.1.2. Presentation of Local Regional Evaluation index
As mentioned earlier, in terms of local evaluation indicators, the SCRG of a single target is also very important for space optical detection images, because the primary purpose of our background suppression is to improve the contrast between the target and the background, so that the detection platform can better distinguish the target and the background. The higher the SCR of the weak target is, the easier it is to be detected. However, the SCRG of a single target is relatively random. In order to make the verification more convincing, this paper will test multiple targets in multiple images and calculate their average SCRG. The process of calculating the local region SCRG is as follows:
- Threshold segmentation is performed uniformly using the OTSU [49] algorithm to determine the range of pixels of the target itself within a single target region in the labeled image, calculated as follows.
- First, the region around the target is normalized to obtain its normalized histogram, and the mean gray(mg) of this area is calculated. In the following formula, i denotes each individual constituent, which ranges from 0 to L − 1. Pi represents the probability of a pixel with gray level i, and the total number of pixels in this region is n.
- 3.
- Second, for k = 0, 1… L − 1, the cumulative sums P1(k) and P2(k) are computed as follows:
- 4.
- Third, the cumulative means m1(k) and m2(k) are calculated.
- 5.
- Fourth, interclass variance b2(k) is calculated to obtain the value that maximizes b2(k). If the maximum value is not unique, k* is obtained by averaging the corresponding detected values of k.
- 6.
- Fifth, according to the obtained threshold, threshold segmentation is performed on the area around the target.
- 7.
- Structural element B is set. The region Iƒ after the threshold segmentation is first eroded and then dilated with the aim of removing pulse point noise and retaining the original target region.
- 8.
- The foreground area is finalized with the background image area on the processed image.
- 9.
- The is calculated after background suppression and the of the original image based on the range of pixels is determined for the target and background in the area, where the and are calculated as follows:
3.2. Training Strategies and Implementation Details
Considering that the background of the ground-based image fluctuates greatly, the label of the ground-based image is hardly relatively clean, and the corresponding data that meet the requirements are relatively small; if the network is trained directly on it, by randomizing the initial parameters, it will appear unstable or even unfitting. Therefore, during the experiment, we give priority to training on simulated images for several iterations and choose the parameters that perform best on the validation set to test. Finally, the best result obtained from the training on simulated images is used for the pre-training parameters for ground data without modifying the model. This can compensate for the lack of ground-based data and improve training instability, and make the network training much faster.
As can be seen from the introduction of Section 2.5, we have a total of four datasets. During the training process, we uniformly used SmoothL1 loss with SSIM as the loss function to optimize the entire network. Specifically, in this loss function, the SmoothL1 and SSIM accounted for 0.65 and 0.35, respectively. The optimizer was chosen to be Adam, using β1 = 0.9, β2 = 0.999 and a learning rate η = 2 × 10−4 for training. Space-based simulated images were trained with 600 epochs and ground-based images with 2000 epochs. The learning rate was varied using cosine annealing, where the period was set to the total number of epochs and the minimum learning rate was 1 × 10−6. Finally, the size of batch-size was uniformly set to 2. All experiments were performed on an NVIDIA GTX 2080Ti GPU using PyTorch implementation.
3.3. Comparative Experiments with Different Methods
We compared MBS-Net with some background suppression methods commonly used in optical star images. Among these algorithms, Median-Blur [9], Top-Hat [43] and BM3D [8] are the traditional algorithms. SExtractor [50] is a commonly used astronomical software. DnCNN [51] and BSC-Net [29] are background suppression algorithms based on deep learning. Our algorithm mainly improves the signal-to-noise ratio of the target and achieves image enhancement by suppressing the complex background. In order to make the experimental results more intuitive and sufficient, we chose multiple real data sets for quantitative measurement and qualitative analysis, and visualized the images after the suppression of many different types of backgrounds.
- Global quantitative evaluation results on different datasets: There are four data sets for experimental training. A is a simulation image data set with relatively small background fluctuation, and B, C, D are real ground star images with complex background and large background fluctuation. As we can see, Table 1, Table 2 and Table 3 show the experimental results of different global evaluation indicators (PSNR, SSIM, BSF), respectively. From the experimental data, we can clearly see that, compared with the traditional background suppression algorithm, the suppression effect of the algorithm based on deep learning is more obvious and stable; in most cases, it is better than the traditional algorithm in three commonly used global evaluations. In addition, we can find that the MBS-Net algorithm proposed in this paper performs best on four datasets. Among these deep learning algorithms, on the three real data sets of B, C and D, our proposed algorithm outperforms the BSC-Net proposed by Li et al. last year by an average of 3.73 dB on PSNR, 2.54 on SSIM, and 6.98 on BSF. This fully shows that the proposed algorithm in this paper can achieve a background suppression function that is superior to other algorithms in three global evaluation indicators.
 Table 1. The quantitative PSNR results of various algorithms on different datasets.
Table 1. The quantitative PSNR results of various algorithms on different datasets. Table 2. The quantitative SSIM results of various algorithms on different datasets.
Table 2. The quantitative SSIM results of various algorithms on different datasets. Table 3. The quantitative BSF results of various algorithms on different datasets.
Table 3. The quantitative BSF results of various algorithms on different datasets.
- 2.
- Local target regions quantitative evaluation results on different datasets: The improvement in target signal-to-noise ratio is one of the most important criteria to test the effect of the algorithm. For this reason, we randomly selected several targets from each test image in three real test data, and calculated the SCRG of the local area of these targets. We selected five of the above algorithms for comparison. Specific results are in Table 4. We find that when the filter size changes, the results of traditional algorithms vary greatly. However, deep learning algorithms do not have these drawbacks and they are very stable. Among these algorithms, we can see that the average target signal-to-noise ratio gain of MBS-Net reaches 1.54, which is significantly higher than other algorithms. This means that our algorithm not only works well in overall background suppression, but also achieves more prominent results in retaining targets and improving signal-to-noise ratio.
 Table 4. The quantitative average SCRG results of various algorithms on different datasets.
Table 4. The quantitative average SCRG results of various algorithms on different datasets.
- 3.
- Partial image visualization after background suppression: Figure 6, Figure 7 and Figure 8 below show the background suppression results of images containing stray light and clouds so that we can see the effect of different algorithms more clearly and intuitively. In these visual results, we enlarge a local area containing the target, add the target’s SCRG, and show a three-dimensional gray scale of the whole image, which allows us to inspect the suppression effect of the algorithm from both the overall and local perspectives. We find that traditional algorithms can only improve the signal-to-noise ratio of partial targets at some times. In general, the overall background suppression effect is not stable. Median filtering only reduces the variance of the background by using a smooth background indiscriminately. The other two traditional methods improve the signal-to-noise ratio by reducing the gray level of the background. When these methods encounter complex clouds and stray light backgrounds, the background suppression effect is poor. On the contrary, the three algorithms based on deep learning are more robust. In the display of stray light and cloud background test images, the MBS-Net algorithm we proposed has the best effect; the improvement in the target’s signal-to-noise ratio is higher than other algorithms. Intuitively, the target is also more completely preserved. This is because first our proposed algorithm focuses on the different types of backgrounds in different images, so that the network can estimate the background information before each image feature extraction. Second, the design of multi-level receptive domain module and multi-scale convolution make the semantic information obtained by network feature extraction richer and the ability to distinguish background and target stronger.
 Figure 6. Schematic diagram of local cloud background suppression results.
Figure 6. Schematic diagram of local cloud background suppression results. Figure 7. Schematic diagram of global undulating background suppression results.
Figure 7. Schematic diagram of global undulating background suppression results.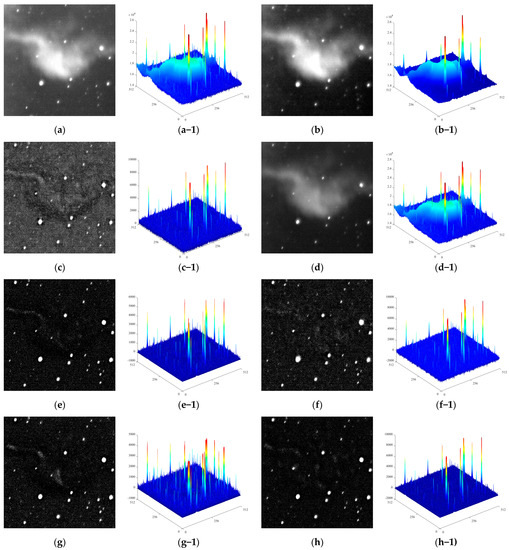 Figure 8. (a) Original Image. (a−1) A 3D grayscale of (a). (b) Median filtering. (b−1) A 3D grayscale of (b). (c) Top-Hat. (c−1) A 3D grayscale of (c). (d) BM3D. (d−1) A 3D grayscale of (d). (e) DnCNN. (e−1) A 3D grayscale of (e). (f) Source-extractor. (f−1) A 3D grayscale of (f). (g) BSC-Net. (g−1) A 3D grayscale of (g). (h) MBS-Net. (h−1) A 3D grayscale of (h).
Figure 8. (a) Original Image. (a−1) A 3D grayscale of (a). (b) Median filtering. (b−1) A 3D grayscale of (b). (c) Top-Hat. (c−1) A 3D grayscale of (c). (d) BM3D. (d−1) A 3D grayscale of (d). (e) DnCNN. (e−1) A 3D grayscale of (e). (f) Source-extractor. (f−1) A 3D grayscale of (f). (g) BSC-Net. (g−1) A 3D grayscale of (g). (h) MBS-Net. (h−1) A 3D grayscale of (h).
4. Discussion
In this section, we will discuss the role of each module and multi-scale convolution, and analyze the experimental results under different network structures to verify that the addition of each module is beneficial to the overall network model. In addition, we also pay attention to the real-time performance of the algorithm, and compare the test time and parameters with different depths.
4.1. Discussion on Ablation Experiment
The MBS-Net network model framework used in this paper is based on U-Net. In order to validate our ideas and the soundness of each component, excluding other confounding factors, we conduct ablation experiments on the ground-based image dataset without using the parameter migration approach. Specifically, we divide the ablation experiment into two parts, and use the SSIM and PSNR in the test set as evaluation indicators. In the first part, we study the influence of three components on the background suppression effect, which is divided into the following six different combinations for verification.
As can be seen from the above Table 5, we can see that the background suppression effect has an increase when the BIE and MUFE module are added separately. The improvement effect of the MUFE component is more obvious, which is increased by 0.45 db on PSNR and 5.6 × 10−3 on SSIM. Compared with using the MUFE component alone, after adding two components at the same time, the PSNR and SSIM of the prediction graph and label are further improved. In particular, the average PSNR of the predicted values improved by 0.52 dB and the SSIM by 1.01 × 10−2 more. These results fully illustrate that the three modules we added are all beneficial to improve the model effect, and all modules are in a harmonious relationship with each other, and the combination of any two modules does not lead to a decrease in effectiveness.

Table 5.
The quantitative results of ablation studies.
In addition to the ablation experiments on the three main modules, we also conducted ablation experiments on the convolutional blocks, including the regular 3 × 3 convolution as well as the multi-scale convolution proposed in this paper. From Table 6, we can see that in the comparison of the individual convolutional blocks, the number of parameters and flops of our proposed multi-scale convolution block is less than that of the regular 3 × 3 convolution. In terms of validating the MBS-Net algorithm’s training effect, we inserted two convolutional blocks into the full MBS-Net. From the change curve of the loss function and PSNR in Figure 9 below, it is seen that after inserting the multi-scale convolutional block, the MBS-Net is more stable in training and fits faster; in addition, the PSNR of the image is higher. This further indicates that with fewer parameters, the convolutional block also enables the improvement of the performance of the network.

Table 6.
Params and Flops of different model structures.
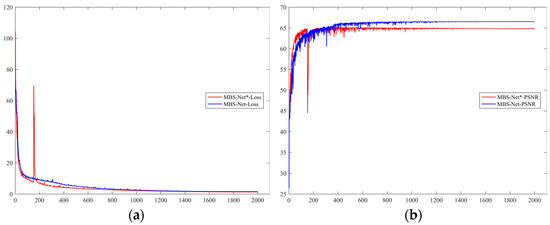
Figure 9.
Diagram of Loss and PSNR variation. (a) Schematic diagram of loss variation curve. (b) Schematic diagram of PSNR.
We think there are two reasons for this. Firstly, it is because the network with the inserted multi-scale convolution block enriches the features of the image through the convolutional operation of different convolutional-size kernels. Simultaneously, the multi-scale convolution block enables the network to encode and decode the feature information of interest in the image from a global perspective, which improves the network’s ability to extract features from the background and the target. Secondly, the network width is widened without making the network deeper, which does not lead to information loss of weak targets.
4.2. Analysis of Different Depth of MUFE
From the above, we can see that the second module of the network, MUFE, is composed of a multi-level U-Net. The size of its layers affects the performance of the algorithm, but we do not know the number of layers that is appropriate. In real projects, we need to balance the effectiveness of the model and the speed of the operation. In addition, the feature extraction stage occupies a lot of parameters and computation, so the effect of multiscale depth on the effectiveness and speed needs to be discussed. With other parameters fixed, we conducted experiments using three real datasets for different depths of the feature extraction module and calculated the test time, number of parameters and computation. The specific results are shown in Table 7, the size of the input image is 512 × 512 and the number of test sets varies from dataset to dataset.

Table 7.
Params, Flops and test time of different networks on three datasets.
From the results in the above table and the following Figure 10, as the depth of MUFE decreases, the time of testing the model on three real data sets reduces, but the difference is not very large. In addition, compared with other depth models, the four-layer deep model performs best on the PSNR index. If the number of layers continues to be added, the effect is not improved. This means that a depth of four layers is relatively appropriate for the network, balancing effectiveness with operational speed.
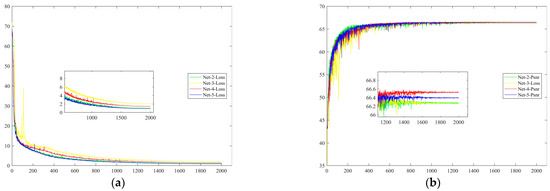
Figure 10.
Loss and PSNR variation diagram of different deep networks. (a) Schematic diagram of loss variation curve. (b) Schematic diagram of PSNR.
5. Conclusions
In this paper, we propose an image enhancement network, MBS-Net, based on background suppression. It is an end-to-end network structure, mainly for ground-based optical star detection images. In terms of specific network structure design, we aim at resolving the four problems existing in the background suppression algorithm based on deep learning that have been identified in the past. According to the composition and characteristics of the star map, we build three main components, and add them to the classic image segmentation network. From the above results and analysis of many comparative experiments and extensive ablation experiments, our proposed algorithm is superior to some existing traditional algorithms and deep learning algorithms on multiple datasets. It effectively solves the background suppression problem of star maps in complex environments and improves the signal-to-noise ratio of space debris, which is conducive to the detection of space debris in actual projects.
Author Contributions
Conceptualization, L.L. and Z.N.; methodology, L.L.; software, L.L and Y.L.; validation, L.L.; formal analysis, L.L.; resources, Q.S. and Z.N.; data curation, Q.S.; writing—original draft preparation, L.L.; writing—review and editing, Z.N.; visualization, L.L; supervision, Z.N. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded in part by the Youth Science Foundation of China (Grant No.61605243).
Data Availability Statement
Part of code and data can be found at the following link: https://github.com/GFKDliulei1998/Background-Suppression.git (accessed on 21 June 2023).
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Parameter settings of Dhyana 4040: The sky position captured by the device is random. The exposure time is about 100 ms. The PSF is a two-dimensional Gaussian and in an area with a radius of 1.5–2.0 pixels; the energy concentration degree is 80%. The field of view is 3 × 3 degrees, the image size is 4096 × 4096, and the pixel size is about 2.6 arcsec per pixel. The image is 16 bits and the maximum pixel is 65,535.
References
- Liou, J.C.; Krisko, P. An update on the effectiveness of post mission disposal in LEO. In Proceedings of the 64th International Astronautical Congress, Beijing, China, 23–27 September 2013; IAC-13-A6.4.2. International Astronautical Federation: Beijing, China, 2013. [Google Scholar]
- Kessler, D.J.; Cour-Palais, B.G. Collision frequency of artificial satellites: The creation of a debris belt. J. Geophys. Res. 1978, 83, 2637–2646. [Google Scholar] [CrossRef]
- Masias, M.; Freixenet, J.; Lladó, X.; Peracaula, M. A review of source detection approaches in astronomical images. Mon. Not. R. Astron. Soc. 2012, 422, 1674–1689. [Google Scholar] [CrossRef]
- Diprima, F.; Santoni, F.; Piergentili, F.; Fortunato, V.; Abbattista, C.; Amoruso, L.; Cordona, T. An efficient and automatic debris detection framework based on GPU technology. In Proceedings of the 7th European Conference on Space Debris, Darmstadt, Germany, 18–24 April 2017. [Google Scholar]
- Nixon, M.S.; Aguado, A.S. Feature Extraction and Image Processing. Newnes 2002, 5, 67–97. [Google Scholar]
- Kouprianov, V. Distinguishing features of CCD astrometry of faint GEO objects. Adv. Space Res. 2008, 41, 1029–1038. [Google Scholar] [CrossRef]
- Ruia, Y.; Yan-ninga, Z.; Jin-qiub, S.; Yong-penga, Z. Smear Removal Algorithm of CCD Imaging Sensors Based on Wavelet Trans-form in Star-sky Image. Acta Photonica Sin. 2011, 40, 413–418. [Google Scholar] [CrossRef]
- Dabov, K.; Foi, A.; Katkovnik, V.; Egiazarian, K. Image Denoising by Sparse 3-D Transform-Domain Collaborative Filtering. IEEE Trans. Image Process. 2007, 16, 2080–2095. [Google Scholar] [CrossRef]
- Yair, W.; Erick, F. Contour Extraction of Compressed JPEG Images. J. Graph. Tools 2001, 6, 37–43. [Google Scholar]
- Wei, M.S.; Xing, F.; You, Z. A real-time detection and positioning method for small and weak targets using a 1D morphology-based approach in 2D images. Light Sci. Appl. 2018, 7, 18006. [Google Scholar] [CrossRef]
- Wang, X.; Zhou, S. An Algorithm Based on Adjoining Domain Filter for Space Image Background and Noise Filtrating. Comput. Digit. Eng. 2012, 40, 98–99. [Google Scholar]
- Yan, M.; Fei, W.U.; Wang, Z. Removal of SJ-9A Optical Imagery Stray Light Stripe Noise. Spacecr. Recovery Remote Sens. 2014, 35, 72–80. [Google Scholar]
- Chen, H.; Zhang, Y.; Zhu, X.; Wang, X.; Qi, W. Star map enhancement method based on background suppression. J. PLA Univ. Sci. Technol. Nat. Sci. Ed. 2015, 16, 7–11. [Google Scholar]
- Zou, Y.; Zhao, J.; Wu, Y.; Wang, B. Segmenting Star Images with Complex Backgrounds Based on Correlation between Objects and 1D Gaussian Morphology. Appl. Sci. 2021, 11, 3763. [Google Scholar] [CrossRef]
- Batson, J.; Royer, L. Noise2self: Blind denoising by self-supervision. In Proceedings of the International Conference on Machine Learning, PMLR, Long Beach, CA, USA, 9–15 June 2019; pp. 524–533. [Google Scholar]
- Hernán Gil Zuluaga, F.; Bardozzo, F.; Iván Ríos Patiño, J.; Tagliaferri, R. Blind microscopy image denoising with a deep residual and multiscale encoder/decoder network. arXiv e-prints 2021, arXiv:2105.00273. [Google Scholar]
- Soh, J.W.; Cho, N.I. Deep universal blind image denoising. In Proceedings of the 2020 IEEE 25th International Conference on Pattern Recognition (ICPR), Milan, Italy; 2021; pp. 747–754. [Google Scholar]
- Liu, P.; Zhang, H.; Lian, W.; Zuo, W. Multi-level wavelet convolutional neural networks. IEEE Access 2019, 7, 74973–74985. [Google Scholar] [CrossRef]
- Zhao, Y.; Jiang, Z.; Men, A.; Ju, G. Pyramid real image denoising network. In Proceedings of the 2019 IEEE Visual Communications and Image Processing (VCIP), Sydney, Australia, 1–4 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar]
- Liu, J.-m.; Meng, W.-h. Infrared Small Target Detection Based on Fully Convolutional Neural Network and Visual Saliency. Acta Photonica Sin. 2020, 49, 0710003. [Google Scholar]
- Tian, C.; Fei, L.; Zheng, W.; Xu, Y.; Zuo, W.; Lin, C.W. Deep learning on image denoising: An overview. Neural Netw. 2020, 131, 251–275. [Google Scholar] [CrossRef] [PubMed]
- Liu, G.; Yang, N.; Guo, L.; Guo, S.; Chen, Z. A One-Stage Approach for Surface Anomaly Detection with Background Suppression Strategies. Sensors 2020, 20, 1829. [Google Scholar] [CrossRef]
- Liang-Kui, L.; Shao-You, W.; Zhong-Xing, T. Point target detection in infrared over-sampling scanning images using deep convolutional neural networks. J. Infrared Millim. Waves 2018, 37, 219. [Google Scholar]
- Zhang, K.; Zuo, W.; Zhang, L. FFDNet: Toward a Fast and Flexible Solution for CNN-Based Image Denoising. IEEE Trans. Image Process. 2018, 27, 4608–4622. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Chao, H.; Yang, M. Image Blind Denoising with Generative Adversarial Network Based Noise Modeling. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 3155–3164. [Google Scholar]
- Wu, S.-C.; Zuo, Z.-R. Small target detection in infrared images using deep convolutional neural networks. J. Infrared Millim. Waves 2019, 38, 371–380. [Google Scholar]
- Xie, M.; Zhang, Z.; Zheng, W.; Li, Y.; Cao, K. Multi-Frame Star Image Denoising Algorithm Based on Deep Reinforcement Learning and Mixed Poisson–Gaussian Likelihood. Sensors 2020, 20, 5983. [Google Scholar] [CrossRef]
- Zhang, Z.; Zheng, W.; Ma, Z.; Yin, L.; Xie, M.; Wu, Y. Infrared Star Image Denoising Using Regions with Deep Reinforcement Learning. Infrared Phys. Technol. 2021, 117, 103819. [Google Scholar] [CrossRef]
- Li, Y.; Niu, Z.; Sun, Q.; Xiao, H.; Li, H. BSC-Net: Background Suppression Algorithm for Stray Lights in Star Images. Remote Sens. 2022, 14, 4852. [Google Scholar] [CrossRef]
- Chen, K.; Zou, Z.; Shi, Z. Building extraction from remote sensing images with sparse token transformers. Remote Sens. 2021, 13, 4441. [Google Scholar] [CrossRef]
- Zhang, Z.; Jiang, Y.; Jiang, J.; Wang, X.; Luo, P.; Gu, J. Star: A structure-aware lightweight transformer for real-time image enhancement. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision, Montreal, QC, Canada, 11–17 October 2021; pp. 4106–4115. [Google Scholar]
- Chen, K.; Li, W.; Lei, S.; Chen, J.; Jiang, X.; Zou, Z.; Shi, Z. Continuous remote sensing image super-resolution based on context interaction in implicit function space. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Peng, L.; Zhu, C.; Bian, L. U-shape transformer for underwater image enhancement. IEEE Trans. Image Process. 2023, 32, 3066–3079. [Google Scholar] [CrossRef] [PubMed]
- Wang, X. Target trace acquisition method in serial star images of moving background. Opt. Precis. Eng. 2008, 16, 524–530. [Google Scholar]
- Tao, J.; Cao, Y.; Ding, M. Progress of Space Debris Detection Technology. Laser Optoelectron. Prog. 2022, 59, 1415010. [Google Scholar]
- Guo, S.; Yan, Z.; Zhang, K.; Zuo, W.; Zhang, L. Toward convolutional blind denoising of real photographs. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 15–20 June 2019; pp. 1712–1722. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Mei, Y.; Fan, Y.; Zhang, Y.; Yu, J.; Zhou, Y.; Liu, D.; Fu, Y.; Huang, T.S.; Shi, H. Pyramid Attention Networks for Image Restoration. arXiv 2020, arXiv:2004.13824. [Google Scholar]
- Zhao, H.-S.; Shi, J.-P.; Qi, X.-J.; Wang, X.-G.; Jia, J.-Y. Pyramid scene parsing network. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Bolei, Z.; Khosla, A.; Lapedriza, A.; Oliva, A.; Torralba, A. Object Detectors Emerge in Deep Scene CNNs. In Proceedings of the 2015 International Conference on Learning Representations (ICLR), San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the 18th International Conference on Medical Image Computing and Computer-Assisted Intervention (MICCAI), Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE conference on computer vision and pattern recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Bai, X.; Zhou, F.; Xue, B. Image enhancement using multi scale image features extracted by top-hat transform. Opt. Laser Technol. 2012, 44, 328–336. [Google Scholar] [CrossRef]
- Liu, Y.; Zhao, C.; Xu, Q. Neural Network-Based Noise Suppression Algorithm for Star Images Captured During Daylight Hours. Acta Opt. Sin. 2019, 39, 0610003. [Google Scholar]
- Kahr, E.; Montenbruck, O.; O’Keefe KP, G. Estimation and analysis of two-line elements for small satellites. J. Space-Craft Rocket. 2013, 50, 433–439. [Google Scholar] [CrossRef]
- Schrimpf, A.; Verbunt, F. The star catalogue of Wilhelm IV, Landgraf von Hessen-Kassel. arXiv Prepr. 2021, arXiv:2103.10801. [Google Scholar]
- Wang, Y.; Niu, Z.; Huang, J.; Li, P.; Sun, Q. Fast Simulation Method for Space-Based Optical Observation Images of Massive Space Debris. Laser Optoelectron. Prog. 2022, 59, 1611006. [Google Scholar]
- Huang, K.; Mao, X.; Liang, X.G. A Novel Background Suppression Algorithm for Infrared Images. Acta Aeronaut. Et Astronau-Tica Sin. 2010, 31, 1239–1244. [Google Scholar]
- Otsu, N. A Threshold Selection Method from Gray-Level Histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Bertin, E.; Arnouts, S. SExtractor: Software for source extraction. Astron. Astrophys. Suppl. Ser. 1996, 117, 393–404. [Google Scholar] [CrossRef]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a gaussian denoiser: Residual learning of deep cnn for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).