An Efficient Fault Detection and Exclusion Method for Ephemeris Monitoring
Abstract
:1. Introduction
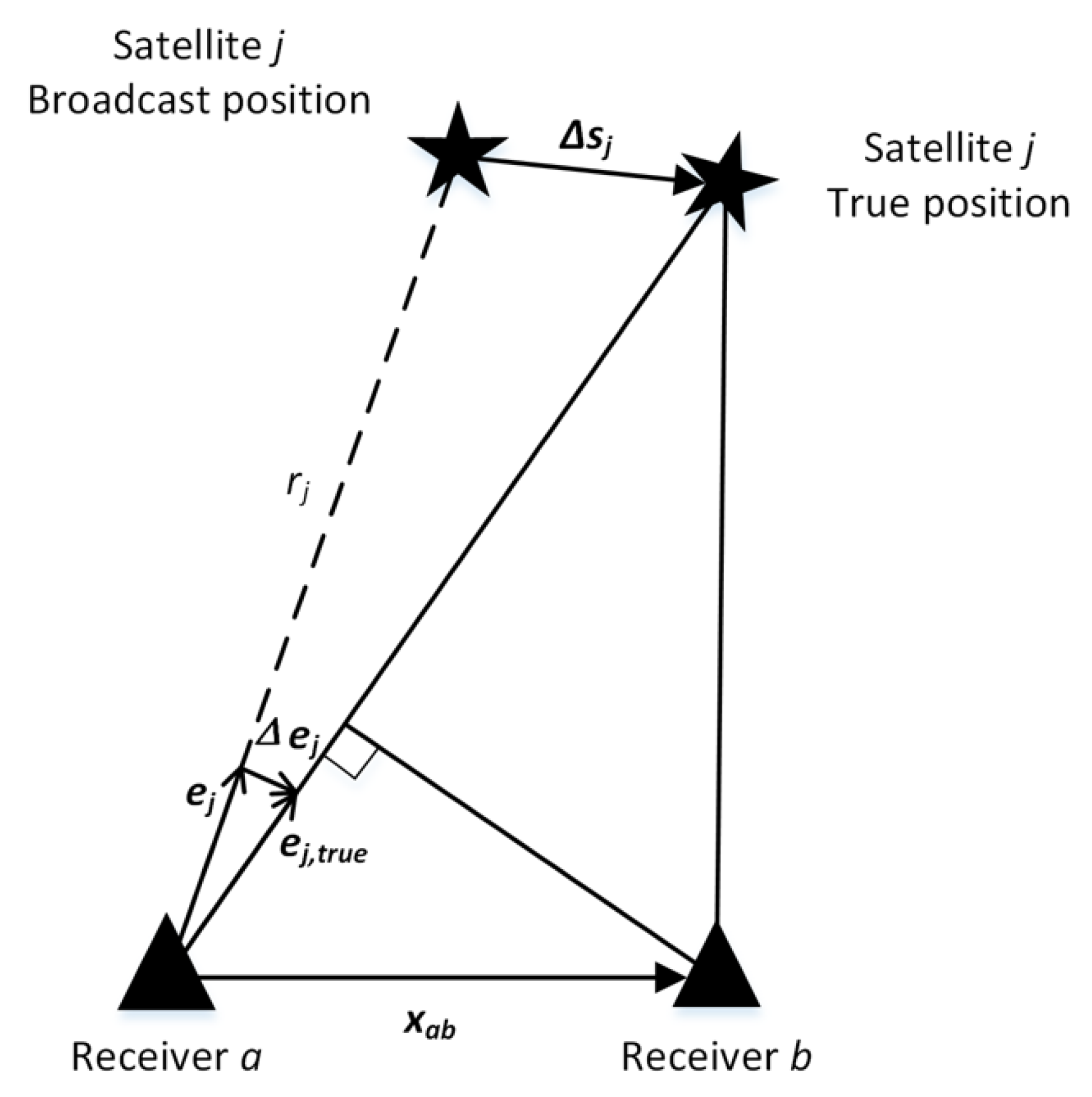
2. Overview of Ephemeris Monitor
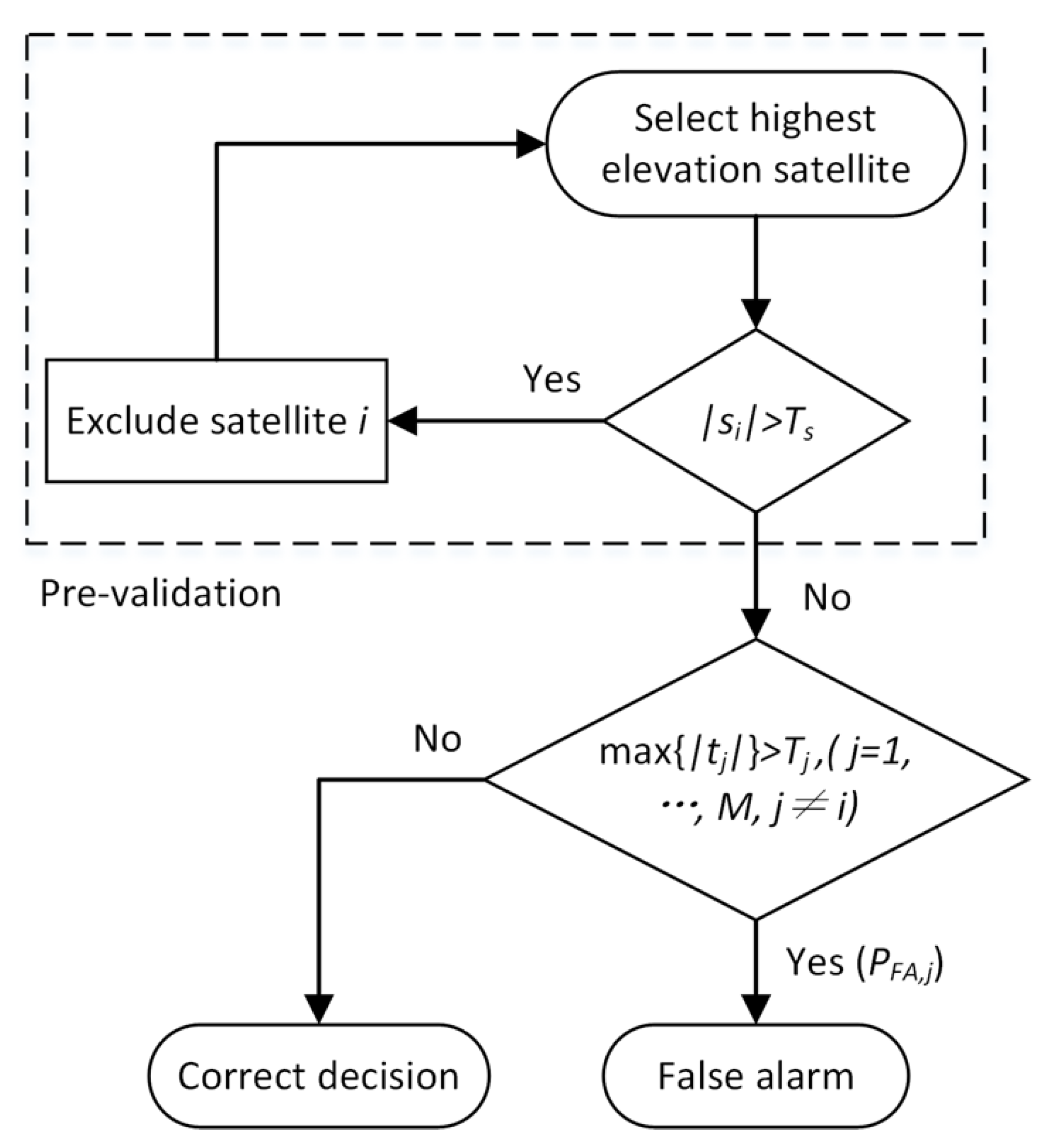
3. FDE Method with Pre-Validation
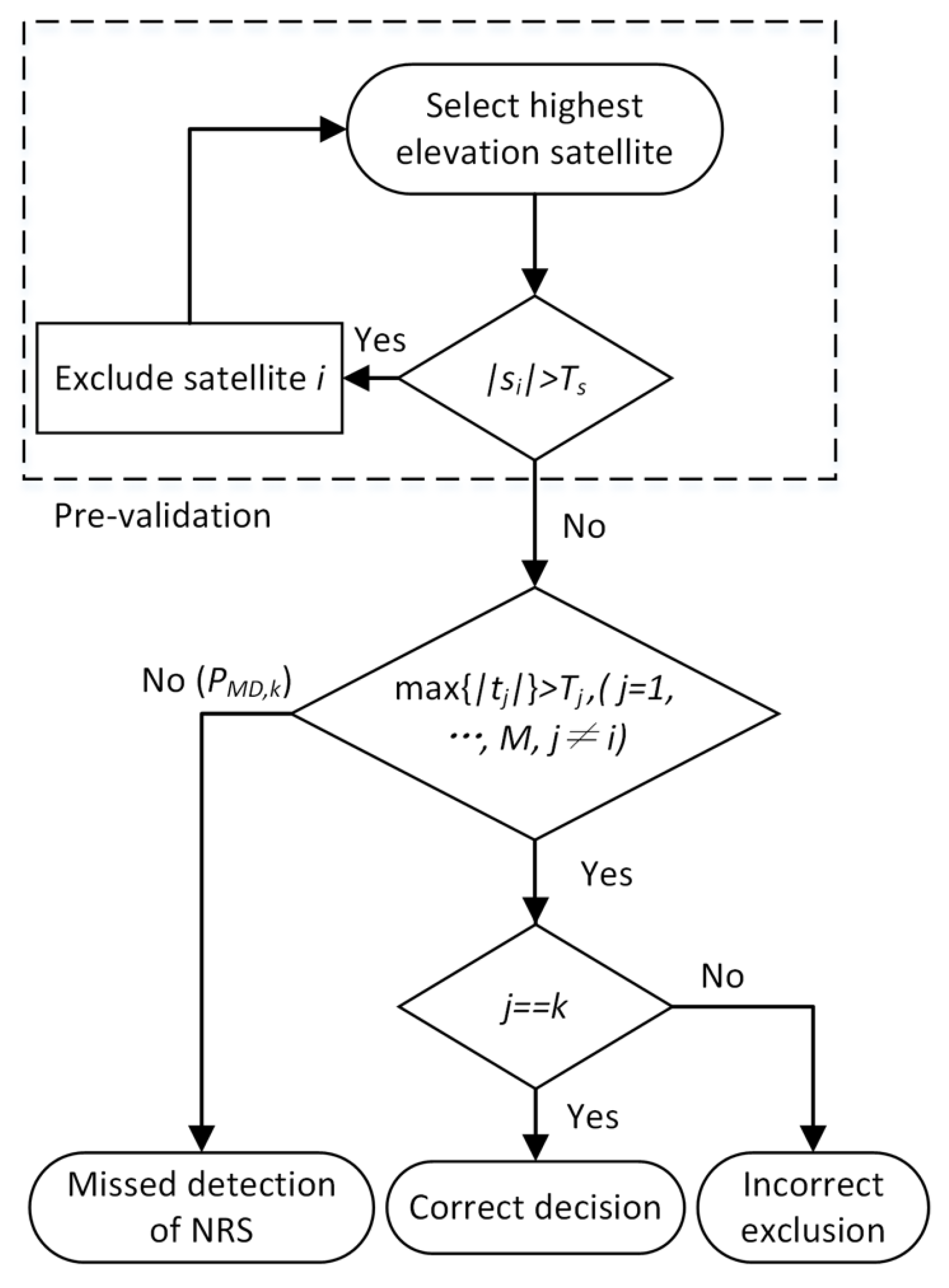
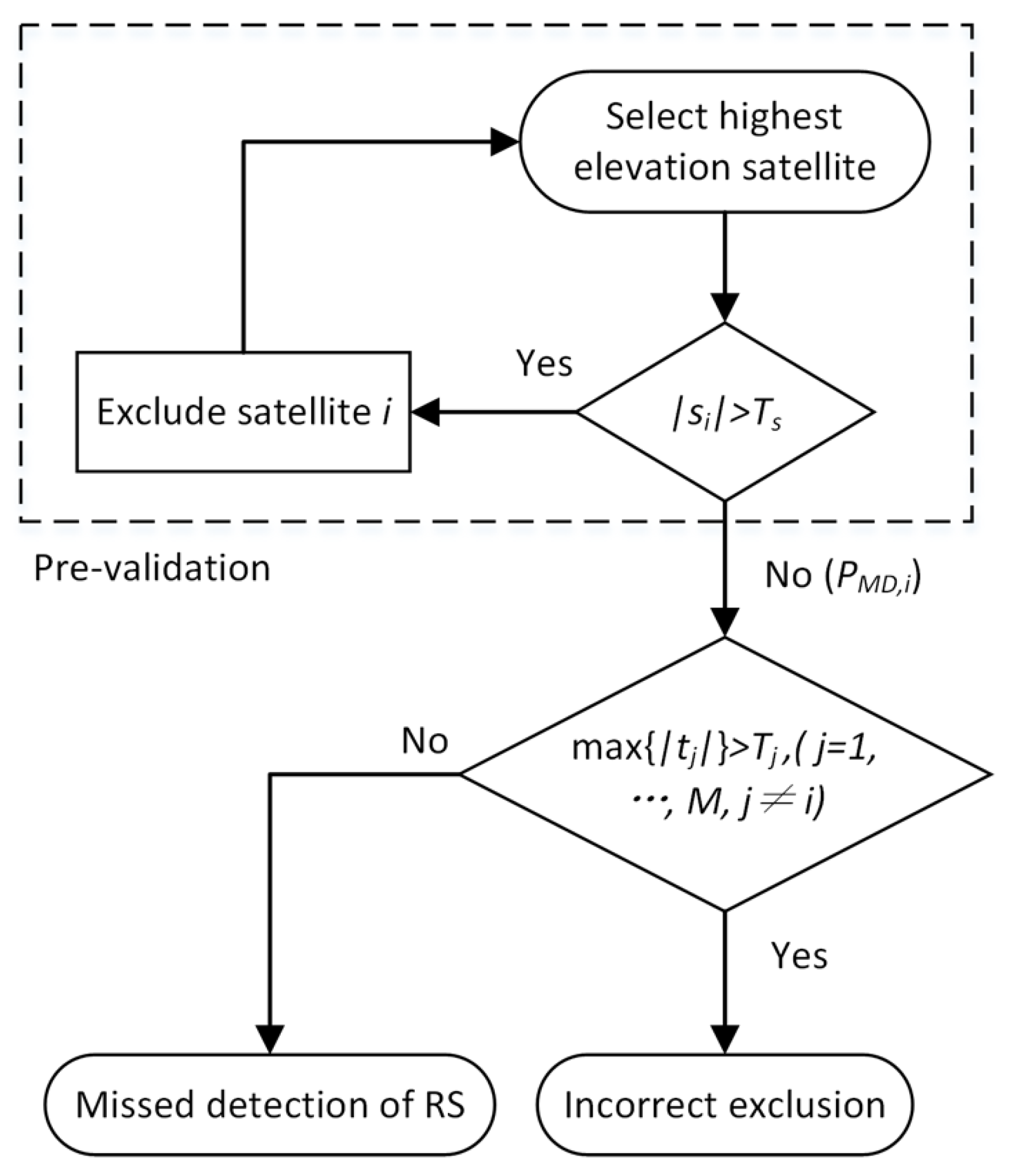
4. DD-FDE Method
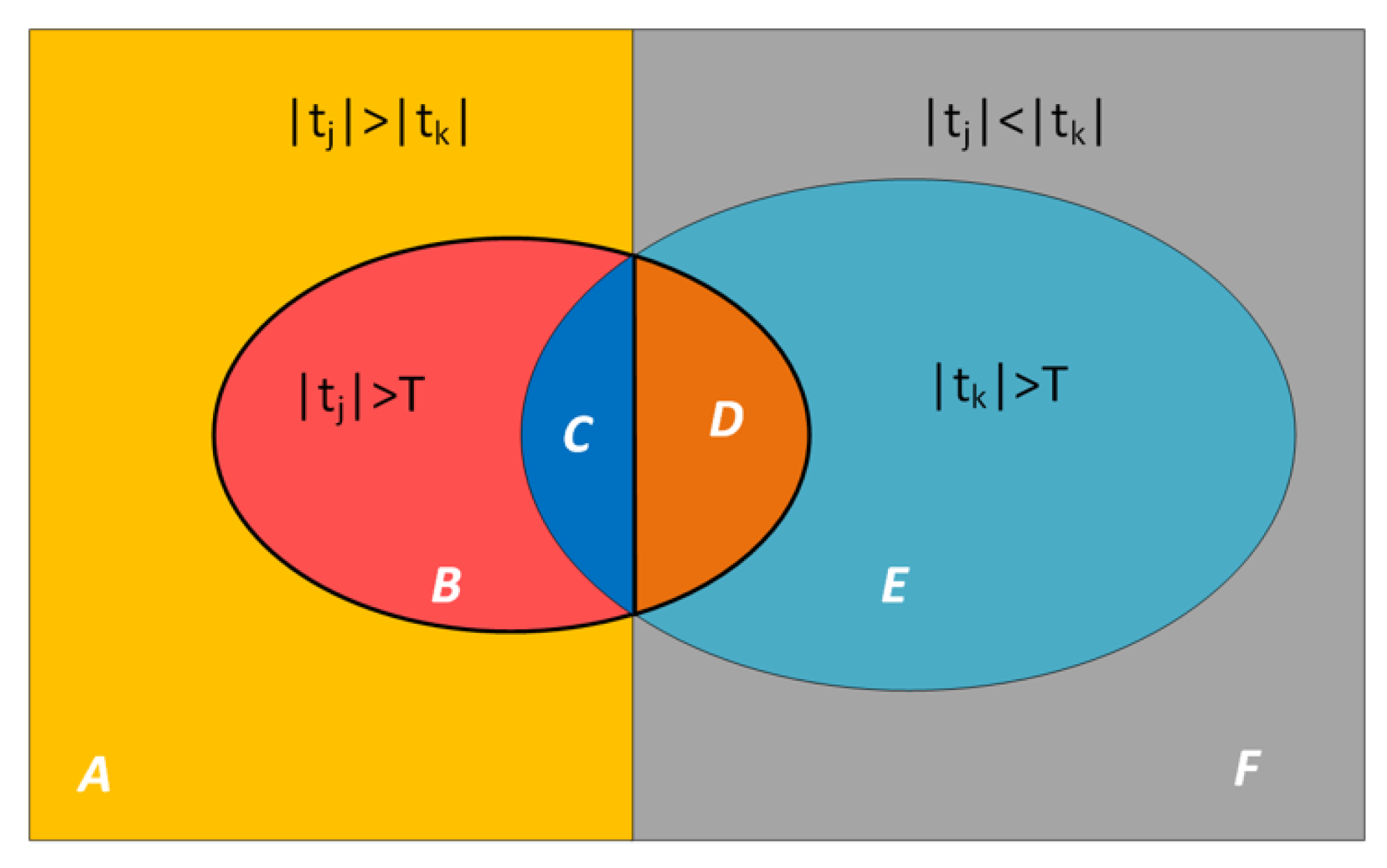
4.1. Statistical Decisions
4.2. Test Risks and MDE Derivation
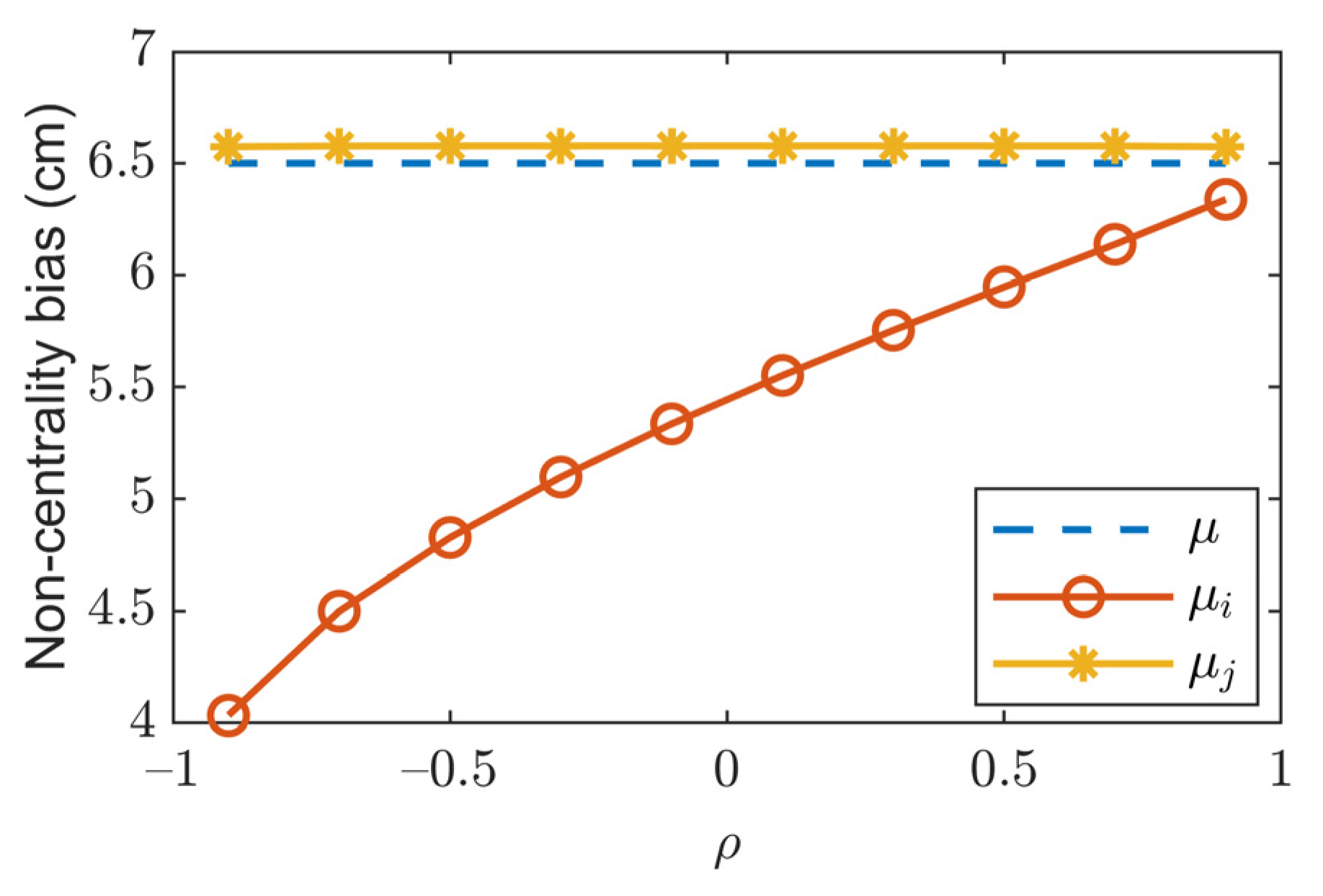
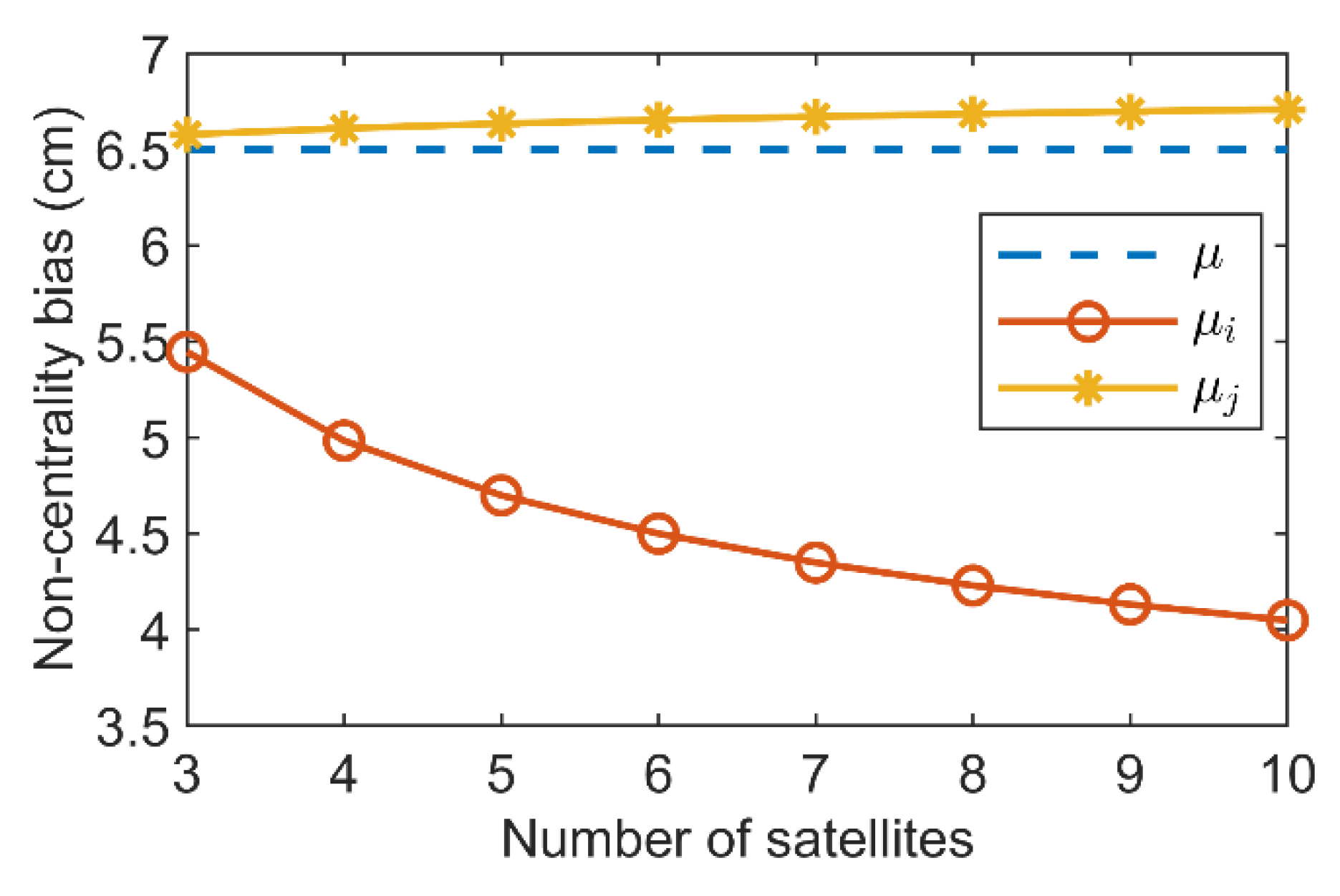
5. Numerical Results of DD-FDE Method
6. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- ED-114A; Minimum Operational Performance Standards Specification for Global Navigation Satellite Ground Based Augmentation System Ground Equipment to Support Category I Operations. EUROCAE: Saint-Denis, France, 2019. Available online: https://standards.globalspec.com/std/13497674/EUROCAE%20ED%20114 (accessed on 29 August 2022).
- SARPS. GBAS CAT II/III Development Baseline SARPs. Icao Navigation Systems Panel. Available online: http://www.icao.int/safety/airnavigation/documents/gnss_cat_ii_iii.pdf (accessed on 29 August 2022).
- Brenner, M.; Liu, F. Ranging Source Fault Detection Performance for Category III GBAS. In Proceedings of the ION GNSS 2010, Portland, OR, USA, 21–24 September 2010; pp. 2618–2632. [Google Scholar]
- Jiang, Y.; Milner, C.; Macabiau, C. Code-Carrier Divergence for Dual Frequency GBAS. GPS Solut. 2017, 21, 769–781. [Google Scholar] [CrossRef]
- Pullen, S.; Lee, J.; Luo, M.; Pervan, B.; Chan, F.; Gratton, L. Ephemeris Protection Level Equations and Monitor Algorithms for GBAS. In Proceedings of the ION GNSS 2001, Salt Lake City, UT, USA, 11–14 September 2001; pp. 1738–1749. [Google Scholar]
- Tu, R.; Zhang, R.; Fan, L.; Han, J.; Zhang, P.; Wang, X.; Lu, X. Real-Time Monitoring of the Dynamic Variation of Satellite Orbital Maneuvers Based on BDS Observations. Measurement 2021, 168, 108331. [Google Scholar] [CrossRef]
- Gratton, L.; Pervan, B.; Pullen, S. Orbit Ephemeris Monitors for Category I LAAS. In Proceedings of the ION PLANS 2004, Monterey, CA, USA, 26–29 April 2004; pp. 429–438. [Google Scholar]
- Pervan, B.; Gratton, L. Orbit Ephemeris Monitors for Local Area Differential GPS. IEEE Trans. Aerosp. Electron. Syst. 2005, 41, 449–460. [Google Scholar] [CrossRef]
- Khanafseh, S.; Patel, J.; Pervan, B. Ephemeris Monitor for GBAS Using Multiple Baseline Antennas with Experimental Validation. In Proceedings of the ION GNSS+ 2017, Portland, OR, USA, 25–29 September 2017; pp. 4197–4209. [Google Scholar]
- Patel, J.; Khanafseh, S.; Pervan, B. Detecting Hazardous Spatial Gradients at Satellite Acquisition in GBAS. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 3214–3230. [Google Scholar] [CrossRef]
- Jiang, Y. Ephemeris Monitor with Ambiguity Resolution for CAT II/III GBAS. GPS Solut. 2020, 24, 116–122. [Google Scholar] [CrossRef]
- Ken, F.; Mcdonald, J.; Johnson, B. Observed Nominal Atmospheric Behavior Using Honeywell’s GAST D Ionosphere Gradient Monitor. In Proceedings of the CSG Meeting, Montreal, MB, Canada, 17–20 May 2014. [Google Scholar]
- Jiang, Y.; Wang, J. A New Approach to Calculate the Vertical Protection Level in A-RAIM. J. Navig. 2014, 67, 711–725. [Google Scholar] [CrossRef]
- DO-253; Minimum Operational Performance Standards for GPS Local Area Augmentation System Airborne Equipment. RTCA: Washington, DC, USA, 2017. Available online: https://standards.globalspec.com/std/10168693/RTCA%20DO-253 (accessed on 29 August 2022).
- Annex 10—Aeronautical Telecommunications-Volume I-Radio Navigational Aids. International Civil Aviation Organization. Available online: https://store.icao.int/en/annex-10-aeronautical-telecommunications-volume-i-radio-navigational-aids (accessed on 29 August 2022).
- Pervan, B.; Chan, F.-C. Detecting Global Positioning Satellite Orbit Errors Using Short-Baseline Carrier-Phase Measurements. J. Guid. Control Dyn. 2003, 26, 122–131. [Google Scholar] [CrossRef]
- Jefferson, D.C.; Bar-Sever, Y.E. Accuracy and Consistency of Broadcast GPS Ephemeris Data. In Proceedings of the ION GPS 2000, Salt Lake City, UT, USA, 19–22 September 2000; pp. 391–395. [Google Scholar]
- Tang, H.; Pullen, S.; Enge, P.; Gratton, L.; Pervan, B.; Brenner, M.; Scheitlin, J.; Kline, P. Ephemeris Type A Fault Analysis and Mitigation for LAAS. In Proceedings of the IEEE/ION Position, Location and Navigation Symposium, Indian Wells, CA, USA, 4–6 May 2010; pp. 654–666. [Google Scholar]
- Li, L.; Liu, X.; Jia, C.; Cheng, C.; Li, J.; Zhao, L. Integrity Monitoring of Carrier Phase-Based Ephemeris Fault Detection. GPS Solut. 2020, 24, 43–55. [Google Scholar] [CrossRef]
- Yang, L.; Wang, J.; Knight, N.L.; Shen, Y. Outlier Separability Analysis with a Multiple Alternative Hypotheses Test. J. Geod. 2013, 87, 591–604. [Google Scholar] [CrossRef]

| Test Result | |||||
|---|---|---|---|---|---|
| Real Case | |||||
| A + F | C + D | B | E | ||
| Correct decision | PFA | PFA | PFA | ||
| PMD | Correct decision | PIE | PIE | ||
| PMD | PIE | Correct decision | PIE | ||
| PMD | PIE | PIE | Correct decision | ||
| Test Results | ||||||
|---|---|---|---|---|---|---|
| Real Case | For all , | For all , | For one or more , | For one or more , | ||
| Correct decision | PFA | PFA | PFA | |||
| PMD | Correct decision | PIE | PIE | |||
| PMD | PIE | Correct decision | PIE | |||
| PMD | PIE | PIE | Correct decision | |||
| Correct decision | PFA | PFA | PFA | ||
| PMD | Correct decision | PIE | PIE | ||
| PMD | PIE | Correct decision | PIE | ||
| PMD | PIE | PIE | Correct decision |
| 0.9 | 1.8 × 10−9 | 8.2 × 10−9 | 8.2 × 10−9 |
| 0.6 | 3.3 × 10−11 | 1.0 × 10−8 | 1.0 × 10−8 |
| 0.3 | 1.7 × 10−13 | 1.0 × 10−8 | 1.0 × 10−8 |
| 0 | 7.5 × 10−17 | 1.0 × 10−8 | 1.0 × 10−8 |
| 0.9 | 3.7 × 10−8 | 1.3 × 10−7 | 1.3 × 10−7 |
| 0.6 | 1.4 × 10−9 | 1.7 × 10−7 | 1.7 × 10−7 |
| 0.3 | 1.9 × 10−11 | 1.7 × 10−7 | 1.7 × 10−7 |
| 0 | 2.8 × 10−14 | 1.7 × 10−7 | 1.7 × 10−7 |
| 0.9 | 1.6 × 10−7 | 6.7 × 10−9 | 3.3 × 10−9 |
| 0.6 | 1.7 × 10−7 | 1.0 × 10−8 | 1.3 × 10−10 |
| 0.3 | 1.7 × 10−7 | 1.0 × 10−8 | 1.2 × 10−12 |
| 0 | 1.7 × 10−7 | 1.0 × 10−8 | 1.7 × 10−15 |
| 0.9 | 1.6 × 10−7 | 6.7 × 10−9 | 3.1 × 10−14 | |
| 0.6 | 1.7 × 10−7 | 1.0 × 10−8 | 2.4 × 10−9 | |
| 0.3 | 1.7 × 10−7 | 1.0 × 10−8 | 8.6 × 10−9 | |
| 0 | 1.7 × 10−7 | 1.0 × 10−8 | 1.0 × 10−8 |
| 0.9 | 1.4 × 10−16 | 9.6 × 10−28 | 9.6 × 10−28 | |
| 0.6 | 3.0 × 10−25 | 5.8 × 10−18 | 5.8 × 10−18 | |
| 0.3 | 1.7 × 10−42 | 7.4 × 10−17 | 7.4 × 10−17 | |
| 0 | 1.4 × 10−112 | 1.0 × 10−16 | 1.0 × 10−16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Li, W.; Zhang, H. An Efficient Fault Detection and Exclusion Method for Ephemeris Monitoring. Remote Sens. 2023, 15, 3259. https://doi.org/10.3390/rs15133259
Jiang Y, Li W, Zhang H. An Efficient Fault Detection and Exclusion Method for Ephemeris Monitoring. Remote Sensing. 2023; 15(13):3259. https://doi.org/10.3390/rs15133259
Chicago/Turabian StyleJiang, Yiping, Wang Li, and Hengwei Zhang. 2023. "An Efficient Fault Detection and Exclusion Method for Ephemeris Monitoring" Remote Sensing 15, no. 13: 3259. https://doi.org/10.3390/rs15133259
APA StyleJiang, Y., Li, W., & Zhang, H. (2023). An Efficient Fault Detection and Exclusion Method for Ephemeris Monitoring. Remote Sensing, 15(13), 3259. https://doi.org/10.3390/rs15133259





