Surface-Related Multiples Elimination for Waterborne GPR Data
Abstract
1. Introduction
2. Materials and Methods
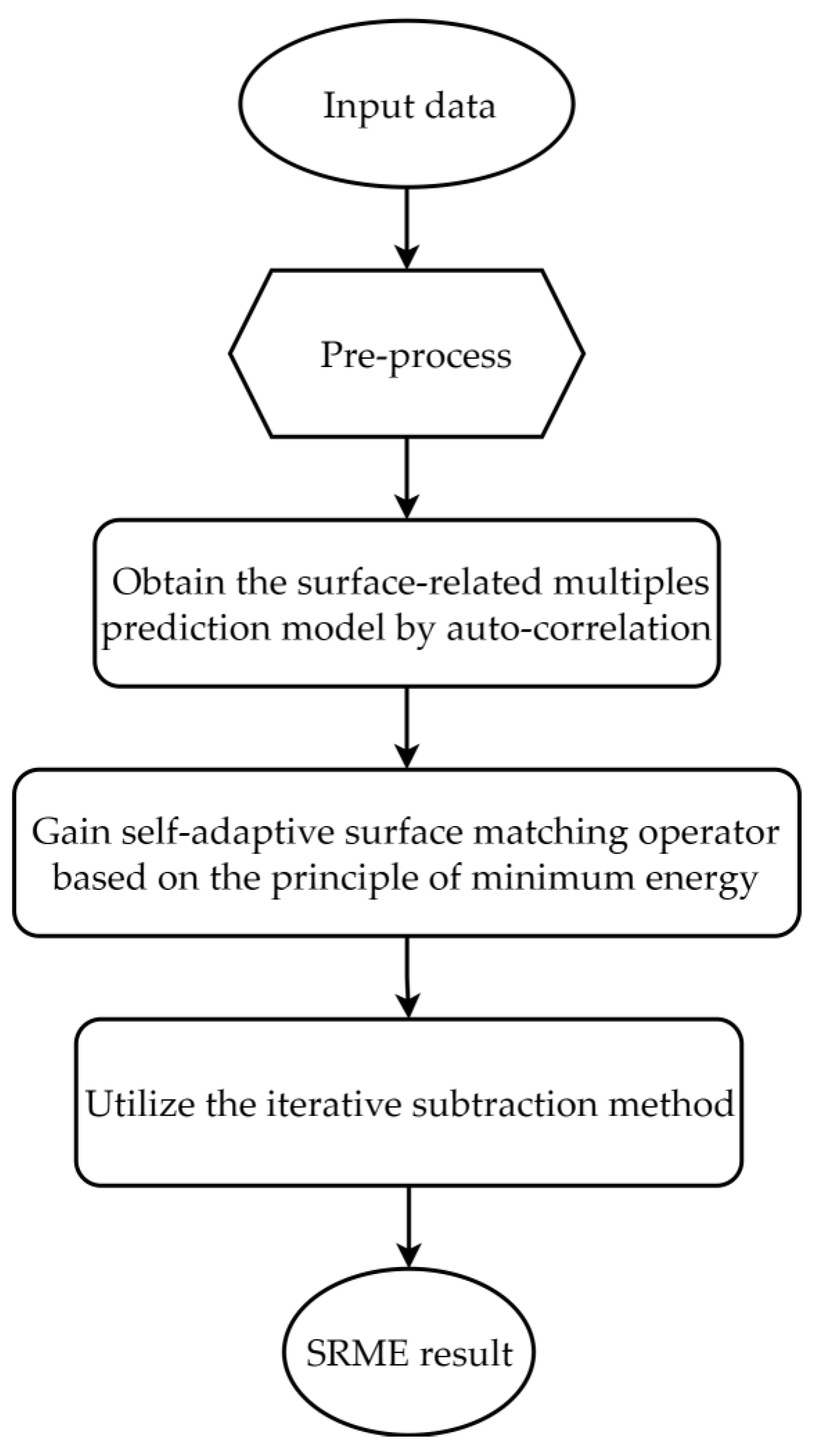
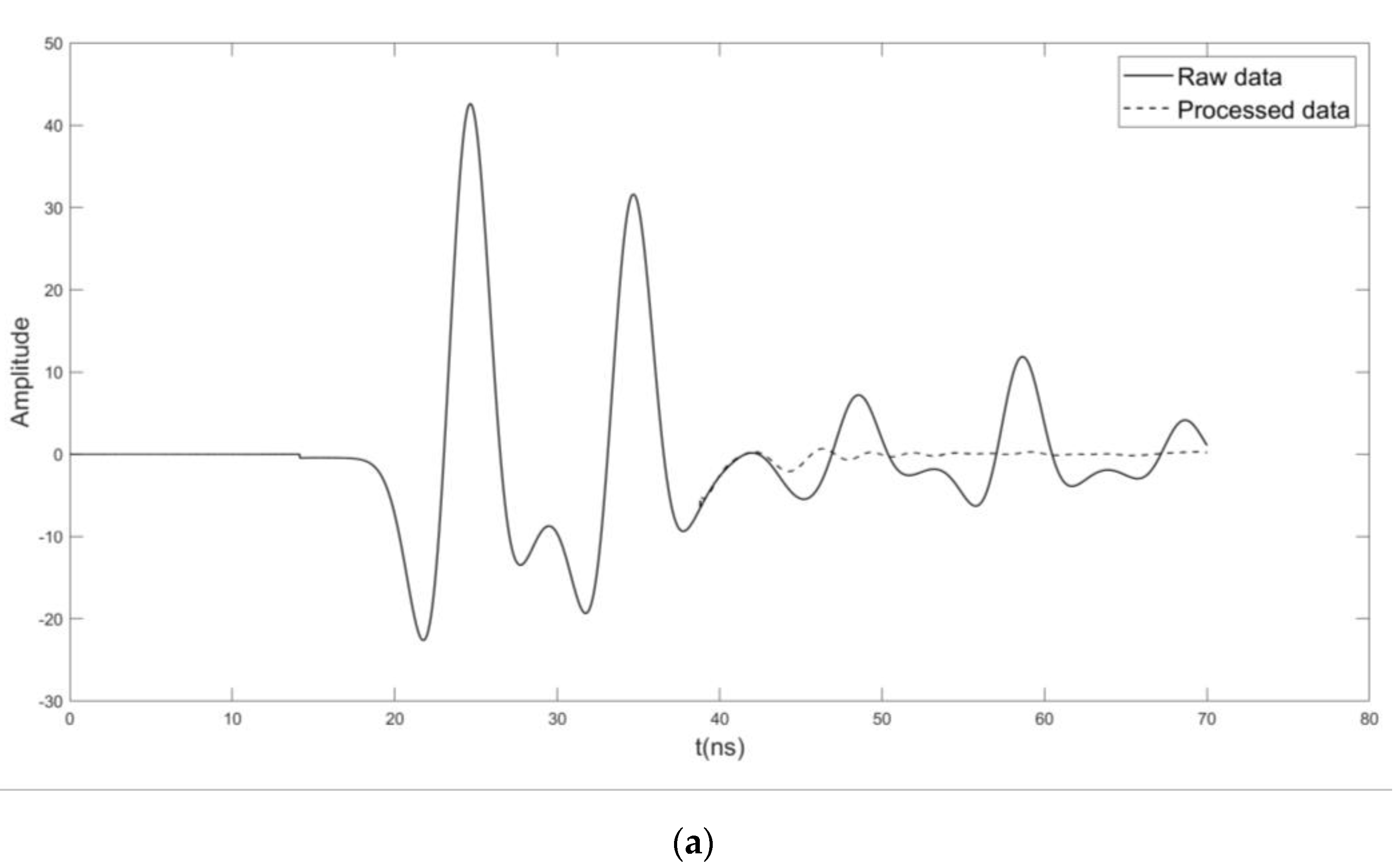
2.1. Principles of the SRME Method
2.2. Workflow
2.3. Synthetic Datasets
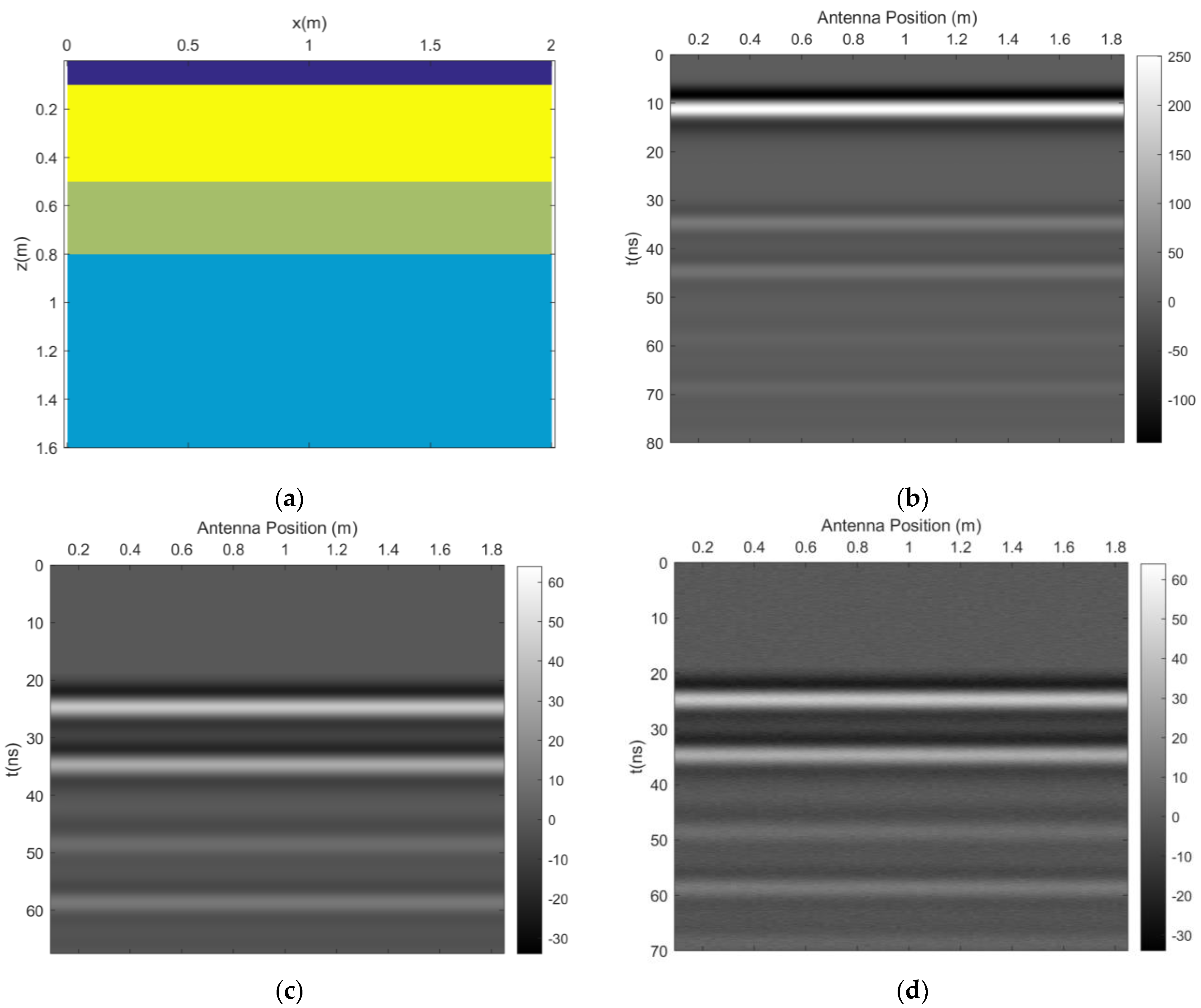
2.3.1. Underwater Horizontal Layered Model
2.3.2. Underwater Undulating Interface Model
2.4. Real Case Datasets
3. Results
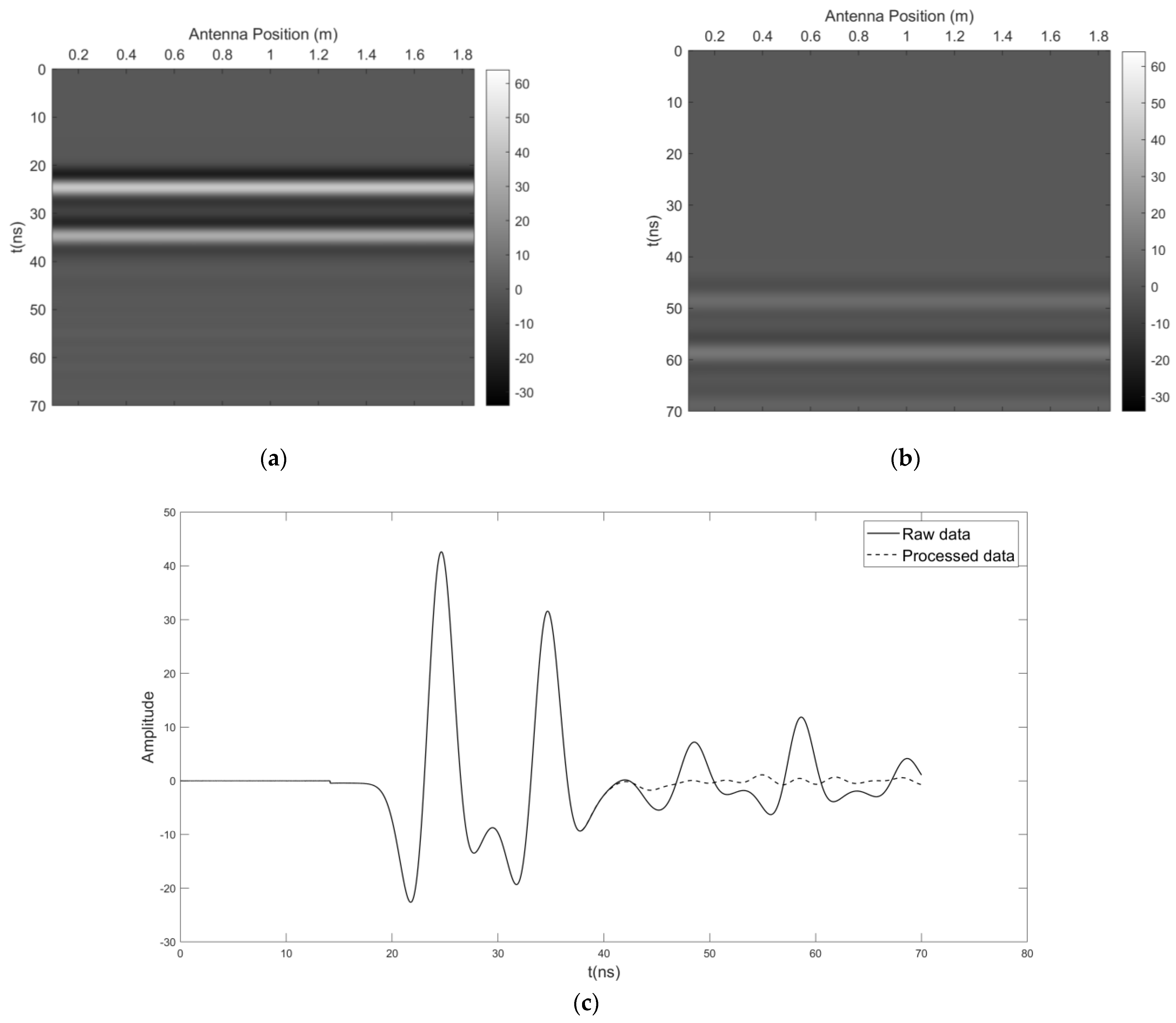
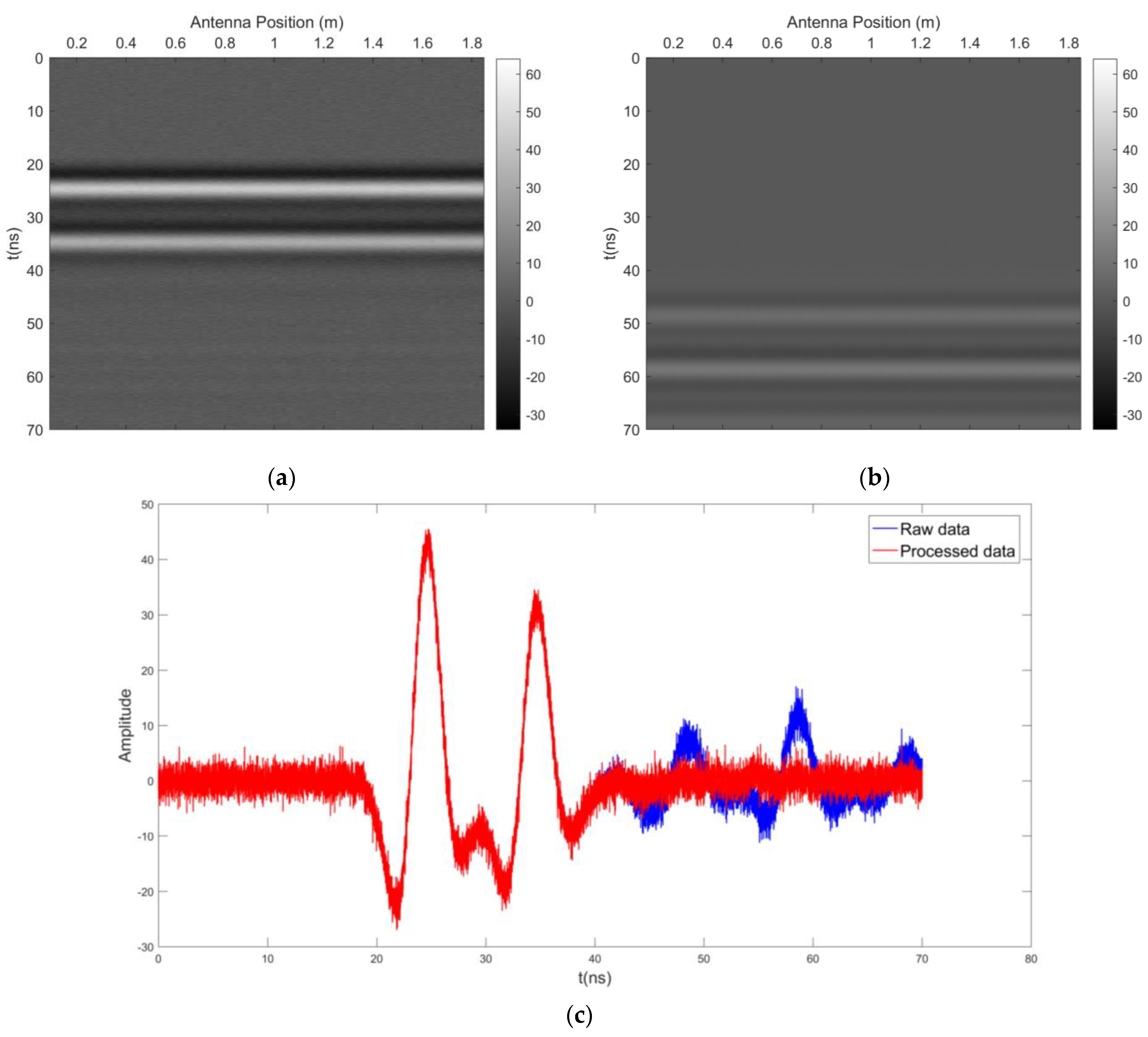
3.1. Synthetic Datasets
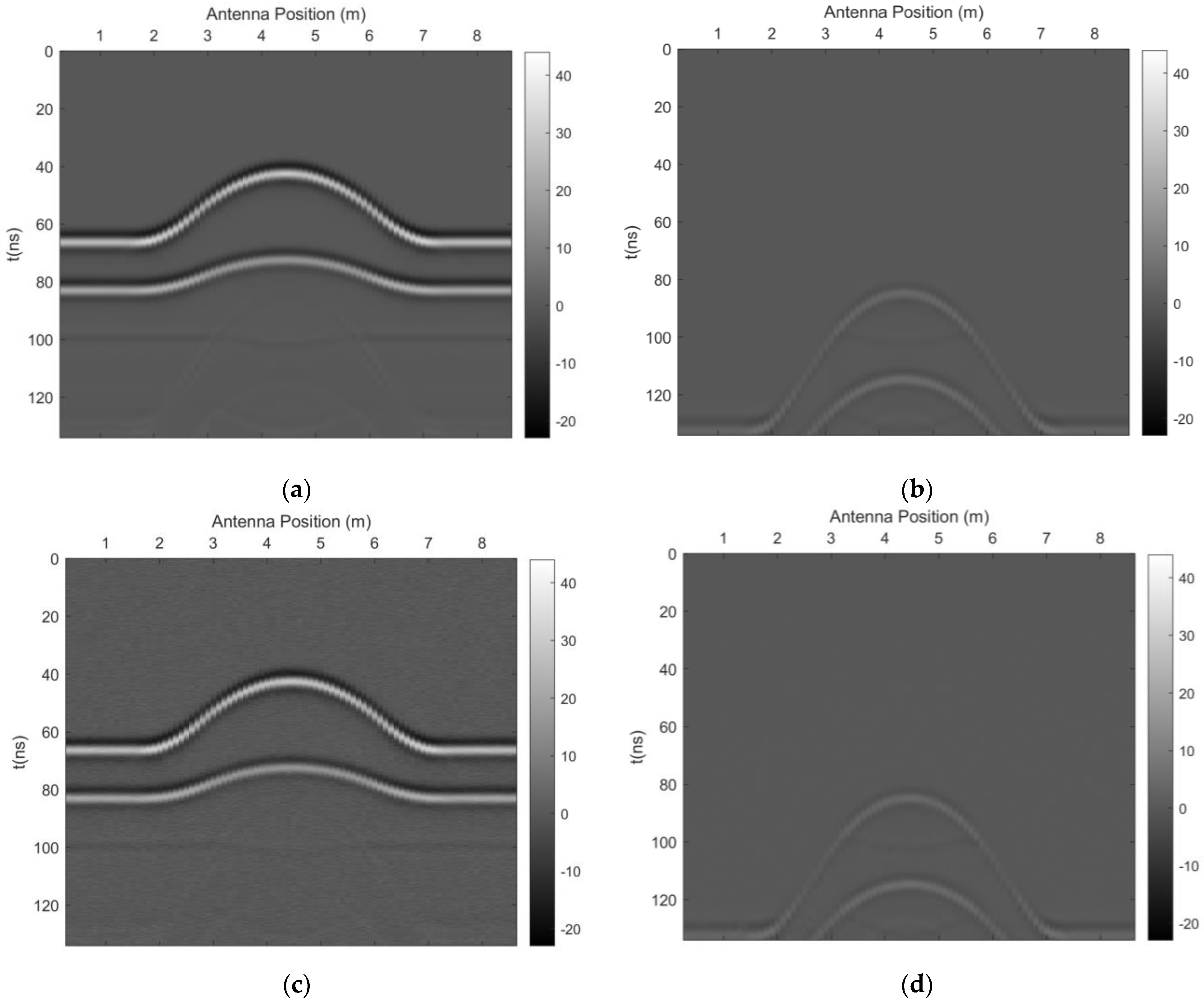
3.1.1. Underwater Horizontal Layered Model
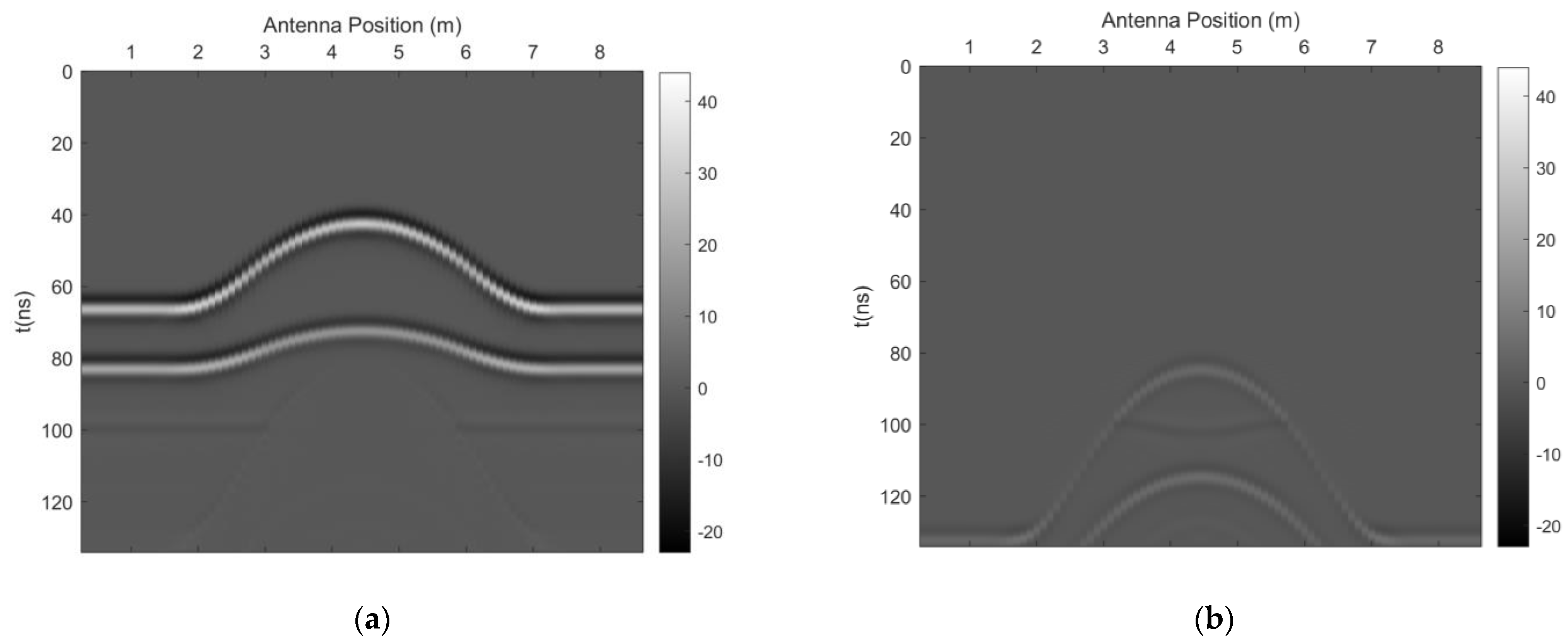
3.1.2. Underwater Undulating Interface Model
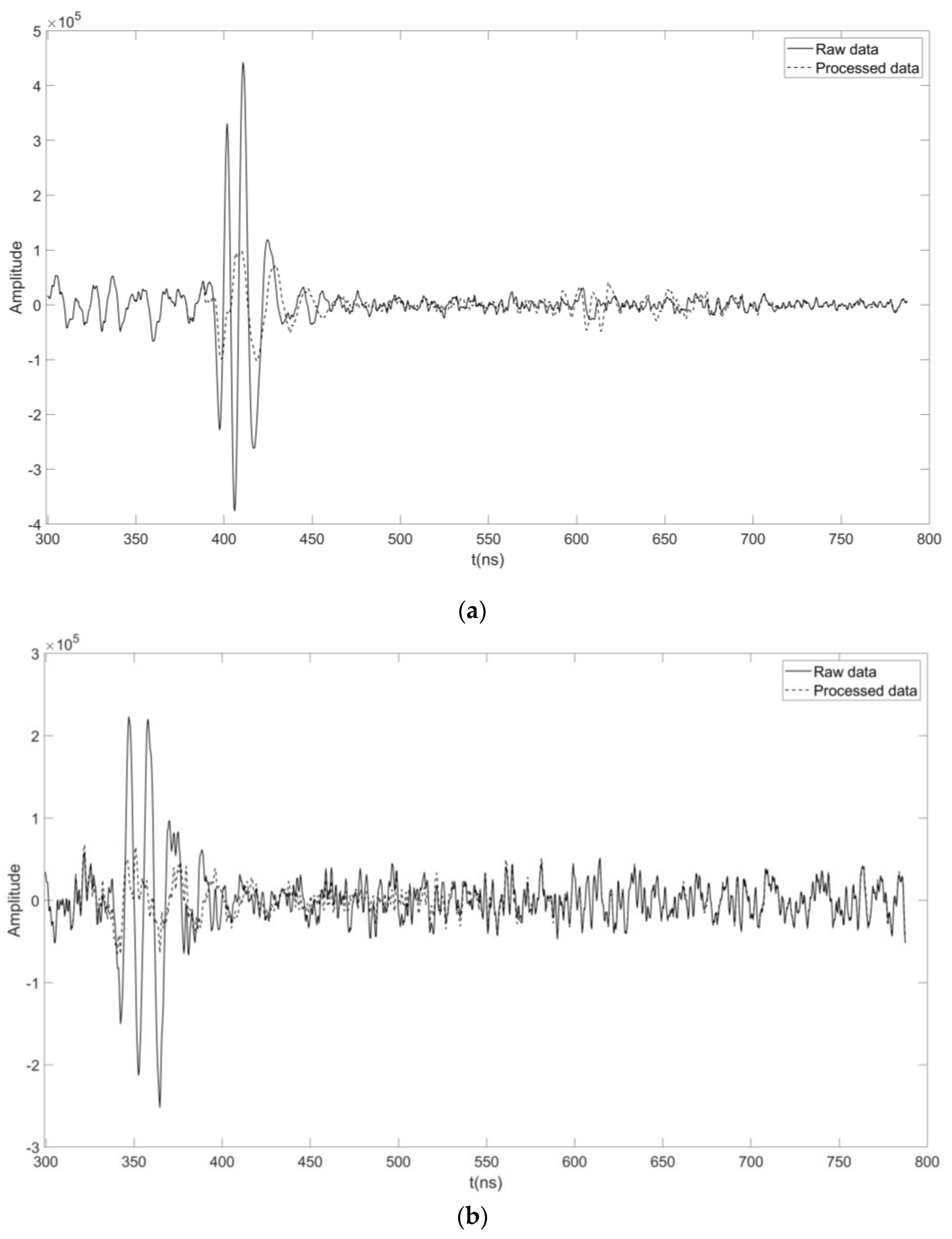
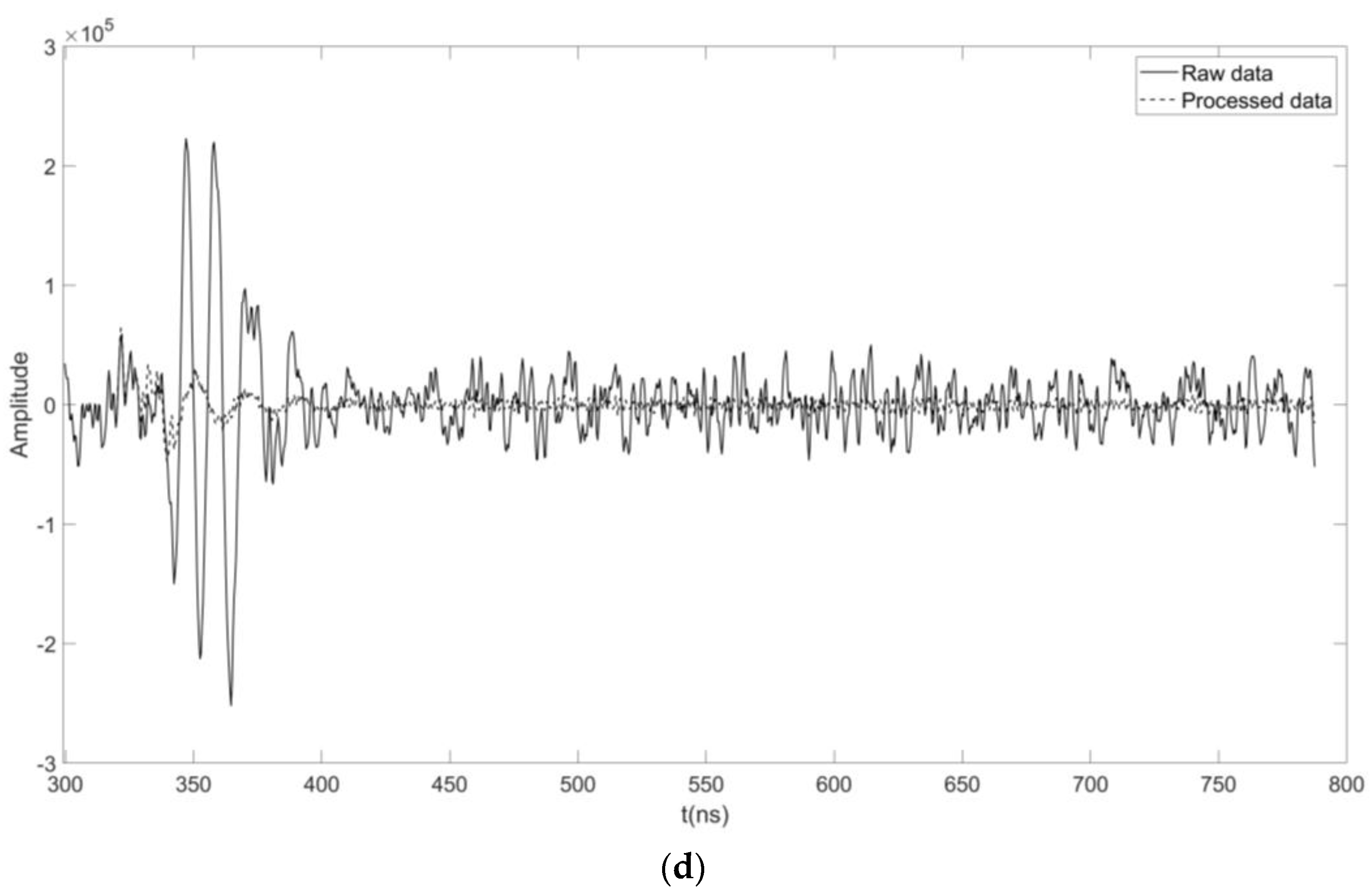
3.2. Real Case Datasets
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Benson, A.K. Applications of ground penetrating radar in assessing some geological hazards: Examples of groundwater contamination, faults, cavities. J. Appl. Geophy. 1995, 33, 177–193. [Google Scholar] [CrossRef]
- Alani, A.M.; Tosti, F. GPR applications in structural detailing of a major tunnel using different frequency antenna systems. Constr. Build. Mater. 2018, 158, 1111–1122. [Google Scholar] [CrossRef]
- Dinh, K.; Gucunski, N.; Zayed, T. Automated visualization of concrete bridge deck condition from GPR data. NDT E Int. 2019, 102, 120–128. [Google Scholar] [CrossRef]
- Barone, P.M.; Pettinelli, E.; Bellomo, T.; Scarpati, C. Applications of GPR to archaeology and geology: The example of the regio III in Pompeii (Naples, Italy). In Proceedings of the 4th International Workshop on Advanced Ground Penetrating Radar, IREA, Naples, Italy, 27–29 June 2007. [Google Scholar] [CrossRef]
- Chapman, H.; Adcock, J.; Gater, J. An approach to mapping buried prehistoric palaeosols of the Atlantic seaboard in Northwest Europe using GPR, geoarchaeology and GIS and the implications for heritage management. J. Archaeol. Sci. 2009, 36, 2308–2313. [Google Scholar] [CrossRef]
- Beres, M.; Haeni, F.P. Application of ground-penetrating-radar Methods in Hydrogeologie Studies. Ground Water. 1991, 29, 375–386. [Google Scholar] [CrossRef]
- Yang, C.H.; Jean, L.K.; Chen, J.N.; Tong, L.T. Underwater profiling by DC tomography and GPR methods. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 1997; pp. 654–656. [Google Scholar] [CrossRef]
- Manik, H.; Furusawa, M. Combined underwater acoustic and radar instruments for assessing fish near seabed and mapping seabed. In Proceedings of the 3rd International Symposium on Underwater Technology, Tokyo, Japan, 16–19 April 2002. [Google Scholar] [CrossRef]
- Sun, W.; Xu, Q.; Xie, G.; Shang, X.Y. Application of ground penetrating radar with GPS in underwater topographic survey. In Proceedings of the 2nd International Conference on Artificial Intelligence, Management Science and Electronic Commerce, Dengfeng China, 8–10 August 2011. [Google Scholar] [CrossRef]
- Truman, C.C.; Asmussen, L.E.; Allison, H.D. Ground-penetrating radar: A tool for mapping reservoirs and lakes. J. Soil. Water Conserv. 1991, 46, 370–373. [Google Scholar]
- Shean, D.E.; Marchant, D.R. Seismic and GPR surveys of Mullins Glacier, mcmurdo dry valleys, Antarctica: Ice thickness, internal structure and implications or surface ridge formation. J. Glaciol. 2010, 56, 48–64. [Google Scholar] [CrossRef]
- Saintenoy, A.; Friedt, J.-M.; Booth, A.D.; Tolle, F.; Bernard, E.; Laffly, D.; Marlin, C.; Griselin, M. Deriving ice thickness, glacier volume and bedrock morphology of Austre Lovénbreen (Svalbard) using GPR. Near. Surf. Geophys. 2013, 11, 253–262. [Google Scholar] [CrossRef]
- Liu, H.; Xie, X.; Sato, M. New ground penetrating radar system for quantitative characterization of snow and sea ice. In Proceedings of the ET International Radar Conference 2013, Xi’an, China, 14–16 April 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Liu, H.; Takahashi, K.; Sato, M. Measurement of Dielectric Permittivity and Thickness of Snow and Ice on a Brackish Lagoon Using GPR. J-STARS. 2014, 7, 820–827. [Google Scholar] [CrossRef]
- Lapazaran, J.J.; Otero, J.; Martín-Espanol, A.; Navarro, F.J. On the errors involved in ice-thickness estimates I: Ground-penetrating radar measurement errors. J. Glaciol. 2016, 62, 1008–1020. [Google Scholar] [CrossRef]
- Moorman, B.J.; Michel, F.A. Bathymetric mapping and sub-bottom profiling through lake ice with ground-penetrating radar. J. Paleolimnol. 1997, 18, 61–73. [Google Scholar] [CrossRef]
- Dugan, H.A.; Doran, P.T.; Tulaczyk, S.; Mikucki, J.A.; Arcone, S.A.; Auken, E.; Schamper, C.; Virginia, R.A. Subsurface imaging reveals a confined aquifer beneath an ice-sealed Antarctic lake. Geophys. Res. Lett. 2015, 42, 96–103. [Google Scholar] [CrossRef]
- Bandini, F.; Kooij, L.; Mortensen, B.K.; Caspersen, M.B.; Thomsen, L.G.; Olesen, D.; Bauer-Gottwein, P. Mapping inland water bathymetry with Ground Penetrating Radar (GPR) on board Unmanned Aerial Systems (UASs). J. Hydrol. 2023, 616, 128789. [Google Scholar] [CrossRef]
- Qin, T.; Zhao, Y.H.; Lin, G.C.; Hu, S.F.; An, C.; Geng, D.X.; Rao, C.F. Underwater archaeological investigation using ground penetrating radar: A case analysis of Shanglinhu Yue Kiln sites (China). J. Appl. Geophy. 2018, 154, 11–19. [Google Scholar] [CrossRef]
- Mellett, J.S. Profiling of ponds and bogs using ground-penetrating radar. J. Paleolimnol. 1995, 14, 233–240. [Google Scholar] [CrossRef]
- Fisher, T.G.; Loope, W.L.; Pierce, W.; Jol, H.M. Big lake records preserved in a little lake’s sediment: An example from Silver Lake, Michigan, USA. J. Paleolimnol. 2007, 37, 365–382. [Google Scholar] [CrossRef]
- Zhao, Y.H.; Wu, J.S.; Xie, X.Y.; Chen, J.; Ge, S.C. Multiple suppression in GPR image for testing back-filled grouting within shield tunnel. In Proceedings of the XIII International Conference on Ground Penetrating Radar, Lecce, Italy, 16 August 2010. [Google Scholar] [CrossRef]
- Xie, X.Y.; Qin, H.; Yu, C.; Liu, L.B. An automatic recognition algorithm for GPR images of RC structure voids. J. Appl. Geophy. 2013, 99, 125–134. [Google Scholar] [CrossRef]
- Zhang, L.L.; Slob, E. Electromagnetic Marchenko scheme based internal multiple elimination for lossless media. In Proceedings of the 9th International Workshop on Advanced Ground Penetrating Radar, Edinburgh, Scotland, 28–30 June 2017. [Google Scholar] [CrossRef]
- Berkhout, A.J. Seismic Migration: Imaging of Acoustic Energy by Wave Field Extrapolation, A. Theoretical Aspects, 2nd ed.; Elsevier: Amsterdam, The Netherlands, 1984. [Google Scholar]
- Verschuur, D.J.; Berkhout, A.J.; Wapenaar, C.P.A. Adaptive surface-related multiple elimination. Geophysics 1992, 57, 1166–1177. [Google Scholar] [CrossRef]
- Berkhout, A.J.; Verschuur, D.J. Estimation of multiple scattering by iterative inversion, Part I: Theoretical considerations. Geophysics 1997, 62, 1586–1595. [Google Scholar] [CrossRef]
- Verschuur, D.J.; Berkhout, A.J. Estimation of multiple scattering by iterative inversion, Part II: Practical aspects and examples. Geophysics 1997, 62, 1596–1611. [Google Scholar] [CrossRef]
- Jakubowicz, H. Wave Equation Prediction and Removal of Interbed Multiples. In SEG Technical Program Expanded Abstracts; Society of Exploration Geophysicists: Houston, TX, USA, 1998; pp. 1527–1530. [Google Scholar] [CrossRef]
- Berkhout, A.J.; Verschuur, D.J. Removal of internal multiples with the common-focus-point (CFP) approach: Part 1-Explanation of the theory. Geophysics 2005, 70, V45–V60. [Google Scholar] [CrossRef]
- Verschuur, D.J. Seismic Multiple Removal Techniques: Past, Present and Future, 2nd ed.; EAGE Publications: Houten, The Netherlands, 2013; pp. 84–91. [Google Scholar]
- Levinson, N. The Wiener RMS error criterion in filter design and prediction. J. Math. Phys. 1946, 25, 261–278. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]










| Layer | Thickness (m) | |
|---|---|---|
| Air | 0.1 | 1 |
| Water | 0.4 | 81 |
| Silt | 0.3 | 25 |
| Bedrock | 0.8 | 5 |
| Layer | Thickness (m) | |
|---|---|---|
| Air | 0.3 | 1 |
| Water | 0.7 (thinnest)/1.1 (thickest) | 81 |
| Silt | 0.5 (thinnest)/1.5 (thickest) | 25 |
| Bedrock | 1.1 | 5 |
| Method | Noise | SNR (dB) |
|---|---|---|
| SRME | None | 11.1235 |
| Predictive deconvolution | None | 11.5178 |
| SRME | 4% Gaussian random noise | 11.1853 |
| Predictive deconvolution | 4% Gaussian random noise | 11.4822 |
| Method | Location | Noise | SNR (dB) |
|---|---|---|---|
| SRME | 1 m | None | 12.6812 |
| 4.5 m | None | 13.5961 | |
| 1 m | 4% Gaussian random noise | 12.4715 | |
| 4.5 m | 4% Gaussian random noise | 13.1093 | |
| Predictive deconvolution | 1 m | None | 18.9891 |
| 4.5 m | None | 13.857 | |
| 1 m | 4% Gaussian random noise | 17.5618 | |
| 4.5 m | 4% Gaussian random noise | 12.7906 |
| Method | Location | SNR (dB) |
|---|---|---|
| SRME | 63 m | 0.8394 |
| Predictive deconvolution | 63 m | 0.3683 |
| SRME | 94 m | 1.2340 |
| Predictive deconvolution | 94 m | 0.2646 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shen, R.; Zhao, Y.; Cheng, H.; Hu, S.; Chen, S.; Ge, S. Surface-Related Multiples Elimination for Waterborne GPR Data. Remote Sens. 2023, 15, 3250. https://doi.org/10.3390/rs15133250
Shen R, Zhao Y, Cheng H, Hu S, Chen S, Ge S. Surface-Related Multiples Elimination for Waterborne GPR Data. Remote Sensing. 2023; 15(13):3250. https://doi.org/10.3390/rs15133250
Chicago/Turabian StyleShen, Ruiqing, Yonghui Zhao, Hui Cheng, Shufan Hu, Shifeng Chen, and Shuangcheng Ge. 2023. "Surface-Related Multiples Elimination for Waterborne GPR Data" Remote Sensing 15, no. 13: 3250. https://doi.org/10.3390/rs15133250
APA StyleShen, R., Zhao, Y., Cheng, H., Hu, S., Chen, S., & Ge, S. (2023). Surface-Related Multiples Elimination for Waterborne GPR Data. Remote Sensing, 15(13), 3250. https://doi.org/10.3390/rs15133250










