Abstract
The crop drought risk assessment is an important basis for mitigating the effects of drought on crops. The study of drought using crop growth models is an integral part of agricultural drought risk research. The current Decision Support System for Agrotechnology Transfer (DSSAT) model is not sufficiently sensitive to moisture parameters when performing simulations, and most studies that conduct different scenario simulations to assess crop drought vulnerability are based on the site-scale. In this paper, we improved the moisture sensitivity of the Crop Environment Resource Synthesis System (CERES)-Wheat to improve the simulation accuracy of winter wheat under water stress, and then we assessed the drought intensity in the Beijing-Tianjin-Hebei region and constructed a gridded vulnerability curve. The grid vulnerability curves (1 km × 1 km) were quantitatively characterized using key points, and the drought risk distribution and zoning of winter wheat were evaluated under different return periods. The results show that the stress mechanism of coupled water and photosynthetic behavior improved the CERES-Wheat model. The accuracy of the modified model improved in terms of the above-ground biomass and yield compared with that before the modification, with increases of 20.39% and 11.45% in accuracy, respectively. The drought hazard intensity index of winter wheat in the study area from 1970 to 2019 exhibited a trend of high in the southwest and low in the southeast. The range of the multi-year average drought hazard intensity across the region was 0.29–0.61. There were some differences in the shape and characteristic covariates of the drought vulnerability curves among the different sub-zones. In terms of the cumulative loss rates, almost the entire region had a cumulative drought loss rate of 49.00–54.00%. Overall, the drought risk index decreased from west to east and from north to south under different return periods. This quantitative evaluation of the drought hazard intensity index provides a reference for agricultural drought risk evaluation.
1. Introduction
Drought is one of the most complex and devastating natural hazards []. In recent years, global climate change and the development of human life, the economy and urbanization have led to an increase in the frequency of and damage caused by droughts [,]. The impacts of drought include economic, natural and social impacts [], with drought having a significant impact on agriculture. Globally, the average annual loss of agricultural production due to drought has exceeded USD 6 billion and is still increasing []. Between 1983 and 2009, about three-quarters of the global crops’ harvested crop area (454 million hectares) experienced yield losses due to drought, with cumulative yield losses equivalent to USD 166 billion. With respect to the global average, a drought can reduce the agricultural gross domestic product (GDP) by 0.8%, and the degree of impact varies from country to country []. For the same drought disaster intensity, the higher the level of regional agricultural vulnerability, the more severe the disaster losses. Therefore, in-depth research on the quantification of agricultural drought vulnerability is of great significance for regional agricultural drought risk prevention and the formulation of disaster mitigation strategies.
Research on drought risk assessment is growing in the international community [], and there is a proliferation of assessment methods. Most studies consider the agricultural drought risk as the superimposed effect of the exposure, the environmental sensitivity and the vulnerability of the crop in the process of coping with drought in agricultural systems. A risk index system was constructed to comprehensively evaluate the risk level of a region and carry out zoning [,,]. Zhang et al. [] developed a multi-indicator assessment model to evaluate the agricultural drought risk in terms of the hazard, vulnerability, exposure and drought resistance based on the fuzzy characteristics of variables. Existing machine learning approaches have made great progress in drought stress monitoring and diagnosis []. An et al. [] used a deep learning convolutional neural network (DCNN) for drought stress identification. In addition, numerous studies have been conducted on the drought monitoring of plants and images using machine learning algorithms [,]. A number of studies have also focused on the analysis of precipitation indices that affect drought vulnerability, such as the use of the standardized precipitation index (SPI) to characterize agricultural drought conditions [,]. Thomas et al. [] used a combination of the SPI, surface water drought index and groundwater drought index to assess the drought vulnerability. Kar et al. [] used multiple factors including watershed topographic characteristics, soil type and rainfall deviation to evaluate the spatial and temporal variability of drought characteristics, and then identified and analyzed the areas vulnerable to drought. Some scholars considered farmers as the mainstay of agricultural production and focused more on a drought vulnerability assessment from the microscopic perspective of farmers’ households [,]. The impact of the farmers’ own characteristics on the drought sensitivity and adaptive capacity is considered. Drought vulnerability studies based on indicator systems are mostly represented by qualitative or semi-quantitative risk maps, which are useful for understanding the spatial and temporal distribution characteristics of the drought risk. However, there is the problem that the selection of indicators is too subjective, and it is difficult to determine the physical significance associated with the composite vulnerability index and to estimate the corresponding agricultural losses under different drought intensities.
Agricultural drought vulnerability curves can enable the quantitative assessment of the crop vulnerability level and estimation of the extent of agricultural damage under different drought hazard intensities. Three main types of data can be used to construct these curves: actual disaster data, systematic surveys and model simulation data [,]. The first type is more dependent on disaster case data, while the second type is more work-intensive and mixed with more human factors to investigate. Vulnerability curves constructed with the help of crop growth models are less limited by disaster data and can quantify the relationship between the degree of drought and crop yield loss from the perspective of physical processes, so they are gradually becoming a hot research topic [,,].
Currently, the commonly used crop growth models include the FAO Crop Model to Simulate Yield Response to Water (AquaCrop) [,], Agricultural Production Systems Simulator (APSIM) [], Environmental Policy-Integrated Climate (EPIC) [,,] and Decision Support System for Agrotechnology Transfer (DSSAT) [,] models. Scholars use appropriate crop growth models to evaluate agricultural drought vulnerability according to the major crops in the region. For example, Wang et al. [] concluded that the EPIC model was less sensitive to the crop yield during severe drought and was not good at modeling the soil moisture when crops were under water stress. They proposed to construct physical vulnerability curves for crops based on the water stress and yield loss contribution of the EPIC model, and then performed a vulnerability evaluation and yield loss rate risk evaluation. The DSSAT model is a globally used crop modeling platform that has been widely used in agriculture in recent years []. It has a daily time step and considers the effects of moisture, nitrogen and sunshine length on crop growth and development []. The DSSAT-CERES (Crop Environment Resource Synthesis System)-Wheat model has been used for more applications in the Chinese region [,]. However, the DSSAT model is more sensitive to nitrogen than water, and its water module only considers the relationship between the possible water uptake and the actual transpiration, making it less accurate for simulating crop yield loss under different water stresses. Moreover, this model is mainly used to simulate the effect of different irrigation amounts on crop yield reduction based on field experiments or to analyze the risk of future climate change on crop yield reduction at the regional scale [,].
The DSSAT model is not sufficiently sensitive to moisture parameters when performing simulations, and few studies have used the correlation between the water stress and the yield loss rate to construct regionally gridded crop drought vulnerability curves. The CERES-Wheat model has been utilized less in constructing vulnerability curves using scenario simulation methods []. The main objectives of this study paper were (1) to make moisture improvements to the CERES-Wheat model, improve its moisture sensitivity and evaluate the modified model; (2) to set up a scenario simulation of winter wheat growth in the study area with a spatial resolution of 1 km × 1 km, construct a gridded vulnerability curve and characterize the vulnerability curve; and (3) to assess the drought risk of winter wheat in the study area. The results of this paper provide a quantitative estimation of the small-scale winter wheat drought loss risk and a basis for refined disaster prevention and mitigation strategies.
2. Data and Methods
2.1. Study Area
The Beijing-Tianjin-Hebei region (36°05′N–42°40′N, 113°27′E–119°50′E) was selected as the study area, which is bordered by the Bohai Sea to the east, the Taihang Mountains to the south, Shanxi to the west and Inner Mongolia to the north. The study area covers a total area of 216,000 km2, accounting for 2.2% of China’s national territory. Figure 1 shows the study area and distribution of winter wheat.
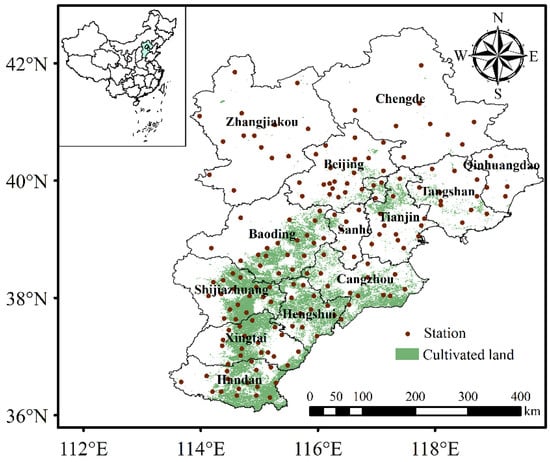
Figure 1.
The study area and distribution of winter wheat.
2.2. Data
In this paper, the extraction method of the winter wheat planting area was based on the decision tree method, using multi-temporal MODIS (Moderate-Resolution Imaging Spectroradiometer) data with different phenological characteristics and spectral differences of winter wheat and other vegetation, and completing the area stitching and projection conversion in MRT (MODIS Reprojection Tool) [,,]. The NDVI (normalized difference vegetation index) for October, November and May/June was selected to build a decision tree to extract the 2010 winter wheat planting area in the study area, which is in general agreement with other studies in the literature [].
The daily meteorological data from 1970 to 2019 were obtained from the China Meteorological Administration (CMA) (http://data.cma.cn/ (accessed on 20 January 2020)), including daily maximum temperature, daily minimum temperature, precipitation and sunshine hours data. Based on the sunshine hours, the daily solar radiation was calculated using the Angstrom–Prescott equation []. The meteorological data were spatially interpolated to a resolution of 1 km using the kriging method. The digital elevation model (DEM) data were obtained from the Shuttle Radar Topography Mission (SRTM) data provided by the Resource and Environmental Science and Data Center (http://www.redc.cn/Default.aspx (accessed on 11 October 2022)), with a spatial resolution of 1 km. The daily minimum temperature, daily maximum temperature, precipitation and sunshine hours data for the winter wheat growing period (15 November to 20 May) in the Beijing-Tianjin-Hebei region from 1970 to 2019 were integrated into each meteorological data for each growing period (49 growing periods). The meteorological data and DEM elevation data were graded and mapped using the natural breakpoint method. Figure 2 shows the meteorological data and DEM data for the wheat growing periods from 1970 to 2019 in the Beijing-Tianjin-Hebei region.
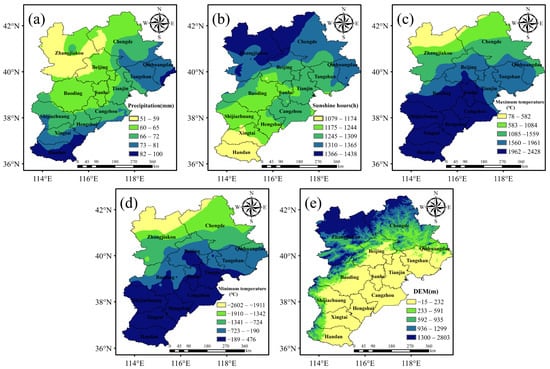
Figure 2.
Meteorological geographical data for the wheat growing periods from 1970 to 2019 partitioning in the Beijing-Tianjin-Hebei region: (a) average annual precipitation, (b) average annual sunshine hours, (c) average annual maximum temperature, (d) average annual minimum temperature and (e) DEM.
In this study, a dataset composed of crop growth and development and farmland soil moisture ten-day values from 1991 to 2010 from agrometeorological stations was utilized. The dataset was obtained from the China Meteorological Data Network (http://data.cma.cn/ (accessed on 11 April 2022)), including basic information about the stations (station number, name, latitude, longitude and elevation) and basic growth information about winter wheat.
Two datasets were used for the regional soil-scale simulations: a China dataset of soil properties for land surface modeling [], and a China dataset of soil hydraulic parameters’ pedotransfer functions for land surface modeling [,], both of which had a spatial resolution of 1 km. In this simulation, the model used 11 parameters, including the soil thickness, sand, powder, clay, gravel, bulk weight, pH, saturated water content, water content, bulk density, saturated hydraulic conductivity, field water-holding capacity and wilting coefficient.
2.3. Methods
2.3.1. Improving the Moisture-Sensitive DSSAT Model
The DSSAT, one of the most widely used crop growth simulation models worldwide, has distinct application characteristics [,]. The DSSAT family of models has some generic modules, but each crop has its own module []. The CERES-Wheat model is a sub-model embedded in the DSSAT, which is able to simulate various environmental (including weather and soil) and management factors (crop variety, growing conditions, fertilizer and irrigation) on a day-by-day basis. Transpiration is one of the most important mechanisms of plant water transport. The CERES-Wheat model uses the relative transpiration method to calculate the root water uptake as the minimum crop water requirement for the day and the model-simulated root water uptake [].
where is the actual plant water uptake on day , is the crop water requirement on day , and is the model-simulated root water uptake on day , is the coefficient of root uptake, , are the actual soil water content and wilting water content of the soil layer, is the root length density (cm/cm3) and is the thickness of the soil layer (cm).
The effect of the soil water content on plant transpiration and photosynthesis was taken into account. Coupling the stress mechanisms of the soil water content on plant transpiration and photosynthetic behavior, the relationship between the actual soil water availability and the critical soil water availability affecting photosynthetic production was used to construct the effect factor of the water stress on photosynthesis. This factor reflected the discounting effect of photosynthesis during the water deficit. The sensitivity of the model to water was improved by embedding the water stress effect factor on photosynthesis in the CERES-Wheat model:
where is the effect of water stress on photosynthesis, is the actual soil water content (cm3/cm3), is the wilting water content (cm3/cm3), is the critical soil water content (cm3/cm3) affecting photosynthetic production, is the proportion of soil water available for photosynthesis that is readily absorbed by plants and is the amount of water held in the field (cm3/cm3).
The DSSAT model source code is written in Fortran. In this paper, the stress mechanisms of the soil water content on plant transpiration and photosynthesis behavior were coupled, and the new effect factors were embedded into the soil evapotranspiration file. The modified model was used to simulate winter wheat growth.
2.3.2. Model Accuracy Evaluation and Parameter Calibration
In this paper, the CERES-Wheat model was improved by embedding factors for the effect of water stress on photosynthesis. The above-ground biomass and yield were simulated using the modified model, and the standard root mean square error (nRMSE) of the simulated and measured values was calculated and compared with the pre-model improvement. For different species of crops, the genetic parameters used in the DSSAT varied from variety to variety. It was necessary to calibrate the genetic parameters of the crop to the actual measurements before conducting the simulation. The parameter localization process was as follows. First, the daily meteorological data, soil data and management data for each prefecture were entered into the CERES-Wheat model. Second, the model-simulated phenological periods were compared with the actual measured phenological periods, and the generalized likelihood uncertainty estimation (GLUE) method was used to calculate the genetic parameters. This method was a direct debugging of a set of model parameters, and the degree of simulation between the simulation results and the measured results was the evaluation criterion. After several adjustments, parameters such as the vernalization coefficient, photoperiod response and grain-filling phase duration were finally determined.
2.3.3. Drought Hazard Intensity Index
In this paper, a spatial rasterization run of the CERES-Wheat model was used to simulate the growth of wheat on grid cells within the study area. The water stress indicator was defined as the difference between the actual and potential evapotranspiration []. The water stress was used as the main factor to describe the intensity of the drought-causing factors, as the magnitude of the water stress and the number of days of stress together affect the intensity of the drought in a crop during a reproductive period. The number of days of stress is the number of days when the moisture stress value is greater than 0, i.e., the number of days when the actual evapotranspiration is less than the potential evapotranspiration. Therefore, the water stress value and the number of days affected by water stress throughout the growing period were used to extract and construct the drought hazard intensity index (DHI) as an indicator for evaluating drought-causing factors in wheat:
where is the drought hazard intensity index for grid of year , is the water stress index at day , is the actual evapotranspiration (mm) and is the potential evapotranspiration (mm). The is in the range (0,1) and the closer the DHI is to 1, the drier it is.
2.3.4. Gridded Drought Vulnerability Curves
In order to determine the effect of water stress on the crop yield, two scenarios were set: sufficient nutrients and irrigation (scenario Y1) and no irrigation (scenario Y2). These two scenarios can be considered as reaching the point of excluding the effects of temperature stress on crop growth. The differences between the corresponding indicators simulated in scenario Y1 and scenario Y2 for the entire growing season were the loss due to the degree of exposure to drought.
where is the degree of yield loss due to drought throughout the growing period in grid of year ; and are the yield values in scenarios Y1 and Y2, respectively.
According to numerous studies, logistic functions can adequately describe the relationship between the DHI and the corresponding yield loss rate [,]. Therefore, a physical vulnerability curve was defined based on the DHI and the corresponding yield loss rate, and the relationship between the two was modeled using a logistic regression analysis as follows:
where is the yield loss rate of the evaluation unit, is the drought hazard intensity index of the evaluation unit and is the parameter to be fitted.
Three characteristic parameters were calculated to characterize the phase change based on the vulnerability curve function [], where these key points were calculated by deriving Equation (9) such that both the second and third order derivatives were zero. Table 1 lists the key point covariates of the vulnerability curves. The three characteristic parameters were as follows: (1) the starting point of rapid loss growth (V1) is the dividing point between the initial and developmental phases of the vulnerability curve, marking the shift from slow to rapid loss growth; (2) the inflection point of rapid loss growth (V2) is the peak point of loss growth, located in the middle of the developmental phase of the vulnerability curve; (3) the end point of rapid loss growth (V3) is the dividing point between the developmental and end phases of the vulnerability curve phase and the end of the vulnerability curve, marking the final slow growth phase of losses, which will remain at a relatively stable high value. In addition, the cumulative yield loss rate (CYL) was also used as one of the parameters for the evaluation of the vulnerability curve. The CYL was obtained by integrating Equation (9) over DHI values of (0, 1) to describe the overall vulnerability.

Table 1.
Key point covariates of the vulnerability curve.
2.3.5. Drought Risk Assessment
From a system engineering perspective, the drought risk can be considered to be a system []. In this paper, the exposure was set to 1 in areas planted with winter wheat and 0 in areas not planted with winter wheat, without considering drought mitigation capacity []. The winter wheat drought risk was a function of the drought hazard and vulnerability. The drought hazard was determined by the drought hazard intensity index and the vulnerability was determined by the yield loss rate determined by the vulnerability curve.
where represent drought risk, hazard, vulnerability and exposure, respectively; represents drought risk and is used to indicate the degree of regional drought risk. The higher the value, the greater the degree of drought risk and the greater the vulnerability to drought. represents the winter wheat drought hazard intensity index and is used to indicate the degree of drought disturbance; and is used to indicate winter wheat drought vulnerability: the higher the value, the greater the potential damage caused.
Table 2 presents the drought risk classification for winter wheat. The drought risk was classified into five classes based on the natural breakpoint method according to the 1970–2019 average risk index, and thus the drought risk in the study area was zoned.

Table 2.
Drought risk classification for winter wheat.
3. Results
3.1. Model Accuracy Evaluation and Parameter Localization
Table 3 and Figure 3 demonstrate the simulated and measured values of the above-ground biomass throughout the growing period before and after the model modification. The accuracy of the model in simulating both aboveground biomass and yield was improved after improving the water sensitivity by embedding the effect factor of the water stress on photosynthesis. For trial NO. 1, the modified model exhibited the greatest improvement relative to the pre-modification model, with a 4.89% reduction in error. In the example trial, the improved model in trial NO. 2 exhibited less improvement, with a 1.61% reduction in error (Table 3). The modified CERES-Wheat model simulated above-ground biomass values closer to the measured values than the pre-modification model simulation, with an average accuracy increase of 20.39%. The changes in the improved results compared to the pre-modification results generally began to manifest only halfway through the growing period and became more significant as the period progressed, providing a more accurate simulation of winter wheat growth.

Table 3.
The nRMSE of simulated and measured values before and after modification of the above-ground biomass model.
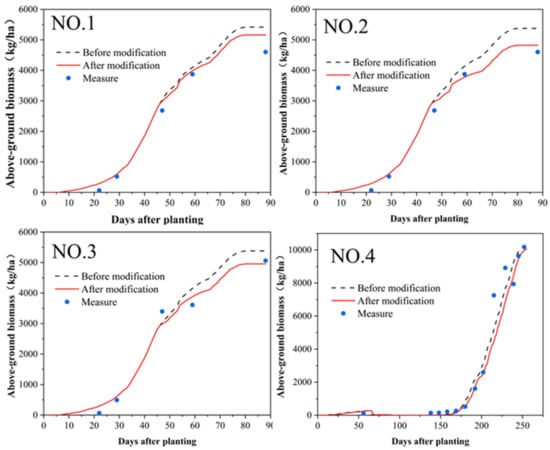
Figure 3.
Simulated and measured values of above-ground biomass throughout the growing period before and after model modification.
In terms of the yield, Figure 4 compares the measured and simulated yield values before and after the model modification. The nRMSE of the simulated value of the model before modification was 17.56%. The scatter of the simulated yield of the modified model and the actual value was closer to the 1:1 trend line, and the nRMSE was 15.55%, i.e., 11.45% more accurate than before the modification. This shows that the modified model simulated the yield variation of winter wheat more accurately.
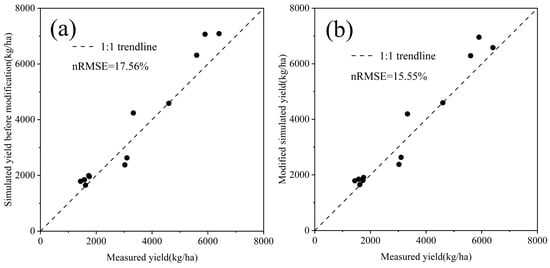
Figure 4.
(a) Original model and (b) modified model simulated yield values vs. measured values.
In the simulation of the study area, the GLUE method is used to determine the genetic parameters of the winter wheat in the study area based on the phenological data. Figure 5 shows the simulated anthesis and maturity stages compared to the measured values when the genetic parameters are localized. The localized model simulated both anthesis and maturity values close to the 1:1 trend line, with a correlation coefficient (R2) of 0.66 between the simulated anthesis and measured anthesis. The fit of the simulated maturity was better than that of the anthesis, with a correlation coefficient of 0.80 between the simulated and measured maturity. In general, the model achieved a good level of accuracy at this spatial scale.
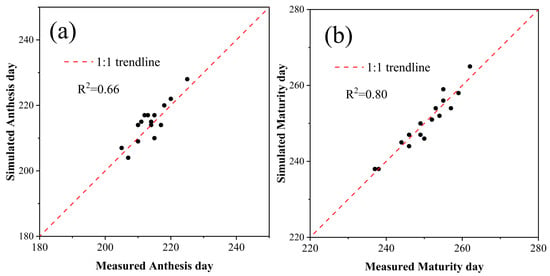
Figure 5.
Comparison of simulated and measured values for the (a) anthesis and (b) maturity stages after localization of genetic parameters.
3.2. Drought Hazard Intensity Assessment
In this paper, the interpolated meteorological data and genetic parameters of each component from 1970 to 2019 were input into the modified CERES-Wheat model using 1 km × 1 km as the evaluation unit. Without irrigation, the daily water stress indices for each evaluation unit in the study area were output, and finally the drought hazard intensity index (DHI) was calculated for each evaluation unit during a growing period. Figure 6 shows the spatial distribution of the DHI for winter wheat in a time series. In most years, the DHI for winter wheat exhibited a trend of high in the southwest and low in the southeast. The range of the multi-year average DHI across the region was 0.29, 0.61. Overall, most of the central region was the driest region in the entire study area, with a multi-year average DHI of greater than 0.5. In terms of the time series of the DHI in Beijing, Tianjin and Hebei, the drought hazard was higher in 1985 than in other years, with the highest DHI, and the DHI exceeded 0.6 in more than 50% of the wheat planted area. The areas with DHI values of greater than 0.57 in other years were mainly concentrated in Baoding. In 1990, 2000 and 2015, the DHI was lower, and the proportions of areas with DHI values of less than 0.30 were 35.86%, 34.75% and 42.75%, respectively. The distribution of the drought hazard intensity shows that the upper edge of the municipal boundary between Xingtai and Hengshui was the boundary, with a small intensity index below the dividing line and a large intensity index above the dividing line.
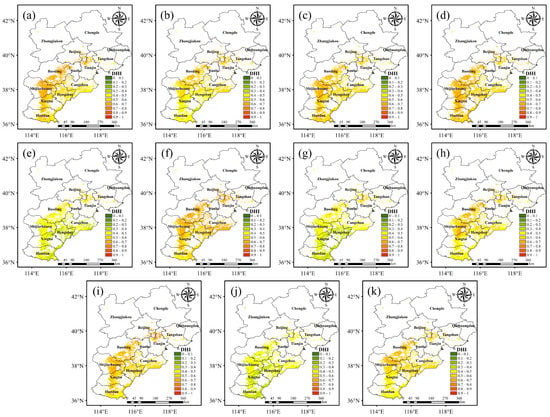
Figure 6.
The spatial distribution of the DHI for winter wheat in a time series: (a) 1970, (b) 1975, (c) 1980, (d) 1985, (e) 1990, (f) 1995, (g) 2000, (h) 2005, (i) 2010, (j) 2015 and (k) 2018.
Due to the small variation in the vulnerability curves for the same crop within a small area, zoning based on factors affecting the drought vulnerability was required to achieve a more accurate analysis of the DHI and vulnerability. In order to analyze the correlations between the annual average DHI and five factors, including precipitation, sunshine hours, daily maximum temperature, daily minimum temperature and DEM elevation data, a correlation analysis was conducted using the Pearson correlation coefficient. Table 4 shows the correlation coefficients between each element and the DHI.

Table 4.
Correlation coefficients of each factor with the drought hazard intensity index.
As each factor passed the confidence test, the natural breakpoint method was used to reassign values to the graded values, followed by aggregation of the various types of data and finally, the study area was divided into 12 zones. Figure 7 shows the partitioning of the winter wheat in the study area. Table 5 shows the proportions of the total winter wheat acreage in the different zones, with zones NO.7 and NO.8 accounting for the largest proportions (16.30% and 15.93%, respectively) and NO.1 accounting for the smallest proportion (only 0.14%).
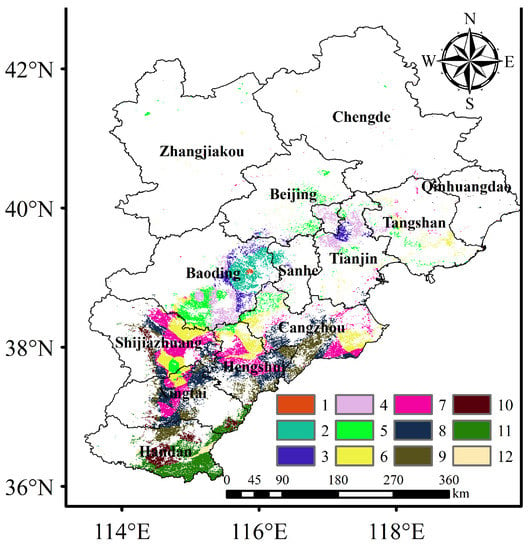
Figure 7.
Winter wheat zoning in the Beijing-Tianjin-Hebei region.

Table 5.
Winter wheat zoning in the Beijing-Tianjin-Hebei region.
3.3. Gridded Vulnerability Curves and Characterization
Based on the corrected genetic parameters, the modified CERES-Wheat model was used to simulate the growth of winter wheat in each grid under both the adequate irrigation and no irrigation scenarios. The vulnerability curves for the different partitions were fitted using a logistic approach based on the 48-year drought hazard intensity index and the corresponding yield loss rates. Since there was little variation in the vulnerability curves for the same crop within a small area, each grid within the partition fit this partition-fitted curve. Figure 8 presents scatter plots of the drought vulnerability curves and yield loss rates for the 12 sub-zones. In general, the fits for NO.10, 11 and 12 were better than those for the other sub-regions, with R2 values of 0.53, 0.50 and 0.58, respectively. Based on the scattered points in Figure 8, it can be seen that the distribution of the drought intensity in the other sub-zones was similar except for sub-regions 1 and 12, and the drought hazard indices were within the range of 0.4–0.6.
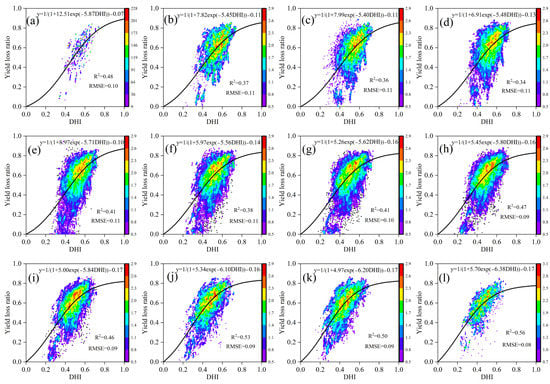
Figure 8.
Drought vulnerability curves for winter wheat in different sub-zones ((a–l) represent Nos. 1–12).
Figure 9 shows the covariates of the drought vulnerability characteristics of winter wheat in different sub-zones. The vulnerability curve was analyzed in terms of four aspects: the starting point of rapid loss growth, the inflection point of rapid loss growth, the end point of rapid loss growth and the cumulative loss rate. Figure 9 shows that there were some differences in the shape of drought vulnerability and the coordinates of the key points in different sub-zones. The drought hazard intensity and loss rate corresponding to the starting point of rapid loss growth were mainly distributed in the range of (0, 0.20) and (0, 0.15), the drought hazard intensity and loss rate corresponding to the inflection point of rapid loss growth were mainly distributed in the range of (0.25, 0.40) and (0.3, 0.4), and the drought hazard intensity and loss rate corresponding to the end point of rapid loss growth were mainly distributed in the range of (0.60, 0.70) and (0.50, 0.55). The range of loss rates was smaller compared to the drought hazard intensities. Overall, the coordinates of the rapid growth endpoints of losses were similar in different sub-zones, indicating that yield loss rates were similar in different zones when winter wheat drought hazard intensities were at their strongest. In terms of the starting point for rapid loss growth, the DHI1 of the starting point for rapid loss growth in NO.11 was 0.05. This indicated that the yield loss rate of winter wheat in this sub-zone entered a rapid growth phase after the intensity of the drought disaster exceeded 0.05, and the starting point for drought tolerance was lower than that in other sub-zones. In terms of the inflection point for rapid growth in losses, the DHI2 of the inflection point for rapid growth in NO.1 was 0.43. This indicated that the growth rate of winter wheat yield loss in this zone began to decelerate when the drought hazard intensity exceeded 0.43. In terms of the rapid growth endpoint, the DHI3 of the rapid growth endpoint for NO.1 was 0.65. This indicated that the growth rate of the winter wheat yield loss rate in this zone started to slow down significantly when the drought hazard intensity exceeded 0.65, and the loss rate was close to the peak. The DHI3 for the rapid growth endpoint of loss for NO.11 was 0.47. This indicated that the loss rate approached the peak of the zone at drought hazard intensities above 0.47, and that the loss rate of winter wheat was hit by the drought hazard and entered the high loss stage more quickly than in other areas. In terms of cumulative loss rates, the cumulative drought loss rates ranged from 49.00% to 54.00% for almost the entire region. The cumulative loss rate of 54.34% for the drought vulnerability curve of NO.11 indicated that winter wheat production was more vulnerable to drought hazards and that drought hazards hit production more strongly in this zone.
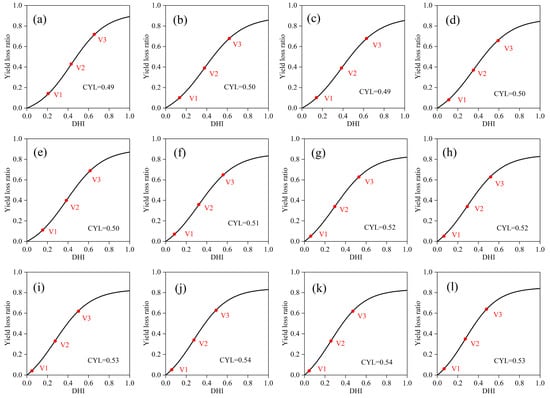
Figure 9.
Characteristic drought vulnerability curve parameters for winter wheat in different sub-zones ((a–l) represent Nos.1–12).
Based on the drought intensity indices under different return periods, the yield loss rates of winter wheat due to drought under different return periods were plotted in combination with the constructed drought vulnerability curves so as to assess the drought vulnerability of winter wheat. Figure 10 shows the distribution of the yield loss rates for fixed drought risk levels for winter wheat in the Beijing-Tianjin-Hebei region. For the case of the drought intensity index of once every 2 years, the yield loss rates were all distributed in the range of (0.3, 0.5): the ranges of (0.3, 0.4) and (0.4, 0.5) each accounted for about half of the total area. In addition, the distribution of the yield loss rates was more similar for the drought intensity index return periods of 20 and 25 years. When the drought intensity index had a return period of 50 years, the yield loss rate was more evenly distributed across the region, with yield loss rates of >0.7.
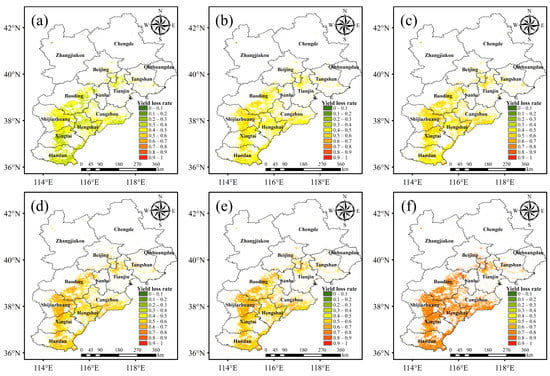
Figure 10.
Distribution of yield loss rates for fixed risk levels of winter wheat drought in the Beijing-Tianjin-Hebei region for return periods of (a) 2, (b) 5, (c) 10, (d) 20, (e) 25 and (f) 50 years.
3.4. Drought Risk Assessment
Figure 11 shows the distribution of the drought risk zones for winter wheat in the Beijing-Tianjin-Hebei region under different return periods. As can be seen from Figure 11a, the risk was in the low, relatively low and moderate risk classes for the entire region for a return period of once every 2 years. The relatively low risk level accounted for the largest area (75.71%), indicating that the lower drought risk had a 2-year return period in most areas. The moderate risk level accounted for 19.33% of the total area under winter wheat cultivation, mostly in Shijiazhuang and Baoding. The low risk level accounted for 7.03% of the total area, and was distributed in the southern part of Handan City, i.e., where moisture is more abundant. As can be seen from Figure 11b, for the 5-year return period, the proportion of the area with a moderate risk was the largest (62.69%), while the proportion of the area with a relatively low risk was 36.00%, and the boundary between the moderate and relatively low risk areas was the upper boundary between Xingtai and Hengshui cities. As can be seen from Figure 11c, the proportion of the area with moderate risk was the largest (75.00%) for a return period of 10 years. In addition, the area with relatively high drought risk levels exceeded the area with a relatively low risk for this return period. As can be seen in Figure 11d, the moderate risk and relatively high risk level areas each accounted for half of the total area for a return period of 25 years. As can be seen from Figure 11f, the entire region had a relatively high risk level for a return period of 50 years, with the relatively high and high drought risk areas accounting for 39.64% and 60.36%, respectively. Overall, the drought risk index decreased from west to east and from north to south, and the drought risk was higher. This indicates that the precipitation levels in the Beijing-Tianjin-Hebei region are not sufficient for normal winter wheat growth levels and artificial irrigation is necessary.
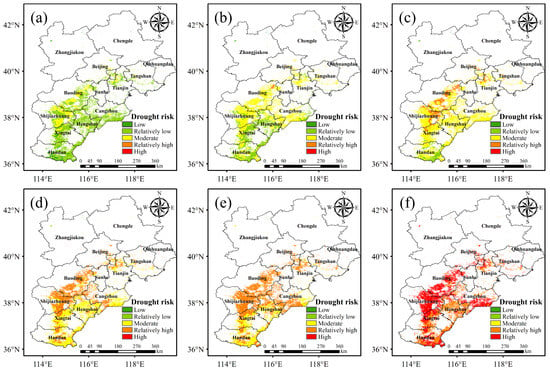
Figure 11.
Distribution of winter wheat drought risk zones in the Beijing-Tianjin-Hebei region for return periods of (a) 2, (b) 5, (c) 10, (d) 20, (e) 25 and (f) 50 years.
4. Discussion
4.1. Sensitivity Analysis of Model Parameters
The model parameters reveal the characteristics of crop growth and play a crucial role in the simulation results of the model [,]. Not only do the individual parameters themselves influence the model, but the parameters also work together to influence the model through their interactions []. Crop models often include many uncertain parameters that can lead to uncertainty in predictions. A parameter sensitivity analysis can provide a better understanding of the internal mechanisms and processes of crop growth models []. Relatively little literature focuses directly on the global sensitivity of the soil parameters of winter wheat in the DSSAT-CERES, especially under different moisture treatment conditions. Therefore, in this paper, a sensitivity analysis comparing the results of the model before and after modification of the DSSAT model parameters is conducted using the extended Fourier amplitude sensitivity test (EFAST) global sensitivity analysis method. This paper focuses on the sensitivity to water before and after the modification, so 10 soil parameters are selected and the relevant literature [,] is referenced to determine the range of values for each parameter (Table 6).

Table 6.
Meaning of soil parameters and range of values.
The CERES sensitivity response is assumed to differ between the fully irrigated and limited irrigation treatments []. Six irrigation scenarios are set up (Table 7), with irrigation levels categorized as fully irrigated (50 mm) and not irrigated. The irrigation level of 50 mm is divided into four drought periods: the greening period (I1), plucking period (I2), spike period (I3) and grouting period (I4). The meteorological data required for the model were obtained from Bazhou station, which is located in the more central part of the study area, and the observation data include precipitation, sunshine hours and daily maximum and minimum temperatures.

Table 7.
Irrigation treatments in winter wheat under different periods of irrigation treatment.
Figure 12 presents a plot of the global sensitivity indices for the maximum leaf area index, above-ground biomass and yield to 10 soil parameters under six different irrigation treatments. The sensitivity of the maximum leaf area index to each parameter differs before and after the modification under the different irrigation treatments, and the sensitivity indices change considerably. As can be seen from Figure 12a1, the leaf area index simulated using the modified model is more sensitive to SLLL, SSAT and SLOC, and the SSAT is the parameter with the largest sensitivity index. In contrast, the leaf area index is more sensitive to the SDUL and SLLL simulated using the original model, which is in agreement with He et al.’s study of the DSSAT model [,]. The modified model has the greatest change in the sensitivity index of the SSAT for the original model, with the mean sensitivity index increasing from 0.01 to 0.75, indicating that the modified model is more sensitive to the SSAT. In addition, the mean sensitivity index for the SLLL decreases from 0.79 to 0.53, and that for the SDUL decreases from 0.25 to 0.04, indicating that the model improvements are mainly focused on the SSAT. The sensitivity of the maximum leaf area index simulated using the modified model to the SSAT decreases as the irrigation satisfaction rate increases. The sensitivity indices of the above-ground biomass and yield of winter wheat simulated using the original and modified models exhibit similar patterns to the maximum leaf area index under different irrigation treatments. The above-ground biomass and yield simulated using the modified model are mainly sensitive to the SSAT and SLLL. The SSAT is the most sensitive parameter, accounting for more than 70% of the total effect, followed by the SLLL, which accounts for more than 50% of the total effect. In addition, the modified model has different sensitivity indices for the SLOC under different irrigation treatments.
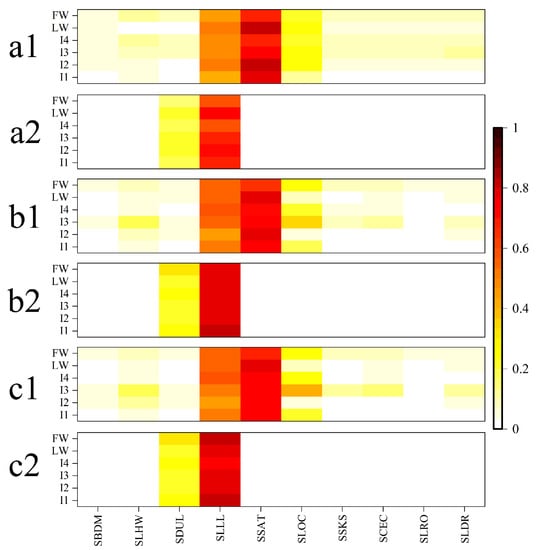
Figure 12.
Global sensitivity indices of the (a) maximum leaf area index, (b) above-ground biomass and (c) yield to 10 soil parameters simulated using the modified model and the original model for the 2015 wheat growing season, where 1 represents the improved model and 2 represents the original model.
4.2. Advantages and Limitations
DSSAT models have been used extensively to evaluate the impact of drought on agriculture. Most use meteorological factors in combination with the yield to evaluate the impacts of drought [,]. Itoh et al. [] used the DSSAT to simulate the yield changes in winter wheat and then investigated the correlations between the yield and the standardized precipitation evapotranspiration index (SPEI) and soil moisture deficit index (SMDI). Wei et al. [] used meteorological factors and the yield loss rates, combined with a semi-logarithmic function, to construct a drought loss risk curve. Historical meteorological data have also been combined with drought stress trials and input into the DSSAT model to evaluate the drought risk by directly outputting the yield loss rates []. However, few studies have used the DSSAT-CERES model for scenario simulation and thus for assessing crop drought vulnerability. In addition, the models lack accuracy in simulating areas where drought is frequent []. In this paper, the stress mechanisms of moisture and photosynthetic behavior are coupled to improve the CERES-Wheat model, and the modified model is used to assess the drought vulnerability of winter wheat. The modified model compensates for the simulation errors caused by the model’s moisture module, resulting in an improvement in the modified model’s simulation accuracy. The accuracies of both the above-ground biomass and yield simulations improved compared to the pre-modification results, with accuracy increases of 20.39% and 11.45%, respectively. In this study, vulnerability curves are fitted to different partitioned grids rather than to individual grids. In the future, vulnerability curves will be fit to each grid, but as there is little variation in the vulnerability curves for the same crop at small scales, it is more representative to use partitioned fits for vulnerability curves. In this paper, rainfed scenarios and fully irrigated scenarios are simulated, and multiple scenarios will be considered in future simulations.
5. Conclusions
In this study, the stress mechanisms of water and photosynthetic behavior were coupled to improve the CERES-Wheat model and enhance the accuracy of crop simulations. Based on the modified CERES-Wheat model for the simulation in the study area from 1970 to 2019, the drought vulnerability curve on a 1 km grid scale was constructed to quantitatively evaluate the drought hazard intensity index, vulnerability and drought risk of winter wheat. These results show that the accuracies of the above-ground biomass and yields simulated using the modified model increased by 20.39% and 11.45% compared to those of the original model. The drought hazard intensity index for winter wheat in the study area during 1970–2018 exhibited a trend of high in the southwest to low in the southeast in the time series. The shapes and characteristic parameters of the drought vulnerability curves differed somewhat between sub-areas. Furthermore, the drought risk index decreased from west to east and from north to south under different return periods, and the drought risk was higher. These results indicate that the precipitation levels in the Beijing-Tianjin-Hebei region are not sufficient for normal growth levels, and artificial irrigation is necessary. A method is proposed for an agricultural drought risk evaluation to provide a reference for mitigating the winter wheat drought risk.
Author Contributions
Conceptualization, H.Y. and Z.L.; methodology, Z.L.; software, Z.L.; validation, H.Y., Z.L. and Q.D.; formal analysis, H.Y.; resources, Z.D.; writing—original draft preparation, Z.L.; writing—review and editing, Z.L. and Q.D.; supervision, H.Y.; project administration, H.Y.; funding acquisition, H.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by the National Key R&D Program of China (grant number 2021YFC3000203).
Data Availability Statement
Not applicable.
Acknowledgments
The soil datasets were provided by the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn, accessed on 16 June 2023).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tan, C.; Yang, J.; Wang, X.; Qin, D.; Huang, B.; Chen, H. Drought disaster risks under CMIP5 RCP scenarios in Ningxia Hui Autonomous Region, China. Nat. Hazards 2020, 100, 909–931. [Google Scholar] [CrossRef]
- Yuan, X.; Zhou, Y.; Jin, J.; Wei, Y. Risk analysis for drought hazard in China: A case study in Huaibei Plain. Nat. Hazards 2013, 67, 879–900. [Google Scholar] [CrossRef]
- Zhang, Q.; Yao, Y.; Wang, Y.; Wang, S.; Wang, J.; Yang, J.; Wang, J.; Li, Y.; Shang, J.; Li, W. Characteristics of drought in Southern China under climatic warming, the risk, and countermeasures for prevention and control. Theor. Appl. Climatol. 2019, 136, 1157–1173. [Google Scholar] [CrossRef]
- Tsakiris, G. Drought Risk Assessment and Management. Water Resour. Manag. 2017, 31, 3083–3095. [Google Scholar] [CrossRef]
- Wei, Y.; Jin, J.; Jiang, S.; Ning, S.; Cui, Y.; Zhou, Y. Simulated Assessment of Summer Maize Drought Loss Sensitivity in Huaibei Plain, China. Agronomy 2019, 9, 78. [Google Scholar] [CrossRef]
- Kim, W.; Iizumi, T.; Nishimori, M. Global Patterns of Crop Production Losses Associated with Droughts from 1983 to 2009. J. Appl. Meteorol. Climatol. 2019, 58, 1233–1244. [Google Scholar] [CrossRef]
- González Tánago, I.; Urquijo, J.; Blauhut, V.; Villarroya, F.; De Stefano, L. Learning from experience: A systematic review of assessments of vulnerability to drought. Nat. Hazards 2016, 80, 951–973. [Google Scholar] [CrossRef]
- Singh, G. Salinity-related desertification and management strategies: Indian experience. Land Degrad. Dev. 2009, 20, 367–385. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, Q.; Yao, Y. Drought vulnerability assessment for maize in the semiarid region of northwestern China. Theor. Appl. Climatol. 2020, 140, 1207–1220. [Google Scholar] [CrossRef]
- Sivakumar, V.L.; Krishnappa, R.R.; Nallanathel, M. Drought vulnerability assessment and mapping using Multi-Criteria decision making (MCDM) and application of Analytic Hierarchy process (AHP) for Namakkal District, Tamilnadu, India. Mater. Today Proc. 2021, 43, 1592–1599. [Google Scholar] [CrossRef]
- Zhang, D.; Wang, G.; Zhou, H. Assessment on agricultural drought risk based on variable fuzzy sets model. Chin. Geogr. Sci. 2011, 21, 167–175. [Google Scholar] [CrossRef]
- Zhou, J.; Zhou, J.; Ye, H.; Ali, M.L.; Chen, P.; Nguyen, H.T. Yield estimation of soybean breeding lines under drought stress using unmanned aerial vehicle-based imagery and convolutional neural network. Biosyst. Eng. 2021, 204, 90–103. [Google Scholar] [CrossRef]
- An, J.; Li, W.; Li, M.; Cui, S.; Yue, H. Identification and Classification of Maize Drought Stress Using Deep Convolutional Neural Network. Symmetry 2019, 11, 256. [Google Scholar] [CrossRef]
- Jin, Z.; Zhuang, Q.; Tan, Z.; Dukes, J.S.; Zheng, B.; Melillo, J.M. Do maize models capture the impacts of heat and drought stresses on yield? Using algorithm ensembles to identify successful approaches. Glob. Change Biol. 2016, 22, 3112–3126. [Google Scholar] [CrossRef]
- Das Choudhury, S.; Saha, S.; Samal, A.; Mazis, A.; Awada, T. Drought stress prediction and propagation using time series modeling on multimodal plant image sequences. Front. Plant Sci. 2023, 14, 1003150. [Google Scholar] [CrossRef] [PubMed]
- Dai, M.; Huang, S.; Huang, Q.; Leng, G.; Guo, Y.; Wang, L.; Fang, W.; Li, P.; Zheng, X. Assessing agricultural drought risk and its dynamic evolution characteristics. Agric. Water Manag. 2020, 231, 106003. [Google Scholar] [CrossRef]
- Du, L.; Tian, Q.; Yu, T.; Meng, Q.; Jancso, T.; Udvardy, P.; Huang, Y. A comprehensive drought monitoring method integrating MODIS and TRMM data. Int. J. Appl. Earth Obs. Geoinf. 2013, 23, 245–253. [Google Scholar] [CrossRef]
- Thomas, T.; Jaiswal, R.K.; Galkate, R.; Nayak, P.C.; Ghosh, N.C. Drought indicators-based integrated assessment of drought vulnerability: A case study of Bundelkhand droughts in central India. Nat. Hazards 2016, 81, 1627–1652. [Google Scholar] [CrossRef]
- Kar, S.K.; Thomas, T.; Singh, R.M.; Patel, L. Integrated assessment of drought vulnerability using indicators for Dhasan basin in Bundelkhand region, Madhya Pradesh, India. Curr. Sci. 2018, 115, 338–346. [Google Scholar] [CrossRef]
- Zarafshani, K.; Maleki, T.; Keshavarz, M. Assessing the vulnerability of farm families towards drought in Kermanshah province, Iran. Geojournal 2020, 85, 823–836. [Google Scholar] [CrossRef]
- Zarafshani, K.; Sharafi, L.; Azadi, H.; Hosseininia, G.; De Maeyer, P.; Witlox, F. Drought vulnerability assessment: The case of wheat farmers in Western Iran. Glob. Planet. Chang. 2012, 98–99, 122–130. [Google Scholar] [CrossRef]
- Kim, H.; Park, J.; Yoo, J.; Kim, T. Assessment of drought hazard, vulnerability, and risk: A case study for administrative districts in South Korea. J. Hydro-Environ. Res. 2015, 9, 28–35. [Google Scholar] [CrossRef]
- Dabanli, I. Drought hazard, vulnerability, and risk assessment in Turkey. Arab. J. Geosci. 2018, 11, 538. [Google Scholar] [CrossRef]
- Tan, G.; Shibasaki, R. Global estimation of crop productivity and the impacts of global warming by GIS and EPIC integration. Ecol. Model. 2003, 168, 357–370. [Google Scholar] [CrossRef]
- Liu, J.G. A GIS-based tool for modelling large-scale crop-water relations. Environ. Model. Softw. 2009, 24, 411–422. [Google Scholar] [CrossRef]
- Liu, W.F.; Yang, H.; Folberth, C.; Wang, X.Y.; Luo, Q.Y.; Schulin, R. Global investigation of impacts of PET methods on simulating crop-water relations for maize. Agric. For. Meteorol. 2016, 221, 164–175. [Google Scholar] [CrossRef]
- Zhu, X.; Xu, K.; Liu, Y.; Guo, R.; Chen, L. Assessing the vulnerability and risk of maize to drought in China based on the AquaCrop model. Agric. Syst. 2021, 189, 103040. [Google Scholar] [CrossRef]
- Fawen, L.; Manjing, Z.; Yaoze, L. Quantitative research on drought loss sensitivity of summer maize based on AquaCrop model. Nat. Hazards 2022, 112, 1065–1084. [Google Scholar] [CrossRef]
- Keating, B.A.; Carberry, P.S.; Hammer, G.L.; Probert, M.E.; Robertson, M.J.; Holzworth, D.; Huth, N.I.; Hargreaves, J.N.G.; Meinke, H.; Hochman, Z.; et al. An overview of APSIM, a model designed for farming systems simulation. Eur. J. Agron. 2003, 18, 267–288. [Google Scholar] [CrossRef]
- Guo, H.; Wang, R.; Garfin, G.M.; Zhang, A.Y.; Lin, D.G.; Liang, Q.O.; Wang, J.A. Rice drought risk assessment under climate change: Based on physical vulnerability a quantitative assessment method. Sci. Total Environ. 2021, 751, 141481. [Google Scholar] [CrossRef]
- Wang, Z.; Jiang, J.; Ma, Q. The drought risk of maize in the farming-pastoral ecotone in Northern China based on physical vulnerability assessment. Nat. Hazards Earth Syst. Sci. 2016, 16, 2697–2711. [Google Scholar] [CrossRef]
- Li, R.; Tsunekawa, A.; Tsubo, M. Assessment of agricultural drought in rainfed cereal production areas of northern China. Theor. Appl. Climatol. 2017, 127, 597–609. [Google Scholar] [CrossRef]
- Wei, Y.; Jin, J.; Cui, Y.; Ning, S.; Fei, Z.; Wu, C.; Zhou, Y.; Zhang, L.; Liu, L.; Tong, F. Quantitative assessment of soybean drought risk in Bengbu city based on disaster loss risk curve and DSSAT. Int. J. Disaster Risk Reduct. 2021, 56, 102126. [Google Scholar] [CrossRef]
- Yassi, A.; Syaiful, S.A.; Ruslan, A.; Ridwan, I.; Andari, G. Simulation and production of soybean plant growth (Glycine max (L) Merrill) using the DSSAT model with different scenarios of water supply and compost. IOP Conf. Ser. Earth Environ. Sci. 2019, 343, 12014. [Google Scholar] [CrossRef]
- Yao, N.; Li, Y.; Liu, Q.; Zhang, S.; Chen, X.; Ji, Y.; Liu, F.; Pulatov, A.; Feng, P. Response of wheat and maize growth-yields to meteorological and agricultural droughts based on standardized precipitation evapotranspiration indexes and soil moisture deficit indexes. Agric. Water Manag. 2022, 266, 107566. [Google Scholar] [CrossRef]
- Paff, K.; Asseng, S. A Crop Simulation Model for Tef (Eragrostis tef (Zucc.) Trotter). Agronomy 2019, 9, 817. [Google Scholar] [CrossRef]
- Chen, X.G.; Li, Y.; Yao, N.; Liu, D.L.; Javed, T.; Liu, C.C.; Liu, F.G. Impacts of multi-timescale SPEI and SMDI variations on winter wheat yields. Agric. Syst. 2020, 185, 102955. [Google Scholar] [CrossRef]
- Shen, H.; Chen, Y.; Wang, Y.; Xing, X.; Ma, X. Evaluation of the Potential Effects of Drought on Summer Maize Yield in the Western Guanzhong Plain, China. Agronomy 2020, 10, 1095. [Google Scholar] [CrossRef]
- Hu, Y.; Liu, Y.; Tang, H.; Xu, Y.; Pan, J. Contribution of Drought to Potential Crop Yield Reduction in a Wheat-Maize Rotation Region in the North China Plain. J. Integr. Agric. 2014, 13, 1509–1519. [Google Scholar] [CrossRef]
- Li, Y.; Huang, H.; Ju, H.; Lin, E.; Xiong, W.; Han, X.; Wang, H.; Peng, Z.; Wang, Y.; Xu, J.; et al. Assessing vulnerability and adaptive capacity to potential drought for winter-wheat under the RCP 8.5 scenario in the Huang-Huai-Hai Plain. Agric. Ecosyst. Environ. 2015, 209, 125–131. [Google Scholar] [CrossRef]
- Jia, H.; Wang, J.; Cao, C.; Pan, D.; Shi, P. Maize drought disaster risk assessment of China based on EPIC model. Int. J. Digit. Earth 2012, 5, 488–515. [Google Scholar] [CrossRef]
- Vannoppen, A.; Gobin, A. Estimating Farm Wheat Yields from NDVI and Meteorological Data. Agronomy. 2021, 11, 946. [Google Scholar] [CrossRef]
- Tuvdendorj, B.; Zeng, H.; Wu, B.; Elnashar, A.; Zhang, M.; Tian, F.; Nabil, M.; Nanzad, L.; Bulkhbai, A.; Natsagdorj, N. Performance and the Optimal Integration of Sentinel-1/2 Time-Series Features for Crop Classification in Northern Mongolia. Remote Sens. 2022, 14, 1830. [Google Scholar] [CrossRef]
- Zhang, J.; He, Y.; Lin, Y.; Liu, P.; Zhou, X.; Huang, Y. Machine Learning-Based Spectral Library for Crop Classification and Status Monitoring. Agronomy 2019, 9, 496. [Google Scholar] [CrossRef]
- Wang, T.; Lv, C.; Yu, B. Assessing the Potential Productivity of Winter Wheat Using WOFOST in the Beijing-Tianjin-Hebei Region. J. Nat. Resour. 2010, 25, 475–487. (In Chinese) [Google Scholar]
- Li, H.; Lian, Y.; Wang, X.; Ma, W.; Zhao, L. Solar constant values for estimating solar radiation. Energy 2011, 36, 1785–1789. [Google Scholar] [CrossRef]
- Wei, S.; Dai, Y.; Liu, B.; Zhu, A.; Duan, Q.; Wu, L.; Ji, D.; Ye, A.; Yuan, H.; Zhang, Q.; et al. A China Dataset of Soil Properties for Land Surface Modeling; National Tibetan Plateau Data Center: Beijing, China, 2021. (In Chinese) [Google Scholar]
- Dai, Y.; Shangguan, W.; Duan, Q.; Liu, B.; Fu, S.; Niu, G. Development of a China Dataset of Soil Hydraulic Parameters Using Pedotransfer Functions for Land Surface Modeling. J. Hydrometeorol. 2013, 14, 869–887. [Google Scholar] [CrossRef]
- Shangguan, W.; Dai, Y. A China Dataset of Soil Hydraulic Parameters Pedotransfer Functions for Land Surface Modeling (1980); National Tibetan Plateau Data Center: Beijing, China, 2022. (In Chinese) [Google Scholar]
- Shen, H.; Gao, Y.; Guo, F.; Wang, Y.; Ma, X. A modified DSSAT-CERES model for simulating summer maize growth under film mulching. Agron. J. 2021, 113, 4819–4831. [Google Scholar] [CrossRef]
- Timsina, J.; Humphreys, E. Performance of CERES-Rice and CERES-Wheat models in rice-wheat systems: A review. Agric. Syst. 2006, 90, 5–31. [Google Scholar] [CrossRef]
- Jones, J.W.; Hoogenboom, G.; Porter, C.H.; Boote, K.J.; Batchelor, W.D.; Hunt, L.A.; Wilkens, P.W.; Singh, U.; Gijsman, A.J.; Ritchie, J.T. The DSSAT cropping system model. Eur. J. Agron. 2003, 18, 235–265. [Google Scholar] [CrossRef]
- Camargo, G.G.T.; Kemanian, A.R. Six crop models differ in their simulation of water uptake. Agric. For. Meteorol. 2016, 220, 116–129. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.; Wang, C.; Cui, L.; Yan, D. Risk early warning of maize drought disaster in Northwestern Liaoning Province, China. Nat. Hazards 2014, 72, 701–710. [Google Scholar] [CrossRef]
- Geerts, S.; Raes, D.; Garcia, M.; Taboada, C.; Miranda, R.; Cusicanqui, J.; Mhizha, T.; Vacher, J. Modeling the potential for closing quinoa yield gaps under varying water availability in the Bolivian Altiplano. Agric. Water Manag. 2009, 96, 1652–1658. [Google Scholar] [CrossRef]
- Wu, Y.; Guo, H.; Zhang, A.; Wang, J. Establishment and characteristics analysis of a crop-drought vulnerability curve: A case study of European winter wheat. Nat. Hazards Earth Syst. Sci. 2021, 21, 1209–1228. [Google Scholar] [CrossRef]
- Guo, H.; Zhang, X.; Lian, F.; Gao, Y.; Lin, D.; Wang, J.A. Drought Risk Assessment Based on Vulnerability Surfaces: A Case Study of Maize. Sustainability 2016, 8, 813. [Google Scholar] [CrossRef]
- Ma, H.; Malone, R.W.; Jiang, T.; Yao, N.; Chen, S.; Song, L.; Feng, H.; Yu, Q.; He, J. Estimating crop genetic parameters for DSSAT with modified PEST software. Eur. J. Agron. 2020, 115, 126017. [Google Scholar] [CrossRef]
- Raymundo; Sexton-Bowser, S.; Ciampitti, I.A.; Morris, G.P. Crop modeling defines opportunities and challenges for drought escape, water capture, and yield increase using chilling-tolerant sorghum. Plant Direct. 2021, 5, e349. [Google Scholar] [CrossRef]
- Varella, H.; Guérif, M.; Buis, S. Global sensitivity analysis measures the quality of parameter estimation: The case of soil parameters and a crop model. Environ. Model. Softw. 2010, 25, 310–319. [Google Scholar] [CrossRef]
- Ma, H.; Wang, J.; Liu, T.; Guo, Y.; Zhou, Y.; Yang, T.; Zhang, W.; Sun, C. Time series global sensitivity analysis of genetic parameters of CERES-maize model under water stresses at different growth stages. Agric. Water Manag. 2023, 275, 108027. [Google Scholar] [CrossRef]
- Li, Z.; Jin, X.; Liu, H.; Xu, X.; Wang, J. Global sensitivity analysis of wheat grain yield and quality and the related process variables from the DSSAT-CERES model based on the extended Fourier Amplitude Sensitivity Test method. J. Integr. Agric. 2019, 18, 1547–1561. [Google Scholar] [CrossRef]
- Kassie, B.T.; Asseng, S.; Rotter, R.P.; Hengsdijk, H.; Ruane, A.C.; Van Ittersum, M.K. Exploring climate change impacts and adaptation options for maize production in the Central Rift Valley of Ethiopia using different climate change scenarios and crop models. Clim. Chang. 2015, 129, 145–158. [Google Scholar] [CrossRef]
- He, W.; Yang, J.Y.; Zhou, W.; Drury, C.F.; Yang, X.M.; Reynolds, W.D.; Wang, H.; He, P.; Li, Z.T. Sensitivity analysis of crop yields, soil water contents and nitrogen leaching to precipitation, management practices and soil hydraulic properties in semi-arid and humid regions of Canada using the DSSAT model. Nutr. Cycl. Agroecosyst. 2016, 106, 201–215. [Google Scholar] [CrossRef]
- DeJonge, K.C.; Ascough, J.C.; Ahmadi, M.; Andales, A.A.; Arabi, M. Global sensitivity and uncertainty analysis of a dynamic agroecosystem model under different irrigation treatments. Ecol. Model. 2012, 231, 113–125. [Google Scholar] [CrossRef]
- Zhuo, W.; Huang, H.; Gao, X.; Li, X.; Huang, J. An Improved Approach of Winter Wheat Yield Estimation by Jointly Assimilating Remotely Sensed Leaf Area Index and Soil Moisture into the WOFOST Model. Remote Sens. 2023, 15, 1825. [Google Scholar] [CrossRef]
- Itoh, Y.; Bröcker, M.J.; Sekine, S.; Söll, D.; Yokoyama, S. Dimer-Dimer Interaction of the Bacterial Selenocysteine Synthase SelA Promotes Functional Active-Site Formation and Catalytic Specificity. J. Mol. Biol. 2014, 426, 1723–1735. [Google Scholar] [CrossRef]
- Geng, S.M.; Yan, D.H.; Yang, Z.Y.; Zhang, Z.B.; Yang, M.J.; Kan, G.Y. Characteristics Analysis of Summer Maize Yield Loss Caused by Drought Stress in the Northern Huaihe Plain, China. Irrig. Drain. 2018, 67, 251–268. [Google Scholar] [CrossRef]
- Ran, H.; Kang, S.; Hu, X.; Li, S.; Wang, W.; Liu, F. Capability of a solar energy-driven crop model for simulating water consumption and yield of maize and its comparison with a water-driven crop model. Agric. For. Meteorol. 2020, 287, 107955. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).