Real-Time Tomographic Inversion of Truncated Ionospheric GNSS Radio Occultations

Abstract

This paper presents a new way of combining Abel inversion and the Chapman model with a linearly increasing scale height to retrieve ionospheric electron density vertical profiles from truncated-sounding radio-occultation data. A linear Vary–Chap model is used to cover the blind region due to data truncation, with parameters estimated by enumeration of the possible values in a grid centered around a set of parameters compatible with ionospheric physics. The resulting electron density is estimated with its corresponding error from the linear least-squares solution presenting the smaller post-fit residual on the input GNSS carrier-phase measurements. The results, tested on a set of representative GNSS RO measurements obtained by COSMIC/FORMOSAT-3, show that this method can retrieve EDVPs with a predominant absolute and relative error of ${10}^{10}{\mathrm{e}}^{-}{\mathrm{m}}^{-3}$ and 5%, respectively, and in less than 10 s per profile, which makes this method suitable for near real-time applications in upcoming missions such as EUMETSAT Polar System-Second Generation.

1. Introduction

Global navigation satellite system (GNSS) radio-occultation (RO) missions, such as GPS/MET (Hernández-Pajares et al. [1]), CHAMP (Jakowski et al. [2]), COSMIC/ FORMOSAT-3 (Olivares-Pulido et al. [3]), GRACE, PAZ (Cardellach et al. [4]), FY3C/GNOS RO (Mao et al. [5]), and the future EPS-SG (Hernández-Pajares et al. [6]), are of great benefit to ionospheric sounding and modeling. As the GNSS signal travels along the line of sight (LOS) between the GNSS transmitter and the receiver on board the low earth orbiter (LEO) satellite, it scans the ionospheric regions above and below the maximum ionospheric electron density peak (see Figure 1). The effect of the ionosphere on the GNSS signal (i.e., the ionospheric delay) changes in accordance with the vertical electron density (VED). Consequently, it is possible to directly retrieve the vertical electron density profile (VEDP) from the GNSS signal with inversion techniques (Hernández-Pajares et al. [1], Pedatella et al. [7]). This is based on the fact that the dual-frequency measurements provided by GNSS receivers on board LEOs in RO scenarios, with a negative elevation angle, are very sensitive to vertical gradients.

In general, VEDP retrieval techniques are limited to the sounded regions, which span the top and bottom sides of the ionosphere. However, some missions presently under preparation, e.g., EPS-SG, instead of sounding the whole range of the top and bottom sides of the ionosphere, will only scan the regions below the LEO orbit, thus providing truncated measurements and, consequently, posing a problem for full VEDP retrieval. For example, the new EPS-SG satellites orbiting at 817 km height are conceived for neutral atmospheric sounding, thus focusing their measurements in the region closer to the earth’s surface. Nevertheless, this also provides opportunities for ionospheric sounding, although with RO measurements whose impact parameter (the shortest distance from the straight line that contains both the receiver and transmitter coordinates to the center of the earth) is below 500 km (see layout in Figure 1).

The problem with truncated radio-occultation data is twofold: (1) the missing observations may account for a significant part of the RO measurements (e.g., more than 40% for EPS-SG), and (2) the long length through the blind area reduces the accuracy of the RO inversion at the usual starting point of the inversion, affecting the whole profile estimation. Regarding the modeling of the blind region, the Chapman model has usually been a first attempt to model the missing data (Chapman [8]). However, Olivares-Pulido et al. [3] have advocated more realistic models in order to be consistent with the constraints imposed by observational data from the COSMIC/FORMOSAT-3 mission. Furthermore, Hernández-Pajares et al. [6] introduced the Vary–Chapman extrapolation technique (VCET), and showed that provided the electron density profile is well known below a given ceiling height, e.g., ∼500 km, it is possible to extrapolate the VEDP further up. The VCET is based on the predominant linear relationship between the scale height, H, and the temperature observed above the maximum ionospheric electron density peak (Olivares-Pulido et al. [3]). Moreover, such a linear model is in good agreement with the climate models presented in Prol et al. [9], which are based on top-sounding data as well (Prol et al. [10]).

In order to develop VEDP retrieval techniques with truncated RO data sets, Lyu et al. [11] combined the linear Vary–Chap model presented in Olivares-Pulido et al. [3] with an Abel inversion method to determine the VEDP with topside-truncated data sets of dual-frequency RO GNSS measurements, gathered from the LEO height, e.g., ∼800 km. Lyu et al. [11] proposed two models, different from each other in terms of accuracy and computational speed. The most accurate model, the Abel–Vary–Chap hybrid (AVHIRO) method consists of the simultaneous computation of the bottom and top sides by the Powell minimization method. However, the high computational load (above 20 min in a standard I7 processor system under Linux) prevents its usage at the operational level. Alternatively, the simple estimation method for the retrieval of the electron density profiles (SEEIRO) only requires around 15 s per profile, at the expense of yielding profiles of lower resolution than those computed by AVHIRO.

This work presents a completely new approach regarding the AVHIRO method (hereinafter AVHIROv2), with the goal of high accuracy and computational speed compliant with the constraints of operational services. The structure of this work is as follows: the second section introduces the details of AVHIROv2 and the modeling of the blind region. The third section presents the results and discusses the performance of AVHIROv2 with respect to the most accurate of the previous models: AVHIRO. The final fourth section presents the conclusions.

Figure 1. From Lyu et al. [11]. Layout of the truncated RO measurements scenario studied in this work, showing up, as a conceptual example, some transmitter-receiver rays illuminating three layers, in green, magenta, and orange colors. The height interval used to fit the Vary–Chap model is also represented (light blue color). The LEO orbit at around 800 km height is represented in red, and the illuminated part of the ionosphere is placed between the top and lowest thick blue lines, indicating the electron density peak height by means of the middle thick blue line.

Figure 1. From Lyu et al. [11]. Layout of the truncated RO measurements scenario studied in this work, showing up, as a conceptual example, some transmitter-receiver rays illuminating three layers, in green, magenta, and orange colors. The height interval used to fit the Vary–Chap model is also represented (light blue color). The LEO orbit at around 800 km height is represented in red, and the illuminated part of the ionosphere is placed between the top and lowest thick blue lines, indicating the electron density peak height by means of the middle thick blue line.

2. Modified AVHIRO Model

The model presented in this work is a completely new update of the AVHIRO model introduced by Lyu et al. [11], hence the name AVHIROv2. AVHIRO consists of the combination of the Abel inversion method with a linear Vary–Chap model introduced in Olivares-Pulido et al. [3]. The Abel inversion solves the electron density for the impact parameter height range corresponding to the LOS between the receiver and transmitter. The input GNSS data consist of carrier-phase measurements only; therefore, the ambiguity term is also estimated along with the electron density. Figure 1 provides the layout for stating the system of equations that link observational data (namely, the carrier phases $L_1$ and $L_2$, both measured in Frequencies $f_1$ and $f_2$, respectively) with the known crossing lengths $l_{j,i}$ of the corresponding jth line of sight that crosses each given ith layer (with geocentric height $r\in [r_i-\Delta r/2,r_i+\Delta r/2]$), and with the unknown electron density values $N_e$ and carrier-phase ambiguity in length units $B_I\equiv B_1-B_2$. The ionospheric combination of $L_1$ and $L_2$, $L_I$, which removes all the non-dispersive terms, e.g., geometric distance, clocks, tropospheric delay, and yields the following equation with S, the slant total electron content (STEC), and the ambiguity term $B_I$:

$$L_I=\alpha ·S+B_I,$$

(1)

where $\alpha =1.05\times {10}^{-17}$ m${}^3$, and the STEC term, S, corresponds to the integration of the ionospheric electron density, $N_e$, along the line of sight between the receiver and the satellite as follows:

$$S={\int }_{{\overrightarrow{r}}_{rec}}^{{\overrightarrow{r}}_{sat}}{N}_{e}dl.$$

(2)

The tomographic model assumes that the electron density is constant within voxels (or pixels in 2D), e.g., Hernández-Pajares et al. [12]. With this hypothesis, Equation (2) can be numerically computed as the summation of the electron density within each ionospheric layer times the segment of the LOS within that layer, namely:

$$S=\sum _{i=1}^{i=N}{N}_{e,i}·l_i,$$

(3)

where the index i runs over the number ionospheric pierce points (IPPs) of the GNSS signal, and N is the total number of IPPs. Note that, for negative elevation angles, the illuminated layers are typically pierced twice. Therefore, by assuming spherical symmetry, Equation (3) can be modified accordingly, thus yielding the following expression:

$$S=2\sum _{i=1}^{i=N/2}{N}_{e,i}·l_i,$$

(4)

with i being now the index that runs over the number of layers sounded by the GNSS signal. It is important to emphasize that the conditions that yield Term 2 in Equation (4) are twofold: spherical symmetry and negative elevation angle. Alternatively, a more general separability assumption with the electron density replaced by the shape function could be considered (Hernández-Pajares et al. [1]).

Replacing the STEC term in Equation (1) with Equation (4) leads to the following equation, which holds for each observation:

$$L_I=2\alpha \left(\sum _i{N}_{e,i}·l_i\right)+B_I,$$

(5)

where, for sake of simplicity, we have omitted the upper value of the IPPs index, N. Note, however, that Equation (5) implicitly assumes that all the ionospheric regions above and below the LEO orbit are sounded. Nevertheless, the goal of this work is to retrieve VEDP from incomplete radio-occultation GNSS data. Therefore, the observational data $L_I$ must be corrected by a term corresponding to the STEC within the blind region, $S_b$, thus yielding the following expression, with the summation restricted to the bottom illuminated layers:

$${\widehat{L}}_I\equiv L_I-\alpha S_b=2\alpha \left(\sum _i{N}_{e,i}·l_i\right)+B_I.$$

(6)

Finally, in this context, we can express in detail the ionospheric combination of carrier phases, within the region where observations are available, as:

$${\left({\widehat{L}}_I\right)}_j=2\alpha \left(\sum _i{N}_{e,i}·l_{j,i}\right)+B_I,$$

(7)

where the index j corresponds to the numbering for the measurements. Therefore, expanding over the measurements index, the following system of equations unfolds:

$$\begin{array}{ccc}{\left({\widehat{L}}_I\right)}_1\hfill & =& B_I\hfill \\ {\left({\widehat{L}}_I\right)}_2\hfill & =& \alpha \left(2l_{2,1}{N}_{e,1}\right)+B_I\hfill \\ {\left({\widehat{L}}_I\right)}_3\hfill & =& \alpha \left(2l_{3,1}{N}_{e,1}\right)+B_I\hfill \\ \hfill & \dots & \\ {\left({\widehat{L}}_I\right)}_j\hfill & =& \alpha \left(2l_{j,1}{N}_{e,1}+2l_{j,2}{N}_{e,2}+\dots +2l_{j,i}{N}_{e,i}\right)+B_I\hfill \\ \hfill & \dots & \\ {\left({\widehat{L}}_I\right)}_p\hfill & =& \alpha \left(2l_{p,1}{N}_{e,1}+2l_{p,2}{N}_{e,2}+\dots +2l_{p,M}{N}_{e,M}\right)+B_I\hfill \end{array}$$

(8)

where M is the number of layers that the model defines, i.e., up to 500 km, and p is the $p_{th}$ impact parameter, sorted in descending order. Note that M must be such that redundancy is possible in each and all of the layers, to allow for error estimation by linear least-squares (LLS) method. For example, in the system deployed in Equation (8), ${\left({\widehat{L}}_I\right)}_2$ and ${\left({\widehat{L}}_I\right)}_3$ are observations belonging to the same layer ($N_1$).

Now, the question is how to estimate $S_b$. For this, we used the following method:

1.

Within a grid, for each value of the electron density peak and height, scale height, and scale height vertical gradient ($N_m,h_m,H_0$, and $\frac{\partial H}{\partial h}$, respectively), compute $S_b$ as the integration of the electron density according to the Vary–Chap model (see a detailed introduction in Section 2 of Olivares-Pulido et al. [3] and corresponding equations):

$$S_b={\int }_{h_{bl}}^{h_{bu}}{N}_{e}dh$$

(9)

$$N_e=N_m{e}^{\frac{1}{2}(1-z-e^{-z})},wherez=\frac{h-h_m}{H}$$

(10)

$$H=\frac{\partial H}{\partial h}(h-h_m)+H_0$$

(11)

where $h_{bl}$ and $h_{bu}$ are the lower and upper height boundaries for the blind region, respectively; $N_m$ is the maximum electron density; h is the height, $h_m$, the height where $N_m$ is located; and two parameters for the linear Vary–Chap model, $H_0$ and the derivative of the scale height with height, $\frac{\partial H}{\partial h}$.

Note the difficulty involved in estimating with gradient-based search the proposed model, exclusively based on carrier-phase data (without background model) and estimating the carrier phase ambiguity (see more details in Lyu et al. [11]), in contrast to other models (Healy and Culverwell [13]).

2.

Secondly, for each tuple $\left(N_m,h_m,H_0,\frac{\partial H}{\partial h}\right)$ in the possible values of the grid nodes, an LLS solution is computed for Equation (6).

3.

The optimal EDVP is the one, among the different grid values of $S_b$, with the smallest LLS RMS for Equation (8).

4.

Finally, AVHIROv2 results can be extrapolated into the top side with the VCET method (Hernández-Pajares et al. [6]), thus providing a combined method that retrieves the full EDVP with truncated data. Note that the extrapolation is computed by means of the new EDVP obtained in the previous point.

In order to compute the above algorithm, it is necessary to previously set up the size of the grid. This grid is implemented in accordance with the ranges of the parameters $N_m$, $h_m$, $H_0$, and $\frac{\partial H}{\partial h}$. The ranges for those parameters are estimated as follows:

• The ranges for $N_m$ and $h_m$ are centered around values computed by an empirical model, summarized in the next section, and based on correlations between the ambiguous but precise observation of maximum STEC values provided by $L_I$ and the corresponding impact parameter, with $N_m$ and $h_m$.
• The ranges for $H_0$ and $\frac{\partial H}{\partial h}$ are centered around typical values of 30 km and $0.05$, respectively, as per Olivares-Pulido et al. [3].

2.1. The Radio-Occultation-Based F2-Peak Empirical Model (GRID2EDP)

Central values for the ranges of $N_m$ and $h_m$ are estimated by means of the GNSS raw ionospheric radio-occultation data to the empirical electronic density peak (GRID2EDP) empirical model, presented as well in this paper.

GRID2EDP is a simple model that captures the correlations empirically found between:

• $h_m$ and the impact parameter of RO STEC peak $h_{Sm}$;
• $N_m$ and the difference of STEC at the peak vs. the value at minimum RO elevation, $S_m-S\left(E_{min}\right)$.

The last correlation is computed by linear regression. Thus, GRID2EDP directly provides a guess of the electron density peak value and height from the raw RO measurements and corresponding impact parameters.

In order to assess the hypothesis of linear correlation between such parameters, we have conducted a cross-correlation analysis with a data set that contains representative weeks within a solar cycle. In this regard, the data selected are measurements taken from the COSMIC/FORMOSAT-3 RO within four representative weeks in the previous solar cycle (see Figure 2 and Hernández-Pajares et al. [6] for details).

The testing data sets consist of four representative weeks, excepting one or two days per week that were used for characterizing the GRID2EDP performance: Day 267 of Year 2011 (from Scenario 1, Days 261–267), 358 of Year 2011 (from Scenario 2, Days 352–358), 240 of Year 2008 (from Scenario 3, Days 234–240), and Days 348 and 349 of Tear 2006, the ones with high geomagnetic activity in Scenario 4 (Days 346–352).

Figure 3 shows the cross-correlation between $h_m$ and $h_{Sm}$ (top), and between $N_m$ with $S_m$ (bottom). The plot at the top-left side indicates that the parameter of the impact of the ionospheric combination $L_I=L_1-L_2$ of phase COSMIC/FORMOSAT-3 measurements between 6500 km and below 6870 km of the geocentric distance (to avoid global $S_m$ due to sporadic E-layer) follows a rather linear trend with respect to $h_m$.

Similarly, the plot at the bottom-left side depicts a linear trend correlation between $\Delta S\equiv S_m-S\left(E_{min}\right)$ and $N_m$, where $E_{min}$ is the minimum (most negative) elevation angle.

The data set (also known as the training set) on both plots on the left side was used for the computation of the arithmetic mean and the standard distribution (blue dots and blue bars, respectively), with 5 km binned data of the impact parameter for $h_m$ vs. $h_{Sm}$ (top-left plot), and also for the computation of the linear regression of $N_m$ vs. $\Delta S\equiv S_m-S\left(E_{min}\right)$ (bottom-left plot). The testing data set on the right-side plots (red dots) show good agreement with those empirical parameters.

Finally, since the correlation between $S_m$ and $N_m$ is invariant under shifting of S by a constant, we conducted the cross-correlation analysis with $\Delta S\equiv S_m-S\left(E_{min}\right)$, thus avoiding the computation of the ambiguity term $B_I$.

The $h_m$ intervals for the grid are centered around the values estimated with GRID2EDP and span $3\sigma$ to take into account the limited number of ROs and associated lack of Gaussianity for some intervals. We used eleven values for each parameter (including their central values) evenly distributed within their intervals. Regarding the $N_m$ vs. $S_m-S\left(E_{min}\right)$ component of GRID2EDP, we computed a single linear regression over the training dataset and associated standard deviations.

Table 1. Example of configuration parameters for the grid set up. $N_{m,0}$ and $h_{m,0}$ are the central values for the intervals of $N_m$ and $h_m$, respectively.

Parameter	Range or Value
$N_m$	11 values in $[N_{m,0}-3{\sigma }_{N_m},N_{m,0}+3{\sigma }_{N_m}]$
$h_m$	11 values in $[h_{m,0}-3{\sigma }_{h_m},h_{m,0}+3{\sigma }_{h_m}]$
$H_0$	Cappellari model (Equation (12))
$\frac{\partial H}{\partial h}$	0.075

summarizes the values for the ranges of $N_m$ and $h_m$.

2.2. Model Initialization

The developed model is initialized with the parameters presented in Table 1. It also summarizes the configuration of the grid used in this study. Regarding the initial scale height $H_0$, the Cappellari model (Cappellari et al. [14]) can be used as a central value, which relates the scale height $H_0$ and $h_m$ as follows:

$$H_0=\frac{1}{2}\left(h_m-50\right).$$

(12)

Finally, the scale height derivative $\frac{\partial H}{\partial h}$ is set to a typical value of 0.075 (Olivares-Pulido et al. [3]). Adopting these values as those around which the exploration is performed speeds up the computations without compromising the accuracy.

3. Results

The performance analysis of AVHIROv2 was carried out in the height range corresponding to the observation impact parameter heights (below 500 km), where AVHIROv2 provides not only electron densities but also the corresponding error estimates. For this analysis, we have considered a set of +3000 representative radio occultations corresponding to the four weeks of COSMIC/FORMOSAT-3 GNSS RO measurements studied in Hernández-Pajares et al. [6] after an artificial truncation at 500 km impact height. Those four weeks are representative of the previous solar cycle (see Figure 2).

In order to assess the performance of AVHIROv2, we computed the RMS for its relative difference with respect to the profile obtained with the same model but with the complete (i.e., non-truncated) COSMIC/FORMOSAT-3 GNSS RO measurements: the spherical symmetry-based Abel inversion (SAI). The reason for selecting SAI is that it does not require any external product, as opposed, for example, to the improved Abel inversion (IAI, Hernández-Pajares et al. [1]). IAI is a bit more precise (see IAI and SAI assessment vs. external ionosonde measurements at Hernández-Pajares et al. [1]), but it would require global ionospheric maps of VTEC (GIMs) computed and assessed externally within the International GNSS Service (IGS) (see Hernández-Pajares et al. [6,15], Roma-Dollase et al. [16]).

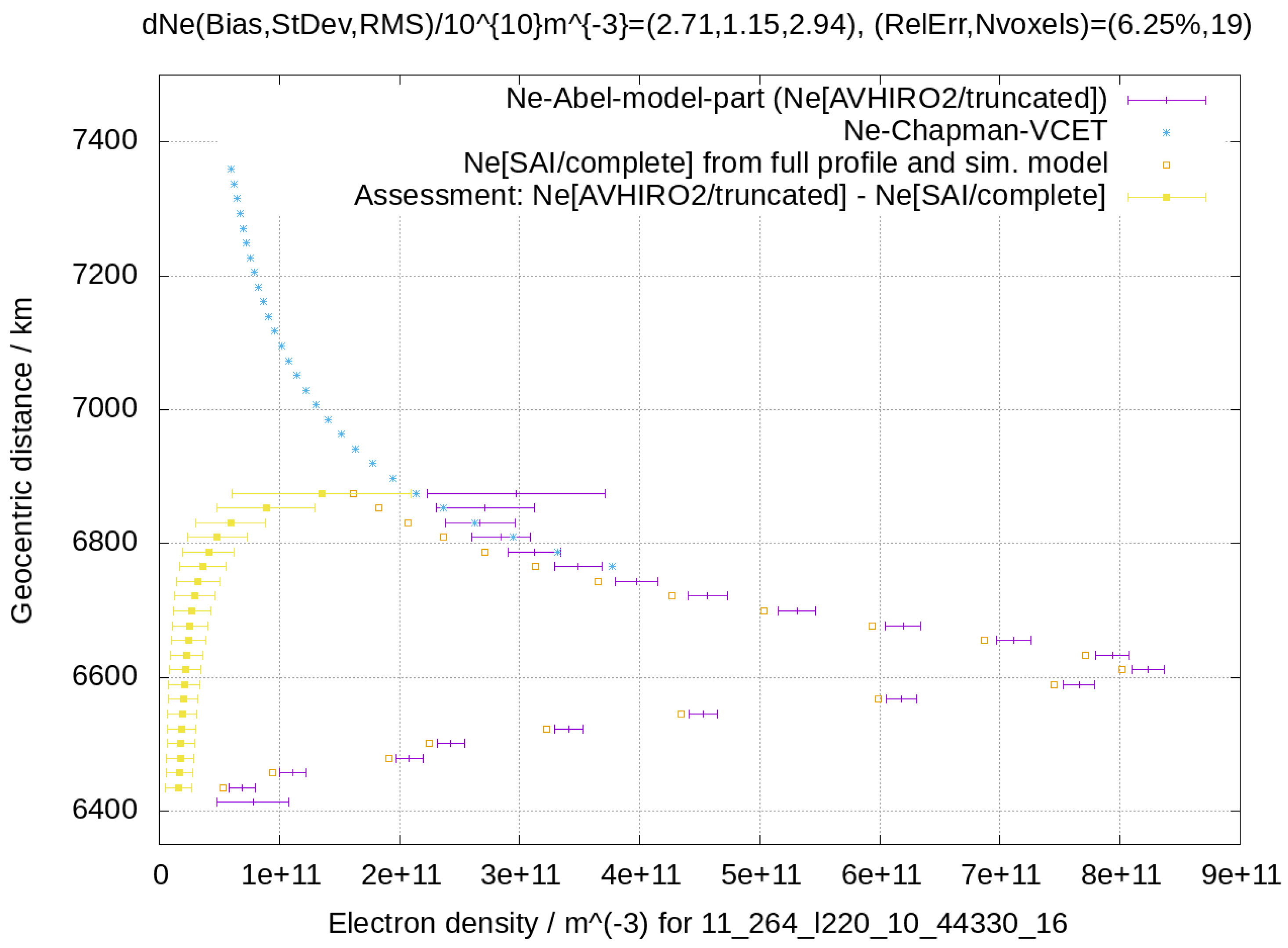
Figure 4 shows the VEDP (magenta points) obtained by the technique proposed in this work. The differences with respect to the full-profile SAI (empty orange squares) are always slightly outside the AVHIROv2 VEDP error bars, and they increase around the truncated height. However, the VCET profile (blue stars) stays within the error bars of the AVHIROv2 profile, except for the points at the beginning and at the end of the region where both VEDPs overlap.

Figure 5 shows the RMS histograms for the absolute (left) and relative (right) RMS differences between AVHIROv2 and SAI VEDPs. The mode for the absolute RMS is less than $2.5\times {10}^{10}{\mathrm{e}}^{-}/{\mathrm{m}}^3$, and the relative RMS is centered around $5\%$. The distribution is skewed due to some outliers that appear for some profiles near the top side. For example, there are some outliers shown in Figure 4. However, the AVHIROv2 error estimation allows for their detection (horizontal bars along the magenta VEDP shown in Figure 4).

Finally, Figure 6 shows that the AVHIROv2 error estimation is sensitive to the actual error, i.e., the error estimates are typically reliable indicators of the actual errors.

Table 2. Summary of performance in the selected COSMIC radio occultations truncated to 500 km of highest impact parameter with pros and cons of AVHIRO and AVHIROv2. Best values of each row are highlighted in bold.

	AVHIRO	AVHIROv2
Number of common radio occultations	3426 (+90% of the total ones)
Ne bias/$({10}^{10}$ m${}^{-3}$)	1.249	1.298
Ne standard deviation/$({10}^{10}$ m${}^{-3}$)	4.072	3.234
Ne RMS/$({10}^{10}$ m${}^{-3}$)	4.260	3.485
Ne Relative Accuracy	15.54%	12.71%
CPU time per preprocessed RO	20 min	1.2 s
Suitable for NRT service?	No	Yes
Required external information?	No	No
Required inputs	2-frequency GPS carrier-phase RO meas.,
	predicted GPS and LEO orbits (both methods)

summarizes the performance of inverting truncated ROs below 500 km vs. the result with the complete ROs for AVHIROv2 and AVHIRO (SEEIRO performs worse than AVHIRO; therefore, it has not been considered for the comparison. For further details, see Lyu et al. [11]). The comparison has been carried out over the common representative set of 3426 radio occultations and without removing any outliers in both datasets.

AVHIRO presents a bias value of $1.298\times {10}^{10}$ m${}^{-3}$, which is about 3% smaller than the one from AVHIROv2, $1.249\times {10}^{10}$ m${}^{-3}$. Nevertheless, the standard deviation and RMS ($3.234\times {10}^{10}$ m${}^{-3}$ and $3.485\times {10}^{10}$ m${}^{-3}$, respectively) are $26\%$ and $22\%$ smaller for AVHIROv2 than for AVHIRO.

Another major difference is the CPU time required per preprocessed RO. In this regard, the computational speed developed by AVHIROv2 is three orders of magnitude higher than the computation performed by AVHIRO. This implies that AVHIROv2 is suitable for NRT services, as opposed to AVHIRO, and none of them require external information. In other words, they all are autonomous models, with GPS carrier-phase measurements being the only input data needed.

4. Conclusions

In this work, we have presented AVHIROv2, which combines in an accurate and fast fashion the Abel inversion method with a linear Vary–Chap model for the retrieval of ionospheric electron density vertical profiles from truncated RO data for the bottom side of the ionosphere, i.e., below 500 km.

The linear Vary–Chap model provides the means to estimate the contribution of the blind region, $S_b$, to the observed STEC. In this regard, it has been crucial the implementation of a new proposed empirical model (GRID2EDP), which directly provides a guess of the electron density peak value and height from the raw RO measurements and corresponding impact parameters. Then, with the parameters estimated by GRID2EDP, the Abel inversion retrieves the ionospheric electron density vertical profile at the bottom side with a very low computational burden.

We have compared the results in a common representative dataset with the most accurate previous method, AVHIRO. The results show that although the error bias is 3% larger for AVHIROv2 than for AVHIRO, the overall error RMS is 22% smaller for the former. Namely, the Ne error for AVHIROv2 is 3.485 $\times {10}^{10}$ m${}^{-3}$ (12.7%), whereas, for AVHIRO, the Ne error is 4.260 $\times {10}^{10}$ m${}^{-3}$ (15.5%). Furthermore, the computational speed is three orders of magnitude higher for AVHIROv2 than for AVHIRO.

Although some profiles present some deviations near the top side, which are well represented by the estimated error, AVHIROv2 does not present extreme transition effects formerly reported in some cases with AVHIRO.

Finally, AVHIROv2 results can be extrapolated into the top side with the VCET method (Hernández-Pajares et al. [6]), thus providing a combined method that retrieves the full EDVP with truncated data.

Future improvements, such as implementing the separability hypothesis (Hernández-Pajares et al. [1,6]), would require the availability of global ionospheric maps of VTEC in real time, such as those computed in the International GNSS Service (IGS, Liu et al. [17]).