Uncertainty of CYGNSS-Derived Heat Flux Variations at Diurnal to Seasonal Time Scales over the Tropical Oceans
Abstract
1. Introduction
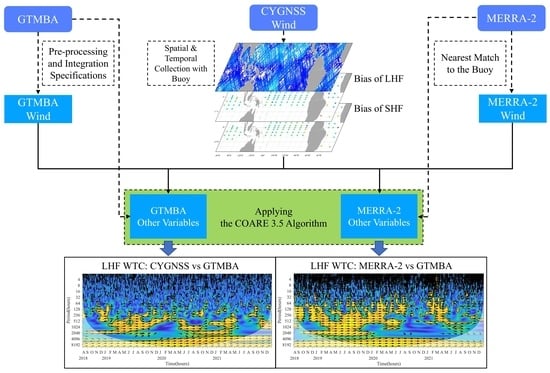
2. Data and Methods
2.1. Turbulent Heat Flux Calculation
2.2. CYGNSS Wind Product
2.3. MERRA-2 Reanalysis Data
2.4. GTMBA Buoy Array Data
2.5. The Design of Sensitivity Experiments
2.6. Major Evaluation Indicators
3. Results
3.1. Statistical Metrics of the Heat Fluxes Derived from Different Datasets
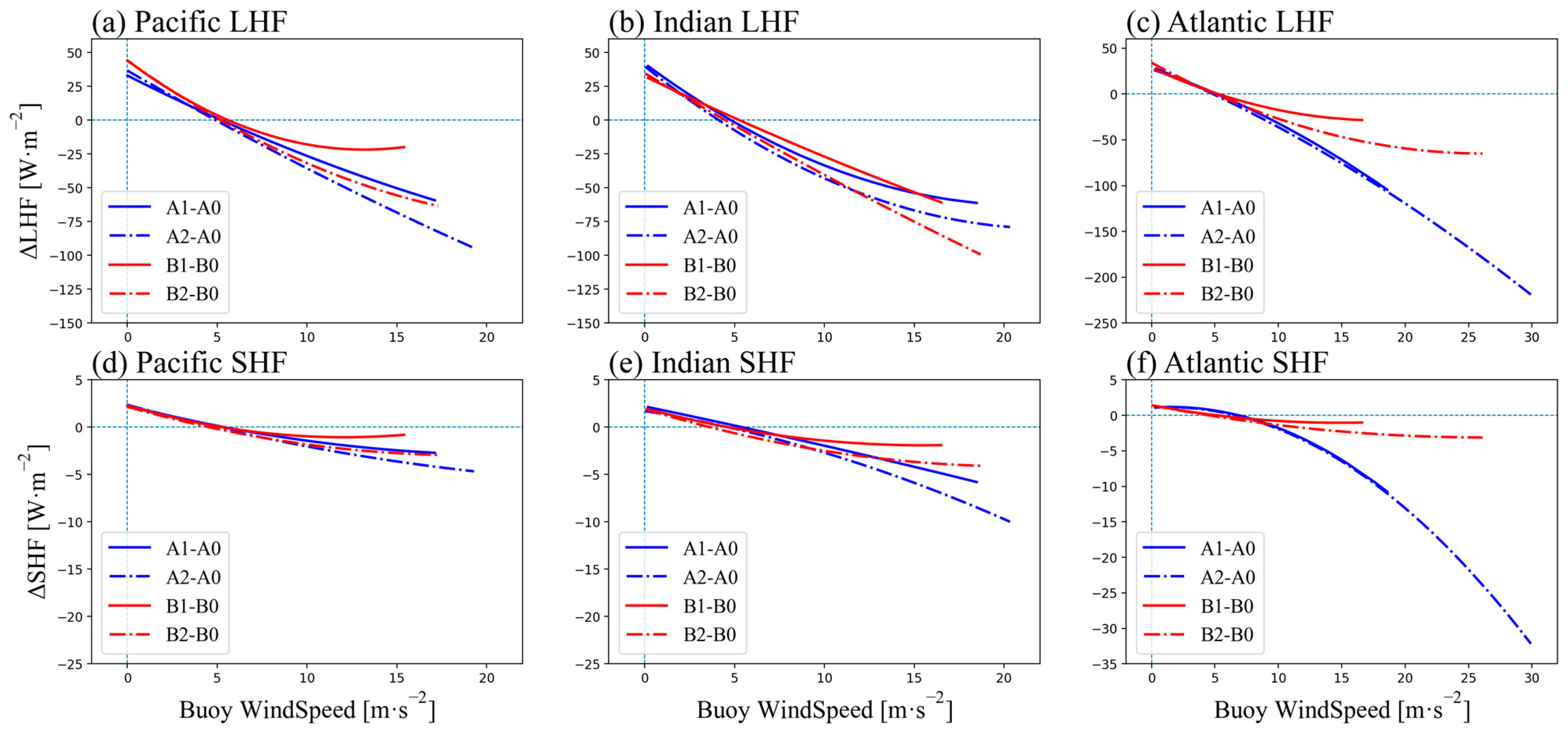
3.2. Sensitivities of Different Input Wind Speed Datasets for the Heat Flux Calculation
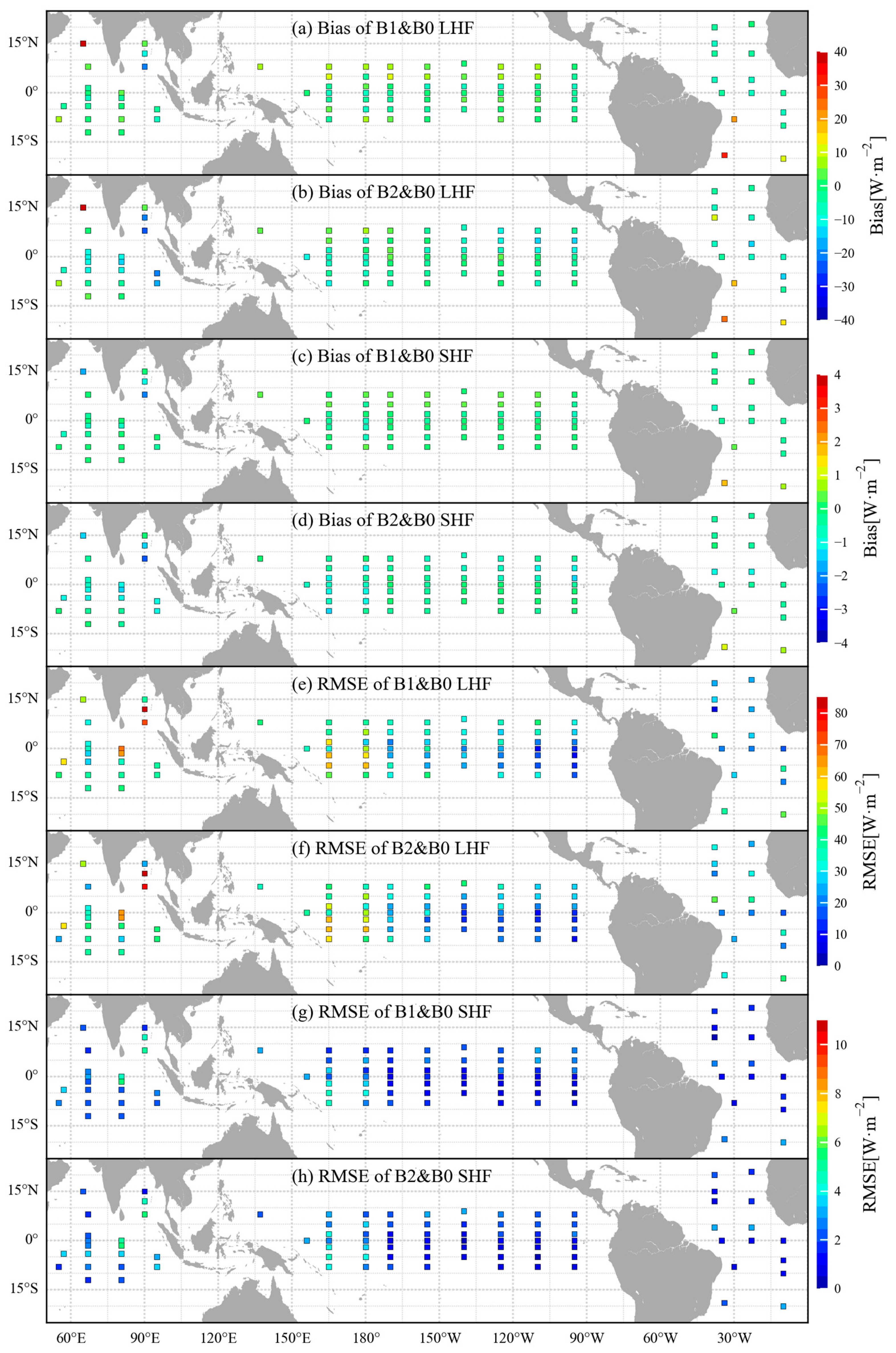
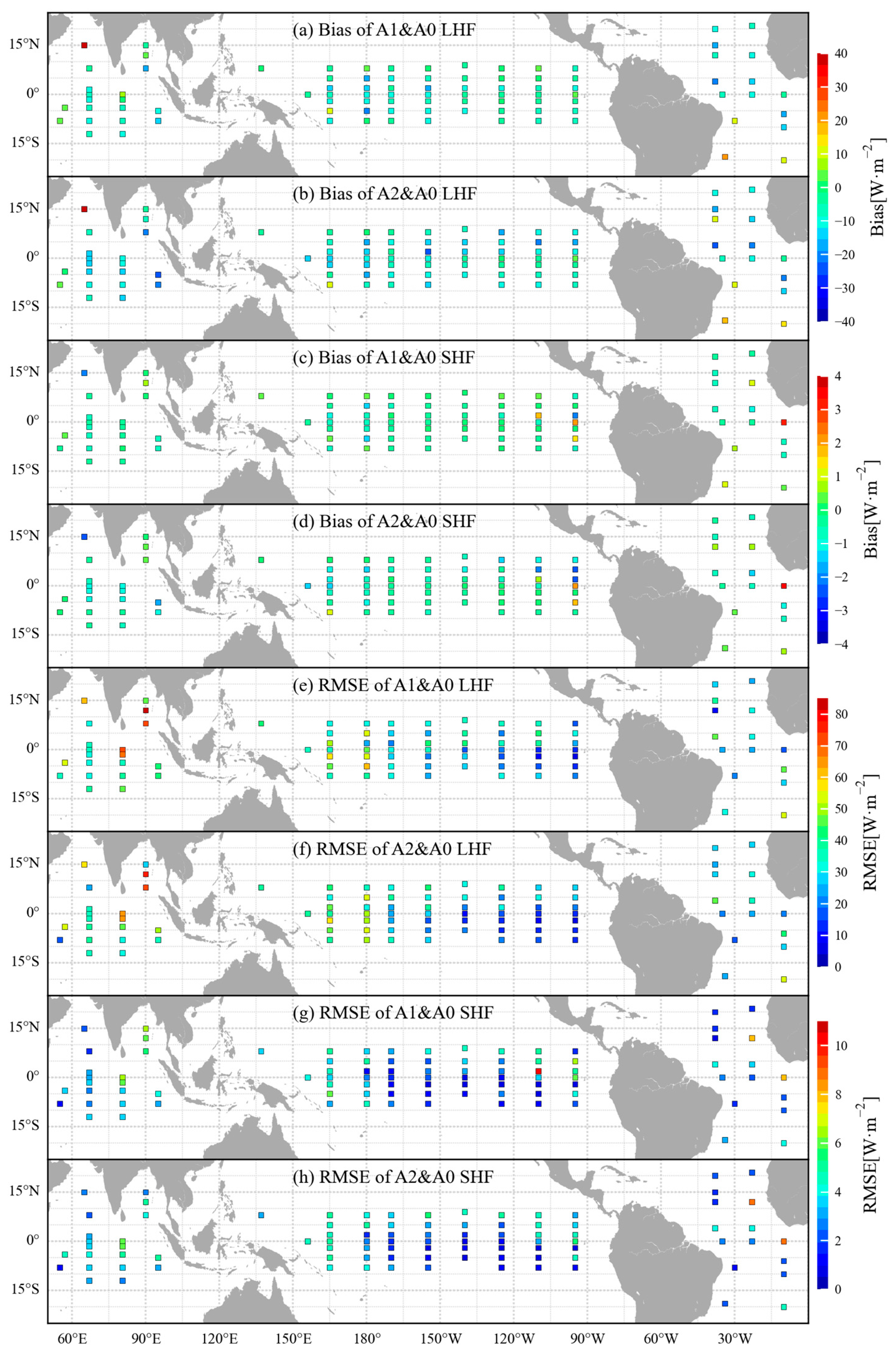
3.3. Spatial Distribution of Mean Bias and RMSE in the Heat Fluxes
3.4. Wavelet Coherence Analysis of the Hourly Heat Fluxes
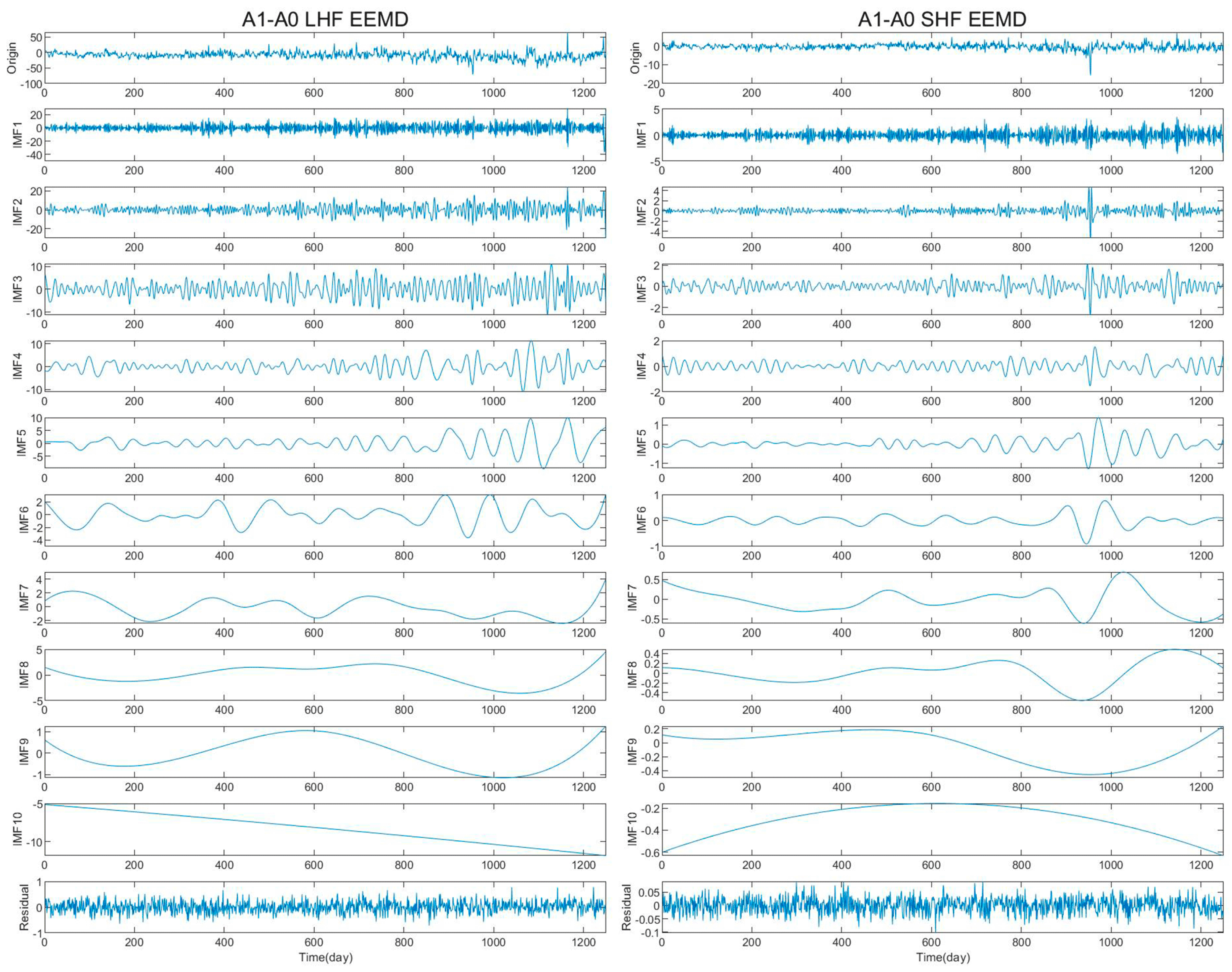
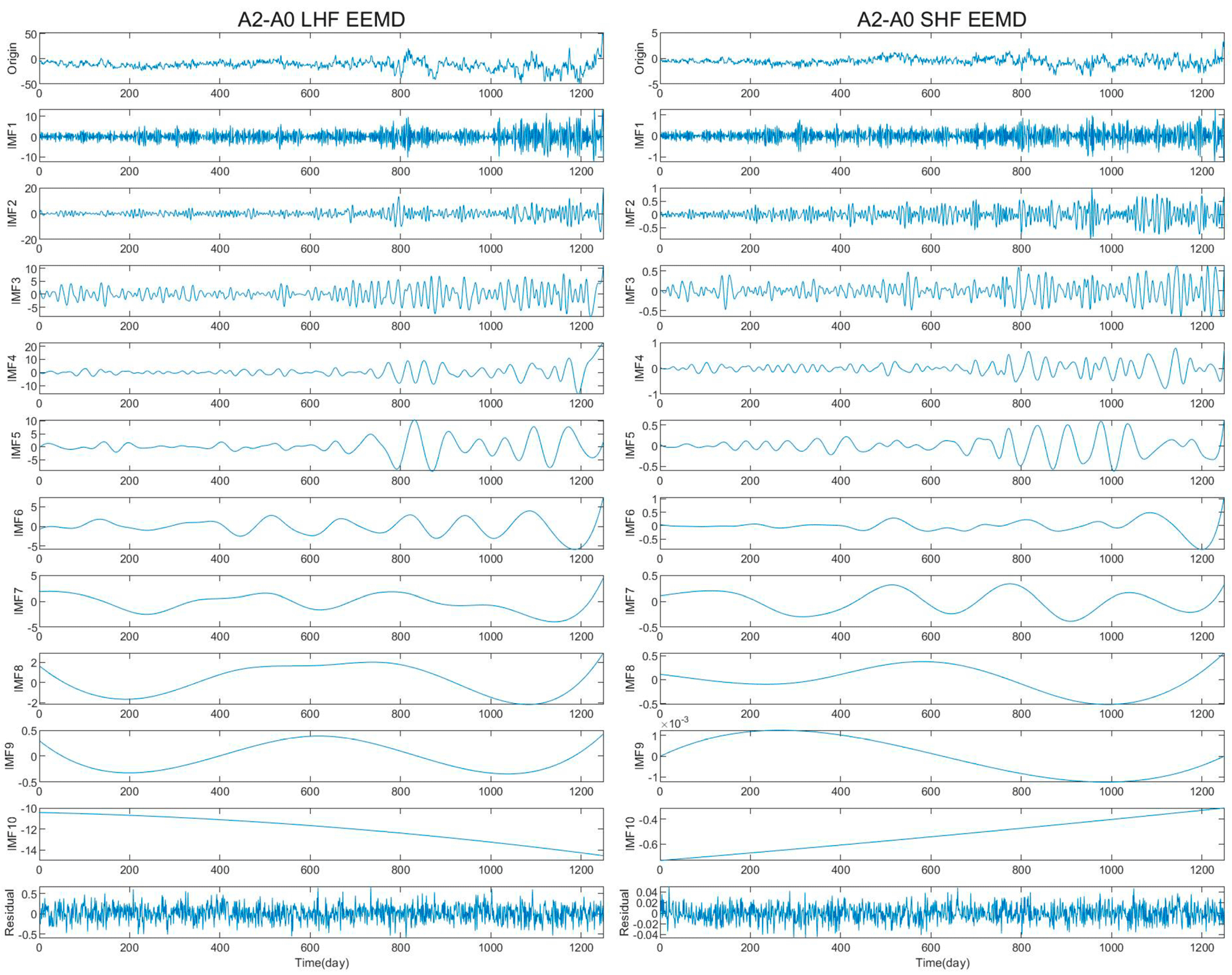
3.5. Contributions of Wind Speed and Other Variables to Heat Fluxes Calculation
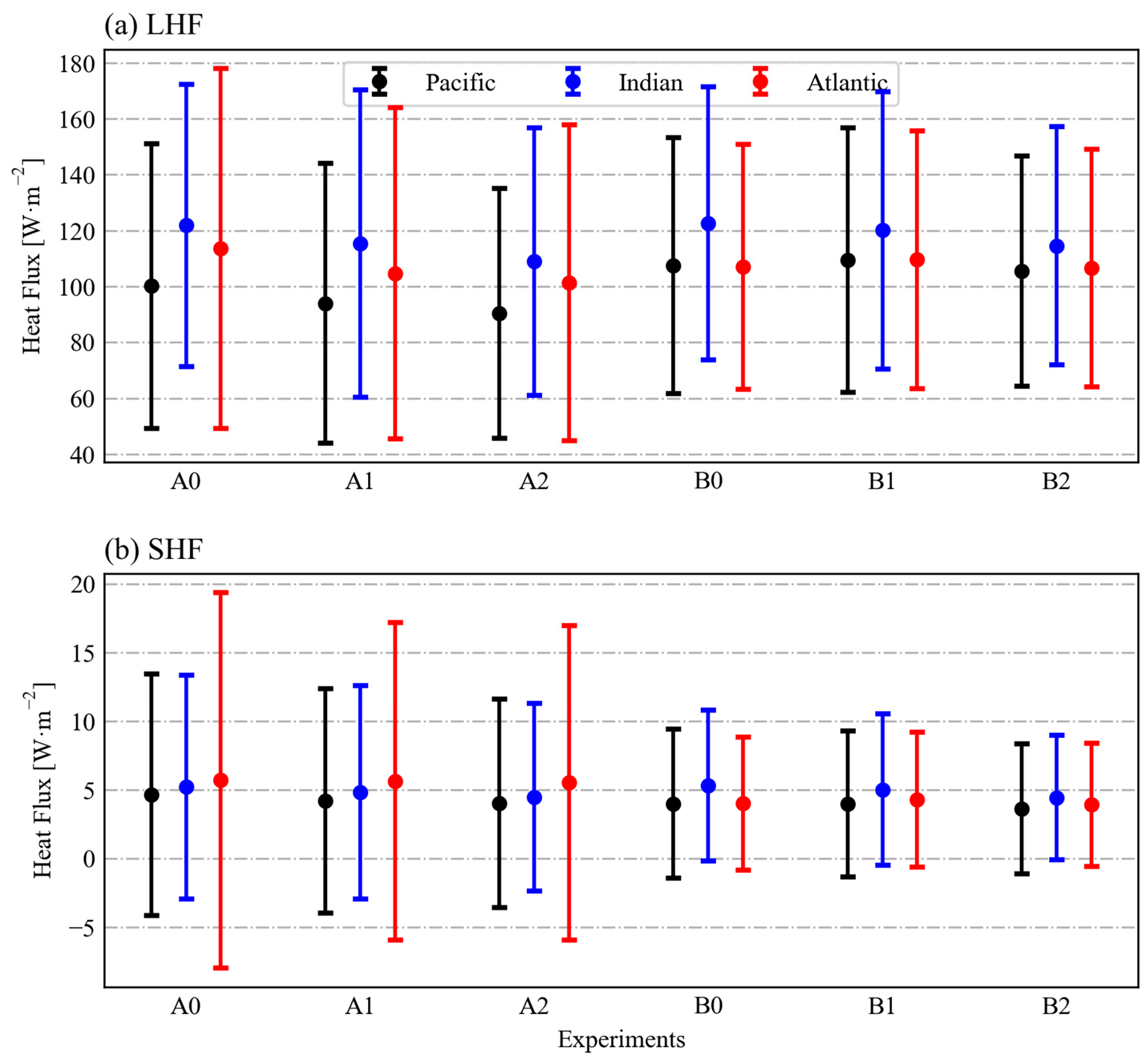
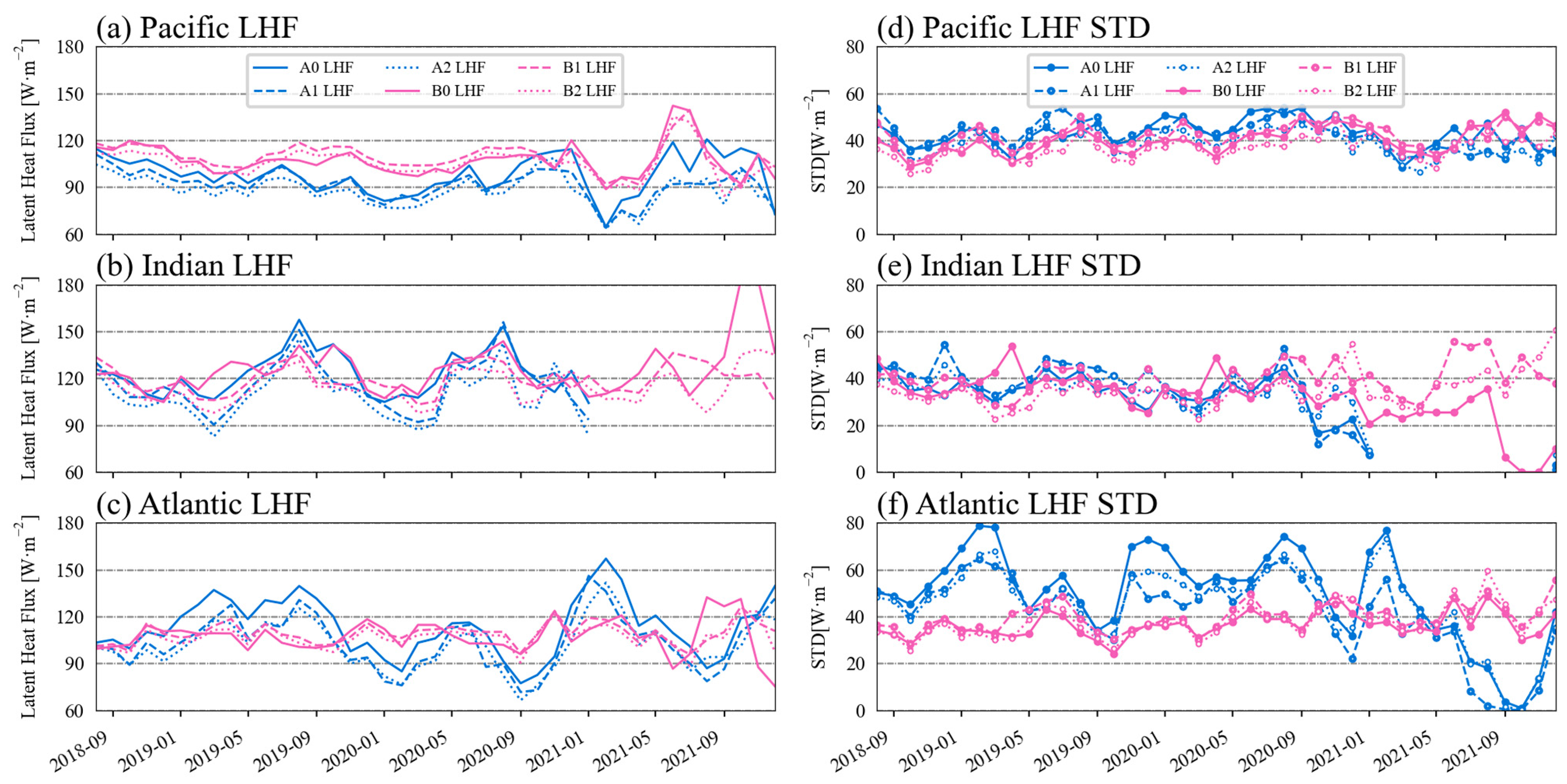
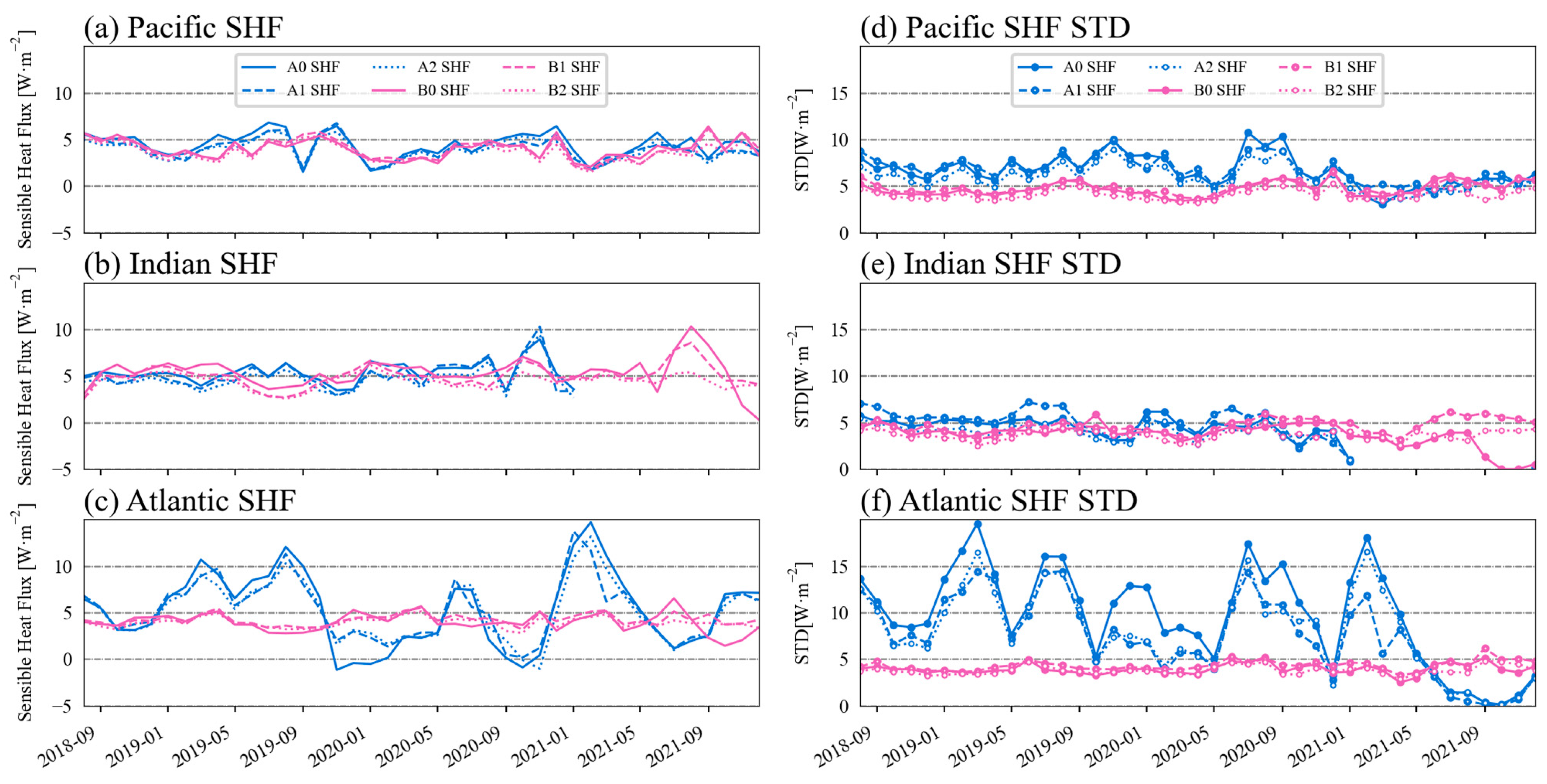
3.6. Uncertainty of the Heat Fluxes in Different Ocean Basins
4. Discussion and Conclusions
5. Summary
- (1)
- The turbulent heat fluxes derived from the CYGNSS and MERRA-2 wind speeds show overall consistency with those calculated from buoy wind speed, especially in the high-density matching regions. However, the CYGNSS wind speed had limitations in calculating heat fluxes at high wind speeds, particularly in latent heat flux estimation.
- (2)
- The heat fluxes calculated from the CYGNSS and MERRA-2 wind speeds had differences in the biases and RMSEs when compared to those calculated from buoy winds, mainly at sites located near the equator in the western Pacific Ocean, the Arabian Sea, and the Bay of Bengal, and near the Gulf of Guinea.
- (3)
- The LHF and SHF derived from the CYGNSS showed uncertainty at the synoptic, sub-synoptic and diurnal time scales, and thus, should be further validated before application.
- (4)
- The EEMD results show that the contribution of the CYGNSS wind speed to the LHF and SHF differences can reach a total of 50% and 57% at the high-frequency band, with typical periods of 3–7 days. The MERRA-2 specific humidity had the most significant contribution to the LHF difference in the periods of 192 and 500 days, while its temperature had the largest contribution (16%) to the difference in the SHF in the period of about 1 year.
- (5)
- The monthly LHF and SHF time series in the Pacific and Indian Oceans were generally consistent with each other. However, significant differences were found in the Atlantic Ocean, which may be attributed to the differences in the input SST, rather than the input wind speed.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A

References
- Zhang, G.J.; Mcphaden, M.J. The Relationship between Sea Surface Temperature and Latent Heat Flux in the Equatorial Pacific. J. Clim. 1995, 8, 589–605. [Google Scholar] [CrossRef]
- Ma, Z.; Fei, J.; Huang, X.; Cheng, X. Contributions of surface sensible heat fuxes to tropical cyclone. Part I: Evolution of tropical cyclone intensity and structure. J. Atmos. Sci. 2015, 72, 120–140. [Google Scholar] [CrossRef]
- Hsu, C.W.; DeMott, C.A.; Branson, M.D.; Reeves Eyre, J.; Zeng, X. Ocean surface flux algorithm effects on tropical Indo-Pacific intraseasonal precipitation. Geophys. Res. Lett. 2022, 49, e2021GL096968. [Google Scholar] [CrossRef] [PubMed]
- Liu, W.T.; Katsaros, K.B.; Businger, J.A. Bulk Parameterization of Air-Sea Exchanges of Heat and Water Vapor Including the Molecular Constraints at the Interface. J. Atmos. Sci. 1979, 36, 1722–1735. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Rogers, D.P.; Edson, J.B.; Young, G.S. Bulk parameterization of air-sea fluxes for Tropical Ocean-Global Atmosphere Coupled-Ocean Atmosphere Response Experiment. J. Geophys. Res. Ocean. 1996, 101, 3747–3764. [Google Scholar] [CrossRef]
- Edson, J.B.; Jampana, V.; Weller, R.A.; Bigorre, S.P.; Plueddemann, A.J.; Fairall, C.W.; Miller, S.D.; Mahrt, L.; Vickers, D.; Hersbach, H. On the exchange of momentum over the open ocean. J. Phys. Oceanogr. 2013, 43, 1589–1610. [Google Scholar] [CrossRef]
- Cronin, M.F.; Gentemann, C.L.; Edson, J.; Ueki, I.; Bourassa, M.; Brown, S.; Clayson, C.A.; Fairall, C.W.; Farrar, J.T.; Gille, S.T.; et al. Air-sea fluxes with a focus on heat and momentum. Front. Mar. Sci. 2019, 6, 430. [Google Scholar] [CrossRef]
- Bentamy, A.; Piolle, J.F.; Grouazel, A.; Danielson, R.; Gulev, S.; Paul, F.; Azelmat, H.; Mathieu, P.; von Schuckmann, K.; Sathyendranath, S.; et al. Review and assessment of latent and sensible heat flux accuracy over the global oceans. Remote Sens. Environ. 2017, 201, 196–218. [Google Scholar] [CrossRef]
- Tomita, H.; Kubota, M.; Cronin, M.F.; Iwasaki, S.; Konda, M.; Ichikawa, H. An assessment of surface heat fluxes from J-OFURO2 at the KEO and JKEO sites. J. Geophys. Res. Ocean. 2010, 115, C03018. [Google Scholar] [CrossRef]
- Tomita, H.; Hihara, T.; Kako, S.; Kubota, M.; Kutsuwada, K. An introduction to J-OFURO3, a third-generation Japanese ocean flux data set using remote-sensing observations. J. Oceanogr. 2019, 75, 171–194. [Google Scholar] [CrossRef]
- Roberts, J.B.; Robertson, F.R.; Clayson, C.A.; Bosilovich, M.G. Characterization of turbulent latent and sensible heat flux exchange between the atmosphere and ocean in MERRA. J. Clim. 2012, 25, 821–838. [Google Scholar] [CrossRef]
- Al Senafi, F.; Anis, A.; Menezes, V. Surface Heat Fluxes over the Northern Arabian Gulf and the Northern Red Sea: Evaluation of ECMWF-ERA5 and NASA-MERRA2 Reanalyses. Atmosphere 2019, 10, 504. [Google Scholar] [CrossRef]
- Decker, M.; Brunke, M.A.; Wang, Z.; Sakaguchi, K.; Zeng, X.; Bosilovich, M.G. Evaluation of the Reanalysis Products from GSFC, NCEP, and ECMWF Using Flux Tower Observations. J. Clim. 2012, 25, 1916–1944. [Google Scholar] [CrossRef]
- Josey, S.A.; Yu, L.; Gulev, S.; Jin, X.; Tilinina, N.; Barnier, B.; Brodeau, L. Unexpected impacts of the Tropical Pacific array on reanalysis surface meteorology and heat fluxes. Geophys. Res. Lett. 2014, 41, 6213–6220. [Google Scholar] [CrossRef]
- Valdivieso, M.; Haines, K.; Balmaseda, M.; Chang, Y.-S.; Drevillon, M.; Ferry, N.; Fujii, Y.; Koehl, A.; Storto, A.; Toyoda, T.; et al. An assessment of air–sea heat fluxes from ocean and coupled reanalyses. Clim. Dyn. 2017, 49, 983–1008. [Google Scholar] [CrossRef]
- Huang, B.; Liu, C.; Ren, G.; Zhang, H.; Zhang, L. The Role of Buoy and Argo Observations in Two SST Analyses in the Global and Tropical Pacific Oceans. J. Clim. 2019, 32, 2517–2535. [Google Scholar] [CrossRef]
- Tomita, H.; Kutsuwada, K.; Kubota, M.; Hihara, T. Advances in the estimation of global surface net heat flux based on satellite observation: J-OFURO3 V1.1. Front. Mar. Sci. 2021, 8, 612361. [Google Scholar] [CrossRef]
- Pokhrel, S.; Dutta, U.; Rahaman, H.; Chaudhari, H.; Hazra, A.; Saha, S.K.; Veeranjaneyulu, C. Evaluation of different heat flux products over the tropical Indian Ocean. Earth Space Sci. 2020, 7, e2019EA000988. [Google Scholar] [CrossRef]
- Carvalho, D.; Rocha, A.; Gómez-Gesteira, M.; Santos, C.S. Comparison of reanalyzed, analyzed, satellite-retrieved and NWP modelled winds with buoy data along the Iberian Peninsula coast. Remote Sens. Environ. 2014, 152, 480–492. [Google Scholar] [CrossRef]
- Tomita, H.; Hihara, T.; Kubota, M. Improved satellite estimation of near-surface humidity using vertical water vapor profile information. Geophys. Res. Lett. 2018, 45, 899–906. [Google Scholar] [CrossRef]
- Robertson, F.R.; Roberts, J.B.; Bosilovich, M.G.; Bentamy, A.; Clayson, C.A.; Fennig, K.; Schröder, M.; Tomita, H.; Compo, G.P.; Gutenstein, M.; et al. Uncertainties in Ocean Latent Heat Flux Variations over Recent Decades in Satellite-Based Estimates and Reduced Observation Reanalyses. J. Clim. 2020, 33, 8415–8437. [Google Scholar] [CrossRef]
- Tomita, H.; Kubota, M. An analysis of the accuracy of Japanese Ocean Flux data sets with Use of Remote sensing Observations (J-OFURO) satellite-derived latent heat flux using moored buoy data. J. Geophys. Res. Ocean. 2006, 111, C07007. [Google Scholar] [CrossRef]
- Ruf, C.S.; Atlas, R.; Chang, P.S.; Clarizia, M.P.; Garrison, J.L.; Gleason, S.; Katzberg, S.J.; Jelenak, Z.; Johnson, J.T.; Majumdar, S.J.; et al. New Ocean Winds Satellite Mission to Probe Hurricanes and Tropical Convection. Bull. Am. Meteorol. Soc. 2016, 97, 385–395. [Google Scholar] [CrossRef]
- Asharaf, S.; Waliser, D.E.; Posselt, D.J.; Ruf, C.S.; Zhang, C.; Putra, A.W. CYGNSS ocean surface wind validation in the tropics. J. Atmos. Ocean. Technol. 2021, 38, 711–724. [Google Scholar] [CrossRef]
- Yi, Y.; Johnson, J.T.; Wang, X. Diurnal Variations in Ocean Wind Speeds Measured by CYGNSS and Other Satellites. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Crespo, J.A.; Posselt, D.J.; Asharaf, S. CYGNSS Surface Heat Flux Product Development. Remote Sens. 2019, 11, 2294. [Google Scholar] [CrossRef]
- Lin, J.; Wang, Y.; Xu, T. CYGNSS Sea Surface Heat Flux Product Validation and Its Applicability. In Proceedings of the OCEANS 2022 Hampton Roads, Hampton Roads, VA, USA, 17–20 October 2022; IEEE: New York, NY, USA, 2022; pp. 1–6. [Google Scholar] [CrossRef]
- Li, X.; Yang, J.; Yan, Y.; Li, W. Exploring CYGNSS mission for surface heat flux estimates and analysis over tropical oceans. Front. Mar. Sci. 2022, 9, 1001491. [Google Scholar] [CrossRef]
- Li, X.; Yang, D.; Yang, J.; Han, G.; Zheng, G.; Li, W. Validation of NOAA CyGNSS Wind Speed Product with the CCMP Data. Remote Sens. 2021, 13, 1832. [Google Scholar] [CrossRef]
- Ricciardulli, L.; Mears, C.; Manaster, A.; Meissner, T. Assessment of CYGNSS Wind Speed Retrievals in Tropical Cyclones. Remote Sens. 2021, 13, 5110. [Google Scholar] [CrossRef]
- Hammond, M.L.; Foti, G.; Gommenginger, C.; Srokosz, M. An Assessment of CyGNSS v3.0 Level 1 Observables over the Ocean. Remote Sens. 2021, 13, 3500. [Google Scholar] [CrossRef]
- Brunke, M.A.; Zeng, X.; Anderson, S. Uncertainties in sea surface turbulent flux algorithms and data sets. J. Geophys. Res. Ocean. 2002, 107, 3141. [Google Scholar] [CrossRef]
- Fairall, C.W.; Bradley, E.F.; Hare, J.E.; Grachev, A.A.; Edson, J.B. Bulk parameterization of air-sea fluxes: Updates and verification for the COARE algorithm. J. Clim. 2003, 16, 571–591. [Google Scholar] [CrossRef]
- Brunke, M.A.; Fairall, C.W.; Zeng, X.; Eymard, L.; Curry, J.A. Which Bulk Aerodynamic Algorithms are Least Problematic in Computing Ocean Surface Turbulent Fluxes? J. Clim. 2003, 16, 619–635. [Google Scholar] [CrossRef]
- Rienecker, M.M.; Suarez, M.J.; Gelaro, R.; Todling, R.; Bacmeister, J.; Liu, E.; Bosilovich, M.G.; Schubert, S.D.; Takacs, L.; Kim, G.-K.; et al. MERRA: NASA’s Modern-Era Retrospective Analysis for Research and Applications. J. Clim. 2011, 24, 3624–3648. [Google Scholar] [CrossRef]
- Global Modeling and Assimilation Office (GMAO). MERRA-2 tavg1_2d_flx_Nx: 2d,1-Hourly, Time-Averaged, Single-Level, Assimilation, Surface Flux Diagnostics V5.12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015. [CrossRef]
- Global Modeling and Assimilation Office (GMAO). MERRA-2 tavg1_2d_slv_Nx: 2d,1-Hourly, Time-Averaged, Single-Level, Assimilation, Single-Level Diagnostics V5.12.4; Goddard Earth Sciences Data and Information Services Center (GES DISC): Greenbelt, MD, USA, 2015. [CrossRef]
- Grinsted, A.; Moore, J.C.; Jevrejeva, S. Application of the cross wavelet transform and wavelet coherence to geophysical time series. Nonlinear Proc. Geophys. 2004, 11, 561–566. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Yan, Y.; Song, X.; Wang, G.; Chen, C. Importance of high-frequency (≤30-day) wind variability to the annual climatology of the surface latent heat flux inferred from the global tropical moored buoy array. J. Geophys. Res. Ocean. 2022, 127, e2021JC018094. [Google Scholar] [CrossRef]
- Ruf, C.S.; Gleason, S.; McKague, D.S. Assessment of CYGNSS wind speed retrieval uncertainty. IEEE J-STARS 2018, 12, 87–97. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.S. Statistical derivation of wind speeds from CYGNSS data. IEEE Trans. Geosci. Remote Sens. 2020, 58, 3955–3964. [Google Scholar] [CrossRef]
- Prigent, A.; Lübbecke, J.F.; Bayr, T.; Latif, M.; Wengel, C. Weakened SST variability in the tropical Atlantic Ocean since 2000. Clim. Dyn. 2020, 54, 2731–2744. [Google Scholar] [CrossRef]
- Ren, H.; Zuo, J.; Li, W. The Impact of Tropical Atlantic SST Variability on the Tropical Atmosphere during Boreal Summer. J. Clim. 2021, 34, 6705–6723. [Google Scholar] [CrossRef]
- Leyba, I.M.; Solman, S.A.; Saraceno, M. Trends in sea surface temperature and air–sea heat fluxes over the South Atlantic Ocean. Clim. Dyn. 2019, 53, 4141–4153. [Google Scholar] [CrossRef]
- Swain, D.; Rahman, S.H.; Ravichandran, M. Comparison of NCEP turbulent heat fluxes with in situ observations over the south-eastern Arabian Sea. Meteorol. Atmos. Phys. 2009, 104, 163–175. [Google Scholar] [CrossRef]
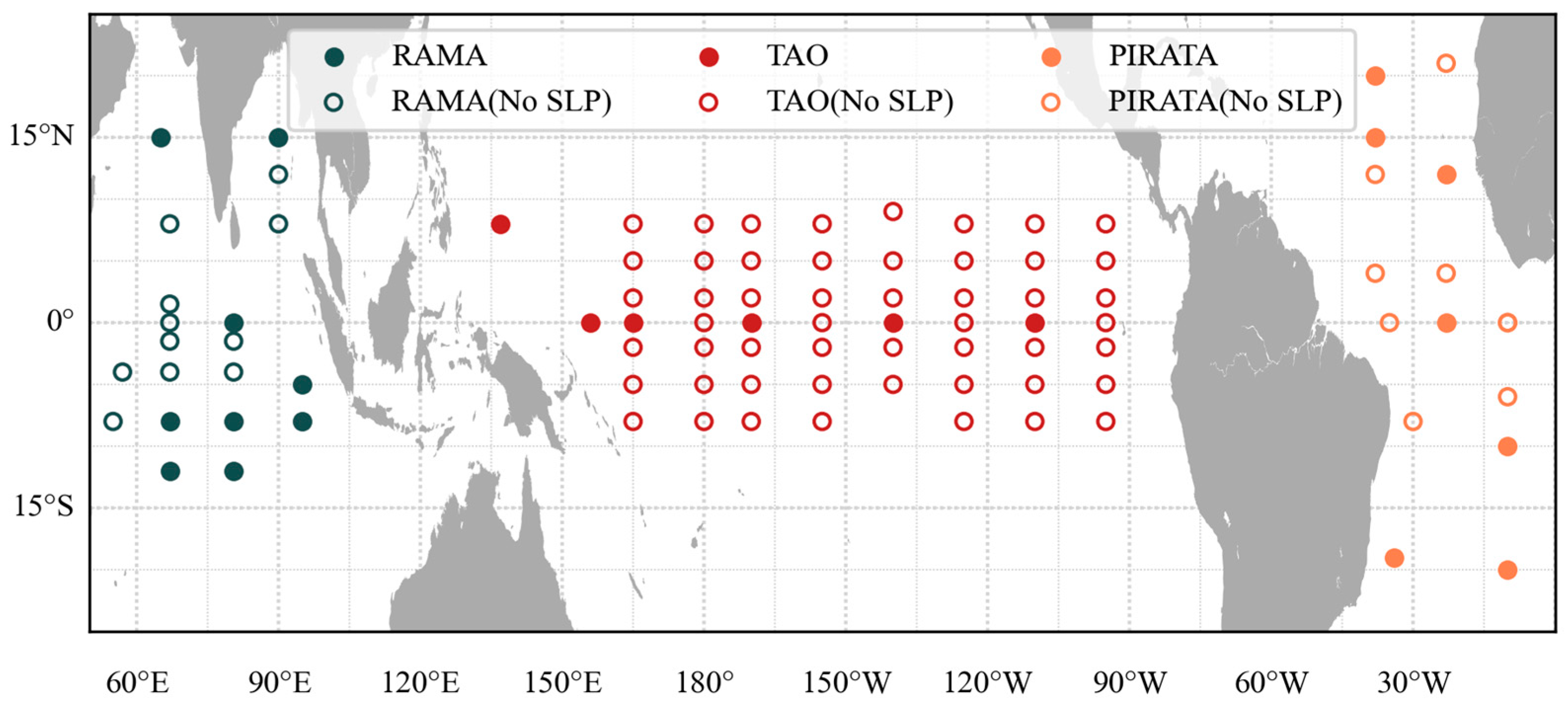
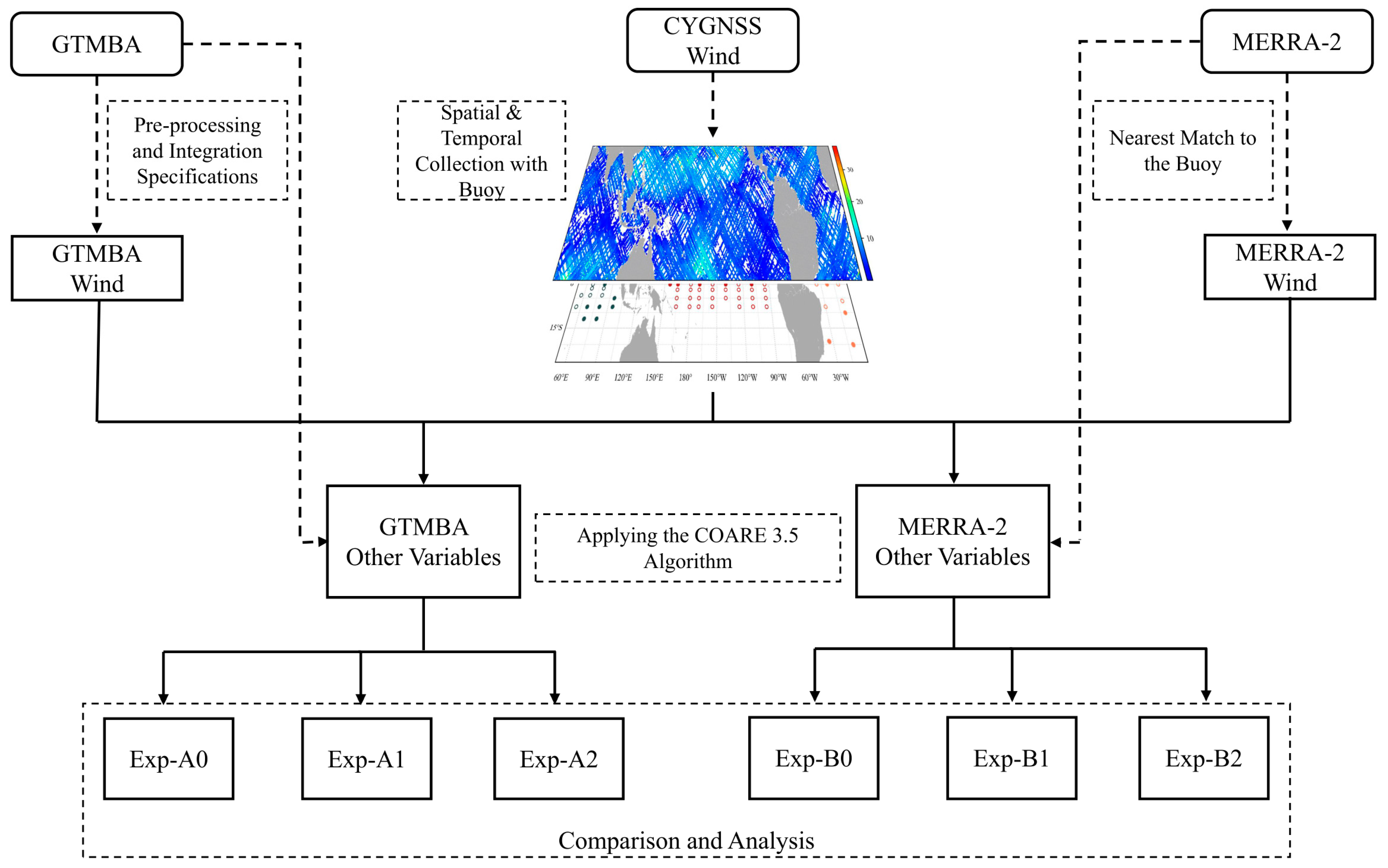



| Data Collection | Variable | Spatial Res | Temporal Res | Spatial Coverage | Time Span |
|---|---|---|---|---|---|
| M2T1NXFLX | 𝜌𝑎, 𝑞𝑠 | 0.625° × 0.5° | 1 h from 00:30 UTC | 40°S~40°N | 1 August 2018~31 December 2021 |
| M2T1NXSLV | 𝑞a, SLP, 𝑇𝑠, 𝑇𝑎, 𝑈 |
| Experiments | Output Variables | Input Variables | ||
|---|---|---|---|---|
| Description | Symbol | Wind Speed | Other Variables | |
| Buoy Original | A0 | LHFA0 SHFA0 | 𝑈Buoy | 𝑇𝑎 Buoy 𝑇𝑠 Buoy 𝑞a Buoy 𝑞𝑠 Buoy 𝜌𝑎 Buoy |
| CYGNSS Wind + Buoy Variable | A1 | LHFA1 SHFA1 | 𝑈CYGNSS | |
| MERRA-2 Wind + Buoy Variable | A2 | LHFA2 SHFA2 | 𝑈MERRA2 | |
| Buoy Wind + MERRA-2 Variable | B0 | LHFB0 SHFB0 | 𝑈Buoy | 𝑇𝑎 MERRA2 𝑇𝑠 MERRA2 𝑞a MERRA2 𝑞𝑠 MERRA2 ρa MERRA2 |
| CYGNSS Wind + MERRA-2 Variable | B1 | LHFB1 SHFB1 | 𝑈CYGNSS | |
| MERRA-2 Wind + MERRA-2 Variable | B2 | LHFB2 SHFB2 | 𝑈MERRA2 | |
| (a) A1–A0 Turbulent Heat Fluxes, EEMD | ||||||
| IMF | LHF | SHF | ||||
| Mean Period | IMFs Variance | Contribution | Mean Period | IMFs Variance | Contribution | |
| 1 | 2.9562 | 39.8189 | 31.48% | 2.9667 | 0.9454 | 40.69% |
| 2 | 6.9197 | 23.3616 | 18.47% | 6.3887 | 0.3762 | 16.19% |
| 3 | 13.2169 | 11.3026 | 8.93% | 14.3563 | 0.2314 | 9.96% |
| 4 | 27.4505 | 8.2958 | 6.56% | 26.0208 | 0.1382 | 5.95% |
| 5 | 65.7368 | 9.389 | 7.42% | 55.5111 | 0.1017 | 4.37% |
| 6 | 124.9 | 1.8314 | 1.45% | 113.5455 | 0.0469 | 2.02% |
| 7 | 416.3333 | 1.6232 | 1.28% | 356.8571 | 0.0816 | 3.51% |
| 8 | 624.5 | 3.4955 | 2.76% | 624.5 | 0.0581 | 0.25% |
| (b) A2–A0 Turbulent Heat Fluxes, EEMD | ||||||
| IMF | LHF | SHF | ||||
| Mean Period | IMFs Variance | Contribution | Mean Period | IMFs Variance | Contribution | |
| 1 | 3.2868 | 9.7569 | 10.22% | 3.1701 | 0.0987 | 17.85% |
| 2 | 7.8801 | 8.9691 | 9.4% | 7.0765 | 0.057 | 10.31% |
| 3 | 15.2317 | 6.7156 | 7.04% | 14.6941 | 0.0421 | 7.62% |
| 4 | 38.4308 | 17.6207 | 18.46% | 30.4634 | 0.0511 | 9.24% |
| 5 | 71.3714 | 9.2526 | 9.69% | 62.45 | 0.0446 | 8.06% |
| 6 | 146.9412 | 3.969 | 4.16% | 156.125 | 0.0531 | 0.96% |
| 7 | 416.3333 | 2.3369 | 2.45% | 312.25 | 0.0396 | 7.16% |
| 8 | 624.5 | 1.8754 | 1.96% | 624.5 | 0.0748 | 13.53% |
| (c) B0–A0 Turbulent Heat Fluxes, EEMD | ||||||
| IMF | LHF | SHF | ||||
| Mean Period | IMFs Variance | Contribution | Mean Period | IMFs Variance | Contribution | |
| 1 | 3.3086 | 11.4619 | 8.92% | 3.313 | 0.3726 | 10.85% |
| 2 | 7.7337 | 10.0341 | 7.81% | 7.6391 | 0.2825 | 8.23% |
| 3 | 16.8784 | 9.4895 | 7.39% | 15.5155 | 0.2504 | 7.29% |
| 4 | 35.1831 | 9.1559 | 7.13% | 35.1831 | 0.4092 | 11.92% |
| 5 | 75.697 | 11.0604 | 8.61% | 69.3889 | 0.3671 | 10.69% |
| 6 | 192.1538 | 29.6947 | 23.11% | 208.1667 | 0.2131 | 6.21% |
| 7 | 499.6 | 18.1702 | 14.14% | 356.8571 | 0.5524 | 16.09% |
| 8 | 624.5 | 1.2988 | 1.01% | 624.5 | 0.1915 | 5.58% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lin, J.; Wang, Y.; Pan, H.; Wei, Z.; Xu, T. Uncertainty of CYGNSS-Derived Heat Flux Variations at Diurnal to Seasonal Time Scales over the Tropical Oceans. Remote Sens. 2023, 15, 3161. https://doi.org/10.3390/rs15123161
Lin J, Wang Y, Pan H, Wei Z, Xu T. Uncertainty of CYGNSS-Derived Heat Flux Variations at Diurnal to Seasonal Time Scales over the Tropical Oceans. Remote Sensing. 2023; 15(12):3161. https://doi.org/10.3390/rs15123161
Chicago/Turabian StyleLin, Jinsong, Yanfeng Wang, Haidong Pan, Zexun Wei, and Tengfei Xu. 2023. "Uncertainty of CYGNSS-Derived Heat Flux Variations at Diurnal to Seasonal Time Scales over the Tropical Oceans" Remote Sensing 15, no. 12: 3161. https://doi.org/10.3390/rs15123161
APA StyleLin, J., Wang, Y., Pan, H., Wei, Z., & Xu, T. (2023). Uncertainty of CYGNSS-Derived Heat Flux Variations at Diurnal to Seasonal Time Scales over the Tropical Oceans. Remote Sensing, 15(12), 3161. https://doi.org/10.3390/rs15123161