A SAR Image-Despeckling Method Based on HOSVD Using Tensor Patches
Abstract
1. Introduction
2. Materials and Methods
2.1. Statistics of Log-Transformed Speckle
2.2. Searching Similar Patches of SAR Images
2.2.1. Measure for Non-Local Similarity
2.2.2. Computation of Gradient
2.3. Tensor and Third-Order Tensor Decomposition
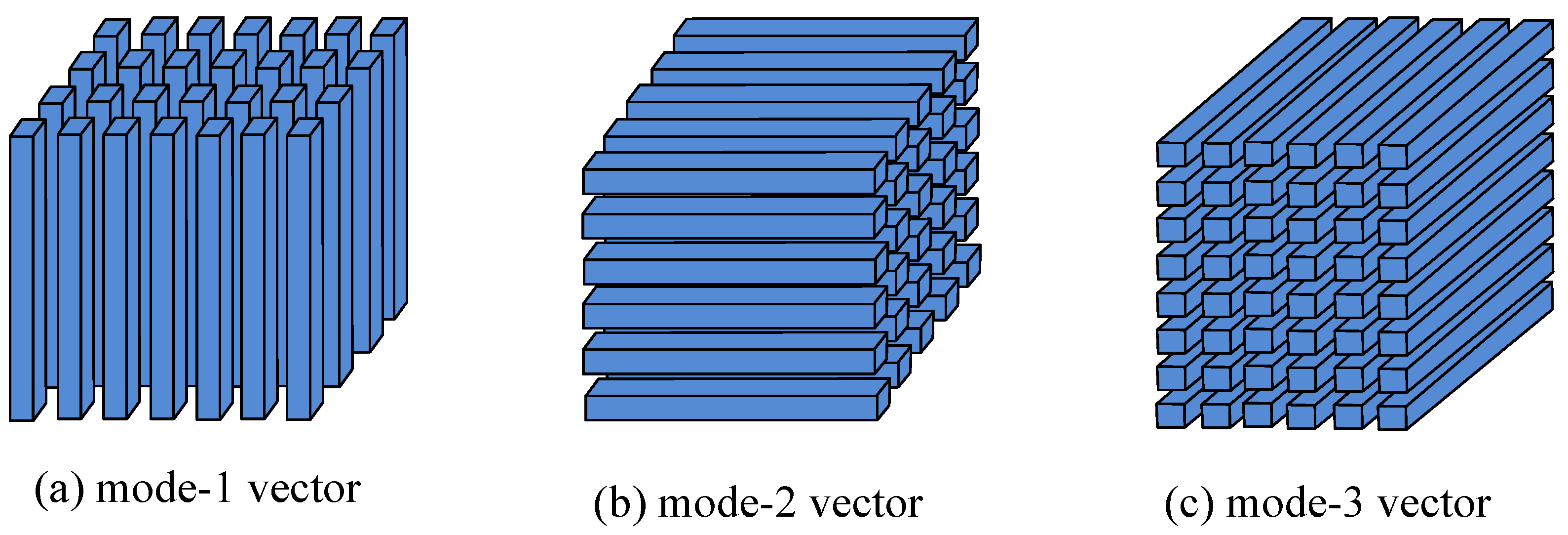
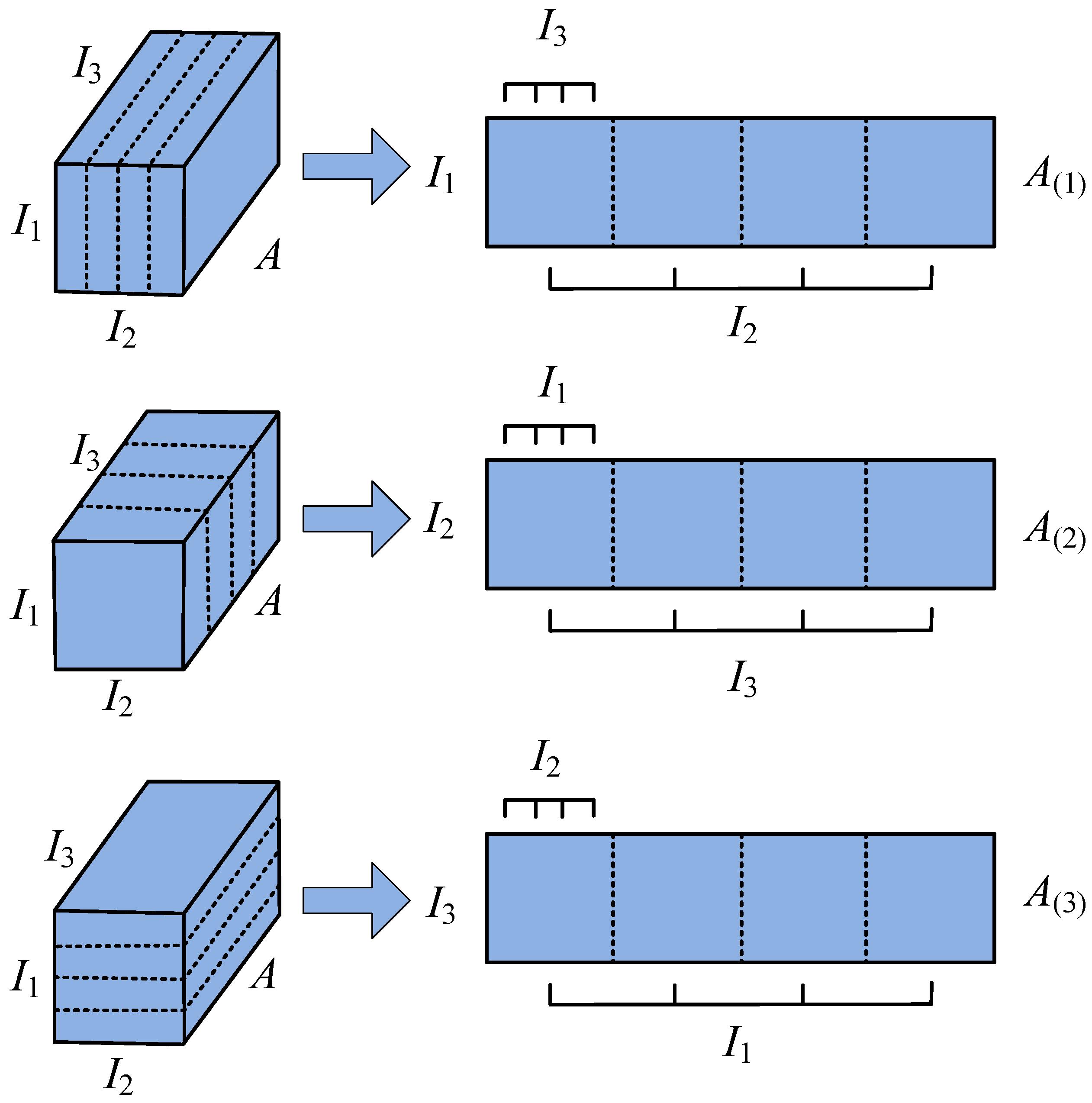
2.3.1. Definition of Tensor
2.3.2. Higher-Order Singular Value Decomposition
2.4. SAR Image Despeckling Based on the Iterative Low-Rank Tensor Patch Approximation Algorithm
2.5. Soft-Thresholding Proximal Operator
2.6. Residual Iteration and Adaptive Weight Setting to
2.7. Aggregation of Despeckled Tensor Patches
| Algorithm 1 Iterative low-rank tensor patch approximation algorithm for SAR image despeckling |
| Input: SAR image Y, the ENL L, the number of reference patches K, and iteration F |
| Output: despeckled SAR image X |
| 1: Initialization: |
| Initialize , , SAR image patch tensor A |
| 2: Iteration: |
| ➀ Outer loop: for n = 1:F do |
| (I) Re-estimate by (28) |
| (II) Re-estimate noise variance by (28) |
| ➁ Inner loop: for t = 1:T do |
| (I) Compute and core tensor of by HOSVD via Equation (14) |
| (II) For each in core calculate the via Equation (22) |
| (III) Apply threshold to in via Equation (27) |
| (IV) Estimate despeckling patches tensor by (23) |
| End for |
| ➂ Obtain the nth step despeckled SAR image via Equation (33) |
| End for |
| ➃ Obtain the despeckled SAR image X |
3. Results
3.1. Experiments on Simulated Multiplicative Noise Images
3.2. Experiments on Real SAR Images
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Moreira, A.; Prats-Iraola, P.; Younis, M.; Krieger, G.; Hajnsek, I.; Papathanassiou, K.P. A tutorial on synthetic aperture radar. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–43. [Google Scholar] [CrossRef]
- Ren, H.; Yu, X.; Zou, L.; Zhou, Y.; Wang, X.; Bruzzone, L. Extended convolutional capsule network with application on SAR automatic target recognition. Signal Process. 2021, 183, 108021. [Google Scholar] [CrossRef]
- Baraha, S.; Sahoo, A.K.; Modalavalasa, S. A systematic review on recent developments in nonlocal and variational methods for SAR image despeckling. Signal Process. 2022, 196, 108521. [Google Scholar] [CrossRef]
- Ponmani, E.; Saravanan, P. Image denoising and despeckling methods for SAR images to improve image enhancement performance: A survey. Multimed. Tools Appl. 2021, 80, 26547–26569. [Google Scholar] [CrossRef]
- Wang, G.; Bo, F.; Chen, X.; Lu, W.; Hu, S.; Fang, J. A collaborative despeckling method for SAR images based on texture classification. Remote Sens. 2022, 14, 1465. [Google Scholar] [CrossRef]
- Bo, F.; Lu, W.; Wang, G.; Zhou, M.; Wang, Q.; Fang, J. A Blind SAR Image Despeckling Method Based on Improved Weighted Nuclear Norm Minimization. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar] [CrossRef]
- Lee, J.S. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI-2, 165–168. [Google Scholar] [CrossRef]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 157–166. [Google Scholar] [CrossRef]
- Kuan, D.T.; Sawchuk, A.A.; Strand, T.C.; Chavel, P. Adaptive noise smoothing filter for images with signal-dependent noise. IEEE Trans. Pattern Anal. Mach. Intell. 1985, PAMI-7, 165–177. [Google Scholar] [CrossRef]
- Ranjani, J.J.; Thiruvengadam, S. Dual-tree complex wavelet transform based SAR despeckling using interscale dependence. IEEE Trans. Geosci. Remote Sens. 2010, 48, 2723–2731. [Google Scholar] [CrossRef]
- Bianchi, T.; Argenti, F.; Alparone, L. Segmentation-based MAP despeckling of SAR images in the undecimated wavelet domain. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2728–2742. [Google Scholar] [CrossRef]
- Tao, R.; Wan, H.; Wang, Y. Artifact-free despeckling of SAR images using contourlet. IEEE Geosci. Remote Sens. Lett. 2012, 9, 980–984. [Google Scholar]
- Hou, B.; Zhang, X.; Bu, X.; Feng, H. SAR image despeckling based on nonsubsampled shearlet transform. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2012, 5, 809–823. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Li, X.; Kuang, G. SAR image speckle reduction based on nonconvex hybrid total variation model. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1231–1249. [Google Scholar] [CrossRef]
- Maji, S.K.; Thakur, R.K.; Yahia, H.M. SAR image denoising based on multifractal feature analysis and TV regularisation. IET Image Process. 2020, 14, 4158–4167. [Google Scholar] [CrossRef]
- Zhang, Z.; Xu, Y.; Yang, J.; Li, X.; Zhang, D. A survey of sparse representation: Algorithms and applications. IEEE Access 2015, 3, 490–530. [Google Scholar] [CrossRef]
- Jiang, J.; Jiang, L.; Sang, N. Non-local sparse models for SAR image despeckling. In Proceedings of the 2012 International Conference on Computer Vision in Remote Sensing, Xiamen, China, 16–18 December 2012; pp. 230–236. [Google Scholar]
- Wang, P.; Zhang, H.; Patel, V.M. SAR image despeckling using a convolutional neural network. IEEE Signal Process. Lett. 2017, 24, 1763–1767. [Google Scholar] [CrossRef]
- Lattari, F.; Gonzalez Leon, B.; Asaro, F.; Rucci, A.; Prati, C.; Matteucci, M. Deep learning for SAR image despeckling. Remote Sens. 2019, 11, 1532. [Google Scholar] [CrossRef]
- Liu, S.; Gao, L.; Lei, Y.; Wang, M.; Hu, Q.; Ma, X.; Zhang, Y.D. SAR speckle removal using hybrid frequency modulations. IEEE Trans. Geosci. Remote Sens. 2020, 59, 3956–3966. [Google Scholar] [CrossRef]
- Vitale, S.; Ferraioli, G.; Pascazio, V. Multi-objective CNN-based algorithm for SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2020, 59, 9336–9349. [Google Scholar] [CrossRef]
- Liu, Z.; Lai, R.; Guan, J. Spatial and transform domain CNN for SAR image despeckling. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’05), San Diego, CA, USA, 20–25 June 2005; Volume 2, pp. 60–65. [Google Scholar]
- Deledalle, C.A.; Denis, L.; Tupin, F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef] [PubMed]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2011, 50, 606–616. [Google Scholar] [CrossRef]
- Cozzolino, D.; Parrilli, S.; Scarpa, G.; Poggi, G.; Verdoliva, L. Fast adaptive nonlocal SAR despeckling. IEEE Geosci. Remote Sens. Lett. 2013, 11, 524–528. [Google Scholar] [CrossRef]
- Chen, G.; Li, G.; Liu, Y.; Zhang, X.P.; Zhang, L. SAR image despeckling based on combination of fractional-order total variation and nonlocal low rank regularization. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2056–2070. [Google Scholar] [CrossRef]
- Guo, Q.; Zhang, C.; Zhang, Y.; Liu, H. An efficient SVD-based method for image denoising. IEEE Trans. Circuits Syst. Video Technol. 2015, 26, 868–880. [Google Scholar] [CrossRef]
- Ozcan, C.; Sen, B.; Nar, F. Sparsity-driven despeckling for SAR images. IEEE Geosci. Remote Sens. Lett. 2015, 13, 115–119. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, C.; Zhao, H.; Yu, W. Low-rank modeling and its applications in image analysis. ACM Comput. Surv. (CSUR) 2014, 47, 1–33. [Google Scholar] [CrossRef]
- Zhao, Y.Q.; Yang, J. Hyperspectral image denoising via sparse representation and low-rank constraint. IEEE Trans. Geosci. Remote Sens. 2014, 53, 296–308. [Google Scholar] [CrossRef]
- Liang, D.; Jiang, M.; Ding, J. Fast patchwise nonlocal SAR image despeckling using joint intensity and structure measures. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6283–6293. [Google Scholar] [CrossRef]
- Aghababaei, H.; Ferraioli, G.; Vitale, S.; Zamani, R.; Schirinzi, G.; Pascazio, V. Nonlocal model-free denoising algorithm for single-and multichannel SAR data. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–15. [Google Scholar] [CrossRef]
- Kolda, T.G.; Bader, B.W. Tensor decompositions and applications. SIAM Rev. 2009, 51, 455–500. [Google Scholar] [CrossRef]
- Liu, J.; Musialski, P.; Wonka, P.; Ye, J. Tensor completion for estimating missing values in visual data. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 208–220. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Ely, G.; Aeron, S.; Hao, N.; Kilmer, M. Novel methods for multilinear data completion and de-noising based on tensor-SVD. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Washington, DC, USA, 23–28 June 2014; pp. 3842–3849. [Google Scholar]
- Xue, J.; Zhao, Y.; Liao, W.; Chan, J.C.W. Nonlocal low-rank regularized tensor decomposition for hyperspectral image denoising. IEEE Trans. Geosci. Remote Sens. 2019, 57, 5174–5189. [Google Scholar] [CrossRef]
- Yang, H.; Park, Y.; Yoon, J.; Jeong, B. An improved weighted nuclear norm minimization method for image denoising. IEEE Access 2019, 7, 97919–97927. [Google Scholar] [CrossRef]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. Multiscale Model. Simul. 2005, 4, 490–530. [Google Scholar] [CrossRef]
- Jang, S.; Nam, H.; Lee, Y.J.; Jeong, B.; Lee, R.; Yoon, J. Data-adapted moving least squares method for 3-D image interpolation. Phys. Med. Biol. 2013, 58, 8401. [Google Scholar] [CrossRef]
- De Lathauwer, L.; De Moor, B.; Vandewalle, J. A multilinear singular value decomposition. SIAM J. Matrix Anal. Appl. 2000, 21, 1253–1278. [Google Scholar] [CrossRef]
- Gandy, S.; Recht, B.; Yamada, I. Tensor completion and low-n-rank tensor recovery via convex optimization. Inverse Probl. 2011, 27, 025010. [Google Scholar] [CrossRef]
- Shen, Z.; Sun, H. Iterative Adaptive Nonconvex Low-Rank Tensor Approximation to Image Restoration Based on ADMM. J. Math. Imaging Vis. 2019, 61, 627–642. [Google Scholar] [CrossRef]
- Deledalle, C.A.; Denis, L.; Tabti, S.; Tupin, F. MuLoG, or how to apply Gaussian denoisers to multi-channel SAR speckle reduction? IEEE Trans. Image Process. 2017, 26, 4389–4403. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Zhang, L.; Mou, X.; Zhang, D. FSIM: A feature similarity index for image quality assessment. IEEE Trans. Image Process. 2011, 20, 2378–2386. [Google Scholar] [CrossRef] [PubMed]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Di Martino, G.; Poderico, M.; Poggi, G.; Riccio, D.; Verdoliva, L. Benchmarking framework for SAR despeckling. IEEE Trans. Geosci. Remote Sens. 2013, 52, 1596–1615. [Google Scholar] [CrossRef]












| Patch size | 5 × 5 | 6 × 6 | 7 × 7 | 8 × 8 | 9 × 9 |
| PSNR | 23.11 | 23.14 | 23.26 | 23.24 | 23.19 |
| SSIM | 0.679 | 0.681 | 0.687 | 0.680 | 0.679 |
| Patch number | 100 | 150 | 200 | 250 | 300 |
| PSNR | 23.23 | 23.27 | 23.33 | 23.31 | 23.38 |
| SSIM | 0.683 | 0.687 | 0.691 | 0.693 | 0.695 |
| Patch stack number | 30 | 40 | 50 | 60 | 70 |
| PSNR | 23.07 | 23.25 | 23.40 | 23.42 | 23.37 |
| SSIM | 0.683 | 0.687 | 0.691 | 0.693 | 0.695 |
| Search window | 10 × 10 | 15 × 15 | 20 × 20 | 25 × 25 | 30×30 |
| PSNR | 23.21 | 23.34 | 23.41 | 23.43 | 23.45 |
| SSIM | 0.686 | 0.691 | 0.697 | 0.696 | 0.698 |
| L = 1 | L = 2 | L = 4 | L = 8 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | PSNR | FSIM | SSIM | PSNR | FSIM | SSIM | PSNR | FSIM | SSIM | PSNR | FSIM | SSIM | |
| House | Noisy image | 12.16 | 0.427 | 0.096 | 14.71 | 0.504 | 0.152 | 17.32 | 0.584 | 0.225 | 20.04 | 0.663 | 0.316 |
| PPB | 25.13 | 0.786 | 0.642 | 27.16 | 0.840 | 0.724 | 29.02 | 0.877 | 0.786 | 30.39 | 0.893 | 0.823 | |
| FANS | 25.34 | 0.804 | 0.757 | 28.66 | 0.854 | 0.811 | 31.17 | 0.883 | 0.842 | 32.95 | 0.903 | 0.860 | |
| SAR-BM3D | 24.62 | 0.836 | 0.772 | 28.14 | 0.877 | 0.816 | 30.90 | 0.905 | 0.845 | 32.12 | 0.922 | 0.863 | |
| Mulog | 25.01 | 0.835 | 0.783 | 28.36 | 0.870 | 0.822 | 31.15 | 0.894 | 0.847 | 32.97 | 0.914 | 0.862 | |
| Proposed | 25.54 | 0.813 | 0.733 | 28.28 | 0.857 | 0.797 | 30.76 | 0.888 | 0.836 | 32.38 | 0.904 | 0.854 | |
| Monarch | Noisy image | 13.47 | 0.536 | 0.258 | 16.04 | 0.614 | 0.349 | 18.75 | 0.691 | 0.444 | 21.52 | 0.762 | 0.546 |
| PPB | 23.00 | 0.826 | 0.716 | 24.72 | 0.866 | 0.790 | 25.99 | 0.892 | 0.835 | 27.63 | 0.916 | 0.873 | |
| FANS | 24.21 | 0.856 | 0.805 | 26.57 | 0.895 | 0.864 | 28.52 | 0.919 | 0.900 | 30.23 | 0.938 | 0.924 | |
| SAR-BM3D | 23.61 | 0.853 | 0.800 | 26.13 | 0.890 | 0.856 | 28.13 | 0.915 | 0.893 | 29.84 | 0.933 | 0.919 | |
| Mulog | 23.80 | 0.866 | 0.813 | 26.24 | 0.901 | 0.867 | 28.43 | 0.924 | 0.904 | 30.30 | 0.942 | 0.929 | |
| Proposed | 23.51 | 0.843 | 0.750 | 26.04 | 0.890 | 0.825 | 28.28 | 0.921 | 0.890 | 30.30 | 0.943 | 0.920 | |
| Napoli | Noisy image | 14.64 | 0.606 | 0.229 | 17.27 | 0.628 | 0.337 | 20.08 | 0.759 | 0.463 | 22.97 | 0.826 | 0.593 |
| PPB | 21.74 | 0.713 | 0.561 | 23.23 | 0.783 | 0.659 | 24.94 | 0.845 | 0.741 | 26.40 | 0.885 | 0.800 | |
| FANS | 22.26 | 0.710 | 0.598 | 24.24 | 0.804 | 0.703 | 26.24 | 0.869 | 0.784 | 28.12 | 0.910 | 0.848 | |
| SAR-BM3D | 22.64 | 0.760 | 0.639 | 24.42 | 0.825 | 0.724 | 26.36 | 0.880 | 0.802 | 28.12 | 0.916 | 0.865 | |
| Mulog | 22.43 | 0.735 | 0.628 | 24.08 | 0.801 | 0.704 | 26.02 | 0.861 | 0.778 | 27.96 | 0.908 | 0.843 | |
| Proposed | 22.33 | 0.780 | 0.600 | 24.15 | 0.826 | 0.690 | 26.14 | 0.881 | 0.775 | 28.04 | 0.915 | 0.842 | |
| R1 | R2 | R3 | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Methods | ENL1 | ENL2 | MoR | Time | ENL1 | ENL2 | MoR | Time | ENL1 | ENL2 | MoR | Time |
| Noisy image | 2.90 | 2.62 | - | - | 2.20 | 2.62 | - | - | 22.47 | 12.78 | - | - |
| PPB | 55.58 | 366.65 | 1.00 | 23.08 | 1345.02 | 340.70 | 0.99 | 22.36 | 1327.92 | 1181.27 | 1.00 | 23.11 |
| FANS | 32.65 | 74.58 | 1.02 | 1.62 | 100.75 | 98.03 | 1.11 | 1.74 | 525.66 | 770.60 | 1.01 | 1.58 |
| SAR-BM3D | 19.63 | 22.27 | 0.99 | 24.31 | 127.05 | 77.99 | 0.99 | 24.54 | 3837.38 | 111.76 | 0.99 | 24.09 |
| Mulog | 29.74 | 69.61 | 1.07 | 10.25 | 216.92 | 144.60 | 1.38 | 10.02 | 878.76 | 859.67 | 1.01 | 11.36 |
| Proposed | 38.04 | 151.58 | 0.96 | 50.63 | 137.74 | 151.58 | 0.99 | 49.47 | 401.67 | 951.58 | 0.98 | 49.33 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fang, J.; Mao, T.; Bo, F.; Hao, B.; Zhang, N.; Hu, S.; Lu, W.; Wang, X. A SAR Image-Despeckling Method Based on HOSVD Using Tensor Patches. Remote Sens. 2023, 15, 3118. https://doi.org/10.3390/rs15123118
Fang J, Mao T, Bo F, Hao B, Zhang N, Hu S, Lu W, Wang X. A SAR Image-Despeckling Method Based on HOSVD Using Tensor Patches. Remote Sensing. 2023; 15(12):3118. https://doi.org/10.3390/rs15123118
Chicago/Turabian StyleFang, Jing, Taiyong Mao, Fuyu Bo, Bomeng Hao, Nan Zhang, Shaohai Hu, Wenfeng Lu, and Xiaofeng Wang. 2023. "A SAR Image-Despeckling Method Based on HOSVD Using Tensor Patches" Remote Sensing 15, no. 12: 3118. https://doi.org/10.3390/rs15123118
APA StyleFang, J., Mao, T., Bo, F., Hao, B., Zhang, N., Hu, S., Lu, W., & Wang, X. (2023). A SAR Image-Despeckling Method Based on HOSVD Using Tensor Patches. Remote Sensing, 15(12), 3118. https://doi.org/10.3390/rs15123118






