Pixel-Wise Attention Residual Network for Super-Resolution of Optical Remote Sensing Images

Abstract

The deep-learning-based image super-resolution opens a new direction for the remote sensing field to reconstruct further information and details from captured images. However, most current SR works try to improve the performance by increasing the complexity of the model, which results in significant computational costs and memory consumption. In this paper, we propose a lightweight model named pixel-wise attention residual network for optical remote sensor images, which can effectively solve the super-resolution task of multi-satellite images. The proposed method consists of three modules: the feature extraction module, feature fusion module, and feature mapping module. First, the feature extraction module is responsible for extracting the deep features from the input spatial bands with different spatial resolutions. Second, the feature fusion module with the pixel-wise attention mechanism generates weight coefficients for each pixel on the feature map and fully fuses the deep feature information. Third, the feature mapping module is aimed to maintain the fidelity of the spectrum by adding the fused residual feature map directly to the up-sampled low-resolution images. Compared with existing deep-learning-based methods, the major advantage of our method is that for the first time, the pixel-wise attention mechanism is incorporated in the task of super-resolution fusion of remote sensing images, which effectively improved the performance of the fusion network. The accuracy assessment results show that our method achieved superior performance of the root mean square error, signal-to–reconstruction ratio error, universal image quality index, and peak signal noise ratio compared to competing approaches. The improvements in the signal-to-reconstruction ratio error and peak signal noise ratio are significant, with a respective increase of 0.15 and 0.629 dB for Sentinel-2 data, and 0.196 and 1 dB for Landsat data.

1. Introduction

In recent decades, remote sensing images have been widely used and satisfactory results have been achieved in target recognition [1], land cover classification [2], agricultural inspection [3], aerosol monitoring [4], and other fields [5,6,7,8]. The rise of remote sensing prompted a growing need for images with more refined details [9]. However, it is impractical to simultaneously satisfy high spatial resolution, high spectral resolution, and high temporal resolution. In fact, a single sensor must make a trade-off between them. As the spatial resolution increases, the instantaneous field of view (IFOV) decreases, and to ensure the signal-to-noise ratio of the imagery, the spectral bandwidth needs to be broadened, and hence a finer spectral resolution cannot be achieved [10]. Alongside that, although each sensor has a predetermined time revisit period, the actual time revisit period of available images often falls short of expectations due to cloud cover, shadows, and other negative atmospheric influences. It is apparent that the lack of spatial and temporal information limits the application potential of remote sensing images [11,12,13].

One feasible solution is to fully leverage the information correlation among multiple images to enhance the low-resolution images, improving their local resolution and/or spectral resolution. This process incorporates richer feature information, allowing for a more comprehensive and mutually interpretable representation of the same scene when combined with high-resolution images. With the development of the aerospace industry, more and more satellites have been launched into space for earth observation, providing a large and sufficient source of data for the enhancement of low-resolution images. Since the first Landsat satellite was launched in 1972, the Landsat program has continued to acquire surface imagery, providing millions of valuable images, making it the longest record of surface observations to date and facilitating scientific investigations on a global scale [14,15]. Among them, Landsat 8, launched in 2013, and Landsat 9, launched in 2021, carry the Land Imager (OLI), which includes nine bands with a spatial resolution of 30 m, including a 15 m panchromatic band of, achieving a revisit cycle of 16 days [16]. Landsat satellite imagery with a 30 m spatial resolution can be used both as fine images to fuse with lower spatial resolution imagery, and as coarse images to fuse with higher resolution imagery. The pairing of MODIS and Landsat is typical of the former, and based on the frequent revisit cycles of MODIS satellites, the guidance of Landsat data is expected to generate daily Earth observation reflectivity products [17,18,19]. In this case, the choice of a coarse image is more extensive, and it may be either Google Imagery [20], SPOT5 [21], or Sentinel-2 [22]. Google images have a resolution of 0.3 m, but are updated slowly and historical images with definite dates cannot be downloaded. Although SPOT has a wealth of historical imagery, as a commercial remote sensing system, it is not freely available to the public. The Sentinel 2A satellite, launched in 2015, and the Sentinel 2B satellite, launched in 2017, form a dual-satellite system with a revisit cycle of five days [23]. Due to the similarity in band specifications, the overlapping coverage, same coordinate system, and open access, Sentinel 2 MSI images can be combined with Landsat OLI images to form HR–LR pairs for super-resolution enhancement [24,25].

Recently, the advancement of deep learning has brought a fresh vitality to the super-resolution processing of remote sensing images. The learning-based methods effectively take full advantage of the spectral correlation and spatial correlation present in remote sensing images, enabling the establishment of nonlinear connections between low-resolution (LR) and high-resolution (HR) images. Initially, the research focus of remote sensing image super-resolution mainly revolved around discussing the applicability of existing models to remote sensing images. Leibel et al. retrained the SRCNN model on Sentinel 2 images and demonstrated its ability to enhance single-band images from Sentinel 2 [26]. Tuna et al. employed the SRCNN and VDSR models in conjunction with the IHS transform on SPOT and Pleiades satellite remote sensing images to enhance their resolution by a multiplicative factor of 2, 3, and 4 [27]. Since 2017, there has been a proliferation of specialized super-resolution models designed for remote sensing applications. Lei et al. introduced a novel approach known as the combined local–global network (LGCNet) to acquire multi-level representations of remote sensing (RS) images by integrating outputs from various convolutional layers. Through experimentation on a publicly accessible remote sensing dataset (UC Merced), it was demonstrated that the proposed model exhibited superior accuracy and visual performance compared to both SRCNN and FSRCNN [28]. Xu et al. introduced the deep memory connected network (DMCN), which leverages memory connections to integrate image details with environmental information [29]. Furthermore, the incorporation of dense residual blocks serves as an effective approach to enhance the efficacy of convolutional neural network (CNN)-based architectures. Jiang et al. introduced a deep distillation recursive network (DDRN) to address the challenge of video satellite image super-resolution [30]. The DDRN comprises a series of ultra-dense residual blocks (UDB), a multi-scale purification unit (MSPU), and a reconstruction module. The MSPU module specifically addresses the loss of high-frequency components during the propagation of information. Deeba et al. have introduced the wide remote sensing residual network (WRSR) as an advanced technique for super-resolution in remote sensing. This novel approach aims to enhance accuracy and minimize losses through three key strategies: widening the network, reducing its depth, and implementing additional weight-normalization operations [31]. Huan et al. contend that the utilization of a single up-sampling operation results in the loss of LR image information. To address this issue, they propose incorporating complementary blocks of global and local features in the reconstruction structure as a means of alleviating that problem [32]. Lu et al. proposed a multi-scale residual neural network (MRNN) based on multi-scale features of objects in remote sensing images [33]. The feature extraction module of the network extracts information from objects at various scales, including large, medium, and small scales. Subsequently, a fusion network is employed to effectively integrate the extracted features from different scales, thereby reconstructing the image in a manner that aligns with human visual perception.

Although CNN-based methods are widely used in various tasks and have achieved excellent performance, the homogeneous treatment of input data across channels imposes limitations on the representational capacity of convolutional neural networks (CNNs). To address these challenges, attention mechanisms have emerged as a viable solution, enhancing the representation of feature information and enabling the network to focus on salient features while suppressing irrelevant ones. The squeeze-and-excitation (SE) block, proposed by Hu et al., enhances the representation capability of the network by explicitly modeling the interdependencies between channels and adaptively recalibrating the channel feature responses [34]. Zhang et al. proposed a highly sophisticated residual channel attention network (RCAN) that incorporates a residual error (RIR) structure, enabling the network to emphasize the learning of high-frequency information [35]. Woo et al. presented the convolutional block attention module (CBAM), which utilizes both channel and spatial attention module mappings to sequentially infer attention mapping. This attention mapping is subsequently multiplied with the input feature mapping to achieve adaptive feature refinement [36]. Dai et al. proposed a deep second-order attention network (SAN) to enhance feature representation and feature correlation learning. They incorporated a second-order channel attention (SOCA) module, which utilized global covariance pooling to learn feature interdependencies and generate more discriminative representations [37]. Niu et al. argued that channel attention overlooks the correlation between different layers and presented the holistic attention network (HAN). HAN consists primarily of a layer attention module (LAM) and a channel-space attention module (CSAM). The LAM adaptively highlights hierarchical features by considering the correlations among different layers, while the CSAM learns the confidence level of each channel’s positions to selectively capture more informative features [38]. The majority of the aforementioned approaches exhibit a satisfactory performance. However, the intricate architecture of the developed attention module results in elevated operational expenses for remote sensing images. By incorporating channel attention and spatial attention in an optimized manner, pixel attention enables the acquisition of feature information using fewer parameters and with a reduced computational complexity [39]. Therefore, it is very suitable for super-resolution tasks of remote sensing images. In this paper, we proposed a lightweight pixel-wise attention residual network (PARNet) for remote sensing image enhancement. Compared with the existing CNN-based sharpening methods, the main contributions of this paper can be summarized as follow:

• We propose a lightweight SR network to improve the spatial resolution of optical remote sensing images.
• Our method can raise the spatial resolution of Landsat 8 bands at 30 m into 10 m, which is also applicable to other satellite image super-resolution enhancement tasks, such as Sentinel-2.
• For the first time, the pixel attention mechanism is included in the super resolution fusion task of remote sensing images.
• Our method effectively identifies information on land cover and land use change (LULC), atmospheric cloud disturbance, and surface smog, and makes reasonable judgments in the fusion process.

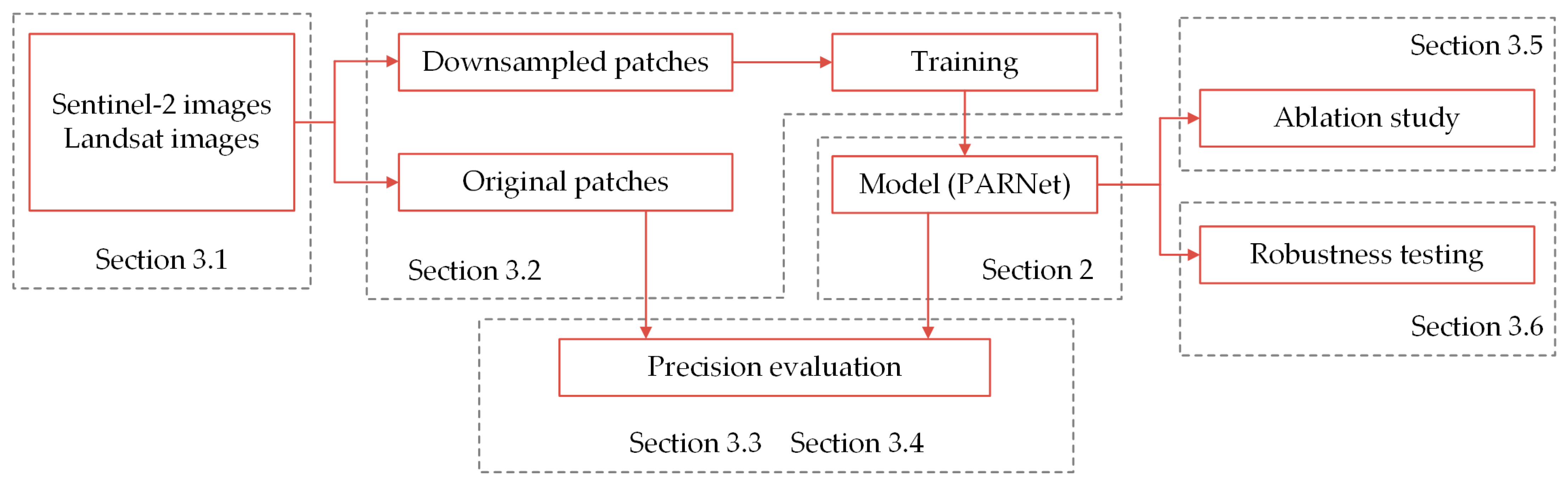
This paper is organized in the following way. As shown in Figure 1, the structure of the proposed PARNet network is presented in detail in Section 2. In Section 3, we evaluate the experimental results quantitatively and qualitatively in terms of accuracy metrics and visual presentation, verifying the necessity of pixel-wise attention mechanism and reconstruction module, and test the anti-interference capability of our model on Landsat data. Section 4 gives a full discussion of the whole experiment and suggests the next focus. Finally, Section 5 concludes the paper.

2. Proposed Method

In this paper, we propose a method termed pixel-wise attention residual network (PARNet). As shown in Figure 2, The proposed method consists of three modules: the feature extraction module, feature fusion module, and feature mapping module. The details are introduced as follows.

2.1. Feature Extracting

The feature extraction module first extracts the shallow features from the concatenated LR and HR bands using a convolution operation, followed by deeper features from a series of aligned Resblocks. All features are connected in the channel dimension and the number of channels is subsequently reduced by a convolution layer.

The structure of our Resblock is shown in Figure 3. Deeper and more complex feature information is extracted from two identical parallel branches and then fused prior to the output of the convolution layer. Each branch consists of a constant scale layer behind the convolution layer and the activation layer. Besides this, to transmit the spectral information, the input of Resblock is stacked directly on the output side, using a skip connection layer. The operation of the m-th Resblock can be expressed as:

$$\{\begin{array}{l}{x}_{m_1}=\lambda \phi (w_{m_1}\times x_{m-1}+b_{m_1})\\ x_{m_2}=\lambda \phi (w_{m_2}\times x_{m-1}+b_{m_2})\\ x_{cat}=Cat(x_{m1},x_{m2})\\ x_m=w_{m3}\times x_{cat}+b_{m3}+x_{m-1}\end{array},$$

(1)

where x_m1, x_m2, and x_cat are intermediate results, λ is the residual scaling with a factor of 0.2, {w_m, b_m} is the weight matrix and the basis of the convolution in Resblock, x_m−1 and x_m denote the input and the output of Resblock, respectively, and φ refers to the LeakyRelu activation function, which is specifically designed for solving the Dead ReLU problem.

The output of each Resblock is connected to the channel dimension. To prevent the generation of overly complex models, the number of channels is controlled by a 3 × 3 convolutional layer to produce a deeper feature map before feature fusion. These operations can be expressed as follows:

$$\{\begin{array}{l}{x}_{cat}=Cat(x_1,x_2,\cdots ,x_m)\\ x_{out}=w_{out}\times x_{cat}+b_{out}\end{array},$$

(2)

where x₁, x₂, and x_m are the outputs corresponding to each Resblock, {w_out, b_out} is the weight matrix and the basis of the convolution, and x_out is the final depth feature maps of the whole feature extraction module.

2.2. Pixel-Wise Attention Scheme

Before presenting the feature fusion module, it is necessary to introduce the pixel-wise attention scheme. Inspired by channel attention [34] and spatial attention [36], the pixel-wise attention scheme was first proposed in AIM 2020 challenge [39]. As shown in Figure 4, pixel-wise attention uses only a 1 × 1 convolution layer and a sigmoid function to generate a C × H × W attention map, which is then multiplied by the input features. Note that C is the number of channels, while H and W are the height and width of the features.

The PA layer can be described as

$$x_k=f_{PA}(x_{k-1})\times x_{k-1}$$

(3)

where f_PA(·)is the structure of a 1 × 1 convolution layer, followed by a sigmoid function. x_k−1 and x_k denote the input and output feature maps of PA.

2.3. Feature Fusing

It should be noted that in previous work on SR, the reconstruction module fundamentally comprised mainly up-sampling, a fully connected layer, and a convolution layer [40,41,42]. Few researchers have placed attention mechanisms at the feature fusion stage.

In this work, we propose the PA-based reconstruction (PA-REC) component. Experimental results show that introducing PA could significantly improve the final performance with little parameter cost. As shown in Figure 5, a PA layer is adopted between two convolution layers, each of which is tracked by a LeakyRelu activator. Subsequently, a convolution layer makes the channel of the spatial residual image to be the same as the up-sampled LR bands, followed by a constant scaling layer. The PA–REC can be formulated as follows:

$$\{\begin{array}{l}{x}_{f_1}=\phi (w_{f_1}\times x_1+b_{f_1})\\ x_{f_2}=\phi (f_{PA}(x_{f_1})\times x_{f_1})\\ x_{f_3}=\phi (w_{f_3}\times x_{f_2}+b_{f_3})\\ x_2=\lambda (w_{f_4}\times x_{f_3}+b_{f_4})\end{array},$$

(4)

where x₁ and x₂ denote the input and output of this component, {w_f, b_f} mean the weight matrix and basis of the convolution layers of the PA-REC, and x_f1, x_f2, and x_f3 are the intermediate results.

2.4. Feature Mapping

Given that the HR target has the same spectral content as the input LR, the fused residual feature map is added directly to the up-sampled low-resolution images to maintain the fidelity of the spectrum.

3. Experiments

3.1. Data

A brief introduction about Sentinel-2, Landsat 8, and Landsat 9 is given here. Sentinel-2 consists of two identical satellites, Sentinel-2A and Sentinel-2B, with a revisit period of ten days for one satellite and 5-day revisit period for the two satellites. Sentinel-2 carries a multispectral imager (MSI) covering 13 spectral bands with 4 bands at 10 m (B2–B4, B8), 6 bands at 20 m (B5–B7, B8a, B11–B12), and 3 bands at 90 m (B1, B9–B10). The Landsat8 satellite carries an operational land imager (OLI) consisting of seven multispectral bands (B1–B7) with a resolution of 30 m, a panchromatic band of 15 m (B8), and a cirrus band of 30 m (B9). Landsat 9 builds upon the observation capabilities established by Landsat 8, enhancing the radiometric resolution of the OLI-2 sensor from 12 bits in Landsat 8 to an even more advanced 14 bits. This heightened radiometric resolution enables the sensor to discern more subtle variations, particularly in dimmer regions such as bodies of water or dense forests. For convenience, we have reconciled Landsat 8 and 9 as Landsat in the following sections. A description of the Sentinel-2 and Landsat parameters is described in

Table 1. Information for all bands of the Sentinel-2 MSI sensor.

	Band	Wavelength (nm)	Resolution (m)
Visible	B1	433–453	60
	B2	458–523	10
	B3	543–578	10
Red	B4	650–680	10
Red-Edge	B5	698–713	20
	B6	733–748	20
	B7	773–793	20
Near-Infrared	B8	785–900	10
	B8a	855–875	20
Water Vapour	B9	935–955	60
SWIR-Cirrus	B10	1360–1390	60
SWIR	B11	1565–1655	20
	B12	2100–2280	20

and

Table 2. Information for all bands of the Landsat OLI sensor.

	Band	Wavelength for Landsat-8 (nm)	Wavelength for Landsat-9 (nm)	Resolution (m)
Visible	B1	433–453	430–450	30
	B2	450–515	450–510	30
	B3	525–600	530–590	30
Red	B4	630–680	640–670	30
Near-Infrared	B5	845–885	850–880	30
SWIR	B6	1560–1660	1570–1650	30
	B7	1360–1390	1360–1380	30
Panchromatic	B8	500–680	500–680	15

.

Four level 1C products of Sentinel-2 and Landsat were acquired from the European Space Agency (ESA) Copernicus Open Access Center (https://scihub.copernicus.eu/, accessed on 31 December 2022) and the United States Geological Survey (USGS) Earth Explorer (https://earthexplorer.usgs.gov/, accessed on 1 January 2023), respectively. Four pairs of Landsat–Sentinel images were selected globally for training, as shown in the black box in Figure 6A–E, showing the geographic locations in detail. Vignettes of the four image pairs and respective acquisition times are shown in the top right panel. Of these, the first group had the longest collection interval between Landsat imagery and Sentinel-2 imagery, 13 days apart, followed by the third group, 1 day apart, and the remaining two groups were collected on the same day. In addition, the first two pairs represent the agricultural region of Florida, USA, and the Andes in western Argentina, both which have a simple composition of geomorphological types, while the other two cover the Yangtze River Delta and Pearl River Delta of China, respectively. Each landform type is complex and contains at least three different types of cover. All images were captured under low cloud cover conditions.

3.2. Experimental Details

N_2× represents the 20 m→10 m network for Sentinel-2 images and N_3× represents the 45 m→15 m network for Landsat images. Two networks were trained separately with different super-resolution factors, which were f = 2 for the N_2× and f = 3 for the N_3×.

For the N_2× network, we separated the Sentinel-2 bands into three sets A = {B2, B3, B4, B8} (GSD = 10 m), B = {B5, B6, B7, B8a, B11, B12} (GSD = 20 m), and C= {B1, B9} (GSD = 60 m). As B10 has poor radiometric quality, it was excluded. The dataset C was also excluded here, as we only focus on the N_2× network.

For the N_3× network, the Landsat images were first cropped to the same coverage as Sentinel-2, which is 7320 × 7320 in the panchromatic (GSD = 15 m) band and 3660 × 3660 in the multispectral (GSD = 30 m) bands, respectively. The Landsat bands were also separated into two sets, S = {B1, B2, B3, B4, B5, B6, B7} (GSD = 30 m) and P = {B8} (GSD = 15 m). Due to the limitations of the equipment, we super-resolved a portion of the spectral bands in S, which is D = {B1, B2, B3, B4}.

N_2× and N_3× are similar in many ways except for the input. N_2× takes the bands in B as the LR input and produces SR images with 10 m GSD using the HR information from 10 m bands, while N_3× takes 30 m bands in D into 10 m using the information from the panchromatic band B8 and 10 m bands of Sentinel-2.

Since images with a GSD = 10 m corresponding to bands of 20 m do not exist in reality, these down-sampled images are used as the input to generate the SR image to its original GSD according to Wald’s protocol [43]. The original images are then used as validation data to assess the accuracy of the model we trained. As shown in Figure 7, the Gaussian filter with a pixel standard deviation σ = 1/s pixels was used to perform blurring on the original image. Then, we down-sampled the blurry image by averaging s × s windows, where s = 2 for N_2× and s = 3 for N_3×.

As shown in

Table 3. Training and testing split.

Network	GSD	Patches	Split
$N_{2\times }$	10 m 20 m	(90, 90) (45, 45)	Training	80%
			Validation	10%
			Testing	10%
$N_{3\times }$	10 m	(60, 60)	Training	80%
	15 m	(40, 40)	Validation	10%
	30 m	(20, 20)	Testing	10%

, we segmented the entire down-sampled image into small patches without duplicate pixels. The patch size for N_2× is 90 × 90 at 10 m bands and 45 × 45 at 20 m bands. For N_3×, the patch size of the input 10 m bands of Sentinel-2, the multispectral bands, and the panchromatic band of Landsat are 60 × 60, 40 × 40, and 20 × 20, respectively. A total of 3721 patches were sampled per image. Among them, 80% are used as training data, 10% are used as validation data, and the remaining 10% are used as testing data.

All networks are implemented in the Keras framework with TensorFlow 2.4 as the back end. The training is performed in the GPU mode of an Intel core I9 CPU equipped with Windows 3.6 GHz, NVIDIA GeForce RTX 2080, and 16 GB of RAM. Each model was trained for 200 epochs with batch = 10 batch size, L1-norm as the loss function, and Nadam [44] with β₁ = 0.9, β₂ = 0.999, and ɛ = 10⁻⁸ as the optimizer. We use an initial learning rate of l r = 1 × 10⁻⁴, which is halved whenever the validation loss does not decrease for 1 consecutive epoch. To ensure the stability of the optimization, we normalize the raw 0~10,000 reflectance values to 0–1 prior to processing.

3.3. Quantitative Evaluation Metrics

To assess the effectiveness of our method, we take the deep-learning-based methods of SRCRR and DSenNet as the benchmark methods. All parameters of the baseline are set as suggested in the original publication. In this paper, we adopted five indicators for quantitative assessment, namely the root mean square error (RMSE), signal-to-reconstruction ratio error (SRE), universal image quality index (UIQ) [45], peak signal-to-noise ratio (PSNR), and the Brenner gradient function (Brenner). Among these assessment metrics, RMSE, SRE, UIQ, and PSNR are employed for evaluating the performance of the downscaling experiments. On the other hand, the Brenner metric is utilized for evaluating the quality of the original images. In what follows, we use y to represent the reference image, x to present the super-resolved image, and µ and σ stand for the mean and standard deviation, respectively.

The root mean square error (RMSE) measures the overall spectral differences between the reference image and the super-resolved image; the smaller, the better (n is the number of pixels in x).

$$RMSE(x,y)=\sqrt{\frac{1}{n}{\displaystyle \sum {(y-x)}^2}}$$

(5)

The signal-to-reconstruction ratio error (SRE) is measured in decibels (dB), which measures the error relative to the average image intensity, making the error comparable between images of different brightness; the higher, the better.

$$SRE(x,y)=10{\log }_{10}\frac{{\mu }_x^2}{\Vert y-x\Vert 2/n}$$

(6)

The universal image quality index (UIQI), which is a general objective image quality index, portrays the distortion of the reconstructed image with respect to the reference image in three aspects: correlation loss, brightness distortion, and contrast distortion. UIQI is unitless, with a maximum value of 1. In general, the larger the UIQI value, the closer the reconstructed image is to the reference image.

$$UIQI(x,y)=\frac{{\sigma }_{xy}}{{\sigma }_x{\sigma }_y}\cdot \frac{2{\mu }_x\cdot {\mu }_y}{{({\mu }_x)}^2+{({\mu }_y)}^2}\cdot \frac{2{\sigma }_x{\sigma }_y}{{\sigma }_x^2+{\sigma }_y^2}$$

(7)

The peak signal-to-noise ratio (PSNR) measures the quality of the reconstructed image, and the value varies from 0 to infinity; the higher the PSNR, the better the quality of the reconstructed image, as more detailed information is recovered by the model based on the coarse image. Here, Max(y) takes the maximal value of y.

$$PSNR(x,y)=20{\log }_{10}(\frac{Max(y)}{RMSE(y,x)})$$

(8)

The gradient function (Brenner) serves as a widely used metric for assessing image sharpness. It is calculated as the squared difference in grayscale values separated by two pixels. A higher Brenner value indicates a sharper image.

$$Brenner={\displaystyle {\sum }_y{{\displaystyle {\sum }_x(f(x+2,y)-f(x,y))}}^2}$$

(9)

where f(x, y) represents the gray value of pixel (x, y) corresponding to image f.

3.4. Experimental Results

In this section, we compare our results with the bicubic up-sampling methods, SRCNN and DSen2, using five metric indicators: RMSE, SRE, UIQ, PSNR, and Brenner. SRCNN, which is a pioneering deep learning model in the field of super-resolution reconstruction, possesses a simple structure, with only three convolutional layers having the kernel sizes of 9 × 9, 1 × 1, and 5 × 5, respectively [46]. To achieve networks capable of super-resolving arbitrary Sentinel 2 images without additional training, Lanaras et al. conducted extensive sampling on a global scale and proposed the DSen2 model. This model employs a series of residual blocks comprising convolutional layers, activation functions, and constant scaling to extract high-frequency information from the input layer, which is then added to the LR image as the output. Being an end-to-end learning network for image data, DSen2 can also be applied to other super-resolution tasks involving multispectral sensors of varying resolutions [47].

3.4.1. Evaluation at a Lower Scale

N_2× Sentinel-2 SR. The sharpening results for each Sentinel-2 datum on the test set are shown in

Table 4. Results of the sharpening 20 m bands for Sentinel-2, evaluated at a lower scale (input 40 m, output 20 m). The best results are shown in bold.

		RMSE	SRE	UIQ	PSNR
Florida	Bicubic	0.0074	26.0532	0.9518	69.7297
	SRCNN	0.0034	29.7953	0.9885	84.5335
	DSen2	0.0027	30.8831	0.9926	89.2141
	PARNet	0.0026	31.1194	0.9934	90.1849
Andes	Bicubic	0.0089	33.8328	0.9542	76.7907
	SRCNN	0.0046	36.8410	0.9874	89.2641
	DSen2	0.0031	38.8696	0.9943	97.1335
	PARNet	0.0030	39.0517	0.9947	97.8848
Yangtze River Delta	Bicubic	0.0070	25.1262	0.9086	67.5037
	SRCNN	0.0031	29.1560	0.9837	84.5205
	DSen2	0.0024	30.2961	0.9901	89.0881
	PARNet	0.0024	30.4028	0.9907	89.5992
Pearl River Delta	Bicubic	0.0081	21.5454	0.9283	64.2546
	SRCNN	0.0031	26.1132	0.9890	83.7916
	DSen2	0.0027	26.8411	0.9922	86.6477
	PARNet	0.0026	26.9198	0.9925	86.9322

, where the data in the table are average values from 20 m bands. It can be seen that the deep-learning-based method is significantly better than the interpolation-based bicubic up-sampling method. Compared with SRCNN, DSen2 further improves accuracy, especially in PSNR, showing a significant improvement of 7.8694 on the Andes dataset. Our method slightly outperformed DSen2, with a decrease of ~0.15 in SRE and an increase of ~0.6294 dB in PSNR.

N_3× Landsat SR.

Table 5. Results of the sharpening bands for Landsat were evaluated at a lower scale (input 90 m, output 30 m). The best results are shown in bold.

		RMSE	SRE	UIQ	PSNR
Florida	Bicubic	0.0112	17.6273	0.8738	61.2077
	SRCNN	0.0051	21.1488	0.9736	76.4707
	DSen2	0.0047	21.5048	0.9774	78.0028
	PARNet	0.0045	21.6874	0.9793	78.8305
Andes	Bicubic	0.0096	14.7899	0.8266	59.2376
	SRCNN	0.0038	19.0964	0.9743	77.1665
	DSen2	0.0036	19.3724	0.9774	78.3122
	PARNet	0.0035	19.5349	0.9796	79.1877
Yangtze River Delta	Bicubic	0.005	18.5645	0.7844	65.2543
	SRCNN	0.0024	21.7451	0.9502	78.4773
	DSen2	0.0021	22.6235	0.9644	81.8125
	PARNet	0.0020	22.8246	0.9682	82.9704
Pearl River Delta	Bicubic	0.0104	26.0121	0.8717	64.9336
	SRCNN	0.0046	29.7617	0.9764	80.6697
	DSen2	0.0043	30.1678	0.9801	82.3914
	PARNet	0.0040	30.4069	0.9821	83.5550

shows the average sharpening results of Landsat. Our method shows a visible advantage over others on Landsat super-resolution, with a 1.8 × 10⁻⁴ decrease in RMSE and an increase of ~0.1963 in SRE, and ~1.006 dB in PSNR.

Figure 8 and Figure 9 further show the density scatter plots of the reference bands and the fused bands generated by DSen2, SRCNN, and PARNet in bands 1–4. Validation data in the Pearl River Delta from 5 December 2021 show that the fusion results are generally close to the true value across all spectral bands. Compared with other methods, our method is closer to the true value. The advantage of our method was more apparent in the Yangtze River Delta on 26 February 2022, where our result remained symmetrically distributed on either side of the diagonal, while the scatterplots in which DSen2 and SRCNN lie show significant deviations. This phenomenon is due to the fact that DSen2 and SRCNN do not mine the deep features of the image sufficiently. Of these, the architecture of SRCNN is the shallowest, consisting of only three convolutional layers, which are unable to achieve the deep features of the image, and as a result, the slopes of the regression equation in the scatter plot are also the lowest. Note that the slopes of DSen2 are slightly larger than those of the SRCNN, but generally, this is by less than 0.6, and the percentage of the depth features lost should not be underestimated. For our method, the slope of the regression equation is close to one on both B1 and B4, and rises to 0.881 on B2, with only slight overfitting on B3. These results indicate that our method is far superior to DSen2 and SRCNN in its ability to explore deep features.

In addition to the advantages in quality evaluation metrics and density scatter plots, our method also shows satisfactory results in terms of the number of model parameters and model size.

Table 6. Comparison of the number of model parameters and model size.

	SRCNN	DSen2	PARNet
Model Params	52,004	1,786,116	836,356
Memory Size (MB)	0.644	20.5	9.85

shows the comparison of the number of model parameters and model size between SRCNN, DSen2, and PARNet, where the model size is in MB. Among them, the SRCNN model has the simplest structure, with only three convolutional layers, so the model parameters and memory size are the smallest, which are 52,004 and 644 KB, respectively. Followed by our PARNet with 836,356 and 9.85 MB. The DSen2 model has the maximum number of model parameters and memory size, which are 52,004 and 644 KB, respectively. Compared with DSen2, the number of model parameters and memory size of our method are less than half of DSen2. Combined with the previous quality evaluation performance, it can be concluded that our method is a lightweight and accurate model.

3.4.2. Evaluation at the Original Scale

In order to prove that our method is equally applicable to real-scale Sentinel-2, we performed an additional verification on the original dataset without down-sampling. As shown in Figure 10, the super-resolved image is clearly sharper and brings out additional detail compared to the respective initial input. Figure 11 shows a further check on the original Landsat dataset. Compared to the original 20 m scene, the super-resolved image carries over the extensive feature information from Sentinel-2 imagery. The previously blurry patches of color morphed into clear exterior shapes. As can be seen from the results, the super-resolved images show higher similarity to the original RGB images.

In the human perception, there is little difference in the super-resolution results obtained from three deep-learning-based methods, whether using Sentinel-2 data or Landsat images. Therefore, we performed additional evaluations using the Brenner gradient, as shown in

Table 7. Results of the sharpening bands for Sentinel-2, evaluated at the original scale (input 20 m, output 10 m). The best results are shown in bold.

		B5	B6	B7	B8a
Brenner	Bicubic	0.4440	0.5883	0.8133	0.9799
	SRCNN	1.5489	2.0811	2.8447	3.3578
	DSen2	1.5798	2.1246	2.8918	3.3844
	PARNet	1.5804	2.1267	2.8989	3.3801

and

Table 8. Results of the sharpening bands for Landsat, evaluated at the original scale (input 30 m, output 10 m). The best results are shown in bold.

		B1	B2	B3	B4
Brenner	Bicubic	0.1198	0.1464	0.1907	0.3222
	SRCNN	0.5885	0.7074	0.9220	1.5432
	DSen2	0.6219	0.7599	0.9693	1.5564
	PARNet	0.6344	0.7758	0.9708	1.5975

. It is evident that the Brenner values derived from the deep learning methods exhibit a clear advantage. Furthermore, the results generated by DSen2 are comparable to our PARNet model, but surpass SRCNN. On the first three bands of Sentinel-2, the PARNet model slightly outperforms DSen2 and consistently outperforms DSen2 across all four bands of Landsat. Considering that our network width is half of DSen2 and the model parameters are also less than half of DSen2, we assert that our proposed model is more cost effective.

3.5. The Impact of the PA–RECblock

Here, we confirmed the influence of the PA–REC block on network performance through an Ablation study. In the first place, we removed the PA–REC block from our PARNet network and denoted it as $N_{3\times }^1$. Second, $N_{3\times }^2$ contains the PA–REC block without the PA layer. In contrast, $N_{3\times }^3$ has the same structure as PARNet.

As shown in

Table 9. The impact of the PA–REC block. The symbol ✓ represents the inclusion relationship and refers to the non-inclusion relationship. The values in the table are the average of the four Landsat datasets. The best results are shown in bold.

Model	${\mathit{N}}_{3\mathit{\times }}^1$	${\mathit{N}}_{3\mathit{\times }}^2$	${\mathit{N}}_{3\mathit{\times }}^3$
PA			✓
REC		✓	✓
RMSE	0.00385	0.00352	0.00351
SRE	22.95978	23.60991	23.61343
UIQI	0.97223	0.97720	0.97733
PSNR	79.17943	81.08414	81.13586

, after adding the PA–REC block, all evaluation metrics improved compared to the initial model $N_{3\times }^1$, particularly on the SRE and PSNR, which have increased by 0.65365 and 1.95643 dB, respectively. In addition, even though there is no PA layer in the REC block, the structure consisting of convolution layers, activation functions, and constant scaling can still achieve a high accuracy result and the addition of the PA layer results in the best performance.

3.6. Robustness of the Model

Due to variations in the sampling times of multiple sensors, the images captured by different sensors are not completely identical and exhibit dissimilarities. These dissimilarities manifest in various aspects, including changes in land use and land cover (LULC), atmospheric cloud cover, traces of human activity, etc. In the case of low-resolution ground truth (GT) images, the divergent high-resolution (HR) data can provide misleading guidance. Consequently, the ability to mitigate the interference caused by error information becomes a critical challenge for multi-sensor image super-resolution, and it reflects the robustness of the model. This section investigates the interference resistance of our model to error messages.

As shown in Figure 12, the differences between images from different sampling times are common, with agricultural land changing from vegetation to bare soil in only a single day (a–c), not to mention longer time intervals. Compared with (d), the bare land in (f) increased as a result of crop harvesting. In addition to the LULC changes, traces of human activity also contribute to this difference. On 18 January 2022, the Sentinel-2 MSI sensor captured a scene of heavy smoke from the ground burning in (g), while the Landsat satellite missed this record by coming in 13 days late. On the same day, atmospheric cloud cover prevented Sentinel-2 from being able to capture a clear image in (j), which was avertedly avoided by the late Landsat, which obtained a non-cloud-covered image. Even though there are so many differences between the images captured by Sentinel-2 MSL and Landsat OLI, the fused images still demonstrate a tendency toward the original state, while achieving richer spatial detail. These findings indicate that our network is capable of identifying the changing scenes and making reasonable judgments about the true appearance of the changed region.

4. Discussion

To meet the demand for high spatial and temporal resolutions of remote sensing images, we proposed a lightweight pixel-wise attention residual network (PARNet) for remote sensing super-resolution tasks, which can harmonize the differences in spatial resolution between different sensors and add information about spatial detail to the sensor images with a low and medium spatial resolution, with the help of sensor images with high spatial resolution, thereby achieving a level of spatial resolution comparable to that of high spatial resolution images. The resulting remote sensing products with high spatial and temporal resolution can better serve in applications such as change detection and time series analysis.

In comparison to the existing models such as SRCNN and DSen2, our algorithm put more effort into mining rich local characteristics. As shown in Figure 8 and Figure 9, the predicted values from our method are significantly closer to the reference values on the Pearl River Delta dataset, as well as the Yangtze River Delta dataset. Most importantly, we introduce the pixel-wise attention mechanism into the super-resolution of remote sensing images for the first time. Pixel-wise attention, as a combination of spatial attention and channel attention, provides a more precise regulation of the correlation between feature information, thereby improving the learning and reconstruction efficiency of the network. As Table 9 indicates, the fusion network obtained the best performance when delivering the PA layer to the REC block. Alongside that, although we introduced the pixel-wise attention mechanism into the network framework, it should be noted that the parameters of our network are controlled around 836 K, which is less than half of the 1786 K parameters in DSen2, and outperform DSen2 in all of the quality assessment metrics referenced in this paper. These results reveal that our network achieves an improved balance between convergence performance and computational cost.

Due to the nonuniform acquisition times, the images collected by various sensors are not entirely identical. These variances include changes in LULC, atmospheric cloud cover, human activity traces, etc. For low-resolution GT images, the discrepant HR provides a kind of misleading guidance. Therefore, the ability to avoid the interference of error information is a problem to be faced by multi-sensor image super-resolution, and is a reflection of the robustness of the model. We also explored the interference resistance of our model to error messages. The results in Figure 12 indicate that our method can successfully identify the changing scenes and make reasonable judgements about the true appearance of the changed region, which indicates the high robustness of our model. In future research, a greater emphasis will be placed on establishing super-resolution products of remote sensing images with high spatial and temporal coverage, and applying them to specific environmental monitoring tasks to assign the super-resolution technology a greater role.

5. Conclusions

In this paper, we proposed a lightweight pixel-wise attention residual network (PARNet) for super-resolving optical remote sensing images. The proposed method is generalizable and can be applied to different super-resolution scenarios of remote sensing images. Compared with the existing deep-learning-based methods, the major advantage of our method is that we incorporate the pixel-wise attention mechanism in the feature fusion step, which effectively improved the performance of the fusion network. The 3D feature map generated by pixel-attention adaptively adjusts the pixel-level features in all feature maps to enhance the more important feature weights, and it significantly improves the performance of the network. Furthermore, our model allows for effective control over a number of parameters, thereby reducing the computational costs associated with remote sensing image super-resolution tasks. Additionally, our model exhibits strong robustness against the interference of erroneous HR information. Our model shows significant improvements in the SRE and PSNR on four test datasets. Specifically, it achieves improvements of 0.15 dB and 0.629 dB for Sentinel-2 data, and 0.196 dB and 1 dB for Landsat data. These results indicate that the proposed method is competitive with existing methods.