Abstract
When vortex electromagnetic waves propagate through a turbulent atmosphere, the amplitude and phase of the electromagnetic waves are disturbed, creating the scintillation effect. According to the scintillation index of vortex waves, a new method of retrieving the turbulent refraction structure parameter was proposed using a genetic algorithm, and the feasibility of this method was verified by simulated experiments. The numerical results showed that the inversed value obtained by the genetic algorithm was close to the real parameter when the turbulent inner scale and outer scale were fixed. However, there was a gap between the inversed value and the real parameter when only the turbulent outer scale was fixed. These results suggest that vortex wave data can be used for turbulent refraction structure parameter inversion, and they provide new research directions for atmospheric remote sensing.
1. Introduction
Atmospheric turbulence is an irregular atmospheric motion composed of many atmospheric vortices of different sizes [1]. The turbulence enhances the vertical and horizontal exchange of momentum, heat, water vapor, and pollutants in the atmosphere [2]. In aeronautical meteorology, atmospheric turbulence has a significant impact on aircraft. It is well known that aircraft bumpiness caused by turbulence affects passengers’ flight experiences and increases aircraft fatigue damage [3,4]. Furthermore, flight attitude changes can make an aircraft difficult to control, leading to serious flight accidents [5,6]. Therefore, it is necessary to study atmospheric turbulence and its detection.
At present, the ultrasonic anemometer, the radiosonde, wind profile radar, lidar, and other instruments are commonly used to detect turbulence structure [7,8,9]. The ultrasonic anemometer has the advantages of providing a fast response, stable performance, simple maintenance, and high credibility; however, it can only obtain turbulence information for a single point, and it cannot obtain the vertical atmospheric profile [10]. A radiosonde can detect the whole atmospheric profile and calculate turbulence structure, although its spatio-temporal resolution is too sparse to be applied to actual early warnings [11]. The detecting principle of wind profile radar is based on the Doppler effect, and its sample space and stratification height are fixed [2,12]. It can probe horizontal and vertical wind velocity, signal-to-noise ratios, and the refraction structure constant at different heights to provide rich data for studying atmospheric turbulence. Moreover, it has other advantages, such as high spatial and temporal resolution, high precision, and high operational reliability. However, it can only be used to detect clear-air turbulence.
When light is transmitted in the atmosphere, its related characteristics also show irregular changes due to random variation in the atmospheric refraction structure, which leads to a series of turbulence effects. Therefore, an optical transmission method was developed to invert the atmospheric turbulence profile through the relationship between the optical turbulent effect and the atmospheric refraction structure parameters. Optical transmission methods include SCIDAR (scintillation detection and range), SLODAR (slope detection and ranging), MASS (multi-aperture scintillation sensor), S-DIMM+ (solar differential Image motion monitor plus), and RTS lidar (residual turbulent scintillation lidar), as well as the first continuous vertical turbulence monitor, 24hSHIMM. In the 1970s, Vernin and Roddier proposed SCIDAR, a method for measuring atmospheric turbulence using starlight scintillation that was based on Tatarskii’s research on the light intensity scintillation model proposed by the Kolmogorov theory [13]. SCIDDAR retrieves a turbulence profile using the covariance of two stars’ light intensity fluctuations, as observed by a large aperture telescope. Therefore, this method requires two stars in the observed angle, and it can be difficult to find an appropriate telescope location [14]. Inspired by SCIDAR, in 2000, Wilson proposed SLODAR to retrieve atmospheric turbulence profiles by measuring the wavefront slopes of binary stars and calculating their cross-correlations and autocorrelations [15]. Compared with SCIDAR, SLODAR is low-cost, but it cannot accurately measure near-surface turbulence intensity. MASS is a non-mainstream method based on light intensity scintillation, and it retrieves turbulence profiles by detecting the spatial scintillation characteristics of a single star [16]. However, its spatial resolution and accuracy are low, and so it needs to be combined with DIMM. In 2010, Scharmer and Van Werkhoven proposed the S-DIMM+ method for daytime detection, which was developed from the DIMM method, although it could not measure wind speed and required large aperture telescopes [17]. In 2020, Kovadlo et al. used wavefront sensor data to determine the altitudes of atmospheric turbulent layers within a boundary layer, and this method’s results were in agreement with typical altitudes [18]. RTS lidar uses backscattered light intensity fluctuations to retrieve turbulence parameters. However, its probing height can only be below 2 km, and its accuracy is affected by laser stability [19]. The 24hSHIMM method for continuously monitoring atmospheric optical turbulence is affected by sky background noise [20]. Although there are many detection methods derived from optical transmission theory, each has its own advantages and disadvantages. Therefore, the development of new detection methods has continued to be of interest.
In recent years, with the development of communication technology, a new wireless communication technology with orbital angular momentum, has been explored and applied [21,22]. In 2007, inspired by the study of vortex beams with orbital angular momentum (OAM), Thide et al., from the Swedish Institute of Space Physics, proposed the concept of an electromagnetic wave vortex (EM vortex) by combining the theories and technologies related to vortex beams [23]. The EM vortex was proposed to improve the capacity and efficiency of a communication system. In 2011, the St. George’s Island Lighthouse and the terrace of the Governor’s Palace in the Venice witnessed the world’s first 2.414 GHz EM vortex communication experiment [24]. The 442 m distance achieved may become an important milestone in wireless communication. Tsinghua University also tested a 27.5 km OAM communication in 2016, and these successful cases have brought hope to the communication sector [25]. However, vortex waves are prone to atmospheric turbulence during their propagation, resulting in a variety of disturbed effects, including scintillation, phase fluctuation, and spiral spectrum dispersion [26]. These disturbed effects can reflect the turbulence energy distribution and provide inspiration for the development of a new turbulence detection methods. Therefore, in this paper, we imitated the optical transmission method to retrieve the refraction structure parameter , reflecting the turbulence strength. Because vortex waves are generated simply and continuously and their band ranges vary, its application scenarios in meteorological detection are diverse. It is hoped that the research in this paper can provide some ideas for vortex waves to be applied in meteorological detection, such as for atmospheric duct inversion, cloud-based height determination, etc.
The remainder of this paper is organized as follows. Section 2 introduces the simulated model, including the vortex waves and turbulence spectrum. Then, the genetic algorithm and objective function for inversion are introduced. Section 3 presents the inversion results of the refraction structure parameter from the vortex waves. Finally, the conclusions of this work are summarized in Section 4.
2. Simulations and Inversion Methods
2.1. Vortex Waves Simulation
According to the basic theory of electrodynamics, an electromagnetic field carries not only linear momentum but also angular momentum. Angular momentum can be further divided into intrinsic and extrinsic rotations related to polarization. The external rotation of a particle is called the orbital angular momentum, and this parameter is related to the wave front. Therefore, the basic principle of simulating a vortex wave is that the ordinary electromagnetic wave superimposes a phase rotation factor related to the spatial phase angle . Since the Laguerre–Gaussian vortex wave is the most classical and easy to realize [27], the cylindrical coordinate system expression of the Laguerre–Gaussian wave with an OAM state transmitting along the z-axis is written as:
where , is the waist radius, is the wave length, is the topological charge, is the radial value, is the associated Laguerre polynomial, is the normalization constant, is the radius of the curvature, and is the Gouy phase-shift representing the additional phase-shift generated during the propagation of the Gaussian waves. Here, the topological charge can be any integer. When the topological charge is used, the center intensity of a vortex wave is zero, and the intensity has a hollow distribution.
Figure 1 shows the distribution of the intensities and the angle phases of vortex waves at their source and as transmitted for a distance in free space. A vacuum also causes energy dispersion and phase-changes in the vortex waves.

Figure 1.
The vortex waves propagate in a vacuum. (a,b) The intensity and phase of an electromagnetic wave before propagation. (c,d) The intensity and phase of an electromagnetic wave in free space.
2.2. Phase-Screen Simulating Turbulence
Atmospheric turbulence is the phenomenon of random changes in atmospheric density resulting in a random refractive index. The refraction structure parameter and the turbulence dissipation rate ε are commonly used in the study of turbulence characteristics. Here, was used to describe the inhomogeneity of atmospheric refractivity. Therefore, it was able to reflect the turbulence strength, and it was also affected by the background temperature and water vapor. ε represented the intensity of the dissipative process in which the turbulence pulsation energy was converted into heat energy, and it was able to directly indicate the turbulence intensity.
In order to simplify the transmission process of electromagnetic waves in turbulence, a common method is to simulate turbulence with a random phase-screen. At present, the main spectrums of a random phase-screen commonly used in theory and experiments are the Kolmogorov spectrum, Von Karman spectrum, Tatarskii spectrum, and Hill spectrum [28]. In this paper, the Kolmogorov spectrum was used for the numerical simulation, and the expression was as follows:
where and are wave numbers in the frequency spectra corresponding to the x-axis and y-axis, is the refraction structure parameter whose values represent the turbulence intensity with the unit m−2/3, is the outer scale and is the inner scale of atmospheric turbulence with the unit m, and .
The simulation of the vortex waves propagating in the random phase-screen was as follows:
I. We fixed the phase-screen size required for the simulation experiment and then divided the phase-screen size into .
II. We obtained the phase spectrum according to the refractivity fluctuation spectrum, which was calculated as follows:
III. Then, the variance in the phase-screen spectrum was obtained as follows:
where denotes the distance between two phase-screens along the z-axis and is the grid distance.
IV. The random phase-screen was obtained by fast Fourier transform as follows:
where FFT represents the fast Fourier transform operator and the parameter C is a complex random matrix where the mean value is 0 and the variance is 1. Its discrete form is:
In the above process, is the distance between two phase-screens along the z-axis and and are grid intervals in the x and y directions, respectively, where . Further, and are the number of grids in two directions, respectively, and are the lengths in the x and y directions of the phase plate, where and , and and are the frequency intervals in the x direction and the y direction. Lastly, A and B are Gaussian random numbers whose real and imaginary parts have a mean of 0 and a variance of 1.
If the power spectrum is used to simulate turbulence, the low-frequency components will be lost. Therefore, in order to increase the authenticity of the power spectrum, superimposed low-frequency subharmonics were adopted. On the basis of resampling Fourier low-frequency subharmonics, interpolation and merging were carried out. The discrete expression for generating sub-harmonics is:
where is the subharmonic series and the frequency intervals of the subharmonic are and . The phase after subharmonic compensation can be obtained by adding formula (7) to formula (6). The phase produced by this method contained more low-frequency information so as to improve the statistical characteristics of the phase simulation on a large scale.
When the vortex waves are transmitted in the atmospheric turbulence modeled by the phase screen method, the transmission process is divided into two parts [29]. In the first part, the vortex waves are directly affected by the atmospheric turbulence to produce an additional phase, which can be expressed in the cylindrical coordinate system as follows:
where denotes the additional phase caused by the turbulence and represents the vortex wave fields passing through the phase-screen. In addition to the turbulent effects, there is also a variational wavefront phase when the vortex waves travel in vacuum. Therefore, in the second part, the vortex waves fields become before the vortex wave propagates through the vacuum to the next phase-screen, and here, denotes the position of the next phase-screen [30]. Therefore, the vortex waves passing through the vacuum can be simulated as follows:
Step 1. The Fourier transform can be applied to the vortex wave fields to obtain the frequency domain .
Step 2. The vacuum phase factor can be added, as follows:
Step 3. The spatial field can be obtained by the inverse Fourier transform.
The vortex waves propagate through a phase screen and a vacuum whose distance is . According to the parameter settings of the phase screen method, the vortex waves propagate with new additional phases continuously until they reach the receiver.
2.3. Scintillation Index
When the vortex waves are transmitted in random media such as atmospheric turbulence, the fluctuations in the electromagnetic intensity are called scintillations [31]. The scintillation index (SI) is often used to describe the strength of this phenomenon. The SI is generally defined as:
where denotes the instantaneous strength of the receiving surface and represents the system average. Here, the electromagnetic field obtained by numerical simulation is a discrete field, and the average of the intensity can be approximated by
Some past studies have shown that the scintillation index and the refraction structure parameter have a numerical relationship [32], such as that seen in weak turbulence conditions, as follows:
where is a constant that can be measured according to the field measurement and , where is the wavelength of the electromagnetic wave. represents the detection range and is the refraction structure parameter to be retrieved. It can be seen from Equation (10) that there is an approximate nonlinear relationship between the SI and , which indicates that can be derived from the SI of the vortex waves.
2.4. Genetic Algorithm
In order to correlate the change in the scintillation index during turbulence with the refraction structure parameter , the corresponding mapping model was established using a genetic algorithm. A genetic algorithm (GA) is a type of algorithm that simulates the evolutionary process of natural selection [33]. It performs a multi-direction search by maintaining a population of potential solutions, and it supports the formation and exchange of this information in the population. A GA is a classic optimization algorithm, and they were first proposed in the 1970s. With its hidden parallelism and self-learning habit, a GA is suitable for dealing with large and changing data problems. Figure 2 shows the flow chart of a GA.
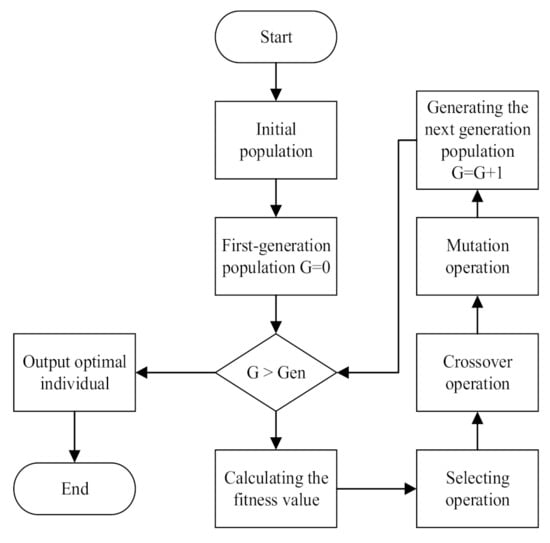
Figure 2.
The flow chart of GA implementation.
In a GA, all solution sets are called populations, and each individual in a population is called a chromosome. A chromosome is made up of multiple genes, each of which corresponds to a variable. The fitness value of a chromosome can be calculated from the objective function. Since the inversion problem is a minimum problem for each chromosome, the smaller the fitness value, the closer the variable is to the true value. In each iteration, the chromosome can be updated by crossover and mutation operations. In practical problems, the parameters of the group need to be set.
According to the literature [30], the value of ranges from 10−12 to 10−14 m−2/3. In general, the assigned value of close to the ground can be 10−13 m−2/3. Therefore, the initial value of was randomly generated from 10−12 to 10−14 m−2/3. The population size was set to 100, and the chromosome length was set to the number of variables to be calculated. Then, the individual fitness was set to 10−4. Before the global search, the refraction structure parameter was digitally encoded, and the crossover and mutation probabilities were set to 0.2. Binary coding was used for crossover evolution, and the optimal solution was decided by roulette wheel selection.
It was necessary to use a GA to optimize the objective function , which represents the fitness value of a chromosome, when retrieving the refraction structure parameters. The specific implementation steps were as follows:
- (1)
- Initialization: one-hundred solution sets were randomly generated in the range of 10−12 to 10−14 m−2/3 as the first generation population.
- (2)
- Fitness evaluation: after initialization, the fitness function value of each chromosome in the current population was calculated according to the fitness function.
- (3)
- Crossover and mutation evolution: binary conversion was performed on each gene, followed by crossover and mutation with a probability of 0.2, followed by conversion to decimal values.
- (4)
- Iteration: If the fitness values of all chromosomes were greater than the minimum value in the previous iteration, the chromosome with the smallest fitness value was replaced by the ones in the previous iteration so that the algorithm converged. The iteration was repeated until the maximum number of iterations was reached.
3. Results
3.1. Simulation of Vortex Waves Propagating in a Turbulent Flow
In order to simulate the turbulence spectrum, the refraction structure parameter was set to 4.5 × 10−13 m−2/3 according to the literature [34]. The turbulent inner scale was set as l0 = 1 mm, and the turbulent outer scale was set as L0 = 20 m. Then, the wavelength of the vortex waves was set as λ = 10−3 m, the topological charge was set as s = 4, the radial value was set as p = 0, the waist radius was set as w0 = 0.03 m, and the transmission distance was set as z = 100 m, and these values were set in the forward modeling process. The transmission spacing was set to ∆z = 10 m, and the phase-screen size was set to L = 5 m. Through the Kolmogorov spectrum simulation, the phase-screen could be generated as shown in Figure 3. In order to provide the real turbulence spectrum, low-frequency compensation was added to the high-frequency part.
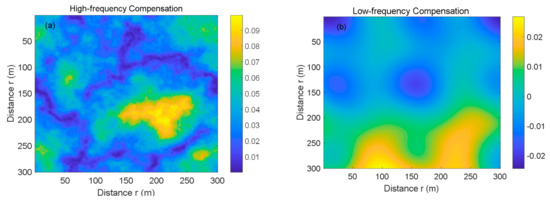
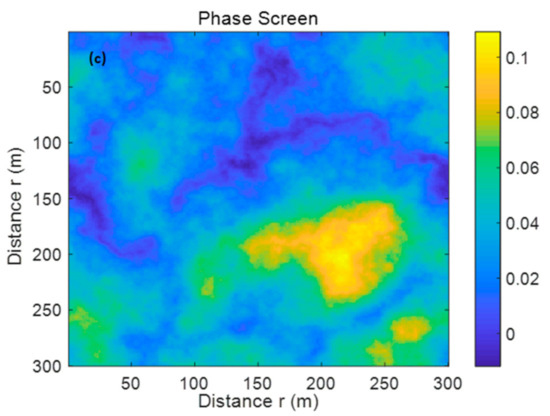
Figure 3.
The high- and low-frequency phase-screen was generated by the Kolmogorov spectrum. (a) High-frequency compensation, (b) low-frequency compensation, and (c) synthetic phase-screen.
After the action of the above phase-screen, as Figure 4 shows, the energy and the phase of the vortex waves appeared to be disturbed, which had a large impact on the communication system. However, it was beneficial for turbulence detection. Considering that the beam shapes of both the scalar and vectorial vortex beams appeared to break down after 700 m and no characteristic of a vortex could be observed, we set the transmission distance as z = 100 m, in accordance with the literature [35,36]. In the following experiment, we used this perturbation information to invert the corresponding refraction structure parameters of .
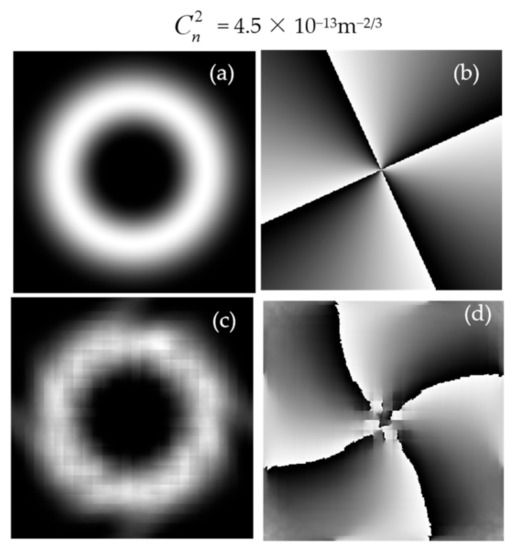
Figure 4.
The vortex waves propagating in the atmospheric turbulence, where is 4.5 × 10−13 m−2/3. (a,b) The intensity and the phase of the electromagnetic wave before propagation. (c,d) The intensity and the phase of the electromagnetic wave in the turbulence.
3.2. Retrieving the Structural Parameters
First, considering that the inner scale l0 and the outer scale L0 are known as l0 = 1 mm and L0 = 10 m, respectively, it was assumed that the real structure parameters were m−2/3.
Since the number of parameters to be retrieved in our paper was one, the number of genes was set as one, and the other parameters were set according to the previous genetic algorithm definition. Through iterative optimization, the optimal individual in the inversion process and the final optimal value obtained by the algorithm could be obtained. Figure 5 shows the convergence process of the inversion parameters and the distribution of the optimal values in the iterative process. It can be seen that the final optimal value, m−2/3, could be obtained after approximately 10 iterations, which was relatively closer to the true value. Therefore, it could be inferred that the GA was able to retrieve the turbulent refraction parameters with few iterations. However, whether the changes in the parameters of the GA had a positive effect on the improvement in the inversion results requires further research and discussion.
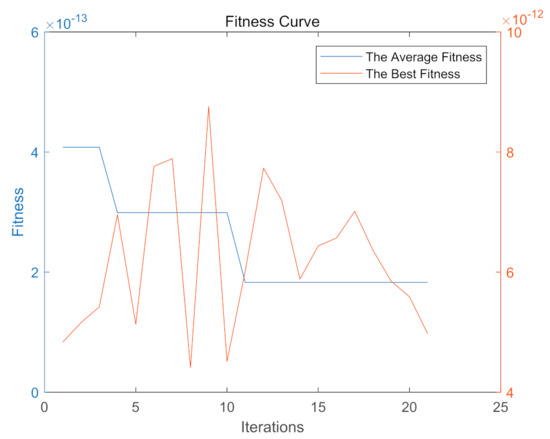
Figure 5.
The convergence process of the inversion parameters and the distribution of the average fitness and the best fitness in the iterative process. The blue line represents the average fitness in the iteration and the red line represents the best fitness of the population.
Further, we compared the distribution of the vortex wave intensity and the angle value obtained from the real and inversion parameters (). It can intuitively be seen in Figure 6 that there was little difference between the electromagnetic field intensity and the angle distribution for the two refraction parameters. After the subtraction of the electromagnetic field after turbulence, it was found that the retrieved intensity was similar. As shown in Figure 6, the maximum and minimum intensities were relatively small, while the radian values of the angle differences ranged from −π to π. Therefore, there was a certain difference in the angle distribution. In brief, this showed that the method proposed in this paper provided a new idea for the inversion of turbulent refraction parameters ().

Figure 6.
The difference between the electromagnetic field intensity and the angle distribution for the two refraction parameters. (a) Intensity difference and (b) angle distribution difference.
Then, due to the change in the inner scale l0 affecting the inversion of the parameter , it was assumed that the true l0 = 5 mm and m−2/3, and the outer scale was assumed to be L0 = 10 m while the inner scale was unknown. The GA was further used for inversion in this case. Figure 7 shows the convergence process of the inversion parameters and the optimal value distribution in the iterative process. Here, the average fitness was plotted in a y-log scale. The combination of the inner scale l0 and the turbulence parameters for converged and found better individuals after approximately seven iterations, where l0 = 2.205 mm and m−2/3. Similarly, by comparing the differences in the electromagnetic field intensity and the angle distribution, Figure 8 shows that there were large differences in the intensities and angle distributions of the vortex electromagnetic fields that were retrieved, which means that the addition of the inner scale parameter made the inversion problem more complex, and the uncertainty increased. Therefore, through the analysis of the above inversion process, we deduced that the scintillation index could be used to invert the turbulent refraction structure parameters. However, the number and setting of the inversion parameters had a large influence on the final results, which may also be a direction for future research.
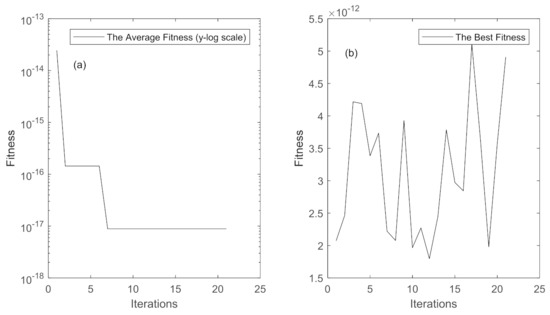
Figure 7.
The convergence process of the inversion parameters and the distribution of the average fitness and the best fitness in the iterative process. The line in (a) represents the average fitness in a y-log scale and the line in (b) represents the best fitness of the population.

Figure 8.
The difference in the electromagnetic field intensities and angle distributions between the two refraction parameters. (a) Intensity difference and (b) angle distribution difference.
4. Conclusions
Although there are many methods for detecting atmospheric turbulence, most continue to have some problems, such as large detection errors or inconvenience. Thus, developing new detection methods is still of notable interest in turbulence research. Therefore, according to the characteristics of vortex wave transmission in turbulence, this study proposed a new method for retrieving the turbulence structure parameters from vortex wave data and preliminarily discussed the inversion results by means of numerical simulations. The above experiments showed the following: (1) When considering the known inner and outer scales of turbulence, the refraction structure parameters retrieved from the vortex wave data were close to the simulated real values, and there were some tolerable errors. However, the differences in the distributions of the vortex wave’s angle obtained from the real value and the retrieved value were obvious. (2) When the outer scale was known and the inner scale was unknown, the intensities and angle distributions retrieved were quite different, which meant that the unknowability of the inner scale made the inversion problem more complicated, and the uncertainty of the inversion results increased. In general, the method proposed in this paper can roughly achieve the inversion of turbulent structure parameters.
However, the new method also has some shortcomings. Firstly, in the process of the multiphase simulation, the selection of the grid interval , the phase-screen interval , and the grid number had large effects on whether the phase-screen could correctly reflect the change characteristics of the turbulence [37]. Therefore, the rationality of the parameter setting requires further discussion. Secondly, the vortex wave’s own parameters, such as the wavelength , waist radius , topological charge , and inner and outer scale size, also affected the vortex wave transmission characteristics, and so the setting of these parameters also requires further study. Finally, the application of the new method to actual detection data may also be a future research focus.
Author Contributions
Methodology, Q.L.; validation, Z.S., S.Z. and P.G.; investigation, Z.L.; resources, M.H. and J.G.; writing—original draft preparation, Q.L. and Z.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Natural Science Foundation of Hunan Province, grant number 2021JJ40668, and the Research Projects of the National University of Defense Technology, grant number ZK19-21.
Data Availability Statement
The data can be downloaded from: Qixiang, L. (17 November 2022). A Preliminary Study on the Inversion Method of the Refraction Structure Parameter from the Vortex Electromagnetic Waves (Version 1.0). 4TU. ResearchData. doi: https://figshare.com/s/ea1a4df236113b1ce119 (accessed on 21 November 2022).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Wacławczyk, M.; Nowak, J.L.; Siebert, H.; Malinowski, S.P. Detecting Nonequilibrium States in Atmospheric Turbulence. J. Atmos. Sci. 2022, 79, 2757–2772. [Google Scholar] [CrossRef]
- Ren, Y.; Zhang, H.; Zhang, X.; Wu, B.; Cai, X.; Song, Y.; Zhu, T. Coupled-decoupled turbulence structures of stable boundary layer during heavy haze pollution events. Atmos. Res. 2022, 281, 106465. [Google Scholar] [CrossRef]
- Dutton, J.A.; Panofsky, H.A. Clear Air Turbulence: A Mystery May Be Unfolding: High altitude turbulence poses serious problems for aviation and atmospheric science. Science 1970, 167, 937–944. [Google Scholar] [CrossRef]
- Storer, L.N.; Williams, P.D.; Gill, P.G. Aviation turbulence: Dynamics, forecasting, and response to climate change. Pure Appl. Geophys. 2019, 176, 2081–2095. [Google Scholar] [CrossRef]
- Williams, J.K. Using random forests to diagnose aviation turbulence. Mach. Learn. 2014, 95, 51–70. [Google Scholar] [CrossRef] [PubMed]
- Lv, Y.; Guo, J.; Li, J.; Cao, L.; Chen, T.; Wang, D.; Chen, D.; Han, Y.; Guo, X.; Xu, H.; et al. Spatiotemporal characteristics of atmospheric turbulence over China estimated using operational high-resolution soundings. Environ. Res. Lett. 2021, 16, 054050. [Google Scholar] [CrossRef]
- O’connor, E.J.; Illingworth, A.J.; Brooks, I.; Westbrook, C.; Hogan, R.; Davies, F.; Brooks, B.J. A Method for Estimating the turbulent kinetic energy dissipation rate from a vertically pointing doppler lidar, and independent evaluation from balloon-borne in Situ measurements. J. Atmos. Ocean. Technol. 2010, 27, 1652–1664. [Google Scholar] [CrossRef]
- Shupe, M.D.; Brooks, I.M.; Canut, G. Evaluation of turbulent dissipation rate retrievals from Doppler Cloud Radar. Atmos. Meas. Tech. 2012, 5, 1375–1385. [Google Scholar] [CrossRef]
- He, Y.; Zhu, X.; Sheng, Z.; He, M.; Feng, Y. Observations of Inertia Gravity Waves in the Western Pacific and Their Characteristic in the 2015/2016 Quasi-biennial Oscillation Disruption. J. Geophys. Res. Atmos. 2022, 127, 037208. [Google Scholar] [CrossRef]
- Peña, A.; Dellwik, E.; Mann, J. A method to assess the accuracy of sonic anemometer measurements. Atmos. Meas. Tech. 2019, 12, 237–252. [Google Scholar] [CrossRef]
- Ko, H.-C.; Chun, H.-Y. Potential sources of atmospheric turbulence estimated using the Thorpe method and operational radiosonde data in the United States. Atmos. Res. 2022, 265, 105891. [Google Scholar] [CrossRef]
- Ji, Q.; Zhu, X.; Sheng, Z.; Tian, T. Spectral Analysis of Gravity Waves in the Martian Thermosphere during Low Solar Activity Based on MAVEN/NGIMS Observations. Astrophys. J. 2022, 938, 97. [Google Scholar] [CrossRef]
- Shepherd, H.W.; Osborn, J.; Wilson, R.W.; Butterley, T.; Avila, R.; Dhillon, V.S.; Morris, T.J. Stereo-SCIDAR: Optical turbulence profiling with high sensitivity using a modified SCIDAR instrument. Mon. Not. R. Astron. Soc. 2013, 437, 3568–3577. [Google Scholar] [CrossRef]
- Butterley, T.; Wilson, R.W.; Sarazin, M. Determination of the profile of atmospheric optical turbulence strength from SLODAR data. Mon. Not. R. Astron. Soc. 2006, 369, 835–845. [Google Scholar] [CrossRef]
- Kornilov, V.; Tokovinin, A.; Shatsky, N.; Voziakova, O.; Potanin, S.; Safonov, B. Combined MASS-DIMM instruments for atmospheric turbulence studies. Mon. Not. R. Astron. Soc. 2007, 382, 1268–1278. [Google Scholar] [CrossRef]
- Wang, Z.; Zhang, L.; Kong, L.; Bao, H.; Guo, Y.; Rao, X.; Zhong, L.; Zhu, L.; Rao, C. A modified S-DIMM+: Applying additional height grids for characterizing daytime seeing profiles. Mon. Not. R. Astron. Soc. 2018, 478, 1459–1467. [Google Scholar] [CrossRef]
- Sathe, A.; Mann, J. Measurement of turbulence spectra using scanning pulsed wind lidars. J. Geophys. Res. Atmos. 2012, 117, D01201. [Google Scholar] [CrossRef]
- Kovadlo, P.G.; Shikhovtsev, A.Y.; Kopylov, E.A.; Kiselev, A.V.; Russkikh, I.V. Study of the Optical Atmospheric Distortions using Wavefront Sensor Data. Russ. Phys. J. 2021, 63, 1952–1958. [Google Scholar] [CrossRef]
- Manninen, A.J.; Marke, T.; Tuononen, M.; O’Connor, E.J. Atmospheric Boundary Layer Classification with Doppler Lidar. J. Geophys. Res. Atmos. 2018, 123, 8172–8189. [Google Scholar] [CrossRef]
- Griffiths, R.; Osborn, J.; Farley, O.; Butterley, T.; Townson, M.J.; Wilson, R. Demonstrating 24-hour continuous vertical monitoring of atmospheric optical turbulence. Opt. Express 2023, 31, 6730. [Google Scholar] [CrossRef]
- Zheng, F.; Chen, Y.; Ji, S.; Duan, G. Research status and prospects of orbital angular momentum technology in wireless communication. Prog. Electromagn. Res. 2020, 168, 113–132. [Google Scholar] [CrossRef]
- Ren, J.; Leung, K.W.; Liu, D.Q.; Luk, K.M.; Mao, J.-F. Orbital angular momentum radiator multiplexing electromagnetic waves in free space. Opt. Express 2020, 28, 345–359. [Google Scholar] [CrossRef] [PubMed]
- Mohammadi, S.M.; Daldorff, L.K.S.; Bergman, J.E.S.; Karlsson, R.L.; Thide, B.; Forozesh, K.; Carozzi, T.D.; Isham, B. Orbital angular momentum in radio—A system study. IEEE Trans. Antennas Propag. 2009, 58, 565–572. [Google Scholar] [CrossRef]
- Tamburini, F.; Mari, E.; Sponselli, A.; Thidé, B.; Bianchini, A.; Romanato, F. Encoding many channels on the same frequency through radio vorticity: First experimental test. New J. Phys. 2012, 14, 033001. [Google Scholar] [CrossRef]
- Zhang, C.; Zhao, Y. Orbital angular momentum nondegenerate index mapping for long distance transmission. IEEE Trans. Wirel. Commun. 2019, 18, 5027–5036. [Google Scholar] [CrossRef]
- Mabena, C.M.; Roux, F.S. Optical orbital angular momentum under strong scintillation. Phys. Rev. A 2019, 99, 013828. [Google Scholar] [CrossRef]
- Ruffato, G.; Massari, M.; Romanato, F. Generation of high-order Laguerre-Gaussian modes by means of spiral phase plates. Opt. Lett. 2014, 39, 5094–5097. [Google Scholar] [CrossRef]
- Blaunstein, N.; Kopeika, N. Optical Waves and Laser Beams in the Irregular Atmosphere; CRC Press: Boca Raton, FL, USA, 2017; pp. 1–26. [Google Scholar] [CrossRef]
- Dipankar, A.; Sagaut, P. A new phase-screen method for electromagnetic wave propagation in turbulent flows using large-eddy simulation. J. Comput. Phys. 2009, 228, 7729–7741. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L. Laser Beam Propagation Through Random Media, 2nd ed.; SPIE Optical Engineering Press: Bellingham, WA, USA, 2005; pp. 47–50. [Google Scholar]
- Baykal, Y. Scintillation index in strong oceanic turbulence. Opt. Commun. 2016, 375, 15–18. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, W.; Qian, X.; Rao, R. Simulation of the scintillation index of plane wave propagating through general non-Kolmogorov atmospheric turbulence path. Acta Opt. Sin. 2015, 35, 33–39. [Google Scholar] [CrossRef]
- Mirjalili, S. Genetic algorithm. In Evolutionary Algorithms and Neural Networks; Springer: Cham, Switzerland, 2019. [Google Scholar] [CrossRef]
- Kwiecień, J. The effects of atmospheric turbulence on laser beam propagation in a closed space—An analytic and experimental approach. Opt. Commun. 2019, 433, 200–208. [Google Scholar] [CrossRef]
- Cheng, W.; Joseph, W.H.; Zhan, Q. Propagation of scalar and vector vortex beams through turbulent atmosphere. In Proceedings of the SPIE 7200, Atmospheric Propagation of Electromagnetic Waves III, San Jose, CA, USA, 24 February 2009. [Google Scholar]
- Zhang, J.; Ji, Q.; Sheng, Z.; He, M.; He, Y.; Zuo, X.; He, Z.; Qin, Z.; Wu, G. Observation based climatology Martian atmospheric waves perturbation Datasets. Sci. Data 2022, 10, 4. [Google Scholar] [CrossRef] [PubMed]
- Jia, P.; Cai, D.; Wang, D.; Basden, A. Simulation of atmospheric turbulence phase screen for large telescope and optical interferometer. Mon. Not. R. Astron. Soc. 2015, 447, 3467–3474. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).