Estimation of the Two-Dimensional Direction of Arrival for Low-Elevation and Non-Low-Elevation Targets Based on Dilated Convolutional Networks
Abstract
1. Introduction
2. Signal Model
2.1. L-Shaped Array Signal Model
2.2. Low-Elevation-Target Signal Model
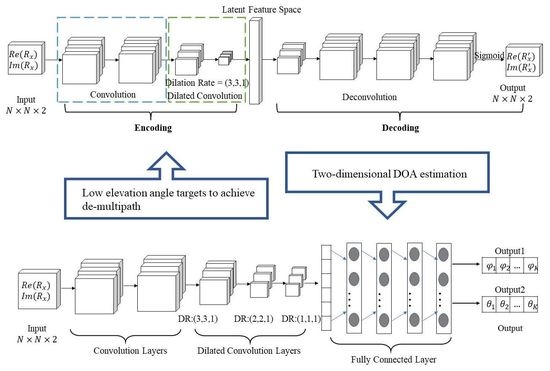
3. Dilated Convolution Network Model
3.1. Dilated Convolutional Autoencoder Mode
Dilated Convolution
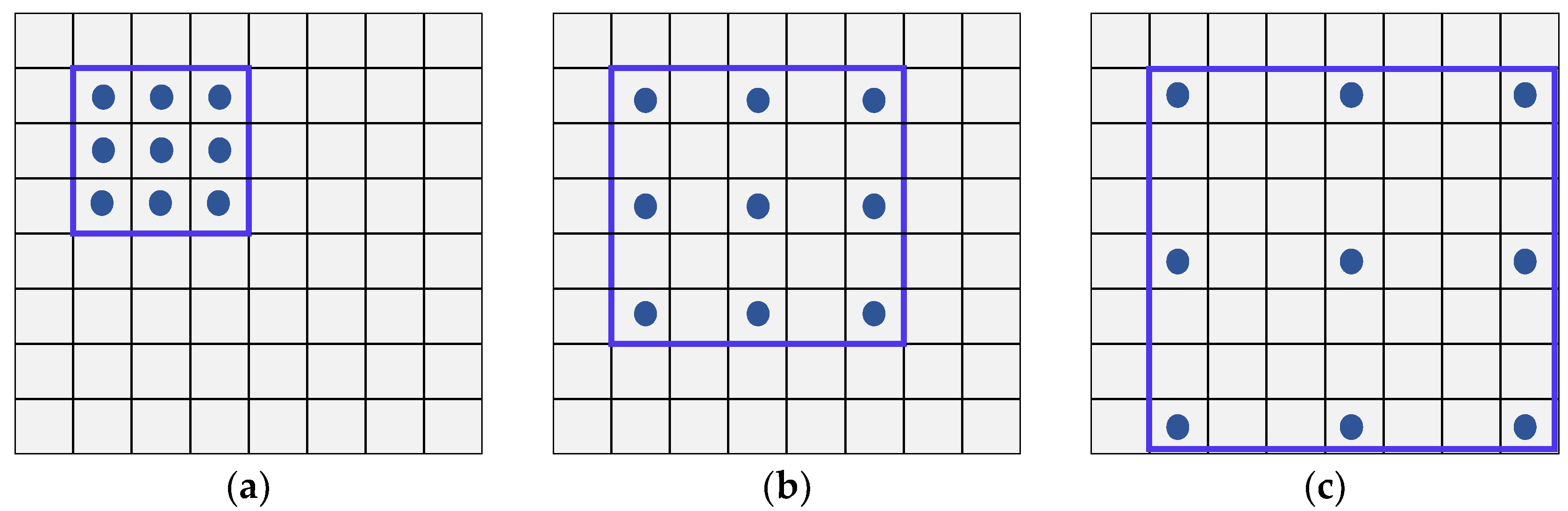
3.2. Dilated Convolutional Neural Network Model
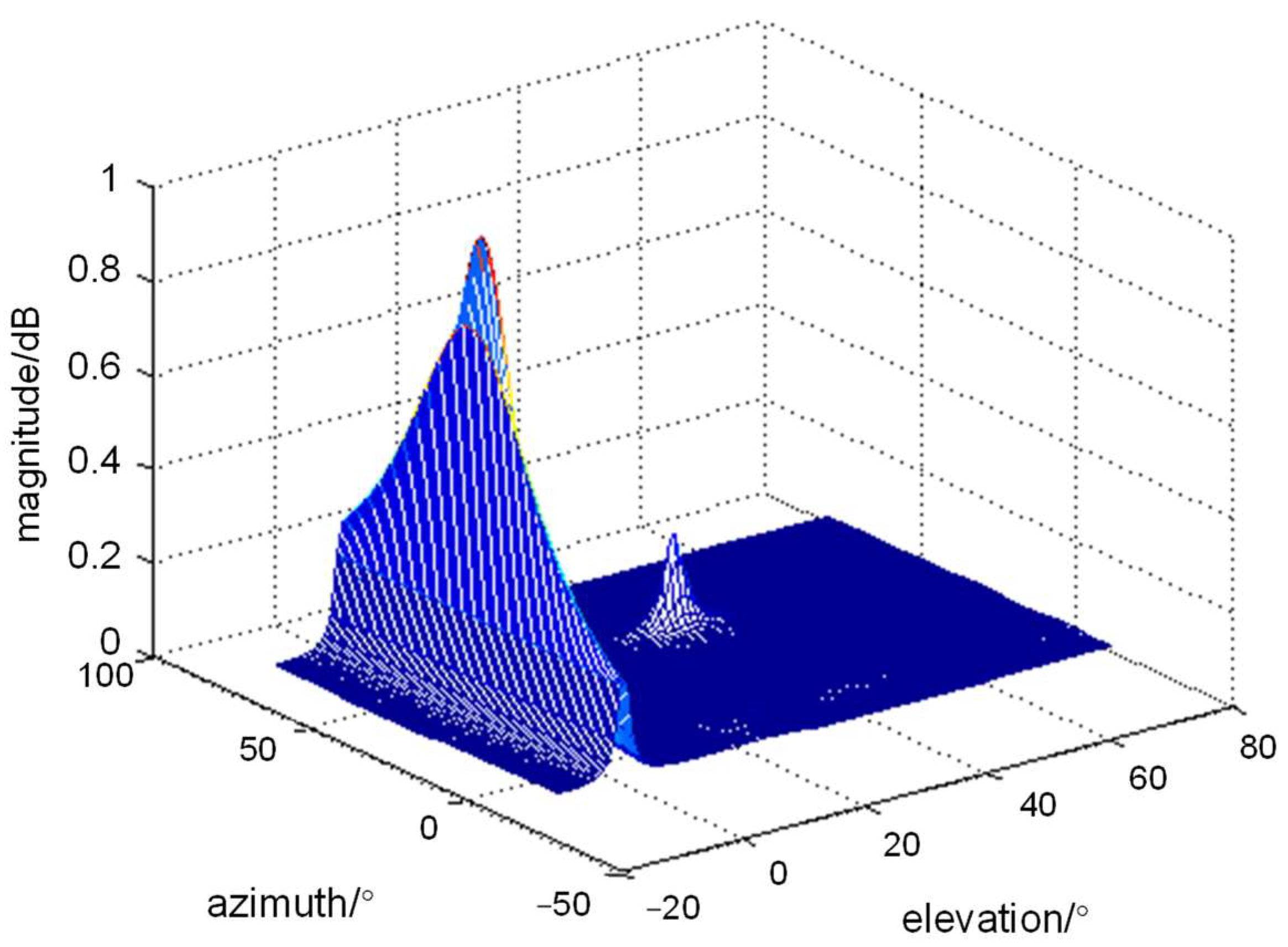
4. Simulation Experiments and Analysis of Results
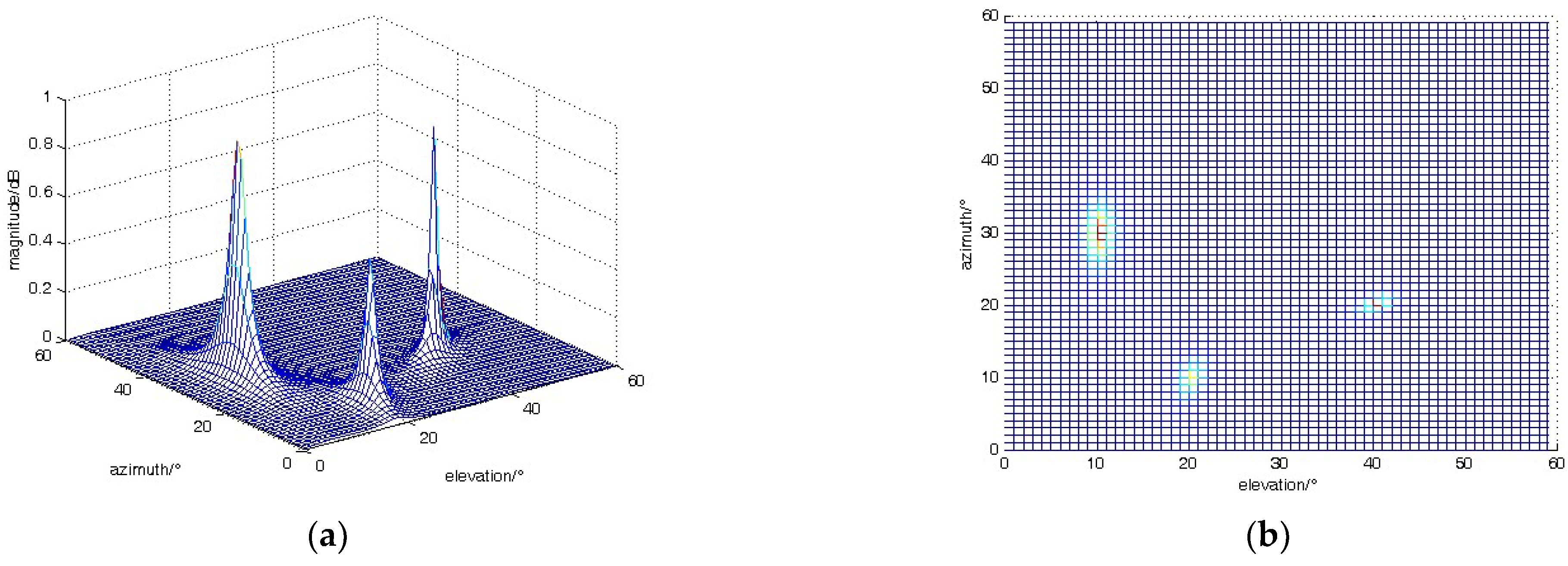
4.1. Verification of Dilated Convolutional Autoencoder Mode Validity
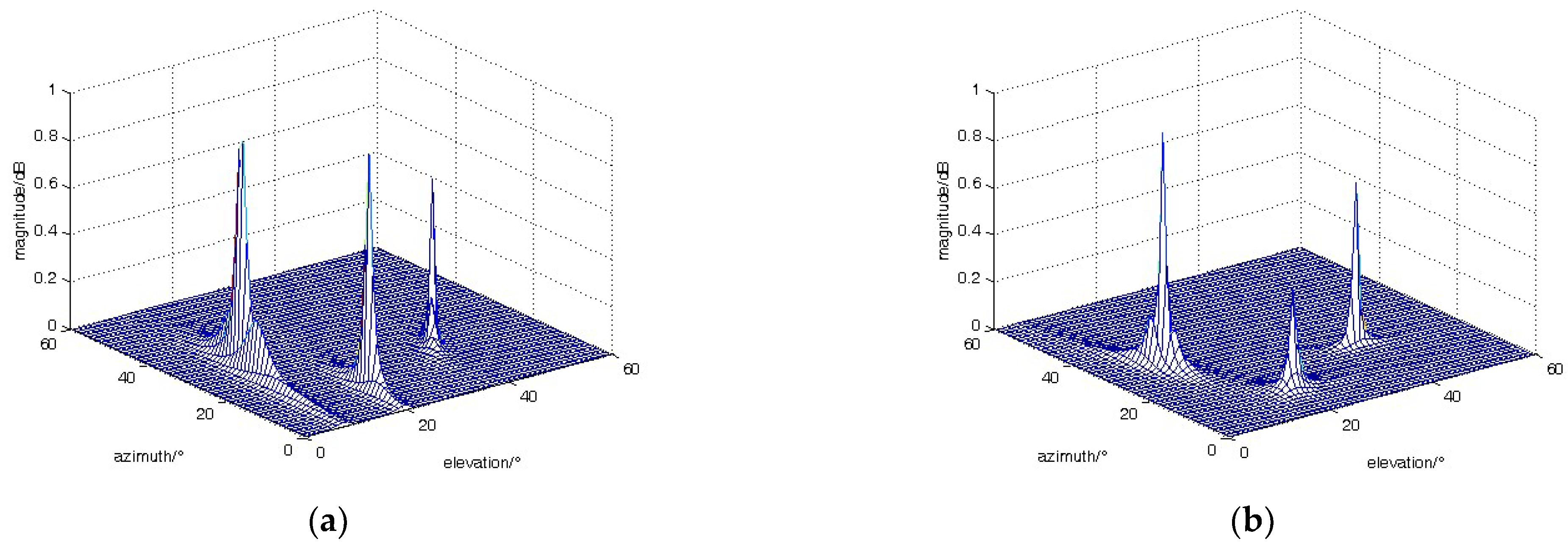
4.2. Verification of Dilated Convolutional Neural Network Model Validity
4.3. RMSE of 2D DOA Estimation at Different SNRs with Non-Low-Elevation Targets
4.4. RMSE of 2D DOA Estimation at Different SNRs with Low-Elevation Targets
5. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Richards, M. Fundamentals of Radar Signal Processing, 2nd ed.; IET: London, UK, 2014; pp. 1–16. [Google Scholar]
- Ning, G.; Zhang, S.; Zhang, J. Velocity-independent two-dimensional direction-of-arrival estimation algorithm with three parallel linear arrays. IET Signal Process. 2022, 1, 106–116. [Google Scholar] [CrossRef]
- Zhang, H.; Gao, K.; Xing, J. 2D Direction-of-arrival Estimation for Sparse L-shaped Array based on Recursive Gridding. In Proceedings of the 9th Asia-Pacific Conference on Antennas and Propagation (APCAP), Xiamen, China, 4–7 August 2020. [Google Scholar]
- Xiong, Y.; Li, Z.; Wen, F. 2D DOA Estimation for Uniform Rectangular Array with One-bit Measurement. In Proceedings of the IEEE 11th Sensor Array and Multichannel Signal Processing Workshop (SAM), Hangzhou, China, 8–11 June 2020. [Google Scholar]
- Zhao, X.; Zhou, J.; Fan, H. Improved 2D-MUSIC estimation for low intercept coprime MIMO radar. J. Phys. Conf. Ser. 2021, 1971, 012007. [Google Scholar] [CrossRef]
- Yin, Q.; Zou, L. A Robert High Resolution Approach to 2D Signal Parameters Estimation-DOA Matrix Method. J. China Inst. Commun. 1991, 4, 1–7, 44. [Google Scholar]
- Liang, L.; Shi, Y.; Shi, Y. Two-dimensional DOA estimation method of acoustic vector sensor array based on sparse recovery. Digit. Signal Process. 2022, 120, 103294. [Google Scholar] [CrossRef]
- Liu, S.; Zhao, J.; Wu, D. 2D DOA estimation by a large-space T-shaped array. Digit. Signal Process. 2022, 130, 103699. [Google Scholar] [CrossRef]
- Wang, H.; He, P.; Yu, W. Two-dimensional DOA Estimation Based on Generalized Coprime Double Parallel Arrays. J. Signal Process. 2022, 38, 223–231. [Google Scholar]
- Ma, J.; Wei, S.; Ma, H. Two-dimensional DOA Estimation for Low-angle Target Based on ADMM. J. Electron. Inf. Technol. 2022, 44, 2859–2866. [Google Scholar]
- Su, X.; Liu, Z.; Peng, B. A Sparse Representation Method for Coherent Sources Angle Estimation with Uniform Circular Array. Int. J. Antennas Propag. 2019, 2019, 3849791. [Google Scholar] [CrossRef]
- Park, H.; Li, J. Efficient sparse parameter estimation-based methods for two-dimensional DOA estimation of coherent signals. IET Signal Process. 2020, 14, 643–651. [Google Scholar] [CrossRef]
- Liang, H.; Li, X. Two-Dimensional DOA Estimation of Coherent Signals Based on the Toeplitz Matrix Reconstruction. Electron. Inf. Warf. Technol. 2012, 27, 23–27. [Google Scholar]
- Molaei, A.; Zakeri, B.; Andargoli, S. Two-dimensional DOA estimation for multi-path environments by accurate separation of signals using k-medoids clustering. IET Commun. 2019, 13, 1141–1147. [Google Scholar] [CrossRef]
- Agatonovic, M.; Stanković, Z.; Milovanovic, I. Efficient Neural Network Approach for 2d DOA Estimation based on Antenna Array Measurements. Prog. Electromagn. Res. 2013, 137, 741–758. [Google Scholar] [CrossRef]
- Zhu, W.; Zhang, M.; Li, P. Two-Dimensional DOA Estimation via Deep Ensemble Learning. IEEE Access 2020, 8, 124544–124552. [Google Scholar] [CrossRef]
- Yang, X.; Liu, L.; Li, L. A Method for Estimating 2D Direction of Arrival Based on Coprime Array with L-shaped Structure. J. Xi’an Jiaotong Univ. 2020, 54, 144–149. [Google Scholar]
- Sinha, A.; Bar-Shalom, Y.; Blair, W. Radar measurement extraction in the presence of sea-surface multipath. IEEE Trans. Aerosp. Electron. Syst. 2003, 39, 550–567. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Y.; Yun, Y. Direct signal DOA estimation algorithm in radar low angle bearing environment. Aerosp. Electron. Warf. 2009, 25, 29–31. [Google Scholar]
- Gu, J.; Wei, P.; Tai, H. 2-D Direction-of-Arrival Estimation of Coherent Signals using Cross-Correlation Matrix. Signal Process. 2008, 88, 75–85. [Google Scholar] [CrossRef]
- Zhao, F.; Hu, G.; Zhou, H.; Zhan, C. CAE-CNN-Based DOA Estimation Method for Low-Elevation-Angle Target. Remote Sens. 2023, 15, 185. [Google Scholar] [CrossRef]
- Vu, T.; Yang, H.; Nguyen, V. Multimodal Learning using Convolution Neural Network and Sparse Autoencoder. In Proceedings of the IEEE International Conference on Big Data and Smart Computing, Jeju Island, Republic of Korea, 13–16 February 2017. [Google Scholar]
- Firat, O.; Vural, F. Representation Learning with Convolutional Sparse Autoencoders for Remote Sensing. In Proceedings of the 21st Signal Processing and Communications Applications Conference (SIU), Haspolat, Turkey, 24–26 April 2013. [Google Scholar]
- Yao, J.; Wang, D.; Hu, H. ADCNN: Towards Learning Adaptive Dilation for Convolutional Neural Networks. Pattern Recognit. 2022, 123, 108369. [Google Scholar] [CrossRef]
- Chalavadi, V.; Jeripothula, P.; Datla, R. mSODANet: A Network for Multi-Scale Object Detection in Aerial Images using Hierarchical Dilated Convolutions. Pattern Recognit. 2022, 126, 108548. [Google Scholar] [CrossRef]
- Nair, V.; Hinton, G.E. Rectified Linear Units Improve Restricted Boltzmann Machines. In Proceedings of the International Conference on Machine Learning, Haifa, Israel, 21–24 June 2010. [Google Scholar]
- Su, X.; Hu, P.; Liu, Z. Mixed Near-Field and Far-Field Source Localization Based on Convolution Neural Networks via Symmetric Nested Array. IEEE Trans. Veh. Technol. 2021, 70, 7908–7920. [Google Scholar] [CrossRef]












| Type | Target Number | RMSE/° | RMSEe/° | RMSEa/° | ||
|---|---|---|---|---|---|---|
| LUA | 2 | 99.98 | 100 | 0.3697 | 0.2901 | 0.4352 |
| 3 | 99.97 | 100 | 0.3083 | 0.2710 | 0.3412 | |
| LSA | 2 | 99.99 | 100 | 0.3507 | 0.2548 | 0.4256 |
| 3 | 100 | 100 | 0.2768 | 0.2602 | 0.2759 |
| Type | Model | PE/% | PE/% | RMSE/° | RMSEe/° | RMSEa/° | |
|---|---|---|---|---|---|---|---|
| Low | Non-Low | ||||||
| LUA | DCNN | 85.74 | 97.35 | 1.6782 | 1.5757 | 1.5302 | 1.7946 |
| DCAE-DCNN | 99.98 | 100 | 0.3441 | 0.2913 | 0.2893 | 0.3898 | |
| LSA | DCNN | 87.36 | 96.77 | 1.6813 | 1.6710 | 1.6276 | 1.7125 |
| DCAE-DCNN | 99.99 | 100 | 0.2975 | 0.2851 | 0.2720 | 0.3124 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, G.; Zhao, F.; Liu, B. Estimation of the Two-Dimensional Direction of Arrival for Low-Elevation and Non-Low-Elevation Targets Based on Dilated Convolutional Networks. Remote Sens. 2023, 15, 3117. https://doi.org/10.3390/rs15123117
Hu G, Zhao F, Liu B. Estimation of the Two-Dimensional Direction of Arrival for Low-Elevation and Non-Low-Elevation Targets Based on Dilated Convolutional Networks. Remote Sensing. 2023; 15(12):3117. https://doi.org/10.3390/rs15123117
Chicago/Turabian StyleHu, Guoping, Fangzheng Zhao, and Bingqi Liu. 2023. "Estimation of the Two-Dimensional Direction of Arrival for Low-Elevation and Non-Low-Elevation Targets Based on Dilated Convolutional Networks" Remote Sensing 15, no. 12: 3117. https://doi.org/10.3390/rs15123117
APA StyleHu, G., Zhao, F., & Liu, B. (2023). Estimation of the Two-Dimensional Direction of Arrival for Low-Elevation and Non-Low-Elevation Targets Based on Dilated Convolutional Networks. Remote Sensing, 15(12), 3117. https://doi.org/10.3390/rs15123117