Quantitative Assessment of Sea Surface Salinity Estimates Using a High-Frequency Radar in Ise Bay, Japan
Abstract
1. Introduction
2. Materials and Methods
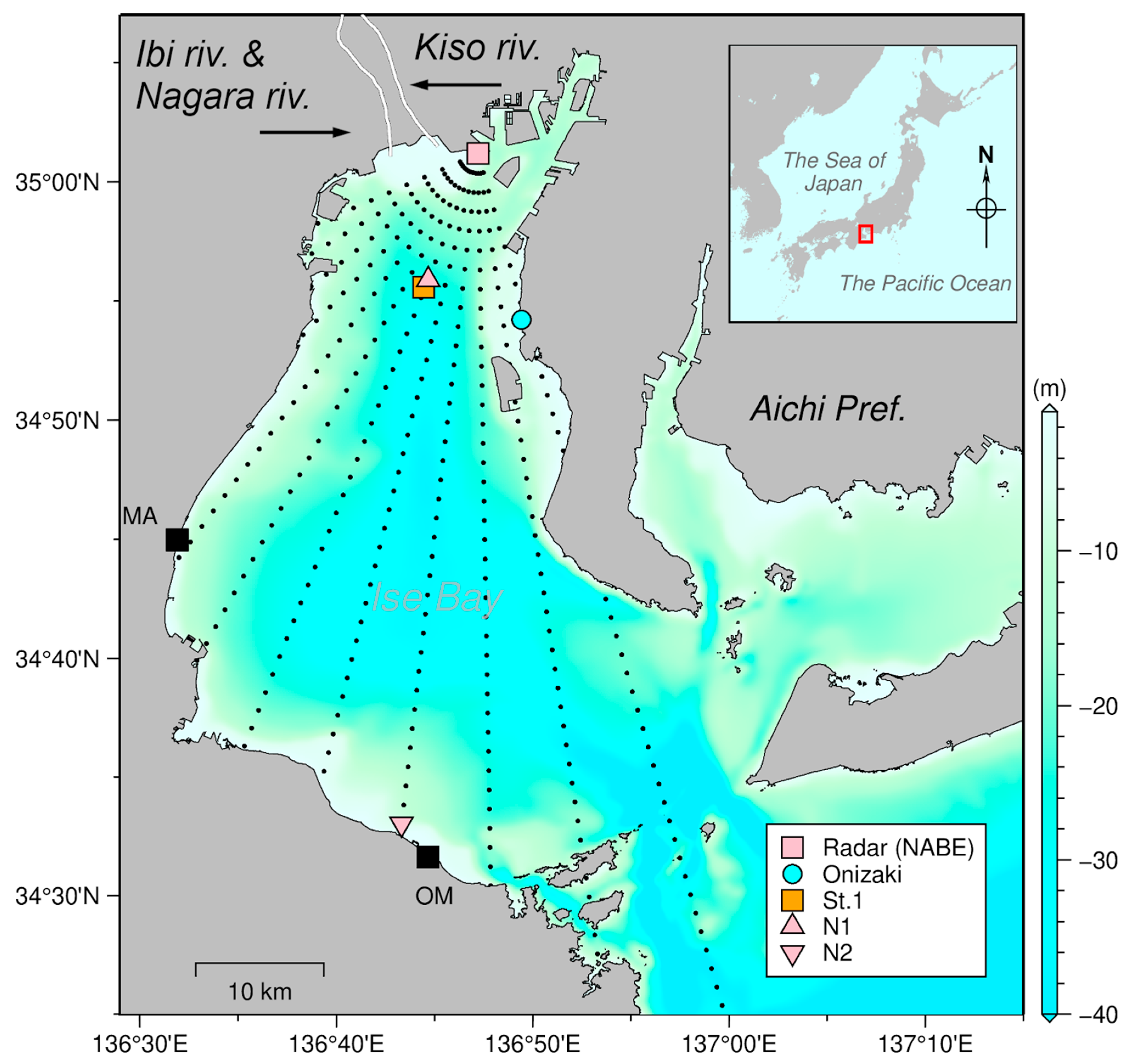
2.1. Study Site
2.2. Materials
2.3. Theory and Methods
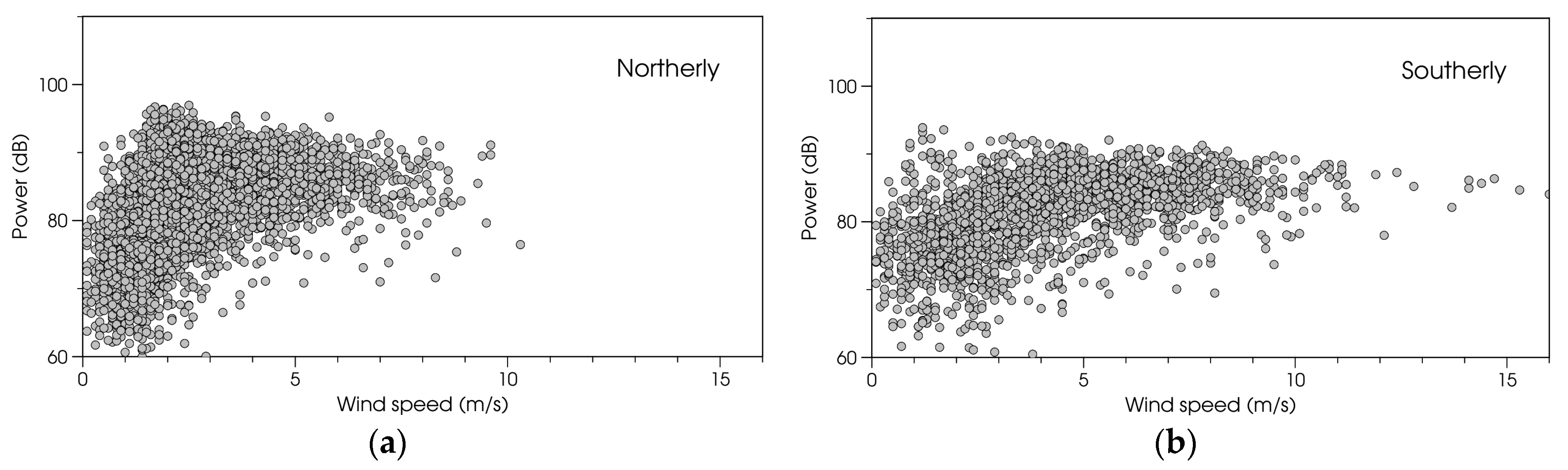
2.3.1. Effects of the Wave Spectrum and SSS on Received Power
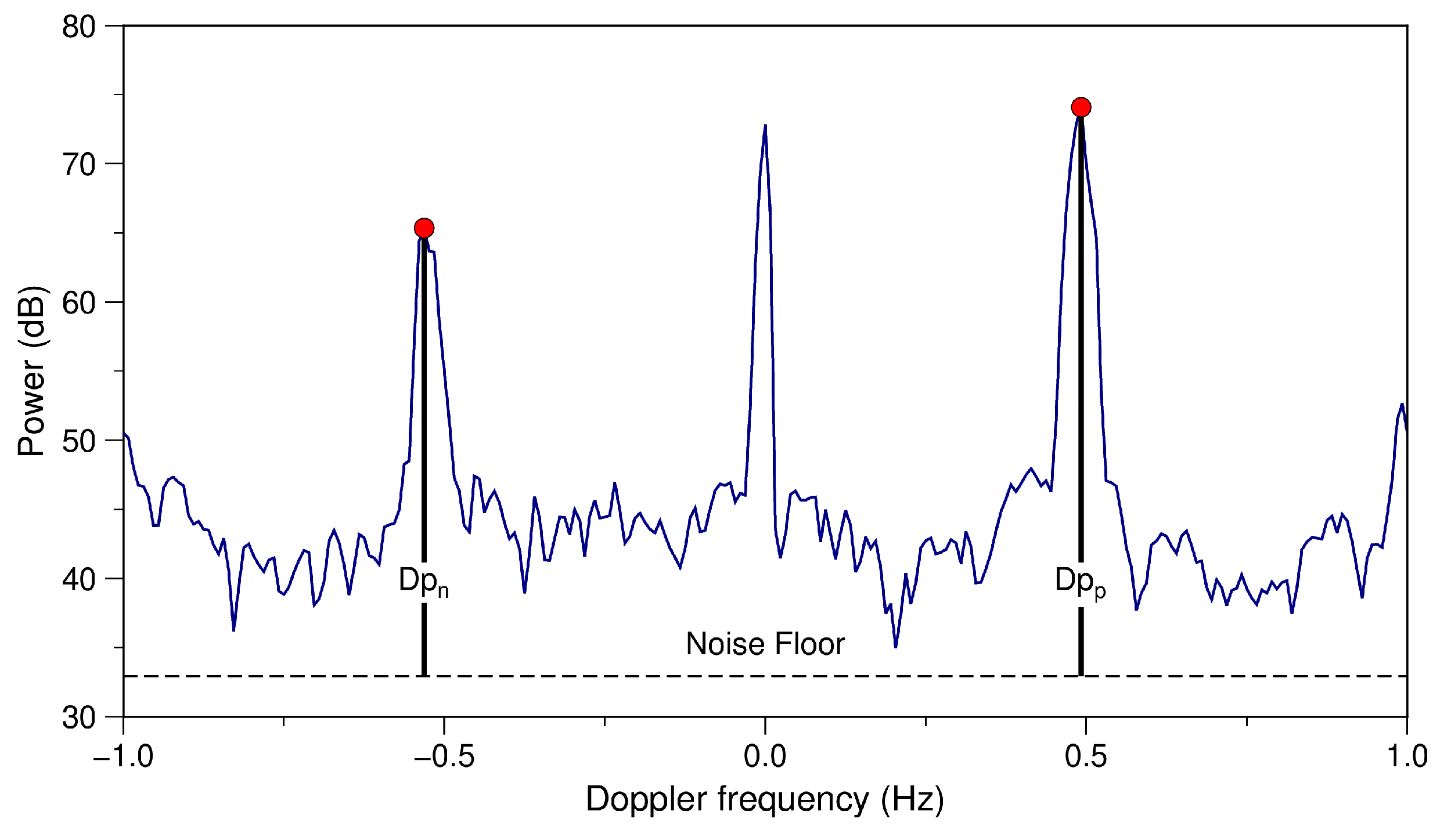
2.3.2. Radar Observation Point for Obtaining the Reference Values and Definition of Received Power
2.4. Calculation of the Effect of Wave Spectra and Electric Conductivity on Received Power
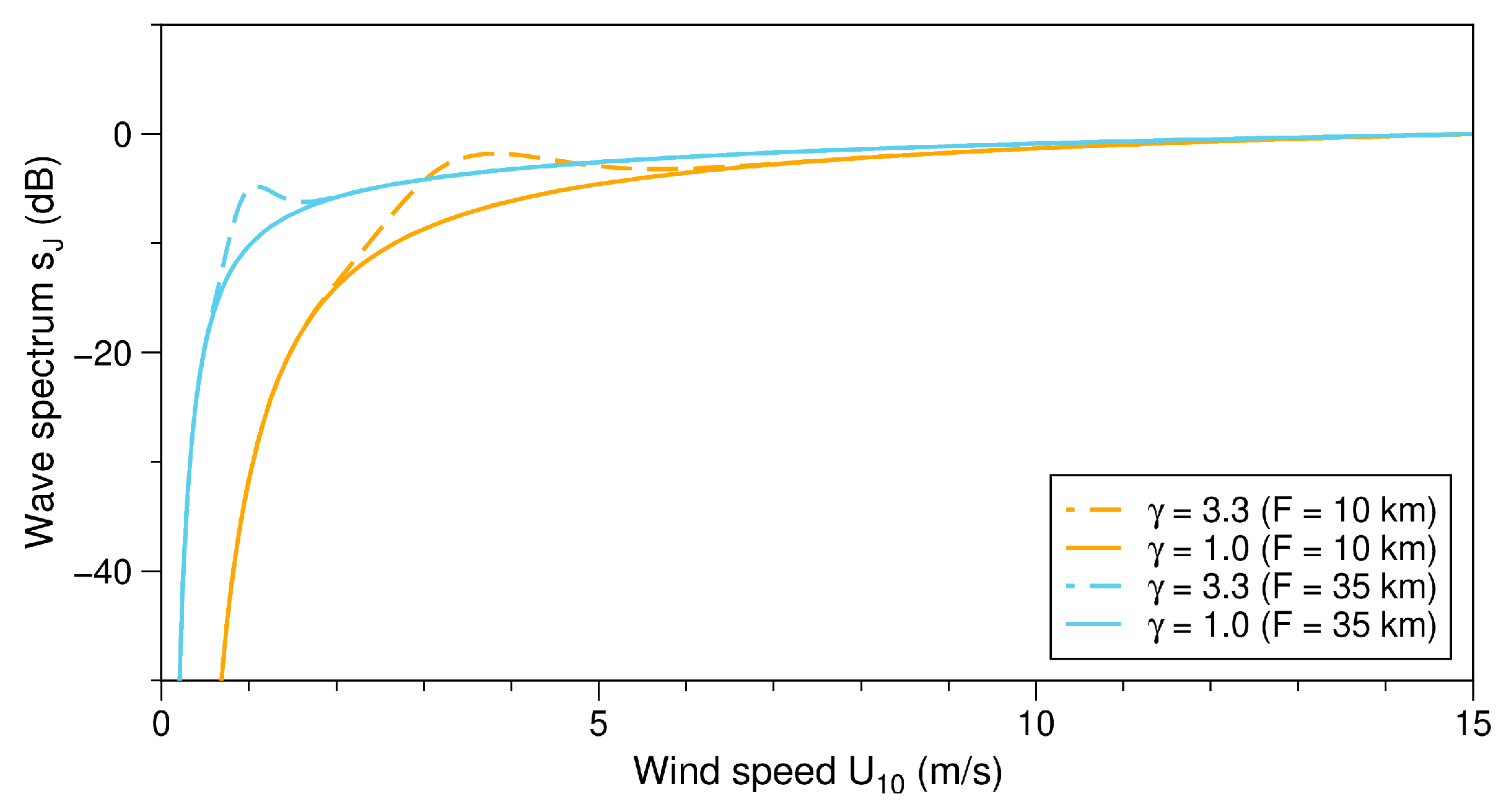
2.4.1. Wave Spectra
2.4.2. Electric Conductivity
2.5. Determination of the Salinity Estimation Parameters
3. Results
3.1. Parameter Setup
3.2. SSS Estimates
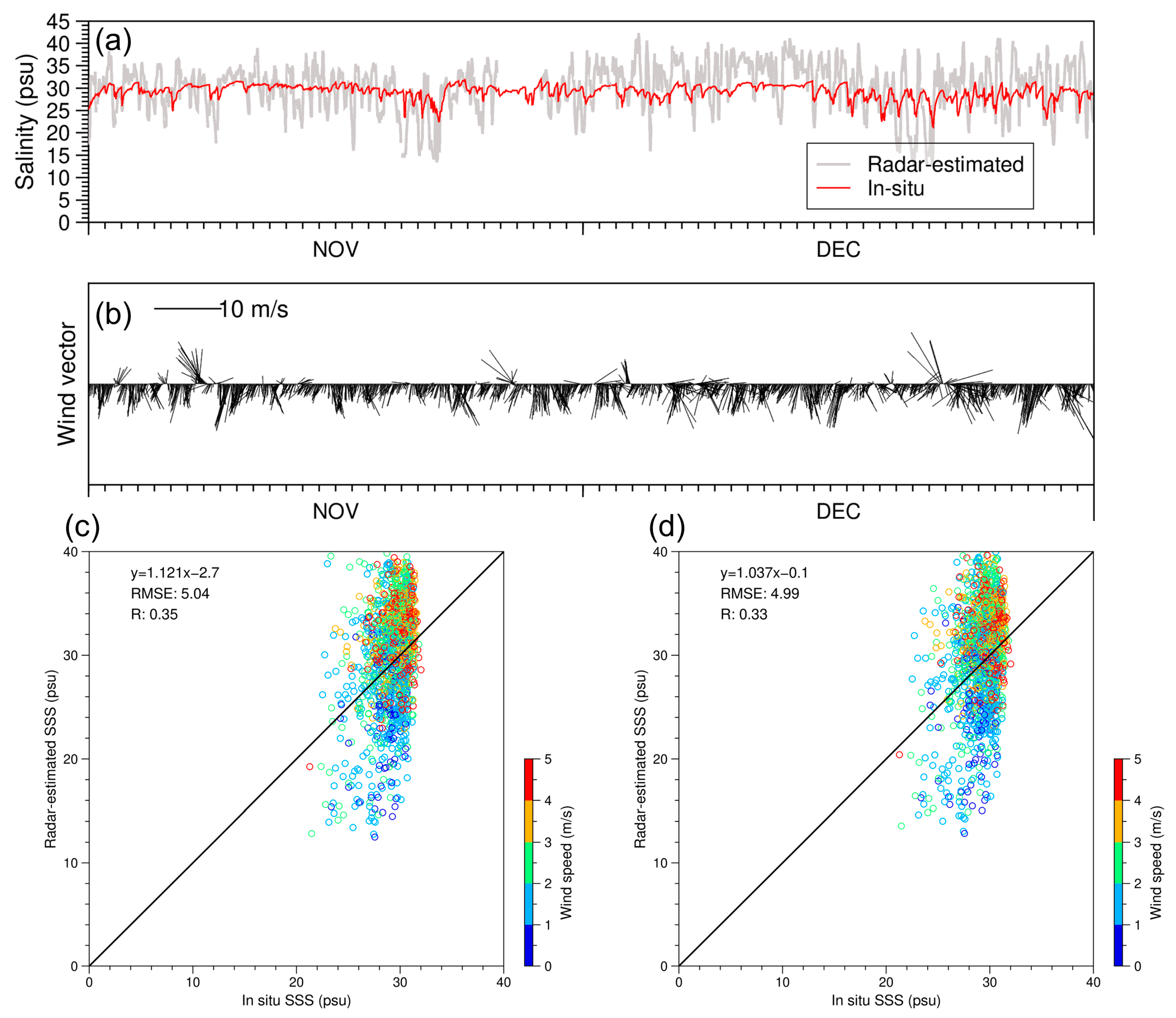
3.2.1. Comparison with In Situ Observations
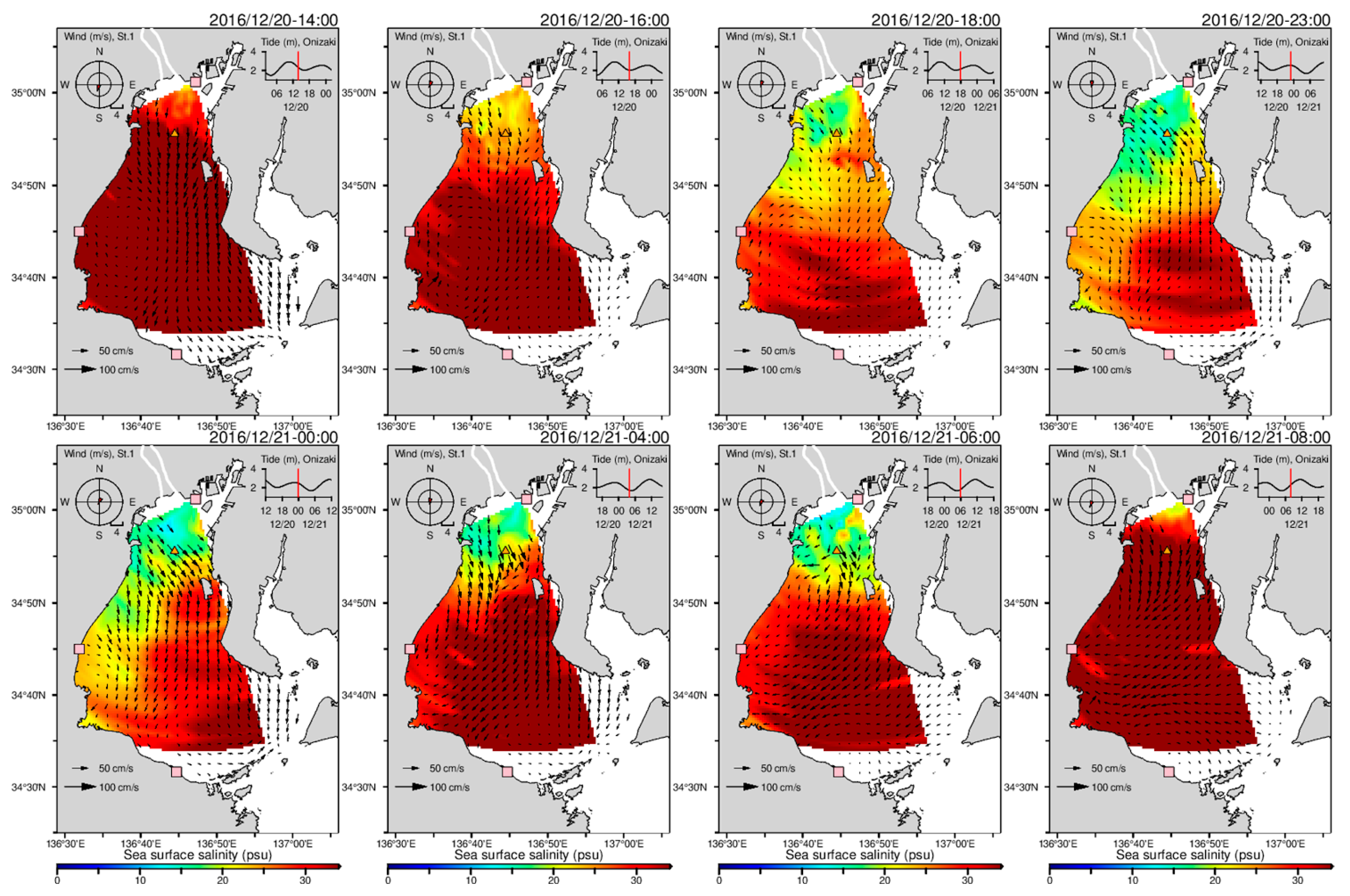
3.2.2. Distribution of Sea Surface Salinity
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Fujii, S.; Heron, M.L.; Kim, K.; Lai, J.-W.; Lee, S.-H.; Wu, X.; Wu, X.; Wyatt, L.R.; Yang, W.-C. An overview of developments and applications of oceanographic radar networks in Asia and Oceania countries. Ocean Sci. J. 2013, 48, 69–97. [Google Scholar] [CrossRef]
- Rubio, A.; Mader, J.; Corgnati, L.; Mantovani, C.; Griffa, A.; Novellino, A.; Quentin, C.; Wyatt, L.; Schulz-Stellenfleth, J.; Horstmann, J.; et al. HF radar activity in European coastal seas: Next steps toward a pan-European HF radar network. Front. Mar. Sci. 2017, 4, 8. [Google Scholar] [CrossRef]
- Roarty, H.; Cook, T.; Hazard, L.; George, D.; Harlan, J.; Cosoli, S.; Wyatt, L.; Fanjul, E.A.; Terrill, E.; Otero, M.; et al. The global high frequency radar network. Front. Mar. Sci. 2019, 6, 164. [Google Scholar] [CrossRef]
- Lorente, P.; Aguiar, E.; Bendoni, M.; Berta, M.; Brandini, C.; Cáceres-Euse, A.; Capodici, F.; Cianelli, D.; Ciraolo, G.; Corgnati, L.; et al. Coastal high-frequency radars in the Mediterranean—Part 1: Status of operations and a framework for future development. Ocean Sci. 2022, 18, 761–795. [Google Scholar] [CrossRef]
- Lipa, B.; Barrick, D.; Saitoh, S.-I.; Ishikawa, Y.; Awaji, T.; Largier, J.; Garfield, N. Japan tsunami current flows observed by HF radars on two continents. Remote Sens. 2011, 3, 1663–1679. [Google Scholar] [CrossRef]
- Fuji, R.; Hinata, H. Temporal variability of tsunami arrival detection distance revealed by virtual tsunami observation experiments using numerical simulation and 1-month HF radar observation. J. Oceanogr. 2017, 73, 725–741. [Google Scholar] [CrossRef]
- Grilli, S.T.; Grosdidier, S.; Guérin, C.A. Tsunami detection by high-frequency radar beyond the continental shelf: I: Algorithms and validation on idealized case studies. Pure Appl. Geophys. 2016, 173, 3895–3934. [Google Scholar] [CrossRef]
- Hinata, H.; Fujii, S.; Furukawa, K.; Kataoka, T.; Miyata, M.; Kobayashi, T.; Mizutani, M.; Kokai, T.; Kanatsu, N. Propagating tsunami wave and subsequent resonant response signals detected by HF radar in the Kii Channel, Japan. Estuar. Coast. Shelf Sci. 2011, 95, 268–273. [Google Scholar] [CrossRef]
- Toguchi, Y.; Fujii, S.; Hinata, H. Tsunami waves and tsunami-induced natural oscillations determined by HF radar in Ise Bay, Japan. J. Geophys. Res. Ocean. 2018, 123, 2965–2980. [Google Scholar] [CrossRef]
- Wyatt, L.R. A relaxation method for integral inversion applied to HF radar measurement of the ocean wave directional spectrum. Int. J. Remote Sens. 1990, 11, 1481–1494. [Google Scholar] [CrossRef]
- Gurgel, K.-W.; Essen, H.-H.; Schlick, T. An empirical method to derive ocean waves from second-order Bragg scattering: Prospects and limitations. IEEE J. Ocean. Eng. 2006, 31, 804–811. [Google Scholar] [CrossRef]
- Basañez, A.; Lorente, P.; Montero, P.; Álvarez-Fanjul, E.; Pérez-Muñuzuri, V. Quality assessment and practical interpretation of the wave parameters estimated by HF radars in NW Spain. Remote Sens. 2020, 12, 598. [Google Scholar] [CrossRef]
- Heron, M.; Rose, R. On the application of HF ocean radar to the observation of temporal and spatial changes in wind direction. IEEE J. Ocean. Eng. 1986, 11, 210–218. [Google Scholar] [CrossRef]
- Shen, W.; Gurgel, K.-W.; Voulgaris, G.; Schlick, T.; Stammer, D. Wind-speed inversion from HF radar first-order backscatter signal. Ocean Dyn. 2012, 62, 105–121. [Google Scholar] [CrossRef]
- Wyatt, L.R. Progress towards an HF radar wind speed measurement method using machine learning. Remote Sens. 2022, 14, 2098. [Google Scholar] [CrossRef]
- Meadows, L.A.; Whelan, C.; Barrick, D.; Kroodsma, R.; Ruf, C.; Teague, C.C.; Meadows, G.A.; Wang, S. High frequency radar and its application to fresh water. J. Great Lakes Res. 2013, 39, 183–193. [Google Scholar] [CrossRef]
- Gurgel, K.-W.; Essen, H.-H.; Kingsley, S. High-frequency radars: Physical limitations and recent developments. Coast. Eng. 1999, 37, 201–218. [Google Scholar] [CrossRef]
- Fernandez, D.M.; Meadows, L.A.; Vesecky, J.F.; Teague, C.C.; Paduan, J.D.; Hansen, P. Surface current measurements by HF radar in freshwater lakes. IEEE J. Ocean. Eng. 2000, 25, 458–471. [Google Scholar] [CrossRef]
- Diercks, A.R.; Howden, S.D.; Barrick, D. HF Radar Signal Propagation as a Function of Salinity—A Case Study in the Mississippi Sound. In Proceedings of the AGU Fall Meeting Abstracts, San Francisco, CA, USA, 1 December 2016; Volume 2016, pp. OS13B–1825. [Google Scholar]
- Halverson, M.; Pawlowicz, R.; Chavanne, C. Dependence of 25-Mhz HF radar working range on near-surface conductivity, sea state, and tides. J. Atmos. Ocean. Technol. 2017, 34, 447–462. [Google Scholar] [CrossRef]
- Tarantolo, P.J. Electromagnetic Probing of Salt with High Frequency Radar. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 1978. [Google Scholar]
- Yoshii, T. Measuring Sea Surface Salinity and Sea Surface Temperature Using Ocean Radar; Central Research Institute of Electric Power, Environmental Science Research Laboratory, Rep. No. V09038. 2010. Available online: https://criepi.denken.or.jp/hokokusho/pb/reportDetail?reportNoUkCode=V09038 (accessed on 14 March 2023).
- Yoshii, T.; Sakai, S.; Tsubono, T.; Matsuyama, M.; Tada, A.; Nakamura, T. Consideration of impact factors on data acquisition for ocean radar with VHF band. In Proceedings of the 2008 International Conference on Radar, Adelaide, Australia, 2–5 September 2008; IEEE: San Francisco, CA, USA, 2008; pp. 682–687. [Google Scholar]
- Font, J.; Camps, A.; Borges, A.; Martín-Neira, M.; Boutin, J.; Reul, N.; Kerr, Y.H.; Hahne, A.; Mecklenburg, S. SMOS: The challenging sea surface salinity measurement from space. Proc. IEEE 2010, 98, 649–665. [Google Scholar] [CrossRef]
- Kerr, Y.H.; Waldteufel, P.; Wigneron, J.-P.; Delwart, S.; Cabot, F.; Boutin, J.; Escorihuela, M.-J.; Font, J.; Reul, N.; Gruhier, C.; et al. The SMOS mission: New tool for monitoring key elements of the global water cycle. Proc. IEEE 2010, 98, 666–687. [Google Scholar] [CrossRef]
- Bai, Y.; Pan, D.; Cai, W.-J.; He, X.; Wang, D.; Tao, B.; Zhu, Q. Remote sensing of salinity from satellite-derived CDOM in the Changjiang River dominated East China Sea. J. Geophys. Res. Ocean. 2013, 118, 227–243. [Google Scholar] [CrossRef]
- Fujiwara, T.; Takahashi, T.; Kasai, A.; Sugiyama, Y.; Kuno, M. the role of circulation in the development of hypoxia in Ise Bay, Japan. Estuar. Coast. Shelf Sci. 2002, 54, 19–31. [Google Scholar] [CrossRef]
- Isewan Environmental Database. Available online: www.isewan-db.go.jp (accessed on 18 January 2023).
- Water Information System. Available online: http://www1.river.go.jp/ (accessed on 18 January 2023).
- Environmental Conservation Survey Results in Ise Bay. Available online: https://www1.kaiho.mlit.go.jp/KAN4/kaisyo/kasoho/kasoho.html (accessed on 14 March 2023).
- Barrick, D. First-order theory and analysis of MF/HF/VHF scatter from the sea. IEEE Trans. Antennas Propag. 1972, 20, 2–10. [Google Scholar] [CrossRef]
- Gurgel, K.-W.; Essen, H.-H.; Schlick, T. Tracking of fresh-water plumes in Dutch coastal waters by means of HF Radar. In Proceedings of the IEEE 1999 International Geoscience and Remote Sensing Symposium, IGARSS’99 (Cat. No.99CH36293), Hamburg, Germany, 28 June–2 July 1999; IEEE: Hamburg, Germany, 1999; Volume 5, pp. 2548–2550. [Google Scholar]
- Barrick, D.E. Theory of HF and VHF propagation across the rough sea, 1, the effective surface impedance for a slightly rough highly conducting medium at grazing incidence. Radio Sci. 1971, 6, 517–526. [Google Scholar] [CrossRef]
- Barrick, D.E.; Peake, W.H. A review of scattering from surfaces with different roughness scales. Radio Sci. 1968, 3, 865–868. [Google Scholar] [CrossRef]
- Guinard, N.W.; Ransone, J.T.; Daley, J.C. Variation of the NRCS of the sea with increasing roughness. J. Geophys. Res. 1971, 76, 1525–1538. [Google Scholar] [CrossRef]
- Knight, P.; Robson, J.A.W. Empirical formula for groundwave field-strength calculation. Electron. Lett. 1984, 20, 740. [Google Scholar] [CrossRef]
- Barrick, D.E.; Weber, B.L. On the nonlinear theory for gravity waves on the ocean’s surface. Part II: Interpretation and applications. J. Phys. Oceanogr. 1977, 7, 11–21. [Google Scholar] [CrossRef]
- Chelton, D.B.; McCabe, P.J. A review of satellite altimeter measurement of sea surface wind speed: With a proposed new algorithm. J. Geophys. Res. 1985, 90, 4707. [Google Scholar] [CrossRef]
- Schroeder, L.C.; Boggs, D.H.; Dome, G.; Halberstam, I.M.; Jones, W.L.; Pierson, W.J.; Wentz, F.J. The relationship between wind vector and normalized radar cross section used to derive SEASAT-A satellite scatterometer winds. J. Geophys. Res. 1982, 87, 3318. [Google Scholar] [CrossRef]
- Sekine, Y.; Nakamura, S. Variation in wind in the region around Ise Bay. Bull. Fac. Bioresour. 2002, 28, 1–9. [Google Scholar]
- Tian, Y.; Wen, B.; Zhou, H.; Wang, C.; Yang, J.; Huang, W. Wave height estimation from first-order backscatter of a dual-frequency high frequency radar. Remote Sens. 2017, 9, 1186. [Google Scholar] [CrossRef]
- Fofonoff, N.P.; Millard, R.C., Jr. Algorithms for the Computation of Fundamental Properties of Seawater; UNESCO Technical Papers in Marine Sciences; 44; UNESCO: Paris, France, 1983. [Google Scholar]
- Tanaka, Y.; Ikeda, K. Analyse of relationship between hypoxia and age in Ise Bay by using numerical simulation. J. Japan Soc. Civ. Eng. Ser. B2 2015, 71, I_1261–I_1266. [Google Scholar] [CrossRef]
- Annual Tropical Cyclone Report 2016. Available online: https://www.metoc.navy.mil/jtwc/products/atcr/2016atcr.pdf (accessed on 18 January 2023).
- Fujiwara, T.; Sanford, L.P.; Nakatsuji, K.; Sugiyama, Y. Anti-cyclonic circulation driven by the estuarine circulation in a gulf type ROFI. J. Mar. Syst. 1997, 12, 83–99. [Google Scholar] [CrossRef]
- Fujiwara, T. Buoyancy-driven current during cooling periods in Ise Bay, Japan. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Murakami, T.; Kawasaki, K.; Okubo, Y.; Kim, J. Numerical analysis of flow and density structures in Ise Bay Area at Tokai Heavy Rain. Proc. Coast. Eng. JSCE 2007, 54, 371–375. [Google Scholar] [CrossRef]
- Hasselmann, K.; Barnett, T.P.; Bouws, E.; Carlson, H.; Cartwright, D.E.; Enke, K.; Ewing, J.A.; Gienapp, A.; Hasselmann, D.E.; Kruseman, P.; et al. Measurements of wind-wave growth and swell decay during the Joint North Sea Wave Project (JONSWAP). Ergänzungsh. zur Dtsch. Hydrogr. Zeitschrift, R.A. 1973, 12, 1–95. [Google Scholar]
- Pierson, W.J.; Moskowitz, L. A proposed spectral form for fully developed wind seas based on the similarity theory of S. A. Kitaigorodskii. J. Geophys. Res. 1964, 69, 5181–5190. [Google Scholar] [CrossRef]
- Zhou, H.; Wen, B. Wave height extraction from the first-order Bragg peaks in high-frequency radars. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2296–2300. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, C.; Yang, J.; Tian, Y.; Wen, B. Wind and current dependence of the first-order Bragg scattering power in high-frequency radar sea echoes. IEEE Geosci. Remote Sens. Lett. 2017, 14, 2428–2432. [Google Scholar] [CrossRef]
- International Telecommunication Union. Final Acts WRC-12, Resolution 612, Use of the radiolocation service between 3 and 50 MHz to support oceanographic radar operations. In Proceedings of the World Radiocommunication Conference, Geneva, Switzerland, 23 January–17 February 2012. [Google Scholar]







| Parameter | Value |
|---|---|
| Beam forming method | Digital beamforming (DBF) |
| Radar type | Frequency modulated interrupted continuous wave (FMICW) |
| Center frequency | 24.515 MHz |
| Sweep bandwidth | 100 kHz |
| Frequency sweep interval | 0.5 s |
| Maximum transmission power | 200 W |
| Range resolution | 1.5 km |
| Azimuth resolution | 7.5° |
| Antenna type | 1 transmission and 8 receiving antenna of 3-element Yagi |
| Data update cycle | 1 h |
| Location | SST (°C) | ||||
|---|---|---|---|---|---|
| AUG | SEP | OCT | NOV | DEC | |
| Upper part of the bay (range 1.5–15 km) | 27.5 | 27.5 | 21.5 | 18.5 | 14.0 |
| Lower part of the bay (range > 15 km) | 27.5 | 27.0 | 22.5 | 18.5 | 14.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Toguchi, Y.; Fujii, S. Quantitative Assessment of Sea Surface Salinity Estimates Using a High-Frequency Radar in Ise Bay, Japan. Remote Sens. 2023, 15, 3088. https://doi.org/10.3390/rs15123088
Toguchi Y, Fujii S. Quantitative Assessment of Sea Surface Salinity Estimates Using a High-Frequency Radar in Ise Bay, Japan. Remote Sensing. 2023; 15(12):3088. https://doi.org/10.3390/rs15123088
Chicago/Turabian StyleToguchi, Yu, and Satoshi Fujii. 2023. "Quantitative Assessment of Sea Surface Salinity Estimates Using a High-Frequency Radar in Ise Bay, Japan" Remote Sensing 15, no. 12: 3088. https://doi.org/10.3390/rs15123088
APA StyleToguchi, Y., & Fujii, S. (2023). Quantitative Assessment of Sea Surface Salinity Estimates Using a High-Frequency Radar in Ise Bay, Japan. Remote Sensing, 15(12), 3088. https://doi.org/10.3390/rs15123088





