A Multivariate Time Series Analysis of Ground Deformation Using Persistent Scatterer Interferometry
Abstract
1. Introduction
2. Materials and Methods
2.1. Geological and Hydrogeological Settings
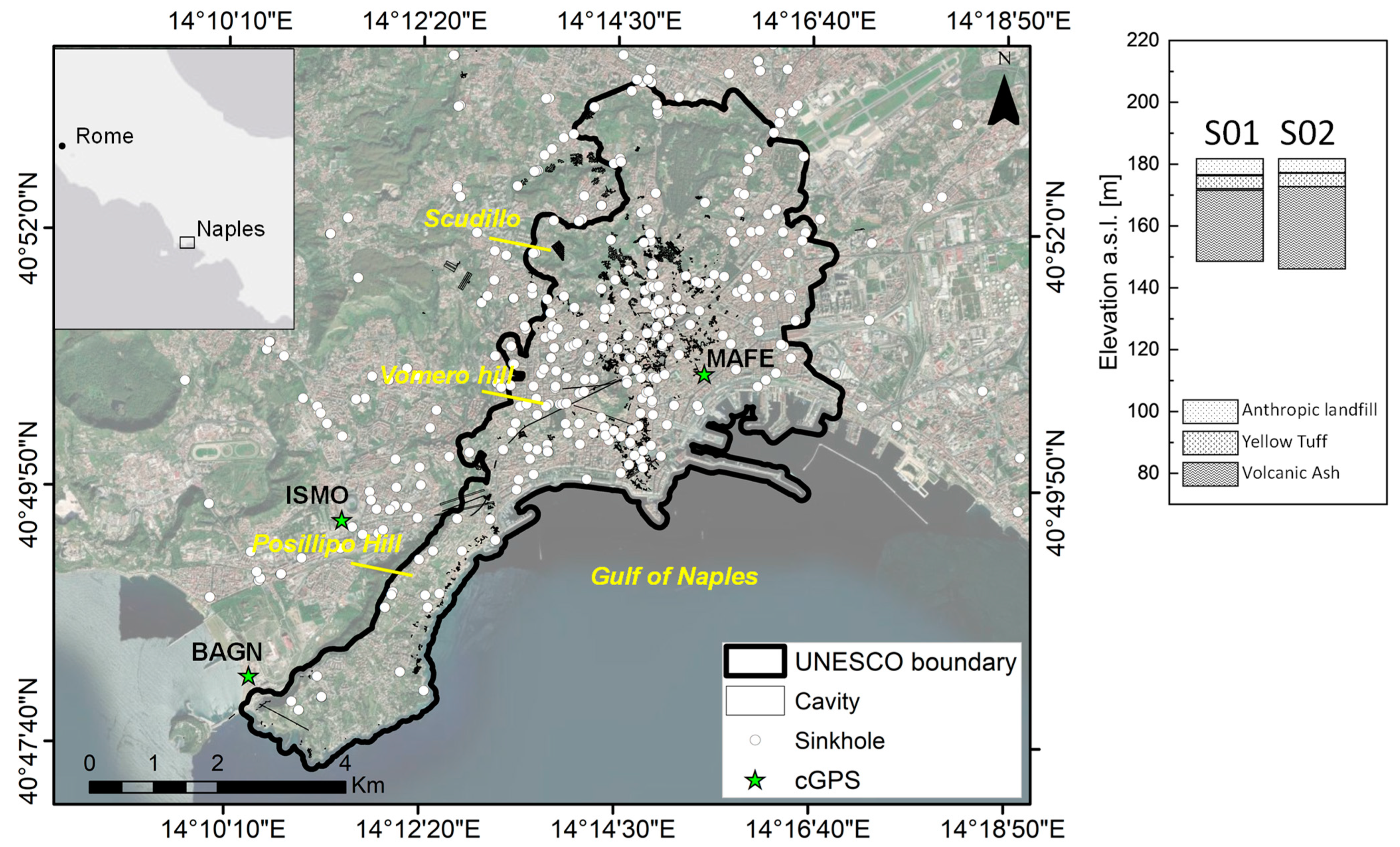
2.2. Neapolitan Cavity System Description
2.3. InSAR Datasets
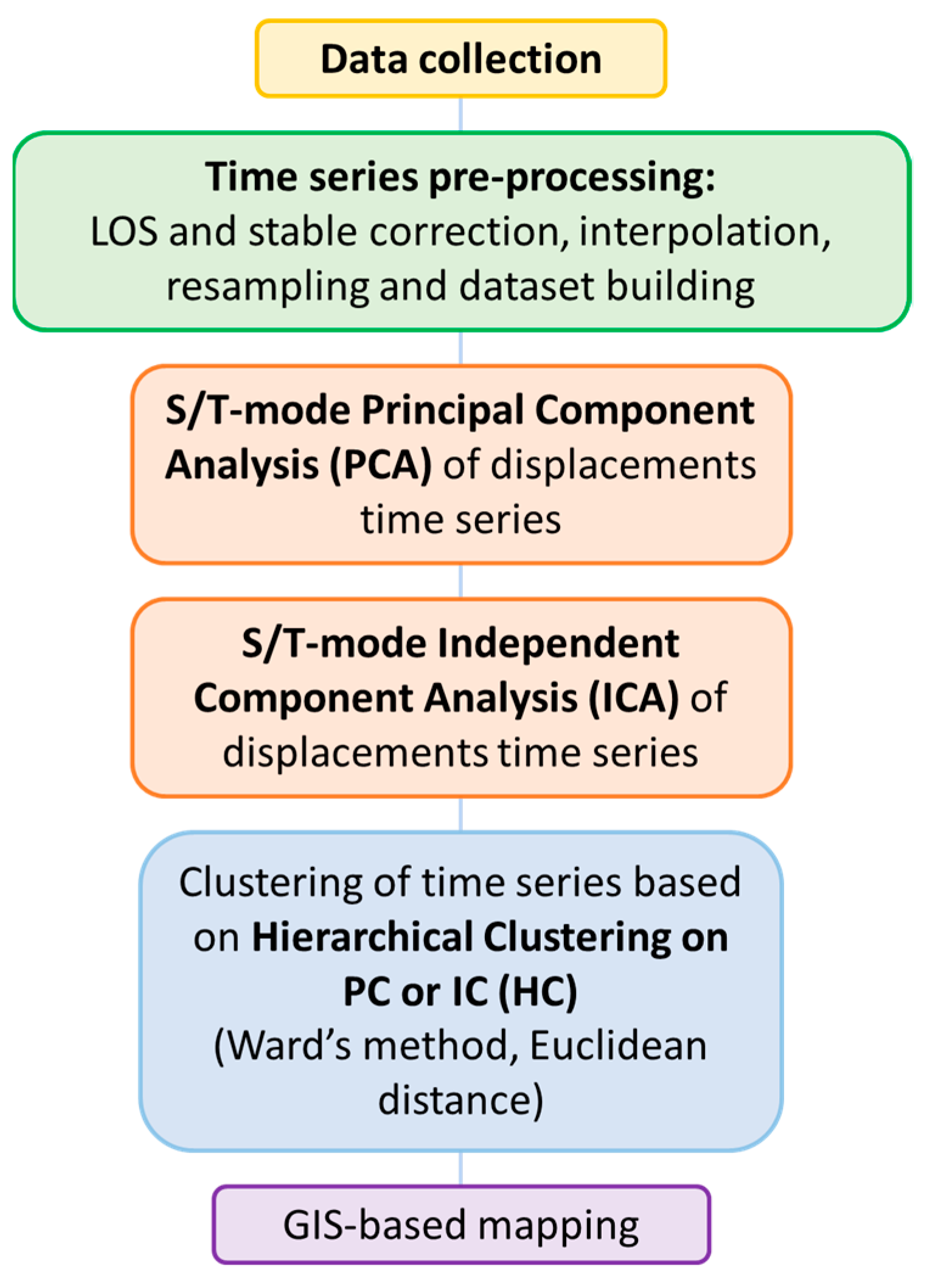
2.4. Methodology
2.4.1. PCA Decomposition
2.4.2. ICA Decomposition
2.4.3. Hierarchical Clustering
3. Results
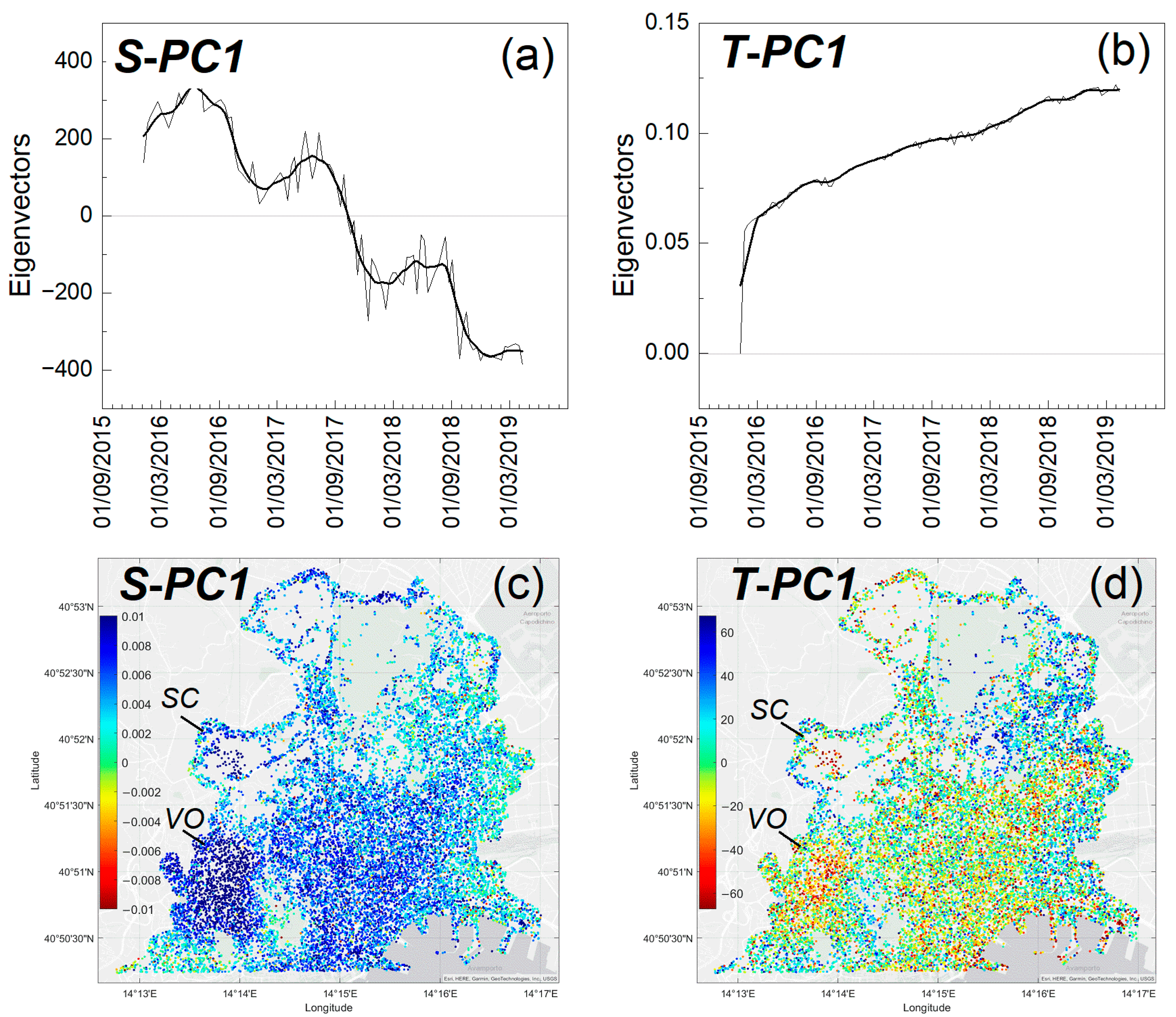
3.1. S- and T-PCA and ICA Results for TerraSAR-X Dataset at Site Scale
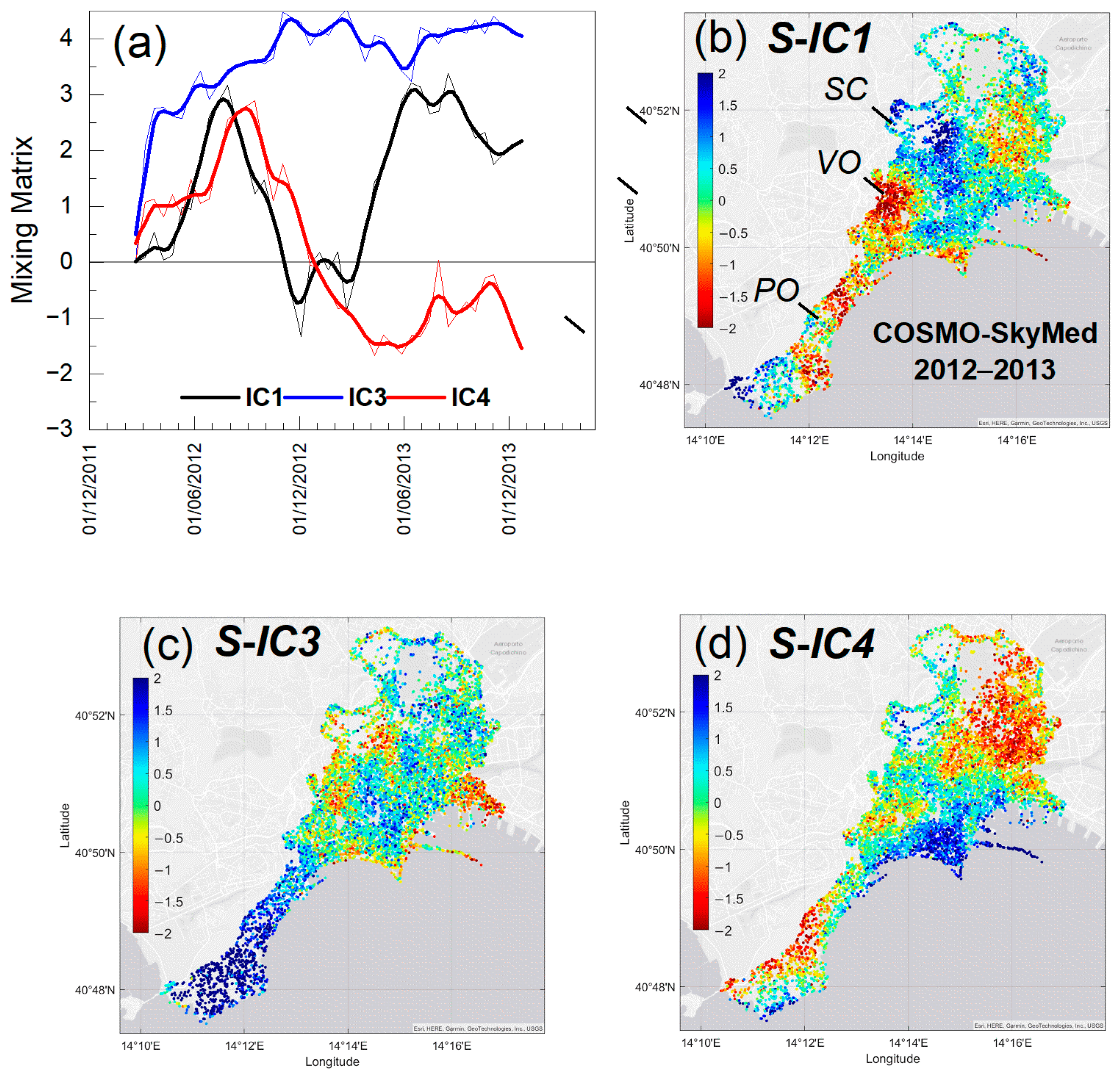
3.2. S-ICA Results for All Datasets at the Site Scale
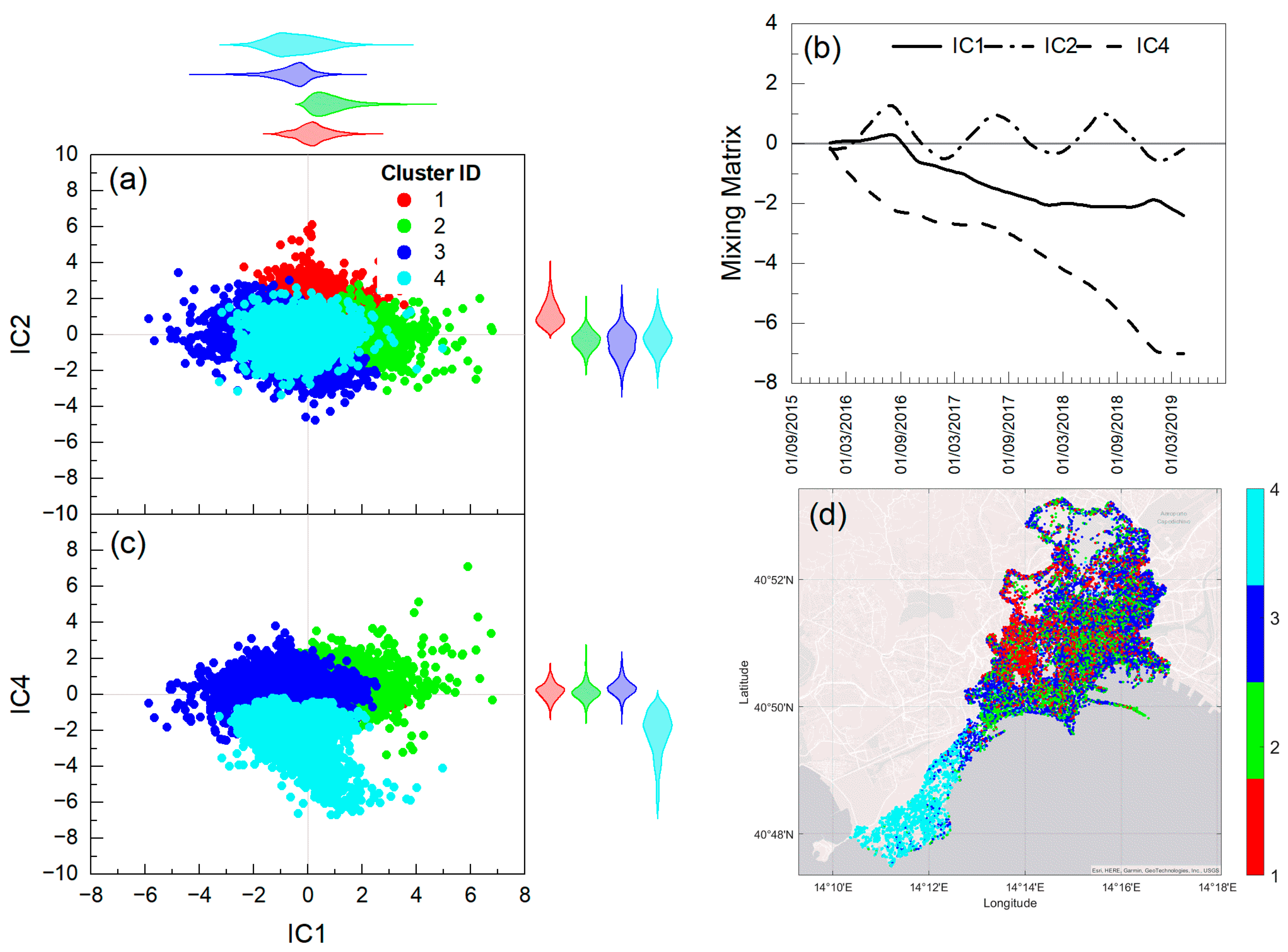
3.3. Clustering Results for S-ICA on TerraSAR-X Dataset at the Site Scale
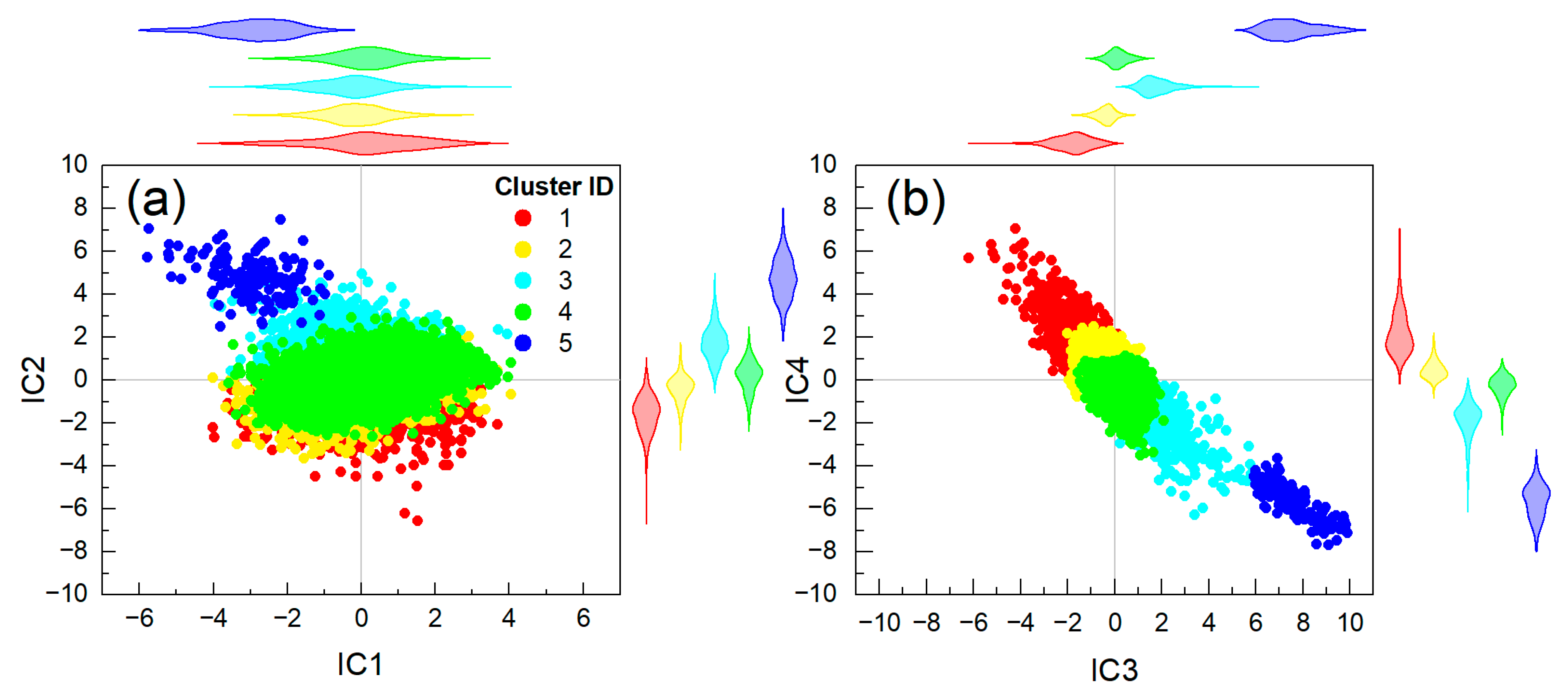
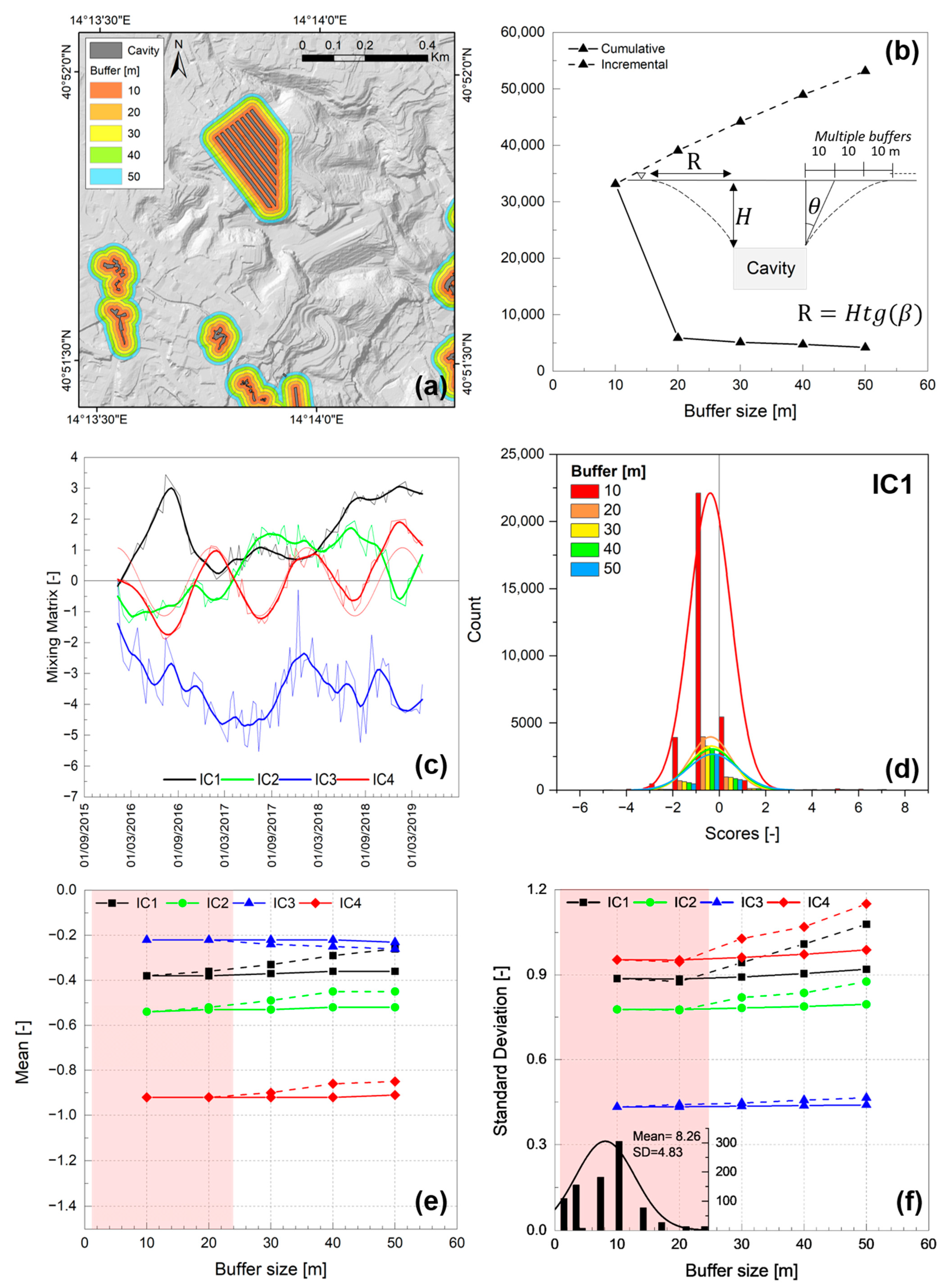
3.4. T-ICA and Clustering for Cavity Classification at the Local Scale
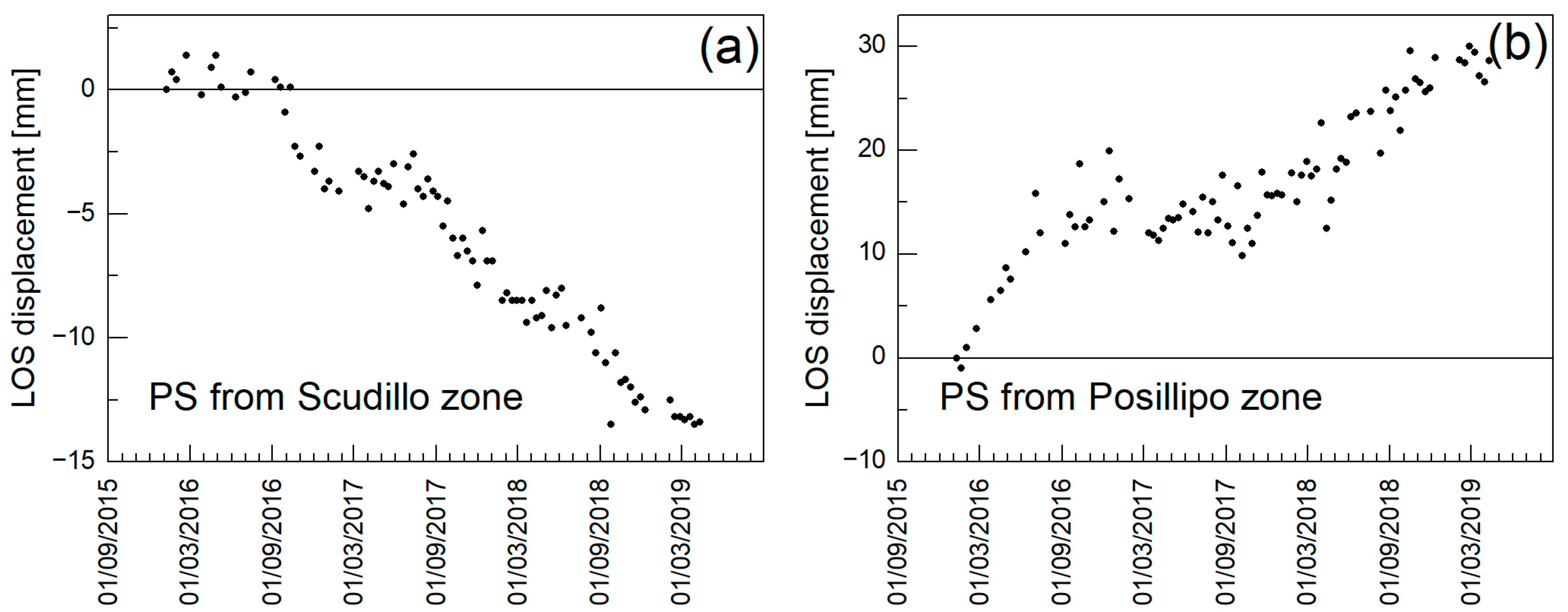
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ferretti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef]
- Bonì, R.; Bosino, A.; Meisina, C.; Novellino, A.; Bateson, L.; McCormack, H. A methodology to detect and characterize uplift phenomena in urban areas using Sentinel-1 data. Remote Sens. 2018, 10, 607. [Google Scholar] [CrossRef]
- Chen, Y.; Tan, K.; Yan, S.; Zhang, K.; Zhang, H.; Liu, X.; Li, H.; Sun, Y. Monitoring land surface displacement over Xuzhou (China) in 2015-2018 through PCA-based correction Applied to SAR interferometry. Remote Sens. 2019, 11, 1494. [Google Scholar] [CrossRef]
- Nespoli, M.; Cenni, N.; Belardinelli, M.E.; Marcaccio, M. The interaction between displacements and water level changes due to natural and anthropogenic effects in the Po Plain (Italy): The different point of view of GNSS and piezometers. J. Hydrol. 2021, 596, 126112. [Google Scholar] [CrossRef]
- Pintori, F.; Serpelloni, E.; Longuevergne, L.; Garcia, A.; Faenza, L.; D’Alberto, L.; Gualandi, A.; Belardinelli, M.E. Mechanical Response of Shallow Crust to Groundwater Storage Variations: Inferences From Deformation and Seismic Observations in the Eastern Southern Alps, Italy. J. Geophys. Res. Solid Earth 2021, 126, e2020JB020586. [Google Scholar] [CrossRef]
- Shi, L.; Gong, H.; Chen, B.; Zhou, C. Land subsidence prediction induced by multiple factors using machine learning method. Remote Sens. 2020, 12, 4044. [Google Scholar] [CrossRef]
- Chaussard, E.; Milillo, P.; Bürgmann, R.; Perissin, D.; Fielding, E.J.; Baker, B. Remote Sensing of Ground Deformation for Monitoring Groundwater Management Practices: Application to the Santa Clara Valley During the 2012–2015 California Drought. J. Geophys. Res. Solid Earth 2017, 122, 8566–8582. [Google Scholar] [CrossRef]
- Gualandi, A.; Liu, Z. Variational Bayesian Independent Component Analysis for InSAR Displacement Time-Series with Application to Central California, USA. J. Geophys. Res. Solid Earth 2021, 126, 4–8. [Google Scholar] [CrossRef]
- Tiampo, K.F.; González, P.J.; Samsonov, S.; Fernández, J.; Camacho, A. Principal component analysis of MSBAS DInSAR time series from Campi Flegrei, Italy. J. Volcanol. Geotherm. Res. 2017, 344, 139–153. [Google Scholar] [CrossRef]
- Bordoni, M.; Bonì, R.; Colombo, A.; Lanteri, L.; Meisina, C. A methodology for ground motion area detection (GMA-D) using A-DInSAR time series in landslide investigations. Catena 2018, 163, 89–110. [Google Scholar] [CrossRef]
- Machado-Machado, E.A.; Neeti, N.; Eastman, J.R.; Chen, H. Implications of space-time orientation for Principal Components Analysis of Earth observation image time series. Earth Sci. Inform. 2011, 4, 117–124. [Google Scholar] [CrossRef]
- Machiwal, D.; Kumar, S.; Meena, H.M.; Santra, P.; Singh, R.K.; Singh, D.V. Clustering of rainfall stations and distinguishing influential factors using PCA and HCA techniques over the western dry region of India. Meteorol. Appl. 2019, 26, 300–311. [Google Scholar] [CrossRef]
- Praene, J.P.; Malet-Damour, B.; Radanielina, M.H.; Fontaine, L.; Rivière, G. GIS-based approach to identify climatic zoning: A hierarchical clustering on principal component analysis. Build. Environ. 2019, 164, 106330. [Google Scholar] [CrossRef]
- Chaussard, E.; Farr, T.G. A New Method for Isolating Elastic From Inelastic Deformation in Aquifer Systems: Application to the San Joaquin Valley, CA. Geophys. Res. Lett. 2019, 46, 10800–10809. [Google Scholar] [CrossRef]
- Garc, A. Exploring ICA for time series decomposition. In Working Paper 11–16 Statistics and Econometrics Series 11; Departamento de Estadística, Universidad Carlos III de Madrid: Getafe, Spain, 2011. [Google Scholar]
- Cardoso, J.; Souloumiac, A. Blind beamforming for non-gaussian signals. IEE Proc. F Radar Signal Process. 1993, 140, 362–370. [Google Scholar] [CrossRef]
- Belouchrani, A.; Meraim, K.A.; Cardoso, J.-F.; Moulines, E. A blind source separation technique based on second order statistics. IEEE Trans. Signal Process. 1997, 45, 434–444. [Google Scholar] [CrossRef]
- Bottiglieri, M.; Falanga, M.; Tammaro, U.; De Martino, P.; Obrizzo, F.; Godano, C.; Pingue, F. Characterization of GPS time series at the Neapolitan volcanic area by statistical analysis. J. Geophys. Res. Atmos. 2010, 115. [Google Scholar] [CrossRef]
- Ebmeier, S.K. Application of independent component analysis to multitemporal InSAR data with volcanic case studies. J. Geophys. Res. Solid Earth 2016, 121, 8970–8986. [Google Scholar] [CrossRef]
- Gaddes, M.E.; Hooper, A.; Bagnardi, M.; Inman, H.; Albino, F. Blind Signal Separation Methods for InSAR: The Potential to Automatically Detect and Monitor Signals of Volcanic Deformation. J. Geophys. Res. Solid Earth 2018, 123, 10226–10251. [Google Scholar] [CrossRef]
- Liu, B.; Dai, W.; Peng, W.; Meng, X. Spatio-temporal analysis of the land subsidence in the UK using Independent Component Analysis. In Proceedings of the 3rd International Workshop on Earth Observation and Remote Sensing Applications, EORSA, Changsha, China, 11–14 June 2014; pp. 294–298. [Google Scholar] [CrossRef]
- Gualandi, A.; Serpelloni, E.; Belardinelli, M.E. Blind source separation problem in GPS time series. J. Geod. 2016, 90, 323–341. [Google Scholar] [CrossRef]
- Cohen-Waeber, J.; Bürgmann, R.; Chaussard, E.; Giannico, C.; Ferretti, A. Spatiotemporal Patterns of Precipitation-Modulated Landslide Deformation From Independent Component Analysis of InSAR Time Series. Geophys. Res. Lett. 2018, 45, 1878–1887. [Google Scholar] [CrossRef]
- Ren, G.; Li, J.; Ren, G.; Li, J. A Study of Angle of Draw in Mining Subsidence Using Numerical Modeling Techniques. 2008. Available online: https://www.researchgate.net/publication/237122395 (accessed on 4 April 2022).
- Whittaker, B.N.; Reddish, D.J. Subsidence Occurrence, Prediction and Control; Elsevier Science: Amsterdam, The Netherlands, 1989. [Google Scholar]
- Tufano, R.; Guerriero, L.; Annibali Corona, M.; Bausilio, G.; Di Martire, D.; Nisio, S.; Calcaterra, D. Anthropogenic sinkholes of the city of Naples, Italy: An update. Nat. Hazards 2022, 112, 2577–2608. [Google Scholar] [CrossRef]
- Ascione, A.; Aucelli, P.P.; Cinque, A.; Di Paola, G.; Mattei, G.; Ruello, M.; Ermolli, E.R.; Santangelo, N.; Valente, E. Geomorphology of Naples and the Campi Flegrei: Human and natural landscapes in a restless land. J. Maps 2020, 17, 18–28. [Google Scholar] [CrossRef]
- Scarpati, C. Volcanism in the city of Naples Emplacement and eruptive mechanisms of large volume Plinian eruptions View project Physics of Volcanism View project. Online Soc. Geol. It. 2015, 33, 88–91. [Google Scholar] [CrossRef]
- Orsi, G.; De Vita, S.; di Vito, M. The restless, resurgent Campi Flegrei nested caldera (Italy): Constraints on its evolution and configuration. J. Volcanol. Geotherm. Res. 1996, 74, 179–214. [Google Scholar] [CrossRef]
- Bevilacqua, A.; De Martino, P.; Giudicepietro, F.; Ricciolino, P.; Patra, A.; Pitman, E.B.; Bursik, M.; Voight, B.; Flandoli, F.; Macedonio, G.; et al. Data analysis of the unsteadily accelerating GPS and seismic records at Campi Flegrei caldera from 2000 to 2020. Sci. Rep. 2022, 12, 19175. [Google Scholar] [CrossRef]
- D’Auria, L.; Giudicepietro, F.; Aquino, I.; Borriello, G.; Del Gaudio, C.; Lo Bascio, D.; Martini, M.; Ricciardi, G.P.; Ricciolino, P.; Ricco, C. Repeated fluid-transfer episodes as a mechanism for the recent dynamics of Campi Flegrei caldera (1989–2010). J. Geophys. Res. Solid Earth 2011, 116, 1–24. [Google Scholar] [CrossRef]
- De Martino, P.; Dolce, M.; Brandi, G.; Scarpato, G.; Tammaro, U. The Ground Deformation History of the Neapolitan Volcanic Area (Campi Flegrei Caldera, Somma–Vesuvius Volcano, and Ischia Island) from 20 Years of Continuous GPS Observations (2000–2019). Remote Sens. 2021, 13, 2725. [Google Scholar] [CrossRef]
- Samsonov, S.V.; Tiampo, K.F.; Camacho, A.G.; Fernández, J.; González, P.J. Spatiotemporal analysis and interpretation of 1993–2013 ground deformation at Campi Flegrei, Italy, observed by advanced DInSAR. Geophys. Res. Lett. 2014, 41, 6101–6108. [Google Scholar] [CrossRef]
- Pepe, S.; De Siena, L.; Barone, A.; Castaldo, R.; D’Auria, L.; Manzo, M.; Casu, F.; Fedi, M.; Lanari, R.; Bianco, F.; et al. Volcanic structures investigation through SAR and seismic interferometric methods: The 2011–2013 Campi Flegrei unrest episode. Remote Sens. Environ. 2019, 234, 111440. [Google Scholar] [CrossRef]
- Castaldo, R.; Tizzani, P.; Solaro, G. Inflating Source Imaging and Stress/Strain Field Analysis at Campi Flegrei Caldera: The 2009–2013 Unrest Episode. Remote Sens. 2021, 13, 2298. [Google Scholar] [CrossRef]
- Matano, F. Analysis and Classification of Natural and Human-Induced Ground Deformations at Regional Scale (Campania, Italy) Detected by Satellite Synthetic-Aperture Radar Interferometry Archive Datasets. Remote Sens. 2019, 11, 2822. [Google Scholar] [CrossRef]
- Terranova, C.; Ventura, G.; Vilardo, G. Multiple causes of ground deformation in the Napoli metropolitan area (Italy) from integrated Persistent Scatterers DinSAR, geological, hydrological, and urban infrastructure data. Earth-Sci. Rev. 2015, 146, 105–119. [Google Scholar] [CrossRef]
- Scarpati, C.; Cole, P.; Perrotta, A. The Neapolitan Yellow Tuff—A large volume multiphase eruption from Campi Flegrei, Southern Italy. Bull. Volcanol. 1993, 55, 343–356. [Google Scholar] [CrossRef]
- Deino, A.L.; Orsi, G.; de Vita, S.; Piochi, M. The age of the Neapolitan Yellow Tuff caldera-forming eruption (Campi Flegrei caldera-Italy) assessed by 40Ar/39Ar dating method. J. Volcanol. Geotherm. Res. 2004, 133, 157–170. [Google Scholar] [CrossRef]
- Basso, N.; Ciotoli, G.; Finoia, M.G.; Guarino, P.M.; Miraglino, P.; Nisio, S. Suscettibilità ai fenomeni di sinkholes antropogenici nel territorio di Napoli. Mem. Descr. Carta Geol. d’It. 2013, XCIII, 73–104. [Google Scholar]
- Guarino, P.M.; Santo, A.; Guarino, P.M.; Santo, A. Planning of geological investigations in areas affected by anthropogenic sinkholes: The case of densely urbanised area northeast of Naples (Italy). EGUGA 2013, 15, EGU2013-4285. [Google Scholar]
- Guarino, P.M.; Nisio, S. Anthropogenic sinkholes in the territory of the city of Naples (Southern Italy). Phys. Chem. Earth Parts A/B/C 2012, 49, 92–102. [Google Scholar] [CrossRef]
- Cennamo, C.; Angelillo, M.; Cusano, C. Structural failures due to anthropogenic sinkholes in the urban area of Naples and the effect of a FRP retrofitting. Compos. Part B Eng. 2017, 108, 190–199. [Google Scholar] [CrossRef]
- Rispoli, C.; Di Martire, D.; Calcaterra, D.; Cappelletti, P.; Graziano, S.F.; Guerriero, L. Sinkholes threatening places of worship in the historic center of Naples. J. Cult. Herit. 2020, 46, 313–319. [Google Scholar] [CrossRef]
- Bevilacqua, A.; Neri, A.; De Martino, P.; Isaia, R.; Novellino, A.; Tramparulo, F.D.; Vitale, S. Radial interpolation of GPS and leveling data of ground deformation in a resurgent caldera: Application to Campi Flegrei (Italy). J. Geod. 2020, 94, 24. [Google Scholar] [CrossRef]
- De Martino, P.; Tammaro, U.; Obrizzo, F. GPS time series at Campi Flegrei caldera (2000–2013). Ann. Geophys. 2014, 57, S0213. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE Trans. Geosci. Remote Sens. 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Ferretti, A.; Fumagalli, A.; Novali, F.; Prati, C.; Rocca, F.; Rucci, A. A new algorithm for processing interferometric data-stacks: SqueeSAR. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3460–3470. [Google Scholar] [CrossRef]
- Giannico, C.; Ferretti, A.; Jurina, L.; Ricci, M. Application of satellite radar interferometry for structural damage assessment and monitoring. In Life-Cycle and Sustainability of Civil Infrastructure Systems, Proceedings of the 3rd International Symposium on Life-Cycle Civil Engineering, IALCCE 2012, Vienna, Austria, 3–6 October 2012; CRC Press: Boca Raton, FL, USA, 2012; pp. 2094–2101. [Google Scholar]
- Notti, D.; Calò, F.; Cigna, F.; Manunta, M.; Herrera, G.; Berti, M.; Meisina, C.; Tapete, D.; Zucca, F. A User-Oriented Methodology for DInSAR Time Series Analysis and Interpretation: Landslides and Subsidence Case Studies. Pure Appl. Geophys. 2015, 172, 3081–3105. [Google Scholar] [CrossRef]
- Jolliffe, I.T. Rotation of principal components: Some comments. J. Climatol. 1987, 7, 507–510. [Google Scholar] [CrossRef]
- Richman, M.B. Rotation of principal components. J. Climatol. 1986, 6, 293–335. [Google Scholar] [CrossRef]
- White, D.; Richman, M.; Yarnal, B. Climate regionalization and rotation of principal components. Int. J. Climatol. 1991, 11, 1–25. [Google Scholar] [CrossRef]
- Ballabio, D. A MATLAB toolbox for Principal Component Analysis and unsupervised exploration of data structure. Chemom. Intell. Lab. Syst. 2015, 8, 1–9. [Google Scholar] [CrossRef]
- Krzanowski, W.J.; Krzanowski, W. Principles of Multivariate Analysis; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Wilks, S.D. Statistical Methods in the Atmospheric Sciences, 4th ed.; Janco, C., Ed.; Elsevier: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Compagnucci, R.H.; Salles, A. Surface Pressure Patterns During The Year Over Southern South America. Int. J. Climatol. 1997, 17, 635–653. [Google Scholar] [CrossRef]
- Salles, A.; Canziani, P.O.; Compagnucci, R.H. The spatial and temporal behaviour of the lower stratospheric temperature over the southern hemisphere: The msu view. Part II: Spatial behaviour. Int. J. Climatol. 2001, 21, 419–437. [Google Scholar] [CrossRef]
- Hyvärinen, A.; Oja, E. A Fast Fixed-Point Algorithm for Independent Component Analysis. Neural Comput. 1997, 9, 1483–1492. [Google Scholar] [CrossRef]
- Ward, J.H., Jr. Hierarchical grouping to optimize an objective function. J. Am. Stat. Assoc. 1963, 58, 236–244. [Google Scholar] [CrossRef]
- Darand, M.; Daneshvar, M.R.M. Regionalization of Precipitation Regimes in Iran Using Principal Component Analysis and Hierarchical Clustering Analysis. Environ. Process. 2014, 1, 517–532. [Google Scholar] [CrossRef]
- Guarino, P.M.; Santo, A.; Forte, G.; De Falco, M.; Niceforo, D.M.A. Analysis of a database for anthropogenic sinkhole triggering and zonation in the Naples hinterland (Southern Italy). Nat. Hazards 2017, 91, 173–192. [Google Scholar] [CrossRef]
- Castellanza, R.; Lollino, P.; Ciantia, M. A methodological approach to assess the hazard of underground cavities subjected to environmental weathering. Tunn. Undergr. Space Technol. 2018, 82, 278–292. [Google Scholar] [CrossRef]
- Perrotti, M.; Lollino, P.; Fazio, N.L.; Pisano, L.; Vessia, G.; Parise, M.; Fiore, A.; Luisi, M. Finite element-based stability charts for underground cavities in soft calcarenites. Int. J. Geomech. 2018, 18, 1–15. [Google Scholar] [CrossRef]
- Scotto, A.; Santolo, D.; Evangelista, L.; Silvestri, F.; Cavuoto, G.; Fiore VDi Punzo, M.; Tarallo, D.; Evangelista, A. Investigations on the stability conditions of a tuff cavity: The Cimitero delle Fontanelle in Naples. Riv. Ital. Di Geotec. 2015, 3, 28. [Google Scholar]
- Chang, L.; Hanssen, R.F. Detection of cavity migration and sinkhole risk using radar interferometric time series. Remote Sens. Environ. 2014, 147, 56–64. [Google Scholar] [CrossRef]
- De Stefano, R.; Repola, L.; Guerriero, L.; Iovane, D.; Morra, V.; Pagano, F.; Di Martire, D. Rockfall threatening cumae archeological site fruition (Phlegraean fields park—Naples). Sustainability 2021, 13, 1390. [Google Scholar] [CrossRef]
- de Silva, F.; di Santolo, A.S. Probabilistic performance-based approaches to the static and seismic assessment of rock cavities. Int. J. Rock Mech. Min. Sci. 2018, 112, 354–368. [Google Scholar] [CrossRef]
- Evangelista, A.; Aversa, S.; Pescatore, T.S.; Pinto, F. Soft rocks in southern Italy and role of volcanic tuffs in the urbanization of Naples. In Proceedings of the II International Symposium on ‘The Geotechnics of Hard Soils and Soft Rocks’, Napoli, Italy, 12–24 October 1998; Volume 3, pp. 1243–1267. [Google Scholar]



| Satellite | Sensor’s Band | Orbit | Inc. Look Angle (°) θ | Acquisition Span | Area (Km2) | No. PS-DSs | Mean PS-DSs Density * | Spatial Resolution (m) * | Revisit Time (Days) |
|---|---|---|---|---|---|---|---|---|---|
| ERS1-2 | C | Desc. | 23 | Jun 1992 Dec 2000 | 31.3 | 8122 | 262 | 20 × 5 | 35 |
| ENVISAT | C | Desc. | 23 | Jun 2003 Jun 2010 | 31.3 | 15,380 | 496 | 20 × 5 | 35 |
| COSMO-SkyMed | X | Desc. | 44 | Feb 2012 Dec 2013 | 31.3 | 252,977 | 8160 | 3 × 3 | 8 |
| TerraSAR-X | X | Desc. | 21.6 | Jan 2016 Apr 2019 | 325.8 | 2,566,269 | 7876.8 | 3 × 3 | 11 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigamonti, S.; Dattola, G.; Frattini, P.; Crosta, G.B. A Multivariate Time Series Analysis of Ground Deformation Using Persistent Scatterer Interferometry. Remote Sens. 2023, 15, 3082. https://doi.org/10.3390/rs15123082
Rigamonti S, Dattola G, Frattini P, Crosta GB. A Multivariate Time Series Analysis of Ground Deformation Using Persistent Scatterer Interferometry. Remote Sensing. 2023; 15(12):3082. https://doi.org/10.3390/rs15123082
Chicago/Turabian StyleRigamonti, Serena, Giuseppe Dattola, Paolo Frattini, and Giovanni Battista Crosta. 2023. "A Multivariate Time Series Analysis of Ground Deformation Using Persistent Scatterer Interferometry" Remote Sensing 15, no. 12: 3082. https://doi.org/10.3390/rs15123082
APA StyleRigamonti, S., Dattola, G., Frattini, P., & Crosta, G. B. (2023). A Multivariate Time Series Analysis of Ground Deformation Using Persistent Scatterer Interferometry. Remote Sensing, 15(12), 3082. https://doi.org/10.3390/rs15123082










