Deep Convolutional Neural Network for Plume Rise Measurements in Industrial Environments
Abstract
1. Introduction
- Proposing Deep Plume Rise Network (DPRNet), a deep learning method for PR measurements, by incorporating PC recognition and image processing-based measurements. We have provided a reproducible algorithm to recognize PCs from RGB images accurately.
- To the best of our knowledge, this paper estimates the PCs’ neutral buoyancy coordinates for the first time, which is of the essence in environmental studies. This online information can help update related criteria, such as the live air-quality health index (AQHI).
- A pixel-level recognition dataset, Deep Plume Rise Dataset (DPRD), containing (1) 2500 fine segments of PCs, (2) the upper and lower boundaries of PCs, (3) the image coordinates of smokestack exit, (4) the centerlines and NBP image coordinates of PCs, is presented. As is expected, the DPRD dataset includes one class, namely PC. Widely-used DCNN-based smoke recognition methods are employed to evaluate our dataset. Furthermore, this newly generated dataset was used for PR measurements.
2. Theoretical Background
2.1. Briggs PR Prediction
2.2. CNN and Convolutional Layer
2.3. Mask R-CNN
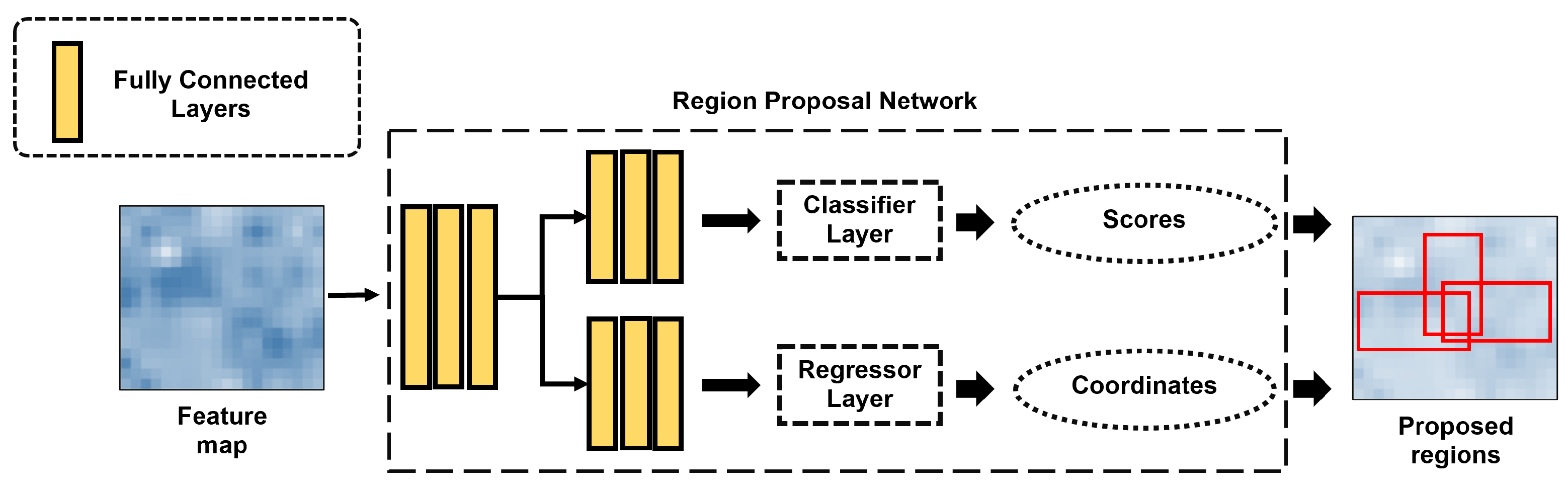
2.3.1. RPN
2.3.2. Loss Function
3. Methodology
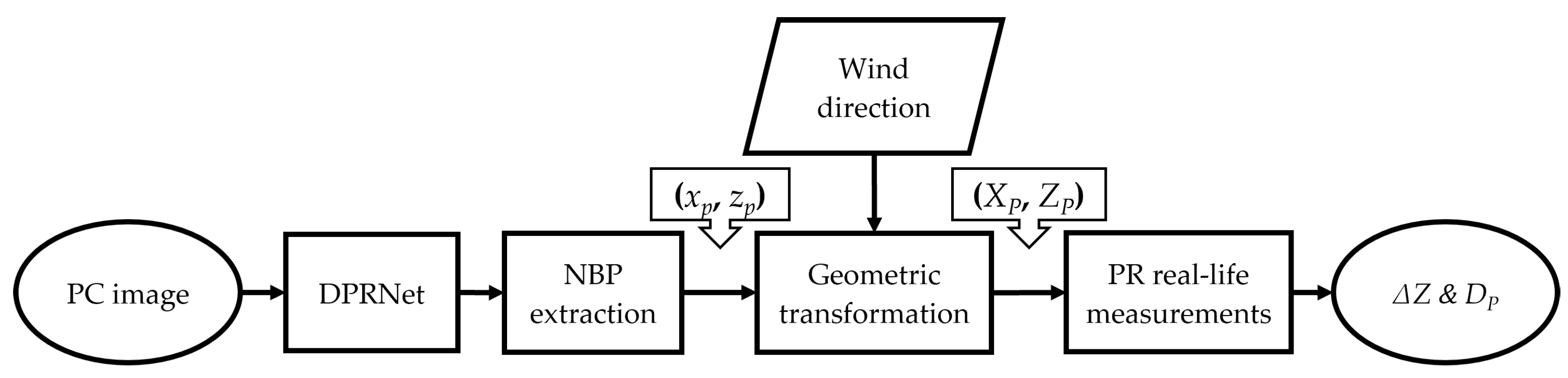
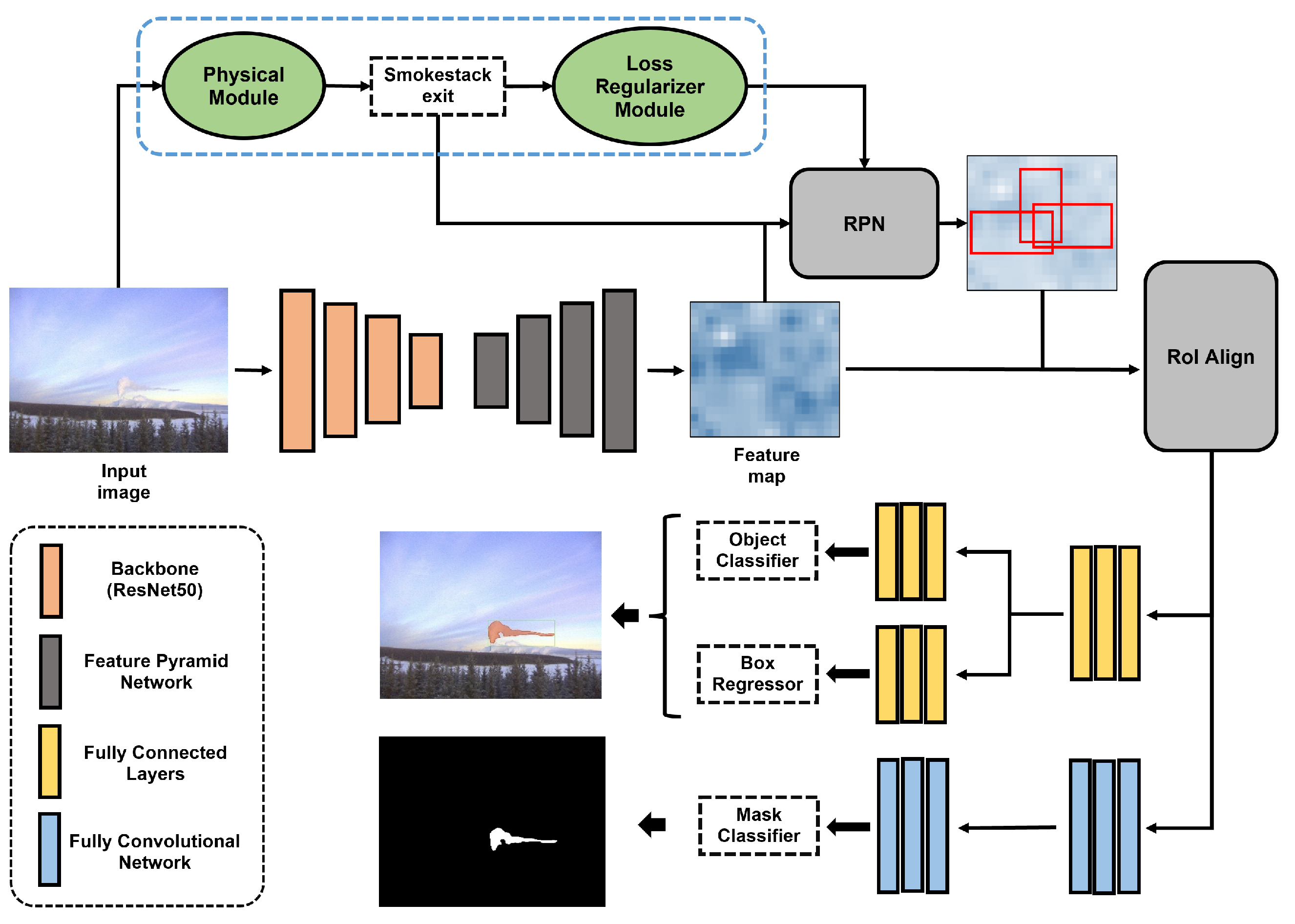
3.1. DPRNet
3.1.1. Physical Module
3.1.2. Loss Regularizer Module
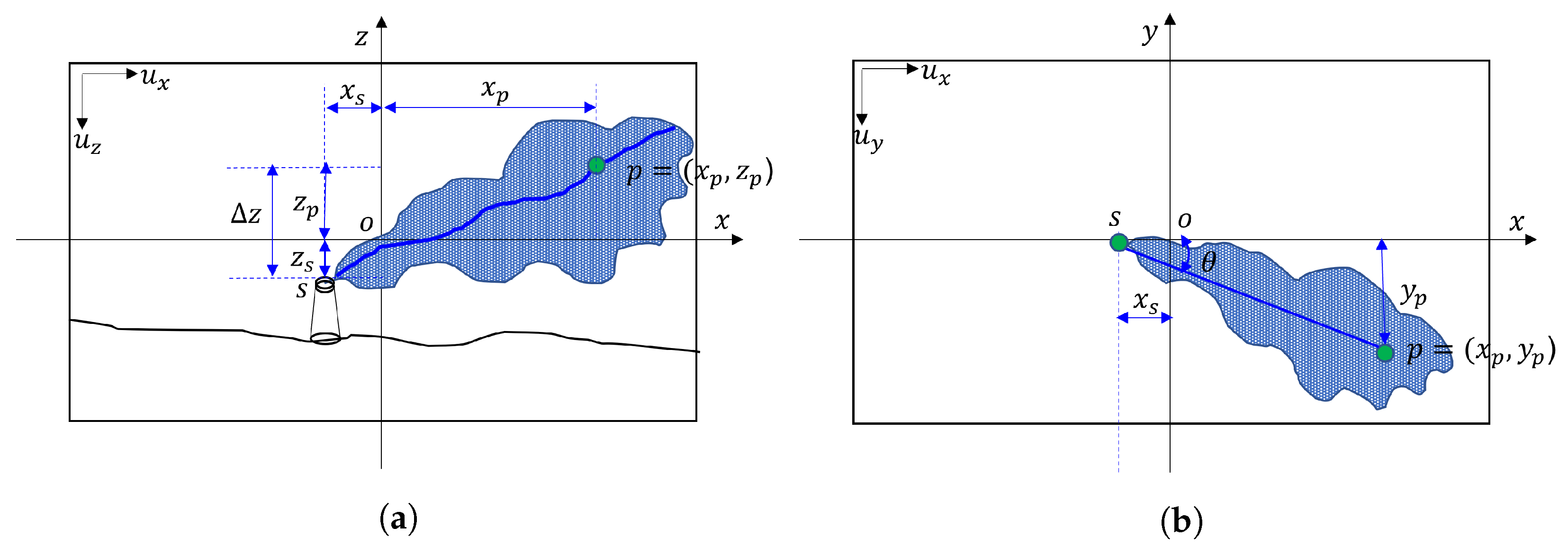
3.2. NBP Extraction
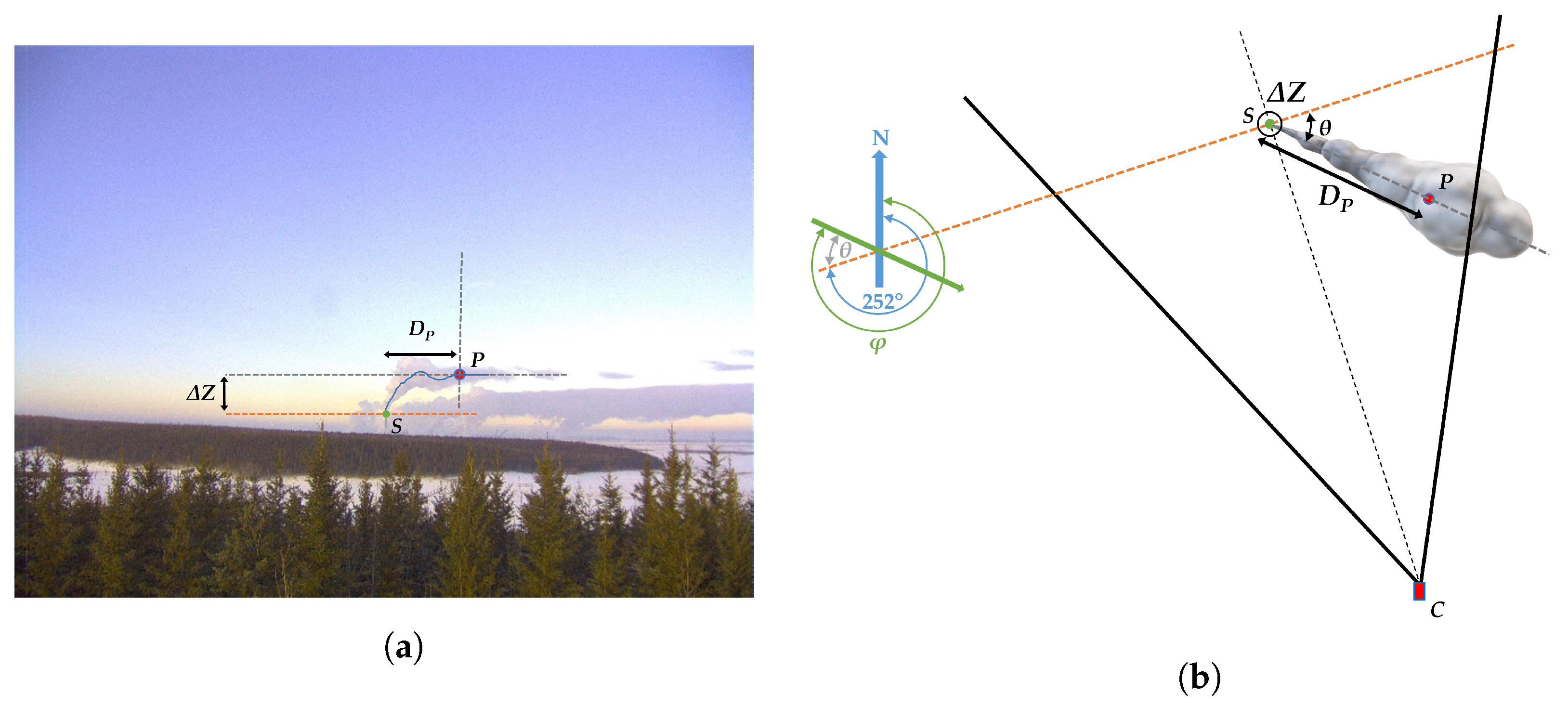
3.3. Geometric Transformation
4. Experimental Results and Discussion
4.1. Site Description
4.2. Deep Plume Rise Dataset (DPRD)
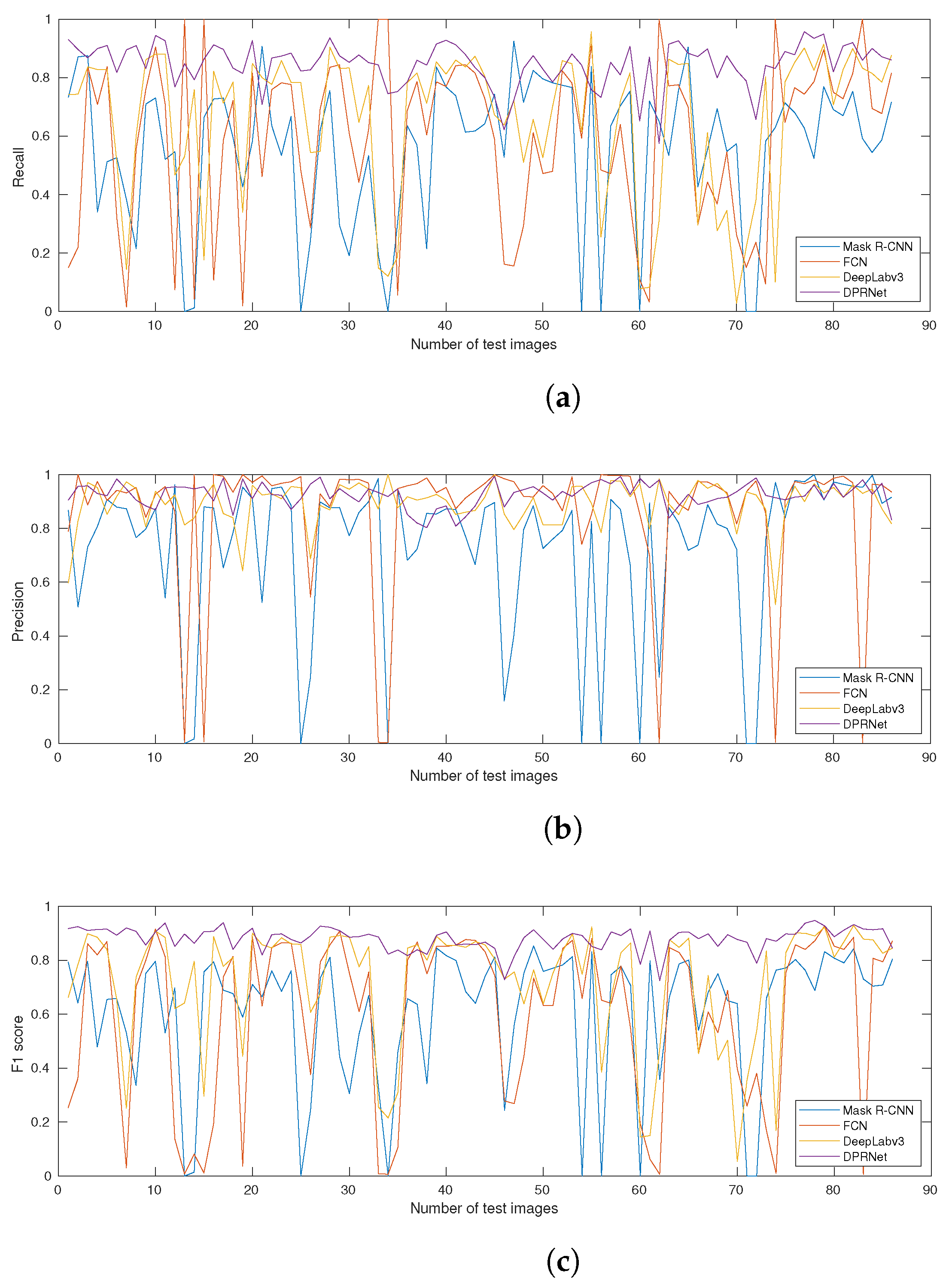
4.3. Model Validation Metrics
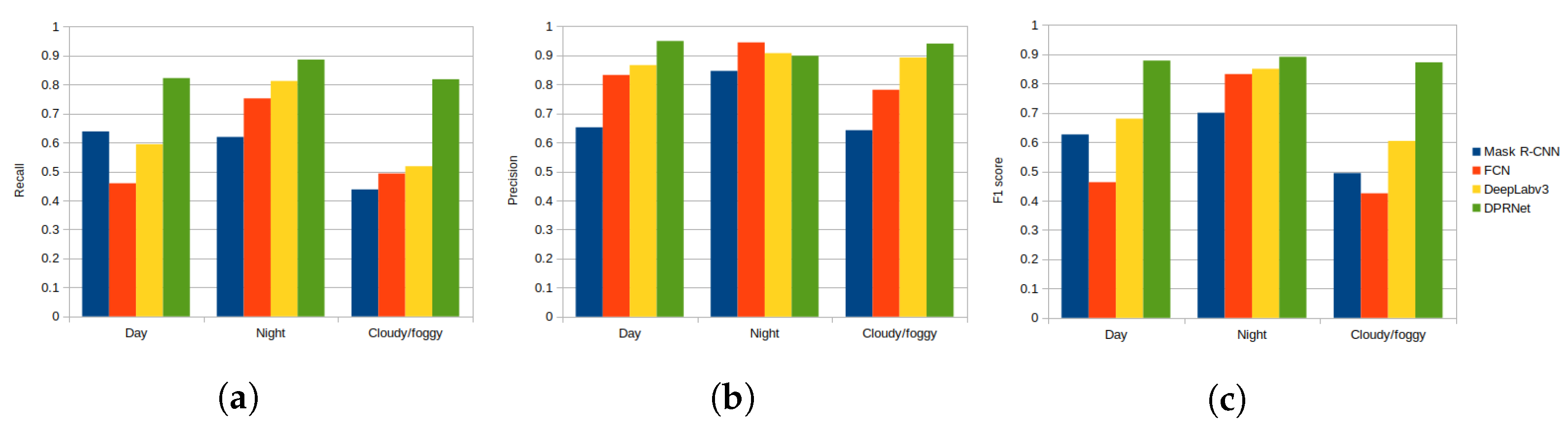
4.4. Comparison with Existing Smoke Recognition Methods
4.5. Plume Rise Measurement
5. Conclusions
- Generalizing DPRNet to predict the PC and PC centerline simultaneously.
- Reinforcing DPRNet to recognize multi-source PCs occurring in industrial environments.
- Conducting comparative studies using meteorological and smokestack measurements between the estimated PR and PR distance from the proposed framework and the Briggs parameterizations equations.
- Briggs parameterization modification via estimated PR and PR distance from the proposed framework.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Briggs, G.A. Plume rise predictions. In Lectures on Air Pollution and Environmental Impact Analyses; Springer: Berlin/Heidelberg, Germany, 1982; pp. 59–111. [Google Scholar]
- Ashrafi, K.; Orkomi, A.A.; Motlagh, M.S. Direct effect of atmospheric turbulence on plume rise in a neutral atmosphere. Atmos. Pollut. Res. 2017, 8, 640–651. [Google Scholar] [CrossRef]
- Briggs, G.A. Plume Rise: A Critical Survey; Technol Report; Air Resources Atmospheric Turbulence and Diffusion Lab.: Oak Ridge, TN, USA, 1969.
- Briggs, G. Plume rise predictions, lectures on air pollution and environment impact analysis. Am. Meteorol. Soc. 1975, 10, 510. [Google Scholar]
- Bieser, J.; Aulinger, A.; Matthias, V.; Quante, M.; Van Der Gon, H.D. Vertical emission profiles for europe based on plume rise calculations. Environ. Pollut. 2011, 159, 2935–2946. [Google Scholar] [CrossRef] [PubMed]
- Bringfelt, B. Plume rise measurements at industrial chimneys. Atmos. Environ. 1968, 2, 575–598. [Google Scholar] [CrossRef]
- Makar, P.; Gong, W.; Milbrandt, J.; Hogrefe, C.; Zhang, Y.; Curci, G.; Žabkar, R.; Im, U.; Balzarini, A.; Baró, R.; et al. Feedbacks between air pollution and weather, part 1: Effects on weather. Atmos. Environ. 2015, 115, 442–469. [Google Scholar] [CrossRef]
- Emery, C.; Jung, J.; Yarwood, G. Implementation of an Alternative Plume Rise Methodology in Camx; Final Report, Work Order No. 582-7-84005-FY10-20; Environ International Corporation: Novato, CA, USA, 2010. [Google Scholar]
- Byun, D. Science Algorithms of the Epa Models-3 Community Multiscale Air Quality (Cmaq) Modeling System; EPA/600/R-99/030; U.S. Environmental Protection Agency: Washington, DC, USA, 1999.
- Rittmann, B.E. Application of two-thirds law to plume rise from industrial-sized sources. Atmos. Environ. 1982, 16, 2575–2579. [Google Scholar] [CrossRef]
- England, W.G.; Teuscher, L.H.; Snyder, R.B. A measurement program to determine plume configurations at the beaver gas turbine facility, port westward, oregon. J. Air Pollut. Control. Assoc. 1976, 26, 986–989. [Google Scholar] [CrossRef]
- Hamilton, P. Paper iii: Plume height measurements at northfleet and tilbury power stations. Atmos. Environ. 1967, 1, 379–387. [Google Scholar] [CrossRef]
- Moore, D. A comparison of the trajectories of rising buoyant plumes with theoretical/empirical models. Atmos. Environ. 1974, 8, 441–457. [Google Scholar] [CrossRef]
- Sharf, G.; Peleg, M.; Livnat, M.; Luria, M. Plume rise measurements from large point sources in israel. Atmos. Environ. Part A Gen. Top. 1993, 27, 1657–1663. [Google Scholar] [CrossRef]
- Webster, H.; Thomson, D. Validation of a lagrangian model plume rise scheme using the kincaid data set. Atmos. Environ. 2002, 36, 5031–5042. [Google Scholar] [CrossRef]
- Gordon, M.; Li, S.-M.; Staebler, R.; Darlington, A.; Hayden, K.; O’Brien, J.; Wolde, M. Determining air pollutant emission rates based on mass balance using airborne measurement data over the alberta oil sands operations. Atmos. Meas. Tech. 2015, 8, 3745–3765. [Google Scholar] [CrossRef]
- Gordon, M.; Makar, P.A.; Staebler, R.M.; Zhang, J.; Akingunola, A.; Gong, W.; Li, S.-M. A comparison of plume rise algorithms to stack plume measurements in the athabasca oil sands. Atmos. Chem. Phys. 2018, 18, 14695–14714. [Google Scholar] [CrossRef]
- Akingunola, A.; Makar, P.A.; Zhang, J.; Darlington, A.; Li, S.-M.; Gordon, M.; Moran, M.D.; Zheng, Q. A chemical transport model study of plume-rise and particle size distribution for the athabasca oil sands. Atmos. Chem. Phys. 2018, 18, 8667–8688. [Google Scholar] [CrossRef]
- Isikdogan, F.; Bovik, A.C.; Passalacqua, P. Surface water mapping by deep learning. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4909–4918. [Google Scholar] [CrossRef]
- Isikdogan, F.; Bovik, A.; Passalacqua, P. Rivamap: An automated river analysis and mapping engine. Remote Sens. Environ. 2017, 202, 88–97. [Google Scholar] [CrossRef]
- Gu, K.; Qiao, J.; Lin, W. Recurrent air quality predictor based on meteorology-and pollution-related factors. IEEE Trans. Ind. Inform. 2018, 14, 3946–3955. [Google Scholar] [CrossRef]
- Gu, K.; Qiao, J.; Li, X. Highly efficient picture-based prediction of pm2. 5 concentration. IEEE Trans. Ind. Electron. 2018, 66, 3176–3184. [Google Scholar] [CrossRef]
- Gubbi, J.; Marusic, S.; Palaniswami, M. Smoke detection in video using wavelets and support vector machines. Fire Saf. J. 2009, 44, 1110–1115. [Google Scholar] [CrossRef]
- Yuan, F. Video-based smoke detection with histogram sequence of lbp and lbpv pyramids. Fire Saf. J. 2011, 46, 132–139. [Google Scholar] [CrossRef]
- Yuan, F. A double mapping framework for extraction of shape-invariant features based on multi-scale partitions with adaboost for video smoke detection. Pattern Recognit. 2012, 45, 4326–4336. [Google Scholar] [CrossRef]
- Yuan, F.; Shi, J.; Xia, X.; Fang, Y.; Fang, Z.; Mei, T. High-order local ternary patterns with locality preserving projection for smoke detection and image classification. Inf. Sci. 2016, 372, 225–240. [Google Scholar] [CrossRef]
- Yuan, F.; Fang, Z.; Wu, S.; Yang, Y.; Fang, Y. Real-time image smoke detection using staircase searching-based dual threshold adaboost and dynamic analysis. IET Image Process. 2015, 9, 849–856. [Google Scholar] [CrossRef]
- Khan, S.; Muhammad, K.; Hussain, T.; Ser, J.D.; Cuzzolin, F.; Bhattacharyya, S.; Akhtar, Z.; de Albuquerque, V.H.C. Deepsmoke: Deep learning model for smoke detection and segmentation in outdoor environments. Expert Syst. Appl. 2021, 182, 115125. [Google Scholar] [CrossRef]
- Shi, Y.-k.; Zhong, Z.; Zhang, D.-X.; Yang, J. A study on smoke detection based on multi-feature. J. Signal Process. 2015, 31, 1336–1341. [Google Scholar]
- Yuan, C.; Liu, Z.; Zhang, Y. Learning-based smoke detection for unmanned aerial vehicles applied to forest fire surveillance. J. Intell. Robot. Syst. 2019, 93, 337–349. [Google Scholar] [CrossRef]
- Filonenko, A.; Hernández, D.C.; Jo, K.-H. Fast smoke detection for video surveillance using cuda. IEEE Trans. Ind. Inform. 2017, 14, 725–733. [Google Scholar] [CrossRef]
- Zen, R.I.; Widyanto, M.R.; Kiswanto, G.; Dharsono, G.; Nugroho, Y.S. Dangerous smoke classification using mathematical model of meaning. Procedia Eng. 2013, 62, 963–971. [Google Scholar] [CrossRef]
- Wang, H.; Chen, Y. A smoke image segmentation algorithm based on rough set and region growing. J. For. Sci. 2019, 65, 321–329. [Google Scholar] [CrossRef]
- Zhao, W.; Chen, W.; Liu, Y.; Wang, X.; Zhou, Y. A smoke segmentation algorithm based on improved intelligent seeded region growing. Fire Mater. 2019, 43, 725–733. [Google Scholar] [CrossRef]
- Ajith, M.; Martínez-Ramón, M. Unsupervised segmentation of fire and smoke from infra-red videos. IEEE Access 2019, 7, 182381–182394. [Google Scholar] [CrossRef]
- Dimitropoulos, K.; Barmpoutis, P.; Grammalidis, N. Higher order linear dynamical systems for smoke detection in video surveillance applications. IEEE Trans. Circuits Syst. Video Technol. 2016, 27, 1143–1154. [Google Scholar] [CrossRef]
- Pham, H.N.; Dang, K.B.; Nguyen, T.V.; Tran, N.C.; Ngo, X.Q.; Nguyen, D.A.; Phan, T.T.H.; Nguyen, T.T.; Guo, W.; Ngo, H.H. A new deep learning approach based on bilateral semantic segmentation models for sustainable estuarine wetland ecosystem management. Sci. Total Environ. 2022, 838, 155826. [Google Scholar] [CrossRef]
- Shi, B.; Patel, M.; Yu, D.; Yan, J.; Li, Z.; Petriw, D.; Pruyn, T.; Smyth, K.; Passeport, E.; Miller, R.D.; et al. Automatic quantification and classification of microplastics in scanning electron micrographs via deep learning. Sci. Total Environ. 2022, 825, 153903. [Google Scholar] [CrossRef]
- Muhammad, K.; Khan, S.; Palade, V.; Mehmood, I.; Albuquerque, V.H.C.D. Edge intelligence-assisted smoke detection in foggy surveillance environments. IEEE Trans. Ind. Inform. 2019, 16, 1067–1075. [Google Scholar] [CrossRef]
- Veerappampalayam Easwaramoorthy, S.; Jaehyuk, C.; Malliga, S.; Obuli Sai, N. Forest fire and smoke detection using deep learning-based learning without forgetting. Fire Ecol. 2023, 19, 9. [Google Scholar]
- Huanjie, T.; Qianyue, D. An adaptive frame selection network with enhanced dilated convolution for video smoke recognition. Expert Syst. Appl. 2023, 215, 119371. [Google Scholar]
- Liu, M.; Xie, X.; Ke, G.; Qiao, J. Simple and efficient smoke segmentation based on fully convolutional network. DEStech Trans. Comput. Sci. Eng. 2019. [Google Scholar] [CrossRef]
- Jia, Y.; Du, H.; Wang, H.; Yu, R.; Fan, L.; Xu, G.; Zhang, Q. Automatic early smoke segmentation based on conditional generative adversarial networks. Optik 2019, 193, 162879. [Google Scholar] [CrossRef]
- Yuan, F.; Zhang, L.; Xia, X.; Wan, B.; Huang, Q.; Li, X. Deep smoke segmentation. Neurocomputing 2019, 357, 248–260. [Google Scholar] [CrossRef]
- Yuan, F.; Dong, Z.; Zhang, L.; Xia, X.; Shi, J. Cubic-cross convolutional attention and count prior embedding for smoke segmentation. Pattern Recognit. 2022, 131, 108902. [Google Scholar] [CrossRef]
- Hwang, B.; Kim, J.; Lee, S.; Kim, E.; Kim, J.; Jung, Y.; Hwang, H. Automatic detection and segmentation of thrombi in abdominal aortic aneurysms using a mask region-based convolutional neural network with optimized loss functions. Sensors 2022, 22, 3643. [Google Scholar] [CrossRef] [PubMed]
- Girshick, R. Fast r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 7–13 December 2015; pp. 1440–1448. [Google Scholar]
- Visscher, A.D. Air Dispersion Modeling: Foundations and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Cimorelli, A.J.; Perry, S.G.; Venkatram, A.; Weil, J.C.; Paine, R.J.; Wilson, R.B.; Lee, R.F.; Peters, W.D.; Brode, R.W. Aermod: A dispersion model for industrial source applications. part i: General model formulation and boundary layer characterization. J. Appl. Meteorol. 2005, 44, 682–693. [Google Scholar] [CrossRef]
- Turner, D.B.; Schulze, R. Atmospheric Dispersion Modeling: Trinity Consultants; Trinity Consultants Inc.,: Oakland, CA, USA, 2007; 408p. [Google Scholar]
- Ji, S.; Xu, W.; Yang, M.; Yu, K. 3d convolutional neural networks for human action recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 221–231. [Google Scholar] [CrossRef]
- He, K.; Gkioxari, G.; Dollár, P.; Girshick, R. Mask r-cnn. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2961–2969. [Google Scholar]
- Albawi, S.; Mohammed, T.A.; Al-Zawi, S. Understanding of a convolutional neural network. In Proceedings of the 2017 International Conference on Engineering and Technology (ICET), Antalya, Turkey, 21–23 August 2017; pp. 1–6. [Google Scholar]
- Chen, X.; Gupta, A. An implementation of faster rcnn with study for region sampling. arXiv 2017, arXiv:1702.02138. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Rafae, G.C.; Paul, W. Digital Image Processing; Addison-Wesley Longman Publishing Co., Inc.: Boston, MA, USA, 1987. [Google Scholar]
- Lothar, B. Introduction to the Operational Calculus; Elsevier & Business Media: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Luhmann, T.; Robson, S.; Kyle, S.; Harley, I. Close Range Photogrammetry: Principles, Techniques and Applications; Whittles Publishing Dunbeath: Dunbeath, UK, 2006; Volume 3. [Google Scholar]
- Geoff, D. Pattern Recognition and Classification: An Introduction; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Chen, L.-C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European conference on computer vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]








| Reported ID | Latitude | Longitude | (m) | (m) | () | (K) |
|---|---|---|---|---|---|---|
| Syn. 12908 | 57.041 | −111.616 | 183.0 | 7.9 | 12.0 | 427.9 |
| Syn. 12909 | 57.048 | −111.613 | 76.2 | 6.6 | 10.1 | 350.7 |
| Syn. 13219 | 57.296 | −111.506 | 30.5 | 5.2 | 8.8 | 355.0 |
| Syn. 16914 | 57.046 | −111.602 | 45.7 | 1.9 | 12.0 | 643.4 |
| Syn. 16915 | 57.046 | −111.604 | 31.0 | 5.0 | 9.0 | 454.5 |
| Syn. 16916 | 57.297 | −111.505 | 31.0 | 5.2 | 9.2 | 355.0 |
| Model | Recall | Precision | F1 Score |
|---|---|---|---|
| Mask R-CNN | 0.556 | 0.727 | 0.607 |
| FCN | 0.591 | 0.859 | 0.599 |
| DeepLabv3 | 0.654 | 0.892 | 0.721 |
| DPRNet | 0.846 | 0.925 | 0.881 |
| Image | Date | Time | (deg.) | (deg.) | (m) | (m) |
|---|---|---|---|---|---|---|
| I1 | 08-Nov-19 | 18-00-13 | 12.16 | −239.8 | 460 | 842 |
| I2 | 09-Nov-19 | 15-00-13 | 3.46 | −248.5 | 126 | 1707 |
| I3 | 14-Nov-19 | 10-00-16 | 10.41 | −241.6 | 338 | 1960 |
| I4 | 16-Nov-19 | 11-00-12 | 10.83 | −241.1 | 427 | 3143 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Koushafar, M.; Sohn, G.; Gordon, M. Deep Convolutional Neural Network for Plume Rise Measurements in Industrial Environments. Remote Sens. 2023, 15, 3083. https://doi.org/10.3390/rs15123083
Koushafar M, Sohn G, Gordon M. Deep Convolutional Neural Network for Plume Rise Measurements in Industrial Environments. Remote Sensing. 2023; 15(12):3083. https://doi.org/10.3390/rs15123083
Chicago/Turabian StyleKoushafar, Mohammad, Gunho Sohn, and Mark Gordon. 2023. "Deep Convolutional Neural Network for Plume Rise Measurements in Industrial Environments" Remote Sensing 15, no. 12: 3083. https://doi.org/10.3390/rs15123083
APA StyleKoushafar, M., Sohn, G., & Gordon, M. (2023). Deep Convolutional Neural Network for Plume Rise Measurements in Industrial Environments. Remote Sensing, 15(12), 3083. https://doi.org/10.3390/rs15123083







