Integrating Remote Sensing and Weather Variables for Mango Yield Prediction Using a Machine Learning Approach
Abstract
1. Introduction
- Comparing a number of ML approaches to determine which best identifies the drivers of mango yield, i.e., in-season canopy reflectance, weather parameters, or both;
- Determining if a ”time series” remote sensing approach can accurately predict mango yield (t/ha) several months (at least 3 months) prior to commercial harvest without the need for infield sampling;
- Assessing the impact of weather on model performance by integrating weather and remote sensing variables in predicting mango orchard yield;
- Evaluating model performance at multiple scale (block level and farm level) and on independent mango farms.
2. Materials and Methods
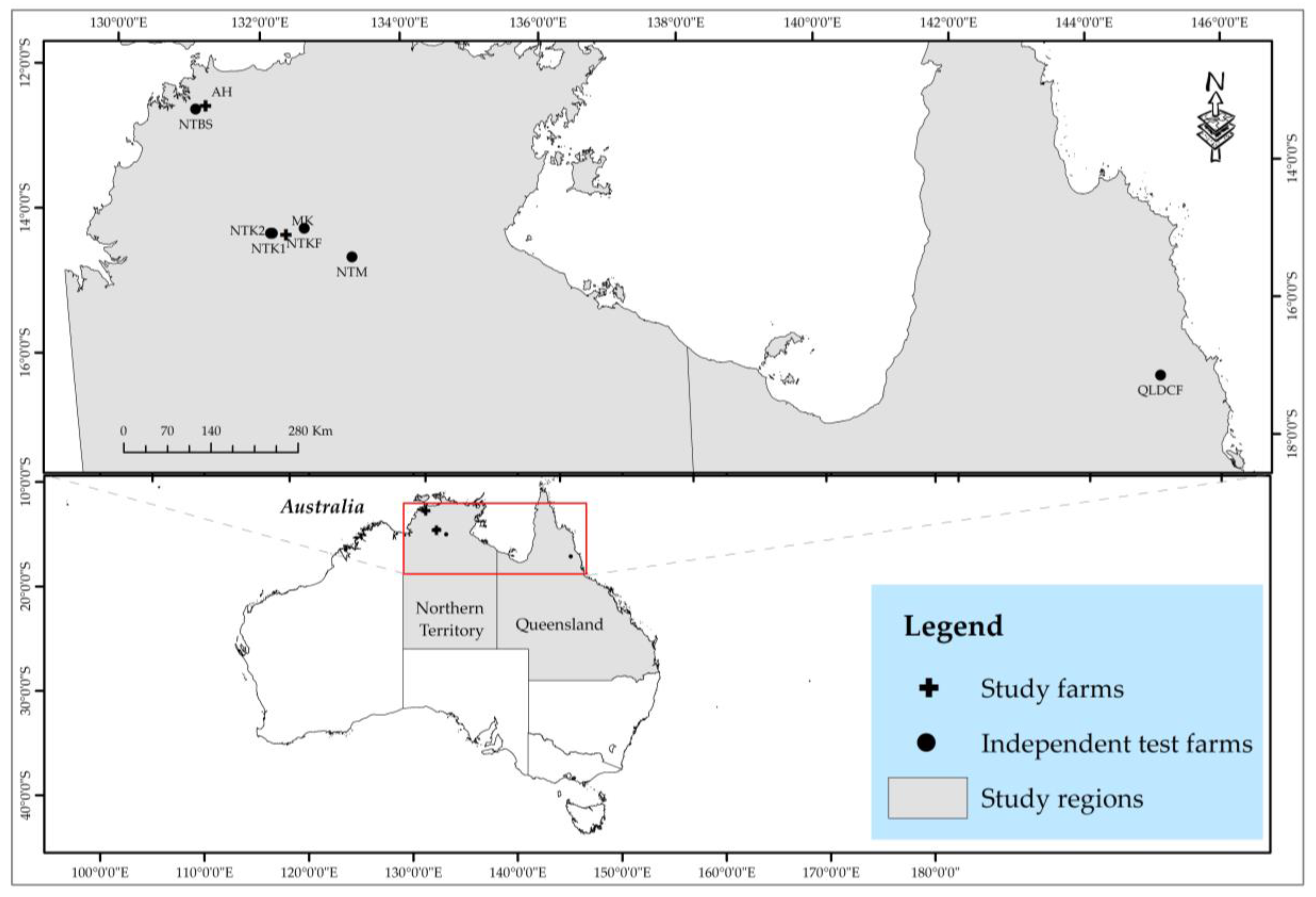
2.1. Study Area
2.2. Data Acquisition and Analysis
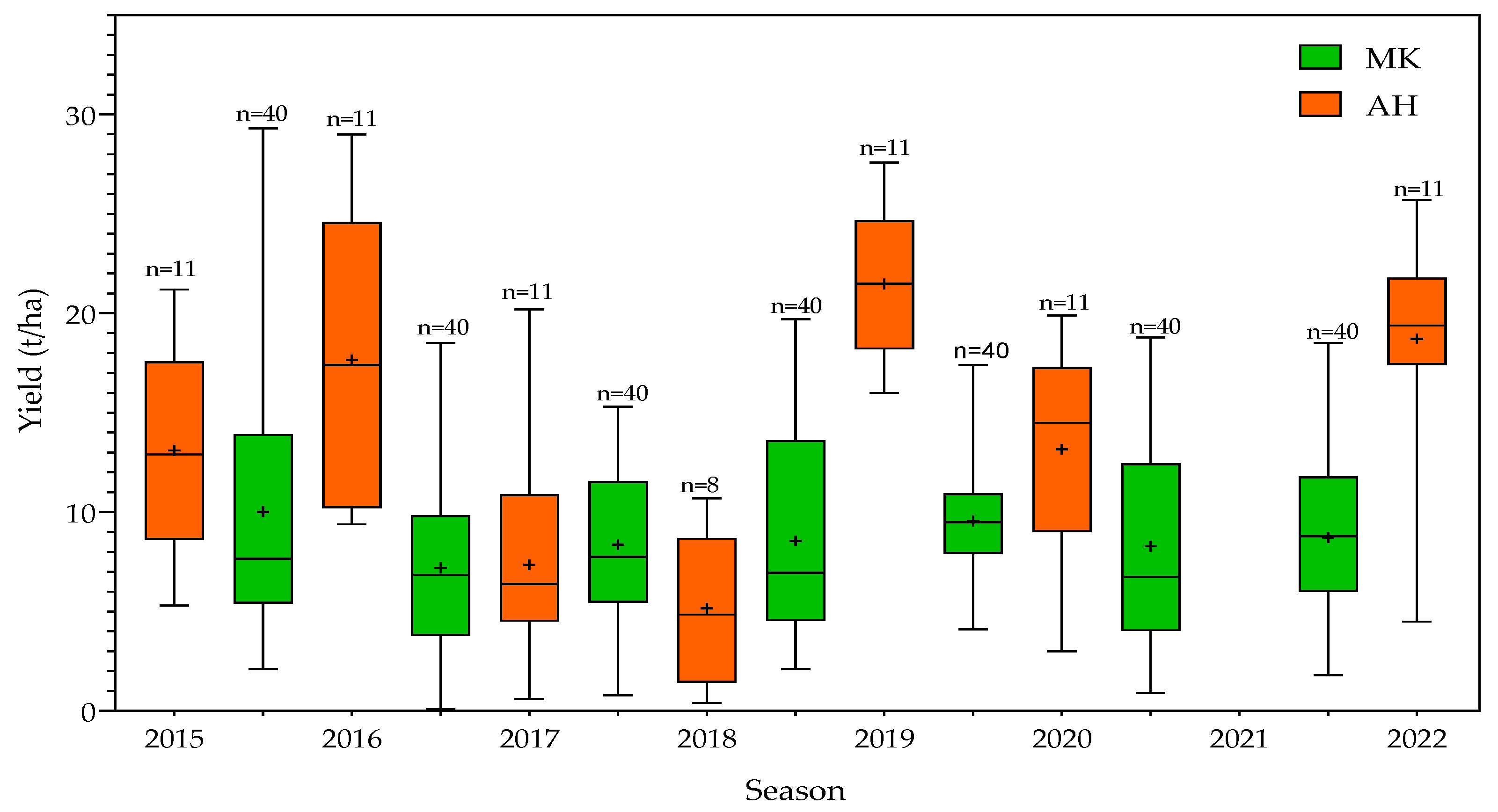
2.2.1. Grower Data
2.2.2. Weather Data
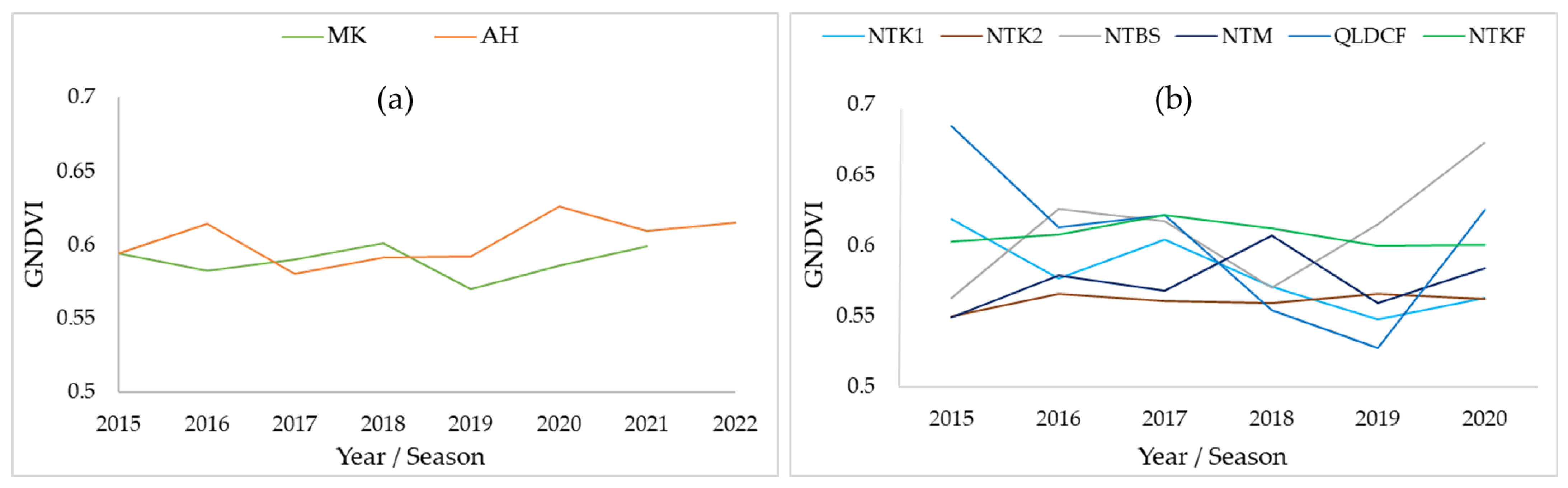
2.2.3. Satellite Remote Sensing Data
2.3. Preparation of Input Variables for Yield Modeling
2.4. Yield Modeling Approaches and Techniques
2.4.1. Cumulative Training Year (CTY) and Leave-One-Year-Out (LOYO) Approaches
2.4.2. Hyperparameter Tuning
2.4.3. Bootstrap Sampling of Training Dataset
2.4.4. Model Prediction and Performance Evaluation
3. Results
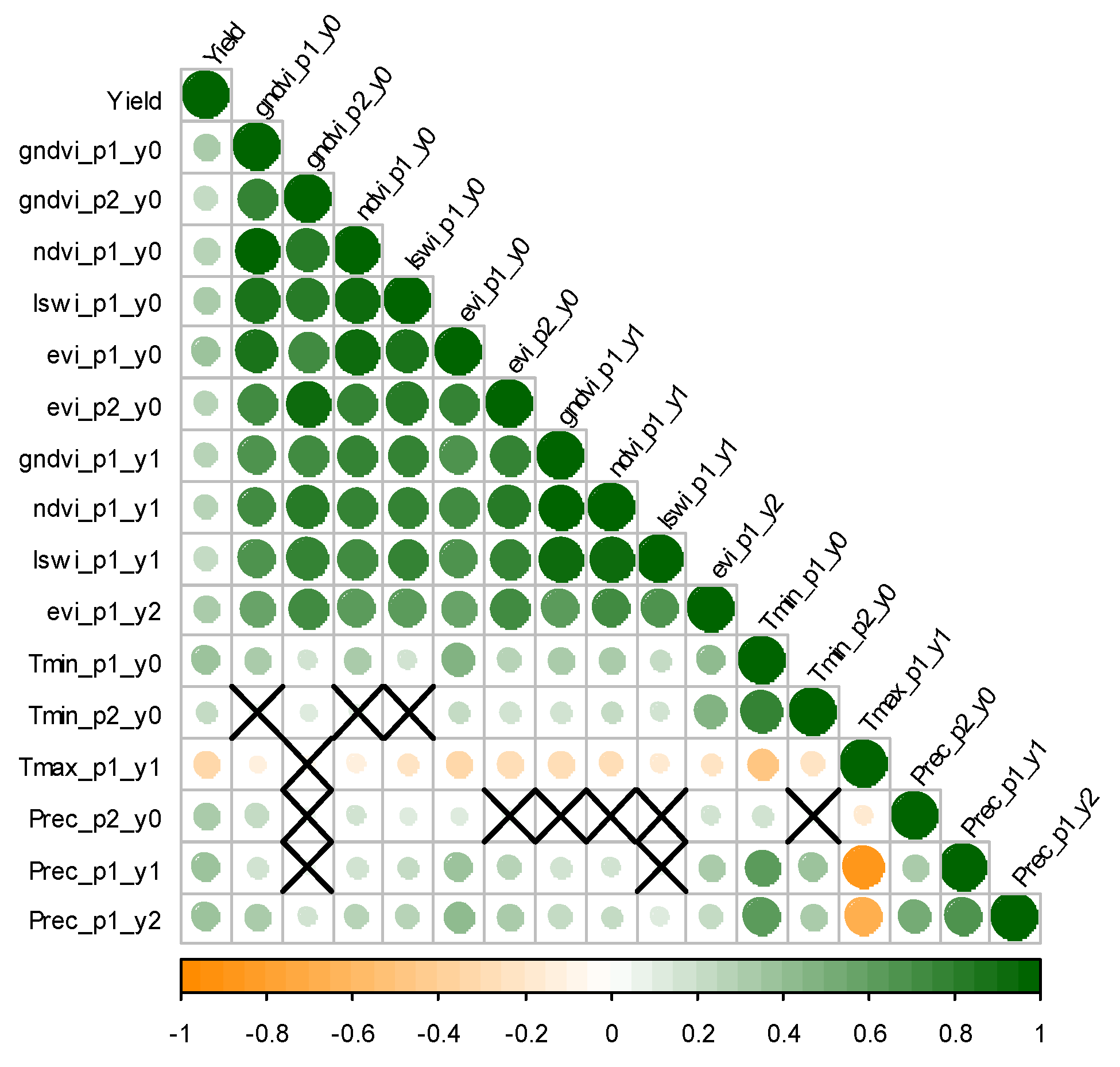
3.1. Relationships among Yield and the Predictor (RS and Weather) Variables
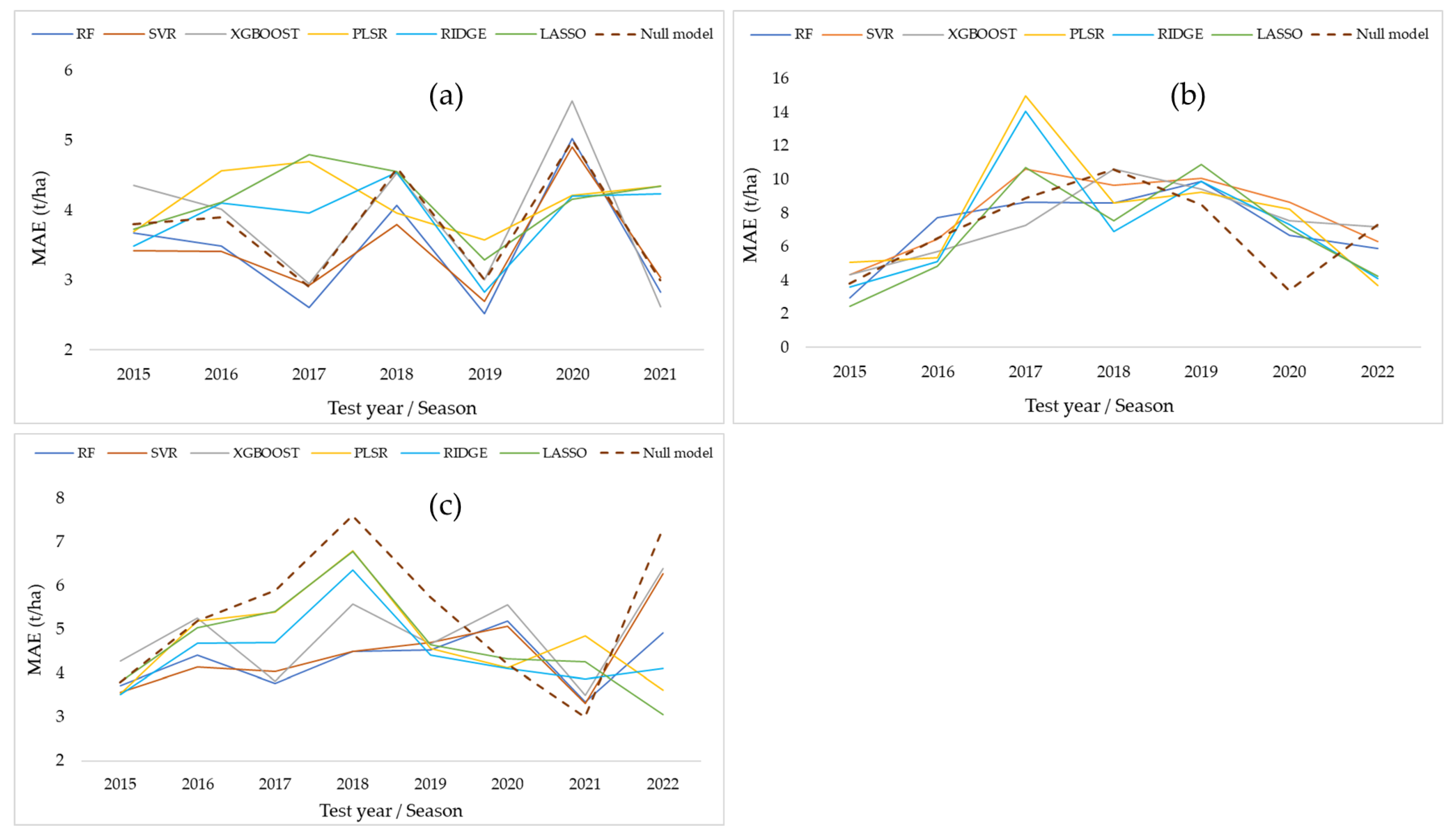
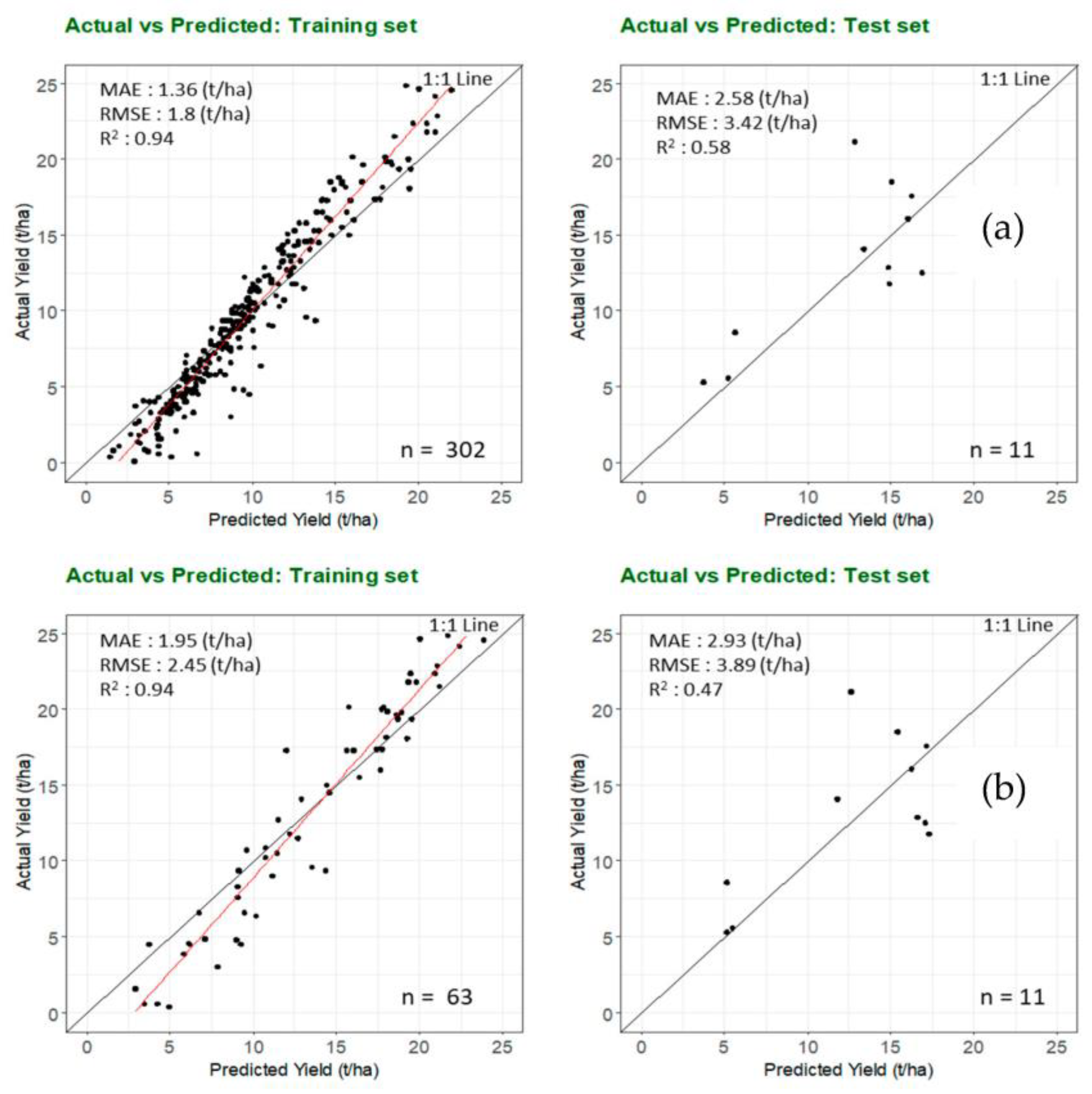
3.2. Predicting Mango Yield at the Block Level and the Farm Level Using RS Variables Only
3.3. Predicting Mango Yield at the Block Level and Farm Level Using RS and Weather Variables
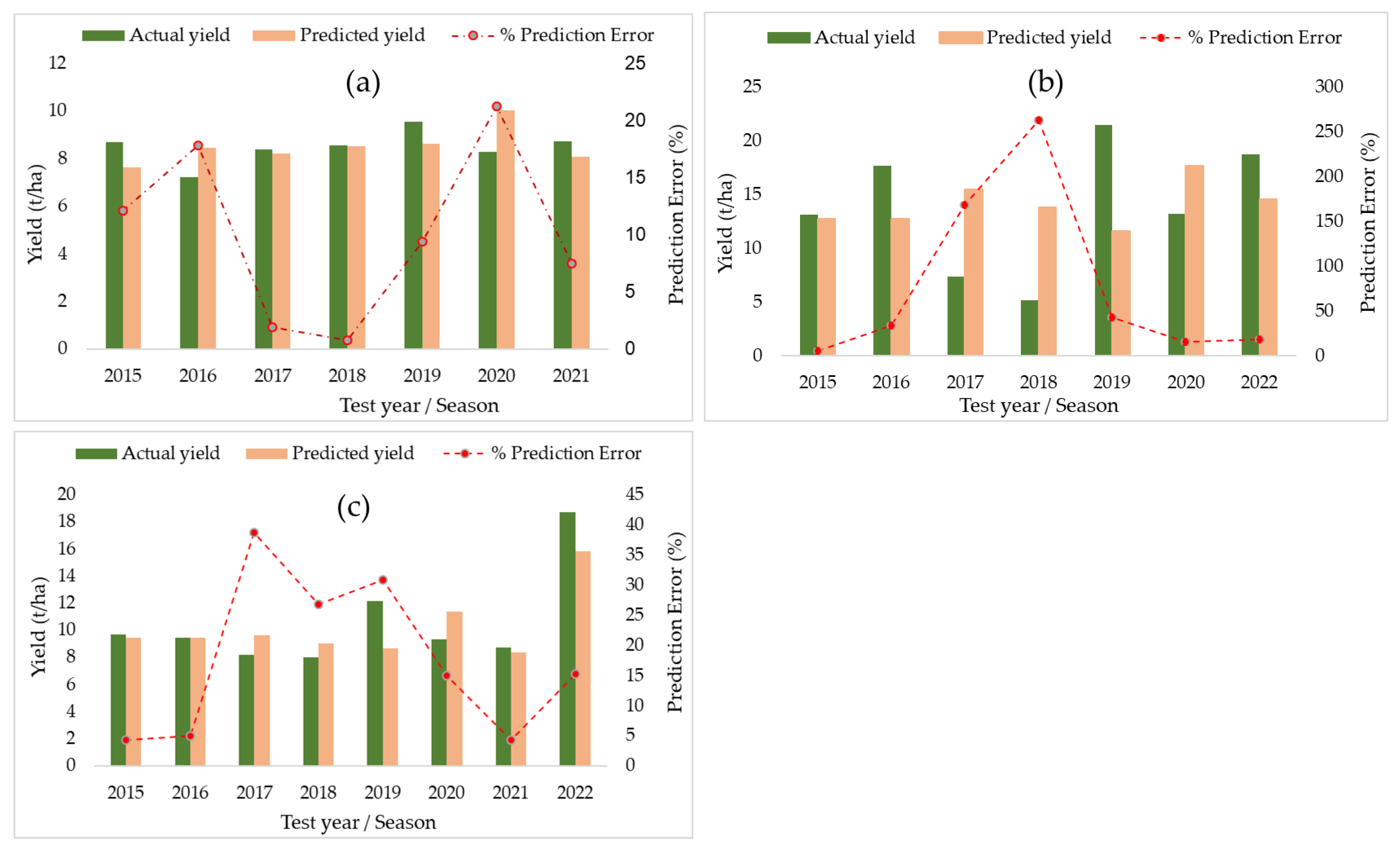
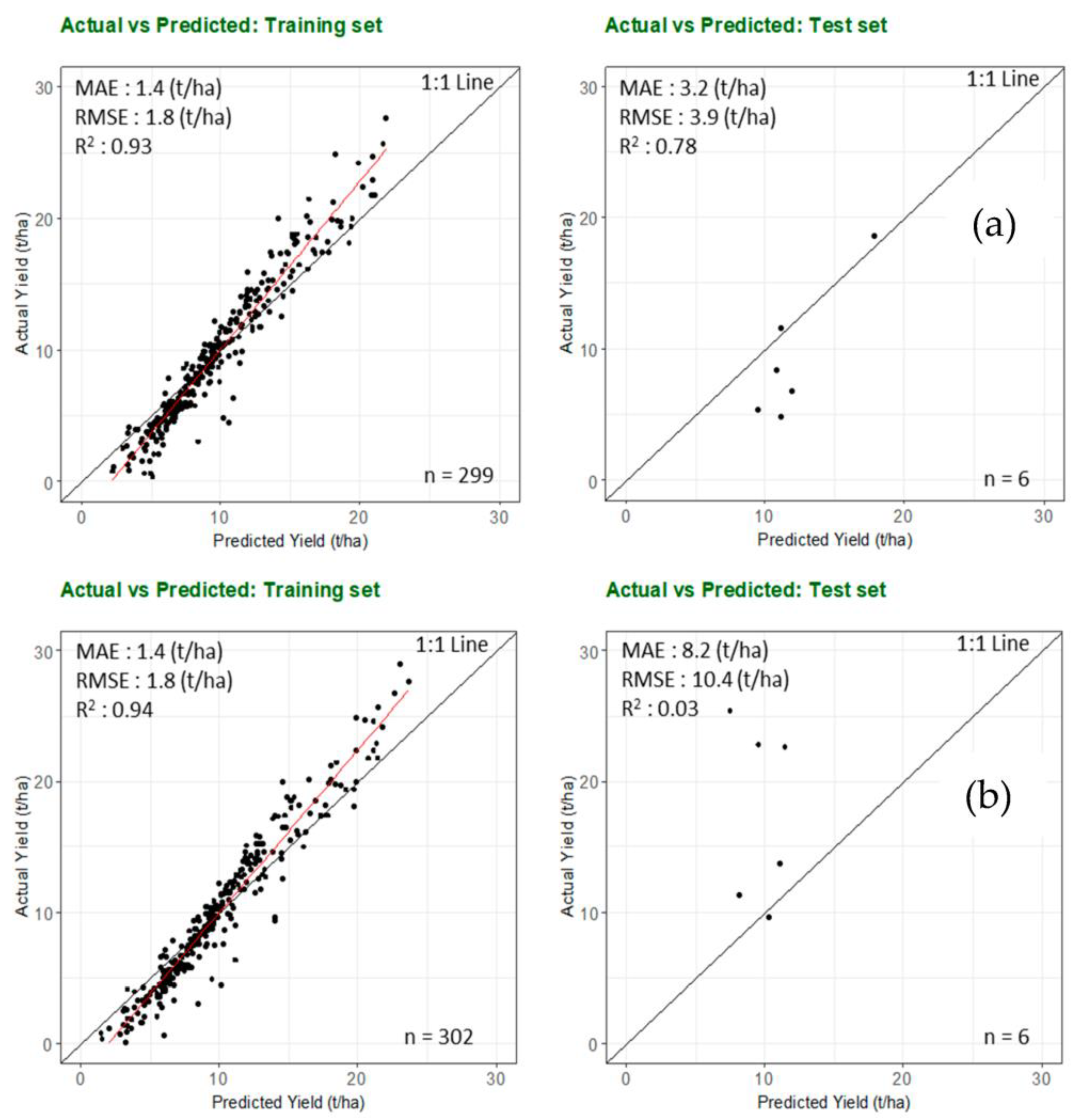
3.4. Predicting Individual Farm Yield from the RS-Based Variables
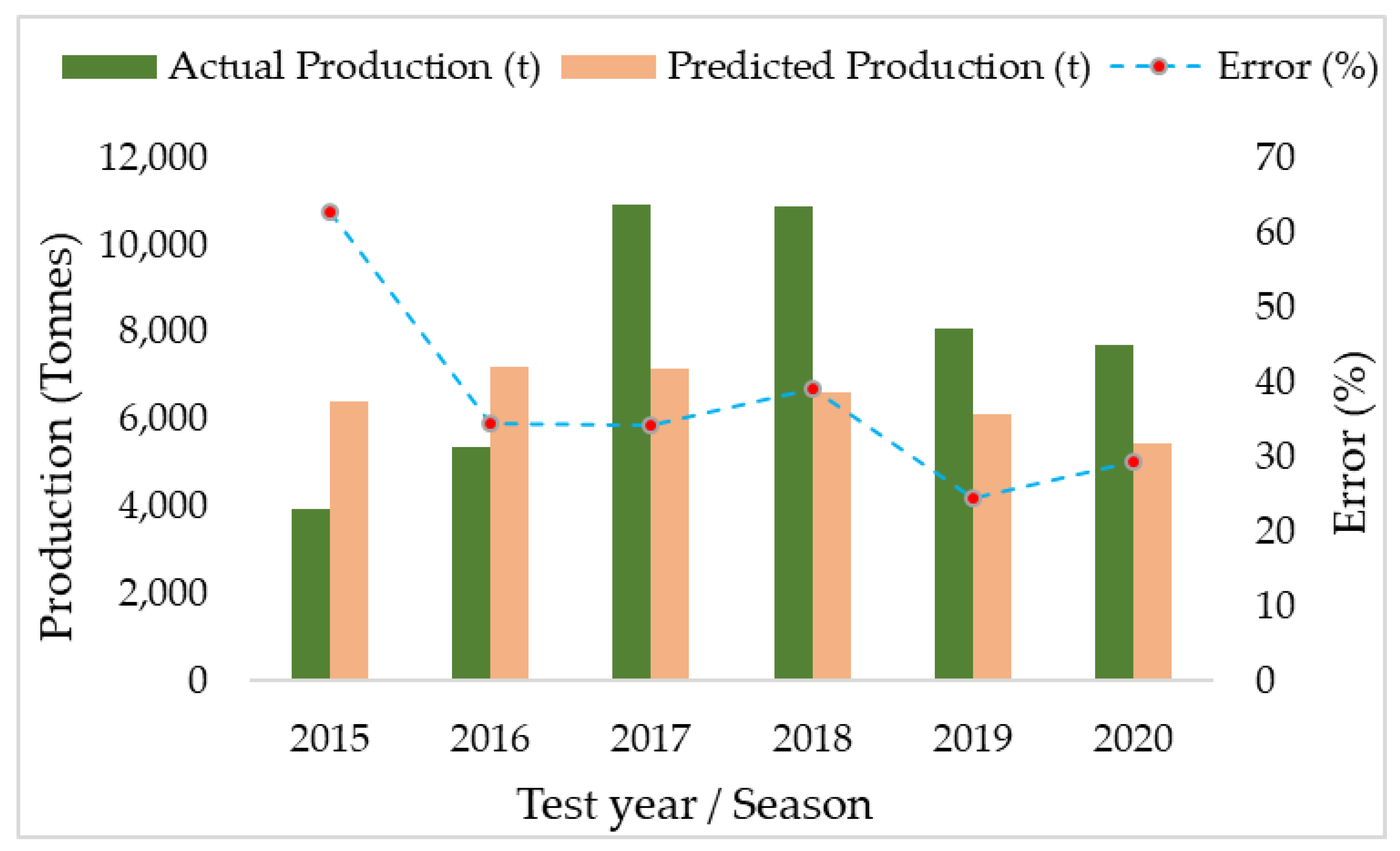
3.5. Validating the Combined Model on Independent Test Farm Locations—RS Variables Only
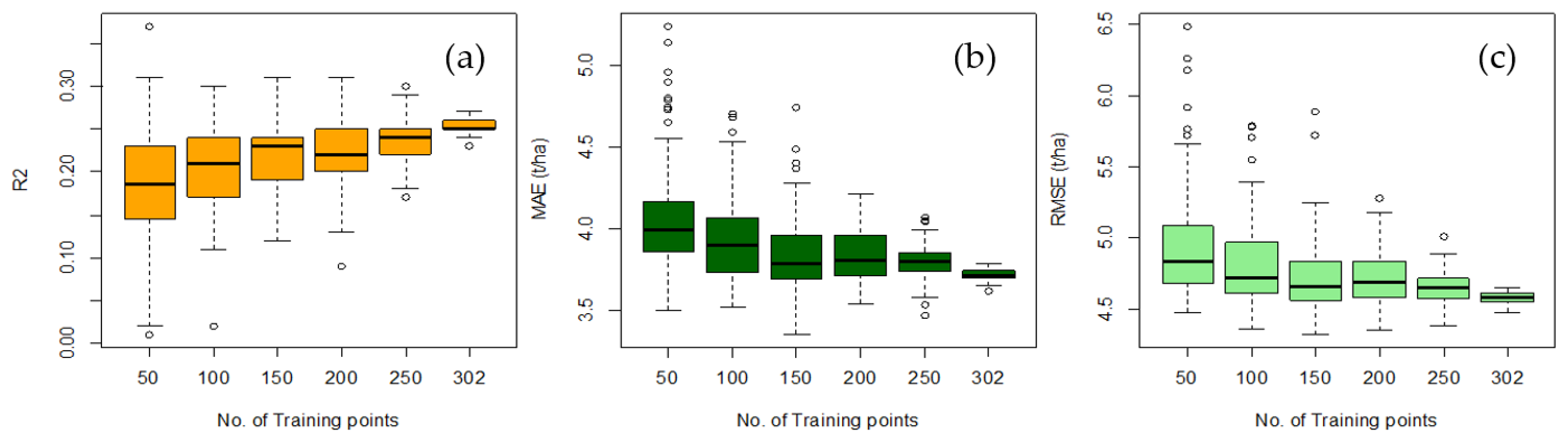
3.6. Impact of Training Dataset Size
4. Discussion
4.1. Predictor and Response Variables Relationship in Yield Modeling
4.2. Block Level and Farm Level Yield Prediction
4.3. Comparison of Model Performance
4.4. Potential for Yield Prediction on Independent Farms
4.5. Bootstrap Results—Varying Training Sample Size
4.6. Challenges with Input Data Quality and Cleaning
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAOSTAT. Value of Agricultural Production. Available online: https://www.fao.org/faostat/en/#data/QV (accessed on 8 January 2023).
- Mitra, S.K. Mango Production in the World—Present Situation and Future Prospect. Int. Soc. Hortic. Sci. 2016, 1111, 287–296. [Google Scholar] [CrossRef]
- Thompson, J.; Morgan, T. Northern Territory’s Lucrative Mango Industry 1000 Workers Short as Fruit-Picking Season Begins. ABC News. Available online: https://www.msn.com/en-au/news/australia/northern-territorys-lucrative-mango-industry-1000-workers-short-as-fruit-picking-season-begins/ar-AA11vvcI (accessed on 3 December 2022).
- NTFA. NT Mangoes. Northern Territory Farmers Association. Available online: https://ntfarmers.org.au/commodities/mangoes/ (accessed on 3 December 2022).
- DTF. Northern Territory Economy: Agriculture, Forestry and Fishing. Northern Territory Government. Available online: https://nteconomy.nt.gov.au/industry-analysis/agriculture,-foresty-and-fishing#horticulture (accessed on 3 December 2022).
- Zhang, Z.; Jin, Y.; Chen, B.; Brown, P. California Almond Yield Prediction at the Orchard Level With a Machine Learning Approach. Front. Plant. Sci. 2019, 10, 809. [Google Scholar] [CrossRef]
- Zarate-Valdez, J.L.; Muhammad, S.; Saa, S.; Lampinen, B.D.; Brown, P.H. Light interception, leaf nitrogen and yield prediction in almonds: A case study. Eur. J. Agron. 2015, 66, 1–7. [Google Scholar] [CrossRef]
- Hoffman, L.A.; Etienne, X.L.; Irwin, S.H.; Colino, E.V.; Toasa, J.I. Forecast performance of WASDE price projections for U.S. corn. Agric. Econ. 2015, 46, 157–171. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A.; Bristow, M. Exploring the Potential of High Resolution WorldView-3 Imagery for Estimating Yield of Mango. Remote Sens. 2018, 10, 1866. [Google Scholar] [CrossRef]
- Anderson, N.T.; Walsh, K.B.; Wulfsohn, D. Technologies for Forecasting Tree Fruit Load and Harvest Timing—From Ground, Sky and Time. Agronomy 2021, 11, 1409. [Google Scholar] [CrossRef]
- Anderson, N.T.; Underwood, J.P.; Rahman, M.M.; Robson, A.; Walsh, K.B. Estimation of fruit load in mango orchards: Tree sampling considerations and use of machine vision and satellite imagery. Precis. Agric. 2018, 20, 823–839. [Google Scholar] [CrossRef]
- Payne, A.B.; Walsh, K.B.; Subedi, P.P.; Jarvis, D. Estimation of mango crop yield using image analysis—Segmentation method. Comput. Electron. Agric. 2013, 91, 57–64. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A.; Brinkhoff, J. Potential of Time-Series Sentinel 2 Data for Monitoring Avocado Crop Phenology. Remote Sens. 2022, 14, 5942. [Google Scholar] [CrossRef]
- Torgbor, B.A.; Rahman, M.M.; Robson, A.; Brinkhoff, J.; Khan, A. Assessing the Potential of Sentinel-2 Derived Vegetation Indices to Retrieve Phenological Stages of Mango in Ghana. Horticulturae 2022, 8, 11. [Google Scholar] [CrossRef]
- Matese, A.; Di Gennaro, S.F. Beyond the traditional NDVI index as a key factor to mainstream the use of UAV in precision viticulture. Sci. Rep. 2021, 11, 2721. [Google Scholar] [CrossRef]
- Verma, H.C.; Ahmed, T.; Rajan, S. Mapping and Area Estimation of Mango Orchards of Lucknow Region by Applying Knowledge Based Decision Tree to Landsat 8 OLI Satellite Images. Int. J. Innov. Technol. Explor. Eng. 2020, 9, 3627–3635. [Google Scholar] [CrossRef]
- Aworka, R.; Cedric, L.S.; Adoni, W.Y.H.; Zoueu, J.T.; Mutombo, F.K.; Kimpolo, C.L.M.; Nahhal, T.; Krichen, M. Agricultural decision system based on advanced machine learning models for yield prediction: Case of East African countries. Smart Agric. Technol. 2022, 2, 100048. [Google Scholar] [CrossRef]
- Krupnik, T.J.; Ahmed, Z.U.; Timsina, J.; Yasmin, S.; Hossain, F.; Al Mamun, A.; Mridha, A.I.; McDonald, A.J. Untangling crop management and environmental influences on wheat yield variability in Bangladesh: An application of non-parametric approaches. Agric. Syst. 2015, 139, 166–179. [Google Scholar] [CrossRef]
- Robson, A.J.; Rahman, M.M.; Muir, J.; Saint, A.; Simpson, C.; Searle, C. Evaluating satellite remote sensing as a method for measuring yield variability in Avocado and Macadamia tree crops. Adv. Anim. Biosci. 2017, 8, 498–504. [Google Scholar] [CrossRef]
- Ye, X.; Sakai, K.; Garciano, L.O.; Asada, S.-I.; Sasao, A. Estimation of citrus yield from airborne hyperspectral images using a neural network model. Ecol. Model. 2006, 198, 426–432. [Google Scholar] [CrossRef]
- Miranda, C.; Santesteban, L.; Urrestarazu, J.; Loidi, M.; Royo, J. Sampling Stratification Using Aerial Imagery to Estimate Fruit Load in Peach Tree Orchards. Agriculture 2018, 8, 78. [Google Scholar] [CrossRef]
- Brinkhoff, J.; Robson, A.J. Block-level macadamia yield forecasting using spatio-temporal datasets. Agric. For. Meteorol. 2021, 303, 108369. [Google Scholar] [CrossRef]
- He, L.; Fang, W.; Zhao, G.; Wu, Z.; Fu, L.; Li, R.; Majeed, Y.; Dhupia, J. Fruit yield prediction and estimation in orchards: A state-of-the-art comprehensive review for both direct and indirect methods. Comput. Electron. Agric. 2022, 195, 106812. [Google Scholar] [CrossRef]
- Sarron, J.; Malézieux, É.; Sané, C.; Faye, É. Mango Yield Mapping at the Orchard Scale Based on Tree Structure and Land Cover Assessed by UAV. Remote Sens. 2018, 10, 1900. [Google Scholar] [CrossRef]
- Bai, X.; Li, Z.; Li, W.; Zhao, Y.; Li, M.; Chen, H.; Wei, S.; Jiang, Y.; Yang, G.; Zhu, X. Comparison of Machine-Learning and CASA Models for Predicting Apple Fruit Yields from Time-Series Planet Imageries. Remote Sens. 2021, 13, 3073. [Google Scholar] [CrossRef]
- Sinha, P.; Robson, A.J. Satellites Used to Predict Commercial Mango Yields. Aust. Tree Crop. Available online: https://www.treecrop.com.au/news/satellites-used-predict-commercial-mango-yields/ (accessed on 12 August 2022).
- Hodges, T.; Botner, D.; Sakamoto, C.; Hays Haug, J. Using the CERES-Maize model to estimate production for the U.S. Cornbelt. Agric. For. Meteorol. 1987, 40, 293–303. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant remote sensing vegetation indices: A review of developments and applications. J. Sens. 2017, 2017, 1353691. [Google Scholar] [CrossRef]
- Bai, T.; Zhang, N.; Mercatoris, B.; Chen, Y. Jujube yield prediction method combining Landsat 8 Vegetation Index and the phenological length. Comput. Electron. Agric. 2019, 162, 1011–1027. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Prueger, J.H. Value of using different vegetative indices to quantify agricultural crop characteristics at different growth stages under varying management practices. Remote Sens. 2010, 2, 562–578. [Google Scholar] [CrossRef]
- Nazir, A.; Ullah, S.; Saqib, Z.A.; Abbas, A.; Ali, A.; Iqbal, M.S.; Hussain, K.; Shakir, M.; Shah, M.; Butt, M.U. Estimation and Forecasting of Rice Yield Using Phenology-Based Algorithm and Linear Regression Model on Sentinel-II Satellite Data. Agriculture 2021, 11, 1026. [Google Scholar] [CrossRef]
- Bolton, D.K.; Friedl, M.A. Forecasting crop yield using remotely sensed vegetation indices and crop phenology metrics. Agric. For. Meteorol. 2013, 173, 74–84. [Google Scholar] [CrossRef]
- Mayer, D.G.; Chandra, K.A.; Burnett, J.R. Improved crop forecasts for the Australian macadamia industry from ensemble models. Agric. Syst. 2019, 173, 519–523. [Google Scholar] [CrossRef]
- Jeong, J.H.; Resop, J.P.; Mueller, N.D.; Fleisher, D.H.; Yun, K.; Butler, E.E.; Timlin, D.J.; Shim, K.M.; Gerber, J.S.; Reddy, V.R.; et al. Random Forests for Global and Regional Crop Yield Predictions. PLoS ONE 2016, 11, e0156571. [Google Scholar] [CrossRef] [PubMed]
- Brdar, S.; Culibrk, D.; Marinkovic, B.; Crnobarac, J.; Crnojevic, V. Support vector machines with features contribution analysis for agricultural yield prediction. In Proceedings of the Second International Workshop on Sensing Technologies in Agriculture, Forestry and Environment (EcoSense 2011), Belgrade, Serbia, 30 April–7 May 2011; pp. 43–47. [Google Scholar]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Freeman, E.A.; Moisen, G.G.; Coulston, J.W.; Wilson, B.T. Random forests and stochastic gradient boosting for predicting tree canopy cover: Comparing tuning processes and model performance. Can. J. For. Res. 2016, 46, 323–339. [Google Scholar] [CrossRef]
- Donovan, J. Australian Mango Varieties. Available online: https://lawn.com.au/australian-mango-varieties/ (accessed on 29 March 2023).
- Fukuda, S.; Spreer, W.; Yasunaga, E.; Yuge, K.; Sardsud, V.; Müller, J. Random Forests modelling for the estimation of mango (Mangifera indica L. cv. Chok Anan) fruit yields under different irrigation regimes. Agric. Water Manag. 2013, 116, 142–150. [Google Scholar] [CrossRef]
- Litvinenko, V.S.; Eckart, L.; Eckart, S.; Enke, M. A brief comparative study of the potentialities and limitations of machine-learning algorithms and statistical techniques. E3S Web Conf. 2021, 266, 2001. [Google Scholar] [CrossRef]
- Kestur, R.; Meduri, A.; Narasipura, O. MangoNet: A deep semantic segmentation architecture for a method to detect and count mangoes in an open orchard. Eng. Appl. Artif. Intell. 2019, 77, 59–69. [Google Scholar] [CrossRef]
- Maya Gopal, P.S.; Bhargavi, R. Performance Evaluation of Best Feature Subsets for Crop Yield Prediction Using Machine Learning Algorithms. Appl. Artif. Intell. 2019, 33, 621–642. [Google Scholar] [CrossRef]
- Gan, H.; Lee, W.S.; Alchanatis, V.; Abd-Elrahman, A. Active thermal imaging for immature citrus fruit detection. Biosyst. Eng. 2020, 198, 291–303. [Google Scholar] [CrossRef]
- Apolo-Apolo, O.E.; Perez-Ruiz, M.; Martinez-Guanter, J.; Valente, J. A Cloud-Based Environment for Generating Yield Estimation Maps From Apple Orchards Using UAV Imagery and a Deep Learning Technique. Front. Plant. Sci. 2020, 11, 1086. [Google Scholar] [CrossRef]
- Marani, R.; Milella, A.; Petitti, A.; Reina, G. Deep neural networks for grape bunch segmentation in natural images from a consumer-grade camera. Precis. Agric. 2020, 22, 387–413. [Google Scholar] [CrossRef]
- Robson, A.J.; Rahman, M.M.; Muir, J. Using Worldview Satellite Imagery to Map Yield in Avocado (Persea americana): A Case Study in Bundaberg, Australia. Remote Sens. 2017, 9, 1223. [Google Scholar] [CrossRef]
- NTG. Weather & Seasons in the Northern Territory. Available online: https://northernterritory.com/plan/weather-and-seasons (accessed on 16 April 2023).
- NTG. Soils of the Northern Territory—Factsheet. Available online: https://depws.nt.gov.au/rangelands/technical-notes-and-fact-sheets/land-soil-vegetation-technical-information (accessed on 8 January 2023).
- Studyprobe. USDA Soil Classification: Understanding Soil Taxonomy. Available online: https://www.studyprobe.in/2021/12/usda-soil-classification.html#:~:text=The%20American%20Method%20of%20Soil%20Classification%20categorizes%20soils,providing%20more%20specific%20information%20about%20the%20soil%27s%20characteristics. (accessed on 18 May 2023).
- Fitchett, J.; Grab, S.W.; Thompson, D.I. Temperature and tree age interact to increase mango yields in the Lowveld, South Africa. S. Afr. Geogr. J. 2014, 98, 105–117. [Google Scholar] [CrossRef]
- USGS. Landsat 1. Available online: https://www.usgs.gov/landsat-missions/landsat-1 (accessed on 8 November 2022).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Culpepper, S.A.; Aguinis, H. R is for Revolution. Organ. Res. Methods 2010, 14, 735–740. [Google Scholar] [CrossRef]
- Rouse Jr, J.; Haas, R.; Schell, J.; Deering, D. Monitoring vegetation systems in the great Plains with ERTS, vol. 351. NASA Spec. Publ. Wash. P. 1974, 1, 309–317. [Google Scholar]
- Gitelson, A.A.; Gritz, Y.; Merzlyak, M.N. Relationships between leaf chlorophyll content and spectral reflectance and algorithms for non-destructive chlorophyll assessment in higher plant leaves. J. Plant Physiol. 2003, 160, 271–282. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Chandrasekar, K.; Sesha Sai, M.V.R.; Roy, P.S.; Dwevedi, R.S. Land Surface Water Index (LSWI) response to rainfall and NDVI using the MODIS Vegetation Index product. Int. J. Remote Sens. 2010, 31, 3987–4005. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Lones, M.A. How to avoid machine learning pitfalls: A guide for academic researchers. arXiv 2021, arXiv:2108.02497. [Google Scholar]
- Kuhn, M. Building Predictive Models in R Using the caret Package. J. Stat. Softw. 2008, 28, 1–26. [Google Scholar] [CrossRef]
- Hastie, T.; Qian, J.; Tay, K. An Introduction to glmnet. CRAN R. Repositary 2021, 1, 1–38. [Google Scholar]
- Mevik, B.-H.; Wehrens, R. Introduction to the pls Package. Help. Sect. “Pls” Package R. Studio Softw. 2015, 2015, 1–23. [Google Scholar]
- Wickham, H. Data Analysis. In ggplot2: Elegant Graphics for Data Analysis; Wickham, H., Ed.; Springer International Publishing: Cham, Switzerland, 2016; pp. 189–201. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics: New York, NY, USA, 2001. [Google Scholar]
- Aarshay, J. Mastering XGBoost Parameter Tuning: A Complete Guide with Python Codes; Analytics Vidhya: Gurugram, India, 2016; Volume 2023. [Google Scholar]
- Beasley, W.H.; Rodgers, J.L. Resampling methods. Sage Handb. Quant. Methods Psychol. 2009, 2009, 362–386. [Google Scholar]
- LaFlair, G.T.; Egbert, J.; Plonsky, L. A Practical Guide to Bootstrapping Descriptive Statistics, Correlations, T Tests, and ANOVAs; Routledge: New York, NY, USA, 2016; pp. 46–77. [Google Scholar]
- Beasley, W.H.; DeShea, L.; Toothaker, L.E.; Mendoza, J.L.; Bard, D.E.; Rodgers, J.L. Bootstrapping to test for nonzero population correlation coefficients using univariate sampling. Psychol. Methods 2007, 12, 414. [Google Scholar] [CrossRef]
- Deines, J.M.; Patel, R.; Liang, S.-Z.; Dado, W.; Lobell, D.B. A million kernels of truth: Insights into scalable satellite maize yield mapping and yield gap analysis from an extensive ground dataset in the US Corn Belt. Remote Sens. Environ. 2021, 253, 112174. [Google Scholar] [CrossRef]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Model. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Perez, R.; Cebecauer, T.; Šúri, M. Chapter 2—Semi-Empirical Satellite Models. In Solar Energy Forecasting and Resource Assessment; Kleissl, J., Ed.; Academic Press: Boston, MA, USA, 2013; pp. 21–48. [Google Scholar] [CrossRef]
- Kouadio, L.; Newlands, N.; Davidson, A.; Zhang, Y.; Chipanshi, A. Assessing the Performance of MODIS NDVI and EVI for Seasonal Crop Yield Forecasting at the Ecodistrict Scale. Remote Sens. 2014, 6, 10193–10214. [Google Scholar] [CrossRef]
- Rahman, M.M.; Robson, A. Integrating Landsat-8 and Sentinel-2 Time Series Data for Yield Prediction of Sugarcane Crops at the Block Level. Remote Sens. 2020, 12, 1313. [Google Scholar] [CrossRef]
- Hatfield, J.L.; Gitelson, A.A.; Schepers, J.S.; Walthall, C.L. Application of Spectral Remote Sensing for Agronomic Decisions. Agron. J. 2008, 100, S117–S131. [Google Scholar] [CrossRef]
- Wiegand, C.; Maas, S.; Aase, J.; Hatfield, J.; Pinter Jr, P.; Jackson, R.; Kanemasu, E.; Lapitan, R. Multisite analyses of spectral-biophysical data for wheat. Remote Sens. Environ. 1992, 42, 1–21. [Google Scholar] [CrossRef]
- Cai, Y.; Guan, K.; Lobell, D.; Potgieter, A.B.; Wang, S.; Peng, J.; Xu, T.; Asseng, S.; Zhang, Y.; You, L. Integrating satellite and climate data to predict wheat yield in Australia using machine learning approaches. Agric. For. Meteorol. 2019, 274, 144–159. [Google Scholar] [CrossRef]
- Cavalcante, Í.H.L. Mango Flowering: Factors Involved in the Natural Environment and Associated Management Techniques for Commercial Crops. 2022. Available online: https://www.mango.org/wp-content/uploads/2022/12/Mango-Flowering-Review_Italo-Cavalcante-atual.pdf (accessed on 5 June 2023).
- Filippi, P.; Whelan, B.M.; Vervoort, R.W.; Bishop, T.F.A. Mid-season empirical cotton yield forecasts at fine resolutions using large yield mapping datasets and diverse spatial covariates. Agric. Syst. 2020, 184, 102894. [Google Scholar] [CrossRef]
- van Klompenburg, T.; Kassahun, A.; Catal, C. Crop yield prediction using machine learning: A systematic literature review. Comput. Electron. Agric. 2020, 177, 105709. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bangert, P. Machine Learning and Data Science in the Power Generation Industry; Elsevier: Amsterdam, The Netherlands, 2021; Volume 543. [Google Scholar]
- Khaki, S.; Wang, L.; Archontoulis, S.V. A cnn-rnn framework for crop yield prediction. Front. Plant Sci. 2020, 10, 1750. [Google Scholar] [CrossRef] [PubMed]
- Brinkhoff, J.; Orford, R.; Suarez, L.A.; Robson, A.R. Data Requirements for Forecasting Tree Crop Yield—A macadamia Case Study. In Proceedings of the European Conference On Precision Agriculture. Available online: https://ssrn.com/abstract=4443667 (accessed on 5 June 2023).
- Teich, D.A. Good Data Quality for Machine Learning Is an Analytics Must. Available online: https://www.techtarget.com/searchdatamanagement/tip/Good-data-quality-for-machine-learning-is-an-analytics-must (accessed on 11 April 2023).
- McDonald, A. Data Quality Considerations for Petrophysical Machine-Learning Models. Petrophysics 2021, 62, 585–613. [Google Scholar]



| Crop | Algorithm/Method | RS Platform | Accuracy | Research Summary | Reference |
|---|---|---|---|---|---|
| Grape | Gaussian process regression | UAV | 85.95% | Evaluated both traditional linear and ML regressions to forecast in-season grape yield | [15] |
| Mango | Fully Convolutional Network (FCN) | RGB Camera | 73.6% | Used MangoNet, a deep CNN based architecture for mango detection using semantic segmentation | [41] |
| Mango | Linear Regression | World View-3 satellite imagery | >90% | Predicted in-season infield mango yield for one season with the 18-tree calibration approach using high resolution RS imagery | [26] |
| Rice | ANN, KNN, SVR and RF | - | 86.5% | Evaluated the performance of the four ML algorithms and to assess the importance of distinct feature sets on the ML algorithms | [42] |
| Citrus | Region Convolutional Neural Network (Faster R-CNN) | Vehicle mounted camera (FLIR A655SC) | 96% | Detected and counted fruits using a combination of a thermal imaging methods and ML to tackle problems associated with color similarity between immature citrus and leaves. | [43] |
| Apple | Faster R-CNN | UAV | >90% | Detected small target fruits from top-view RGB images of apple trees from UAV captures | [44] |
| Farm | Location | Cultivar | No. of Blocks | Avg. Blk Size (ha) | Avg. Yield (t/ha) | Period (Yr) | Age (Yr) | Spacing (m) | Total No. of Data Points |
|---|---|---|---|---|---|---|---|---|---|
| MK | NT | KP | 31 | 5.8 | 8.3 | 2015–2021 | 23 | 6 × 9 | 214 |
| R2E2 | 9 | 5.9 | 9.0 | 18 | 8 × 13 | 62 | |||
| AH | NT | CAL | 11 | 12.1 | 14.1 | 2015–2020, 2022 | 23 | variable | 74 |
| Combined | 3 | 51 | 8 | 350 |
| Vegetation Index | Formula | Reference |
|---|---|---|
| Normalized Difference Vegetation Index (NDVI) | (NIR − R)/(NIR + R) | Rouse Jr et al. [54] |
| Green Normalized Difference Vegetation Index (GNDVI) | (NIR − G)/(NIR + G) | Gitelson et al. [55] |
| Enhanced Vegetation Index (EVI) | 2.5 × ((NIR − R)/(L + NIR + C1 × R − C2 × B)) | Huete et al. [56] |
| Land Surface Water Index (LSWI), also known as the Normalized Difference Water Index (NDWI) | (NIR − SWIR2)/(NIR + SWIR2) | Chandrasekar et al. [57] Gao [58] |
| Predictor Variable Name | Code | Description |
|---|---|---|
| Period 1 of current year’s VI | VI_p1_y0 | Median value of the VI of Period 1 of the current year |
| Period 2 of current year’s VI | VI_p2_y0 | Median value of the VI of Period 2 of the current year |
| Period 1 of last year’s VI | VI_p1_y1 | Median value of the VI of Period 1 of the previous year |
| Period 2 of last year’s VI | VI_p2_y1 | Median value of the VI of Period 2 of the previous year |
| Period 3 of last year’s VI | VI_p3_y1 | Median value of the VI of Period 3 of the previous year |
| Period 1 of last 2 year’s VI | VI_p1_y2 | Median value of the VI of Period 1 of the last 2 years |
| Period 2 of last 2 year’s VI | VI_p2_y2 | Median value of the VI of Period 2 of the last 2 years |
| Period 3 of last 2 year’s VI | VI_p3_y2 | Median value of the VI of Period 3 of the last 2 years |
| Period 1 of current year’s WV | WV_p1_y0 | Median value of the WV of Period 1 of the current year |
| Period 2 of current year’s WV | WV_p2_y0 | Median value of the WV of Period 2 of the current year |
| Period 1 of last year’s WV | WV_p1_y1 | Median value of the WV of Period 1 of the previous year |
| Period 2 of last year’s WV | WV_p2_y1 | Median value of the WV of Period 2 of the previous year |
| Period 3 of last year’s WV | WV_p3_y1 | Median value of the WV of Period 3 of the previous year |
| Period 1 of last 2 year’s WV | WV_p1_y2 | Median value of the WV of Period 1 of last 2 years |
| Period 2 of last 2 year’s WV | WV_p2_y2 | Median value of the WV of Period 2 of last 2 years |
| Period 3 of last 2 year’s WV | WV_p3_y2 | Median value of the WV of Period 3 of last 2 years |
| Algorithm | Hyperparameter Function/Description | Reference |
|---|---|---|
| RF |
| Breiman [64] Jeong et al. [34] Freeman et al. [37] Kuhn [60] |
| SVR |
| Brdar, et al. [35] Kuhn [60] |
| XGBOOST |
| Chen and Guestrin [36] Kuhn [60] |
| PLSR |
| Hastie et al. [65] Mevik and Wehrens [62] |
| RIDGE |
| Hastie et al. [61] Aarshay [66] |
| LASSO |
| Hastie et al. [61] Aarshay [66] |
| Error (%) | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|---|---|---|---|
| Block level | 38.5 | 46.7 | 46.2 | 56.3 | 37.4 | 55.7 | 38.4 | 26.3 |
| Farm level | 4.3 | 5 | 38.6 | 26.7 | 30.9 | 15 | 4.3 | 15.3 |
| Error (%) | 2015 | 2016 | 2017 | 2018 | 2019 | 2020 | 2021 | 2022 |
|---|---|---|---|---|---|---|---|---|
| Block level | 37.4 | 47.1 | 66.1 | 70.7 | 28.7 | 50.9 | 33.6 | 44.5 |
| Farm level | 8.8 | 6.2 | 82.7 | 46.7 | 22 | 5.2 | 3.7 | 39.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Torgbor, B.A.; Rahman, M.M.; Brinkhoff, J.; Sinha, P.; Robson, A. Integrating Remote Sensing and Weather Variables for Mango Yield Prediction Using a Machine Learning Approach. Remote Sens. 2023, 15, 3075. https://doi.org/10.3390/rs15123075
Torgbor BA, Rahman MM, Brinkhoff J, Sinha P, Robson A. Integrating Remote Sensing and Weather Variables for Mango Yield Prediction Using a Machine Learning Approach. Remote Sensing. 2023; 15(12):3075. https://doi.org/10.3390/rs15123075
Chicago/Turabian StyleTorgbor, Benjamin Adjah, Muhammad Moshiur Rahman, James Brinkhoff, Priyakant Sinha, and Andrew Robson. 2023. "Integrating Remote Sensing and Weather Variables for Mango Yield Prediction Using a Machine Learning Approach" Remote Sensing 15, no. 12: 3075. https://doi.org/10.3390/rs15123075
APA StyleTorgbor, B. A., Rahman, M. M., Brinkhoff, J., Sinha, P., & Robson, A. (2023). Integrating Remote Sensing and Weather Variables for Mango Yield Prediction Using a Machine Learning Approach. Remote Sensing, 15(12), 3075. https://doi.org/10.3390/rs15123075









