Forest Area and Structural Variable Estimation in Boreal Forest Using Suomi NPP VIIRS Data and a Sample from VHR Imagery
Abstract
1. Introduction
2. Materials and Methods
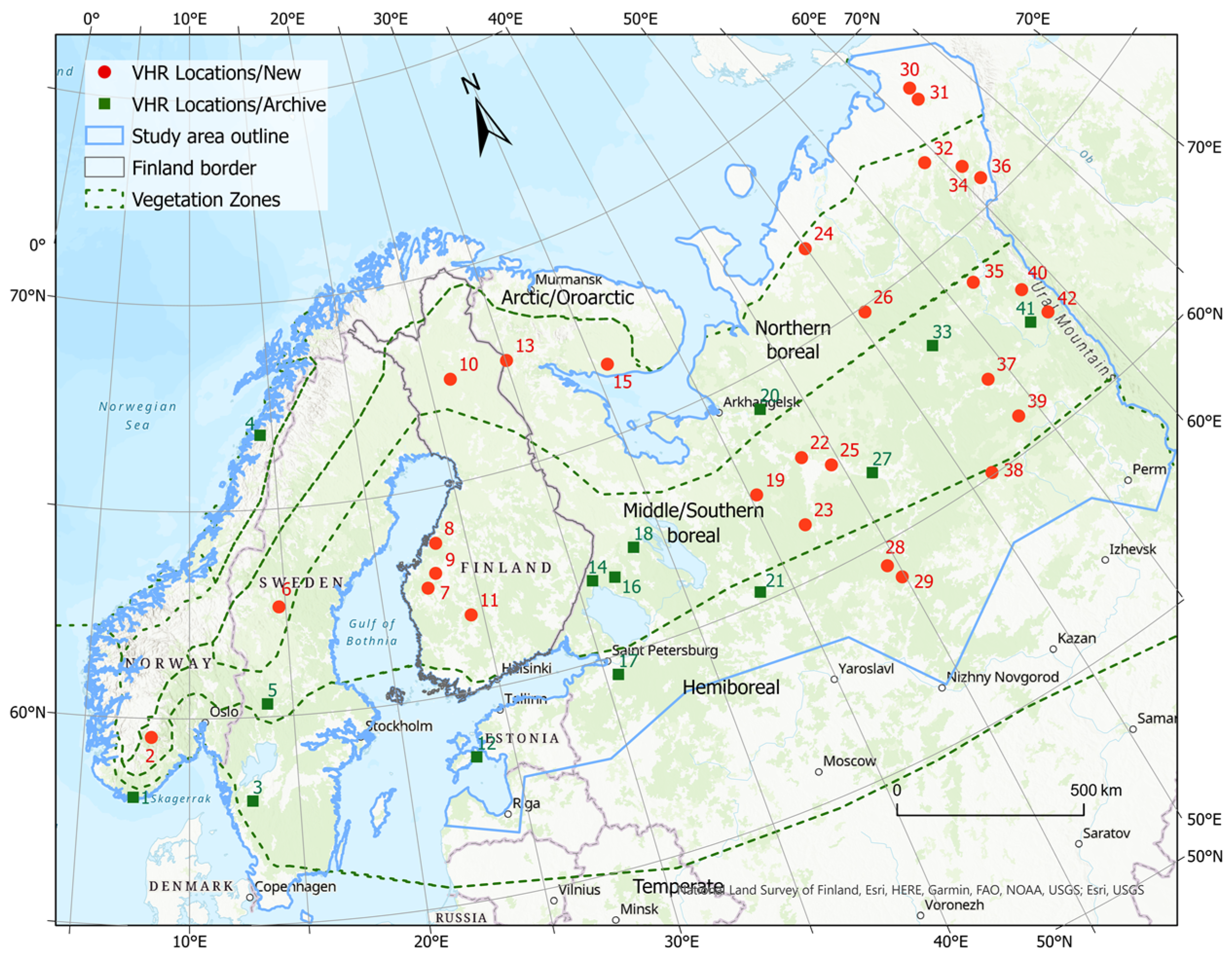
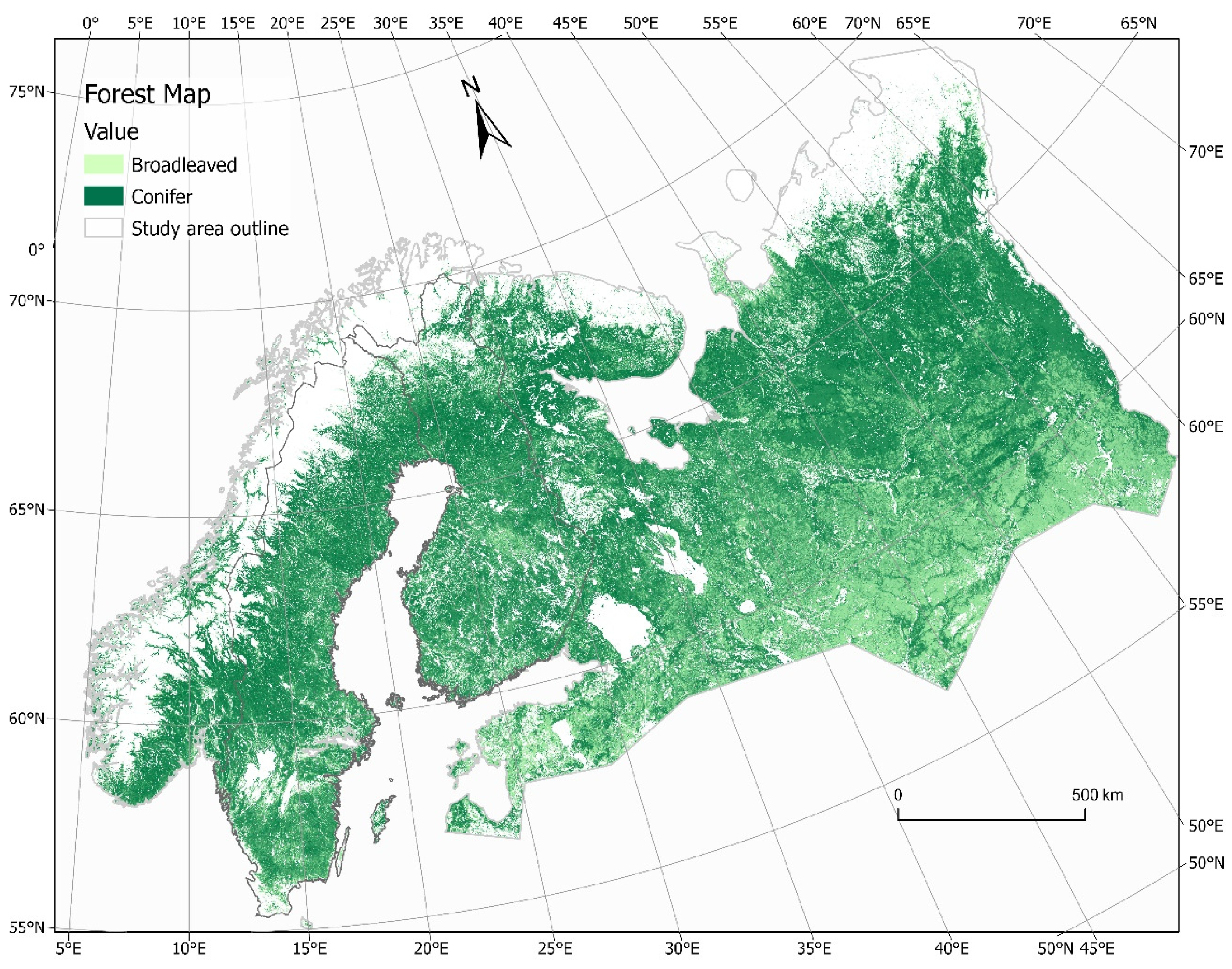
2.1. Study Area and Reference Data
2.2. Suomi NPP VIIRS Data
2.3. VHR Data
2.3.1. Two-Stage Sampling
2.3.2. Visual Interpretation
2.4. Models for Variable Estimation
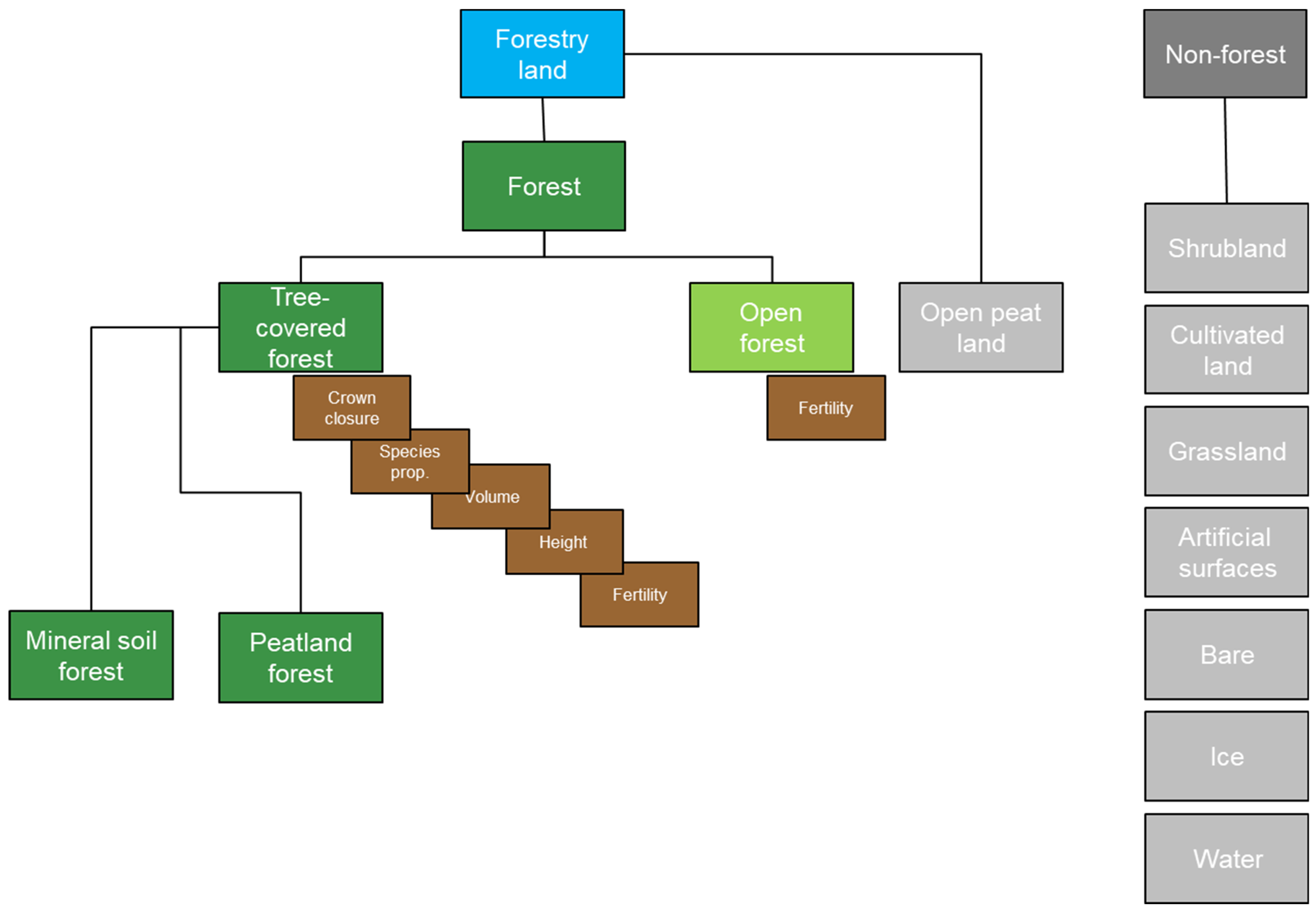
2.4.1. Land Cover Classification
2.4.2. Structural Variables
2.5. Computation of Means and Their Confidence Intervals
2.5.1. Means and Confidence Intervals for Target Variables for VHR Image Areas
2.5.2. Means and Confidence Intervals for Target Variables for Whole Study Area from VHR Images
- is the size of the sampling frame of all possible VHR images. because is a very large number due to the large study area.
- is the number of possible plot locations within each VHR image: ().
- is the number of VHR images;
- is the number of selected plots within a VHR image.
3. Results with Accuracy Considerations
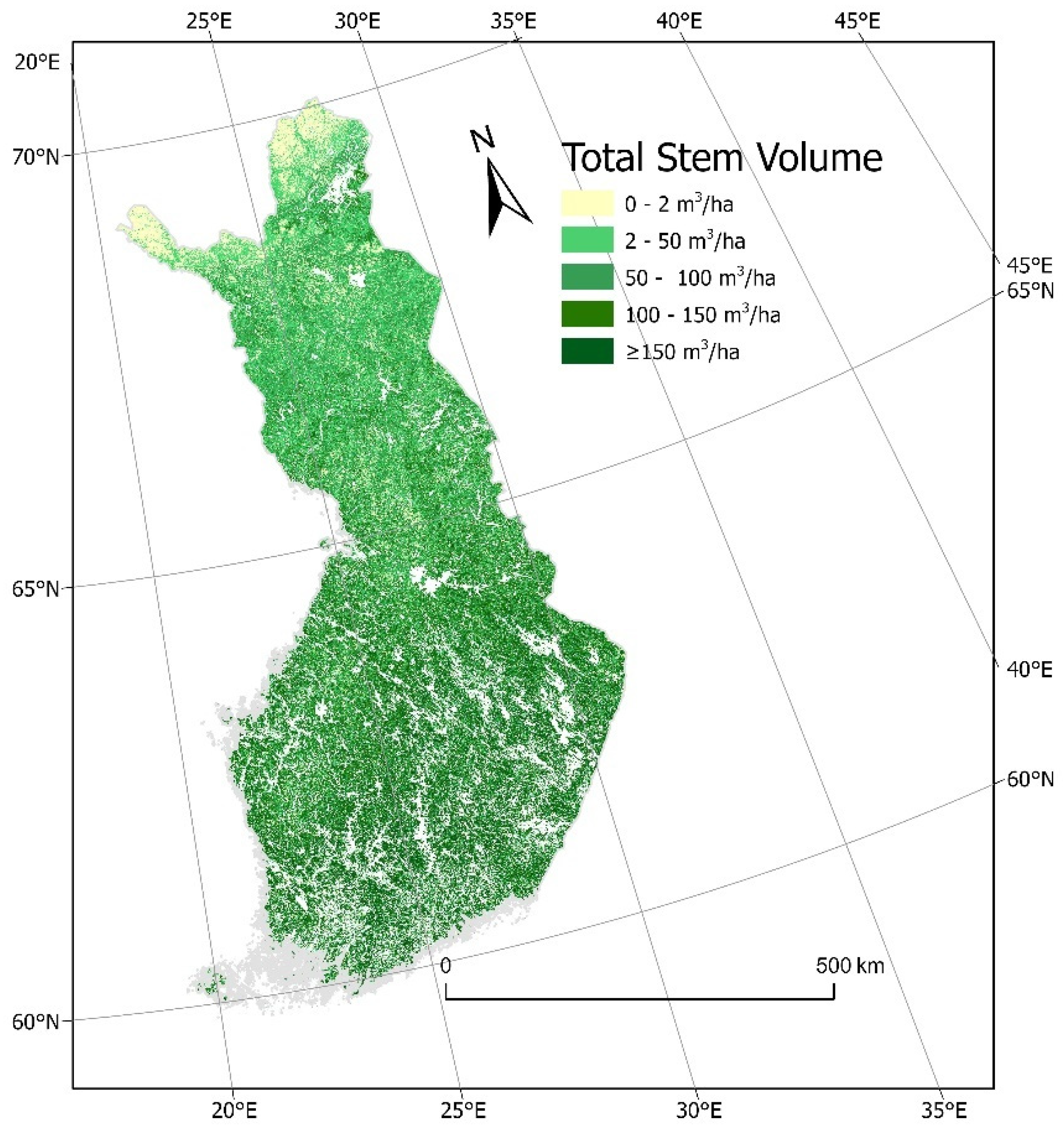
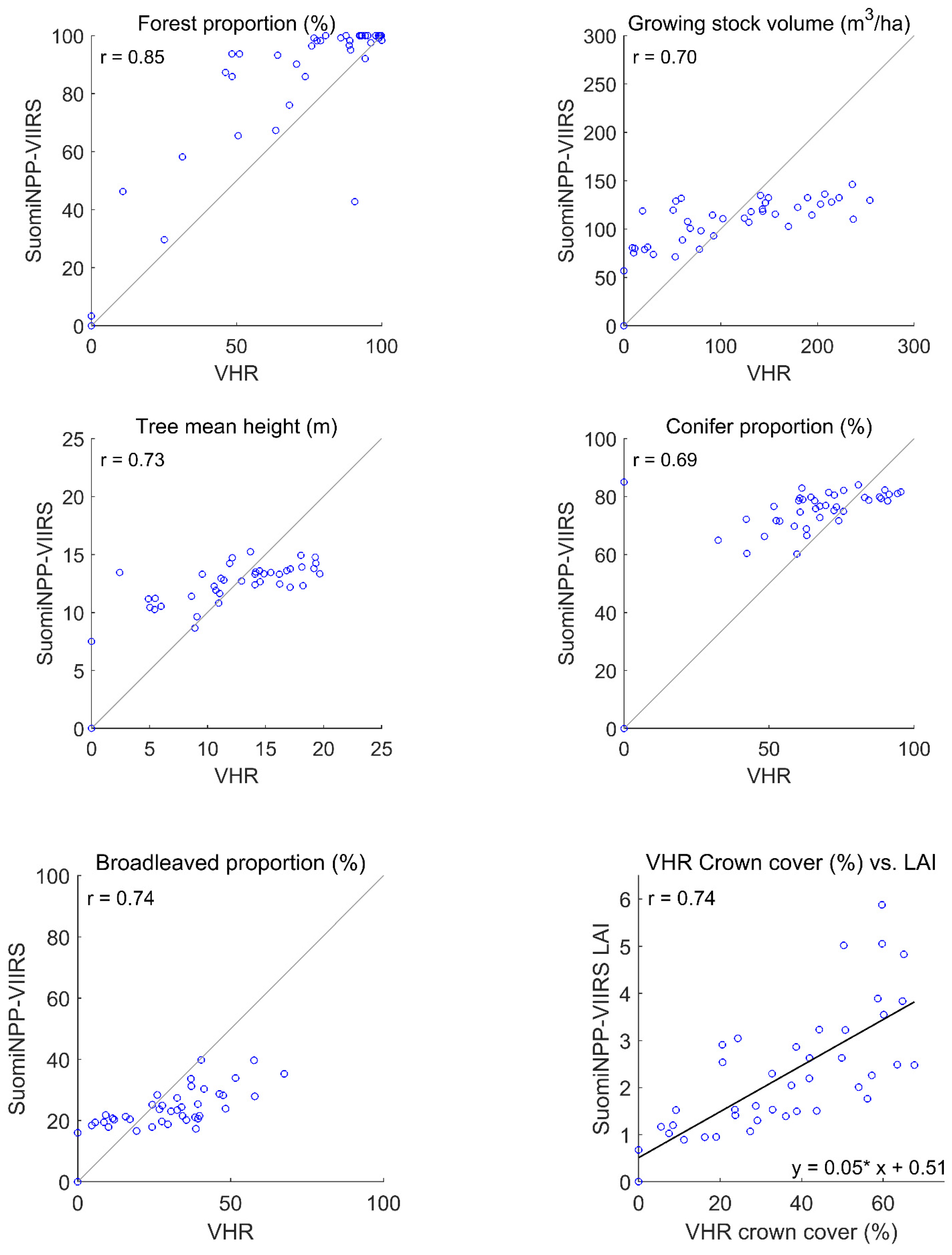
3.1. Forest Variables for the Whole Study Area, Finland, and Sweden
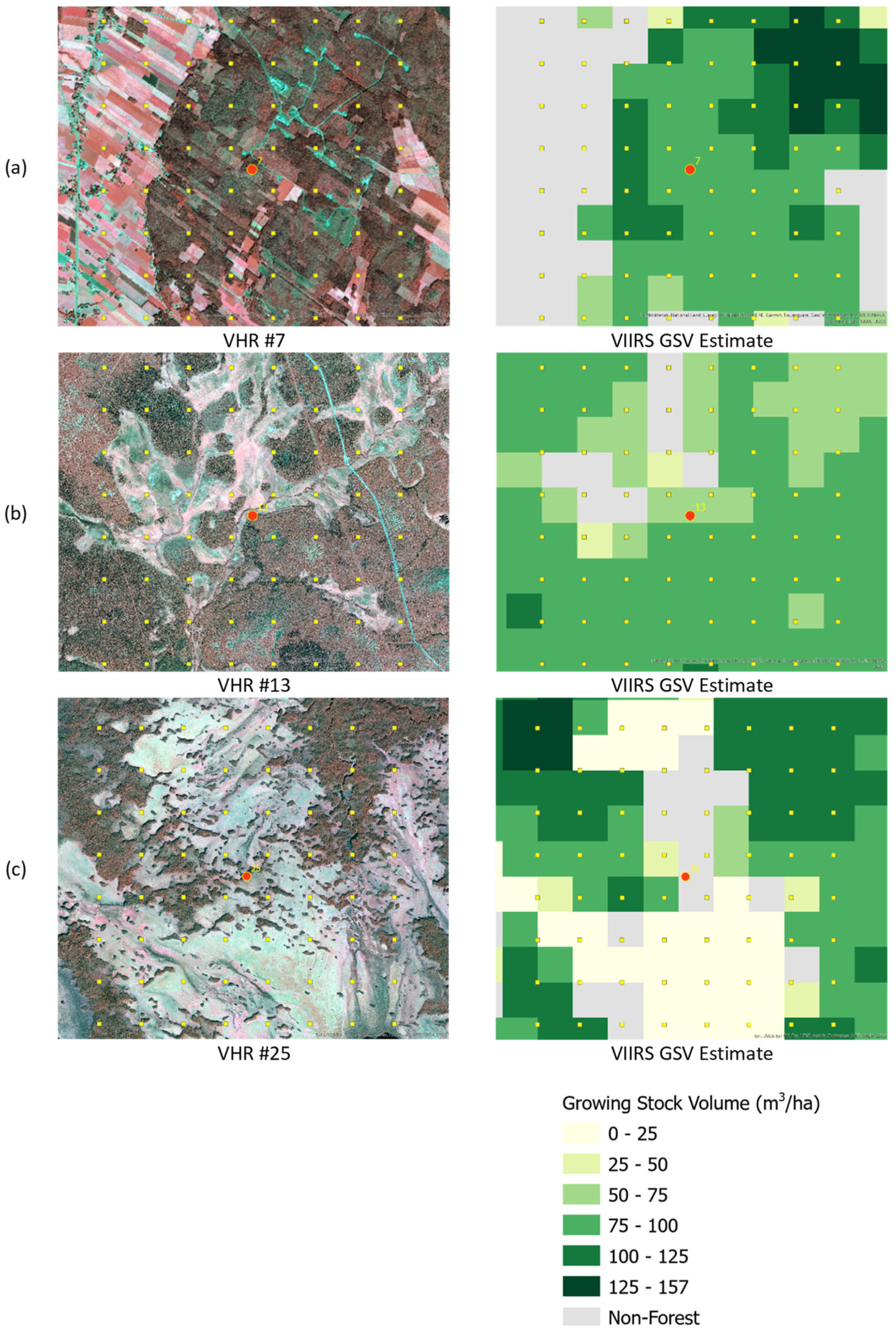
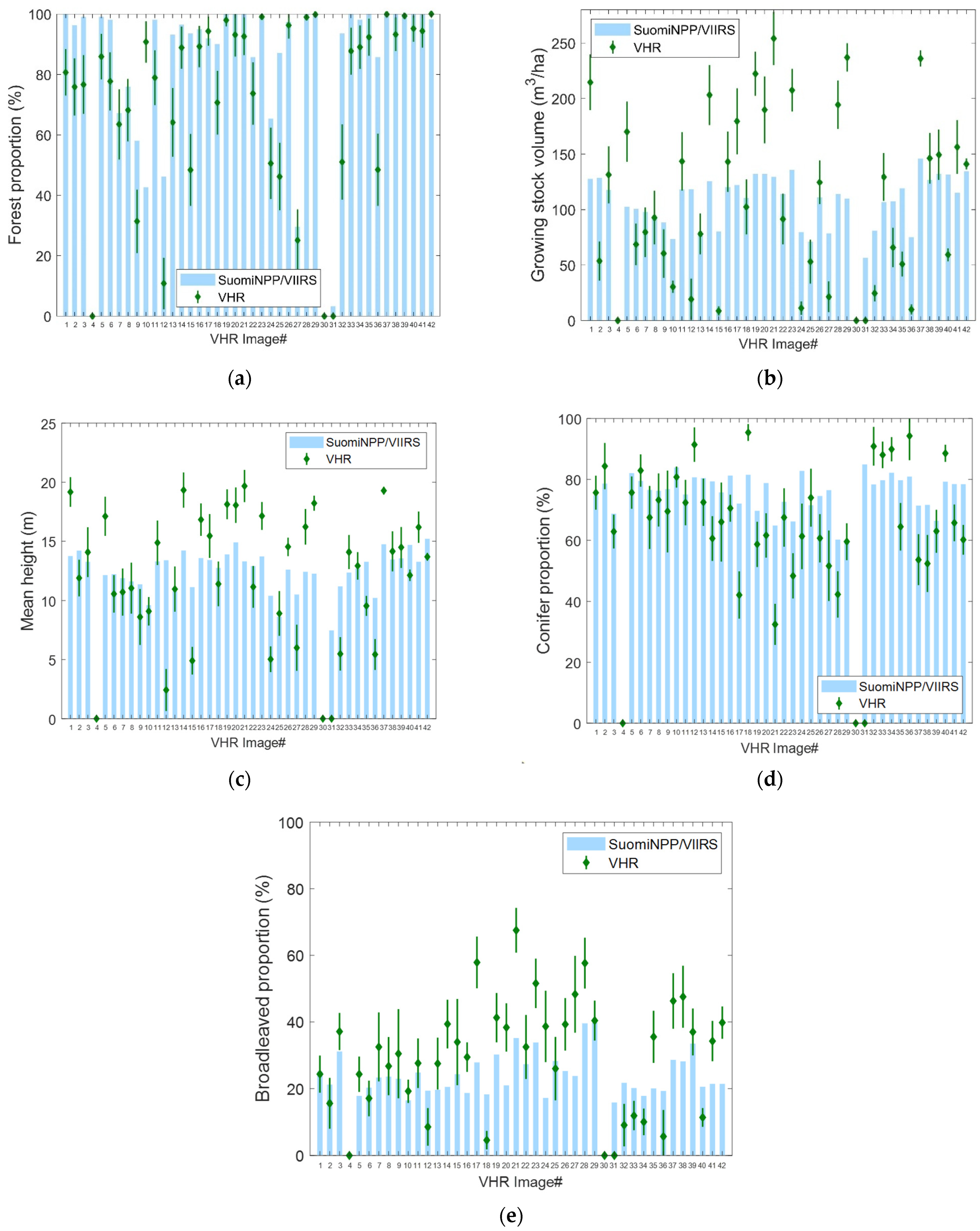
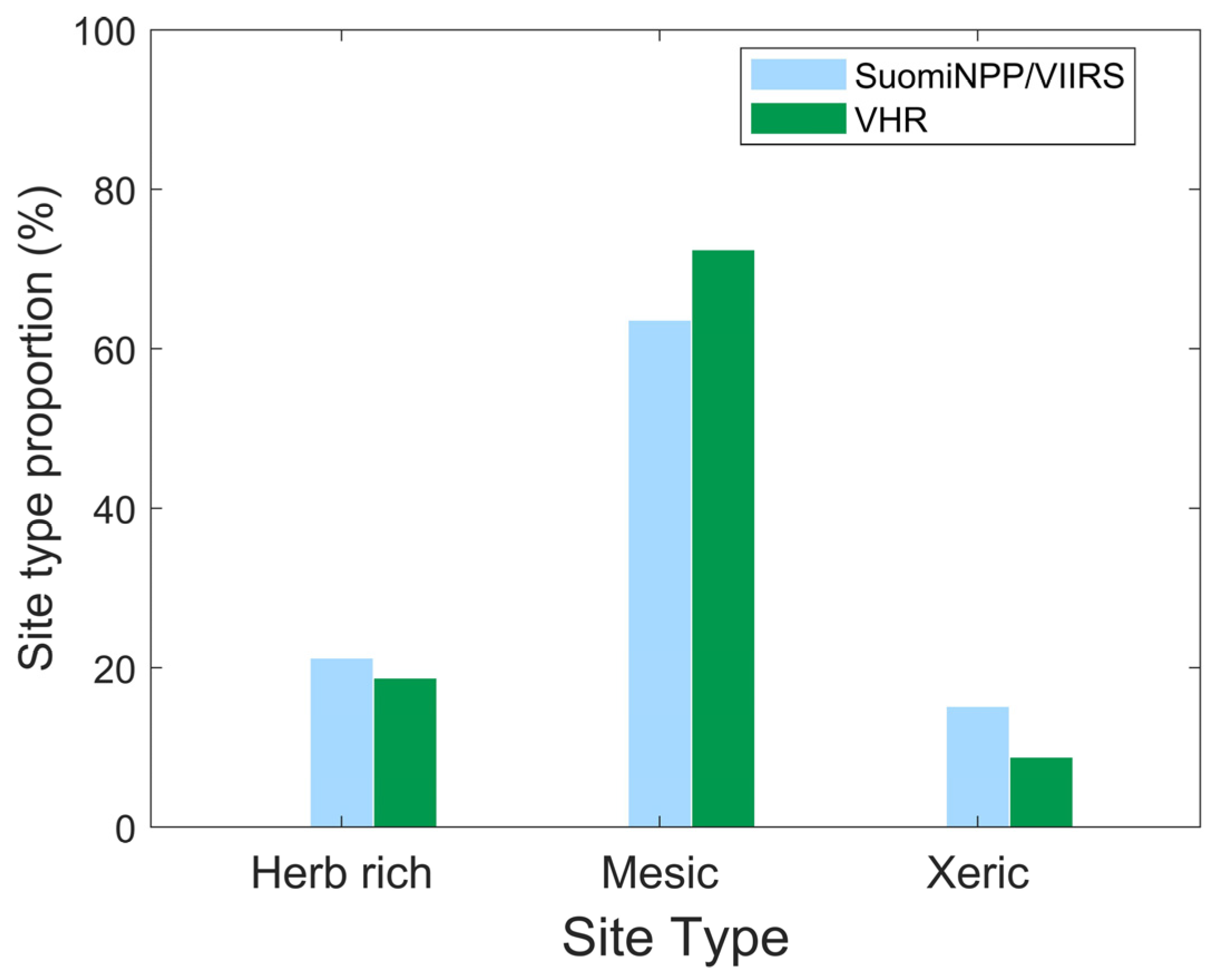
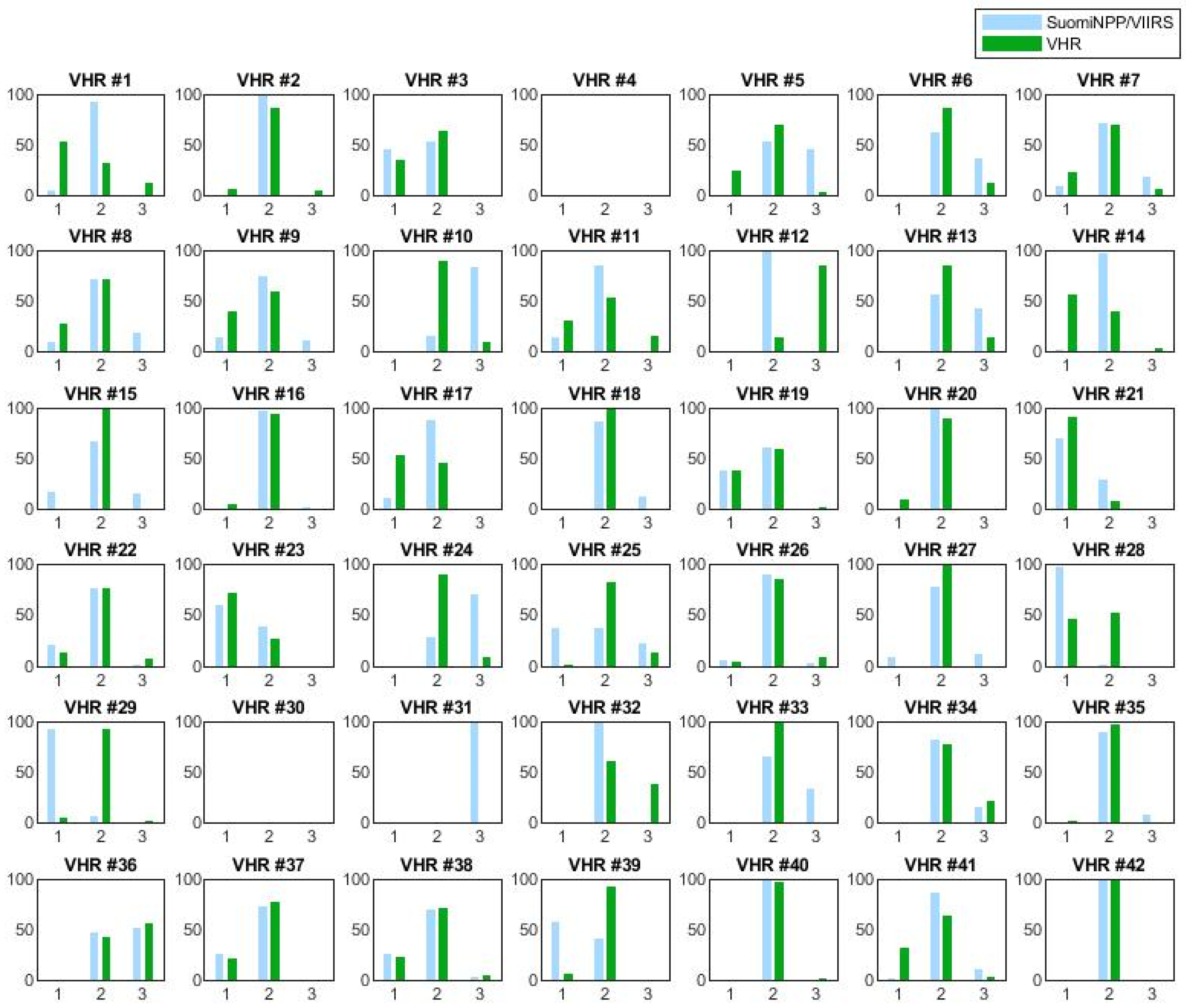
3.2. Comparison of VIIRS Map and VHR Plot Assessment by VHR Image Areas
4. Discussion
4.1. General Approach
4.2. VIIRS Map and VHR Sample Agreement for Whole Area
4.3. Agreement with NFI Data and Worldcover
4.4. Agreement at VHR Image Locations
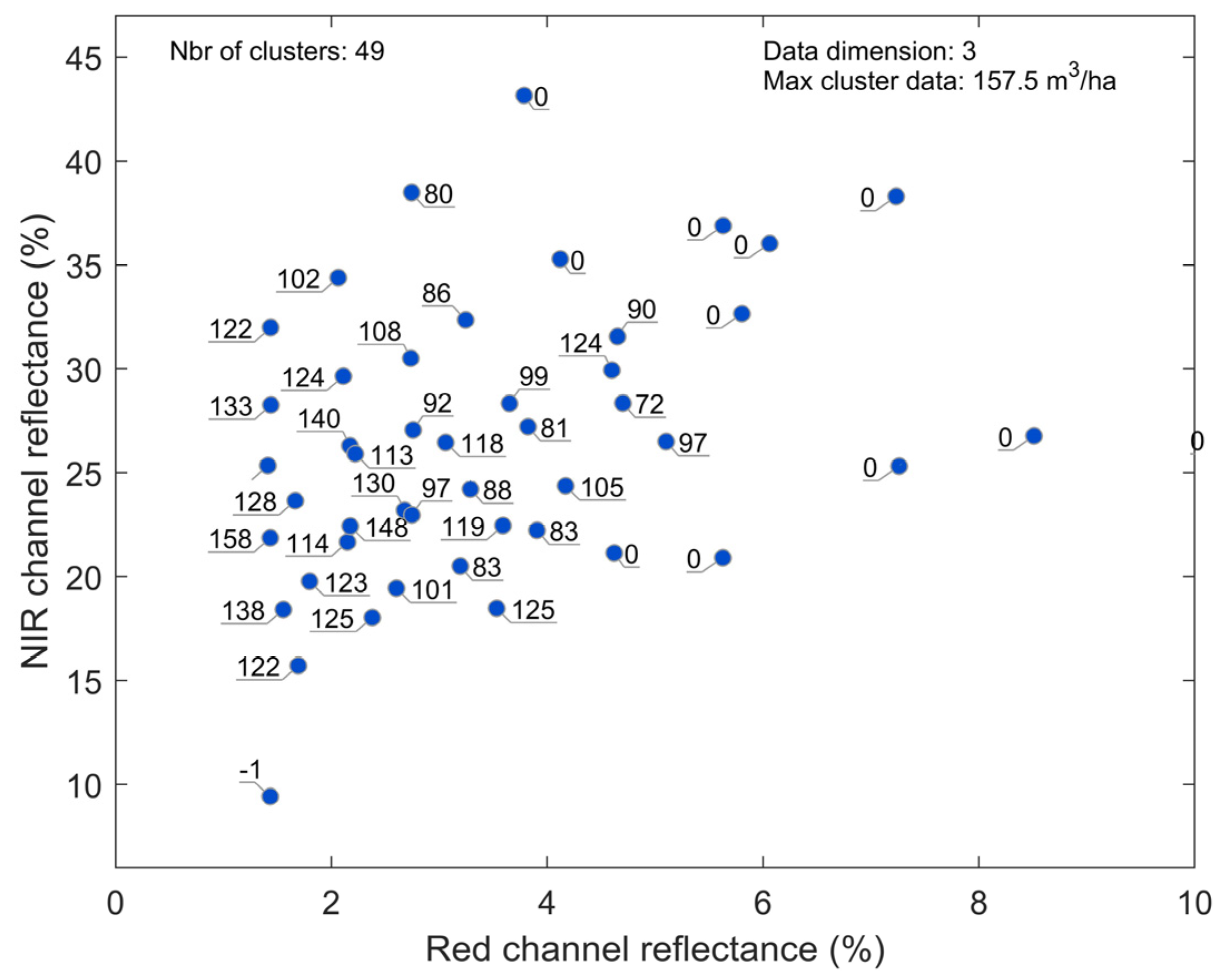
4.5. Calibration Tests
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- FAO. Global Forest Resources Assessment 2020 Key Findings; FAO: Rome, Italy, 2020. [Google Scholar]
- Nabuurs, G.J.; Masera, K.O.; Andrasko, P.; Benitez-Ponce, R.; Boer, M.; Dutschke, E.; Elsiddig, J.; Ford-Robertson, P.; Frumhoff, T.; Karjalainen, O.; et al. Chapter 9: Forestry—AR4 WGIII. Available online: https://archive.ipcc.ch/publications_and_data/ar4/wg3/en/ch9.html (accessed on 28 December 2022).
- Lier, M.; Köhl, M.; Korhonen, K.T.; Linser, S.; Prins, K.; Talarczyk, A. The New EU Forest Strategy for 2030: A New Understanding of Sustainable Forest Management? Forests 2022, 13, 245. [Google Scholar] [CrossRef]
- Zanaga, D.; Van De Kerchove, R.; De Keersmaecker, W.; Souverijns, N.; Brockmann, C.; Quast, R.; Wevers, J.; Grosu, A.; Paccini, A.; Vergnaud, S.; et al. ESA WorldCover 10 m 2020 V100. 2021. Available online: https://zenodo.org/record/5571936 (accessed on 17 January 2023).
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Kangas, A.; Gove, J.H.; Scott, C.T. Introduction; Springer: Dordrecht, The Netherlands, 2006; pp. 3–11. [Google Scholar]
- McRoberts, R. The National Forest Inventory of the United States of America. J. For. Sci. 2008, 24, 127–135. [Google Scholar]
- Tomppo, E.; Olsson, H.; Ståhl, G.; Nilsson, M.; Hagner, O.; Katila, M. Combining National Forest Inventory Field Plots and Remote Sensing Data for Forest Databases. Remote Sens. Environ. 2008, 112, 1982–1999. [Google Scholar] [CrossRef]
- Liu, H.; Gong, P.; Wang, J.; Wang, X.; Ning, G.; Xu, B. Production of Global Daily Seamless Data Cubes and Quantification of Global Land Cover Change from 1985 to 2020—IMap World 1.0. Remote Sens. Environ. 2021, 258, 112364. [Google Scholar] [CrossRef]
- Häme, T.; Stenberg, P.; Andersson, K.; Rauste, Y.; Kennedy, P.; Folving, S.; Sarkeala, J. AVHRR-Based Forest Proportion Map of the Pan-European Area. Remote Sens. Environ. 2001, 77, 76–91. [Google Scholar] [CrossRef]
- Shimada, M.; Itoh, T.; Motooka, T.; Watanabe, M.; Shiraishi, T.; Thapa, R.; Lucas, R. New Global Forest/Non-Forest Maps from ALOS PALSAR Data (2007–2010). Remote Sens. Environ. 2014, 155, 13–31. [Google Scholar] [CrossRef]
- Martone, M.; Rizzoli, P.; Wecklich, C.; González, C.; Bueso-Bello, J.L.; Valdo, P.; Schulze, D.; Zink, M.; Krieger, G.; Moreira, A. The Global Forest/Non-Forest Map from TanDEM-X Interferometric SAR Data. Remote Sens. Environ. 2018, 205, 352–373. [Google Scholar] [CrossRef]
- Pulella, A.; Santos, R.A.; Sica, F.; Posovszky, P.; Rizzoli, P. Multi-Temporal Sentinel-1 Backscatter and Coherence for Rainforest Mapping. Remote Sens 2020, 12, 847. [Google Scholar] [CrossRef]
- Ruiz-Ramos, J.; Marino, A.; Boardman, C.; Suarez, J. Continuous Forest Monitoring Using Cumulative Sums of Sentinel-1 Timeseries. Remote Sens. 2020, 12, 3061. [Google Scholar] [CrossRef]
- Congalton, R.G.; Gu, J.; Yadav, K.; Thenkabail, P.; Ozdogan, M. Global Land Cover Mapping: A Review and Uncertainty Analysis. Remote Sens. 2014, 6, 12070–12093. [Google Scholar] [CrossRef]
- Schepaschenko, D.; See, L.; Lesiv, M.; McCallum, I.; Fritz, S.; Salk, C.; Moltchanova, E.; Perger, C.; Shchepashchenko, M.; Shvidenko, A.; et al. Development of a Global Hybrid Forest Mask through the Synergy of Remote Sensing, Crowdsourcing and FAO Statistics. Remote Sens. Environ. 2015, 162, 208–220. [Google Scholar] [CrossRef]
- Schuck, A.; Päivinen, R.; Häme, T.; Van Brusselen, J.; Kennedy, P.; Folving, S. Compilation of a European Forest Map from Portugal to the Ural Mountains Based on Earth Observation Data and Forest Statistics. For. Policy Econ. 2003, 5, 187–202. [Google Scholar] [CrossRef]
- Sexton, J.O.; Song, X.-P.; Feng, M.; Noojipady, P.; Anand, A.; Huang, C.; Kim, D.-H.; Collins, K.M.; Channan, S.; Dimiceli, C.; et al. Global, 30-m Resolution Continuous Fields of Tree Cover: Landsat-Based Rescaling of MODIS Vegetation Continuous Fields with Lidar-Based Estimates of Error. Int. J. Digit. Earth 2013, 8947, 130321031236007. [Google Scholar] [CrossRef]
- Pflugmacher, D.; Rabe, A.; Peters, M.; Hostert, P. Mapping Pan-European Land Cover Using Landsat Spectral-Temporal Metrics and the European LUCAS Survey. Remote Sens. Environ. 2019, 221, 583–595. [Google Scholar] [CrossRef]
- Büttner, G. CORINE Land Cover and Land Cover Change Products. Remote Sens. Digit. Image Process. 2014, 18, 55–74. [Google Scholar]
- Hame, T.; Salli, A.; Andersson, K.; Lohi, A. A New Methodology for the Estimation of Biomass of Conifer dominated Boreal Forest Using NOAA AVHRR Data. Int. J. Remote Sens. 1997, 18, 3211–3243. [Google Scholar] [CrossRef]
- Miettinen, J.; Carlier, S.; Häme, L.; Mäkelä, A.; Minunno, F.; Penttilä, J.; Pisl, J.; Rasinmäki, J.; Rauste, Y.; Seitsonen, L.; et al. Demonstration of Large Area Forest Volume and Primary Production Estimation Approach Based on Sentinel-2 Imagery and Process Based Ecosystem Modelling. Int. J. Remote. Sens. 2021, 42, 9492–9514. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark Map of Forest Carbon Stocks in Tropical Regions across Three Continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated Carbon Dioxide Emissions from Tropical Deforestation Improved by Carbon-Density Maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Avitabile, V.; Herold, M.; Heuvelink, G.B.M.; Lewis, S.L.; Phillips, O.L.; Asner, G.P.; Armston, J.; Ashton, P.S.; Banin, L.; Bayol, N.; et al. An Integrated Pan-Tropical Biomass Map Using Multiple Reference Datasets. Glob. Chang. Biol. 2016, 22, 1406–1420. [Google Scholar] [CrossRef] [PubMed]
- Potapov, P.; Li, X.; Hernandez-Serna, A.; Tyukavina, A.; Hansen, M.C.; Kommareddy, A.; Pickens, A.; Turubanova, S.; Tang, H.; Silva, C.E.; et al. Mapping Global Forest Canopy Height through Integration of GEDI and Landsat Data. Remote Sens. Environ. 2021, 253, 112165. [Google Scholar] [CrossRef]
- Duncanson, L.; Kellner, J.R.; Armston, J.; Dubayah, R.; Minor, D.M.; Hancock, S.; Healey, S.P.; Patterson, P.L.; Saarela, S.; Marselis, S.; et al. Aboveground Biomass Density Models for NASA’s Global Ecosystem Dynamics Investigation (GEDI) Lidar Mission. Remote Sens. Environ. 2022, 270, 112845. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 Imagery for Forest Variable Prediction in Boreal Region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Santoro, M.; Cartus, O.; Carvalhais, N.; Rozendaal, D.M.A.; Avitabile, V.; Araza, A.; de Bruin, S.; Herold, M.; Quegan, S.; Rodríguez-Veiga, P.; et al. The Global Forest Above-Ground Biomass Pool for 2010 Estimated from High-Resolution Satellite Observations. Earth Syst. Sci. Data 2021, 13, 3927–3950. [Google Scholar] [CrossRef]
- Cajander, A.K. Forest Types and Their Significance. Silva Fenn. 1949, 56, 7396. [Google Scholar] [CrossRef]
- Lambin, E.F.; Mayaux, P. Calibration of Tropical Forest Area Estimates at Coarse Spatial Resolution with Fine Resolution Data. Int. Geosci. Remote Sens. Symp. 1995, 2, 1003–1005. [Google Scholar] [CrossRef]
- Deppe, F. Forest Area Estimation Using Sample Surveys and Landsat MSS and TM Data. Photogramm. Eng. Remote Sens. 1998, 64, 285–292. [Google Scholar]
- Kuusela, K. The Dynamics of Boreal Coniferous Forests; SITRA: Manama, Bahrain, 1990; ISBN 951-563-274-9. [Google Scholar]
- INSPIRE Infrastructure for Spatial Information in Europe. D2.8.I.2 Data Specification on Geographical Grid Systems-Technical Guidelines. 2014. Available online: https://inspire.ec.europa.eu/documents/Data_Specifications/INSPIRE_Specification_GGS_v3.0.1.pdf (accessed on 17 January 2023).
- The Multi-Source National Forest Inventory of Finland—Methods and Results 2015—Jukuri. Available online: https://jukuri.luke.fi/handle/10024/543826 (accessed on 6 April 2022).
- Katila, M.; Rajala, T.; Kangas, A. Assessing Local Trends in Indicators of Ecosystem Services with a Time Series of Forest Resource Maps. Silva Fenn. 2020, 54, 1–19. [Google Scholar] [CrossRef]
- Korhonen, K.T.; Ahola, A.; Heikkinen, J.; Henttonen, H.M.; Hotanen, J.-P.; Ihalainen, A.; Melin, M.; Pitkänen, J.; Räty, M.; Sirviö, M.; et al. Forests of Finland 2014–2018 and Their Development 1921–2018. Silva Fenn. 2021, 55, 10662. [Google Scholar] [CrossRef]
- Härmä, P.; Teiniranta, R.; Törmä, M.; Repo, R.; Järvenpää, E. (22) (PDF) The Production of Finnish CORINE Land Cover 2000 Classification. Available online: https://www.researchgate.net/publication/253513467_The_production_of_Finnish_CORINE_land_cover_2000_classification (accessed on 8 April 2022).
- Rahman, H.; Dedieu, G. SMAC: A Simplified Method for the Atmospheric Correction of Satellite Measurements in the Solar Spectrum. Int. J. Remote Sens. 1994, 15, 123–143. [Google Scholar] [CrossRef]
- Cochran, W.G. Sampling Techniques, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 1977; ISBN 0-471-16240-X. [Google Scholar]
- Häme, T.; Kilpi, J.; Ahola, H.A.; Rauste, Y.; Antropov, O.; Rautiainen, M.; Sirro, L.; Bounpone, S. Improved Mapping of Tropical Forests with Optical and SAR Imagery, Part I: Forest Cover and Accuracy Assessment Using Multi-Resolution Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 74–91. [Google Scholar] [CrossRef]
- Olofsson, P.; Foody, G.M.; Herold, M.; Stehman, S.V.; Woodcock, C.E.; Wulder, M.A. Good Practices for Estimating Area and Assessing Accuracy of Land Change. Remote Sens. Environ. 2014, 148, 42–57. [Google Scholar] [CrossRef]
- Zhang, J.; Goodchild, M.F. Uncertainty in Geographical Information; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar] [CrossRef]
- Hansen, W.D.; Fitzsimmons, R.; Olnes, J.; Williams, A.P. An Alternate Vegetation Type Proves Resilient and Persists for Decades Following Forest Conversion in the North American Boreal Biome. J. Ecol. 2021, 109, 85–98. [Google Scholar] [CrossRef]
- Larsen, J.A. The Boreal Ecosystem; Academic Press: Cambridge, MA, USA, 1980; ISBN 0-12-436880-8. [Google Scholar]
- Henttonen, H.M.; Nöjd, P.; Suvanto, S.; Heikkinen, J.; Mäkinen, H. Size-Class Structure of the Forests of Finland during 1921–2013: A Recovery from Centuries of Exploitation, Guided by Forest Policies. Eur. J. For. Res. 2020, 139, 279–293. [Google Scholar] [CrossRef]
- Ho, T.K. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Heiskanen, J.; Rautiainen, M.; Korhonen, L.; Mõttus, M.; Stenberg, P. Retrieval of Boreal Forest LAI Using a Forest Reflectance Model and Empirical Regressions. Int. J. Appl. Earth Obs. Geoinf. 2011, 13, 595–606. [Google Scholar] [CrossRef]
- Finnish Statistical Yearbook of Forestry | Natural Resources Institute Finland. Available online: https://www.luke.fi/en/statistics/about-statistics/statistical-publications/finnish-statistical-yearbook-of-forestry (accessed on 9 September 2022).
- Nilsson, P.; Roberge, C.; Fridman, J.; Wulff, S. Skogsdata 2019; Official Statistics of Sweden: Örebro, Sweden, 2019. [Google Scholar]
- Global Forest Resources Assessments, FAO. Available online: https://www.fao.org/forest-resources-assessment/remote-sensing/fra-2020-remote-sensing-survey/methodology/en/ (accessed on 13 September 2022).
- Olofsson, P.; Stehman, S.V.; Woodcock, C.E.; Sulla-Menashe, D.; Sibley, A.M.; Newell, J.D.; Friedl, M.A.; Herold, M. A Global Land-Cover Validation Data Set, Part I: Fundamental Design Principles. Int. J. Remote Sens. 2012, 33, 5768–5788. [Google Scholar] [CrossRef]
- Mäkelä, A.; Pulkkinen, M.; Mäkinen, H. Bridging Empirical and Carbon-Balance Based Forest Site Productivity—Significance of below-Ground Allocation. For. Ecol. Manag. 2016, 372, 64–77. [Google Scholar] [CrossRef]
- Häme, T.; Sirro, L.; Dees, M.; Mäkelä, A.; Penttilä, J.; Marin, G.; Tomé, M. Helping Forest Owners to Manage Forest Carbon—the Forest Flux Project. GI Forum 2021, 9, 137–142. [Google Scholar] [CrossRef]
- Poso, S. A method of combining photo and field samples in forest inventory. In Communicationes Instituti Forestalis Fenniae; Instituti Forestalis Fenniae: Joensuu, Finland, 1972; pp. 1–133. [Google Scholar]



| Band I | Center Wavelength (µm) | Wavelength Range (µm) |
|---|---|---|
| 1 | 0.64 | 0.6–0.68 |
| 2 | 0.865 | 0.85–0.88 |
| 3 | 1.61 | 1.58–1.64 |
| Time Range | Number of Images |
|---|---|
| 13 May–19 June | 58 |
| 20 June 20–11 July | 53 |
| 21 August–11 September | 65 |
| 12 September–30 September | 62 |
| Image# | Instrument | Date | Image# | Instrument | Date | Image# | Instrument | Date |
|---|---|---|---|---|---|---|---|---|
| 1 | WV1 | 7 August 2013 | 15 | P1B | 18 August 2015 | 29 | P1B | 21 August 2015 |
| 2 | P1B | 13 August 2015 | 16 | WV1 | 2 June 2013 | 30 | P1B | 31 July 2015 |
| 3 | P1A | 19 September 2014 | 17 | P1A | 25 July 2014 | 31 | P1A | 31 July 2015 |
| 4 | WV1 | 30 July 2013 | 18 | WV1 | 28 May 2013 | 32 | P1B | 30 June 2015 |
| 5 | P1B | 20 September 2014 | 19 | P1B | 20 August 2015 | 33 | WV1 | 25 September 2014 |
| 6 | P1B | 4 July 2015 | 20 | WV1 | 31 May 2013 | 34 | P1B | 30 June 2015 |
| 7 | P1A | 16 August 2015 | 21 | WV1 | 18 September 2014 | 35 | P1A | 30 June 2015 |
| 8 | P1A | 1 July 2015 | 22 | P1A | 6 August 2015 | 36 | P1A | 30 June 2015 |
| 9 | P1A | 16 August 2015 | 23 | P1A | 20 August 2015 | 37 | P1A | 7 August 2015 |
| 10 | P1A | 18 August 2015 | 24 | P1B | 29 July 2015 | 38 | P1B | 30 June 2015 |
| 11 | P1A | 3 July 2015 | 25 | P1B | 21 August 2015 | 39 | P1A | 12 August 2015 |
| 12 | P1A | 14 July 2014 | 26 | P1B | 24 July 2015 | 40 | P1A | 7 August 2015 |
| 13 | P1B | 17 August 2015 | 27 | WV1 | 8 June 2014 | 41 | WV1 | 8 August 2014 |
| 14 | P1B | 24 July 2014 | 28 | P1B | 21 August 2015 | 42 | P1A | 7 August 2015 |
| Variable | VIIRS Map | VHR 95% Ci-Low | Expected Value | VHR 95% Ci-High |
|---|---|---|---|---|
| Forest area (km2) | 2,140,589 | 1,840,672 | 2,114,126 | 2,416,984 |
| Forest proportion (%) * | 72.8 | 62.6 | 71.9 | 82.2 |
| Growing stock volume (1000m3) * | 23,332,420 | 152,960 | 217,332 | 296,081 |
| Growing stock volume (m3/ha) * | 109.0 | 83.1 | 102.8 | 122.5 |
| Forest height (m) | 12.5 | 10.2 | 11.9 | 13.6 |
| Conifer proportion (%) | 74.9 | 63.7 | 68.5 | 73.4 |
| BL proportion (%) | 25.1 | 26.6 | 31.5 | 36.3 |
| Class | Forest Proportion from VHR Plots, (%) | Area, 95% Confidence Interval (%) | V, 95% Confidence Interval | |
|---|---|---|---|---|
| Mineral Soil Forest | 58.3 | (48.8, 67.7) | 125.3 | (101.6, 149.0) |
| Peat Forest | 8.2 | (4.6, 11.8) | 11.0 | (7.1, 14.9) |
| Mineral Soil + Peat Forest | 66.5 | (57.7, 75.2) | 111.2 | (89.9, 132.4) |
| Open Forest | 5.4 | (3.3, 7.5) | 0.0 | n/a |
| Mineral Soil + Peat Forest and Open Forest | 71.9 | (62.6, 82.2) | 102.8 | (83.1, 122.5) |
| Variable | VIIRS Map | NFI FI |
|---|---|---|
| Forest area (km2) | 258,346 | 226,600 1 |
| Forest proportion (%) 2 | 77.0 | 67.0 |
| Growing stock volume (1000 m3) | 2,707,466 | 2,506,000 1 |
| Growing stock volume (m3/ha) | 104.8 | 110.6 1 |
| Conifer proportion (%) | 77.5 | 80.0 3 |
| BL proportion (%) | 22.6 | 20.0 3 |
| Variable | VIIRS Map | NFI SE |
|---|---|---|
| Forest area (km2) | 320,879 | 301,910 1 |
| Forest proportion (%) 2 | 71.6 | 67.0 |
| Growing stock volume (1000 m3) | 3,451,799 | 3,574,000 |
| Growing stock volume (m3/ha) | 107.5 | 118.4 1 |
| Conifer proportion (%) | 77.8 3 | 80.4 3 |
| BL proportion (%) | 22.2 3 | 19.6 3 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Häme, T.; Astola, H.; Kilpi, J.; Rauste, Y.; Sirro, L.; Mutanen, T.; Parmes, E.; Rasinmäki, J.; Imangholiloo, M. Forest Area and Structural Variable Estimation in Boreal Forest Using Suomi NPP VIIRS Data and a Sample from VHR Imagery. Remote Sens. 2023, 15, 3029. https://doi.org/10.3390/rs15123029
Häme T, Astola H, Kilpi J, Rauste Y, Sirro L, Mutanen T, Parmes E, Rasinmäki J, Imangholiloo M. Forest Area and Structural Variable Estimation in Boreal Forest Using Suomi NPP VIIRS Data and a Sample from VHR Imagery. Remote Sensing. 2023; 15(12):3029. https://doi.org/10.3390/rs15123029
Chicago/Turabian StyleHäme, Tuomas, Heikki Astola, Jorma Kilpi, Yrjö Rauste, Laura Sirro, Teemu Mutanen, Eija Parmes, Jussi Rasinmäki, and Mohammad Imangholiloo. 2023. "Forest Area and Structural Variable Estimation in Boreal Forest Using Suomi NPP VIIRS Data and a Sample from VHR Imagery" Remote Sensing 15, no. 12: 3029. https://doi.org/10.3390/rs15123029
APA StyleHäme, T., Astola, H., Kilpi, J., Rauste, Y., Sirro, L., Mutanen, T., Parmes, E., Rasinmäki, J., & Imangholiloo, M. (2023). Forest Area and Structural Variable Estimation in Boreal Forest Using Suomi NPP VIIRS Data and a Sample from VHR Imagery. Remote Sensing, 15(12), 3029. https://doi.org/10.3390/rs15123029







