Abstract
To monitor the Very-Low-Frequency (VLF) environment, a VLF detection system has been installed in Suizhou, China, a location with the longitude almost identical to that of the NWC transmitter in Australia. In the years 2019 and 2020, two solar eclipses crossed the NWC–Suizhou path at different locations. Each solar eclipse event represents a naturally occurring controlled experiment, but these two events are unique in that similar levels of electron density variation occurred at different locations along the VLF propagation path. Therefore, we conducted a comparative study using the VLF measurements during these two eclipses. Previous studies mostly estimated a pair of the reflection height (h′) and sharpness parameter (β) using the Long Wavelength Propagation Capability code, whereas, in this study, we use the VLF amplitude and phase as constraints in order to find the electron density change that best explains the VLF measurements. The eclipse measurements could be best explained if the path-averaged β value was 0.56 and 0.62 km−1 for the 2019 and 2020 eclipse, respectively. The VLF reflection height increased from 71.5 to 73.3 km for the 2019 eclipse and from 71.1 to 72.8 km for the 2020 eclipse. The best-fit β values were consistent with the Faraday International Reference Ionosphere model and statistical studies, and the h′ change was also consistent with previous studies and theoretical calculations. Moreover, present results suggested that VLF signals collected by a single receiver were not sensitive to where the electron density change occurs along the propagation path but reflected the average path condition. Therefore, a network of VLF receivers is required in order to monitor in real time the spatial extent of the space weather events that disturb the lower ionosphere.
1. Introduction
The D-region ionosphere is the region of enhanced electron densities at altitudes of 60–90 km that only appears during daytime conditions, as being primarily produced by the ionization of Nitric Oxide (NO) by solar Lyman-α radiation (1214 Å) [1,2]. After sunset, the solar inputs disappear, and the D-region relaxes to a state of very weak ionization. This region is of particular importance for the transition and transport processes between the neutral atmosphere and upper ionosphere [3] and is closely correlated with various atmospheric [4], magnetospheric [5,6], and solar events [7,8], including lightning discharge [9,10,11,12], gravity waves [13], radiation belt particle precipitation [14,15,16,17], gamma-ray bursts [7], solar eclipses [18], and flares [19]. Moreover, the collisional damping in the D-region ionosphere plays a critical role in the attenuation of radio waves, especially the Very-Low-Frequency (VLF, 3–30 kHz) waves, which have been used for navigation and long-range communications before the invention of the Global Positioning System (GPS) [20].
Measuring the D-region ionosphere is particularly difficult not only due to its extremely low level of electron density, but the fact that this region is too high for balloon-borne instruments and too low for space-borne instruments as well. Both high-power Incoherent Scatter Radars (ISRs) and riometers can remotely sense the D-region ionosphere, but with limited resolution in space. Sounding rockets can directly measure the D-region condition but only at a given location and a specific time. On the other hand, the VLF remote sensing technique represents the most sensitive and affordable approach for D-region measurements [21,22,23]. It is from this perspective that various VLF detection systems/networks have been developed, for example, the Atmospheric Weather Electromagnetic System for Observation, Modeling, and Education (AWESOME) instrument [24] and the Antarctic-Arctic Radiation-belt (Dynamic) Deposition-VLF Atmospheric Research Konsortium (AARDDVARK) [25]. With wavelengths of tens of kilometers, VLF waves bounce within the Earth and ionosphere (EI) waveguide and can propagate for long distances with relatively low attenuation. Abnormal changes in VLF signals, especially those from navy transmitters, are usually caused by the electron density disturbance in the D-region ionosphere [4], which, in most cases, is due to intense space weather events, for example, solar eclipses [26].
Solar eclipses have historically provided great opportunities for the studies of ionosphere formation and radio wave propagation [27,28,29]. In general, positive changes in VLF amplitude were observed for propagation paths shorter than 2000 km, whereas negative changes were observed for propagation paths longer than 10,000 km [30]. The 2009 total solar eclipse has been found to cause an increase in VLF reflection height by ~0.6 km and an increase in the sharpness parameter by ~0.012 km−1 [31]. Using measurements of tweek radio atmospherics, Singh et al. [32] revealed that this eclipse led to an increase in reflection height by ~5 km. Moreover, Pal et al. [33] studied the solar eclipse that occurred on 15 January 2010 and found an increase of ~3 km for the reflection height. The 2017 solar eclipse crossed the continental United States, and Cohen et al. [34] reported measurements of this eclipse at 11 different locations. Xu et al. [18] modeled this eclipse using a first-principles chemistry model and a Finite-Difference Time-Domain (FDTD) model, and the abnormal VLF measurements in Utah have been well explained. Moreover, Tripathi et al. [35] studied the 2020 solar eclipse using both tweek and transmitter signals and emphasized that “each solar eclipse, depending upon its time of occurrence, duration, and geographical location has a particular impact on the Earth’s ionosphere”.
To investigate VLF waves emitted from both natural and anthropogenic sources, a VLF receiving system has been designed at Wuhan University and installed in Suizhou, China. The longitude of this location is almost identical with the NWC transmitter in Australia. In 2019 and 2020, two solar eclipses crossed this path at different locations with different intersection angles. Each solar eclipse event represents a naturally occurring controlled experiment, and these two events are unique in that similar levels of electron density variation occurred at different locations along the VLF propagation path. By modeling and comparing the VLF measurements during these two eclipses, we aim at better understanding the VLF technique, especially related to the question about if and how to remotely sense the location of electron density disturbance using VLF measurements. In this study, we report measurements of NWC signals at the Suizhou station during this controlled experiment. Using a well-constrained ionospheric inversion method, we also estimate the eclipse-induced D-region disturbance with a view towards better understanding the solar eclipse effects and VLF propagation in the EI waveguide.
2. VLF Instrument and Eclipse Measurement
The VLF receiver utilized for the present eclipse study was developed and assembled at Wuhan University. It mainly consists of magnetic loop antennas, an analog front end, and a digital receiver. This receiver can detect radio waves with frequencies of 1–50 kHz. Similar to other VLF receivers, for example, AWESOME [24], the magnetic loop antennas were set up in both East–West and North–South directions to configure an orthogonal antenna system. The analog front end converts the induced current into voltage signals, filters the background noise, and amplifies the signal [36]. The digital receiver mainly comprised an analog to digital converter, a USB interface, and a GPS synchronization module, providing a timing accuracy of ~100 ns for the detection system [36,37]. With a dynamic range of ~110 dB, this system is highly sensitive to VLF waves emitted by lightning discharges and navy transmitters [38,39] and represents one of the most sensitive VLF receivers that are currently operational for subionospheric studies [40,41,42]. In this study, we report measurements of the VLF signals from the NWC transmitter, which is located at the North West Cape, Australia (21.82°S, 114.17°E) and operates at 19.8 kHz with an emitting power of 1 MegaWatt. The amplitude and phase are obtained by considering that transmitter signals are modulated using the Minimum Shifting Key (MSK) method [43,44,45].
The receiving site in Suizhou (31.57°N, 113.32°E) is particularly noteworthy in that its longitude is almost identical with the NWC transmitter. This location was purposely chosen in order to monitor in real time the disturbance induced by space weather events in the lower ionosphere. Transmitter signals have been widely used to probe the D-region electron density, but this inversion problem is poorly constrained in nature, the accuracy of which is largely limited by the cleanliness of VLF measurements and the assumptions used in the ionospheric inversion. A receiving site with the same longitude as the transmitter, such as the Suizhou site, can somewhat minimize the influence from the terminator effects during equinox periods. Therefore, the NWC–Suizhou path is ideally suitable for studies of subionospheric remote sensing and space weather events. In the following, we compare two solar eclipse events measured by the WHU VLF wave detection system in Suizhou.
The first eclipse occurred on 26 December 2019, started approximately at 02:30 UT from Saudi Arabia, and ended approximately at 08:06 UT in the Pacific Ocean, with a total duration of nearly 6 h. Figure 1 shows the totality path (solid line) and the northern and southern limits (such as the eclipse occurred on 20 April 2023, we could get dashed lines and date available at: https://eclipse.gsfc.nasa.gov/SEpath/SEpath2001/SE2023Apr20Hpath.html, accessed on 20 April 2023). The northern and southern limits represent the upper and lower boundaries of the annular eclipse belt (~200 km wide). The vertical line shows the NWC–Suizhou path and is color-coded using the solar obscuration rate, with red denoting 100% obscuration and blue denoting 0% obscuration. The obscuration data were calculated using the method described in [46]. The totality path crossed the VLF propagation path almost at the midpoint (1.5°N, 113.8°E) at 06:00 UT with an intersection angle of nearly 90°. This intersection is marked as point ‘A’ in Figure 1a. Figure 1b shows the solar obscuration factor along the NWC–Suizhou path as the eclipse moved from the Indian Ocean to the Pacific Ocean between 12:40 and 15:40 LT (Local time at the Suizhou station, Beijing time, UTC+8). The colored line in Figure 1a is a vertical slice of the obscuration factors shown in Figure 1b, corresponding to the occurrence time of eclipse maximum.
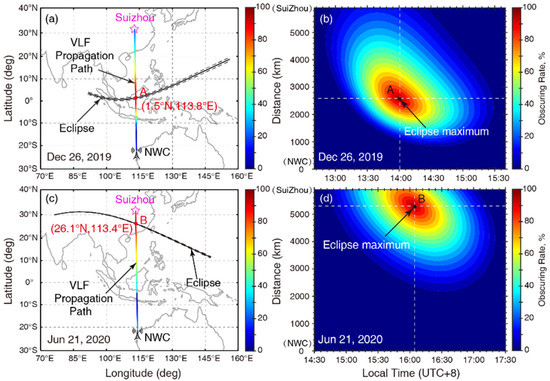
Figure 1.
(a) Totality path (solid) and northern and southern limits (dashed) of the solar eclipse occurred on 26 December 2019. The vertical line shows the VLF propagation path between NWC and our receiver in Suizhou and is color-coded using the obscuration rate during eclipse maximum. (b) Solar obscuration factor along the VLF propagation path between 12:40 and 15:40 LT (Local time at the Suizhou station, UTC+8). Panels (c,d) show similar results but for the eclipse occurred on 21 June 2020 between 14:30 and 17:30 LT (UTC+8).
The second eclipse occurred on 21 June 2020 and propagated from Africa to the Pacific Ocean between 04:50 and 08:30 UT, with a total duration of ~4 h. The corresponding totality path and solar obscuration rates are shown in Figure 1c,d, respectively. Different from the first eclipse, this eclipse crossed the NWC–Suizhou path at a location close to the receiver end, approximately 700 km away from Suizhou, and the intersection angle is approximately 70°. The latitude and longitude of the intersection are 26.1°N and 113.4°E, as marked using point ‘B’ in Figure 1c,d. A direct comparison between Figure 1b,d show that solar input was blocked at point A and B during the 2019 and 2020 eclipses, respectively, and similar levels of electron density change were placed at different locations along the VLF propagation path.
The NWC signals that were recorded in Suizhou during the 2019 and 2020 eclipses are shown in Figure 2. Figure 2a,b show the amplitude and phase change in the NWC signal between 12:40 and 15:40 LT (UTC+8) during the solar eclipse that occurred on 26 December 2019. These data are calculated using measurements from both North–South and East–West antennas and correspond to the total horizontal magnetic field. To better illustrate the eclipse effects, we also plotted the amplitude and phase measurements in the same time window a day before (red line) and after (green line) this eclipse. The average value of amplitude and phase measured during these two quiet days was considered as the baseline and plotted using the black line in Figure 2.
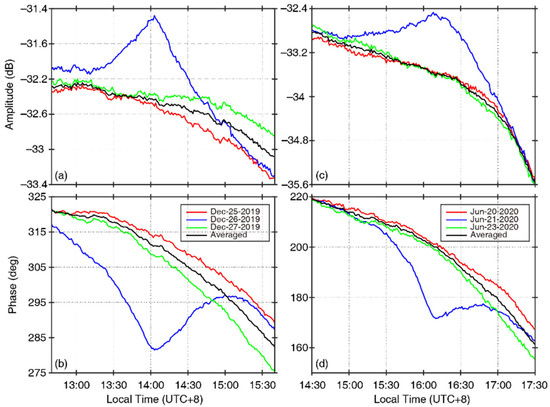
Figure 2.
(a) Amplitude and (b) Phase measurements of VLF signals from the NWC transmitter during the solar eclipse on 26 December 2019, as well as the VLF measurements a day before and after the eclipse. Panels (c,d) show similar results but for the eclipse that occurred on 21 June 2020.
Following previous studies [45,47,48,49], we mainly focus on the net effects caused by solar eclipses, which are obtained by subtracting the baseline values from the eclipse-day measurements. The net amplitude and phase changes during the 2019 eclipse are shown as black lines in Figure 3a,b, respectively. We mainly focus on the net effects between 12:07 and 15:03 LT since the eclipse effects become prominent in this time period. Figure 2c,d and Figure 3c,d show similar results but for the 2020 eclipse event. For this eclipse, we mainly focus on the net effects between 14:28 and 17:28 LT. The amplitude change is approximately 1 dB for both eclipse events, whereas the phase change is ~29.6° for the 2019 eclipse and ~28.5° for the 2020 eclipse. These subtle differences may be related to the difference in the locations at which the totality path crossed the VLF propagation path (see Figure 1). The absolute value of VLF phase has been long found to be not steady [47,48] and phase instability has been observed, even for those transmitters in the United States [45], although they are usually considered to be highly phase stable [49]. Therefore, we investigate the relative change in VLF amplitude and phase in this study.
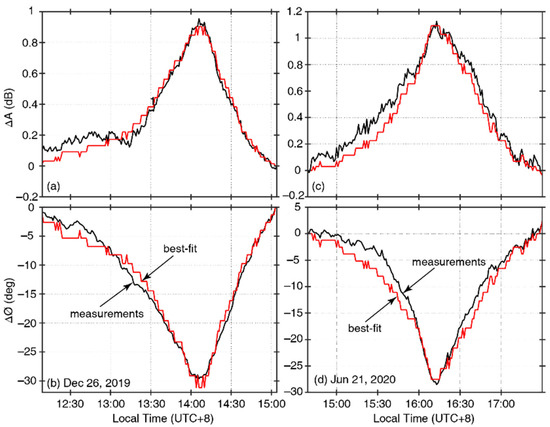
Figure 3.
Comparison of (a) amplitude (∆A) and (b) phase changes (∆ϕ) between modeling results and real measurements during the solar eclipse on 26 December 2019. Panels (c,d) show similar results but for the eclipse that occurred on 21 June 2020.
3. Ionospheric Inversion
To interpret the eclipse measurements, we modeled the propagation of VLF waves from NWC to Suizhou using a Finite-Difference-Time-Domain (FDTD) model and estimated the influence on the D-region ionosphere produced by solar eclipses. Specifically, we first simulated the VLF response to all possible ionospheric conditions as described by the Wait’s (WS) profile [50]. The ionospheric conditions during these two eclipses were then derived by finding out the set of h′ and β values that best explained the eclipse measurements using a well-constrained inversion method, which has been widely utilized in previous subionospheric studies [18,51,52]. Finally, we estimated the variation in D-region electron density for these two eclipses separately and checked if they were consistent (1) with each other, (2) with the reduction in solar input, and (3) with previous studies.
The FDTD model [53] was first developed for modeling the electromagnetic pulse emitted by lighting discharge and has been recently modified for VLF transmitter simulations [54]. This model explicitly solves the Maxwell’s and Langevin equations and calculates the electromagnetic fields and currents in the simulation domain. This model can simulate waves with frequencies of ~100 Hz–500 kHz and utilize arbitrary ground conductivity, ionospheric density, atmospheric density, and the Earth’s magnetic field as the input. The amplitude and phase along the ground are extracted at discrete frequencies by calculating the discrete Fourier transforms. This FDTD model has been utilized in various space physics studies, including lightning discharge [55], lightning-produced electron precipitation [56], and solar eclipses [18]. It has been validated through direct comparison with the Long Wavelength Propagation Capability code [57] and a full-wave model [58]; good agreements have been obtained [54,59]. The simulation domain is set to be 8000 km in the radial direction and 110 km in the vertical direction. The grid size is 1 km × 1 km (radial, vertical) for altitudes below 70 km and 1 km × 0.5 km (radial, vertical) for altitudes above 70 km. The time step of FDTD simulations is chosen to be 0.1 µs.
We further investigate the electron density variation during the two eclipses using the WS profile. This profile approximates the electron density at altitudes from 60 to 90 km using two parameters: the effective reflection height h′ with units of (km) and the sharpness parameter β with units of (km−1). Recent studies have compared this profile with the Faraday International Reference Ionosphere (FIRI) model [60,61], a model that is specifically proposed for the lower ionosphere and represents, to date, the most accurate model for the D-region. This model is derived from first-principles chemistry simulations but deliberately calibrated using real rocket measurements. h′ and β are, in general, good proxies of the electron density around the reflection altitudes of VLF waves in the D-region and have been extensively employed in previous studies of VLF remote sensing data. In the WS formula, the electron density ne (m−3) at altitude h (km) can be calculated using the following formula:
In this study, we varied h′ between 60 and 90 km with 0.1 km steps and β between 0.3 and 0.65 km−1 with 0.01 km−1 steps. This β range was chosen since it was typical of FIRI profiles during daytime conditions [51,62]. As a solar eclipse resembles a brief day-night transition, typical h′ values of daytime conditions were assumed for the pre-eclipse and recovery stages. The above-mentioned FDTD model was employed to calculate the expected amplitude and phase at the Suizhou station for all these h′ and β combinations (h′: 60–90 km, β: 0.3–0.65 km−1). For each simulation, h′ was assumed to be the same for the entire VLF propagation path, and the electron density was assumed to be homogeneous. By adopting this assumption, the best-fit h′ and β values reported in this study represented the path-averaged ionospheric conditions. Cummer et al. [22] estimated the uncertainties induced by this assumption and concluded that VLF propagation was “controlled by the path-averaged ionospheric height and sharpness, even in the presence of significant inhomogeneities in” h′ and β.
The inversion method was similar to that described in [18,51,52,53], and the idea was to find out the h′ and β pairs that best explained the VLF measurements from all possible combinations with reasonable constraints. Xu et al. [51] demonstrated the applicability of this method in estimating the D-region electron density using ground-based VLF measurements. Gołkowski et al. [52] utilized this method to quantify the ionospheric perturbations from lightning discharge. Shao et al. [62] utilized a similar method to probe the ionospheric disturbance caused by lightning discharge and found that the D-region electron density decreased in response to lightning discharge.
The ionospheric inversion was explicitly performed in two steps. First, we calculated the VLF amplitude and phase that would be received under different ionospheric conditions, namely, different combinations of h′ and β values. These data were pre-tabulated and used as a lookup table in the next step to represent the ionospheric condition at a specific moment during the evolution of solar eclipses. Second, we searched all possible combinations of h′ and β values in order to find out the sequence of h′ and β values that best explained the measured amplitude and phase.
The parametric search (the second step of ionospheric inversion) was conducted with the following steps. First, we fit the relative amplitude change during solar eclipses (black curves in Figure 2). For a given β value, we used all h′ values that were less than or equal to 75 km as the initial ionospheric conditions, corresponding to the pre-eclipse VLF measurements (the first data point). As for the next data point, we searched forward in the ascending order of h′ until a value was found, the amplitude difference between which and the initial condition was consistent with that of the first two data points in VLF measurements. This step was repeated for all the data points of VLF measurements. We then conducted this procedure of amplitude fitting for all β values between 0.3 and 0.65 km−1 with a step of 0.01 km−1. This ensured a good fit to the amplitude data, whereas the corresponding agreement with the phase data varied with different β values.
The parametric search was performed with three reasonable constraints: (1) β was invariant along the VLF propagation path and with time during solar eclipses; (2) the h′ value at the beginning of solar eclipses was less than or equal to 75 km (≤75 km); (3) h′ was assumed to increase and decrease during the development and recovery stages of solar eclipses, respectively, representing the day–night transition. As will be explained in the following, the first constraint was used since rocket measurements [63] and first principles simulations [18] found that β changed insignificantly during solar eclipses. The second constraint was used considering the occurrence time of solar eclipses.
The first constraint was adopted for two reasons. First, Mechtly et al. [63] reported measurements of electron density during the solar eclipse that occurred on 12 November 1966. The slope of the electron density profile was found to change insignificantly during this eclipse event. Second, previous eclipse studies estimated the h′ and β change caused by solar eclipses without using this constraint. Although there existed a large discrepancy among previous studies, the β change was found to be 0.01–0.03 km−1 in most cases [30,31,33,35,64]. Moreover, Xu et al. [18] modeled the electron density change in the D- and E-region ionosphere using measurements of solar input by the Solar Dynamic Observatory (SDO) satellite and a widely used D-region chemistry model: the Sodankylä Ion and Neutral Chemistry (SIC) model [65]. Although this study was performed for solar eclipse in North America, it had been clearly shown that the steepness of electron densities at altitudes of 60–90 km did not change noticeably, and the electron density profile shifted parallelly towards lower values during solar eclipses. Indeed, the electron density variation at D-region altitudes was roughly proportional to the square root of solar Lyman-α variation and governed by the background NO density profile [65,66]. The NO concentration was not expected to change significantly during solar eclipses, and thus the sharpness parameter would not change significantly. As such, we opted to assume that β was invariant during solar eclipses in the present study, and this assumption helped reduce one degree of freedom in the ionospheric inversion problem. The second constraint was used considering the occurrence time of solar eclipses (daytime).
Figure 3a,b show the best-fit that we found for the 2019 eclipse. The amplitude data were well reproduced since we chose the h′ values that matched these measurements, but the agreements in phase were not as good. With the same h′ change, for example, from 71 to 73 km, different β values could have caused less or more dramatic phase changes, and there only existed single or limited sets of h′ and β values that could explain both the amplitude and phase measurements. This point was better illustrated in the best-fit results that we found for the 2020 eclipse, as shown in Figure 3c,d. The agreements to the VLF measurements during the 2020 event were, in general, worse than the 2019 event, especially during the pre-eclipse stage at the first ~30 min (~15:00–15:30 LT). It was possible to choose a set of h′ values that better fit the amplitude measurements, but the agreements in phase, in turn, became even worse. The results shown in Figure 3c,d were obtained by balancing the agreements in amplitude and phase, and thus represented the best-fit. One sees clearly from Figure 3 that the best-fit h′ and β values that we found for the 2019 and 2020 eclipses could satisfactorily explain the VLF measurements.
The variation in electron density derived from ionospheric inversion is shown in Figure 4. Figure 4a shows the variation in electron density at 60–90 km as derived from the set of best-fit h′ and β values for the 2019 eclipse. The white line shows the best-fit h′ values and the best-fit β value is 0.56 km−1. The electron density changed significantly during the 2019 eclipse, with a reduction of 63.7% at 73 km altitude and an increase in reflection height from 71.5 to 73.3 km (∆h′ = 1.8 km). Figure 4b shows the electron density variation at 73 km altitude, as well as the temporal evolution of solar input during the 2019 solar eclipse. The overall trend in solar input variation, as calculated using the average value of obscuration rates along the VLF propagation path, is similar to our inversion results. The time difference between 100% obscuration of solar input (~14:01 LT) and VLF response (~14:06 LT) is approximately 5 min, which is consistent with previous studies [31,67].
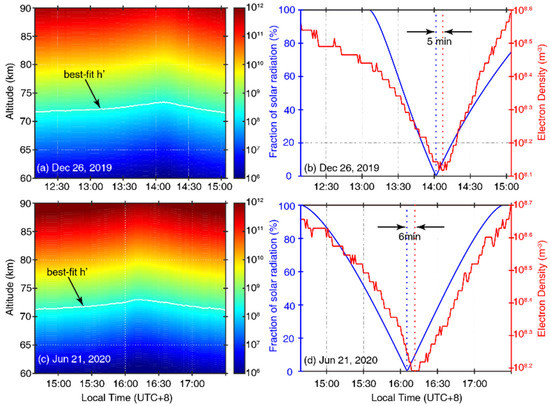
Figure 4.
(a) Temporal evolution of electron density at altitudes of 60–90 km between 12:07 and 15:03 LT (UTC+8) for the solar eclipse that occurred on 26 December 2019. (b) The change in electron density at 73 km altitude, as well as the solar input, for the 2019 eclipse. Panels (c,d) show similar results but for the solar eclipse occurred on 21 June 2020.
Figure 4c,d show similar results but for the 2020 eclipse. The best-fit β value is 0.62 km−1, and the h′ value changed from 71.1 to 72.8 km during this eclipse. As shown in Figure 4d, the electron density change at 73 km altitude follows more closely with the variation in solar input during this eclipse. The time difference is approximately 6 min between 100% obscuration of solar input (~16:05 LT) and VLF response (~16:11 LT). As the temporal resolution of VLF data used in the present analysis is 1 min, we consider this time difference as being consistent with the 2019 event.
4. Validation of the Inversion Results
To examine if the best-fit h′ and β values were reasonable, we compared the inversion results with the FIRI model [60], previous studies [30,31,33,35,64,67,68], as well as theoretical calculations [69]. Figure 5a shows the comparison of electron density profiles between the FIRI profiles and the pre-eclipse profiles that we found for the 2019 and 2020 solar eclipses, whereas Figure 5b shows the profiles that were close to the best-fit profiles derived from VLF measurements. FIRI represented, to date, the most accurate model for the D-region electron density. As clearly shown in Figure 5b, in the altitude range that was critical for VLF reflection during daytime conditions (65–75 km), the pre-eclipse ionospheric profiles that we found for the 2019 and 2020 eclipse events were consistent with the FIRI model, especially the curve marked in cyan.
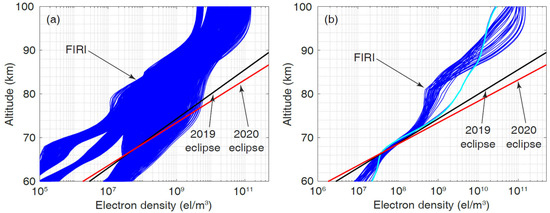
Figure 5.
(a) Comparison of electron density profiles between the FIRI model and the pre-eclipse profiles derived from VLF measurements for the 2019 and 2020 solar eclipses. (b) The FIRI profiles that are close to the pre-eclipse ionospheric conditions that we found for the 2019 and 2020 solar eclipses. The cyan line is closest to the pre-eclipse ionospheric conditions. The best-fit h′ and β value is 71.5 km and 0.56 km−1 for the pre-eclipse ionospheric condition of the 2019 eclipse, respectively. The best-fit h′ and β values are 71.1 km and 0.62 km−1 for the pre-eclipse ionospheric conditions of the 2020 eclipse, respectively.
McCormick et al. [61] performed a statistical study on typical daytime β values. β was found to be mostly in the range between 0.35 and 0.65 km−1, with the occurrence being almost equal between 0.4 and 0.6 km−1. Therefore, the best-fit β values of 0.56 and 0.62 that we found for the 2019 and 2020 eclipses were not unreasonable.
Table 1 shows the comparison of our findings with previous studies, specifically the h′ and β values for the D-region ionosphere during eclipse maximum and the change in h′ (∆h′) and β (∆β) reported in previous VLF-eclipse studies [30,31,33,35,64,67,68]. There existed a large discrepancy in terms of h′ and β estimates among previous studies. ∆h′ was found to be mostly in the range of 1–3 km, with the largest value being 8 km, whereas ∆β was mostly in the range of 0.01–0.03 km−1, with the largest value being 0.07 km−1. The h′ and ∆h′ values that we found for the 2019 and 2020 eclipses were close to those of [31,35,68].

Table 1.
h′ and β values for the D-region ionosphere during eclipse maximum and the change in h′ (∆h′) and β (∆β) reported in previous VLF-eclipse studies.
For the sake of completeness, we further compared the best-fit results with an analytical formula that described the relation between the change in VLF phase (∆ϕ) and reflection height (∆h′) [69]:
where λ is the wavelength of NWC signals (~15.1 km), d is the length of the VLF propagation path from NWC to Suizhou (~5940 km), and a is the Earth radius (~6370 km). The phase change measured during the 2019 eclipse was 29.6°, and, according to Equation (2), this corresponded to a change of 1.78 km in the reflection height. As for the 2020 eclipse, the phase change was 28.5°, and ∆h′ was found to be 1.72 km. In contrast, our inversion results suggested changes in reflection height of 1.8 and 1.7 km for the 2019 and 2020 eclipse, respectively. Both were in excellent agreement with the theoretical calculations.
5. Conclusions and Discussion
In this study, we reported measurements of VLF signals from the NWC transmitter measured during the 2019 and 2020 solar eclipse events in Suizhou, China. The totality path crossed different locations along the VLF propagation path, and these two eclipses provided a unique opportunity to investigate the effects of solar eclipses on the D-region ionosphere. Therefore, we conducted a comparative study using the VLF data collected during these two events. Using a FDTD model and a well-constrained inversion method, we further quantified the influence of these two solar eclipses on the D-region ionosphere.
The two eclipses reported in this study constituted a naturally occurring controlled experiment: the totality path crossed the VLF propagation path almost perpendicularly at the midpoint during the 2019 solar eclipse, whereas the 2020 eclipse crossed this path at a location close to the receiver end. During these two eclipses, the solar input was blocked by the Moon, leading to similar levels of electron density variation but at different locations along the NWC–Suizhou path. A direct comparison between these two events could help better understand the VLF technique, especially related to the question about if and how to remotely sense the location of electron density disturbance using VLF measurements. An amplitude change of ~1 dB was measured during both events, whereas the phase changes were 29.6° and 28.5° for the 2019 and 2020 eclipse, respectively. We only investigated the 2019 and 2020 solar eclipses in this study mainly because of the rarity of these two events. Since deployment, our receiver in Suizhou has only recorded these two eclipse events, and they constituted a naturally occurring controlled experiment. With more eclipse events recorded in the future, we plan to conduct a statistical study to better quantify the effects of solar eclipse on VLF propagation.
Our VLF measurements could be best explained if the path-averaged β values were 0.56 and 0.62 km−1 for the 2019 and 2020 eclipse, respectively. These β values were larger than those reported in previous studies [30,31,33,35,64,67,68], which typically found β in the range of 0.3–0.5 km−1. However, we examined these results using the FIRI model, and the best-fit β values turned out to be consistent with FIRI profiles and the statistical study reported in [61]. On the other hand, the VLF reflection height was found to increase from 71.5 to 73.3 km for the 2019 eclipse (∆h′ = 1.8 km) and from 71.1 to 72.8 km for the 2020 eclipse (∆h′ = 1.7 km). The reflection heights at the eclipse maximums were 73.3 and 72.8 km for the 2019 and 2020 event, respectively. These two values seemed slightly lower than those of typical nighttime conditions, but were, in fact, not unreasonable since they represented the path-averaged h′ values. The h′ and ∆h′ values obtained using the present inversion method were close to those reported in [31,35,68].
According to the relation between the phase change and reflection height [69], a phase change of 29.6° measured during the 2019 eclipse corresponded to an increase in h′ by 1.78 km. As for the 2020 eclipse, ∆h′ was ~1.72 km. Both showed excellent agreements with our ionospheric inversion results. Different from previous eclipse studies, in this work, we matched the amplitude measurements and used the phase measurements to evaluate the goodness of fit with three constraints. These constraints were motivated by first-principle chemistry simulations and previous eclipse studies. The agreement obtained with theoretical calculations was a good validation of our ionosphere-inversion method, as well as the constraints.
h′ was directly related to the electron density at the reflection altitudes of VLF waves and had a larger control over the amplitude change. As the net amplitude change measured during the two eclipses was similar, ∆h′ was found to be similar for these two events. With two parameters describing the entire D-region ionosphere, β in the WS profile was not a well-defined parameter and represented the steepness of electron density at or close to h′. With the same h′ change, a larger β value could lead to less or more dramatic phase changes, and thus the best-fit β value was found to be different for the two eclipses. As shown in Figure 5, the best-fit β values were not a typical of daytime ionospheric conditions, although they were slightly larger than what had been often used in sub-ionospheric remote sensing.
A direct comparison between the 2019 and 2020 eclipses suggested that VLF signals were not sensitive to where the electron density change occurs along the propagation path but reflected the average path condition. Present results, to some extent, supported the usage of h′ and β for describing the average condition of the D-region ionosphere along the VLF propagation path. A main problem in VLF remote sensing is that it is still unclear if and how this technique can be used to identify the location of electron density disturbance along the transmitter–receiver path, for example, as caused by energetic electron precipitation from the radiation belts. Our study demonstrated that the VLF measurements recorded at a single site reflected the path-averaged condition of D-region ionosphere. Numerous studies have been devoted to identifying the location and spatial extent of electron density variation [5,70] since such knowledge is of particular importance for the estimation of atmospheric chemical changes produced by precipitation of energetic particles from the radiation belts. In light of our results, a single VLF receiver can be used to monitor the path-averaged electron density disturbance in the D-region. However, a network of VLF receivers is required in order to monitor in real time the spatial extent of the space weather events that disturb the lower ionosphere.
Author Contributions
Data curation, W.X., X.G. and B.N.; methodology, W.X., X.G., S.W. and W.C.; validation, X.G., S.W., X.M. and Z.L.; investigation, W.C. and W.X.; writing—original draft preparation, W.C. and W.X.; writing—review and editing, W.C., W.X., X.G., B.X., Q.W. and B.N.; project administration, W.X., X.G. and B.N.; funding acquisition, W.X., X.G. and B.N. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by the National Key R&D Program of China (Grant No. 2022YFF0503700), the National Natural Science Foundation of China (Grant Nos. 42188101, 42025404, 41974186, 42174188, 41904144, 41904143, 42174190, 41874195, 42274205, and 42274199), the B-type Strategic Priority Program of the Chinese Academy of Sciences (Grant No. XDB41000000), and the Pre-research projects on Civil Aerospace Technologies (Grant Nos. D020308, D020104, and D020303). This project was supported by the open fund of Hubei Luojia Laboratory (Grant No. 220100051).
Data Availability Statement
The simulation data and analysis codes used to generate all figures and results in this paper are available at https://doi.org/10.5281/zenodo.6948560. More VLF data recorded at the Suizhou station can be obtained after a request is made to Xudong gu (guxudong@whu.edu.cn).
Acknowledgments
We are grateful to the editor and anonymous reviewers for their assistance in evaluating this paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Brasseur, G.P.; Solomon, S. Aeronomy of the Middle Atmosphere: Chemistry and Physics of the Stratosphere and Mesosphere, 3rd ed.; Springer: Dordrecht, The Netherlands, 2006; pp. 443–531. [Google Scholar]
- Budden, K.G. Radio Waves in the Ionosphere; Cambridge University Press: Cambridge, UK, 2009; pp. 474–781. [Google Scholar]
- Codrescu, M.V.; Fuller-Rowell, T.J.; Roble, R.G.; Evans, D.S. Medium Energy Particle Precipitation Influences on the Mesosphere and Lower Thermosphere. J. Geophys. Res. Space Phys. 1997, 102, 19977–19987. [Google Scholar] [CrossRef]
- Inan, U.S.; Cummer, S.A.; Marshall, R.A. A Survey of ELF and VLF Research on Lightning-Ionosphere Interactions and Causative Discharges. J. Geophys. Res. Space Phys. 2010, 115, A00E36. [Google Scholar] [CrossRef]
- Clilverd, M.A.; Nunn, D.; Lev-Tov, S.J.; Inan, U.S.; Dowden, R.L.; Rodger, C.J.; Smith, A.J. Determining the Size of Lightning-Induced Electron Precipitation Patches. J. Geophys. Res. Space Phys. 2002, 107, SIA 10-1–SIA 10-11. [Google Scholar] [CrossRef]
- Xu, W.; Marshall, R.A.; TyssØy, H.N.; Fang, X. A Generalized Method for Calculating Atmospheric Ionization by Energetic Electron Precipitation. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028482. [Google Scholar] [CrossRef]
- Fishman, G.J.; Inan, U.S. Observation of an Ionospheric Disturbance Caused by a Gamma-Ray Burst. Nature 1988, 331, 418–420. [Google Scholar] [CrossRef]
- Thomson, N.R.; Clilverd, M.A. Solar Flare Induced Ionospheric D-Region Enhancements from VLF Amplitude Observations. J. Atmos. Sol.-Terr. Phys. 2001, 63, 1729–1737. [Google Scholar] [CrossRef]
- Inan, U.S.; Bell, T.F.; Rodriguez, J.V. Heating and Ionization of the Lower Ionosphere by Lightning. Geophys. Res. Lett. 1991, 18, 705–708. [Google Scholar] [CrossRef]
- Rodger, C.J.; Cho, M.; Clilverd, M.A.; Rycroft, M.J. Lower Ionospheric Modification by Lightning-EMP: Simulation of the Night Ionosphere over the United States. Geophys. Res. Lett. 2001, 28, 199–202. [Google Scholar] [CrossRef]
- Hosseini, P.; Gołkowski, M.; Hared, V. Remote Sensing of Radiation Belt Energetic Electrons Using Lightning Triggered Upper Band Chorus. Geophys. Res. Lett. 2019, 46, 37–47. [Google Scholar] [CrossRef]
- Xu, W.; Marshall, R.A.; Kero, A.; Sousa, A. Chemical Response of the Upper Atmosphere Due to Lightning-Induced Electron Precipitation. J. Geophys. Res. Atmos. 2021, 126, e2021JD034914. [Google Scholar] [CrossRef]
- Fritts, D.; Alexander, M. Gravity Wave Dynamics and Effects in the Middle Atmosphere. Rev. Geophys. 2003, 41, 1003. [Google Scholar] [CrossRef]
- Bortnick, J.; Inan, U.S.; Bell, T.F. Temporal Signatures of Radiation Belt Electron Precipitation Induced by Lightning-Generated MR Whistler Waves: 2. Global Signatures. J. Geophys. Res. Space Phys. 2006, 111, A02204. [Google Scholar] [CrossRef]
- Xu, W.; Marshall, R.A.; Fang, X.; Turunen, E.; Kero, A. On the Effects of Bremsstrahlung Radiation During Energetic Electron Precipitation. Geophys. Res. Lett. 2018, 45, 1167–1176. [Google Scholar] [CrossRef]
- Ni, B.; Hua, M.; Gu, X.; Fu, S.; Xiang, Z.; Cao, X.; Ma, X. Artificial Modification of Earth’s Radiation Belts by Ground-Based Very-Low-Frequency (VLF) Transmitters. Sci. China Earth Sci. 2022, 65, 391–413. [Google Scholar] [CrossRef]
- Hua, M.; Li, W.; Ni, B.; Ma, Q.; Green, A.; Shen, X.; Claudepierre, S.G.; Bortnik, J.; Gu, X.; Fu, S.; et al. Very-Low-Frequency Transmitters Bifurcate Energetic Electron Belt in near-Earth Space. Nat. Common. 2020, 11, 4847. [Google Scholar] [CrossRef]
- Xu, W.; Marshall, R.A.; Kero, A.; Turunen, E.; Drob, D.; Sojka, J.; Rice, D. VLF Measurements and Modeling of the D-Region Response to the 2017 Total Solar Eclipse. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7613–7622. [Google Scholar] [CrossRef]
- Han, F.; Cummer, S.A. Midlatitude Daytime D Region Ionosphere Variations Measured from Radio Atmospherics. J. Geophys. Res. Space Phys. 2010, 115, A10314. [Google Scholar] [CrossRef]
- Barr, R.; Jones, D.L.; Rodger, C.J. ELF and VLF Radio Waves. J. Atmos. Sol.-Terr. Phys. 2000, 62, 1689–1718. [Google Scholar] [CrossRef]
- Hardman, S.F.; Rodger, C.J.; Dowden, R.L.; Brundell, J.B. Measurements of the VLF Scattering Pattern of the Structured Plasma of Red Sprites. IEEE Antennas Propag. Mag. 1998, 40, 29–38. [Google Scholar] [CrossRef]
- Cummer, S.A.; Inan, U.S.; Bell, T.F. Ionospheric D Region Remote Sensing Using VLF Radio Atmospherics. Radio Sci. 1998, 33, 1781–1792. [Google Scholar] [CrossRef]
- Cohen, M.B.; Inan, U.S.; Fishman, G. Terrestrial Gamma Ray Flashes Observed Aboard the Compton Gamma Ray Observatory/Burst and Transient Source Experiment and ELF/VLF Radio Atmospherics. J. Geophys. Res. Atmos. 2006, 111, D24109. [Google Scholar] [CrossRef]
- Cohen, M.B.; Inan, U.S.; Paschal, E.W. Sensitive Broadband ELF/VLF Radio Reception with the AWESOME Instrument. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3–17. [Google Scholar] [CrossRef]
- Belcher, S.R.G.; Clilverd, M.A.; Rodger, C.J.; Cook, S.; Thomson, N.R.; Brundell, J.B.; Raita, T. Solar Flare X-Ray Impacts on Long Sub ionospheric VLF Paths. Space Weather 2021, 19, e2021SW002820. [Google Scholar] [CrossRef]
- Schaal, R.E.; Mendes, A.M.; Ananthakrishnan, S.; Kaufmann, P. VLF Propagation Effects Produced by the Eclipse. Nature 1970, 226, 1127–1129. [Google Scholar] [CrossRef]
- Bracewell, R.N. Theory of Formation of an Ionospheric Layer below E Layer Based on Eclipse and Solar Flare Effects at 16 Kc/Sec. J. Atmos. Terr. Phys. 1952, 2, 226–235. [Google Scholar] [CrossRef]
- Lynn, K.J.W. The Total Solar Eclipse of 23 October 1976 Observed at VLF. J. Atmos. Terr. Phys. 1981, 43, 1309–1316. [Google Scholar] [CrossRef]
- Sears, R.D.; Heaps, M.G.; Niles, F.E. Modeling the Ion Chemistry of the D Region: A Case Study Based upon the 1966 Total Solar Eclipse. J. Geophys. Res. Space Phys. 1981, 86, 10073–10086. [Google Scholar] [CrossRef]
- Clilverd, M.A.; Rodger, C.J.; Thomson, N.R.; Lichtenberger, J.; Steinbach, P.; Cannon, P.; Angling, M.J. Total Solar Eclipse Effects on VLF Signals: Observations and Modeling. Radio Sci. 2001, 36, 773–788. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, A.; Maurya, A.K.; Singh, R. Changes in the D Region Associated with Three Recent Solar Eclipses in the South Pacific Region. J. Geophys. Res. Space Phys. 2016, 121, 5930–5943. [Google Scholar] [CrossRef]
- Singh, R.; Veenadhari, B.; Maurya, A.K.; Cohen, M.B.; Kumar, S.; Selvakumaran, R.; Pant, P.; Singh, A.K.; Inan, U.S. D-Region Ionosphere Response to the Total Solar Eclipse of 22 July 2009 Deduced from ELF-VLF Tweek Observations in the Indian Sector. J. Geophys. Res. Space Phys. 2011, 116, A10301. [Google Scholar] [CrossRef]
- Pal, S.; Chakrabarti, S.K.; Mondal, S.K. Modeling of Sub-Ionospheric VLF Signal Perturbations Associated with Total Solar Eclipse, 2009 in Indian Subcontinent. Adv. Space Res. 2012, 50, 196–204. [Google Scholar] [CrossRef]
- Cohen, M.B.; Gross, N.C.; Higginson-Rollins, M.A.; Marshall, R.A.; Gołkowski, M.; Liles, W.; Rodriguez, D.; Rockway, J. The Lower Ionospheric VLF/LF Response to the 2017 Great American Solar Eclipse Observed Across the Continent. Geophys. Res. Lett. 2018, 45, 3348–3355. [Google Scholar] [CrossRef]
- Tripathi, G.; Singh, S.B.; Kumar, S.; Singh, A.K.; Singh, R.; Singh, A.K. Effect of 21 June 2020 Solar Eclipse on the Ionosphere Using VLF and GPS Observations and Modeling. Adv. Space Res. 2022, 69, 254–265. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, G.; Ni, B.; Zhao, Z.; Gu, X.; Zhou, C.; Wang, F. Development of Ground-Based ELF/VLF Receiver System in Wuhan and Its First Results. Adv. Space Res. 2016, 57, 1871–1880. [Google Scholar] [CrossRef]
- Chen, Y.; Ni, B.; Gu, X.; Zhao, Z.; Yang, G.; Zhou, C.; Zhang, Y. First Observations of Low Latitude Whistlers Using WHU ELF/VLF Receiver System. Sci. China Technol. Sci. 2017, 60, 166–174. [Google Scholar] [CrossRef]
- Wang, S.W.; Gu, X.D.; Luo, F.; Peng, R.; Chen, H.; Li, G.; Ni, B.; Zhao, Z.Y.; Yuan, D. Observations and analyses of the sunrise effect for NWC VLF transmitter signals. Chin. J. Geophys. 2020, 63, 4300–4311. [Google Scholar] [CrossRef]
- Gu, X.; Li, G.; Pang, H.; Wang, S.; Ni, B.; Luo, F.; Peng, R.; Chen, L. Statistical Analysis of Very Low Frequency Atmospheric Noise Caused by the Global Lightning Using Ground-Based Observations in China. J. Geophys. Res. Space Phys. 2021, 126, e2020JA029101. [Google Scholar] [CrossRef]
- Yi, J.; Gu, X.; Cheng, W.; Tang, X.; Chen, L.; Ni, B.; Zhou, R.; Zhao, Z.; Wang, Q.; Zhou, L. A Detailed Investigation of Low Latitude Tweek Atmospherics Observed by the WHU ELF/VLF Receiver: 2. Occurrence Features and Associated Ionospheric Parameters. Earth Planet. Phys. 2020, 4, 238–245. [Google Scholar] [CrossRef]
- Zhou, R.; Gu, X.; Yang, K.; Li, G.; Ni, B.; Yi, J.; Chen, L.; Zhao, F.; Zhao, Z.; Wang, Q.; et al. A Detailed Investigation of Low Latitude Tweek Atmospherics Observed by the WHU ELF/VLF Receiver: I. Automatic Detection and Analysis Method. Earth Planet. Phys. 2020, 4, 120–130. [Google Scholar] [CrossRef]
- Gu, X.; Wang, Q.; Ni, B.; Xu, W.; Wang, S.; Yi, J.; Hu, Z.; Li, B.; He, F.; Chen, X.; et al. First Results of the Wave Measurements by the WHU VLF Wave Detection System at the Chinese Great Wall Station in Antarctica. J. Geophys. Res. Space Phys. 2022, 127, e2022JA030784. [Google Scholar] [CrossRef]
- Pasupathy, S. Minimum Shift Keying: A Spectrally Efficient Modulation. IEEE Commun. Mag. 1979, 17, 14–22. [Google Scholar] [CrossRef]
- Paschal, E.W. Phase Measurements of Very-Low-Frequency Signals from the Magnetosphere; Stanford University: Stanford, CA, USA, 1988. [Google Scholar]
- Gross, N.C.; Cohen, M.B.; Said, R.K.; Gołkowski, M. Polarization of Narrowband VLF Transmitter Signals as an Ionospheric Diagnostic. J. Geophys. Res. Space Phys. 2018, 123, 901–917. [Google Scholar] [CrossRef]
- Chakrabarti, S.K.; Sasmal, S.; Basak, T.; Chakraborty, S.; Tucker, R.L. Modeling D-Region Ionospheric Response of the Great American TSE of August 21, 2017 from VLF Signal Perturbation. Adv. Space Res. 2018, 62, 651–661. [Google Scholar] [CrossRef]
- Thomson, N.R. Experimental Daytime VLF Ionospheric Parameters. J. Atmos. Terr. Phys. 1993, 55, 173–184. [Google Scholar] [CrossRef]
- Thomson, N.R.; Clilverd, M.A.; McRae, W.M. Nighttime Ionospheric D Region Parameters from VLF Phase and Amplitude. J. Geophys. Res. Space Phys. 2007, 112, A07304. [Google Scholar] [CrossRef]
- McCrae, W.; Thomson, N. VLF Phase and Amplitude: Daytime Ionospheric Parameters. J. Atmos. Sol.-Terr. Phys. 2000, 62, 609–618. [Google Scholar] [CrossRef]
- Wait, J.R. Characteristics of the Earth-Ionosphere Waveguide for VLF Radio Waves; National Bureau of Standards: Gaithersburg, MD, USA, 1964; p. NBS TN 300.
- Xu, W.; Marshall, R.A.; Bortnik, J.; Bunnell, J.W. An Electron Density Model of the D- and E-Region Ionosphere for Trans ionospheric VLF Propagation. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029288. [Google Scholar] [CrossRef]
- Gołkowski, M.; Renick, C.; Cohen, M.B. Quantification of Ionospheric Perturbations from Lightning Using Overlapping Paths of VLF Signal Propagation. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028540. [Google Scholar] [CrossRef]
- Marshall, R.A. An Improved Model of the Lightning Electromagnetic Field Interaction with the D-Region Ionosphere. J. Geophys. Res. Space Phys. 2012, 117, A03316. [Google Scholar] [CrossRef]
- Marshall, R.A.; Wallace, T.; Turbe, M. Finite-Difference Modeling of Very-Low-Frequency Propagation in the Earth-Ionosphere Waveguide. IEEE Trans. Antennas Propag. 2017, 65, 7185–7197. [Google Scholar] [CrossRef]
- Marshall, R.A.; Snively, J.B. Very Low Frequency Sub Ionospheric Remote Sensing of Thunderstorm-Driven Acoustic Waves in the Lower Ionosphere. J. Geophys. Res. Atmos. 2014, 119, 5037–5045. [Google Scholar] [CrossRef]
- Marshall, R.A.; Xu, W.; Sousa, A.; McCarthy, M.; Millan, R. X-Ray Signatures of Lightning-Induced Electron Precipitation. J. Geophys. Res. Space Phys. 2019, 124, 10230–10245. [Google Scholar] [CrossRef]
- Ferguson, J.A. Computer Programs for Assessment of Long-Wavelength Radio Communications, Version 2.0: User’s Guide and Source Files; Space and Naval Warfare Systems Center: San Diego, CA, USA, 1998. [Google Scholar]
- Lehtinen, N.G.; Inan, U.S. Full-Wave Modeling of Trans ionospheric Propagation of VLF Waves. Geophys. Res. Lett. 2009, 36, L03104. [Google Scholar] [CrossRef]
- Gasdia, F.; Marshall, R.A. A New Longwave Mode Propagator for the Earth–Ionosphere Waveguide. IEEE Trans. Antennas Propag. 2021, 69, 8675–8688. [Google Scholar] [CrossRef]
- Friedrich, M.; Torkar, K.M. FIRI: A Semiempirical Model of the Lower Ionosphere. J. Geophys. Res. Space Phys. 2001, 106, 21409–21418. [Google Scholar] [CrossRef]
- McCormick, J.C.; Cohen, M.B. A New Four-Parameter D-Region Ionospheric Model: Inferences from Lightning-Emitted VLF Signals. J. Geophys. Res. Space Phys. 2021, 126, e2021JA029849. [Google Scholar] [CrossRef]
- Shao, X.M.; Lay, E.H.; Jacobson, A.R. Reduction of Electron Density in the Night-Time Lower Ionosphere in Response to a Thunderstorm. Nat. Geosocial. 2013, 6, 29–33. [Google Scholar] [CrossRef]
- Mechtly, E.A.; Seino, K.; Smith, L.G. Lower Ionosphere Electron Densities Measured During the Solar Eclipse of November 12, 1966. Radio Sci. 1969, 4, 371–375. [Google Scholar] [CrossRef]
- Guha, A.; De, B.K.; Roy, R.; Choudhury, A. Response of the Equatorial Lower Ionosphere to the Total Solar Eclipse of 22 July 2009 during Sunrise Transition Period Studied Using VLF Signal. J. Geophys. Res. Space Phys. 2010, 115, A11302. [Google Scholar] [CrossRef]
- Turunen, E.; Matveinen, H.; Tolvanen, J.; Ranta, H. D-region ion chemistry model. In STEP Handbook of Ionospheric Models; Schunk, R.W., Ed.; SCOSTEP Secretariat: Boulder, CO, USA, 1996; pp. 1–25. [Google Scholar]
- Verronen, P.T.; Andersson, M.E.; Marsh, D.R.; Kovács, T.; Plane, J.M.C. WACCM-D—Whole Atmosphere Community Climate Model with D-Region Ion Chemistry. J. Adv. Model. Earth Syst. 2016, 8, 954–975. [Google Scholar] [CrossRef]
- Phanikumar, D.V.; Kwak, Y.S.; Patra, A.K.; Maurya, A.K.; Singh, R.; Park, S.M. Response of the Mid-Latitude D-Region Ionosphere to the Total Solar Eclipse of 22 July 2009 Studied Using VLF Signals in South Korean Peninsula. Adv. Space Res. 2014, 54, 961–968. [Google Scholar] [CrossRef]
- Venkatesham, K.; Singh, R.; Maurya, A.K.; Dube, A.; Kumar, S.; Phanikumar, D.V. The 22 July 2009 Total Solar Eclipse: Modeling D Region Ionosphere Using Narrowband VLF Observations. J. Geophys. Res. Space Phys. 2019, 124, 616–627. [Google Scholar] [CrossRef]
- Pant, P.; Mahra, H. Effect of solar eclipse on VLF propagation. Indian J. Radio Space Phys. 1994, 23, 399–402. [Google Scholar]
- Clilverd, M.A.; Rodger, C.J.; Nunn, D. Radiation Belt Electron Precipitation Fluxes Associated with Lightning. J. Geophys. Res. Space Phys. 2004, 109, A12208. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).