Baseline Calibration of L-Band Spaceborne Bistatic SAR TwinSAR-L for DEM Generation
Abstract
1. Introduction
2. Materials and Methods
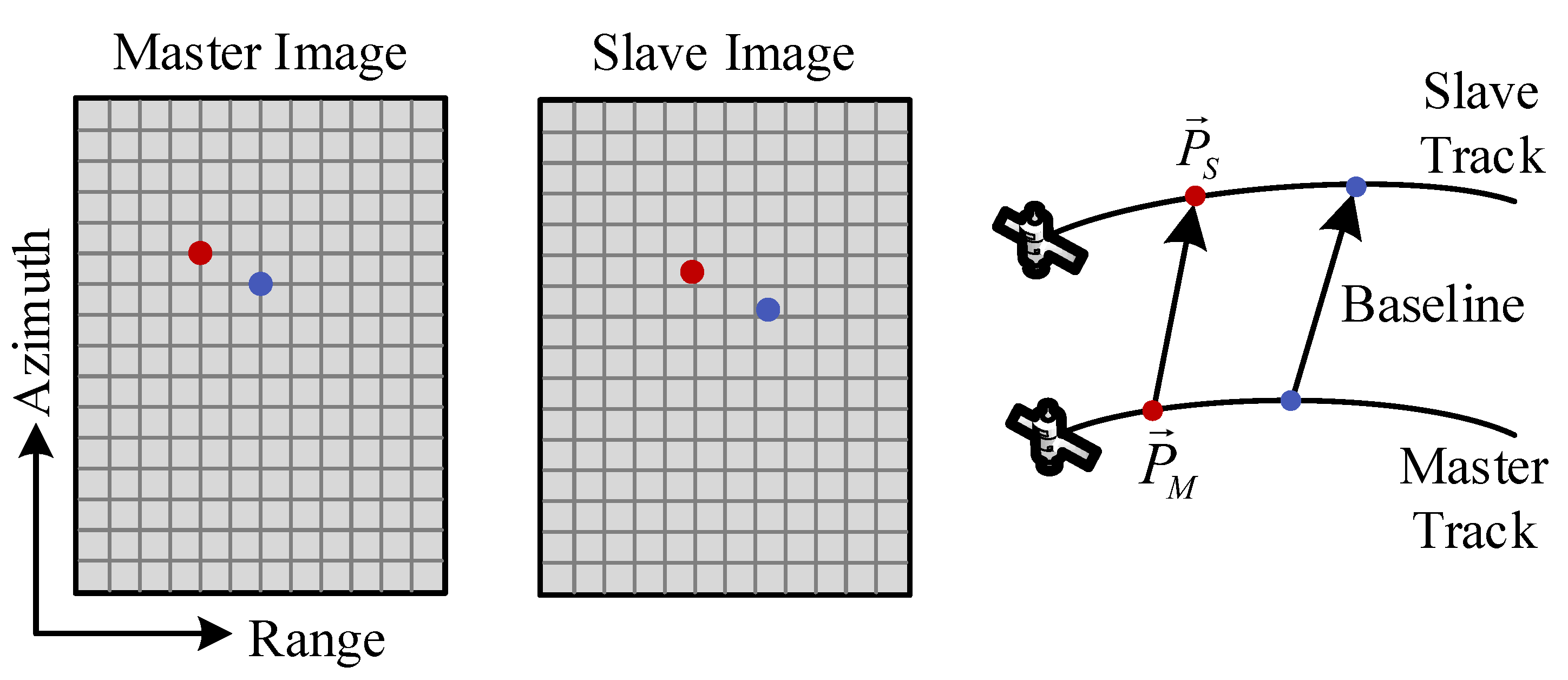
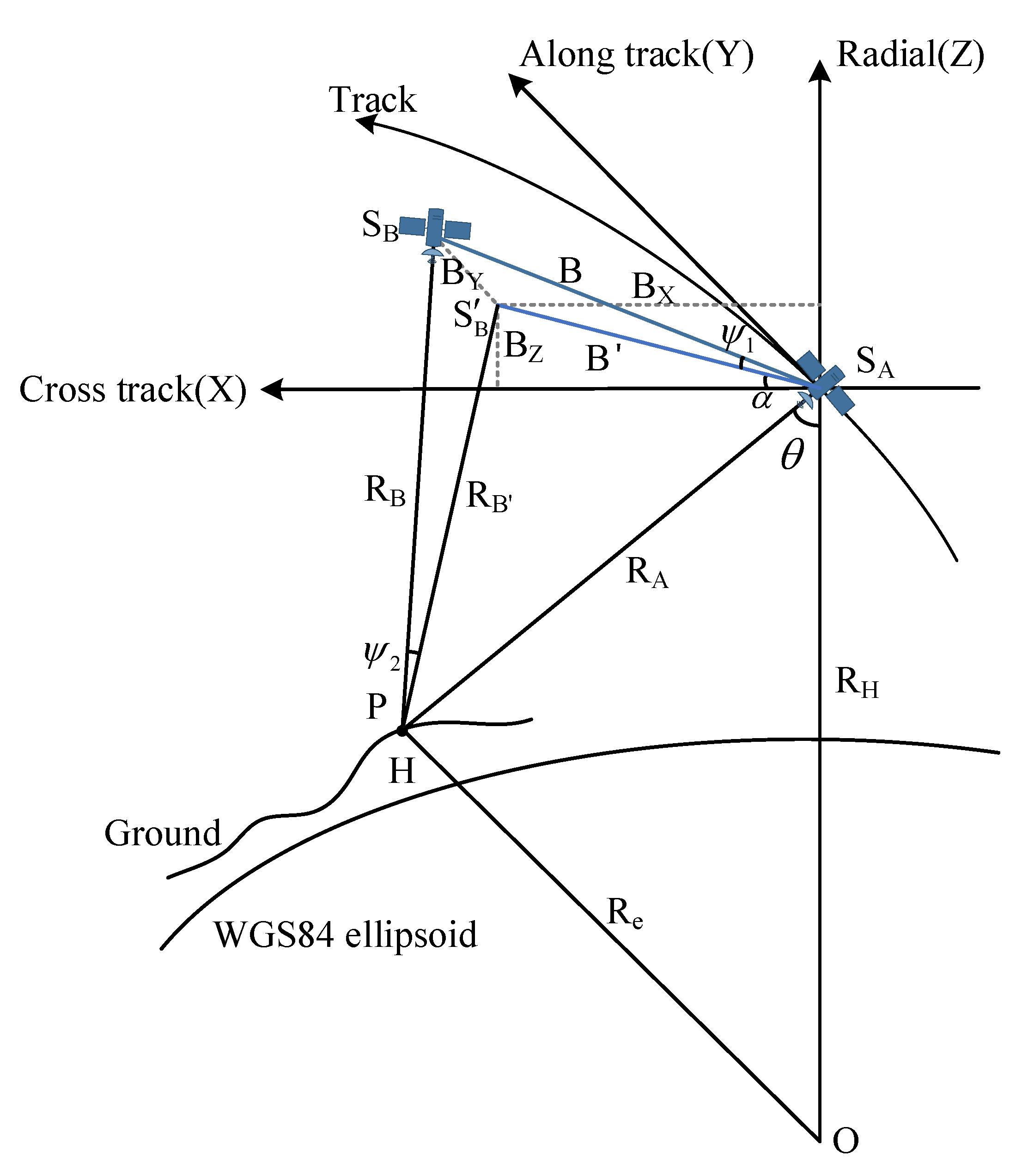
2.1. Baseline Model
2.2. Baseline Calibration Model
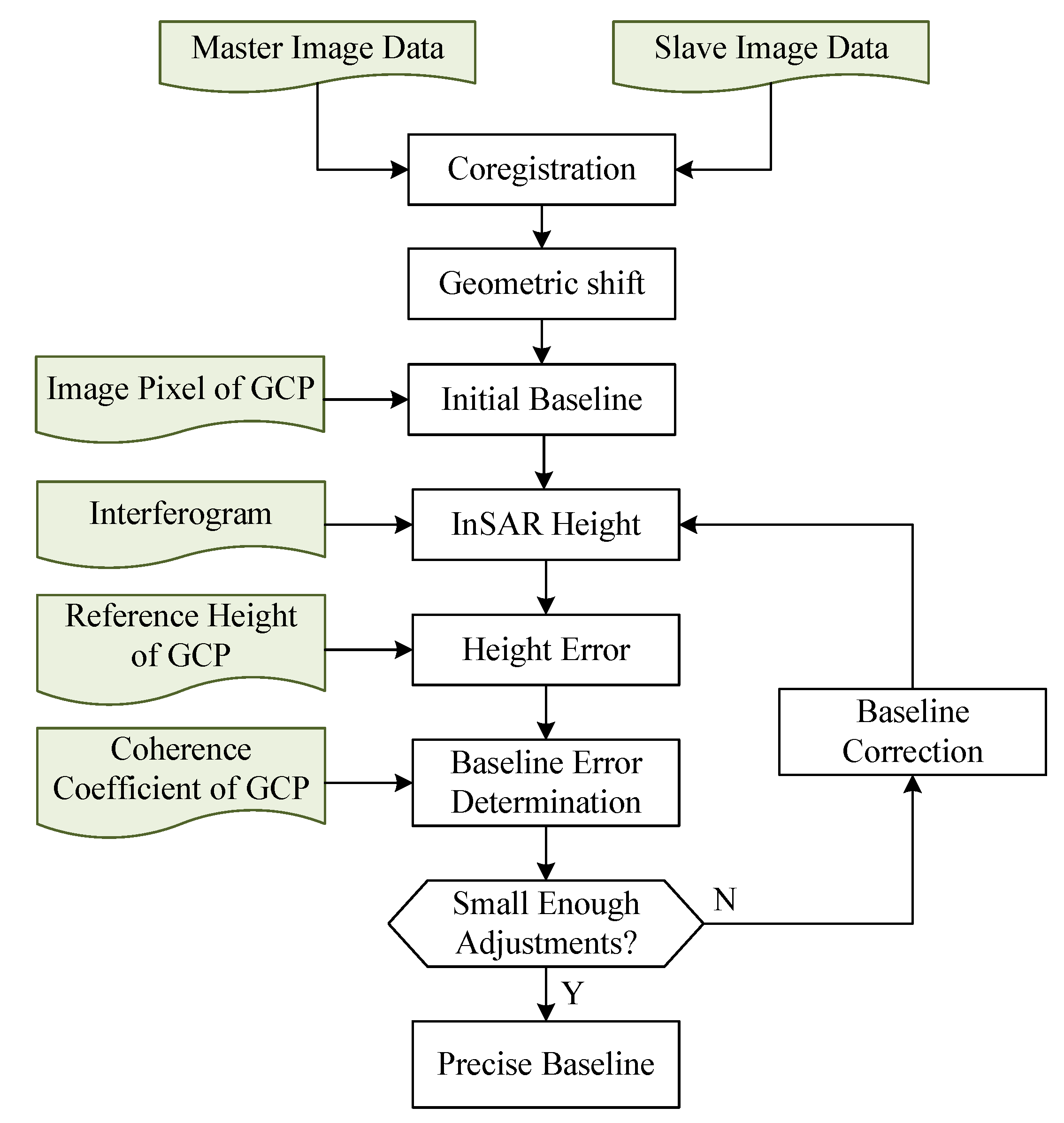
2.3. Baseline Calibration Method
3. Results and Analysis
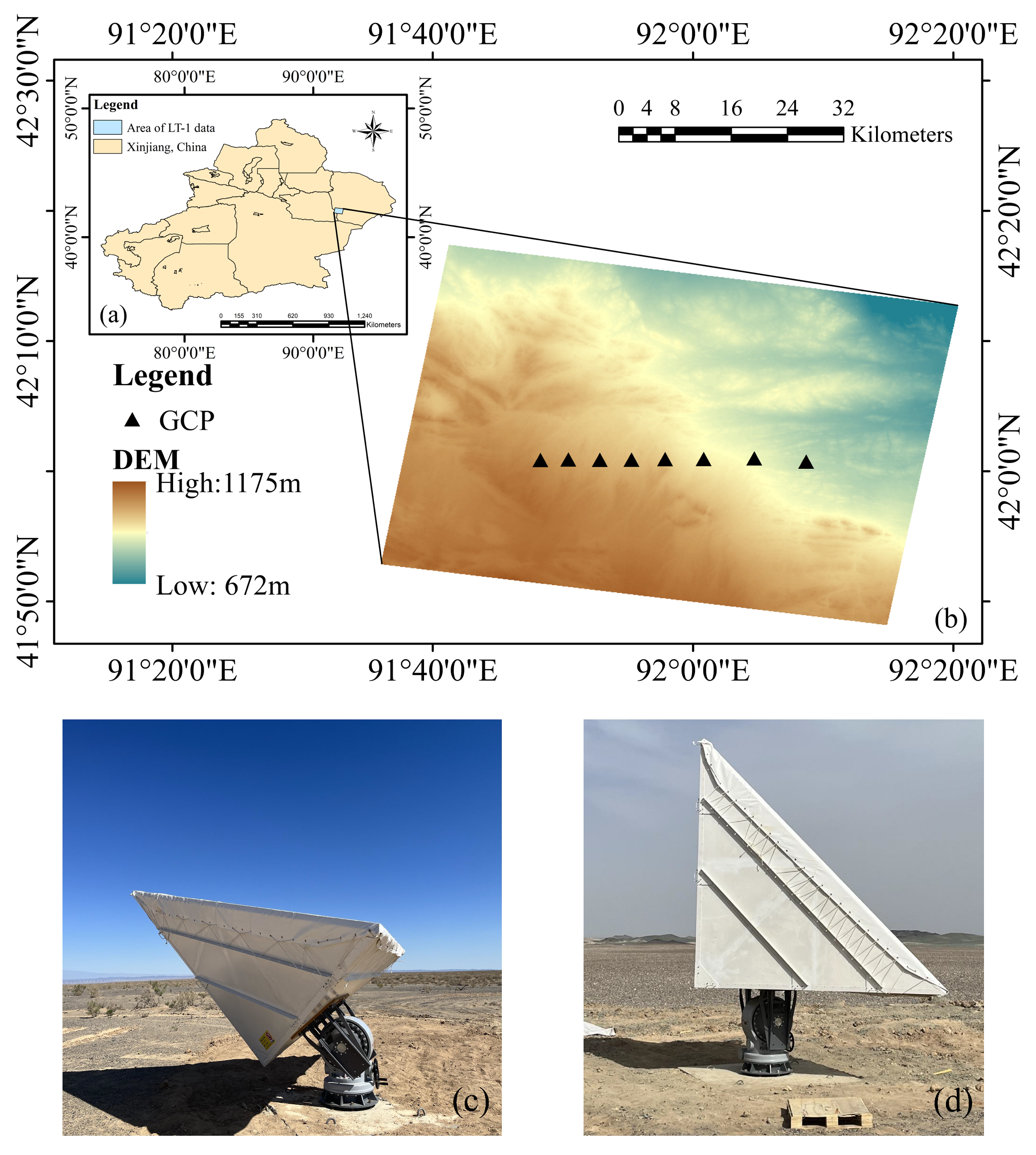
3.1. Study Area and Data
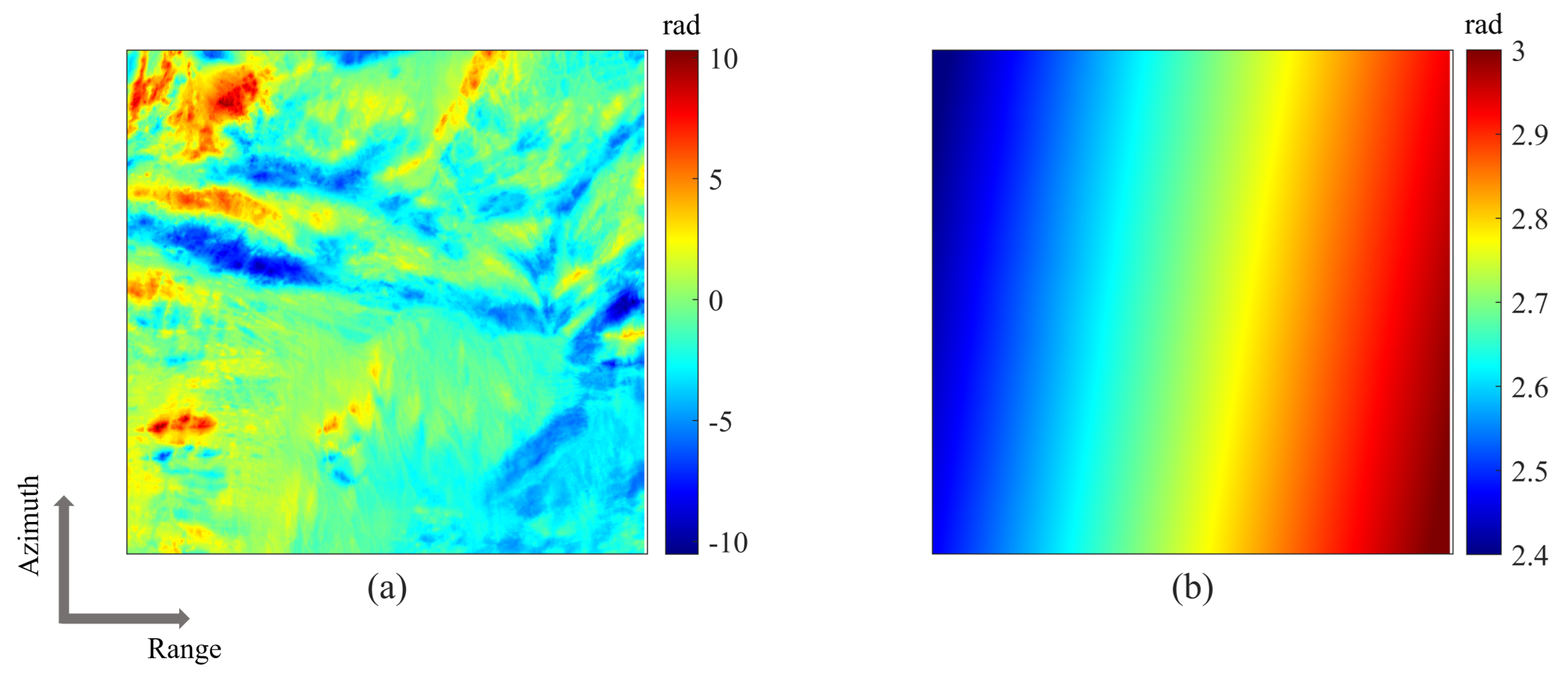
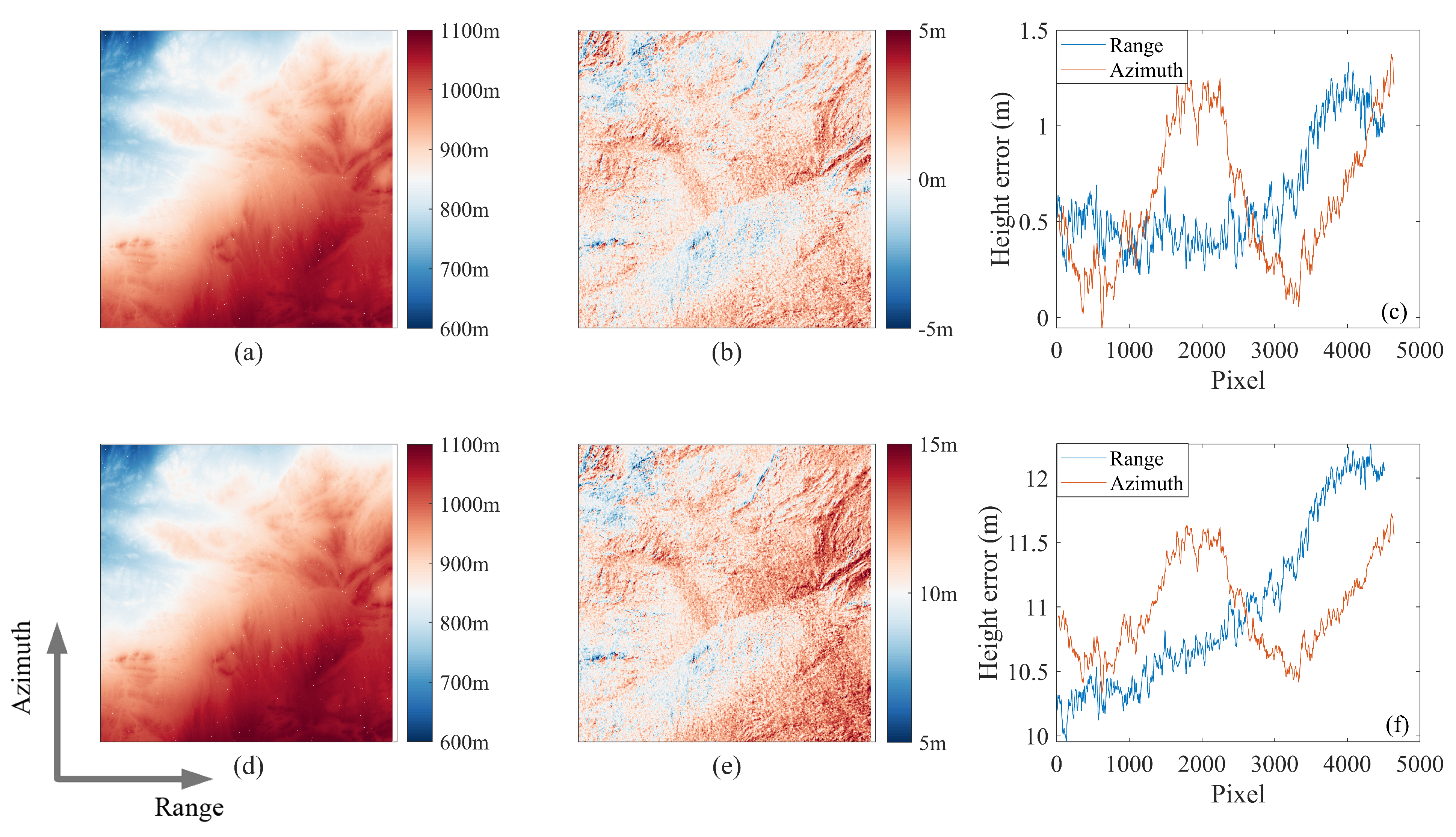
3.2. Baseline Estimation
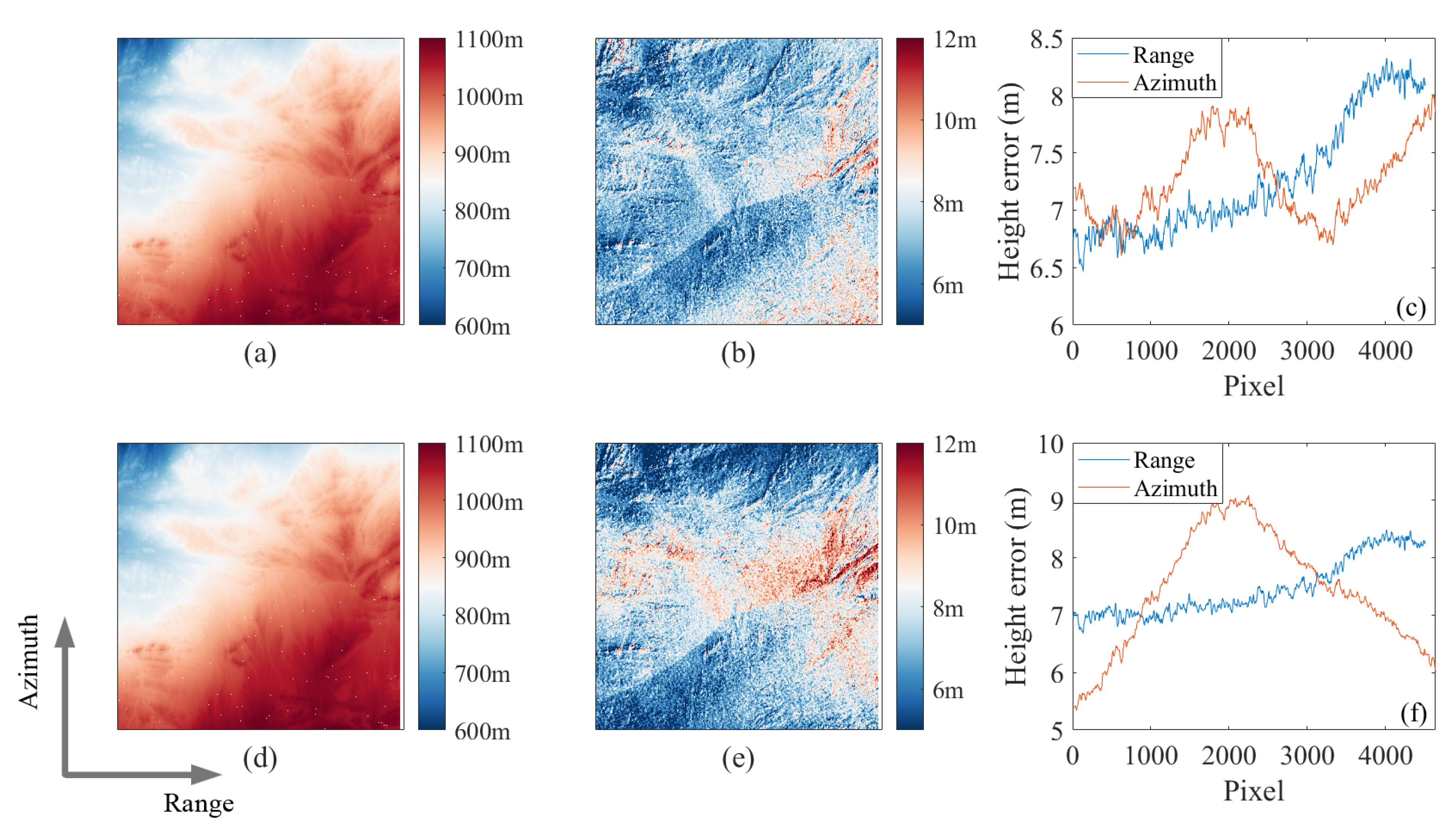
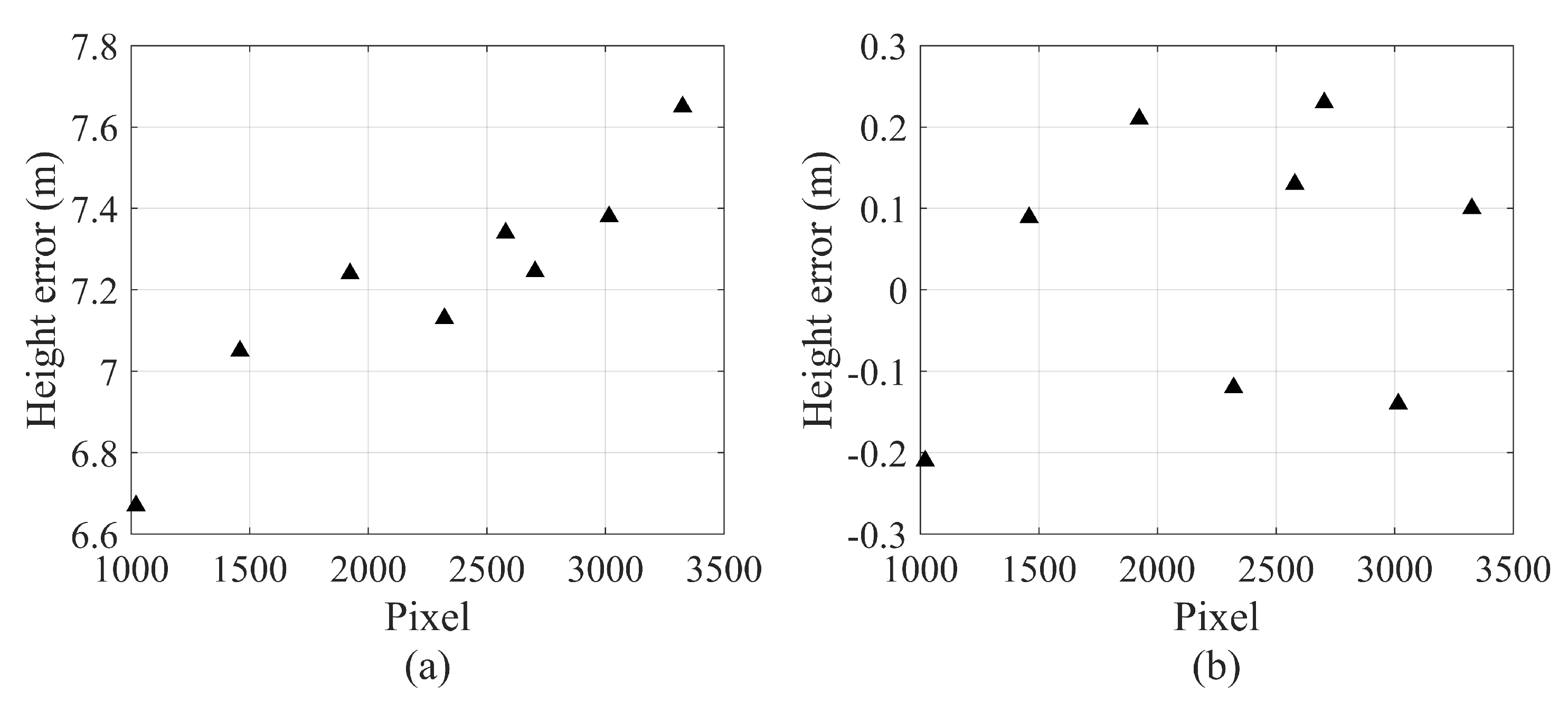
3.3. Baseline Calibration
4. Discussion
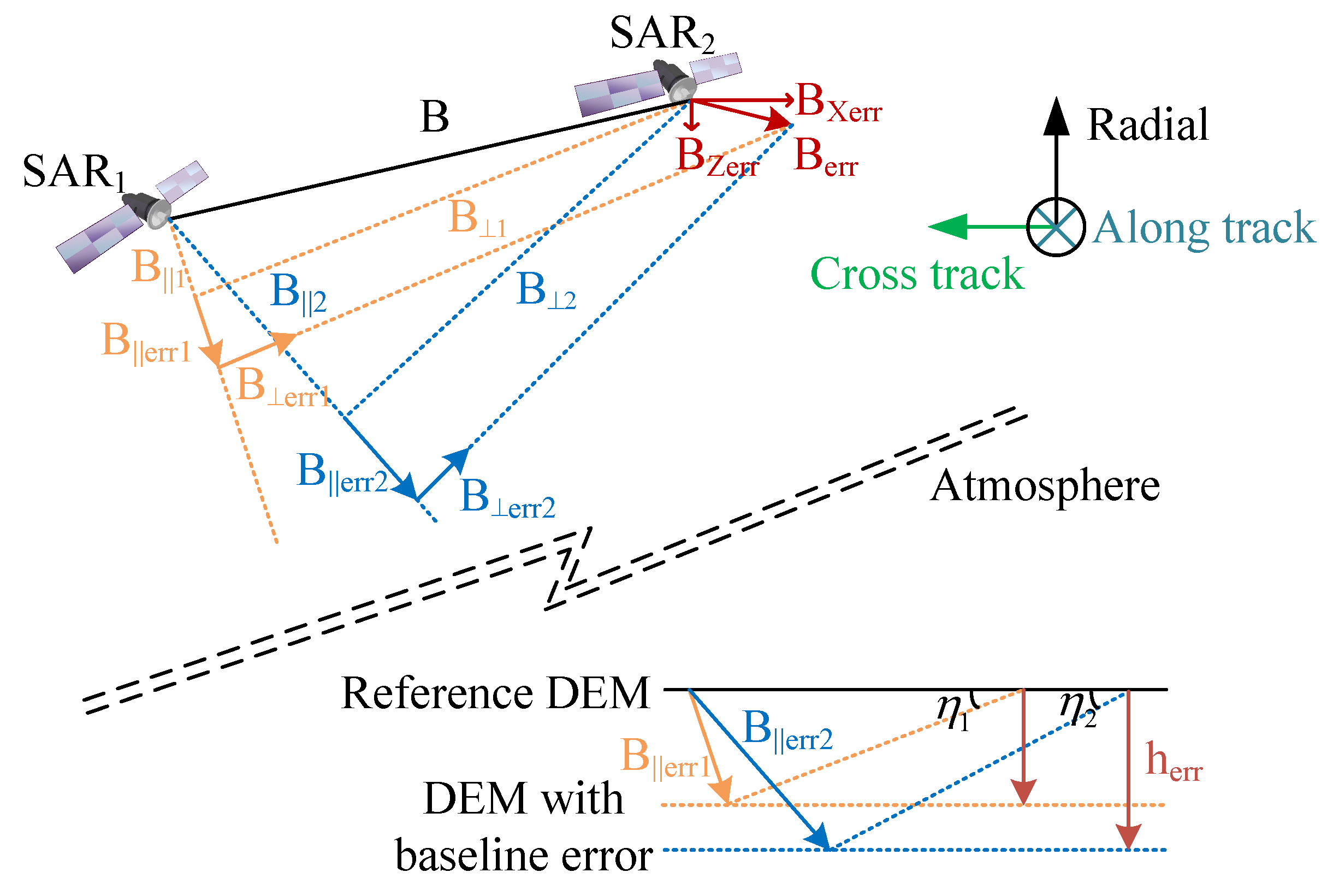
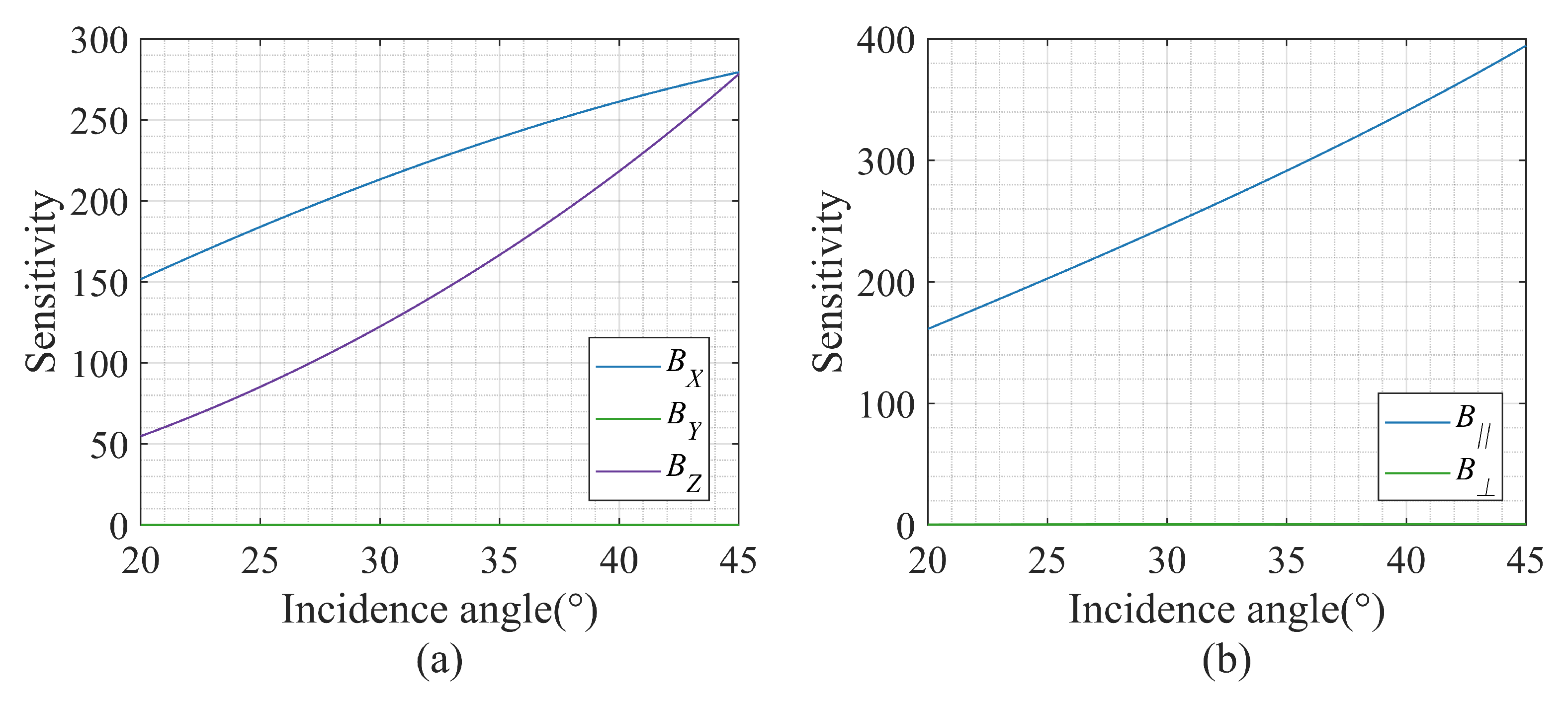
4.1. Error Transfer Analysis
4.1.1. First-Order Terms
4.1.2. High-Order Terms
4.2. Penetration Depth
4.3. DEM Adjustment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Second-Order Terms
References
- Krieger, G.; De, Z.F. Relativistic effects in bistatic SAR processing and system synchronization. In Proceedings of the 9th European Conference on Synthetic Aperture Radar, EUSAR 2012, Nuremberg, Germany, 23–26 April 2012; pp. 231–234. [Google Scholar]
- Breit, H.; Younis, M.; Balss, U.; Niedermeier, A.; Grigorov, C.; Hueso-Gonzalez, J.; Krieger, G.; Eineder, M.; Fritz, T. Bistatic synchronization and processing of TanDEM-X data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2011, Vancouver, BC, Canada, 24–29 July 2011; pp. 2424–2427. [Google Scholar]
- Wang, R.; Deng, Y. Bistatic SAR System and Signal Processing Technology; Springer: Singapore, 2018. [Google Scholar] [CrossRef]
- Zhang, H.; Deng, Y.; Wang, R.; Wang, W.; Jia, X.; Liu, D.; Li, C. End-to-end bistatic InSAR raw data simulation for TwinSAR-L mission. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2019, Yokohama, Japan, 28 July–2 August 2019; pp. 3519–3522. [Google Scholar] [CrossRef]
- Jin, G.; Liu, K.; Liu, D.; Liang, D.; Zhang, H.; Ou, N.; Zhang, Y.; Deng, Y.; Li, C.; Wang, R. An advanced phase synchronization scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2020, 58, 1735–1746. [Google Scholar] [CrossRef]
- Liang, D.; Liu, K.; Yue, H.; Chen, Y.; Deng, Y.; Zhang, H.; Li, C.; Jin, G.; Wang, R. An advanced non-interrupted synchronization scheme for bistatic synthetic aperture radar. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2019, Yokohama, Japan, 28 July–2 August 2019; pp. 1116–1119. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, H.; Ou, N.; Liu, K.; Liang, D.; Deng, Y.; Wang, R. First demonstration of multipath effects on phase synchronization scheme for LT-1. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2590–2604. [Google Scholar] [CrossRef]
- Mou, J.; Hong, J.; Wang, Y.; Du, S.; Xing, K.; Qiu, T. LT-1 Baseline Calibration Method Based on Improved Baseline Calibration Model. In Proceedings of the 2022 IEEE International Geoscience and Remote Sensing Symposium, IGARSS 2022, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7452–7455. [Google Scholar] [CrossRef]
- Zebker, H.A.; Farr, T.G.; Salazar, R.P.; Dixon, T.H. Mapping the world’s topography using radar interferometry: The TOPSAT mission. Proc. IEEE 1994, 82, 1774–1786. [Google Scholar] [CrossRef]
- Zink, M.; Bachmann, M.; Brautigam, B.; Fritz, T.; Hajnsek, I.; Moreira, A.; Wessel, B.; Krieger, G. TanDEM-X: The new global DEM takes shape. IEEE Geosci. Remote Sens. Mag. 2014, 2, 8–23. [Google Scholar] [CrossRef]
- Xie, H.; Zhan, Y.; Zeng, G.; Pan, X. LEO mega-constellations for 6G global coverage: Challenges and opportunities. IEEE Access 2021, 9, 164223–164244. [Google Scholar] [CrossRef]
- Pinheiro, M.; Reigber, A. Improving TamDEM-X DEMs accuracy using large-baseline data from the science phase. In Proceedings of the 11th European Conference on Synthetic Aperture Radar, EUSAR 2016, Hamburg, Germany, 6–9 June 2016; pp. 1–6. [Google Scholar]
- González, J.H.; Bachmann, M.; Krieger, G.; Fiedler, H. Development of the TanDEM-X calibration concept: Analysis of systematic errors. IEEE Trans. Geosci. Remote Sens. 2010, 48, 716–726. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. TanDEM-X: A satellite formation for high-resolution SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef]
- Qi, Y.; Wang, Y.; Hong, J.; Du, S. Additional Reference Height Error Analysis for Baseline Calibration Based on a Distributed Target DEM in TwinSAR-L. Remote Sens. 2021, 13, 2750. [Google Scholar] [CrossRef]
- Kroes, R.; Montenbruck, O.; Bertiger, W.; Visser, P. Precise GRACE baseline determination using GPS. GPS Solut. 2005, 9, 21–31. [Google Scholar] [CrossRef]
- Small, D.; Werner, C.; Nuesch, D. Baseline modelling for ERS-1 SAR interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, IGARSS 1993, Tokyo, Japan, 18–21 August 1993; pp. 1204–1206. [Google Scholar]
- Xu, B.; Li, Z.; Zhu, Y.; Shi, J.; Feng, G. SAR Interferometric Baseline Refinement Based on Flat-Earth Phase without a Ground Control Point. Remote Sens. 2020, 12, 233. [Google Scholar] [CrossRef]
- González, J.H.; Antony, J.; Bachmann, M.; Krieger, G.; Zink, M.; Schrank, D.; Schwerdt, M. Bistatic system and baseline calibration in TanDEM-X to ensure the global digital elevation model quality. ISPRS J. Photogramm. Remote Sens. 2012, 73, 3–11. [Google Scholar] [CrossRef]
- Liu, G.; Hanssen, R.F.; Guo, H.; Yue, H.; Perski, Z. Nonlinear model for InSAR baseline error. IEEE Trans. Geosci. Remote Sens. 2016, 54, 5341–5351. [Google Scholar] [CrossRef]
- Du, Y.; Fu, H.; Liu, L.; Feng, G.; Peng, X.; Wen, D. Orbit error removal in InSAR/MTInSAR with a patch-based polynomial model. Int. J. Appl. Earth Obs. Geoinf. 2021, 102, 102438. [Google Scholar] [CrossRef]
- Liu, Z.; Jung, H.S.; Lu, Z. Joint correction of ionosphere noise and orbital error in L-band SAR interferometry of interseismic deformation in southern California. IEEE Trans. Geosci. Remote Sens. 2013, 52, 3421–3427. [Google Scholar] [CrossRef]
- Yang, Q.; Wang, J.; Wang, Y.; Lu, P.; Jia, H.; Wu, Z.; Li, L.; Zan, Y.; Wang, R. Image-Based Baseline Correction Method for Spaceborne InSAR With External DEM. IEEE Trans. Geosci. Remote Sens. 2023, 61, 1–16. [Google Scholar] [CrossRef]
- Hanssen, R.F. Radar Interferometry: Data Interpretation and Error Analysis; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Crosetto, M. Calibration and validation of SAR interferometry for DEM generation. ISPRS J. Photogramm. Remote Sens. 2003, 57, 213–227. [Google Scholar] [CrossRef]
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The shuttle radar topography mission–A new class of digital elevation models acquired by spaceborne radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Tu, J.; Gu, D.; Wu, Y.; Yi, D. Error modeling and analysis for InSAR spatial baseline determination of satellite formation flying. Math. Probl. Eng. 2012, 2012, 140301. [Google Scholar] [CrossRef]
- Antony, J.M.W.; Gonzalez, J.H.; Schwerdt, M.; Bachmann, M.; Krieger, G.; Zink, M. Results of the TanDEM-X Baseline Calibration. IEEE J. Sel. Top. Appl. Earth Obs. Remote. Sens. 2013, 6, 1495–1501. [Google Scholar] [CrossRef]
- Dall, J. InSAR Elevation Bias Caused by Penetration Into Uniform Volumes. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2319–2324. [Google Scholar] [CrossRef]
- Gisinger, C.; Schubert, A.; Breit, H.; Garthwaite, M.; Balss, U.; Willberg, M.; Small, D.; Eineder, M.; Miranda, N. In-depth verification of Sentinel-1 and TerraSAR-X geolocation accuracy using the Australian corner reflector array. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1154–1181. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Y. A fast offset estimation approach for InSAR image subpixel registration. IEEE Geosci. Remote. Sens. Lett. 2011, 9, 267–271. [Google Scholar] [CrossRef]
- Zhao, S.; Gu, D.; Yi, B.; Yi, D. Error analysis for the baseline estimation and calibration of distributed InSAR satellites. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium. IGARSS 2016, Beijing, China, 10–15 July 2016; pp. 4179–4182. [Google Scholar] [CrossRef]
- Fritz, T.; Rossi, C.; Yague-Martinez, N.; Rodriguez-Gonzalez, F.; Lachaise, M.; Breit, H. Interferometric processing of TanDEM-X data. In Proceedings of the 2011 IEEE International Geoscience and Remote Sensing Symposium. IGARSS 2011, Vancouver, BC, Canada, 24–29 July 2011; pp. 2428–2431. [Google Scholar] [CrossRef]
- Sharma, J.J.; Hajnsek, I.; Papathanassiou, K.P.; Moreira, A. Estimation of Glacier Ice Extinction Using Long-Wavelength Airborne Pol-InSAR. IEEE Trans. Geosci. Remote Sens. 2013, 51, 3715–3732. [Google Scholar] [CrossRef]
- Xiong, S.; Muller, J.-P.; Li, G. The Application of ALOS/PALSAR InSAR to Measure Subsurface Penetration Depths in Deserts. Remote Sens. 2017, 9, 638. [Google Scholar] [CrossRef]
- Gaber, A.; Koch, M.; Griesh, M.H.; Motoyuki, S.; Farouk, E. Near-surface imaging of a buried foundation in the Western Desert, Egypt, using space-borne and ground penetrating radar. J. Archaeol. Sci. 2013, 40, 1946–1955. [Google Scholar] [CrossRef]
- Hallikainen, M.T.; Ulaby, F.T.; Dobson, M.C.; El-Rayes, M.A.; Wu, L.K. Microwave dielectric behavior of wet soil-part 1: Empirical models and experimental observations. IEEE Trans. Geosci. Remote Sens. 1985, 1, 25–34. [Google Scholar] [CrossRef]
- Michael, S.; Paul, M.; Brian, E.; Craig, A.; Stefan, E. Canopy height estimation with TanDEM-X in temperate and boreal forests. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 82, 101904. [Google Scholar] [CrossRef]
- Gruber, A.; Wessel, B.; Huber, M.; Roth, A. Operational TanDEM-X DEM calibration and first validation results. ISPRS J. Photogramm. Remote Sens. 2012, 73, 39–49. [Google Scholar] [CrossRef]
- Rizzoli, P.; Martone, M.; Gonzalez, C.; Wecklich, C.; Tridon, D.B.; Bräutigam, B.; Bachmann, M.; Schulze, D.; Fritz, T.; Huber, M.; et al. Generation and performance assessment of the global TanDEM-X digital elevation model. ISPRS J. Photogramm. Remote Sens. 2017, 132, 119–139. [Google Scholar] [CrossRef]


| Parameter | Value |
|---|---|
| Central incidence angle | 44.41 |
| Bistatic angle | 0.16 |
| Orbit height | 607 km |
| Height of ambiguity | 78.48 m |
| Resolution (azimuth × range) | 1.99 m × 1.66 m |
| Image pixel (azimuth × range) | 23,248 × 22,914 |
| Multi-look number (azimuth × range) | 5 × 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mou, J.; Wang, Y.; Hong, J.; Wang, Y.; Wang, A. Baseline Calibration of L-Band Spaceborne Bistatic SAR TwinSAR-L for DEM Generation. Remote Sens. 2023, 15, 3024. https://doi.org/10.3390/rs15123024
Mou J, Wang Y, Hong J, Wang Y, Wang A. Baseline Calibration of L-Band Spaceborne Bistatic SAR TwinSAR-L for DEM Generation. Remote Sensing. 2023; 15(12):3024. https://doi.org/10.3390/rs15123024
Chicago/Turabian StyleMou, Jingwen, Yu Wang, Jun Hong, Yachao Wang, and Aichun Wang. 2023. "Baseline Calibration of L-Band Spaceborne Bistatic SAR TwinSAR-L for DEM Generation" Remote Sensing 15, no. 12: 3024. https://doi.org/10.3390/rs15123024
APA StyleMou, J., Wang, Y., Hong, J., Wang, Y., & Wang, A. (2023). Baseline Calibration of L-Band Spaceborne Bistatic SAR TwinSAR-L for DEM Generation. Remote Sensing, 15(12), 3024. https://doi.org/10.3390/rs15123024








