A Combined Deep Learning and Prior Knowledge Constraint Approach for Large-Scale Forest Disturbance Detection Using Time Series Remote Sensing Data

Abstract

The scale and severity of forest disturbances across the globe are increasing due to climate change and human activities. Remote sensing analysis using time series data is a powerful approach for detecting large-scale forest disturbances and describing detailed forest dynamics. Various large-scale forest disturbance detection algorithms have been proposed, but most of them are only suitable for detecting high-magnitude forest disturbances (e.g., fire, harvest). Conversely, more continuous, subtle, and gradual lower-magnitude forest disturbances (e.g., thinning, pests, and diseases) have been subject to less focus. Deep learning (DL) can distinguish subtle differences in information within time series data, offering new opportunities to capture forest disturbances in a complete and detailed way. This study proposes an approach for analyzing forest dynamics across large areas and long time periods by combining DL time series classification and prior knowledge constraint. The approach consists of two stages: (1) an improved self-attention model used for time series classification to identify sequences with forest disturbance characteristics; (2) developed skip-disturbance recovery index (S-DRI) characterizing the temporal context, using prior knowledge constraint to identify forest disturbance years in time series with disturbance characteristics. In this study, the year of forest disturbances in five study areas located in the United States, Canada, and Poland from 2001 to 2020 was mapped. A total of 3082 manually interpreted test data with different disturbance causal agents (such as fire, harvest, conversion, hurricane, and pests) were sampled from five research areas for validation. Our approach was also evaluated against two forest disturbance benchmark datasets derived from LandTrendr and the Global Forest Change (GFC) dataset. The results demonstrate that our approach achieved an overall accuracy of 87.8%, surpassing the accuracy of LandTrendr (84.6%) and the Global Forest Change dataset (81.4%). Furthermore, our approach demonstrated lower omission rates (ranging from 10.0% to 67.4%) in detecting subtle to severe causal agents of forest disturbance, in comparison to LandTrendr (with a range of 18.0% to 81.6%) and GFC (with a range of 15.0% to 88.8%). This study, which involved mapping large-scale and long-term forest disturbance in multiple regions, revealed that our approach can be applied to new areas without a requirement for complex parameter adjustments. These results demonstrate the potential of our approach in generating comprehensive and detailed forest disturbance data, thus providing a new and effective method in this domain.

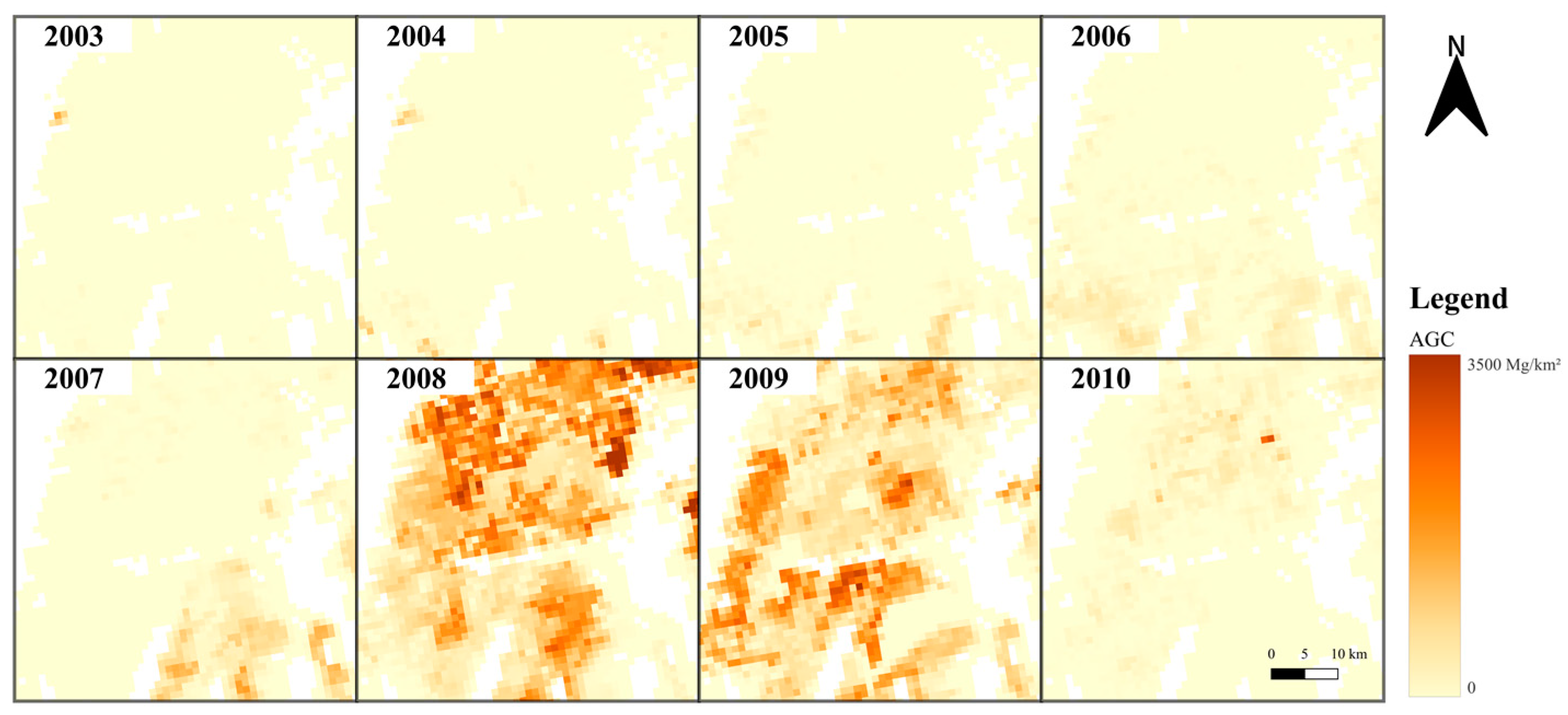
1. Introduction

There is growing evidence that more intense forest disturbance events have become more frequent in recent decades, posing significant challenges to biological habitats and ecological sustainability [1,2,3]. Natural disturbances, such as fire, drought, hurricanes, etc., alongside human activities, such as deforestation, urbanization, and agricultural land reclamation, significantly impact the composition, structure, and function of the forest system. These disturbance events release massive amounts of carbon stored in forest vegetation into the atmosphere while also disrupting forest oxygen-release functions [4,5]. Forest disturbances can cause permanent alterations in forest functions with considerable effects on the global forest carbon budget and other vital ecosystem services, including the water cycle and energy balance [6,7]. There is an urgent need for retrospective analysis and compilation of basic data on forest disturbance, which will facilitate the development of sustainable forest conservation policies and mitigate the increase in carbon emissions generated by the forest disturbance.

Detecting and characterizing change over time is the natural first step toward identifying the driver of the change and understanding the change mechanism [8]. Remote sensing data have long been used for forest cover research as they capture natural and anthropogenic activities on a broad spatial scale and have natural temporal properties [9,10,11]. The Landsat Archives provide a long-term, large-scale collection of satellite images in standard format that can be used on a large scale to detect changes caused by forest disturbance [12]. In 2008, free and open access to all Landsat archives continued to revolutionize the use of Landsat data [13]. The use of Landsat time series analysis and extraction of spectral trajectory features is a mainstream method for current systematic forest disturbance monitoring, with significant progress [8,14,15,16,17,18,19,20].

Many forest disturbance detection and Landsat-based change detection algorithms based on time series remote sensing data have been developed and widely used. Among them, the threshold method (e.g., VCT), trajectory fitting method (e.g., CCDC), and trajectory segmentation method (e.g., LandTrendr) are the most often used methods for forest disturbance detection [13,15,16]. These methods have been proven to be effective in detecting forest disturbances, but the reliabilities often depend on the severity of the disturbance events themselves [21]. Ideally, forest disturbance has significant time series variability characteristics that are sufficient to pass a fixed threshold for detection [18]. However, data gaps and noise due to clouds, snow, or satellite system failures still make it challenging to extract reliable changes from the remote sensing time series [22,23,24]. The spectral response to non-stand replacement disturbance is subtle and delayed; therefore, some algorithms tend not to consider detecting non-stand replacement disturbance or take a conservative approach to avoid errors due to factors, such as data noise and phenological changes. Most products or methods used for detecting forest disturbance are sensitive to sudden and rapid stand replacement disturbances (e.g., harvest, fire) but ineffective for detecting non-stand replacing disturbances (e.g., insect pests, drought) that persist over many years and change gradually [21,25,26]. The goal of forest management is to mitigate or adapt to the impacts of constantly changing disturbance conditions, and subtle long-term disturbances often lead to more varied stand structures, which also need to be addressed [27]. Therefore, new methods are needed to comprehensively and accurately detect forest disturbances, not solely relying on the severity of the disturbance events themselves.

DL is powerful in modeling and learning capabilities and can extract information about real-world changes from remote sensing data [28]. Current studies using DL for forest disturbance detection are mainly based on computer vision techniques, which do not capture long-term forest dynamics information. Most of the studies have been evaluated with little reference data from a small area and only for single disturbance causal agent detection, which limits the transferability of the proposed approaches [29,30]. In remote sensing, the detection of forest disturbances is inherently difficult because low-magnitude and very small size disturbance image textures are not obvious, similar to other background noise [31].

DL is well adapted to complex spatial and temporal patterns and has the ability to detect and differentiate land cover with very similar spectral characteristics [32,33]. Using time series remote sensing data can provide dynamic change information of the Earth’s surface. In recent years, DL-based time series classification models have been used to obtain periodic information on vegetation dynamics, mowing frequency, land use, and other land surface change information from remote sensing data, such as convolutional neural network (CNN), long short-term memory (LSTM), and recurrent neural network (RNN) [34,35,36,37]. The transformer was first proposed for applications in natural language processing [38]. It has been used in other areas, such as computer vision and sequence generation, due to its efficient performance, demonstrating its advances [38,39,40]. In recent studies, the transformer has been used for time series prediction and classification, showing superior performance on multiple datasets [41,42]. In contrast to RNN and CNN, the self-attention mechanism of the transformer allows neural networks to extract features from observations at specific time steps of the input time series of values [42]. Rußwurm et al. [43] compared six DL models based on Sentinel-2 raw and pre-processed data for crop-type classification, showing better performance for self-attention neural networks than the CNN.

Free open access to data and increased computing power solve the limited availability of the excessive computational demand for temporal stacks of large-scale satellite images [44,45]. Numerous studies have shown that the use of time dependence and spectral change is more suitable for forest disturbance detection [13,31]. However, the inherent variability, dropouts, and extraneous data present in remote sensing time series data pose significant challenges in achieving end-to-end forest disturbance detection using DL [46]. If the remote sensing time series can be aligned and trimmed to equivalent lengths, it is possible to use DL time series classification to distinguish between low-magnitude disturbances and spectral changes caused by noise [46]. DL can identify a sequence of forest disturbance events, and the exact timing of the forest disturbance can be determined by utilizing simpler statistical methods or relying on prior knowledge of the disturbance times present within the sequence. Prior knowledge constraints integrate logical rules into deep learning models, encode human intentions and domain knowledge into the model to control the output results, and avoid heavy reliance on large amounts of labeled data for training [47]. Forest disturbance can be considered a time-varying process that can be effectively monitored through time series analysis and characteristics extraction [48]. Based on the time-varying characteristics of forest disturbances, integrating prior knowledge constraints into deep learning time series classification models to detect forest disturbances can avoid top-down approaches to eliminate noise-induced variation and focus more on lower-magnitude disturbances.

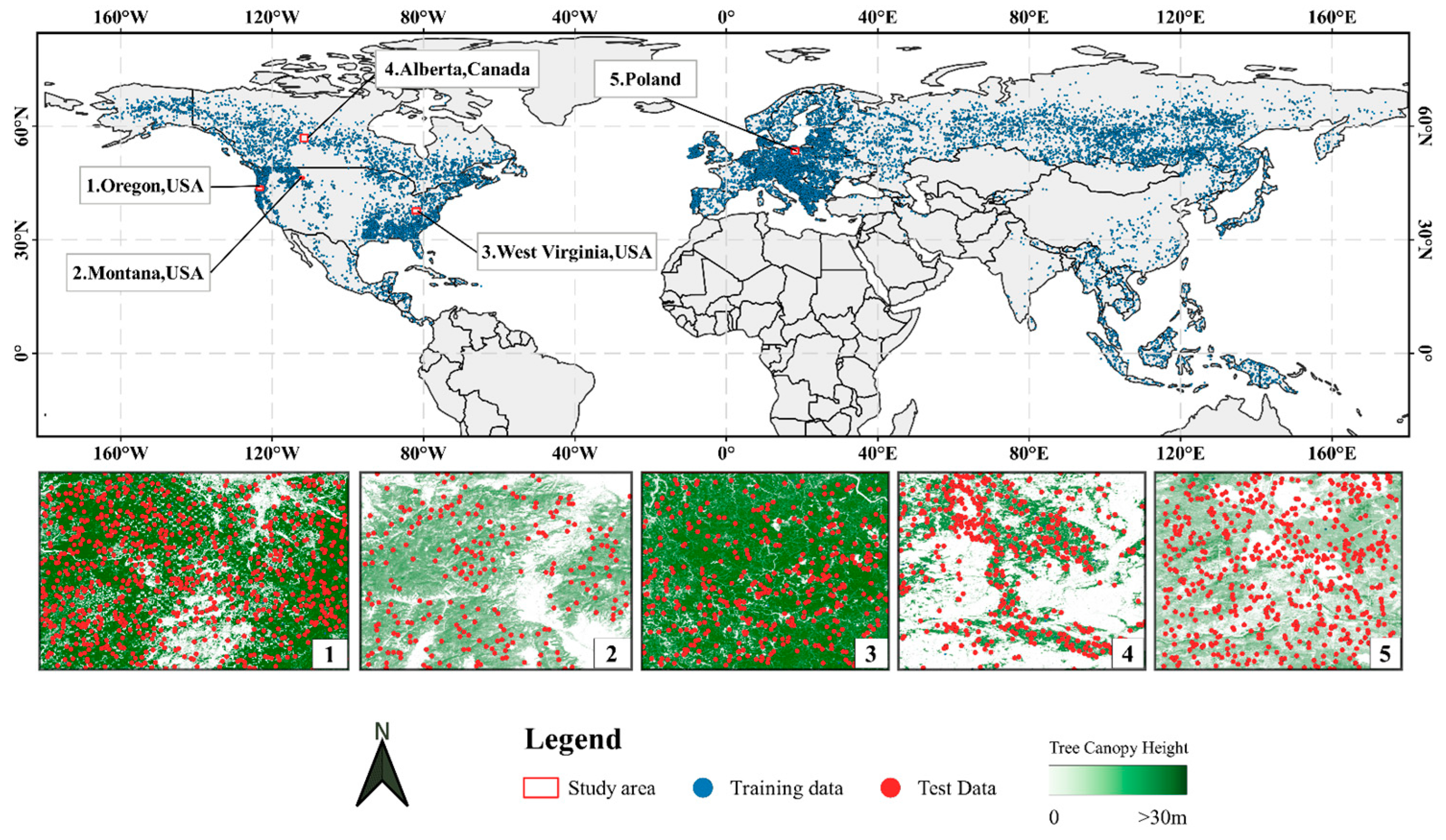
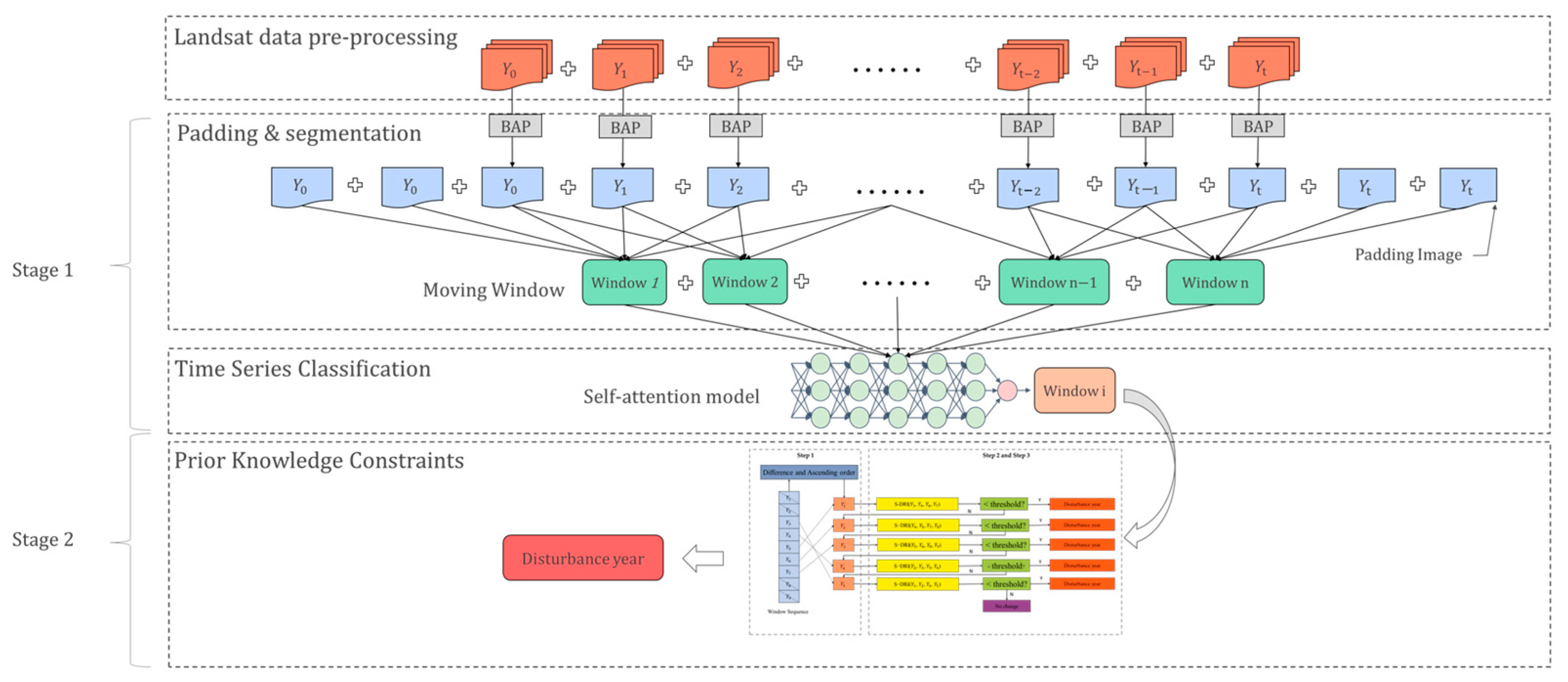
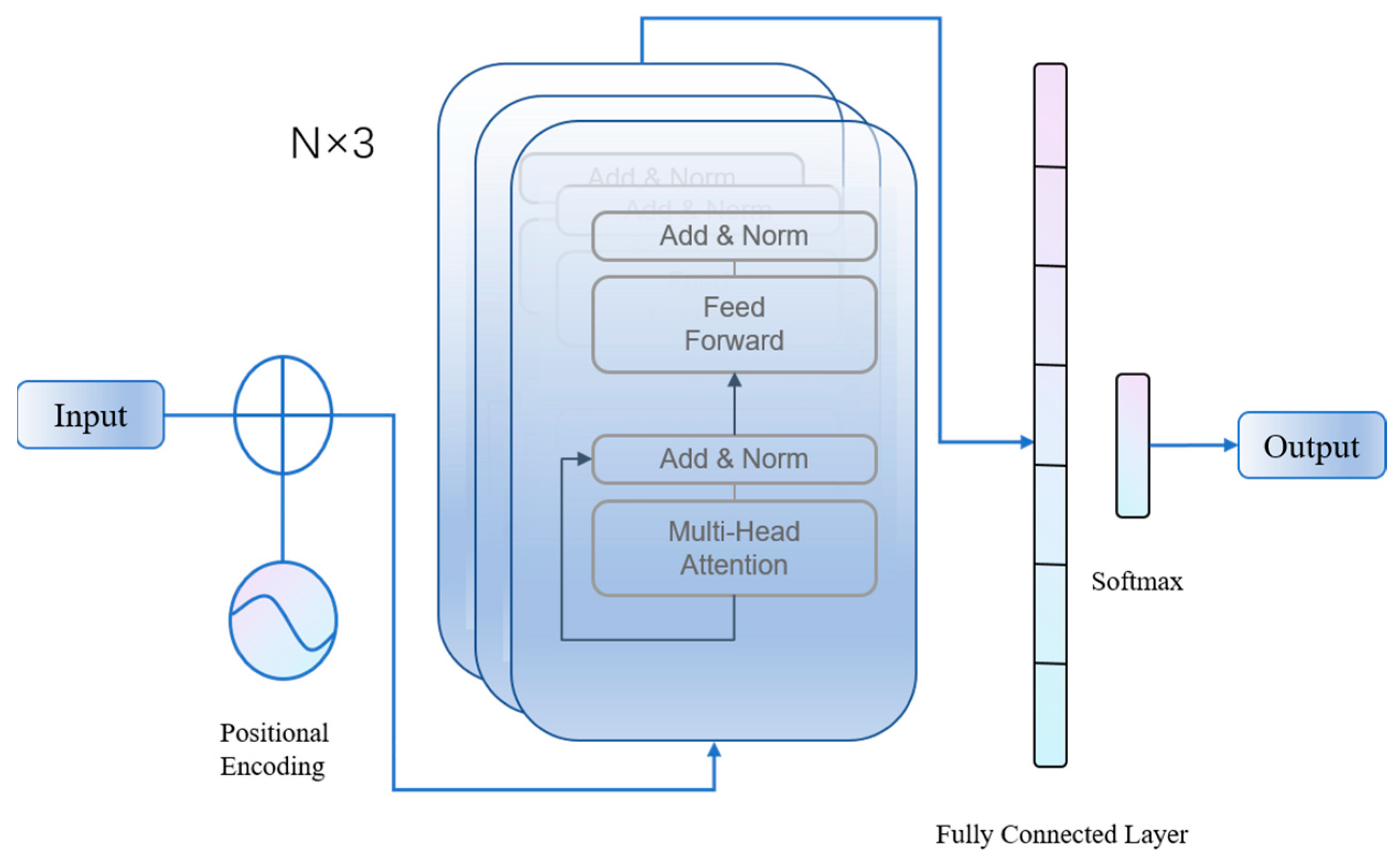
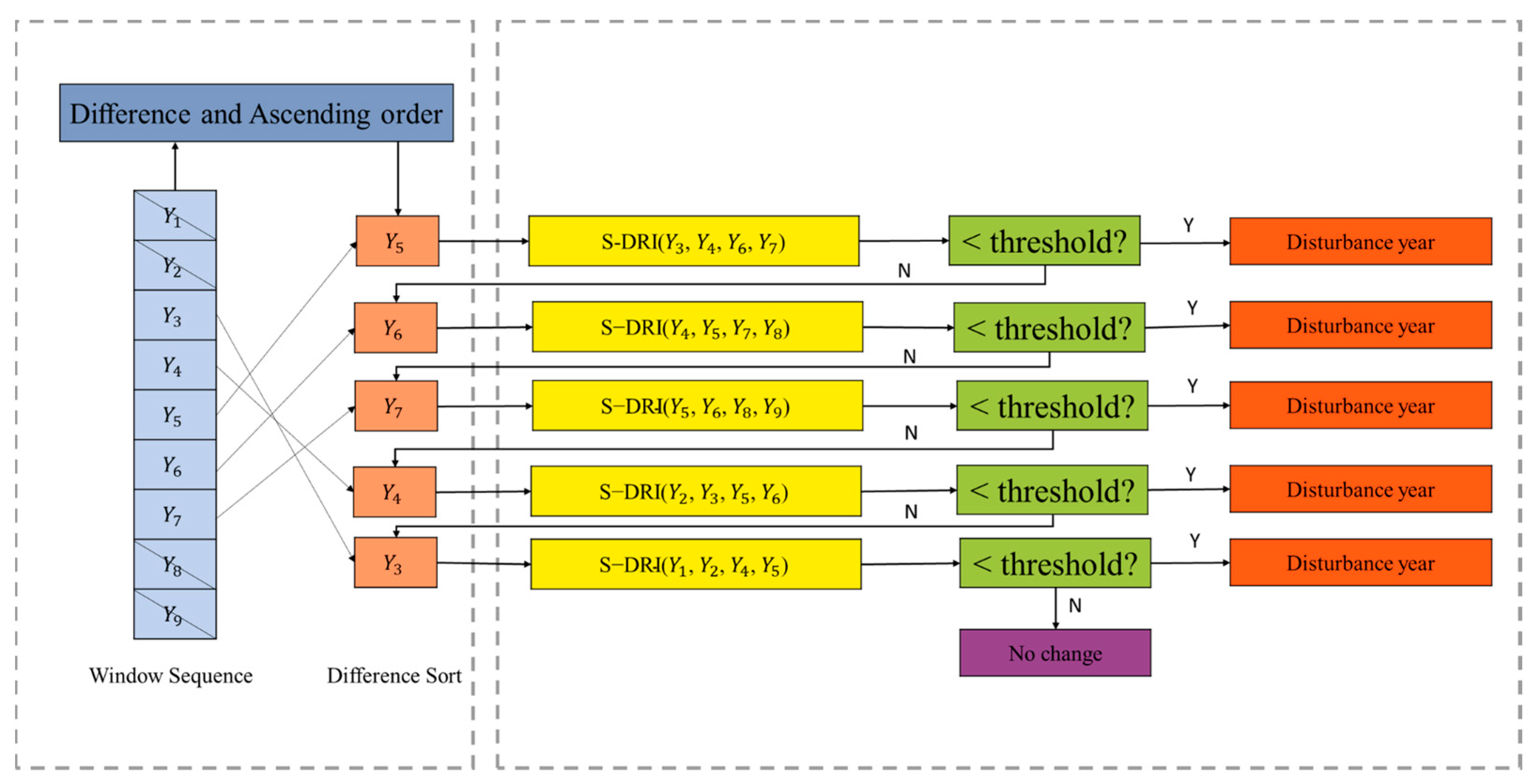
In this paper, we proposed a forest disturbance detection model that combines DL classification and prior knowledge constraints to achieve comprehensive and accurate detection of forest disturbances using time series remote sensing data. The proposed approach involves a two-phase process for mapping forest disturbance: (1) Use a moving window algorithm to align and segment remote sensing time series; then, classify time series based on DL to pinpoint the time window where the disturbance event occurred. (2) Define and apply the prior knowledge constraints to locate the specific year of the disturbance event in the identified window. We illustrated the effectiveness of our model by analyzing time series Landsat images spanning two decades (2001 to 2020) and testing on forests in study areas located in Oregon, West Virginia, Montana, Alberta, and Poland. In addition, our approach is compared with results from the LandTrendr and GFC dataset and explores the omission of the different forest disturbance causal agent classes.

2. Materials and Methods

2.1. Study Area

Natural disasters, climate change, and land use change are interrelated, and different regions have different spatial and temporal disturbance patterns and dominant disturbance causal agents. To comprehensively evaluate the performance of the forest disturbance detection approach in different environments, five regions located in North America and Europe were selected as the study areas for this study, as shown in Figure 1. There are diverse forest types and disturbance causal agents in the selected study areas. Most of the study areas are covered by forest and vary greatly in elevation, climate, forest populations, and disturbance causal agents. The area, forest cover, elevation, and major species of trees and the disturbance causal agents of each study area are summarized in

Table 1. Description of area, forest cover, elevation, forest species groups, and disturbance causal agents in study area.

	Study Area	Area (ha)	Forest (%)	Elevation (m)	Forest Species Groups	Disturbance Causal Agents
1	Oregon, USA	1,468,571	88.3	−17~1915	Douglas fir, Ponderosa pine, Western red cedar	Harvest, Fire, Thinning
2	Montana, USA	526,423	61.1	368~3376	Red pine, Yellow pine, Chinese pine, Spruce	Pests and diseases, Harvest
3	West Virginia, USA	2,932,182	90.3	164~1433	Torch pine, Short-leaf pine, White pine, Spruce	Mining, Harvest, Thinning
4	Alberta, Canada	2,492,891	92.7	217~866	Aspen poplar, Balsam poplar, Paper birch	Fire, Mining, Harvest
5	Poland	2,009,051	35.8	−8~289	Pine, Birch, Poplar	Hurricanes, Harvest

[25,49].

2.2. Data and Pre-Processing

2.2.1. Landsat Imageries and Spectral Indices

In this study, remote sensing time series were created using Landsat imageries from three sensors, namely Landsat 5 TM, Landsat 7 ETM+, and Landsat 8 OLI. We utilized the best available pixel (BAP) algorithm to produce continuous, cloud-free, and phenological consistent image composites [51]. The BAP algorithm uses the Landsat Ecosystem Disturbance Adaptive Processing System (LEDAPS) algorithm to generate surface reflectance values for the six Landsat optical bands. Clouds and their shadows were detected and masked using the function of mask (Fmask) algorithm [52,53,54]. The BAP algorithm calculates four separate scores for each pixel: the sensor score, the acquisition day of year score, the distance to cloud or cloud shadow score, and the atmospheric opacity score. All scores were summed to provide a total score for each pixel, and the pixel with the highest score was used in the image composite. Details on the pixel scoring rules and annual BAP development can be found in White et al. [51]. In this study, the maximum cloud cover in the Landsat scenes used was set to be below 70%, the maximum atmospheric opacity was 0.3, and the minimum atmospheric opacity was 0.2. Given that all study areas are situated in mid-latitudes of the Northern Hemisphere, the annual acquisition day of year score selects the closest day to August 1 as the first clear pixel, with ±30 days from the designated target day of the year. This study used BAP to produce annual composite images for five TSAs from 2000 to 2020.

For the forest not being disturbed, the canopy closure is relatively high with low shortwave-infrared reflectance (SWIR). After the disturbance, the bare soil and low vegetation increased the reflectance of SWIR in the area [55,56]. Due to the superior performance of SWIR in indicating vegetation change, spectral indices involving SWIR, such as normalized burn ratio (NBR) and normalized difference vegetation index (NDVI), were widely used in detecting forest disturbance [7,26,57,58]. Numerous studies have shown that NBR responds significantly to forest change and is suitable for detecting the occurrence of forest disturbance [16,23,26,59]. In this study, the NBR spectral index was used to construct time series for detecting pixel-level forest disturbance.

2.2.2. Reference Data

It is necessary to collect sufficient data for training the DL model. Forest disturbance is a rare event, with an average frequency of 1 in 1000 years per tree experiencing stand replacement disturbance, and collecting manually interpreted training data is a labor-intensive exercise [60]. We designed a method for obtaining reference data. First, a classifier was trained to distinguish between forest and non-forest areas. Then, sampling points were randomly generated in the forest areas, with a minimum distance of 3 km between two points to avoid spatial autocorrelation issues [1]. Manual interpretation based on high-resolution images and Landsat time series was conducted to determine the forest disturbance history for all samples and exclude samples that fell outside of forests.

The collected reference data include training datasets for the self-attention model for training and validation and a test dataset for evaluating the forest disturbance detection approach. Figure 1 shows a total of 18,240 reference data points (blue points) collected for training the time series classifier, of which 45% experienced at least one disturbance between 1988 and 2019. The training datasets for North America and Asia were generated using the aforementioned process, and the European dataset was provided by Senf et al. [61]. The study area in this study does not include the training data. To evaluate the model performance, 3082 reference samples (red points) were collected from the 5 study areas as the test dataset. Between 2001 and 2020, 2047 forest pixels remained unchanged and 1035 pixels experienced disturbances. The disturbance time and the disturbance causal agent classes of the test data were labeled by visually interpreting the time series of Landsat images and the publicly available medium- to high-resolution images. Figure 2 shows the distribution of the number of disturbance causal agents for the test data in each study area. A description of the disturbance causal agent classes is shown in

Table A1. Forest disturbance causal agent classes and descriptions.

Class	Description
Harvest	Harvesting refers to the removal of trees from a forest for the purpose of timber production or other uses.
Thinning	Thinning is a forestry practice that involves the selective removal of trees from a forest to improve the growth and health of the remaining trees.
Conversion	Conversion refers to the process of changing the land use of a forested area, typically to a non-forest use such as agriculture, urban development, or infrastructure development.
Fire	Fires can occur naturally or be intentionally set and can have significant impacts on forest.
Pests and diseases	Pests and diseases can impact forests by attacking and killing trees, which can lead to de-creased tree density and reduced forest productivity.
Wind	Wind events such as storms, hurricanes, and cyclones can have significant impacts on forests, causing damage to trees and other vegetation through wind and wind-borne de-bris.
Others	Other events that cause tree mortality and canopy cover reduction.

.

2.3. Forest Disturbance Detection Model

To detect the annual forest disturbance using Landsat time series data, a two-stage forest disturbance detection approach, consisting of DL time series classification and prior knowledge constraint, was proposed in this study (Figure 3). In the first stage, we apply the moving window algorithm to segment the time series into multiple window sequences, where each window sequence corresponds to a specific time period for a given pixel. We then use a trained self-attention model to classify each window sequence, indicating whether the sequence contains a forest disturbance event. The second stage applies a prior knowledge constraint to the window sequences containing the disturbance event that was identified by the self-attention model in the first stage to determine the specific year of the forest disturbance.

To facilitate a better understanding of the methods proposed in this study, we defined several concepts. For a given time series $\mathrm{Y}=\left\{{\mathrm{Y}}_0,\dots ,{\mathrm{Y}}_{\mathrm{t}}\right\}$, it is a sequential order of spectral values of a pixel during the detection period. The $\mathrm{s}$ sample long sub-signal ${\left\{{\mathrm{Y}}_{\mathrm{i}}\right\}}_{\mathrm{i}=\mathrm{a}}^{\mathrm{a}+\mathrm{s}} (0\le \mathrm{a}<\mathrm{a}+\mathrm{s}\le \mathrm{t})$ is a window sequence, where $\mathrm{s}$ represents the move window size. In the remainder of this article, we use the above notation.

2.3.1. Padding and Segmentation

This study involves a time classifier that performs time series classification tasks, which requires first transforming input remote sensing data of varying lengths into fixed-length inputs for the classifier to use. We used a moving window algorithm to segment the remote sensing time series data into a number of window sequences [37]. A key part of mining time series data is to identify the movements and/or components within them by segmenting the time series, which can efficiently discover the critical time segments via the moving window [62]. The moving window algorithm progressively moves the window within the time detection period of each pixel, creating a new sequence based on the values that fall into the window at each step (Figure 4a). This new sequence is called a window sequence. The number of strides refers to the number of steps by which the window is shifted. The size of the window sequence, i.e., the number of composite images containing observations in the sequence, controls the amount of information available in the trajectory [37]. The window sequence corresponded to a period of time for a given forest pixel, and a label indicated whether a disturbance event occurred or not during the period or not is assigned to that window sequence (Figure 4a). In this study, we tested the window sizes of 7, 9, and 11 progressively to explore the effect of window size on the recognition of a window sequence. To improve the efficiency of the model operation, moving window sizes of 7, 9, and 11 use strides of 2, 2, and 4, respectively.

For forest disturbance detection, an ideal window sequence should contain the pre-disturbance forest features and the post-disturbance recovery features (as shown in Figure 4aII). For better detection of early or late disturbance events within the detection period, before segmenting time series with a moving window, padding was applied using the shifting method to reduce information loss at the edges of the time series, as shown in Figure 4b. Specifically, the padding operation simulates forest time series information (for example, in Figure 4b, we observed that the window sequence with padding operation has trajectories similar to the raw spectral values) and ensures that disturbance events within the detection period are included in the created window sequence with sufficient information, thereby improving the accuracy of time series classification models [63]. In this study, we performed $\lfloor \mathrm{s}/2\rfloor$ times padding on the edges of the time series using $Y_0$ and $Y_t$, respectively. For example, in Figure 4b, when using the moving window of size 9, the edges of the time series were padded four times using the NBR values of 2000 and 2020, respectively.

2.3.2. Self-Attention Model

In this study, a self-attention mechanism in the transformer model is used for time series classification [38]. Let $X=\left\{{\mathrm{x}}_1,{ \mathrm{x}}_2,\dots ,{ \mathrm{x}}_n\right\}$ be the input sequence of length $n$; the self-attention mechanism computes the key $K=W_k^T X$, query $Q=W_q^T X$, and value $V=W_v^T X$ vectors originate from the input matrix $X$ transformed by linear transformation, where $W_k$, $W_q$, and $W_v$ are the learned weight matrices. Attention scores are computed between all pairs of positions in the input sequence using the dot product between the query and key vectors, followed by softmax activation. The output representation for each position in the input sequence is computed as the weighted sum of the value vectors. This results in the generic formulation of self-attention, as shown in Equation (1).

$$\mathrm{Attention}\left(Q,K,V\right)=\mathrm{softmax}\left(\frac{Q{K}^T}{\sqrt{d_k}}\right)V$$

(1)

where $d_k$ is the dimensionality of the query and key vectors, and the attention scores are scaled by $\sqrt{d_k}$ for better gradient backpropagation.

In this study, the encoder architecture of the transformer network was used [38]. The schematic architecture of the used model is shown in Figure 5. Since the input data are continuous time series data, the word embedding step was no longer required. For the transformer, as a feed-forward architecture that was insensitive to the order of the inputs, position encoding was added in order to make it aware of the sequential nature of the time series. The time series with location encoding was converted to a higher-dimensional feature representation by using a 3-layer transformer encoder block. Each block applies multi-head self-attention and dense layers to each time instance independently and introduces skip connections and layer normalization for better gradient flow and model stability. The output of the last transformer block is reduced to a single vector of size by applying global maximum pooling along the time dimension. This reduced representation was then projected to the scores of each class using a final fully connected layer with a softmax activation function.

The self-attention model takes, as input, a sequence created using a moving window algorithm and produces a binary classification result indicating whether there is forest disturbance within the window sequence. Rußwurm et al. [43] developed a self-attention model to classify land cover types using Sentinel-2 multispectral images. In this study, we improved the self-attention model proposed by Rußwurm et al. [43] to identify window sequences containing forest disturbance events [38]. To reduce the risk of overfitting in model training, we reduced the dimension of its hidden state $D_h$, the number of self-attention layers $L$, and the number of self-attention heads $H$. The final model parameters were $L=3$, $D_h=128$, $H=1$.

The model was trained and tested using the training data and the test data from the reference dataset (Figure 1). For samples that underwent disturbances, we segmented them using a moving window, obtained the window sequence that the disturbance event fell into, and labeled as Disturbance. For undisturbed reference samples, a moving window is used to segment the time series, and one of the resulting window sequences is randomly selected and labeled as No change. Only one window sequence was selected for each reference sample; we then trained the time series classifier using the labeled window sequences. For model training, we split the input data set into three parts: training, validation, and test data. The training dataset was used to train the model, while after each training epoch, the current performance was evaluated on the validation set to monitor the convergence and trigger learning parameter changes. The test data for the self-attention model come from five study areas, and the strategy for obtaining window sequences and labels is consistent with the strategy used to obtain window sequences for training.

The loss function used in the self-attention model is the binary cross-entropy function, which has been typically used in neural networks for classification tasks [64]. The optimization algorithm used was Adam, and the batch size was 128 [65]. The initial learning rate was set to 1× 10⁻³, and the learning rate decay was 1 × 10⁻². The maximum number of training epochs in the model was set to 200. An early stopping mechanism was implemented to prevent overfitting by ending the training when the loss function did not change for 10 epochs.

2.3.3. Prior Knowledge Constraints

To identify the specific year of a forest disturbance occurring in the windows sequence that contains disturbance events, the prior knowledge presenting the temporal changes in the spectral index before and after disturbance events was introduced. Forest disturbances in time series data usually coincide with sudden drops in NBR values. While spectral changes caused by noise are temporary and quickly return to normal values, disturbance-induced spectral changes are more persistent and last for several years, featuring prominent patterns [16]. Based on this prior knowledge, we proposed S-DRI to constrain forest disturbances in the window sequence. The S-DRI for a given year (target year refers to a specific year in the time series that is being analyzed) is the first-order linear regression slope of the NBR values for the previous and subsequent years. The slope indicates the direction and magnitude of the spectral index change in the time series and is used to determine whether a disturbance occurred. The S-DRI for the target year is calculated as shown in Equation (2). In this study, the S-DRI of the target year used the NBR values for each of the two previous and subsequent years and the target year.

$$\mathrm{S}-\mathrm{DRI}=\frac{\sum i\left(Y_i-\overline{Y}\right)}{\sum i^2}$$

(2)

where $Y_i$ denotes the NBR value of the $i$ year distance from the target year, $i\in \left\{-2,-1,1,2\right\}$. $\overline{Y}$ denotes the mean value of the NBR involved in the calculation.

Based on prior knowledge of the time-varying features of forest disturbance, we use S-DRI to constrain disturbance events in window sequences labeled as Disturbance by self-attention models (Figure 6). The strategy is as follows: First, we calculate the first-order difference ($\Delta Y$) of spectral values in window sequences to analyze the change magnitude between adjacent years (Equation (3)). To prioritize the detection of larger outliers or years that deviate from the spectral trend in the time series, the S-DRI values for the target years are sequentially calculated via the $\Delta Y$ magnitude of the year. In other words, the S-DRI values for each target year are calculated starting from the year with the largest difference in NBR values and then gradually moving towards years with smaller differences, until all target years have been computed. This approach avoids exploring known invalid or irrelevant solutions. Next, the S-DRI value of the target year is compared to a predefined threshold. If the S-DRI value exceeds the threshold, we assume that it is a false disturbance caused by noise and continue, calculating the S-DRI value of the next target year. If the S-DRI value is less than or equal to the predefined threshold, the current year is output. There are two stop criteria in this workflow: (1) the window sequence has a target year that meets the requirements of the predefined threshold, and (2) the maximum number of iterations has been reached. If none of the target years met the set threshold after all iterations, it was considered that there was no change in the forest in the window sequence. In a window sequence, only the target years that meet the S-DRI calculation criteria are calculated, such as $Y_3$ to $Y_7$ in Figure 6.

$$\Delta Y=Y_i-Y_{i-1}$$

(3)

2.4. Results Assessment Method

The disturbance detection accuracy was assessed using the binary classification metrics. In this study, a total of 3082 forest pixels were manually interpreted in five study areas and collected as test data. The overall accuracy (OA), producer’s accuracy (PA), and user’s accuracy (UA) were used to assess the accuracy of the forest disturbance detection (as shown in

Table 2. Confusion matrix for the evaluation of forest disturbance detection results.

Map Class	Reference Data		User’s Accuracy
	No Change	Disturbance
No change	TP	FP	$\frac{TP}{TP+FP}$
Disturbance	FN	TN	$\frac{TN}{FN+TN}$
Producer’s Accuracy	$\frac{TP}{TP+FN}$	$\frac{TN}{FP+TN}$

and Equation (4)). The OA measures the proportion of correctly classified samples among all samples. The PA measures the proportion of truly positive samples among all samples classified as positive. The UA measures the proportion of truly positive samples among all samples labeled as positive. It is worth noting that a strict time definition was used in the evaluation of forest disturbance detection results. The inconsistent output disturbance times (e.g., if a disturbance occurred in 2007 but the model detected it in 2006 or 2008) were considered as failures of the model in detecting forest disturbances. In Table 2, output results with inconsistent disturbance time are considered as FP.

The method proposed in this study requires setting two parameters: the size of the moving window and the predefined S-DRI threshold. Different parameter settings may result in different model output results. Therefore, we conducted a grid search to test all possible combinations to find the best parameters for each input set [37]. The grid search involved 60 (3 × 20) model setups, each defined by a combination of window sizes and S-DRI values, in order to determine the optimal configuration. Specifically, we used window sizes of 7, 9, and 11 and S-DRI values ranging from −0.1 to 0, with an interval of 0.005. This study includes a time series classification model. When searching for window sizes, we also calculated the overall accuracy of the time series classification models with different window sizes. The method used to preprocess the testing dataset for evaluating the classification accuracy of the self-attention model is consistent with the preprocessing strategy used for the training dataset.

To further evaluate the performance of the proposed forest disturbance detection method, the results of the forest disturbance detected in this study were compared to those detected by the LandTrendr and the GFC dataset [16,25,66]. LandTrendr and GFC use time series of Landsat satellite images to detect changes in forest cover and provide important data for land management decisions. Utilizing the functions and datasets provided in Google Earth Engine (GEE, https://earthengine.google.com, accessed on 1 July 2022), we downloaded the forest disturbance maps of LandTrendr (use parameters as shown in

Table A2. Parameters used in the LandTrendr algorithm.

Parameter	Configuration
Base index	NBR
Max Segments	6
SpikeThreshold	0.9
VertexCountOvershoot	3
PreventOneYearRecovery	True
RecoveryThreshold	0.25
PvalThreshold	0.05
BestModelProportion	0.75
MinObservationsNeeded	6

) and GFC, and we extracted the pixel values of the test dataset for evaluation. In this study, the performance of the three methods for forest disturbance detection was evaluated using a confusion matrix. In addition, we also evaluated the omission (Equation (5)) of different disturbance causal agents of the three methods.

$$Overall Accuracy=\frac{TP+TN}{TP+FP+FN+TN}$$

(4)

$$Omission\left(i\right)=1-\frac{TN\left(i\right)}{FP\left(i\right)+TN\left(i\right)}$$

(5)

where $i$ is forest disturbance causal agent class.

3. Results

3.1. Optimal Parameters

The evaluation results of the test dataset using different parameter combinations obtained through the grid search are shown in

Table 3. Evaluation results of the test dataset based on different parameter combinations from the grid search.

Window Size	Self-Attention Model	S-DRI	Disturbance Detection
	OA		OA	PA	UA
7	95.5%	−0.05	86.9%	66.5~97.4%	87.0~91.6%
9	95.1%	−0.05	87.0%	66.5~97.3%	87.1~91.6%
11	95.5%	−0.05	87.8%	68.9~97.4%	87.0~91.4%

. For each window size, only the best parameter setup with the highest accuracy for the S-DRI value is shown. The results show that the OA of the self-attention models with different window sizes is very close, about 95%, with a difference of less than 1%. This difference may be caused by the randomness of DL or the machine environment. Increasing the window size does not improve the accuracy of the model, indicating that the change information in the continuous seven-year remote sensing time series provides sufficient evidence to distinguish whether the forest has been disturbed.

We also observed that the optimal S-DRI threshold for different window sizes was −0.05, indicating that this is the best balance between filtering out noise and detecting disturbance in the window sequence. When the window size was changed with the same S-DRI, it could be observed that the OA of the test dataset improved with an increase in the window size. Based on the OA of the self-attention model of different window sizes, the time series classifier does not improve accuracy as the window size increases, indicating that a larger window size is beneficial in providing more temporal information that confirms the disturbance years according to prior knowledge constraints, thus enabling the model to detect more disturbance events that fall on the edge of the window sequence due to the moving window. For example, when the window size increases from 9 to 11, the PA increases from 66.5~97.4% to 68.9~97.4%. However, it does not mean that we should use a larger window size because a larger window size means a sequence containing more noise and a greater probability of multiple disturbances. With an increase in window size, the UA of the model decreased from 87.0~91.6% to 87.0~91.4%. In view of both methods’ efficiency and accuracy, a window size of 11 and S-DRI of −0.05 were, therefore, identified as the best-performing combination of parameters in this study.

Figure 7 illustrates the distribution of S-DRI values for disturbance and no-change years in the training dataset and testing dataset of the study areas. The median values of S-DRI for no-change samples were concentrated around 0, while the S-DRI values for disturbed samples ranged from −0.07 (Montana) to −0.16 (Oregon). A threshold of −0.05 could effectively detect forest disturbances within the study area. The widths of the upper and lower boundaries of the boxplots in different study areas reflect, to some extent, the abundance of low- and high-magnitude disturbances contained in the area. For example, Oregon has high forest cover (NBR of about 0.8), and disturbances include more high-magnitude spectral variation (harvest, fire) and less low-magnitude spectral variation (thinning), resulting in larger box dispersion and smaller medians. Figure 8 demonstrates the application of S-DRI in determining disturbance events in window sequences, and S-DRI can capture disturbance events caused by abrupt spectral changes (conversion and thinning) as well as changes that persisted over many years, such as forest cover loss due to pests and diseases. In addition, through regression using multi-year spectral values, S-DRI can also distinguish noise caused by image composites, phenological changes, or sensor failures (Figure 8d).

3.2. Accuracy Assessment

The evaluation results of the three methods on 3082 test data in five study areas are shown in

Table 4. Confusion matrix of forest disturbance detection assessment.

	Map Class	Reference Data		PA	UA	OA
		No Change	Disturbance
Ours	No change	1992	322	97.3%	86.1%	87.8%
	Disturbance	55	713	68.9%	92.8%
LandTrendr	No change	2023	451	98.8%	81.8%	84.6%
	Disturbance	24	584	56.4%	96.1%
GFC	No change	1981	508	96.8%	79.6%	81.4%
	Disturbance	66	527	50.9%	88.9%

. An assessment of the discrimination between no change/disturbance samples indicated that our approach created reliable maps of forest disturbance. Our approach has the highest OA at 87.8%, which is higher than LandTrendr’s 84.6% and GFC’s 81.4%. The forest disturbance detection was the focus of the study. The disturbance class’s producer accuracy of our approach was relatively high, at 68.9%, indicating that our approach captures more accurate forest disturbances. LandTrendr evaluated 2049 samples for the no-change class, out of which only 24 were detected as the disturbance class. However, the relatively low UA (81.8%) for the no-change class indicates that LandTrendr identifies some disturbance pixels as no change. GFC had high disturbance time confusion and disturbance event dropouts; therefore, the disturbance class has a lower UA (88.9%) and PA (50.9%).

Table 5. Omission rate of three approaches to detect different disturbance causal agent classes.

	Harvest	Conversion	Fire	Wind	Thinning	Pest and Diseases	Other
Number	361	172	194	60	93	98	57
Ours	16.3%	18.0%	18.6%	10.0%	40.9%	32.7%	67.4%
LandTrendr	27.4%	32.0%	18.0%	20.0%	63.4%	66.4%	81.6%
GFC	25.5%	40.7%	27.3%	15.0%	60.2%	88.8%	69.4%

shows the omission rate of three approaches to detect different disturbance causal agent classes. The map omission via the test dataset disturbance agent class indicates that the three methods provide lower omission for high-magnitude disturbances (wind, harvesting, and fire), while disturbances with lower magnitude and longer duration (thinning, pest, and diseases) have high omission. The omission of low-magnitude disturbances affects forest disturbance detection significantly. Our approach is more sensitive to detecting harvest, conversion, wind, thinning, and pest diseases, with significantly lower omission than the other two approaches, especially in detecting complex land use changes (conversion, 18.0%) and long-term pest diseases (pest and diseases, 32.7%).

3.3. Mapping Forest Disturbance

Estimates of the area of forest disturbance in these study areas indicated that approximately 20% of the forest had experienced at least one disturbance in the period of 2001–2020. The three approaches provided relatively consistent spatial and temporal distributions of forest disturbance in Oregon, West Virginia, Alberta, and Poland (Figure 9). Visually, the different methods provided the spatial extent of continuously active human activities and severe natural disasters that are temporally consistent with the historical record observed.

However, three methods mapped significantly different forest disturbance detection results in Montana. Previous studies indicate that the presence of bark beetles in Montana State’s pine forests was documented as early as the late 1990s. In 2009, the forests experienced the largest outbreak of bark beetles on record [67]. Based on the high-resolution remote sensing imageries in this area, it was found that the forests in the area began to change from deep green to reddish brown around 2008 and then turned to dark gray between 2009 and 2010. To further evaluate the spatial and temporal distribution of tree damage caused by the bark beetle, we cited the bark-beetle-caused tree mortality disturbance dataset of Berner et al. [68] as a supplement (Figure 10). The dataset shows that the southeastern part of the region was infested with bark beetles in 2007, causing severe damage to forests in the northern part of the Montana study area in 2008. By 2009, the infestation had shifted to the southwest, causing damage to forests throughout the study area. Our approach provides forest disturbance mapping results that are more consistent with this dataset.

Fine-scale differences between the various approaches are highlighted by selecting an example from each study area, as shown in Figure 11. GFC has a longer detection period and does not face any composite image limitations (Figure 11b). However, GFC ignores disturbances occurring in partially mixed pixels (Figure 11a) and may result in the omission and incorrect detection of low-magnitude disturbances (Figure 11e). LandTrendr and our approach both utilize composite images during the vegetation growing season (July–September). Therefore, disturbances occurring after the vegetation growing season can only be detected in the next year’s growing season. As a result, both LandTrendr and our method cannot detect the Oregon wildfires in October 2020 (Figure 11b) and fail to completely detect the harvest of the rapid recovery (Figure 11a). LT-GEE (LandTrendr-GEE) filters out some small changes based on statistical patterns in spatial and temporal dimensions in order to filter out noise, which makes it have a high PA of the no-change class but overlooks some of the real disturbances (Figure 11c,e) [69]. In addition, the LT-GEE fits the time series and prevents one-year recovery, which may produce omission at the end of the detection period (Figure 11a,d) [70]. Our approach is more complete and accurate in mapping the forest disturbance. It is also noteworthy that S-DRI identifies the disturbance year with the greatest spectral change, while the persistent infestation of trees by pests and diseases causes our approach to have a temporal delay (1 year) in detecting some disturbance (Figure 11e). Compared to other methods, our approach exhibits enhanced regularity and continuity in detecting forest disturbance boundaries associated with thinning and harvesting activities, with significantly fewer omissions and fragmented patches (Figure 11f).

4. Discussion

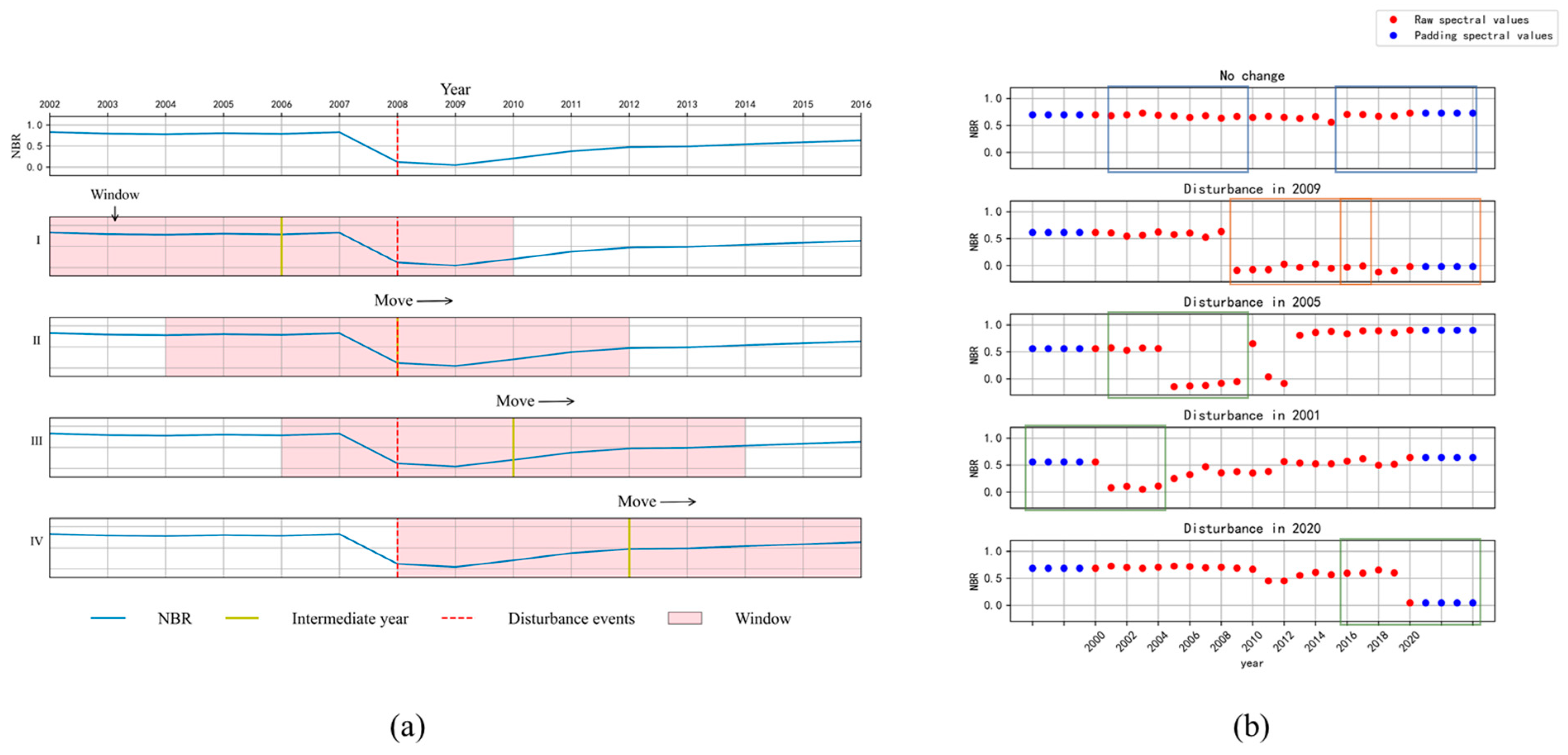
An accurate understanding of forest dynamics is critical for both effective forest management and mitigating the effects of climate change. The work presented here demonstrates a novel approach for detecting forest disturbances using DL time series classification and prior knowledge constraint. During the detection period, the moving window algorithm processes the time series of pixels as a window sequence and evaluates the window sequence with an improved self-attention model to obtain an interval estimate of the disturbance time. The a priori knowledge constraints are applied to the resulting window sequence with disturbance events to determine the exact year of disturbance. The results demonstrate that the combination of DL time series classification models and prior knowledge constraints can help detect forest disturbances of varying magnitudes, from subtle to severe. This approach provides comprehensive and detailed insight into forest dynamics and can support effective forest management and climate change mitigation efforts.

A key innovation of our work lies in the combination of DL time series classification and prior knowledge constraints to detect the history of forest disturbance. Landsat-based forest cover and change mapping using supervised expert-driven classification is a well-established and accepted methodology [71]. Recent studies have shown that utilizing robust reference data and carefully constructed models results in disturbance maps with higher accuracy, such as stacked generalization, secondary classification, and ensemble methods [22,23,26]. However, these methods rely on the foundation of forest disturbance detection algorithms, such as LandTrendr, to provide evidence. In previous studies, the main applications of DL in forest disturbance detection have been in semantic segmentation and time series regression and forecasting [30,72,73,74,75]. When used for large-scale disturbance detection, these methods still have more limitations, such as the need for labor-intensive manual annotation and higher-quality images. Our study employed a method based on time series deep learning and prior knowledge constraints, effectively addressing the challenge of detecting low-amplitude disturbances. In the study, the deep learning time series classifier differentiated between stable forests and disturbances, while the application of prior knowledge constraints reduced the learning cost of the model. Our method is applicable for detecting disturbances of varying magnitudes on a global scale, as demonstrated by the validation results across multiple study areas worldwide. These results provide evidence of the reliability of our method.

Ideally, noise due to cloud contamination, smoke obscuration, and sensor failure in the time series should be completely removed before time series analysis, but complete elimination of this noise is not possible without human intervention [23]. The differences in spectral indices based on spectral reflectance ratio between observations before and after low-magnitude forest disturbances are very similar to the spectral changes caused by phenological variations and solar angle differences [76,77]. Using high-magnitude threshold rules can remove these noisy and erroneous spectral changes, but it is difficult to capture low-magnitude disturbances [26]. Evaluation of the results for different disturbance causal agents shows that ignoring low-magnitude disturbances (e.g., thinning, pests, and diseases) is still an important factor affecting the accuracy of the model. The self-attention model uses multi-year spectral trajectory profiles to track forest disturbances, filtering out most spectral changes caused by noise, which helps the knowledge constraint (S-DRI) run in a high-confidence window sequence. By doing so, a lower threshold can be used to detect the occurrence of forest disturbance, avoiding oversensitivity to spectral changes. When we attempted to detect forest disturbance using S-DRI alone for each pixel throughout the detection period without employing a moving window and DL time series classification, there was a significant decrease in OA of the test dataset. Specifically, the OA decreased to 68.1%, as expected.

The time series classification task is complicated by extraneous, erroneous, and unaligned data of variable length [46]. The moving window solves the problem of the fixed input data dimension of the time series classification model, and the priori knowledge constraint is used to determine the exact years of disturbance events. The window can be moved infinitely to process new images after the self-attention model has been trained, providing more efficient use of the forest detection data.

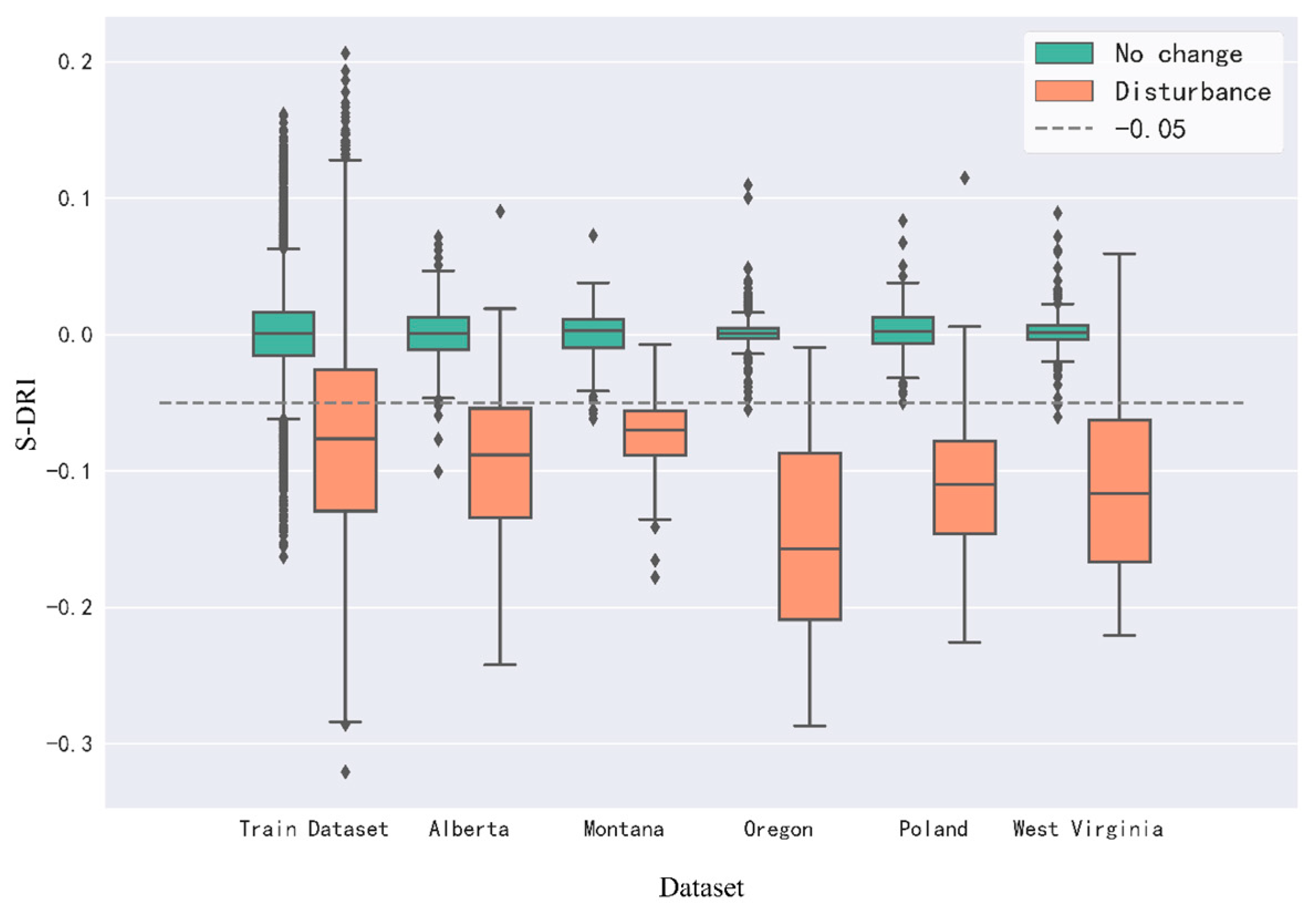
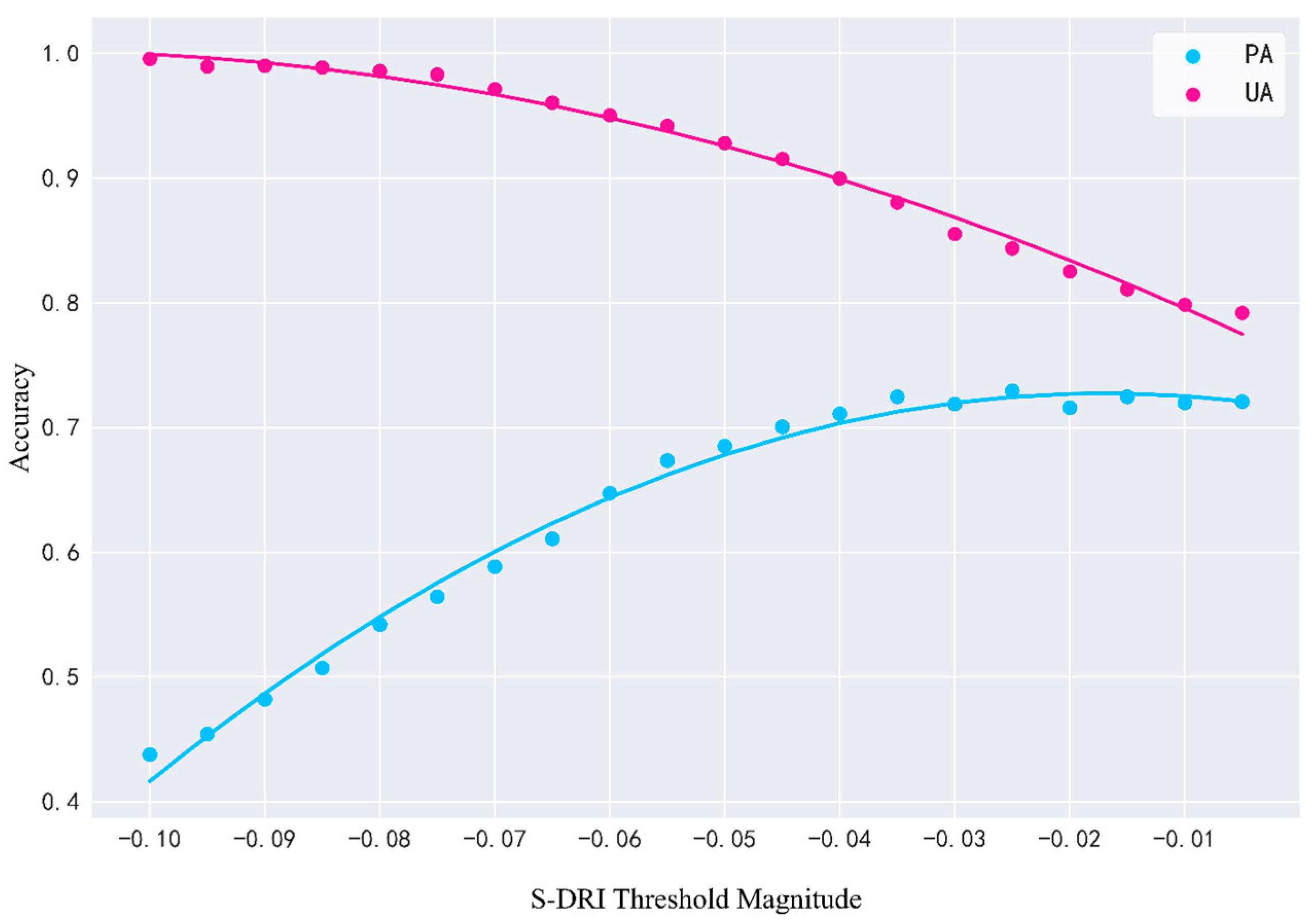
Optimizing the threshold for S-DRI allows for the detection of lower-magnitude disturbances while effectively distinguishing most noise, striking a balance between sensitivity and specificity. To demonstrate this briefly, the predefined threshold was fine-turned to evaluate the impact on our approach performance. We sequentially adjusted the threshold of S-DRI from −0.1 to 0 in intervals of 0.005 and evaluated the disturbance class PA and UA of the test dataset. As shown in Figure 12, when lower thresholds were used, low-magnitude disturbances and noise were removed, while significantly high-magnitude disturbances with distinctive features were retained. This resulted in lower UA and higher PA. With the increased S-DRI threshold, more of the low-magnitude disturbances can be effectively retained, and the UA correspondingly increases. Meanwhile, high thresholds allowed some noise to pass through constraints, resulting in lower PA. When the threshold is adjusted to a certain value (−0.035), most of the disturbance can be detected, and the UA does not increase, even if the threshold is adjusted again. However, as the threshold increases, it also allows more false disturbances to pass the detection, resulting in a continued decrease in UA. The threshold of S-DRI was the only parameter that needed to be adjusted when the algorithm was applied in different regions and could be adjusted by removing low-magnitude disturbances to obtain the required degree of disturbance map.

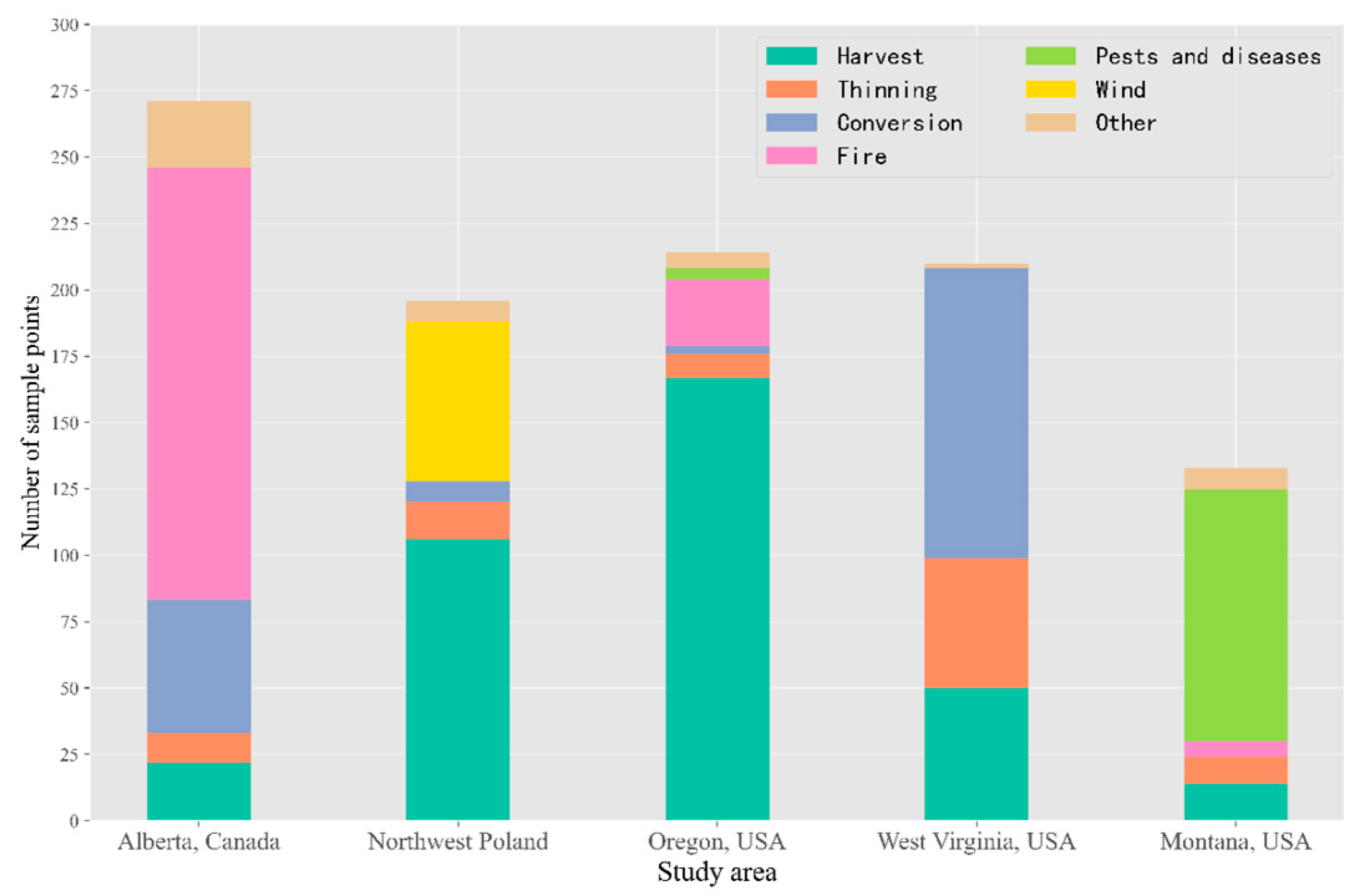
The accuracy provided in this study may be slightly underestimated because strict definitions were used in this study without allowing any leeway for time adjustments [78]. Disturbances that occur after the vegetation growth period are not detected by our approach and LandTrendr until the following year (e.g., one fire in Oregon is not detectable using both approaches). In the assessment of the results, temporal inconsistencies were considered to be omissions in the disturbance detection; therefore, all three approaches have a low UA for the no-change class. In addition, GFC detection only targets stand replacement disturbances, and non-stand replacement disturbances included in the test data also involve accuracy calculation, especially in Montana, where GFC can only correctly detect 31 out of 137 changed pixels, resulting in a lower OA.

When mapping the forest disturbance, our approach still suffers from some limitations. It is observed from the S-DRI threshold adjustment (Figure 12) that even with a higher S-DRI threshold, the approach only has about 70~75% PA, which is caused by the omission in the self-attention model or spectral index application limitations. Due to the low-magnitude disturbance area being rare with difficult visual interpretation, the forest disturbance agents in the randomly generated training samples mainly include the harvest, wildfire, and conversion [79]. Improving data quality and balancing the samples can enhance the capability of time series classification models to detect low-magnitude disturbances (thinning, pests, and diseases, etc.), although it requires more effort. Furthermore, the reduction in forest cover caused by factors, such as pests, diseases, and droughts, persists for several years. In subsequent studies, it is necessary to develop new conceptual definitions to describe the entire disturbance process. Cohen et al. [26] showed that the use of multiple spectral bands/indices is very beneficial for forest disturbance detection and may solve the problem that some disturbances cannot be monitored using a single band (e.g., due to the similarity of NBR index values between water and forests, it is difficult to detect disturbances where forests are converted into water). Multiple DL-based multivariate time series learning frameworks have been proposed, and using multiple indexes/bands to detect forest change should be considered in a future study [42]. During the later stages of our analysis of forest change (2018–2020), we identified an issue where the accuracy of the results became increasingly incorrect in all three models. This issue arose because spectral changes over multiple years continued to be an essential criterion for disturbance determination. However, time series constructed from composite images did not contain sufficient data at the end of the detection period, which contributed to decreased accuracy. The use of multi-source remote sensing data and a near-real-time change monitoring approach may solve this problem. This will be the focus of further work [58].

5. Conclusions

Detailed access to long time series and large areas of forest disturbances can be challenging without relying solely on the severity of the disturbance event itself. DL allows for the capture of subtle land changes and adaptation to complex temporal–spatial patterns. However, its use for detecting forest disturbances is not widespread. This study presents a novel approach that combines DL time series classification with prior knowledge constraint to address this issue. The integration of DL and prior knowledge constraint in window sequences with disturbance features allows for a reduction in processing changes caused by noise while enabling the detection of more low-magnitude disturbances. The prior knowledge constraint uses rules that consider temporal contextual information to accurately determine the year of the disturbance. The approach can be used for long time series analysis and is easily transferable to new regions without the need for complex parameter tuning. This study offers a fresh perspective on how DL can be used to comprehensively detect forest disturbances on a large scale.