Net Primary Productivity Estimation of Terrestrial Ecosystems in China with Regard to Saturation Effects and Its Spatiotemporal Evolutionary Impact Factors
Abstract
1. Introduction
2. Research Region and Data
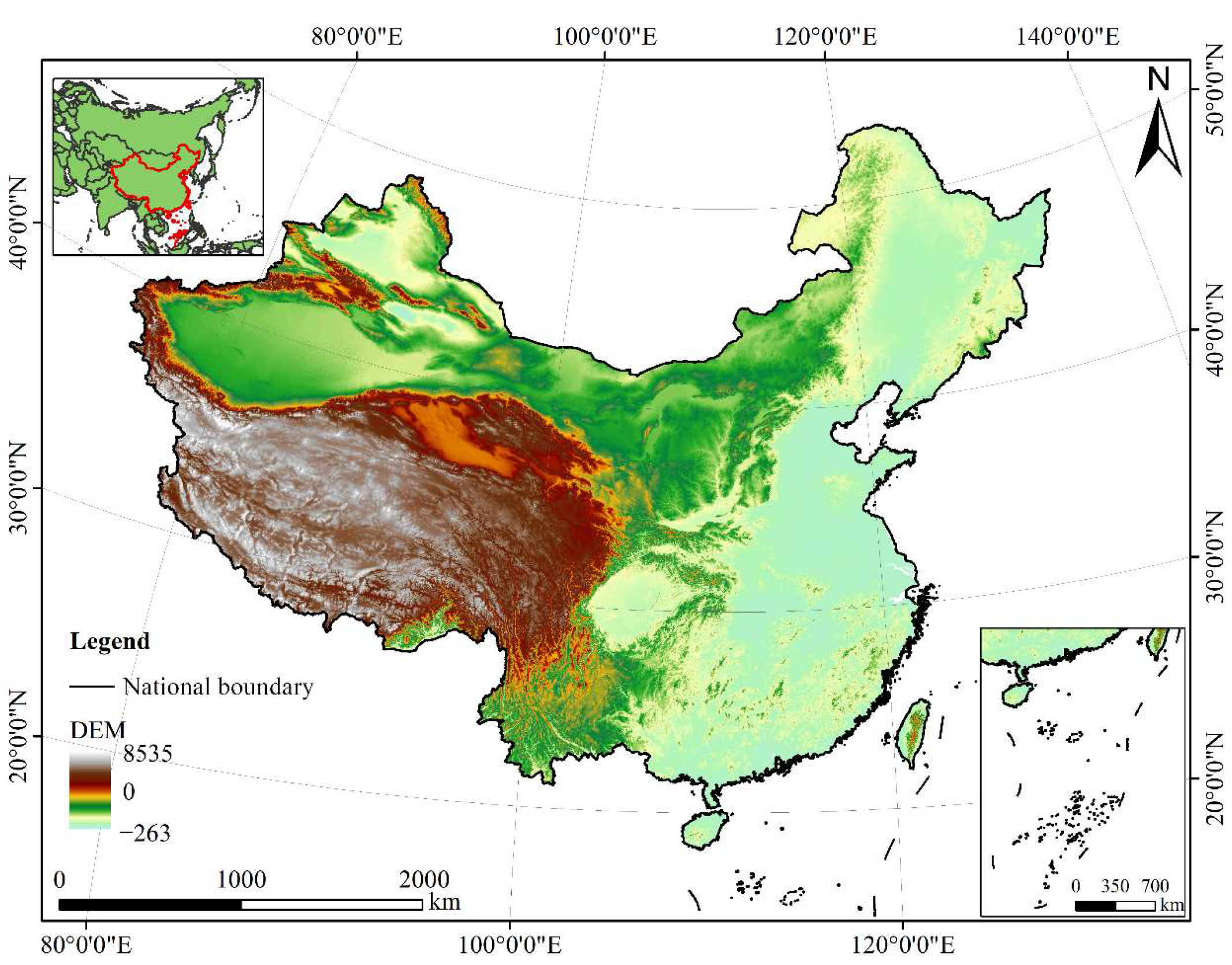
2.1. Research Region
2.2. Material and Processing
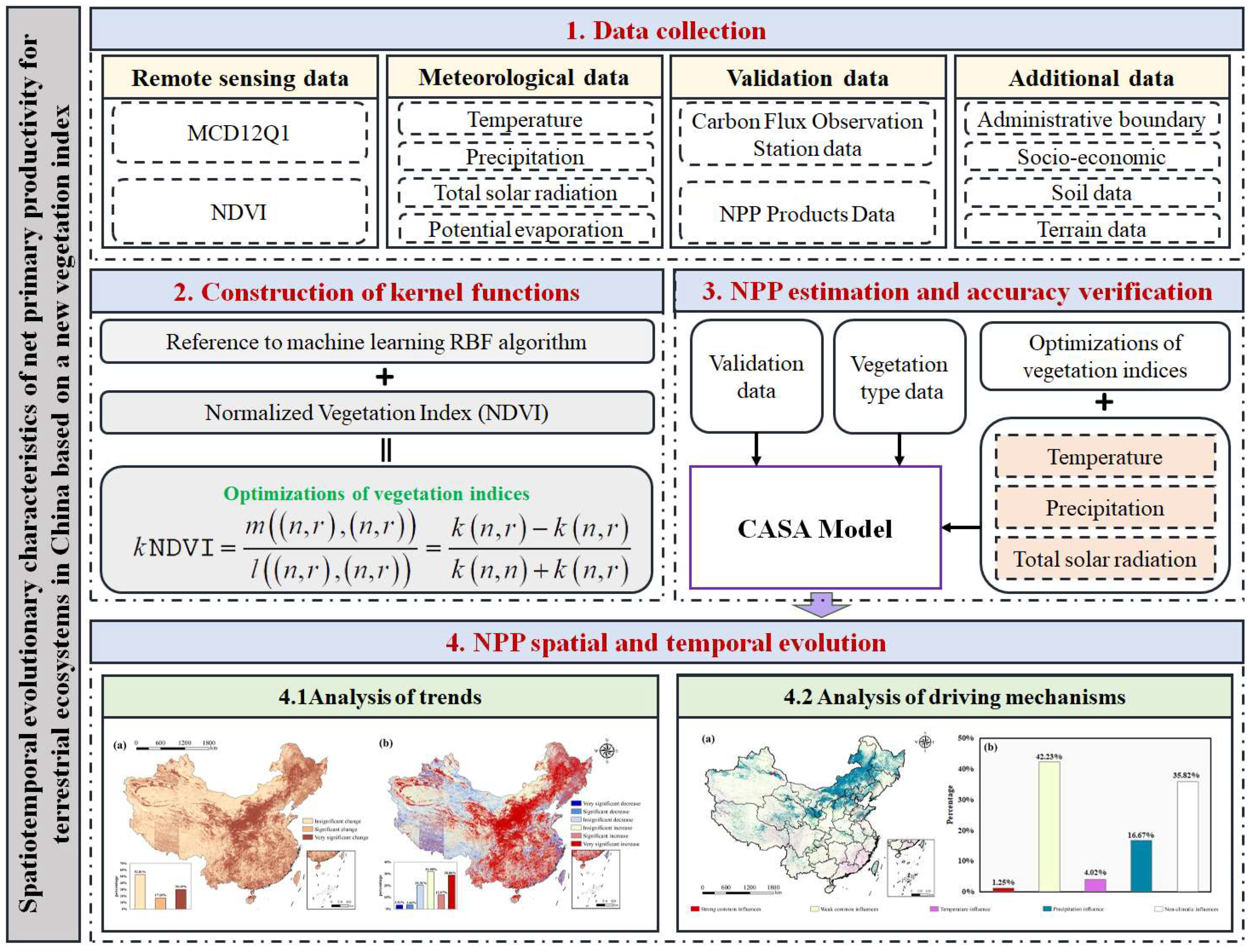
3. Methods
3.1. Construction of kNDVI
3.2. NPP Estimation Model
3.3. NPP Trend Analysis
3.4. Driving Mechanisms of NPP Changes
3.4.1. Response of NPP to Climatic Factors
3.4.2. The Role of Climate and Human Activities in NPP Changes
4. Results and Analysis
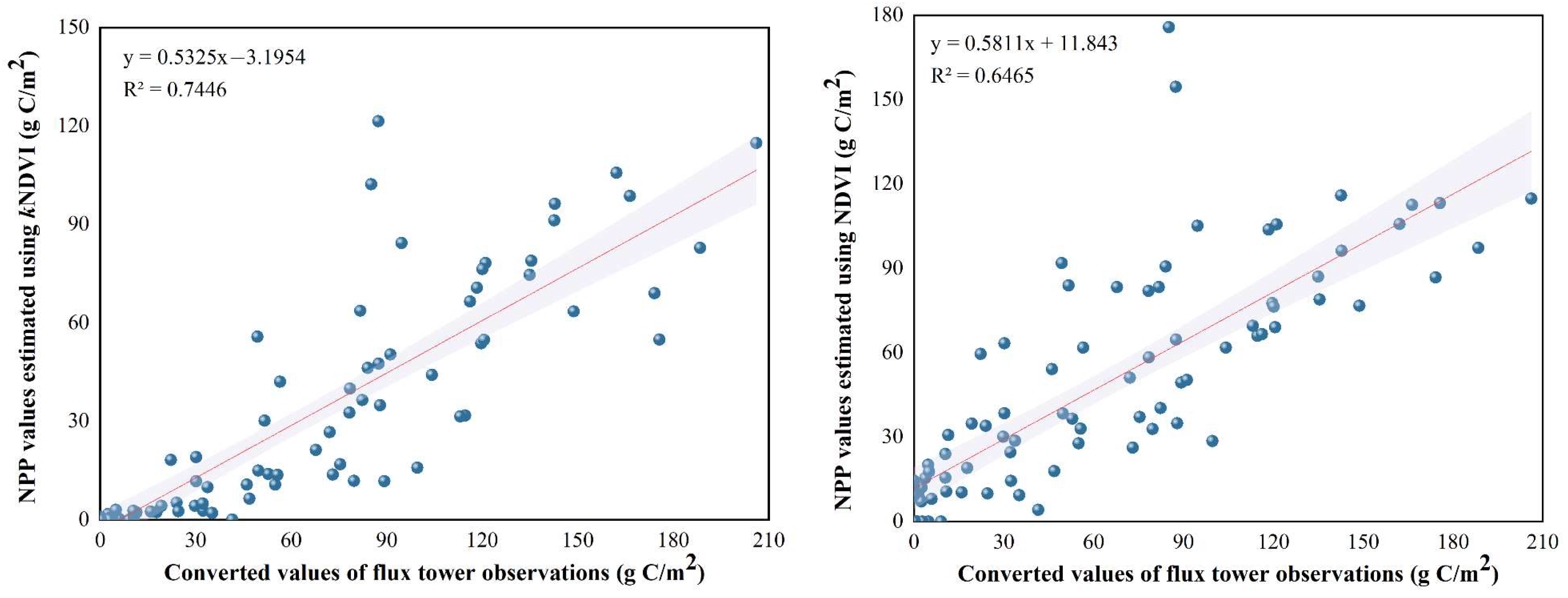
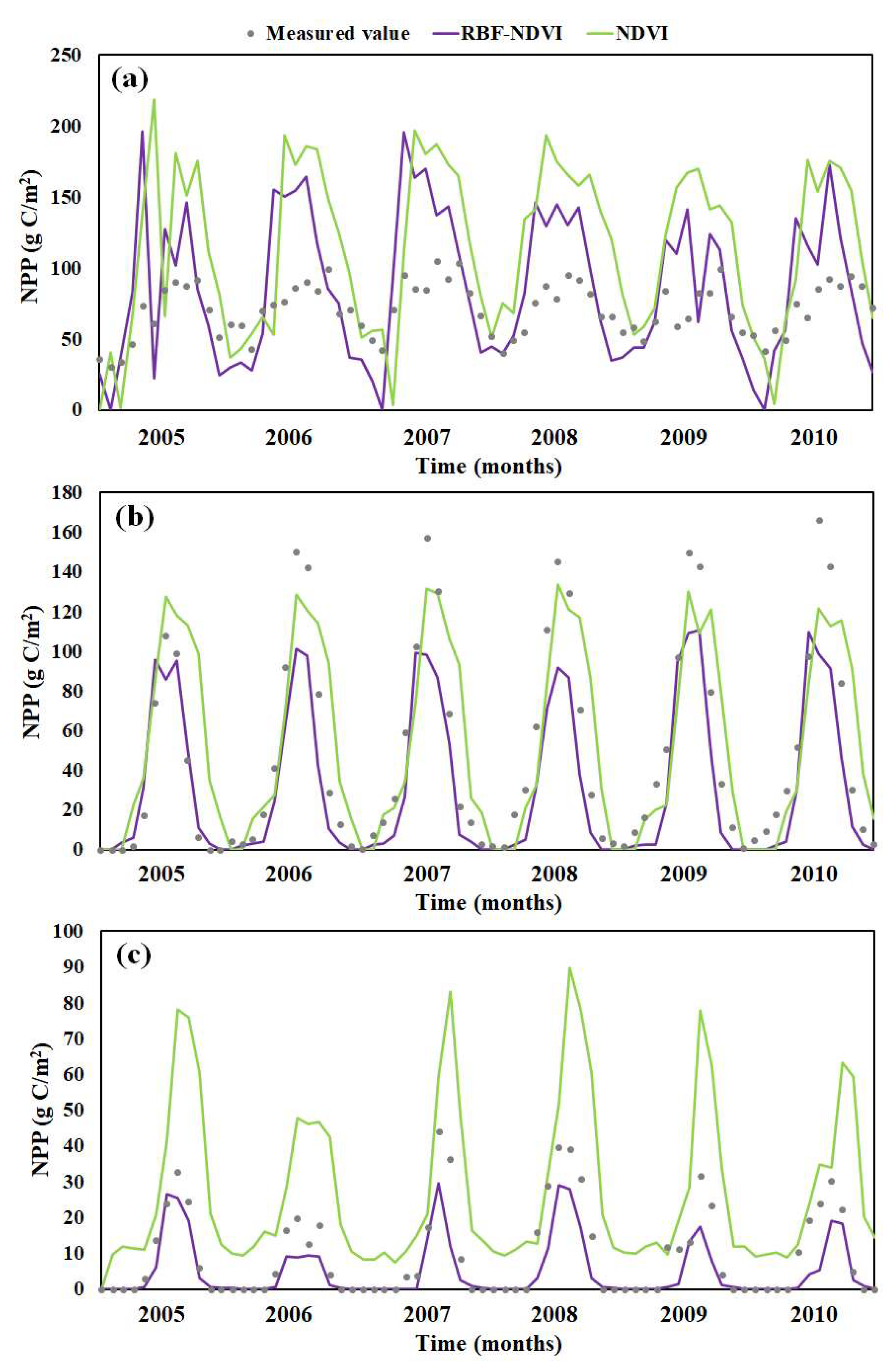
4.1. Accuracy Validation of NPP
4.2. Characteristics of Spatiotemporal Variation in NPP
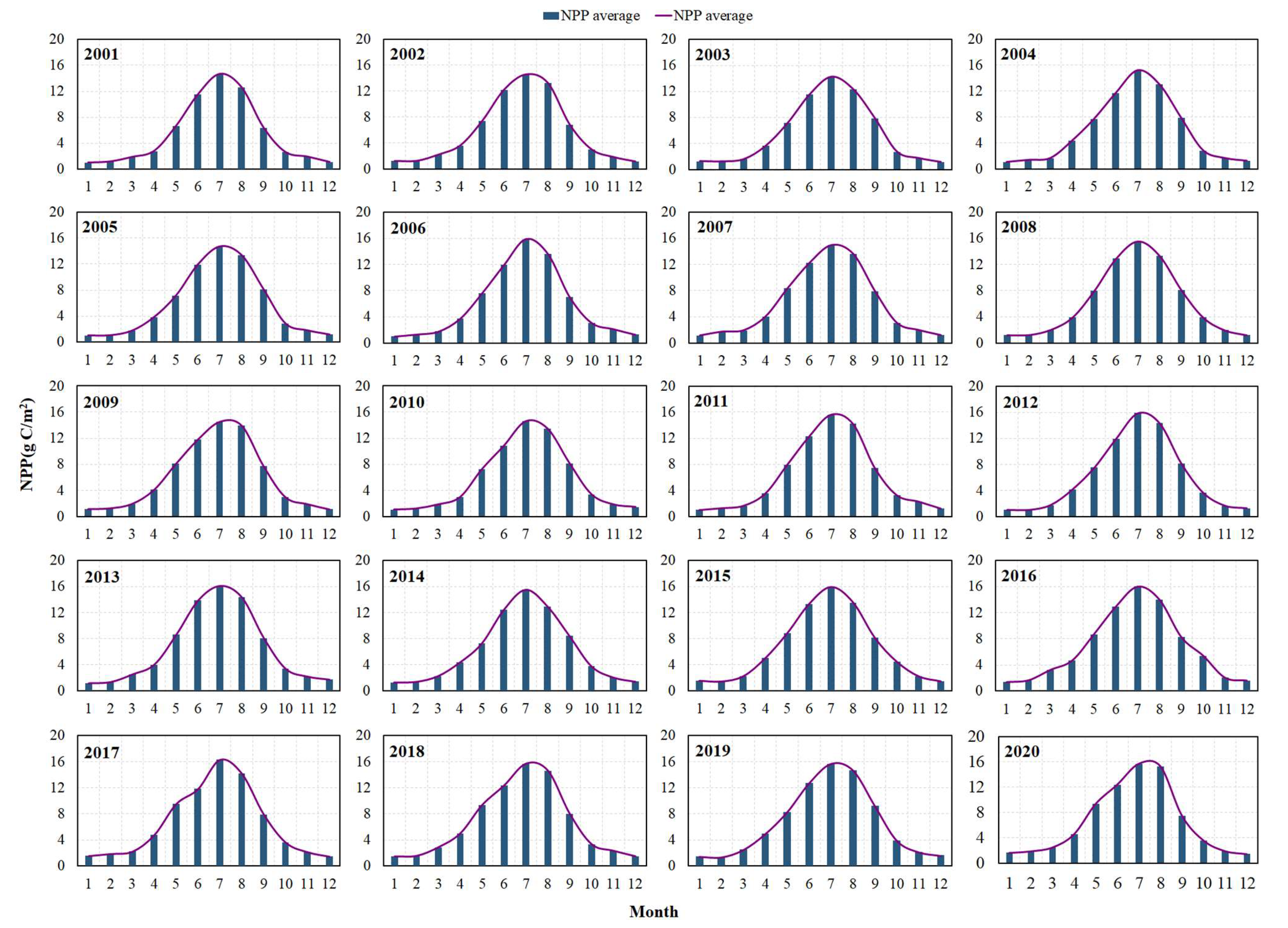
4.2.1. Temporal Trends
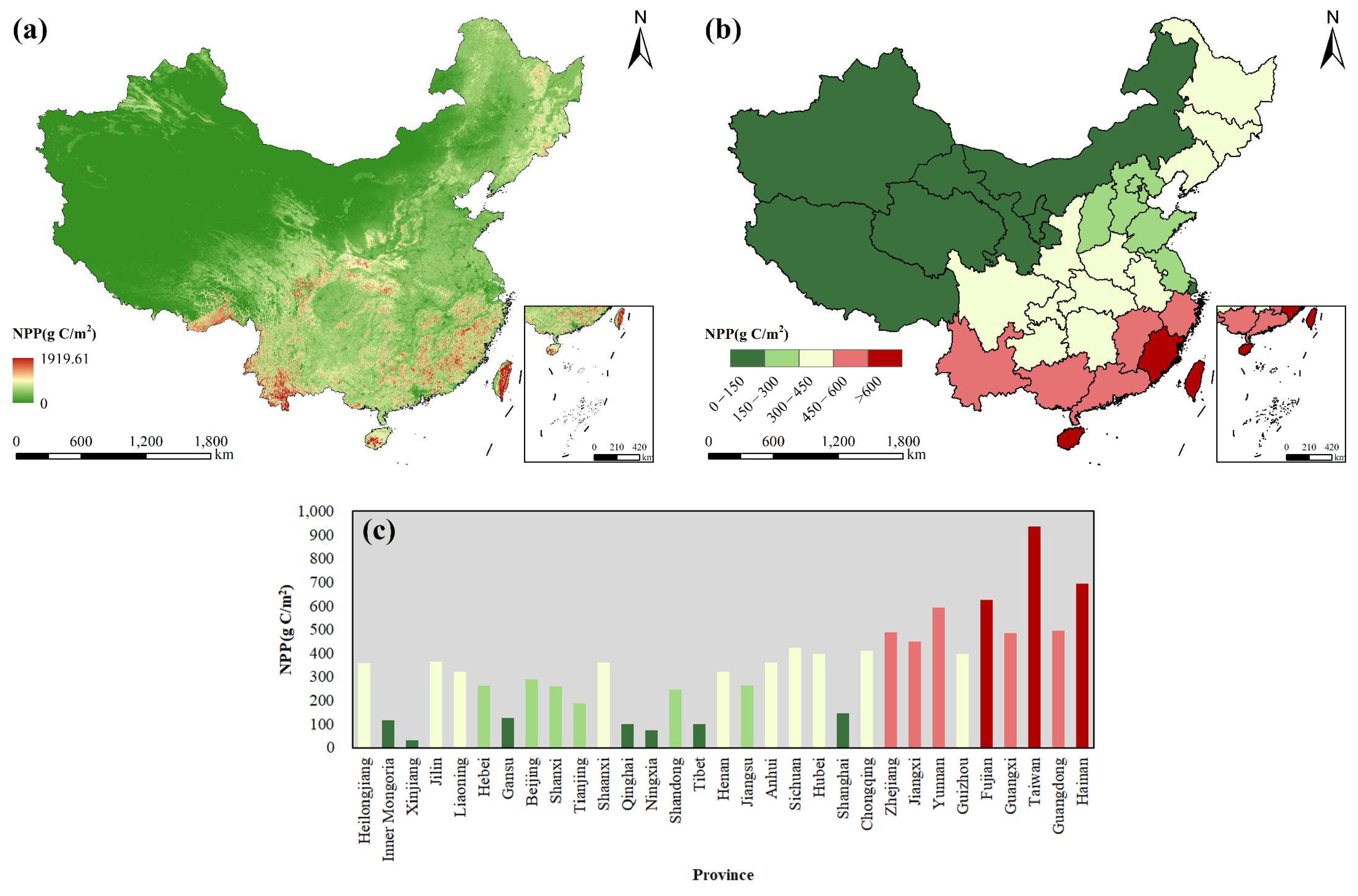
4.2.2. Spatial Distribution Characteristics
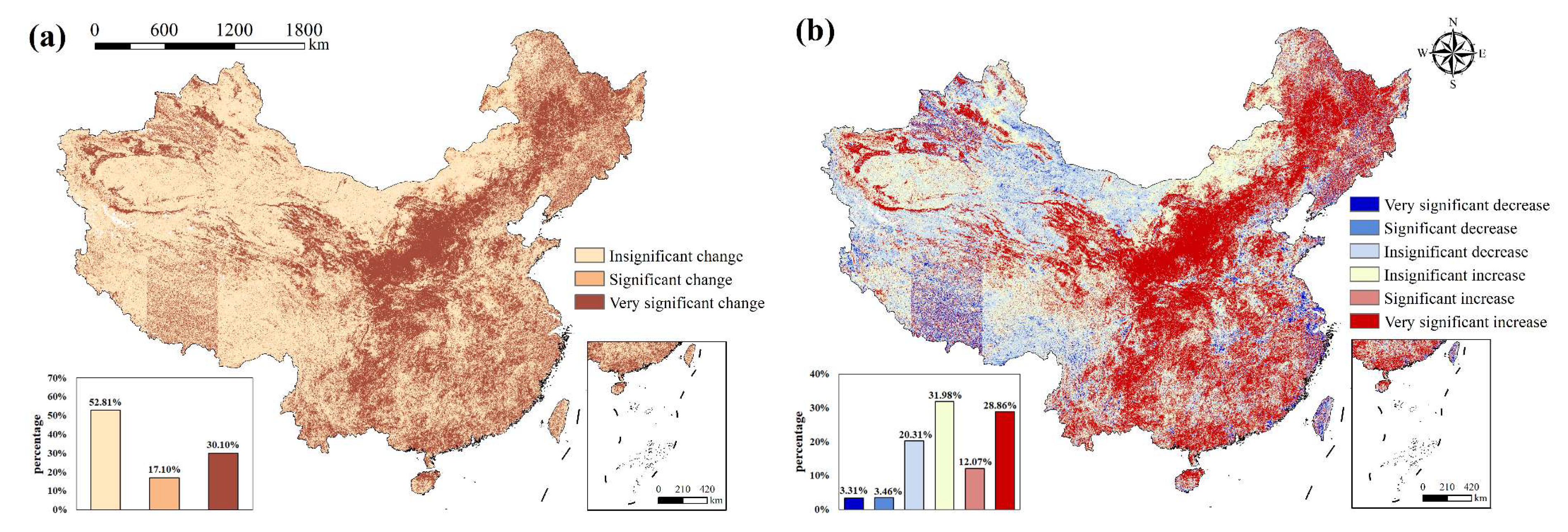
4.2.3. Spatial Variation Characteristics
4.3. Analysis of the Mechanisms Driving the Spatiotemporal Evolution of NPP in China in the Studied Period
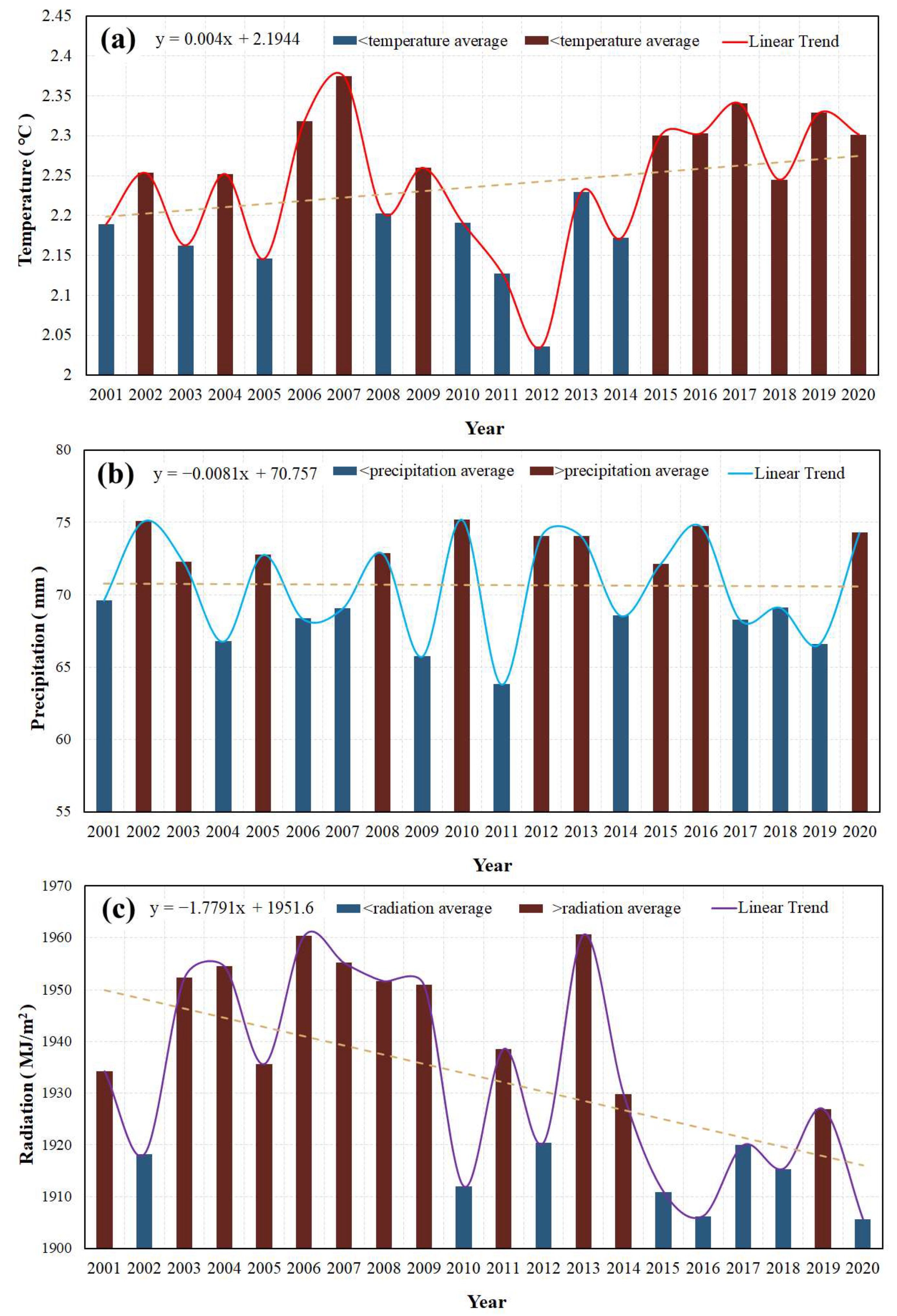
4.3.1. Trends in Climate Change and their Impact on Vegetation NPP
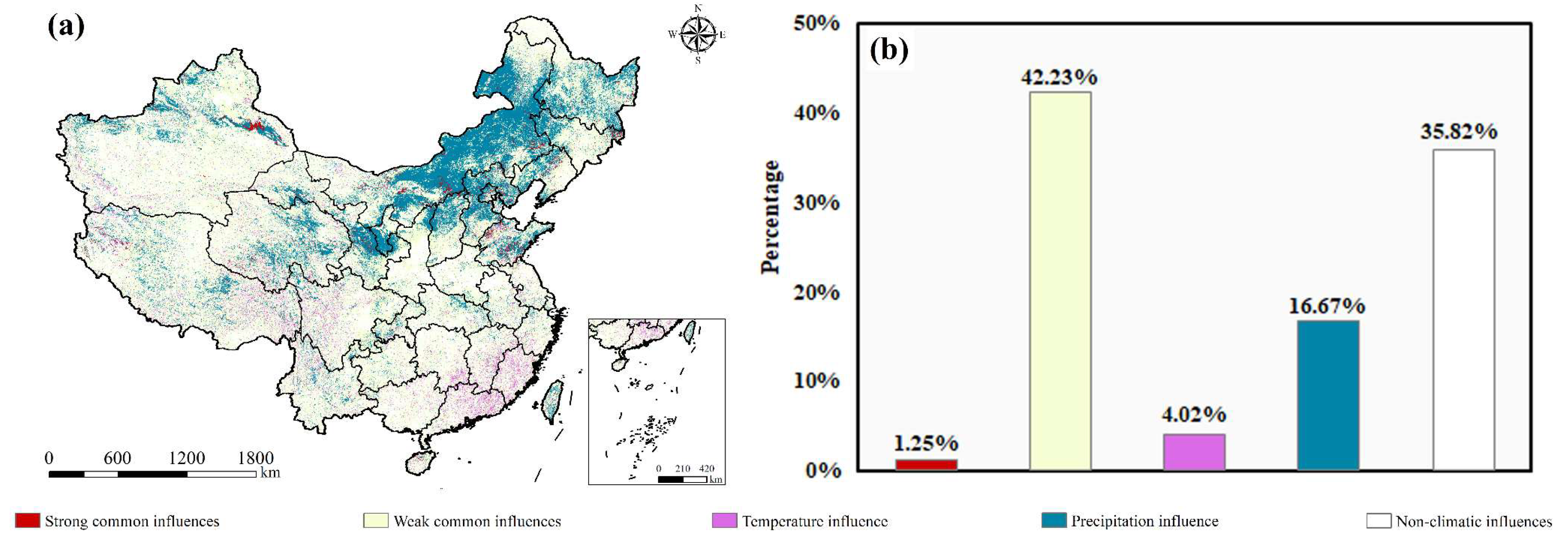
4.3.2. Relative Contributions of Climate and Human Activities to NPP Changes
5. Discussion
5.1. Relationship between Drivers and NPP Changes at Each Stage
5.2. Comparison with Other NPP Reports
5.3. Limitations and Prospects
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Y.; Hu, Q.; Zou, F. Spatio-Temporal Changes of Vegetation Net Primary Productivity and Its Driving Factors on the Qinghai-Tibetan Plateau from 2001 to 2017. Remote Sens. 2021, 13, 1566. [Google Scholar] [CrossRef]
- Liu, G.; Shao, Q.; Fan, J.; Ning, J.; Rong, K.; Huang, H.; Liu, S.; Zhang, X.; Niu, L.; Liu, J. Change Trend and Restoration Potential of Vegetation Net Primary Productivity in China over the Past 20 Years. Remote Sens. 2022, 14, 1634. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Wang, Q.; Du, X.; Li, J.; Gang, C.; Zhou, W.; Wang, Z. Evaluating the Responses of Net Primary Productivity and Carbon Use Efficiency of Global Grassland to Climate Variability along an Aridity Gradient. Sci. Total Environ. 2019, 652, 671–682. [Google Scholar] [CrossRef]
- Ning, K.; Chen, J.; Li, Z.; Liu, C.; Nie, X.; Liu, Y.; Wang, L.; Hu, X. Land Use Change Induced by the Implementation of Ecological Restoration Programs Increases Future Terrestrial Ecosystem Carbon Sequestration in Red Soil Hilly Region of China. Ecol. Indic. 2021, 133, 108409. [Google Scholar] [CrossRef]
- Zhang, F.; Zhang, Z.; Kong, R.; Chang, J.; Tian, J.; Zhu, B.; Jiang, S.; Chen, X.; Xu, C.Y. Changes in Forest Net Primary Productivity in the Yangtze River Basin and Its Relationship with Climate Change and Human Activities. Remote Sens. 2019, 11, 1451. [Google Scholar] [CrossRef]
- Redmann, R.E. Primary Productivity. In Encyclopedia of Entomology; Springer: Dordrecht, The Netherlands, 2008. [Google Scholar] [CrossRef]
- Running, S.W.; Hunt, E.R. Generalization of a Forest Ecosystem Process Model for Other Biomes, BIOME-BGC, and an Application for Global-Scale Models; Woodhead Publishing Limited: Shaxton, UK, 1993. [Google Scholar]
- Chen, W.; Chen, J.; Liu, J.; Cihlar, J. Atmospheric Disturbances I Mineralization • Canopy Radiation Model C, N CO:On C-Budget. Glob. Biogeochem. Cycles 2000, 14, 827–838. [Google Scholar] [CrossRef]
- David McGuire, A.; Melillo, J.M.; Kicklighter, D.W.; Pan, Y.; Xiao, X.; Helfrich, J.; Moore, B.; Vorosmarty, C.J.; Schloss, A.L. Equilibrium Responses of Global Net Primary Production and Carbon Storage to Doubled Atmospheric Carbon Dioxide: Sensitivity to Changes in Vegetation Nitrogen Concentration. Global Biogeochem. Cycles 1997, 11, 173–189. [Google Scholar] [CrossRef]
- Wilcox, B.P. Ecohydrology Bearing-Invited Commentary Transformation Ecosystem Change and Ecohydrology: Ushering in a New Era for Watershed Management. Ecohydrology 2010, 130, 126–130. [Google Scholar]
- Wang, C.; Jiang, Q.; Deng, X.; Lv, K.; Zhang, Z. Spatio-Temporal Evolution, Future Trend and Phenology Regularity of Net Primary Productivity of Forests in Northeast China. Remote Sens. 2020, 12, 3670. [Google Scholar] [CrossRef]
- Qi, S.; Chen, S.; Long, X.; An, X.; Zhang, M. Quantitative Contribution of Climate Change and Anthropological Activities to Vegetation Carbon Storage in the Dongting Lake Basin in the Last Two Decades. Adv. Sp. Res. 2023, 71, 845–868. [Google Scholar] [CrossRef]
- Zhou, Z.; Qin, D.; Chen, L.; Jia, H.; Yang, L.; Dai, T. Novel Model for NPP Prediction Based on Temperature and Land Use Changes: A Case in Sichuan and Chongqing, China. Ecol. Indic. 2022, 145, 109724. [Google Scholar] [CrossRef]
- Yin, C.; Luo, M.; Meng, F.; Sa, C.; Yuan, Z.; Bao, Y. Contributions of Climatic and Anthropogenic Drivers to Net Primary Productivity of Vegetation in the Mongolian Plateau. Remote Sens. 2022, 14, 3383. [Google Scholar] [CrossRef]
- Xiao, X.; Hollinger, D.; Aber, J.; Goltz, M.; Davidson, E.A.; Zhang, Q.; Moore, B. Satellite-Based Modeling of Gross Primary Production in an Evergreen Needleleaf Forest. Remote Sens. Environ. 2004, 89, 519–534. [Google Scholar] [CrossRef]
- Bao, G.; Bao, Y.; Qin, Z.; Xin, X.; Bao, Y.; Bayarsaikan, S.; Zhou, Y.; Chuntai, B. Modeling Net Primary Productivity of Terrestrial Ecosystems in the Semi-Arid Climate of the Mongolian Plateau Using LSWI-Based CASA Ecosystem Model. Int. J. Appl. Earth Obs. Geoinf. 2016, 46, 84–93. [Google Scholar] [CrossRef]
- Liang, L.; Geng, D.; Yan, J.; Qiu, S.; Shi, Y.; Wang, S.; Wang, L.; Zhang, L.; Kang, J. Remote Sensing Estimation and Spatiotemporal Pattern Analysis of Terrestrial Net Ecosystem Productivity in China. Remote Sens. 2022, 14, 1902. [Google Scholar] [CrossRef]
- Bidoglio, G.; De Plano, A.; Avogadro, A.; Murray, C.N. Migration Behaviour and Chemical Speciation of Np and Am under Nuclear Waste Repository Conditions. Inorg. Chim. Acta 1984, 95, 1–3. [Google Scholar] [CrossRef]
- Xu, X.; Jiang, H.; Guan, M.; Wang, L.; Huang, Y.; Jiang, Y.; Wang, A. Vegetation Responses to Extreme Climatic Indices in Coastal China from 1986 to 2015. Sci. Total Environ. 2020, 744, 140784. [Google Scholar] [CrossRef]
- Wang, S.; Zhang, L.; Huang, C.; Qiao, N. An NDVI-Based Vegetation Phenology Is Improved to Be More Consistent with Photosynthesis Dynamics through Applying a Light Use Efficiency Model over Boreal High-Latitude Forests. Remote Sens. 2017, 9, 695. [Google Scholar] [CrossRef]
- Wu, W. The Generalized Difference Vegetation Index (GDVI) for Dryland Characterization. Remote Sens. 2014, 6, 1211. [Google Scholar] [CrossRef]
- Xue, J.; Su, B. Significant Remote Sensing Vegetation Indices: A Review of Developments and Applications. J. Sens. 2017, 2017, 17. [Google Scholar] [CrossRef]
- Shan, N.; Xi, L.; Zhang, Q.; Lin, N.; Xu, D.; Cao, B. Better Revisiting Chlorophyll Content Retrieval with Varying Senescent Material and Solar-Induced Chlorophyll Fluorescence Simulation on Paddy Rice during the Entire Growth Stages. Ecol. Indic. 2021, 130, 108057. [Google Scholar] [CrossRef]
- Kang, X.; Huang, C.; Zhang, L.; Zhang, Z.; Lv, X. Downscaling Solar-Induced Chlorophyll Fluorescence for Field-Scale Cotton Yield Estimation by a Two-Step Convolutional Neural Network. Comput. Electron. Agric. 2022, 201, 107260. [Google Scholar] [CrossRef]
- Camps-Valls, G.; Campos-Taberner, M.; Moreno-Martínez, Á.; Walther, S.; Duveiller, G.; Cescatti, A.; Mahecha, M.D.; Muñoz-Marí, J.; García-Haro, F.J.; Guanter, L.; et al. A Unified Vegetation Index for Quantifying the Terrestrial Biosphere. Sci. Adv. 2021, 7, eabc7447. [Google Scholar] [CrossRef] [PubMed]
- Shi, S.; Zhu, L.; Luo, Z.; Qiu, H. Quantitative Analysis of the Contributions of Climatic and Anthropogenic Factors to the Variation in Net Primary Productivity, China. Remote Sens. 2023, 15, 789. [Google Scholar] [CrossRef]
- Fu, J.; Gong, Y.; Zheng, W.; Zou, J.; Zhang, M.; Zhang, Z.; Qin, J.; Liu, J.; Quan, B. Spatial-Temporal Variations of Terrestrial Evapotranspiration across China from 2000 to 2019. Sci. Total Environ. 2022, 825, 153951. [Google Scholar] [CrossRef]
- Liu, J.; Wang, Z.; Duan, Y.; Li, X.; Zhang, M.; Liu, H.; Xue, P.; Gong, H.; Wang, X.; Chen, Y.; et al. Effects of Land Use Patterns on the Interannual Variations of Carbon Sinks of Terrestrial Ecosystems in China. Ecol. Indic. 2023, 146, 109914. [Google Scholar] [CrossRef]
- Kong, R.; Zhang, Z.; Huang, R.; Tian, J.; Feng, R.; Chen, X. Projected Global Warming-Induced Terrestrial Ecosystem Carbon across China under SSP Scenarios. Ecol. Indic. 2022, 139, 108963. [Google Scholar] [CrossRef]
- Su, S.; Zeng, Y.; Zhao, D.; Zheng, Z.; Wu, X. Optimization of Net Primary Productivity Estimation Model for Terrestrial Vegetation in China Based on CERN Data. Acta Ecol. Sin. 2022, 42, 1276–1289. [Google Scholar] [CrossRef]
- Zhu, W.; Pan, Y.; He, H.; Yu, D.; Hu, H. Simulation of Maximum Light Use Efficiency for Some Typical Vegetation Types in China. Chinese Sci. Bull. 2006, 51, 457–463. [Google Scholar] [CrossRef]
- Yin, C.; Chen, X.; Luo, M.; Meng, F.; Sa, C.; Bao, S.; Yuan, Z.; Zhang, X.; Bao, Y. Quantifying the Contribution of Driving Factors on Distribution and Change of Net Primary Productivity of Vegetation in the Mongolian Plateau. Remote Sens. 2023, 15, 1986. [Google Scholar] [CrossRef]
- Li, Y.; Xie, Z.; Qin, Y.; Zheng, Z. Estimating Relations of Vegetation, Climate Change, and Human Activity: A Case Study in the 400 Mm Annual Precipitation Fluctuation Zone, China. Remote Sens. 2019, 11, 1159. [Google Scholar] [CrossRef]
- Li, M.; Chu, R.; Shen, S.; Islam, A.R.M.T. Dynamic Analysis of Pan Evaporation Variations in the Huai River Basin, a Climate Transition Zone in Eastern China. Sci. Total Environ. 2018, 625, 496–509. [Google Scholar] [CrossRef]
- Zhang, M.; Yuan, N.; Lin, H.; Liu, Y.; Zhang, H. Quantitative Estimation of the Factors Impacting Spatiotemporal Variation in NPP in the Dongting Lake Wetlands Using Landsat Time Series Data for the Last Two Decades. Ecol. Indic. 2022, 135, 108544. [Google Scholar] [CrossRef]
- Tu, H.; Guli, J.; Yu, T.; Li, X.; Chen, B. Analysis of Spatio temporal Variation Characteristics and Influencing Factors of Net Primary Productivity in Terrestrial Ecosystems of China. Acta Ecol. Sin. 2023, 43, 1219–1233. [Google Scholar] [CrossRef]
- Yang, S.; Zhang, J.; Wang, J.; Zhang, S.; Bai, Y.; Shi, S.; Cao, D. Spatiotemporal Variations of Water Productivity for Cropland and Driving Factors over China during 2001–2015. Agric. Water Manag. 2022, 262, 107328. [Google Scholar] [CrossRef]
- An, X.; Jin, W.; Zhang, H.; Liu, Y.; Zhang, M. Analysis of Long-Term Wetland Variations in China Using Land Use/Land Cover Dataset Derived from Landsat Images. Ecol. Indic. 2022, 145, 109689. [Google Scholar] [CrossRef]
- Fan, J.; Li, D.; Zhou, H. Comparison of GLOPEM and MOD17A3NPP. J. Shaanxi Meteorol. 2013, 1, 21–25. [Google Scholar]
- Chen, P. Monthly 1-Km Raster Dataset of Net Primary Productivity of Chinese Terrestrial Ecosystems North of 18°N Latitude (1985–2015). J. Glob. Chang. Data Discov. 2019, 3, 35–41. [Google Scholar] [CrossRef]
- Liang, W.; Quan, Q.; Wu, B.; Mo, S. Response of Vegetation Dynamics in the Three-North Region of China to Climate and Human Activities from 1982 to 2018. Sustainability 2023, 15, 73. [Google Scholar] [CrossRef]
- Zhang, Y.; She, J.; Long, X.; Zhang, M. Spatio-Temporal Evolution and Driving Factors of Eco-Environmental Quality Based on RSEI in Chang-Zhu-Tan Metropolitan Circle, Central China. Ecol. Indic. 2022, 144, 109436. [Google Scholar] [CrossRef]
- Shi, Z.; Wang, Y.; Zhao, Q.; Zhang, L.; Zhu, C. The Spatiotemporal Changes of NPP and Its Driving Mechanisms in China from 2001 to 2020. Ecol. Environ. Sci. 2022, 31, 2111–2123. [Google Scholar]
- Ma, Z.; Cui, H.; Ge, Q. Prediction of Net Primary Productivity Change Pattern in China Based on Vegetation Dynamic Models. Acta Geogr. Sin. 2022, 77, 1821–1836. [Google Scholar] [CrossRef]
- Li, D.; Wang, Z. The Characteristics of NPP of Terrestrial Vegetation in China Based on MOD17A3 Data. Ecol. Environ. Sci. 2018, 27, 397–405. [Google Scholar] [CrossRef]
- Naeem, S.; Zhang, Y.; Tian, J.; Qamer, F.M.; Latif, A.; Paul, P.K. Quantifying the Impacts of Anthropogenic Activities and Climate Variations on Vegetation Productivity Changes in China from 1985 to 2015. Remote Sens. 2020, 12, 1113. [Google Scholar] [CrossRef]
- Cervantes-Duarte, R.; González-Rodríguez, E.; Funes-Rodríguez, R.; Ramos-Rodríguez, A.; Torres-Hernández, M.Y.; Aguirre-Bahena, F. Variability of Net Primary Productivity and Associated Biophysical Drivers in Bahía de La Paz (Mexico). Remote Sens. 2021, 13, 1644. [Google Scholar] [CrossRef]
- Sun, J.; Niu, H.; Yuan, M. Spatial Pattern Change and Analysis of NPP in Terrestrial Vegetation Ecosystem in China. Trans. Chinese Soc. Agric. Mach. 2020, 51, 162–168. [Google Scholar] [CrossRef]
- Martínez, B.; Sánchez-Ruiz, S.; Campos-Taberner, M.; García-Haro, F.J.; Gilabert, M.A. Exploring Ecosystem Functioning in Spain with Gross and Net Primary Production Time Series. Remote Sens. 2022, 14, 1310. [Google Scholar] [CrossRef]
- Rafique, R.; Zhao, F.; De Jong, R.; Zeng, N.; Asrar, G.R. Global and Regional Variability and Change in Terrestrial Ecosystems Net Primary Production and NDVI: A Model-Data Comparison. Remote Sens. 2016, 8, 177. [Google Scholar] [CrossRef]
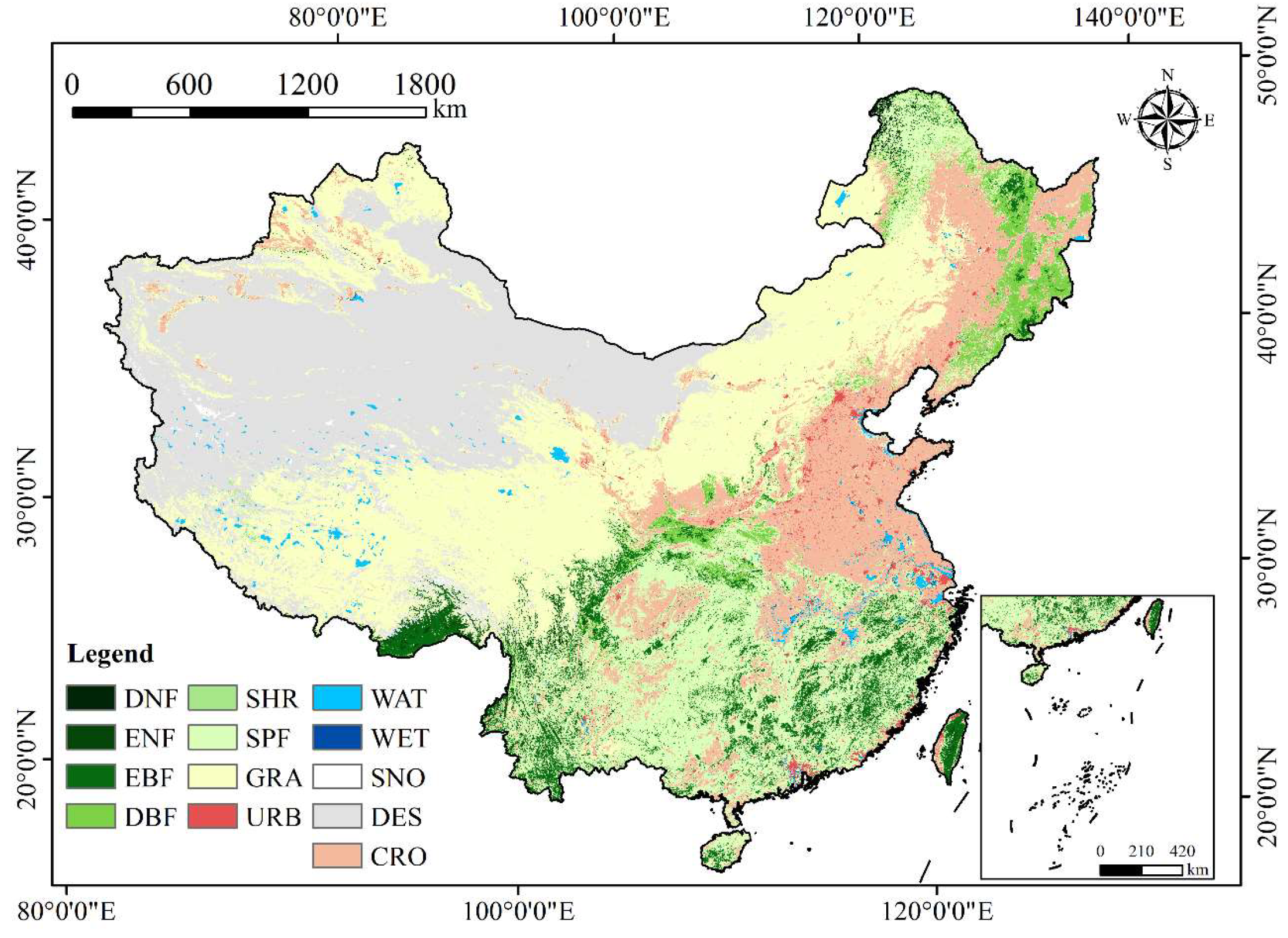





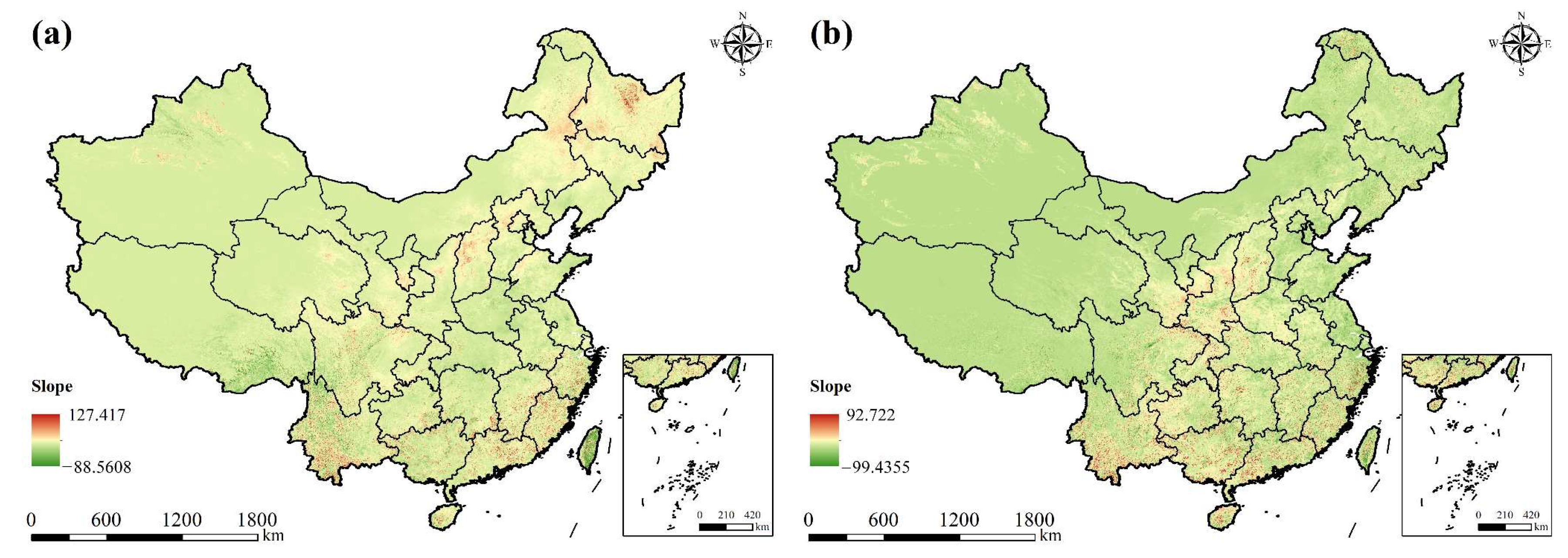

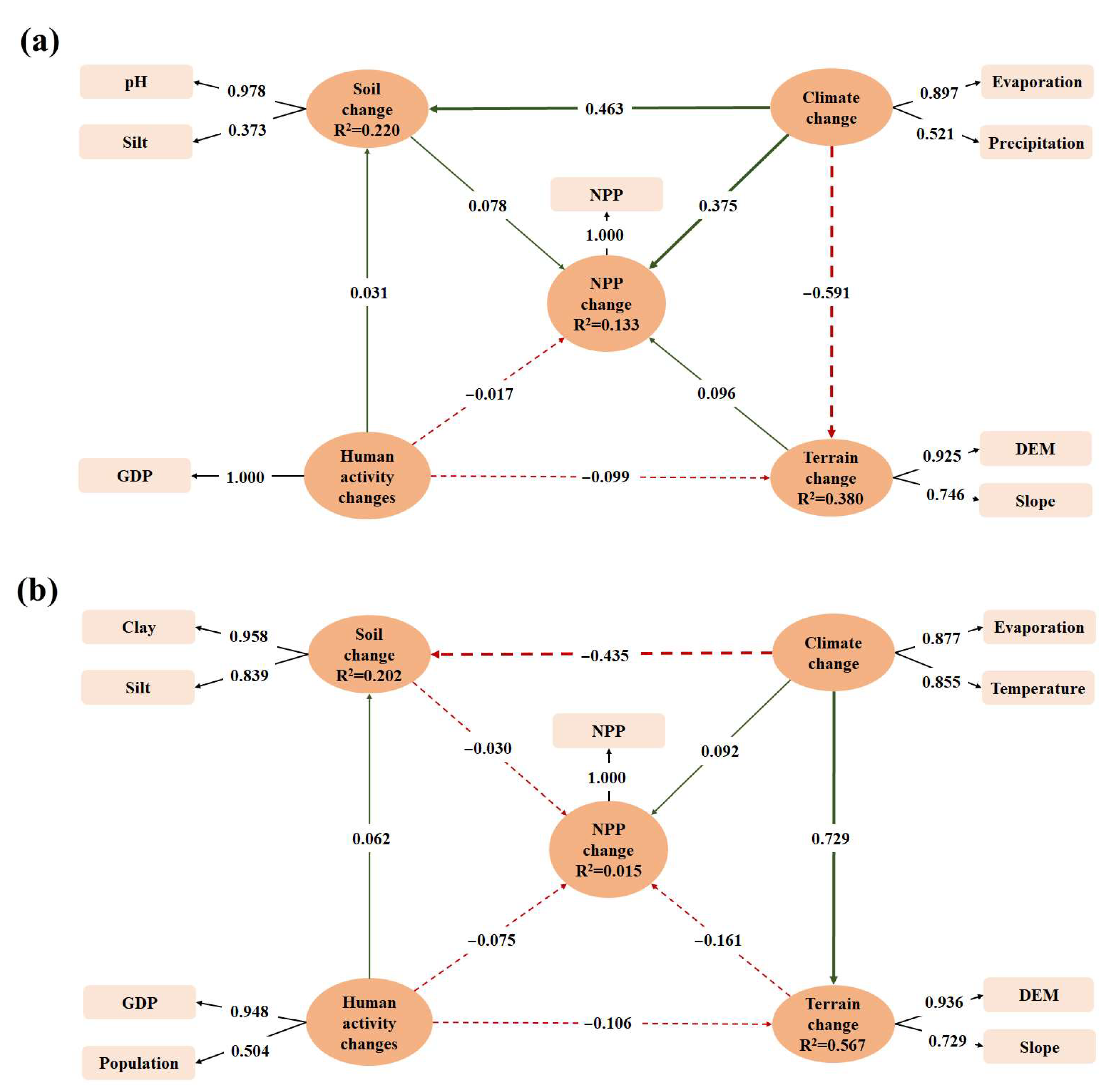
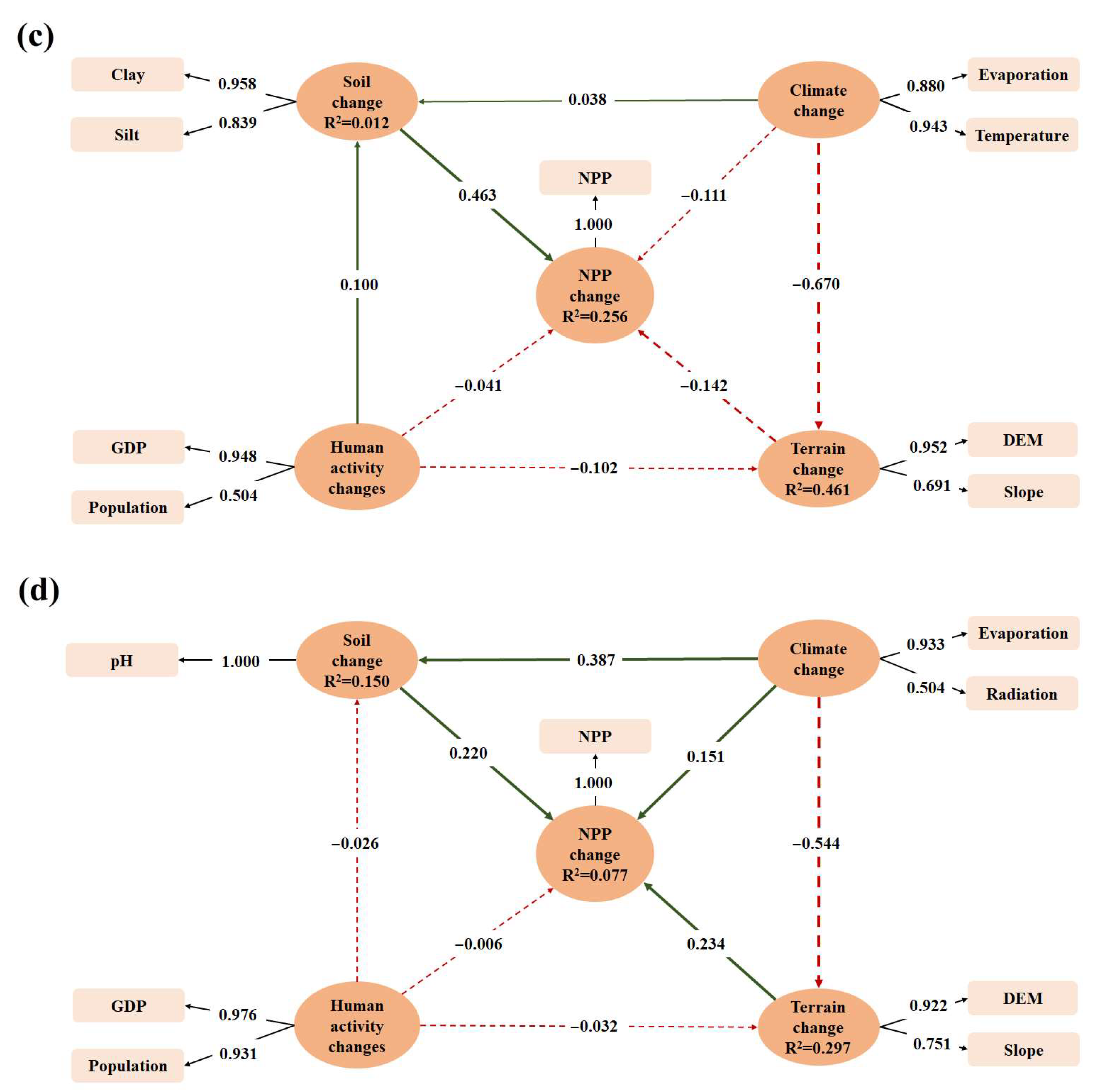
| Class | Class Names | Acronym | εmax |
|---|---|---|---|
| 1 | Deciduous Needleleaf Forest | DNF | 0.485 |
| 2 | Evergreen Needleleaf Forest | ENF | 0.389 |
| 3 | Evergreen Broadleaf Forest | EBF | 0.985 |
| 4 | Deciduous Broadleaf Forest | DBF | 0.692 |
| 5 | Shrublands | SHR | 0.429 |
| 6 | Sparse forests | SPF | 0.475 |
| 12 | Grasslands | GRA | 0.542 |
| 13 | Urban and built-up | URB | 0.542 |
| 15 | Water | WAT | 0.542 |
| 16 | Wetlands | WET | 0.542 |
| 17 | Snow and ice | SNO | 0.542 |
| 20 | Deserts | DES | 0.542 |
| 21 | Croplands | CRO | 0.542 |
| Station Name | Longitude (°) | Latitude (°) | Vegetation Type |
|---|---|---|---|
| Changbaishan | 128.096 | 42.402 | Forest |
| Qianyanzhou | 115.063 | 26.747 | Forest |
| Dinghushan | 112.536 | 23.173 | Forest |
| Xishuangbanna | 101.266 | 21.950 | Forest |
| Haibei | 101.331 | 37.665 | Shrub |
| Dang Xiong | 91.066 | 30.497 | Grassland |
| Inner Mongolia | 116.675 | 43.545 | Grassland |
| Yucheng | 116.640 | 36.958 | Farmland |
| Data Types | Data Sources |
|---|---|
| vegetation type | https://doi.org/10.5067/MODIS/MCD12Q1.006 (accessed on 10 August 2022) |
| NDVI | http://www.vito-eodata.be (accessed on 6 June 2022) |
| temperature | http://www.geodata.cn (accessed on 2 September 2022) |
| precipitation | http://www.geodata.cn (accessed on 2 September 2022) |
| evaporation | http://www.geodata.cn (accessed on 2 September 2022) |
| radiation | https://doi.org/10.24381/cds.68d2bb30 (accessed on 30 August 2022) |
| carbon flux | http://www.cnern.org.cn (accessed on 30 October 2022) |
| MOD17A3HGF | https://doi.org/10.5067/MODIS/MOD17A3HGF.061 (accessed on 30 October 2022) |
| ChinaNPP_1985_2015 | http://www.geodoi.ac.cn/ (accessed on 30 October 2022) |
| GLO-PEM NPP | https://www.resdc.cn/ (accessed on 30 October 2022) |
| administrative divisions | http://ngcc.sbsm.gov.cn/ (accessed on 15 June 2022) |
| soil | http://dx.doi.org/10.3334/ORNLDAAC/1247 (accessed on 19 September 2022) |
| GDP | https://www.resdc.cn/ (accessed on 19 September 2022) |
| population | https://www.resdc.cn/ (accessed on 19 September 2022) |
| DEM | http://www.gscloud.cn/ (accessed on 15 June 2022) |
| Driving Factor | FC | PT | PP |
|---|---|---|---|
| Strong common influence | FC ≤ F0.05 | PT < P0.05 | PP < P0.05 |
| Weak common influence | FC ≤ F0.05 | PT > P0.05 | PP > P0.05 |
| Temperature influence | FC ≤ F0.05 | PT < P0.05 | PP > P0.05 |
| Precipitation influence | FC ≤ F0.05 | PT > P0.05 | PP > P0.05 |
| Non-climatic influence | FC ≥ F0.05 | / | / |
| Time Periods | 2001–2005 | 2005–2010 | 2010–2015 | 2015–2020 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Construct | VIF | Loading | CR | AVE | VIF | Loading | CR | AVE | VIF | Loading | CR | AVE | VIF | Loading | CR | AVE |
| Soil | 0.669 | 0.548 | 0.712 | 0.569 | 0.896 | 0.811 | ||||||||||
| pH | 1.030 | 0.978 | 1.030 | 0.925 | * | * | 1.028 | 1.000 | ||||||||
| Clay | * | * | * | * | 1.729 | 0.958 | * | * | ||||||||
| Silt | 1.030 | 0.373 | 1.030 | 0.533 | 1.729 | 0.839 | * | * | ||||||||
| Climate | 0.685 | 0.538 | 0.857 | 0.750 | 0.908 | 0.832 | 0.703 | 0.563 | ||||||||
| Evaporation | 1.008 | 0.897 | 1.335 | 0.877 | 1.820 | 0.880 | 1.027 | 0.933 | ||||||||
| Temperature | * | * | 1.335 | 0.855 | 1.820 | 0.943 | * | * | ||||||||
| Precipitation | 1.008 | 0.521 | * | * | * | * | * | * | ||||||||
| Radiation | * | * | * | * | * | * | 1.027 | 0.504 | ||||||||
| Human activity | – | – | 0.738 | 0.607 | 0.713 | 0.576 | 0.953 | 0.910 | ||||||||
| GDP | 1.000 | 1.000 | 1.107 | 0.976 | 1.042 | 0.948 | 3.222 | 0.976 | ||||||||
| Population | * | * | 1.107 | 0.521 | 1.042 | 0.504 | 3.222 | 0.931 | ||||||||
| Terrain | 0.827 | 0.707 | 0.824 | 0.704 | 0.814 | 0.692 | 0.827 | 0.707 | ||||||||
| DEM | 1.238 | 0.925 | 1.241 | 0.936 | 1.236 | 0.952 | 1.235 | 0.922 | ||||||||
| Slope | 1.238 | 0.746 | 1.241 | 0.729 | 1.236 | 0.691 | 1.235 | 0.751 | ||||||||
| Study | Remote-Sensing Indicator Sources | Impact Factors |
|---|---|---|
| This study | NDVI (MOD13Q1) | temperature, precipitation, solar radiation, evaporation, GDP, population, pH, clay, silt, DEM, slope |
| [45] | NPP (MOD17A3HGF) | - |
| [48] | - | temperature, precipitation |
| [44] | NDVI (AVHRR/MOD13A3) | precipitation, relative humidity, sunshine hours, temperature, wind speed |
| [43] | NPP (MOD17A3HGF) | temperature, precipitation |
| [36] | NPP (MOD17A3HGF) | temperature, precipitation |
| [49] | FPAR (MCD43A1 and MCD43A2) | temperature, precipitation |
| [46] | ANPP (ChinaNPP_1985_2015) | temperature, precipitation |
| [47] | NPP(Aqua-MODIS) | temperature, Chlorophyll-a, photosynthetically available radiation, relative surface density, wind stress curl, salinity, nitrates, phosphates |
| [50] | NDVI (GIMMS) | CO2 concentration, climate, land use change |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, S.; Zhang, H.; Zhang, M. Net Primary Productivity Estimation of Terrestrial Ecosystems in China with Regard to Saturation Effects and Its Spatiotemporal Evolutionary Impact Factors. Remote Sens. 2023, 15, 2871. https://doi.org/10.3390/rs15112871
Qi S, Zhang H, Zhang M. Net Primary Productivity Estimation of Terrestrial Ecosystems in China with Regard to Saturation Effects and Its Spatiotemporal Evolutionary Impact Factors. Remote Sensing. 2023; 15(11):2871. https://doi.org/10.3390/rs15112871
Chicago/Turabian StyleQi, Shuaiyang, Huaiqing Zhang, and Meng Zhang. 2023. "Net Primary Productivity Estimation of Terrestrial Ecosystems in China with Regard to Saturation Effects and Its Spatiotemporal Evolutionary Impact Factors" Remote Sensing 15, no. 11: 2871. https://doi.org/10.3390/rs15112871
APA StyleQi, S., Zhang, H., & Zhang, M. (2023). Net Primary Productivity Estimation of Terrestrial Ecosystems in China with Regard to Saturation Effects and Its Spatiotemporal Evolutionary Impact Factors. Remote Sensing, 15(11), 2871. https://doi.org/10.3390/rs15112871












