Abstract
As the fundamental regulator of energy exchange in the vegetation–soil–atmosphere circulation system, soil moisture is a key parameter for drought monitoring and is indispensable to the land surface hydrological processes. In order to overcome the constraints of the Perpendicular Drought Index, PDI (performs poorly over the fields with dense vegetation and hard to construct the soil line), and the Temperature Vegetation Drought Index, TVDI (requires similar atmospheric forcing and large enough dimension of mapping area), in soil moisture monitoring, a new drought index (Normalized Temperature Drought Index, NTDI) is proposed to explore the spatiotemporal changes of soil moisture by substituting red and near-infrared reflectances with vegetation index and normalized land surface temperature on the basis of the PDI framework. Victoria, Australia, was selected as the study area as it experiences many severe droughts and has been affected for more than ten years. Time series of satellite-based data were applied to evaluate the effectiveness and applicability of the NTDI at the regional scale. Results indicated that the expression of the soil line representing the water condition of the bare soil is easier to obtain in the new trapezoid framework and has good fits with the coefficients of determination (R2) of more than 0.8. Compared with PDI, TVDI and Modified PDI (MPDI) at the cropping sites, NTDI exhibits a relatively better performance in soil moisture monitoring for most days where the R2 achieved can reach to more than 0.7 on DOY 242, 254 and 272. Meanwhile, spatial–temporal mappings of the four drought indices from satellite data were conducted, and the NTDI presented the slightly seasonal variation and effectively described the real spatial characteristics of regional drought. Overall, the NTDI seems to a viable approach and can provide insight into spatial and temporal soil moisture monitoring at different scales.
1. Introduction
Drought is a multiattribute and long-term disaster characterized by prolonged water shortage, which can lead to severe influence on sustainable development of resources and environment, especially agricultural production and socioeconomic activities [1,2]. The severe degree and extent of drought are determined by its strength, time of duration, spatiotemporal distribution and economic situations in the local area [3]. Agricultural drought monitoring is tied to global food security and is recognized as one of the most significant contributions to humans, as seen in the definition of short-period drought of the topsoil during a vital moment during the growth season. Therefore, how to realize the real-time and effective estimation of agricultural drought has drawn increasing attention from scientists all over the world.
Drought is now becoming one of the most common climate disasters in Australia, and stream flows would possibly expect to drop by 5–45% in Victoria’s western watersheds by 2030 [4]. According to the Australian Bureau of Meteorology, many regions of Australia were still in significant drought as at late 2019. More than eight catastrophic droughts have struck Victoria, the second smallest but most densely inhabited state in Australia. Many areas of Victoria may continue to be affected for more than ten years. Policymakers and scientists have given quantitative drought evaluation and prediction a lot of scientific attention during the last few decades. On the basis of regional hydrologic records and meteorological observations, many traditional drought monitoring models were created, such as the Standardized Precipitation Index (SPI), the Rainfall Anomaly Index (RAI) and the Standardized Precipitation Evapotranspiration Index (SPEI) [5,6,7,8]. Although these models provide valuable drought information by spatial interpolation of sample data on unsampled locations, the results are often poorly distributed and are occasionally not available for timely drought detection, which can pose high uncertainties in water stress or drought monitoring.
Compared with the conventional methods, the remote sensing technique is regarded as an effective way to monitor soil moisture (SM) status and drought conditions. It can be applied to monitor land surface parameters, for example, albedo, vegetation indices (VIs) and land surface temperature (LST), etc. These models typically use different optical bands to compute LST and VIs from satellite data. The Normalized Difference Vegetation Index (NDVI) represents the level of chlorophyll content and vegetation growth. It has been extensively used for drought modelling and significant connections between timely integrated NDVI and related drought factors including precipitation and SM [9,10,11]. Numerous NDVI-based indicators also have been proposed including the Vegetation Condition Index (VCI) and the Anomaly Vegetation Index (AVI) [12,13]. However, NDVI is easily saturated and strongly influenced by soil background over sparse vegetation-covered regions. A time lag also frequently occurs between NDVI response and drought [14,15]. The satellite-derived LST effectively indicates energy exchange in the soil–atmosphere circulation system at large scales and responses relatively to the sensitive energy flux caused by closed stomata of stressed plants through transpiration [16,17]. Many LST-based indices were used to investigate water stress and monitor drought such as the Temperature Condition Index (TCI), the Crop Water Stress Index (CWSI) and Normalized Difference Temperature Index (NDTI) [18,19,20]. LST is particularly responsive to the fluctuations in SM over lower vegetation covered areas, but the vegetation canopy severely influences the connection between LST and SM over densely vegetation covered areas [3]. In general, LST typically increases and SM decreases when NDVI decreases, regardless of other factors in the development of drought. Collectively, LST and NDVI constitute a trapezoid feature space and provide real-time approaches for the quantitative exploration of drought monitoring. The Temperature Vegetation Dryness Index (TVDI) has been used according to the frames of the NDVI-LST space [21]. Given the complexity and limitations of the NDVI-LST space, the Perpendicular Drought Index (PDI) was proposed by Ghulam et al., and near infrared (NIR) and red reflectances were used to construct a Red-NIR space according to the spectral patterns of SM [22]. Not long after, Ghulam et al. developed a modified Perpendicular Drought Index (MPDI) by considering the fraction of vegetation for regional vegetated surface drought estimation [23,24]. Zormand et al. evaluated the potential of PDI, MPDI and TVDI during 2003–2013 [25]. Results indicated that, compared to the monthly scale, PDI, MPDI and TVDI could better represent wet and dry conditions at the yearly scale, and SPI could be effectively replaced by MPDI for monitoring and mapping agricultural drought. Wang et al. used PDI and TVDI to construct the joint and combination models and monitored SM across the whole winter wheat season from sowing to harvesting [26]. Results demonstrated that the joint and combination models both performed well in SM estimation with the root mean squared error (RMSE) of 1.49% and 1.48% at 0–20 cm, respectively.
However, PDI performed poorly over heavily vegetated farmland and uneven terrain with different soil types. In MPDI, the vegetation reflectances in the NIR and red bands are site-specific and empirically determined. For the different vegetation growth, MPDI is easily affected by vegetation growth states, levels of stress and greenness, etc. In this present paper, the normalized LST-VI feature space is used to construct a new drought index according to the definition of PDI. The new drought index substitutes NIR and red reflectance with normalized LST and VI to improve its sensitivity to water variations and vegetation status. In this paper, intercomparison of SM estimates from the new drought index, PDI, MPDI and TVDI is performed using field observations and satellite data over the whole of Victoria, Australia. Then, the maps of the four drought indices are presented based on two kinds of satellite data. Finally, the effects of different spatial resolutions of the satellite data on the new drought index are discussed.
2. Materials
2.1. Characteristics of the Study Area
The research is conducted in the Victoria state located in the south-eastern part of Australia, which covers a total of 237,659 km² (Figure 1). It extends in longitude from 140°58′E to 149°59′E and in latitude from 33°59′S to 39°12′S with an altitude of 1000~2000 m. The land cover types in this area are complex including predominantly cereal crops, pasture/grassland and woody vegetation. The woody vegetation contains softwood plantations, hardwood, remnant vegetation and native forests, which are mostly found in the Victorian Alps and Big Desert Wilderness Area. The pasture/grassland and crops are primarily farmed in Victoria’s western, northern, and centre, but they are also increasingly being planted in the region’s heavy rainfall areas in the south. In Victoria, the weather can be semiarid moderate with scorching summers or temperate and chilly around the coast. The warmest areas in Victoria are the Mallee and upper Wimmera, with typical winter temperatures of 15 °C and 32 °C in summer. There are places in Victoria that are colder than others, such as the Victorian Alps, where temperatures in winter are less than 9 °C and in the highest parts are below 0 °C. The rainy period is generally in winter from July to August. The mean annual rainfall in certain areas of the northeast surpasses 1800 mm but is just 280 mm or less in the Mallee, where summer precipitation is greater. Many areas of Victoria have seen substantial rainfall deficits recently, and the Bureau of Meteorology (BOM) predicts that this will lead to a 20–40% increase for the occurrence of drought during the ensuing decades.

Figure 1.
Overview of study area and details of pasture and crop sites.
2.2. Datasets and Observations
2.2.1. MODIS Data
The Moderate Resolution Imaging Spectroradiometers (MODIS) is onboard the Aqua and Terra satellites that provides 36 bands and lots of products with worldwide coverage in 1–2 days. In order to obtain time series of monitoring the surface biophysical variables, the NDVI calculated from MOD09GA product and LST deduced from MOD11A1 product were chosen to monitor drought in semi-arid regions, which were both acquired from NASA website. The MOD09GA data are daily atmospheric correction reflectance products at 500 m resolution and the MOD11A1 data are daily LST with a spatial resolution of 1 km. The two products have been radiometrically corrected and fully calibrated. The MODIS Reprojection Tool (MRT) was performed to convert the original sinusoidal projection system to a common Universal Transverse Mercator (UTM) coordinate system and resample the MOD09GA images to unify the relative resolution using the nearest neighbour algorithm with a pixel size of 1 km × 1 km. As it is well known, cloud contamination strongly affects the satellite-derived NDVI and LST. Thus, in this study, daytime and cloud-free MOD09GA and MOD11A1 data for a total of 18 days in 2019 were selected to eliminate the effects of clouds and missing pixels. Table 1 shows the details of 18 MODIS images including overpass time, date and day of year (DOY).

Table 1.
Details of MODIS images for 18 days and four corresponding Landsat-8 data in 2019.
2.2.2. Landsat-8 Data
Landsat satellite has two payloads including Operational Land Image (OLI) and Thermal Infrared Sensor (TIRS) with 11 spectral bands and a 16-day recycle period. The multispectral data has spatial resolution of 30 m, while the TIRS has two bands at 100 m resolution. All Landsat-8 data were collected from the USGS website. Radiometric correction and atmospheric correction for multispectral bands were carried out by ENVI 5.3 software. In this study, the Landsat-8 images on 1 January, 26 June, 14 September and 30 December were selected to match the dates of MODIS data. Table 1 shows the details of the four Landsat-8 images. The multispectral and thermal data were radiometric calibration in ENVI 5.3 to implement the conversion from digital number (DN) to radiance. Then, the FLAASH Atmospheric Correction toolbox was used to conduct the atmospheric correction for the Landsat-8 radiance images. Finally, the four atmospheric correction images were geometrically corrected using ground control points (GCPs). In order to establish the NDVI-LST feature space using Landsat-8 data, further data-processing steps were required: (1) all images were resampled to unify the spatial resolution to 30 m for multispectral and thermal bands; (2) NDVI values were deduced from the NIR and red bands, and a subset corresponding to the research site was relatively accomplished; (3) thermal bands of Landsat-8 data were used to retrieve LST values based on the monowindow algorithm [27]; (4) finally, the elevations were applied to calibrate the LST to eliminate the effects of topography and solar radiation [28,29].
2.2.3. Field Measurements
The field measurements including SM and soil temperature were obtained from Agriculture Victoria with SM probes installed on a range of cropping and pasture sites across Victoria. Sensors on the capacitance probes manufactured in South Australia recorded absolute soil water content every hour, which helps the crop planting industry to make early decisions in a period of time through monthly analysis. These data were plotted to show the change of soil water content with time. At each site, eight measurements were taken from eight probes, and the collected data were sent to the server through the mobile phone network. The server stores the data and makes it available for analysis using drawing software. The SM measuring probes in cropping regions measured areas every 10 cm with the depth ranging from 30 cm to 1 m, while the pasture monitoring probe was 80 cm long and had 8 sensors inside, which provided soil temperature and SM content every 10 cm. Eight cropping monitoring sites were evenly distributed in northern and western Victoria, and seven pasture monitoring sites were located in central and southern part of Victoria. Figure 2 shows the SM observations for 18 days at each cropping site. It is obvious from Figure 1 that the SM fluctuates seasonally in most cropping monitoring sites except for Werrimul, Ouyen and Speed, located in northwest Victoria. Hamilton has a wide range of SM values from 0.1 to 0.4 cm3/cm3. It is easily inferred that the SM value has a growing trend from northwest to southwest Victoria in winter. In addition, meteorological data such as humidity, wind speed and precipitation were also obtained at each site. Meanwhile, to reduce the influences of terrain undulation on the temperature, digital elevation model (DEM) data providing a consistent and topographic maps of all land surfaces between 56°S and 60°N were used in this study. Each tile was in GeoTIFF format at 90 m resolution. The DEMs of all regions over the whole of Victoria were collected and mosaicked together.
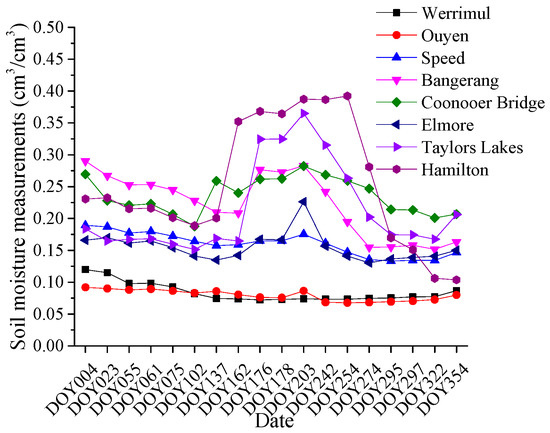
Figure 2.
SM observations for 18 days at cropping sites.
3. Methodology
3.1. The Red–NIR Spectral Space
The vegetation canopy intensively absorbs the incident radiances in the red band and strongly reflects the NIR wavelength. Thus, the reflectance in the NIR spectral region becomes higher as the vegetation density thickens, which can significantly reflect the information about the vegetation. Therefore, various VIs were generated from the Red-NIR spectral space, such as the NDVI, the Ratio Vegetation Index (RVI) and the Difference Vegetation Index (DVI) [30]. In addition, the location of a random pixel depends on not only vegetation cover but also water status. As illustrated in Figure 3, the pixels corresponding to satellite data are distributed in a triangular framework. For pixels completely covered by bare soil, with the increase in the red reflectance values, the amount of SM decreases distinctly, forming a certain line in the Red-NIR space, called the soil line. L is a line passing through the origin of the spectral space and is perpendicular to the soil line. The PVI, representing the distance from the soil line to a given pixel, was proposed to depict vegetation cover. As the PVI values increase, the land cover types vary from the bare soil to the partial and full vegetation cover. The other two edges, defined as the wet and dry edges, were produced to represent the smallest and largest water stress areas over various vegetation cover, respectively [31].
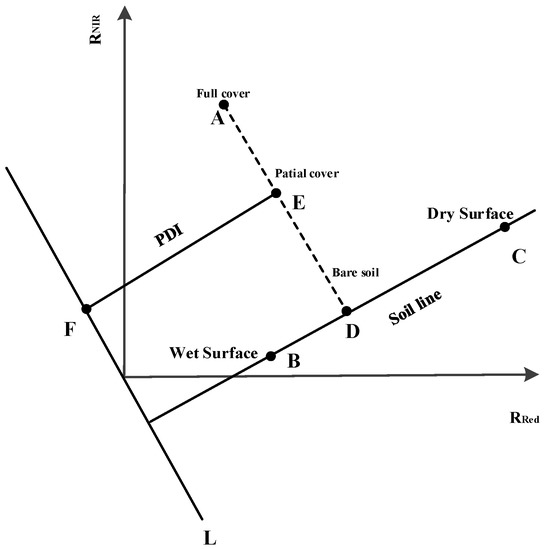
Figure 3.
The Red-NIR spectral space [22].
In order to consider the interaction mechanism between vegetation and soil in the spectral space, Ghulam et al. proposed the PDI according to the scattering characteristics of remote sensing imagery [22]. The equation of the PDI can be expressed as follows:
where and represent the surface reflectances of NIR and red bands retrieved from satellite data. is the slope of the soil line, which is related to the land cover conditions of the research region. The PDI is rather effective for SM retrieval and drought monitoring over bare soil, while some limitations hinder the application of PDI in areas covered by dense vegetation. Therefore, Ghulam et al. developed the MPDI on the basis of the PDI by introducing the vegetation fraction concept [23,24]. The MPDI can be calculated in the following form:
where and stand for the surface reflectances of pure vegetation in the NIR and red bands, which are usually set to 0.05 and 0.5 [24]. is the vegetation coverage, which can be calculated using NDVI [32]. The MPDI fully considers the vegetation growth and SM conditions to improve drought monitoring accuracy in areas with various vegetation cover. Zhang et al. validated the MPDI using SM measurements at different depths of soil layers in Henan province, China, and Zormand et al. compared the PDI and MPDI to monitor drought in northeast Iran during 2003–2013 [25,33].
3.2. The LST–NDVI Feature Space
As shown in Figure 4, the scatterplots of NDVI and LST constitute a triangle shape when the research area is wide enough to accommodate a large range of surface SM and fraction vegetation coverage. In the NDVI-LST space, LST is shown on the x-axis, and NDVI is displayed on the y-axis. Similarly, as shown in the Red-NIR spectral space in Figure 3, pixels with low LST and high NDVI values represent the dense vegetation coverage, which is distributed around the upper vertex of the triangle. From the upper vertex to the lower two vertices, the two lines also indicate the wet and dry edges, respectively. The dry edge stands for minimum evapotranspiration or SM, while the wet edge means maximum SM and potential evapotranspiration under various land cover types. The base of the triangle shows the direction of SM status from water-saturated soil to dry bare soil.
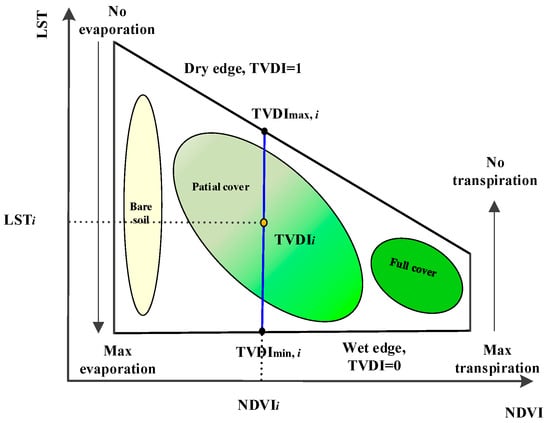
Figure 4.
The NDVI-LST feature space [21].
Sandholt et al. developed the TVDI to investigate SM and drought status based the NDVI-LST feature space [21]. The TVDI is obtained as follows:
where and are the highest and lowest LSTs corresponding to a given NDVI. The expressions of and are shown in the following form:
where , , and are empirical coefficients, which can be estimated by linear regression analysis. Many studies were conducted to monitor drought according to TVDI characterized with performance of SM and vegetation [34,35,36,37]. Meanwhile, in order to improve the SM monitoring accuracy, many improvements about the TVDI conducted from satellite data were also performed in recent years [38,39,40,41,42,43].
3.3. The NDVI–LSTnor Feature Space
For the dry edge in NDVI-LST space, the principle of the triangle in Figure 4 is that is expected to have a negative relationship with variations of NDVI. However, for the pixels in regions that are covered by bare soil, the scatterplots of LST apparently deviate from the main trend of the dry edge [14]. Compared with the original triangular NDVI-LST space, Liu et al. also discovered that the feature space was biparabolic, and LST seemed to be positively correlated with changes of NDVI over the low biomass vegetation-covered regions [44,45]. Therefore, the base of the triangle shown in Figure 4 would not perform as a horizontal line. With the increase in NDVI and LST, the positions of the pixels in this line move away from dry to wet bare soil. Thus, the line might be regarded as the soil line in the NDVI-LST space.
Therefore, the NDVI-LST space seems to be similar to the conceptual triangular Red-NIR spectral space shown in Figure 3. In order to further investigate the common characteristics between the two spaces, the LST requires normalization to produce comparable SM, and the values of normalized LST vary from 0 to 1 [46,47]. The observed minimum and maximum LSTs are used to normalize LST, and they are usually fixed for a given NDVI when the limiting edges of the study area are determined. The normalized LST can be calculated using the following formula:
where is the normalized LST.
As illustrated in Figure 5, the NDVI–LSTnor feature space is newly established when the NDVI values are displayed against the LSTnor values for pixels covered from bare soil to fully vegetation. Similarly, pixels with low LSTnor and high NDVI values are scattered around the upper vertex of the triangle. From the upper vertex to the lower two vertices, the left line is the wet edge indicating the maximum water availability over different land cover conditions, while the right line is the dry edge with the minimum SM. Thus, compared with the pixels around the dry edge, those located closer to the coordinate origin have lower water stress. The pixels distributed around the bare soil represent the soil line, perpendicular to the iso-lines produced by pixels with equal SM values. The line can be characterized as follows:
where and are the slope and intercept of the soil line. It should be noted that soil cover, particle size and organic matter highly affect the extraction of the soil line. Thus, the application of the soil line equation extracted from satellite data is site-specific and invalid globally. It should be considered that in most studies, the corresponding position of the soil line is relatively important and different for any study region and satellite image.

Figure 5.
The NDVI–LSTnor feature space.
3.4. Design of the New Drought Index
Similar framework can be found when the NIR and red reflectances in Figure 3 are substituted with NDVI and LSTnor in Figure 5, respectively. Water availability can be expressed with the distance of the specific pixel to the line passing through the coordinate origin and perpendicular to the soil line. Therefore, referring to the definition of PDI, a new index called normalized temperature drought index (NTDI) was firstly proposed and expressed in the following:
With respect to extremely wet soil or a water body, the positions of the pixels are close to the coordinate origin, representing that the distance is the least amount with smallest value of NTDI and largest amount of SM. As the pixel moves away from the origin towards the dry edge along the iso-lines parallel to the soil line, the higher values the NTDI has, the lower moisture content the soil possesses. Extremely dry surface has the furthest distance from the origin, where the drought value generally reaches to the maximum.
The flowchart of constructing the four drought indices is presented in Figure 6. Compared with the PDI, MPDI and TVDI, the NTDI has the following advantages: (1) highly sensitive to SM and effectively a reflection of water variations in comparison with PDI and MPDI; (2) easier to construct the soil line and find the fitting expression; (3) the boundary fitting between the wet and dry edges in a specific space is not necessary; and (4) the drought index can be used over the sparsely vegetated or bare soil-covered regions and has no limitations of land cover types. However, terrain and latitude variations will be the main factor responsible for the inaccurate estimation of LST and NTDI.
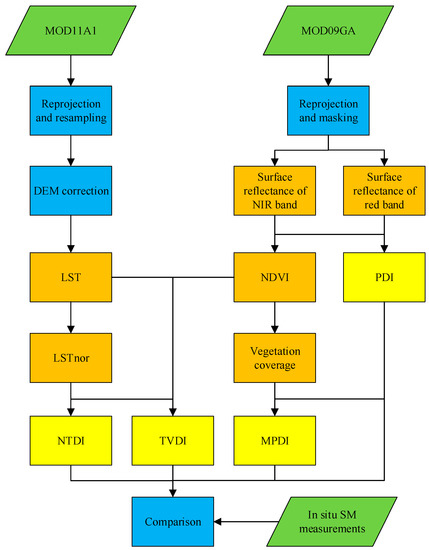
Figure 6.
The flowchart of constructing the four drought indices and SM monitoring.
4. Results
4.1. Estimation of Soil Line for NTDI
The NDVI–LSTnor trapezoid framework including soil line and dry edge with NDVI pixels against corresponding LSTnor from DOY 004 to DOY 354 is shown in Figure 7. The determination of the soil line and dry edge in the framework is conducted using the enhanced edges determination method proposed by Tang et al. [48]. From Figure 7, the framework with soil line (red lines), dry edge (blue lines) and wet edge (not shown) presented for most days is similar to the trapezoid space shown in Figure 5. Some issues need to be explained in the presented framework.
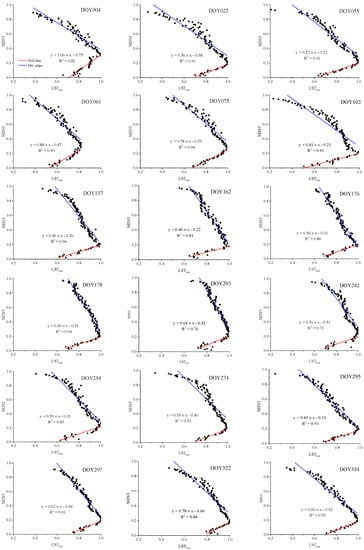
Figure 7.
The scatterplots of the dry edge and soil line in the NDVI-LSTnor space for 18 images.
(1) As discussed in Section 3.2, the dry edges representing the negative relationship between NDVI and LSTnor are derived from the dry edges in the NDVI-LST space. It is clear that there are good fits between NDVI and LSTnor for most of the days. The LSTnor in some frameworks has small ranges on individual days from DOY137 to 242. It can be explained that the values of LST generally fluctuate with changes of seasons. As illustrated in Table 1, DOY 137, 162, 176, 178, 203 and 242 are mostly distributed from May to August, which exactly correlate to winter in Australia. At that time, the climate in Victoria is mild and humid, which is affected by the midlatitude westerly wind.
(2) Actually, the pixels corresponding to the dry edges and soil lines represent the distribution of maximum values of LST for each NDVI in the NDVI-LST feature space. The soil lines represent the maximum water stress over the bare soil-covered regions with the NDVI values ranging from 0 to 0.2. The framework is constrained by the dry edge, soil line and not-shown wet edge shapes like a biparabolic, without a regular trapezoid, which also has a similar result with the research conducted by Tao et al. and Liu et al. [44,45,49]. For all days, the pixels corresponding to the soil line have good fits with the coefficients of determination (R2) of more than 0.8 except for DOY 203 and 242. Compared with the Red-NIR spectral space, the proposed method has a high sensitivity to the water condition of the bare soil, and soil line can be easily expressed. Therefore, the NTDI method is more feasible for the drought monitoring and SM retrieval in this study.
4.2. Comparison of PDI, MPDI, TVDI and NTDI Using MODIS Data at Crop Sites
In order to evaluate the effectiveness of PDI, MPDI, TVDI and NTDI in SM retrieval, the four drought indices were estimated based on Equations (1)–(3) and (8) with the 18 MODIS images in 2019. SM measurements at crop sites were provided to evaluate the feasibility of these drought indices using the R2 and RMSE. Table 2 shows the estimated results between observed volumetric surface soil water contents and retrieved drought indices with 0.01 and 0.05 confidence levels for 18 days. Results indicate the NTDI has a good correlation with SM for most days, especially on DOY 242, 254 and 274, with an R2 of more than 0.7. Similarly, TVDI and MPDI also performed well on those three days compared with other days. However, a poor correlation relationship is found in 4 of 13 sites where the R2 achieved is nearly or lower than 0.1. That is probably because some particular pixels are affected by clouds or missing in the LST images. Thus, the corresponding drought indices will be misestimated, and the general distribution of these pixels is not consistent with that of the surrounding ones. Furthermore, judging from the values of RMSE, the results acquired from the NTDI and PDI are rather close for most of days, with the difference in RMSE of less than 0.06, and are relatively higher than that produced by the MPDI and TVDI for almost all of the 18 days. In general, the NTDI conducts a more accurate capture of the variation of SM than the other three drought indices. It is also suitable for the drought monitoring over sparsely vegetated or bare soil-covered areas regardless of the other ancillary data.

Table 2.
The SM estimated results using drought indices based on the 18 MODIS images.
4.3. Spatial–Temporal Estimation of Drought Indices from MODIS Images
In order to assess the effectiveness of NTDI over the large-scale areas, four MODIS images (DOY 004, 176, 254 and 354, 2019) were used to evaluate the difference in the drought monitoring between NTDI and other drought indices, including TVDI, PDI and MPDI, over the Victoria state in Australia. The year 2019 is considered a slightly dry year with 277 mm annual precipitation. DOY 004, 176, 254 and 354 are dates representing the significant climate characteristics of the year.
Figure 8 shows the monitoring results of each drought index over the whole Victoria state. The smaller the index value, the larger the SM and the wetter the soil surface. From Figure 8, the values of NTDI on all four days are generally higher than other three drought indices, which can be possibly explained by two reasons: (1) The agricultural Murray Darling Basin (MDB), covering most areas of Victoria, experienced the driest period on record from early 2017 to the end of 2019 (more than 100 mm lower than the period of 1965–1967) due to large rainfall deficits (see the Bureau’s drought report: http://www.bom.gov.au/climate/drought/, accessed on 23 November 2022). Studies found the flash drought occurred in early 2019 and June 2019 with sustained rainfall anomalies [50]. (2) Affected by the El Niño-Southern Oscillation (ENSO), parts of Victoria, especially the densely vegetation-covered east coast regions, were devastated by the 2019–2020 Australian bushfire season stretching from June 2019 to March 2020 (see the NASA Global Precipitation Measurement report: https://gpm.nasa.gov/applications/water/drought-and-australia-wildfire-season, accessed on 26 November 2022). Meanwhile, it can be seen that the values of all the drought indices are higher over the Big Desert Wilderness Area located in the northwest region of the Victoria. Moreover, there is a relatively wet area in the eastern part called the Victorian Alps with a very high altitude, where the largest proportion of woody vegetation is mainly distributed and the values of the four drought indices are much lower. From DOY 004 to 354, NDTI, MPDI and TVDI present the slightly seasonal variation of dry summer (DOY 004, 354) and wet winter (DOY 176, 254). However, PDI indicates opposite results with lower values on all of four days. The possible reason is that PDI does not eliminate the contribution of the vegetation layer, which will lead to the overestimation of surface drought conditions.


Figure 8.
The dryness maps of four drought indices from MODIS data.
Figure 9 shows frequency distributions of the four drought indices from DOY 004 to 354. The four drought indices are normalized with the values from 0 to 1. From the frequency distribution, NTDI values are distributed between the range of 0.5 and 1.0 for the four days. The greatest numbers of pixels are almost concentrated on a pixel value of 0.8, which demonstrates that the whole region in Victoria is relatively dry. The phenomenon can be explained and proved using the Australian Bureau’s drought report, as above. NTDI can effectively describe the spatial characteristics of regional dryness distribution. PDI pixels are normally concentrated between the range of 0.1 and 0.6, which represents that the dryness is significantly underestimated. MPDI value has a very large range, with the greatest numbers of pixels ranging from 0.5 to 0.7. Two peaks are obviously located in the frequency distribution of MPDI on DOY 004 and 354. The majority of the pixels are focused on a different value range in TVDI. The dryness on DOY 254 is lower than that on other days. From the frequency distribution of MPDI and TVDI, the whole Victoria is drier on DOY 004 and 354.
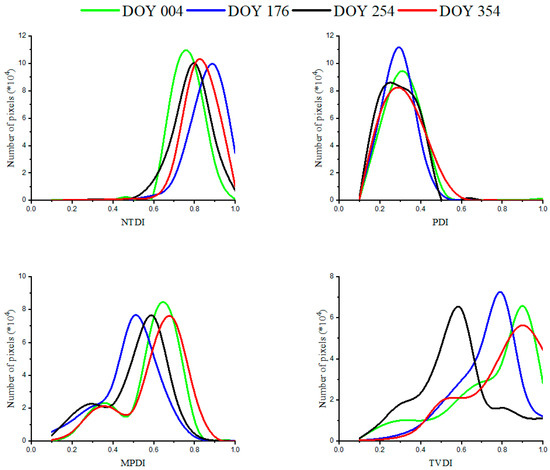
Figure 9.
A comparison of frequency distributions of the four drought indices maps from MODIS data.
It is worth pointing that the four drought indices in the Big Desert Wilderness Area are high. Some regions near the east coast are also in the same situation due to the bushfire in 2019. However, the SM in the desert area is not as low as expected from the dryness values of PDI. Meanwhile, the SM content near the east coast is generally quite high in the PDI, MPDI and TVDI maps. Compared with the three drought indices, NTDI maps faithfully display the significant water status and exhibit good dryness monitoring capabilities under different seasonal conditions.
4.4. Spatial–Temporal Estimation of Drought Indices from Landsat-8 Images
In order to compare with the MODIS data in the same period, four Landsat-8 images (DOY 001, 177, 257 and 353, 2019) were conducted to evaluate the applicability of the four VIs in small-scale regions. Figure 10 illustrates the spatial distribution of NTDI, PDI, MPDI and TVDI estimated from Landsat-8 images on DOY 001, 177, 257 and 353. Trends for the four drought indices presented in Figure 10 indicate that overall, the four indices perform consistently with the corresponding indices in Figure 8. A similar trend is observed that the values of NTDI and TVDI are much higher than that of PDI and MPDI in the same period, especially in the northern part of these maps due to lack of precipitation. From DOY 001 to 257, NTDI and TVDI values decrease because of the occurrence of rainfall in winter, and DOY 257 has the lowest NTDI and TVDI values. From DOY 257 to 353, the two drought indices values rise, which indicates that the values will increase from September to December in most regions if there is no precipitation, especially in dry desert and poor rangeland. For PDI and MPDI, the maps do not demonstrate any particular dynamic changes of index values over the four dates. They cannot indicate the differences of seasonal characteristics, although the four periods are very different regarding water status over the whole year. Meanwhile, MPDI and PDI values exhibit an opposite phenomenon that the desert land in the northern part is wetter than any other regions, which shows unusual dryness and water status.
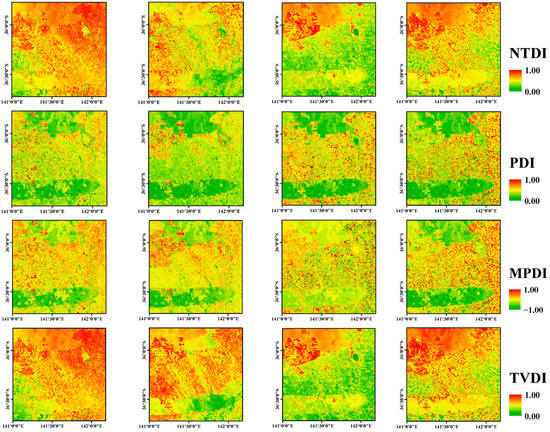
Figure 10.
The dryness maps of four drought indices from Landsat-8 data.
To further illustrate the ability of the four drought indices for dryness monitoring, Figure 11 shows the frequency distribution of NTDI, PDI, MPDI and TVDI maps from DOY 001 to 353. Compared with Figure 9, the frequency distributions of the four drought indices perform similar characteristics for the four days. NTDI values also are distributed in the high value range, and the number of high-value pixels are concentrated on a pixel value of 0.8 except on DOY 257. The dryness on DOY 257 is generally low possibly because of the short-term precipitation reported by Australian Bureau of Meteorology. PDI values have an extremely low range from 0.1 to 0.6, which underestimates the dryness of this region. MPDI and TVDI also have very large ranges, and the number of high-value pixels are concentrated in the higher value range on DOY 001 and 353.
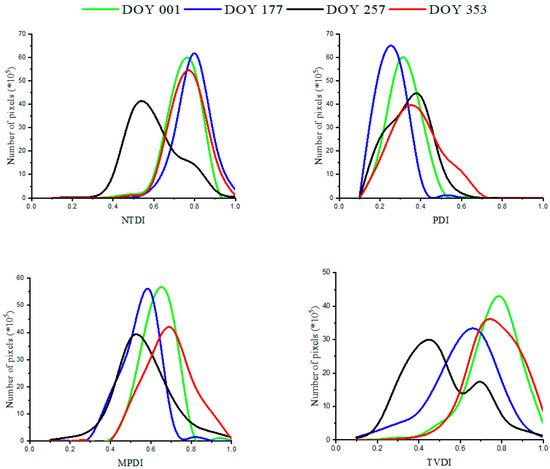
Figure 11.
A comparison of frequency distributions of the four drought indices maps from Landsat-8 data.
4.5. Influences of Different Spatial Resolution on NTDI
In order to evaluate the influences of the spatial resolution of the two satellite datasets on NTDI, the NDVI–LSTnor feature space is significantly conducted based on 1 km MODIS and 30 m Landsat-8 images for the four corresponding days. The MODIS data were clipped with the shape of Landsat-8 images, and the two satellite datasets are compared to examine the effects on the NTDI. Figure 12 shows the feature spaces constituted by the NDVI and the LSTnor using the MODIS data for DOY 004, 176, 254 and 354. As shown in Figure 12, the frames of the NDVI–LSTnor feature spaces are close to the conceptual trapezoid or triangle shape. The blue and red lines represent the dry edge and soil line, respectively. The distinct division of dry edge and soil line demonstrates that the feature space formed by the NDVI and the LSTnor is feasible and effective. However, the wet edge, the left edge of the frames in Figure 12, is not consistent with the distribution in the feature spaces except DOY 254. It can be explained that there are not enough pixels with high SM values in this small area. Figure 13 shows the feature spaces constituted by the NDVI and the LSTnor based on the Landsat-8 data for DOY 001, 177, 257 and 353. Compared with the wet edges in Figure 12, different results are shown in Figure 13 because of the higher spatial resolution of Landsat-8 data. The wet edges are almost consistent and constant in the space. The division of the dry edge and soil line is also clear, and the frames are significantly trapezoidal for the four days. These findings indicate that the Landsat-8 data are more suitable for the establishment of the NDVI–LSTnor feature space than MODIS data in this small area, and the feature space is applicable to construct the NTDI.

Figure 12.
Map of NDVI-LSTnor feature space based on the MODIS data on DOY 004, 176, 254 and 354 (the blue and red lines refer to dry edge and soil line).

Figure 13.
Map of NDVI-LSTnor feature space based on the Landsat-8 data on DOY 001, 177, 257 and 353 (the blue and red lines refer to dry edge and soil line).
To further analyse the difference of the NTDI values based on the two satellite datasets, the Landsat-8 data are resampled to 1 km and compared with the NTDI values of MODIS images for the four corresponding days. Figure 14 shows the scatterplots between the NTDI values from resampled Landsat-8 and MODIS data. As shown in Figure 14, the NTDI values from MODIS data have a good relationship with that from resampled Landsat-8 data on DOY 254. The R2 is 0.628, and the RMSE is 0.075. Figure 14 shows the lowest relationship between the NTDI values from the two satellite datasets on DOY 176, and the scatterplots of NTDI are distributed in the high values. It is obvious that NTDI values from resampled Landsat-8 data are overall greater than that from MODIS data on DOY 176 and 354. Figure 15 shows the frequency distribution of differences between NTDI values from MODIS and resampled Landsat-8 data for the four days. It can be seen that the differences on DOY 176 and 354 are mostly lower than 0, which also can be seen from Figure 14. Though a good relationship between the NTDI values for the two satellite datasets in Figure 14, the differences are obviously higher than 0 on DOY 254 in Figure 15, which means most of NTDI values from MODIS data are greater than that from resampled Landsat-8 data. Therefore, the spatial resolution will influence the NDVI–LSTnor feature space and effectiveness and applicability of NTDI. Large regions need to be selected when the spatial resolution is coarse.

Figure 14.
The scatterplots between the NTDI values from resampled Landsat-8 and MODIS data.

Figure 15.
The frequency distribution of differences between NTDI values from MODIS and resampled Landsat-8 data for the four days.
5. Discussions
As discussed above, the parameterization scheme of NTDI will affect the accuracy in the SM monitoring. Precise extraction of the dry edge and soil line makes it possible to reduce the error and uncertainty in the calculation of NTDI. In the NDVI-LST feature space, many methods were proposed to extract the dry and wet edges precisely. Linear or quadratic functions of NDVI for determination of maximum and minimum LST at dry and wet edges were often used to establish the relationship between drought index and LST with consideration of the high sensitivity of SM to LST [44,51,52]. The LST of a water body or a well-irrigated agricultural field was taken as a wet edge [46,53]. Observed dry and wet edges were limited by the specific region from the remote sensing data. Theoretical limiting edges were determined using the energy balance model with a robust physical basis to reduce the uncertainty caused by the observed dry and wet edges [54]. In this study, the enhanced edges determination method proposed by Tang et al. was used to obtain the dry and wet edges [48]. Theoretical limiting edges will be closer to the dry edge and soil line in the NDVI–LSTnor trapezoid feature space.
The effect of topography on LST and restrictions of the study area are the main error sources in drought monitoring. As is known, a wide change of both land use cover from bare soil to full vegetation cover and surface SM from dry to wet conditions were needed for the establishment of TVDI. However, for NTDI, the restriction will be not a required condition. For the NDVI–LSTnor trapezoid feature space, extraction of the soil line will affect the calculation of NTDI. Furthermore, the effect of topography on LST also strongly limited the feasibility of the new drought index. Studies showed that LST decreased 6 °C with the elevation rising 1 km in heterogeneous regions [28,29,55]. In this study, Victoria has different land cover types with a significant difference in elevation, including the Big Desert Wilderness Area located in the northwest region and the wet area in the eastern part called the Victorian Alps with a very high altitude. Thus, terrain becomes an essential factor that cannot be ignored in this region.
6. Conclusions
In order to improve the sensitivity of PDI and MPDI to SM and reduce the reliance of TVDI on the land cover types, a new parameterization scheme was developed in this paper by substituting NIR and red reflectance with normalized LST and NDVI according to the frame of PDI. The normalized temperature drought index (NTDI) was firstly developed to improve its sensitivity to water variations and vegetation status. Time series of MODIS and Landsat-8 data were applied to evaluate the effectiveness and applicability of NTDI at crop sites over the whole of Victoria, Australia. It can be concluded as follows:
(1) The NDVI–LSTnor trapezoid framework is derived from the NDVI-LST feature space with a good negative relationship between NDVI and LSTnor. The LSTnor calculated from LST generally fluctuates with the changes of seasons and represents the water stress under different land cover types. In the NDVI-LSTnor feature space, the fitting expression of soil lines representing the water condition of bare soil is easy to obtainand has good fits with R2 of more than 0.8 for most of the days.
(2) PDI, MPDI, TVDI and NTDI were estimated to evaluate the effectiveness and applicability in SM monitoring based on MODIS data at cropping sites in Victoria, Australia. The results indicated that NTDI has a better fitting relationship with SM for most of days, especially on DOY 242, 254 and 274 with the R2 of more than 0.7 when compared with the other three drought indices. The RMSE produced by the NTDI and PDI has a similar value for most days with a difference of less than 0.06. Therefore, the NTDI can substantially capture the spatial and temporal changes of SM with reasonable estimation accuracy.
(3) The spatial distributions of the four indices calculated from MODIS and Landsat-8 data are conducted to further analyse the difference in the drought monitoring ability. Overall, the NTDI and TVDI have higher values than PDI and MPDI according to the maps and frequency distribution for all of four days. Meanwhile, the area called Big Desert Wilderness Area located in the northwest region of the Victoria has very high values of all drought indices, which represents the real dryness condition in that region. NTDI also presents the slightly seasonal variation and describes the spatial characteristics of the regional drought distribution.
However, errors resulting from the establishment of the feature space and terrain will lead to drought index estimation uncertainty and ill-posed problems. Further theoretical verification and field work are needed to evaluate the NTDI in different regions, as well as to optimize the parameterization scheme on the site scale. Time series field measurements are conducted to evaluate the applicability of the new drought index over regions with different land cover types.
Author Contributions
Methodology, L.T.; software, Y.D.; validation, L.T., Y.D. and Y.W.; formal analysis, L.T.; investigation, Y.W.; writing—original draft preparation, L.T.; writing—review and editing, D.R.; funding acquisition, L.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Director Fund of the International Research Center of Big Data for Sustainable Development Goals (CBAS2022DF018), National Natural Science Foundation of China (41901278).
Data Availability Statement
The datasets reported in this paper can be accessed through: https://agriculture.vic.gov.au (in situ soil moisture observation data of pasture and crop sites in Victoria, last accessed on: 10 October 2022); https://search.earthdata.nasa.gov/search (MOD09GA, MOD11A1 products, last accessed: 10 October 2022); and http://earthexplorer.usgs.gov/ (Landsat-8 data, last accessed: 10 October 2022).
Acknowledgments
We thank Dale Boyd, who serves in Agriculture Victoria, for giving us great technical support and lots of valuable ground SM observations.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goddard, S.; Harms, S.K.; Reichenbach, S.E.; Tadesse, T.; Waltman, W.J. Geospatial decision support for drought risk management. Commun. ACM 2003, 46, 35–37. [Google Scholar] [CrossRef]
- Riebsame, W.E.; Changnon, S.A.; Karl, T.R. Drought and Natural Resources Management in the United States: Impacts and Implications of the 1987-89 Drought; Routledge: England, UK, 2019. [Google Scholar]
- Son, N.T.; Chen, C.F.; Chen, C.R.; Chang, L.Y.; Minh, V.Q. Monitoring agricultural drought in the Lower Mekong Basin using MODIS NDVI and land surface temperature data. Int. J. Appl. Earth Obs. Geoinf. 2012, 18, 417–427. [Google Scholar] [CrossRef]
- Sheldon, F.; Thoms, M.C. Relationships between flow variability and macroinvertebrate assemblage composition: Data from four Australian dryland rivers. River Res. Appl. 2006, 22, 219–238. [Google Scholar] [CrossRef]
- McKee, T.B. Drought monitoring with multiple time scales. In Proceedings of the 9th Conference on Applied Climatology, Boston, MA, USA, 15–20 January 1995. [Google Scholar]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–183. [Google Scholar]
- Van Rooy, M. A rainfall anomally index independent of time and space. Notos 1965, 14, 43–48. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Peters, A.J.; Walter-Shea, E.A.; Ji, L.; Vina, A.; Hayes, M.; Svoboda, M.D. Drought monitoring with NDVI-based standardized vegetation index. Photogramm. Eng. Remote Sens. 2002, 68, 71–75. [Google Scholar]
- Dong, Z.; Wang, L.; Gao, M.F.; Zhu, X.C.; Feng, W.B.; Li, N. Ratio Drought Index (RDI): A soil moisture index based on new NIR-red triangle space. Int. J. Remote Sens. 2023, 1–14. [Google Scholar] [CrossRef]
- Tian, Q.; Lu, J.Z.; Chen, X.L. A novel comprehensive agricultural drought index reflecting time lag of soil moisture to meteorology: A case study in the Yangtze River basin, China. Catena 2022, 209, 105804. [Google Scholar] [CrossRef]
- Chen, W.-Y.; Xiao, Q.-G.; Sheng, Y.-W. Application of the anomaly vegetation index to monitoring heavy drought in 1992. Remote Sens. Environ. 1994, 9, 106–112. [Google Scholar]
- Kogan, F.N. Droughts of the late 1980s in the United States as derived from NOAA polar-orbiting satellite data. Bull. Am. Meteorol. Soc. 1995, 76, 655–668. [Google Scholar] [CrossRef]
- Lu, Y.; Tao, H.; Wu, H. Dynamic drought monitoring in Guangxi using revised temperature vegetation dryness index. Wuhan Univ. J. Nat. Sci. 2007, 12, 663–668. [Google Scholar] [CrossRef]
- Qin, Q.; Ghulam, A.; Zhu, L.; Wang, L.; Li, J.; Nan, P. Evaluation of MODIS derived perpendicular drought index for estimation of surface dryness over northwestern China. Int. J. Remote Sens. 2008, 29, 1983–1995. [Google Scholar] [CrossRef]
- McVicar, T.R.; Jupp, D.L. The current and potential operational uses of remote sensing to aid decisions on drought exceptional circumstances in Australia: A review. Agric. Syst. 1998, 57, 399–468. [Google Scholar] [CrossRef]
- Wan, Z.; Wang, P.; Li, X. Using MODIS land surface temperature and normalized difference vegetation index products for monitoring drought in the southern Great Plains, USA. Int. J. Remote Sens. 2004, 25, 61–72. [Google Scholar] [CrossRef]
- Idso, S.; Reginato, R.; Jackson, R.; Pinter, J.P. Measuring yield-reducing plant water potential depressions in wheat by infrared thermometry. Irrig. Sci. 1981, 2, 205–212. [Google Scholar] [CrossRef]
- Kogan, F.N. Application of vegetation index and brightness temperature for drought detection. Adv. Space Res. 1995, 15, 91–100. [Google Scholar] [CrossRef]
- McVicar, T.; Jupp, D.; Yang, X.; Tian, G. Linking regional water balance models with remote sensing. In Proceedings of the 13th Asian Conference on Remote Sensing, Ulaanbaatar, Mongolia, 7–11 October 1992; p. B6. [Google Scholar]
- Sandholt, I.; Rasmussen, K.; Andersen, J. A simple interpretation of the surface temperature/vegetation index space for assessment of surface moisture status. Remote Sens. Environ. 2002, 79, 213–224. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Zhan, Z. Designing of the perpendicular drought index. Environ. Geol. 2007, 52, 1045–1052. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Kusky, T.; Li, Z.L. A re-examination of perpendicular drought indices. Int. J. Remote Sens. 2008, 29, 6037–6044. [Google Scholar] [CrossRef]
- Ghulam, A.; Qin, Q.; Teyip, T.; Li, Z.-L. Modified perpendicular drought index (MPDI): A real-time drought monitoring method. ISPRS J. Photogramm. Remote Sens. 2007, 62, 150–164. [Google Scholar] [CrossRef]
- Zormand, S.; Jafari, R.; Koupaei, S.S. Assessment of PDI, MPDI and TVDI drought indices derived from MODIS Aqua/Terra Level 1B data in natural lands. Nat. Hazards 2017, 86, 757–777. [Google Scholar] [CrossRef]
- Wang, H.; He, N.; Zhao, R.; Ma, X. Soil water content monitoring using joint application of PDI and TVDI drought indices. Remote Sens. Lett. 2020, 11, 455–464. [Google Scholar] [CrossRef]
- Qin, Z.; Karnieli, A.; Berliner, P. A mono-window algorithm for retrieving land surface temperature from Landsat TM data and its application to the Israel-Egypt border region. Int. J. Remote Sens. 2001, 22, 3719–3746. [Google Scholar] [CrossRef]
- Liu, Z.F.; Yao, Z.J.; Wang, R. Evaluating the surface temperature and vegetation index (Ts/VI) method for estimating surface soil moisture in heterogeneous regions. Hydrol. Res. 2018, 49, 689–699. [Google Scholar] [CrossRef]
- Yan, H.; Zhou, G.; Yang, F.; Lu, X. DEM correction to the TVDI method on drought monitoring in karst areas. Int. J. Remote Sens. 2018, 40, 2166–2189. [Google Scholar] [CrossRef]
- Rouse, J.J.; Haas, R.H.; Schell, J.A.; Deering, D.W. Monitoring Vegetation Systems in the Great Plains with Erts. In Proceedings of the Third Earth Resources Technology Satellite-1 Symposium, Washington, DC, USA, 10–14 December 1973; p. 309. [Google Scholar]
- Zhang, J.; Zhang, Q.; Bao, A.; Wang, Y. A new remote sensing dryness index based on the near-infrared and red spectral space. Remote Sens. 2019, 11, 456. [Google Scholar] [CrossRef]
- Baret, F.; Clevers, J.; Steven, M. The robustness of canopy gap fraction estimates from red and near-infrared reflectances: A comparison of approaches. Remote Sens. Environ. 1995, 54, 141–151. [Google Scholar] [CrossRef]
- Zhang, J.H.; Zhou, Z.M.; Yao, F.M.; Yang, L.M.; Hao, C. Validating the Modified Perpendicular Drought Index in the North China Region Using In Situ Soil Moisture Measurement. IEEE Geosci. Remote Sens. Lett. 2015, 12, 542–546. [Google Scholar] [CrossRef]
- Chen, J.; Wang, C.; Jiang, H.; Mao, L.; Yu, Z. Estimating soil moisture using Temperature–Vegetation Dryness Index (TVDI) in the Huang-huai-hai (HHH) plain. Int. J. Remote Sens. 2011, 32, 1165–1177. [Google Scholar] [CrossRef]
- Chen, S.L.; Wen, Z.M.; Jiang, H.; Zhao, Q.J.; Zhang, X.Y.; Chen, Y. Temperature Vegetation Dryness Index Estimation of Soil Moisture under Different Tree Species. Sustainability 2015, 7, 11401–11417. [Google Scholar] [CrossRef]
- Du, L.; Song, N.; Liu, K.; Hou, J.; Hu, Y.; Zhu, Y.; Wang, X.; Wang, L.; Guo, Y. Comparison of Two Simulation Methods of the Temperature Vegetation Dryness Index (TVDI) for Drought Monitoring in Semi-Arid Regions of China. Remote Sens. 2017, 9, 177. [Google Scholar] [CrossRef]
- Shi, S.; Yao, F.; Zhang, J.; Yang, S. Evaluation of Temperature Vegetation Dryness Index on Drought Monitoring over Eurasia. IEEE Access 2020, 8, 30050–30059. [Google Scholar] [CrossRef]
- Maduako, I.N.; Ndukwu, R.I.; Ifeanyichukwu, C.; Igbokwe, O. Multi-Index Soil Moisture Estimation from Satellite Earth Observations: Comparative Evaluation of the Topographic Wetness Index (TWI), the Temperature Vegetation Dryness Index (TVDI) and the Improved TVDI (iTVDI). J. Indian Soc. Remote Sens. 2016, 45, 631–642. [Google Scholar] [CrossRef]
- Zhao, S.; Cong, D.; He, K.; Yang, H.; Qin, Z. Spatial-temporal variation of drought in China from 1982 to 2010 based on a modified temperature vegetation drought index (mTVDI). Sci. Rep. 2017, 7, 17473. [Google Scholar] [CrossRef]
- Zhu, W.; Jia, S.; Lv, A. A time domain solution of the Modified Temperature Vegetation Dryness Index (MTVDI) for continuous soil moisture monitoring. Remote Sens. Environ. 2017, 200, 1–17. [Google Scholar] [CrossRef]
- Li, C.B.; Adu, B.; Li, H.H.; Yang, D.H. Spatial and temporal variations of drought in Sichuan Province from 2001 to 2020 based on modified temperature vegetation dryness index (TVDI). Ecol. Indic. 2022, 141, 109106. [Google Scholar] [CrossRef]
- Wang, H.; Li, Z.S.; Zhang, W.J.; Ye, X.; Liu, X.F. A Modified Temperature-Vegetation Dryness Index (MTVDI) for Assessment of Surface Soil Moisture Based on MODIS Data. Chin. Geogr. Sci. 2022, 32, 592–605. [Google Scholar] [CrossRef]
- Dai, R.; Chen, S.B.; Cao, Y.J.; Zhang, Y.F.; Xu, X.T. A Modified Temperature Vegetation Dryness Index (mTVDI) for Agricultural Drought Assessment Based on MODIS Data: A Case Study in Northeast China. Remote Sens. 2023, 15, 1915. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, L.X.; Yue, H. Biparabolic NDVI-T-S Space and Soil Moisture Remote Sensing in an Arid and Semi arid Area. Can. J. Remote Sens. 2015, 41, 159–169. [Google Scholar] [CrossRef]
- Liu, Y.; Yue, H. The Temperature Vegetation Dryness Index (TVDI) Based on Bi-Parabolic NDVI-T-s Space and Gradient-Based Structural Similarity (GSSIM) for Long-Term Drought Assessment across Shaanxi Province, China (2000–2016). Remote Sens. 2018, 10, 959. [Google Scholar] [CrossRef]
- Carlson, T. An overview of the “triangle method” for estimating surface evapotranspiration and soil moisture from satellite imagery. Sensors 2007, 7, 1612–1629. [Google Scholar] [CrossRef]
- Zhang, D.J.; Tang, R.L.; Tang, B.H.; Wu, H.; Li, Z.L. A Simple Method for Soil Moisture Determination From LST-VI Feature Space Using Nonlinear Interpolation Based on Thermal Infrared Remotely Sensed Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 638–648. [Google Scholar] [CrossRef]
- Tang, R.; Li, Z.-L.; Tang, B. An application of the Ts–VI triangle method with enhanced edges determination for evapotranspiration estimation from MODIS data in arid and semi-arid regions: Implementation and validation. Remote Sens. Environ. 2010, 114, 540–551. [Google Scholar] [CrossRef]
- Tao, L.; Ryu, D.; Western, A.; Boyd, D. A new drought index for soil moisture monitoring based on MPDI-NDVI trapezoid space using MODIS data. Remote Sens. 2021, 13, 122. [Google Scholar] [CrossRef]
- Nguyen, H.; Wheeler, M.C.; Hendon, H.H.; Lim, E.-P.; Otkin, J.A. The 2019 flash droughts in subtropical eastern Australia and their association with large-scale climate drivers. Weather Clim. Extrem. 2021, 32, 100321. [Google Scholar] [CrossRef]
- Zhu, W.; Lv, A.; Jia, S.; Yan, J. A new contextual parameterization of evaporative fraction to reduce the reliance of the Ts− VI triangle method on the dry edge. Remote Sens. 2017, 9, 26. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Jensen, K.H. Combining the triangle method with thermal inertia to estimate regional evapotranspiration—Applied to MSG-SEVIRI data in the Senegal River basin. Remote Sens. Environ. 2008, 112, 1242–1255. [Google Scholar] [CrossRef]
- Jiang, L.; Islam, S. A methodology for estimation of surface evapotranspiration over large areas using remote sensing observations. Geophys. Res. Lett. 1999, 26, 2773–2776. [Google Scholar] [CrossRef]
- Zhang, D.; Tang, R.; Zhao, W.; Tang, B.; Wu, H.; Shao, K.; Li, Z.-L. Surface Soil Water Content Estimation from Thermal Remote Sensing based on the Temporal Variation of Land Surface Temperature. Remote Sens. 2014, 6, 3170–3187. [Google Scholar] [CrossRef]
- Ran, Q.; Zhang, Z.; Zhang, G.; Zhou, Q. DEM correction using TVDI to evaluate soil moisture status in China. Sci. Soil Water Conserv. 2005, 3, 32–36. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).