Abstract
Urban tree species identification performs a significant role in tree management and the sustainable development of cities. Conventionally, multispectral or hyperspectral remote sensing images are applied to identify species. However, spectral profiles of trees on images are easily affected by surroundings and illuminations, resulting in urban trees of different species possibly having similar spectral features. The handheld laser scanning (HLS) technique can capture 3D structural information of trees and be confirmed to be effective in reducing the problem of spectral similarity through tree structural properties (TSP). TSP usually varies in different leaf conditions, especially TSP of tropical tree species. In this study, we investigated the effects of leaves on urban tropical tree species identification using HLS. A total of 89 metrics that characterized the TSP were evaluated, including 19 branches, 12 stems, 45 crowns, and 13 entire tree metrics. All metrics were derived under different leaf conditions. The correlation and importance of these metrics were further evaluated. Our results demonstrated that crown metrics perform the most important role in urban species identification in leaf-on and leaf-off conditions and that the combination of metrics derived in different leaf conditions can improve the identification accuracy. Furthermore, we discovered 9 robust metrics that perform well in all leaf conditions, including 3 crowns, 2 branches, 2 stems, and 2 entire tree metrics. These metrics give a deep understanding of numerous structural properties and provide a significant reference for the relevant structure-based classification of other tropical species. This study also illustrated that HLS could help to overcome the spectrum-related limitations and improve the efficiency of species identification and sustainable forest management.
1. Introduction
Information about species distribution in urban areas performs a significant role in tree management and conservation. Studies of tree species classification were commonly implemented by identifying spectral features from remote sensing images, such as multispectral and hyperspectral images [1,2]. However, the performance of spectral features is limited by the similarity problem, i.e., the spectral features of the same species may be different due to some factors, such as varying shapes in details and the surrounding environment [3], or the spectral features of different species may be similar [4]. This problem can be reduced by considering tree structures that vary between species because of the different branching patterns and foliage distributions [5]. The light detection and ranging (LiDAR) technology that measures distances using roundtrip time of pulsed laser energy between targets and sensors [6] can capture and represent tree structure information via three-dimensional (3D) point clouds.
The conventional terrestrial LiDAR (TLS) emits laser pulses from a sensor standing on the ground. To capture as complete as possible the structural information, time-consuming preparations and point cloud fusion are required [7]. HLS technology, which places a laser scanning sensor on a handheld moving platform, is able to capture dense and complete tree point clouds economically and efficiently [8]. Its flexible mobility not only reduces the occlusion effect (i.e., the trees far away from the scanner may be occluded by trees near the scanner, causing an incomplete point cloud of trees away from the scanner) but also simplifies the complex preparation and co-registration procedures. Additionally, performance of HLS for forest inventory evaluation has been validated. For instance, Chen et al. [9] achieved an estimation of the diameter at the breast height (DBH) of an arbor forest in the Haidian District in Beijing with an RMSE of 1.58 cm using ZEB-REVO-RT. Oveland et al. [10] and Su et al. [11] accurately estimated the DBH of boreal forest in the southeastern part of Norway with an RMSE of 14.3% using GeoSLAM ZEB1. However, many studies used HLS to estimate the inventory of trees in forests, rarely focusing on inventory surveys of urban trees. To bridge this gap, this study aims to investigate the potential of HLS for urban tree inventory.
Species identification from 3D point clouds usually relies on tree structural properties (TSP) characterized by structural metrics, such as tree height, crown diameter, and DBH [12,13]. Over decades, many structural metrics have been developed and applied to classify species, such as explicit structural parameters [3], quantitative structural features [14], and salient geometric features [15]. These metrics can be divided into two categories according to their extraction methods. One category is metrics that are extracted directly from individual tree point clouds. Explicit structural parameters and salient geometric features both belong to this category. Another category is metrics that are extracted from the reconstructed 3D tree model, which is hierarchically generated by cylinder fitting [14]. Metrics extracted from point clouds mainly represent external geometric characteristics, while metrics extracted from 3D models can describe internal and external geometric characteristics of trees. Most studies concentrate on optimization and improvement of identification accuracy by combining diverse types of data or developing optimized algorithms [16,17]. A comprehensive and thorough understanding of the contribution of structural metrics for species identification is rarely studied [18,19], such as the relationship between derived metrics and specific structural properties of different species and the importance of different types of structural metrics for species identification [20]. Therefore, we proposed to estimate the performance and importance of existing structural metrics for tree species identification using HLS in an urban setting.
A challenge for urban tree species identification based on structural metrics is that structural metrics would change with leaf conditions [21]. Different leaf conditions result in different tree structures [22], thus influencing structural metric values and species identification accuracy. However, related studies demonstrated that leaf condition shows varied influences on the identification of different species. Hamraz et al. [23] demonstrated that leaf-off data could provide more useful information for the identification of mixed temperate species in southeastern Kentucky, while Shi et al. [5] indicated no greatly different performance between leaf-on and leaf-off conditions for the identification of species in Central Europe but the combination of metrics derived under two leaf conditions could improve identification accuracy. The influence of leaf conditions on tropical species identification was rarely studied. Thus, we propose to evaluate certain influences of leaf conditions on tropical species identification in an urban setting.
In this study, we collected 89 structural metrics from previous studies, including 19 in branches, 12 in stems, 45 in crowns, and 13 of entire tree metrics. Under the assumption that leaf conditions may affect the extraction of structural metrics and urban tropical species identification results, an experiment evaluating the specific influence of leaf conditions on species identification was conducted. We removed leaf points by combining the TLSeparation [24] algorithm and manual refinement. TLSeparation is a method developed for the separation of wood and leaf points from individual tree point clouds based on 3D geometric features and has been set as a Python library. All metrics were extracted under two leaf conditions (leaf-on and leaf-off).
2. Materials and Methods
2.1. Study Site and Research Data
Hong Kong (HK) is located south of China (22°08′–22°35′N, 113°49′–114°31′E). The certain climate, namely, long rainy summer and tiny temperate differences in four seasons, creates a great environment for vegetation, resulting in considerable tropical and subtropical tree species diversity. To improve the sustainable development of HK, the government invests enormous efforts in managing urban trees. Information on most trees has been collected and kept, including location, species, and basic structural parameters. Compared to forests, urban trees tend to have low density, and their structural characteristics are less affected by neighboring trees [25]. These make HK urban trees good study objects.
For the selection of tree species, we proposed three rules, i.e., separability, availability, and invariability. Separability means target samples can be greatly separated spatially to ensure the completion of individual tree point cloud and structural metrics extraction. There should be clear boundaries between target trees and neighbors. Availability indicates that enough trees of species are available to be measured. Invariability indicates that the general shape of the target species is not easily affected by neighbors. Following these three rules, four species were finally selected from the dominant species in Hong Kong [26,27,28], i.e., Aleurites moluccana (L.) Willd (AM), Ficus altissima Blume (FA), Delonix regia (Boj. ex Hook.) Raf. (DR), and Hibiscus tiliaceus L. (HT). AM and HT have spherical crowns with simple and complex structures, respectively, while FA and DR have upright funnel crowns with complex and simple structures, respectively. The simple and complex structure stands for the number of main branches of a tree. The number of main branches of AM are relatively smaller than the number of main branches of HT and FA. A total of 85 AM, 69 FA, 65 DR, and 68 HT trees were chosen as research samples (Figure 1). Basic structural parameters, i.e., tree height (TH), DBH, and crown width (CS) of all trees, were simultaneously measured in the field (Table 1). TH and CS were measured by a laser rangefinder. DBH was measured by a tree caliper. The height difference between the lowest and highest points of a tree is defined as TH. The maximum horizontal difference of a crown is defined as CS. The trunk diameter at a tree height of 1.3 m is defined as DBH.
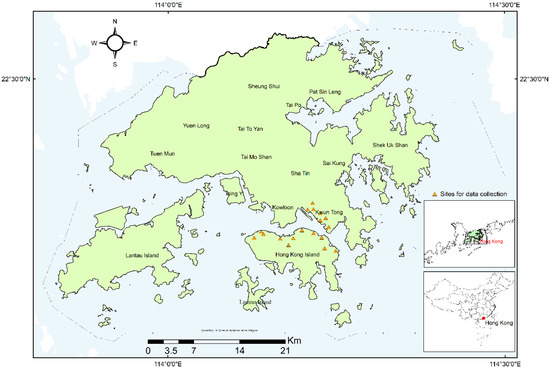
Figure 1.
Research site. The yellow icons are the site for the tree point cloud collection. The collected trees are mainly in the park or along the roadside in Hong Kong Island and Kwun Tong District.

Table 1.
Basic structural information of each species. Subscript “avg”, “median”, and “sd” indicate the average, median, and standard deviation values, respectively. The unit of TH and CS is m and the unit of DBH is mm.
Tree point clouds (Figure 2) were collected during May and December in the year 2020 by ZEB Horizon (https://geoslam.com/solutions/zeb-horizon/) accessed on 10 May 2023, which is a lightweight personal HLS developed by GeoSLAM Ltd., consisting of 16 sensors with a wavelength of 903 nm. This equipment can capture approximately 300,000 points per second with a relative accuracy of up to 6 mm. The scanning range is up to 100 m. Its field of view is 360° horizontally and 270° vertically. A detailed description of ZEB Horizon is listed in Table 2.
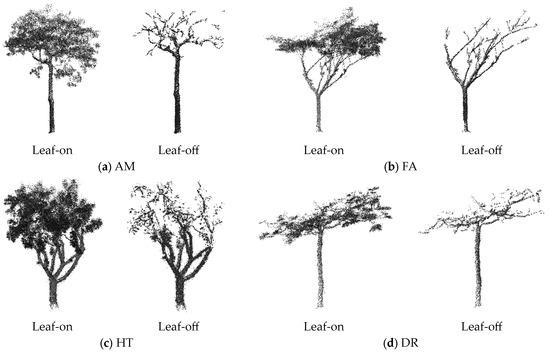
Figure 2.
Point cloud examples of four species. The four species are (a) Aleurites moluccana, (b) Ficus altissima, (c) Hibiscus tiliaceus, (d) Delonix regia.

Table 2.
Datasheet of ZEB Horizon.
To capture as complete as possible information about trees, we held the scanner and walked around the target trees twice. The captured point cloud was automatically processed using GeoSLAM Hub software which utilizes simultaneous localization and mapping (SLAM) algorithm to locate the scanner and register 3D point cloud [29]. The accuracy of the SLAM algorithm used in GeoSLAM Hub is less than 3 cm [30]. Processed point clouds are outputted in LAS 1.2 format.
A statistical outlier removal approach was applied to reduce noise points. The average distances of each point to neighbors were computed. Then, points farther than the sum value of average distance and standard deviation of point distances were regarded as noise [31]. Subsequently, ground points were removed using a cloth simulation filtering algorithm, which simulates the drop procedure of cloth to the ground surface [32]. The noise removal and ground point removal were conducted with CloudCompare 2.0 software [33].
2.2. Individual Tree Point Cloud Segmentation
A four-phased approach was employed to segment individual trees (Figure 3). In phases 1–3, Canopy Height Model (CHM) was first created by rasterizing elevation differences. Based on CHM, we employed Marker-controlled Watershed Segmentation (MCWS) algorithm to coarsely segment individual trees. The marker was able to alleviate over-segmentation by determining segmented object locations [34]. We used tree locations, which were detected through fitting cylinders to stem using Density-based Spatial Clustering of Applications with Noise Algorithm (DBSCAN) at tree height of 1.3–1.4 m [35], as markers of the MCWS algorithm.
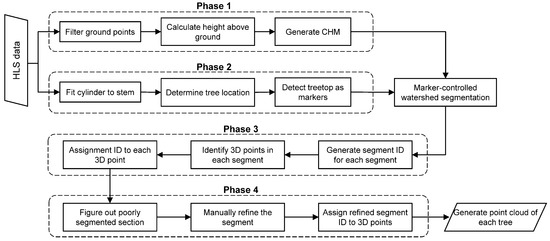
Figure 3.
Procedure of individual tree segmentation.
After coarse segmentation, each 2D segment was assigned a segment ID, and the segmentation of the 3D point cloud was conducted (i.e., the points located within a segment were assigned the corresponding segment ID). In phase 4, unsuccessfully segmented trees were filtered. Subsequently, manual refinement was executed to further separate individual tree points clouds.
2.3. Structural Metric Derivation
Many structural metrics have been developed for species identification. We divided existing metrics into four categories based on the part of a tree that structural metrics are related to, i.e., branch, stem, crown, and entire tree metrics. Eighty-nine metrics were derived in this study (Table 3 and Table 4). Branch and stem metrics were extracted based on the construction of TreeQSM which was developed by Raumonen et al. [36]. Before QSM construction, several parameters (i.e., PatchDiam1, PatchDiam2Min, and PatchDiam2Max) were optimized by grid search based on four tree point clouds (a tree for each species). PatchDiam1 was used to control patch size during the first cover sets generation. PatchDiam2Min and PatchDiam2Max controlled minimum and maximum patch size during the second cover sets generation, respectively. Testing ranges of three parameters were [0.06, 0.08, 0.12, 0.14] (PatchDiam1), [0.02, 0.03, 0.04, 0.05] (PatchDiam2Min), and [0.05, 0.07, 0.11, 0.13] (PatchDiam2Max).

Table 3.
Definition of stem, branch, and entire tree metrics.

Table 4.
Definition of crown metrics.
Then, model precision was calculated for each QSM by comparing the average difference of TH, DBH, and CS between derived and field-measured parameters. The smaller differences, the more precise the QSM. Optimized parameters were finally selected according to model precision. Afterwards, QSM was built five times for each tree using same input parameters to reduce the uncertainty, unreliability, and stochasticity. The appropriate model was estimated by calculating mean distance between cylinder models and points of the trunk and all branches by the select-optimum function of TreeQSM. The optimized structural parameters were output by this function. In addition, a part of the crown and entire tree metrics were extracted directly from the point cloud. Other metrics were extracted from gridding tree point clouds (tree points were gridded using an edge with a length of 0.02). Derivation of all metrics was conducted using MATLAB software. The detailed definition and format of eighty-nine metrics were listed in Supplementary File.
All metrics were derived under two leaf conditions, respectively, to investigate the effect of leaf points on tree structures and species identification. Leaf-on condition means individual tree point clouds contain leaf points, and leaf-off condition means leaf points were not contained in individual tree point clouds. Leaf-off condition was achieved by removing leaf points using the TLSeparation algorithm developed by Vicari et al. [24] and manual refinement. TLSeparation is likely to introduce significant underestimation of crown structural complexity [25]. Manual refinement thus was used to improve separation results of TLSeparation and to obtain better leaf-off individual tree point clouds. According to the work of Demol et al. [37] and Lau et al. [38], TreeQSM has limitations on the 3D model reconstruction of small branches, especially branches whose diameters are thicker than 20 cm. Therefore, this study mainly focuses on the extraction of structural metrics of first- and second-order branches.
Removal of highly related metrics not only saves computing power but also boosts the performance of identification models. We used Pearson’s correlation coefficient, a measure of the correlation between two sets of data [39], to analyze the relationship between all metrics. The threshold of r was used to split highly correlated and lowly correlated metrics [40]. We used a popular threshold of 0.7 to distinguish the correlation coefficient (i.e., |r| > 0.7 demonstrates a high correlation, otherwise demonstrating a low correlation) [41,42].
2.4. Metric Importance Assessment and Metric Selection
A hybrid method was proposed to evaluate the importance of individual metrics (i.e., incorporate the importance assessment with identification procedure). During classifier construction, the metric that made the split, the corresponding changes of Gini impurity and the number of affected samples were all tracked once a split was done. The times a metric was used to split a node can be counted by Gini impurity (Equation (1)), which is a measurement used to determine how the features of a dataset should split nodes to form the tree [43]. The more frequently a metric is used during a classifier construction, the more important it is [43]. After classifier construction, the total gain that measures the decrease in node impurity of each metric can be computed. Accordingly, the importance ranking of all metrics can be generated. The importance assessment procedure was achieved using the Python library skicit-learn [44].
where is the number of classes. is the probability of samples belonging to class at a given node.
Redundant and irrelevant metrics adversely affect the performance of identification models with the increase in metric dimensions [45,46]. For example, highly related or insignificant metrics increase dimensions without improving identification accuracy [16,47]. Metric selection seeks to find appropriate metrics for improving identification efficiency by maximizing the performance of identification models and minimizing metric numbers [48]. In this study, structural metrics were selected based on correlation analysis and importance assessment. In each pair, the metric that had lower importance values (|r| < 0.7) was removed. When the importance of the two metrics was the same, their total |r| values were compared. Then, metrics that have relatively higher total |r| values were removed. In addition, an accumulated importance was introduced to evaluate the importance of metric types for tropical species identification. The accumulated importance equals to the total sum of importance values of all metrics of the same type.
2.5. Tropical Species Classification
Machine learning approaches have been commonly applied to solve identification problems. Among various machine learning models, XGBoost has shown great ability on a metric-based identification problem in recent years [49]. It is an optimized and scalable end-to-end tree-boosting system based on a gradient-decision tree and provides a parallel tree-boosting method which fits many large or small trees to the reweighted version of the training data [50]. We employed XGBoost to identify species using selected structural metrics. Overall, trees were divided into two datasets. About 20% of trees were randomly selected as dataset 2 for evaluating the robustness and reliability of identification models and selected structural metrics. The rest 80% of the trees were used as dataset 1. Approximately 70% of trees of dataset 1 were used as training data and 30% as testing data to show the performance of the identification model. The model trained using training data in dataset 1 was implemented to identify species of dataset 2. Training and testing of identification models were implemented under two leaf conditions, respectively, to explore the effect of leaves on species identification.
The performance of XGBoost model is controlled by a number of parameters. Obtaining the performance of each parameter value is time-consuming and computationally intensive. We integrated a grid search that can exhaustively search subsets from parameter space and cross-validation to find optimal parameter sets. A five-step strategy was proposed for parameter optimization: (1) Determine learning rate and an optimum number of trees; (2) Tune parameters of each tree; (3) Optimize regularization parameters; (4) Decrease learning rate and repeat the above-mentioned steps; and (5) Finish parameter optimization until model accuracy does not increase. The experiment was carried out with the “scikit-learn” package [44].
The performance of selected metrics and identification model was evaluated by three assessment approaches (Equations (2)–(4)), namely, overall accuracy (), user’s accuracy (, and procedure’s accuracy (). illustrated the general performance of the identification model on four species. and were used for each species to reduce the influence of imbalanced samples between species on result assessment. evaluates identification results from the point of view of species, and evaluates identification results from perspective of model. To each species, demonstrated rate of correct prediction made by identification model compared to all predictions. demonstrated rate of correct predictions compared to true sample.
where is the number of precisely predicted samples, is the count of all samples, is the number of predicted samples of a species, is the number of samples predicted as that species, and is the number of true samples of a species.
3. Results
3.1. Validation of HLS-Based Tree Structure Characterization
The differences between manually measured and HLS-derived metrics, including mean, standard deviation (SD), and median of difference values, are listed in Table 5. Overall mean differences of DBH, TH, and CS are 4.35 mm, 0.69 m, and 0.82 m, respectively, demonstrating that HLS can effectively capture basic structural information of trees. In terms of specific species, FA has relatively larger errors than others in TH and DBH. This may be because some aerial roots of FA influenced the automated measurement of structural metrics. For CS, the possible reason for the large differences between manually measured and HLS-derived metrics is human vision error.

Table 5.
Difference between manual measured and HLS-derived metrics. Sd means standard deviation. MPE means the mean percentage error (unit is %).
3.2. Correlation of Structural Metrics and Metric Selection
The number of highly correlated metrics in leaf-on conditions is larger than in leaf-off conditions (Figure 4 and Figure 5), demonstrating that the diversity of inner structures represented by metrics derived under leaf-off conditions is more remarkable than external structures represented by metrics derived under leaf-on conditions. With regard to metric types, the correlation coefficient of metrics, especially branch and crown metrics, tends to be larger in leaf-on than in leaf-off conditions. About half of crown metrics have high correlation coefficient values under two-leaf conditions. This notion may be explained by two possible situations: (1) existing crown metrics represent the same or similar characteristics of a crown using various formats; and (2) some metrics may not be appropriate to tropical species. Metrics with high correlation coefficients under two leaf conditions predominantly relate to branch length, CS, crown cover, crown length, stem length, TH, and tree volume.
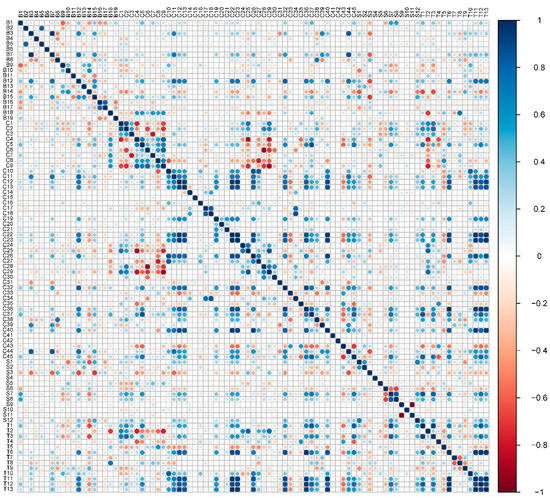
Figure 4.
Correlation coefficient of all metrics under leaf-on condition. The higher the positive correlation, the blue is darker. The higher the negative correlation, the red is darker.
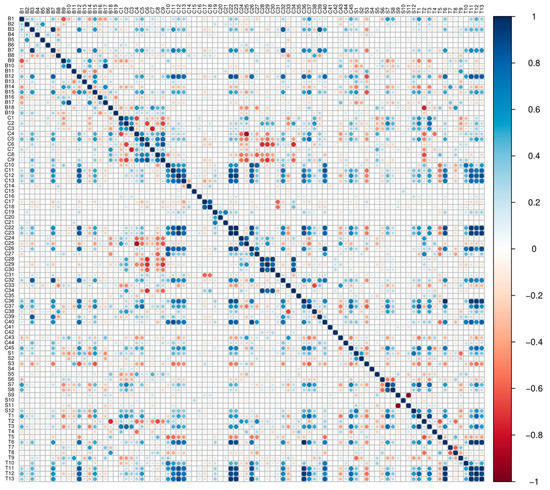
Figure 5.
Correlation coefficient of all metrics under leaf-off condition. The higher the positive correlation, the darker the blue is. The higher the negative correlation, the darker the red is.
The metric selection was conducted on the basis of assessment of the correlation coefficient and the importance of all metrics in the first calculation. Under the leaf-on condition, 42 metrics were removed, including 6 branch metrics, 24 crown metrics, 4 stem metrics, and 8 entire tree metrics. Under leaf-off condition, 38 metrics were removed, including 4 branch metrics, 22 crown metrics, 4 stem metrics, and 8 entire tree metrics. Although most crown metrics were developed in previous studies, many of them are similar or have relatively low importance for species classification. The same situation was observed in entire tree-related metrics. The remaining metrics under two leaf conditions are listed in Table 6.

Table 6.
Remaining metrics under leaf-on and leaf-off conditions after removing highly correlated metrics.
3.3. Importance of Structural Metrics
Among all structural metrics, crown structural metrics were found to be the predominant metrics for differentiating four tropical species in HK under two leaf conditions according to accumulated importance values of each type (Table 7). Their accumulated importance values remain the largest in the four types of metrics, and no significant difference was observed between the two leaf conditions. This finding agrees that crown structure is a fundamental attribute of a tree [51]. The aforementioned situation may also be the reason many previous studies predominantly used crown metrics to classify species from point cloud [5,52,53]. The performance of branch and stem metrics significantly varies under different leaf conditions. Branch metrics perform increasingly important roles from leaf-on to leaf-off conditions, while stem metrics show an opposite trend. This situation may be because the internal structural and morphological characteristics of trees were shown clearer under leaf-off conditions. Thus, branch metrics more explicitly express differences between species.

Table 7.
Overall accumulated importance of each type of metric.
From the importance of individual metrics, the stem shape metric performs the most important role in tropical species identification under all leaf conditions (Figure 6). This notion agrees with the demonstration of Stal et al. [54], wherein stem properties are important parameters of a tree. However, unlike commonly used stem metrics such as DBH for species identification, the most important stem metric in this study is S5. Two possible reasons for this situation are as follows: (1) in comparison with DBH, which only measures the diameter of a stem, stem radial irregularity the takes size and shape of a stem into consideration. Taking HT and AM as an example, S5 can still identify them when stem diameters are the same because the trunk of AM tends to grow straighter, and the shape of AM trunk is closer to the perfect circle. However, the HT trunk has greater irregularity. (2) S5 has lower relationships with other metrics, making identification models more sensitive to its variations between species.
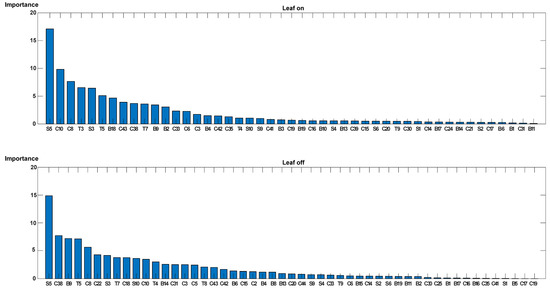
Figure 6.
Importance ranking of the structural metrics under leaf-on and leaf-off conditions.
In addition, some structural metrics perform different roles in tropical tree species identification under different leaf conditions. When leaves exist, C10 and C8 are identified as important metrics for species identification (ranking as second and third). However, under leaf-off conditions, C10 and C8 become less important. Meanwhile, B9 and C38 become the second and third most important metrics. Unlike commonly used metrics in previous studies, such as TH, CS, and DBH [18,19], the first 15 important metrics under two-leaf conditions are more concrete and tangible, especially the first five metrics. In the first five metrics under leaf-on conditions, the crown shape is described through the ratio between CS and TH and the ratio between the horizontal and vertical spread. The ratio between metrics and TH is also proven to perform better because it can reduce the influence of tree ages [3]. Stem shape is described through S5, and TH is the mean height of all tree grids. Moreover, the first five metrics under leaf-off condition characterize properties of stem diameter, crown volume, branch length, stem volume, and CS by stem radial irregularity, the ratio of crown volume to the number of crown points, the mean length of first-order branches, the ratio between the number stem grids and entire tree grids, and the ratio of the vertical length of the crown to the horizontal length of the crown, respectively.
We discovered nine robust metrics that consistently show large importance values under two leaf conditions, including three crown metrics, two branch metrics, two stem metrics, and two entire tree metrics, namely, S5, C10, C8, S3, T5, B18, T7, B9, and C3. These metrics appear in the first 15 metrics under two leaf conditions but with different rankings. The frequently employed branch length and branch volume were also verified to be effective and efficient for tropical species classification. Three robust crown metrics are more appropriate to tropical species from the aspect of ecosystem and plant morphology compared with the commonly used crown metrics, such as crown diameter, crown cover area, and crown base height [55,56,57]. Shenkin et al. [51], who studied the role of ecosystem and phylogeny on crown size and shape, demonstrated that crown vertical length and crown volume of tropical species vary more across gradients than crown diameter and projected crown area.
The crown depth and crown base height can be affected by structures and leaves of the upper crown [58]. Specifically, the sparse structure and compound leaves of the upper crown could allow lateral light to effectively penetrate deeper into the canopy, allowing the crown bottom to maintain a positive carbon balance and grow deeper [49,59]. These phenomena are reasons why crown metrics C3, C8, and C38, which describe the characteristics of the crown bottom, crown vertical length (also called crown depth), and crown volume, respectively, outperformed other commonly used metrics in tropical species classification. The two entire tree metrics relate to tree volume, confirming again the effectiveness of tree volume for the classification of species, not only for boreal and temperate species [60] but also for tropical species.
3.4. Results of Species Identification
Identification results under different leaf conditions are shown in Table 8. Overall accuracy values indicated that the selected first 15 important metrics could identify tropical species with an accuracy of approximately 70%. The overall accuracy obtained under the leaf-on condition is slightly better than that under the leaf-off condition in the two datasets. In terms of performance on each species, noticeable differences can be observed. The and values of AM and HT are generally higher than those of FA and DR under two leaf conditions in two datasets. This may be explained from the aspect of plant morphology, i.e., AM and HT have a spherical crown, while FA and DR trees have an upright funnel crown. Structural metrics may be more sensitive to spherical shapes than to upright funnel shapes. There are also differences in specific classification performance on two species that have similar shapes. To the spherical crown, leaf condition has smaller influences on simple structure, while to the upright funnel crown, the leaf condition has a larger influence on the simple structure than on the complex tree structure.

Table 8.
Identification results of four tropical species under leaf-on and leaf-off conditions.
The combination of metrics derived under two leaf conditions improved overall classification accuracy from 70.27% to 81.7% (Table 9). However, the performance of specific species significantly varies. The combination of metrics derived under two leaf conditions improves classification results of FA and DR, with the procedure’s accuracy increasing from 55.56% to 75.00% and from 37.5% to 75.00%, respectively, showing that the combination of metrics derived under two leaf conditions could improve classification results of upright funnel crown, while the combination of metrics derived under two leaf condition shows different performance on AM and HT in testing data (i.e., datasets 1 and 2). In dataset 1, of AM achieved using the combination of metrics derived under two leaf conditions is slightly larger than that achieved using metrics derived under the leaf-on condition but is smaller than that achieved under the leaf-off condition. However, in dataset 2, of AM achieved using the combination of metrics derived under two-leaf condition is less than that achieved using metrics derived under leaf-on and leaf-off conditions. value of HT achieved using the combination of metrics derived from two leaf conditions is less than that achieved using metrics derived under leaf-on but larger than that achieved using metrics derived under the leaf-off condition in dataset 1. However, the identification result of HT using the combination of metrics derived under two leaf conditions is larger than that using metrics derived under single leaf conditions in dataset 2.

Table 9.
Confusion matrix of classification results of four tropical species under combination of structural metrics derived under two leaf conditions.
4. Discussion
4.1. Performance Analysis
Several studies have identified tropical species based on structural properties characterized by structural metrics from point clouds in recent years. However, the importance of these metrics was rarely compared. In this study, we extracted 89 structural metrics that represent traits of different parts of a tree from the HLS point cloud, including branch, crown, stem, and entire tree metrics, and assessed their correlations and importance for tropical species identification under different leaf conditions. The identification performance of these metrics was also evaluated.
Our correlation coefficient analysis illustrated that about half of existing structural metrics are highly correlated. Among them, approximately two-thirds of branch and stem metrics have high correlation coefficient values, and more than half of crown and entire tree metrics have high correlation coefficient values. This notion may be explained by two possible situations: (1) existing crown metrics represent the same or similar characteristics of a crown using various formats; and (2) some metrics may not be appropriate to tropical species. Thus, it is essential to find effective and efficient metrics for tropical species identification. According to important assessment results, the structural properties of the crown and stem were identified as the most important components for the identification of tropical species. This finding may also be the reason many studies mainly used crown metrics to classify species. In addition, stem metrics perform important roles. However, different from other studies which use DBH, the most important stem metric is stem radial irregularity. There are two possible reasons: (1) in comparison with DBH that only measures the diameter of a stem, stem radial irregularity takes the size and shape of a stem into consideration. (2) stem radial irregularity has a lower relationship with other metrics, making the identification model more sensitive to its variations between species.
Several robust and more concrete metrics were discovered, providing reference significance to further studies. Identification results demonstrated that leaf condition affects species identification. Based on overall accuracy, the leaf-off condition could slightly improve the performance of structural metrics, while combination of metrics derived under two leaf conditions could significantly improve identification accuracy. This could be due to the fact that metrics derived under the leaf-off condition can better represent inner crown and branch structures compared to metrics derived under leaf-on condition. The combination of metrics derived under two leaf conditions integrated the internal and external structural properties of a tree, thus obtaining better identification results. However, specific influence of leaf conditions on the identification of tropical trees depends on the species. This may relate to the surrounding environment, plant morphology, and ecology.
4.2. Influence Factors
This study obtained positive importance assessment and species identification results. Each species has at least two misidentified trees. This situation may be due to the effects of the surrounding environment and their growth-defense tradeoffs [61]. Tomé and Burkhart [62] illustrated that the growth of individual trees on particular sites could be affected by local neighbors and competition status. Park trees in Hong Kong usually have high species diversity and a complex growth environment [63]. To adapt to various external stress conditions and maximize survival efficiency, plants evolve a complex and sophisticated regulatory mechanism to mediate the balance of growth and external stress [64,65]. This adaptation leads to the convergence of tree traits, resulting in the structure differs from the common pattern of their corresponding species, lowering variation between species [66,67]. In addition, to maintain the neatness and beauty, trees in the park are sometimes pruned, resulting that the precision of their external shape and structural characteristics are affected. Samples used in this study are selected from parks which away from residential areas and near forests to minimize the influence of pruning and maintenance activities. It is difficult to completely reduce the impact of pruning activities. This study was conducted on four tropical species growing in a park in Hong Kong. The limited number of species, certain environments, and ecosystems may also affect the assessment of the importance and applicability of selected important metrics. In addition, tree point clouds were obtained by holding the scanner and walking around trees twice. During the generation of tree point clouds, the point clouds need to be registered, and repeated points need to be removed by GeoSLAM Hub software. This procedure may be affected by system errors of GeoSLAM Hub software, thus influencing the quality of tree point clouds and the extraction of structural metrics.
Furthermore, four species were selected as examples of tropical species for assessment of structural metrics. Although some inefficient and highly correlated metrics were detected and optimal metric sets were proposed in this study, it is not enough to be used as a standard guideline for the identification of all tropical species. We will try to explore the capability and applicability of structural metrics on more species and samples in diverse environments. Branch and stem metrics derived under all leaf conditions are extracted on the basis of the construction of 3D tree models. The 3D model was constructed by hierarchically fitting cylinders to stems and branches. However, branch points, particularly high-order branch points within the crown, may be misidentified under leaf-on condition. Accordingly, metrics related to traits of high-order branches may be inaccurate. This is the reason the importance of branch metrics is relatively low.
4.3. Application Analysis
Our study affirmed that HLS could be used to reduce obscuration effects and obtain structural measurements. Meanwhile, HLS can easily handle forest inventory and structural heterogeneity, tree growth modeling, and tree structural health monitoring. The application in other fields, such as 3D model construction of buildings and survey of individual trees and forests, can be performed using HLS. This study explored the importance and performance of numerous existing structural metrics for species identification, evaluated their correlation, and discussed the association of structural metrics, identification, and structural properties. Results of our capability test showed that good identification results could be obtained with several important and optimal metrics instead of many metric sets. This method not only decreases identification time but also saves computing power, providing a significant reference for later work.
4.4. Potential Improvement
Our assessment of structural metrics indicated that identifying species based on the structural characteristics of a species is practical and feasible, but there is still space for improvement. Many structural metrics were included and evaluated in this study, and optimal metrics were verified to be effective for tropical species identification. Some properties of trees, such as texture traits of foliage, crown, and stem, cannot be resolved. According to crown criteria illustrated by González-Orozco et al. [68] and Trichon [69], the division within a crown remarkably varies between species. Some crowns do not have clear divisions, while others have two or more divisions with each component. Foliage texture has many types, for example, smooth, mottled, granular, grainy, and spotted [68]. If these texture features can be taken into consideration, species identification using structural metrics derived from the HLS point cloud will be improved. Traditionally, species identification is conducted based on multispectral or hyperspectral photographs, which can represent spectral information of crowns and leaves. If structural characteristics and spectral information can be integrated as features for species identification, more details and knowledge of trees may enhance identification precision. In addition, structural metrics and the influence of leaves were explored based on standalone trees. Their performance on trees in dense forests is still unknown. Therefore, further experiments are worth being designed and carried out to exploit and improve the robustness, practicality, and applicability.
5. Conclusions
This study evaluated the correlation coefficient between 89 existing structural metrics, including crown, stem, branch, and entire tree metrics, and assessed the use of these metrics for tropical species classification under different leaf conditions using HLS point cloud. Approximately two-thirds of branch and stem metrics are highly correlated, and more than half of crown and entire tree metrics are highly correlated. In terms of metric importance, crown, and stem metrics were identified as the most important components. Leaf conditions (i.e., leaf-on and leaf-off) were found to have an influence on tropical species classification. The combination of metrics derived under leaf-on, and leaf-off conditions can significantly improve the identification accuracy of four tropical species. Furthermore, we investigated fifteen optimal metrics based on correlation analysis and importance metrics, and nine robust structural metric sets were proposed and validated. The most important structural metrics discovered in this study are more concrete compared to commonly used structural metrics. For example, we found CS characterized by the ratio between the horizontal and vertical maximum spread of a crown is more significant than horizontal spread and spread area for species identification. Although plenty of structural metrics were developed, many of them are identical. It is essential to investigate efficient structural metrics for the identification of more species, such as boreal and temperate species. Our exploration of the connection between metrics and structural properties and assessment of the importance of identification of four tropical species provide a significant reference for further research, not only studies on the effectiveness of structural metrics but also studies on the identification of other tropical species.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/rs15112826/s1, Figure S1: Illustration of stem metric derivation. Figure S2: Illustration of crown metrics. Figure S3: Illustration of crown profile and relevant metrics. Table S1: Detailed definition and format of stem structural metrics. Table S2: Detailed definition and format of branch structural metrics. Table S3: Detailed definition and format of entire tree structural metrics. Table S4: Detailed definition and format of crown structural metrics. References [70,71,72,73,74] are cited in the supplementary materials.
Author Contributions
Conceptualization, M.S.W.; methodology, M.S.W. and M.W.; validation, M.W.; formal analysis and investigation, M.W.; writing—original draft preparation, M.W.; writing—review and editing, M.S.W.; visualization, M.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by General Research Fund (Grant Nos. 15603920 and 15609421) and the Collaborative Research Fund (Grant No. C5062-21GF) from the Research Grants Council, Hong Kong, China. M.S. Wong also acknowledged the support from the project 1-CD81, Research Institute for Land and Space, the Hong Kong Polytechnic University, Hong Kong, China.
Data Availability Statement
The data that support the findings of this study are available from the corresponding author upon reasonable request.
Acknowledgments
We express our gratitude to the anonymous reviewers and the editor for their valuable comments and suggestions to improve the manuscript.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Field, C.B.; Barros, V.R. Climate Change 2014–Impacts, Adaptation and Vulnerability: Regional Aspects; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Cao, K.; Zhang, X. An improved Res-UNet model for tree species classification using airborne high-resolution images. Remote Sens. 2020, 12, 1128. [Google Scholar] [CrossRef]
- Lin, Y.; Herold, M. Tree species classification based on explicit tree structure feature parameters derived from static terrestrial laser scanning data. Agric. For. Meteorol. 2016, 216, 105–114. [Google Scholar] [CrossRef]
- Ghiyamat, A.; Shafri, H.Z. A review on hyperspectral remote sensing for homogeneous and heterogeneous forest biodiversity assessment. Int. J. Remote Sens. 2010, 31, 1837–1856. [Google Scholar] [CrossRef]
- Shi, Y.; Skidmore, A.K.; Wang, T.; Holzwarth, S.; Heiden, U.; Pinnel, N.; Zhu, X.; Heurich, M. Tree species classification using plant functional traits from LiDAR and hyperspectral data. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 207–219. [Google Scholar] [CrossRef]
- Alonzo, M.; Bookhagen, B.; Roberts, D.A. Urban tree species mapping using hyperspectral and lidar data fusion. Remote Sens. Environ. 2014, 148, 70–83. [Google Scholar] [CrossRef]
- Bauwens, S.; Bartholomeus, H.; Calders, K.; Lejeune, P. Forest inventory with terrestrial LiDAR: A comparison of static and hand-held mobile laser scanning. Forests 2016, 7, 127. [Google Scholar] [CrossRef]
- Balenović, I.; Liang, X.; Jurjević, L.; Hyyppä, J.; Seletković, A.; Kukko, A. Hand-held personal laser scanning–current status and perspectives for forest inventory application. Croat. J. For. Eng. 2021, 42, 165–183. [Google Scholar] [CrossRef]
- Chen, S.; Liu, H.; Feng, Z.; Shen, C.; Chen, P. Applicability of personal laser scanning in forestry inventory. PLoS ONE 2019, 14, e0211392. [Google Scholar] [CrossRef] [PubMed]
- Oveland, I.; Hauglin, M.; Giannetti, F.; Schipper Kjørsvik, N.; Gobakken, T. Comparing three different ground based laser scanning methods for tree stem detection. Remote Sens. 2018, 10, 538. [Google Scholar] [CrossRef]
- Su, Y.; Guo, Q.; Jin, S.; Guan, H.; Sun, X.; Ma, Q.; Hu, T.; Wang, R.; Li, Y. The development and evaluation of a backpack LiDAR system for accurate and efficient forest inventory. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1660–1664. [Google Scholar] [CrossRef]
- Budei, B.C.; St-Onge, B.; Hopkinson, C.; Audet, F.-A. Identifying the genus or species of individual trees using a three-wavelength airborne lidar system. Remote Sens. Environ. 2018, 204, 632–647. [Google Scholar] [CrossRef]
- Shi, Y.; Wang, T.; Skidmore, A.K.; Heurich, M. Important LiDAR metrics for discriminating forest tree species in Central Europe. J. Photogramm. Remote Sens. 2018, 137, 163–174. [Google Scholar] [CrossRef]
- Åkerblom, M.; Raumonen, P.; Mäkipää, R.; Kaasalainen, M. Automatic tree species recognition with quantitative structure models. Remote Sens. Environ. 2017, 191, 1–12. [Google Scholar] [CrossRef]
- Yao, W.; Krzystek, P.; Heurich, M. Tree species classification and estimation of stem volume and DBH based on single tree extraction by exploiting airborne full-waveform LiDAR data. Remote Sens. Environ. 2012, 123, 368–380. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Latifi, H.; Stereńczak, K.; Modzelewska, A.; Lefsky, M.; Waser, L.T.; Straub, C.; Ghosh, A. Review of studies on tree species classification from remotely sensed data. Remote Sens. Environ. 2016, 186, 64–87. [Google Scholar] [CrossRef]
- Wang, M.; Wong, M.S.; Abbas, S. Tropical Species Classification with Structural Traits Using Handheld Laser Scanning Data. Remote Sens. 2022, 14, 1948. [Google Scholar] [CrossRef]
- Terryn, L.; Calders, K.; Disney, M.; Origo, N.; Malhi, Y.; Newnham, G.; Raumonen, P.; Verbeeck, H. Tree species classification using structural features derived from terrestrial laser scanning. J. Photogramm. Remote Sens. 2020, 168, 170–181. [Google Scholar] [CrossRef]
- Xi, Z.; Hopkinson, C.; Rood, S.B.; Peddle, D.R. See the forest and the trees: Effective machine and deep learning algorithms for wood filtering and tree species classification from terrestrial laser scanning. J. Photogramm. Remote Sens. 2020, 168, 1–16. [Google Scholar] [CrossRef]
- Koenig, K.; Höfle, B. Full-waveform airborne laser scanning in vegetation studies—A review of point cloud and waveform features for tree species classification. Forests 2016, 7, 198. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W.; Seidel, D. Measuring the contribution of leaves to the structural complexity of urban tree crowns with terrestrial laser scanning. Remote Sens. 2021, 13, 2773. [Google Scholar] [CrossRef]
- Sumnall, M.J.; Hill, R.A.; Hinsley, S.A. Comparison of small-footprint discrete return and full waveform airborne lidar data for estimating multiple forest variables. Remote Sens. Environ. 2016, 173, 214–223. [Google Scholar] [CrossRef]
- Hamraz, H.; Contreras, M.A.; Zhang, J. A robust approach for tree segmentation in deciduous forests using small-footprint airborne LiDAR data. Int. J. Appl. Earth Obs. Geoinf. 2016, 52, 532–541. [Google Scholar] [CrossRef]
- Vicari, M.B.; Disney, M.; Wilkes, P.; Burt, A.; Calders, K.; Woodgate, W. Leaf and wood classification framework for terrestrial LiDAR point clouds. Methods Ecol. Evol. 2019, 10, 680–694. [Google Scholar] [CrossRef]
- Arseniou, G.; MacFarlane, D.W. Fractal dimension of tree crowns explains species functional-trait responses to urban environments at different scales. Ecol. Appl. 2021, 31, e02297. [Google Scholar] [CrossRef] [PubMed]
- Government of Hong Kong. The Natural Environment, Plants & Animals in Hong Kong; Conservation, N., Ed.; Government of Hong Kong: Hong Kong, 2021.
- Jim, C.Y. Roadside trees in urban Hong Kong: Part I census methodology. Arboric. J. 1996, 20, 221–237. [Google Scholar] [CrossRef]
- Jim, C.Y. Tree–habitat relationships in urban Hong Kong. Environ. Conserv. 1992, 19, 209–218. [Google Scholar] [CrossRef]
- Ford, K.R.; Breckheimer, I.K.; Franklin, J.F.; Freund, J.; Kroiss, S.; Larson, A.J.; Theobald, E.; HilleRisLambers, J. Competition alters tree growth responses to climate at individual and stand scales. Can. J. For. Res. 2017, 47, 53–62. [Google Scholar] [CrossRef]
- Sammartano, G.; Spanò, A. Point clouds by SLAM-based mobile mapping systems: Accuracy and geometric content validation in multisensor survey and stand-alone acquisition. Appl. Geomat. 2018, 10, 317–339. [Google Scholar] [CrossRef]
- Walfish, S. A review of statistical outlier methods. Pharm. Technol. 2006, 30, 82. [Google Scholar]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. CloudCompare. France: EDF R&D Telecom ParisTech, 11. Available online: https://pcp2019.ifp.uni-stuttgart.de/presentations/04-CloudCompare_PCP_2019_public.pdf (accessed on 10 May 2023).
- Yang, J.; Kang, Z.; Cheng, S.; Yang, Z.; Akwensi, P.H. An Individual Tree Segmentation Method Based on Watershed Algorithm and Three-Dimensional Spatial Distribution Analysis from Airborne LiDAR Point Clouds. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 1055–1067. [Google Scholar] [CrossRef]
- Ester, M.; Kriegel, H.-P.; Sander, J.; Xu, X. A density-based algorithm for discovering clusters in large spatial databases with noise. kdd 1996, 96, 226–231. [Google Scholar]
- Raumonen, P.; Åkerblom, M.; Kaasalainen, M.; Casella, E.; Calders, K.; Murphy, S. Massive-scale tree modelling from TLS data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2015, 2, 189. [Google Scholar] [CrossRef]
- Demol, M.; Wilkes, P.; Raumonen, P.; Krishna Moorthy Parvathi, S.; Calders, K.; Gielen, B.; Verbeeck, H. Volumetric overestimation of small branches in 3D reconstructions of Fraxinus excelsior. Silva Fenn. 2022, 56, 10550. [Google Scholar] [CrossRef]
- Lau, A.; Bentley, L.P.; Martius, C.; Shenkin, A.; Bartholomeus, H.; Raumonen, P.; Malhi, Y.; Jackson, T.; Herold, M. Quantifying branch architecture of tropical trees using terrestrial LiDAR and 3D modelling. Trees 2018, 32, 1219–1231. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y.; Cohen, I. Pearson Correlation Coefficient, in Noise Reduction in Speech Processing; Springer: Berlin/Heidelberg, Germany, 2009; pp. 1–4. [Google Scholar]
- Dormann, C.F.; Elith, J.; Bacher, S.; Buchmann, C.; Carl, G.; Carré, G.; Marquéz, J.R.G.; Gruber, B.; Lafourcade, B.; Leitão, P.J. Collinearity: A review of methods to deal with it and a simulation study evaluating their performance. Ecography 2013, 36, 27–46. [Google Scholar] [CrossRef]
- Schober, P.; Boer, C.; Schwarte, L.A. Correlation coefficients: Appropriate use and interpretation. Anesth. Analg. 2018, 126, 1763–1768. [Google Scholar] [CrossRef] [PubMed]
- Obilor, E.I.; Amadi, E.C. Test for significance of Pearson’s correlation coefficient. Int. J. Innov. Math. Stat. Energy Policies 2018, 6, 11–23. [Google Scholar]
- Shi, X.; Wong, Y.; Li, M.Z.-F.; Palanisamy, C.; Chai, C. A feature learning approach based on XGBoost for driving assessment and risk prediction. Accid. Anal. Prev. 2019, 129, 170–179. [Google Scholar] [CrossRef] [PubMed]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V. Scikit-learn: Machine learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830.45. [Google Scholar]
- Al-Tashi, Q.; Abdulkadir, S.J.; Rais, H.M.; Mirjalili, S.; Alhussian, H. Approaches to multi-objective feature selection: A systematic literature review. IEEE Access 2020, 8, 125076–125096. [Google Scholar] [CrossRef]
- Liu, H.; Motoda, H. Feature Selection for Knowledge Discovery and Data Mining; Springer Science & Business Media: New York, NY, USA, 2012; Volume 454. [Google Scholar]
- Amiri, N.; Heurich, M.; Krzystek, P.; Skidmore, A. Feature Relevance Assessment of Multispectral Airborne Lidar Data for Tree Species Classification. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2018, 42, 31–34. [Google Scholar] [CrossRef]
- Cai, J.; Luo, J.; Wang, S.; Yang, S. Feature selection in machine learning: A new perspective. Neurocomputing 2018, 300, 70–79. [Google Scholar] [CrossRef]
- Manju, N.; Harish, B.; Prajwal, V. Ensemble feature selection and classification of internet traffic using XGBoost classifier. Int. J. Comput. Netw. Inf. Secur. 2019, 11, 37. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A scalable tree boosting system. In Proceedings of the 22nd ACM Sigkdd International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016. [Google Scholar]
- Shenkin, A.; Bentley, L.P.; Oliveras, I.; Salinas, N.; Adu-Bredu, S.; Marimon-Junior, B.H.; Marimon, B.S.; Peprah, T.; Choque, E.L.; Trujillo Rodriguez, L. The influence of ecosystem and phylogeny on tropical tree crown size and shape. Front. For. Glob. Chang. 2020, 3, 501757. [Google Scholar] [CrossRef]
- Harikumar, A.; Bovolo, F.; Bruzzone, L. An internal crown geometric model for conifer species classification with high-density lidar data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2924–2940. [Google Scholar] [CrossRef]
- Li, J.; Hu, B.; Noland, T.L. Classification of tree species based on structural features derived from high density LiDAR data. Agric. For. Meteorol. 2013, 171, 104–114. [Google Scholar] [CrossRef]
- Stal, C.; Verbeurgt, J.; De Sloover, L.; De Wulf, A. Assessment of handheld mobile terrestrial laser scanning for estimating tree parameters. J. For. Res. 2021, 32, 1503–1513. [Google Scholar] [CrossRef]
- Du Toit, F.; Coops, N.C.; Goodbody, T.R.; Stoehr, M.; El-Kassaby, Y.A. Deriving internal crown geometric features of Douglas-fir from airborne laser scanning in a realized-gain trial. For. Int. J. For. Res. 2021, 94, 442–454. [Google Scholar] [CrossRef]
- Kim, S. Individual Tree Species Identification Using LIDAR-Derived Crown Structures and Intensity Data; Citeseer: Princeton, NJ, USA, 2008. [Google Scholar]
- Maschler, J.; Atzberger, C.; Immitzer, M. Individual tree crown segmentation and classification of 13 tree species using airborne hyperspectral data. Remote Sens. 2018, 10, 1218. [Google Scholar] [CrossRef]
- King, D.A. Allometry and life history of tropical trees. J. Trop. Ecol. 1996, 12, 25–44. [Google Scholar] [CrossRef]
- Purves, D.W.; Lichstein, J.W.; Pacala, S.W. Crown plasticity and competition for canopy space: A new spatially implicit model parameterized for 250 North American tree species. PLoS ONE 2007, 2, e870. [Google Scholar] [CrossRef]
- Torabzadeh, H.; Leiterer, R.; Hueni, A.; Schaepman, M.E.; Morsdorf, F. Tree species classification in a temperate mixed forest using a combination of imaging spectroscopy and airborne laser scanning. Agric. For. Meteorol. 2019, 279, 107744. [Google Scholar] [CrossRef]
- Huot, B.; Yao, J.; Montgomery, B.L.; He, S.Y. Growth–defense tradeoffs in plants: A balancing act to optimize fitness. Mol. Plant 2014, 7, 1267–1287. [Google Scholar] [CrossRef]
- Tomé, M.; Burkhart, H.E. Distance-dependent competition measures for predicting growth of individual trees. For. Sci. 1989, 35, 816–831. [Google Scholar]
- Jim, C.Y. The urban forestry programme in the heavily built-up milieu of Hong Kong. Cities 2000, 17, 271–283. [Google Scholar] [CrossRef]
- Simonovsky, M.; Komodakis, N. Dynamic edge-conditioned filters in convolutional neural networks on graphs. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 26 June 2017. [Google Scholar]
- Xie, Z.; Nolan, T.M.; Jiang, H.; Yin, Y. AP2/ERF transcription factor regulatory networks in hormone and abiotic stress responses in Arabidopsis. Front. Plant Sci. 2019, 10, 228. [Google Scholar] [CrossRef] [PubMed]
- MacFarlane, D.W.; Kane, B. Neighbour effects on tree architecture: Functional trade-offs balancing crown competitiveness with wind resistance. Funct. Ecol. 2017, 31, 1624–1636. [Google Scholar] [CrossRef]
- Poorter, L.; Bongers, L.; Bongers, F. Architecture of 54 moist-forest tree species: Traits, trade-offs, and functional groups. Ecology 2006, 87, 1289–1301. [Google Scholar] [CrossRef] [PubMed]
- González-Orozco, C.E.; Mulligan, M.; Trichon, V.; Jarvis, A. Taxonomic identification of Amazonian tree crowns from aerial photography. Appl. Veg. Sci. 2010, 13, 510–519. [Google Scholar] [CrossRef]
- Trichon, V. Crown typology and the identification of rain forest trees on large-scale aerial photographs. In Tropical Forest Canopies: Ecology and Management: Proceedings of ESF Conference, Oxford University, 12–16 December 1998; Springer: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Colaço, A.F.; Trevisan, R.G.; Molin, J.P.; Rosell-Polo, J.R. A method to obtain orange crop geometry information using a mobile terrestrial laser scanner and 3D modeling. Remote Sens. 2017, 9, 763. [Google Scholar] [CrossRef]
- Cupec, R.; Vidović, I.; Filko, D.; Đurović, P. Object recognition based on convex hull alignment. Pattern Recognit. 2020, 102, 107199. [Google Scholar] [CrossRef]
- Di Gennaro, S.F.; Matese, A. Evaluation of novel precision viticulture tool for canopy biomass estimation and missing plant detection based on 2.5 D and 3D approaches using RGB images acquired by UAV platform. Plant Methods 2020, 16, 91. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Hyyppä, J. A comprehensive but efficient framework of proposing and validating feature parameters from airborne LiDAR data for tree species classification. Int. J. Appl. Earth Obs. Geoinf. 2016, 46, 45–55. [Google Scholar] [CrossRef]
- Liu, H.; Wu, C. Incorporating crown shape information for identifying ash tree species. Photogramm. Eng. Remote Sens. 2018, 84, 495–503. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).