Denoising and Accuracy Evaluation of ICESat-2/ATLAS Photon Data for Nearshore Waters Based on Improved Local Distance Statistics
Abstract
1. Introduction
2. Materials and Methods
2.1. Experiment Areas
2.2. ICESat-2 ATL03 Data
3. Research Methods
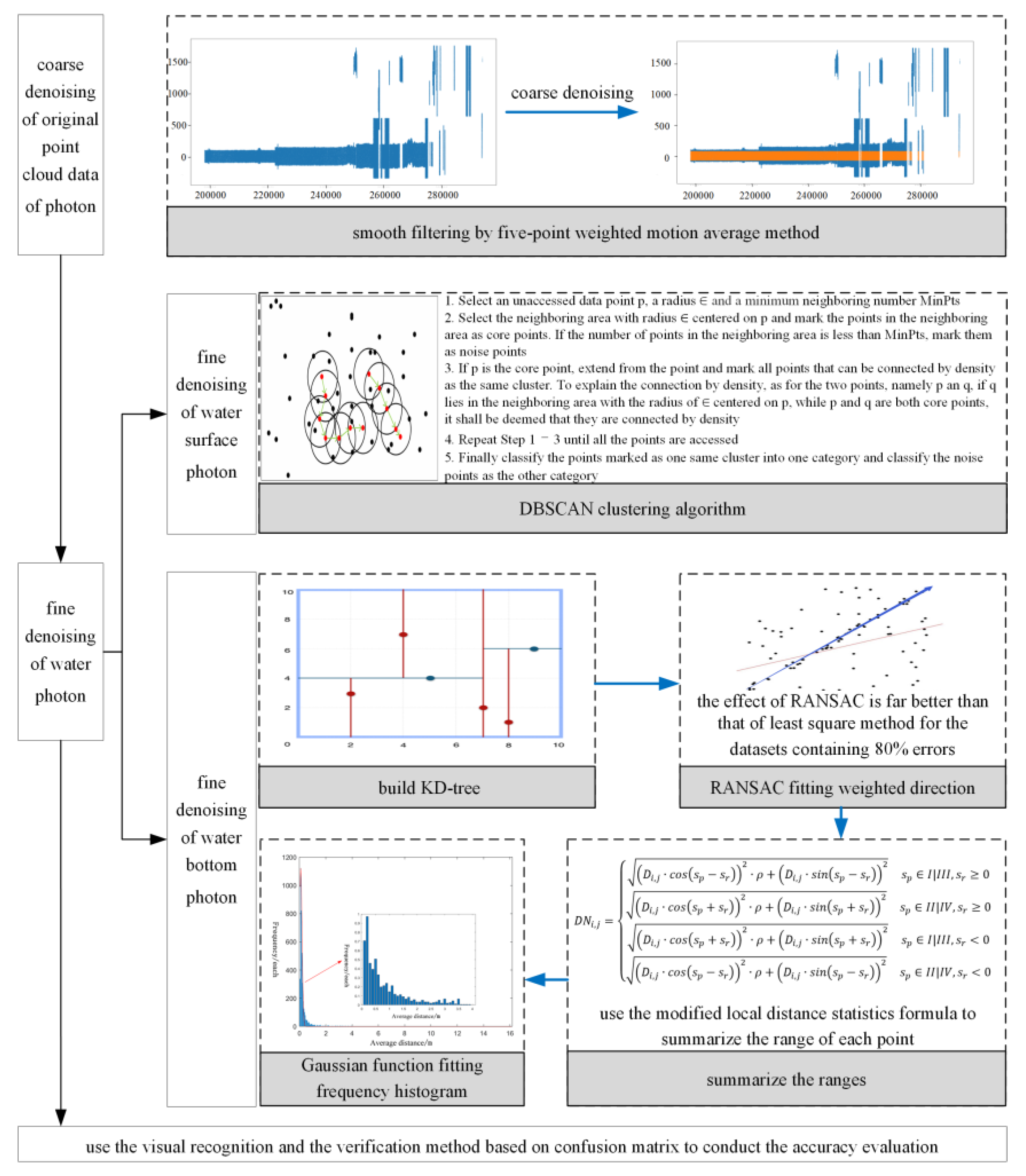
3.1. Photon Coarse Denoising
3.2. Photon Fine Denoising
3.2.1. Fine Denoising of Water Surface Photon
3.2.2. Fine Denoising of Water Bottom Photon
- (1)
- Build the KD tree indexes for the water bottom photons so as to improve the indexing speed and then search the nearest K points around each point. The KD tree is constructed according to the steps provided in Appendix B.
- (2)
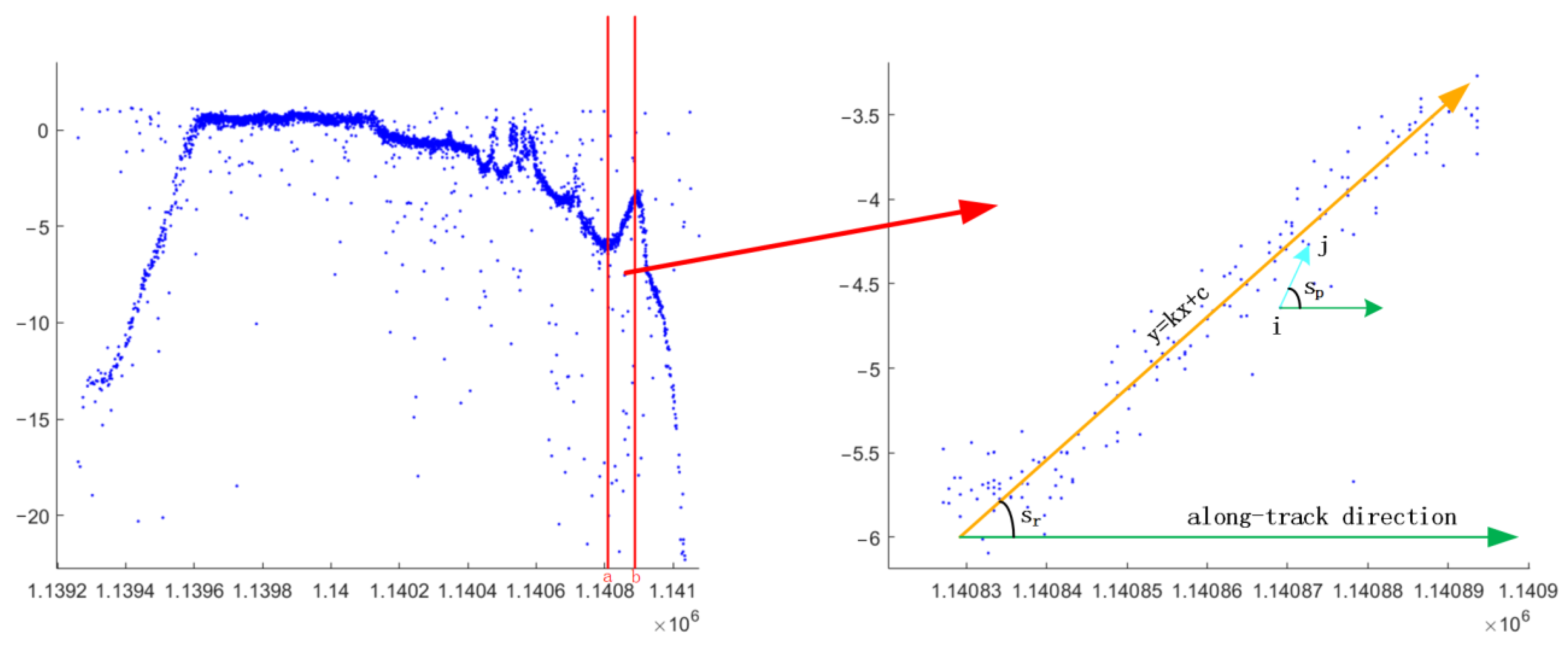
- Divide the intervals in the along-track direction according to 20 m for the water bottom photons and carry out RANSAC (Random Sample Consensus) straight-line fitting on all the photons in each interval. The basic idea of the RANSAC algorithm is given in Appendix C. The fitted straight line slope is the slope of the terrain trend direction in this interval and it is weighted in this direction.
- (3)
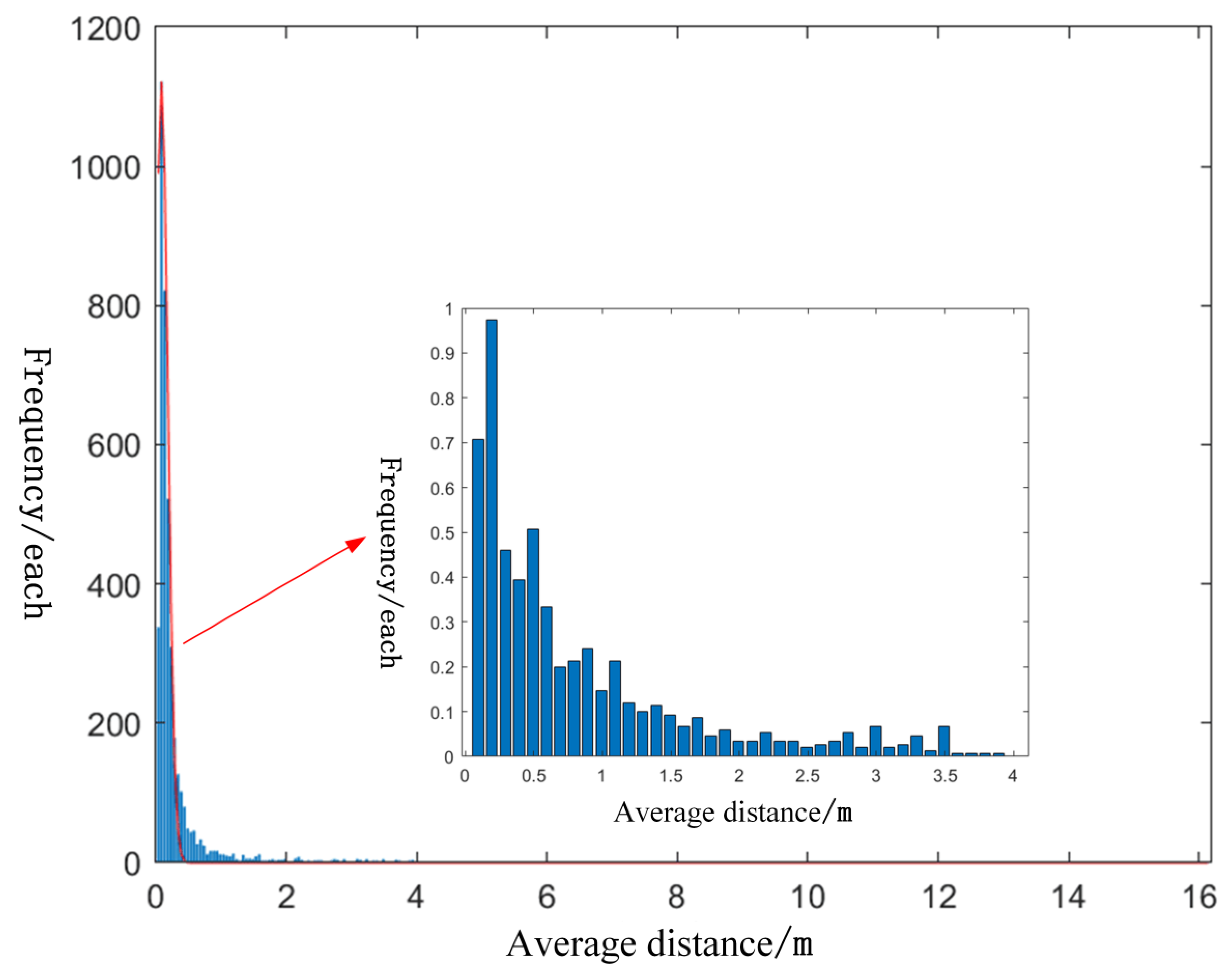
- According to the modified distance formula, the average values of the local distance sum of the nearest K points from each point are counted.
- (4)
- Because there are many fine sands in the water bottom area near the sea surface, ATL03 single-photon data will penetrate to the bottom through fine sands in this area, with obvious layering. Thus, it is required to remove the water bottom photons in shallow water areas. According to the elevation of water bottom point cloud data, the distribution histogram is built to divide the point cloud data into N intervals according to the equal elevation interval and count the total number of photons in each elevation interval. The average value of the elevation histogram is calculated and then look through the histogram to find the most elevation sections continuously larger than the average value for DBSCAN clustering denoising.
- (5)
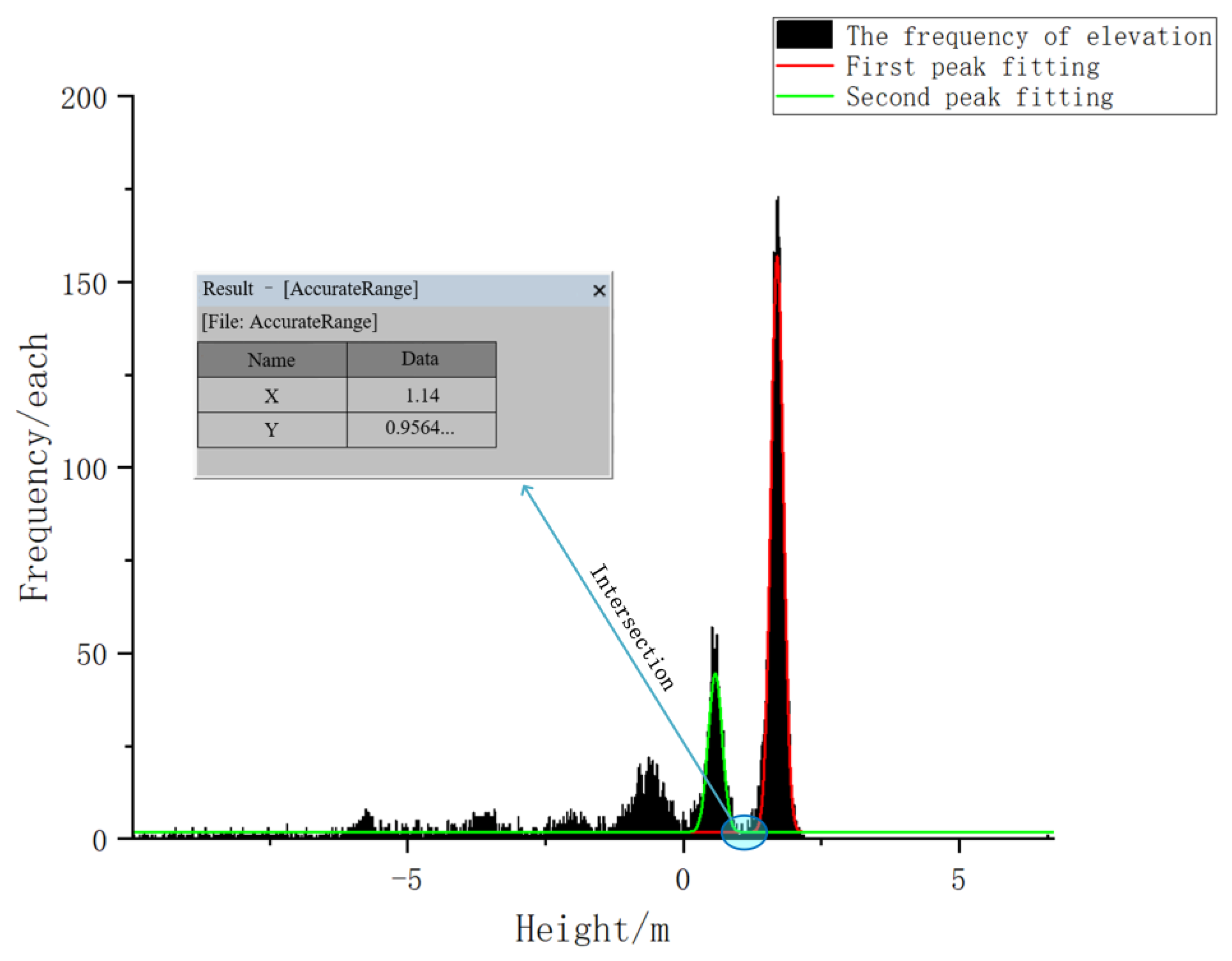
- Conduct the frequency statistics on the average distance , and produce the frequency histogram with 0.1 as the spacing. Conduct the Gaussian curve fitting on , and search the final elevation section whose frequency is lower than with the peak value of as the average value of the Gaussian curve based on the Gaussian curve half-width and full-height theorem. refers to the difference between the abscissa of the elevation section and the average value . The average distance threshold is set to be the sum of the average value and t-fold . Those whose average distance is larger than the threshold shall be noise photon while the rest shall be water bottom signal photons.
3.3. Accuracy Evaluation
4. Data Processing and Results
4.1. Point Cloud Denoising Experiment
4.1.1. Threshold Selection for Photon Separation
4.1.2. Threshold Selection for Gaussian Curve Fitting
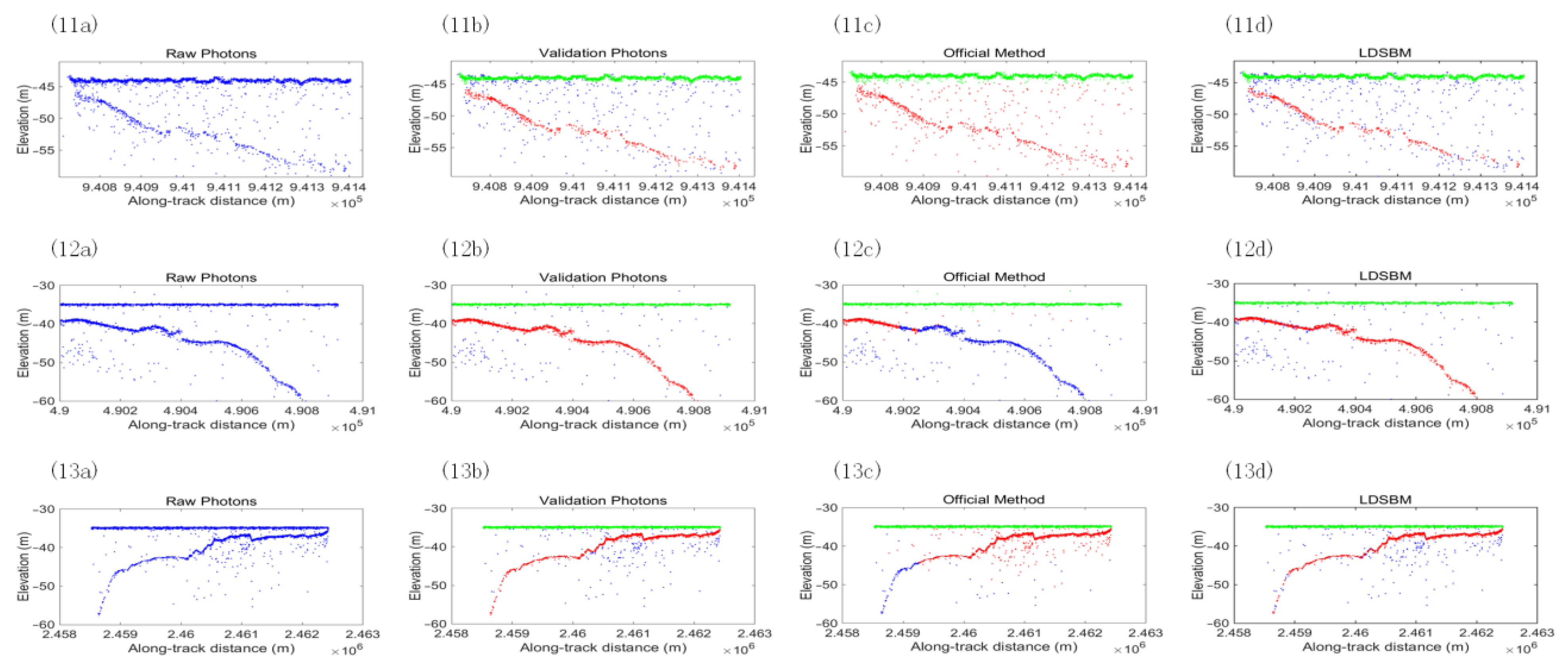
4.2. Denoising Results
5. Discussion
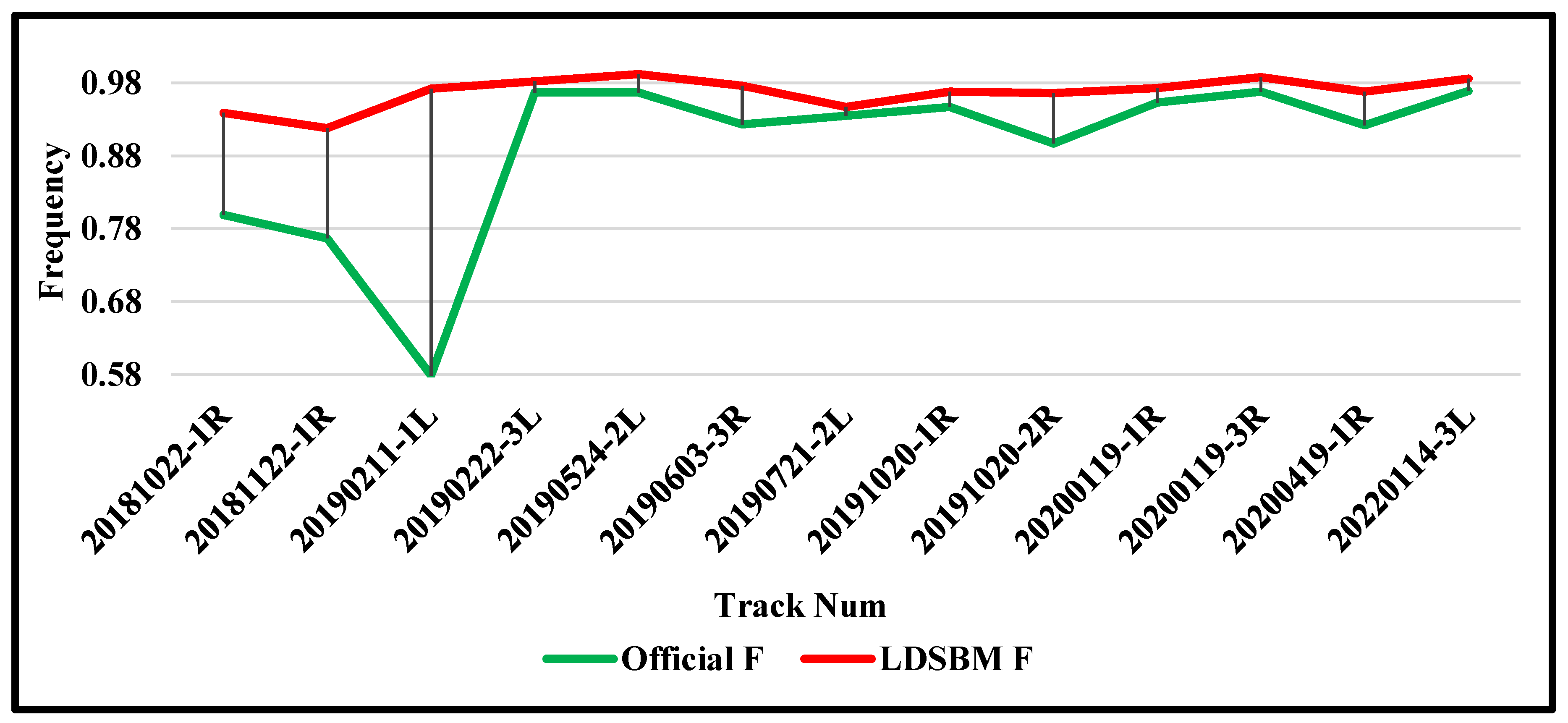
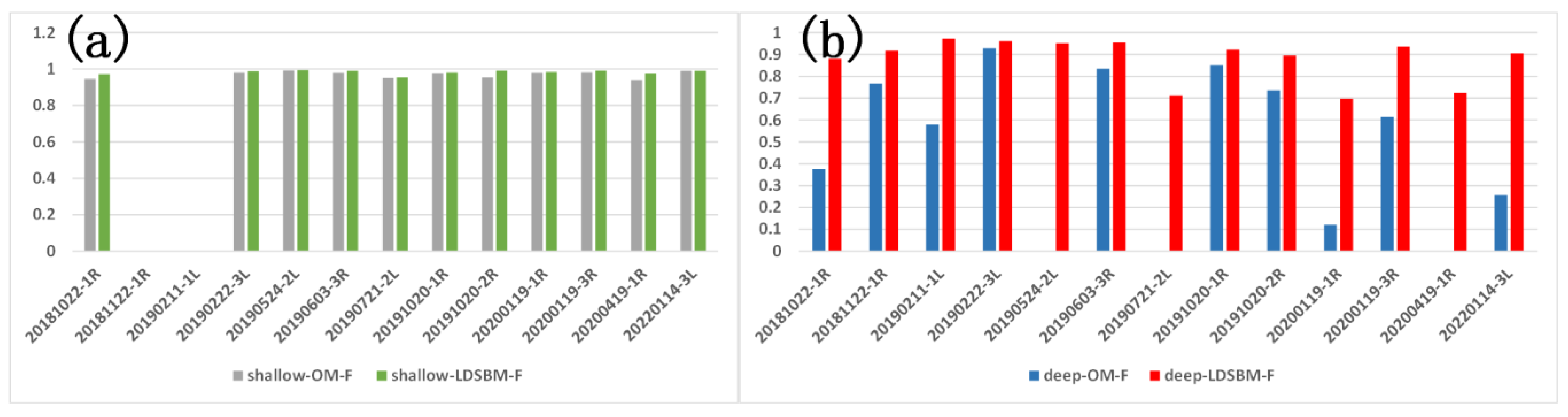
5.1. Global Precision Discussion
5.2. Delamination Precision Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- (1)
- Select an unused data point p, a radius ∈ and a minimum neighboring number MinPts.
- (2)
- Select the neighboring area with radius ∈ centered on p and mark the points in the neighboring area as core points. If the number of points in the neighboring area is less than MinPts, mark them as noise points.
- (3)
- If p is the core point, extend from the point and mark all points that can be connected by density as the same cluster. To explain the connection by density, as for the two points, namely p and q, if q lies in the neighboring area with the radius of ∈ centered on p, while p and q are both core points, it shall be deemed that they are connected by density.
- (4)
- Repeat Step 1–3 until all the points are accessed.
- (5)
- Finally classify the points marked as one same cluster into one category and classify the noise points as the other category.
Appendix B
Appendix C
References
- Westaway, R.M.; Lane, S.N.; Hicks, D.M. Remote sensing of clear-water, shallow, gravel-bed rivers using digital photogrammetry. Photogramm. Eng. Remote Sens. 2001, 67, 1271–1282. [Google Scholar]
- Brown, C.J.; Beaudoin, J.; Brissette, M.; Gazzola, V. Multispectral multibeam echo sounder backscatter as a tool for improved seafloor characterization. Geosciences 2019, 9, 126. [Google Scholar] [CrossRef]
- Hua, L.W.; Bi, Y.L.; Hao, L. The research of artificial shoreline extraction based on airborne LIDAR data. J. Phys. Conf. Ser. 2021, 2006, 012048. [Google Scholar] [CrossRef]
- Paravolidakis, V.; Ragia, L.; Moirogiorgou, K.; Zervakis, M.E. Automatic coastline extraction using edge detection and optimization procedures. Geosciences 2018, 8, 407. [Google Scholar] [CrossRef]
- Xu, N.; Ma, Y.; Zhang, W.; Wang, X.H.; Yang, F.; Su, D. Monitoring Annual Changes of Lake Water Levels and Volumes over 1984–2018 Using Landsat Imagery and ICESat-2 Data. Remote Sens. 2020, 12, 4004. [Google Scholar] [CrossRef]
- Abdalati, W.; Zwally, H.J.; Bindschadler, R.; Csatho, B.; Farrell, S.L.; Fricker, H.A.; Harding, D.; Kwok, R.; Lefsky, M.; Markus, T.; et al. The ICESat-2 laser altimetry mission. Proc. IEEE 2010, 98, 735–751. [Google Scholar] [CrossRef]
- Parrish, C.E.; Magruder, L.A.; Neuenschwander, A.L.; Forfinski-Sarkozi, N.; Alonzo, M.; Jasinski, M. Validation of ICESat-2 ATLAS bathymetry and analysis of ATLAS’s bathymetric mapping performance. Remote Sens. 2019, 11, 1634. [Google Scholar] [CrossRef]
- Xu, N.; Ma, X.; Ma, Y.; Zhao, P.; Yang, J.; Wang, X.H. Deriving Highly Accurate Shallow Water Bathymetry from Sentinel-2 and ICESat-2 Datasets by a Multitemporal Stacking Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 6677–6685. [Google Scholar] [CrossRef]
- Babbel, B.J.; Parrish, C.E.; Magruder, L.A. ICESat-2 elevation retrievals in support of satellite-derived bathymetry for global science applications. Geophys. Res. Lett. 2021, 48, e2020GL090629. [Google Scholar] [CrossRef]
- Neuenschwander, A.; Pitts, K. The ATL08 land and vegetation product for the ICESat-2 Mission. Remote Sens. Environ. 2019, 221, 247–259. [Google Scholar] [CrossRef]
- Chen, Y.; Le, Y.; Zhang, D.; Wang, Y.; Qiu, Z.; Wang, L. A photon-counting LiDAR bathymetric method based on adaptive variable ellipse filtering. Remote Sens. Environ. 2021, 256, 112326. [Google Scholar] [CrossRef]
- Xie, C.; Chen, P.; Pan, D.; Zhong, C.; Zhang, Z. Improved Filtering of ICESat-2 Lidar Data for Nearshore Bathymetry Estimation Using Sentinel-2 Imagery. Remote Sens. 2021, 13, 4303. [Google Scholar] [CrossRef]
- Hsu, H.-J.; Huang, C.-Y.; Jasinski, M.; Li, Y.; Gao, H.; Yamanokuchi, T.; Wang, C.-G.; Chang, T.-M.; Ren, H.; Kuo, C.-Y.; et al. A semi-empirical scheme for bathymetric mapping in shallow water by ICESat-2 and Sentinel-2: A case study in the South China Sea. ISPRS J. Photogramm. Remote Sens. 2021, 178, 1–19. [Google Scholar] [CrossRef]
- Wang, B.; Ma, Y.; Zhang, J.; Zhang, H.; Zhu, H.; Leng, Z.; Zhang, X.; Cui, A. A noise removal algorithm based on adaptive elevation difference thresholding for ICESat-2 photon-counting data. Int. J. Appl. Earth Obs. Geoinf. 2023, 117, 103207. [Google Scholar] [CrossRef]
- Wang, Z.; Xi, X.; Nie, S.; Wang, C. Bathymetric Method of Nearshore Based on ICESat-2/ATLAS Data—A Case Study of the Islands and Reefs in The South China Sea. In Proceedings of the IGARSS 2022-2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; IEEE: Piscataway Township, NJ, USA, 2022; pp. 2868–2871. [Google Scholar]
- Zhang, G.; Xing, S.; Xu, Q.; Li, P.; Wang, D. A Pre-Pruning Quadtree Isolation Method with Changing Threshold for ICESat-2 Bathymetric Photon Extraction. Remote Sens. 2023, 15, 1629. [Google Scholar] [CrossRef]
- Magruder, L.; Brunt, K.; Neumann, T.; Klotz, B.; Alonzo, M. Passive ground-based optical techniques for monitoring the on-orbit ICESat-2 altimeter geolocation and footprint diameter. Earth Space Sci. 2021, 8, e2020EA001414. [Google Scholar] [CrossRef]
- Le, Y.; Hu, M.; Chen, Y.; Yan, Q.; Zhang, D.; Li, S.; Zhang, X.; Wang, L. Investigating the Shallow-Water Bathymetric Capability of Zhuhai-1 Spaceborne Hyperspectral Images Based on ICESat-2 Data and Empirical Approaches: A Case Study in the South China Sea. Remote Sens. 2022, 14, 3406. [Google Scholar] [CrossRef]
- Ma, Y.; Xu, N.; Liu, Z.; Yang, B.; Yang, F.; Wang, X.H.; Li, S. Satellite-derived bathymetry using the ICESat-2 lidar and Sentinel-2 imagery datasets. Remote Sens. Environ. 2020, 250, 112047. [Google Scholar] [CrossRef]
- Koblinsky, C.J.; Clarke, R.T.; Brenner, A.C.; Frey, H. Measurement of river level variations with satellite altimetry. Water Resour. Res. 1993, 29, 1839–1848. [Google Scholar] [CrossRef]
- Ye, J.; Qiang, Y.; Zhang, R.; Liu, X.; Deng, Y.; Zhang, J. High-precision digital surface model extraction from satellite stereo images fused with ICESat-2 data. Remote Sens. 2021, 14, 142. [Google Scholar] [CrossRef]
- Li, R.; Li, H.; Hao, T.; Qiao, G.; Cui, H.; He, Y.; Hai, G.; Xie, H.; Cheng, Y.; Li, B. Assessment of ICESat-2 ice surface elevations over the Chinese Antarctic Research Expedition (CHINARE) route, East Antarctica, based on coordinated multi-sensor observations. Cryosphere 2021, 15, 3083–3099. [Google Scholar] [CrossRef]
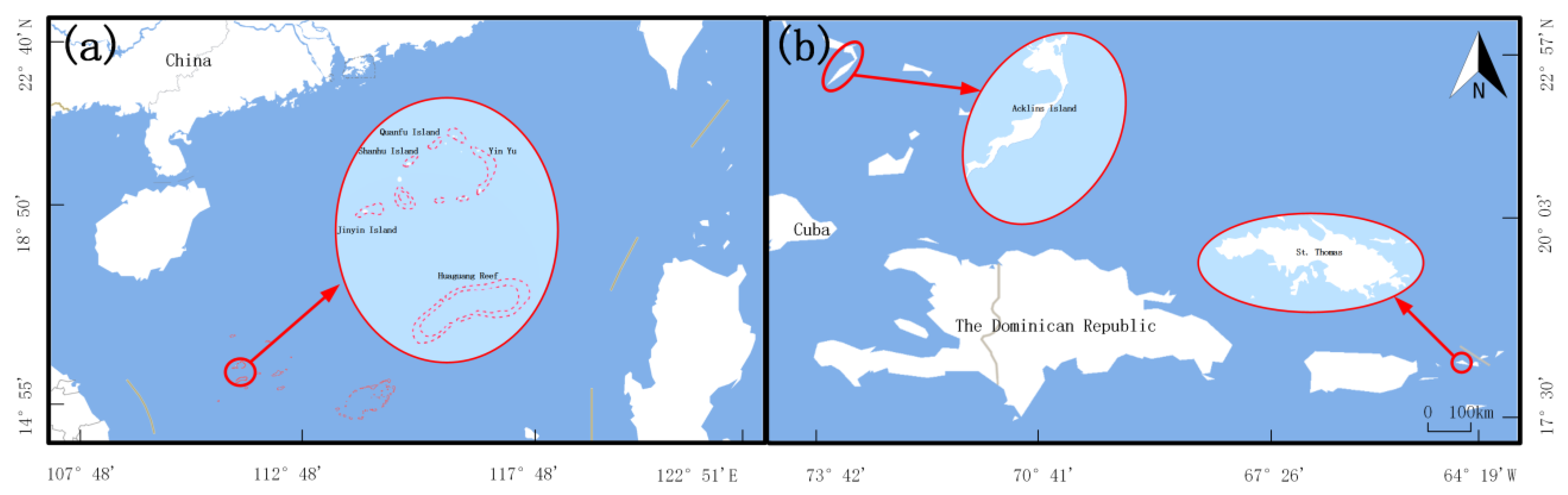
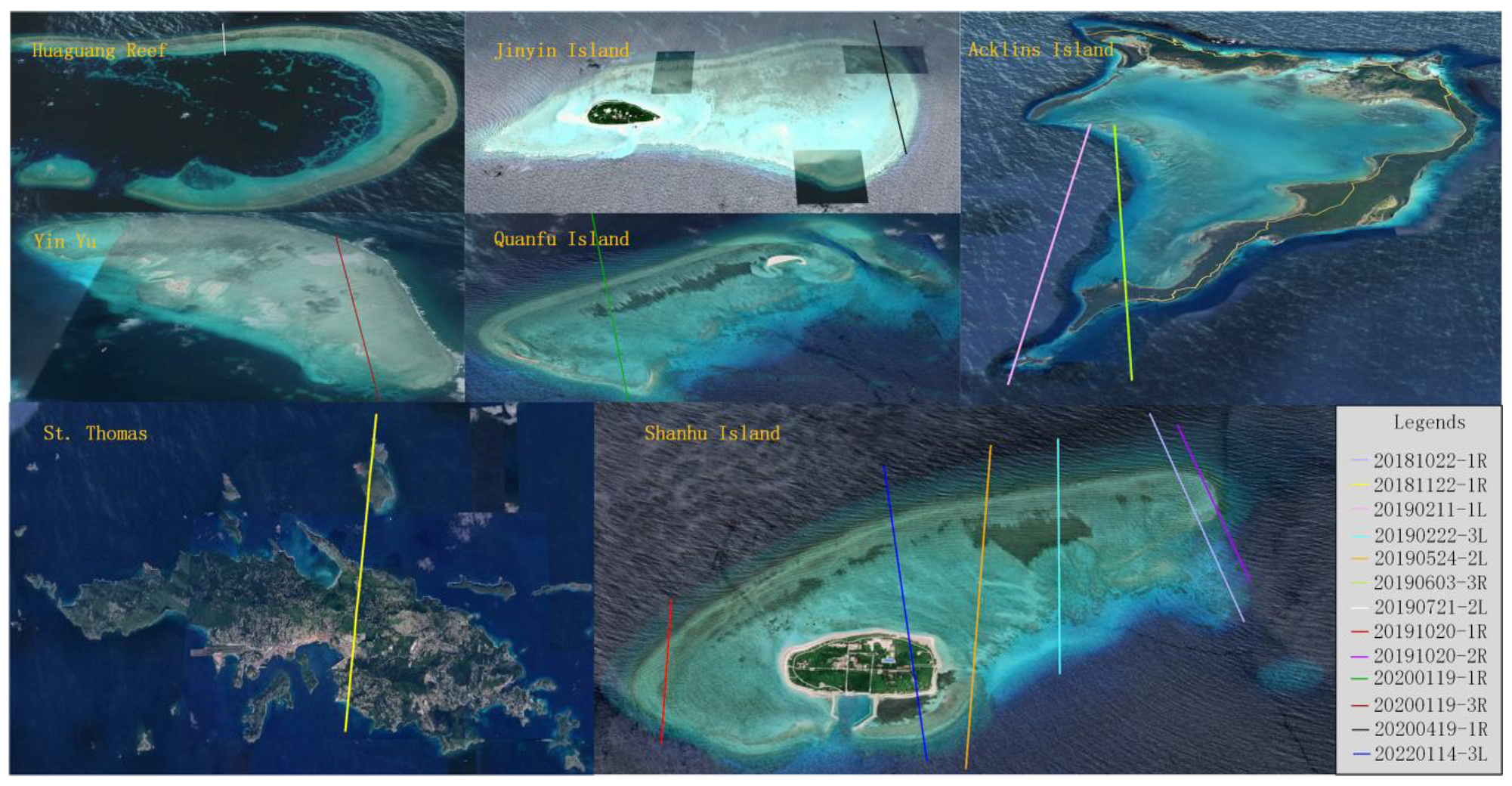

| Name of the ATL03 Dataset | Local Acquisition Time | Beam No. Used | Photon Reference |
|---|---|---|---|
| ATL03_20181022073835_03620101_005_01 | 15:38 | GT1R | 5,525,850~5,531,700 |
| ATL03_20190222135159_08570207_005_01 | 21:51 | GT3L | 611,220~620,235 |
| ATL03_20190524093136_08570307_005_01 | 17:31 | GT2L | 9,873,740~9,884,740 |
| ATL03_20190721183749_03620401_005_01 | 02:37 | GT2L | 1,169,050~1,171,420 |
| ATL03_20191020141751_03620501_005_01 | 22:17 | GT1R | 1,759,220~1,760,930 |
| ATL03_20191020141751_03620501_005_01 | 22:17 | GT2R | 1,380,710~1,383,610 |
| ATL03_20200119095733_03620601_005_01 | 17:57 | GT1R | 5,316,850~5,328,140 |
| ATL03_20200119095733_03620601_005_01 | 17:57 | GT3R | 5,489,800~5,504,320 |
| ATL03_20200419053723_03620701_005_01 | 13:37 | GT1R | 11,042,060~11,061,510 |
| ATL03_20220114231625_03621401_005_01 | 07:20 | GT3L | 4,621,580~4633590 |
| ATL03_20181122060325_08340107_005_01 | 14:03 | GT1R | 1,645,587~1,648,704 |
| ATL03_20190211025118_06820207_005_01 | 10:51 | GT1L | 417,804~420,731 |
| ATL03_20190603091752_10100301_005_01 | 17:17 | GT3R | 344,236~348,241 |
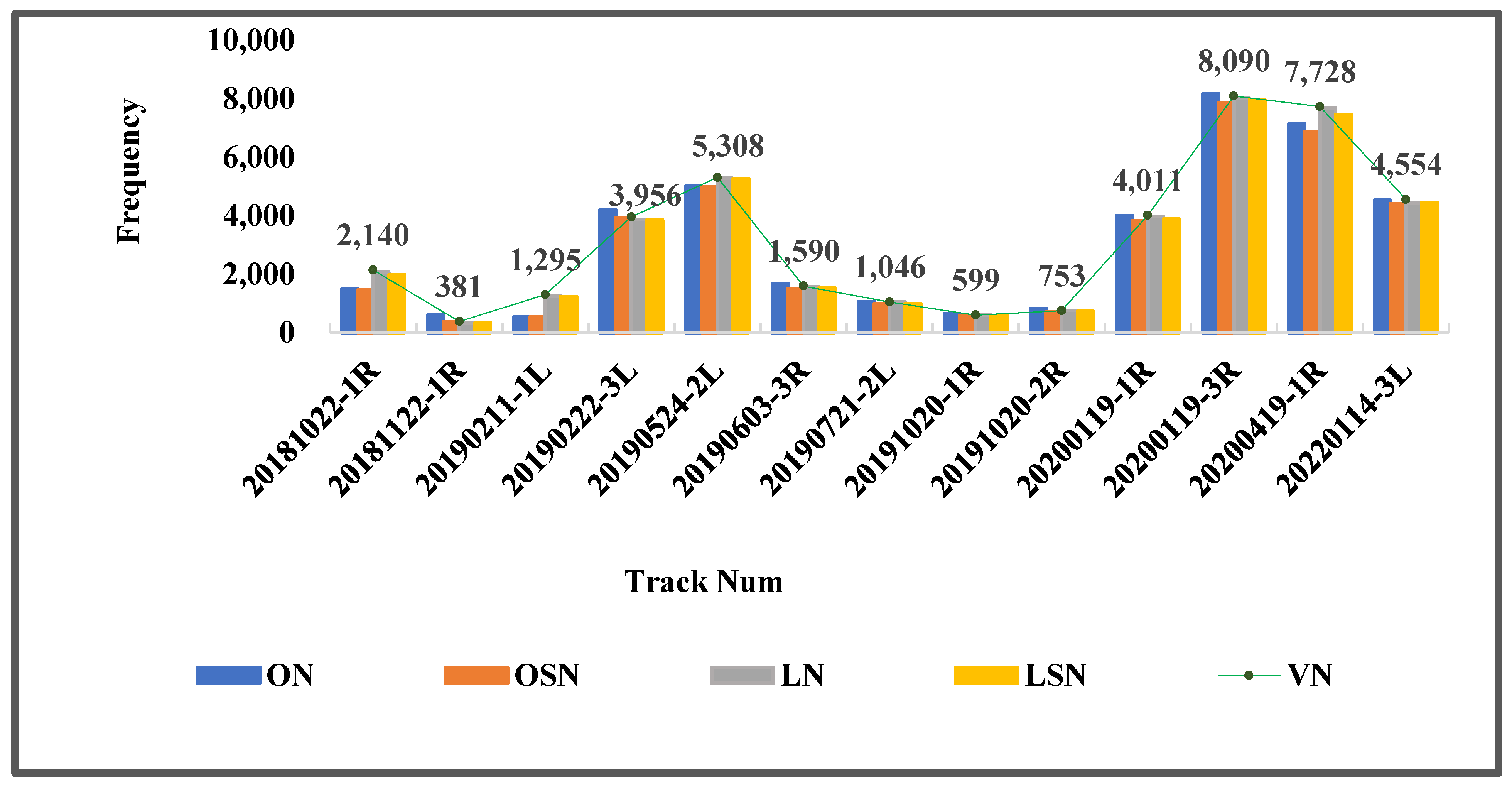
| ATL03 | ON | OSN | LN | LSN | VN | RN |
|---|---|---|---|---|---|---|
| 20181022-1R | 1505 | 1456 | 2064 | 1974 | 2140 | 3045 |
| 20181122-1R | 612 | 381 | 338 | 330 | 381 | 622 |
| 20190211-1L | 542 | 532 | 1248 | 1236 | 1295 | 1408 |
| 20190222-3L | 4202 | 3945 | 3876 | 3845 | 3956 | 4242 |
| 20190524-2L | 5007 | 4987 | 5273 | 5249 | 5308 | 6018 |
| 20190603-3R | 1671 | 1506 | 1560 | 1537 | 1590 | 1784 |
| 20190721-2L | 1064 | 986 | 1061 | 998 | 1046 | 1199 |
| 20191020-1R | 653 | 593 | 601 | 581 | 599 | 665 |
| 20191020-2R | 826 | 708 | 754 | 728 | 753 | 937 |
| 20200119-1R | 4000 | 3818 | 3973 | 3883 | 4011 | 4948 |
| 20200119-3R | 8164 | 7867 | 8015 | 7957 | 8090 | 8850 |
| 20200419-1R | 7134 | 6851 | 7682 | 7461 | 7728 | 10,650 |
| 20220114-3L | 4531 | 4401 | 4437 | 4433 | 4554 | 5122 |
| ATL03 | OM | LDSBM | ||||
|---|---|---|---|---|---|---|
| R | P | F | R | P | F | |
| 20181022-1R | 0.680 | 0.967 | 0.799 | 0.922 | 0.956 | 0.939 |
| 20181122-1R | 1.000 | 0.623 | 0.767 | 0.866 | 0.976 | 0.918 |
| 20190211-1L | 0.411 | 0.982 | 0.579 | 0.954 | 0.990 | 0.972 |
| 20190222-3L | 0.997 | 0.939 | 0.967 | 0.972 | 0.992 | 0.982 |
| 20190524-2L | 0.940 | 0.996 | 0.967 | 0.989 | 0.995 | 0.992 |
| 20190603-3R | 0.947 | 0.901 | 0.923 | 0.967 | 0.985 | 0.976 |
| 20190721-2L | 0.943 | 0.927 | 0.935 | 0.954 | 0.941 | 0.947 |
| 20191020-1R | 0.990 | 0.908 | 0.947 | 0.970 | 0.967 | 0.968 |
| 20191020-2R | 0.940 | 0.857 | 0.897 | 0.967 | 0.966 | 0.966 |
| 20200119-1R | 0.952 | 0.955 | 0.953 | 0.968 | 0.977 | 0.973 |
| 20200119-3R | 0.972 | 0.964 | 0.968 | 0.984 | 0.993 | 0.988 |
| 20200419-1R | 0.887 | 0.960 | 0.922 | 0.965 | 0.971 | 0.968 |
| 20220114-3L | 0.972 | 0.971 | 0.969 | 0.973 | 0.999 | 0.986 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, J.; Zhong, J.; Mo, F.; Liu, R.; Li, X.; Yang, X.; Zeng, J. Denoising and Accuracy Evaluation of ICESat-2/ATLAS Photon Data for Nearshore Waters Based on Improved Local Distance Statistics. Remote Sens. 2023, 15, 2828. https://doi.org/10.3390/rs15112828
Xie J, Zhong J, Mo F, Liu R, Li X, Yang X, Zeng J. Denoising and Accuracy Evaluation of ICESat-2/ATLAS Photon Data for Nearshore Waters Based on Improved Local Distance Statistics. Remote Sensing. 2023; 15(11):2828. https://doi.org/10.3390/rs15112828
Chicago/Turabian StyleXie, Junfeng, Jincheng Zhong, Fan Mo, Ren Liu, Xiang Li, Xiaomeng Yang, and Junze Zeng. 2023. "Denoising and Accuracy Evaluation of ICESat-2/ATLAS Photon Data for Nearshore Waters Based on Improved Local Distance Statistics" Remote Sensing 15, no. 11: 2828. https://doi.org/10.3390/rs15112828
APA StyleXie, J., Zhong, J., Mo, F., Liu, R., Li, X., Yang, X., & Zeng, J. (2023). Denoising and Accuracy Evaluation of ICESat-2/ATLAS Photon Data for Nearshore Waters Based on Improved Local Distance Statistics. Remote Sensing, 15(11), 2828. https://doi.org/10.3390/rs15112828







