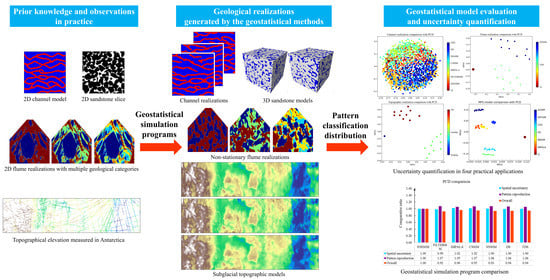
A Pattern Classification Distribution Method for Geostatistical Modeling Evaluation and Uncertainty Quantification
Abstract
1. Introduction
2. Background of the Geostatistical Evaluation Methods
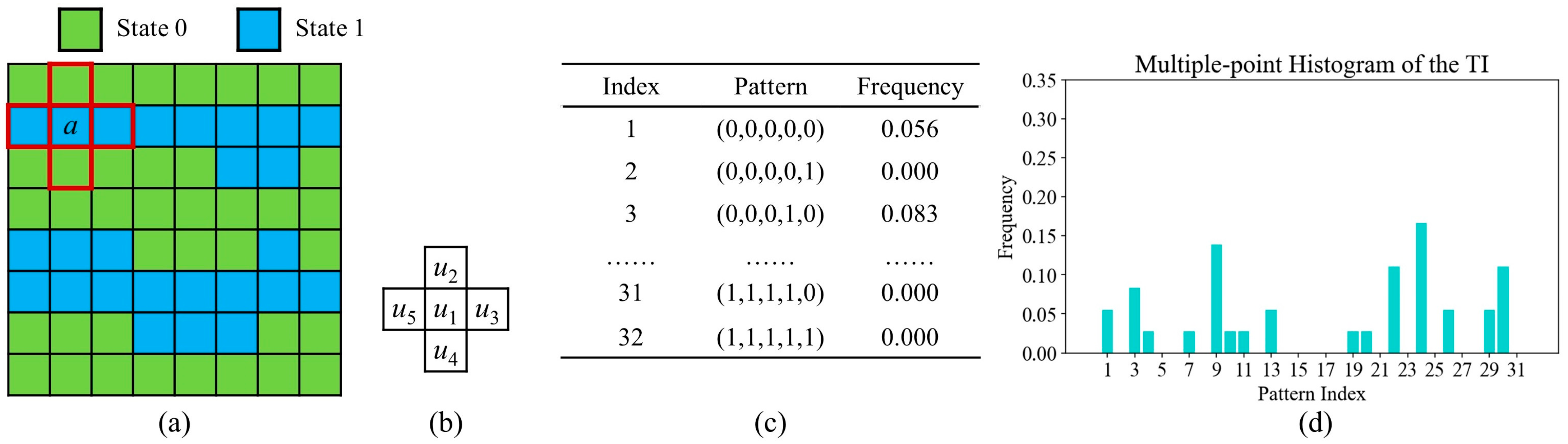
2.1. Multiple-Point Histogram
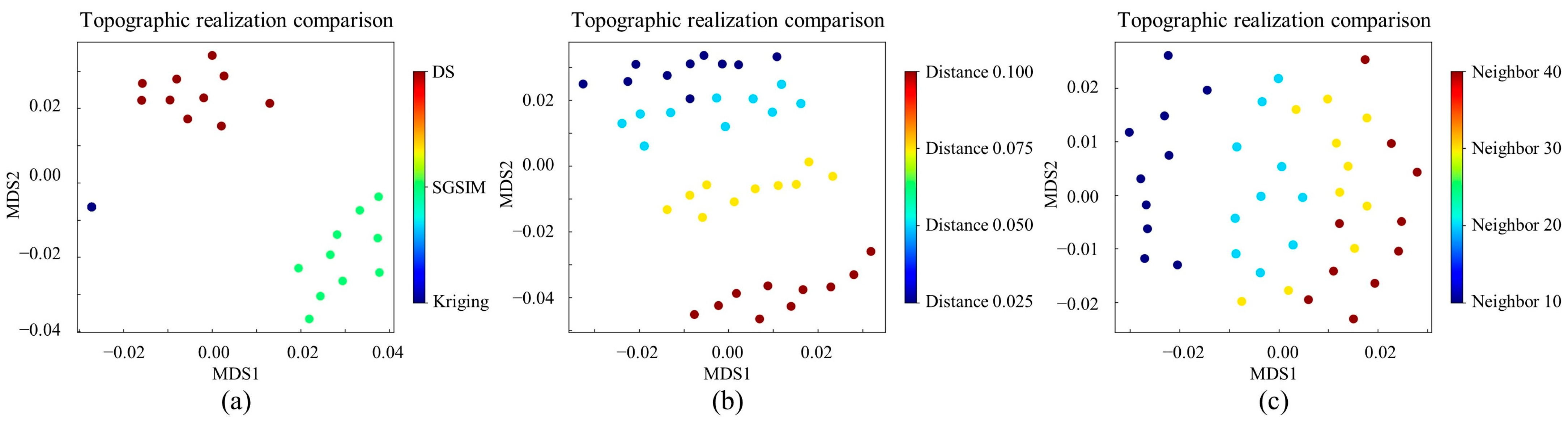
2.2. Analysis of Distance
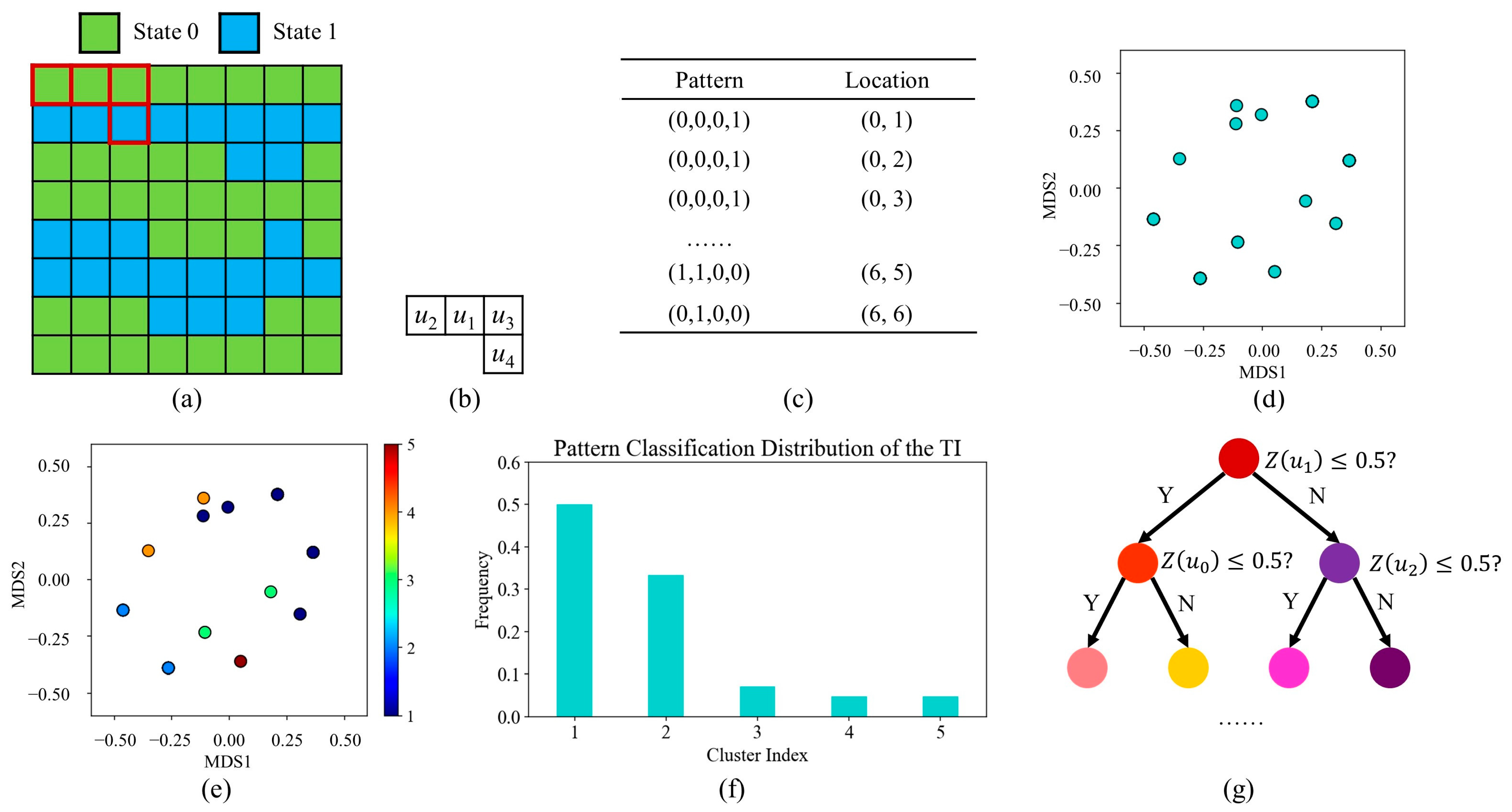
3. The Key Principles of Pattern-Classification Distribution
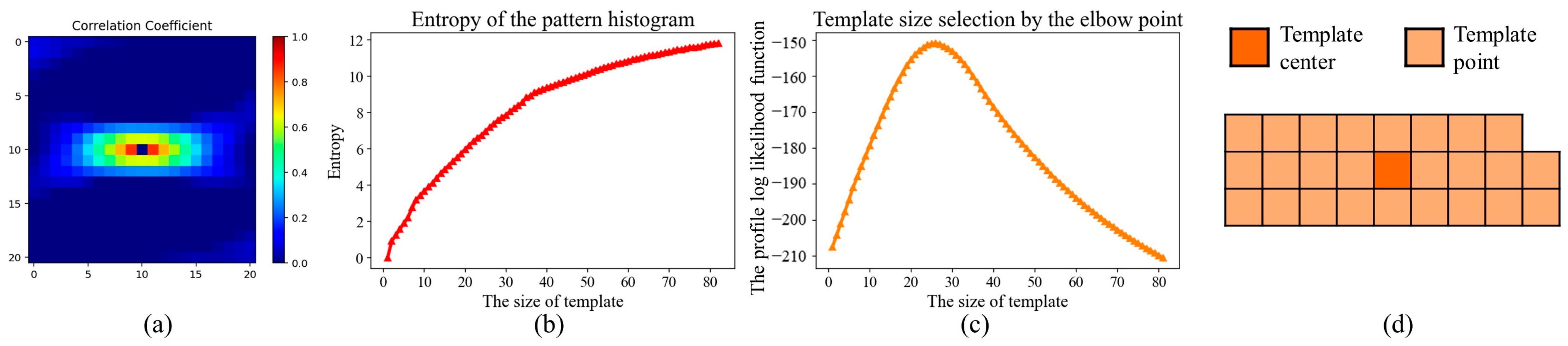
3.1. The Correlation-Driven Template-Design Program
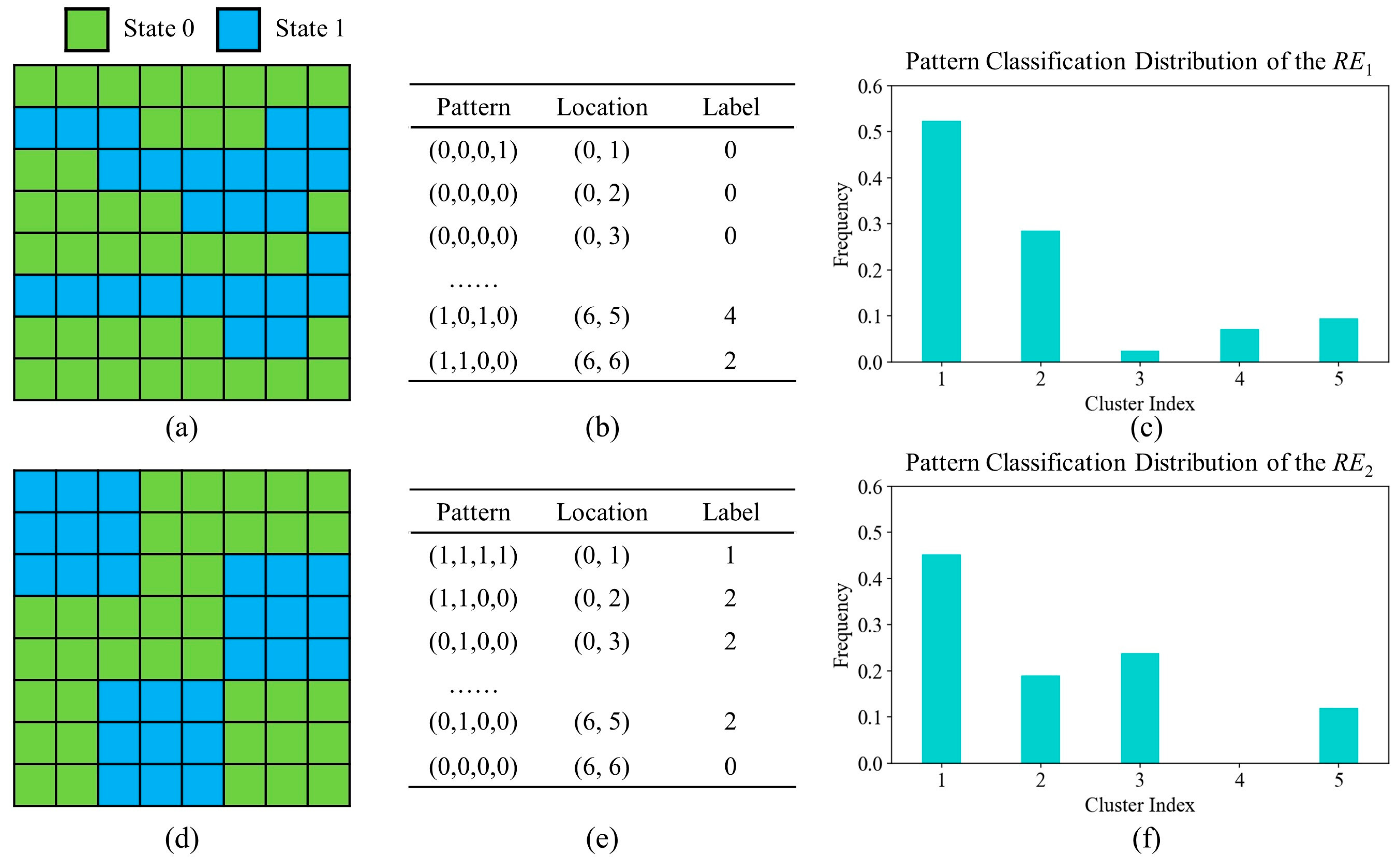
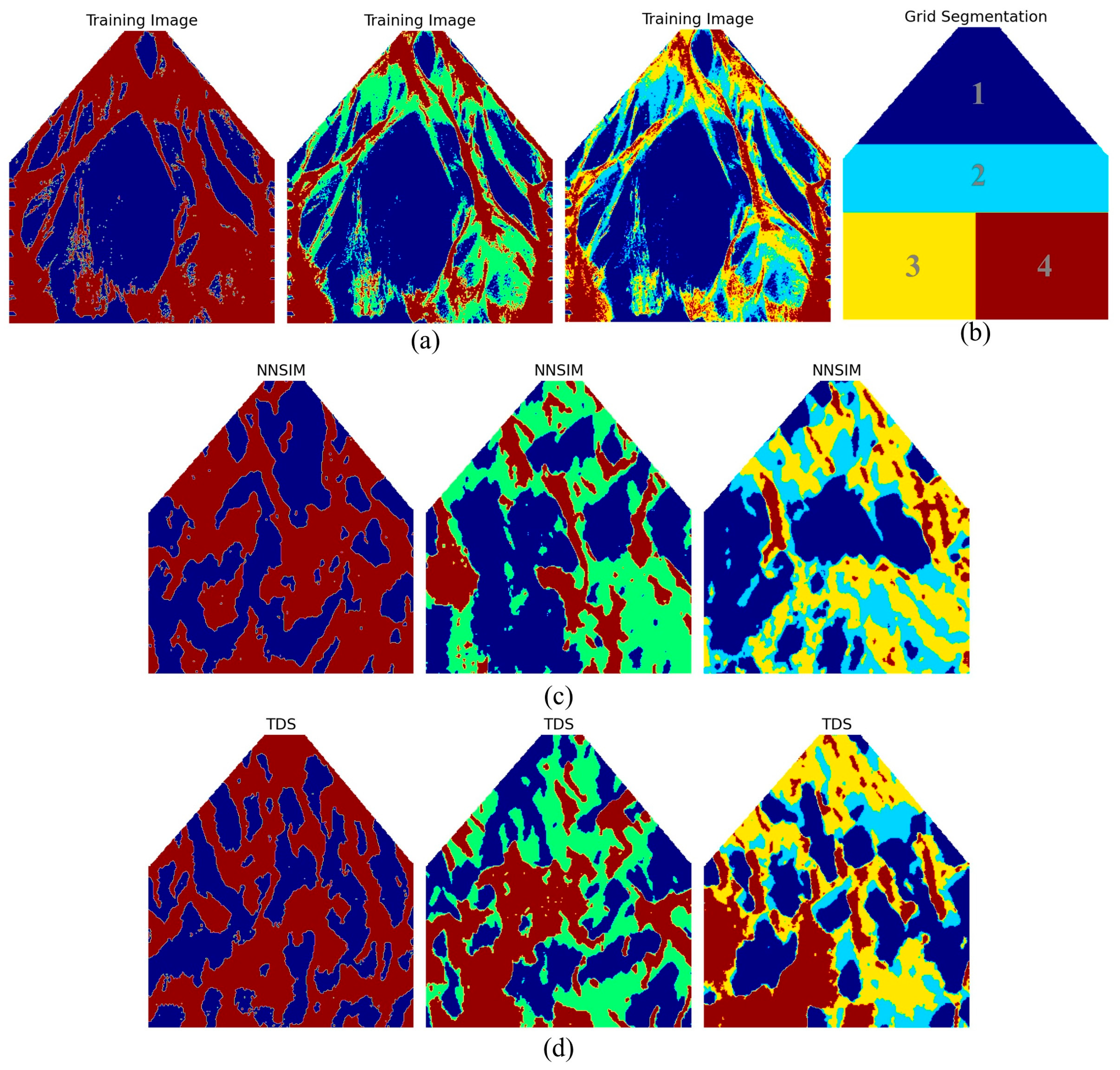
3.2. Geological Model Characterization Using Hierarchical Clustering and Decision Tree
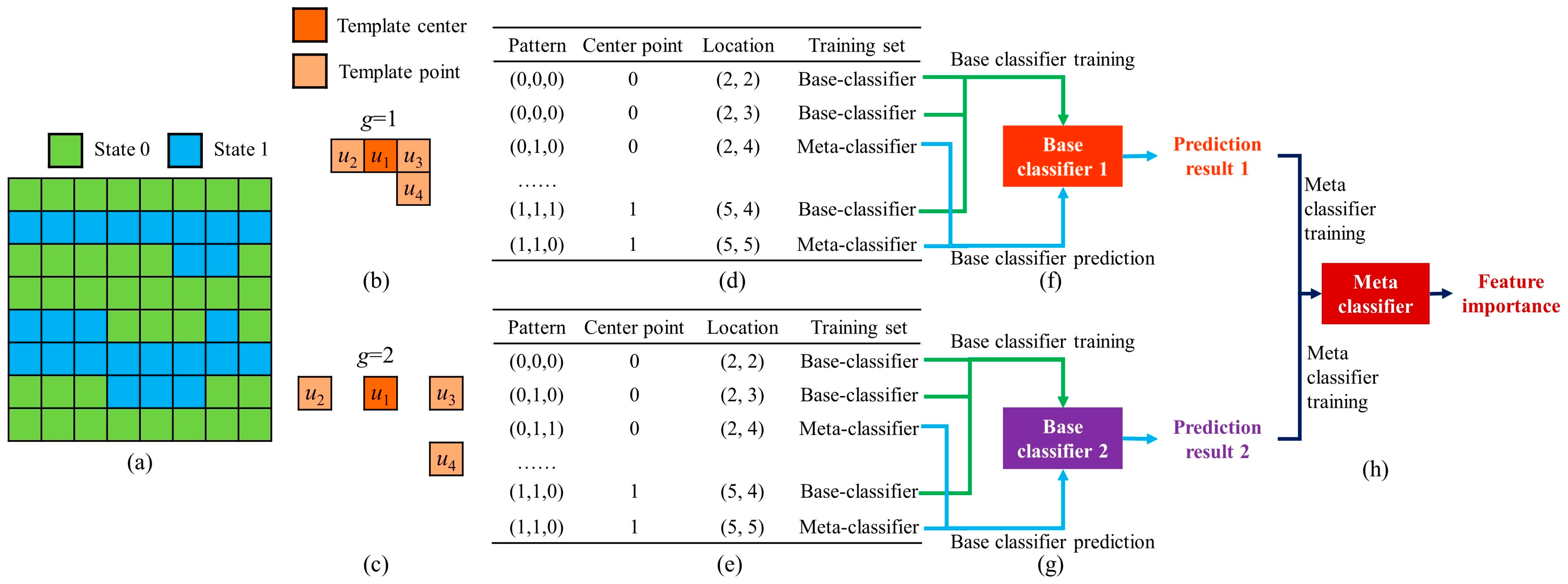
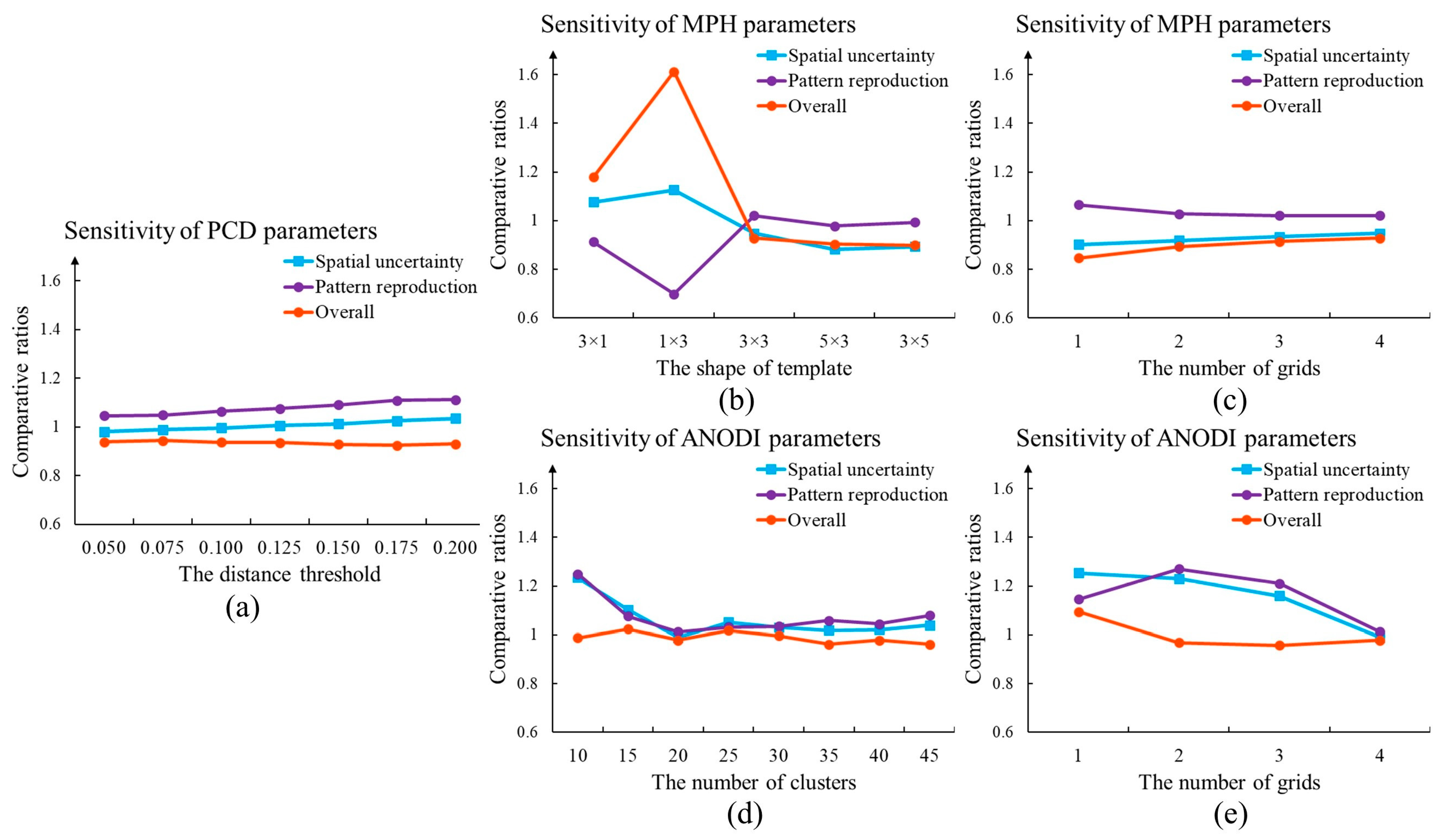
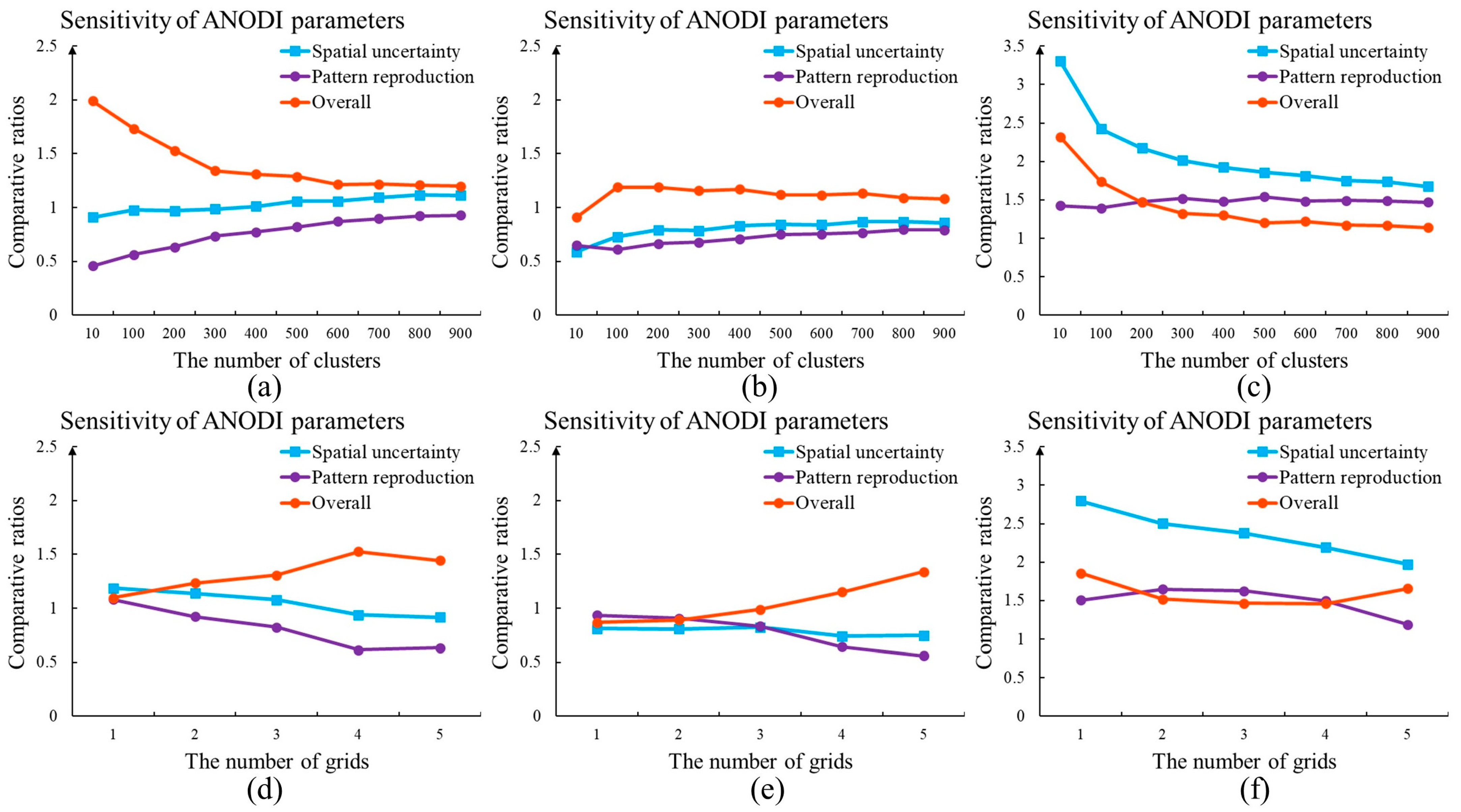
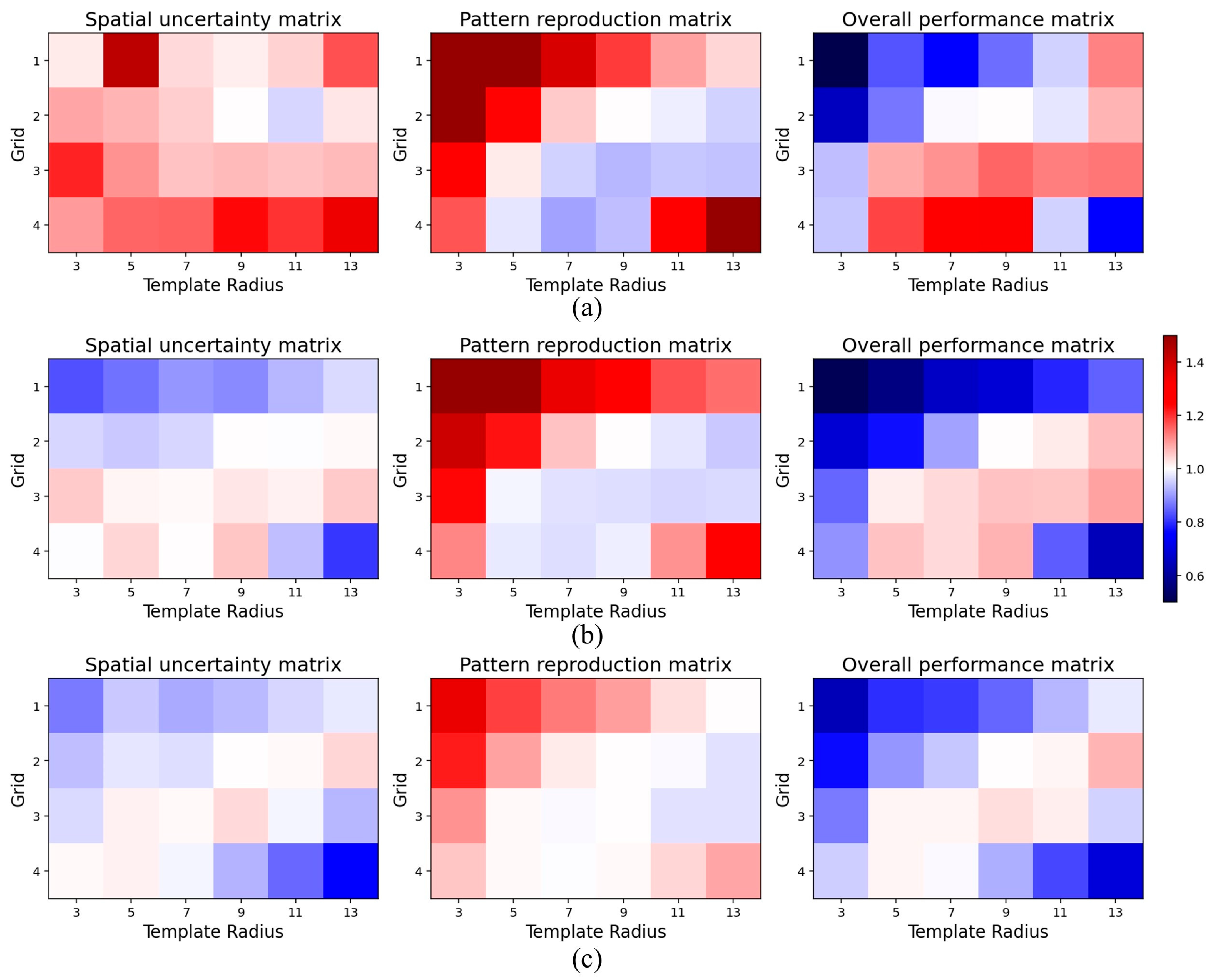
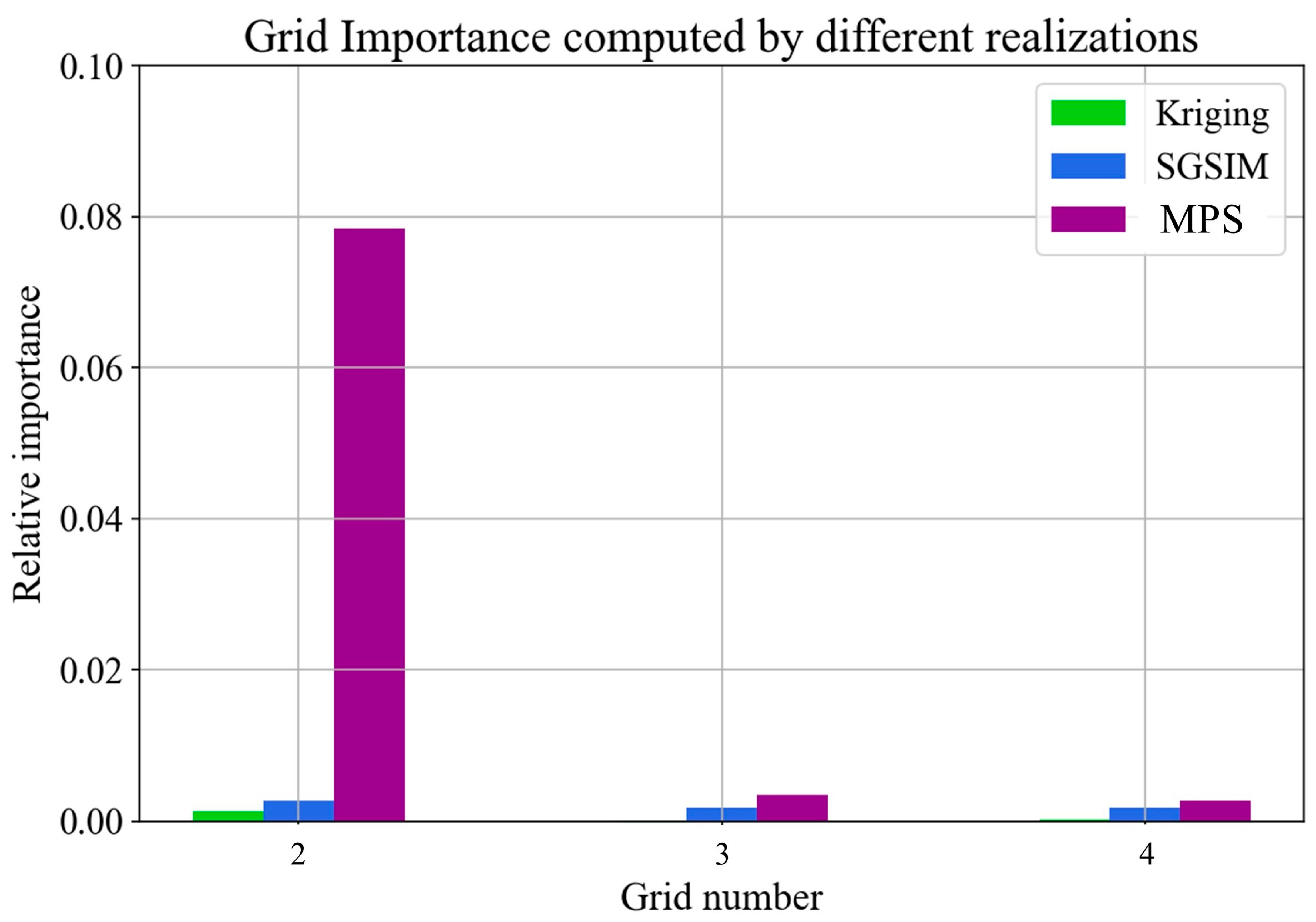
3.3. Automatic Resolution Importance Assignment with a Stacking Strategy
4. Applications
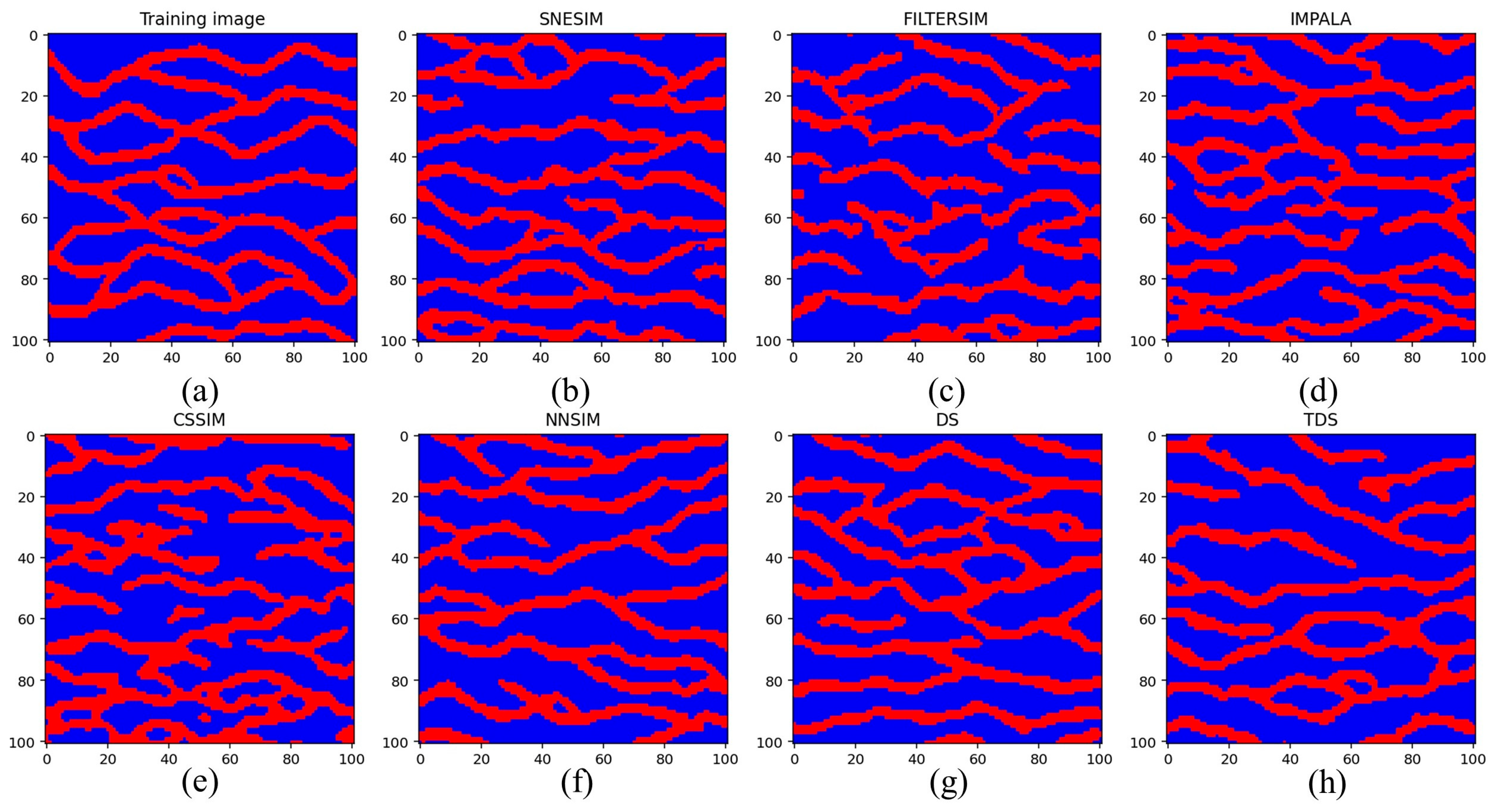
4.1. A 2D Benchmark Channel Model with Anisotropic Structures
4.2. A 2D Non-Stationary Flume System with Morphologically Complex Structures
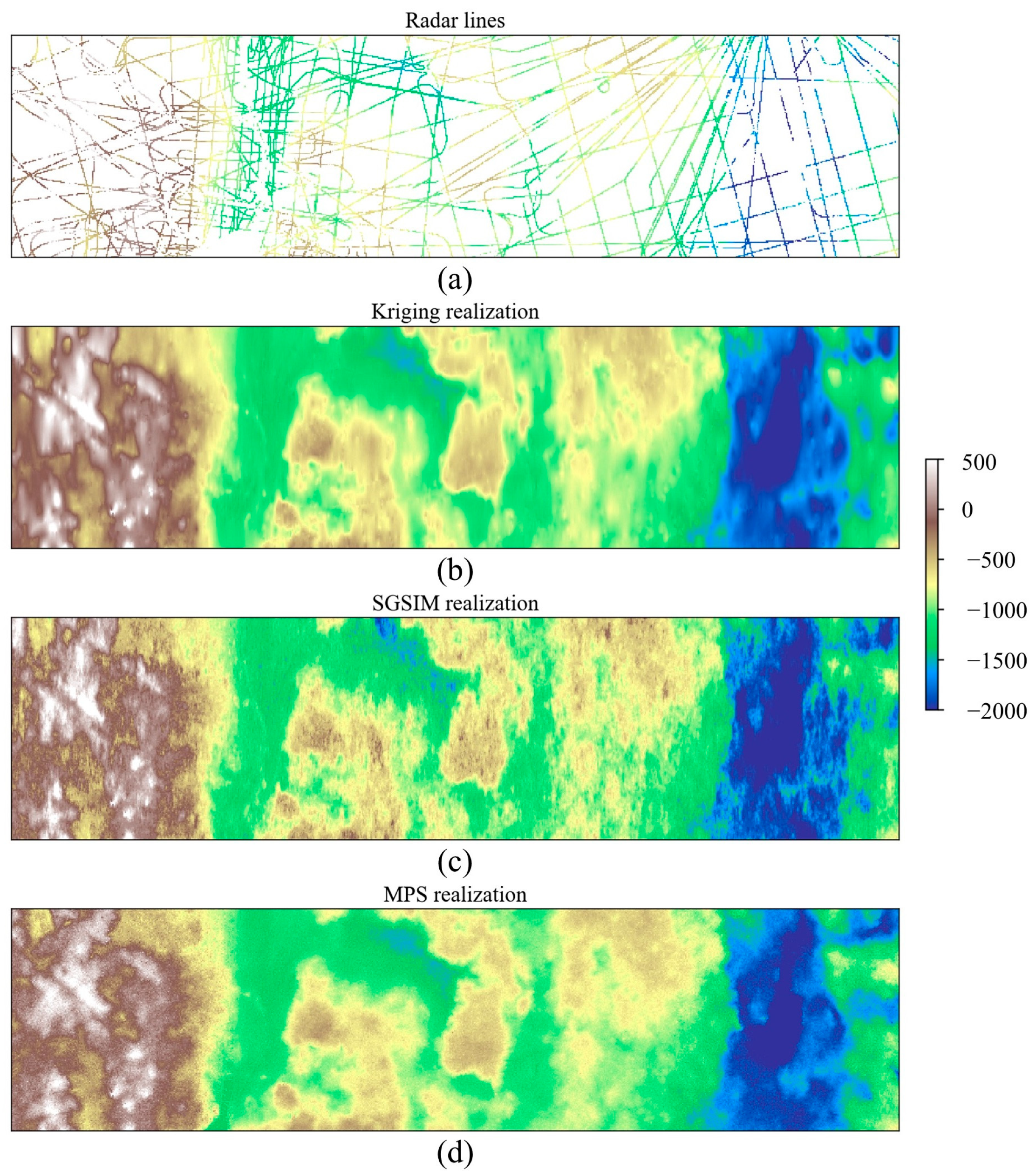
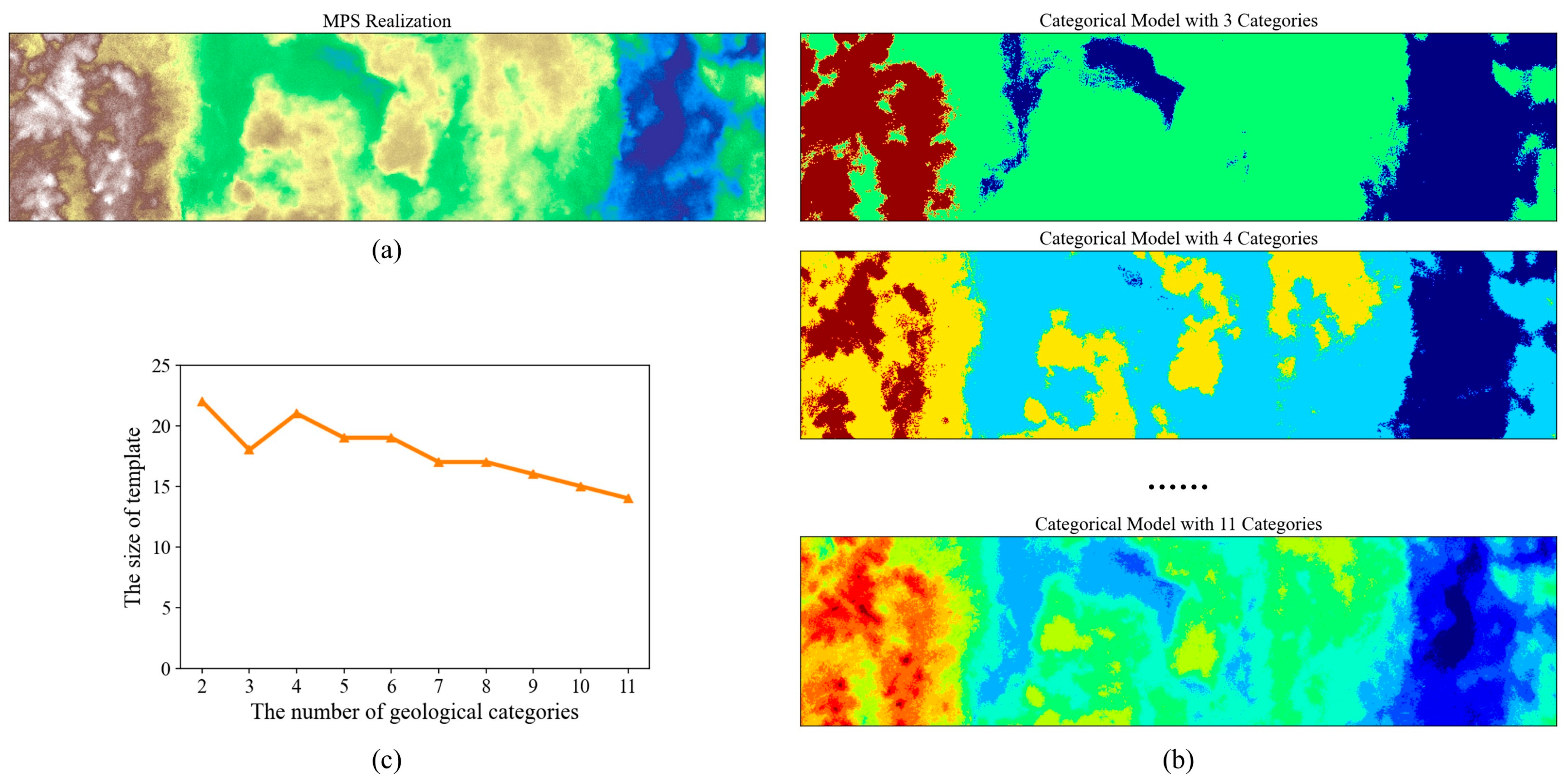
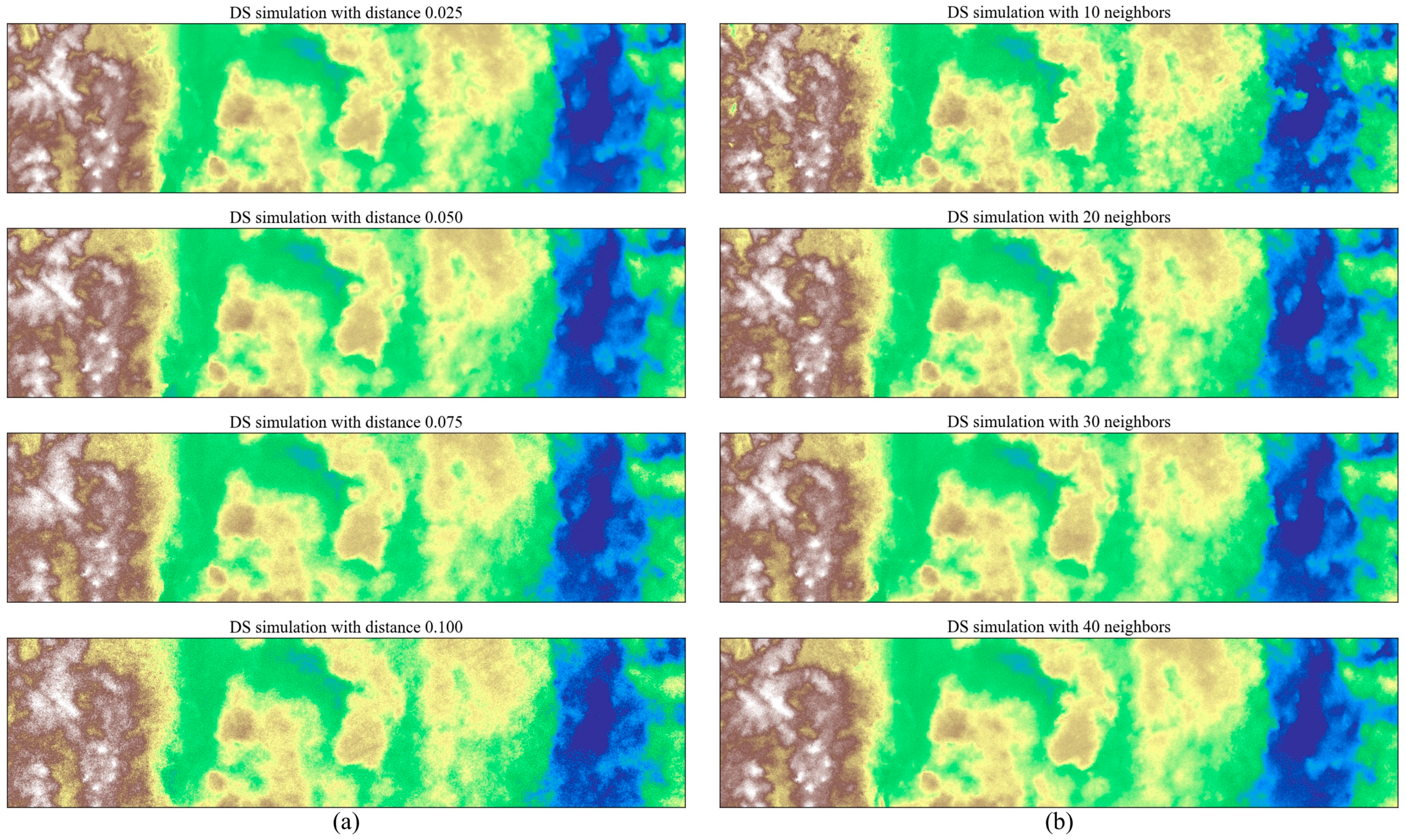
4.3. A 2D Subglacial-Bedrock-Elevation Model with Continuous Variable
4.4. A 3D Sandstone Model from a 2D Slice
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Scheidt, C.; Fernandes, A.M.; Paola, C.; Caers, J. Quantifying natural delta variability using a multiple-point geostatistics prior uncertainty model. J. Geophys. Res. Earth Surf. 2016, 121, 1800–1818. [Google Scholar] [CrossRef]
- Hoffimann, J.; Scheidt, C.; Barfod, A.; Caers, J. Stochastic simulation by image quilting of process-based geological models. Comput. Geosci. 2017, 106, 18–32. [Google Scholar] [CrossRef]
- Hoffimann, J.; Bufe, A.; Caers, J. Morphodynamic analysis and statistical synthesis of geomorphic data: Application to a flume experiment. J. Geophys. Res. Earth Surf. 2019, 124, 2561–2578. [Google Scholar] [CrossRef]
- Zhang, T.; Liu, D. Reconstructing digital terrain models from ArcticDEM and worldview-2 imagery in Livengood, Alaska. Remote Sens. 2023, 15, 2061. [Google Scholar] [CrossRef]
- Leong, W.J.; Horgan, H.J. DeepBedMap: A deep neural network for resolving the bed topography of Antarctica. Cryosphere 2020, 14, 3687–3705. [Google Scholar] [CrossRef]
- MacKie, E.J.; Schroeder, D.M.; Zuo, C.; Yin, Z.; Caers, J. Stochastic modeling of subglacial topography exposes uncertainty in water routing at Jakobshavn Glacier. J. Glaciol. 2021, 67, 75–83. [Google Scholar] [CrossRef]
- Yin, Z.; Zuo, C.; MacKie, E.J.; Caers, J. Mapping high-resolution basal topography of West Antarctica from radar data using non-stationary multiple-point geostatistics (MPS-bedmappingV1). Geosci. Model Dev. 2022, 15, 1477–1497. [Google Scholar] [CrossRef]
- Hadjipetrou, S.; Mariethoz, G.; Kyriakidis, P. Gap-filling sentinel-1 offshore wind speed image time series using multiple-point geostatistical simulation and reanalysis data. Remote Sens. 2023, 15, 409. [Google Scholar] [CrossRef]
- Mariethoz, G.; Caers, J. Multiple-Point Geostatistics: Stochastic Modeling with Training Image; Wiley: New York, NY, USA, 2014. [Google Scholar]
- Zuo, C.; Pan, Z.; Yin, Z.; Guo, C. A nearest neighbor multiple-point statistics method for fast geological modeling. Comput. Geosci. 2022, 167, 105208. [Google Scholar] [CrossRef]
- Liu, G.; Fang, H.; Chen, Q.; Cui, Z.; Zeng, M. A feature-enhanced MPS approach to reconstruct 3D deposit models using 2D geological cross sections: A case study in the Luodang Cu deposit, Southwestern China. Nat. Resour. Res. 2022, 31, 3101–3120. [Google Scholar] [CrossRef]
- Gravey, M.; Mariethoz, G. QuickSampling v1.0: A robust and simplified pixel-based multiple-point simulation approach. Geosci. Model Dev. 2020, 13, 2611–2630. [Google Scholar] [CrossRef]
- Bai, H.; Ge, Y.; Mariethoz, G. Utilizing spatial association analysis to determine the number of multiple grids for multiple-point statistics. Spat. Stat. 2016, 17, 83–104. [Google Scholar] [CrossRef]
- Zuo, C.; Pan, Z.; Gao, Z.; Gao, J. Correlation-driven direct sampling method for geostatistical simulation and training image evaluation. Phys. Rev. E 2019, 99, 053310. [Google Scholar] [CrossRef]
- Zhang, T.; Switzer, P.; Journel, A. Filter-based classification of training image patterns for spatial simulation. Math. Geol. 2006, 38, 63–80. [Google Scholar] [CrossRef]
- Honarkhah, M.; Caers, J. Stochastic simulation of patterns using distance-based pattern modeling. Math. Geosci. 2010, 42, 487–517. [Google Scholar] [CrossRef]
- Zuo, C.; Yin, Z.; Pan, Z.; MacKie, E.J.; Caers, J. A tree-based direct sampling method for surface and subsurface hydrological modeling. Water Resour. Res. 2020, 56, e2019WR026130. [Google Scholar] [CrossRef]
- Strebelle, S.; Cavelius, C. Solving speed and memory issues in multiple-point statistics simulation program SNESIM. Math. Geosci. 2014, 46, 171–186. [Google Scholar] [CrossRef]
- Straubhaar, J.; Malinverni, D. Addressing conditioning data in multiple-point statistics simulation algorithms based on a multiple grid approach. Math. Geosci. 2014, 46, 187–204. [Google Scholar] [CrossRef]
- Song, S.; Mukerji, T.; Hou, J. Bridging the gap between geophysics and geology with generative adversarial networks (GANs). IEEE Trans. Geosci. Remote. Sens. 2022, 60, 1–11. [Google Scholar]
- Li, X.; Li, B.; Liu, F.; Li, T.; Nie, X. Advances in the application of deep learning methods to digital rock technology. Adv. Geo-Energy Res. 2022, 8, 5–18. [Google Scholar] [CrossRef]
- Song, S.; Mukerji, T.; Hou, J. GANSim: Conditional facies simulation using an improved progressive growing of generative adversarial networks (GANs). Math. Geosci. 2021, 53, 1413–1444. [Google Scholar] [CrossRef]
- Zhang, T.F.; Tilke, P.; Dupont, E.; Zhu, L.C.; Liang, L.; Bailey, W. Generating geologically realistic 3D reservoir facies models using deep learning of sedimentary architecture with generative adversarial networks. Pet. Sci. 2019, 16, 541–549. [Google Scholar] [CrossRef]
- Laloy, E.; Hérault, R.; Jacques, D.; Linde, N. Training-image based geostatistical inversion using a spatial generative adversarial neural network. Water Resour. Res. 2018, 54, 381–406. [Google Scholar] [CrossRef]
- Chen, Q.; Cui, Z.; Liu, G.; Yang, Z.; Ma, X. Deep convolutional generative adversarial networks for modeling complex hydrological structures in Monte-Carlo simulation. J. Hydrol. 2022, 610, 127970. [Google Scholar] [CrossRef]
- Gringarten, E.; Deutsch, C.V. Teacher’s aide variogram interpretation and modeling. Math. Geol. 2001, 33, 507–534. [Google Scholar] [CrossRef]
- Sahimi, M.; Tahmasebi, P. Reconstruction, optimization, and design of heterogeneous materials and media: Basic principles, computational algorithms, and applications. Phys. Rep. 2021, 939, 1–82. [Google Scholar] [CrossRef]
- Renard, P.; Allard, D. Connectivity metrics for subsurface flow and transport. Adv. Water Resour. 2013, 51, 168–196. [Google Scholar] [CrossRef]
- Scheidt, C.; Li, L.; Caers, J. Quantifying Uncertainty in Subsurface Systems; Wiley: New York, NY, USA, 2018. [Google Scholar]
- Song, S.; Mukerji, T.; Hou, J.; Zhang, D.; Lyu, X. GANSim-3D for conditional geomodelling: Theory and field application. Water Resour. Res. 2022, 58, e2021WR031865. [Google Scholar] [CrossRef]
- Boisvert, J.B.; Pyrcz, M.J.; Deutsch, C.V. Multiple-point statistics for training image selection. Nat. Resour. Res. 2007, 16, 313–321. [Google Scholar] [CrossRef]
- Tan, X.J.; Tahmasebi, P.; Caers, J. Comparing training-image based algorithms using an analysis of distance. Math. Geosci. 2014, 46, 149–169. [Google Scholar] [CrossRef]
- Endres, D.M.; Schindelin, J.E. A new metric for probability distributions. IEEE Trans. Inf. Theory. 2003, 49, 1858–1860. [Google Scholar] [CrossRef]
- Zhu, M.; Ghodsi, A. Automatic dimensionality selection from the scree plot via the use of profile likelihood. Comput. Stat. Data Anal. 2006, 51, 918–930. [Google Scholar] [CrossRef]
- Geron, A. Hands-On Machine Learning with Scikit-Learn, Keras & Tensorflow, 2nd ed.; OReilly: Sebastopol, CA, USA, 2019. [Google Scholar]
- Wu, Y.; Tahmasebi, P.; Lin, C.; Dong, C. A comprehensive investigation of the effects of organic-matter pores on shale properties: A multicomponent and multiscale modeling. J. Nat. Gas Eng. 2020, 81, 103425. [Google Scholar] [CrossRef]
- Remy, N.; Boucher, A.; Wu, J. Applied Geostatistics with SGeMS: A User’s Guide; Cambridge University Press: Cambridge, UK, 2009. [Google Scholar]
- Straubhaar, J.; Renard, P.; Mariethoz, G.; Froidevaux, R.; Besson, O. An improved parallel multiple-point algorithm using a list approach. Math. Geosci. 2011, 43, 305–328. [Google Scholar] [CrossRef]
- Guo, C.; Zhang, H.; Zuo, C. A column searching-based multiple-point statistics for efficient image generation. In Proceedings of the 2022 4th International Conference on Communications, Information System and Computer Engineering (CISCE), Shenzhen, China, 17 August 2022. [Google Scholar]
- Mariethoz, G.; Renard, P.; Straubhaar, J. The direct sampling method to perform multiple-point geostatistical simulations. Water Resour. Res. 2010, 46, W11536. [Google Scholar] [CrossRef]
- Meerschman, E.; Pirot, G.; Mariethoz, G.; Straubhaar, J.; Meirvenne, M.V.; Renard, P. A practical guide to performing multiple- point statistical simulations with the direct sampling algorithm. Comput. Geosci. 2013, 52, 307–324. [Google Scholar] [CrossRef]
- Goff, J.A.; Powell, E.M.; Young, D.A.; Blankenship, D.D. Conditional simulation of thwaites glacier (antarctica) bed topography for flow models: Incorporating inhomogeneous statistics and channelized morphology. J. Glaciol. 2014, 60, 635–646. [Google Scholar] [CrossRef]
- Rignot, E.; Mouginot, J.; Scheuchl, B.; Broeke, M.; Wessem, M.J.; Morlighem, M. Four decades of Antarctic Ice sheet mass balance from 1979–2017. Proc. Natl. Acad. Sci. USA 2019, 116, 1095–1103. [Google Scholar] [CrossRef]
- Wu, Y.; Tahmasebi, P.; Yu, H.; Lin, C.; Wu, H.; Dong, C. Pore-scale 3D dynamic modeling and characterization of shale samples: Considering the effects of thermal maturation. J. Geophys. Res. Solid Earth 2020, 125, e2019JB01830. [Google Scholar] [CrossRef]
- Li, B.; Nie, X.; Cai, J.; Zhou, X.; Wang, C.; Han, D. U-Net model for multi-component digital rock modeling of shales based on CT and QEMSCAN images. J. Pet. Sci. Eng. 2020, 216, 110734. [Google Scholar] [CrossRef]
- Comunian, A.; Renard, P.; Straubhaar, J. 3D multiple-point statistics simulation using 2D training images. Comput. Geosci. 2012, 40, 49–65. [Google Scholar] [CrossRef]
- Gueting, N.; Caers, J.; Comunian, A.; Vanderborght, J.; Englert, A. Reconstruction of three-dimensional aquifer heterogeneity from two-dimensional geophysical data. Math. Geosci. 2018, 50, 53–75. [Google Scholar] [CrossRef]
- Zhang, D.; Gao, M.; Liu, F.; Qin, X.; Yin, X.; Fang, W.; Luo, Y. Reconstruction of anisotropic 3D medium using multiple 2D images. J. Pet. Sci. Eng. 2022, 219, 111048. [Google Scholar] [CrossRef]
- Liu, F.; Gao, M.; Li, X.; Lin, H.; Deng, K.; Xu, Y.; Jiang, J. Reconstruction of 3D porous medium using a type of cascaded polymorphic method. Microporous Mesoporous Mater. 2021, 326, 111356. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zuo, C.; Li, Z.; Dai, Z.; Wang, X.; Wang, Y. A Pattern Classification Distribution Method for Geostatistical Modeling Evaluation and Uncertainty Quantification. Remote Sens. 2023, 15, 2708. https://doi.org/10.3390/rs15112708
Zuo C, Li Z, Dai Z, Wang X, Wang Y. A Pattern Classification Distribution Method for Geostatistical Modeling Evaluation and Uncertainty Quantification. Remote Sensing. 2023; 15(11):2708. https://doi.org/10.3390/rs15112708
Chicago/Turabian StyleZuo, Chen, Zhuo Li, Zhe Dai, Xuan Wang, and Yue Wang. 2023. "A Pattern Classification Distribution Method for Geostatistical Modeling Evaluation and Uncertainty Quantification" Remote Sensing 15, no. 11: 2708. https://doi.org/10.3390/rs15112708
APA StyleZuo, C., Li, Z., Dai, Z., Wang, X., & Wang, Y. (2023). A Pattern Classification Distribution Method for Geostatistical Modeling Evaluation and Uncertainty Quantification. Remote Sensing, 15(11), 2708. https://doi.org/10.3390/rs15112708