Simulation Analysis of the Geometric Positioning Accuracy for MEO- and HEO-SAR Satellites

Abstract

Due to the long synthetic aperture time, the large squint angle, and the large imaging width of medium Earth orbit (MEO) and high Earth orbit (HEO) SAR satellites, it is difficult to simulate the geometric positioning accuracy of MEO- and HEO-SAR satellites through the SAR image simulation methods. In this paper, one non-zero Doppler simulation method of geometric positioning accuracy was proposed without simulating SAR images. In order to simulate the geometric positioning accuracy under different errors and imaging observation conditions, the virtual simulation geometric model was constructed by the simulated satellite ephemeris and the coordinates of ground control points (GCPs). On this basis, one geometric accuracy simulation method based on mean value compensation was proposed to simulate the geometric positioning accuracy with GCPs. The experimental results showed that the impact of Doppler center frequency error and velocity error of MEO- and HEO-SAR satellites on geometric positioning accuracy is significant compared with the LEO-SAR satellites, and the maximum error they affect can reach about 1597 m. In addition, the geometric positioning accuracies of MEO- and HEO-SAR satellites with GCPs can be achieved to 1~10 m and 7~29 m, respectively.

1. Introduction

Synthetic aperture radar (SAR) satellites currently operating in orbit are all low Earth orbit (LEO) SAR satellites [1,2], the orbital altitudes of which are within 2000 km, with an average altitude of ~500–800 km. Owing to limited flight altitude, coverage area is small, the surveying and mapping belt is narrow, and the repeated observation period is long. The timeliness of LEO-SAR applications is largely limited. The orbital altitudes of medium Earth orbit (MEO) and high Earth orbit (HEO) SAR satellites are 2000–20,000 km and above 20,000 km, respectively. The advantages of MEO- and HEO-SAR include a short revisit period to a specific region, a wide range of Earth observations and long-term tracking and monitoring of targets [3,4,5]. With the above advantages, MEO- and HEO-SAR satellites have broad application prospects in the military and civilian fields, so it is urgent to analyze the geometric positioning accuracy of MEO- and HEO-SAR satellites.

Due to the measurement errors of satellite orbit parameters and imaging parameters, the geometric positioning accuracy of SAR images is restricted. In SAR image geometric positioning, geometric positioning model is an indispensable step [6]. SAR localization models mainly include the range-Doppler (RD) model [7], Leberl radar collinear model [8], Konecny projection mode [9], rational polynomial coefficient model [10] and range-coplanarity model [11]. Among them, the RD model has the most intuitive and accurate description of SAR imaging geometry and is the most widely used model [12]. In 1982, Curlander [13] proposed the range-Doppler (RD) model, which was later used in SEASAT SAR imagery, and the positioning accuracy was 200 m [14]. Wei Jujie, Lv Guannan, Yang Shucheng and others used the RD model to analyze the positioning accuracy of spaceborne SAR satellites [15,16,17]. After the launch of Gaofen-3, the geometric positioning accuracy of Gaofen-3 was analyzed and obtained an accuracy of 3 m in literature [18,19]. The various positioning methods conducted in the above research were for the LEO-SAR satellites. Jiao et al. used multi-source optical and SAR images to improve the geopositioning accuracy [20]. Ding et al. performed geometric calibration processing on SAR images according to the RD model [21]. Chen et al. used the simulated SAR image to match the real SAR image to correct the orbital model, and then used the RD model for precise geometric rectification [22]. Qiu et al. improved the RD model and proposed a model based on continuously moving geometry [23]. The above research studied positioning accuracy, which was based on LEO-SAR images.

In summary, the research is based on the SAR image and the imaging mode of LEO-SAR satellites is orthogonal side-looking; that is, the Doppler center frequency is generally zero. However, the simulation of MEO- and HEO-SAR satellite images is laborious and inefficient. The synthetic aperture time of MEO- and HEO-SAR satellites are long, which not only generates a squint angle at the moment of imaging, but also makes it difficult to simulate images. Consequently, the simulation method adopted for LEO-SAR satellites is not suitable for MEO- and HEO-SAR satellites. Therefore, a non-zero Doppler simulation method for calculating geometric positioning accuracy is proposed without simulating SAR images. Geometric positioning accuracy is one of the important technical indicators of parameter design and performance evaluation of the SAR system. No research has been conducted on the geometric positioning accuracy of MEO- and HEO-SAR satellites.

In this study, a simulation analysis of the geometric positioning accuracy of MEO- and HEO-SAR satellites was conducted to provide technical support for the design and performance of MEO- and HEO-SAR satellites. First, the positioning errors of the SAR satellites were analyzed. Then, a simulation of MEO- and HEO-SAR satellites was performed using the satellite tool kit (STK) software, and a virtual simulation geometric model was constructed. This model was used to calculate the geometric positioning accuracies of the MEO- and HEO-SAR satellites.

This paper has five parts. Section 2 describes the materials and methods. Section 3 describes the experiment and simulation analysis of the geometric positioning accuracy of satellites. The discussion and conclusion are presented in Section 4 and Section 5, respectively.

2. Material and Methods

2.1. Basic Principles

The geometric positioning accuracy is estimated mainly based on the geometric positioning model. The corresponding geographic coordinates are calculated using the image space coordinates of the ground target on the SAR image. Then, the deviation between the calculated geographical coordinates and the actual geographic coordinates of the ground control point (GCP) is estimated. If there is no error in the geometric parameters at the image moment (e.g., with respect to the orbital position, orbital velocity, slant range and Doppler center frequency), then the difference between the GCP coordinates calculated from the geometric parameters at the image moment and the actual GCP coordinates is zero. If there is an error, this difference shows a non-zero value.

The schematic diagram of the simulation principle is shown in Figure 1. The coordinate vector of the actual ground point A is R_AO = [X, Y, Z]^T. Then, the slant range R between the ground point A and the satellite S can be expressed as,

$$R^2={(X-X_S)}^2+{(Y-Y_S)}^2+{(Z-Z_S)}^2$$

(1)

where, R is the slant range, [X_S, Y_S, Z_S] is the position vector of the satellite and [X, Y, Z] is the position vector of the target point.

The corresponding Doppler center frequency f_D is,

$$fd=-\frac{2}{\lambda R}(R_{SO}-R_{AO})\times V_{SO}$$

(2)

where, f_D is the Doppler center frequency, R_SO and V_SO are the distance vector, $R_{AO}$ is the position vector and λ is the radar wavelength.

Similarly, the slant range $R^{\prime }$ and the corresponding Doppler center frequency $f_D^{\prime }$ can be calculated.

If there is no error in the geometric parameter, then

$$R_{AO}=R_{AO}^{\prime }$$

(3)

where, $R_{AO}^{\prime }$ the position vector at the imaging moment.

If there is an error, then

$$R_{AO}\ne R_{AO}^{\prime }$$

(4)

In Figure 1, S is the phase center of the SAR satellite antenna. R_SO and V_SO are the distance vector [X_S, Y_S, Z_S]^T and velocity vector [X_V Y_V Z_V]^T of the satellite platform, respectively. $R_{SO}^{\prime }$ and $V_{SO}^{\prime }$ are the distance vector and velocity vector at the image moment, respectively. A is the reference coordinate of the actual ground point on the Earth’s surface and $A^{\prime }$ is the ground point position calculated from the simulated SAR image. $R_{AO}$ is the position vector [X, Y, Z]^T of A and $R_{AO}^{\prime }$ the position vector at the imaging moment. R is the distance vector between the SAR satellite and the ground point. $R^{\prime }$ is the distance vector at the imaging moment between the SAR satellite and the ground point.

2.2. Construction of the Simulation Geometric Model

2.2.1. Real Geometric Model Construction

According to the imaging principle of the SAR system, the spatial positioning of a point target is determined by three factors: a model describing the Earth’s shape, the distance from the point target to the sensor, and the Doppler characteristics of the target echo. The RD model has an object–image geometric relationship based on the range condition and Doppler center frequency condition, with a clear geometric and physical meaning [24].

The RD model is presented below in Equation (5).

$$\{\begin{array}{l}\begin{array}{l}\frac{X^2+Y^2}{{(R_e+h)}^2}+\frac{Z^2}{{(R_p+h)}^2}=1\\ R^2={(X-X_S)}^2+{(Y-Y_S)}^2+{(Z-Z_S)}^2\end{array}\hfill \\ f_D=-\frac{2}{\lambda R}(R_{SO}-R_{AO})\times V_{SO}\hfill \end{array}$$

(5)

where, R_e is the average equatorial radius of Earth, and R_p is the Earth’s ellipsoid polar radius and h is the elevation of the target point on the ellipsoid surface.

In Equation (5), the semi-major axis Re and semi-minor axis R_p are known. When the slant range R, Doppler parameter f_D, satellite orbit position and velocity are known, the three-dimensional coordinates of the ground target point can be calculated using Equation (5). The satellite orbital position and velocity can be simulated using the STK software. Thus, the acquisition of slant range R and Doppler parameter f_D is key to creating the simulation.

From the distance and Doppler equations, it can be seen that the slant range R and Doppler parameter f_D have a one-to-one relationship with the three-dimensional coordinates of the ground target point. If there is no error in the SAR system parameters, i.e., if the measured values of the slant range R and Doppler parameter f_D have no error, then the three-dimensional coordinates of the GCP are calculated as the real values. Based on this analysis, the true values of the slant range R and Doppler parameter f_D can be calculated from the true three-dimensional coordinates of the ground target point using the distance and Doppler equations (Equation(5)). Using the aforementioned calculations, a true geometric model was constructed.

2.2.2. Virtual Simulation Geometric Model Construction

In the SAR imaging process, the observed imaging parameters contain errors due to the complexity of the space environment, the time delay of the measurement system and asynchronous timing system. These errors affect the geometric positioning accuracy of ground target points. From the RD positioning model, it is known that the factors affecting the geometric positioning accuracy of the SAR system mainly include the satellite position error, satellite velocity error, Doppler center frequency error, terrain undulation error, slant range measurement error and azimuth time error [19,25,26,27,28,29].

Based on the RD positioning model and considering the factors listed above, a virtual simulation geometry model with errors was constructed, as given by Equation (6).

$$\{\begin{array}{l}\begin{array}{l}\frac{X^2+Y^2}{{(R_e+h+\Delta h)}^2}+\frac{Z^2}{{(R_p+h+\Delta h)}^2}=1\\ {(R+\Delta R)}^2={[X-(X_S+\Delta x)]}^2+{[Y-(Y_S+\Delta y)]}^2+{[Z-(Z_S+\Delta z)]}^2\end{array}\hfill \\ (f_D+\Delta f_1)=-\frac{2}{\lambda R}[(R_{SO}+\Delta r)-R_{AO}]\times (V_{SO}+\Delta v)\hfill \end{array}$$

(6)

where, $\Delta h$ is the terrain undulation error. The Earth is usually assumed to be an ellipsoid. Taking into account the influence of terrain undulation, the radius of the ellipsoid can be adjusted by the ellipsoid height. $\Delta R$ is the slant range measurement error. The slant range from the sensor to the ground point is determined by the propagation time of the signal through the atmosphere. There are two main sources of error in slant range measurements: electrical delay and signal transmission time. $\Delta f_1$ is the Doppler center frequency error. The Doppler center frequency does not affect the azimuth positioning in SAR processing. It is determined based on the azimuth position of the SAR sensor, i.e., the coupling of SAR and orbit time systems, and the angle of the orbital flight track. $\Delta r$ is the satellite position error [Δx, Δy, Δz]^T, and $\Delta v$ is the satellite velocity error. Satellite orbit data are generally collected once in 1s, which does not match the SAR imaging time. Therefore, there is an azimuth time offset, and the azimuth time error affects the fitting accuracy of satellite orbit data.

The virtual simulation geometry model with errors (Equation (6)) can analyze the effects of single and multi-combination error sources on the geometric positioning accuracy.

The model solution calculates the geographic coordinates of ground points using rectangular space coordinates. The least squares method was used to obtain the actual ground point coordinates.

2.2.3. Evaluation Method for Geometric Positioning Accuracy with GCPs

The MEO- and HEO-SAR satellite has a wide imaging range, and it is difficult to simulate SAR images. Positioning accuracy analysis with GCPs is usually performed using an affine transformation. Due to the lack of image-square coordinates of the target point, the simulation of geometric positioning accuracy with GCPs cannot be realized based on the affine transformation model. Therefore, a method based on mean value compensation was proposed to simulate the geometric positioning accuracy with GCPs. Regarding the analysis of errors, the main error images of SAR images are translation error and proportional error, mainly based on translation error [28,29].

First, the error of each ground control point was calculated. Then, the errors were summed up and averaged. The difference between a single error and the average of the errors is calculated. Finally, the difference between the error and the mean value of the error was calculated, and the root mean square (RMS) error was calculated, as seen in Equation (7).

$$RMS=\sqrt{\frac{{\displaystyle {\sum }_{i=1}^n{(E_i-\frac{E_i}{n})}^2}}{n}}$$

(7)

where, E_i is the error of the calculated value, and n is the number of GCPs.

2.3. Simulation Processing Flow

The geometric positioning accuracy without GCPs refers to the difference between the true three-dimensional coordinates of the ground point and the coordinates calculated using the geometric parameters of instantaneous imaging without parameter correction. For a single SAR image, the 2D coordinates (latitude and longitude) of the ground point can be calculated by the RD model only if the elevation information is known. In practical positioning, it is necessary to refer to DEM. Without considering the accuracy of DEM, the geometric positioning performance of SAR satellites can be reflected by the geometric positioning accuracy without GCPs.

The geometric positioning accuracy with GCPs refers to calculating the systematic geometric errors of SAR images in the presence of GCPs and then optimizing the geometric parameters of the imaging moment. Finally, the 3D coordinates of the ground points are calculated using the optimized geometric positioning model, and the difference between the 3D coordinates and the true values is compared. Through the index with the geometric positioning accuracy with GCPs, the geometric positioning level of the SAR image after the optimization of the GCPs can be reflected.

To verify the method for the simulation of geometric positioning accuracy of MEO- and HEO-SAR satellites, the experiment was divided into two parts. The first part was a simulation experiment without GCPs. Satellite positions and velocities were simulated using the STK software. The geographic coordinates of the actual GCPs were then simulated in the imaging area. Based on the RD positioning model, the real satellite-to-ground geometric imaging relationship and the geometric positioning model of the virtual imaging environment were constructed. After obtaining the geometric positioning model, the three-dimensional geographic coordinates without GCPs were calculated. The second part was a simulation experiment with GCPs. Similar to the first part, a geometric positioning model was obtained. Then, points were evenly selected within the corresponding width to calculate the three-dimensional geographic coordinates with GCPs.

The specific flow scheme of the geometric positioning accuracy simulation is shown in Figure 2.

2.3.1. Simulation without GCPs

The simulation without GCPs includes the following six steps: SAR satellite orbit simulation, image area prediction, real geometric imaging relationships, virtual geometric imaging relations, three-dimensional geographic coordinates without GCPs and error statistics.

(1)

SAR satellite orbit simulation. The SAR satellite orbit simulation using STK software was achieved as described in the following steps:

(1.1)

Satellite orbit parameter settings: these include the SAR satellite orbit semi-major axis, orbit eccentricity, orbit inclination parameter, right ascension of the ascending node (RAAN), orbit altitude, satellite orbit type and simulation start and end times.

(1.2)

Sensor parameter setting: the sensor was added to the setup satellite object and the sensor parameters were set by defining the property option attributes.

(1.3)

Satellite position and velocity generation: once the sensor parameters have been set successfully, the satellite position and velocity can be obtained by selecting the position velocity from the Reports and Graph Manager option.

(2)

Image area prediction. Using the simulated MEO- and HEO-SAR orbit parameters, the range of the radar beam covering the Earth’s surface can be predicted according to the satellite’s instantaneous position (including sub-satellite point coordinates and height) and viewing angle. The steps to achieve imaging area prediction mainly include grid settings, coverage resources, coverage analysis time period setting, figure-of-merit (FOM) type selection and display and coverage area generation.

(2.1)

Grid settings: to define the coverage area, a coverage definition object to the scene in step (1) was added and the grid coverage used to define the coverage area boundaries was selected.

(2.2)

Coverage resources: allows the selection of STK objects as coverage resources. The pre-built sensors to be assigned.

(2.3)

Coverage analysis time period setting: we selected the coverage analysis period and then the “Calculate Computer Access” option to calculate coverage.

(2.4)

FOM type selection and display: to simulate the imaging areas of the MEO- and HEO-SAR satellites, two types of objects were provided by STK: coverage definition and FOM. An FOM object on the coverage definition object was created, the FOM type was set as the access duration option, and the minimum value for the calculation criteria was selected. Then the satisfaction field on the definition page in the satisfaction pane was selected, and at least one option for the gate value for satisfaction was selected.

(2.5)

Generation of the coverage area: the extent of the generated area was visualized by selecting the “Show contour” function.

(3)

Simulation of realistic satellite-to-ground geometric imaging relationships. Based on the position and velocity information of the MEO- and HEO-SAR satellites obtained in step (1) and the imaging area predicted in step (2), the real slant range and Doppler center frequency values at the imaging moment were calculated using the Bigemap GIS Office to select the coordinates of the ground point in the visible area using the real geometric model, as shown in Equation (5).

(4)

Virtual imaging geometry relationship simulation. The virtual simulation geometry model with errors (Equation (6)) allows the analysis of both the effect of a single error source on the geometric positioning accuracy and the effect of multiple combined error sources on the geometric positioning accuracy.

(5)

Three-dimensional geographic coordinates without GCPs. Based on the orbital parameters of the MEO- and HEO-SAR satellites obtained from the simulation in step (1) and the virtual simulation geometry model constructed in step (4), the three-dimensional geographic coordinates of the GCP were obtained.

(6)

Error statistics. The three-dimensional geographic coordinates calculated in step (5) were subjected to residual calculation with real three-dimensional geographic coordinates, after which the RMS error of the residuals of the ground points was counted.

2.3.2. Simulation with GCPs

The analysis procedure of geometric positioning accuracy with GCPs was divided into seven steps, of which the first five steps were the same as those without GCPs. The remaining two steps were the calculations of three-dimensional geographic coordinates with GCPs and error statistics.

(1)

Three-dimensional geographic coordinates with GCPs. In the positioning calculation without GCPs, only one ground point was simulated. However, the positioning calculation with GCPs required multiple points to be uniformly selected in the simulation area. Based on the orbital parameters of the MEO- and HEO-SAR satellites obtained from the simulation and the virtual simulation geometry model constructed, the three-dimensional geographical coordinates of the GCPs were solved.

(2)

Error statistics. The residual calculation between the three-dimensional geographic coordinates calculated in step (1) and the real three-dimensional geographic coordinates. The mean value of the positioning error was then calculated, along with the residual of the positioning error and the mean value of each ground point. Finally, the RMS error of the residuals of the ground points was calculated to obtain the geometric positioning accuracy with the GCPs.

3. Experiments and Analysis

3.1. Simulation Data

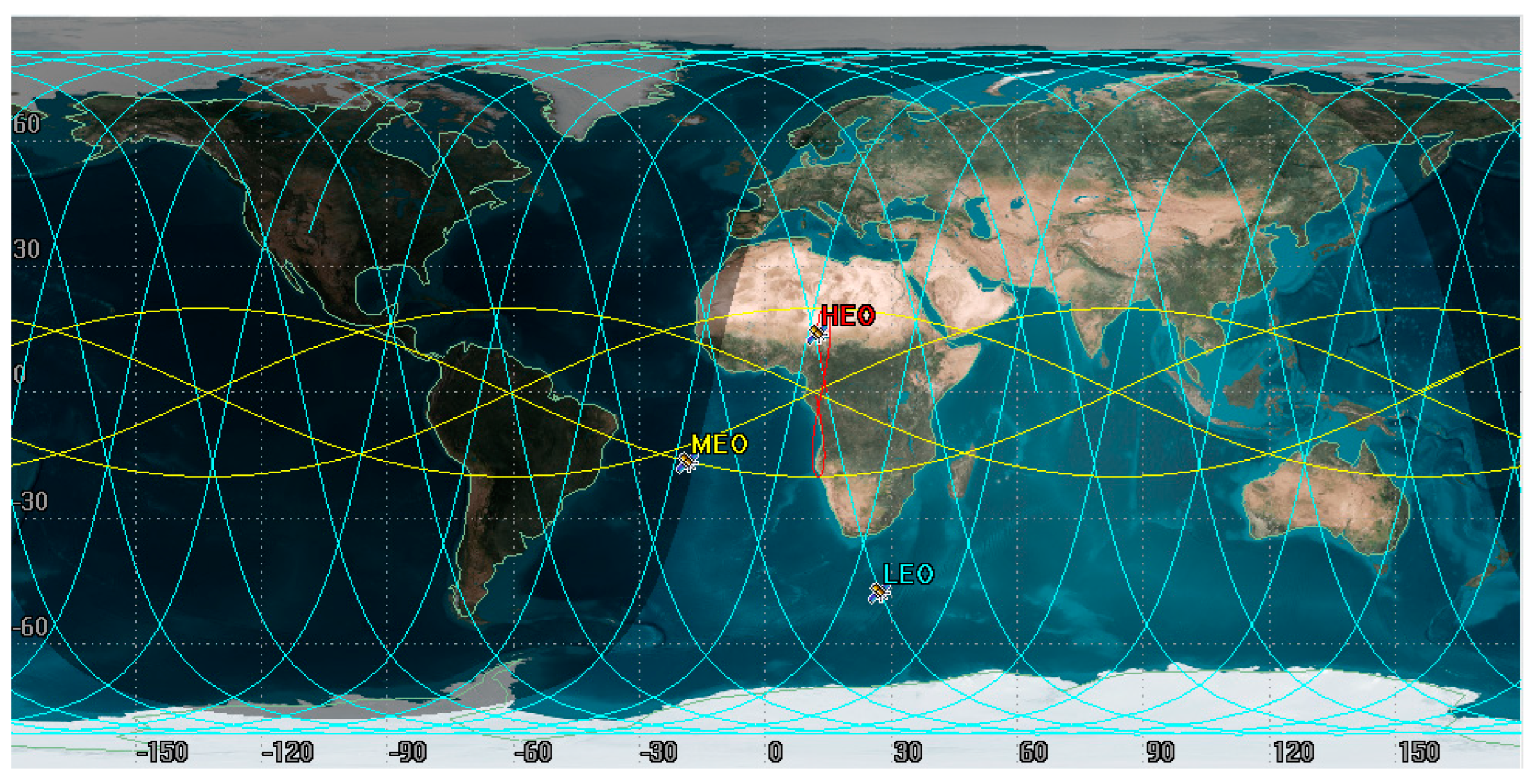
3.1.1. Orbital Data Simulation

The simulation environment was created using STK, and the J4 perturbation model was selected. The orbit data simulation was carried out using the STK software in ascending order of orbit height. The simulation parameters are listed in

Table 1. Simulation parameters of low Earth orbit (LEO), medium Earth orbit (MEO), and high Earth orbit (HEO) synthetic aperture radar (SAR) satellites.

Research Object	Inclination I (°)	Altitude H (km)	Eccentricity	Raan (°)	Sar Sensor
					Min Elevation Angle (°)	Max Elevation Angle (°)	Forward Exclusion Angle (°)	Aft Exclusion Angle (°)
LEO-SAR	98.5	755	0	270	35	70	45	45
MEO-SAR	20	8000	0	0
HEO-SAR	20	36,000	0	40

. The simulation period was set as 24 h.

In the 2D graphics window of STK software, the sub-satellite trajectories of the LEO-, MEO- and HEO-SAR satellites can be displayed, as shown in Figure 3.

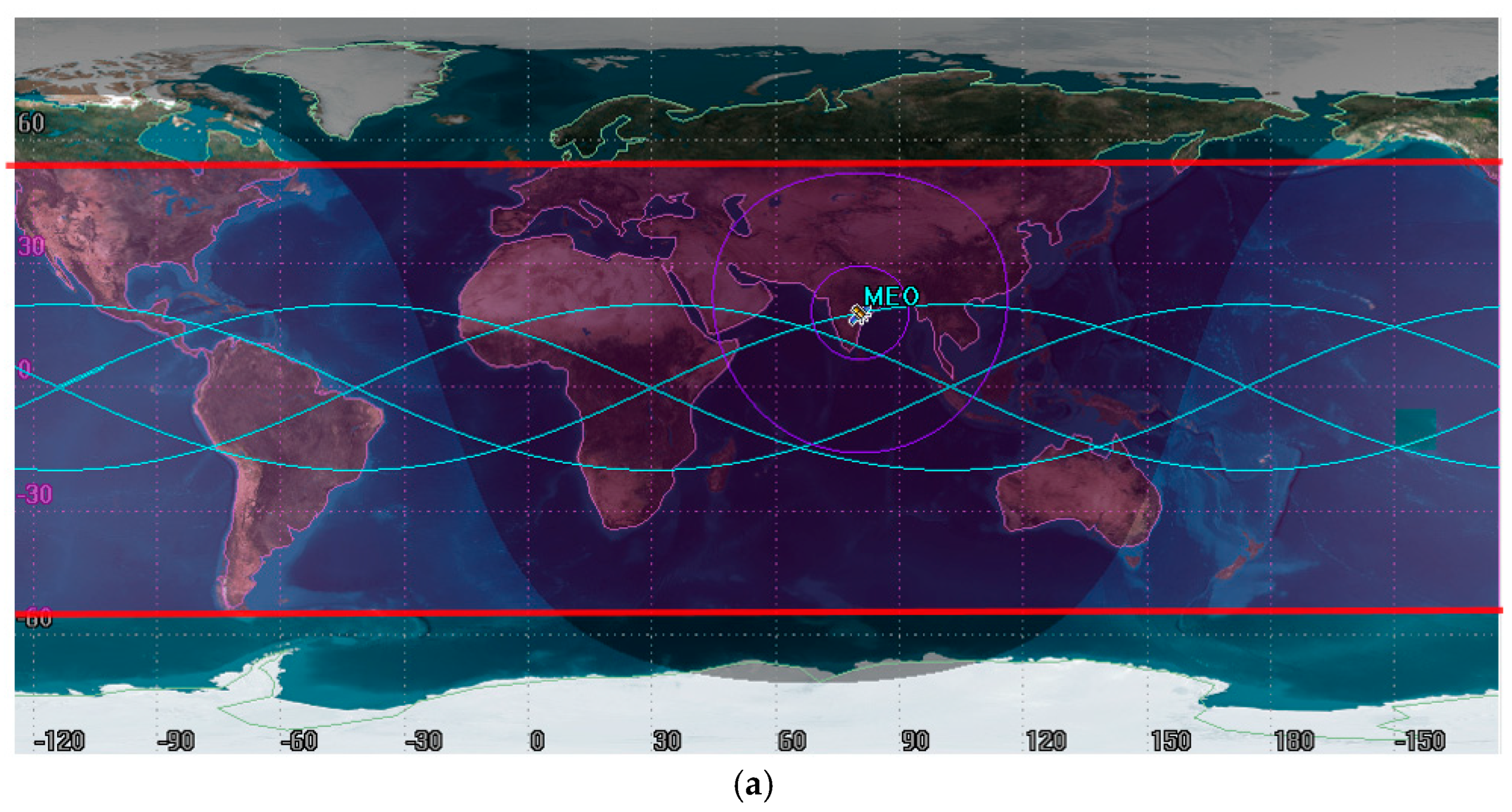
3.1.2. Coverage Analysis

The corresponding parameter settings are listed in

Table 2. Parameter settings for coverage analysis of radar beam.

Project	Parameter
Assets	Sensor
Interval	24 h
Grid spacing	6°
Grid settings	Global
Type of FOM	Access duration
FOM calculation criteria	Minimum
Satisfaction pane selection	At least
Satisfaction threshold	10 s and 120 s

based on the imaging area prediction in Section 2.3.

Considering the characteristics of long synthetic aperture time of MEO- and HEO-SAR satellites, the synthetic aperture time of the MEO-SAR satellite was greater than 10 s as the standard, and that of the HEO-SAR satellite was greater than 120 s as the standard. In this experiment, the threshold values of satisfaction were set to 10 s and 120 s. The coverage area of the MEO-SAR satellite is shown in Figure 4a and that of the HEO-SAR satellite is shown in Figure 4b, where the red line frame is the imaging area.

As seen in Figure 4, the imaging area of the MEO-SAR satellite was within ~50° of north–south latitude, and the imaging area of the HEO-SAR satellite was within ~66° of north–south latitude and spanned ~110° of east–west longitude. The coordinates of the GCPs in the visible area were selected using the Bigemap GIS Office.

Based on the analysis of the imaging area coverage of the MEO- and HEO-SAR satellites, GCPs with different imaging widths were selected within China to simulate and analyze the geometric positioning accuracy. The imaging width ranges were primarily 500, 800, 1000, 1500 and 2000 km, and the different widths shared the same central point P0, as shown in Figure 5.

3.1.3. Selection of Simulation Error

The errors involved in the virtual simulation geometry model include satellite position errors, satellite velocity errors, Doppler center frequency errors, terrain undulation errors, slant range measurement errors and azimuth time errors. With reference to the current level of satellite development technology, data processing level, and external reference data, certain ranges of simulation errors were selected for simulating the geometric positioning accuracy. The values and bases of the specific simulation errors are listed in

Table 3. Values and bases of simulation errors.

Positioning Error Sources	Range Value	Interval Value
DEM	5–25 m	5
Slant range	10–50 m	10
Azimuth time	1–9 ms	2
Doppler center frequency	0–0.7 Hz	0.2
Vertical-track position	1–5 m	1
Along-track position	1–5 m	1
Radial position	1–5 m	1
Vertical-track velocity	0.001–0.01 m/s	0.002
Along-track velocity	0.001–0.01 m/s	0.002
Radial velocity	0.001–0.01 m/s	0.002

.

3.2. Results and Analysis

In our study, relevant experiments were carried out from three aspects.

(1)

Method validation. The geometric positioning accuracy of the LEO-SAR satellite was simulated using the relevant parameters. The effectiveness of the method was verified by comparing it with the measured geometric positioning accuracy of the SAR satellite in orbit.

(2)

Geometric positioning accuracy without GCP simulation. In the simulation imaging area, a GCP was selected. The simulation method proposed in this study was used to simulate the geometric positioning accuracy without GCP. The effects of single and multiple error sources and different satellite orbital positions on the geometric positioning performance of the satellite were analyzed.

(3)

Simulation experiment of the geometric positioning accuracy with GCPs. Several GCPs were evenly selected in the simulation imaging area, and the geometric positioning accuracy with GCPs was calculated separately using the simulation method proposed in this study. The geometric positioning accuracy with GCPs was statistically analyzed. A comparative analysis of the geometric positioning accuracy at different imaging widths and orbital positions was performed.

3.2.1. Method Validation Experiments

For the method validation experiments, four GCPs and satellite positions were selected (Figure 6) based on the range of imaging areas of the LEO-SAR satellite.

(1)

Geometric positioning accuracy of LEO-SAR satellites without error

According to the SAR satellite orbit simulation and imaging area prediction, the LEO-SAR satellite position and velocity and the coordinates of the GCPs in Figure 6 can be determined. According to the real satellite-ground geometric imaging model, the slant distance and Doppler were simulated to calculate the geometric positioning accuracy without error. The geometric positioning accuracy of LEO-SAR satellites without errors at different GCPs are listed in

Table 4. Geometric positioning of ground control points (GCPs) without errors.

Ground Control Point	Geometric Positioning Error (m)
Facility 1	0.0017
Facility 3	0.002
Facility 4	0.0012
Facility 6	0.0022
RMS	0.0018

.

As shown in Table 4, the RMS of the four groups of positioning errors under different GCPs was 0.0018 m. It can be seen that the positioning error of the ground reference point is close to zero, assuming an error of zero. The real satellite-terrestrial geometric imaging relationship is constructed to be valid.

(2)

Geometric positioning accuracy of LEO-SAR satellites with errors

According to the SAR satellite orbit simulation and imaging area prediction, the LEO-SAR satellite position and velocity and the coordinates of the GCPs in Figure 6 can be determined. The corresponding precision values are mentioned in [19]. The positioning error sources for the LEO-SAR satellite was set, and the geometric positioning error was obtained according to the virtual imaging geometric relationship simulation. The geometric positioning errors of LEO-SAR satellites at different GCPs are listed in

Table 5. Geometric positioning errors of ground control points.

Ground Control Point	Geometric Positioning Error (m)
Facility 1	1.85
Facility 3	3.30
Facility 4	1.90
Facility 6	2.37
RMS	2.43

.

As shown in Table 5, the RMS of the four groups of positioning errors under different GCPs was 2.43 m. From previous research literature [19], it is known that the satellite position accuracy can be better than 5 cm, and the velocity accuracy is 0.05 m/s, and the SAR system time error is 30 ns, and the slant range error caused by the atmospheric transmission delay is ~1 m. The error introduced by the imaging processing can be avoided, and the relative elevation error is not considered for the time being. The RMS of the four groups of positioning errors of the satellite under different incidence angles was 2.56 m, which was consistent with the simulation results in Table 5. This indicates that the simulation method proposed in this study is effective.

3.2.2. Simulation Analysis of Geometric Positioning Accuracy without GCPs

(1)

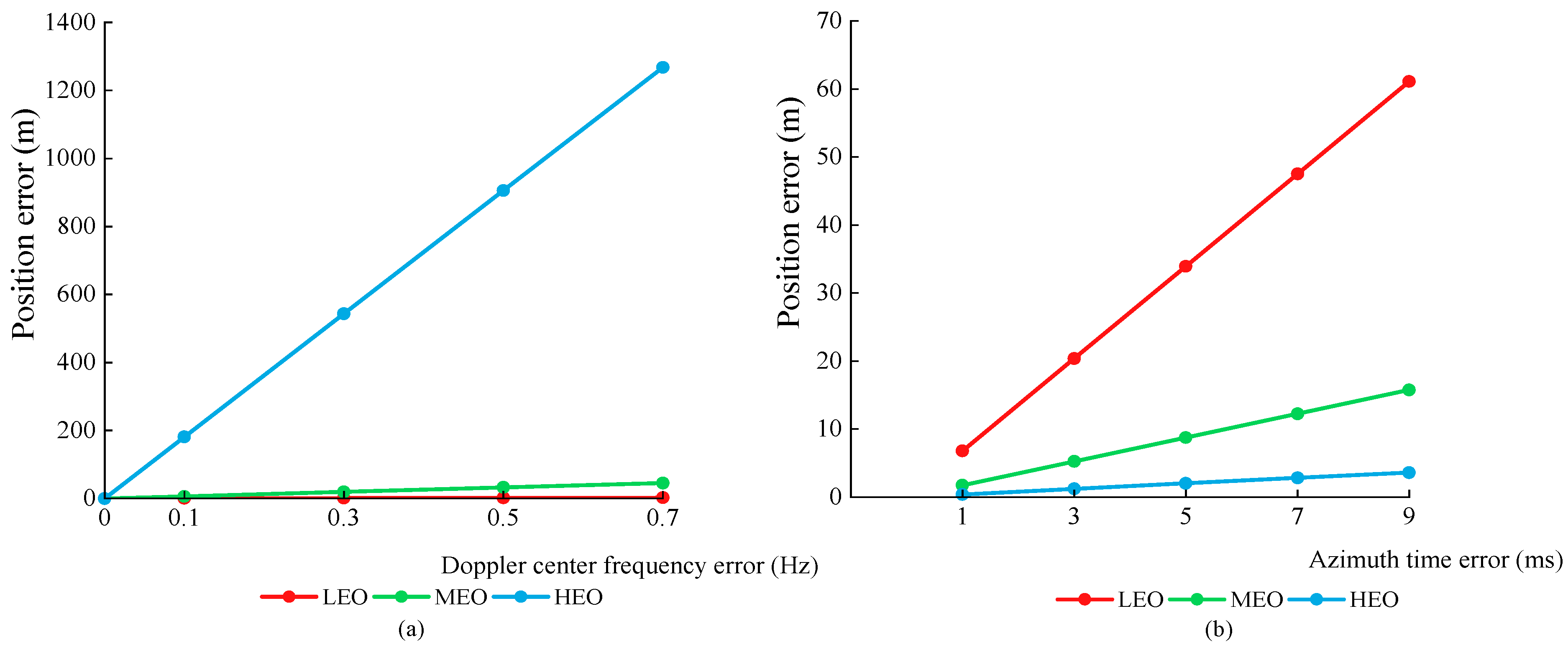
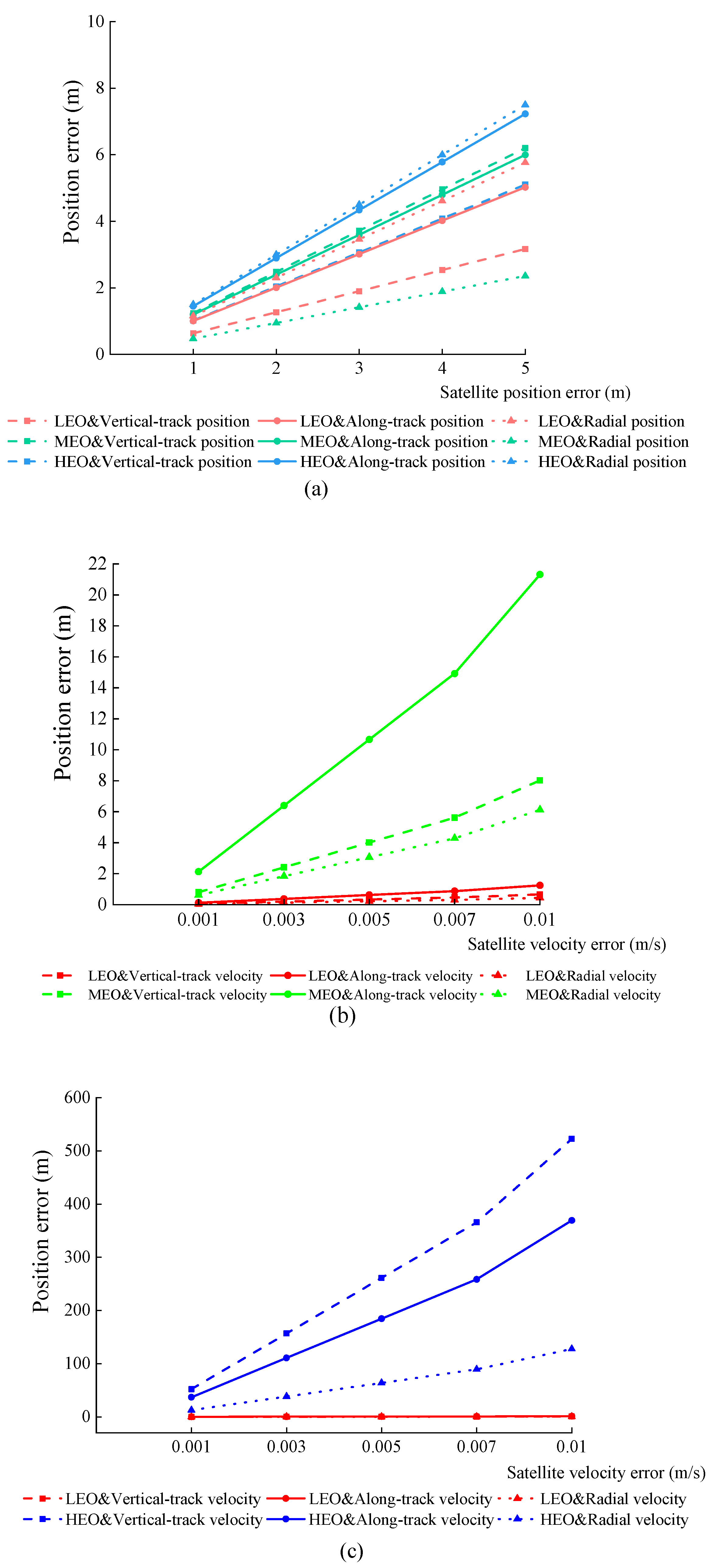
Influence of a single error source on the geometric positioning accuracy of MEO- and HEO-SAR satellites

To analyze the influence of a single error source on the geometric positioning accuracy of the MEO- and HEO-SAR satellites, the satellite positions and velocities of MEO-SAR satellite position 33 and HEO-SAR satellite position 1 were selected (Figure 7).

The satellite position and velocity of MEO-SAR satellite position 33 and HEO-SAR satellite position 1 in Figure 7 and the real ground coordinates P0 in Figure 5 can be known. The simulation of the virtual imaging geometry relationship can be used to verify the positioning errors without GCPs of the three orbiting SAR satellites LEO, MEO and HEO based on the Doppler center frequency error, azimuthal time error, satellite position error and satellite velocity error (the error values are shown in Table 3) in turn, as shown in Figure 8 and Figure 9.

As shown in Figure 8, the geometric positioning accuracy of the SAR satellite is reduced with increasing orbital altitude for the Doppler center frequency error and increased with increasing orbital altitude for the azimuth time error. Two factors affect the azimuth time error: the satellite position and velocity. The differences between the satellite position and velocity at 0 ms and the satellite position and velocity at other azimuth time intervals are presented in

Table 6. Effects of azimuth time intervals on satellite velocity and position.

Azimuth Time Error	Research Object	$\mathbf{\Delta }\mathit{x}$	$\mathbf{\Delta }\mathit{y}$	$\mathbf{\Delta }\mathit{z}$	$\mathbf{\Delta }{\mathit{v}}_{\mathit{x}}$	$\mathbf{\Delta }{\mathit{v}}_{\mathit{y}}$	$\mathbf{\Delta }{\mathit{v}}_{\mathit{z}}$
1 ms	LEO-SAR	0.805	3.914	−6.413	0.002194	0.006707	0.003837
	MEO-SAR	−3.624	−1.487	1.766	0.000432	0.001202	0.000131
	HEO-SAR	0.151	−0.107	0.711	0.000018	0.000012	0.000056
3 ms	LEO-SAR	2.416	11.743	19.239	0.006582	−0.02012	0.011511
	MEO-SAR	10.873	−4.459	5.299	0.001296	0.003607	0.000393
	HEO-SAR	0.453	−0.322	2.135	0.000055	−0.00006	0.000168
5 ms	LEO-SAR	4.027	19.572	32.065	0.01097	0.033534	0.019185
	MEO-SAR	18.122	−7.431	8.832	0.00216	0.006012	0.000654
	HEO-SAR	0.755	−0.536	3.558	0.000091	−0.0001	−0.00028
7 ms	LEO-SAR	5.638	27.401	−44.89	0.015357	0.046947	0.026858
	MEO-SAR	25.371	10.404	12.365	0.003023	0.008417	0.000916
	HEO-SAR	1.057	−0.751	4.981	0.000127	−0.00014	−0.0004
9 ms	LEO-SAR	7.249	35.23	57.716	0.019744	0.060361	0.034532
	MEO-SAR	−32.62	−13.376	15.898	0.003887	−0.010822	−0.001178
	HEO-SAR	1.359	−0.965	6.404	−0.000163	−0.00018	−0.0005

. The difference in the satellite position of the LEO-SAR satellite was much larger than that of the MEO- and HEO-SAR satellites. The existing technology can control the azimuth time error of LEO-SAR satellites within 0 ms, whereas, for MEO- and HEO-SAR satellites, the azimuth time has less influence. Figure 8a shows that the geometric positioning error is more than 1000 m. It can be seen that the Doppler center frequency error has the greatest impact on the geometric positioning accuracy of HEO-SAR satellites.

As shown in Figure 9a, MEO-SAR positioning error > HEO-SAR positioning error > LEO-SAR positioning error when the vertical-track position error is the same; HEO-SAR positioning error > MEO-SAR positioning error > LEO-SAR positioning error when the along-track position error is the same; HEO-SAR positioning error > MEO-SAR positioning error > LEO-SAR positioning error when the radial position error is the same.

Among the satellite orbit parameters, for the MEO-SAR satellite, the values of vertical and along-track position errors were close and large; therefore, they have a more important influence on the geometric positioning accuracy. For the HEO-SAR satellite, the values of the along-track and radial position errors were close to each other and larger than those of LEO and MEO; therefore, they have a more important influence on the geometric positioning accuracy. For the MEO-SAR satellite, the vertical track velocity error reached 20 m, which was much larger than the other two velocity errors; therefore, it has a more important influence on the geometric positioning accuracy. For the HEO-SAR satellite, the vertical-track velocity error reached more than 600 m, which was much larger than the others; therefore, it has a more important influence on the geometric positioning accuracy. When comparing the satellite position with the satellite velocity, the positioning error caused by the satellite position error was less than 10 m, and the impact of satellite velocity on the satellite positioning accuracy was much greater than that of the satellite position.

(2)

Combined effects of multiple error sources on geometric positioning accuracy of MEO- and HEO-SAR satellites

To analyze the effect of multiple error sources on the geometric positioning accuracy of MEO- and HEO-SAR satellites, the satellite positions and velocities of MEO-SAR satellite position 33 and HEO-SAR satellite position 1 were selected (Figure 7).

All error sources to be analyzed were divided into five groups, as shown in Table 3, where the combined error arrangement was combined from the smallest to the largest error, with combination 1 being the smallest value of all errors and the remaining combinations adding the corresponding disturbance values in turn. The positioning error under the influence of the combined error can be obtained based on the virtual imaging geometry relationship simulation, as shown in Figure 10.

From Figure 10, it can be observed that the geometric positioning accuracy of SAR satellites decreases as the orbital altitude increases. The geometric positioning error of SAR satellites increases according to a certain rule, under the influence of the combined error. As can be seen from combinations 1 to 5, the geometric positioning error of MEO-SAR satellites increases by ~33 m between each group, and the geometric positioning error of HEO-SAR satellites increases by ~409 m between each group. The geometric positioning error of the HEO-SAR satellite was much higher than that of the MEO-SAR satellite, and the difference between the two increased as the combined error continued to increase.

(3)

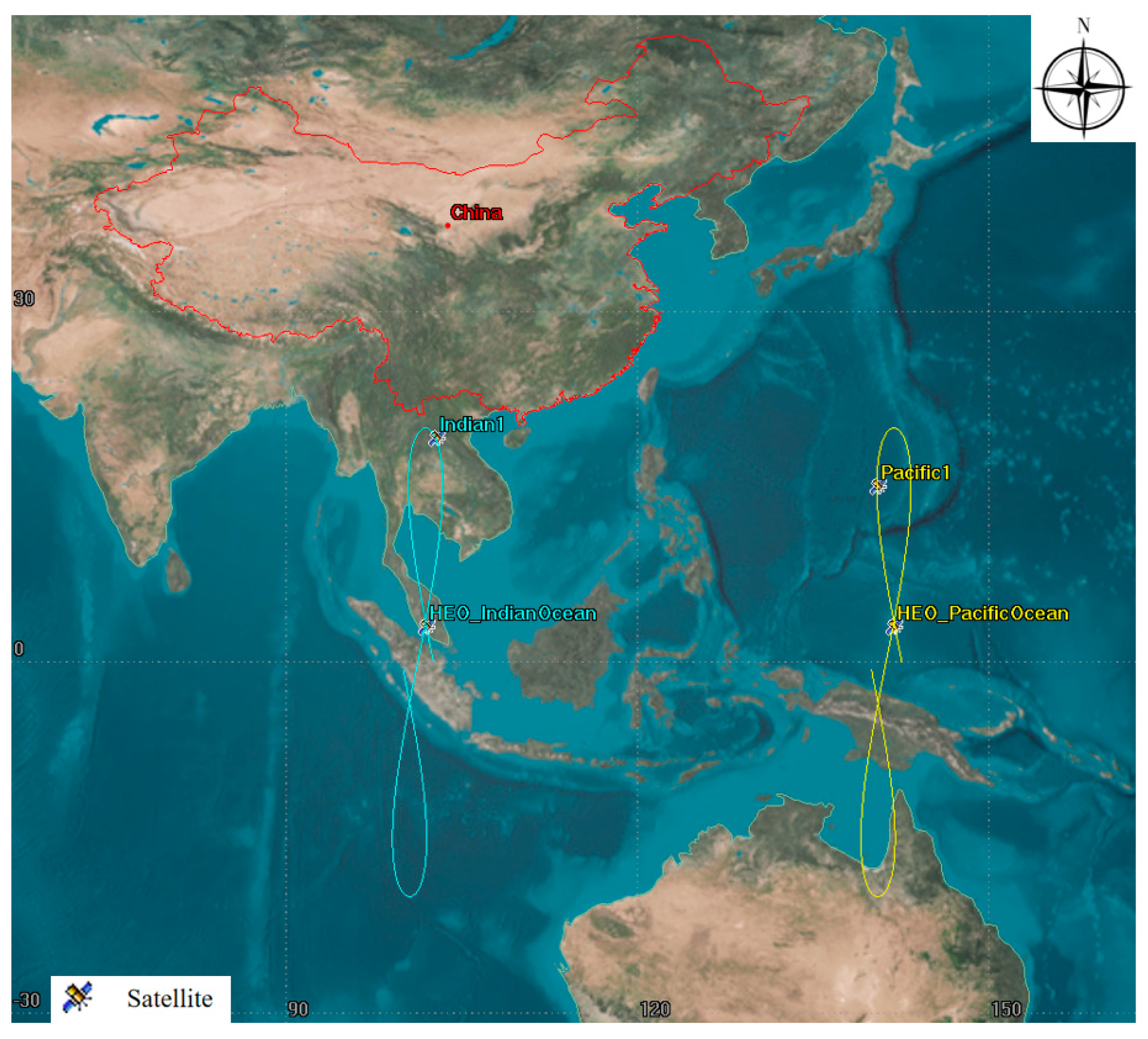
Influence of different orbital positions on the geometric positioning accuracy

Different orbital positions in different regions were selected for the geometric positioning error calculation of the ground points, and six ground points were selected for each of the MEO- and HEO-SAR satellites. A schematic of the ground points and satellite positions is shown in Figure 7.

The position and velocity of the MEO- and HEO-SAR satellites and the coordinates of the six GCPs selected in Figure 7 were determined. The combined error was chosen as the combination with the smallest error value. The positioning errors for different ground points at different satellite orbital positions are shown in Figure 11 and Figure 12.

As shown in Figure 11, the different orbital positions fluctuate within a certain interval of the positioning error for the same combined errors. For each ground point, the MEO-SAR satellite selects an observable position for positioning errors in the range 10–30 m.

Figure 11 shows that the geometric positioning errors of satellite positions 1, 11, 17, 22, 28 and 32 were large, and the satellite positions with large geometric positioning errors were calculated and analyzed in terms of the oblique angle of view with other satellite positions. The positioning error of the MEO SAR satellite is smaller in the side view, whereas the larger the oblique view angle, the more unstable the image, leading to an increase in the positioning error.

As shown in Figure 12, the positioning error trends of HEO-SAR satellites for ground points are the same according to the latitude where the GCPs are located, with the sub-satellite tracks of the HEO-SAR satellite as the boundary (e.g., Places 4 and 5, Places 1 and 6, Places 2 and 3). For Places 4 and 5, it can be seen that the HEO-SAR satellite positioning error is larger at satellite position 2, and the other positions are more stable; for Place 1, it can be seen that the HEO-SAR satellite positioning error is larger at satellite positions 2 and 9, and the other positions are more stable; for Place 6, it can be seen that the HEO-SAR satellite positioning error is larger at satellite positions 2 and 6, and the other positions are more stable; for Place 2 and Place 3, it can be seen that the HEO-SAR satellite positioning error is larger at satellite position 6, and the other positions are more stable. It can be seen from Table 6 that the positioning errors of the different GCPs are larger at satellite positions 2 and 6; that is, the positioning errors are larger at the inflection points of the sub-satellite track of the HEO-SAR satellite.

It can be seen that satellite inflection positions, such as positions 2 and 6, have a large error for ground point positioning, while the other satellite positions in comparison, positions 4 and 8, have a smaller error for ground point positioning, so satellite positions 4 and 8 can be chosen as the optimal solution.

(4)

Influence of different period positions of HEO-SAR satellites on geometric positioning accuracy

Since the sub-satellite track of the HEO-SAR satellite is an unclosed figure-of-eight, and the satellite position changes continuously over time, the sub-satellite tracks of the HEO-SAR satellite for two different periods were selected for the experiment. The sub-satellite tracks of the HEO-SAR satellites at Pacific and Indian Ocean positions with the same width are shown in Figure 13.

The satellite positions and velocities of the HEO-SAR satellite positions Pacific 1 and Indian 1 in Figure 13 and the real coordinates of all GCPs in Figure 5 can be obtained. The average value of the positioning error of the GCPs selected for each width can be calculated to obtain the geometric positioning error without GCPs. The geometric positioning errors without GCPs of the HEO-SAR satellite in the Pacific and Indian Oceans are shown in Figure 14.

From Figure 14, it can be seen that the geometric positioning error of the HEO-SAR satellite without GCPs at the Indian Ocean position is between 229 m and 234 m, which is larger than that at the Pacific Ocean position. The oblique angle of view of the GCP of the HEO-SAR satellite at the Pacific Ocean position is smaller than that of the HEO-SAR satellite at the Indian Ocean position. Therefore, the HEO-SAR satellite can obtain the best positioning accuracy without GCPs at the Pacific Ocean position.

3.2.3. Simulation Analysis of Geometric Positioning Accuracy with GCPs

The magnitude of the imaging width causes each GCP to be at a different location on Earth, and the GCPs are spaced differently, which can cause differences in the geometric positioning accuracy. There were five groups of imaging width magnitudes, with P0 as the center point for uniform point selection, and widths of 500, 800, 1000, 1500 and 2000 km, as shown in Figure 5.

The satellite position and velocity of MEO-SAR satellite position 31 and HEO-SAR satellite position 1 in Figure 7 and the real coordinates of the GCPs in Figure 5 were determined. The residual difference between the positioning error and the mean error at each point was calculated. The positioning accuracy with GCPs was calculated by the RMS error using the residuals.

The positioning errors with and without GCPs for MEO-SAR satellites and those with and without GCPs for HEO-SAR satellites are shown in Figure 15.

From Figure 15, it can be observed that for the same combined errors, the influences of width on the geometric positioning error show variations. For the MEO-SAR satellite, the geometric positioning error without GCPs due to each width was ~44–49 m, and the geometric positioning error with GCPs due to each width was ~31–41 m. For HEO-SAR satellites, the geometric positioning error without GCPs due to each width was ~239–246 m, and the geometric positioning error with GCPs due to each width was ~62–84 m. Figure 15 shows that the geometric positioning accuracy with GCPs of both MEO-SAR and HEO-SAR satellites is higher than that without GCPs, which indicates that those with GCPs will improve the positioning accuracy. However, the geometric positioning accuracy with GCPs gradually decreases as the width increases. When the width increased from 500 to 2000 km, the geometric positioning error with GCPs of the MEO-SAR satellite decreased from approximately 30% to 16% compared to its geometric positioning error without GCPs, and the geometric positioning error with GCPs of the HEO-SAR satellite decreased from approximately 74% to 65% compared to its geometric positioning error without GCPs.

The experiment shows that geometric positioning with GCPs can eliminate some of the systematic errors. Thus, the positioning accuracy is greatly improved, the geometric positioning error is stabilized within a certain range, and the satellite images achieve the best positioning performance.

4. Discussion

4.1. Validity of the Simulation Method

To enable simulation analysis of the geometric positioning accuracy of MEO- and HEO-SAR satellites with and without GCPs, this study first simulated the LEO-SAR satellite.

For the settings of error parameters, refer to Reference [19]. The geometric positioning error of the LEO-SAR satellite was obtained by simulating the virtual imaging geometry model. According to the experimental results in Section 3.2.1, the RMS of the positioning error under different GCPs was 2.43 m, which is consistent with the results (2.56 m) obtained by Reference [19]. This indicated that the simulation method proposed in this study was effective.

4.2. Geometric Positioning Accuracy Characteristics of MEO-SAR Satellite

(1)

According to the experimental results in Section 3.2.2, geometric positioning accuracy decreased as the incidence angle increased. In the case of combined errors, as shown in Table 3, all error sources to be analyzed were divided into five groups. It can be seen from Figure 10 that the combination of errors increased the corresponding interference value and the MEO-SAR satellite geometric positioning accuracy decreased by approximately 33 m between each group.

(2)

In the simulation experiments of geometric positioning accuracy without GCPs, when the combined error was small, the incidence angle had a greater impact on the MEO-SAR satellite. According to the experimental results in Section 3.2.2, the geometric positioning error of the MEO-SAR satellite was approximately 24–48 m at different orbital positions. Positioning accuracy can be improved by numerical control of the angle of incidence and elevation errors.

(3)

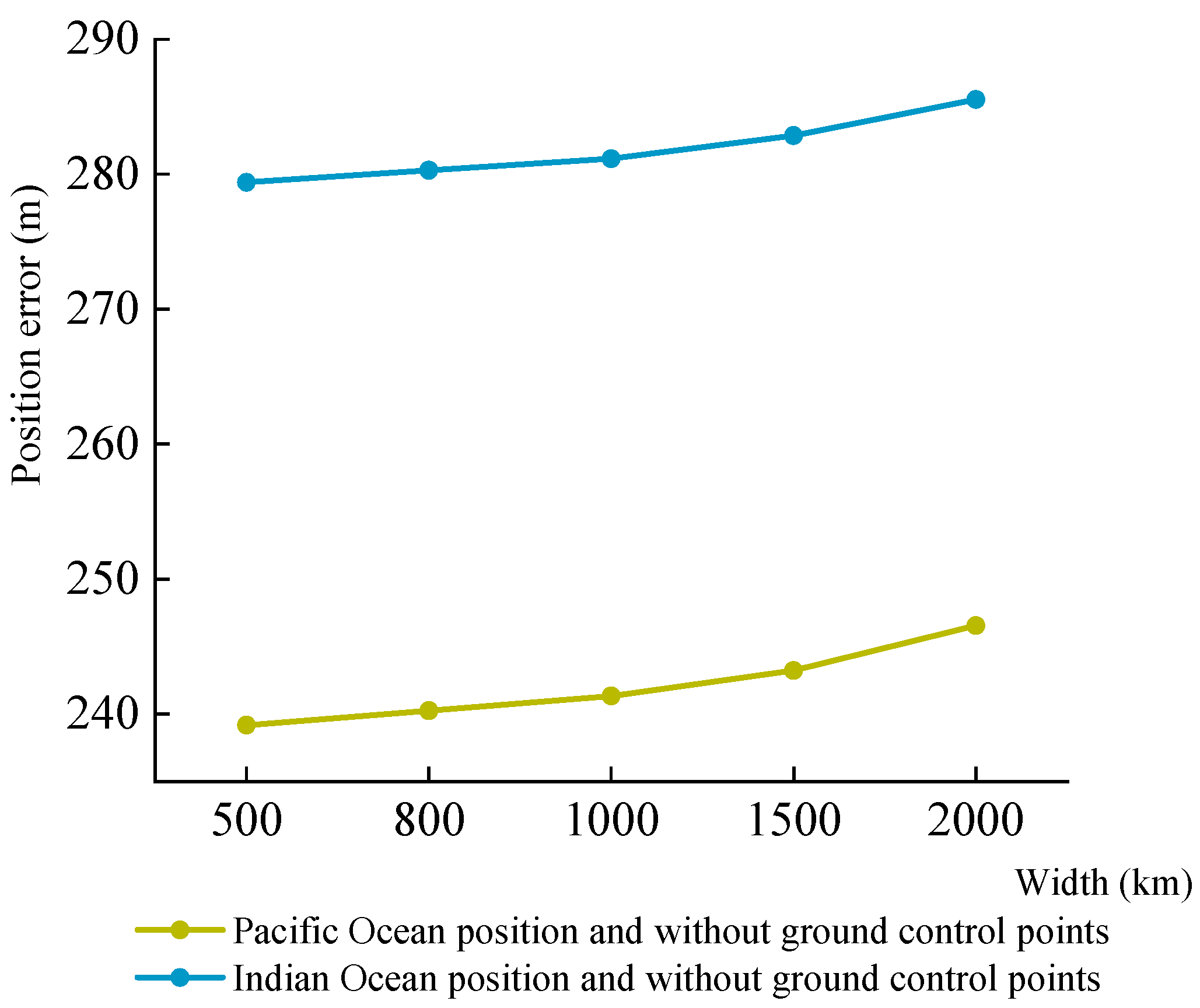
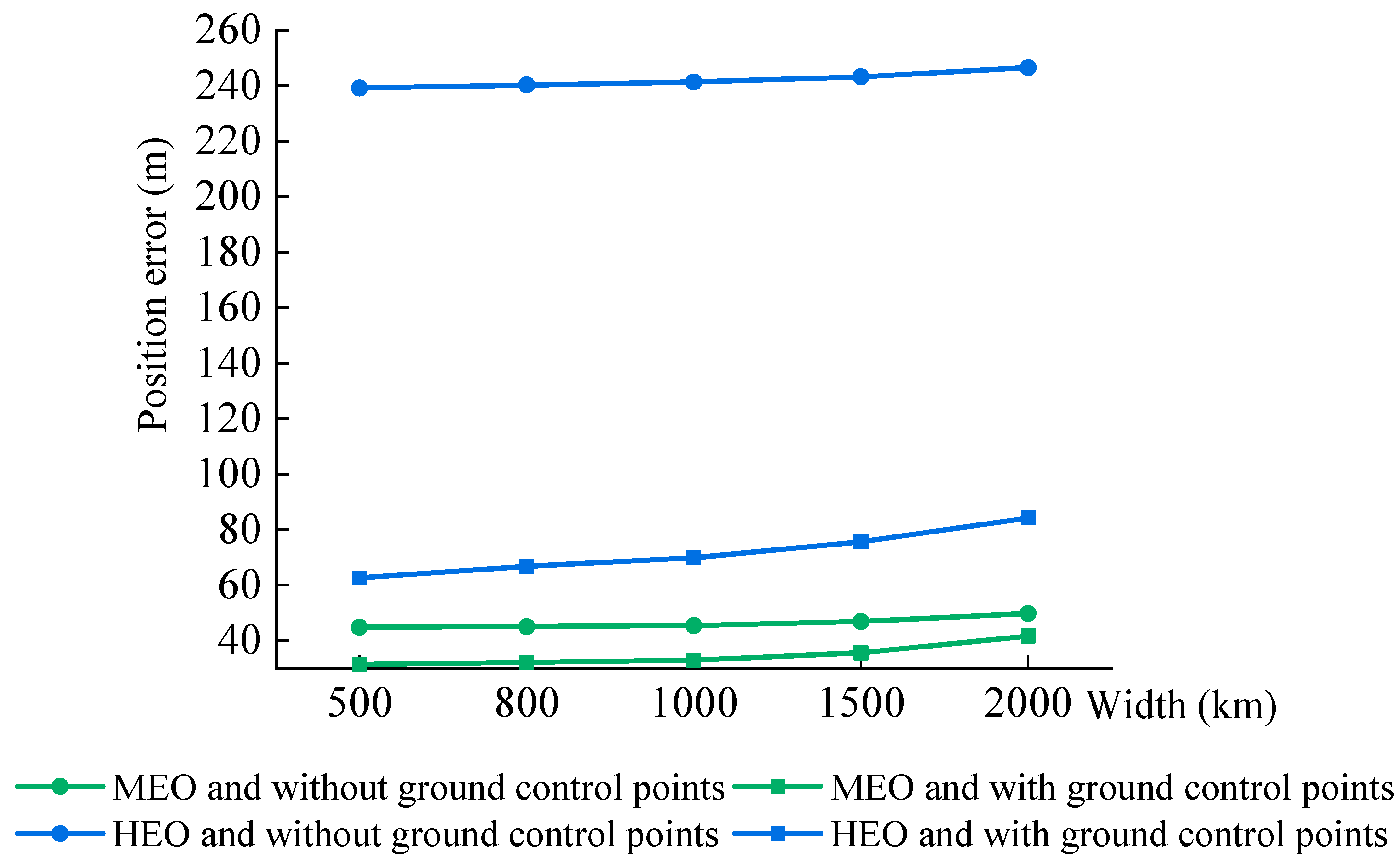
When the simulation experiment of geometric positioning accuracy with GCPs was conducted, part of the systematic errors could be effectively eliminated, and the geometric positioning accuracy of the MEO-SAR satellite was improved. According to the comparative analysis of the experimental results in Section 3.2.3, in the case of combined errors, the geometric positioning error without GCPs of the MEO-SAR satellite was ~44–49 m, whereas the geometric positioning error with GCPs was ~31–41 m.

4.3. Geometric Positioning Accuracy Characteristics of HEO-SAR Satellite

(1)

From Section 3.2.2, it can be seen that among the experimental results of a single error source, the Doppler center frequency error and satellite velocity error had relatively greater negative impacts on the geometric positioning accuracy of the HEO-SAR satellite. It can be seen from Figure 9 that for each 0.1 Hz increase in the Doppler center frequency error, the HEO-SAR satellite positioning error increased by ~182 m. Additionally, Figure 10c shows that for each 0.002 m/s increase in the vertical-track velocity error and radial velocity error, the HEO-SAR satellite positioning error increased by approximately 104 m and 110 m, respectively.

(2)

In the simulation experiments of the geometric positioning accuracy without GCPs, we observed that the intersection point of the figure-of-eight shape could be selected for the geometric positioning accuracy calculation of the HEO-SAR satellite, while the inflection point of the figure-of-eight shape was not suitable for the same. According to the results described in Section 3.2.2, the geometric positioning accuracy calculation results of the HEO-SAR satellite at the intersection of the figure-of-eight track are better than those at the figure-of-eight inflection point, as the latter are not suitable for geometric positioning accuracy calculations at different orbital positions.

(3)

When the simulation experiment of geometric positioning accuracy with GCPs was carried out, the geometric positioning accuracy of the HEO-SAR satellite was improved. According to the comparative analysis of the experimental results in Section 3.2.3, under the influence of multiple error sources, the geometric positioning error without GCPs of the HEO-SAR satellite was ~239–246 m, whereas the geometric positioning error with GCPs was ~62–84 m.

5. Conclusions

This study proposes a simulation method for the geometric positioning accuracy of MEO- and HEO-SAR satellites with and without GCPs. The positions and velocities of the MEO- and HEO-SAR satellites obtained from the RD positioning model were simulated using the STK software. The geographic coordinates of the actual GCPs in the simulated imaging area were combined to construct a virtual simulation geometric model of the GCPs and examined the error between the image point and the object point. The following conclusions were drawn from our analysis and validation:

(1)

In this paper, the corresponding error and simulated LEO-SAR satellite parameters are used for experimental verification. The simulated LEO SAR satellite geometric positioning accuracy reaches 2.43 m. The positioning accuracy of the GF-3 satellite simulated in literature 19 is 2.56 m. Comparing the positioning data of the LEO-SAR satellite and the GF-3, it can be seen that the method proposed in this paper is effective.

(2)

In the geometric positioning accuracy analysis of MEO-SAR satellites, the position of the side-looking mode with a large incidence angle should be selected.

(3)

In the geometric positioning accuracy analysis of HEO-SAR satellites, the Doppler center frequency error and satellite velocity error should be limited.

The method proposed in this paper can provide requirements for the design and index demonstration of MEO- and HEO-SAR satellites. In the future, the coupling characteristics of geometric positioning accuracy and geometric error of MEO- and HEO-SAR satellites can be studied through this method.