Joint Classification of Hyperspectral and LiDAR Data Using Binary-Tree Transformer Network
Abstract
1. Introduction
- To address the issues of inconsistent data structures, insufficient information utilization, and imperfect feature fusion methods, this paper proposes a new binary-tree-style Transformer network that achieves high-precision land-cover classification by fusing heterogeneous data.
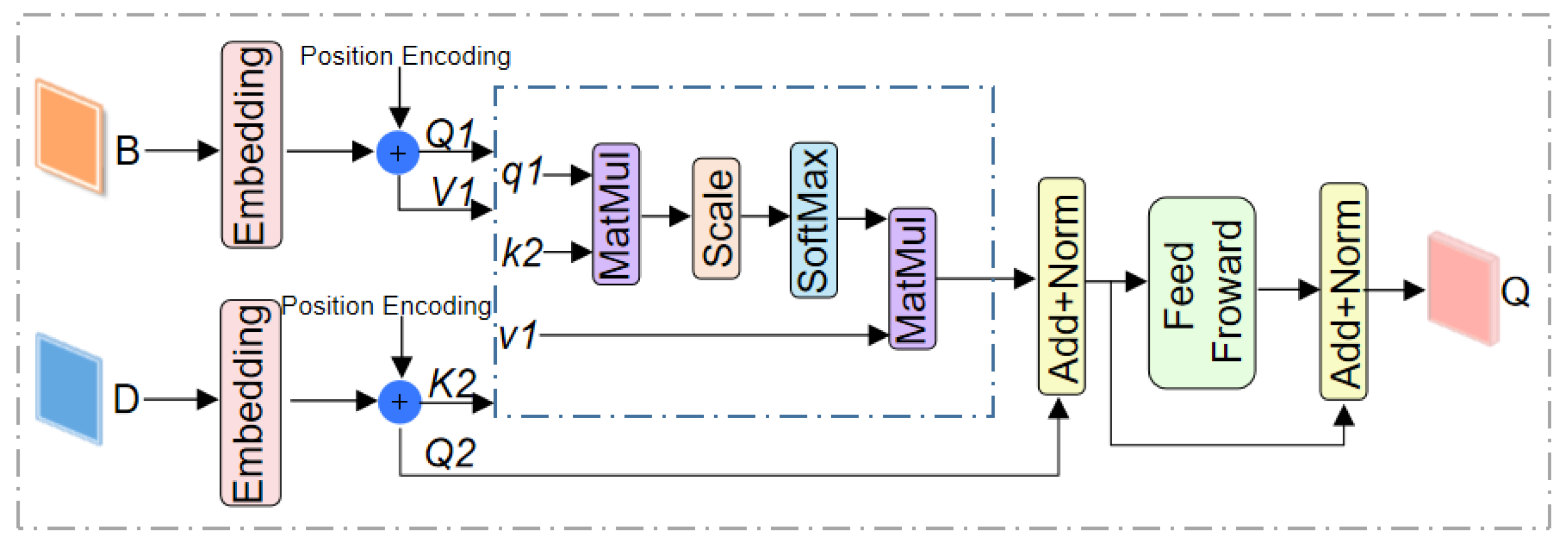
- To fully exploit the complementarity between different modal data, this paper proposes a multi-source Transformer complementor (MSTC) that organically fuses hyperspectral and LiDAR data to better capture the correlations between multi-modal feature information and improve the accuracy of land cover classification. Furthermore, the internal multi-head complementary attention mechanism (MHCA) of this module helps the network better learn the long-distance dependency relationships.
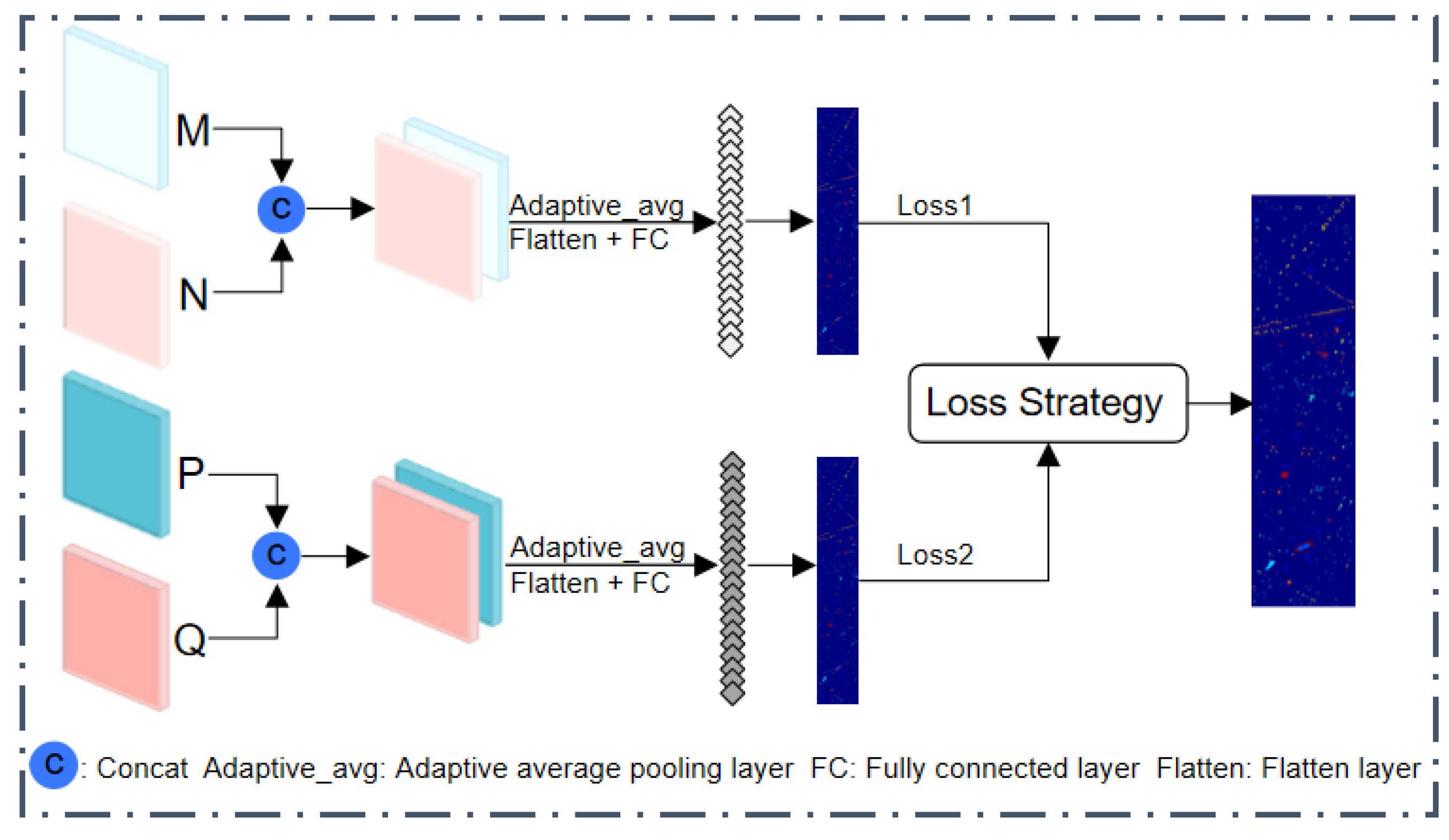
- To fully obtain the feature information of multi-source remote sensing images, this paper proposes a full binary tree structure, named binary feature search tree (BFST), to extract feature maps of the images layer by layer to obtain features at different network levels. The fusion of multi-modal features at different levels is used to obtain multiple image feature representations that are stronger and more stable. This module effectively improves the stability, robustness, and prediction capability of the network.
2. Methodology
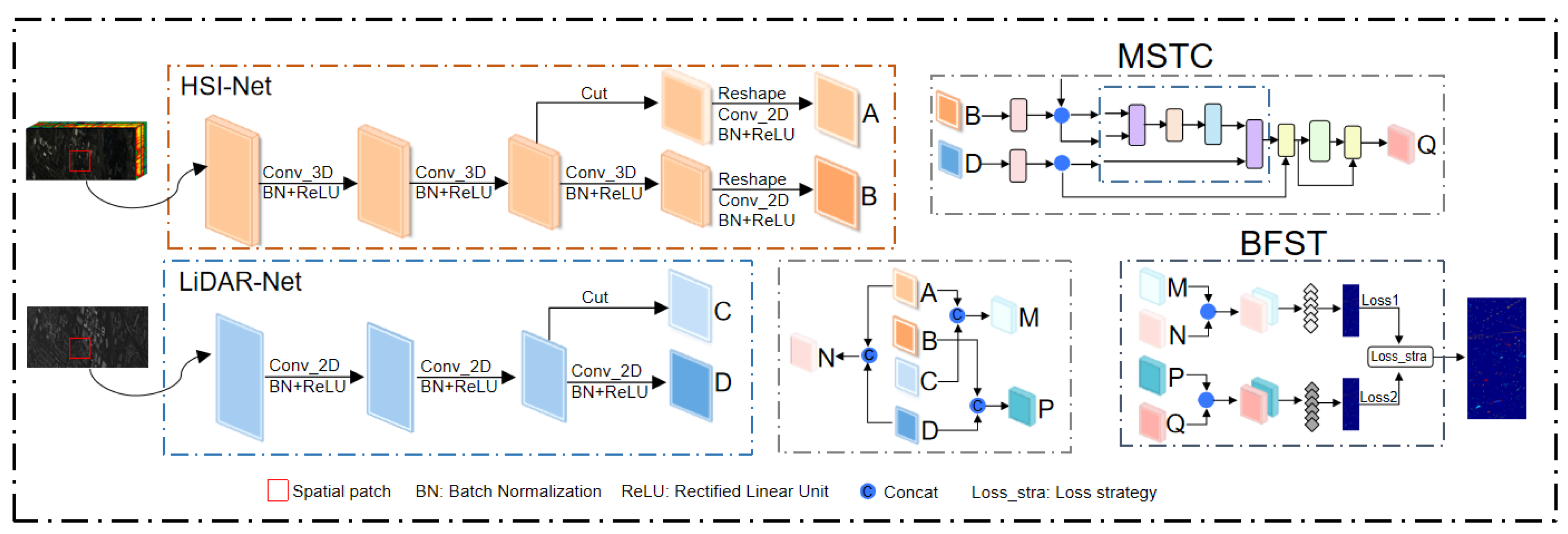
2.1. Overall Framework
2.2. Multi-Source Transformer Complementor
2.3. Binary Feature Search Tree
3. Experiments and Results
3.1. Datasets
3.1.1. Houston Datasets
3.1.2. Trento Datasets
3.2. Experiment Settings
3.3. Evaluation Metrics
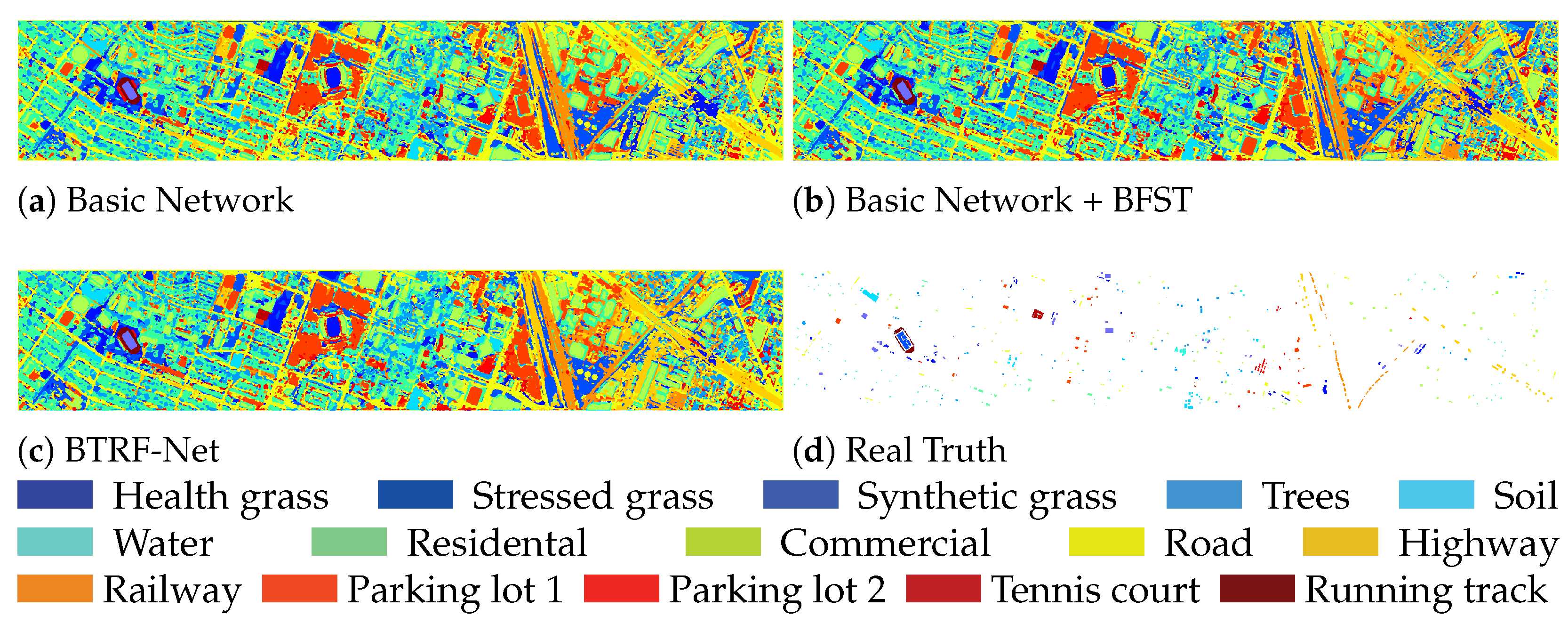
3.4. Comparative Experiments
3.4.1. Comparative Experiments on the Houston Dataset
3.4.2. Comparative Experiments on the Trento Dataset
4. Discussion
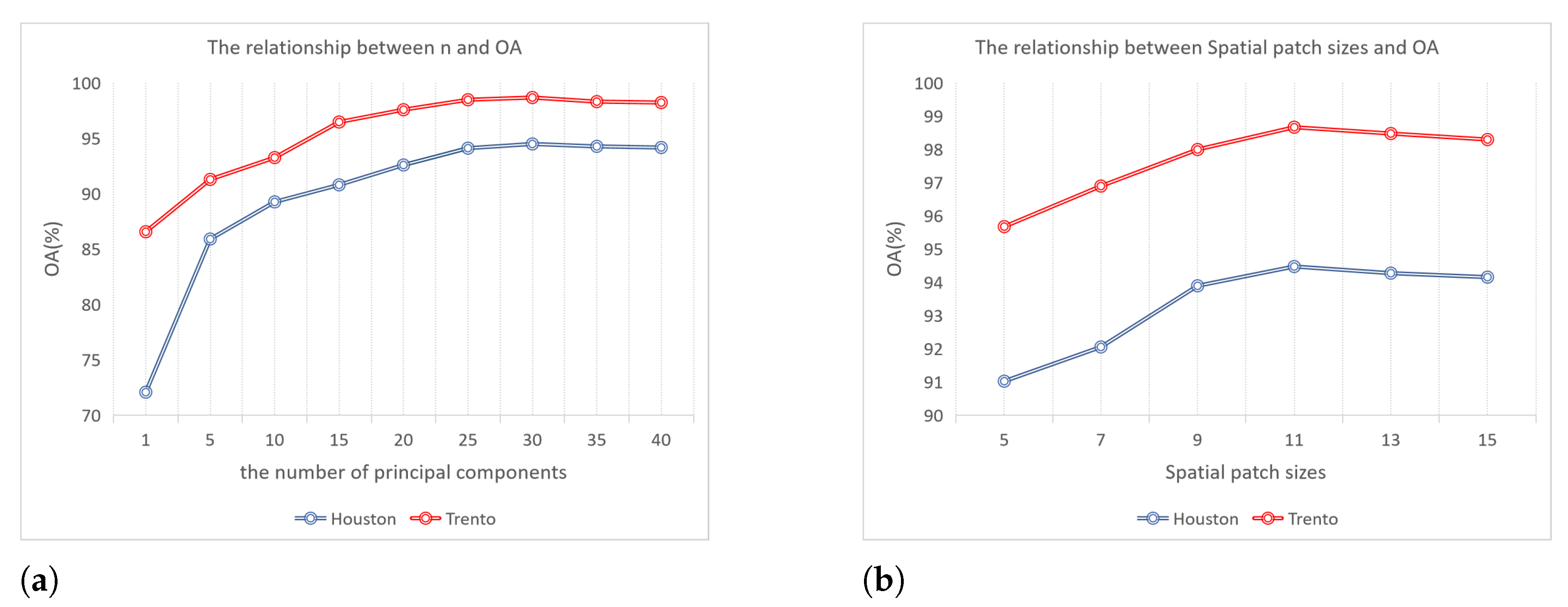
4.1. Parameter Tuning
4.1.1. Principal Component Analysis
4.1.2. Selection of Spatial Patches
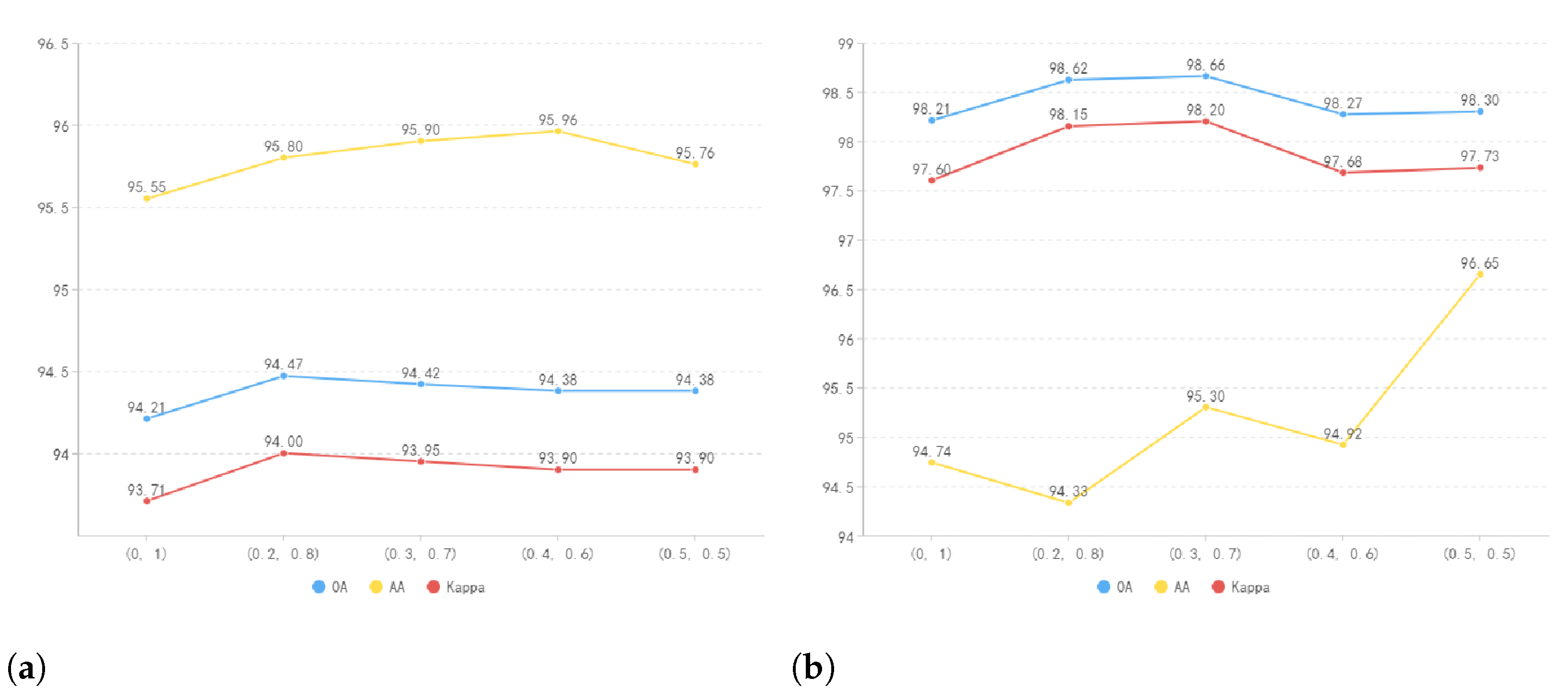
4.1.3. Graphs Comparing BFST Accuracy with Varying Weight Coefficients
4.2. Ablation Experiments
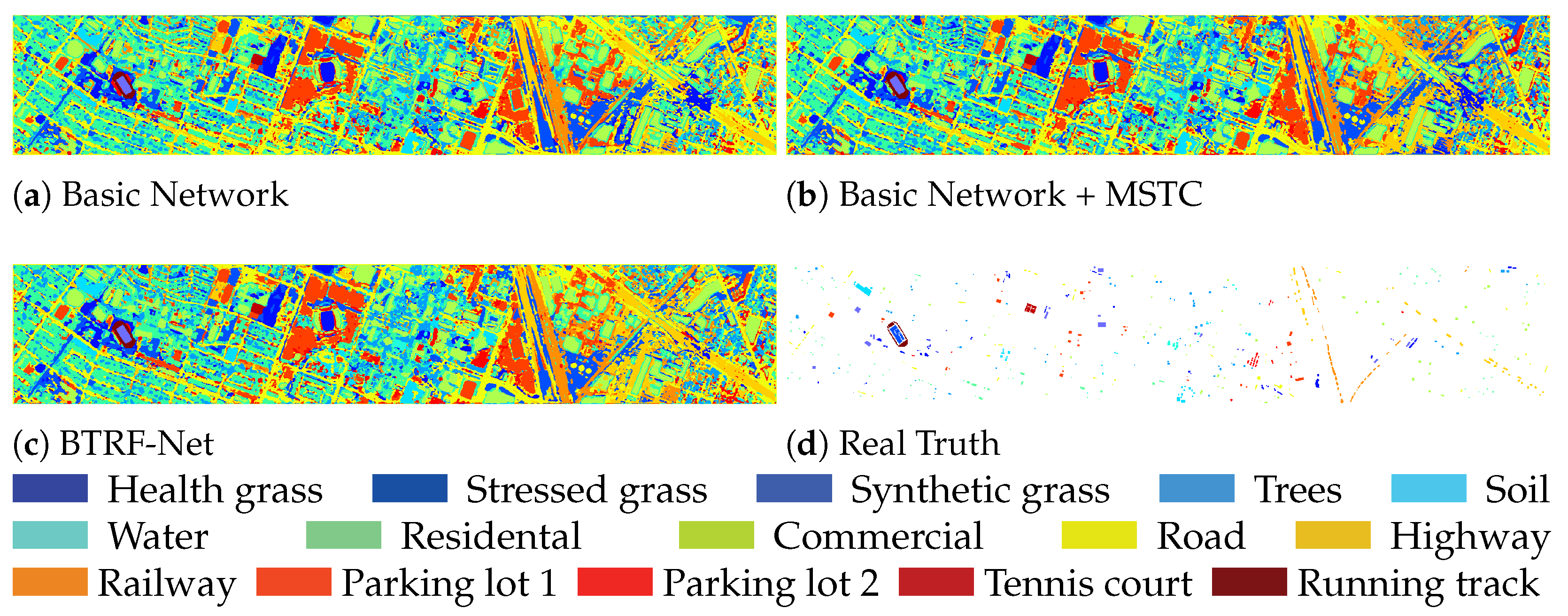
4.2.1. Ablation Experiments of the Multi-Source Transformer Complementor
4.2.2. Ablation Experiments of the Binary Feature Search Tree
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Masser, I. Managing our urban future: The role of remote sensing and geographic information systems. Habit. Int. 2001, 25, 503–512. [Google Scholar] [CrossRef]
- Maes, W.H.; Steppe, K. Estimating evapotranspiration and drought stress with ground-based thermal remote sensing in agriculture: A review. J. Exp. Bot. 2012, 63, 4671–4712. [Google Scholar] [CrossRef] [PubMed]
- Fan, J.; Zhang, X.; Su, F.; Ge, Y.; Tarolli, P.; Yang, Z.; Zeng, C.; Zeng, Z. Geometrical feature analysis and disaster assessment of the Xinmo landslide based on remote sensing data. J. Mount. Sci. 2017, 14, 1677–1688. [Google Scholar] [CrossRef]
- Ghosh, P.; Roy, S.K.; Koirala, B.; Rasti, B.; Scheunders, P. Deep hyperspectral unmixing using transformer network. arXiv 2022, arXiv:2203.17076. [Google Scholar]
- Pham, H.M.; Yamaguchi, Y.; Bui, T.Q. A case study on the relation between city planning and urban growth using remote sensing and spatial metrics. Landsc. Urban Plan. 2011, 100, 223–230. [Google Scholar] [CrossRef]
- Carfagna, E.; Gallego, F.J. Using remote sensing for agricultural statistics. Int. Stat. Rev. 2005, 73, 389–404. [Google Scholar] [CrossRef]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. HybridSN: Exploring 3-D–2-D CNN feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Gabor-filtering-based nearest regularized subspace for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 1012–1022. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral image classification using dictionary-based sparse representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Benediktsson, J.A.; Palmason, J.A.; Sveinsson, J.R. Classification of hyperspectral data from urban areas based on extended morphological profiles. IEEE Trans. Geosci. Remote Sens. 2005, 43, 480–491. [Google Scholar] [CrossRef]
- Gowen, A.A.; O’Donnell, C.P.; Cullen, P.J.; Downey, G.; Frias, J.M. Hyperspectral imaging–an emerging process analytical tool for food quality and safety control. Trends Food Sci. Technol. 2007, 18, 590–598. [Google Scholar] [CrossRef]
- Stuffler, T.; Förster, K.; Hofer, S.; Leipold, M.; Sang, B.; Kaufmann, H.; Penn, B.; Mueller, A.; Chlebek, C. Hyperspectral imaging—An advanced instrument concept for the EnMAP mission (Environmental Mapping and Analysis Programme). Acta Astronaut. 2009, 65, 1107–1112. [Google Scholar] [CrossRef]
- Plaza, A.; Du, Q.; Chang, Y.L.; King, R.L. High performance computing for hyperspectral remote sensing. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2011, 4, 528–544. [Google Scholar] [CrossRef]
- Roy, S.K.; Deria, A.; Hong, D.; Ahmad, M.; Plaza, A.; Chanussot, J. Hyperspectral and LiDAR data classification using joint CNNs and morphological feature learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Plaza, J.; Plaza, A. Fusion of hyperspectral and LiDAR data using sparse and low-rank component analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 6354–6365. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, X.; Ning, X. SVM-based classification of segmented airborne LiDAR point clouds in urban areas. Remote Sens. 2013, 5, 3749–3775. [Google Scholar] [CrossRef]
- Xu, T.; Gao, X.; Yang, Y.; Xu, L.; Xu, J.; Wang, Y. Construction of a Semantic Segmentation Network for the Overhead Catenary System Point Cloud Based on Multi-Scale Feature Fusion. Remote Sens. 2022, 14, 2768. [Google Scholar] [CrossRef]
- Chen, Y.; Li, C.; Ghamisi, P.; Shi, C.; Gu, Y. Deep fusion of hyperspectral and LiDAR data for thematic classification. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), IEEE, Beijing, China, 10–15 July 2016; pp. 3591–3594. [Google Scholar]
- Tomljenovic, I.; Höfle, B.; Tiede, D.; Blaschke, T. Building extraction from airborne laser scanning data: An analysis of the state of the art. Remote Sens. 2015, 7, 3826. [Google Scholar] [CrossRef]
- Zhang, M.; Ghamisi, P.; Li, W. Classification of hyperspectral and LiDAR data using extinction profiles with feature fusion. Remote Sens. Lett. 2017, 8, 957–966. [Google Scholar] [CrossRef]
- Ghamisi, P.; Rasti, B.; Yokoya, N.; Wang, Q.; Hofle, B.; Bruzzone, L.; Bovolo, F.; Chi, M.; Anders, K.; Gloaguen, R.; et al. Multisource and multitemporal data fusion in remote sensing: A comprehensive review of the state of the art. IEEE Geosci. Remote Sens. Mag. 2019, 7, 6–39. [Google Scholar] [CrossRef]
- Hang, R.; Li, Z.; Ghamisi, P.; Hong, D.; Xia, G.; Liu, Q. Classification of hyperspectral and LiDAR data using coupled CNNs. IEEE Trans. Geosci. Remote Sens. 2020, 58, 4939–4950. [Google Scholar] [CrossRef]
- Debes, C.; Merentitis, A.; Heremans, R.; Hahn, J.; Frangiadakis, N.; van Kasteren, T.; Liao, W.; Bellens, R.; Piurica, A.; Gautama, S.; et al. Hyperspectral and LiDAR data fusion: Outcome of the 2013 GRSS data fusion contest. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2014, 7, 2405–2418. [Google Scholar] [CrossRef]
- Pohl, C.; Van Genderen, J.L. Review article multisensor image fusion in remote sensing: Concepts, methods and applications. Int. J. Remote Sens. 1998, 19, 823–854. [Google Scholar] [CrossRef]
- Pedergnana, M.; Marpu, P.R.; Dalla Mura, M.; Dalla Mura, M.; Benediktsson, J.A.; Bruzzone, L. Classification of remote sensing optical and LiDAR data using extended attribute profiles. IEEE J. Sel. Top. Signal Process. 2012, 6, 856–865. [Google Scholar] [CrossRef]
- Réjichi, S.; Chaabane, F. Feature extraction using PCA for VHR satellite image time series spatio-temporal classification. In Proceedings of the 2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), IEEE, Milan, Italy, 26–31 July 2015; pp. 485–488. [Google Scholar]
- Liao, W.; Pižurica, A.; Bellens, R.; Gautama, S.; Philips, W. Generalized graph-based fusion of hyperspectral and LiDAR data using morphological features. IEEE Geosci. Remote Sens. Lett. 2014, 12, 552–556. [Google Scholar] [CrossRef]
- Rasti, B.; Ghamisi, P.; Gloaguen, R. Hyperspectral and LiDAR fusion using extinction profiles and total variation component analysis. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3997–4007. [Google Scholar] [CrossRef]
- Liao, W.; Bellens, R.; Pižurica, A.; Gautama, S.; Philips, W. Combining feature fusion and decision fusion for classification of hyperspectral and LiDAR data. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, IEEE, Quebec City, QC, Canada, 13–18 July 2014; pp. 1241–1244. [Google Scholar]
- Hearst, M.A.; Dumais, S.T.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Ge, C.; Du, Q.; Li, W.; Li, Y.; Sun, W. Hyperspectral and LiDAR data classification using kernel collaborative representation based residual fusion. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2019, 12, 1963–1973. [Google Scholar] [CrossRef]
- Zhong, Y.; Cao, Q.; Zhao, J.; Ma, A.; Zhao, B.; Zhang, L. Optimal decision fusion for urban land-use/land-cover classification based on adaptive differential evolution using hyperspectral and LiDAR data. Remote Sens. 2017, 9, 868. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Xu, Y.; Du, B.; Zhang, L. Multi-source remote sensing data classification via fully convolutional networks and post-classification processing. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, IEEE, Valencia, Spain, 22–27 July 2018; pp. 3852–3855. [Google Scholar]
- Zhang, M.; Li, W.; Du, Q.; Gao, L.; Zhang, B. Feature extraction for classification of hyperspectral and LiDAR data using patch-to-patch CNN. IEEE Trans. Cybern. 2018, 50, 100–111. [Google Scholar] [CrossRef] [PubMed]
- Mohla, S.; Pande, S.; Banerjee, B.; Chaudhuri, S. Fusatnet: Dual attention based spectrospatial multimodal fusion network for hyperspectral and lidar classification. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops, Seattle, WA, USA, 13–19 June 2020; pp. 92–93. [Google Scholar]
- Cao, X.; Zhou, F.; Xu, L.; Meng, D.; Xu, Z.; Paisley, J. Hyperspectral image classification with Markov random fields and a convolutional neural network. IEEE Trans. Image Process. 2018, 27, 2354–2367. [Google Scholar] [CrossRef] [PubMed]
- Hong, D.; Gao, L.; Hang, R.; Zhang, B.; Chanussot, J. Deep encoder–decoder networks for classification of hyperspectral and LiDAR data. IEEE Geosci. Remote Sens. Lett. 2020, 19, 1–5. [Google Scholar] [CrossRef]
- Wu, H.; Prasad, S. Convolutional recurrent neural networks for hyperspectral data classification. Remote Sens. 2017, 9, 298. [Google Scholar] [CrossRef]
- Hu, R.; Singh, A. Unit: Multimodal multitask learning with a unified transformer. In Proceedings of the IEEE/CVF International Conference on Computer Vision, Montreal, BC, Canada, 11–17 October 2021; pp. 1439–1449. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, U.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 5998–6008. [Google Scholar]
- Zhang, G.; Gao, X.; Yang, Y.; Wang, M.; Ran, S. Controllably deep supervision and multi-scale feature fusion network for cloud and snow detection based on medium-and high-resolution imagery dataset. Remote Sens. 2021, 13, 4805. [Google Scholar] [CrossRef]
- Khodadadzadeh, M.; Li, J.; Prasad, S.; Plaza, A. Fusion of hyperspectral and LiDAR remote sensing data using multiple feature learning. IEEE J. Sel. Top. Appl. Earth Observ. Remote Sens. 2015, 8, 2971–2983. [Google Scholar] [CrossRef]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: Theory and applications. Neurocomputing 2006, 70, 489–501. [Google Scholar] [CrossRef]
- Li, W.; Wu, G.; Zhang, F.; Du, Q. Hyperspectral image classification using deep pixel-pair features. IEEE Trans. Geosci. Remote Sens. 2016, 55, 844–853. [Google Scholar] [CrossRef]
- Lee, H.; Kwon, H. Going deeper with contextual CNN for hyperspectral image classification. IEEE Trans. Image Process. 2017, 26, 4843–4855. [Google Scholar] [CrossRef]
- Xu, X.; Li, W.; Ran, Q.; Du, Q.; Gao, L.; Zhang, B. Multisource remote sensing data classification based on convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2017, 56, 937–949. [Google Scholar] [CrossRef]
- Zhang, M.; Li, W.; Tao, R.; Li, H.; Du, Q. Information fusion for classification of hyperspectral and LiDAR data using IP-CNN. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.-L.; Zhao, X.-F.; Cai, W.; He, F.; Cai, Y.-M.; Cai, W.-W. Deep hybrid: Multi-graph neural network collaboration for hyperspectral image classification. Def. Technol. 2023, 23, 164–176. [Google Scholar]
- Ding, Y.; Zhang, Z.; Zhao, X.; Hong, D.; Li, W.; Cai, W.; Zhan, Y. AF2GNN: Graph convolution with adaptive filters and aggregator fusion for hyperspectral image classification. Inf. Sci. 2022, 602, 201–219. [Google Scholar] [CrossRef]
- Ding, Y.; Zhang, Z.; Zhao, X.; Cai, W.; Yang, N.; Hu, H.; Huang, X.; Cao, Y.; Cai, W. Unsupervised self-correlated learning smoothy enhanced locality preserving graph convolution embedding clustering for hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N.; Zhan, Y. Semi-supervised locality preserving dense graph neural network with ARMA filters and context-aware learning for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2021, 60, 1–12. [Google Scholar] [CrossRef]
- Ding, Y.; Zhao, X.; Zhang, Z.; Cai, W.; Yang, N. Graph sample and aggregate-attention network for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2021, 19, 1–5. [Google Scholar] [CrossRef]
- Fang, S.; Li, K.; Li, Z. S²ENet: Spatial–spectral cross-modal enhancement network for classification of hyperspectral and LiDAR data. IEEE Geosci. Remote Sens. Lett. 2022, 19, 1–5. [Google Scholar]
- Wang, N.; Li, W.; Tao, R.; Du, Q. Graph-based block-level urban change detection using Sentinel-2 time series. Remote Sens. Environ. 2022, 274, 112993. [Google Scholar] [CrossRef]
- Ran, S.; Gao, X.; Yang, Y.; Li, S.; Zhang, G.; Wang, P. Building multi-feature fusion refined network for building extraction from high-resolution remote sensing images. Remote Sens. 2021, 13, 2794. [Google Scholar] [CrossRef]



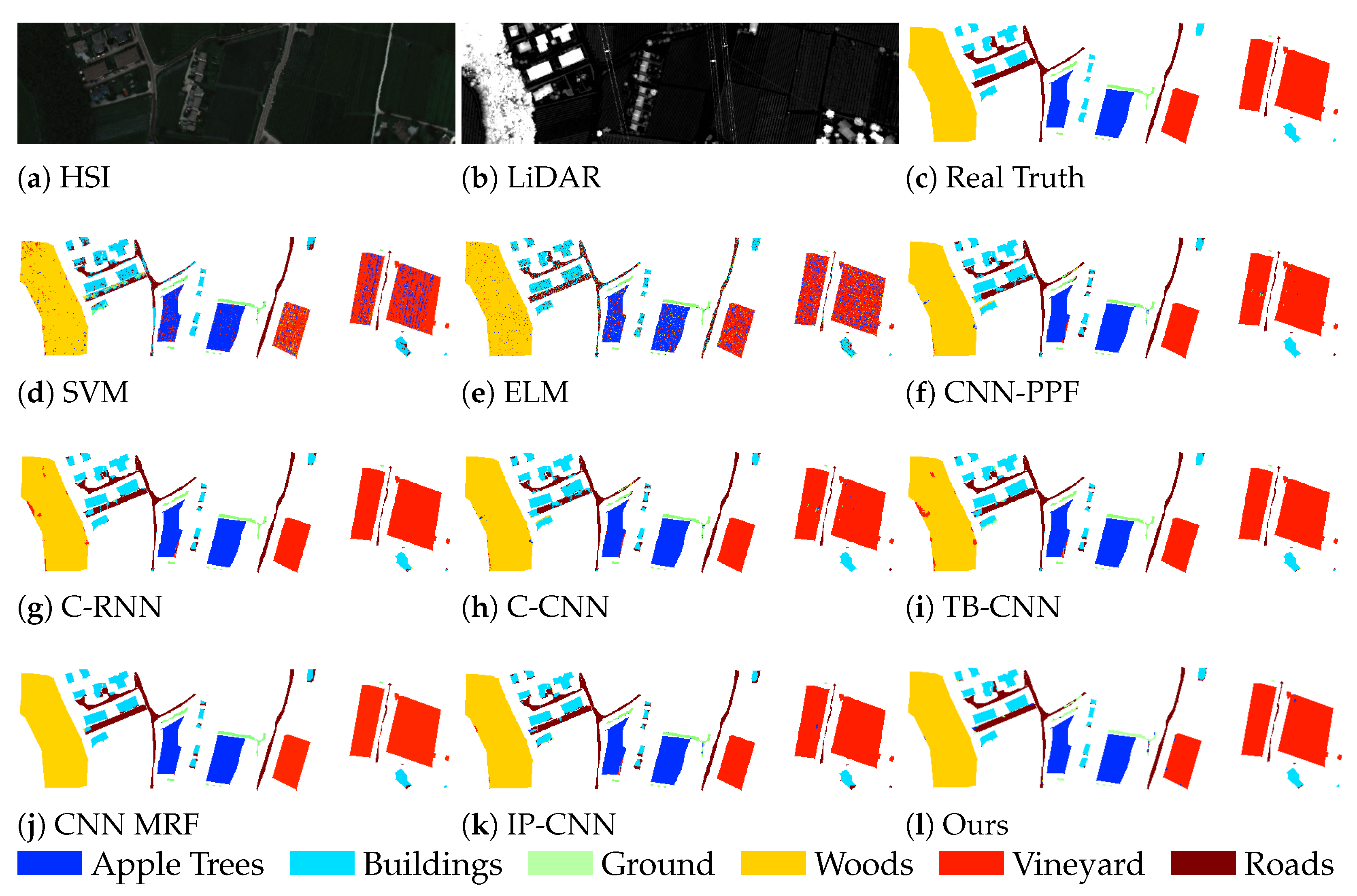
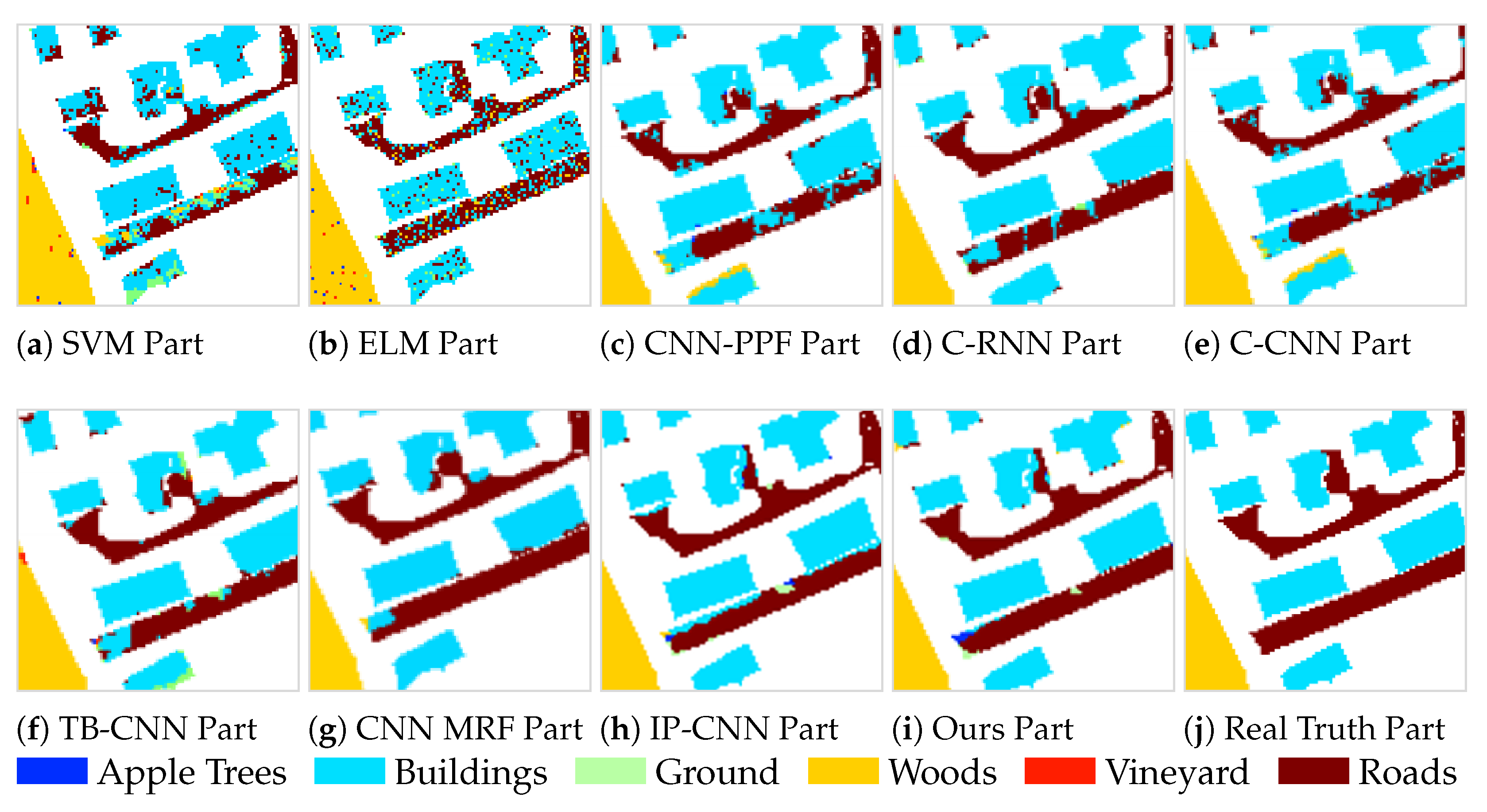


| Class | SVM | ELM | CNN-PPF | C-RNN | C-CNN | TB-CNN | CNN-MRF | IP-CNN | Ours |
|---|---|---|---|---|---|---|---|---|---|
| Healthy grass | 82.43 | 83.10 | 83.57 | 83.00 | 84.89 | 83.10 | 85.77 | 85.77 | 96.88 |
| Stressed grass | 82.05 | 83.70 | 98.21 | 79.41 | 87.40 | 81.20 | 86.28 | 87.34 | 88.57 |
| Synthetic grass | 99.80 | 100.00 | 98.42 | 99.80 | 99.86 | 100.00 | 99.00 | 100.00 | 100.00 |
| Trees | 92.80 | 91.86 | 97.73 | 90.15 | 93.49 | 92.90 | 92.85 | 94.26 | 94.92 |
| Soil | 98.48 | 98.86 | 96.50 | 99.71 | 100.00 | 99.81 | 100.00 | 98.42 | 98.10 |
| Water | 95.10 | 95.10 | 97.20 | 83.21 | 98.77 | 100.00 | 98.15 | 99.91 | 99.15 |
| Residential | 75.47 | 80.04 | 85.82 | 88.06 | 82.81 | 92.54 | 91.64 | 94.59 | 93.33 |
| Commercial | 46.91 | 68.47 | 56.51 | 88.61 | 78.78 | 94.87 | 80.79 | 91.81 | 94.96 |
| Road | 77.53 | 84.80 | 71.20 | 66.01 | 82.51 | 83.85 | 91.37 | 89.35 | 94.03 |
| Highway | 60.04 | 49.13 | 57.12 | 52.22 | 59.41 | 69.89 | 73.35 | 72.43 | 90.18 |
| Railway | 81.02 | 80.27 | 80.55 | 81.97 | 83.24 | 86.15 | 98.87 | 96.57 | 93.11 |
| Parking Lot 1 | 85.49 | 79.06 | 62.82 | 69.83 | 92.13 | 92.60 | 89.38 | 95.60 | 95.51 |
| Parking Lot 2 | 75.09 | 71.58 | 63.86 | 79.64 | 94.88 | 79.30 | 92.75 | 94.37 | 98.71 |
| Tennis Court | 100.00 | 99.60 | 100.00 | 100.00 | 99.77 | 100.00 | 100.00 | 99.86 | 100.00 |
| Running Track | 98.31 | 98.52 | 98.10 | 100.00 | 98.79 | 100.00 | 100.00 | 99.99 | 99.58 |
| OA (%) | 80.49 | 81.29 | 83.33 | 88.55 | 86.90 | 88.91 | 90.61 | 92.06 | 94.47 |
| AA (%) | 83.37 | 84.27 | 83.21 | 90.30 | 89.11 | 90.42 | 92.01 | 93.35 | 95.80 |
| KAPPA (%) | 78.98 | 80.45 | 81.88 | 87.56 | 85.89 | 87.96 | 89.87 | 91.42 | 94.00 |
| Class | SVM | ELM | CNN-PPF | C-RNN | C-CNN | TB-CNN | CNN MRF | IP-CNN | Ours |
|---|---|---|---|---|---|---|---|---|---|
| Apple trees | 88.62 | 92.17 | 90.11 | 98.39 | 93.53 | 98.04 | 99.95 | 99.00 | 95.92 |
| Buildings | 94.04 | 90.91 | 83.34 | 90.46 | 91.97 | 94.56 | 89.97 | 99.40 | 98.04 |
| Ground | 93.53 | 94.36 | 71.13 | 99.79 | 98.33 | 94.36 | 98.33 | 99.10 | 80.33 |
| Woods | 98.90 | 97.12 | 99.04 | 96.96 | 96.50 | 96.57 | 100.00 | 99.92 | 99.83 |
| Vineyard | 88.96 | 78.58 | 99.37 | 100.00 | 98.49 | 99.62 | 100.00 | 99.66 | 99.92 |
| Roads | 91.75 | 63.23 | 89.73 | 81.63 | 71.24 | 74.47 | 97.86 | 90.21 | 97.66 |
| OA (%) | 92.77 | 85.81 | 94.76 | 97.30 | 93.73 | 96.44 | 98.40 | 98.58 | 98.66 |
| AA (%) | 92.63 | 86.06 | 88.97 | 94.54 | 94.23 | 92.94 | 97.04 | 97.88 | 95.30 |
| KAPPA (%) | 95.85 | 81.36 | 93.04 | 96.39 | 93.70 | 95.26 | 97.86 | 98.17 | 98.20 |
| Basic Network | Basic Network + MSTC | BTRF-Net | |
|---|---|---|---|
| OA | 91.60 | 93.54 | 94.47 |
| AA | 93.67 | 94.86 | 95.80 |
| Kappa | 90.88 | 92.98 | 94.00 |
| Basic Network | Basic Network + MSTC | BTRF-Net | |
|---|---|---|---|
| OA | 96.81 | 98.03 | 98.66 |
| AA | 89.68 | 93.37 | 95.30 |
| Kappa | 95.74 | 97.35 | 98.20 |
| Basic Network | Basic Network + BFST | BTRF-Net | |
|---|---|---|---|
| OA | 91.60 | 93.65 | 94.47 |
| AA | 93.67 | 95.01 | 95.80 |
| Kappa | 90.88 | 93.10 | 94.00 |
| Basic Network | Basic Network + BFST | BTRF-Net | |
|---|---|---|---|
| OA | 96.81 | 98.08 | 98.66 |
| AA | 89.68 | 92.51 | 95.30 |
| Kappa | 95.74 | 97.43 | 98.20 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, H.; Yang, Y.; Gao, X.; Zhang, M.; Li, S.; Liu, B.; Wang, Y.; Kou, Y. Joint Classification of Hyperspectral and LiDAR Data Using Binary-Tree Transformer Network. Remote Sens. 2023, 15, 2706. https://doi.org/10.3390/rs15112706
Song H, Yang Y, Gao X, Zhang M, Li S, Liu B, Wang Y, Kou Y. Joint Classification of Hyperspectral and LiDAR Data Using Binary-Tree Transformer Network. Remote Sensing. 2023; 15(11):2706. https://doi.org/10.3390/rs15112706
Chicago/Turabian StyleSong, Huacui, Yuanwei Yang, Xianjun Gao, Maqun Zhang, Shaohua Li, Bo Liu, Yanjun Wang, and Yuan Kou. 2023. "Joint Classification of Hyperspectral and LiDAR Data Using Binary-Tree Transformer Network" Remote Sensing 15, no. 11: 2706. https://doi.org/10.3390/rs15112706
APA StyleSong, H., Yang, Y., Gao, X., Zhang, M., Li, S., Liu, B., Wang, Y., & Kou, Y. (2023). Joint Classification of Hyperspectral and LiDAR Data Using Binary-Tree Transformer Network. Remote Sensing, 15(11), 2706. https://doi.org/10.3390/rs15112706






