A Deep-Learning Scheme for Hydrometeor Type Classification Using Passive Microwave Observations
Abstract
1. Introduction
2. Instruments and Data
2.1. Input Feature
2.2. Ground Truth
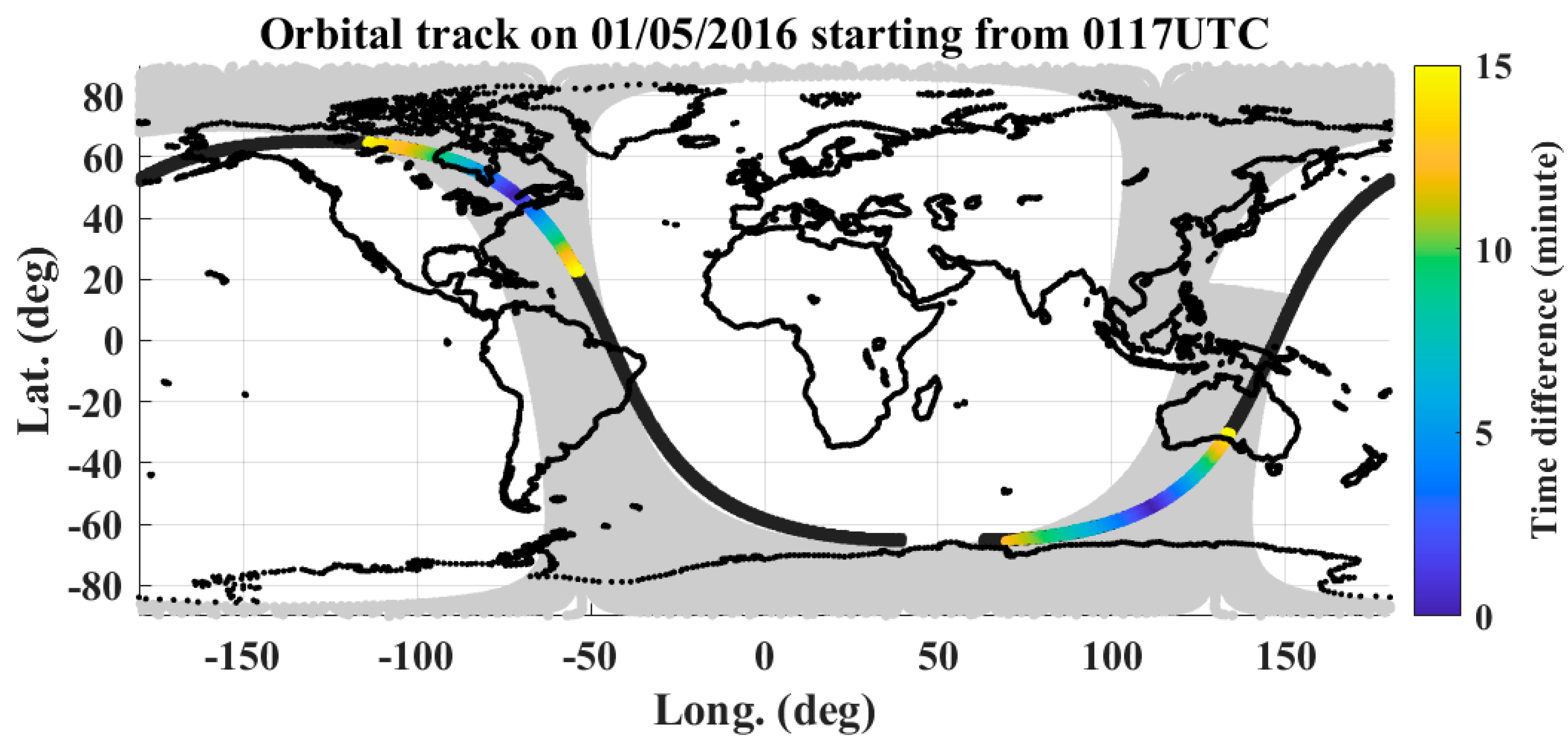
2.3. Collocated and Coincidental Measurements
2.4. Bias Correction
2.5. Data Sub-Setting
3. ResNet-18 Network by Attention Mechanism
3.1. Model Configuration
3.2. Convolutional Embedding Layer
3.3. Bottleneck Residual Block
3.4. Attention Mechanism
3.5. Precipitation Generator
4. Experimental Setting and Results
4.1. Model Training
4.2. Model Validation
5. Conclusions
- (1)
- Utilizing CNN in conjunction with the attention mechanism to learn meaningful feature representations from spatial and temporal dimension space of passive microwave observations for hydrometeor classification;
- (2)
- Exploiting the information content of passive microwave observations for the purpose of hydrometeor classification with the unprecedented inclusion of 118 GHz channels.
Discussions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rosenfeld, D.; Lohmann, U.; Raga, G.B.; O’Dowd, C.D.; Kulmala, M.; Fuzzi, S.; Reissell, A.; Andreae, M.O. Flood or Drought: How Do Aerosols Affect Precipitation? Science 2008, 321, 1309–1313. [Google Scholar] [CrossRef] [PubMed]
- Trenberth, K.E.; Dai, A.; Rasmussen, R.M.; Parsons, D.B. The Changing Character Of Precipitation. Bull. Am. Meteorol. Soc. 2003, 84, 1205–1217. [Google Scholar] [CrossRef]
- Atlas, D.; Ulbrich, C.W. Path- and Area-Integrated Rainfall Measurement by Microwave Attenuation in the 1–3 cm Band. J. Appl. Meteorol. Climatol. 1977, 16, 1322–1331. [Google Scholar] [CrossRef]
- Crow, W.T.; Bolten, J.D. Estimating Precipitation Errors Using Spaceborne Surface Soil Moisture Retrievals. Geophys. Res. Lett. 2007, 34, L08403. [Google Scholar] [CrossRef]
- Shrestha, B.; Cochrane, T.A.; Caruso, B.S.; Arias, M.E.; Wild, T.B. Sediment Management for Reservoir Sustainability and Cost Implications Under Land Use/Land Cover Change Uncertainty. Water Resour. Res. 2021, 57, e2020WR02835. [Google Scholar] [CrossRef]
- Tuttle, S.; Salvucci, G. Empirical evidence of contrasting soil moisture-precipitation feedbacks across the United States. Science 2016, 352, 825–828. [Google Scholar] [CrossRef]
- Allen, M.R.; Ingram, W.J. Constraints on Future Changes in Climate and the Hydrologic Cycle. Nature 2002, 419, 228–232. [Google Scholar] [CrossRef]
- Gherardi, L.A.; Sala, O.E. Enhanced Interannual Precipitation Variability Increases Plant Functional Diversity that in Turn Ameliorates Negative Impact on Productivity. Ecol. Lett. 2015, 18, 1293–1300. [Google Scholar] [CrossRef]
- Donat, M.G.; Alexander, L.V.; Herold, N.; Dittus, A.J. Temperature and Precipitation Extremes in Century-long Gridded Observations, Reanalyses, and Atmospheric Model Simulations. J. Geophys. Res. Atmos. 2016, 121, 11174–11189. [Google Scholar] [CrossRef]
- Samantaray, A.K.; Ramadas, M.; Panda, R.K. Changes in Drought Characteristics Based on Rainfall Pattern Drought Index and the CMIP6 Multi-model Ensemble. Agric. Water Manag. 2022, 266, 107568. [Google Scholar] [CrossRef]
- Sloat, L.L.; Gerber, J.S.; Samberg, L.H.; Smith, W.K.; Herrero, M.; Ferreira, L.G.; Godde, C.M.; West, P.C. Increasing Importance of Precipitation Variability on Global Livestock Grazing Lands. Nat. Clim. Change 2018, 8, 214–218. [Google Scholar] [CrossRef]
- Hunsaker, C.T.; Whitaker, T.W.; Bales, R.C. Snowmelt Runoff and Water Yield Along Elevation and Temperature Gradients in California’s Southern Sierra Nevada1. JAWRA J. Am. Water Resour. Assoc. 2012, 48, 667–678. [Google Scholar] [CrossRef]
- Behrangi, A.; Yin, X.; Rajagopal, S.; Stampoulis, D.; Ye, H. On Distinguishing Snowfall from Rainfall using Near-surface Atmospheric Information: Comparative Analysis, Uncertainties and Uydrologic Importance. Q. J. R. Meteorol. Soc. 2018, 144, 89–102. [Google Scholar] [CrossRef]
- Box, J.E.; Wehrlé, A.; van As, D.; Fausto, R.S.; Kjeldsen, K.K.; Dachauer, A.; Ahlstrøm, A.P.; Picard, G. Greenland Ice Sheet Rainfall, Heat and Albedo Feedback Impacts From the Mid-August 2021 Atmospheric River. Geophys. Res. Lett. 2022, 49, e2021GL097356. [Google Scholar] [CrossRef]
- Loth, B.; Graf, H.-F.; Oberhuber, J.M. Snow Cover Model for Global Cimate Simulations. J. Geophys. Res. Atmos. 1993, 98, 10451–10464. [Google Scholar] [CrossRef]
- Dai, A. Temperature and Pressure Dependence of the Rain-snow Phase Transition over Land and Ocean. Geophys. Res. Lett. 2008, 35, L12802. [Google Scholar] [CrossRef]
- Slater, A.G.; Schlosser, C.A.; Desborough, C.E.; Pitman, A.J.; Henderson-Sellers, A.; Robock, A.; Vinnikov, K.Y.; Entin, J.; Mitchell, K.; Chen, F.; et al. The Representation of Snow in Land Surface Schemes: Results from PILPS 2(d). J. Hydrometeorol. 2001, 2, 7–25. [Google Scholar] [CrossRef]
- Vivekanandan, J.; Zrnic, D.S.; Ellis, S.M.; Oye, R.; Ryzhkov, A.V.; Straka, J. Cloud Microphysics Retrieval Using S-Band Dual-Polarization Radar Measurements. Bull. Am. Meteorol. Soc. 1999, 80, 381–388. [Google Scholar] [CrossRef]
- Liu, H.; Chandrasekar, V. Classification of Hydrometeors Based on Polarimetric Radar Measurements: Development of Fuzzy Logic and Neuro-Fuzzy Systems, and In Situ Verification. J. Atmos. Ocean. Technol. 2000, 17, 140–164. [Google Scholar] [CrossRef]
- Lim, S.; Chandrasekar, V.; Bringi, V.N. Hydrometeor Classification System using Dual-polarization Radar Measurements: Model Improvements and In Situ Verification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 792–801. [Google Scholar] [CrossRef]
- Ryzhkov, A.V.; Schuur, T.J.; Burgess, D.W.; Heinselman, P.L.; Giangrande, S.E.; Zrnic, D.S. The Joint Polarization Experiment: Polarimetric Rainfall Measurements and Hydrometeor Classification. Bull. Am. Meteorol. Soc. 2005, 86, 809–824. [Google Scholar] [CrossRef]
- Park, H.S.; Ryzhkov, A.V.; Zrnić, D.S.; Kim, K.-E. The Hydrometeor Classification Algorithm for the Polarimetric WSR-88D: Description and Application to an MCS. Weather Forecast. 2009, 24, 730–748. [Google Scholar] [CrossRef]
- Scharfenberg, K.A.; Miller, D.J.; Schuur, T.J.; Schlatter, P.T.; Giangrande, S.E.; Melnikov, V.M.; Burgess, D.W.; Andra, D.L.; Foster, M.P.; Krause, J.M. The Joint Polarization Experiment: Polarimetric Radar in Forecasting and Warning Decision Making. Weather Forecast. 2005, 20, 775–788. [Google Scholar] [CrossRef]
- Yang, J.; Zhao, K.; Zhang, G.; Chen, G.; Huang, H.; Chen, H. A Bayesian Hydrometeor Classification Algorithm for C-Band Polarimetric Radar. Remote Sens. 2019, 11, 1884. [Google Scholar] [CrossRef]
- Lukach, M.; Dufton, D.; Crosier, J.; Hampton, J.M.; Bennett, L.; Neely, R.R., III. Hydrometeor Classification of Quasi-Vertical Profiles of Polarimetric Radar Measurements Using a Top-down Iterative Hierarchical Clustering Method. Atmos. Meas. Tech. 2021, 14, 1075–1098. [Google Scholar] [CrossRef]
- Dolant, C.; Langlois, A.; Montpetit, B.; Brucker, L.; Roy, A.; Royer, A. Development of a Rain-on-snow detection Algorithm Using Passive Microwave Radiometry. Hydrol. Process. 2016, 30, 3184–3196. [Google Scholar] [CrossRef]
- Bennartz, R.; Petty, G.W. The Sensitivity of Microwave Remote Sensing Observations of Precipitation to Ice Particle Size Distributions. J. Appl. Meteorol. Climatol. 2001, 40, 345–364. [Google Scholar] [CrossRef]
- Petty, G.W.; Li, K. Improved Passive Microwave Retrievals of Rain Rate over Land and Ocean. Part I: Algorithm Description. J. Atmos. Ocean. Technol. 2013, 30, 2493–2508. [Google Scholar] [CrossRef]
- Skofronick-Jackson, G.M.; Wang, J.R. The Estimation of Hydrometeor Profiles from Wideband Microwave Observations. J. Appl. Meteorol. Climatol. 2000, 39, 1645–1656. [Google Scholar] [CrossRef]
- Wilheit, T.T. Some Comments on Passive Microwave Measurement of Rain. Bull. Am. Meteorol. Soc. 1986, 67, 1226–1232. [Google Scholar] [CrossRef]
- Kedem, B.; Chiu, L.S.; North, G.R. Estimation of Mean Rain Rate: Application to Satellite Observations. J. Geophys. Res. Atmos. 1990, 95, 1965–1972. [Google Scholar] [CrossRef]
- Klaes, K.D.; Cohen, M.; Buhler, Y.; Schlussel, P.; Munro, R.; Luntama, J.P.; von Engelin, A.; Clerigh, E.O.; Bonekamp, H.; Ackermann, J.; et al. An Introduction to the EUMETSAT Polar System. Bull. Am. Meteorol. Soc. 2007, 88, 1085–1096. [Google Scholar] [CrossRef]
- Leppert, K.D.; Cecil, D.J. Signatures of Hydrometeor Species from Airborne Passive Microwave Data for Frequencies 10–183 GHz. J. Appl. Meteorol. Climatol. 2015, 54, 1313–1334. [Google Scholar] [CrossRef]
- Chen, R.; Bennartz, R. Rainfall Algorithms Using Oceanic Satellite Observations from MWHS-2. Adv. Atmos. Sci. 2021, 38, 1367–1378. [Google Scholar] [CrossRef]
- Chen, R.; Bennartz, R. Sensitivity of 89–190-GHz Microwave Observations to Ice Particle Scattering. J. Appl. Meteorol. Climatol. 2020, 59, 1195–1215. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A Logical Calculus of the Ideas Immanent in Nervous Activity. Bull. Math. Biophys. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Qiao, B.; Wu, Z.; Ma, L.; Zhou, Y.; Sun, Y. Effective Ensemble Learning Approach for SST Field Prediction Using Attention-based PredRNN. Front. Comput. Sci. 2022, 17, 171601. [Google Scholar] [CrossRef]
- Sadeghi, M.; Asanjan, A.A.; Faridzad, M.; Nguyen, P.; Hsu, K.; Sorooshian, S.; Braithwaite, D. PERSIANN-CNN: Precipitation Estimation from Remotely Sensed Information Using Artificial Neural Networks–Convolutional Neural Networks. J. Hydrometeorol. 2019, 20, 2273–2289. [Google Scholar] [CrossRef]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Iecognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 26 June–1 July 2016; pp. 770–778. [Google Scholar]
- Blackwell, W.J.; Braun, S.; Bennartz, R.; Velden, C.; DeMaria, M.; Atlas, R.; Dunion, J.; Marks, F.; Rogers, R.; Annane, B.; et al. An Overview of the TROPICS NASA Earth Venture Mission. Q. J. R. Meteorol. Soc. 2018, 144, 16–26. [Google Scholar] [CrossRef]
- Hou, A.Y.; Kakar, R.K.; Neeck, S.; Azarbarzin, A.A.; Kummerow, C.D.; Kojima, M.; Oki, R.; Nakamura, K.; Iguchi, T. The Global Precipitation Measurement Mission. Bull. Am. Meteorol. Soc. 2014, 95, 701–722. [Google Scholar] [CrossRef]
- Bennartz, R.; Bauer, P. Sensitivity of Microwave Radiances at 85-183 GHz to Precipitating Ice Particles. Radio Sci. 2003, 38, 8075. [Google Scholar] [CrossRef]
- Zhang, H.; Wu, C.; Zhang, Z.; Zhu, Y.; Lin, H.; Zhang, Z.; Sun, Y.; He, T.; Mueller, J.; Manmatha, R. Resnest: Split-Attention Networks. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, New Orleans, LA, USA, 18–24 June 2022; pp. 2736–2746. [Google Scholar]
- Chen, J.; Lu, Y.; Yu, Q.; Luo, X.; Adeli, E.; Wang, Y.; Lu, L.; Yuille, A.L.; Zhou, Y. Transunet: Transformers Make Strong Encoders For Medical Image Segmentation. arXiv 2021, arXiv:2102.04306. [Google Scholar]
- Srinivas, A.; Lin, T.-Y.; Parmar, N.; Shlens, J.; Abbeel, P.; Vaswani, A. Bottleneck Transformers For Visual Recognition. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Montreal, Canada, 11–17 October 2021; pp. 16519–16529. [Google Scholar]
- Li, Y.; Yao, T.; Pan, Y.; Mei, T. Contextual Transformer Networks For Visual Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 2022, 45, 1489–1500. [Google Scholar] [CrossRef] [PubMed]
- Prechelt, L. Early Stopping-but When? In Neural Networks: Tricks of the Trade; Springer: Berlin/Heidelberg, Germany, 1998; pp. 55–69. [Google Scholar]
- Paszke, A.; Gross, S.; Massa, F.; Lerer, A.; Bradbury, J.; Chanan, G.; Killeen, T.; Lin, Z.; Gimelshein, N.; Antiga, L. Pytorch: An Imperative Style, High-Performance Deep Learning Library. Adv. Neural Inf. Process. Syst. 2019, 32, 8026–8037. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A Method For Stochastic Optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Ioffe, S.; Szegedy, C. Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift. In Proceedings of the International Conference on Machine Learning, Lille, France, 6–11 July 2015; pp. 448–456. [Google Scholar]
- Xu, B.; Wang, N.; Chen, T.; Li, M. Empirical Evaluation of Rectified Activations in Convolutional Network. arXiv 2015, arXiv:1505.00853. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Bahdanau, D.; Cho, K.; Bengio, Y. Neural Machine Translation by Jointly Learning to Align and Translate. arXiv 2014, arXiv:1409.0473. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is All You Need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local Neural Networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Santoro, A.; Raposo, D.; Barrett, D.G.; Malinowski, M.; Pascanu, R.; Battaglia, P.; Lillicrap, T. A Simple Neural Network Module for Relational Reasoning. Adv. Neural Inf. Process. Syst. 2017, 30, 4974–4983. [Google Scholar]
- Kidd, C.; Becker, A.; Huffman, G.J.; Muller, C.L.; Joe, P.; Skofronick-Jackson, G.; Kirschbaum, D.B. So, How Much of the Earth’s Surface is Covered by Rain Gauges? Bull. Am. Meteorol. Soc. 2017, 98, 69–78. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Chandrasekar, V.; Cifelli, R.; Xie, P. A Machine Learning System for Precipitation Estimation Using Satellite and Ground Radar Network Observations. IEEE Trans. Geosci. Remote Sens. 2020, 58, 982–994. [Google Scholar] [CrossRef]





| Papers | Summary | Active/Passive Data |
|---|---|---|
| Vivekanandan, J., et al. [18] | One of most fundamental algorithms of hydrometeor classification, known as fuzzy logic | Active |
| Liu, Hongping, and V. Chandrasekar [19]; Lim, S., et al. [20] | Improvement algorithms based on [18] | Active |
| Ryzhkov, Alexander V., et al. [21]; Park, Hyang Suk, et al. [22]; Scharfenberg, Kevin A., et al. [23] | Hydrometeor classification algorithm used for U.S. NEXRAD system | Active |
| Yang, Ji, et al. [24]; Lukach, Maryna, et al. [25] | Recent examples of continued efforts on further improved hydrometeor classification methods | Active |
| Klaes, K. Dieter, et al. [26] | Spaceborne passive microwave data have been available for five decades | Passive |
| Dolant, Caroline, et al. [27]; Bennartz, Ralf, and Grant W. Petty [28]; Petty, Grant W., and Ke Li [29]; Skofronick-Jackson, Gail M., and James R. Wan [30]; Wilheit, Thomas T [31]; Kedem, Benjamin, et al. [32] | Passive microwave measurements are particularly useful for global precipitation study | Passive |
| Bennartz, Ralf, and Grant W. Petty [28] | Simulated passive microwave data are responsive to hydrometeor scatter to different degrees between 19 and 150 GHz | Passive |
| Leppert, Kenneth D., and Daniel J. Cecil [33]; Chen, Ruiyao, and Ralf Bennartz [34,35] | Studies using spaceborne and airborne microwave data agree with [28] | Passive |
| Channel Number | Frequency (GHz) | Polarization at Nadir Used in RTTOV |
|---|---|---|
| 1 | 89 | H |
| 2 | 118.75 ± 0.08 | V |
| 3 | 118.75 ± 0.2 | V |
| 4 | 118.75 ± 0.3 | V |
| 5 | 118.75 ± 0.8 | V |
| 6 | 118.75 ± 1.1 | V |
| 7 | 118.75 ± 2.5 | V |
| 8 | 118.75 ± 3.0 | V |
| 9 | 118.75 ± 5.0 | V |
| 10 | 150 | H |
| 11 | 183.31 ± 1.0 | V |
| 12 | 183.31 ± 1.8 | V |
| 13 | 183.31 ± 3.0 | V |
| 14 | 183.31 ± 4.5 | V |
| 15 | 183.31 ± 7.0 | V |
| Data Source | Passive Measurements from MWHS-2 | Retrieval Profiles from DPR | Simulated TBs from RTTOV |
|---|---|---|---|
| Resolution (km) | 16–29 depend on channels | 5 | N/A |
| Gridding method | Measurements of the pixel closest to the center of the grid | Average of all profiles over the grid | N/A |
| Sampling resolution (km) | 25 | ||
| Time difference (min) | 15 | ||
| Year | 2017 for model training/testing; 2016 for model validation | ||
| Version | Channels of TBs | Relative Airmass | Freezing Level |
|---|---|---|---|
| 1 | 1–15 | Y * | N * |
| 2 | 1–15 | Y | Y |
| 3 | 2–15 | Y | N |
| 4 | 1–9, 11–15 | Y | N |
| 5 | 1, 10–15 | Y | N |
| 6 | 1–10 | Y | N |
| 7 | 2–9, 11–15 | Y | N |
| 8 | 1, 10 | Y | N |
| 9 | 1, 5–15 | Y | N |
| 10 | 1–15 | N | Y |
| Precip. Type | Liquid | Mixed | Ice |
|---|---|---|---|
| Liquid | 8902 (84.3%) | 1465 (6.0%) | 1 (0.0%) |
| Mixed | 1662 (15.7%) | 21,124 (86.5%) | 2002 (16.7%) |
| Ice | 0 (0.0%) | 1829 (7.5%) | 10,006 (83.3%) |
| Precip. Type | Liquid | Mixed | Ice | |
|---|---|---|---|---|
| Metrics | ||||
| Bias | 10.5% | −12.1% | 1.5% | |
| Variance | 10.3% | 5.9% | 1% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, R.; Bennartz, R. A Deep-Learning Scheme for Hydrometeor Type Classification Using Passive Microwave Observations. Remote Sens. 2023, 15, 2670. https://doi.org/10.3390/rs15102670
Chen R, Bennartz R. A Deep-Learning Scheme for Hydrometeor Type Classification Using Passive Microwave Observations. Remote Sensing. 2023; 15(10):2670. https://doi.org/10.3390/rs15102670
Chicago/Turabian StyleChen, Ruiyao, and Ralf Bennartz. 2023. "A Deep-Learning Scheme for Hydrometeor Type Classification Using Passive Microwave Observations" Remote Sensing 15, no. 10: 2670. https://doi.org/10.3390/rs15102670
APA StyleChen, R., & Bennartz, R. (2023). A Deep-Learning Scheme for Hydrometeor Type Classification Using Passive Microwave Observations. Remote Sensing, 15(10), 2670. https://doi.org/10.3390/rs15102670






