Performance Analysis of Channel Imbalance Control and Azimuth Ambiguity Suppression in Azimuth Dual Receiving Antenna Mode of LT-1 Spaceborne SAR System
Abstract
1. Introduction
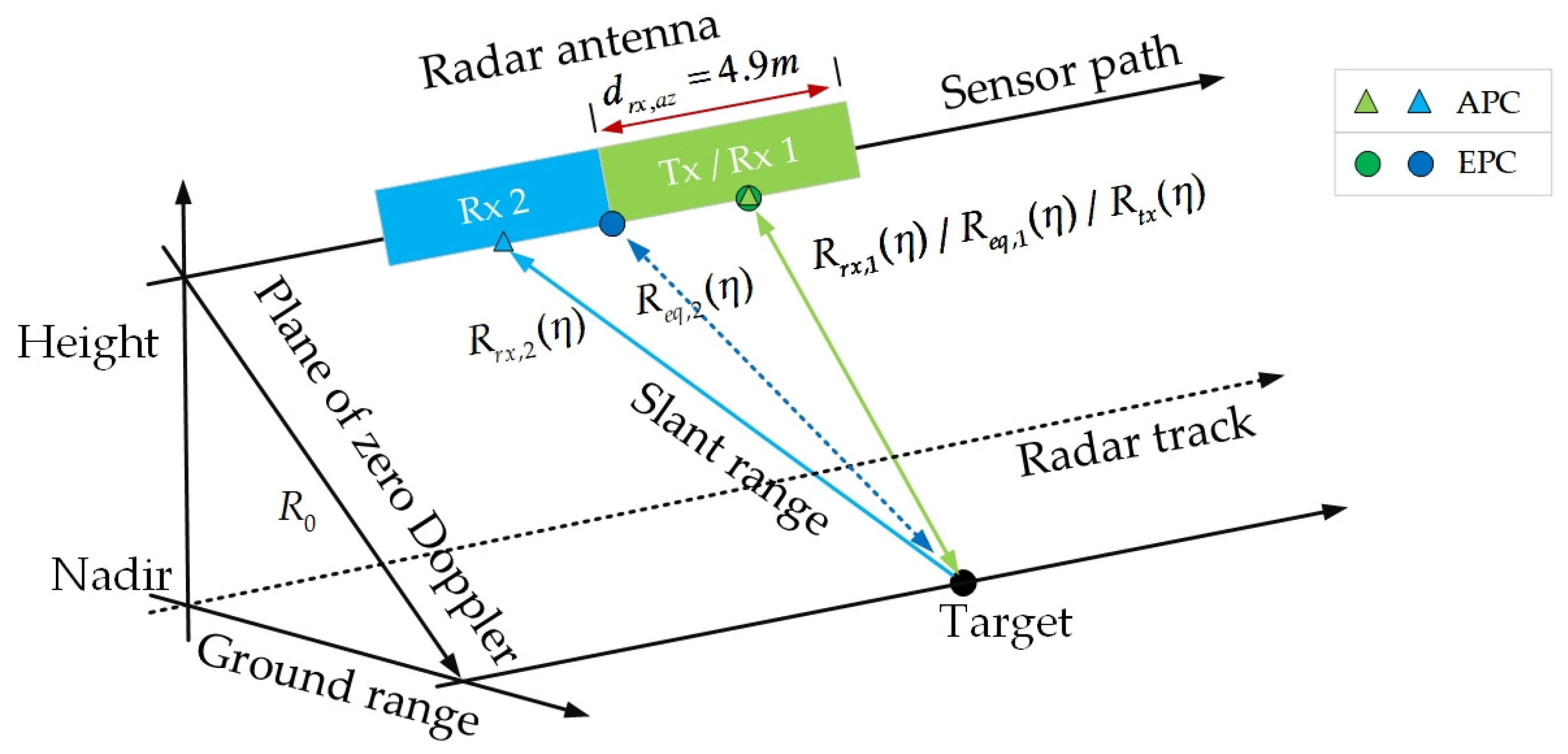
2. LT-1 DRA Mode and Channel Error Model
2.1. LT-1 Signal Model and Channel Constant Amplitude-Phase Error
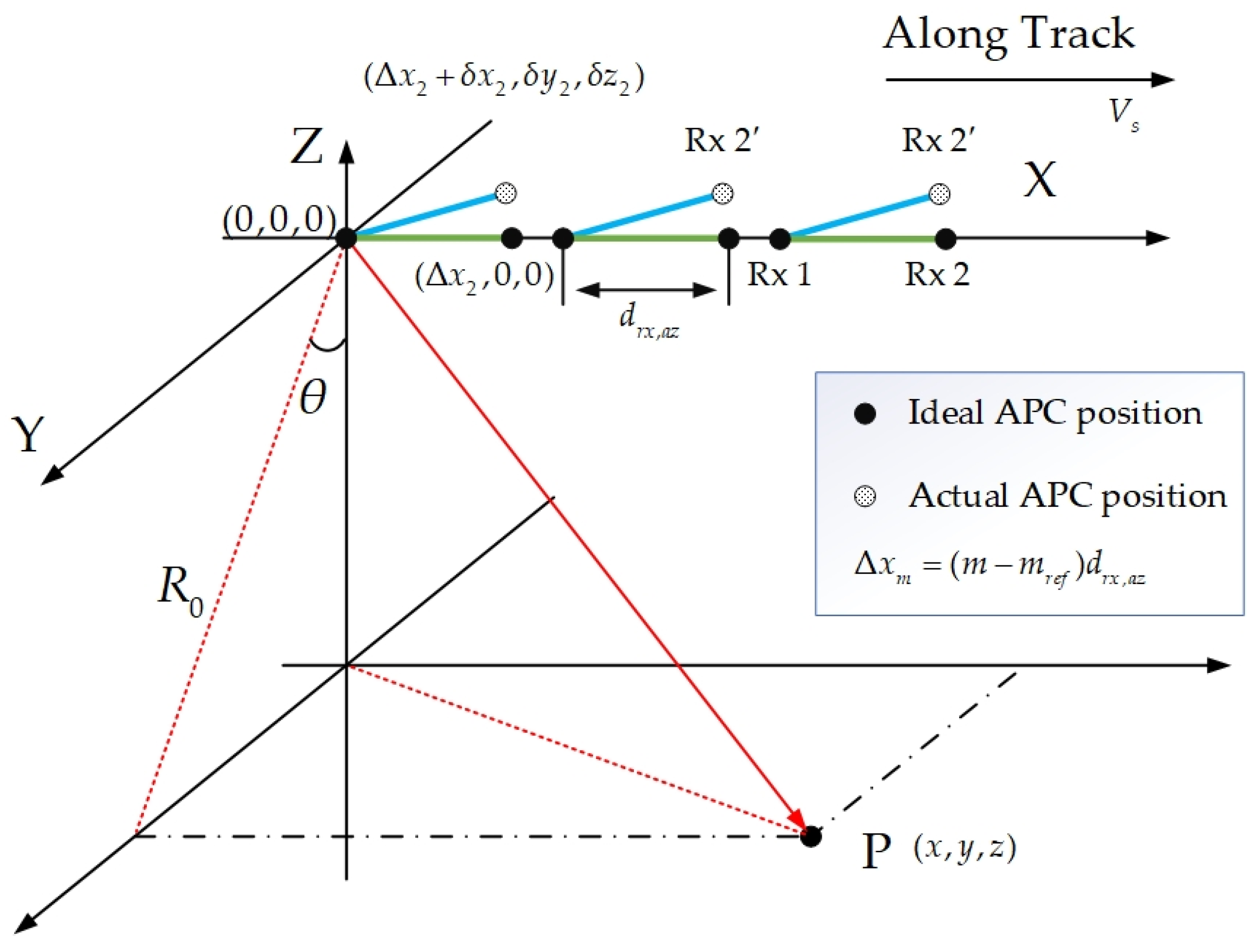
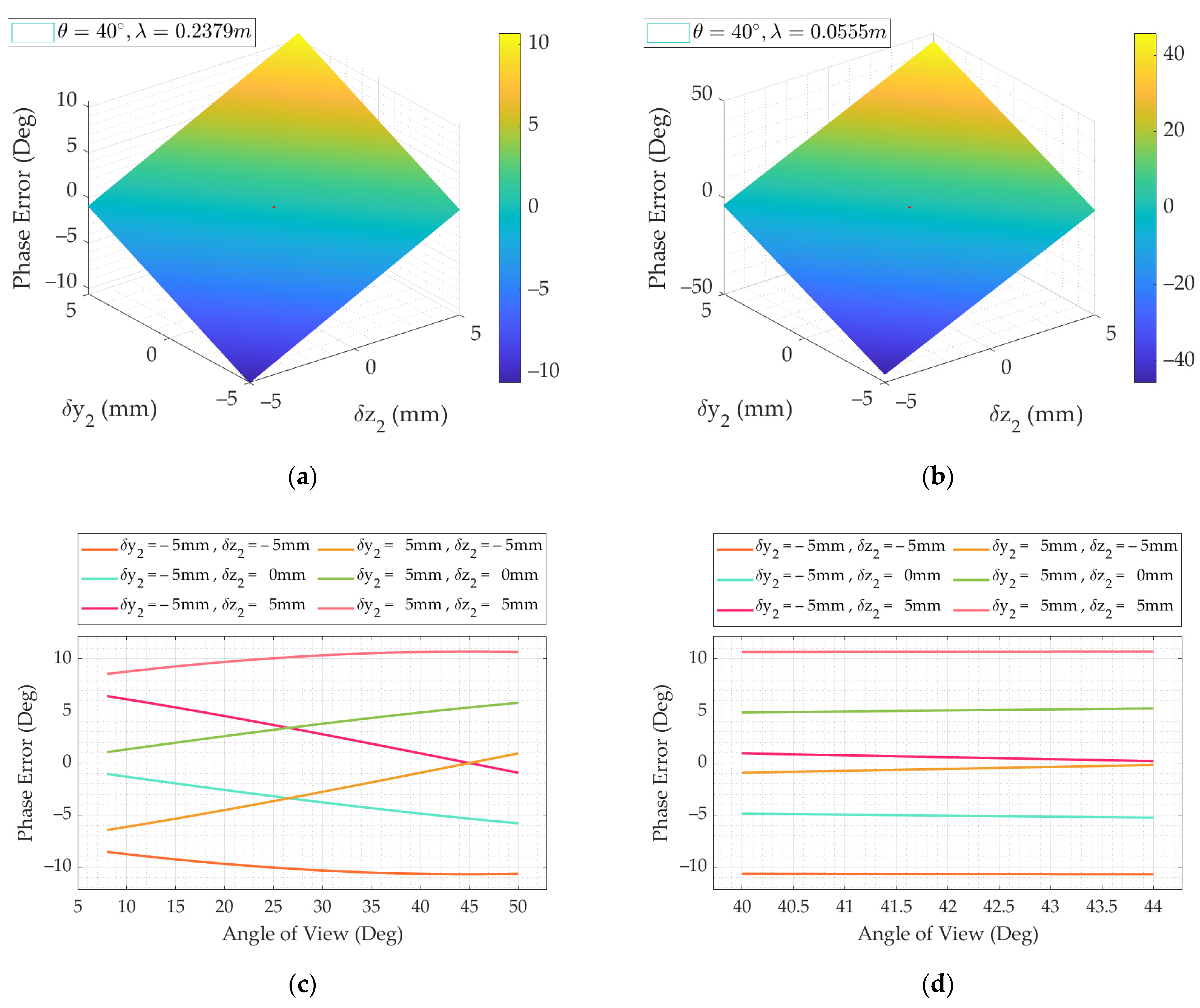
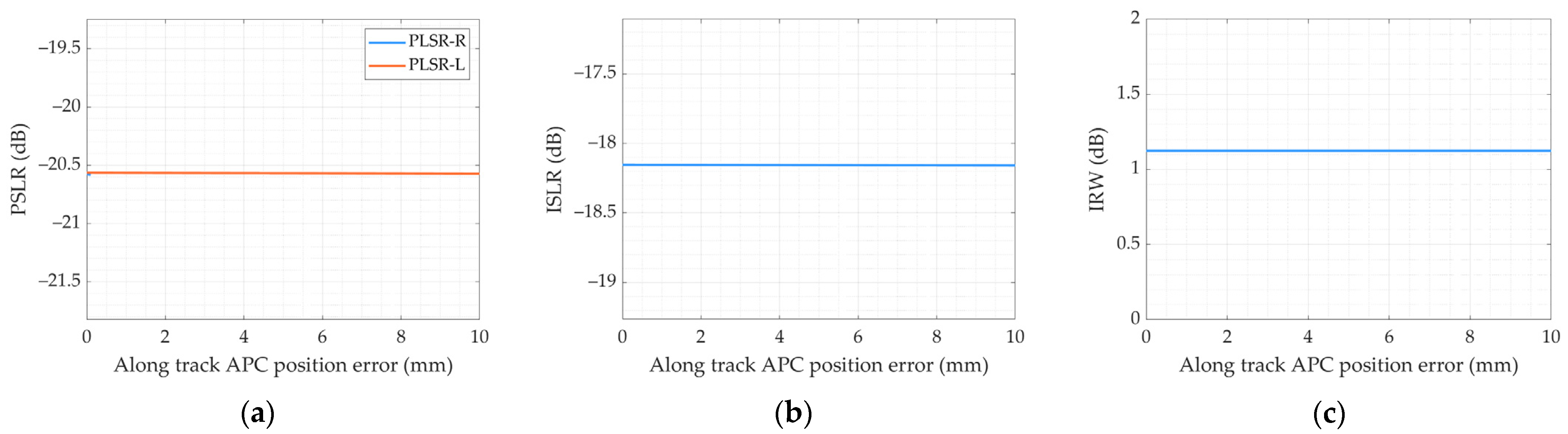
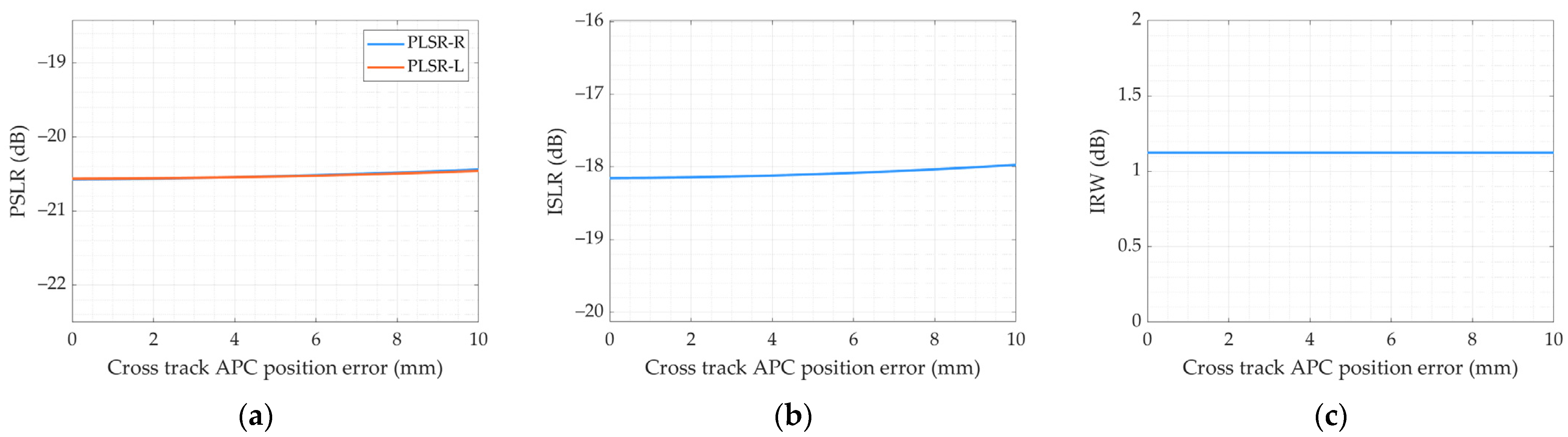
2.2. APC Position Error
- The X-axis direction is the satellite track direction.
- The Y-axis direction is perpendicular to the X-axis direction.
- The Z-axis faces away from the center of the Earth.
- The P point is the target point.
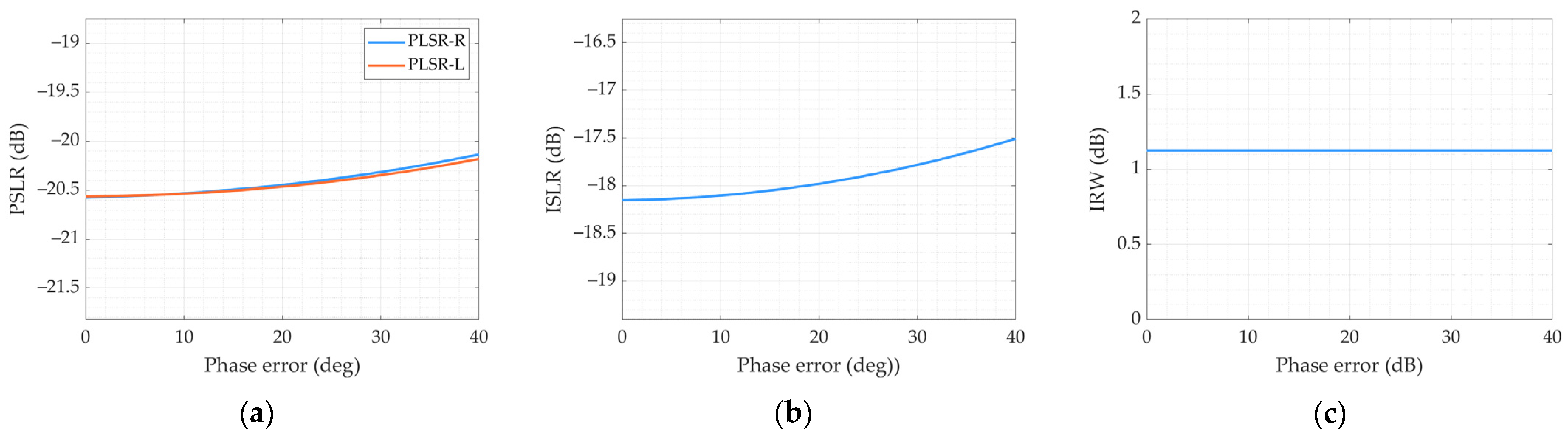
3. Influence of Channel Error on Imaging Performance
4. LT-1 SAR Performance Analysis
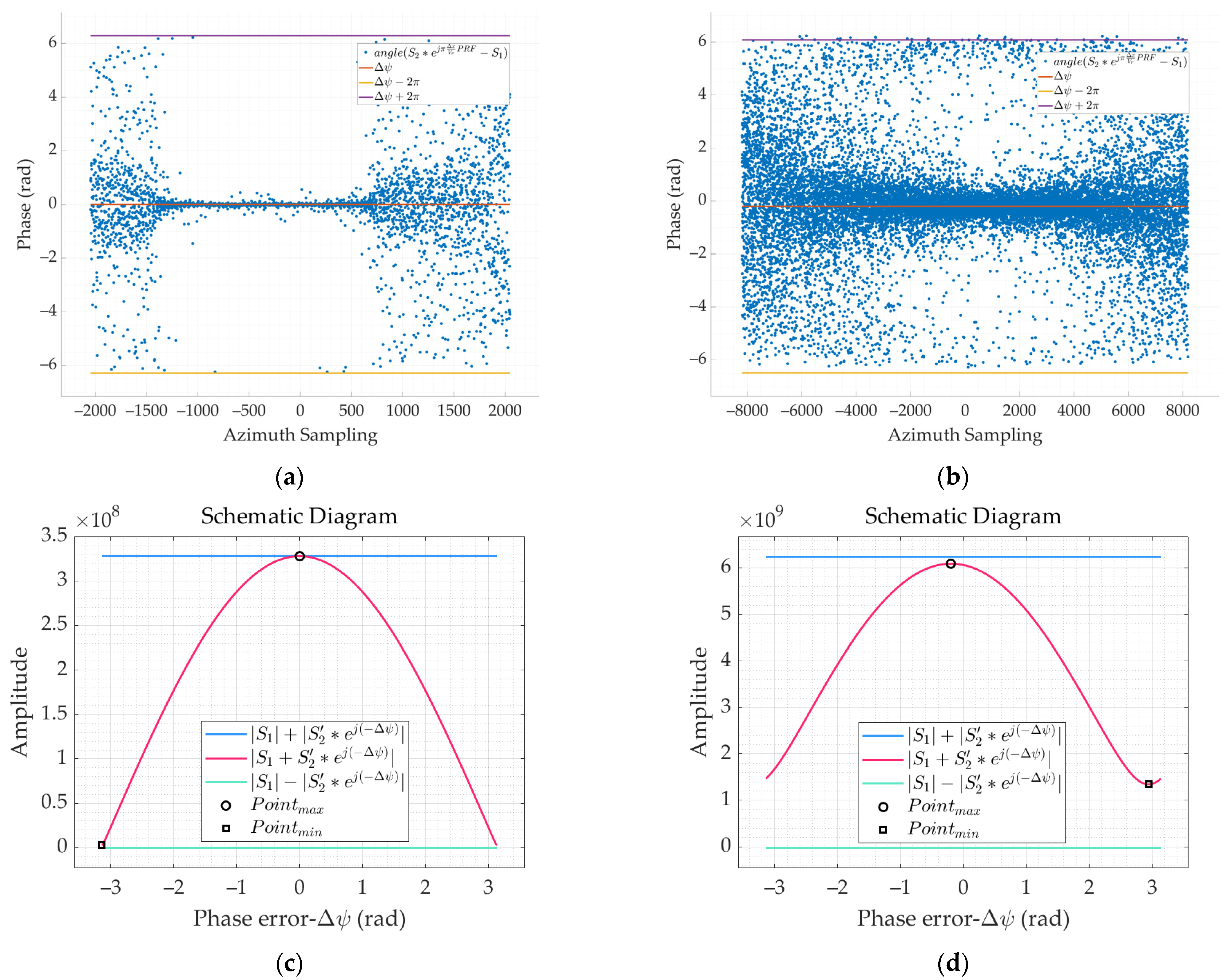
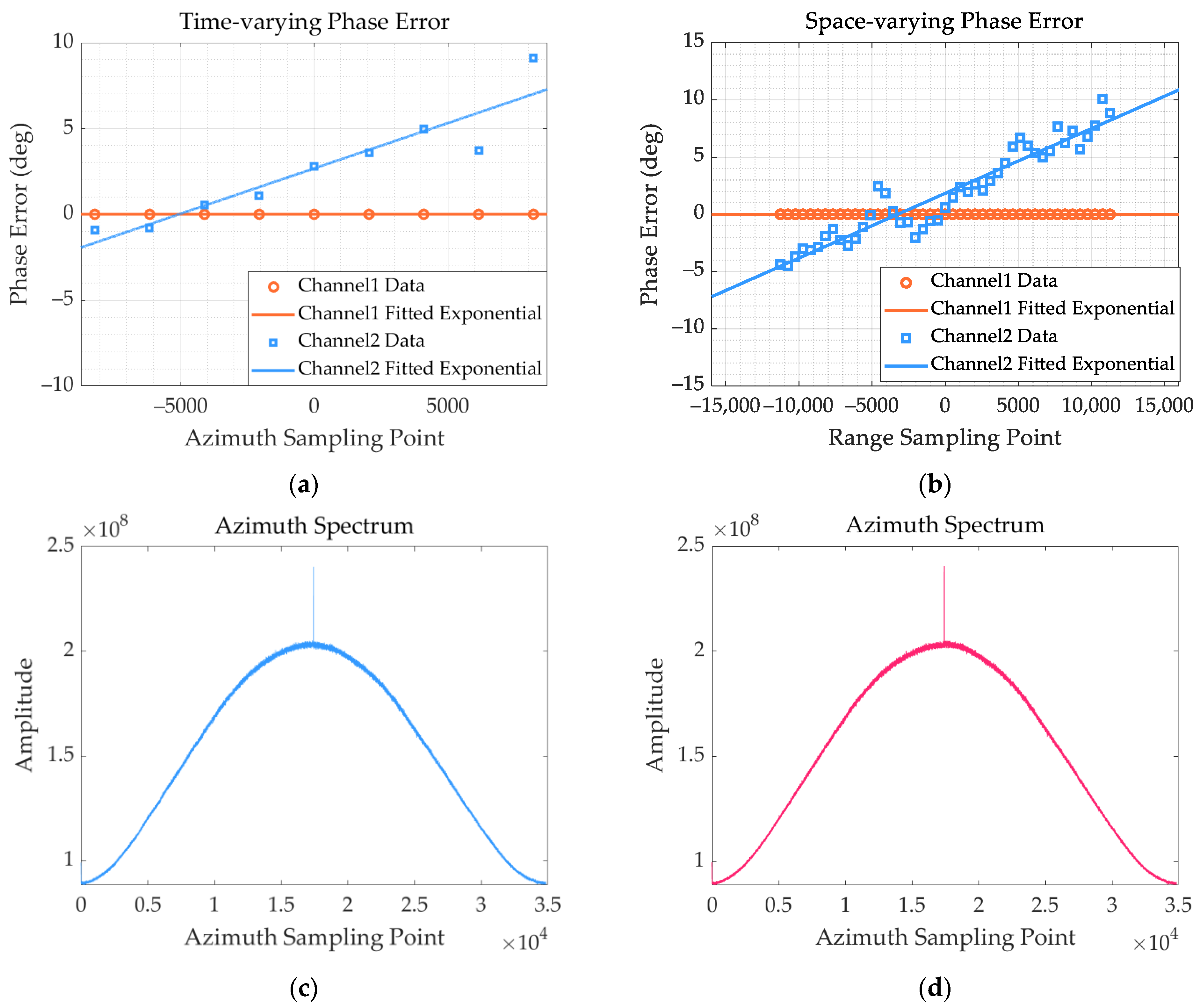
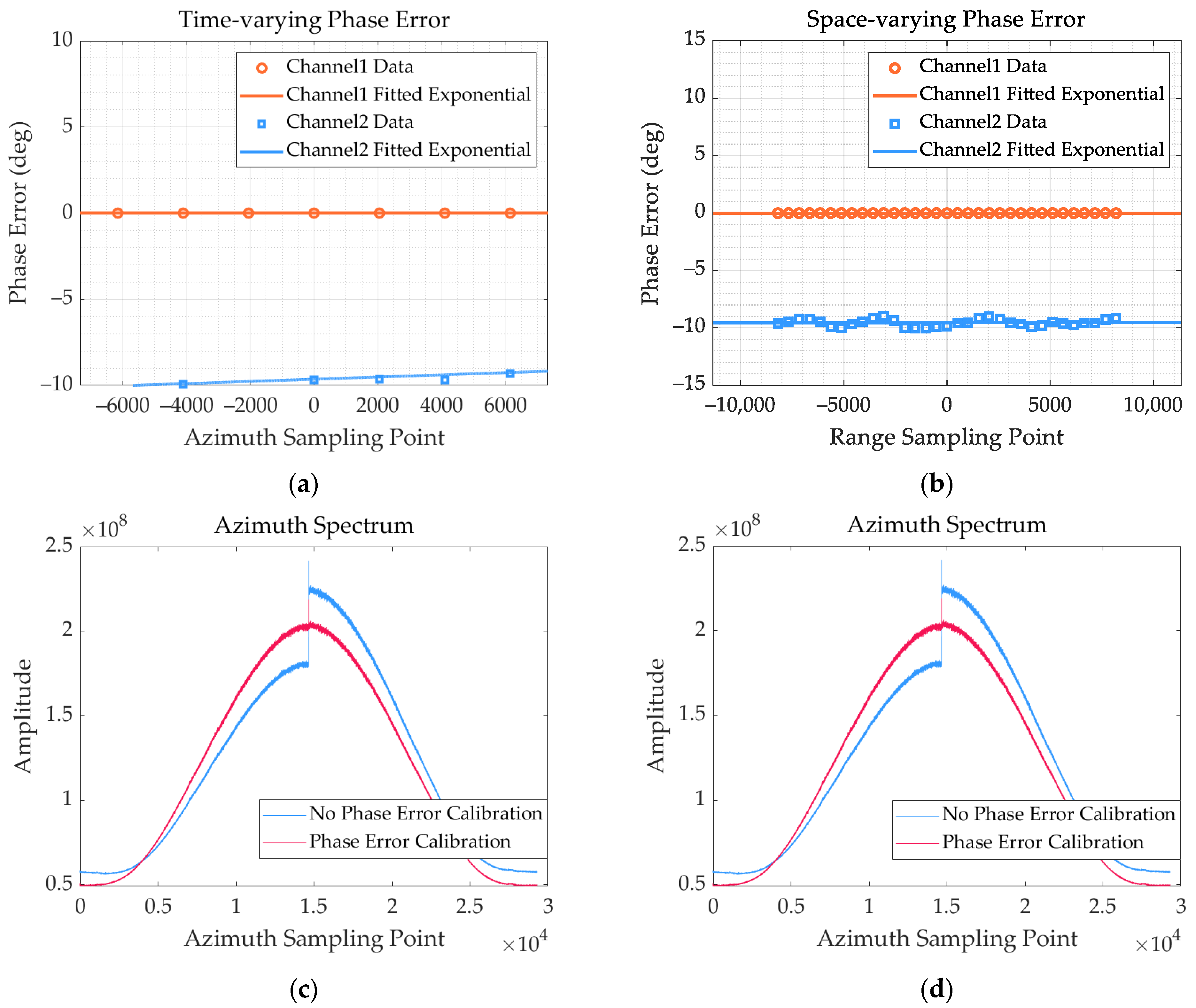
4.1. Consistency Calibration Method for Channel Error
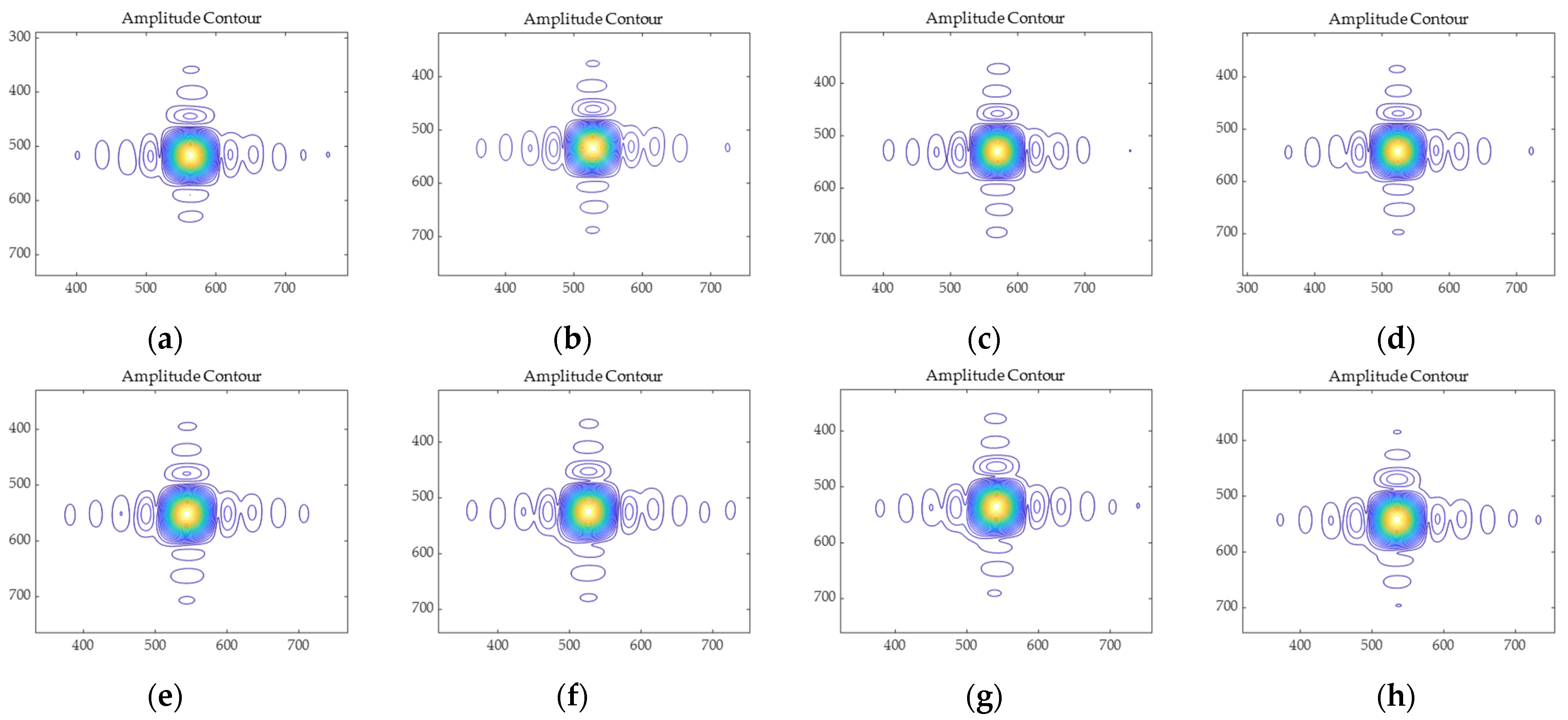
4.2. Calibration Point Imaging Results
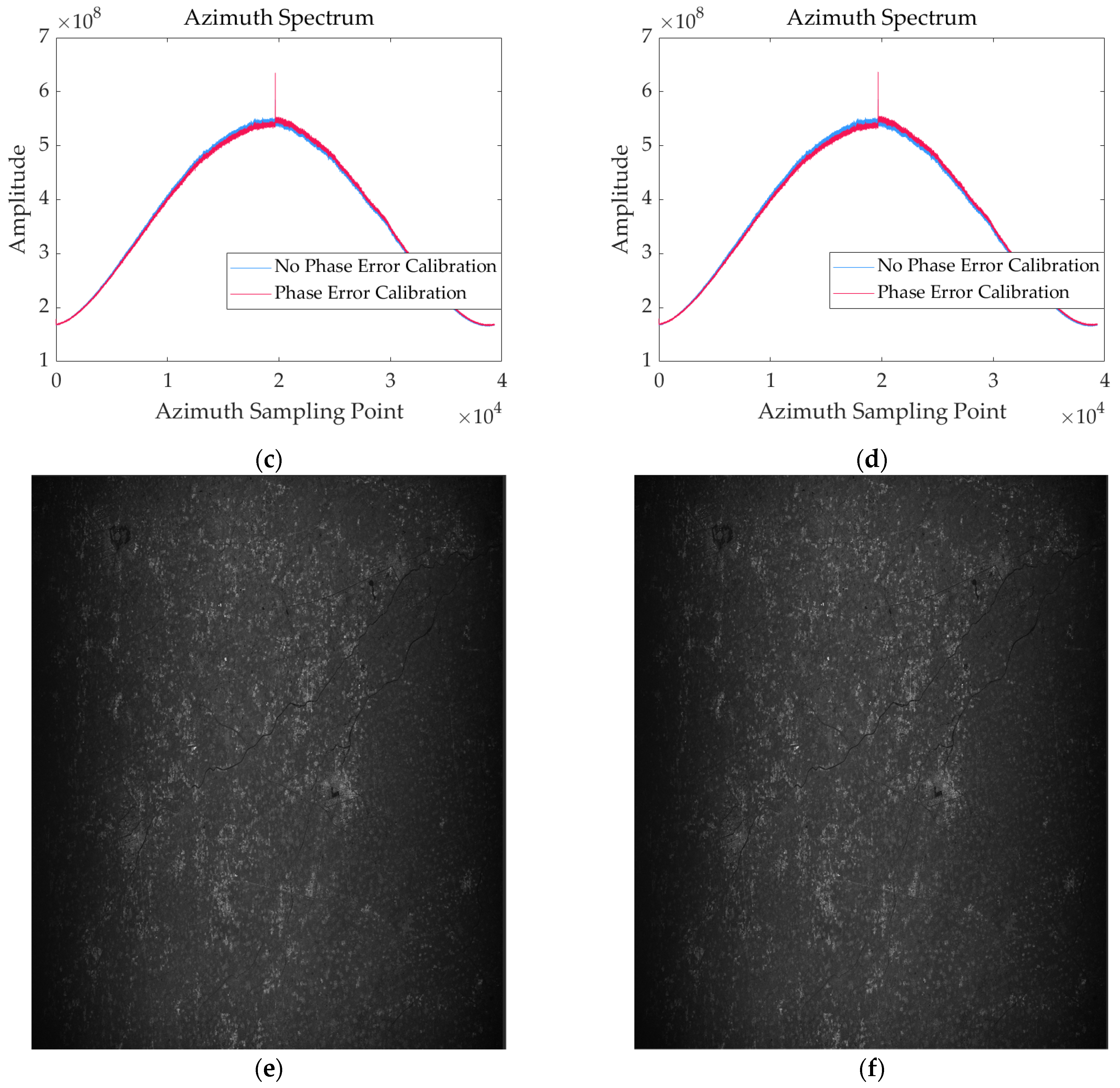
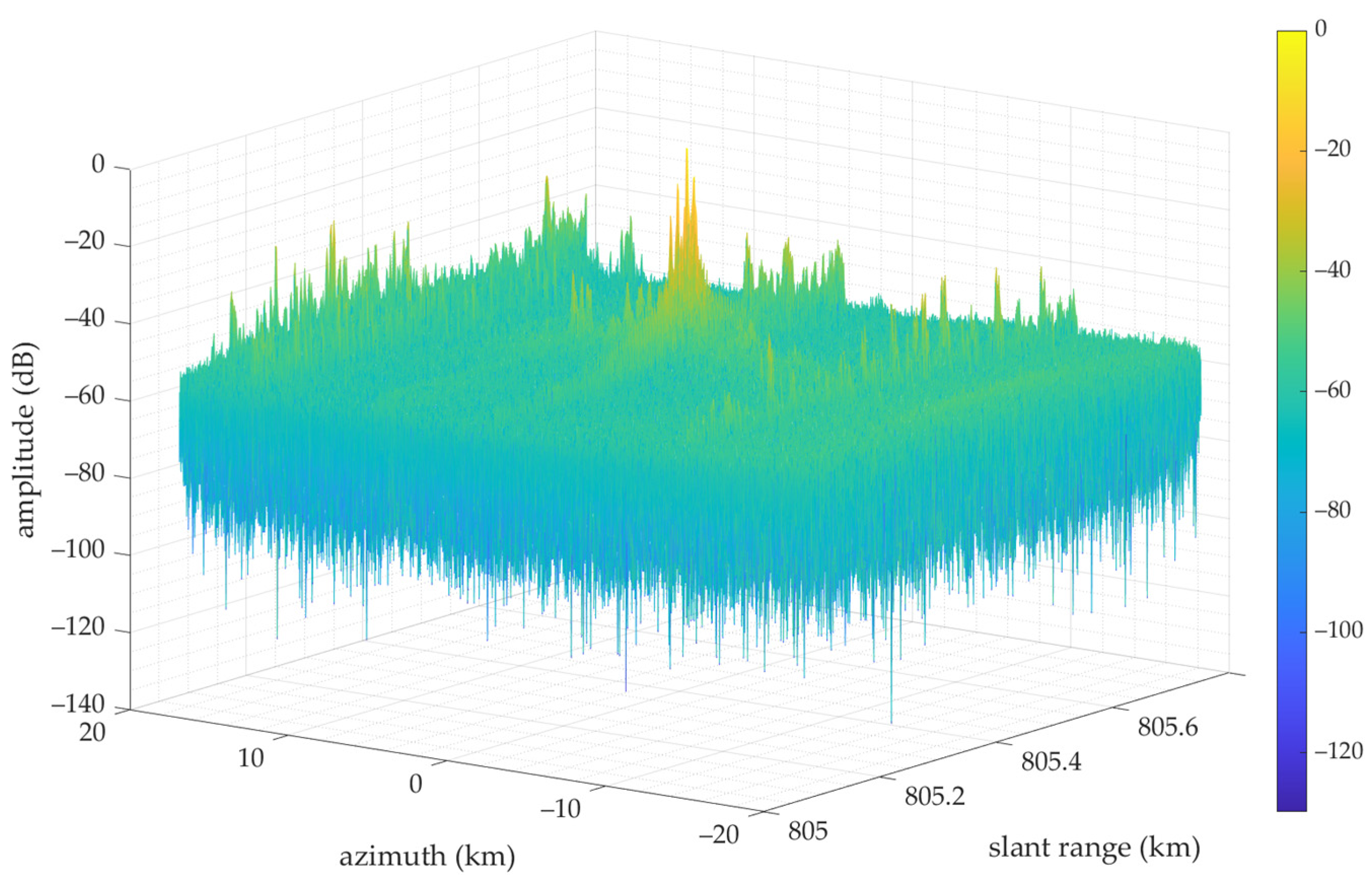
4.3. Scenarios Imaging Results
4.3.1. Wilderness Scenarios
4.3.2. City Scenarios
4.3.3. Land and Sea Interface Scenarios
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Cumming, I.G.; Wong, F.H. Digital processing of synthetic aperture radar data. Artech House 2005, 1, 108–110. [Google Scholar]
- Li, Z.; Wang, H.; Su, T.; Bao, Z. Generation of wide-swath and high-resolution SAR images from multichannel small spaceborne SAR systems. IEEE Geosci. Remote Sens. Lett. 2005, 2, 82–86. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Unambiguous SAR signal reconstruction from nonuniform displaced phase center sampling. IEEE Geosci. Remote Sens. Lett. 2004, 1, 260–264. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Moreira, A. Multidimensional waveform encoding: A new digital beamforming technique for synthetic aperture radar remote sensing. IEEE Trans. Geosci. Remote Sens. 2007, 46, 31–46. [Google Scholar] [CrossRef]
- Jing, W.; Xing, M.; Qiu, C.-W.; Bao, Z.; Yeo, T.-S. Unambiguous reconstruction and high-resolution imaging for multiple-channel SAR and airborne experiment results. IEEE Geosci. Remote Sens. Lett. 2008, 6, 102–106. [Google Scholar] [CrossRef]
- Krieger, G.; Gebert, N.; Younis, M.; Bordoni, F.; Patyuchenko, A.; Moreira, A. Advanced concepts for ultra-wide-swath SAR imaging. In Proceedings of the 7th European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008; pp. 1–4. [Google Scholar]
- Yunkai, D.; Weidong, Y.; Heng, Z.; Wei, W.; Dacheng, L.; Robert, W. Forthcoming spaceborne SAR development. J. Radars 2020, 9, 1–33. [Google Scholar]
- Yingjie, W.; Robert, W.; Weidong, Y.; Qingchao, Z.; Kaiyu, L.; Dacheng, L.; Yunkai, D.; Naiming, O.; Xiaoxue, J.; Heng, Z.; et al. See-Earth: SAR Constellation with Dense Time-SEries for Multi-dimensional Environmental Monitoring of the Earth. J. Radars 2021, 10, 842–864. [Google Scholar] [CrossRef]
- Fu, Z.; Zhang, H.; Zhao, J.; Li, N.; Zheng, F. A Modified 2-D Notch Filter Based on Image Segmentation for RFI Mitigation in Synthetic Aperture Radar. Remote Sens. 2023, 15, 846. [Google Scholar] [CrossRef]
- Currie, A.; Brown, M.A. Wide-swath SAR. In IEE Proceedings F (Radar and Signal Processing); IET: Wales, UK, 1992; pp. 122–135. [Google Scholar]
- Süß, M.; Grafmüller, B.; Zahn, R. A novel high resolution, wide swath SAR system. In Proceedings of the IGARSS 2001. Scanning the Present and Resolving the Future. IEEE 2001 International Geoscience and Remote Sensing Symposium (Cat. No. 01CH37217), Sydney, NSW, Australia, 9–13 July 2001; pp. 1013–1015. [Google Scholar]
- Kim, J.-H.; Younis, M.; Gabele, M.; Prats, P.; Krieger, G. First spaceborne experiment of digital beam forming with TerraSAR-X dual receive antenna mode. In Proceedings of the 2011 8th European Radar Conference, Manchester, UK, 12–14 October 2011; pp. 41–44. [Google Scholar]
- Younis, M.; De Almeida, F.Q.; Bordoni, F.; López-Dekker, P.; Krieger, G. Digital beamforming techniques for multi-channel synthetic aperture radar. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 1412–1415. [Google Scholar]
- Hatooka, Y.; Kankaku, Y.; Arikawa, Y.; Suzuki, S. First result from ALOS-2 operation. In Proceedings of the Earth Observing Missions and Sensors: Development, Implementation, and Characterization III, San Francisco, CA, USA, 18 December 2014; pp. 138–147. [Google Scholar]
- Jin, T.; Qiu, X.; Hu, D.; Ding, C. Unambiguous imaging of static scenes and moving targets with the first Chinese dual-channel spaceborne SAR sensor. Sensors 2017, 17, 1709. [Google Scholar] [CrossRef]
- Qingjun, Z. System design and key technologies of the GF-3 satellite. Acta Geod. Cartogr. Sin. 2017, 46, 269. [Google Scholar]
- Shi, J.; Lü, D.; Wang, Y.; Du, Y.; Pang, Y.; Yang, D.; Wang, X.; Dong, X.; Yang, X. Recent Progress of Earth Science Satellite Missions in China. Chin. J. Space Sci. 2022, 42, 712–723. [Google Scholar] [CrossRef]
- Cai, Y.; Wang, R.; Yu, W.; Liang, D.; Liu, K.; Zhang, H.; Chen, Y. An Advanced Approach to Improve Synchronization Phase Accuracy with Compressive Sensing for LT-1 Bistatic Spaceborne SAR. Remote Sens. 2022, 14, 4621. [Google Scholar] [CrossRef]
- Cai, Y.; Deng, Y.; Zhang, H.; Wang, R.; Wu, Y.; Cheng, S. An Image-Domain Least L 1-Norm Method for Channel Error Effect Analysis and Calibration of Azimuth Multi-Channel SAR. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–14. [Google Scholar] [CrossRef]
- Yang, W.; Guo, J.; Chen, J.; Liu, W.; Deng, J.; Wang, Y.; Zeng, H. A Novel Channel Inconsistency Estimation Method for Azimuth Multichannel SAR Based on Maximum Normalized Image Sharpness. IEEE Trans. Geosci. Remote Sens. 2022, 60, 1–16. [Google Scholar] [CrossRef]
- Shang, M.; Qiu, X.; Han, B.; Ding, C.; Hu, Y. Channel Imbalances and Along-Track Baseline Estimation for the GF-3 Azimuth Multichannel Mode. Remote Sens. 2019, 11, 1297. [Google Scholar] [CrossRef]
- Gebert, N.; de Almeida, F.Q.; Krieger, G. Airborne demonstration of multichannel SAR imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 963–967. [Google Scholar] [CrossRef]
- Li, Z.; Bao, Z.; Wang, H.; Liao, G. Performance improvement for constellation SAR using signal processing techniques. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 436–452. [Google Scholar]
- Feng, J.; Gao, C.; Zhang, Y.; Wang, R. Phase mismatch calibration of the multichannel SAR based on azimuth cross correlation. IEEE Geosci. Remote Sens. Lett. 2012, 10, 903–907. [Google Scholar] [CrossRef]
- Zhang, L.; Gao, Y.; Liu, X. Robust channel phase error calibration algorithm for multichannel high-resolution and wide-swath SAR imaging. IEEE Geosci. Remote Sens. Lett. 2017, 14, 649–653. [Google Scholar] [CrossRef]
- Xiang, J.; Ding, X.; Sun, G.-C.; Zhang, Z.; Xing, M.; Liu, W. An Efficient Multichannel SAR Channel Phase Error Calibration Method Based on Fine-Focused HRWS SAR Image Entropy. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 7873–7885. [Google Scholar] [CrossRef]
- Zhang, S.-X.; Xing, M.-D.; Xia, X.-G.; Liu, Y.-Y.; Guo, R.; Bao, Z. A robust channel-calibration algorithm for multi-channel in azimuth HRWS SAR imaging based on local maximum-likelihood weighted minimum entropy. IEEE Trans. Image Process. 2013, 22, 5294–5305. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.; Lu, P.; Cai, Y.; Li, J.; Yang, T.; Wu, Y.; Wang, R. An Efficient Channel Imbalance Estimation Method Based on Subadditivity of Linear Normed Space of Sub-Band Spectrum for Azimuth Multichannel SAR. Remote Sens. 2023, 15, 1561. [Google Scholar] [CrossRef]
- Laskowski, P.; Bordoni, F.; Younis, M. Antenna pattern compensation in multi-channel azimuth reconstruction algorithm. In Proceedings of the Advanced RF Sensors and Remote Sensing Instruments (ARSI), Noordwijk, The Netherlands, 15 September 2011; pp. 1–10. [Google Scholar]
- Shang, M.; Qiu, X.; Han, B.; Yang, J.; Zhong, L.; Ding, C.; Hu, Y. The space-time variation of phase imbalance for GF-3 azimuth multichannel mode. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 4774–4788. [Google Scholar] [CrossRef]
- Yu, W.; Wang, K.; Wu, J.; Li, S.; Xie, W.; Sun, H.; Ou, N. The LuTan-1 SAR Antenna System. In Proceedings of the EUSAR 2022, 14th European Conference on Synthetic Aperture Radar, Leipzig, Germany, 25–27 July 2022; pp. 1–4. [Google Scholar]
- Maligranda, L. Some remarks on the triangle inequality for norms. Banach J. Math. Anal. 2008, 2, 31–41. [Google Scholar] [CrossRef]
- Mou, J.; Hong, J.; Wang, Y.; Du, S.; Xing, K.; Qiu, T. LT-1 Baseline Calibration Method Based on Improved Baseline Calibration Model. In Proceedings of the IGARSS 2022–2022 IEEE International Geoscience and Remote Sensing Symposium, Kuala Lumpur, Malaysia, 17–22 July 2022; pp. 7452–7455. [Google Scholar]
- Villano, M.; Krieger, G. Spectral-based estimation of the local azimuth ambiguity-to-signal ratio in SAR images. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2304–2313. [Google Scholar] [CrossRef]
- Li, F.K.; Johnson, W.T.K. Ambiguities in Spacebornene Synthetic Aperture Radar Systems. IEEE Trans. Aerosp. Electron. Syst. 1983, AES-19, 389–397. [Google Scholar] [CrossRef]








| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Platform velocity | 7635 | ||
| Carrier frequency | 1.26 | ||
| Nearest slant range | 817 | ||
| Azimuth antenna length | 2 × 4.9 | ||
| Doppler bandwidth | 2761 | ||
| Azimuth sampling frequency | 1795 | ||
| Number of channels | 2 | \ |
| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Platform velocity | 7635 | ||
| Carrier frequency | 1.26 | ||
| Signal bandwidth | 80 | ||
| Signal pulse duration | 70 | ||
| Nearest slant range | 817 | ||
| Azimuth antenna length | 4.9 × 2 | ||
| Rang sampling frequency | 90 | ||
| Azimuth sampling frequency | 1742 | ||
| Number of channels | 2 | \ |
| Calibration Point | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|---|
| Latitude | 42.01435 | 42.01508 | 42.01464 | 42.01483 | 42.01553 | 42.01568 | 42.01648 | 42.01237 |
| Longitude | 91.80460 | 91.84039 | 91.88072 | 91.92124 | 91.96425 | 92.01358 | 92.07841 | 92.14480 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Lu, P.; Cai, Y.; Wu, Y.; Wang, R. Performance Analysis of Channel Imbalance Control and Azimuth Ambiguity Suppression in Azimuth Dual Receiving Antenna Mode of LT-1 Spaceborne SAR System. Remote Sens. 2023, 15, 2765. https://doi.org/10.3390/rs15112765
Xu Z, Lu P, Cai Y, Wu Y, Wang R. Performance Analysis of Channel Imbalance Control and Azimuth Ambiguity Suppression in Azimuth Dual Receiving Antenna Mode of LT-1 Spaceborne SAR System. Remote Sensing. 2023; 15(11):2765. https://doi.org/10.3390/rs15112765
Chicago/Turabian StyleXu, Zongxiang, Pingping Lu, Yonghua Cai, Yirong Wu, and Robert Wang. 2023. "Performance Analysis of Channel Imbalance Control and Azimuth Ambiguity Suppression in Azimuth Dual Receiving Antenna Mode of LT-1 Spaceborne SAR System" Remote Sensing 15, no. 11: 2765. https://doi.org/10.3390/rs15112765
APA StyleXu, Z., Lu, P., Cai, Y., Wu, Y., & Wang, R. (2023). Performance Analysis of Channel Imbalance Control and Azimuth Ambiguity Suppression in Azimuth Dual Receiving Antenna Mode of LT-1 Spaceborne SAR System. Remote Sensing, 15(11), 2765. https://doi.org/10.3390/rs15112765








