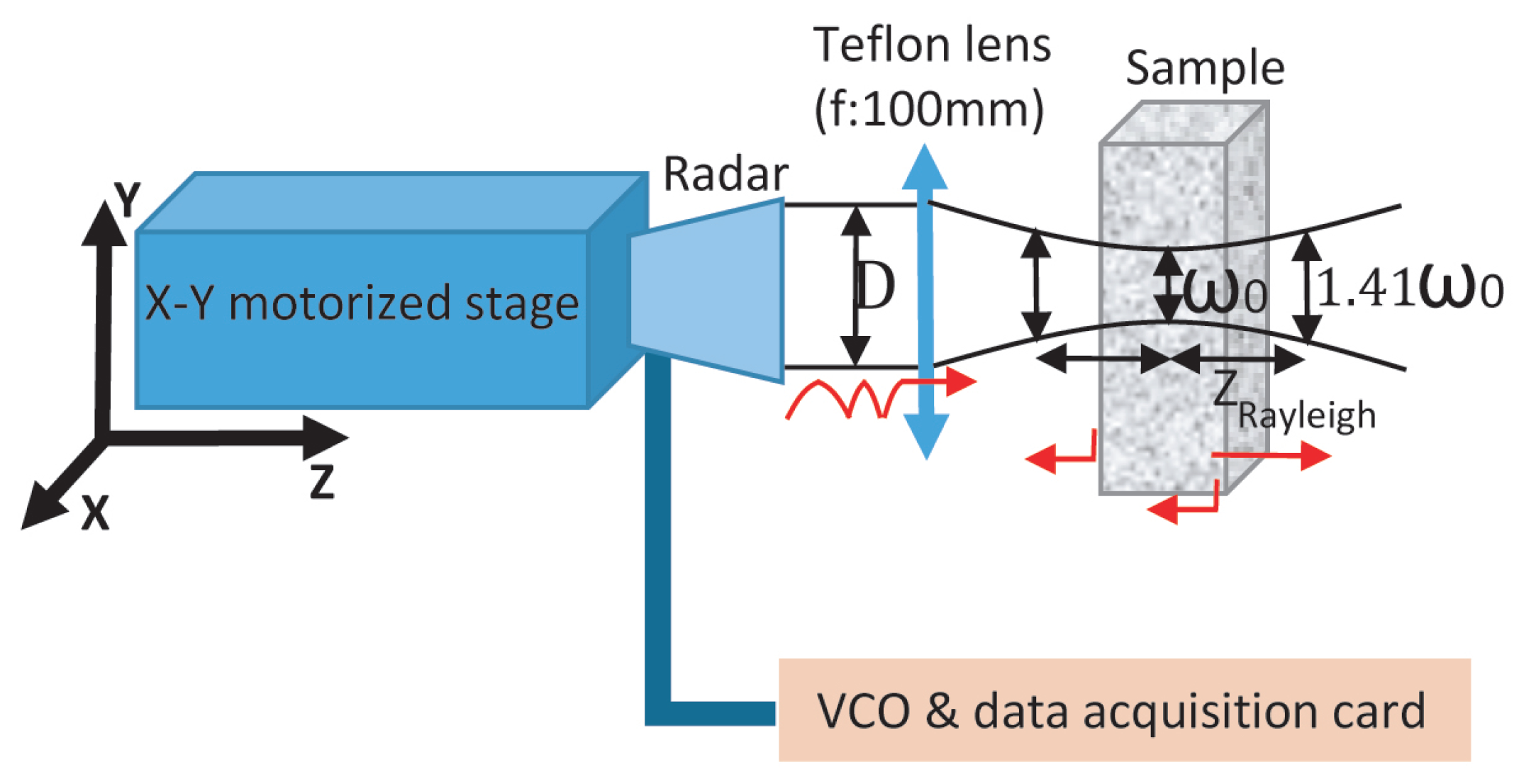
1. Introduction
The detection and characterization of rock fractures and lithological changes are of great importance for the quality control of construction and dielectric composite materials, the characterization of reservoirs, the inspection of cultural heritage objects and geotechnics. Usually, applied methods utilize acoustic or electromagnetic (EM) waves [
1,
2,
3]. In particular, acoustic methods have demonstrated higher penetration depths in rocks than EM signals. However, better axial resolutions can be reached using high-frequency EM microwaves and X-rays. Additionally, the latter have the advantage of being contactless, which is not the case with acoustics methods.
Historically, ground-penetrating radars (GPRs) with frequencies below <20 GHz have been used [
4]. In a recent review [
5], the authors presented the progress in GPR imaging and data processing for applications in different disciplines, such as geology, civil engineering and archaeology. Currently, automated machine learning and classification models have been applied to processing GPR data in order to classify geological structures, obtain dielectric permittivity variations and identify boundaries [
6,
7,
8,
9,
10]. In addition, among the different types of GPR radars, it is worth mentioning multi-frequency holographic radars, which have better spatial resolutions than impulse subsurface radars [
11]. However, one of the limitations of GPRs is the impossibility of measuring millimeter and sub-millimeter fractures due to the range of frequencies that are usually used.
Nevertheless, in order to avoid lateral spatial limitations, a near-field scanning microwave microscope has recently been proposed that measures the dielectric permittivity of minerals with a spatial resolution of tens of microns [
12,
13]. This sub-wavelength resolution is achieved by working in the near field. However, this method is also limited in axial spatial resolution since it works below 3 GHz. Thus, it has not been applied in fracture imaging.
Another approach that has been proposed in recent years uses terahertz time-domain spectroscopy (THz-TDS) to detect
fractures [
14]. The limitation of using this technique is that in most common rocks, the penetration depth is a few millimeters and high time-consuming for imaging large surfaces [
14,
15].
Finally, X-ray microtomography, which is a commonly used method for imaging fractures with high spatial resolutions, has the disadvantages of imaging small volumes (≈mm
), being ionizing, not being compact in size and also being very time-consuming [
16].
One solution to overcome these limitations while keeping a high lateral and axial resolution is working at the EHF band (30–300 GHz). Various applications and implementations of systems using frequency-modulated continuous wave (FMCW) radars within these frequencies have been presented in [
17,
18,
19,
20,
21]. However, so far, there have been no reports on rock applications.
Hence, we propose the use of a 300 GHz FMCW radar to show its feasibility for detecting rock fractures and lithological changes. We present measurements of reservoir rocks, such as dolomite and limestone, and construction rocks, such as granite. The results demonstrated that we could quantify the thicknesses of fractures at the millimeter scale with a centimeter penetration depth, being sensitive to fractures and small lithological changes. The acquisition time for imaging a surface of 121 cm with a spatial step of 1 mm and a penetration depth of 3 cm was around 15 min. In addition, we present a method to obtain 3D fracture reconstructions from radar image measurements.
3. Results
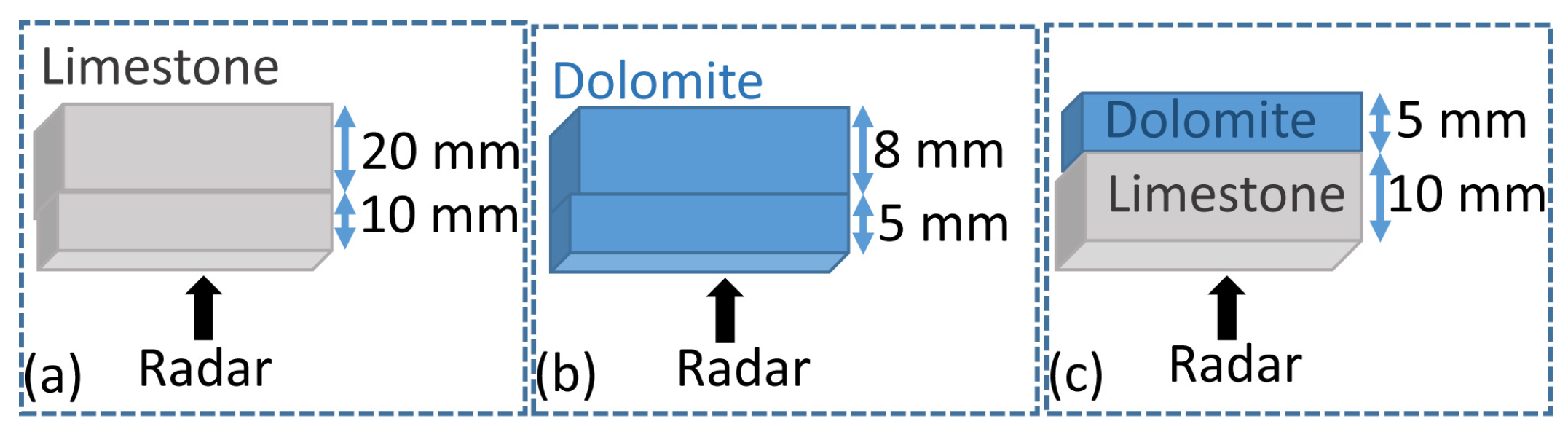
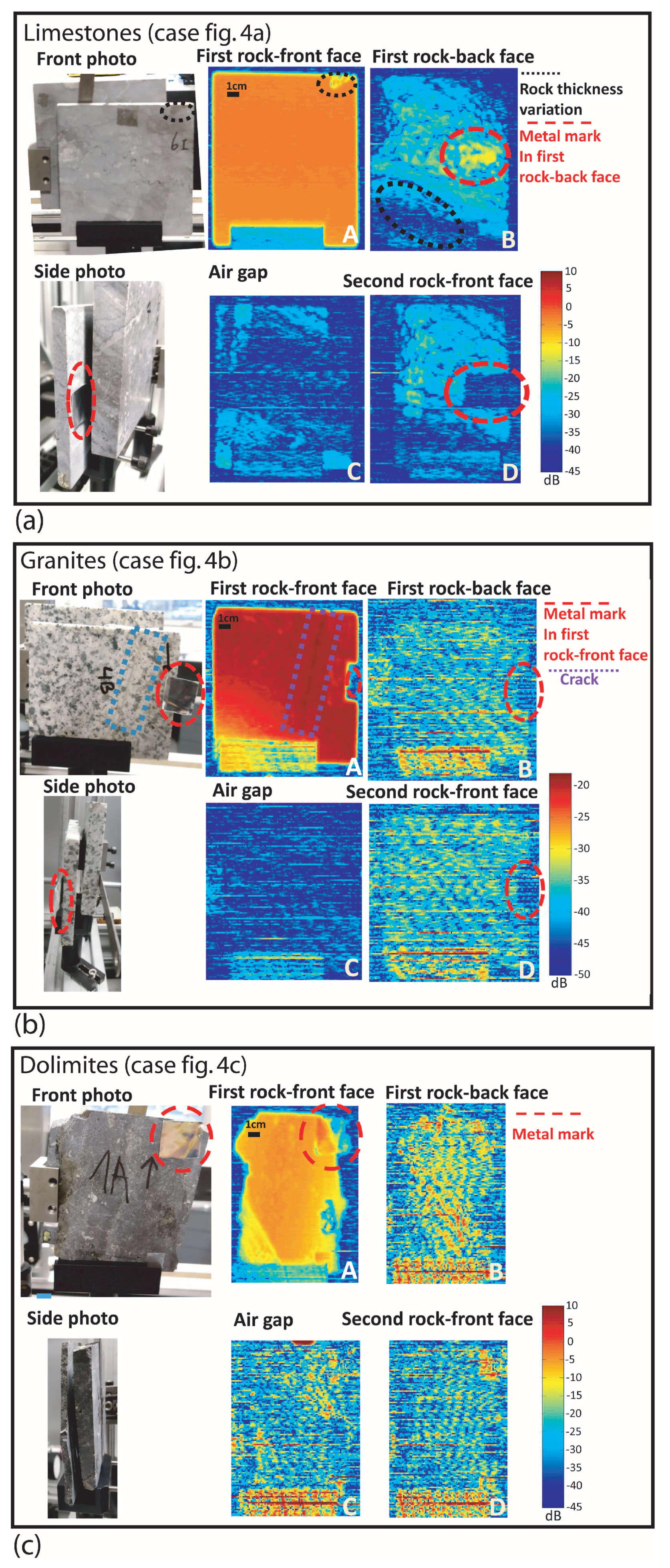
In
Figure 6, we present the fracture detection results for the rock configurations shown in
Figure 4a–c. For all cases, we show the experimental photographs and the radar images obtained in the axial direction. This means the XY surfaces for different z cuts. Firstly, we present the reflection from the front face of the first rock (named ‘A’), then the reflection from its back face (named ‘B’) and the results obtained when situated in the air gap (named ‘C’). Lastly, we show the reflection from the front face of the second rock (named ‘D’). As previously explained, each pixel in the images represents the tone frequency amplitude detected for the selected distance.
As the thicknesses of the rocks varied and they could be a bit tilted regarding the electromagnetic waves, the images presented for Z-slides did not coincide perfectly with the XY planes of the rocks. Moreover, since the rocks were heterogeneous, e.g., contained fossils, intraclasts and ferromagnesian minerals, the ‘B’ and ‘D’ images did present amplitude variations caused by the EM waves traveling at different velocities (
), and because they underwent different absorption and scattering. However, the two faces of the rocks that mimicked the fracture were identified. It should be noted that when EM waves propagated within a rock, the wavelength was shortened since
(where
is the signal frequency). Therefore, within the material, the lateral and axial resolutions of the EM signals were smaller in value (see Equations (
2) and (
4)). This meant that there was an impact on the signal dispersion, depending on the size of the inclusions and fractures.
In the figures, metal marks can be seen. They were metallic tape on the rock that were bigger than the radar lateral resolution to ensure signal reflection. When the electromagnetic signals arrived at the metal, they were fully reflected; thus, a higher amplitude of the frequency tone was measured than that obtained by the variation in the dielectric permittivity of the rock–rock or rock–air interfaces (Fresnell equations). Hence, it helped to identify the rocks’ faces more easily. This is outlined by the red dashed lines.
Especially in the limestone case (
Figure 6a), we identified in images ‘A’ and ‘B’ more attenuated regions that corresponded to variations in the thickness of the rock. We signaled this using black dashed lines. Additionally, as expected, in the ‘B’ image, it can be seen that there were more reflected signals where the metallic mark was (and an absence of them in image ‘D’).
In the granite case, the ‘B’ and ‘D’ images presented pixel amplitudes that varied in a grainy way. This could have been caused by the high heterogeneity of the structures. In the photographs, the high quantity of black crystals, e.g., biotites and amphiboles, is visible, which had sizes in the order of the lateral spatial resolution. In image ‘A’, a crack on the surface is visible. This was generated when cutting the sample and only had a depth of a dozen microns.
Lastly, in the dolomite case, in the ’B’ and ’D’ images, it was possible to detect another kind of variation in the pixel amplitudes. They showed a strong preferential direction. In particular, the latter helped us to identify the front face of the second rock due to the high attenuation of the signals.
In
Figure 7a, we present a photograph and sketches of the experiment shown in
Figure 4d. In the drawings, we added in green some axial cuts with the corresponding numbers of radar images presented in
Figure 7b. The first radar image shows the first face of the first rock (slide 1). Slide 2 is within the first rock. From slides 3 (the back face of the first rock) to 15, the distance between two consecutive slides is 500
m. In
Figure 7a, the blue dashed rectangle signals a thickness variation in the first rock. It was thicker in the bottom part. This is why in slide 4 of
Figure 7b we can see in the upper part the reflection from the first face of the second rock, while the reflection in the bottom part was from the second face of the first rock. We indicated this with white solid rectangles. Additionally, in slide 9, we present in the white solid rectangles the reflections from the middle of the first face of the second rock and in slide 15, we present the last reflection obtained. The reflections from the second rock face were inclined with respect to the boundaries (see the white rectangle in slide 9) because the thickness of the first rock increased at the bottom (see the blue rectangle in
Figure 7a). Therefore, the reflected signals from the lower part of the second rock face arrived later.
The sequence of images from slide 3 to 15 were utilized to make a 3D reconstruction. We used the open-source image processing software FIJI
. We first imported the raw images into FIJI and then subtracted any background noise using the subtract background tool. Next, we used the FIJI plug-in ‘3D viewer’ to obtain the 3D image results. We did not interpolate the images. To help with the visualization, the distances used between the slides were 1.4 mm instead of 500
m.
Figure 7c presents an upper view of the 3D image. Additionally, we provide a video obtained using the same plug-in, showing an animation of the 3D images, in the
Supplementary Materials. In the video, it is possible to notice the variation in the thickness of the first rock. By generating images from different views of the 3D images and using in them the measuring tool from FIJI, it was possible to obtain different parameters for the variation in the thickness and fracture slope of the first rock. We measured a thickness variation of 1.43 mm and in the experiment, it was 1.8 mm. The gap slope (angle between rocks) was obtained using
Figure 7c. We obtained 6.5° for the thicker part and we measured
° in the experiment. In addition, we deduced that the slope in the image appeared clearly when the fracture thickness was around 1.4 mm. This value, as expected, was close to the radar’s axial resolution. However, we could see a gap between the rocks when the distance was around 500
m.
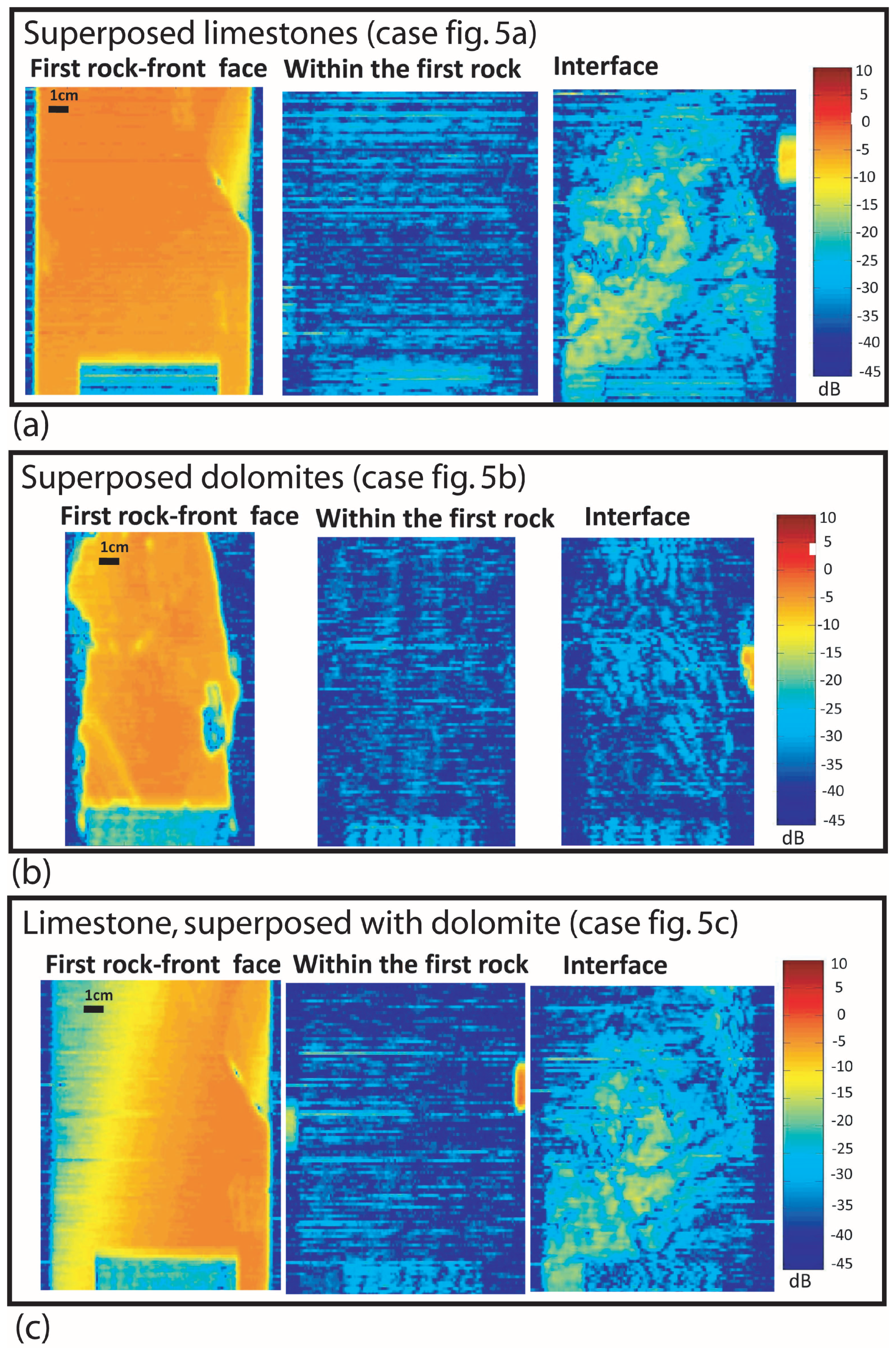
Figure 8 shows the results obtained from the configuration of superposed rocks shown in
Figure 5. For each case, we present the radar image from the front face of the first rock, within the first rock and the interface between them. In particular, the front face of the first rock image in
Figure 8c shows a color change that we do not see in
Figure 8a, which shows the same rock. This indicated that this last rock was tilted with regard to the direction of the electromagnetic signals. Additionally, it should be noted that the rock’s edge in
Figure 8b looks irregular. This was related to the rock shape.
In the reported cases, the interfaces were visible. However, we also performed tests by overlaying granite rocks in which the interfaces were not detected.
Although the aim of the study was to detect fractures and lithological changes, we estimated the refractive indices of the rocks to better understand the images and validate the experimental results obtained using the published indices. To do so, we used the distance found between images ‘A’ and ‘B’ in
Figure 6a–c and the thicknesses of the rocks ‘H’. In the acquisition program, the distance ‘D’ is estimated by considering that the wave propagates in the air. Therefore, with the obtained ‘
’ and ‘
’ values, the refractive indices were estimated using
. Thus,
,
and
. Although these values were approximate since the thicknesses of the samples varied, they are in accordance with the published indices [
25,
26]. In particular, the refractive index of limestone was closer to that of marble as the samples were partially metamorphosed [
22].
The values found showed that the wavelengths were reduced by more than half. If we take a 275 GHz center of frequency for an EM wave propagating in air, we obtain a wavelength of 1 mm, which is reduced to less than 500
m inside a rock. Moreover, as previously mentioned, this also had the impact of more than halving the lateral, as well as the axial, resolution (see Equations (
2) and (
4)). Therefore, the measurements were even more sensitive to smaller rock heterogeneities. This result also contributed toward explaining the amplitude changes between pixels in the images presented in
Figure 6.
We would like to mention that the measurements were carried out and repeated on different days but obtained the same results.
4. Discussion
In this manuscript, we demonstrated that it was possible to clearly detect fractures in rock at a penetration depth of about 1 cm using a 300 GHz radar. However, this depended to a large extent on the dielectric properties of the rocks and their water contents. In particular, the rock samples were not subjected to thermal treatment to evaporate the water contained in their pores and fractures, so the experiments were representative of what is found in nature. Hence, by heating rock samples, a higher penetration could possibly be achieved.
In this work, we did not focus on the heterogeneities or anisotropies of the rocks since this was not the aim of the study. Nevertheless, this information can be seen in the radar images presented in
Figure 6b,c. Chiefly, since the granite samples were isotropic, the variations in pixel amplitudes could have been caused by their high mineral heterogeneities. On the other hand, the dolomite samples were more homogeneous but also anisotropic, with higher porosity and water contents. Hence, the radar images might show a preferential direction caused by the water within the pores. In the limestone case, the pixel amplitudes did not vary as much as those in the two other cases. This could have been caused by the fact that limestone is more homogeneous than granite and less porous than dolomite.
Among the results presented in the case of superposed rocks, dolomite looked the least clear. This could have been due to its significant signal absorption behavior, possibly caused by the large amount of water contained in its pores. However, when we conducted the same experiment on granite (which has less absorption), we found no signals coming from the interface. This could have been caused by the fact that the granite is usually isotropic igneous rocks. On the contrary, this is not generally the case with limestone or dolomite, which are sedimentary rocks. This difference could be explained by
Figure 8a,b, in which we detected signals from the interface even when the samples were not obtained from the same rock (similar refractive indices). Hence, it could have been mainly caused by the different structure orientations between them, i.e., anisotropy. Note that when superposing the rocks, we did not take into account the orientations of their structures and no air layer was visible between them.
As seen in the results obtained by measuring the wedge air gaps (
Figure 7c), the angles found between the rocks were smaller than those measured in the experiments. These results were to be expected considering the effect of the geometry of the reflection of the first face of the second rock, i.e., the electromagnetic waves did not propagate orthogonally with respect to the samples. However, the angles were so small that they did not induce any impact. In the cases where the angles were more than 15 degrees, a formula that relates the dip angles between the reflector and the reflection must be used, as follows (Equation (2.1) in [
27]):
, where
is the angle measured in
Figure 7c. Thus,
, where Z1 and X1 are the distances measured to calculate the angle. The error was estimated by performing a propagation of uncertainty using the equation
. The absolute errors of Z1 and X1 were given by the lateral and axial resolutions of the radar system. Therefore, they were responsible for the sensitivity and accuracy of the detected angles. In our case, the estimated error was 2.3°.
The artificial fractures measured in the study contained air. However, in nature, fractures can also contain water or other minerals. In these cases, other approaches, such as that developed in [
28], should be applied to obtain information on the dielectric permittivity and thicknesses involved in order to identify the fracture content.
5. Conclusions
In this manuscript, we showed that the use of a 300 GHz FMCW radar allowed for the detection and quantification of millimeter fractures with a sensitivity of up to 500 m at a 1 cm penetration depth in reservoir and construction rocks. Radar images of 121 cm with 1 mm pixels were obtained in 15 min. We also showed that with the acquired images, three-dimensional reconstructions of the fractures could be carried out.
In addition, it was possible to measure lithological changes in two different rock types that were superposed and in two superposed samples from the same rock.
All of these results could be useful for the quality control of construction materials, the characterization of reservoirs, the inspection of buildings or architectural art and even the detection of rock erosion.
Although this method could be used to study any rock material, the results will depend on the absorption, porosity and water content of the constituent minerals, among other factors. Therefore, further studies should be carried out on other reservoir and construction rocks in order to obtain results on a wider range of samples of interest. Additionally, the impacts of rock heterogeneities and anisotropies in high-frequency radar images should be studied as well.