SARAL’s Full Mission Reprocessing: Improvement with the GDR-F Standard
Abstract
1. Introduction
2. Materials and Methods
2.1. Orbit
2.2. Microwave Radiometer Derived Parameters
- The sea surface temperature (SST) for a better estimation of the surface emissivity. In the GDR-F products, the NOAA (National Oceanic and Atmospheric Administration) OISST (Optimum Interpolation SST) is used as input.
- The atmospheric temperature lapse rate (γ 800), the temperature decrease slope from the surface to the 800 hPa layer of the atmosphere, that reduces systematic biases over upwelling regions. A climatological map of γ 800 is used as input.
2.3. Level 2 Processing
- -
- Altimeter range;
- -
- SWH (significant Wave Height);
- -
- Sigma naught;
- -
- Square of the mispointing angle.
2.4. Auxiliary Models
3. Results and Discussions
3.1. Validation Overview
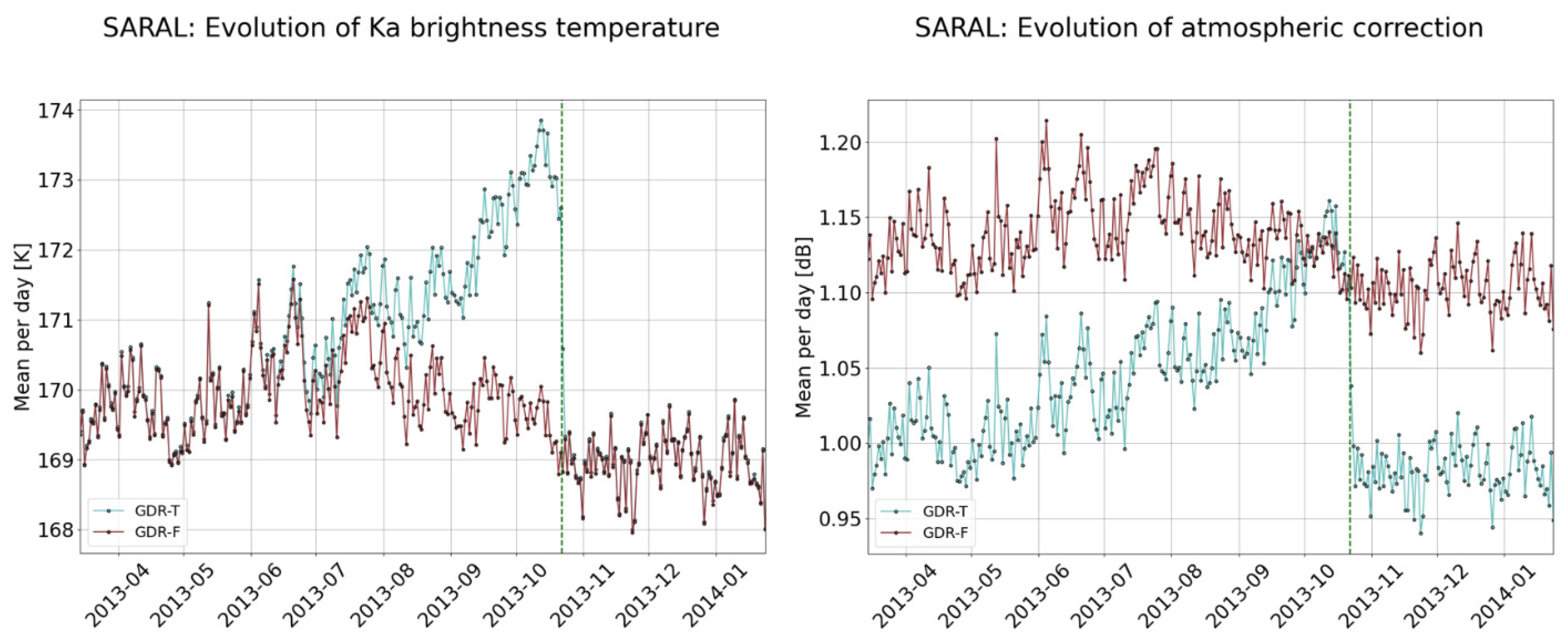
3.2. Analysis of Altimeter and Radiometer Parameters
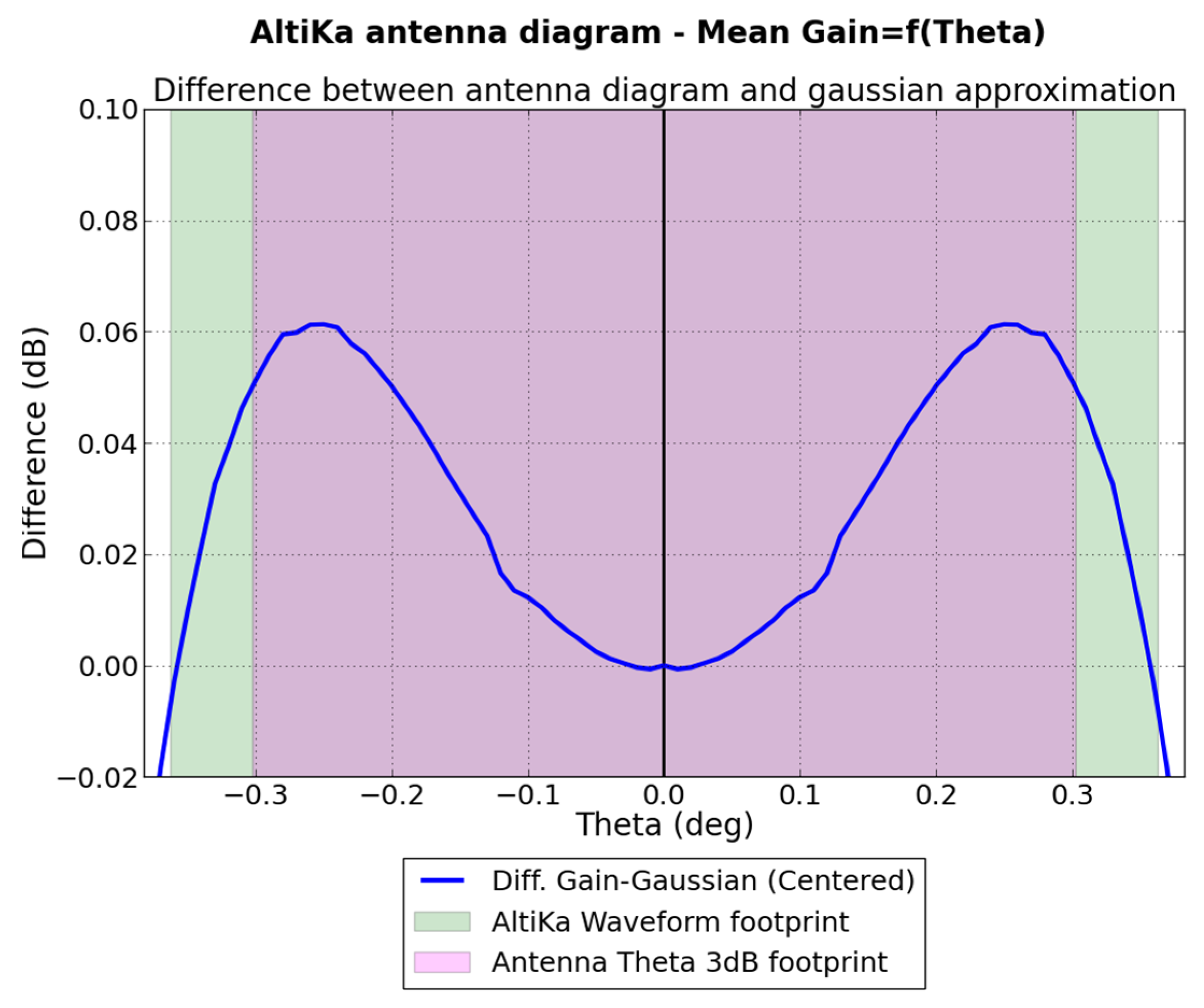
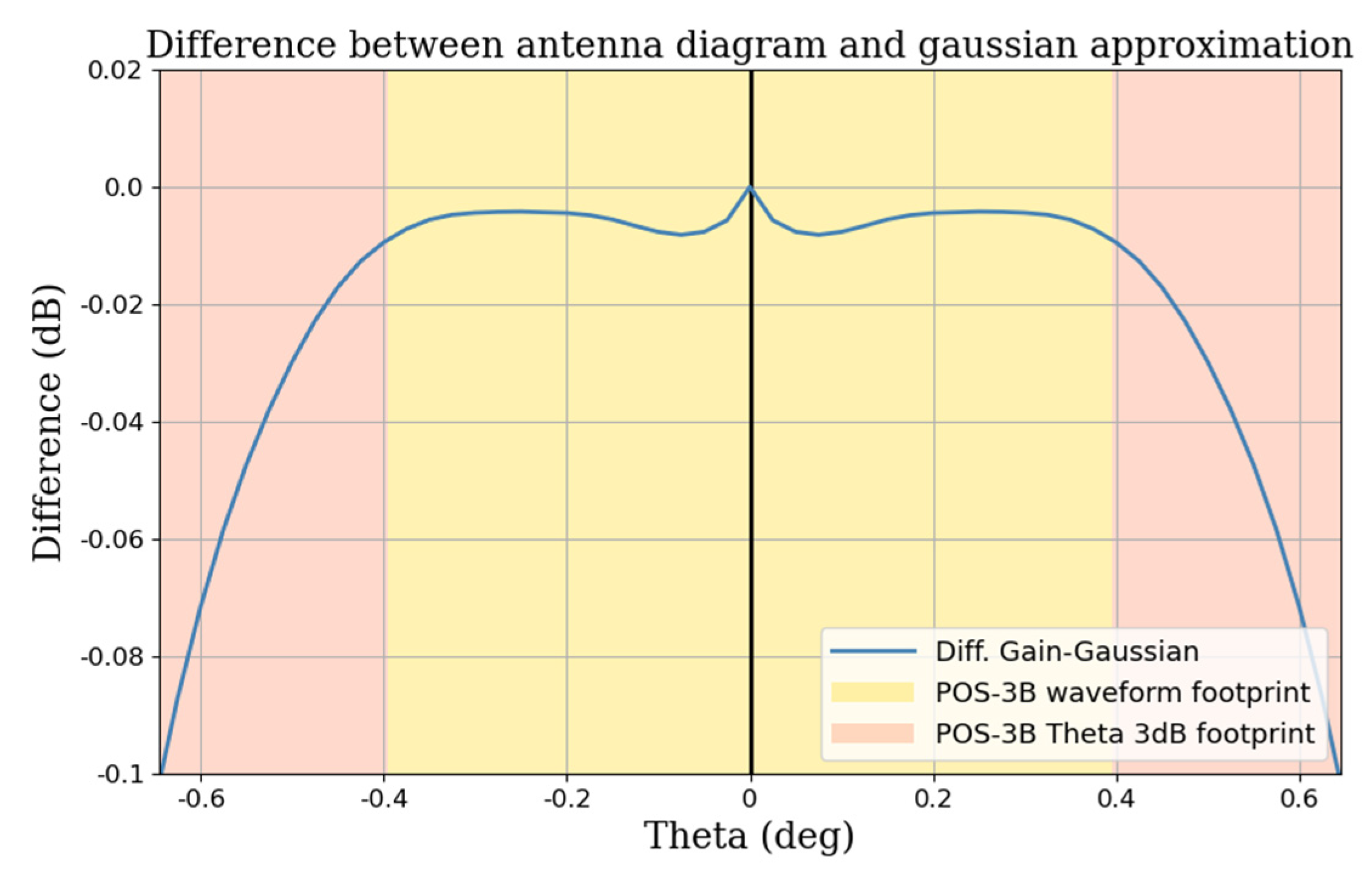
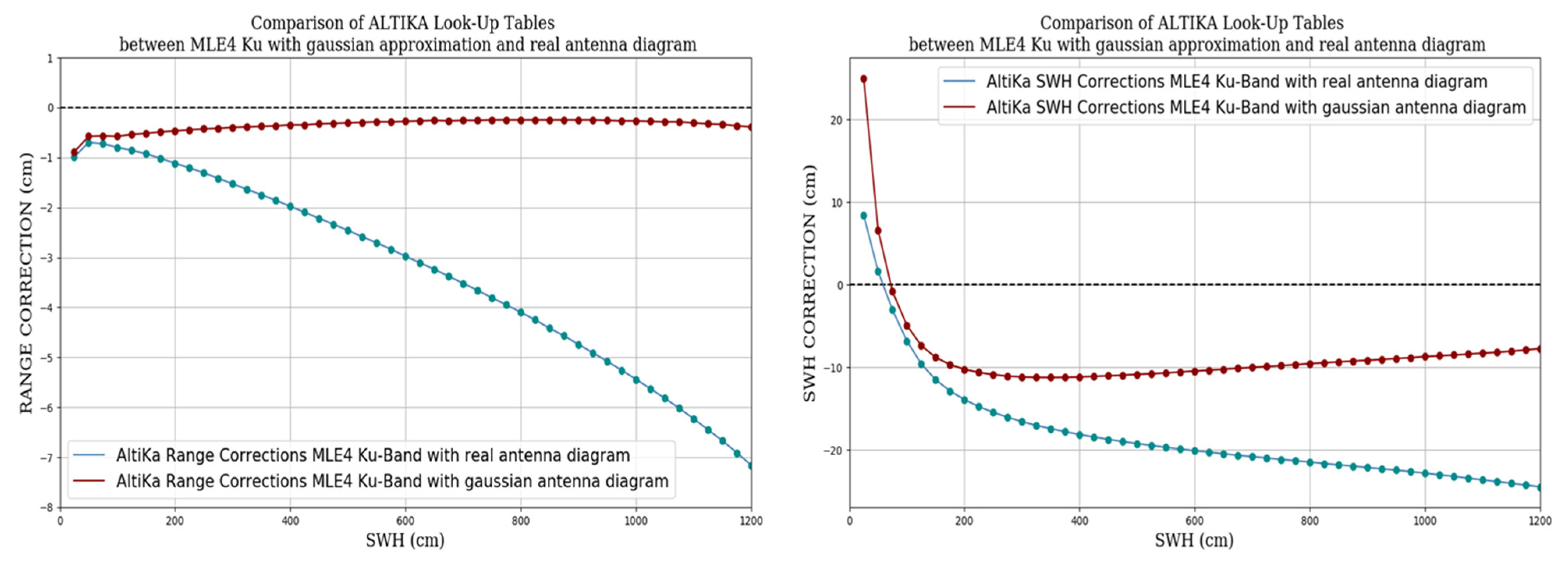
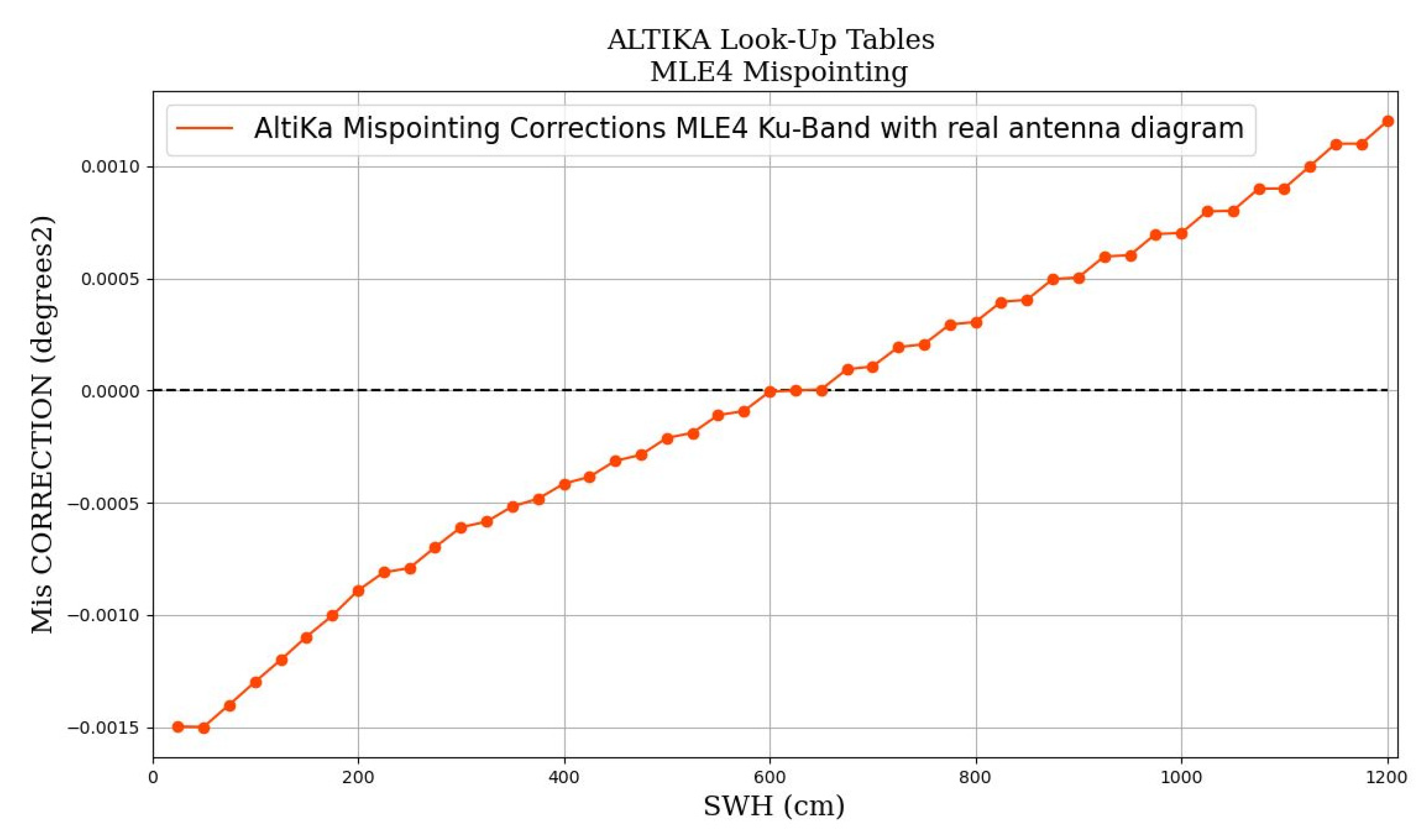
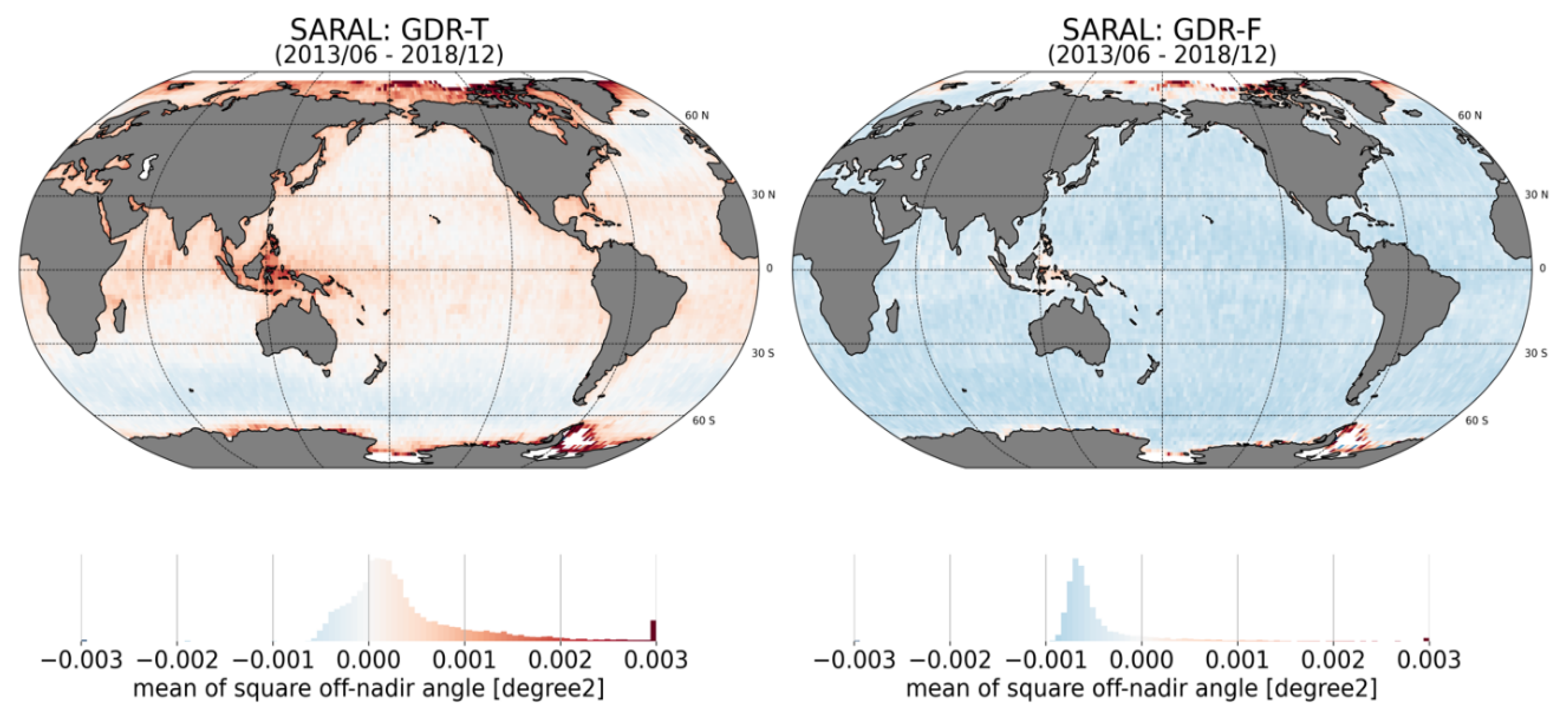
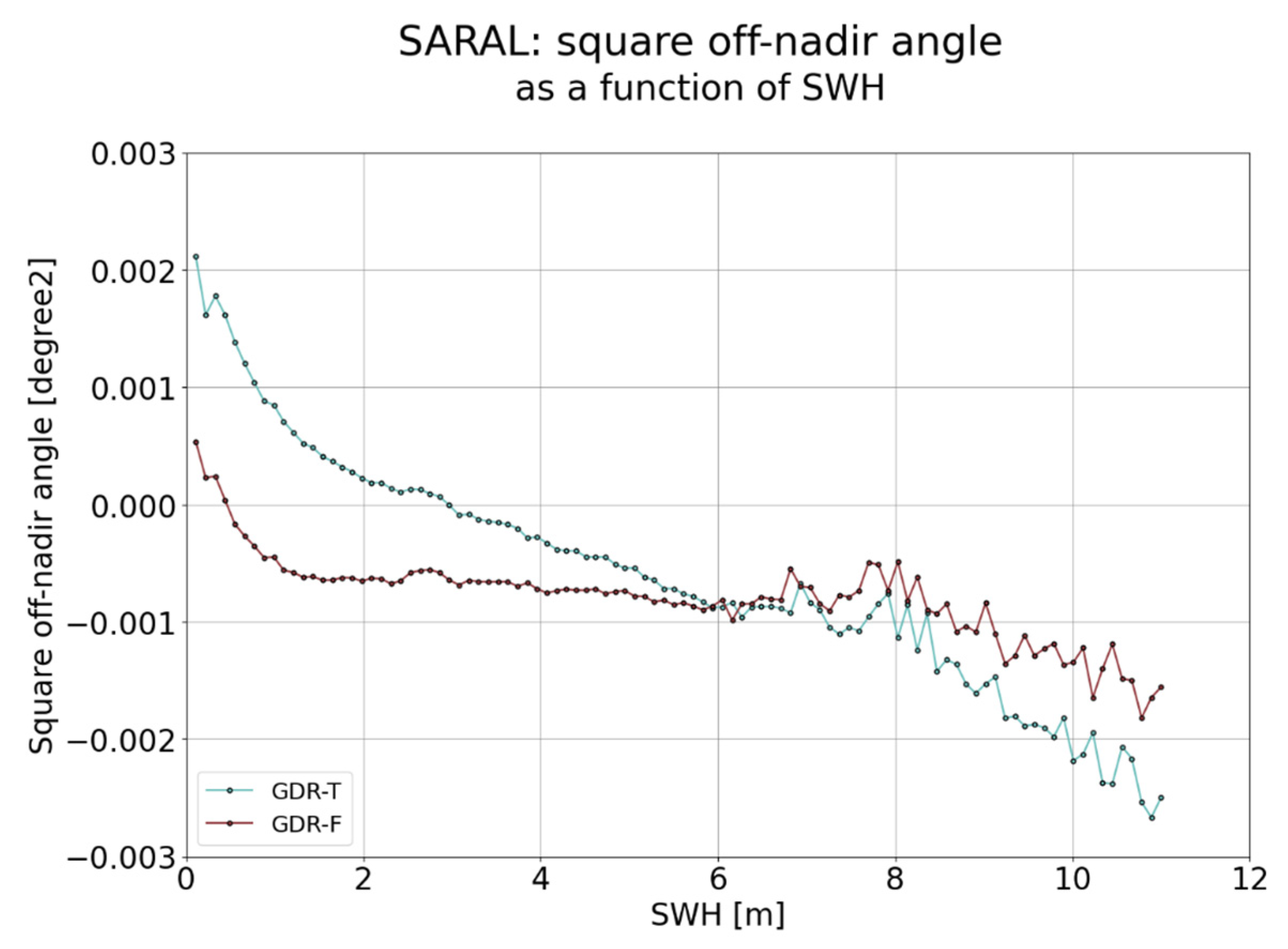
3.2.1. Waveform-Derived Square Off-Nadir Angle
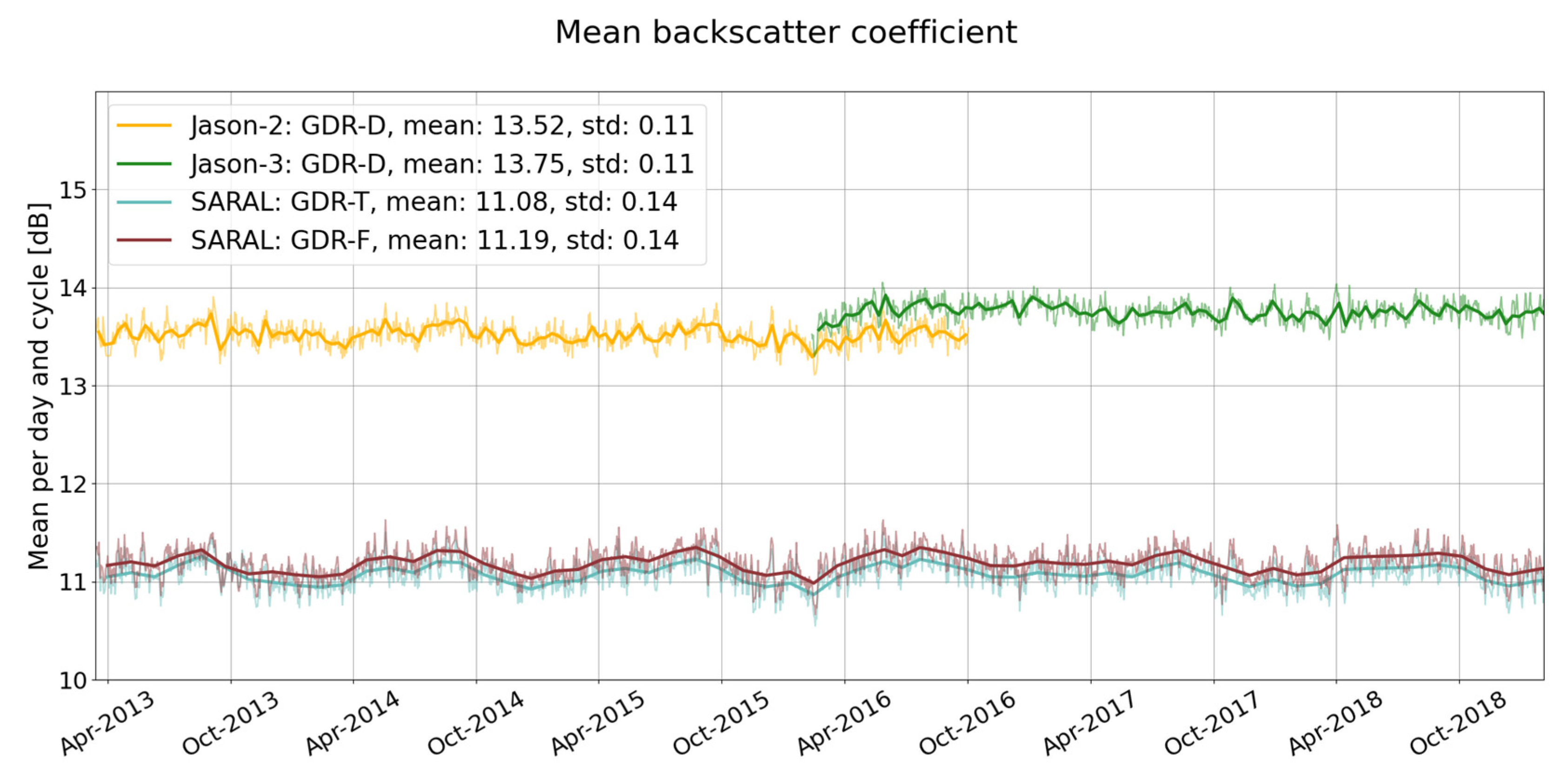
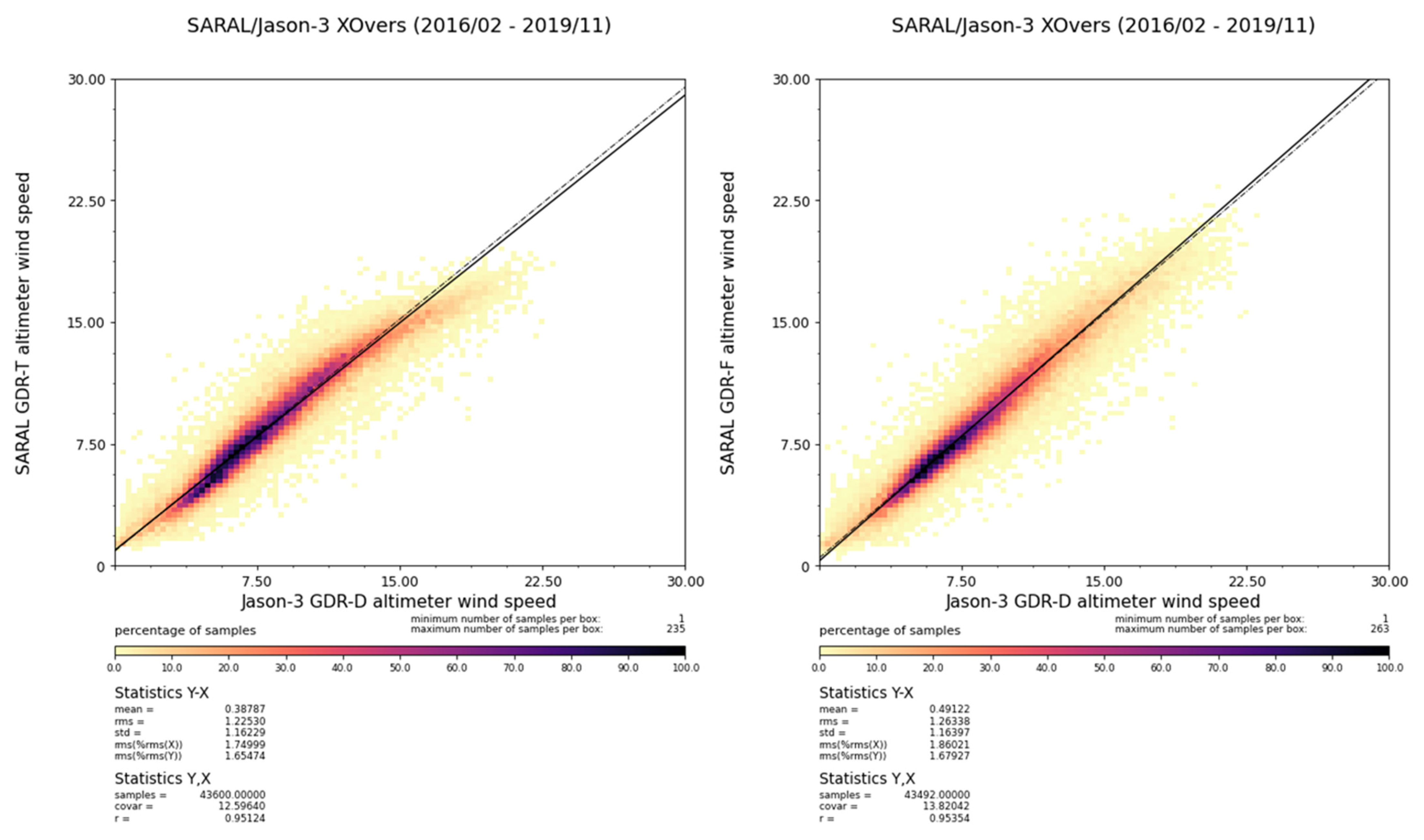
3.2.2. Backscatter Coefficient and Wind Speed
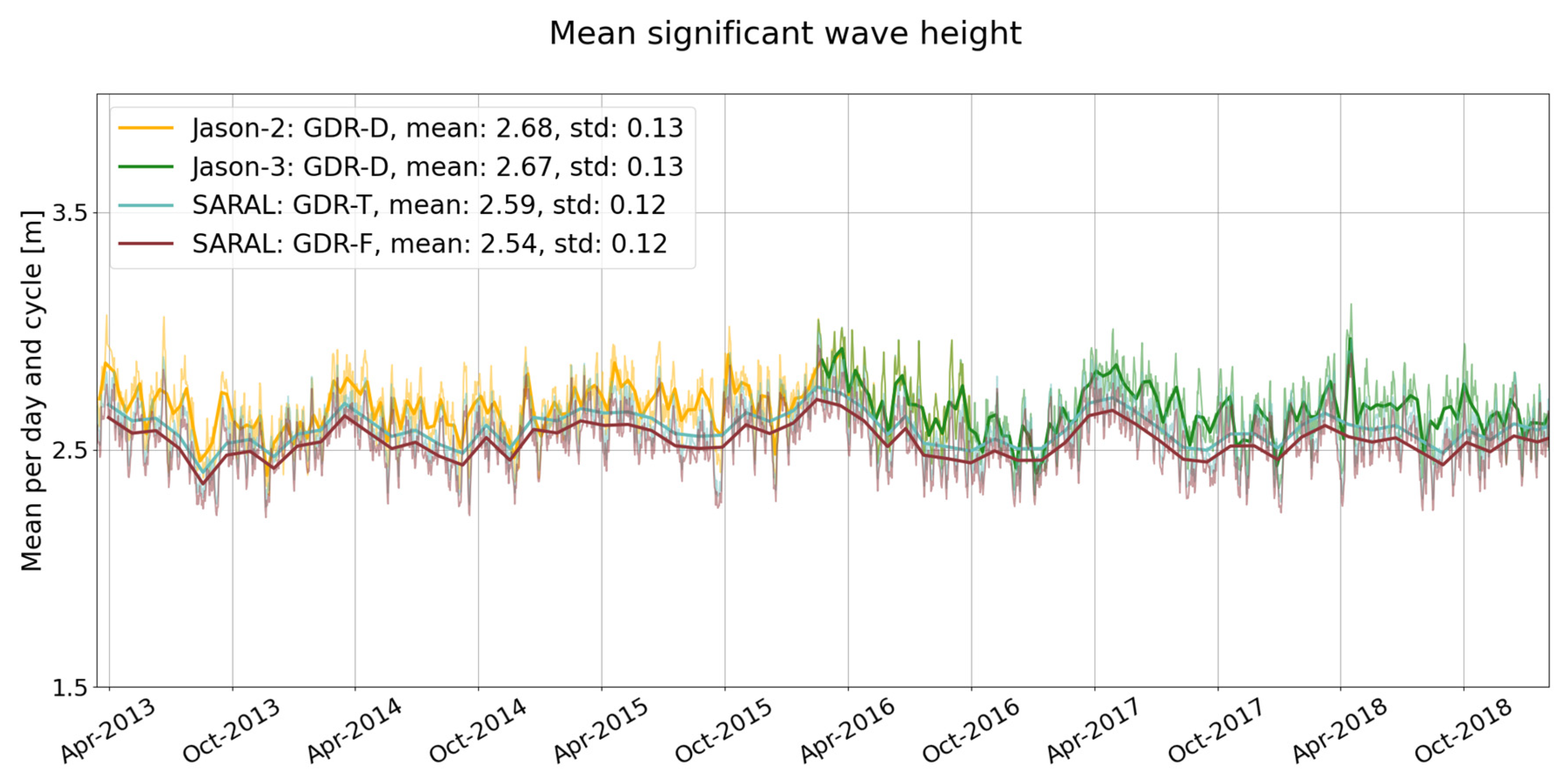
3.2.3. Significant Wave Height (SWH) and Sea State Bias (SSB)
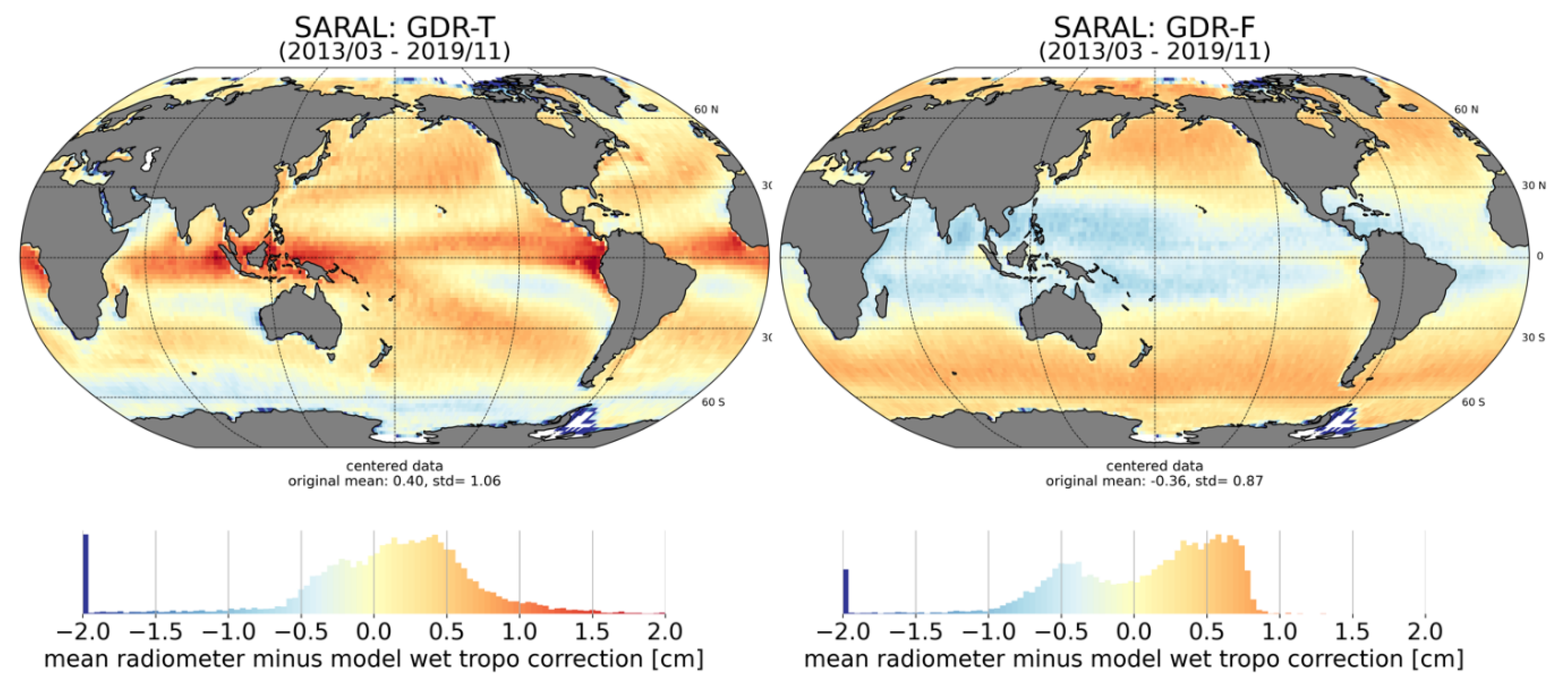
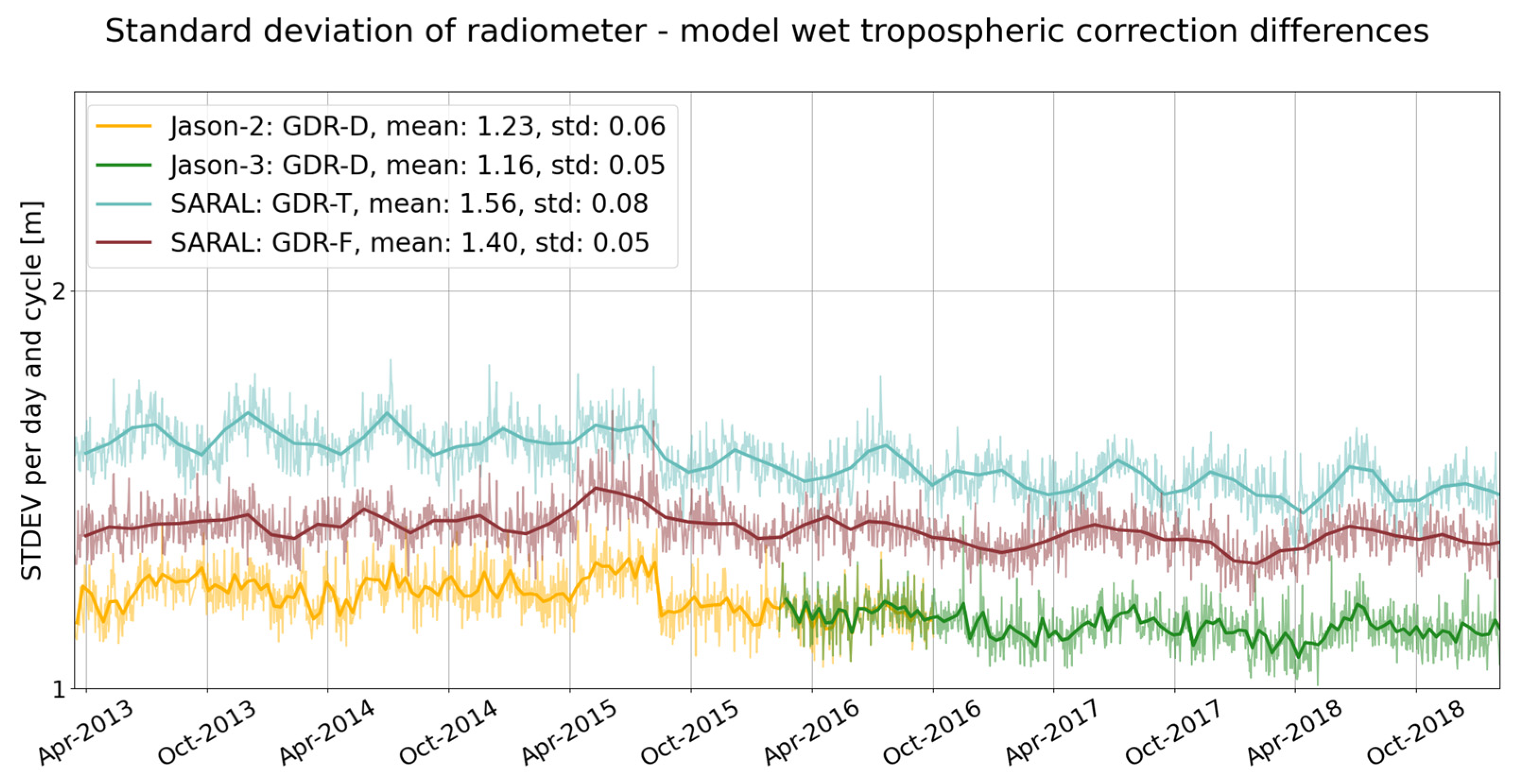
3.2.4. Wet Troposphere Correction (WTC)
3.3. Sea Level Performance
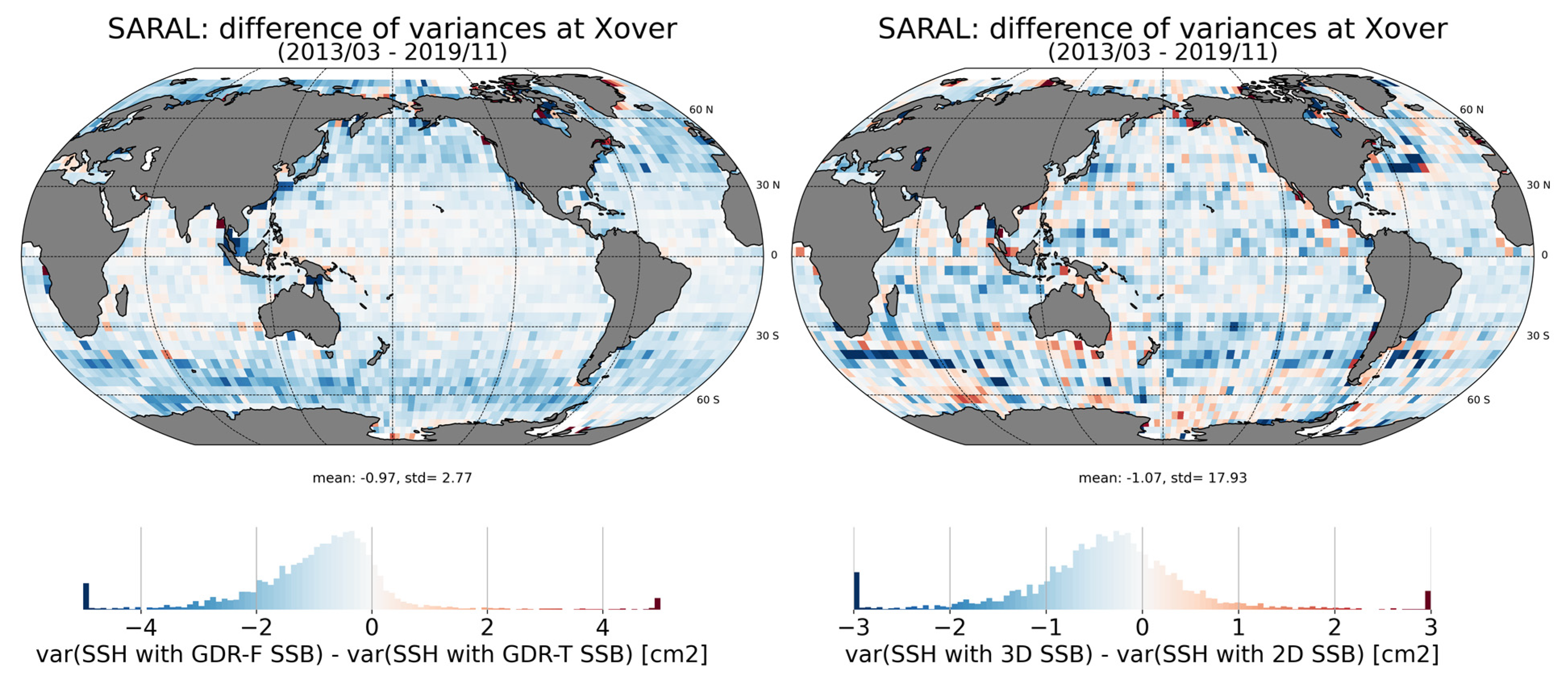
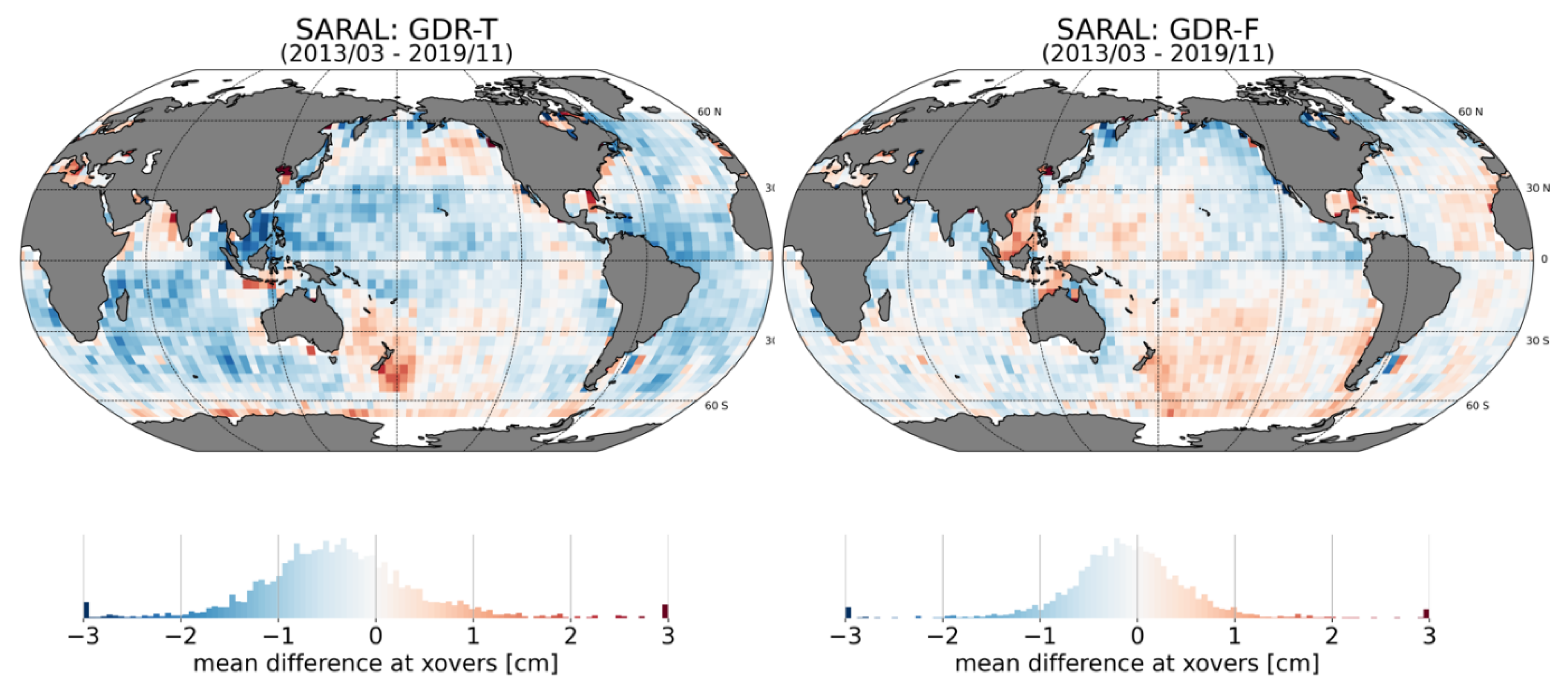
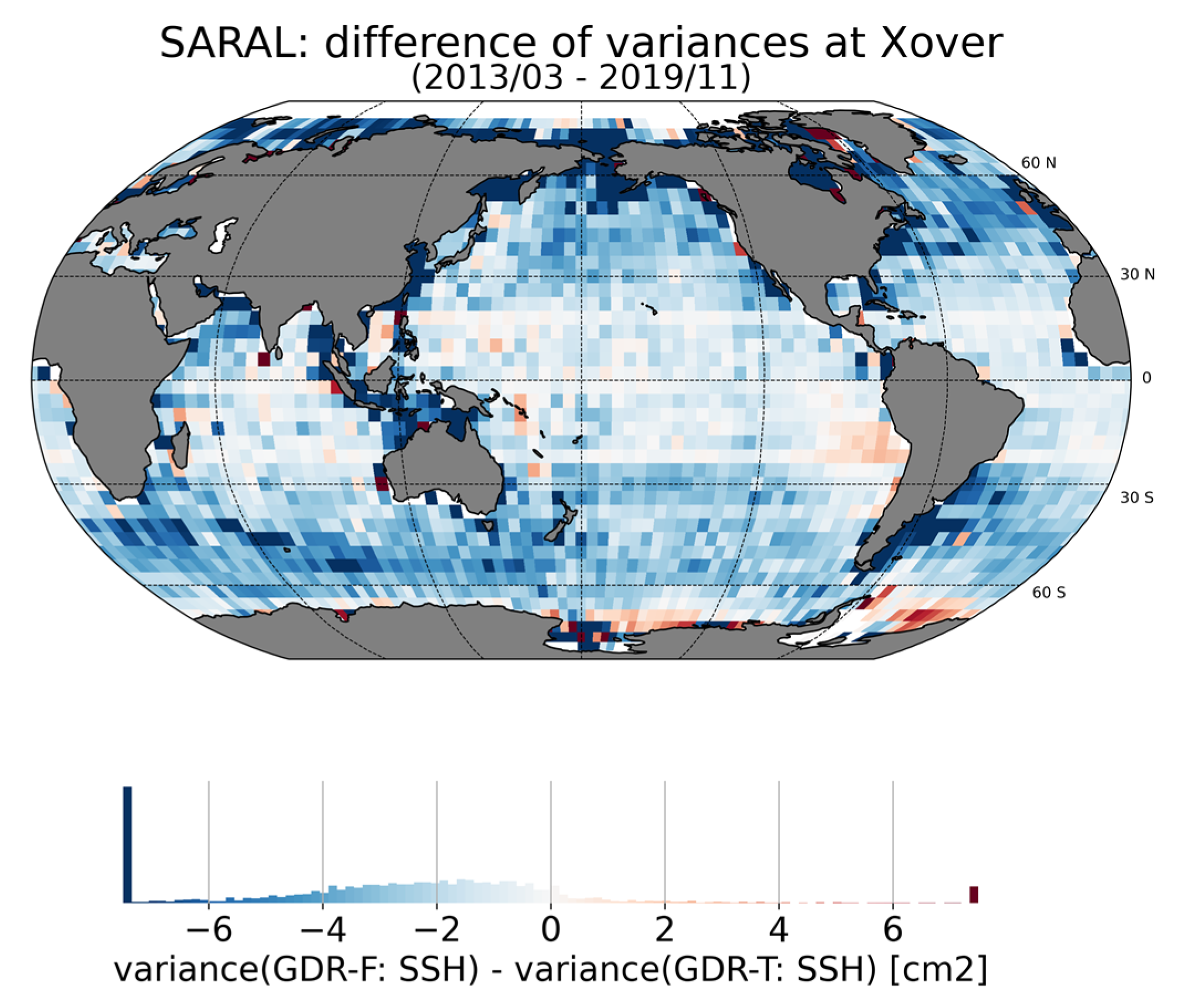
3.3.1. Sea Surface Height (SSH) Cross-Over Analysis
- A maximum time difference of 10 days;
- High-latitude regions are not considered (|latitude| < 66);
- Weighting the crossover distribution by latitudes, where weighting depends on the crossovers’ theoretical density. This also reduces the amplitude of the annual signal.
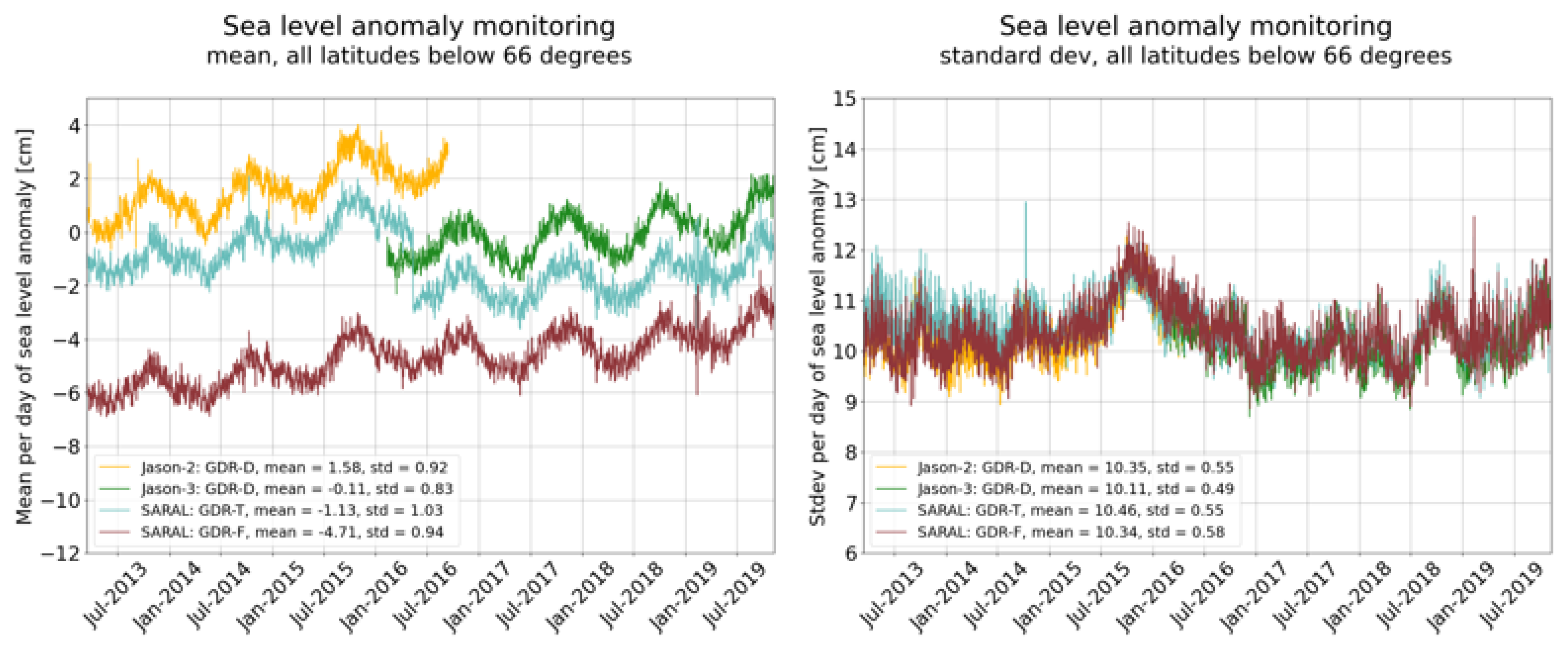
3.3.2. Analysis of Sea Level Anomalies (SLA) and Global Mean Sea Level (GMSL)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Verron, J.; Sengenes, P.; Lambin, J.; Noubel, J.; Steunou, N.; Guillot, A.; Picot, N.; Coutin-Faye, S.; Gairola, R.; Raghava Murthy, D.V.A.; et al. The SARAL/AltiKa altimetry satellite mission. Mar. Geod. 2015, 38 (Suppl. 1), 2–21. [Google Scholar] [CrossRef]
- Jettou, G.; Rousseau, M.; Daguze, J.-A.; Prandi, P.; Bignalet-Cazalet, F. SARAL GDR Quality Assessment Reports. Available online: https://www.aviso.altimetry.fr/en/data/calval/systematic-calval/validation-reports/saral-gdr.html (accessed on 7 May 2023).
- Jettou, G.; Rousseau, M.; Ollivier, A. SARAL/AltiKa Validation and Cross Calibration Activities, Annual Performance Reports. Available online: https://www.aviso.altimetry.fr/en/data/calval/systematic-calval/annual-reports/saral.html (accessed on 7 May 2023).
- Bignalet-Cazalet, F.; Couhert, A.; Queruel, N.; Urien, S.; Carrere, L.; Tran, N.; Jettou, G. SARAL, AltiKa Products Handbook. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/data/tools/SARAL_Altika_products_handbook.pdf (accessed on 7 May 2023).
- Philipps, S.; Prandi, P.; Pignot, V. Saral/Altika Validation and Cross Calibration Activities (Annual Performance Report 2013). 2013. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/calval/validation_report/AL/annual_report_al_2013.pdf (accessed on 7 May 2023).
- Obligis, E.; Rahmani, A.; Eymard, L.; Labroue, S.; Bronner, E. An improved retrieval algorithm for water vapor retrieval: Application to the envisat microwave radiometer. IEEE Trans. Geosci. Remote Sens. 2009, 47, 3057–3064. [Google Scholar] [CrossRef]
- Amarouche, L.; Thibaut, P.; Zanife, O.Z.; Dumont, J.-P.; Vincent, P.; Steunou, N. Improving the Jason-1 ground retracking to better account for attitude effects. Mar. Geod. 2004, 27, 171–197. [Google Scholar]
- Brown, G.S. The average impulse response of a rough surface and its applications. IEEE Trans. Antenna Propag. 1977, AP25, 67–74. [Google Scholar] [CrossRef]
- Thibaut, P.; Poisson, J.C.; Bronner, E.; Picot, N. Relative performance of the MLE3 and MLE4 retracking algorithms on jason-2 altimeter waveforms. Mar. Geod. 2010, 33 (Suppl. 1), 317–335. [Google Scholar] [CrossRef]
- Thibaut, P.; Amarouche, L.; Zanife, O.-Z.; Steunou, N.; Vincent, P.; Raizonville, P. Jason-1 Altimeter Ground Processing Look-Up Correction Tables. Mar. Geod. 2004, 27, 409–431. [Google Scholar] [CrossRef]
- Le Gac, S.; Boy, F.; Guillot, A.; Desjonqueres, J.D.; Picot, N.; Poisson, J.C.; Piras, F.; Bracher, G.; Thibaut, P.; Valladeau, G. Impact of the Antenna Diagram Approximation in Conventional Altimetry WF Processing, Application to SARAL/AltiKa Data, Oral Presentation at OSTST, Reston, USA, 2015. Available online: https://meetings.aviso.altimetry.fr/fileadmin/user_upload/tx_ausyclsseminar/files/OSTST2015/IPM-04-_LeGac_Talk_AltiKaAntennaDiagram_OSTST2015.pdf (accessed on 7 May 2023).
- Scharroo, R.; Lillibridge, J.L. Non-parametric sea-state bias models and their relevance to sea level change studies. In Proceedings of the 2004 Envisat & ERS Symposium, Salzburg, Austria, 6–10 September 2004. [Google Scholar]
- Law-Chune, S.; Aouf, L. Wave effects in global ocean modelling: Parametrizations vs. forcing from a wave model. Ocean Dyn. 2018, 68, 1736–1758. [Google Scholar] [CrossRef]
- Pujol, M.-I.; Schaeffer, P.; Faugere, Y.; Raynal, M.; Dibarboure, G.; Picot, N. Gauging the improvement of recent mean sea surface models: A new approach for identifying and quantifying their errors. J. Geophys. Res. Ocean. 2018, 123, 5589–5911. [Google Scholar] [CrossRef]
- Andersen, O.B.; Stenseng, L.; Piccioni, G.; Knudsen, P. The DTU15 MSS (Mean Sea Surface) and DTU15LAT (Lowest Astronomical Tide) Reference Surface. In Proceedings of the Abstract from ESA Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; Available online: https://orbit.dtu.dk/en/publications/the-dtu15-mss-mean-sea-surface-and-dtu15lat-lowest-astronomical-t (accessed on 7 May 2023).
- Mulet, S.; Rio, M.-H.; Etienne, H.; Artana, C.; Cancet, M.; Dibarboure, G.; Feng, H.; Husson, R.; Picot, N.; Provost, C.; et al. The new CNES-CLS18 global mean dynamic topography. Ocean Sci. 2021, 17, 789–808. [Google Scholar] [CrossRef]
- Carrère, L.; Lyard, F. Modeling the Barotropic Response of the Global Ocean to Atmospheric Wind and Pressure Forcing—Comparisons with Observations. Geophys. Res. Lett. 2003, 30, 8. [Google Scholar] [CrossRef]
- Cartwright, D.E.; Edden, A.C. Corrected tables of tidal harmonics. Geophys. J. Int. 1973, 33, 253–264. [Google Scholar] [CrossRef]
- Desai, S.; Wahr, J.; Beckley, B. Revisiting the pole tide for and from satellite altimetry. J. Geod. 2015, 89, 1233–1243. [Google Scholar] [CrossRef]
- Desai, S.D.; Ries, J.C. Conventional Model Update for Rotational Deformation, in Fall AGU Meeting. New Orleans, LA, USA, 2017. Available online: https://repositories.lib.utexas.edu/handle/2152/75555 (accessed on 7 May 2023).
- Zaron, E.D. Baroclinic tidal sea level from exact repeat mission altimetry. J. Phys. Oceanogr. 2019, 49, 193–210. [Google Scholar] [CrossRef]
- Valladeau, G.; Thibaut, P.; Picard, B.; Poisson, J.C.; Tran, N.; Picot, N.; Guillot, A. Using SARAL/AltiKa to Improve Ka-Band Altimeter Measurements for Coastal Zones, Hydrology and Ice: The PEACHI Prototype. Mar. Geod. 2015, 38 (Suppl. 1), 124–142. [Google Scholar] [CrossRef]
- Gourrion, J.; Vandemark, D.; Bailey, S.; Chapron, B.; Gommenginger, G.P.; Challenor, P.G.; Srokosz, M.A. A two-parameter wind speed algorithm for Ku Band altimeters. J. Atmos. Ocean. Technol. 2002, 19, 2030–2048. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Feng, H.; Guillot, A.; Picot, N. Updated Wind Speed and Sea State Bias Models for Ka-Band Altimetry, 2014 SARAL/AltiKa Workshop, Lake Constance, Germany. Available online: https://meetings.aviso.altimetry.fr/fileadmin/user_upload/tx_ausyclsseminar/files/Poster_PEACHI_ssb_tran2014.pdf (accessed on 7 May 2023).
- Lillibridge, J.; Scharroo, R.; Abdalla, S.; Vandemark, D. One-and Two-Dimensional Wind Speed Models for Ka-Band Altimetry. J. Atmos. Ocean. Technol. 2013, 31, 630–638. [Google Scholar] [CrossRef]
- The WAMDI group. The Wam model–A third generation ocean wave prediction model. J. Phys. Ocenography 1988, 18, 1775–1810. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Zaron, E.D.; Thibaut, P.; Dibarboure, G.; Picot, N. Assessing the effects of sea-state related errors on the precision of high-rate Jason-3 altimeter sea level data. Adv. Space Res. 2019, 68, 963–977. [Google Scholar] [CrossRef]
- Tran, N.; Vandemark, D.; Labroue, S.; Feng, H.; Chapron, B.; Tolman, H.L.; Lambin, J.; Picot, N. Sea state bias in altimeter sea level estimates determined by combining wave model and satellite data. J. Geophys. Res. 2010, 115, C03020. [Google Scholar] [CrossRef]
- Jettou, G.; Rousseau, M. SARAL/AltiKa Validation and Cross Calibration Activities, 2021 Annual Performance Report. Available online: https://www.aviso.altimetry.fr/fileadmin/documents/calval/validation_report/AL/SALP-RP-MA-EA-23530-CLS_Annual_Report_SARAL_2021.pdf#page=108&zoom=100,102,143 (accessed on 7 May 2023).


| MODEL | GDR-T | GDR-F |
|---|---|---|
| DRY TROPOSPHERE RANGE CORRECTION | Using ECMWF atmospheric pressures and models for S1 and S2 atmospheric tides | |
| WET TROPOSPHERE RANGE CORRECTION FROM MODEL | ECMWF model | |
| IONOSPHERE CORRECTION | Global Ionosphere TEC Maps from JPL | |
| SEA STATE BIAS | Hybrid SSB model from [12] | Two empirical solutions were fitted to one year of SARAL GDR-F data: - a 2-parameter model using SWH and wind speed from altimeter measurements (standard version) - a 3-parameter model using SWH, wind speed, and the mean wave period T02 from the Meteo-France WAM model [13] |
| BATHYMETRY | DTM2000.1 | ACE2 (from EAPRS Laboratory) |
| MEAN SEA SURFACE MODEL | MSS CNES-CLS11, MSS CNES CLS15 from cycle 34 | CNES-CLS 2015 model [14] and DTU 2015 model [15] |
| MEAN DYNAMIC TOPOGRAPHY MODEL | MDT CNES-CLS09 | MDT_CNES-CLS-2018 [16] |
| GEOID | MDT CNES-CLS09 | EGM2008 |
| INVERSE BAROMETER CORRECTION | Using ECMWF atmospheric pressures after removing S1 and S2 atmospheric tides | |
| NON-TIDAL HIGH FREQUENCY DEALIASING CORRECTION | Mog2D high-resolution ocean model [17] | |
| OCEAN TIDE | GOT4.8 FES2012 + S1 and M4 ocean tides S1 and M4 load tides are ignored | GOT4.10c model and FES2014b |
| SOLID EARTH TIDE | From tidal potential of Cartwright and Edden [1973] Corrected tables of tidal harmonics [18] | |
| POLE TIDE | Equilibrium model | Desai model [19] with updated Mean Pole Location (MPL) [20] |
| INTERNAL TIDE | None | HRET-v7.0 model [21] |
| WIND SPEED MODEL | ECMWF model | ECMWF model |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jettou, G.; Rousseau, M.; Piras, F.; Simeon, M.; Tran, N. SARAL’s Full Mission Reprocessing: Improvement with the GDR-F Standard. Remote Sens. 2023, 15, 2604. https://doi.org/10.3390/rs15102604
Jettou G, Rousseau M, Piras F, Simeon M, Tran N. SARAL’s Full Mission Reprocessing: Improvement with the GDR-F Standard. Remote Sensing. 2023; 15(10):2604. https://doi.org/10.3390/rs15102604
Chicago/Turabian StyleJettou, Ghita, Manon Rousseau, Fanny Piras, Mathilde Simeon, and Ngan Tran. 2023. "SARAL’s Full Mission Reprocessing: Improvement with the GDR-F Standard" Remote Sensing 15, no. 10: 2604. https://doi.org/10.3390/rs15102604
APA StyleJettou, G., Rousseau, M., Piras, F., Simeon, M., & Tran, N. (2023). SARAL’s Full Mission Reprocessing: Improvement with the GDR-F Standard. Remote Sensing, 15(10), 2604. https://doi.org/10.3390/rs15102604








