Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.1.1. Overview of SDGSAT-1
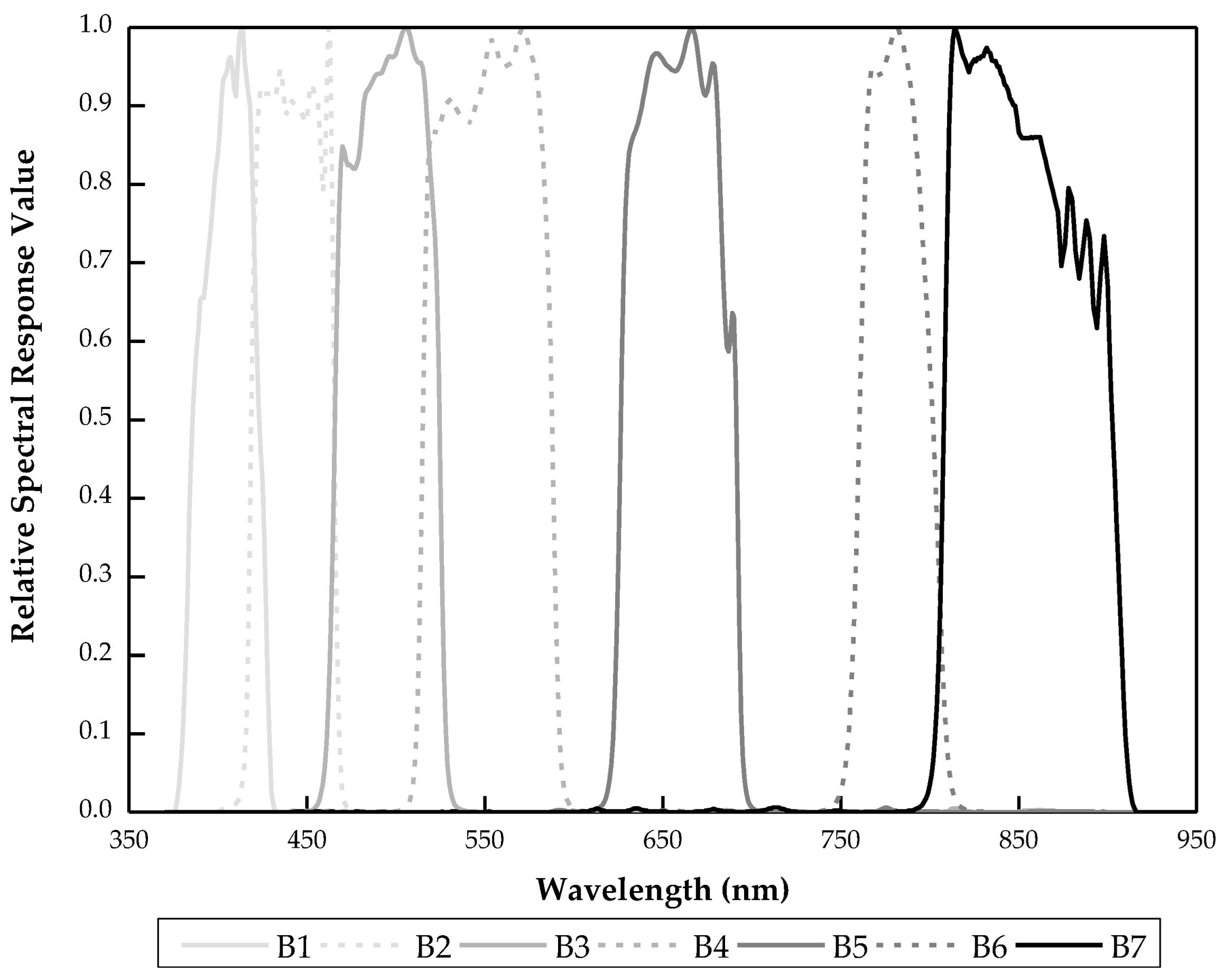
2.1.2. SDGSAT-1 MII
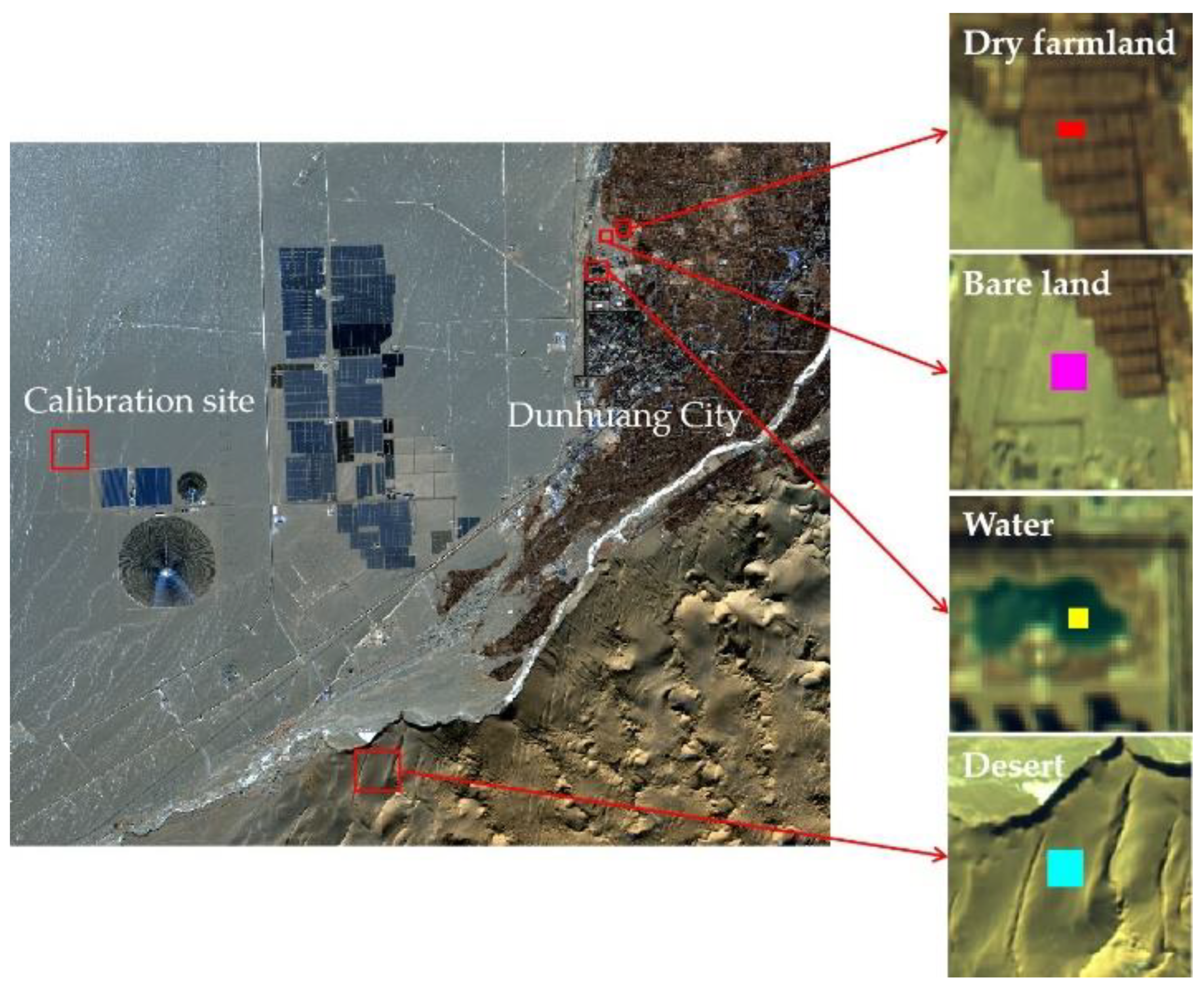
2.1.3. Calibration Site and Image Data Acquisition
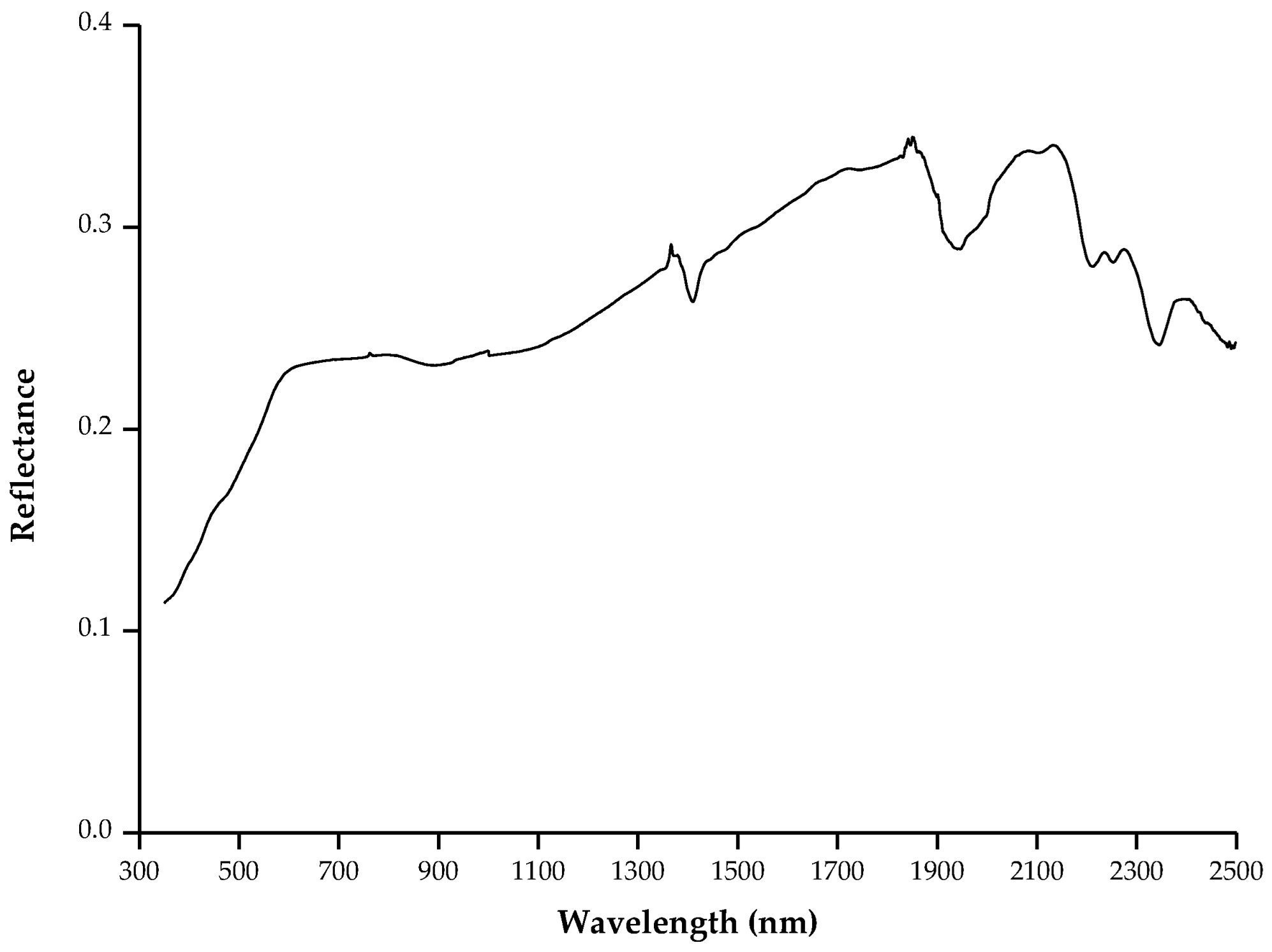
2.1.4. Simultaneous Measurement of Ground Reflectance
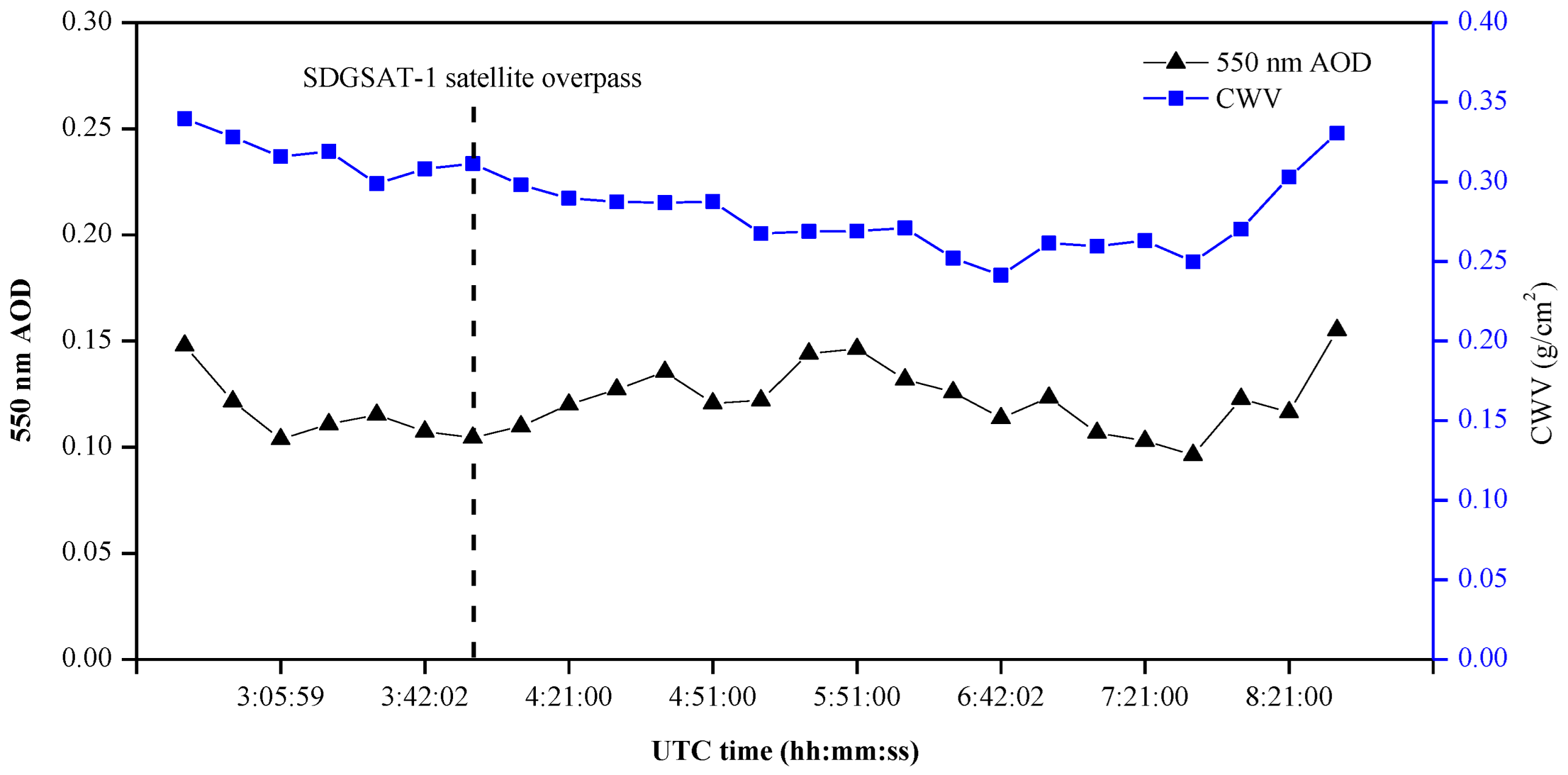
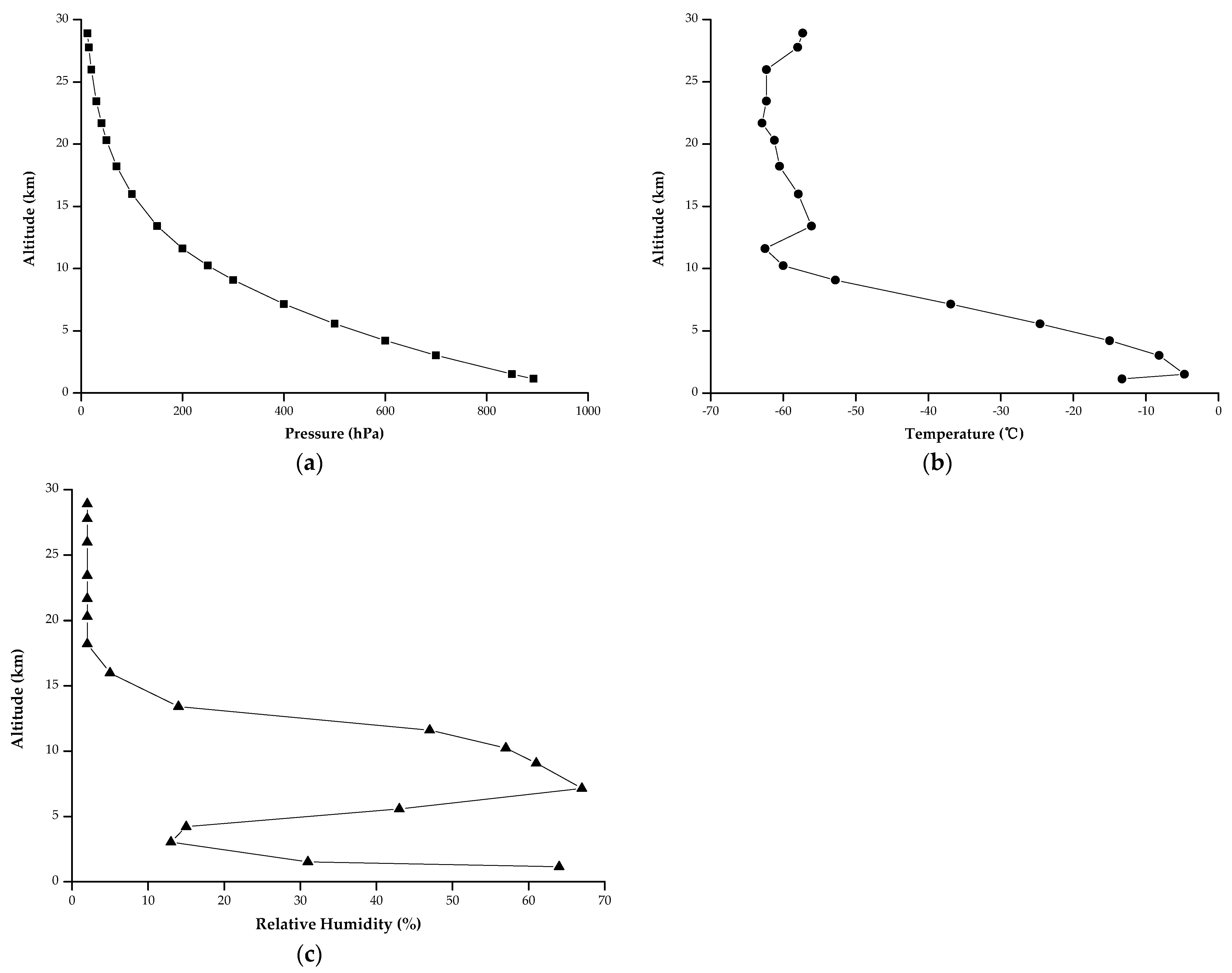
2.1.5. Simultaneous Measurement of Atmospheric Parameters
2.2. Methods
2.2.1. Radiometric Calibration Method
2.2.2. Radiative Transfer Calculations
2.2.3. Calibration Uncertainty Estimation
2.2.4. Cross Validation
3. Results
4. Discussion
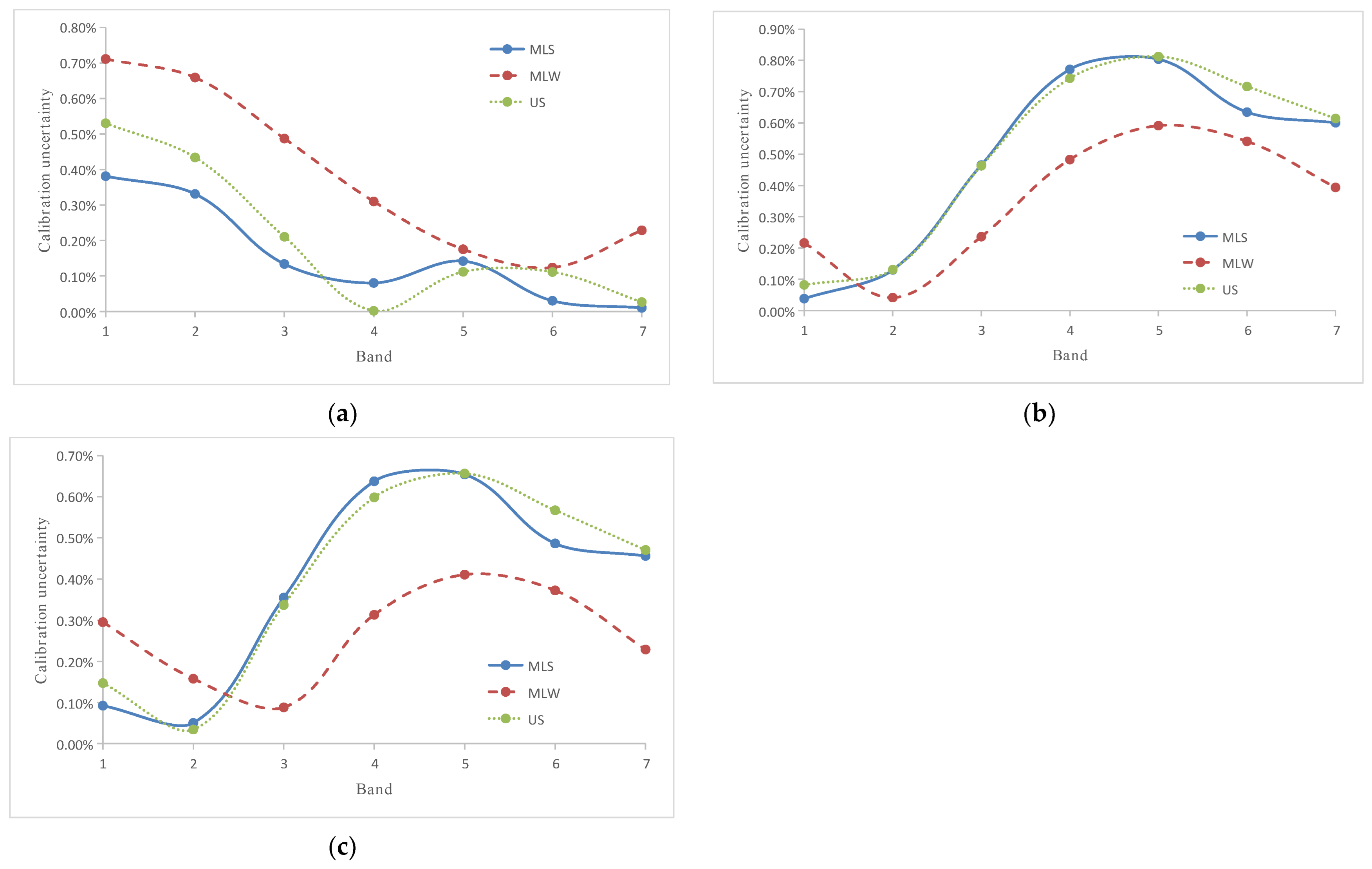
4.1. Uncertainty Analysis
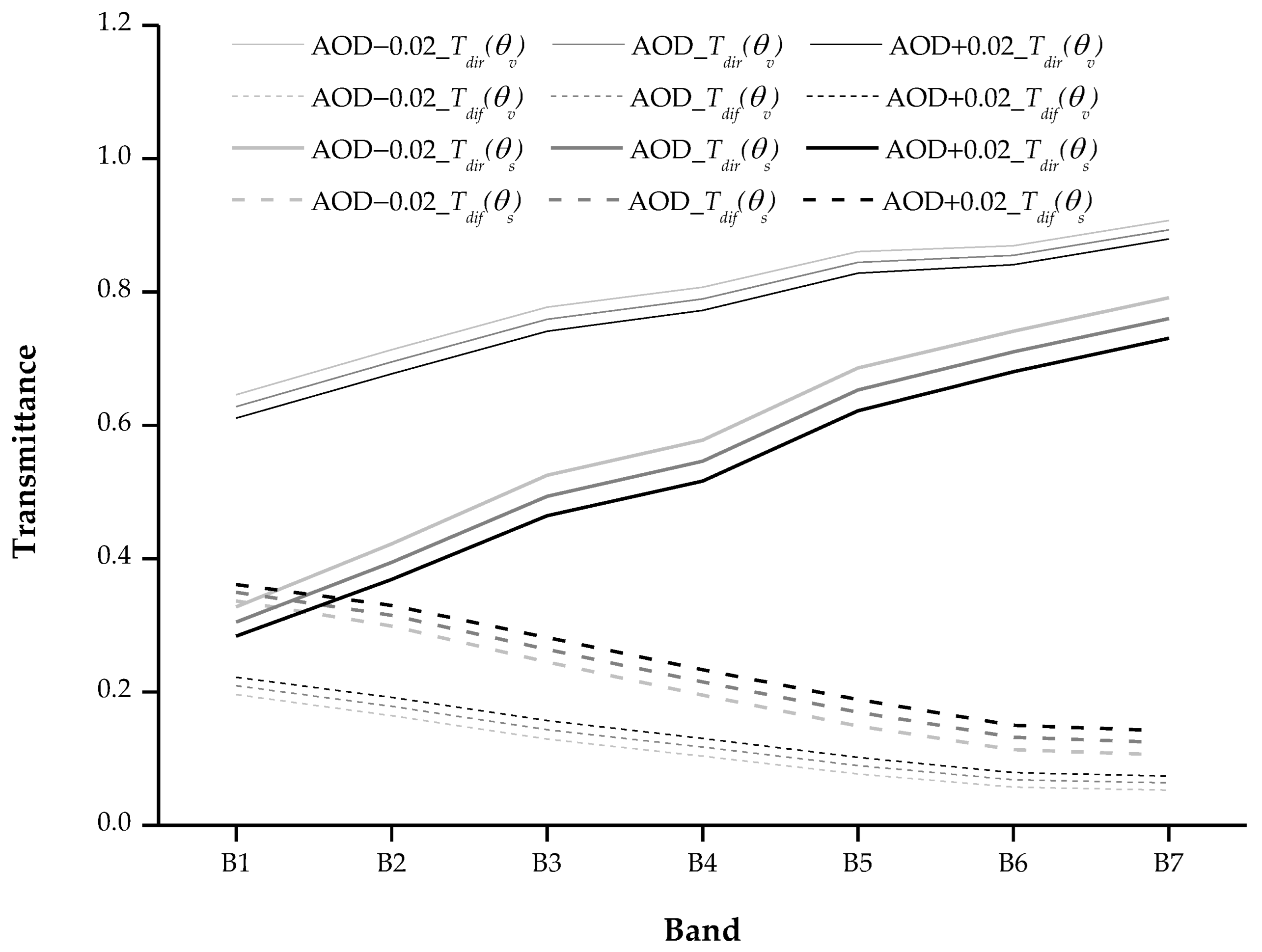
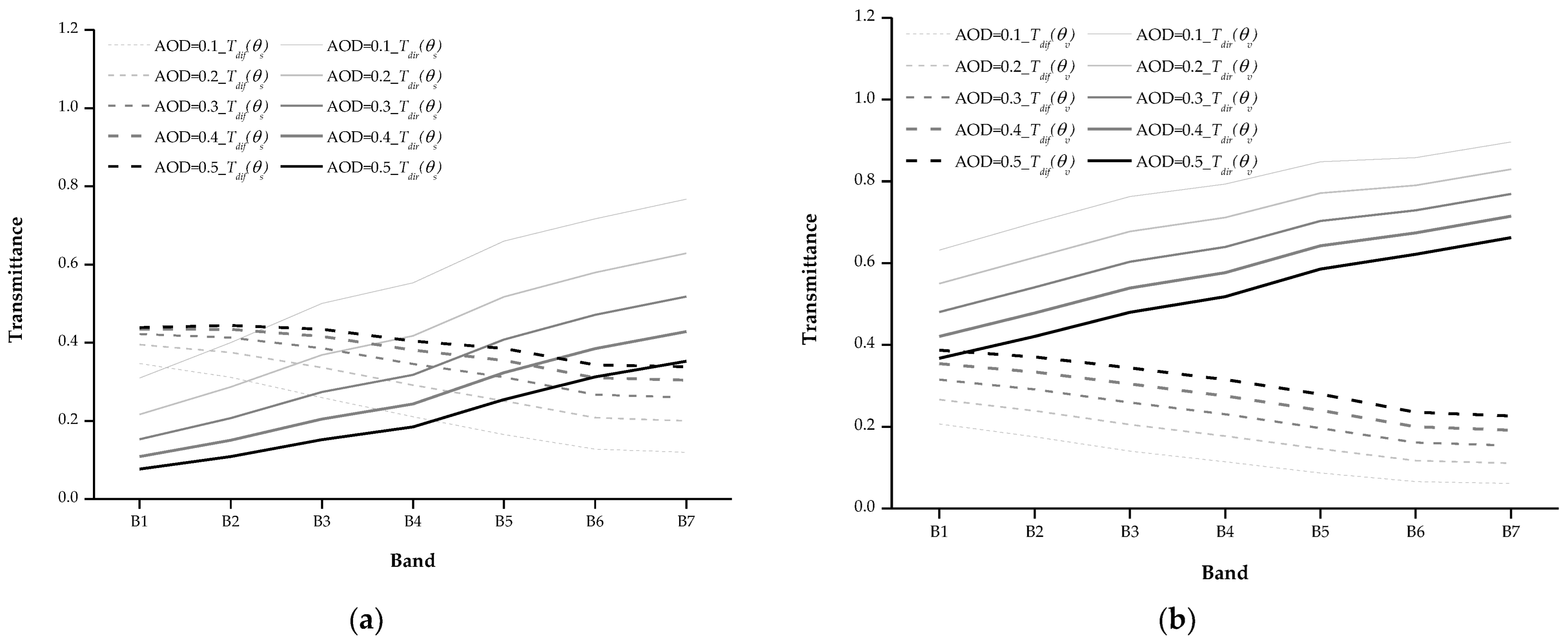
4.1.1. Uncertainty Analysis of Aerosol Model Assumptions
4.1.2. Uncertainty Analysis of Atmospheric Profile Measurements
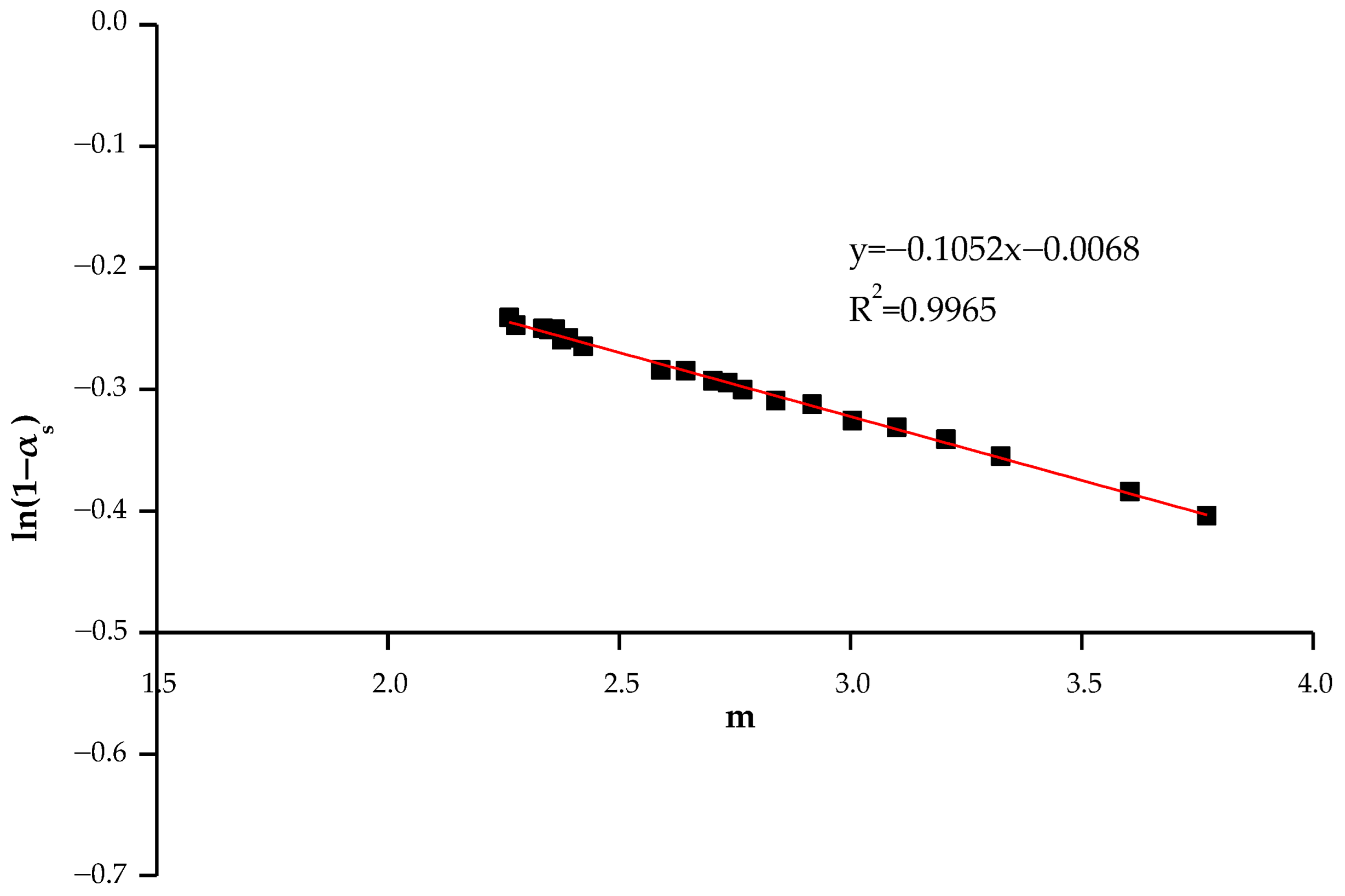
4.1.3. Uncertainty Analysis of AOD Retrieval
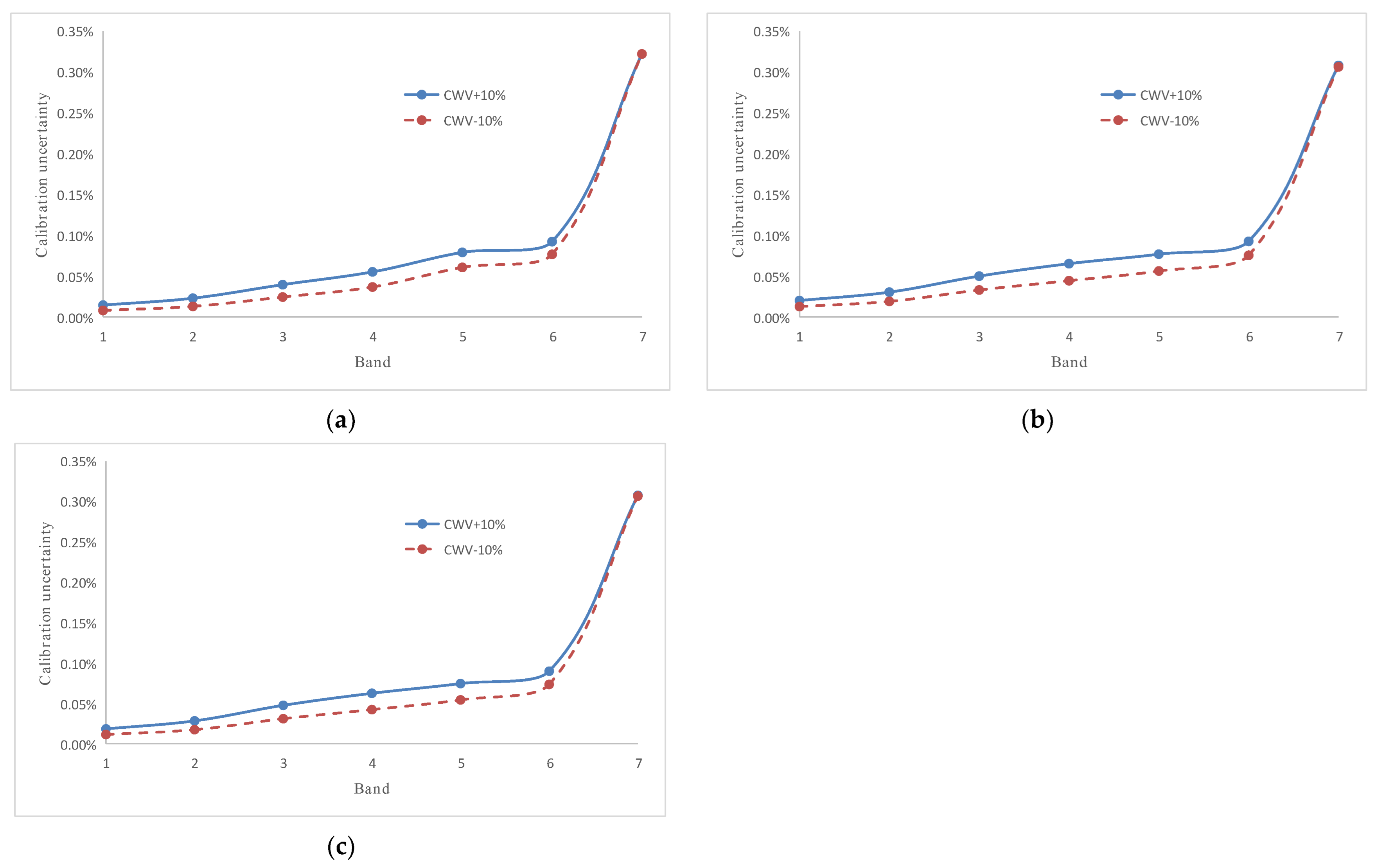
4.1.4. Uncertainty Analysis of Water Vapor Measurement
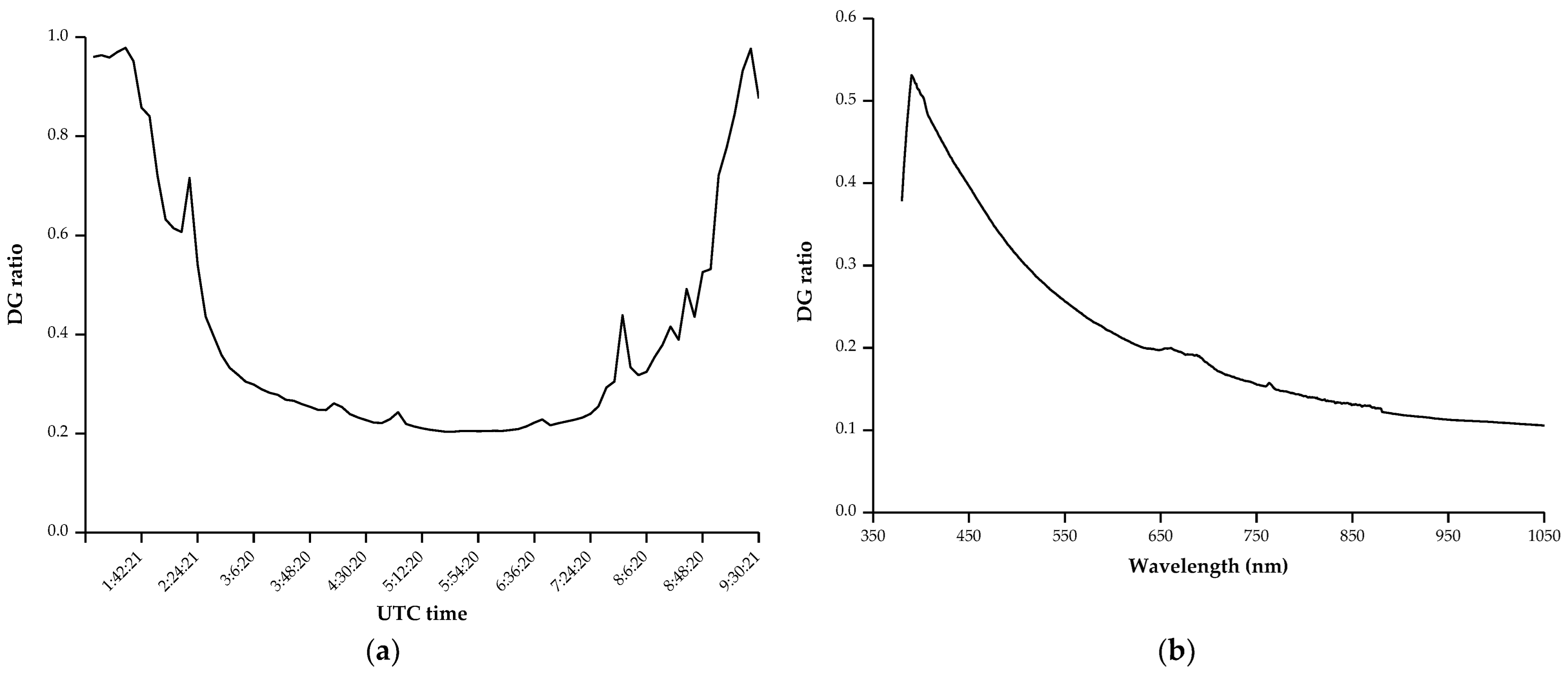
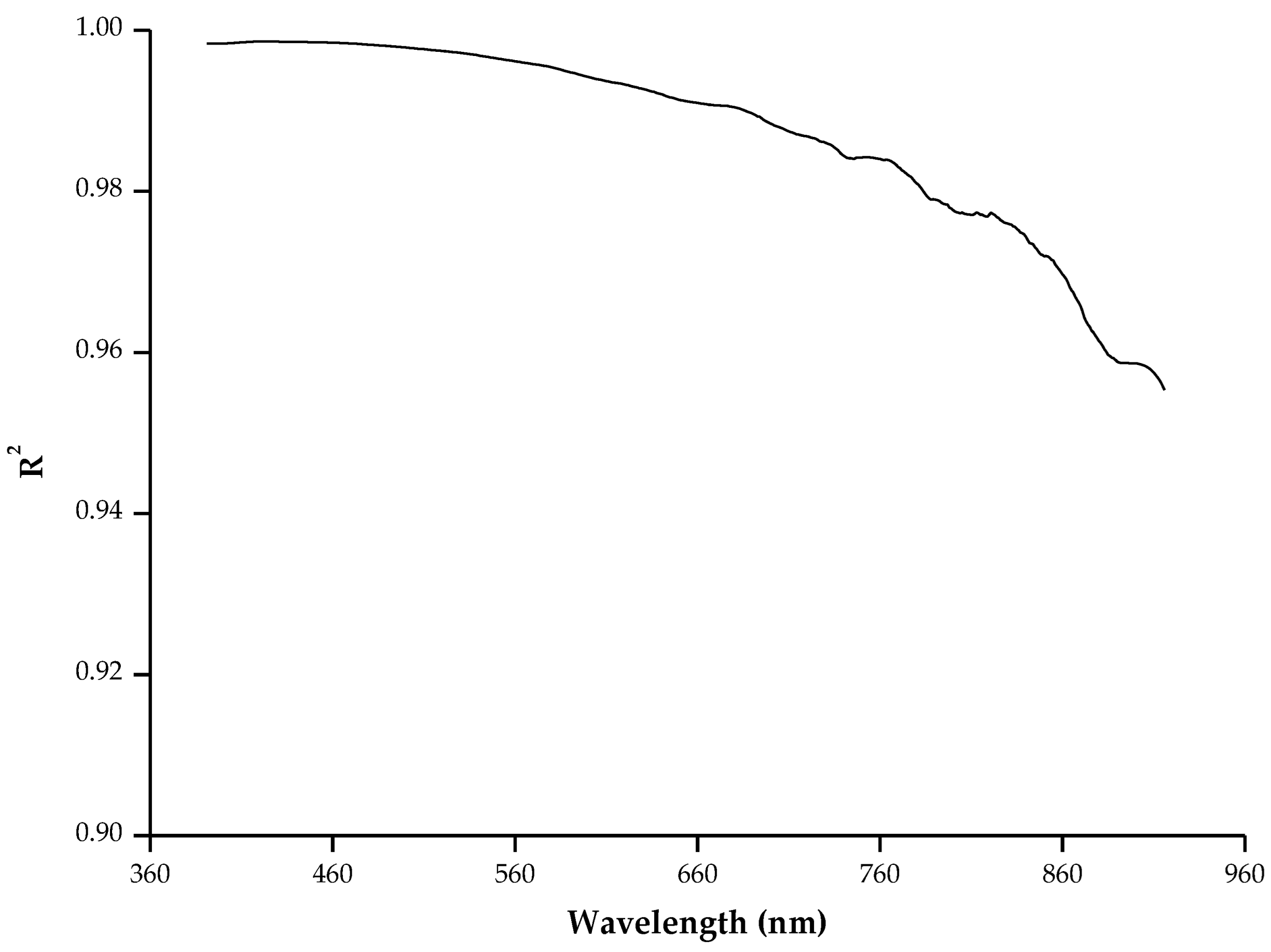
4.1.5. Uncertainty Analysis of Simultaneous Ground Reflectance Measurements
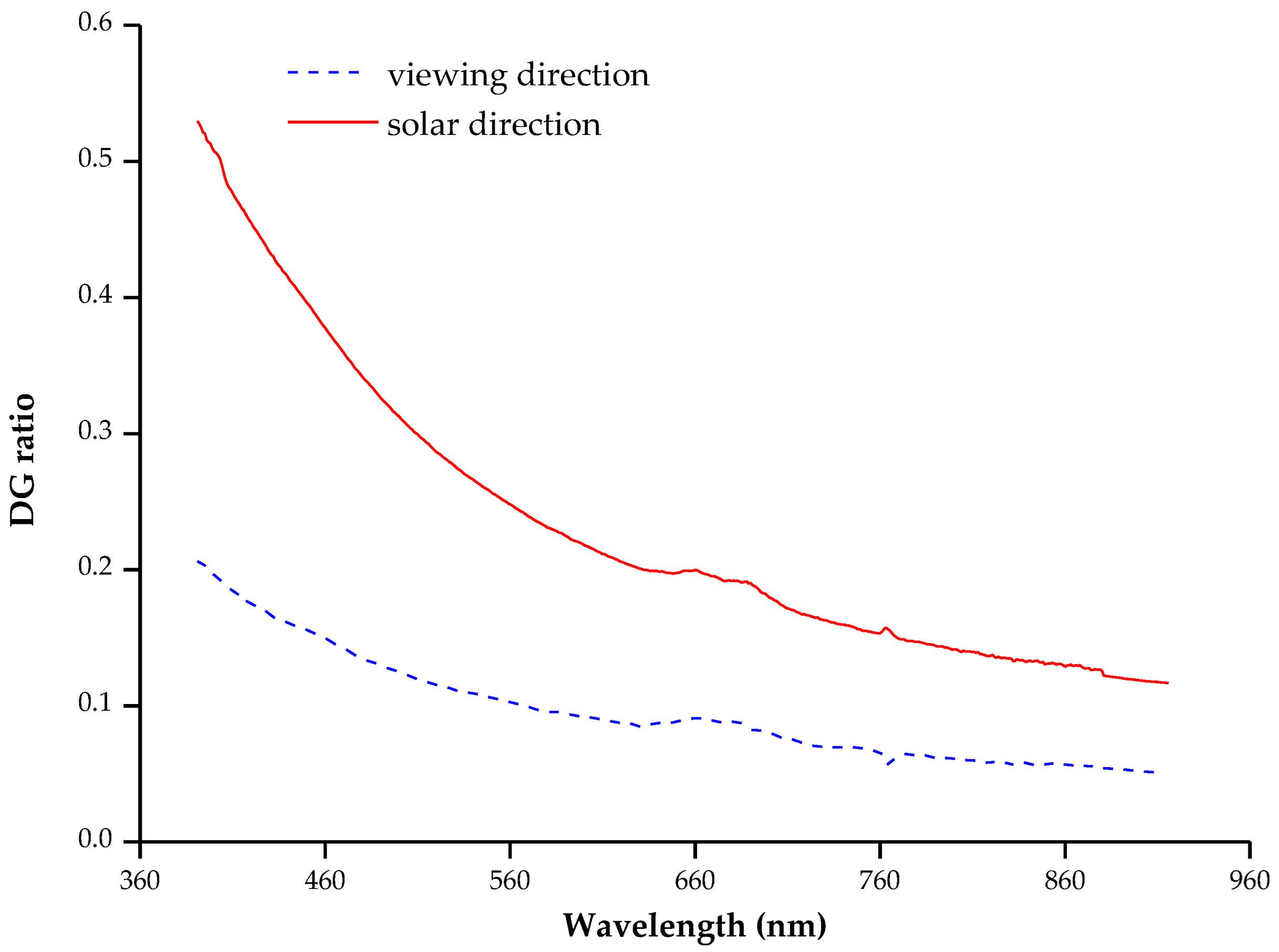
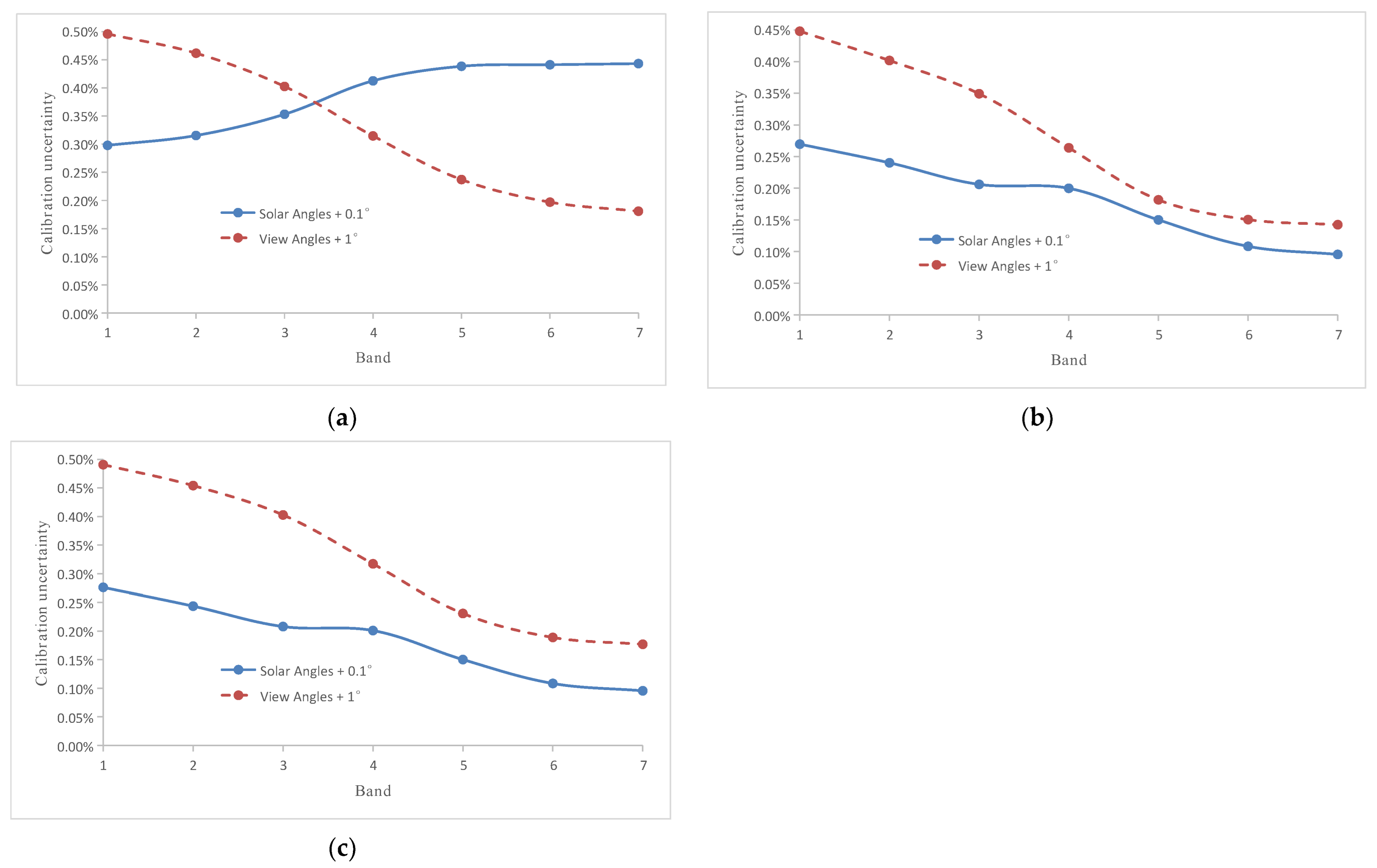
4.1.6. Uncertainty Analysis of Viewing Geometry
4.1.7. Total Calibration Uncertainty Estimation
4.2. Validation
4.2.1. Comparison with Measured Reflectance over the Dunhuang Calibration Site
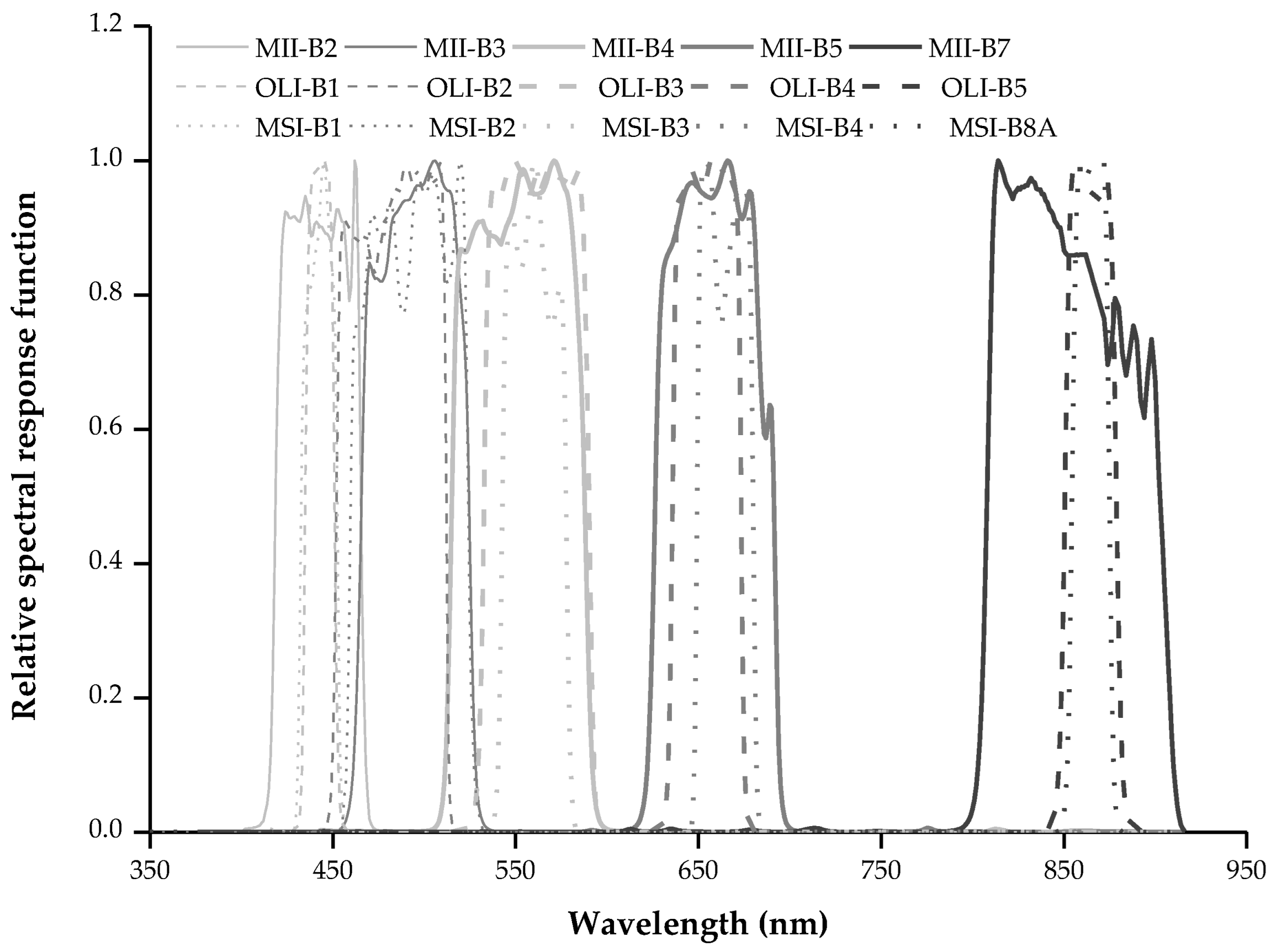
4.2.2. Ground Reflectance Validation Cross-Compared with Landsat-8 OLI and Sentinel-2A MSI over Different Surface Types
5. Conclusions
- (1)
- The radiometric calibration coefficients obtained by the three vicarious calibration methods were reliable, with average relative differences of 2.20% (between the reflectance- and irradiance-based methods) and 1.43% (between the reflectance- and improved irradiance-based methods). The total calibration uncertainties of the reflectance-, irradiance-, and improved irradiance-based methods were 2.77–5.23%, 3.62–5.79%, and 3.50–5.23%, respectively. The largest calibration uncertainty in the reflectance-based method stemmed from the aerosol model assumption, while the retrieval uncertainty of the AOD at 550 nm was the primary calibration uncertainty in the other two methods.
- (2)
- To verify the calibration accuracy of SDGSAT-1 MII, we utilized well-calibrated sensors, Landsat-8 OLI and Sentinel-2A MSI, as reference sensors for cross-comparison with the SDGSAT-1 MII over different surface types. MII retrievals differed less than 0.0075 (7.13%) from OLI retrievals and less than 0.0084 (7.47%) from MSI retrievals when applying calibration coefficients from the reflectance-based method; less than 0.0089 (7.57%) from OLI retrievals and less than 0.0111 (8.65%) from MSI retrievals for the irradiance-based method; and less than 0.0082 (7.33%) from OLI retrievals and less than 0.0101 (8.59%) from MSI retrievals for the improved irradiance-based method. The cross-comparison results showed that the SDGSAT-1 MII calibration accuracy was consistent with those of Landsat-8 OLI and Sentinel-2A MSI, and they showed that the calibration coefficients for the SDGSAT-1 MII are reliable and highly accurate.
- (3)
- Unexpected calibration errors caused by measurement uncertainties in in-situ calibration experiments are hard to detect. Therefore, using different calibration methods and cross-comparing their results is important. In the case of a low AOD (≤0.1), the irradiance- and improved irradiance-based methods showed no obvious advantage over the reflectance-based method, which is therefore recommended under such conditions due to its superiorities of easy operations, low cost, and high accuracy. If DG ratios are not measured, using only the reflectance-based method for calibration under ideal weather conditions is reliable.
- (4)
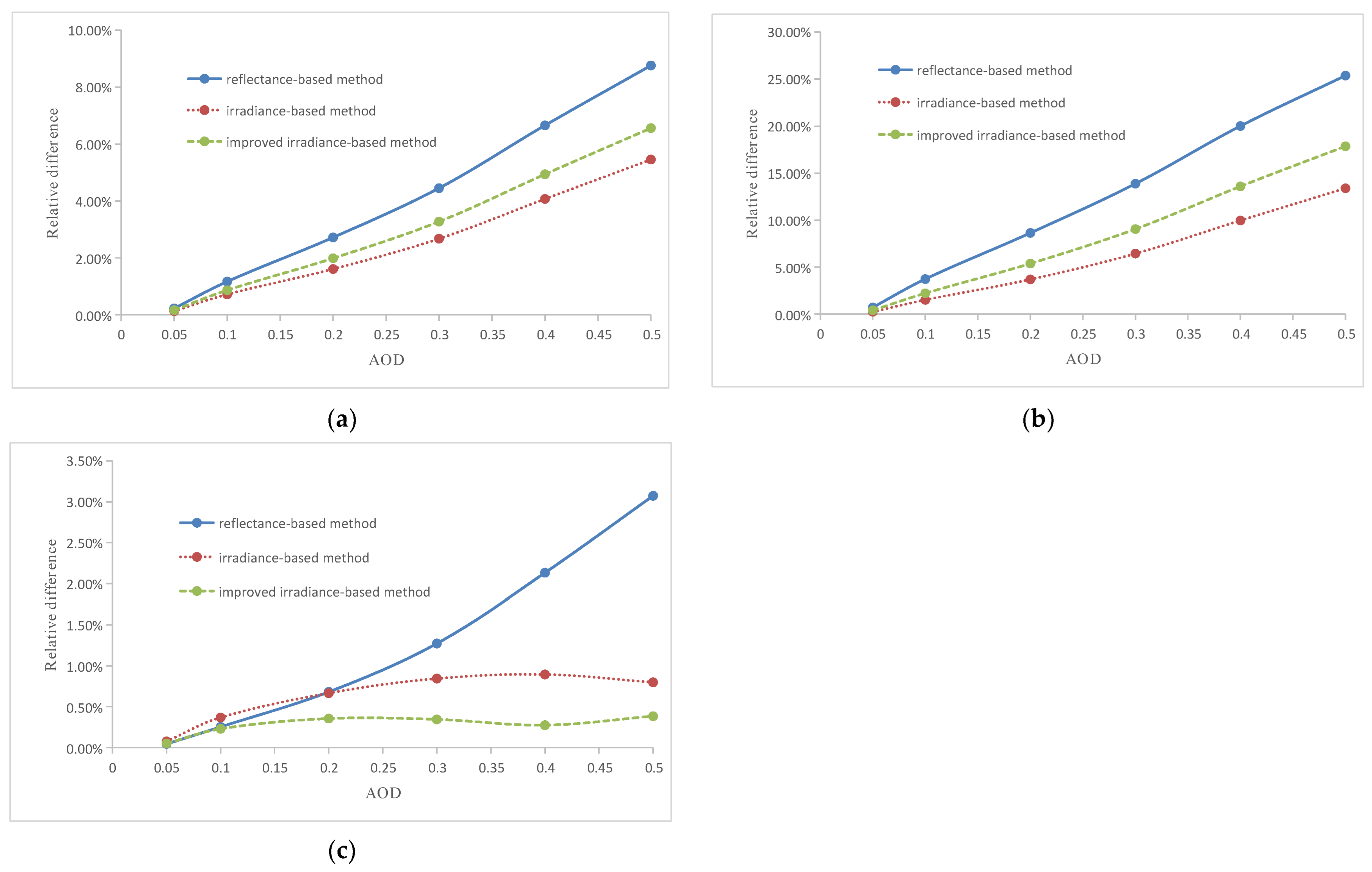
- The performances of the three calibration methods varied for different aerosol types under different AOD conditions. For calibration sites with ground and atmospheric conditions similar to the Dunhuang calibration site, we suggest using the rural and desert aerosol types. When the AOD was 0.1, the reflectance-based method was the best choice, with a total uncertainty of 3.10%, whereas when the AOD was 0.2, 0.3, 0.4, or 0.5, the irradiance-based method had a higher accuracy, with total uncertainties of 3.84%, 4.37%, 5.35%, and 6.47%, than the other two methods. The improved irradiance-based method is recommended when the DG ratio cannot be obtained under a wide-angle measurement (for example, in winter, the range of angle variation is small) or when the atmospheric condition is unstable.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Guo, H.D.; Liang, D.; Sun, Z.C.; Chen, F.; Wang, X.Y.; Li, J.S.; Zhu, L.; Bian, J.H.; Wei, Y.Q.; Huang, L.; et al. Measuring and evaluating SDG indicators with Big Earth Data. Sci. Bull. 2022, 67, 1792–1801. [Google Scholar] [CrossRef] [PubMed]
- Tan, K.; Wang, X.; Niu, C.; Wang, F.; Du, P.J.; Sun, D.X.; Yuan, J.; Zhang, J. Vicarious Calibration for the AHSI Instrument of Gaofen-5 With Reference to the CRCS Dunhuang Test Site. IEEE Trans. Geosci. Remote Sens. 2021, 59, 3409–3419. [Google Scholar] [CrossRef]
- Slater, P.N.; Biggar, S.F.; Holm, R.G.; Jackson, R.D.; Mao, Y.; Moran, M.S.; Palmer, J.M.; Yuan, B. Reflectance- and radiance-based methods for the in-flight absolute calibration of multispectral sensors. Remote Sens. Environ. 1987, 22, 11–37. [Google Scholar] [CrossRef]
- Biggar, S.F. In-Flight Methods for Satellite Sensor Absolute Radiometric Calibration. Ph.D. Thesis, College of Optical Sciences, University of Arizona, Tucson, AZ, USA, 1990. [Google Scholar]
- Xu, W.B.; Shi, J.M.; Zheng, X.B.; Yi, W.N. Design and Application of Global Calibration-Site Network Database. Acta Opt. Sin. 2014, 34, 17–27. [Google Scholar]
- Scott, K.P.; Thome, K.J.; Brownlee, M.R. Evaluation of Railroad Valley playa for use in vicarious calibration. Proc. SPIE 1996, 2818, 158–166. [Google Scholar]
- Thome, K.; Schiller, S.; Conel, J.; Arai, K.; Tsuchida, S. Results of the 1996 Earth Observing System vicarious calibration joint campaign at Lunar Lake Playa, Nevada (USA). Metrologia 1998, 35, 631–638. [Google Scholar] [CrossRef]
- Tsuchida, S.; Sato, I. Cross validation of calibration coefficients for AVNIR and OCTS sensors at the Rogers Dry Lake in USA. J. Remote Sens. Soc. Jpn. 1997, 17, 418–423. [Google Scholar]
- Villa-Aleman, E.; Kurzeja, R.J.; Pendergast, M.M. Temporal, spatial, and spectral variability at the Ivanpah Playa vicarious calibration site. Proc. SPIE 2003, 5093, 320–330. [Google Scholar]
- Rondeaux, G.; Steven, M.; Clark, J.; Mackay, G. La Crau: A European test site for remote sensing validation. Int. J. Remote Sens. 1998, 19, 2775–2788. [Google Scholar] [CrossRef]
- Teillet, P.M.; Thome, K.J.; Fox, N.P.; Morisette, J.T. Earth observation sensor calibration using a global instrumented and automated network of test sites (GIANTS). Proc. SPIE 2001, 4540, 246–254. [Google Scholar]
- Bhaskaran, S.; Phillip, N.; Rahman, A.; Mallick, J. Applications of satellite data for Aerosol Optical Depth (AOD) retrievals and validation with AERONET data. Atmos. Clim. Sci. 2011, 1, 61–67. [Google Scholar] [CrossRef]
- Prata, A.J. Land surface temperature determination from satellites. Adv. Space Res. 1994, 14, 15–26. [Google Scholar] [CrossRef]
- Barry, P.; Jarecke, P.J.; Pearlman, J.; Jupp, D.; Lovell, J.; Campbell, S. Radiometric calibration validation of the Hyperion instrument using ground truth at a site in Lake Frome, Australia. Proc. SPIE 2002, 4480, 242–246. [Google Scholar]
- Wu, D.; Yin, Y.; Wang, Z.; Gu, X.F.; Verbrugghe, M.M.; Guyot, G. Radiometric characterisation of Dunhuang satellite calibration test site (China). In Proceedings of the 7th International Symposium on Physical Measurements and Signatures in Remote Sensing, Courchevel, France, 7–11 April 1997; Volume 4. [Google Scholar]
- Wang, Z.M. Ground test sites for absolute radiometric calibration of China resources satellite. Remote Sens. Land. Resour. 1999, 41, 40–46. [Google Scholar]
- Li, C.R.; Ma, L.L.; Tang, L.L.; Gao, C.X.; Qian, Y.G.; Wang, N.; Wang, X.H. A comprehensive calibration site for high resolution remote sensors dedicated to quantitative remote sensing and its applications. Natl. Remote Sens. Bull. 2021, 25, 198–219. [Google Scholar]
- Thome, K.J.; Crowther, B.G.; Biggar, S.F. Reflectance- and irradiance-based calibration of Landsat-5 Thematic Mapper. Can. J. Remote Sens. 1997, 23, 309–317. [Google Scholar] [CrossRef]
- Thome, K.J.; Markharn, B.L.; Barker, J.L.; Slater, P.N.; Biggar, S.F. Radiometric calibration of Landsat. Photogramm. Eng. Remote Sens. 1997, 63, 853–858. [Google Scholar]
- Markham, B.L.; Barker, J.L.; Kaita, E.; Barsi, J.A.; Helder, D.L.; Palluconi, F.D.; Schott, J.R.; Thome, K.J.; Morfitt, R.; Scaramuzza, P. Landsat-7 ETM+ radiometric calibration: Two years on-orbit. In Proceedings of the Scanning the Present and Resolving the Future. Proceedings. IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, NSW, Australia, 9–13 July 2001; Volume 1, pp. 518–520. [Google Scholar]
- Thome, K.J. Absolute radiometric calibration of Landsat 7 ETM+ using the reflectance-based method. Remote Sens. Environ. 2001, 78, 27–38. [Google Scholar] [CrossRef]
- Czapla-Myers, J.S.; Anderson, N.J.; Biggar, S.F. Early ground-based vicarious calibration results for Landsat 8 OLI. Proc. SPIE 2013, 8866, 205–214. [Google Scholar]
- Czapla-Myers, J.; Mccorkel, J.; Anderson, N.; Thome, K.; Biggar, S.; Helder, D.; Aaron, D.; Leigh, L.; Mishra, N. The Ground-Based Absolute Radiometric Calibration of Landsat 8 OLI. Remote Sens. 2015, 7, 600–626. [Google Scholar] [CrossRef]
- Liu, Y.K.; Ma, L.L.; Wang, N.; Qian, Y.G.; Qiu, S.; Li, C.R.; Tang, L.L. Vicarious radiometric calibration/validation of Landsat-8 operational land imager using a ground reflected radiance-based approach with Baotou site in China. J. Appl. Remote Sens. 2017, 11, 1. [Google Scholar] [CrossRef]
- Biggar, S.F.; Dinguirard, M.C.; Gellman, D.I.; Henry, P.J.; Jackson, R.D.; Moran, M.S.; Slater, P.N. Radiometric calibration of SPOT 2 HRV: A comparison of three methods. Proc. SPIE 1991, 1493, 155–162. [Google Scholar]
- Thome, K.J.; Whittington, E.E.; Smith, N.; Nandy, P.; Zalewski, E.F. Ground-reference techniques for the absolute radiometric calibration of MODIS. Proc. SPIE 2000, 4135, 51–59. [Google Scholar]
- Thome, K.J.; Biggar, S.F.; Choi, H.J. Vicarious calibration of Terra Aster, Misr, and Modis. Proc. SPIE 2004, 5542, 290–299. [Google Scholar]
- Zhang, X.W.; Fu, Q.Y.; Han, Q.J.; Pan, Z.Q.; Yang, L. The field radiometric calibration and validation of ZY-3 multispectral sensor. Spectrosc. Spect. Anal. 2014, 34, 2476–2480. [Google Scholar]
- Gao, H.L.; Gu, X.F.; Yu, T.; Gong, H.; Li, J.G.; Li, X.Y. HJ-1A HSI on-orbit radiometric calibration and validation research. Sci. China Technol. Sci. 2010, 53, 3119–3128. [Google Scholar] [CrossRef]
- Brook, A.; Ben-Dor, E. Supervised vicarious calibration (SVC) of multi-source hyperspectral remote-sensing data. Remote Sens. 2015, 7, 6196–6223. [Google Scholar] [CrossRef]
- Li, H.W.; Zhang, H.; Zhang, B.; Chen, Z.C.; Yang, M.H.; Zhang, Y.Q. A Method Suitable for Vicarious Calibration of a UAV Hyperspectral Remote Sensor. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3209–3223. [Google Scholar] [CrossRef]
- Brook, A.; Polinova, M.; Ben-Dor, E. Fine tuning of the SVC method for airborne hyperspectral sensors: The BRDF correction of the calibration nets targets. Remote Sens. Environ. 2018, 204, 861–871. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, B.; Chen, Z.C.; Huang, Z.H. Vicarious Radiometric Calibration of the Hyperspectral Imaging Microsatellites SPARK-01 and -02 over Dunhuang, China. Remote Sens. 2018, 10, 120. [Google Scholar] [CrossRef]
- United Nations. Transforming Our World: The 2030 Agenda for Sustainable Development; United Nations: New York, NY, USA, 2015.
- He, J.T.; Lu, Y.H. The Measurement and Evaluation of Bidirectional Reflectance Characteristics of Dunhuang Radiative Calibration Site. Natl. Remote Sens. Bull. 1997, 1, 246–251. [Google Scholar]
- Hu, X.; Liu, J.; Sun, L.; Rong, Z.; Li, Y.; Zhang, Y.; Zheng, Z.; Wu, R.; Zhang, L.; Gu, X. Characterization of CRCS Dunhuang test site and vicarious calibration utilization for Fengyun (FY) series sensors. Can. J. Remote Sens. 2010, 36, 566–582. [Google Scholar] [CrossRef]
- Hu, X.Q.; Zhang, Y.X.; Qiu, K.M. In-flight Radiometric Calibration for VIR Channels of FY-1C Satellite Sensor by Using Irradiance-based Method. Natl. Remote Sens. Bull. 2003, 7, 458–464. [Google Scholar]
- Fu, Q.Y.; Min, X.J.; Li, X.C.; Sha, C.M.; Li, X.Y.; Ma, G.Q.; Pan, Z.Q.; Guo, Y.; Li, Q.M.; Liu, G.D. In-flight Absolute Calibration of the CBERS-02 CCD Sensor at the Dunhuang Test Site. Natl. Remote Sens. Bull. 2006, 10, 433–439. [Google Scholar]
- Zhang, H.; Zhang, B.; Chen, D.M.; Li, J.S.; Zhao, G.N. Influence of Filter Band Function on Retrieval of Aerosol Optical Depth from Sunphotometer Data. J. Atmos. Ocean. Technol. 2013, 30, 929–941. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, Z.C.; Zhang, B.; Chen, C.Y. Improved Algorithm for Water Vapor Retrieval and Field Calibration in the Channell 940-nm of Sun-photometer. In Proceedings of the 23rd CALCON Technical Conference, Logan, UT, USA, 11–14 August 2014; pp. 11–14. [Google Scholar]
- Zhang, B.; Zhang, H.; Chen, Z.C. Radiometric Calibration of Optical Remote Sensing; Science Press: Beijing, China, 2020; p. 27. [Google Scholar]
- Gao, H.L. Study on the Calibration and Validation of HSI Sensor on HJ-1ASatellite. Ph.D. Thesis, Institute of Remote Sensing Applications, Chinese Academy of Sciences, Beijing, China, 2010. [Google Scholar]
- Gou, Z.Y.; Yan, L.; Chen, W.; Jing, X.; Yin, Z.Y.; Duan, Y.N. In-flight Absolute Radiometric Calibration of UAV Hyperspectral Camera and Its Validation Analysis. Spectrosc. Spect. Anal. 2012, 32, 430–434. [Google Scholar]
- Eck, T.F.; Holben, B.N.; Reid, J.S.; Dubovik, O.; Smirnov, A.; O’Neill, N.T.; Slutsker, I.; Kinne, S. Wavelength dependence of the optical depth of biomass burning, urban, and desert dust aerosols. J. Geophys. Res. 1999, 104, 31333–31349. [Google Scholar] [CrossRef]
- Zhang, Y.X.; Zhang, G.S.; Qiu, K.M.; Wang, Z.Q.; Zhang, L.J. Vicarious Radiometric Calibration of the Remote Sensing Data from Airborne Moderate Resolution Imaging Spectrometer. J. Appl. Meteor. Sci. 1998, 9, 106–112. [Google Scholar]
- Thome, K.J.; Gellman, D.I.; Parada, R.J.; Biggar, S.F.; Slater, P.N.; Moran, M.S. In-flight radiometric calibration of Landsat-5 Thematic Mapper from 1984 to present. Proc. SPIE 1993, 1938, 126–130. [Google Scholar]
- Pang, W.W.; Zheng, X.B.; Lu, J.H.; Li, J.J. Reflectance Characteristics of Dunhuang Radiometric Calibration Test Site. J. Atmos. Environ. Optics. 2015, 10, 472–481. [Google Scholar]
- Thome, K.J. Validation Plan for MODIS Level 1 at-Sensor Radiance; Remote Sensing Group of the Optical Sciences Center, University of Arizona: Tucson, AZ, USA, 1999; pp. 23–28. [Google Scholar]
- Biggar, S.F.; Slater, P.N.; Gellman, D.I. Uncertainties in the in-flight calibration of sensors with reference to measured ground sites in the 0.4–1.1 μm range. Remote Sens. Environ. 1994, 48, 245–252. [Google Scholar] [CrossRef]
- Liu, X.; Bhartia, P.K.; Chance, K.; Froidevaux, L.; Spurr, R.J.D.; Kurosu, T.P. Validation of Ozone Monitoring Instrument (OMI) ozone profiles and stratospheric ozone columns with Microwave Limb Sounder (MLS) measurements. Atmos. Chem. Phys. 2010, 10, 2539–2549. [Google Scholar] [CrossRef]
- Slater, P.N.; Biggar, S.F.; Thome, K.J.; Gellman, D.I.; Spyak, P.R. Vicarious radiometric calibrations of EOS sensors. J. Atmos. Ocean. Technol. 1996, 13, 349–359. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.P.; Acharya, P.K.; Shettle, E.P. MODTRAN®5.2.1 User’s Manual; Spectral Science Inc.: Burlington, MA, USA, 2011. [Google Scholar]
- Bao, S.W.; Chen, H.Y.; Zhang, L.M.; Wang, X.H. Absolute Radiometric Calibration of Optical Remote Sensor Based on Gray-Scale Targets Method and Reflectance Inversion Validation. Acta Opt. Sin. 2021, 41, 204–212. [Google Scholar]


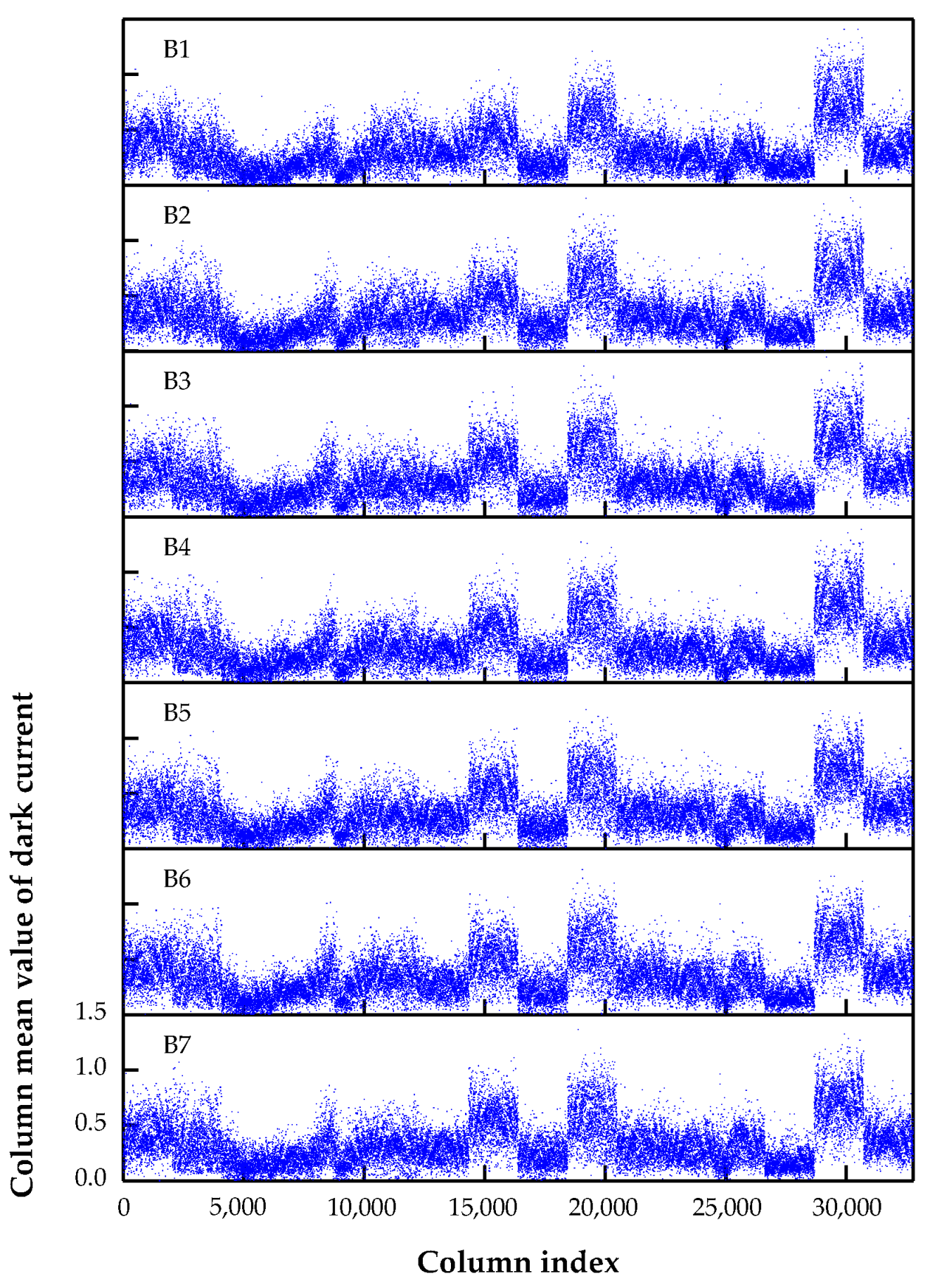


| SDGSAT-1 | Parameters |
|---|---|
| Payloads | MII, GLI, TIS |
| Spectral bands | MII: 7 bands ranging from 374 to 911 nm |
| GLI: 4 bands ranging from 424 to 910 nm | |
| TIS: 3 bands ranging from 8 to 12.5 μm | |
| Swath | 300 km |
| Orbit | Type: sun-synchronous orbit |
| Altitude: 505 km | |
| Inclination: 97.5° | |
| Spatial resolution | MII: 10 m @ 505 km |
| GLI: 10 m @ 505 km (PAN), 40 m @ 505 km (B, G, R) | |
| TIS: 30 m @ 505 km | |
| Revisit period | 11 days |
| SDGSAT-1 MII | Description | Technical Parameters |
|---|---|---|
| Spectral range | B1 | 374–427 nm |
| B2 | 410–467 nm | |
| B3 | 457–529 nm | |
| B4 | 510–597 nm | |
| B5 | 618–696 nm | |
| B6 | 744–813 nm | |
| B7 | 798–911 nm | |
| Spatial resolution | B1–B7 | 10 m @ 505 km |
| Signal-to-noise ratio | B1 | ≥130 |
| B2–B7 | ≥150 | |
| Swath width | B1–B7 | 300 km |
| Modulation transfer function | Static | ≥0.23 |
| Dynamic | ≥0.10 | |
| Dynamic range | B1–B7 | ≥60 dB |
| Digitalizing bits | B1–B7 | 12 bits |
| Date | Overpass Time (UTC) | Solar Zenith (°) | Solar Azimuth (°) | View Zenith (°) | View Azimuth (°) |
|---|---|---|---|---|---|
| 14 December 2021 | 03:45:17 | 68.5554 | 152.2536 | 18.1581 | 304.6388 |
| Atmospheric Parameters | Simultaneous Measurements at Overpass Time |
|---|---|
| 550 nm AOD | 0.1045 |
| CWV | 0.3114 g/cm2 |
| Columnar ozone content | 301.6 DU |
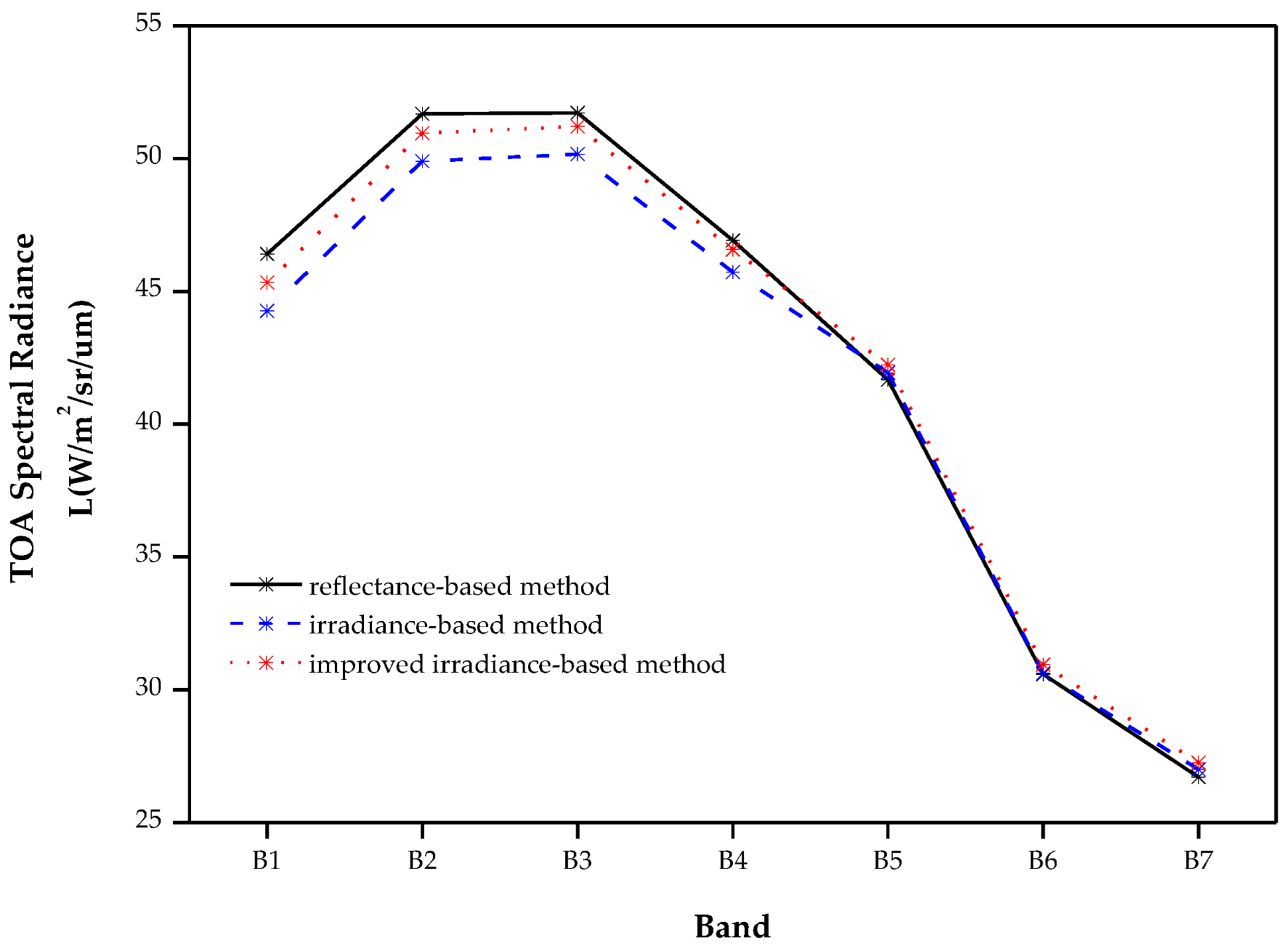
| Band | Relative Difference between Reflectance- and Irradiance-Based Methods | Relative Difference between Reflectance- and Improved Irradiance-Based Methods |
|---|---|---|
| B1 | 4.61% | 2.31% |
| B2 | 3.44% | 1.41% |
| B3 | 3.00% | 0.99% |
| B4 | 2.54% | 0.73% |
| B5 | 0.63% | 1.35% |
| B6 | 0.12% | 1.18% |
| B7 | 1.09% | 2.04% |
| Average relative difference | 2.20% | 1.43% |
| Band | Reflectance-Based Method | Irradiance-Based Method | Improved Irradiance-Based Method |
|---|---|---|---|
| B1 | 0.051616908 | 0.049237722 | 0.050422238 |
| B2 | 0.036291910 | 0.035042783 | 0.035781749 |
| B3 | 0.023327113 | 0.022627800 | 0.023095942 |
| B4 | 0.015849453 | 0.015446672 | 0.015733488 |
| B5 | 0.016096157 | 0.016197140 | 0.016314004 |
| B6 | 0.019731394 | 0.019754163 | 0.019963674 |
| B7 | 0.013811256 | 0.013961794 | 0.014092721 |
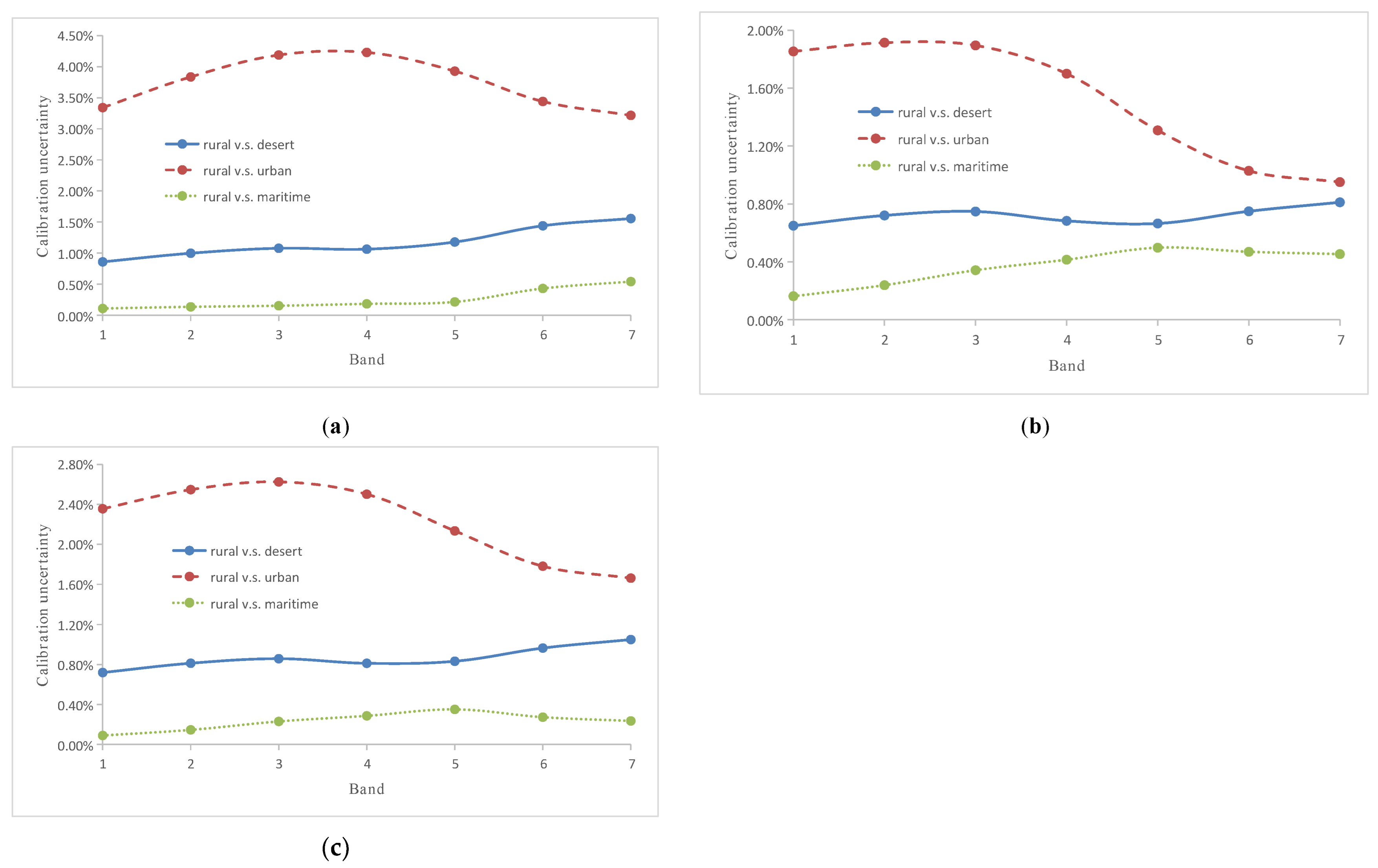
| Method | Rural vs. Desert | Rural vs. Urban | Rural vs. Maritime |
|---|---|---|---|
| Reflectance-based method | 1.17% | 3.74% | 0.25% |
| Irradiance-based method | 0.72% | 1.52% | 0.37% |
| Improved irradiance-based method | 0.86% | 2.23% | 0.23% |
| AOD | Reflectance-Based Method | Irradiance-Based Method | Improved Irradiance-Based Method | |
|---|---|---|---|---|
| AOD = 0.1 | AOD + 0.02 | 1.90% | 7.40% | 5.80% |
| AOD − 0.02 | 1.97% | 8.05% | 6.20% | |
| AOD = 0.2 | AOD + 0.02 | 1.77% | 7.33% | 5.75% |
| AOD − 0.02 | 1.83% | 7.95% | 6.12% | |
| AOD = 0.3 | AOD + 0.02 | 1.62% | 6.93% | 5.44% |
| AOD − 0.02 | 1.65% | 7.39% | 5.72% | |
| AOD = 0.4 | AOD + 0.02 | 1.59% | 7.15% | 5.62% |
| AOD − 0.02 | 1.62% | 7.68% | 5.94% | |
| AOD = 0.5 | AOD + 0.02 | 1.55% | 7.29% | 5.74% |
| AOD − 0.02 | 1.58% | 7.86% | 6.08% | |
| Source of Uncertainty | Reflectance-Based Method (%) | Irradiance-Based Method (%) | Improved Irradiance-Based Method (%) |
|---|---|---|---|
| Assumption of aerosol type | 0.11–4.23 | 0.16–1.91 | 0.09–2.63 |
| Assumption of atmospheric model | 0.01–0.71 | 0.04–0.81 | 0.09–0.66 |
| 550 nm AOD retrieval | 0.03–1.00 | 1.20–4.15 | 0.77–2.83 |
| Water vapor retrieval | 0.01–0.32 | 0.01–0.31 | 0.01–0.31 |
| Ozone measurement | 0.6 | 0.6 | 0.6 |
| Ground reflectance measurement | 1.5 | 1.5 | 1.5 |
| BRDF error | 2.0 | 2.0 | 2.0 |
| Viewing geometries | 0.18–0.50 | 0.10–0.45 | 0.10–0.49 |
| Image misregistration errors | 0.2 | 0.2 | 0.2 |
| Radiative transfer code accuracy | 1.0 | 1.0 | 1.0 |
| DG ratio measurement | / | 2.0 | 2.0 |
| Total uncertainty (Root sum of squares) | 2.77–5.23 | 3.62–5.79 | 3.50–5.23 |
| Total Uncertainty | Reflectance-Based Method (%) | Irradiance-Based Method (%) | Improved Irradiance-Based Method (%) |
|---|---|---|---|
| AOD = 0.1 | 3.10 | 3.55 | 3.58 |
| AOD = 0.2 | 3.96 | 3.84 | 4.00 |
| AOD = 0.3 | 5.28 | 4.37 | 4.76 |
| AOD = 0.4 | 7.24 | 5.35 | 6.03 |
| AOD = 0.5 | 9.21 | 6.47 | 7.42 |
| Band | Inversion | Measurement | Absolute Difference |
|---|---|---|---|
| B1 | 0.136456 | 0.136229 | 0.00023 |
| B2 | 0.155277 | 0.154839 | 0.00044 |
| B3 | 0.175996 | 0.177304 | 0.00131 |
| B4 | 0.206255 | 0.207094 | 0.00084 |
| B5 | 0.233118 | 0.233125 | 0.00001 |
| B6 | 0.236585 | 0.236509 | 0.00008 |
| B7 | 0.233967 | 0.233836 | 0.00013 |
| Sensor | Data Acquisition Time (UTC + 8) | Center Coordinate | Solar Zenith | Solar Azimuth | 550 nm AOD | CWV (g/cm2) |
|---|---|---|---|---|---|---|
| SDGSAT-1 MII | 14 December 2021, 11:45:17 | 40.0913°N, 94.3938°E | 68.5021° | 152.2956° | 0.1045 | 0.3114 |
| Landsat-8 OLI | 14 December 2021, 12:20:23 | 40.3329°N, 95.0782°E | 65.8780° | 161.3918° | 0.1199 | 0.2899 |
| Sentinel-2A MSI | 17 December 2021, 12:32:11 | 40.1419°N, 94.8185°E | 65.0575° | 164.5149° | 0.1229 | 0.2880 |
| SDGSAT-1 MII | Landsat-8 OLI | Sentinel-2A MSI | ||||||
|---|---|---|---|---|---|---|---|---|
| Band | Center Wavelength (nm) | Spectral Range (nm) | Band | Center Wavelength (nm) | Spectral Range (nm) | Band | Center Wavelength (nm) | Spectral Range (nm) |
| B2 | 462 | 410–467 | B1 | 445 | 435–451 | B1 | 443 | 431–454 |
| B3 | 506 | 457–529 | B2 | 509 | 452–512 | B2 | 520 | 458–527 |
| B4 | 571 | 510–597 | B3 | 550 | 533–590 | B3 | 560 | 504–602 |
| B5 | 666 | 618–696 | B4 | 656 | 636–673 | B4 | 654 | 649–680 |
| B7 | 814 | 798–911 | B5 | 859 | 851–879 | B8A | 871 | 855–875 |
| Method | Band | Absolute (Relative) Difference between MII and OLI | Absolute (Relative) Difference between MII and MSI |
|---|---|---|---|
| Reflectance-based method | Coastal/aerosol | 0.0111 (14.04%) | 0.0086 (12.84%) |
| Blue | 0.0133 (13.76%) | 0.0099 (7.12%) | |
| Green | 0.0081 (4.46%) | 0.0041 (2.78%) | |
| Red | 0.0033 (1.83%) | 0.0103 (8.82%) | |
| Near infrared | 0.0016 (1.57%) | 0.0091 (5.81%) | |
| Average difference | 0.0075 (7.13%) | 0.0084 (7.47%) | |
| Irradiance-based method | Coastal/aerosol | 0.0165 (18.45%) | 0.0101 (13.56%) |
| Blue | 0.0078 (8.86%) | 0.0137 (9.10%) | |
| Green | 0.0046 (3.16%) | 0.0076 (3.92%) | |
| Red | 0.0082 (4.09%) | 0.0129 (10.28%) | |
| Near infrared | 0.0074 (3.31%) | 0.0111(6.38%) | |
| Average difference | 0.0089 (7.57%) | 0.0111 (8.65%) | |
| Improved irradiance-based method | Coastal/aerosol | 0.0097 (15.54%) | 0.0110 (15.04%) |
| Blue | 0.0101 (10.12%) | 0.0113 (8.13%) | |
| Green | 0.0068 (4.09%) | 0.0052 (2.78%) | |
| Red | 0.0062 (2.95%) | 0.0126 (10.54%) | |
| Near infrared | 0.0082 (3.94%) | 0.0106 (6.48%) | |
| Average difference | 0.0082 (7.33%) | 0.0101 (8.59%) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Z.; Ma, C.; Zhang, H.; Hu, Y.; Yan, L.; Dou, C.; Li, X.-M. Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China. Remote Sens. 2023, 15, 2578. https://doi.org/10.3390/rs15102578
Cui Z, Ma C, Zhang H, Hu Y, Yan L, Dou C, Li X-M. Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China. Remote Sensing. 2023; 15(10):2578. https://doi.org/10.3390/rs15102578
Chicago/Turabian StyleCui, Zhenzhen, Chao Ma, Hao Zhang, Yonghong Hu, Lin Yan, Changyong Dou, and Xiao-Ming Li. 2023. "Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China" Remote Sensing 15, no. 10: 2578. https://doi.org/10.3390/rs15102578
APA StyleCui, Z., Ma, C., Zhang, H., Hu, Y., Yan, L., Dou, C., & Li, X.-M. (2023). Vicarious Radiometric Calibration of the Multispectral Imager Onboard SDGSAT-1 over the Dunhuang Calibration Site, China. Remote Sensing, 15(10), 2578. https://doi.org/10.3390/rs15102578






