Vicarious CAL/VAL Approach for Orbital Hyperspectral Sensors Using Multiple Sites
Abstract
1. Introduction
2. Materials and Methods
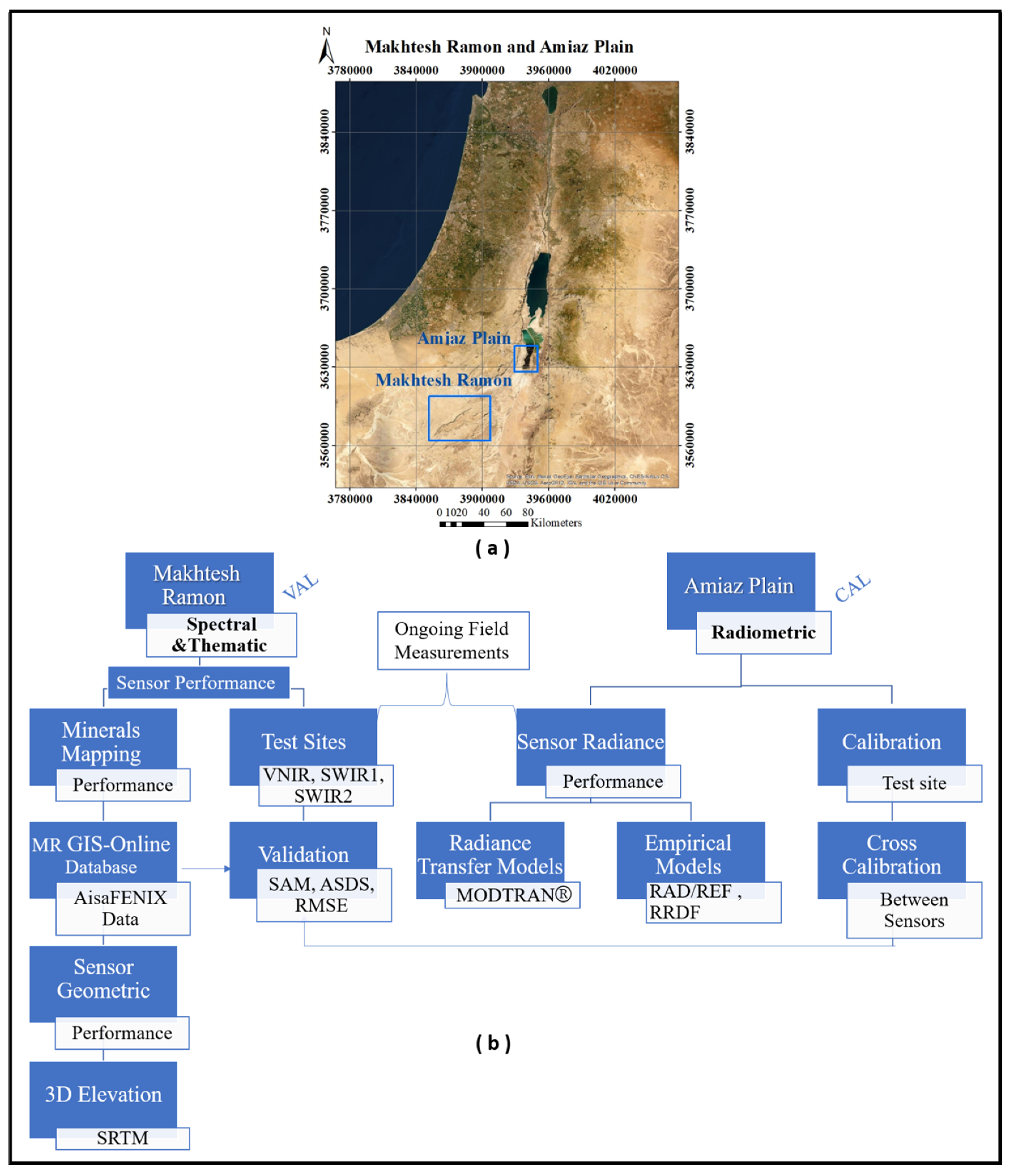
2.1. Test Sites AP and MR
2.2. Stability of the Test Sites
2.3. CAL/VAL Protocol Flowchart
2.4. Field Measurements
2.5. Cross-Calibration of HSR Orbital Sensors Using AP Site
2.6. Sensors’ Image Data
3. Results
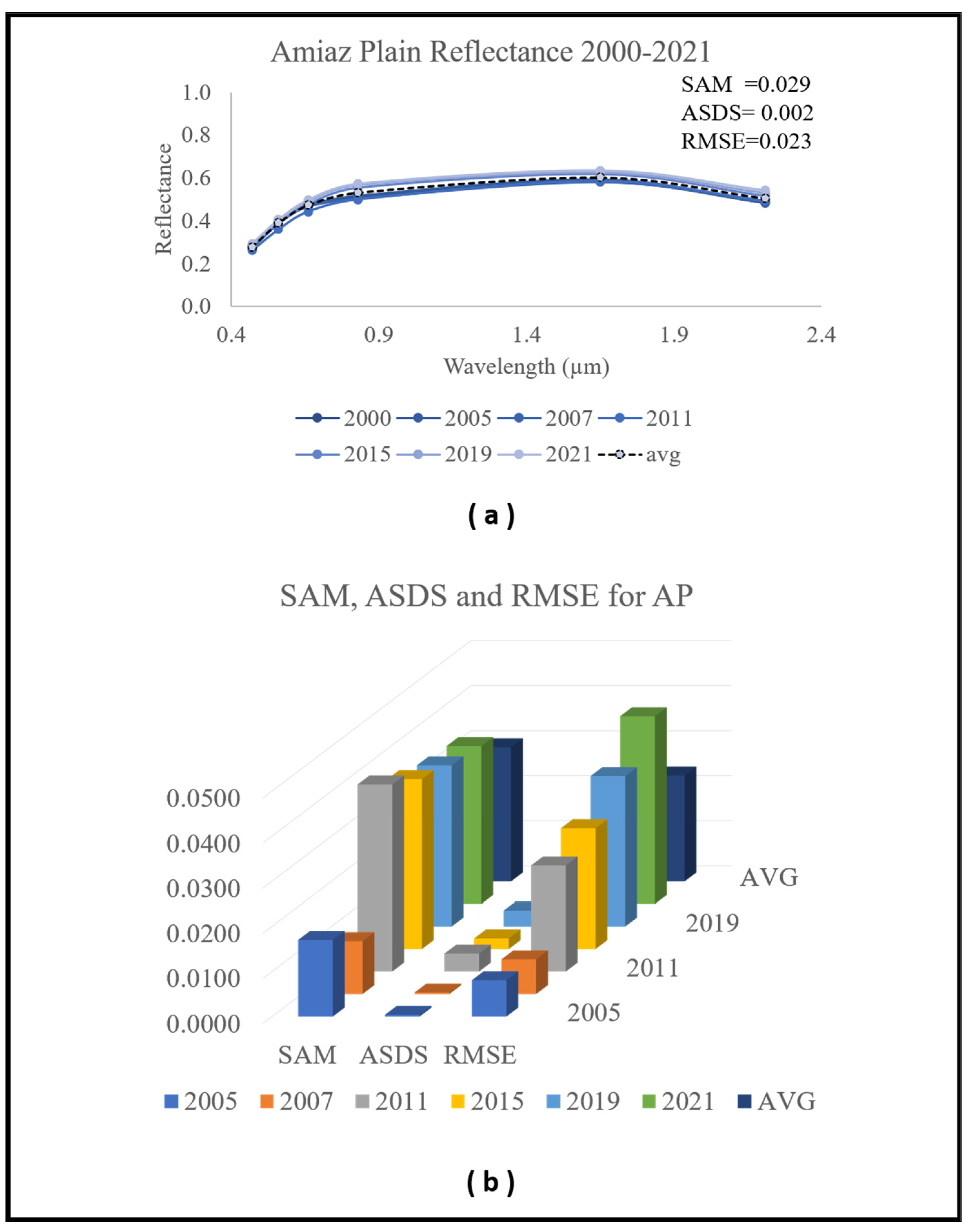
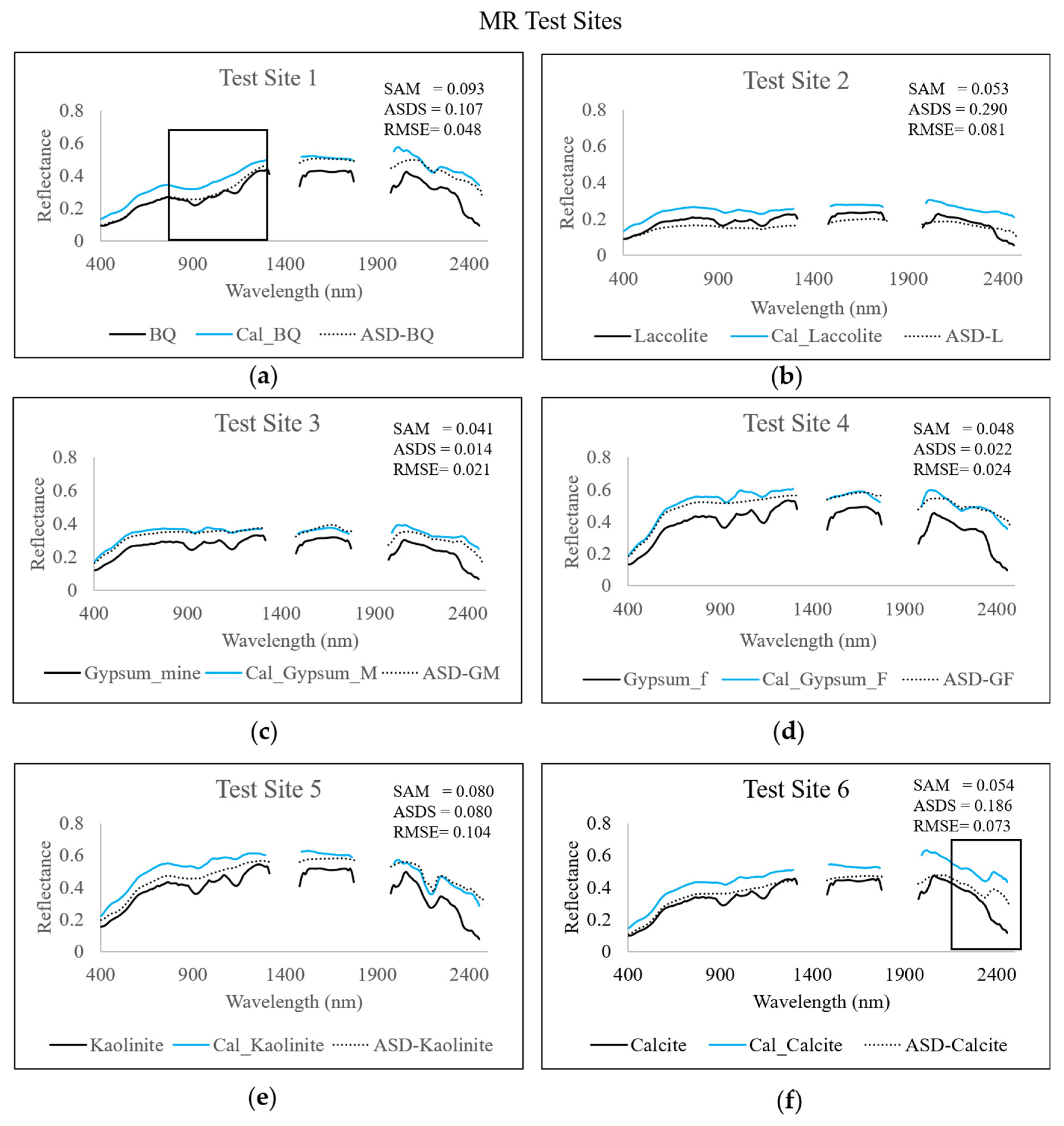
3.1. AP and MR Stability
3.2. AP and MR CAL/VAL Protocol: A Case Study Using the PRISMA HSR Sensor
3.2.1. Evaluate Radiance Performance
3.2.2. Evaluate Spectral Performance—PRISMA L2 Product
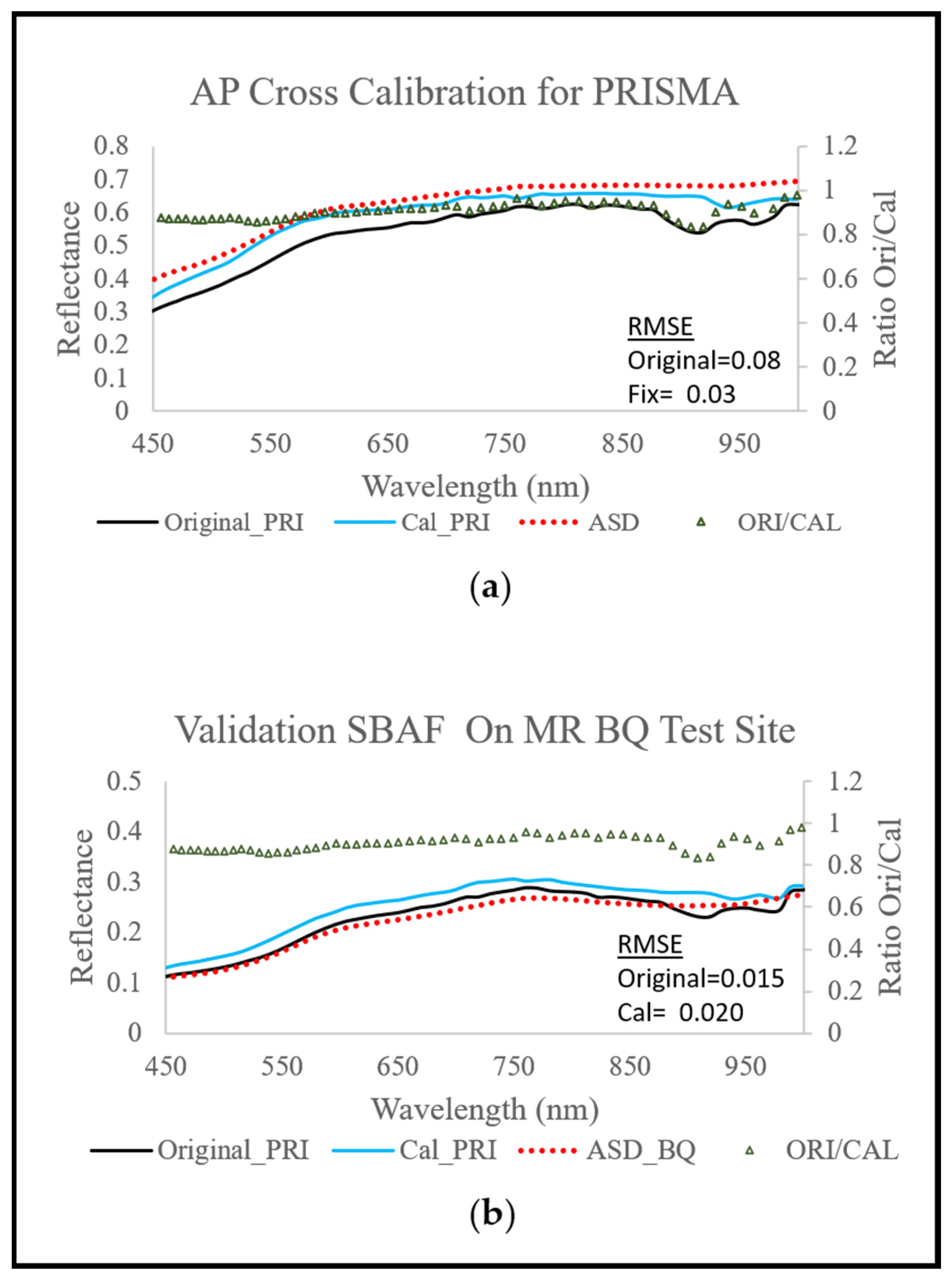
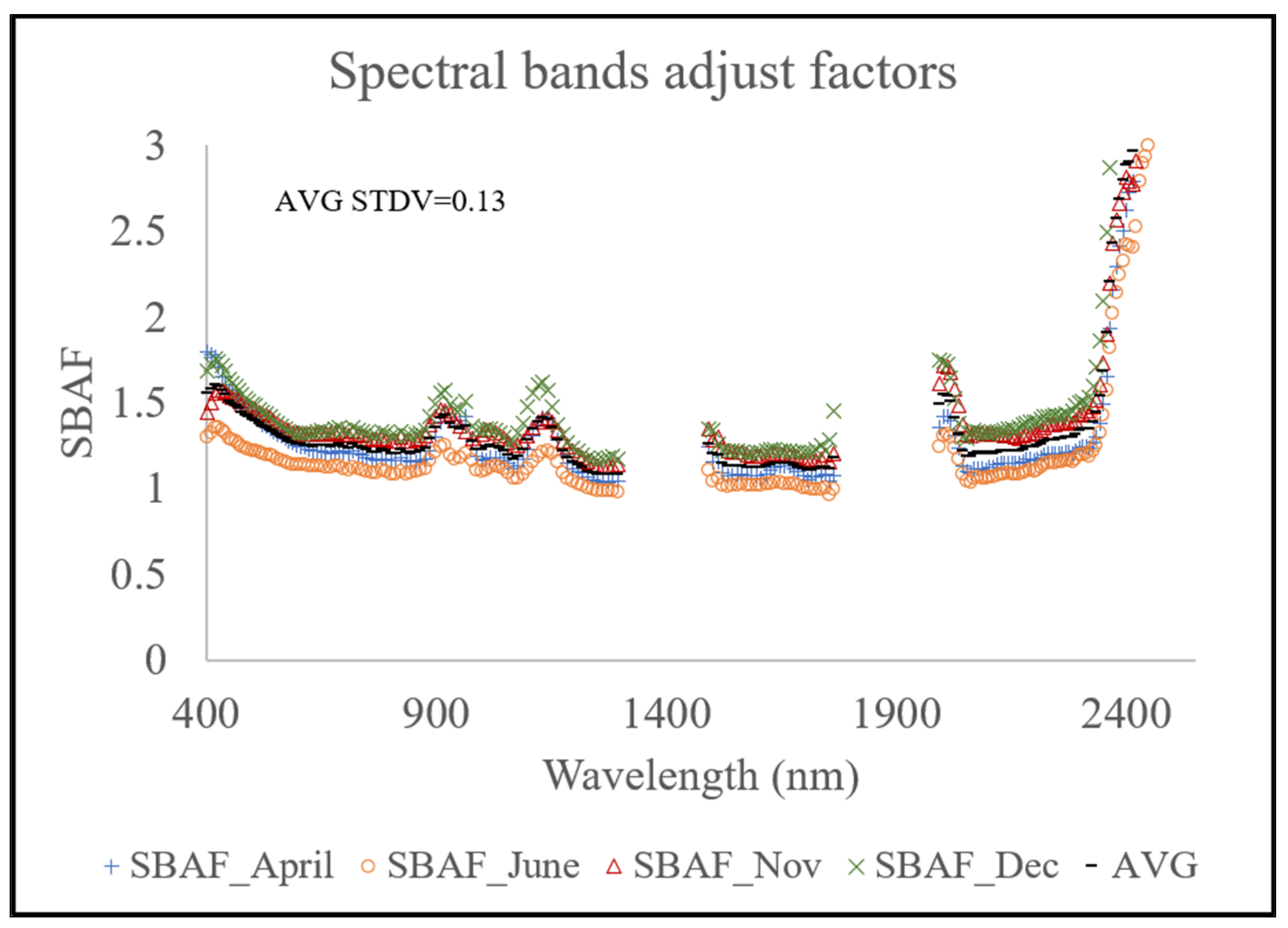
3.2.3. Cross-Calibration and Validation between PRISMA and DESIS Level-2 Products
- p (sensor A)—simulated reflectance for the sensor to be calibrated (PRISMA);
- p (sensor M)—simulated reflectance for the well-calibrated (motherhood) DESIS sensor;
- ρλh—AisaFENIX’s accurate hyperspectral reflectance profile of the surface.
Uncertainty Analysis
3.2.4. Cross-Calibration against a Fixed High-Quality Sensor Image
- p (sensor A)—simulated reflectance for PRISMA (to be calibrated);
- p (sensor M)—simulated reflectance for the well-calibrated (motherhood) sensor AisaFENIX;
- ρλh—ASD field hyperspectral profile of the surface (resampled to PRISMA bands).
3.2.5. Evaluate Sensor’s Thematic Stability
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Mckenzie, I.; Karafolas, N. Fiber optic sensing in space structures: The experience of the European Space Agency (Invited Paper). In Proceedings of the 17th International Conference on Optical Fibre Sensors, Bruges, Belgium, 23 May 2005; Volume 5855, p. 262. [Google Scholar] [CrossRef]
- Chander, G.; Helder, D.L.; Aaron, D.; Mishra, N.; Shrestha, A.K. Assessment of spectral, misregistration, and spatial uncertainties inherent in the cross-calibration study. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1282–1296. [Google Scholar] [CrossRef]
- Bouvet, M.; Thome, K.; Berthelot, B.; Bialek, A.; Czapla-Myers, J.; Fox, N.P.; Goryl, P.; Henry, P.; Ma, L.; Marcq, S.; et al. RadCalNet: A radiometric calibration network for earth observing imagers operating in the visible to shortwave infrared spectral range. Remote Sens. 2019, 11, 2401. [Google Scholar] [CrossRef]
- EMIT Homepage. Available online: https://earth.jpl.nasa.gov/emit/instrument/overview/ (accessed on 10 August 2022).
- EnMAP Homepage. Available online: https://www.enmap.org/ (accessed on 10 August 2022).
- Dubovik, O.; Schuster, G.L.; Xu, F.; Hu, Y.; Bösch, H.; Landgraf, J.; Li, Z. Grand Challenges in Satellite Remote Sensing. Front. Remote Sens. 2021, 2, 619818. [Google Scholar] [CrossRef]
- Thenkabail, P. Remote Sensing Handbook Volume 1: Remotely Sensed Data Characterized, Classification and Accuracies; Taylor & Francis Group, LLC: Abingdon, UK, 2016. [Google Scholar]
- Xu, H.; Zhang, L.; Huang, W.; Li, X.; Si, X.; Xu, W.; Song, Q. On-Board Absolute Radiometric Calibration and Validation Based on Solar Diffuser of HY-1C SCS. Guangxue Xuebao/Acta Opt. Sin. 2020, 40, 30015–30034. [Google Scholar] [CrossRef]
- CAL/VAL Working Groups—Surface Biology and Geology. Available online: https://sbg.jpl.nasa.gov/groups (accessed on 10 August 2022).
- RadCalNet Portal. Available online: https://www.radcalnet.org/#!/ (accessed on 22 July 2022).
- Kieffer, H.H.; Wildey, R.L. Absolute calibration of Landsat instruments using the moon. Photogramm. Eng. Remote Sens. 1985, 51, 1391–1393. [Google Scholar]
- Barnes, R.A.; Eplee, R.E.; Patt, F.S.; Kieffer, H.H.; Stone, T.C.; Meister, G.; Butler, J.J.; McClain, C.R. Comparison of SeaWiFS measurements of the Moon with the U.S. Geological Survey lunar model. Appl. Opt. 2004, 43, 5838–5854. [Google Scholar] [CrossRef] [PubMed]
- Kouyama, T.; Kato, S.; Kikuchi, M.; Sakuma, F.; Miura, A.; Tachikawa, T.; Tsuchida, S.; Obata, K.; Nakamura, R. Lunar calibration for ASTER VNIR and TIR with observations of the Moon in 2003 and 2017. Remote Sens. 2019, 11, 2712. [Google Scholar] [CrossRef]
- Kieffer, H.H.; Stone, T.C.; Barnes, R.A.; Bender, S.C.; Eplee, R.E., Jr.; Mendenhall, J.A.; Ong, L. On-orbit radiometric calibration over time and between spacecraft using the Moon. In Proceedings of the Sensors, Systems, and Next-Generation Satellites VI, Crete, Greece, 8 April 2003; Volume 4881, p. 287. [Google Scholar]
- Chang, I.-L.; Dean, C.; Li, Z.; Weinreb, M.; Wu, X.; Swamy, P.A.V.B. Refined algorithms for star-based monitoring of GOES Imager visible-channel responsivities. In Proceedings of the Earth Observing Systems XVII, San Diego, CA, USA, 15 October 2012; Volume 8510, p. 85100R. [Google Scholar]
- Vermote, E.; Santer, R.; Deschamps, P.Y.; Herman, M. In-flight calibration of large field of view sensors at short wavelengths using Rayleigh scattering. Int. J. Remote Sens. 1992, 13, 3409–3429. [Google Scholar] [CrossRef]
- Kaufman, Y.J.; Holben, B.N. Calibration of the AVHRR visible and near-IR bands by atmospheric scattering, ocean glint and desert reflection. Int. J. Remote Sens. 1993, 14, 21–52. [Google Scholar] [CrossRef]
- Robert, S.F.; Kaufman, Y.J. Calibration of satellite sensors after launch. Appl. Opt. 1986, 25, 1177–1185. [Google Scholar]
- Meygret, A.; Briottet, X.; Henry, P.J.; Hagolle, O. Calibration of SPOT4 HRVIR and Vegetation cameras over Rayleigh scattering. In Proceedings of the Earth Observing Systems V, San Diego, CA, USA, 15 November 2000; Volume 4135, p. 302. [Google Scholar]
- Luderer, G.; Coakley, J.A.; Tahnk, W.R. Using sun glint to check the relative calibration of reflected spectral radiances. J. Atmos. Ocean. Technol. 2005, 22, 1480–1493. [Google Scholar] [CrossRef]
- Khakurel, P.; Leigh, L.; Kaewmanee, M.; Pinto, C.T. Extended pseudo invariant site-based trend-to-trend cross-calibration of optical satellite sensors. Remote Sens. 2021, 13, 1545. [Google Scholar] [CrossRef]
- Loeb, N.G. In-flight calibration of NOAA AVHRR visible and near-IR bands over Greenland and Antarctica. Int. J. Remote Sens. 1997, 18, 477–490. [Google Scholar] [CrossRef]
- Tahnk, W.R.; Coakley, J.A. Updated calibration coefficients for NOAA-14 AVHRR channels 1 and 2. Int. J. Remote Sens. 2001, 22, 3053–3057. [Google Scholar] [CrossRef]
- Ling, W.; Xiuqing, H.; Yupeng, L.; Zhizhao, L.; Min, M. Selection and Characterization of Glaciers on the Tibetan Plateau as Potential Pseudoinvariant Calibration Sites. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2019, 12, 424–436. [Google Scholar] [CrossRef]
- Kwiatkowska, E.J.; Franz, B.A.; Meister, G.; McClain, C.R.; Xiong, X. Cross calibration of ocean-color bands from Moderate Resolution Imaging Spectroradiometer on Terra platform. Appl. Opt. 2008, 47, 6796–6810. [Google Scholar] [CrossRef] [PubMed]
- Chander, G.; Mishra, N.; Helder, D.L.; Aaron, D.B.; Angal, A.; Choi, T.; Xiong, X.; Doelling, D.R. Applications of spectral band adjustment factors (SBAF) for cross-calibration. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1267–1281. [Google Scholar] [CrossRef]
- Obata, K.; Tsuchida, S.; Yamamoto, H.; Thome, K. Cross-calibration between ASTER and MODIS visible to near-infrared bands for improvement of aster radiometric calibration. Sensors 2017, 17, 1793. [Google Scholar] [CrossRef]
- Barsi, J.A.; Alhammoud, B.; Czapla-Myers, J.; Gascon, F.; Haque, M.O.; Kaewmanee, M.; Leigh, L.; Markham, B.L. Sentinel-2A MSI and Landsat-8 OLI radiometric cross comparison over desert sites. Eur. J. Remote Sens. 2018, 51, 822–837. [Google Scholar] [CrossRef]
- Scott, K.P.; Thome, K.J.; Brownlee, M.R. Evaluation of Railroad Valley playa for use in vicarious calibration. In Proceedings of the Multispectral Imaging for Terrestrial Applications, Denver, CO, USA, 4 November 1996; Volume 2818, p. 158. [Google Scholar]
- Bacour, C.; Briottet, X.; Bréon, F.M.; Viallefont-Robinet, F.; Bouvet, M. Revisiting Pseudo Invariant Calibration Sites (PICS) over sand deserts for vicarious calibration of optical imagers at 20 km and 100 km scales. Remote Sens. 2019, 11, 1166. [Google Scholar] [CrossRef]
- Cosnefroy, H.; Leroy, M.; Briottet, X. Selection and characterization of Saharan and Arabian desert sites for the calibration of optical satellite sensors. Remote Sens. Environ. 1996, 58, 101–114. [Google Scholar] [CrossRef]
- Baiocchi, V.; Giannone, F.; Monti, F. How to Orient and Orthorectify PRISMA Images and Related Issues. Remote Sens. 2022, 14, 1991. [Google Scholar] [CrossRef]
- Berthelot, B.; Santer, R. Calibration Test Sites Selection and Characterisation Site Equipment and Auxiliary Data; Vega Technique SAS: Erstein, France, 2008. [Google Scholar]
- Zheng, X.; Huang, Q.; Wang, J.; Wang, T.; Zhang, G. Geometric accuracy evaluation of high-resolution satellite images based on Xianning test field. Sensors 2018, 18, 2121. [Google Scholar] [CrossRef]
- Aerosol Robotic Network (AERONET) Homepage. Available online: https://aeronet.gsfc.nasa.gov/ (accessed on 17 July 2022).
- Heller-Pearlshtien, D.; Pignatti, S.; Greisman-ran, U.; Ben-Dor, E. PRISMA sensor evaluation: A case study of mineral mapping performance over Makhtesh Ramon, Israel. Int. J. Remote Sens. 2021, 42, 5882–5914. [Google Scholar] [CrossRef]
- Heller-Pearlshtien, D.; Ben-Dor, E. CalVal Evaluation of DESIS products in Amiaz Plain and Makhtesh Ramon Test sites. In Proceedings of the 1st DESIS User Workshop—Imaging Spectrometer Space Mission, Calibration and Validation, Applications, Methods, Virtual, 28 September–1 October 2021; pp. 13–21. [Google Scholar]
- Zak, R.; Freund, R. Strain Measurements in Eastern Marginal Shear Zone of Mount Sedom Salt Diapir, Israel. Am. Assoc. Pet. Geol. Bull. 1980, 64, 568–581. [Google Scholar] [CrossRef]
- Weinberger, R.; Bar-Matthews, M.; Levi, T.; Begin, Z.B. Late-Pleistocene rise of the Sedom diapir on the backdrop of water-level fluctuations of Lake Lisan, Dead Sea basin. Quat. Int. 2007, 175, 53–61. [Google Scholar] [CrossRef]
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)-interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Ben-Dor, E.; Kindel, B.; Goetz, A.F.H. Quality assessment of several methods to recover surface reflectance using synthetic imaging spectroscopy data. Remote Sens. Environ. 2004, 90, 389–404. [Google Scholar] [CrossRef]
- Kneizys, F.; Abreu, L.; Anderson, G.; Chetwynd, J.; Shettle, E.; Berk, A.; Bernstein, L.; Robertson, D.; Acharya, P.; Rothman, L.; et al. The MODTRAN 2/3 Report and LOWTRAN-7 Model; Contract F19628-91-C-0132; Ontar Corporation: North Andover, MA, USA, 1996. [Google Scholar]
- MODTRAN®. Available online: http://modtran.spectral.com/modtran_index (accessed on 15 September 2022).
- Brook, A.; Ben-Dor, E. Supervised vicarious calibration (SVC) of hyperspectral remote-sensing data. Remote Sens. Environ. 2011, 115, 1543–1555. [Google Scholar] [CrossRef]
- Farr, T.G.; Rosen, P.A.; Caro, E.; Crippen, R.; Duren, R.; Hensley, S.; Kobrick, M.; Paller, M.; Rodriguez, E.; Roth, L.; et al. The Shuttle Radar Topography Mission. Rev. Geophys. 2007, 45, RG2004. [Google Scholar] [CrossRef]
- Makhtesh Ramon Cal/Val Site. Available online: https://storymaps.arcgis.com/stories/bb5bf09ec7414454a012bfe9bf4b8545 (accessed on 23 July 2022).
- Pignatti, S.; Amodeo, A.; Carfora, M.F.; Casa, R.; Mona, L.; Palombo, A.; Pascucci, S.; Rosoldi, M.; Santini, F.; Laneve, G. PRISMA L1 and L2 Performances within the PRISCAV Project: The Pignola Test Site in Southern Italy. Remote Sens. 2022, 14, 1985. [Google Scholar] [CrossRef]
- Cogliati, S.; Sarti, F.; Chiarantini, L.; Cosi, M.; Lorusso, R.; Lopinto, E.; Miglietta, F.; Genesio, L.; Guanter, L.; Damm, A.; et al. The PRISMA imaging spectroscopy mission: Overview and first performance analysis. Remote Sens. Environ. 2021, 262, 112499. [Google Scholar] [CrossRef]
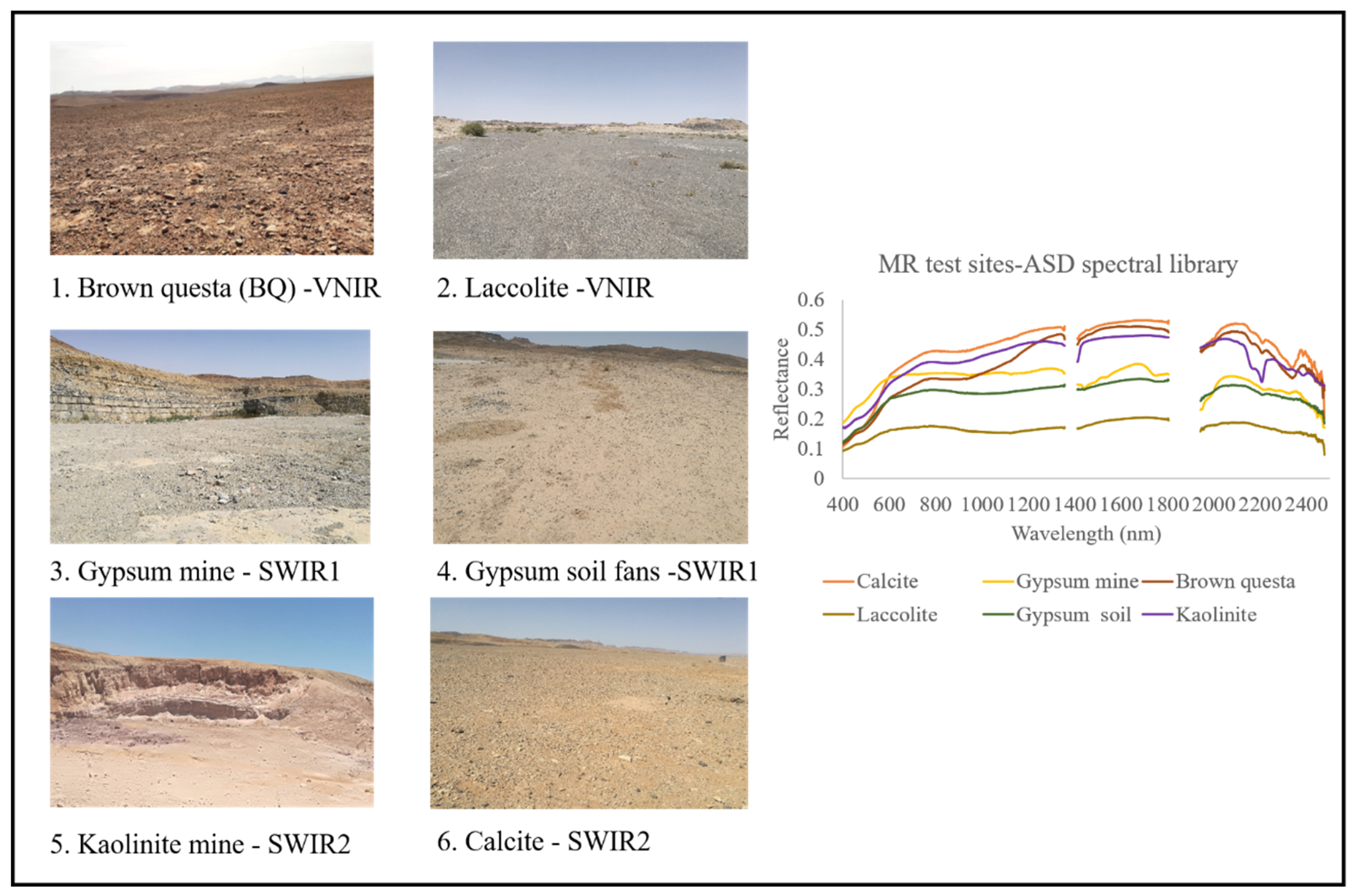
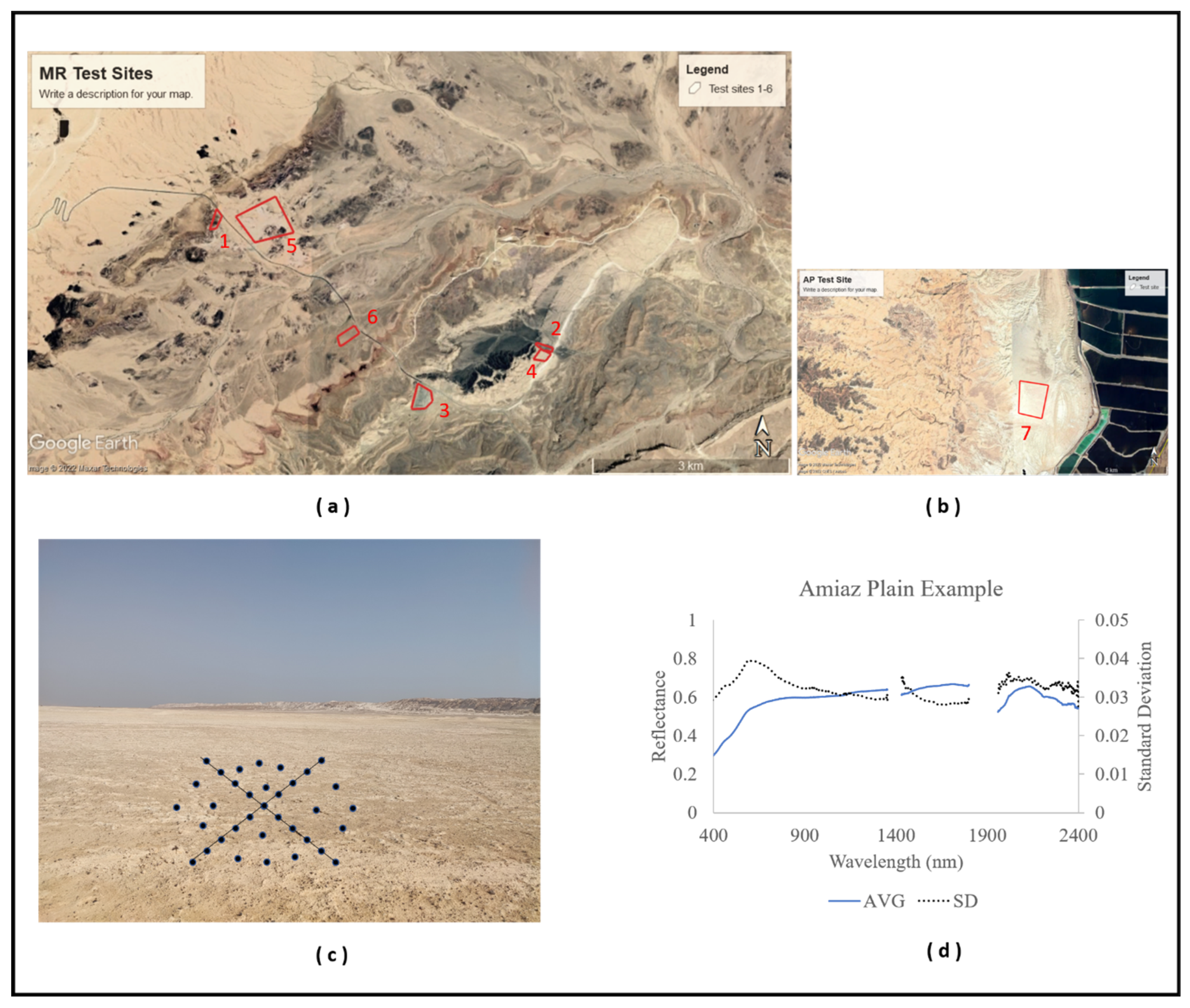


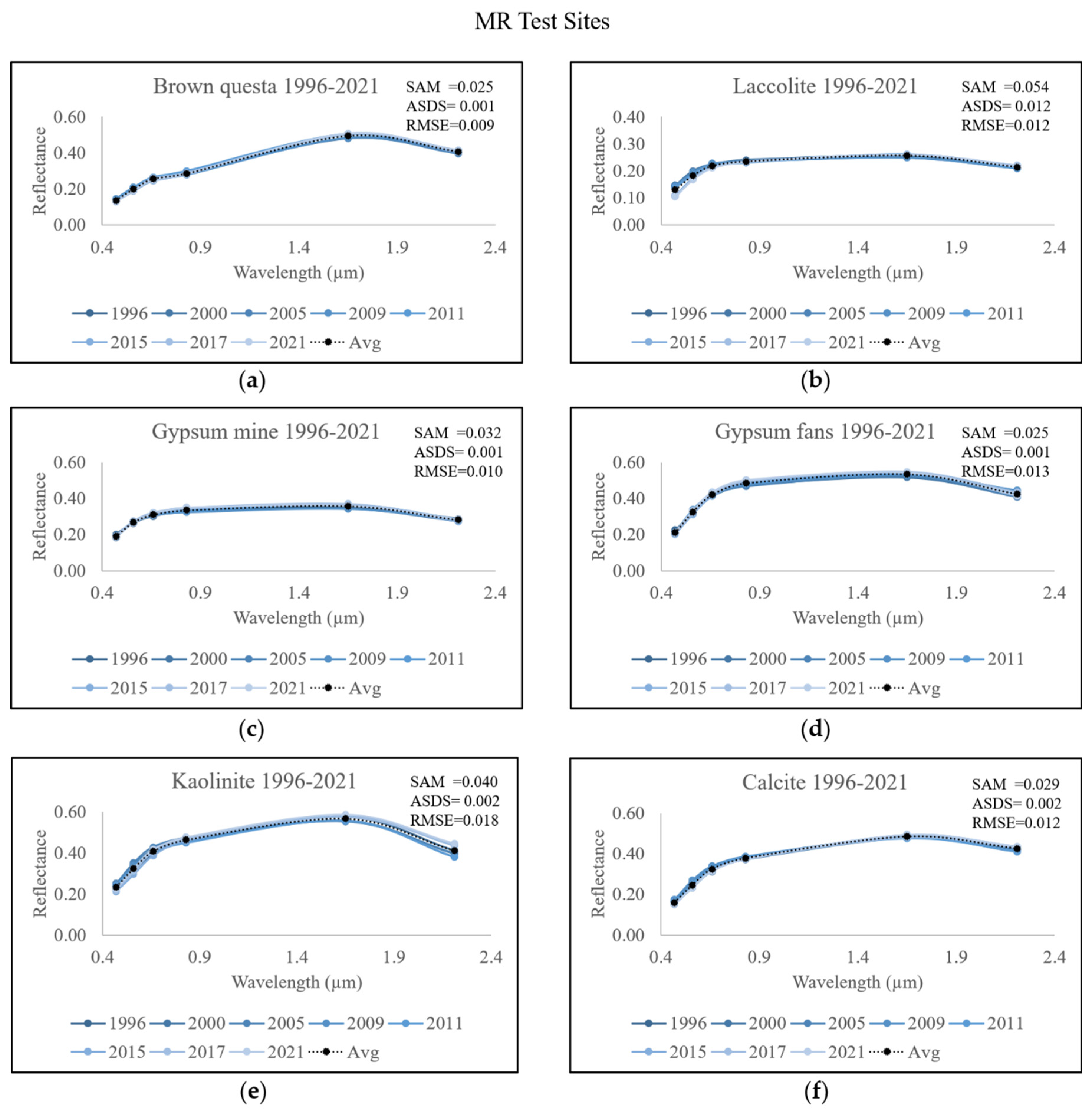
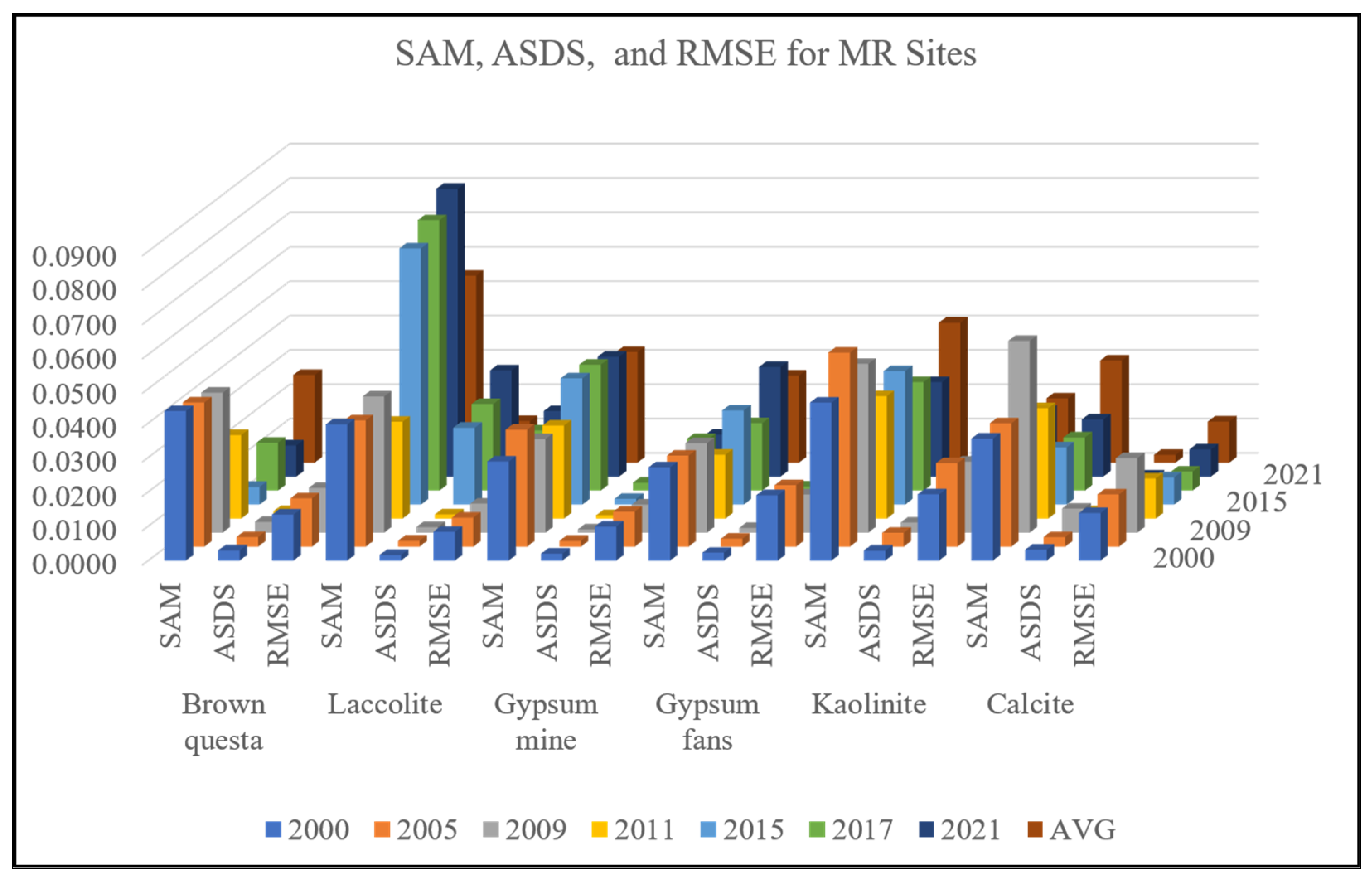
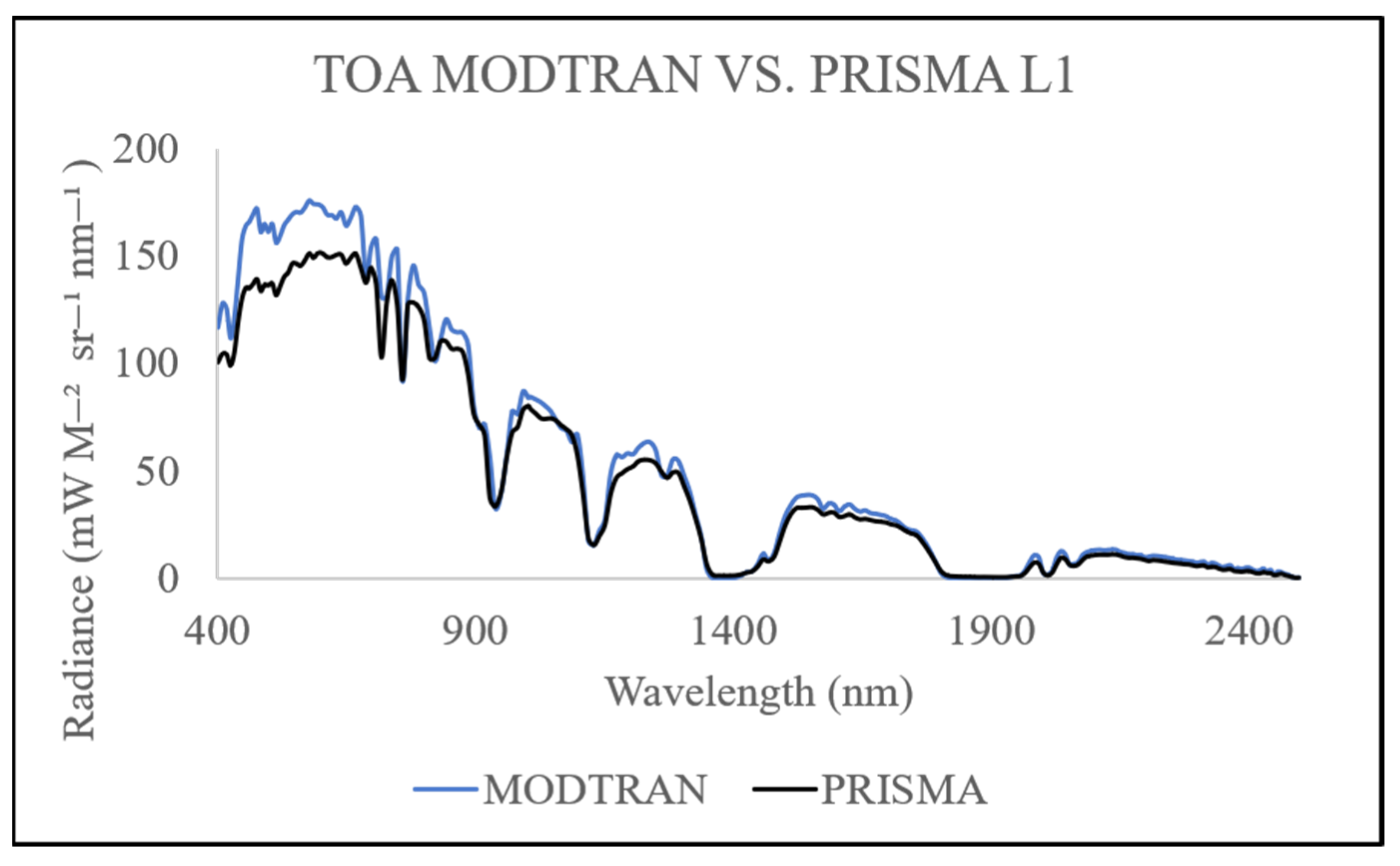
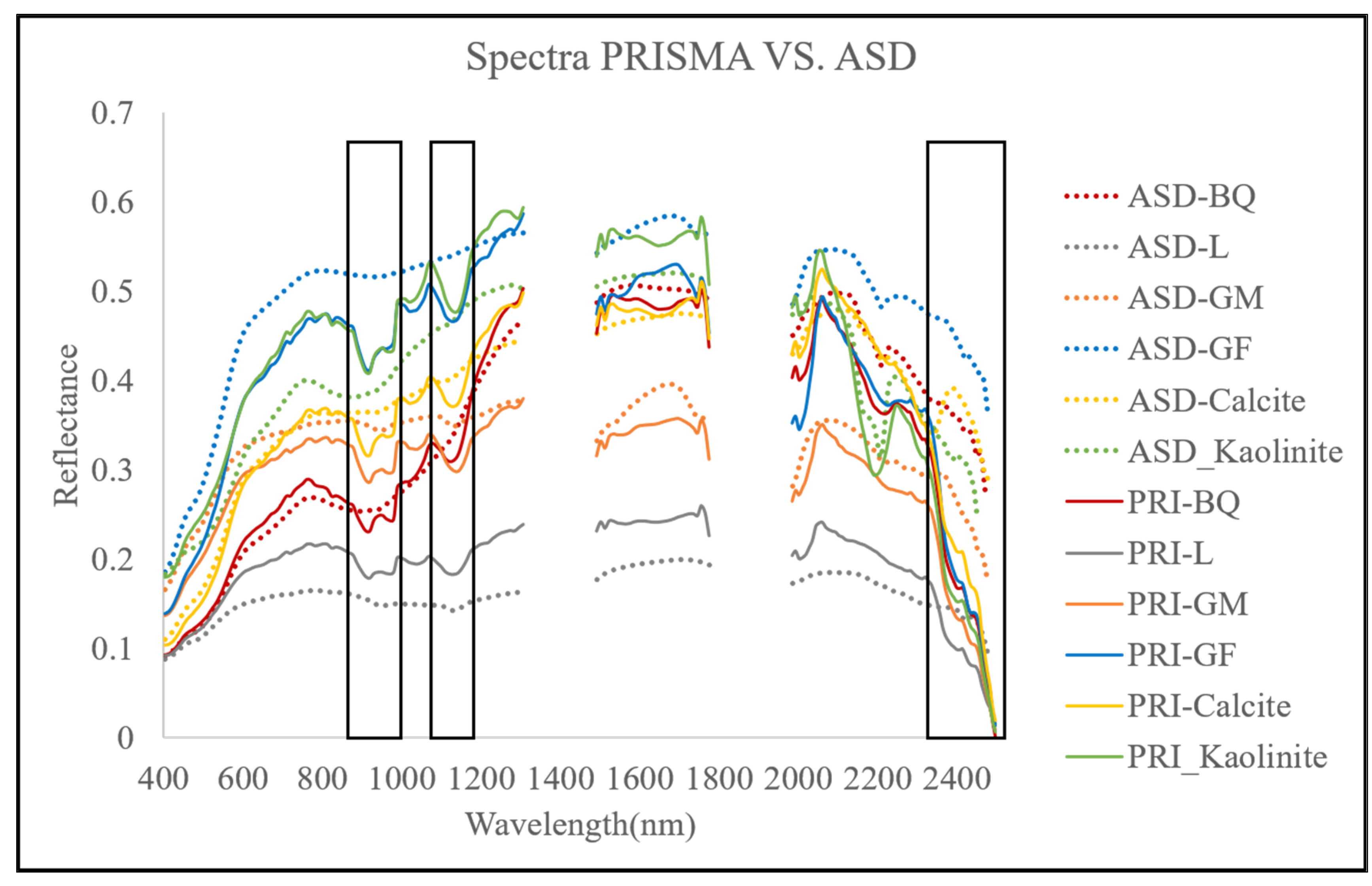



| Test Site | Number | Altitude (Meters Above Sea Level) | Area (Square Meters) |
|---|---|---|---|
| MR Brown questa | 1 | 521 | 28,241 |
| MR Laccolite | 2 | 469 | 17,262 |
| MR Gypsum—old mine | 3 | 498 | 81,473 |
| MR Gypsum—soil fans | 4 | 469 | 27,857 |
| MR Kaolinite—old mine | 5 | 502 | 356,531 |
| MR Calcite | 6 | 503 | 48,578 |
| AP | 7 | −258 | 1,757,943 |
| Sensor | Information | Number of Images | Purpose |
|---|---|---|---|
| Landsat 5 Thematic Mapper 5 (NASA/USGS) | 7 bands, spectral range visible (VIS)–SWIR 0.45–2.35 µm, 30 m GSD (ground sample distance); thermal infrared (TIR) 10.40–12.50 µm, 120 m GSD | 9 | Evaluation of spectral and spatial stability of MR and AP for years 1996–2011 |
| Landsat 8 Operational Land Imager (NASA/USGS) | 11 bands, spectral range VIS–SWIR 0.43–2.29 µm, 30 m GSD; TIR 10.60–12.51 µm, 100 m GSD; panchromatic 0.5–0.68 µm | 6 | Evaluation of spectral and spatial stability of MR and AP for years 2015–2021 |
| PRISMA PRecursore IperSpettrale della Missione Applicativa Italian Space Agency (ASI) | 234 bands, range of 400–2500 nm, 30 m GSD; full-width half maximum (FWHM) ≤12 nm, swath 30 km, sensor altitude 615 km L1 TOA radiometric image, L2B ground radiometric image, and L2D atmosphere- corrected data cube. Acquired from PRISMA’s website | 15 | Validation of CAL/VAL research protocols for AP and MR. Image dates: 2019–2022 |
| DESIS DLR Earth Sensing Imaging Spectrometer German Aerospace Center (DLR) | 235 bands, spectral range 400–1000 nm, 30 m GSD; FWHM ~3.5 nm, swath 30 km, sensor altitude 400 km. L1C radiometric georectified image and L2A atmosphere- corrected data cube. Acquired from DESIS EOweb GeoPortal. | 6 | Validation of CAL/VAL research protocols for AP and MR. Image dates: 2020–2021 |
| AisaFenix 1K (HSR sensor AisaFENIX—Specim, Spectral Imaging Ltd.) | An airborne campaign using the AisaFENIX 1K over MR and AP was carried out on April 5, 2017, covering the entire MR (200 km²) area and AP (5 km²). 420 bands, spectral range 375–2500 nm, 1.5 m GSD; FWHM: VIS 3.4 (nm), NIR–SWIR, 6.2 (nm), swath 1.8 km | 25 lines on MR 1 line on AP | Establishing high-accuracy reference data for AP and MR, mapping MR main minerals, and summarizing in an online database. Benchmark data for the CAL/VAL protocol [36,46] |
| ASD FieldSpec model FSP 350–2500 nm (Model 3 and Model 4) | Spectral range of 350–2500 nm with 2151 bands, with 3 nm and 8 nm resolution for the VNIR and SWIR regions | Ongoing | In-situ field measurements of radiance and reflectance for validation. Years 2019–2022 |
| The Shuttle Radar Topography Mission (SRTM) | NASA–JPL at a resolution of 1 arc-s (approximately 30 m) [45] | 1 | Creating 3D elevation models of MR. Slope and aspect maps |
| Test Site | Number of ASD Points | SD VNIR | SD SWIR1 | SD SWIR2 | SD All Bands |
|---|---|---|---|---|---|
| Brown questa | 62 | 0.0161 | 0.0250 | 0.0218 | 0.0180 |
| Laccolite | 58 | 0.0117 | 0.0173 | 0.0161 | 0.0129 |
| Gypsum—mine | 61 | 0.0352 | 0.0540 | 0.0627 | 0.0374 |
| Gypsum—soil fans | 50 | 0.0207 | 0.0242 | 0.0318 | 0.0217 |
| Kaolinite | 70 | 0.0226 | 0.0363 | 0.0339 | 0.0254 |
| Calcite | 109 | 0.0205 | 0.0222 | 0.0223 | 0.0224 |
| Test Site | Spectral Range | Wavelength (nm) | SAM | ASDS | RMSE |
|---|---|---|---|---|---|
| Brown questa | VNIR | 402–998 | 0.089 | 0.050 | 0.032 |
| Laccolite | VNIR | 402–998 | 0.060 | 0.020 | 0.020 |
| Gypsum—mine | SWIR1 | 1480–1794 | 0.067 | 0.071 | 0.027 |
| Gypsum—soil fans | SWIR1 | 1480–1794 | 0.066 | 0.073 | 0.042 |
| Kaolinite | SWIR2 | 2001–2400 | 0.144 | 0.300 | 0.103 |
| Calcite | SWIR2 | 2001–2400 | 0.155 | 0.280 | 0.098 |
| Brown questa | VSWIR | 400–2400 | 0.128 | 0.220 | 0.048 |
| Laccolite | VSWIR | 400–2400 | 0.103 | 0.207 | 0.026 |
| Gypsum—mine | VSWIR | 400–2400 | 0.089 | 0.109 | 0.038 |
| Gypsum—soil fans | VSWIR | 400–2400 | 0.092 | 0.123 | 0.075 |
| Kaolinite | VSWIR | 400–2400 | 0. 131 | 0.180 | 0.083 |
| Calcite | VSWIR | 400–2400 | 0.101 | 0.123 | 0.042 |
| Years Compared | X Error (m) | Y Error (m) | SD X | SD Y |
|---|---|---|---|---|
| 2019–2020 | 16.8 | 19.7 | 0.69 | 0.37 |
| 2020–2021 | 243.1 | 66.9 | 0.75 | 1.13 |
| 2021–2022 | 16.9 | 18.3 | 0.43 | 0.23 |
| 2019–2022 | 238.6 | 95.1 | 0.51 | 1.18 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pearlshtien, D.H.; Pignatti, S.; Ben-Dor, E. Vicarious CAL/VAL Approach for Orbital Hyperspectral Sensors Using Multiple Sites. Remote Sens. 2023, 15, 771. https://doi.org/10.3390/rs15030771
Pearlshtien DH, Pignatti S, Ben-Dor E. Vicarious CAL/VAL Approach for Orbital Hyperspectral Sensors Using Multiple Sites. Remote Sensing. 2023; 15(3):771. https://doi.org/10.3390/rs15030771
Chicago/Turabian StylePearlshtien, Daniela Heller, Stefano Pignatti, and Eyal Ben-Dor. 2023. "Vicarious CAL/VAL Approach for Orbital Hyperspectral Sensors Using Multiple Sites" Remote Sensing 15, no. 3: 771. https://doi.org/10.3390/rs15030771
APA StylePearlshtien, D. H., Pignatti, S., & Ben-Dor, E. (2023). Vicarious CAL/VAL Approach for Orbital Hyperspectral Sensors Using Multiple Sites. Remote Sensing, 15(3), 771. https://doi.org/10.3390/rs15030771








