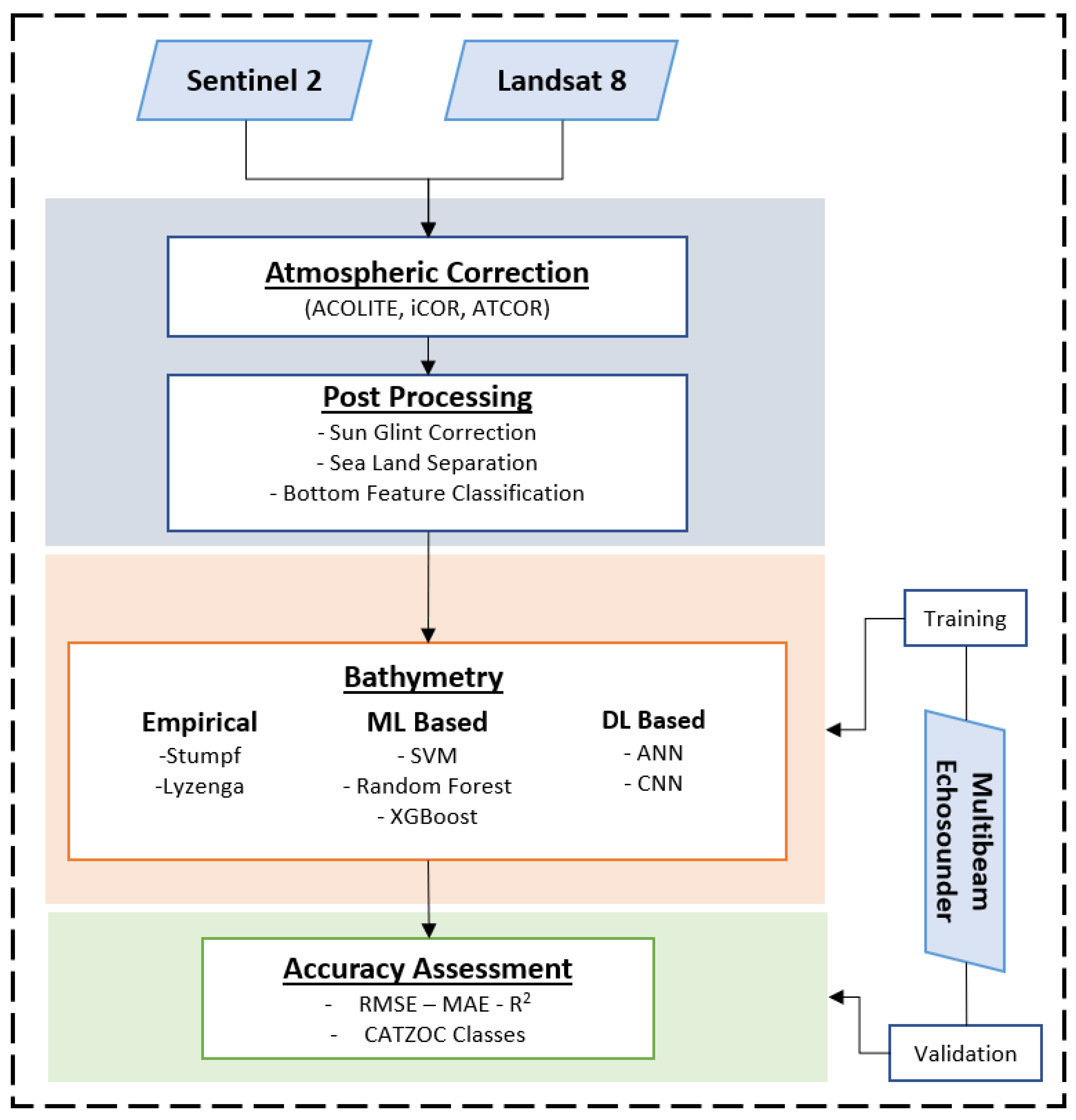
1. Introduction
Shallow water bathymetry is crucial for nautical navigation, but it is also essential for monitoring coastal areas covering underwater topography, sediment loads, detection and identification of human-induced pressures, and the effects of changes in the climate such as sea level rise [
1,
2]. The adverse effects of climate change have been more evident in the last and hottest decade resulting in massive heatwaves and temperature rise, especially in polar regions. Several studies have pointed out that the Antarctic Peninsula and sub-Antarctic islands have faced rapid warming with the highest temperature records and acceleration in snowbank melting [
3,
4,
5]. Thus, there is a need for continuous monitoring of the ecosystem and sea level rise in shallow zones.
The conventional approaches for surveying seas and oceans use single (SBE) and multi-beam echosounders (MBEs). Yet these methods bear certain limitations, such as losing their efficacy as depth decreases, having a limited spatial coverage and temporal resolution, and being subject to logistic restrictions with high operational costs and risks [
1]. Recently, a range of modern tools have been used to assess the ocean’s bathymetry, including remotely operated vehicles, automated underwater vehicles, and airborne LIDAR platforms [
6]. However, according to the study of Ashphaq et al., remote and autonomous technologies are likewise expensive due to costs associated with their purchase and maintenance [
7].
Due to their capacity to collect data across vast spatial areas and to offer high-frequency temporal monitoring, space-borne remote sensing techniques have additionally been developed into a substitute method for obtaining bathymetric data in coastal zones [
8]. The method developed to survey shallow waters with optical satellite images is called satellite-derived bathymetry (SDB). Optical SDB is based on the inverse relationship between the amount of energy reflected from the water column and the depth of water [
1]. As stated by Duan et al., recent studies have focused on SDB technology within the scope of producing bathymetry data [
9]. Remote sensing data eliminate traditional bathymetric surveying because of their low cost, broad regional coverage, and temporal and space-unconstrained sensing abilities [
10]. It is clear that SDB research is rising, as shown in the sharp increase over the past five years according to a literature review in the Web of Science collection using the keywords “satellite”, “remote sensing”, “bathymetry”, etc. Especially, Landsat 8 and Sentinel 2 open-source optical satellites have shown expanded research capability on the optical SDB field and provide high potential in bathymetry estimation of coastal and inland regions [
9,
11,
12,
13].
It can be stated that initial studies based on linear and logarithmic band ratio-based algorithms [
14,
15] were followed by machine learning (ML) algorithms and DL-based approaches that are nowadays available based on a chronological review of empirical SDB studies. The initial use of ML-based SDB mapping was introduced by Ceyhun and Yalcın [
16], and the popular use of ML-based approaches was observed coupled with the support vector machine (SVM) algorithm [
9,
17], followed by the random forest (RF) [
9,
18,
19,
20] and XGBoost algorithms [
21,
22]. Among them, the use of XGBoost in optical SDB is relatively new, and only two studies have been undertaken to infer bathymetric depth from Sentinel 2 satellite images. Susa’s study, drawing attention to the current use of XGBoost, suggested further investigation of its performance [
22]. The DL-based SDB mapping is a recent research attempt, which mainly focuses on determining the local spatial correlation between the reflectance information and the water depth. Initial studies used artificial neural networks (ANNs) for SDB mapping and reported considerable improvements in accuracy with respect to classical models [
23,
24]. Another study by Dickens and Armstrong used recurrent neural networks (RNNs) on Orbview 3 satellite images to derive SDB in Pacific islands [
25]. A more recent study used convolutional neural networks (CNNs) to identify the relationship and produce SDB maps at spatial resolutions compatible with multispectral images [
26]. Recently, Wan and Ma used a deep belief network with a data perturbation (DBN-DP) model on Quickbird and Worldview 2 images in which R
2 correlation and RMSE metrics in comparison with other models used in the study were reported [
27]. A recent study published in 2023 compared basic empirical models and ML-based methods (RF, SVM, and NN) in SDB mapping of the Ganquan Dao area and their findings provided higher inversion results with ML-based methods in up to 15 m depth. The authors of the study pointed out that a comparative analysis of empirical and ML-based methods in different water depths is still scarce and inconclusive [
28].
The atmospheric correction process is frequently addressed as a crucial step when satellite images are used for bathymetry extraction [
29,
30]. The complexity of the water column in coastal waters caused by factors such as water quality and sediment heterogeneity has an impact on the proper measurement of water depth. This situation suggests a stricter requirement for atmospheric correction accuracy [
12]. Several recent studies have experimentally compared the performance of various atmospheric correction algorithms and examined the comparative correlation between ground-based depth measurements and/or image band ratios and estimated depth [
30,
31]. Among these studies, Caballero and Stumpf showed that the performance of atmospheric correction directly affects empirical methods based on band ratio [
30]. Ceyhun and Yalcin stated that machine learning-based approaches in particular do not consider the behavioral mechanism of electromagnetic radiation in water; therefore, the effect of atmospheric correction is minimal [
16]. On the other hand, Duan et al. obtained significant correlation differences depending on the atmospheric correction model on the machine learning-based SVM algorithm, and they stated that there is still a need for a systematic comparison of the effects of different atmospheric correction algorithms on different SDB models [
9].
This study focuses on estimating and mapping the bathymetry on Horseshoe Island, Antarctic Peninsula, by performing a comprehensive evaluation of atmospheric correction effects on SDB with Landsat 8 and Sentinel 2 images, and by comparing the performance of ML- and DL-based models with the basic empirical models. To the best of our knowledge, this study is one of the first studies to conduct a thorough evaluation of SDB mapping with optical satellite images in Antarctica, considering sensor platforms, atmospheric correction methods, and empirical SBD models.
The main contributions of this study to the literature are the following:
Demonstration of a comparative performance evaluation of empirical SDB mapping approaches with an extension of the most current ML- and DL-based methods in Antarctica.
Evaluation of the effects of the state-of-the-art atmospheric correction methods on SDB mapping for a region with complex and challenging atmospheric conditions such as Antarctica.
Investigation of the suitability of open source mid-resolution optical satellites, Landsat 8 and Sentinel 2, in SDB mapping of Antarctica.
2. Study Area and Data
Antarctica is a unique and fragile environment that is characterized by its extreme cold, dry, and windy conditions. It is the coldest, driest, and windiest continent on Earth, and its landscape is dominated by ice and snow [
32]. The Antarctic continent is covered by a thick ice sheet that averages about 2100 m in thickness. The ice sheet holds approximately 70% of the Earth’s freshwater, making it a crucial part of the planet’s climate system [
33]. Despite its harsh conditions, Antarctica is home to a wide range of plant and animal life, including penguins, seals, and several species of algae and bacteria. However, the biodiversity of the continent is relatively low compared with other regions of the world due to its isolation and extreme environmental conditions. In recent years, the environment in Antarctica has been threatened by climate change which has caused the ice to melt and the sea level to rise [
34].
Bathymetry of the Antarctic region is important for understanding the topography of the ocean floor and related processes. The region is characterized by a complex network of ocean currents and glaciers, which significantly impacts the region’s bathymetry. There have been several efforts to map the bathymetry of the Antarctic region using satellite data and other observations [
35,
36,
37,
38]. These studies utilized a number of data sources, including aerial gravity, satellite altimetry, single beam and multibeam echo sounding, and various methods. One important example is the International Bathymetric Chart of the Southern Ocean (IBCSO), which is a digital map of the ocean floor in the Southern Hemisphere. IBCSO was created using data from a variety of sources, including satellite altimetry, ship-based measurements, and in situ sensors [
39]. However, there is a gap in evaluating the efficacy of optical satellite images in SDB mapping for this region.
Due to their free data and extensive coverage areas, Landsat 8 and Sentinel 2 satellites successfully meet this need for optical multispectral data, and SDB studies derived from these satellites have been widely used in recent years [
9,
30,
31]. Landsat 8 satellite carries two different sensors, Operational Land Imager (OLI) and Thermal Infrared (TIR). These sensors provide 11 bands of multispectral data from the Coastal Aerosol region of the electromagnetic spectrum to the Thermal Infrared. The temporal resolution of the Landsat 8 satellite is 16 days. Its spatial resolution is 30 m for the visible- and shortwave-infrared regions. Sentinel 2 is a satellite constellation consisting of the Sentinel 2A and Sentinel 2B satellites. It provides 13 bands of multispectral data in the spectrum ranging from the Coastal Aerosol region to the Shortwave Infrared (SWIR). The common temporal resolution of the Sentinel 2 satellite constellation is five days. The near-infrared resolution of the Sentinel 2 satellites for the visible and near-infrared (NIR) bands is 10 m. Landsat 8 and Sentinel 2 provide good coverage of the global land surface, inland waters, and the sea [
30,
40,
41]. These satellites have recently demonstrated tremendous potential for bathymetry applications in coastal, inland, and open sea waters [
11,
12,
13,
42].
Since the meteorological conditions of Horseshoe Island in Antarctica are quite challenging, the potential to provide data with optical satellites is low. Taking this issue and the year 2019 as a reference, which was the date of the previous Arctic research expedition in which multibeam echosounder (MBE) measurements were performed, an archive search was carried out through the USGS Earth Explorer [
43] and Copernicus Open Access Hub [
44] portals by defining a time period of 2 years for Landsat 8 and Sentinel 2 satellite images. During the search, cloudiness was not taken into consideration in the first stage, and image selections were made by evaluating the cloudiness rate of the study area based on the results obtained within the scope of the scan results. The initial results of the scan for the period of 2017–2021 provided 5 Landsat 8 and 3 Sentinel 2 cloud-free images (
Table 1). Among them, Landsat 8 images dated 19 February 2018 and Sentinel 2 images dated 24 January 2019 were used in this study due to their temporal proximity to the in situ MBE data.
Processing levels of the acquired data:
- -
For Landsat 8 data, the L1GT level is radiometrically corrected, geometrically corrected using a limited number of ground points and digital elevation models, and is provided in 16-bit data form. Top of atmosphere (TOA) reflectance values can be obtained from these data by basic coefficient transformations.
- -
For Sentinel 2 data, the L1C level is again radiometrically and geometrically corrected, and the TOA reflectance values can be obtained from these data with basic coefficient transformations.
As understood from this information, the images to be used within the scope of the study can only be obtained at basic processing levels, and they need atmospheric correction to reach the surface reflectance values required in satellite-based SDB studies.
The dense MBE data provided as point cloud data with horizontal resolution below 1 m are used as the main training and validation dataset. This dataset was collected with the R2SONIC 2022 instrument during the Turkish Antarctic Expedition (TAE)-III to the region between 29 January–6 March. These data embody a maximum measurement error margin of around 1 m horizontally and 1 cm vertically for 400 m, which is the maximum depth it can measure within its technical capabilities [
45]. In this context, a total of 10,000 bathymetric point data, 2500 homogeneously for each 5 m interval for 0–20 m depth, were randomly selected. Of these 10,000 point data, 8000 were used for model training and 2000 were used for validation. During the analysis, 5 m depth intervals were evaluated separately in addition to 0–10 m and 0–20 m intervals for holistic evaluation. The study region and bathymetric model obtained from these data are presented in
Figure 1.
Aerosol optical depth (AOD) data that were then measured by ship-borne Microtops II sun photometers through The Maritime Aerosol Network (MAN) component of the Aerosol Robotic Network (AERONET) [
46] were obtained from the NASA AERONET website [
47] to be used in iCOR and ATCOR atmospheric models.
4. Results
This section presents the analysis results of SDB estimation on the coasts of Horseshoe Island in a comparative structure. The evaluation includes (i) comparing the effects of ACOLITE, ATCOR, and iCOR atmospheric correction algorithms on SDB estimation, (ii) comparing SDB algorithm performances, and (iii) comparing the performances of Landsat 8 and Sentinel 2 visible bands on SBD estimation. The evaluation was carried out for 5 m depth intervals up to 20 m depth. In addition, 0–10 m, 0–15 m, and 0–20 m intervals were examined to check the estimation consistency among increasing depth ranges. Furthermore, all possible visible band pairs were evaluated for Stumpf, SVM, RF, and XGBoost algorithms to investigate the potential effects. ANN- and CNN-based algorithms used RGB images directly in their estimations.
The RMSE- and MAE-based results proved that RF and XGBoost provided the highest performance for the whole sensor, depth, and atmospheric correction configurations. The ANN and CNN algorithms ranked second, and their accuracies were highly close to each other according to the RMSE and MAE values. SVM, Lyzenga, and Stumpf BR algorithms followed the DL-based algorithms again with comparable performances while Stumpf BG and Stumpf GR were ranked last in this comparison (
Table A1,
Table A2,
Table A3,
Table A4,
Table A5 and
Table A6). Based on the investigation of the best-performing RF and XGBoost algorithms (
Figure 7 and
Figure 8), it can be asserted that using different band configurations such as BG, GR, and BR has nearly no impact on the performance of algorithms, except for the Stumpf algorithm where the BR combination provided comparatively stable results. Moreover, notably lower RMSE values were detected in the 0–15 m and 0–20 m intervals than the BG and GR combinations for Landsat 8, while the same situation was not observable for Sentinel 2 (
Table 4). It is worth mentioning that DL-based models presented the best results in this study. Our experiments demonstrated that changing the loss functions and increasing the model depth (more than three convolutional layers), and feeding the models, either with the log values of RGB bands or a combination of their log ratios, did not provide significant improvements.
The atmospheric correction algorithms had a slight effect on the results, where all sensor and algorithm configurations provided similar performances across different input images resulting from three atmospheric correction algorithms. At this point, it is worth mentioning that, our findings reflect the correlative behavior of surface reflectance values with in situ depths in log space; thus, this finding does not necessarily indicate the similarity of absolute surface reflectance values obtained by these atmospheric correction algorithms. For the ease of application, ACOLITE is more automated and requires no additional input information.
The sensor-based evaluation proved that Sentinel 2 provided higher accuracies in the 0–5 m, 5–10 m, and 0–10 m depth intervals, while the performance of the Landsat 8 was higher for the remaining 5 m intervals and wider depth ranges (0–15 m and 0–20 m). As expected from previous studies, the accuracies reduced with increasing depths; however, ML-based algorithms minimized this increment and provided comparatively consistent mapping performances.
R2 is another important indicator that represents the model’s ability to construct the relationship between reflectance and depth. Depth intervals for R2 are defined differently than the RMSE, which are 0–5, 0–10, 0–15, and 0–20, to investigate the correlation changes in increasing interval ranges. When the results of correlation analysis were investigated, it was similarly seen that Landsat 8 images provided high and consistent correlation characteristics except for the 0–5 m depth ranges. For Sentinel 2, a decrease in correlation was observable through larger depths such as the 0–15 m and 0–20 m ranges. The SDB algorithms had a small effect, with slightly higher correlations of RF than XGBoost. The results also provided that there is no significant effect of the three atmospheric correction methods on the correlation performance.
The last step of the study was to evaluate the performance in terms of category of zone of confidence (CATZOC) classification. The CATZOC levels are specified in the relevant International Hydrographic Organization (IHO) standard documents [
74], which comprise the requisite accuracy in various depth ranges (
Table 5) [
27]. SDB results of the study were mainly clustered at Level A2/B and C, while the performance of XGBoost and RF at 0–5 m intervals with Sentinel 2 images satisfied Level A1. Lastly, the performance at 0–20 m, the widest range for all combinations, was evaluated as Level C and Level D (
Table A7,
Table A8 and
Table A9).
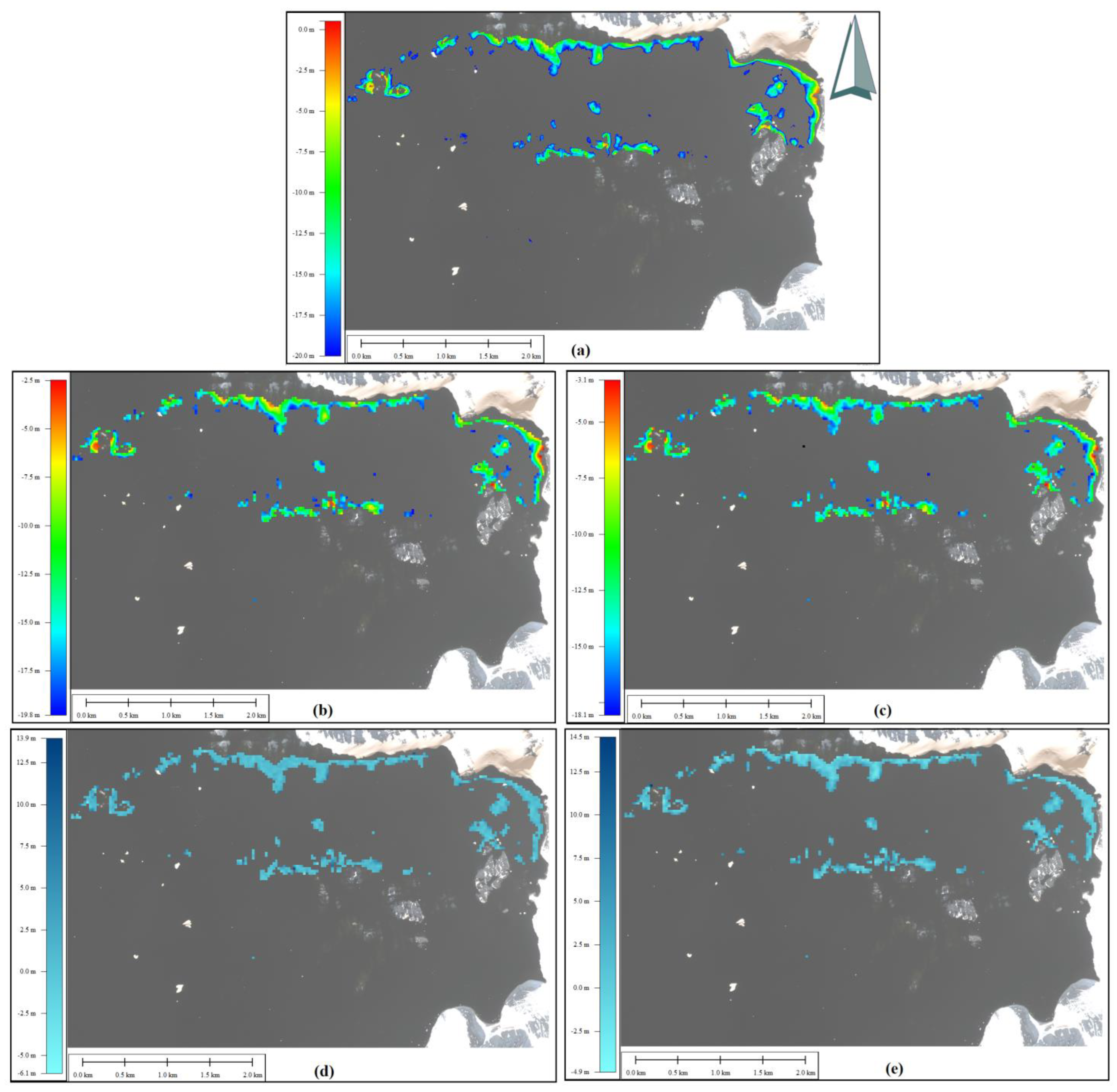
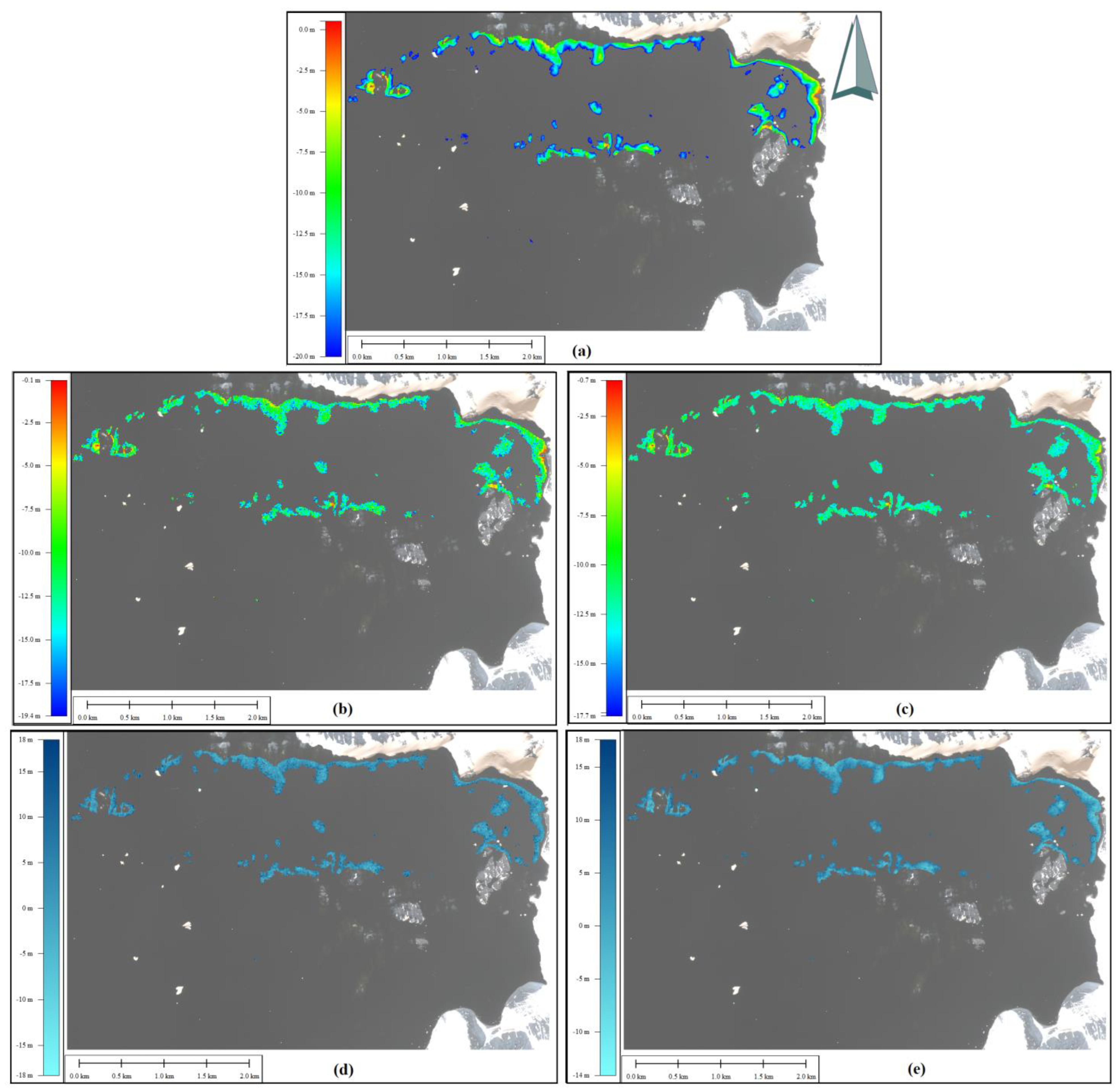
The final products of the 0–20 m range bathymetry inversion were created as raster grid maps for both RF and XGBoost methods, and Landsat 8 and Sentinel 2 images (
Figure 9 and
Figure 10). In addition, change rasters were also constructed in regard to the grid map of the in situ MBE data for comparison purposes. When these maps are visually investigated, it can be interpreted that both algorithms provide similar results and that they are mostly comparable to the MBE map. The results obtained from Landsat 8 are more in line with MBE in higher depths (
Figure 9b,c vs.
Figure 10b,c). Additionally, the difference maps from Landsat 8 provided smaller difference ranges (lighter blue) when compared with Sentinel 2 forms (
Figure 9d,e vs.
Figure 10d,e). Smother boundaries of the Sentinel 2-based maps match well with the MBE data, while the step effect and boundary discontinuities are visible for the Landsat 8-based maps related to higher spatial resolution of the Sentinel 2 images. Lastly, the higher performance of Sentinel 2 in coastal regions (0–5 m depth) is visible on the maps.
5. Discussion
When the results are investigated through the algorithm context, it can clearly be seen that ML- and DL-based algorithms cope well with the non-linear behavior of the reflectance–depth relationship, and provide highly accurate and consistent results for 5 m depth intervals. Although the decrease in accuracy with increasing depth is observable for all methods, this phenomenon is less effective in these models. They also performed well in wider-depth ranges of 0–10 m, 0–15 m, and 0–20 m, indicating their consistent performance. The performance of Lyzenga ranked as the fifth, followed by Stumpf BR and SVM. The worst results were obtained with Stumpf BG and Stumpf GR combinations for Landsat 8, which faced dramatic RMSE and MAE increases in wider depth intervals. While not providing the highest accuracy, SVM was the most consistent method with stable RMSE and MAE values across all atmospheric correction, sensor, and band combinations.
In the sensor context, Landsat 8 provided higher accuracy with lower RMSE and higher R
2 values in higher depths (greater than 10 m) and wider depth ranges (0–15 and 0–20 m), but faced difficulties in 0–5 m and 0–10 m depth intervals. Sentinel 2 provided better results in 0–5 m, 5–10 m, and 0–10 m intervals; however, its performance dramatically reduced especially in wide depth ranges (higher RMSE, MAE, and lower R
2), where it could not build a correlation with in situ MBE data. From these results, it can be commented that Sentinel 2 copes well with depth heterogeneity, which is observable on the shallower parts due to its high spatial resolution, while it exerted a disadvantage in deeper regions where depth became more homogenous. However, higher spatial resolution provides reflectance heterogeneity. This finding points out that, although previous research concluded that higher resolution results in higher accuracy [
22,
75], the spatial heterogeneity of the depth and conformity of image spatial resolution is another factor to be considered. The findings of Ashphaq et al., 2022, also compared the performance of Landsat 8, Sentinel 2, and ASTER-Terra images in SDB mapping of a turbid coastal water region, and they concluded that they could reach the highest correlation and the lowest accuracy with Landsat 8 images, which supports our findings that spatial resolution is not a direct indicator of higher accuracy [
76]. On the other hand, we determined that the advantage of Sentinel 2 is its construction of boundary geometries quite accurately compared with Landsat 8, mainly as a result of its higher spatial resolution.
When the results are analyzed in the context of atmospheric correction, this study’s findings show that, particularly when using ML-based techniques, the effects of the three selected atmospheric correction models on building the relationship between surface reflectance and in situ depth measurements are minimal. This finding conflicts with Duan’s [
9] and Abdul Gafoor’s [
21] studies, which employed ML-based methods for bathymetric modeling and found noticeable effects of atmospheric correction on modeling, but it is quite consistent with the study conducted by Ceyhun and Yilmaz [
16]. It should be highlighted that the proper application of the atmospheric correction to the data is still a factor to be considered. At this point, the ACOLITE model is the most parametrically automated model. In particular, the AOT value calculated by the model agreed with the value (0.030) obtained from the AERONET Microtops Level 2.0 dataset obtained in 2019 in the relevant season. The Wv parameter also agreed with 0.8 cm, which is the average of the summer season between 2019 and 2021. While running the ACOLITE model, the area of interest can be introduced as vector data, and the result data can be obtained only for this area. Although AOT can be calculated as image based for the iCOR model, this approach is primarily based on the calculation of land surfaces; thus, the AOT and Wv values obtained from the AERONET Microtops Level 2.0 dataset were defined manually. The only parameter that can be intervened for ATCOR is Wv, for which 1.0 cm was chosen as the closest value to the Aeronet data. To summarize, iCOR and ATCOR have some limitations related to AOT retrieval and the aerosol model; however, these limitations can be minimized by the use of AERONET OC data.
Although the proposed approaches and the findings of this study point out efficient SDB mapping capabilities in such a region with complex characteristics, it is worth mentioning that SDB is influenced by several factors such as water quality, wave structure, salinity, and illumination conditions related to seasonal differences, which are not directly investigated in this study. Moreover, performance of the recently investigated XGBoost was similar to the RF; however, its advantages on other ML algorithms is mainly observed with high-dimensional datasets [
22]. Therefore, its performance should be further checked with a multi-temporal image-based SBD approach. This work used ANN- and CNN-based architectures in SDB mapping, although the performance of recently introduced DL-based architectures remains to be investigated in the future. Lastly, we plan to extend the study to different regions and other sensors for possible performance improvement, and to wider applicability testing of our findings.