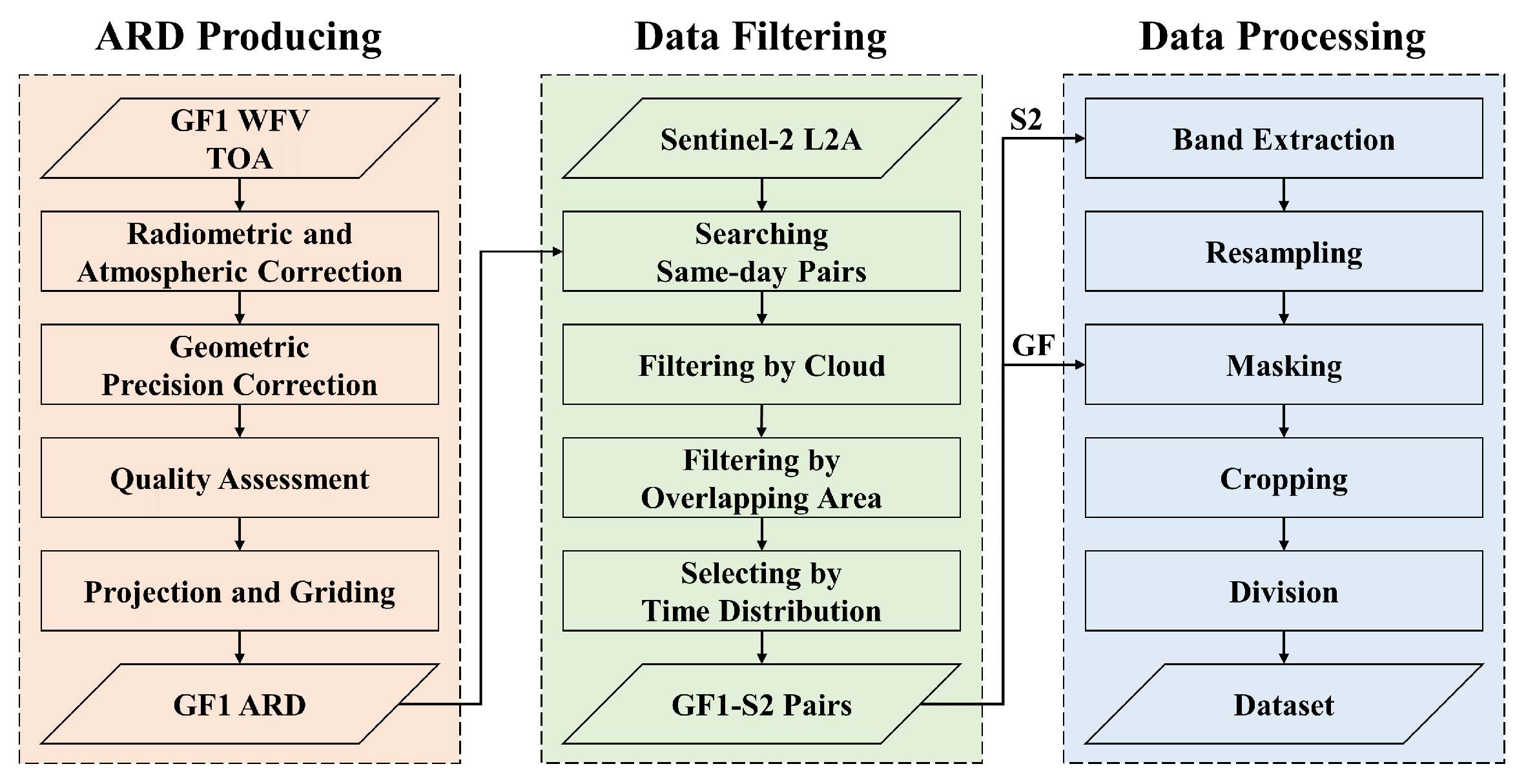
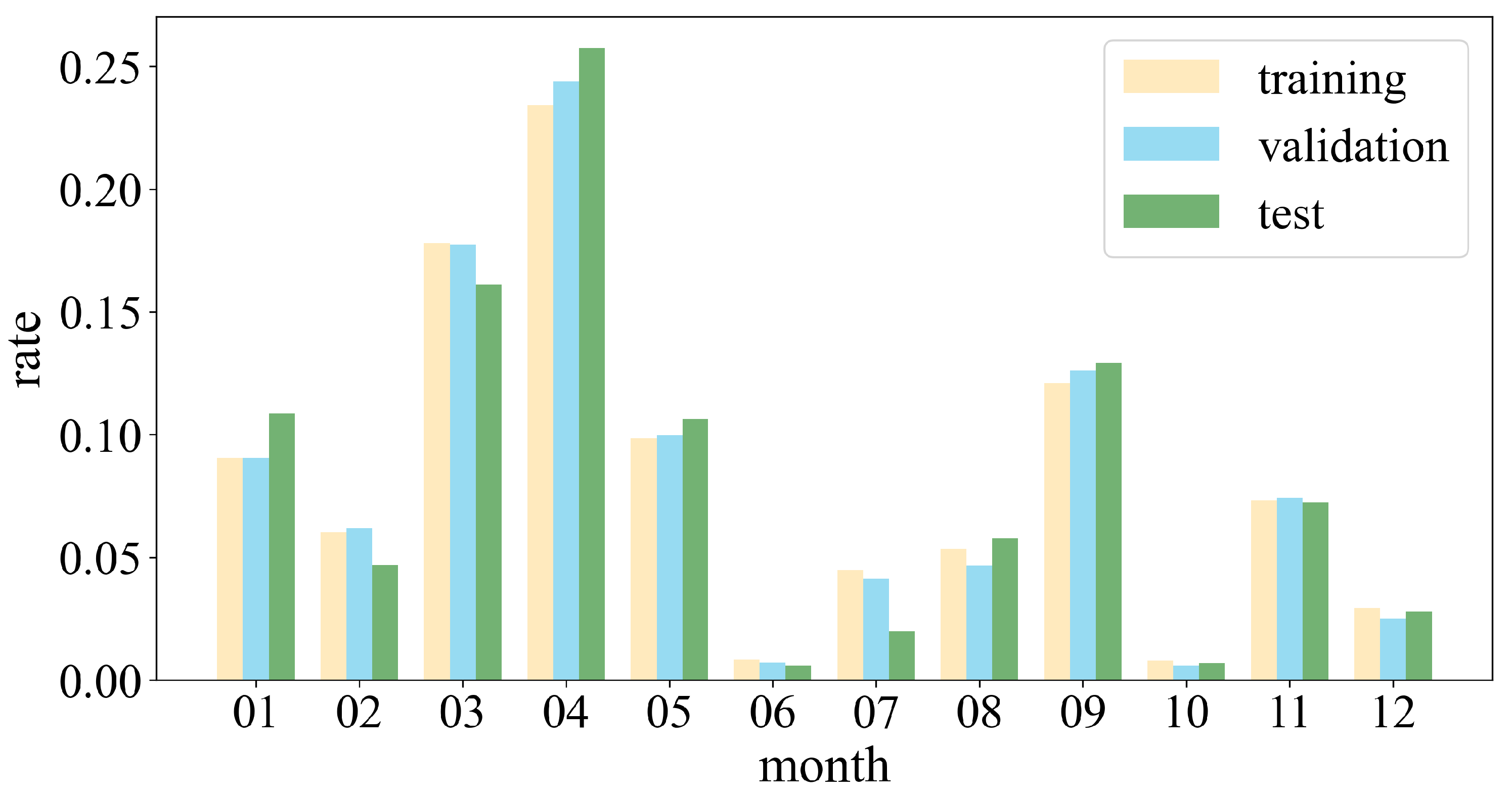
1. Introduction
Since numerous Earth observation satellites have been launched in recent years, the enormous potential of combining data from different platforms has been discovered [
1,
2,
3]. The temporal coverage is expected to significantly increase when observations from multiple sensors are combined [
4]. Higher-temporal-resolution data provides a solid data foundation for time series analysis in many Earth-monitoring applications, such as land cover change detection [
5], terrestrial ecosystem monitoring [
6], urban expansion [
7], and flood response [
8,
9].
A large amount of medium-resolution satellite imagery has been archived since the open data policy was adopted for Gaofen (GF) satellites in 2019. However, the publicly available GF1 data is in the 1A/B processing stage, necessitates additional efforts to construct spatially and temporally consistent time series before most analyses, particularly for large-scale and long-term analyses [
10]. Therefore, analysis ready data (ARD) is desperately needed to relieve users of costly pre-processing steps. As defined by the Committee on Earth Observation Satellites (CEOS), ARD is satellite data that has been processed to a minimum set of requirements and organized into a form that allows immediate analysis with minimal additional user effort and interoperability both through time and with other datasets (
http://ceos.org/ard/ (accessed on 22 February 2023)). Specifically, GF1-ARD provides surface reflectance (SR) after atmospheric and geometric correction. Furthermore, GF1-ARD contains a quality assessment band, projected and tiled onto the same UTM-based military grid reference system (MGRS) as Sentinel-2.
Sentinel-2 (S2) is a suitable candidate to create a virtual constellation (VC) with GF1-ARD to produce temporally denser products. GF1-WFV has a four-day revisit cycle. However, GF1-WFV weekly observations cannot fulfil the requirements of these applications due to the need for continuous and fine-grained monitoring and environmental factors. These environmental factors, include challenging solar geometries, frequent snow and ice cover, persistent cloud cover, and other poor atmospheric effects [
11,
12], all of which can negatively affect the images. Therefore, it is an appealing idea to combine data from GF1-WFV and S2 into a single dataset, and this combination of multiple sensor data is termed “VC”. The European Space Agency launched two satellites for the S2 mission, S-2A and S-2B, in 2015 and 2017, respectively. Both S-2A and S-2B have a repeat cycle of ten days, while they have a joint revisit period of five days. The multi-spectral instrument (MSI) onboard both S2 satellites provides thirteen spectral bands with a spatial resolution of 10 to 60 m, depending on the wavelength. Meanwhile, four wide field viewing (WFV) sensors onboard the GF1 satellites contain four spectral bands with a spatial resolution of 16 m. S2 and GF1 share similarities in band specification, as shown in
Table 1. Furthermore, they both have sun-synchronous polar orbits. Because of these similarities, they are favourable for developing more frequent multi-sensor ARD products.
Over the past few decades, many investigations have been conducted to produce harmonized data from multiple sensors. These works can be generally divided into two categories: bandpass alignment [
13,
14,
15,
16,
17] and spatio-temporal fusion [
18,
19,
20]. Since there usually exists disparity in spatial resolution between different sensors, these two categories of methods generate synergies in different application scenarios. The former is only required to temporally align the radiometric characteristics of multi-source imagery, where sensor-to-sensor variations are required to be minimized. Furthermore, the latter is also expected to achieve image super-resolution, which improves the spatial resolution of the coarser input to a finer spatial resolution. For example, the NASA Harmonized Landsat and Sentinel-2 (HLS) project combines the visible bands of the Landsat-8 OLI (30 m) and Sentinel-2 MSI (10 m) to produce more frequent reflectance products at 30 m [
1]. Based on this, researchers have attempted to bridge the spatial resolution gap between Landsat-8 and Sentinel-2 to yield a 10 m harmonized dataset [
19]. In this study, we focus on producing denser GF1-ARD products with the aid of Sentinel-2 to promote the temporal resolution of GF1-ARD. Hence, the required spatial resolution of the output products is 16 m and the first category of methods is taken into account.
The goal of multi-sensor bandpass alignment is to promote the consistency of sequential observations across various sensors. Furthermore, temporally consistency can be defined as data collected in a short period of time with similar values [
21]. Reflectance inconsistencies in multi-temporal and multi-sensor data may be introduced by factors such as, misregistration, different viewing geometry [
22,
23,
24], atmospheric and cloud contamination, sensor degradation and calibration variations [
25], distinct spectral bandpass and spatial resolution [
1,
26], and other processing problems [
13]. As a result, bandpass alignment is inevitably implemented in order to produce harmonized data from multiple sensors.
Bandpass alignment can be decomposed into two processes, including making the time sequence of a single sensor consistent and coordinating the radiometric characteristics consistent across different sensors. In this study, we assume the first consistency has been guaranteed, concentrating on the second process. As a result, the bandpass alignment is converted into the transformation from S2 imagery to GF1-ARD-like data. The majority of current studies focus on the alignment between Landsat and S2, but few have investigated the combination of GF1-ARD and data from other sensors. At the same time, most of the work involving GF1 data is limited to a small region, and the temporal consistency is not systematically studied [
27,
28]. Therefore, it is worthwhile to conduct a global investigation into the bandpass alignment of GF1-ARD products and data from other platforms.
Most of the current models are built on the linear model, which is ineffective for aligning S2 to GF1-ARD. Although S2 and GF1 have similar sensor characteristics, their relationships become complicated when each sensor goes through its own series of processing steps from digital numbers to SR. Meanwhile, the linear model is unsatisfactory when generalizing to a global scale. As a result, researchers have developed local-derived bandpass alignment, such as in permafrost regions [
3], Australia [
14], and arctic–boreal regions [
15]. These experiments demonstrate that locally derived bandpass alignment is superior to globally harmonized products. Since the modelling capability of the linear model is constrained due to the limited globally shared parameters, more powerful regional-adaptive models are therefore desired to achieve the alignment from S2 to GF1-ARD.
Taking advantages of the fast development of deep learning techniques [
29], it is becoming increasingly popular to train deep neural networks for image enhancement [
30,
31,
32,
33,
34]. The bandpass alignment can be viewed as a special case of image enhancement tasks in computer vision, with the goal of adjusting the input closer to the GF1-ARD products rather than better visualization results. However, the backbone of these models is the deep convolutional neural network (CNN), composed of the local operations of convolution and pooling [
35,
36]. These stacked local operations will result in large receptive fields and therefore inevitably produce an unacceptably blurry output. Without the guidance of global knowledge, these models will make erroneous local decisions that lead to artefacts in uniform areas [
31]. In addition, the transformation parameters should be shared in relatively large areas since the differences between GF1-ARD and Sentinel-2 L2A products are sensor-related. In summary, the favoured model should achieve a nearly pixel-wise transformation in a relatively larger area.
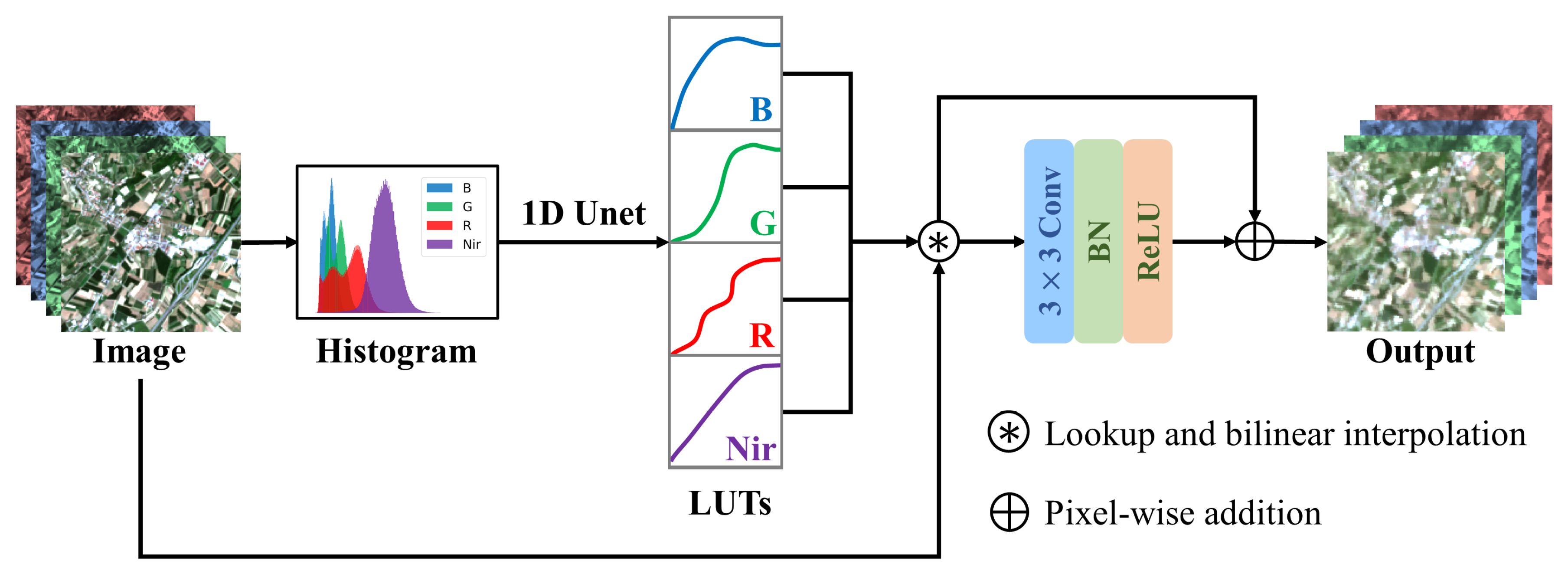
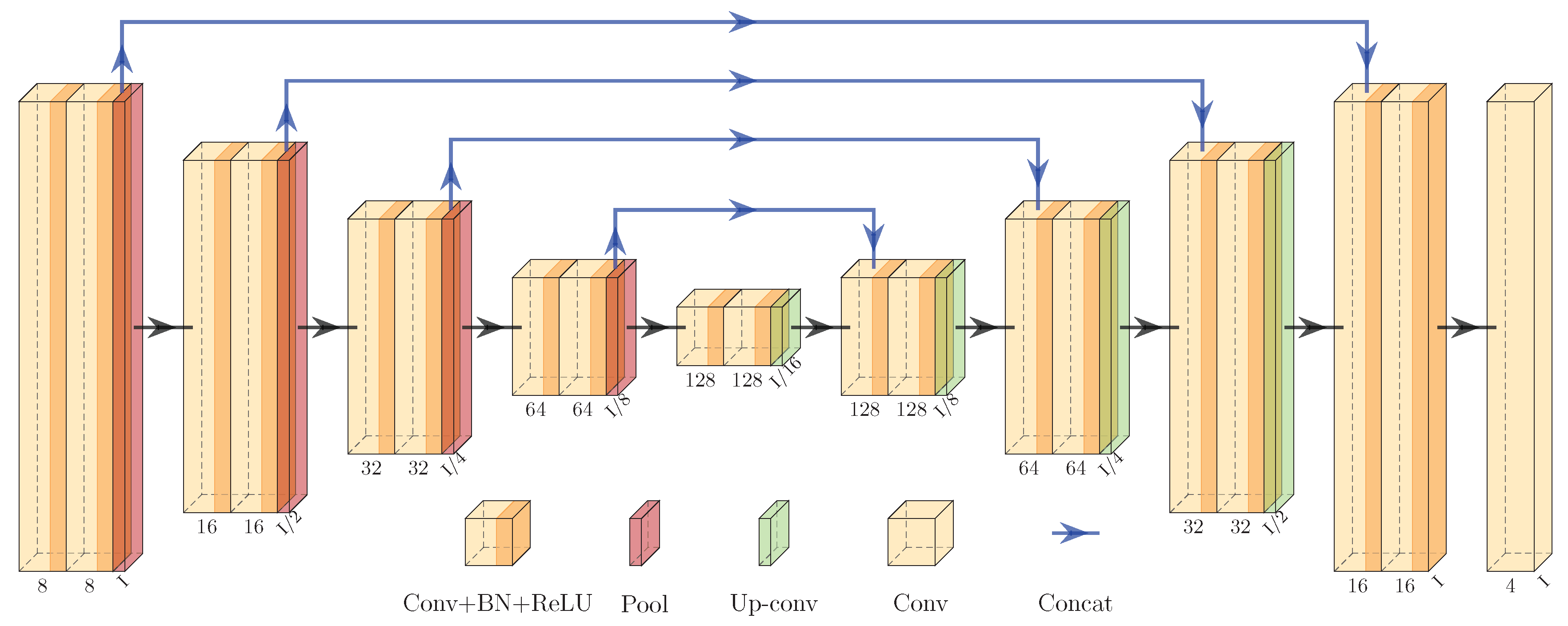
Guided by the above principles, we propose to learn tile-adaptive lookup tables (LUTs) with a U-shaped network (UNet) to produce fast and robust bandpass alignment. Inspired by the research of [
30,
33], the LUTs are used to enhance the linear model. The primary difference between our model and the preceding models is how the LUTs are learned. Our model generates the LUTs from the histogram of a tile, while these models are developed by images. As previously mentioned, the bandpass alignment can be regarded as an image enhancement task, and histogram matching is one of the most widely used methods. Histogram matching can be viewed as a process of finding LUTs based on the histograms of the input image pair. However, this is not applicable in our task since only the source S2 imagery is provided for the inference while the target GF1-ARD imagery is not. Motivated by the basic principles of histogram matching, we believe the expected LUTs are highly correlated with the input radiance distribution. Yet, it is challenging to learn a good mapping function from a histogram to LUTs. This issue can be effectively resolved by a deep learning model, which has strong non-linear and generalization abilities due to its deep structure. Therefore, we innovatively propose to learn tile-wise LUTs from the histograms of bands based on UNet. Furthermore, we add a single CNN layer with a
kernel to lessen the burden of the registration error between S2 and GF1-ARD. Furthermore, such a small kernel hardly blurs the final output because the spatial resolution of the S2 input is inherently higher.
To validate the effectiveness of the proposed model, experiments have been conducted across two years at three diverse study sites. The radiance distribution and true colour images after the transformation are comprehensively visualized. Moreover, the normalized difference vegetation index (NDVI) is employed to demonstrate the excellent consistency of the temporally aligned data. The temporal frequency of data is further assessed to illustrate the giant promotion of the time series’ frequency after combining S2.
3. Results
In the following experiments, the proposed model is evaluated on our dataset. The linear model learned by ordinary least squares (OLS) is compared to illustrate the competitive performance of our model. The ablation study and visualization results are shown to demonstrate the effectiveness of this model. Moreover, the temporal frequency of the data is assessed after the bandpass alignment. Finally, the temporal consistency of the combined time sequence is measured.
3.1. Performance Comparison
The coefficient of determination (
) is adopted to quantify the goodness of fit of the model. In this regression task, the
is a statistical measure of how well the transformed S2 bands approximate the GF1-ARD bands. An
of 1 indicates that the regression predictions perfectly fit the data. In addition, we calculate the root-mean-squared error (RMSE) to measure the absolute difference between the prediction results and the ground truth. The smaller the difference between these the values pairs, the closer the relationship. Moreover, the OLS regression is derived between equivalent bands from the S2 and GF1-ARD, and the fitting model is formulated as follows:
where
y is the GF1-ARD product and
x is the prediction result, which can be the output of the linear model or our model.
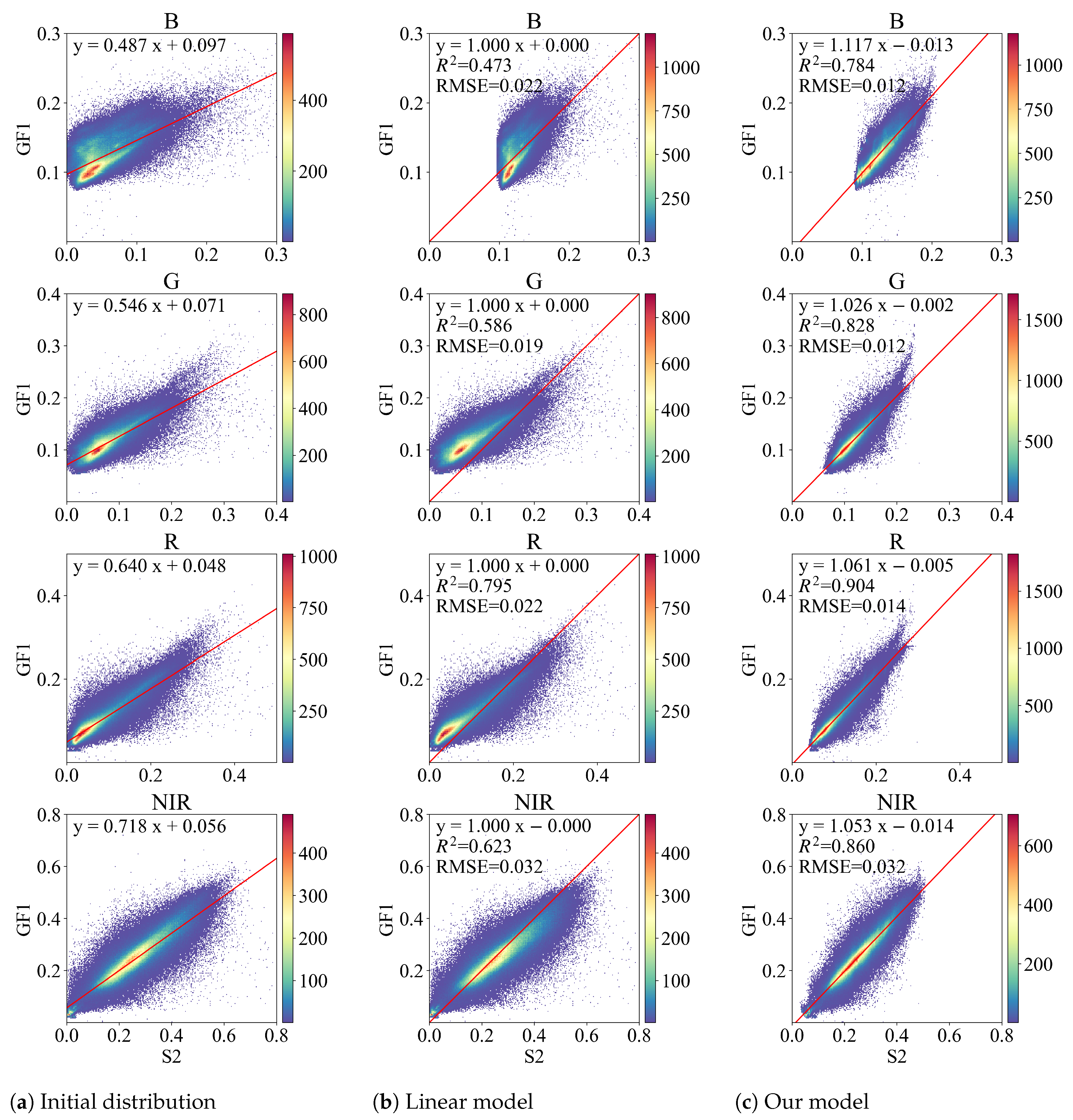
Table 3 presents a quantitative comparison between the linear and proposed models in the test dataset. We observed that the linear correlation between S2 and GF1-ARD, especially in the blue band, is not significant enough. The
values in blue, red, and NIR bands are less than 0.8, and those in the blue band are even less than 0.5. In contrast, the linear correlation between the GF1-ARD and the prediction of our model is greatly improved. The
values of all bands are close to or greater than 0.8. In addition, the RMSE values are considerably lower than those of the linear model, especially the RMSE in the blue band, which is almost reduced by a factor of 2.
Figure 6 further displays the scatter plots between the GF1-ARD and different variables, including the initial S2 data and the prediction of the linear model and the output of our model. The parameters of the linear and proposed models are determined by samples in the training dataset. It is worth noting that the red solid line in
Figure 6a is learned using OLS regression with the S2 and GF1-ARD representing the
x and
y in Equation (
7), consistent with
Table 3. Since the OLS is a linear transformation, the line fitted by the S2 after OLS transformation and GF1-ARD is
. Meanwhile, the red line in
Figure 6c is learned with the prediction of our model and the GF1-ARD. As seen in
Figure 6a, the scatters are not well located around the red solid line calculated by OLS regression, indicating a low linear correlation between S2 and GF1-ARD. In contrast, the scatters of our model are distributed more tightly, consistent with the previous quantitative results.
However, there still exists scatters that fall far apart and cannot be transformed well by our model. The remaining differences are caused by several factors, including misregistration, different viewing geometry, and mixed pixels. Despite the fact that our model employs a CNN module, the registration error cannot be fully addressed because a local operation cannot perfectly align the S2–GF1 pair spatially. Meanwhile, the viewing geometry differs even though the S2–GF1 pairs are observed on the same day. Correspondingly, the reflectance may vary greatly due to the terrain, particularly in mountain shadow regions. Moreover, the effects of mixed pixels vary because of the difference in spatial resolution. We downsampled S2 from 16 m to 30 m in the data processing, whereas the mixed pixels in the downsampled S2 are still less than those in the 30 m GF1-ARD. As a result, even if our model is powerful, the bandpass alignment will never be perfect because the observation conditions cannot be strictly identical.
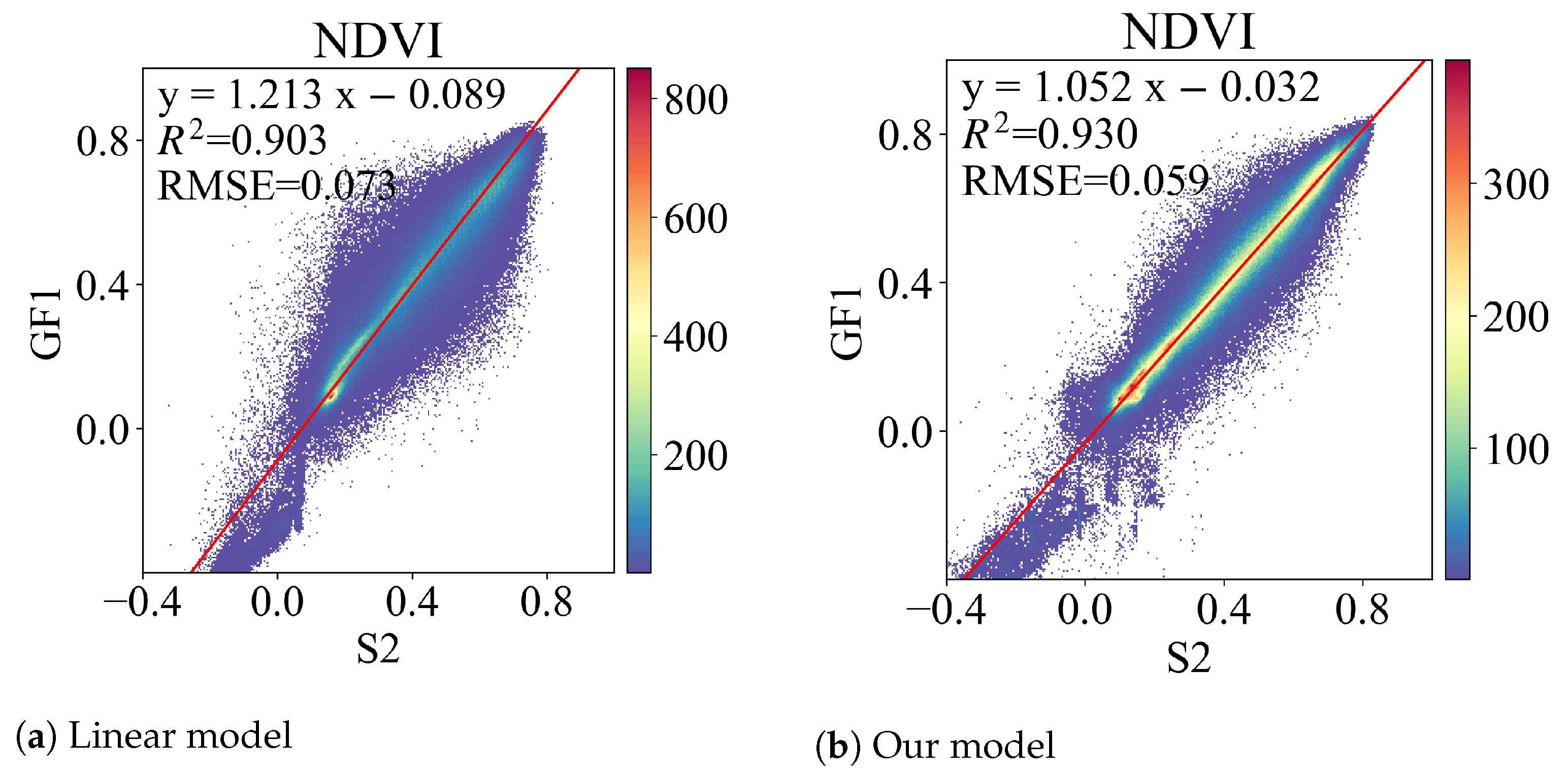
Furthermore, since the NDVI is one of the most simple yet effective vegetation indices, we extends the quantitative comparison to the NDVI. The NDVI is calculated using two bands by the following formula:
where
and
stand for the reflectance in the near-infrared (NIR) and red bands, respectively. An NDVI value near one indicates a high level of green plant cover, while a value near zero denotes a lack of vegetation, possibly in urban areas. Water, clouds, or snow are the primary causes of negative NDVI values. The quantitative and qualitative results are shown in
Table 4 and
Figure 7, respectively. Even when
for the red and NIR bands is less than 0.8, the linear model’s NDVI
can reach 0.9, which can be attributed to two factors. First, the red and NIR bands have a relatively stronger linear correlation. Second, normalization enables the NDVI to be a successful descriptor of vegetation variations in the presence of atmospheric effects, sensor calibration degradation, and radiometric degradation in the red and NIR bands (reviewed by [
44]). Our model increases the NDVI
even higher to 0.93 while decreasing the RMSE from 0.073 to 0.059. Accordingly, the scattering points in
Figure 7b are more centred around the red fitting line. Additionally, we find that the fitting is worse in areas with reflectance values lower than 0, which should be the area devoid of vegetation. As a result, the NDVI
can be further promoted in practical applications, and we believe that the data that our model transforms is acceptable for qualitative and quantitative vegetation cover analysis.
3.2. Ablation Study
The improvement in the performance of our model can be attributed to two designs: the histogram-based LUTs and the CNN module. The following experiments are extended to illustrate the validity of these factors. It is worth noting that hyperparameters in the ablation experiments remain unchanged unless otherwise specified, and the early stopping strategy is adopted to select the best model. To better explore these two factors, we design several comparable models based on the proposed model. The “GlobalLUTs” refers to a global shared LUT model that has no relation to the tile histograms, whereas “TileLUTs” indicates a model that is based on the tile histograms. Moreover, a CNN module is added when the model name is suffixed with “-Conv”. All these comparisons are shown in
Table 5.
Table 5 presents the quantitative results of the comparable models, and we find that both factors are important. Since
can better describe the differences in model performance, we focus more on it in the following analyses. Histogram-based LUTs are far more powerful than global LUTs, which boost the
of GlobalLUTs and GlobalLUTs-Conv by nearly 0.3 and 0.2, respectively, in the blue band. The tile-adaptive transformation can adjust the LUTs in different scenes, allowing it to succeed in the blue band with low linear correlation. At the same time, we discover that the improvement in the other three bands is less obvious, because their linear correlations prior to transformation are higher than that of the blue band. In addition, the CNN module also plays an important role in our model. The CNN model benefits both the GlobalLUTs and TileLUTs, increasing the
in the NIR band by nearly 0.07 and 0.05, respectively. Since the kernel size of the CNN module is only three, this finding demonstrates that even the pixel-level registration error matters in the bandpass alignment task. The positive effects of the CNN module are illustrated in
Section 3.3.4.
3.3. Visualization Results
3.3.1. True Colour Combination
To better visualize the transformed imagery, we exhibit the true colour combination of tiles. Notably, the reflectance products are multiplied by 10,000 before being saved as UInt16 data. Hence, a mapping function is required to display the images. However, the dynamic stretching methods based on histogram statistics are not desirable in this case. Under different stretching parameters, the relative values of pixels cannot be maintained. As a result, this makes it impractical to evaluate the similarity between the transformed image and the target image. Therefore, the fixed-parameter stretching shown in
Table 6 is adopted to present the imagery. The table records a three-stage stretching in which the values in the last three columns of UInt16 are mapped to the corresponding values of Byte.
Figure 8 displays the stretched results of three tiles, which are spread across three study sites over different months. As can be seen, there exists significant variations between S2 and GF1-ARD after the fixed stretching. This implies that their reflectances vary greatly, consistent with the scatter distribution in
Figure 6a. The transformed S2 images are much closer to the GF1-ARD after bandpass alignment, demonstrating the necessity of it before combining multiple sensors. In addition, the overall colour of our model’s prediction is more realistic and closer to the target, whereas the linear model’s tends to whiter.
3.3.2. Batch Visualization
The ultimate goal of our model is to automatically batch transform the S2 imagery into GF1-ARD products. The key processes of the proposed model are a lookup operation and a single
convolution, both of which require little time and computation. Meanwhile, the tile-adaptive LUTs are created using a UNet with only 0.17 M parameters. As a result, our model supports batch conversion of large amounts of data. To exemplify this, we use the trained model to transform all involved tiles in our dataset and then count the time it takes. In the inferring phase, the conversion and thumbnail creation of these 119 tiles take a total of 785 s, with one tile taking an average of 4.1 s. Our experiments are carried out on a NVIDIA RTX A6000. In addition, thirty tiles are selected from each of the three study sites, and their true colour images are depicted in
Figure 9.
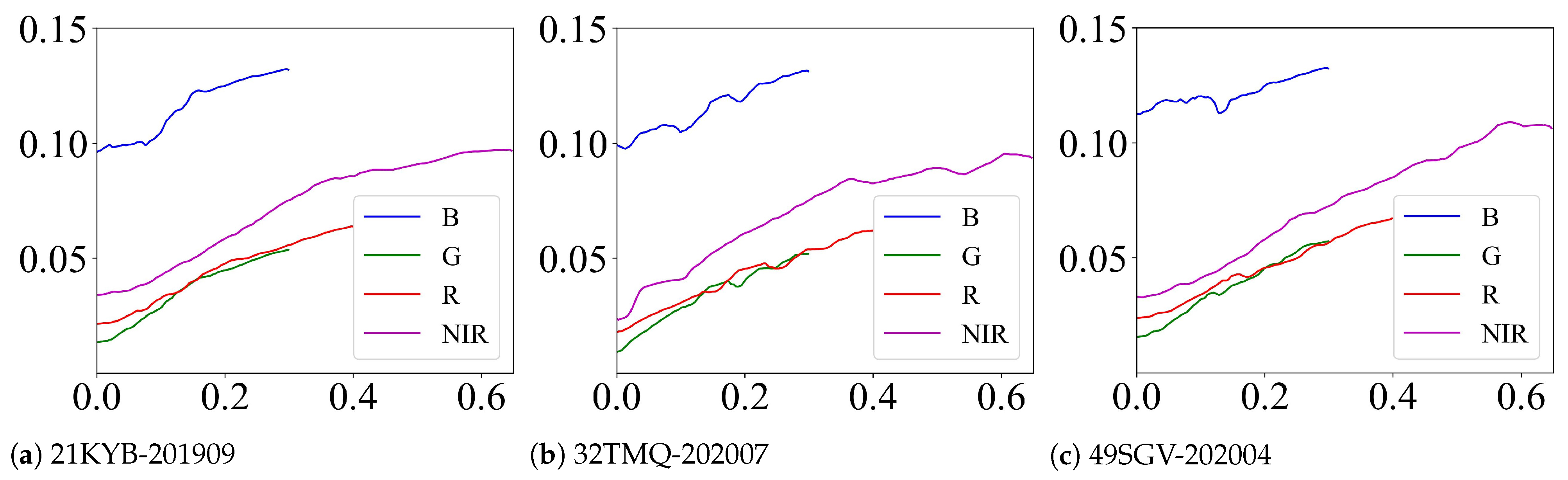
3.3.3. Visualization of LUTs
The LUTs of the previous three tiles are further displayed in
Figure 10. The learned LUTs can describe a more complicated transformation function that the linear model cannot. For example, as the input increases, the LUTs of “21KYB-201909” tend to rise monotonically. The rising rate, however, varies in stages, with the rising rate at the beginning and end being gentler than in the middle. Meanwhile, we find that the LUTs of “49SGV-202004” approach linear transformation, consistent with the similar visualization results of the last row in
Figure 8. Due to powerful capabilities of LUTs, the quantitative and qualitative results outperform the linear model. In addition, since most of the scatters are distributed in the former part of the space, we truncate the blue, green, red, and NIR bands with 0.3, 0.3, 0.4, and 0.6, respectively. Therefore, the length of the curve varies across the bands. As a result, the fixed-length LUT can be effectively exploited, and the degrees of fineness can be adaptively adjusted according to the distribution range of each band. Moreover, all the blue curves have a higher intercept value, which matches the scatter distribution of the blue band in
Figure 6a.
3.3.4. Spatial Misregistration
We select a local region in “21KYB-201909” as an example to present the spatial details of images in
Figure 11. The first row shows the true colour combination of the selected local region. As previously mentioned, even though S2 is downsampled to 30 m, it still has more spatial details and sharper edges than GF1-ARD. The output of the linear model is as detailed as S2 because it is a pixel-wise transformation. In contrast, our model’s prediction is slightly blurrier than S2 since one
convolutional operation is employed. However, the minor loss of spatial details makes it closer to the target GF1-ARD. In addition, we display zoomed-in views of the red cross point in the second row to illustrate the spatial misregistration between S2 and GF1-ARD. We find that there is one pixel offset in the row direction. Thus, the offset is preserved in the prediction of the linear model. In comparison, our model modifies the spatial location and approaches the target GF1-ARD, demonstrating the effectiveness of the simple CNN module. Meanwhile, we observe that there is still complex spatial distortion except for the pixel-level offset. This distortion is hard to eliminate and prevents further improvement of the bandpass alignment.
3.4. Temporal Frequency Assessment
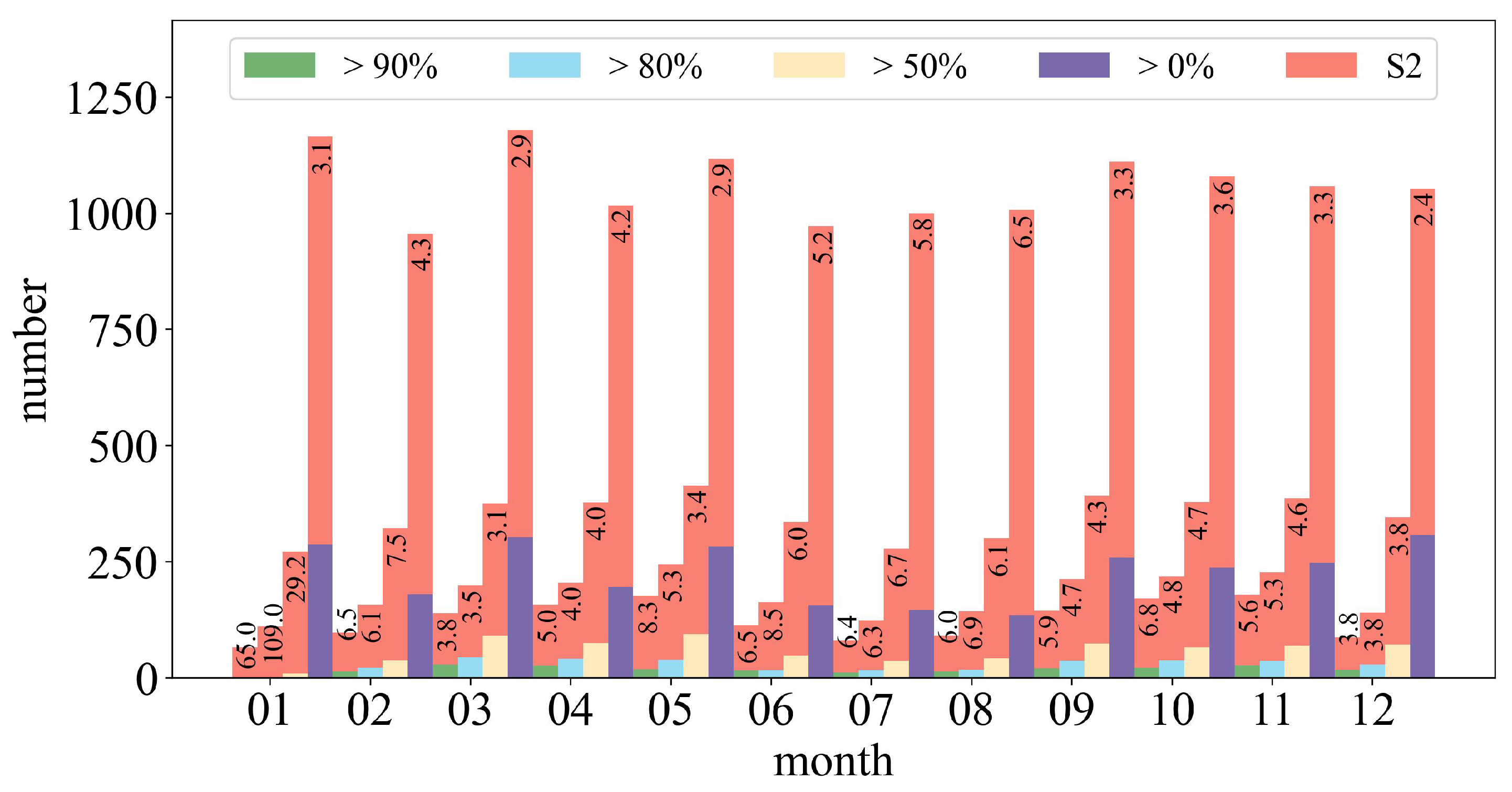
We assess the volume of the S2 L2A and GF1-ARD images available at study site A (69 tiles in total) in 2020. Specifically, we investigate the amount at different valid data levels in
Figure 12, where valid data refers to the pixels after removing no data and cloud regions.
We find that the total number of GF1-ARD data is large, while the expected data with a valid data rate greater than 80% are much lower. Meanwhile, the amount of valid data varies by month, and the volume decreases in summer and winter due to increased cloud cover, rain, and snow. For instance, in June, only seventeen images have a valid coverage ratio greater than 80%. Fortunately, the S2 to GF1-ARD ratio in these seasons is significantly higher than in others. After merging the S2 data, the temporal frequency of th eGF1-ARD data is significantly increased, which is critical in months when little data is available. Meanwhile, we find that the number of available data is drastically increased, even at the first levels, which greatly benefits the time series analysis.
Furthermore, to better illustrate the combined effectiveness of merging the S2 data, we give an example of tile “49SGA” from November 2020 to December 2020 in
Figure 13. To imitate the circumstances of practical application, the GF1-ARD with a valid data rate greater than 80% is filtered out, and there are only three images in two months. After combining the S2 data, the frequency of the collection is twice as dense as before. The distributions of the S2 and GF1-ARD are complementary, where the S2 has more data in November and the GF1 has more data in December. As a result, combining the data provides a much denser sequence with less cloud contamination.