Spatiotemporal Analysis of Rainfall and Droughts in a Semiarid Basin of Brazil: Land Use and Land Cover Dynamics
Abstract
1. Introduction
2. Materials and Methods
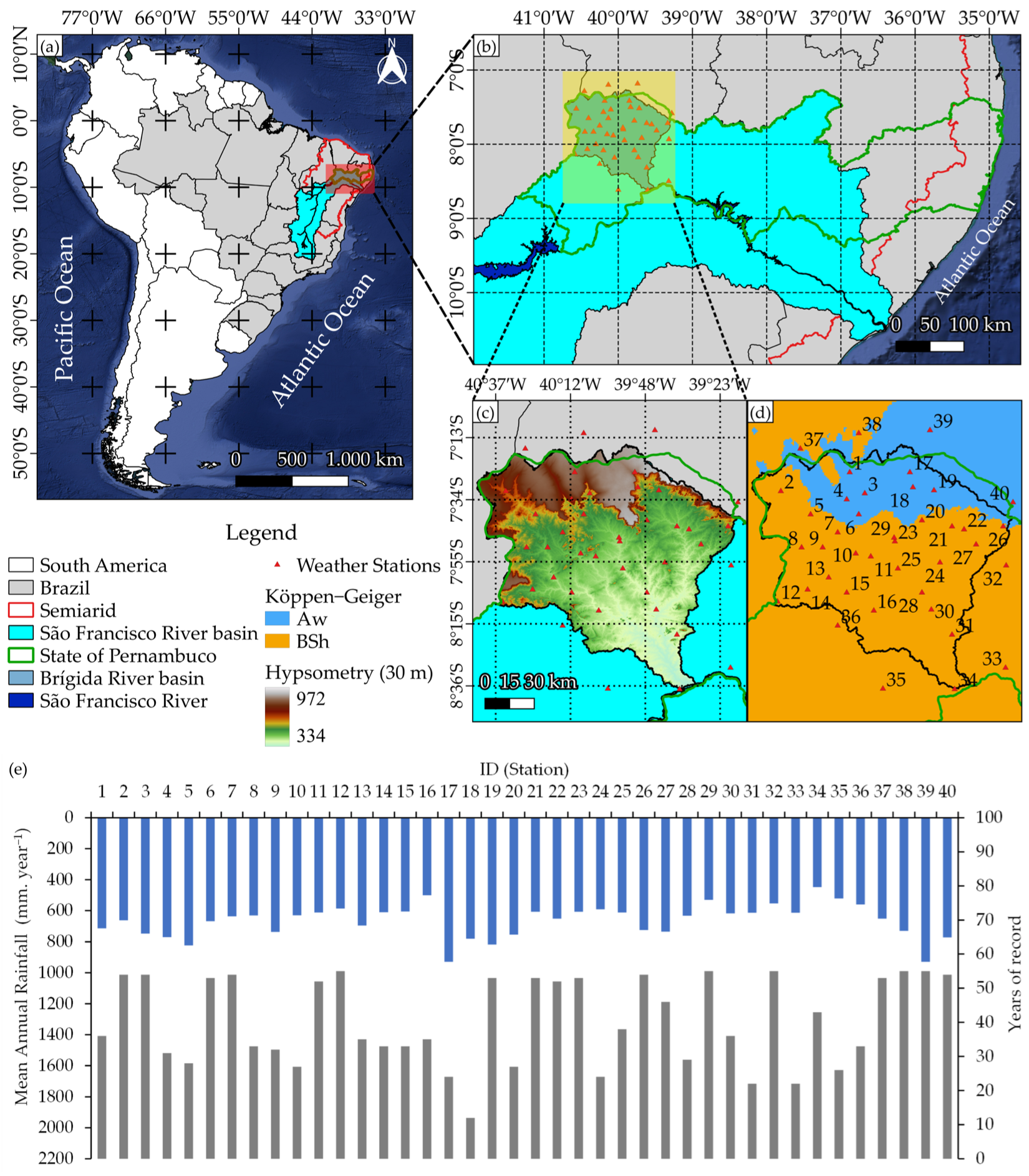
2.1. Characterization of the Study Site
2.2. Rainfall Data
2.3. Standard Precipitation Index (SPI)
2.4. Statistical Analysis
- Exponential Model:
- Spherical Model:
- Gaussian Model:
2.4.1. Universal Kriging (UK)
2.4.2. Sequential Gaussian Simulation (SGS)
2.4.3. Ordinary Cokriging
2.5. Assessment of Geostatistics Methods
2.6. Analysis of Biophysical Indexes and Land Use and Land Cover (LULC)
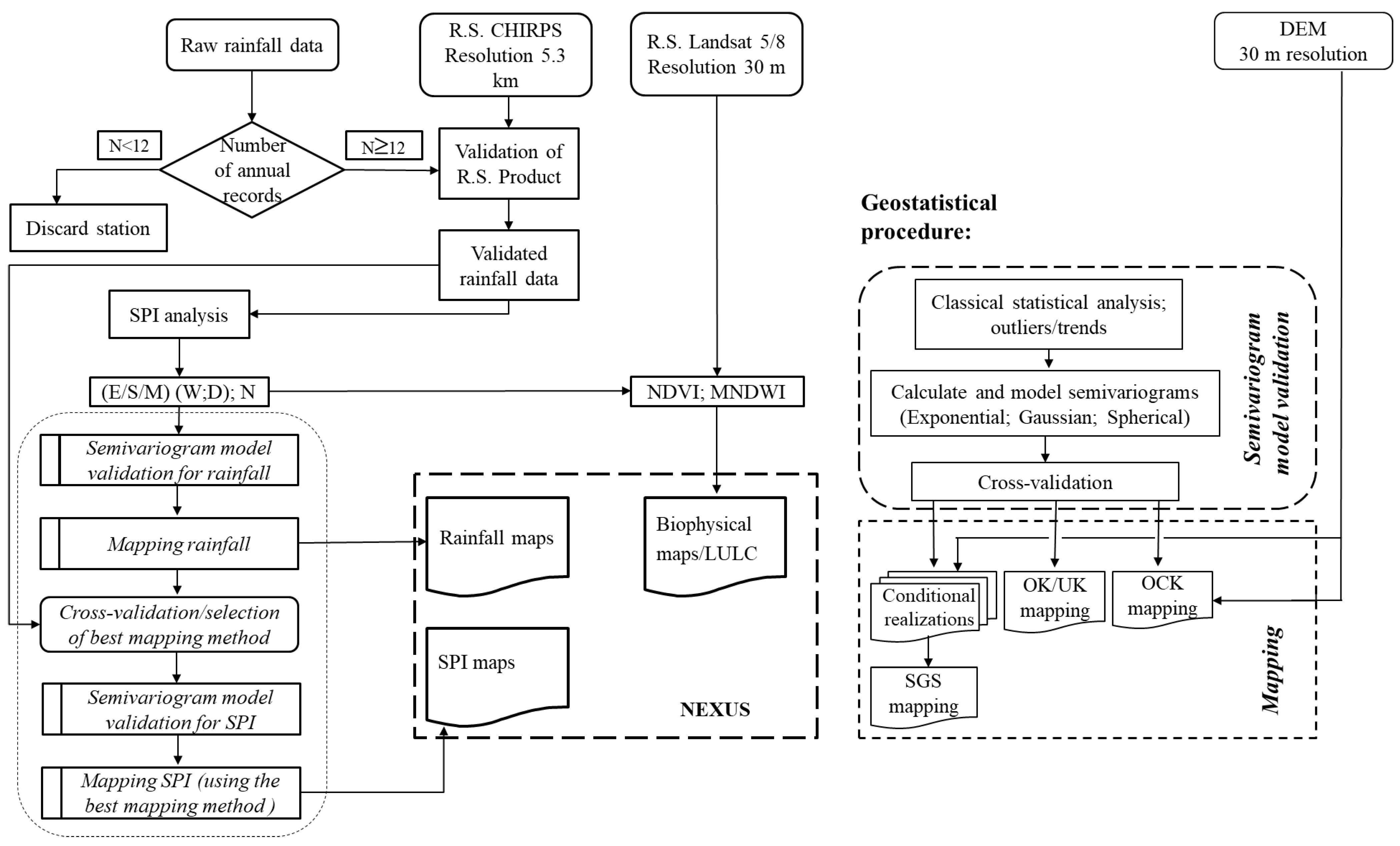
2.7. Flowchart of the Data Analysis and Processing Steps
3. Results and Discussion
3.1. Rainfall via CHIRPS and SPI
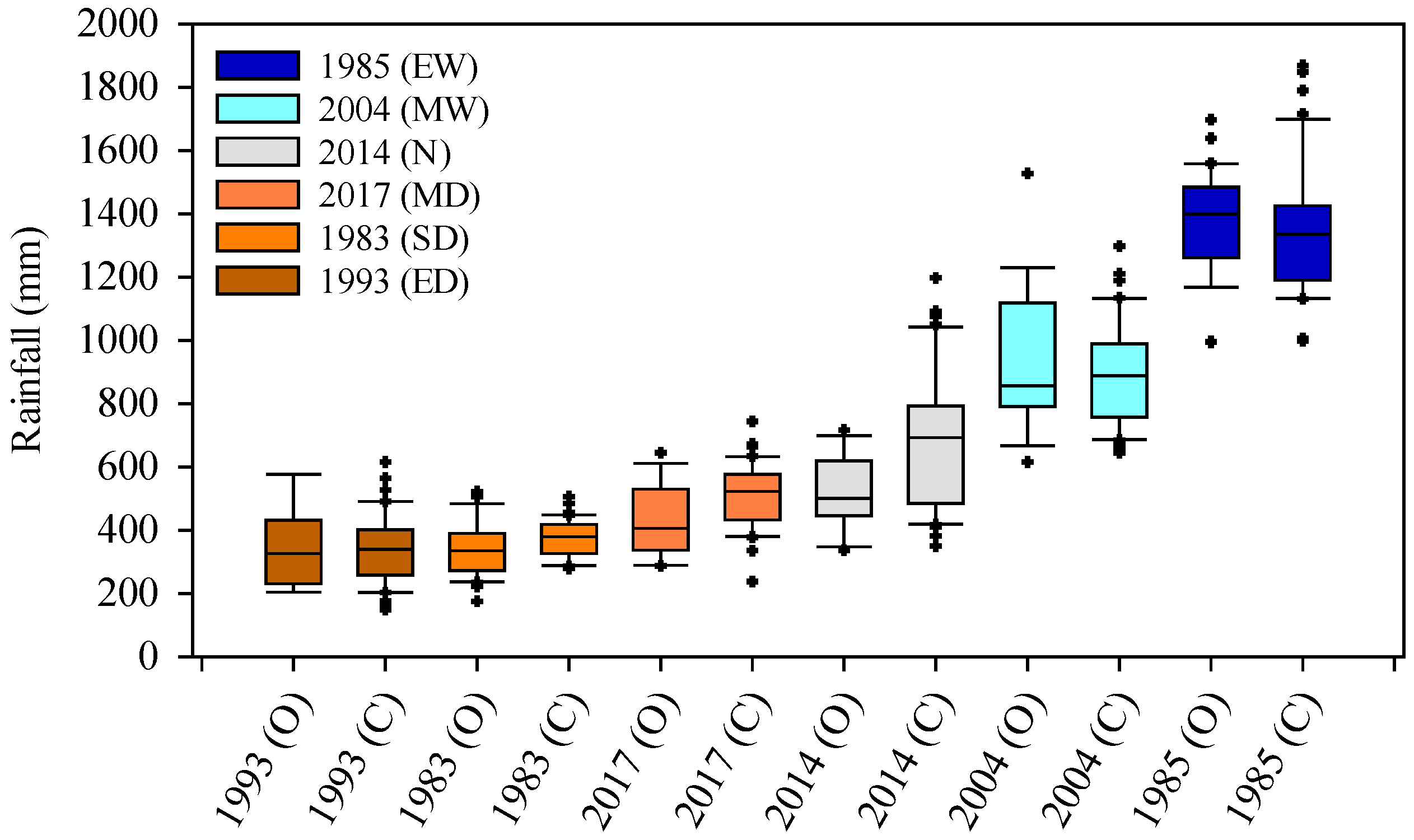
3.2. Statistical Analysis of Annual Rainfall
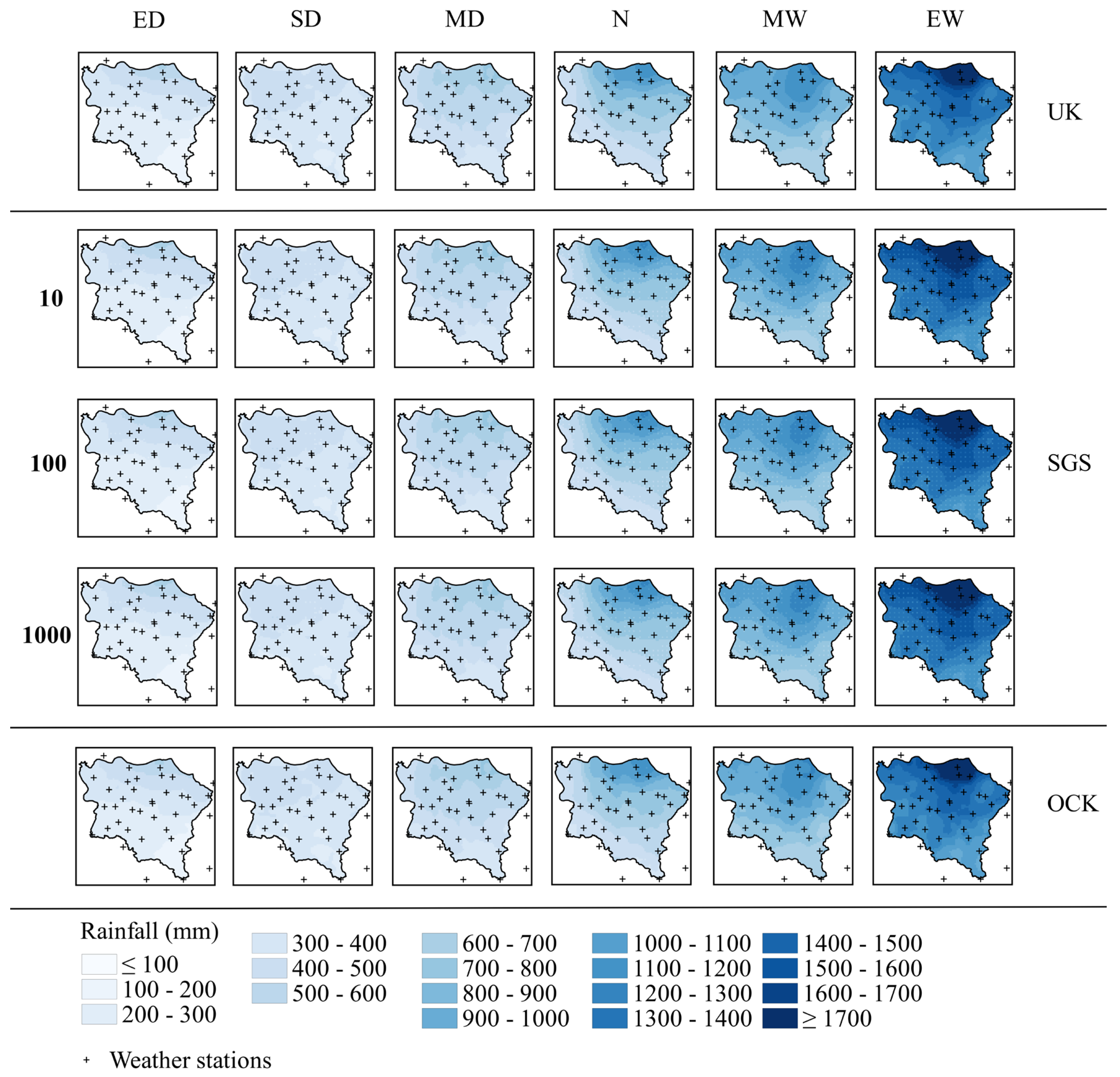
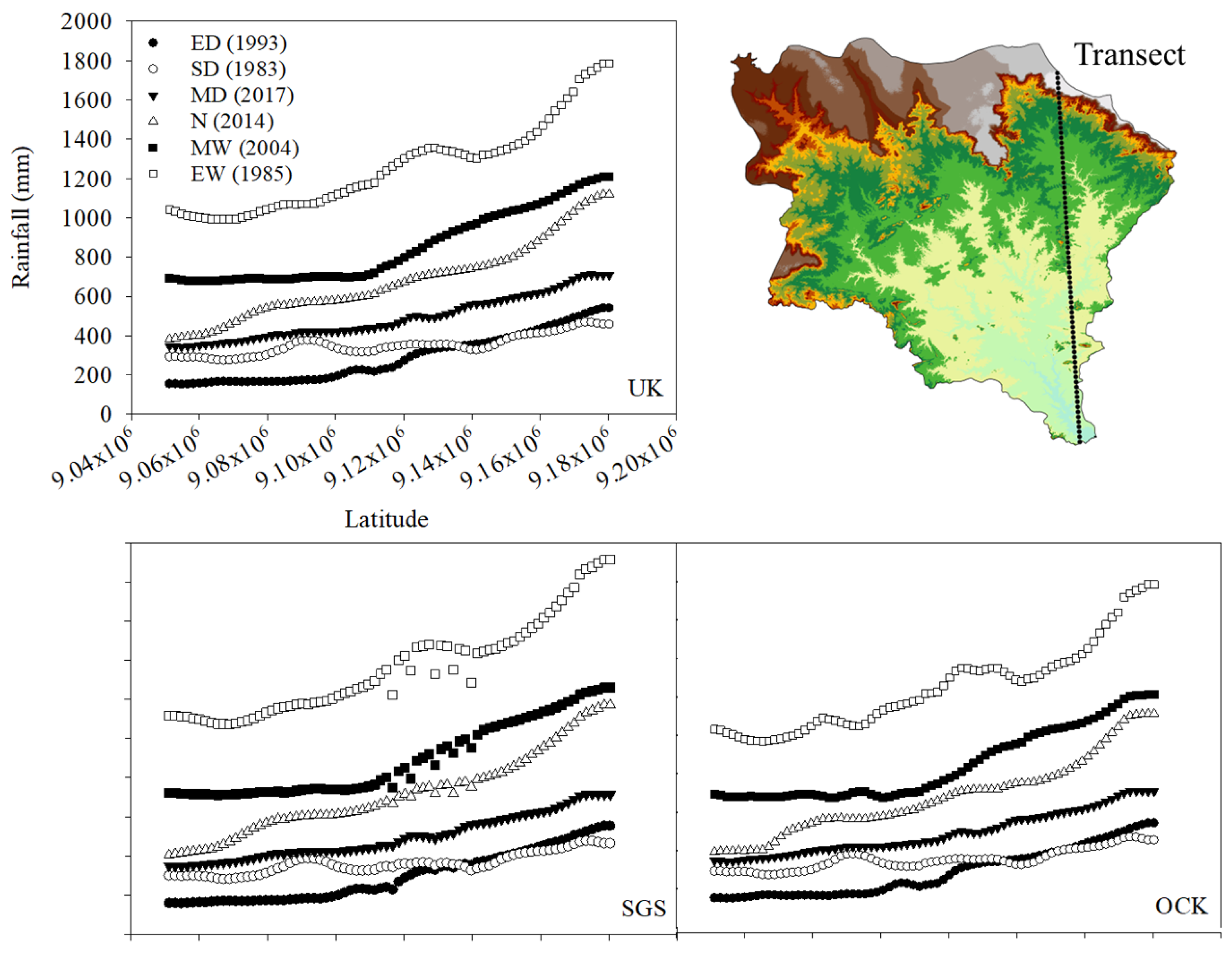
3.3. Universal Kriging
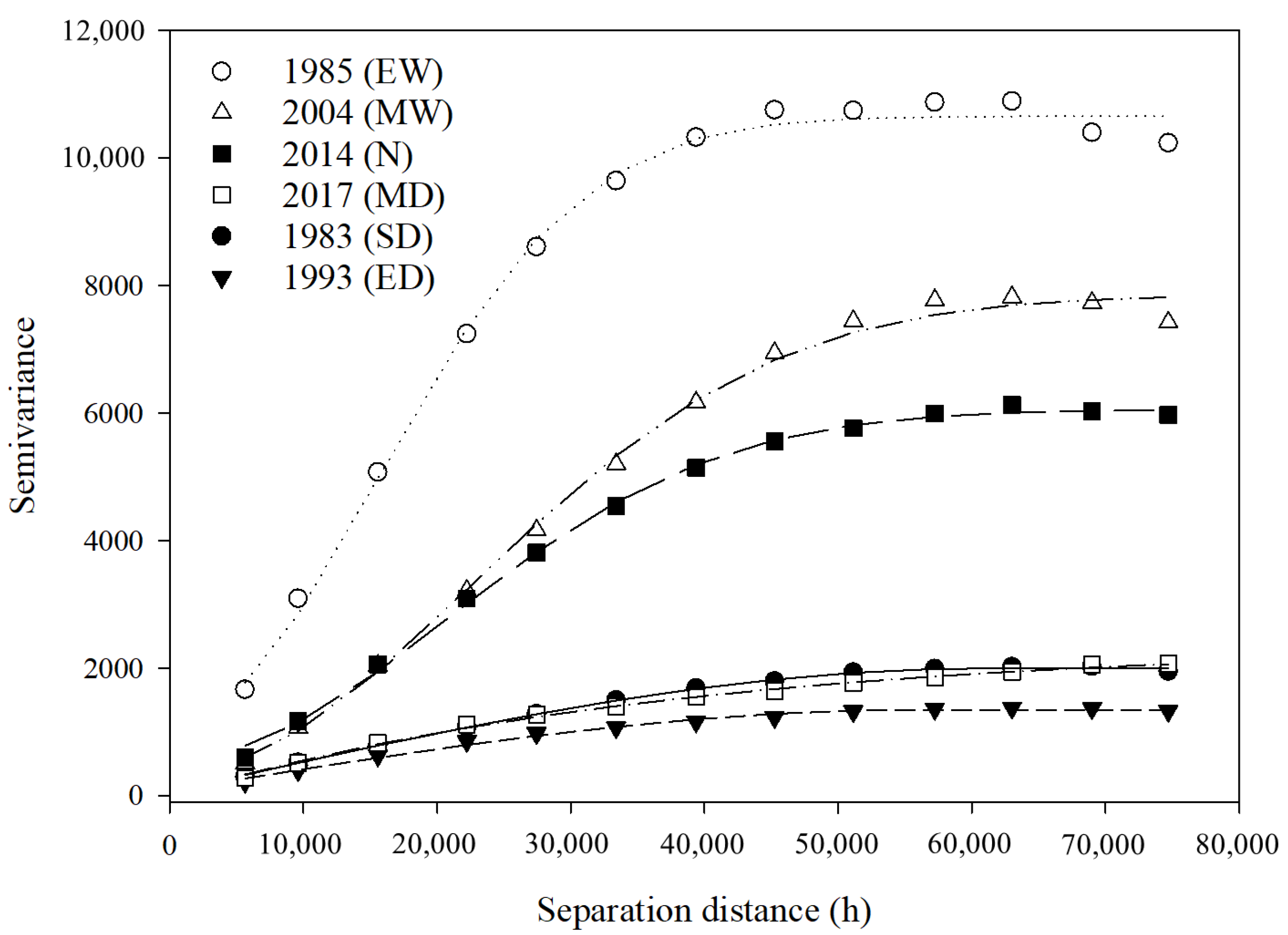
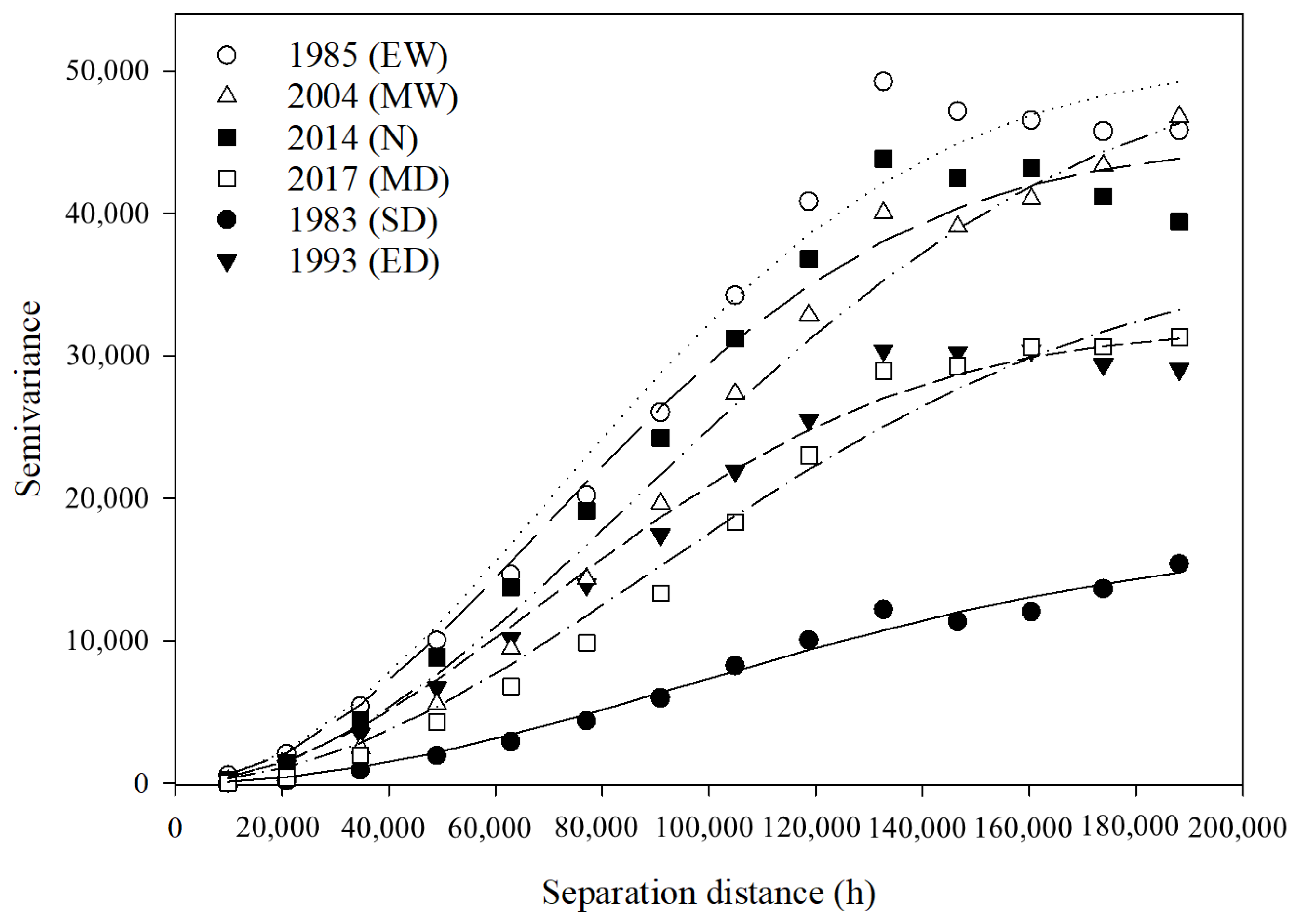
3.4. Cross-Semivariogram Models of Annual Rainfall
3.5. Spatiotemporal Analysis (Rainfall UK, SGS and Cokriging)
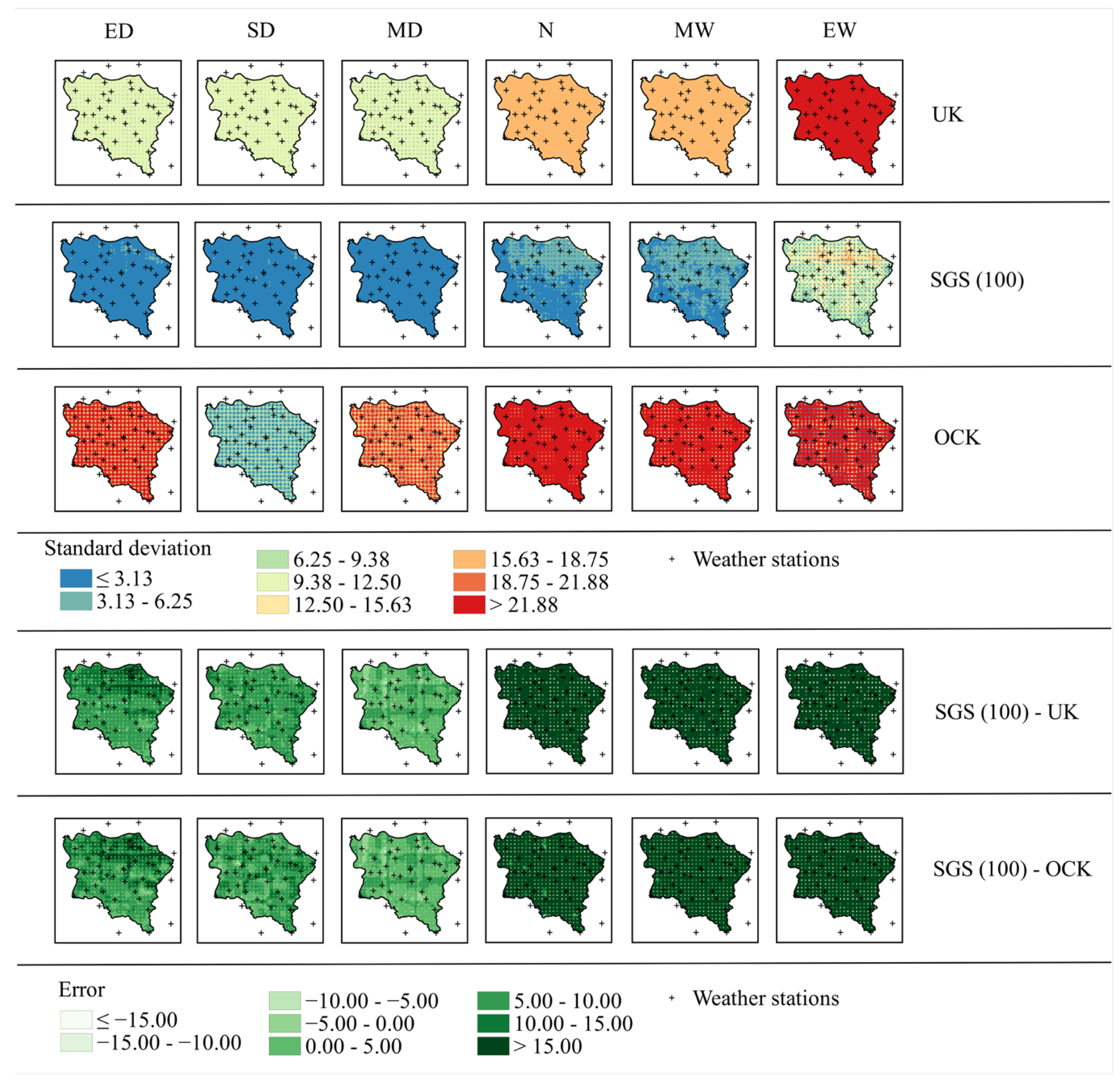
3.6. Performance of Different Interpolation (UK, SGS, OCK) Methods for Annual Rainfall Estimation in the Study Area
3.7. SPI Semivariogram Models
3.8. SPI SGS
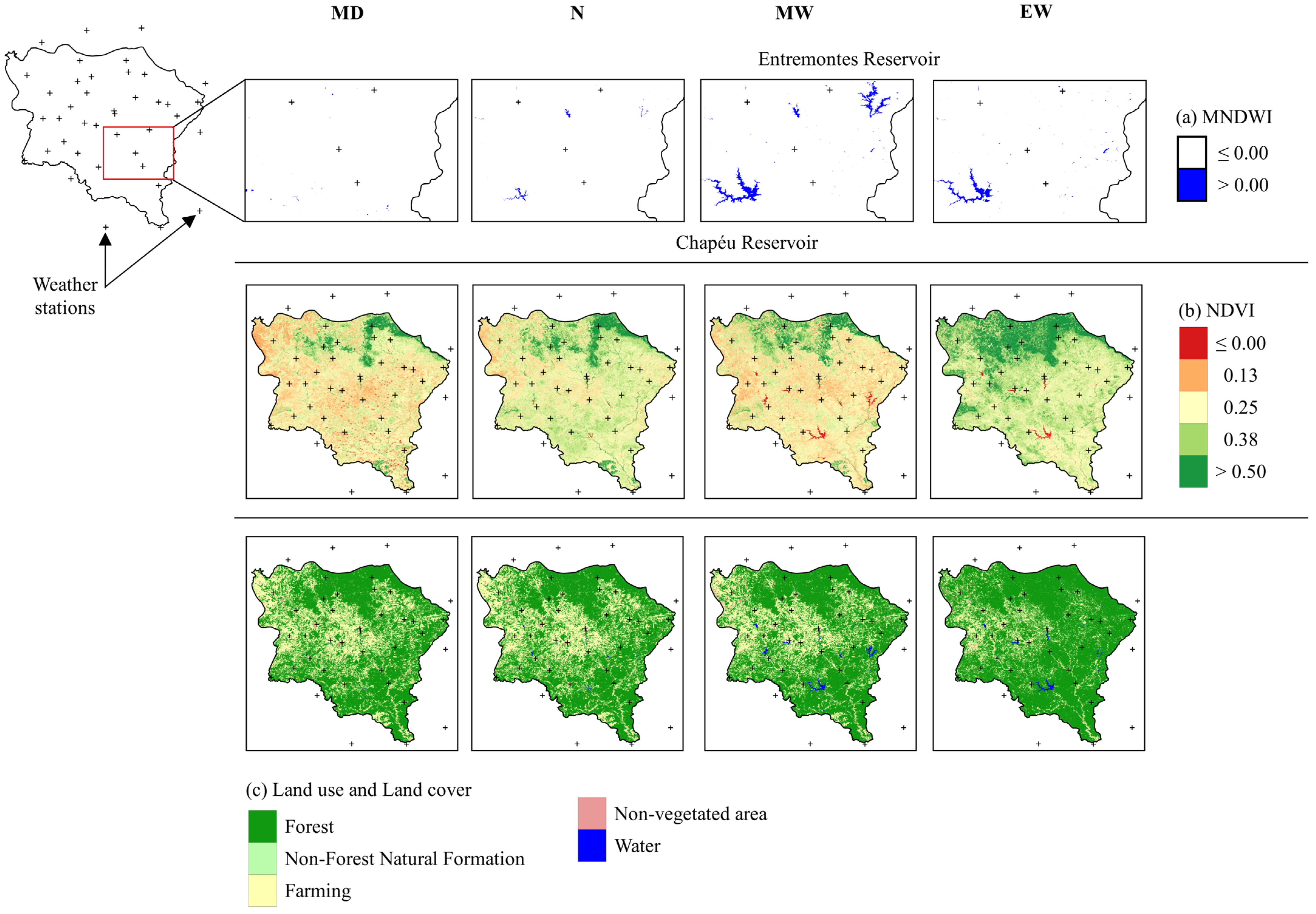
3.9. Analysis of Biophysical Indexes and Land Use and Land Cover (LULC)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Cristiano, E.; ten Veldhuis, M.C.; van de Giesen, N. Spatial and temporal variability of rainfall and their effects on hydrological response in urban areas—A review. Hydrol. Earth Syst. Sci. 2017, 21, 3859–3878. [Google Scholar] [CrossRef]
- Peña-Angulo, D.; Nadal-Romero, E.; González-Hidalgo, J.C.; Albaladejo, J.; Andreu, V.; Bagarello, V.; Barhi, H.; Batalla, R.J.; Bernal, S.; Bienes, R.; et al. Spatial variability of the relationships of runoff and sediment yield with weather types throughout the Mediterranean basin. J. Hydrol. 2019, 571, 390–405. [Google Scholar] [CrossRef]
- Kim, J.; Lee, J.; Kim, D.; Kang, B. The role of rainfall spatial variability in estimating areal reduction factors. J. Hydrol. 2019, 568, 416–426. [Google Scholar] [CrossRef]
- Peña-Angulo, D.; Nadal-Romero, E.; González-Hidalgo, J.C.; Albaladejo, J.; Andreu, V.; Barhi, H.; Bernal, S.; Biddoccu, M.; Bienes, R.; Campo, J.; et al. Relationship of weather types on the seasonal and spatial variability of rainfall, runoff, and sediment yield in the western Mediterranean basin. Atmosphere 2020, 11, 609. [Google Scholar] [CrossRef]
- Da Silva, J.L.B.; Moura, G.B.D.A.; da Silva, M.V.; Lopes, P.M.O.; Guedes, R.V.D.S.; Silva, F.D.F.E.; Ortiz, P.F.S.; Rodrigues, J.A.D.M. Changes in the water resources, soil use and spatial dynamics of Caatinga vegetation cover over semiarid region of the Brazilian Northeast. Remote Sens. Appl. Soc. Environ. 2020, 20, 100372. [Google Scholar] [CrossRef]
- Santos, J.F.S.; Naval, L.P. Spatial and temporal dynamics of water footprint for soybean production in areas of recent agricultural expansion of the Brazilian savannah (Cerrado). J. Clean. Prod. 2020, 251, 119482. [Google Scholar] [CrossRef]
- Singh, V.P. Handbook of Applied Hydrology, 2nd ed.; McGraw-Hill Education—Europe: London, UK, 2016; ISBN 0071835091. [Google Scholar]
- Paredes-Trejo, F.J.; Barbosa, H.A.; Kumar, T.V.L. Validating CHIRPS-based satellite precipitation estimates in Northeast Brazil. J. Arid Environ. 2017, 139, 26–40. [Google Scholar] [CrossRef]
- Rodrigues, D.T.; Gonçalves, W.A.; Spyrides, M.H.C.; e Silva, C.M.S. Spatial and temporal assessment of the extreme and daily precipitation of the Tropical Rainfall Measuring Mission satellite in Northeast Brazil. Int. J. Remote Sens. 2019, 41, 549–572. [Google Scholar] [CrossRef]
- Neto, R.M.B.; Santos, C.A.G.; Silva, J.F.C.B.D.C.; da Silva, R.M.; dos Santos, C.A.C.; Mishra, M. Evaluation of the TRMM product for monitoring drought over Paraíba State, northeastern Brazil: A trend analysis. Sci. Rep. 2021, 11, 1097. [Google Scholar] [CrossRef]
- McKee, T.B.; Doesken, N.J.; Kleist, J. The Relationship of Drought Frequency and Duration to Time Scales. In Proceedings of the 8th Conference on Applied Climatology, Anaheim, CA, USA, 17–22 January 1993; pp. 179–184. [Google Scholar]
- Juliani, B.H.T.; Okawa, C.M.P. Application of a standardized precipitation index for meteorological drought analysis of the semi-arid climate influence in Minas Gerais, Brazil. Hydrology 2017, 4, 26. [Google Scholar] [CrossRef]
- Brito, S.S.B.; Cunha, A.P.M.A.; Cunningham, C.C.; Alvalá, R.C.; Marengo, J.A.; Carvalho, M.A. Frequency, duration and severity of drought in the Semiarid Northeast Brazil region. Int. J. Climatol. 2018, 38, 517–529. [Google Scholar] [CrossRef]
- Santos, C.A.G.; Brasil Neto, R.M.; de Araújo Passos, J.S.; da Silva, R.M. Drought assessment using a TRMM-derived standardized precipitation index for the upper São Francisco River basin, Brazil. Environ. Monit. Assess. 2017, 189, 250. [Google Scholar] [CrossRef]
- Tsesmelis, D.E.; Leveidioti, I.; Karavitis, C.A.; Kalogeropoulos, K.; Vasilakou, C.G.; Tsatsaris, A.; Zervas, E. Spatiotemporal Application of the Standardized Precipitation Index (SPI) in the Eastern Mediterranean. Climate 2023, 11, 95. [Google Scholar] [CrossRef]
- Toté, C.; Patricio, D.; Boogaard, H.; van der Wijngaart, R.; Tarnavsky, E.; Funk, C. Evaluation of satellite rainfall estimates for drought and flood monitoring in Mozambique. Remote Sens. 2015, 7, 1758–1776. [Google Scholar] [CrossRef]
- Mariano, D.A.; dos Santos, C.A.; Wardlow, B.D.; Anderson, M.C.; Schiltmeyer, A.V.; Tadesse, T.; Svoboda, M.D. Use of remote sensing indicators to assess effects of drought and human-induced land degradation on ecosystem health in Northeastern Brazil. Remote Sens. Environ. 2018, 213, 129–143. [Google Scholar] [CrossRef]
- Paca, V.H.d.M.; Espinoza-Dávalos, G.E.; Moreira, D.M.; Comair, G. Variability of Trends in Precipitation across the Amazon River Basin Determined from the CHIRPS Precipitation Product and from Station Records. Water 2020, 12, 1244. [Google Scholar] [CrossRef]
- Rouse, J.W.; Haas, R.H.; Schell, J.A.; Deering, D.W.; Harlan, J.C. Monitoring the Vernal Advancement of Retrogradation of Natural Vegetation; NASA: Washington, DC, USA, 1973.
- Galvíncio, J.D.; Sá, I.I.S.; de Moura, M.S.B.; Ribeiro, J.G. Determinação das características físicas, climáticas e da paisagem da bacia hidrográfica do rio Brigida com o auxilio de técnicas de geoprocessamento e sensoriamento remoto. Rev. Geogr. 2007, 24, 83–96. [Google Scholar]
- Santos, C.A.G.; da Silva, R.M.; Silva, A.M.; Neto, R.M.B. Estimation of evapotranspiration for different land covers in a Brazilian semi-arid region: A case study of the Brígida River basin, Brazil. J. S. Am. Earth Sci. 2017, 74, 54–66. [Google Scholar] [CrossRef]
- Da Silva, M.V.; Pandorfi, H.; Lopes, P.M.O.; da Silva, J.L.B.; de Almeida, G.L.P.; Silva, D.A.D.O.; dos Santos, A.; Rodrigues, J.A.D.M.; Batista, P.H.D.; Jardim, A.M.D.R.F. Pilot monitoring of caatinga spatial-temporal dynamics through the action of agriculture and livestock in the brazilian semiarid. Remote Sens. Appl. Soc. Environ. 2020, 19, 100353. [Google Scholar] [CrossRef]
- Da Silva, M.V.; Pandorfi, H.; de Oliveira-Júnior, J.F.; da Silva, J.L.B.; de Almeida, G.L.P.; Montenegro, A.A.d.A.; Mesquita, M.; Ferreira, M.B.; Santana, T.C.; Marinho, G.T.B.; et al. Remote sensing techniques via Google Earth Engine for land degradation assessment in the Brazilian semiarid region, Brazil. J. S. Am. Earth Sci. 2022, 120, 104061. [Google Scholar] [CrossRef]
- Silva, J.R.I.; Montenegro, A.A.D.A.; Farias, C.W.L.D.A.; Jardim, A.M.D.R.F.; da Silva, T.G.F.; Montenegro, S.M.G.L. Morphometric characterization and land use of the Pajeú river basin in the Brazilian semi-arid region. J. S. Am. Earth Sci. 2022, 118, 103939. [Google Scholar] [CrossRef]
- De Lima, I.P.; Jorge, R.G.; de Lima, J.L.M.P. Remote Sensing Monitoring of Rice Fields: Towards Assessing Water Saving Irrigation Management Practices. Front. Remote Sens. 2021, 2, 762093. [Google Scholar] [CrossRef]
- Silva, A.P.; de Lima, I.P.; Santo, M.F.E.S.; Pires, V.C. Assessing changes in drought and wetness episodes in drainage basins using the Standardized Precipitation Index. Die Bodenkult. 2014, 65, 31–37. [Google Scholar]
- Araújo, H.L.; Montenegro, A.A.d.A.; Lopes, I.; de Carvalho, A.A.; e Silva, E.C.; Gonçalves, G.E. Precipitation spatialization in the Brígida river basin in Pernambuco semi-arid. Rev. Bras. Geogr. Fis. 2020, 13, 391–405. [Google Scholar] [CrossRef]
- Marengo, J.A.; Alves, L.M.; Alvala, R.C.S.; Cunha, A.P.; Brito, S.; Moraes, O.L.L. Climatic characteristics of the 2010-2016 drought in the semiarid northeast Brazil region. An. Acad. Bras. Cienc. 2018, 90, 1973–1985. [Google Scholar] [CrossRef]
- Montenegro, A.A.A.; Ragab, R. Hydrological response of a Brazilian semi-arid catchment to different land use and climate change scenarios: A modelling study. Hydrol. Process. 2010, 24, 2705–2723. [Google Scholar] [CrossRef]
- Wanderley, H.S.; de Amorim, R.F.C.; de Carvalho, F.O. Variabilidade espacial e preenchimento de falhas de dados pluviométricos para o estado de Alagoas. Rev. Bras. Meteorol. 2012, 27, 347–354. [Google Scholar] [CrossRef]
- Hengl, T.; Walsh, M.G.; Sanderman, J.; Wheeler, I.; Harrison, S.P.; Prentice, I.C. Global mapping of potential natural vegetation: An assessment of machine learning algorithms for estimating land potential. PeerJ 2018, 2018, e5457. [Google Scholar] [CrossRef]
- Wolff, W.; Duarte, S.N.; Fernandes, R.D.M. Spatialization of the annual and seasonal average precipitations in the state of Santa Catarina, Brazil. J. S. Am. Earth Sci. 2020, 103, 102735. [Google Scholar] [CrossRef]
- Da Silva, M.V.; Pandorfi, H.; Jardim, A.M.D.R.F.; de Oliveira-Júnior, J.F.; da Divincula, J.S.; Giongo, P.R.; da Silva, T.G.F.; de Almeida, G.L.P.; Moura, G.B.D.A.; Lopes, P.M.O. Spatial modeling of rainfall patterns and groundwater on the coast of northeastern Brazil. Urban Clim. 2021, 38, 100911. [Google Scholar] [CrossRef]
- Cunha, A.P.M.A.; Tomasella, J.; Ribeiro-Neto, G.G.; Brown, M.; Garcia, S.R.; Brito, S.B.; Carvalho, M.A. Changes in the spatial–temporal patterns of droughts in the Brazilian Northeast. Atmos. Sci. Lett. 2018, 19, e855. [Google Scholar] [CrossRef]
- Da Silva, R.M.; Santos, C.A.G.; Silva, J.F.C.B.D.C.; Silva, A.M.; Neto, R.M.B. Spatial distribution and estimation of rainfall trends and erosivity in the Epitácio Pessoa reservoir catchment, Paraíba, Brazil. Nat. Hazards 2020, 102, 829–849. [Google Scholar] [CrossRef]
- Medauar, C.C.; Silva, S.A.; Carvalho, L.C.C.; Galvão, Í.M.; Macêdo, P.V. Spatial-temporal variability of rainfall and mean air temperature for the state of Bahia, Brazil. An. Acad. Bras. Cienc. 2020, 92, e20181283. [Google Scholar] [CrossRef]
- De Medeiros, E.S.; de Lima, R.R.; de Olinda, R.A.; dos Santos, C.A.C. Modeling spatiotemporal rainfall variability in Paraíba, Brazil. Water 2019, 11, 1843. [Google Scholar] [CrossRef]
- Page, T.; Beven, K.J.; Hankin, B.; Chappell, N.A. Interpolation of rainfall observations during extreme rainfall events in complex mountainous terrain. Hydrol. Process. 2022, 36, 14758. [Google Scholar] [CrossRef]
- Adhikary, S.K.; Muttil, N.; Yilmaz, A.G. Cokriging for enhanced spatial interpolation of rainfall in two Australian catchments. Hydrol. Process. 2017, 31, 2143–2161. [Google Scholar] [CrossRef]
- Deutsch, C.V.; Journel, A.G. GSLIB: Geostatistical Software Library and User’s Guide, 2nd ed.; Oxford University Press: New York, NY, USA, 1998; ISBN 0195073924. [Google Scholar]
- Méndez-Venegas, J.; Díaz-Viera, M.A.; Herrera, G.S.; Valdés-Manzanilla, A. Geostatistical simulation of spatial variability of convective storms in Mexico City Valley. Geofis. Int. 2013, 52, 111–120. [Google Scholar] [CrossRef][Green Version]
- Wang, G.; Gertner, G.; Singh, V.; Shinkareva, S.; Parysow, P.; Anderson, A. Spatial and Temporal Prediction and Uncertainty Analysis of Rainfall Erosivity for the Revised Universal Soil Loss Equation. Ecol. Modell. 2002, 153, 143–155. [Google Scholar] [CrossRef]
- Goovaerts, P. Geostatistics for Natural Resources Evaluation; Oxford University Press: New York, NY, USA, 1997; ISBN 0195115384. [Google Scholar]
- Isaaks, E.H.; Srivastava, R.M. An Introduction to Applied Geostatistics; Oxford University Press: New York, NY, USA, 1989; ISBN 0195050134. [Google Scholar]
- Goovaerts, P. Geostatistical approaches for incorporating elevation into the spatial interpolation of rainfall. J. Hydrol. 2000, 228, 113–129. [Google Scholar] [CrossRef]
- Cuartas, L.A.; Cunha, A.P.M.D.A.; Alves, J.A.; Parra, L.M.P.; Deusdará-Leal, K.; Costa, L.C.O.; Molina, R.D.; Amore, D.; Broedel, E.; Seluchi, M.E.; et al. Recent Hydrological Droughts in Brazil and Their Impact on Hydropower Generation. Water 2022, 14, 601. [Google Scholar] [CrossRef]
- Agência Pernambucana de Águas e Clima (APAC). Relatório de Situação de Recursos Hídricos do Estado de Pernambuco 2011/2012. Available online: https://www.lai.pe.gov.br/apac/wp-content (accessed on 16 June 2022).
- Instituto de Pesquisa Econômica Aplicada (IPEA). Transposição do Rio São Francisco: Análise de Oportunidade do Projeto; IPEA: Rio de Janeiro, Brazil, 2011; ISBN 1415-4765. [Google Scholar]
- Alvares, C.A.; Stape, J.L.; Sentelhas, P.C.; Gonçalves, J.L.D.M.; Sparovek, G. Köppen’s climate classification map for Brazil. Meteorol. Z. 2013, 22, 711–728. [Google Scholar] [CrossRef] [PubMed]
- Beck, H.E.; Zimmermann, N.E.; McVicar, T.R.; Vergopolan, N.; Berg, A.; Wood, E.F. Present and future köppen-geiger climate classification maps at 1-km resolution. Sci. Data 2018, 5, 180214. [Google Scholar] [CrossRef] [PubMed]
- Instituto Nacional de Meteorologia (INMET). Normais Climatológicas. Available online: https://clima.inmet.gov.br/GraficosClimatologicos/ (accessed on 10 June 2022).
- Soil Survey Staff. Keys to Soil Taxonomy, 9th ed.; US Department of Agriculture: Washington, DC, USA, 2006.
- Gerardo, R.; de Lima, I.P. Sentinel-2 Satellite Imagery-Based Assessment of Soil Salinity in Irrigated Rice Fields in Portugal. Agriculture 2022, 12, 1490. [Google Scholar] [CrossRef]
- Agência Pernambucana de Águas e Clima (APAC). Coordenadas das estações pluviométricas do Estado de Pernambuco. Available online: http://old.apac.pe.gov.br/meteorologia/coordenadas/index.html (accessed on 16 June 2022).
- Warrick, A.W.; Nielsen, D.R. Spatial variability of soil physical properties in the field. In Applications of Soil Physics; Academic Press: New York, NY, USA, 1980. [Google Scholar]
- Journel, A.G. Fundamentals of Geostatistics in Five Lessons; American Geophysical Union: Washington, DC, USA, 1989; ISBN 0-87590-708-3. [Google Scholar]
- Landim, P.M.B. Análise Estatística de Dados Geológicos, 2nd ed.; Edunesp: Rio Claro, Brazil, 2003; ISBN 9788571395046. [Google Scholar]
- Journel, A.G.; Huijbregts, C.J. Mining Geostatistics; Oxford University Press: London, UK, 1978; ISBN 0123910501. [Google Scholar]
- Cambardella, C.A.; Moorman, T.B.; Novak, J.M.; Parkin, T.B.; Karlen, D.L.; Turco, R.F.; Konopka, A.E. Field-Scale Variability of Soil Properties in Central Iowa Soils. Soil Sci. Soc. Am. J. 1994, 58, 1501–1511. [Google Scholar] [CrossRef]
- Vauclin, M.; Vieira, S.R.; Vachaud, G.; Nielsen, D.R. The Use of Cokriging with Limited Field Soil Observations. Soil Sci. Soc. Am. J. 1983, 47, 175–184. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.M.; Stein, A. Comparison of Kriging with External Drift and Regression-Kriging; ITC: Geneve, Switzerland, 2003; p. 17. [Google Scholar]
- Goovaerts, P. Geostatistical modelling of uncertainty in soil science. Geoderma 2001, 103, 3–26. [Google Scholar] [CrossRef]
- Google Earth Engine. Landsat Collections. Available online: https://developers.google.com/earth-engine/datasets/catalog/landsat (accessed on 10 May 2022).
- Xu, H. Modification of normalised difference water index (NDWI) to enhance open water features in remotely sensed imagery. Int. J. Remote Sens. 2006, 27, 3025–3033. [Google Scholar] [CrossRef]
- Molle, F. Geometria de Pequenos Açudes; SUDENE: Recife, Brazil, 1994; Volume 1, ISBN 55655812813.
- MapBiomas Brazil. Coleção 7.1 da Série Anual de Mapas de Cobertura e Uso de Solo do Brasil. Available online: https://mapbiomas.org/colecoes-mapbiomas-1?cama_set_language=pt-BR (accessed on 11 March 2023).
- Mutiga, J.K.; Su, Z.; Woldai, T. Using satellite remote sensing to assess evapotranspiration: Case study of the upper Ewaso Ng’iro North Basin, Kenya. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 100–108. [Google Scholar] [CrossRef]
- Bai, T.; Tahmasebi, P. Sequential Gaussian simulation for geosystems modeling: A machine learning approach. Geosci. Front. 2022, 13, 101258. [Google Scholar] [CrossRef]
- Pereira, G.T.; Teixeira, D.D.B.; de Souza, Z.M.; de Oliveira, I.R.; Marques Júnior, J. Stochastic simulations of calcium contents in sugarcane area. Rev. Bras. Eng. Agric. Ambient. 2015, 19, 767–772. [Google Scholar] [CrossRef]
- Da Silva, T.G.F.; de Queiroz, M.G.; Zolnier, S.; de Souza, L.S.B.; de Souza, C.A.A.; de Moura, M.S.B.; de Araújo, G.G.L.; Neto, A.J.S.; dos Santos, T.S.; de Melo, A.L.; et al. Soil properties and microclimate of two predominant landscapes in the Brazilian semiarid region: Comparison between a seasonally dry tropical forest and a deforested area. Soil Tillage Res. 2021, 207, 104852. [Google Scholar] [CrossRef]
- Panday, P.K.; Coe, M.T.; Macedo, M.N.; Lefebvre, P.; de Castanho, A.D. Deforestation offsets water balance changes due to climate variability in the Xingu River in eastern Amazonia. J. Hydrol. 2015, 523, 822–829. [Google Scholar] [CrossRef]
- Agência Nacional de Águas e Saneamento Básico (ANA). Reservatórios do Semiárido Brasileiro: Hidrologia, Balanço Hídrico e Operação—Reservatório Entremontes. Available online: http://portal1.snirh.gov.br/arquivos/semiarido/204res/SF_Entremontes.pdf (accessed on 1 February 2022).
- Agência Nacional de Águas e Saneamento Básico (ANA). Reservatórios do Semiárido Brasileiro: Hidrologia, Balanço Hídrico e Operação—Reservatório Chapéu. Available online: http://portal1.snirh.gov.br/arquivos/semiarido/204res/SF_Chapéu.pdf (accessed on 1 February 2022).
- De Araújo, J.C.; Mamede, G.L.; De Lima, B.P. Hydrological guidelines for reservoir operation to enhance water governance: Application to the Brazilian Semiarid region. Water 2018, 10, 1628. [Google Scholar] [CrossRef]
- Tomasella, J.; Silva Pinto Vieira, R.M.; Barbosa, A.A.; Rodriguez, D.A.; de Oliveira Santana, M.; Sestini, M.F. Desertification trends in the Northeast of Brazil over the period 2000–2016. Int. J. Appl. Earth Obs. Geoinf. 2018, 73, 197–206. [Google Scholar] [CrossRef]


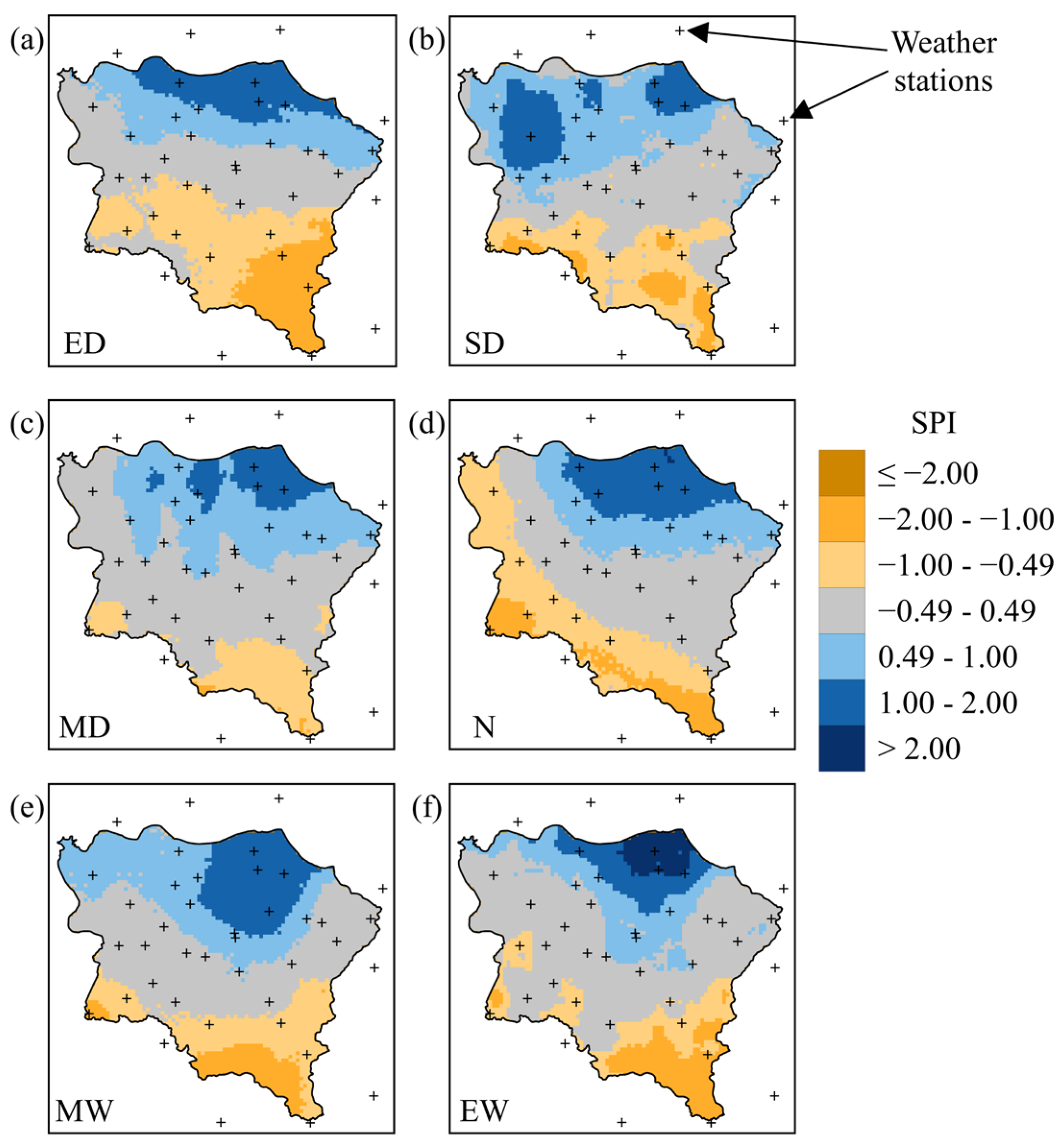
| SPI | Classifications |
|---|---|
| ≥2.00 | Extremely Wet (EW) |
| 1.00 to 1.99 | Severely Wet (SW) |
| 0.50 to 0.99 | Moderately Wet (MW) |
| 0.49 to −0.49 | Normal (N) |
| −0.50 to −0.99 | Moderately Dry (MD) |
| −1.00 to −1.99 | Severely Dry (SD) |
| ≤−2.00 | Extremely Dry (ED) |
| Year | Satellite | Date | Hour (UTM) | Orbit | Point |
|---|---|---|---|---|---|
| ED (1993) | No Landsat images after September and no clouds | ||||
| SD (1983) | No Landsat images | ||||
| MD (2017) | Landsat 8 | 30 September 2017 | 12:47:34 | 217 | 65 |
| 30 September 2017 | 12:47:58 | 217 | 66 | ||
| 7 October 2017 | 12:53:47 | 218 | 65 | ||
| N (2014) | Landsat 8 | 22 September 2014 | 12:47:26 | 217 | 65 |
| 22 September 2014 | 12:47:50 | 217 | 66 | ||
| 13 September 2014 | 12:53:40 | 218 | 65 | ||
| MW (2004) | Landsat 5 | 13 November 2004 | 12:32:25 | 217 | 65 |
| 13 November 2004 | 12:32:49 | 217 | 66 | ||
| 4 November 2004 | 12:38:28 | 218 | 65 | ||
| EW (1985) | Landsat 5 | 24 October 1985 | 12:16:14 | 217 | 65 |
| 24 October 1985 | 12:16:38 | 217 | 66 | ||
| 15 October 1985 | 12:22:31 | 218 | 65 | ||
| Year | SPI | Classification | Year | SPI | Classification | Year | SPI | Classification | Year | SPI | Classification |
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1962 | 0.47 | N | 1976 | −0.33 | N | 1990 | −1.27 | MD | 2004 | 1.32 | MW |
| 1963 | 0.55 | N | 1977 | 0.42 | N | 1991 | −0.81 | N | 2005 | 0.29 | N |
| 1964 | 1.72 | SW | 1978 | −0.04 | N | 1992 | −0.78 | N | 2006 | −0.32 | N |
| 1965 | 0.19 | N | 1979 | 0.70 | N | 1993 | −2.21 | ED | 2007 | −0.62 | N |
| 1966 | 0.11 | N | 1980 | 0.49 | N | 1994 | 0.01 | N | 2008 | 0.59 | N |
| 1967 | 1.09 | MW | 1981 | −0.19 | N | 1995 | 0.29 | N | 2009 | 0.94 | N |
| 1968 | 0.29 | N | 1982 | −1.01 | MD | 1996 | 0.68 | N | 2010 | −0.15 | N |
| 1969 | −0.13 | N | 1983 | −1.98 | SD | 1997 | 0.54 | N | 2011 | 0.41 | N |
| 1970 | −0.48 | N | 1984 | 0.70 | N | 1998 | −1.26 | MD | 2012 | −2.47 | ED |
| 1971 | 0.50 | N | 1985 | 3.30 | EW | 1999 | 0.05 | N | 2013 | −0.78 | N |
| 1972 | −0.65 | N | 1986 | 0.35 | N | 2000 | 0.02 | N | 2014 | −0.27 | N |
| 1973 | 0.67 | N | 1987 | −0.80 | N | 2001 | −0.86 | N | 2015 | −0.37 | N |
| 1974 | 1.84 | SW | 1988 | 1.31 | MW | 2002 | −0.37 | N | 2016 | −1.32 | MD |
| 1975 | 0.12 | N | 1989 | 1.25 | MW | 2003 | −0.70 | N | 2017 | −1.02 | MD |
| Year | Mean | Median | Maximum | Minimum | n | SD | CV (%) | p-Value (KS) |
|---|---|---|---|---|---|---|---|---|
| Extremely Dry (1993) | 329.48 | 280.82 | 843.10 | 138.21 | 930 | 137.17 | 41.63% | 0.14 |
| Severely Dry (1983) | 361.05 | 359.68 | 658.09 | 175.30 | 930 | 76.19 | 21.10% | 0.05 |
| Moderately Dry (2017) | 475.55 | 445.60 | 1001.36 | 212.67 | 930 | 145.69 | 30.64% | 0.10 |
| Normal (2014) | 641.66 | 543.09 | 1444.71 | 333.15 | 930 | 248.55 | 38.74% | 0.16 |
| Moderately Wet (2004) | 854.19 | 824.72 | 1566.14 | 355.03 | 930 | 213.5 | 24.99% | 0.09 |
| Extremely Wet (1985) | 1292.89 | 1237.86 | 2103.26 | 692.42 | 930 | 243.65 | 18.88% | 0.09 |
| SPI Class | Model | Nugget (C0) | Sill (C0 + C1) | Range (A, km) | R2 | DSD (%) | Jack-Knifing | |
|---|---|---|---|---|---|---|---|---|
| M | SD | |||||||
| Extremely Dry (1993) | Spherical | 80 | 1348 | 55.9 | 0.992 | 5.93% | 0.01 | 1.04 |
| Severely Dry (1983) | Spherical | 59 | 1998 | 61.0 | 0.999 | 2.95% | 0.01 | 1.03 |
| Moderately Dry (2017) | Exponential | 1 | 2405 | 114.0 | 0.998 | 0.04% | 0.01 | 1.02 |
| Normal (2014) | Gaussian | 580 | 6059 | 50.2 | 0.998 | 9.57% | 0.01 | 1.06 |
| Moderately Wet (2004) | Gaussian | 370 | 7852 | 55.4 | 0.996 | 4.71% | 0.01 | 1.04 |
| Extremely Wet (1985) | Gaussian | 1160 | 10,660 | 37.6 | 0.996 | 10.88% | 0.01 | 1.04 |
| SPI Class | Model | Nugget (C0) | Sill (C0 + C1) | Range (A, km) | R2 | DSD (%) | Jack-Knifing | |
|---|---|---|---|---|---|---|---|---|
| M | SD | |||||||
| Extremely Dry (1993) | Gaussian | 100 | 32,040 | 168.5 | 0.987 | 0.31% | 0.00 | 1.00 |
| Severely Dry (1983) | Gaussian | 10 | 17,200 | 232.3 | 0.986 | 0.06% | 0.01 | 1.01 |
| Moderately Dry (2017) | Gaussian | 100 | 37,160 | 217.0 | 0.985 | 0.27% | 0.00 | 1.00 |
| Normal (2014) | Gaussian | 100 | 44,920 | 167.5 | 0.979 | 0.22% | 0.00 | 1.00 |
| Moderately Wet (2004) | Gaussian | 100 | 51,300 | 212.9 | 0.990 | 0.19% | 0.00 | 1.00 |
| Extremely Wet (1985) | Gaussian | 100 | 50,690 | 171.9 | 0.979 | 0.20% | 0.00 | 1.00 |
| SPI Class | MBE (mm) | RMSE (mm) | R² | ||||||
|---|---|---|---|---|---|---|---|---|---|
| UK | SGS | OCK | UK | SGS | OCK | UK | SGS | OCK | |
| Extremely Dry (1993) | −0.1415 | −0.0003 | −0.1615 | 55.877 | 0.0029 | 30.632 | 0.9972 | 1.0000 | 0.9992 |
| Severely Dry (1983) | 0.0010 | −0.0001 | 0.0205 | 57.187 | 0.0028 | 36.781 | 0.9895 | 1.0000 | 0.9955 |
| Moderately Dry (2017) | 0.6475 | 0.0000 | 0.6481 | 35.520 | 0.0029 | 35.248 | 0.9984 | 1.0000 | 0.9984 |
| Normal (2014) | 0.1050 | −0.0001 | 0.3873 | 18.392 | 0.0029 | 54.153 | 0.9910 | 1.0000 | 0.9992 |
| Moderately Wet (2004) | 0.3519 | 0.0000 | −0.0886 | 160.142 | 0.0029 | 47.650 | 0.9896 | 1.0000 | 0.9991 |
| Extremely Wet (1985) | 0.4379 | −0.0003 | 0.7608 | 309.794 | 0.0028 | 87.278 | 0.9770 | 1.0000 | 0.9982 |
| SPI Class | Model | Nugget (C0) | Sill (C0 + C1) | Range (A, km) | R2 | DSD (%) | Jack-Knifing | |
|---|---|---|---|---|---|---|---|---|
| M | SD | |||||||
| Extremely Dry (1993) | Spherical | 0.0044 | 0.0833 | 54.2 | 0.992 | 5.28% | 0.01 | 1.04 |
| Severely Dry (1983) | Spherical | 0.0180 | 0.3590 | 60.4 | 0.998 | 5.01% | 0.01 | 1.04 |
| Moderately Dry (2017) | Exponential | 0.0001 | 0.1078 | 97.2 | 0.995 | 0.09% | 0.01 | 1.03 |
| Normal (2014) | Gaussian | 0.0099 | 0.1148 | 47.8 | 0.999 | 8.62% | 0.01 | 1.06 |
| Moderately Wet (2004) | Gaussian | 0.0110 | 0.1710 | 53.7 | 0.997 | 6.43% | 0.01 | 1.05 |
| Extremely Wet (1985) | Spherical | 0.0001 | 0.1832 | 44.4 | 0.995 | 0.05% | 0.01 | 1.03 |
| Year | Total Area of Entremontes Reservoir (m² × 105) | Total Area of Chapéu Reservoir (m² × 105) | Total Volume of Water Stored in Entremontes Reservoir (m³ × 105) | Total Volume of Water Stored in Chapéu Reservoir (m³ × 105) |
|---|---|---|---|---|
| Moderately Dry (2017) | 3.35 | 0 | 6.71 | 0 |
| Normal (2014) | 38.0 | 8.28 | 76.4 | 16.6 |
| Moderately Wet (2004) | 327 | 191 | 659 | 386 |
| Extremely Wet (1985) | 259 | 1.47 | 522 | 2.94 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
de Barros de Sousa, L.; de Assunção Montenegro, A.A.; da Silva, M.V.; Almeida, T.A.B.; de Carvalho, A.A.; da Silva, T.G.F.; de Lima, J.L.M.P. Spatiotemporal Analysis of Rainfall and Droughts in a Semiarid Basin of Brazil: Land Use and Land Cover Dynamics. Remote Sens. 2023, 15, 2550. https://doi.org/10.3390/rs15102550
de Barros de Sousa L, de Assunção Montenegro AA, da Silva MV, Almeida TAB, de Carvalho AA, da Silva TGF, de Lima JLMP. Spatiotemporal Analysis of Rainfall and Droughts in a Semiarid Basin of Brazil: Land Use and Land Cover Dynamics. Remote Sensing. 2023; 15(10):2550. https://doi.org/10.3390/rs15102550
Chicago/Turabian Stylede Barros de Sousa, Lizandra, Abelardo Antônio de Assunção Montenegro, Marcos Vinícius da Silva, Thayná Alice Brito Almeida, Ailton Alves de Carvalho, Thieres George Freire da Silva, and João Luis Mendes Pedroso de Lima. 2023. "Spatiotemporal Analysis of Rainfall and Droughts in a Semiarid Basin of Brazil: Land Use and Land Cover Dynamics" Remote Sensing 15, no. 10: 2550. https://doi.org/10.3390/rs15102550
APA Stylede Barros de Sousa, L., de Assunção Montenegro, A. A., da Silva, M. V., Almeida, T. A. B., de Carvalho, A. A., da Silva, T. G. F., & de Lima, J. L. M. P. (2023). Spatiotemporal Analysis of Rainfall and Droughts in a Semiarid Basin of Brazil: Land Use and Land Cover Dynamics. Remote Sensing, 15(10), 2550. https://doi.org/10.3390/rs15102550








