Monitoring Coastal Erosion Using Remote Images: Comparison between Physically and Remotely Acquired Data on a Limestone Coast
Abstract
1. Introduction
2. Study Area
3. Materials and Methods
3.1. Data Obtained during Fieldwork
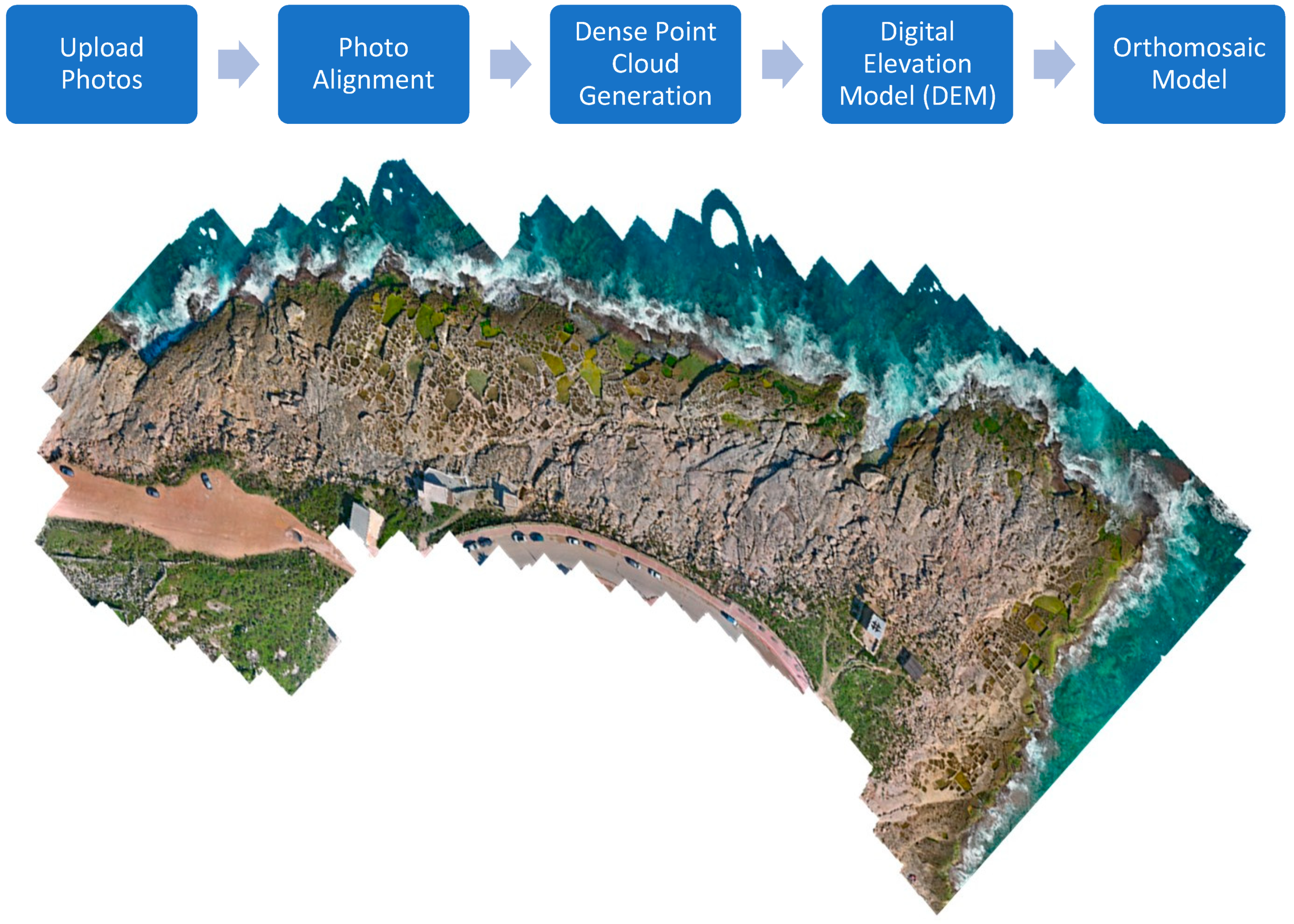
3.2. Aerial Data Acquisition and 3D Model Generation
3.3. Measurements from the 3D Model
- i.
- By applying basic geometric formulas for the volume calculation, according to the boulder shape (e.g., V = l × b × h for cubic boulders, V = 0.5 × l × b × h for triangular boulders) and using the A, B and C axis dimensions acquired:
- ○
- from the in-situ measurements obtained during field trips;
- ○
- from the average boulder dimensions obtained from the model;
- ○
- from the maximum boulder dimensions obtained from the model.
- ii.
- Calculated using Agisoft Metashape software using the in-built function for the volume calculation with the ‘best fit’ option and ‘custom plane’ option. Through the volume calculation facility—by drawing an outline around each boulder—the software calculates the boulder volume from the difference in elevation between each point on the boulder surface and the ground. In the best fit option, the ground level on which the boulder rests is automatically determined by the software from XYZ coordinates of the selected vertices. In the custom plane option, the ground level is determined by the user;
- iii.
- Calculated by multiplying the boulder surface area by the C axis, as derived from the model. This measurement was used as another option to calculate the volume. Through this method, overestimation of the volume (due to inaccurate A and B axis measurements or due to the imbricated position of the boulder) are avoided.
3.4. Correlation Analysis
3.5. Assessment of the Individual Boulder Volume from the Models Generated Using the SfM Techniques
4. Results
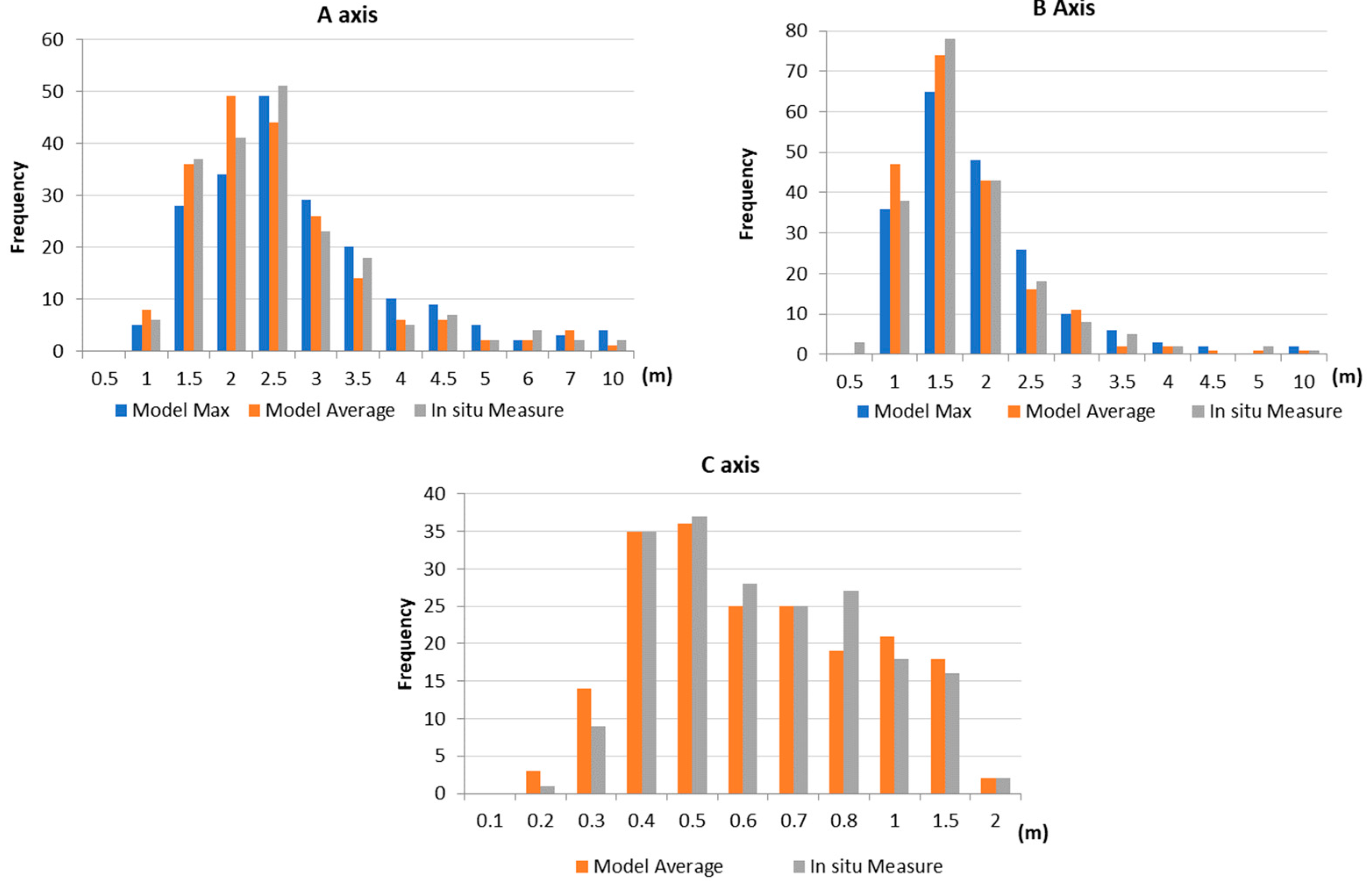
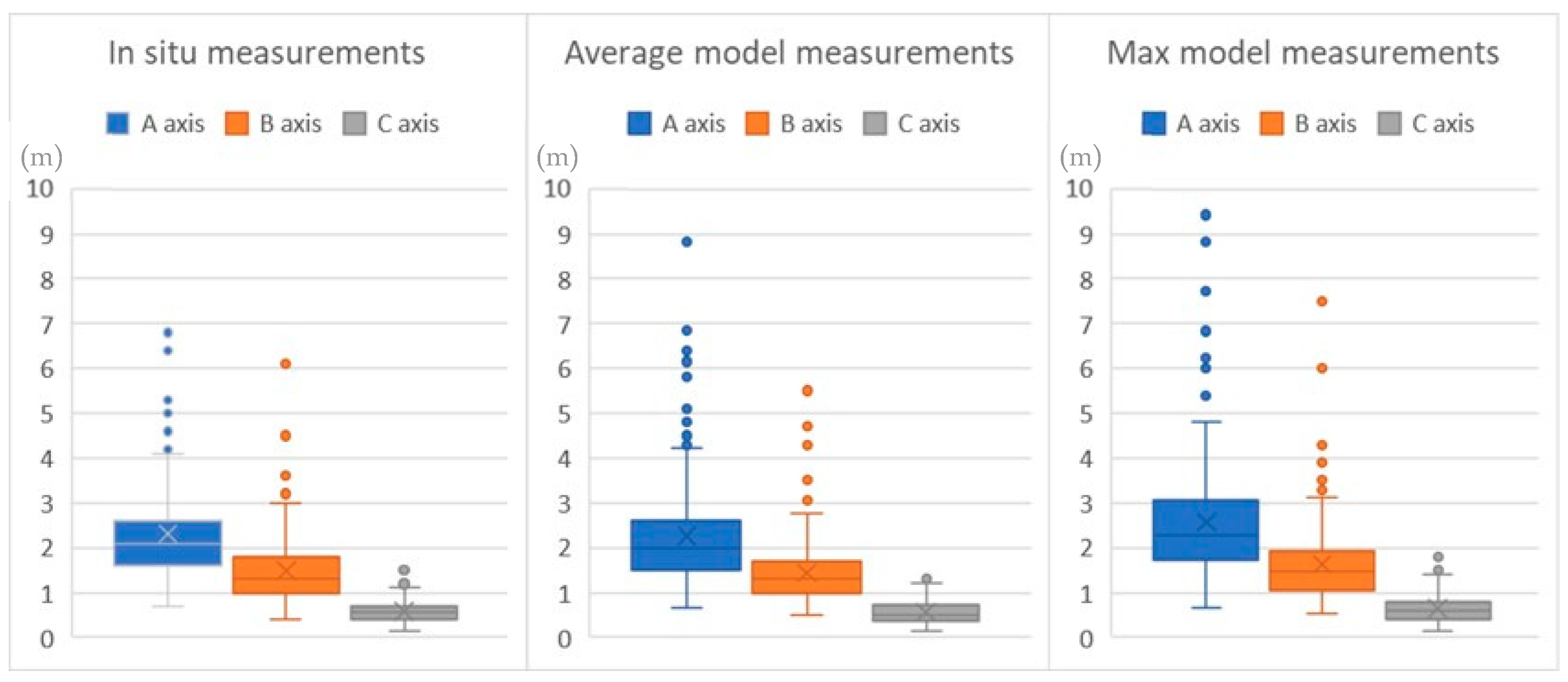
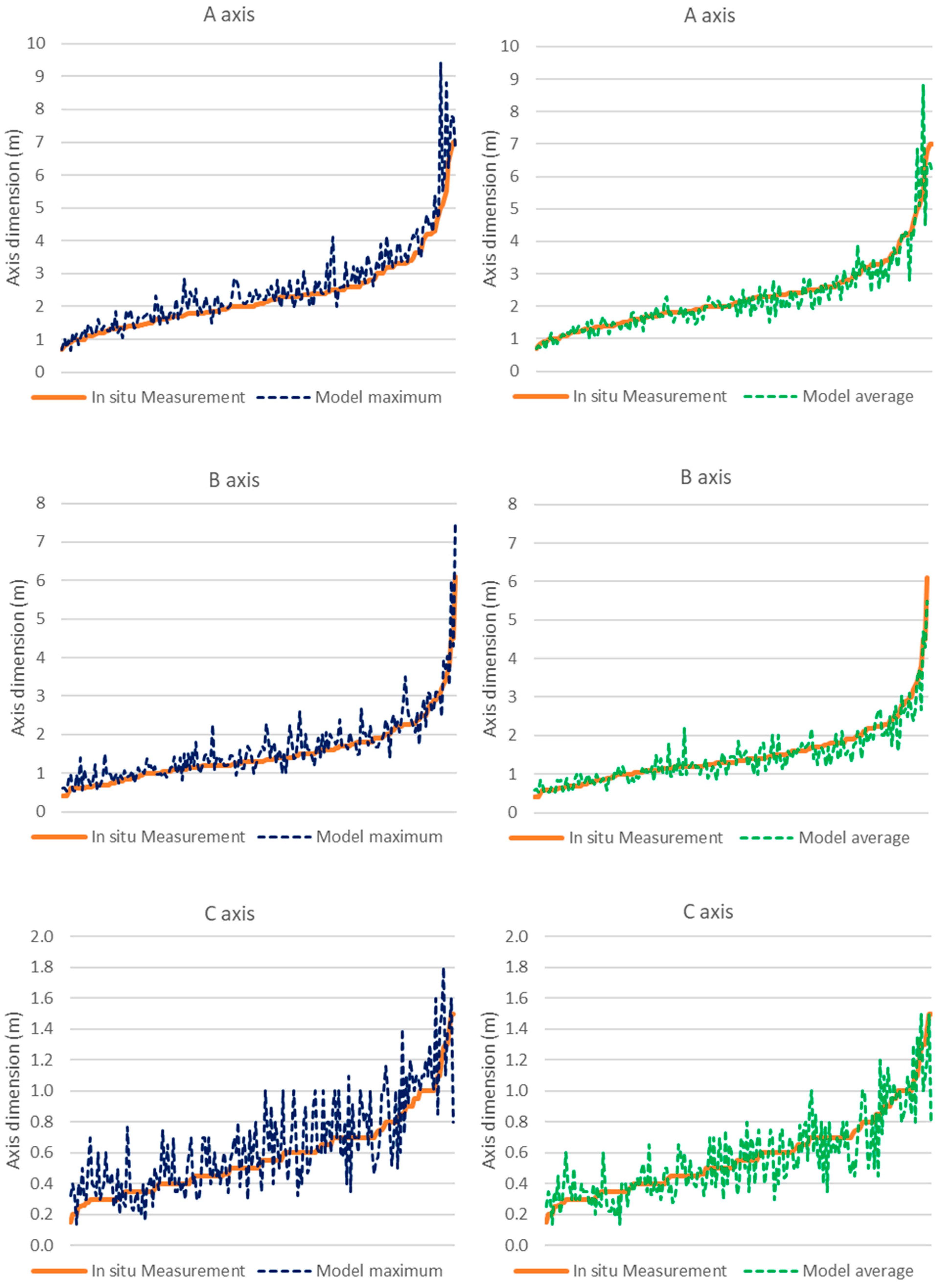
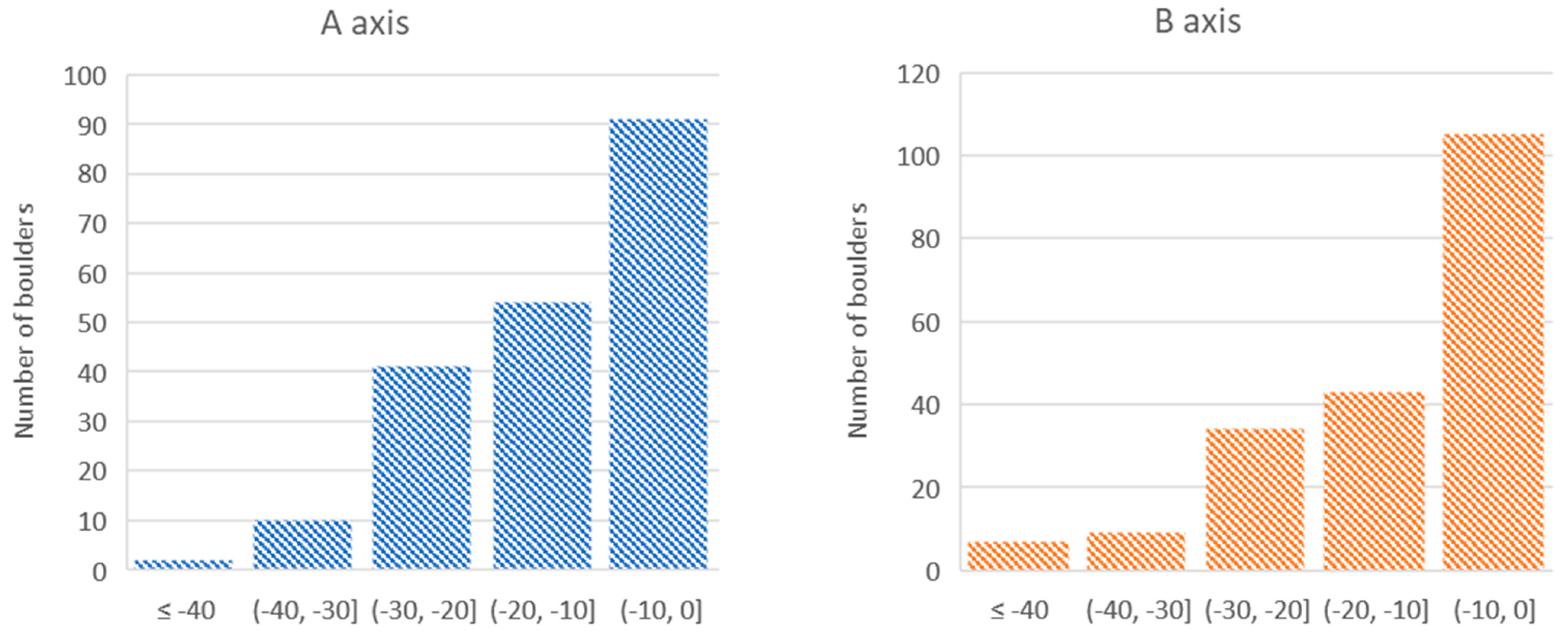
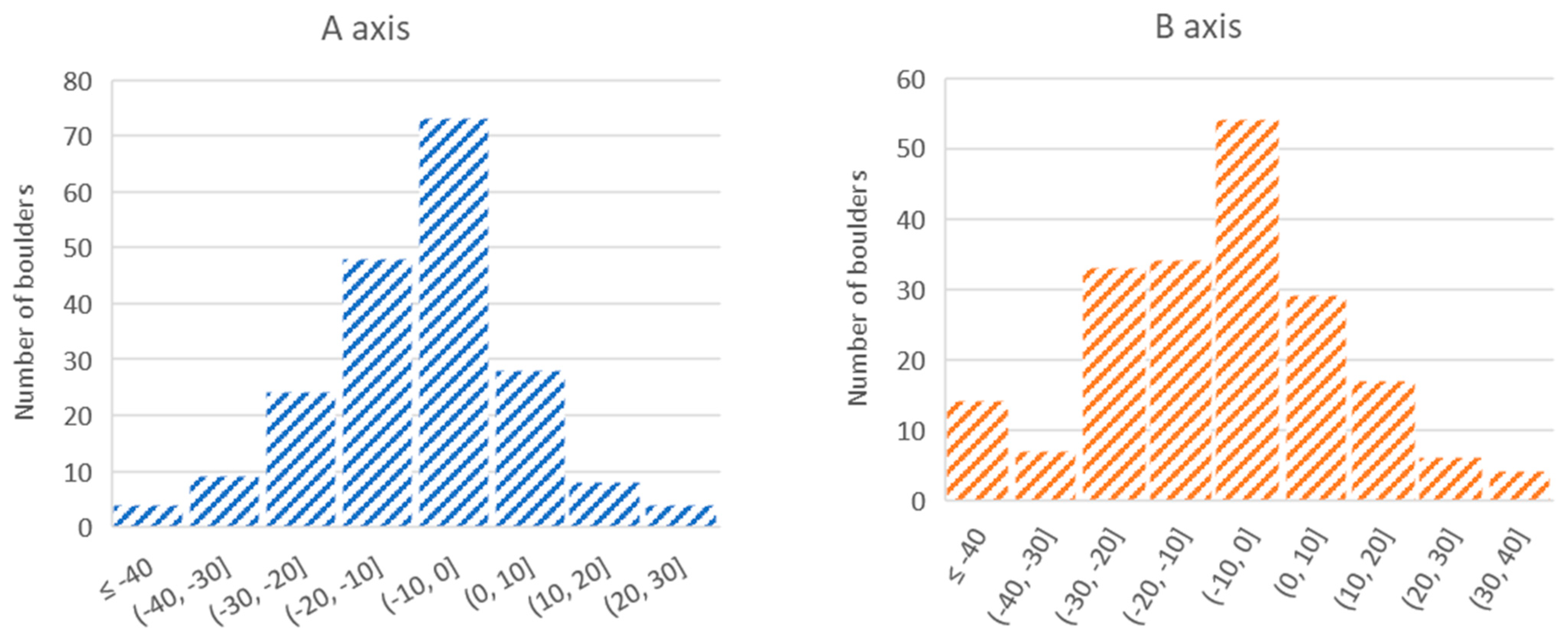
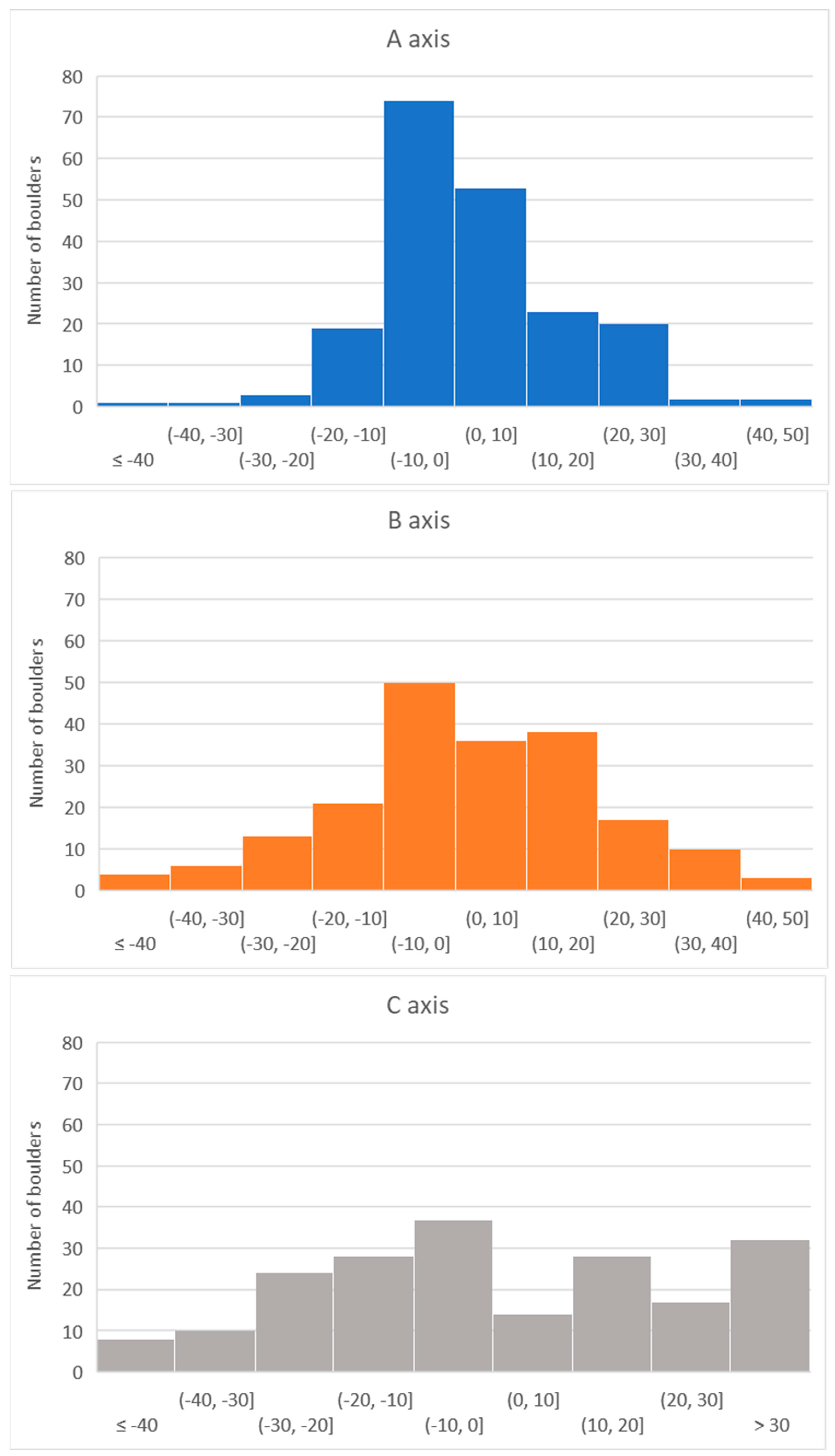
4.1. A, B and C Axis Dimensions
- i.
- the model maximum and model average dimensions for the A and B axes;
- ii.
- the model maximum dimensions and the in-situ measurements for the A and B axes;
- iii.
- the model average and in-situ measurements for the A, B and C axes.
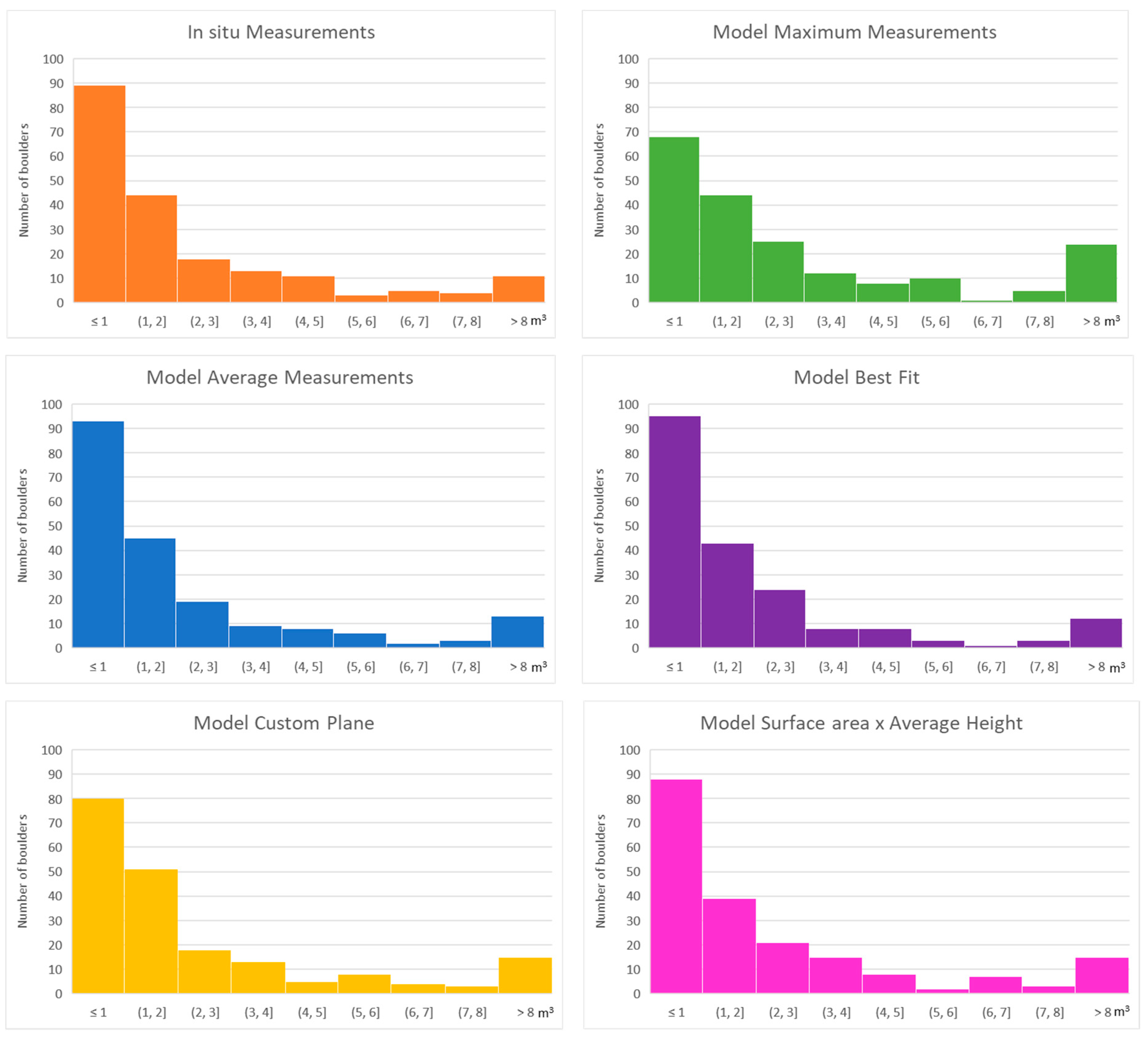
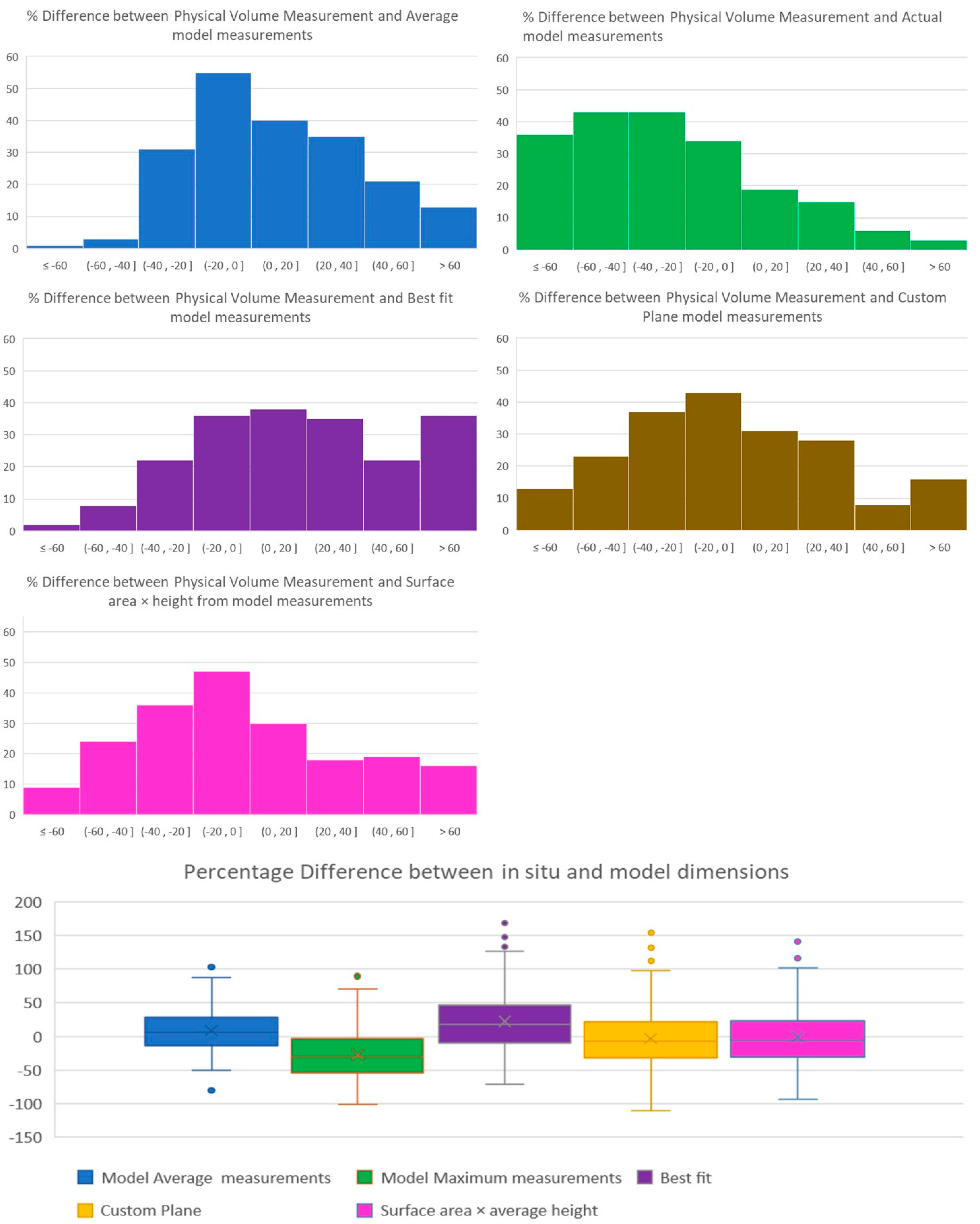
4.2. Boulder Volume Measurements
4.3. Boulder Volume Measurement using SfM
- i.
- Boulder 1 is of a roughly triangular shape with an irregular thickness, positioned on rough, slightly sloping ground;
- ii.
- Boulder 2 is also irregularly shaped; its surface has been partially hewn out as it formed part of a saltpan. During transportation it was overturned and now lies on its side (C axis);
- iii.
- Boulder 3 is roughly cuboid and lies partially inclined on a low scarp;
- iv.
- Boulder 4 is steeply imbricated and lodged between other boulders at the top of a boulder ridge. Its shape is also roughly cuboid;
- v.
- Boulder 5 is irregularly shaped and is located at the front of a cluster of boulders at the foot of the ridge;
- vi.
- Boulder 6 is a very large irregularly shaped mega-boulder of varying thickness. The A and B axes were measured at 7.8 and 7.5 m, respectively. It mostly overlies the shore platform but partially lies over a cluster of boulders that have accumulated in a low channel within the platform itself.
5. Discussion
5.1. Boulder Dimension Measurements
5.2. Biases and Limitations
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Paris, R.; Naylor, L.A.; Stephenson, W.J. Boulders as a signature of storms on rock coasts. Mar. Geol. 2011, 283, 1–11. [Google Scholar] [CrossRef]
- Paris, R.; Fournier, J.; Poizot, E.; Etienne, S.; Morin, J.; Lavigne, F.; Wassmer, P. Boulder and fine sediment transport and deposition by the 2004 tsunami in Lhok Nga (western Banda Aceh, Sumatra, Indonesia): A coupled offshore–onshore model. Mar. Geol. 2010, 268, 43–54. [Google Scholar] [CrossRef]
- Goto, K.; Miyagi, K.; Kawamata, H.; Imamura, F. Discrimination of boulders deposited by tsunamis and storm waves at Ishigaki Island, Japan. Mar. Geol. 2010, 269, 34–45. [Google Scholar] [CrossRef]
- Terry, J.P.; Karoro, R.; Gienko, G.A.; Wieczorek, M.; Lau, A.Y.A. Giant palaeotsunami in Kiribati: Converging evidence from geology and oral history. Isl. Arc 2021, 30, e12417. [Google Scholar] [CrossRef]
- Nott, J. Waves, coastal boulder deposits and the importance of the pre-transport setting. Earth Planet. Sci. Lett. 2003, 210, 269–276. [Google Scholar] [CrossRef]
- Pignatelli, C.; Sanso, P.; Mastronuzzi, G. Evaluation of tsunami flooding using geomorphologic evidence. Mar. Geol. 2009, 260, 6–18. [Google Scholar] [CrossRef]
- Nandasena, N.A.K.; Paris, R.; Tanaka, N. Reassessment of hydrodynamic equations: Minimum flow velocity to initiate boulder transport by high energy events (storms, tsunamis). Mar. Geol. 2011, 281, 70–84. [Google Scholar] [CrossRef]
- Nandasena, N.A.K.; Scicchitano, G.; Scardino, G.; Milella, M.; Piscitelli, A.; Mastronuzzi, G. Boulder displacements along rocky coasts: A new deterministic and theoretical approach to improve incipient motion formulas. Geomorphology 2022, 407, 108217. [Google Scholar] [CrossRef]
- Boesl, F.; Engel, M.; Rodrigo, C.E.; Galang, J.A.; Gonzalo, L.A.; Llanes, F.; Quix, E.; Brückner, H. Digital mapping of coastal boulders—High-resolution data acquisition to infer past and recent transport dynamics. Sedimentology 2020, 67, 1393–1410. [Google Scholar] [CrossRef]
- Ruban, D.A. Finding Coastal Megaclast Deposits: A Virtual Perspective. J. Mar. Sci. Eng. 2020, 8, 164. [Google Scholar] [CrossRef]
- Delle Rose, M.; Martano, P.; Orlanducci, L. Coastal Boulder Dynamics Inferred from Multi-Temporal Satellite Imagery, Geological and Meteorological Investigations in Southern Apulia, Italy. Water 2021, 13, 2426. [Google Scholar] [CrossRef]
- Devoto, S.; Hastewell, L.J.; Prampolini, M.; Furlani, S. Dataset of gravity-induced landforms and sinkholes of the Northeast Coast of Malta (Central Mediterranean Sea). Data 2021, 6, 81. [Google Scholar] [CrossRef]
- Devoto, S.; Macovaz, V.; Mantovani, M.; Soldati, M.; Furlani, S. Advantages of Using UAV Digital Photogrammetry in the Study of Slow-Moving Coastal Landslides. Remote Sens. 2020, 12, 3566. [Google Scholar] [CrossRef]
- Gomez-Pazo, A.; Perez-Alberti, A.; Trenheile, A. Recording inter-annual changes on a boulder beach in Galicia, NW Spain using an unmanned aerial vehicle. Earth Surf. Processes Landf. 2019, 44, 1004–1014. [Google Scholar] [CrossRef]
- Perez-Alberti, A.; Trenhaile, A. An initial evaluation of drone-based monitoring of boulder beaches in Galicia, north-western Spain. Earth Surf. Processes Landf. 2015, 40, 105–111. [Google Scholar] [CrossRef]
- Sedrati, M.; Morales, J.A.; El M’rini, A.; Anthony, E.J.; Bulot, G.; Le Gall, R.; Tadibaght, A. Using UAV and Structure-From-Motion Photogrammetry for the Detection of Boulder Movement by Storms on a Rocky Shore Platform in Laghdira, Northwest Morocco. Remote Sens. 2022, 14, 4102. [Google Scholar] [CrossRef]
- Hoffmeister, D.; Curdt, C.; Bareth, G. Monitoring the sedimentary budget and dislocated boulders in western Greece–results since 2008. Sedimentology 2020, 67, 1411–1430. [Google Scholar] [CrossRef]
- Nagle-McNaughton, T.; Cox, R. Measuring Change Using Quantitative Differencing of Repeat Structure-From-Motion Photogrammetry: The Effect of Storms on Coastal Boulder Deposits. Remote Sens. 2020, 12, 42. [Google Scholar] [CrossRef]
- Pérez-Alberti, A.; Trenhaile, A. Clast mobility within boulder beaches over two winters in Galicia, northwestern Spain. Geomorphology 2015, 248, 411–426. [Google Scholar] [CrossRef]
- Blair, T.C.; McPherson, J.G. Grain-size and textural classification of coarse sedimentary particles. J. Sediment. Res. 1999, 69, 6–19. [Google Scholar] [CrossRef]
- Scerri, S. Sedimentary evolution and resultant geological landscapes. In Landscapes and Landforms of the Maltese Islands, 1st ed.; Gauci, R., Schembri, J., Eds.; Springer: Cham, Switzerland, 2019; pp. 31–47. [Google Scholar]
- Galdies, C. The Climate of Malta: Statistics, Trends and Analysis 1951–2010; National Statistics Office: Valletta, Malta, 2011. [Google Scholar]
- Causon Deguara, J. A study of shore deposits on the coastline between Xgħajra and Żonqor—Marsascala. Unpublished Master of Arts Dissertation, Department of Geography, University of Malta, Msida, Malta, 2015. [Google Scholar]
- Biolchi, S.; Furlani, S.; Antonioli, F.; Baldassini, N.; Causon Deguara, J.; Devoto, S.; Di Stefano, A.; Evans, J.; Gambin, T.; Gauci, R.; et al. Boulder accumulations related to extreme wave events on the eastern coast of Malta. Nat. Hazards Earth Syst. Sci. 2016, 3, 5977–6019. [Google Scholar] [CrossRef]
- Mottershead, D.; Bray, M.; Soar, P.; Farres, P.J. Extreme wave events in the central Mediterranean: Geomorphic evidence of tsunami on the Maltese Islands. Z. Geomorphol. 2014, 58, 385–411. [Google Scholar] [CrossRef]
- Mottershead, D.; Soar, P.; Bray, M.; Hastewell, L.J. Reconstructing Boulder Deposition Histories: Extreme Wave Signatures on a Complex Rocky Shoreline of Malta. Geosciences 2020, 10, 400. [Google Scholar] [CrossRef]
- Causon Deguara, J.; Gauci, R. Evidence of extreme wave events from boulder deposits on the south-east coast of Malta (Central Mediterranean). Nat. Hazards 2017, 86 (Suppl. 2), 543–568. [Google Scholar] [CrossRef]
- Agisoft Metashape User Manual: Professional Edition. 2019. Available online: https://www.agisoft.com/pdf/metashape-pro_1_5_en.pdf (accessed on 1 March 2022).
- Haala, N.; Rothermel, M. Dense multiple stereo matching of highly overlapping UAV imagery. ISPRS Arch. 2012, 39, B1. [Google Scholar] [CrossRef]
- Autret, R.; Dodet, G.; Fichaut, B.; Suanez, S.; David, L.; Leckler, F.; Ardhuin, F.; Ammannd, J.; Grandjean, P.; Allemande, P.; et al. A comprehensive hydro-geomorphic study of cliff-top storm deposits on Banneg Island during winter 2013–2014. Mar. Geol. 2016, 382, 37–55. [Google Scholar] [CrossRef]
- Scicchitano, G.; Pignatelli, C.; Spampinato, C.R.; Piscitelli, A.; Milella, M.; Monaco, C.; Mastronuzzi, G. Terrestrial laser scanner techniques in the assessment of tsunami impact on the Maddalena peninsula (south-eastern Sicily, Italy). EPS 2012, 64, 889–903. [Google Scholar] [CrossRef][Green Version]
- Engel, M.; May, S.M. Bonaire’s boulder fields revisited: Evidence for Holocene tsunami impact on the Leeward Antilles. Quat. Sci. Rev. 2012, 54, 126–141. [Google Scholar] [CrossRef]
- Hoffmeister, D.; Ntageretzis, K.; Aasen, H.; Curdt, C.; Hadler, H.; Willershäuser, T.; Bareth, G.; Brückner, H.; Vött, A. 3D model-based estimations of volume and mass of high-energy dislocated boulders in coastal areas of Greece by terrestrial laser scanning. Z. Geomorphol. 2014, 58 (Suppl. 3), 115–135. [Google Scholar] [CrossRef]
- Mastronuzzi, G.; Pignatelli, C. The boulder berm of Punta Saguerra (Taranto, Italy): A morphological imprint of the Rossano Calabro tsunami of April 24, 1836? EPS 2012, 64, 829–842. [Google Scholar] [CrossRef]
- Biolchi, S.; Denamiel, C.; Devoto, S.; Korbar, T.; Macovaz, V.; Scicchitano, G.; Vilibić, I.; Furlani, S. Impact of the October 2018 storm Vaia on Coastal Boulders in the Northern Adriatic Sea. Water 2019, 11, 2229. [Google Scholar] [CrossRef]
- Biolchi, S.; Furlani, S.; Devoto, S.; Scicchitano, G.; Korbar, T.; Vilibic, I.; Sepic, J. The origin and dynamics of coastal boulders in a semi-enclosed shallow basin: A northern Adriatic case study. Mar. Geol. 2019, 411, 62–77. [Google Scholar] [CrossRef]
- Scicchitano, G.; Scardino, G.; Tarascio, S.; Monaco, C.; Barracane, G.; Locuratolo, G.; Milella, M.; Piscitelli, A.; Mazza, G.; Mastronuzzi, G. The First Video Witness of Coastal Boulder Displacements Recorded during the Impact of Medicane “Zorbas” on Southeastern Sicily. Water 2020, 12, 1497. [Google Scholar] [CrossRef]
- Gienko, G.A.; Terry, J.P. Three-dimensional modeling of coastal boulders using multi-view image measurements. Earth Surf. Processes Landf. 2014, 38, 853–864. [Google Scholar] [CrossRef]
- Lane, S. Slow science, the geographical expedition, and Critical Physical Geography. TCG 2017, 61, 84–101. [Google Scholar] [CrossRef]




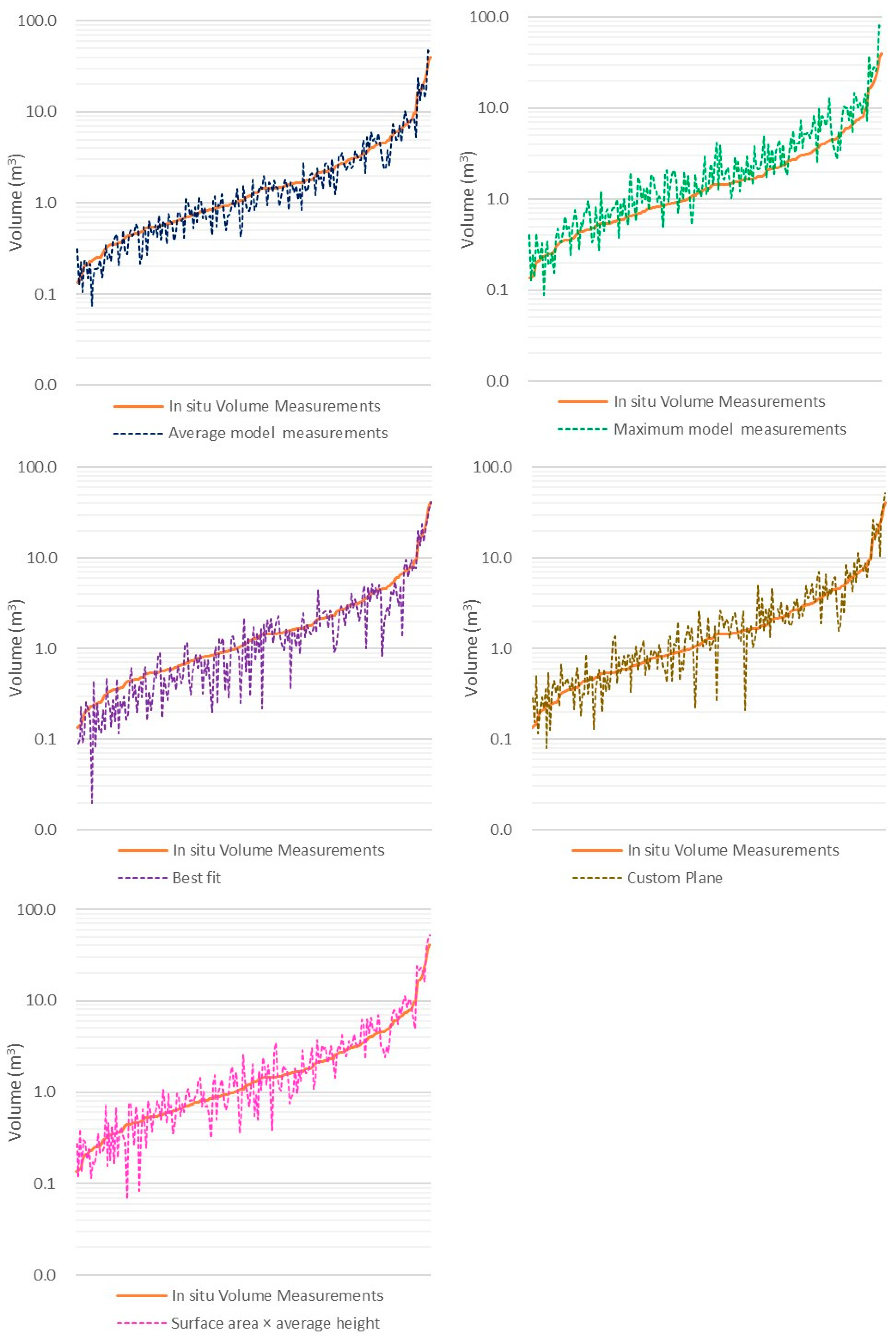







| Correlation between In Situ Measurements and Model Maximum Dimensions | Correlation between In Situ Measurements and Model Average Dimensions | |||
|---|---|---|---|---|
| p(uncorr) | p(uncorr) | |||
| A axis | 0.94 | <0.01 | 0.95 | <0.01 |
| B axis | 0.90 | <0.01 | 0.91 | <0.01 |
| C axis | 0.77 | <0.01 | 0.81 | <0.01 |
| In-Situ Measurements | p Value | |
|---|---|---|
| Model average measurements | 0.96 | <0.01 |
| Model maximum measurements | 0.94 | <0.01 |
| Best fit | 0.91 | <0.01 |
| Custom plane | 0.92 | <0.01 |
| Surface area × average height | 0.93 | <0.01 |
| Method | In-Situ Measurements | Average Model | Maximum Model | Best Fit | Custom Plane | Surface Area × Height |
|---|---|---|---|---|---|---|
| Total volume (m3) | 554.54 | 541.24 | 840.85 | 502.49 | 600.96 | 626.24 |
| Difference from the physical measurements (m3) | −13.30 | 286.32 | −52.05 | 46.42 | 71.70 | |
| Percentage difference from the physical measurements | −2.43% | 41.04% | −9.85% | 8.03% | 12.15% | |
| Boulder (No.) | Volume Calculation Methods | ||||||
|---|---|---|---|---|---|---|---|
| In-Situ Measurements | Average Model | Maximum Model | Best Fit | Custom Plane | Surface Area × Height | SfM | |
| (m3) | (m3) | (m3) | (m3) | (m3) | (m3) | (m3) | |
| 1 (65) irregular shape | 1.29 | 1.79 | 2.93 | 1.74 | 2.23 | 2.02 | 1.46 |
| 2 (20) irregular shape | 1.44 | 1.58 | 1.84 | 2.11 | 2.14 | 1.35 | 1.71 |
| 3 (424) inclined on a scarp | 2.7 | 3.15 | 3.60 | 2.95 | 2.97 | 2.93 | 2.53 |
| 4 (252) imbricated on a ridge | 1.60 | 0.85 | 1.21 | 1.56 | 2.58 | 1.17 | 1.54 |
| 5 (225) in front of a cluster | 3.02 | 2.86 | 7.34 | 2.91 | 2.78 | 3.64 | 2.91 |
| 6 (439) very large | 36.52 | 47.52 | 81.90 | 34.36 | 35.7 | 47.52 | 27.05 |
| Boulder (No.) | % Difference from the SfM Volume | |||||
|---|---|---|---|---|---|---|
| In-Situ Measurements | Average Model | Maximum Model | Best Fit | Custom Plane | Surface Area × Height | |
| % | % | % | % | % | % | |
| 1 (65) irregular shape | −11.64 | 22.60 | 100.68 | 19.18 | 52.74 | 38.36 |
| 2 (20) irregular shape | −15.79 | −7.60 | 7.60 | 23.39 | 25.15 | −21.05 |
| 3 (424) inclined on a scarp | 6.72 | 24.51 | 42.29 | 16.60 | 17.39 | 15.81 |
| 4 (252) imbricated on a ridge | 3.90 | −44.81 | −21.43 | 1.30 | 67.53 | −24.03 |
| 5 (225) in front of a cluster | 3.78 | −1.72 | 152.23 | 0.00 | −4.47 | 25.09 |
| 6 (439) very large | 35.01 | 75.67 | 202.77 | 27.02 | 31.98 | 75.67 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Causon Deguara, J.; Gauci, R.; Inkpen, R. Monitoring Coastal Erosion Using Remote Images: Comparison between Physically and Remotely Acquired Data on a Limestone Coast. Remote Sens. 2023, 15, 36. https://doi.org/10.3390/rs15010036
Causon Deguara J, Gauci R, Inkpen R. Monitoring Coastal Erosion Using Remote Images: Comparison between Physically and Remotely Acquired Data on a Limestone Coast. Remote Sensing. 2023; 15(1):36. https://doi.org/10.3390/rs15010036
Chicago/Turabian StyleCauson Deguara, Joanna, Ritienne Gauci, and Rob Inkpen. 2023. "Monitoring Coastal Erosion Using Remote Images: Comparison between Physically and Remotely Acquired Data on a Limestone Coast" Remote Sensing 15, no. 1: 36. https://doi.org/10.3390/rs15010036
APA StyleCauson Deguara, J., Gauci, R., & Inkpen, R. (2023). Monitoring Coastal Erosion Using Remote Images: Comparison between Physically and Remotely Acquired Data on a Limestone Coast. Remote Sensing, 15(1), 36. https://doi.org/10.3390/rs15010036







