Performance of Haiyang-2 Derived Gravity Field Products in Bathymetry Inversion
Abstract
1. Introduction
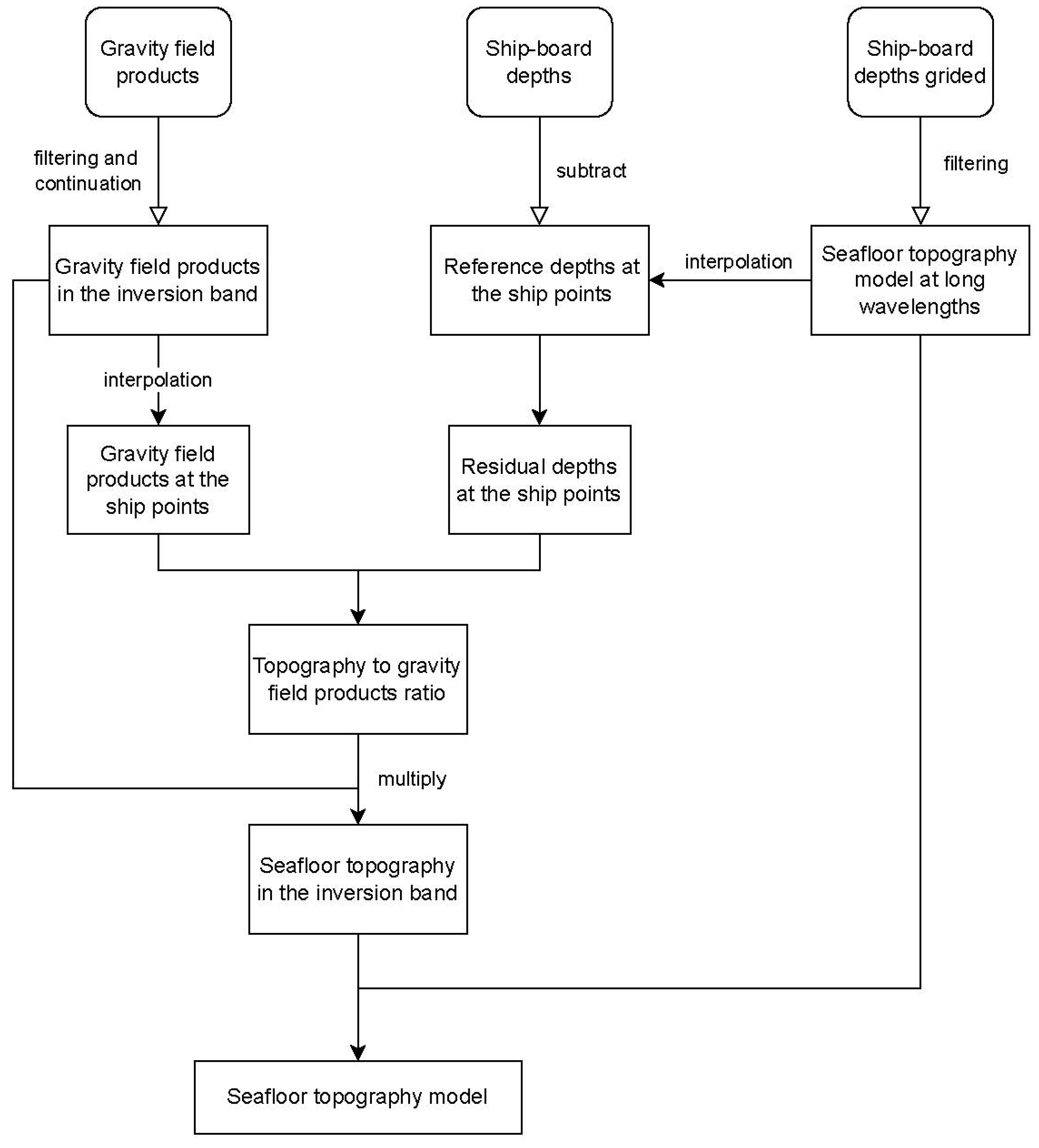
2. Method
2.1. Bathymetry Inversion from GA
- 1.
- Construct long-wavelength water depth . This is achieved by low-pass filtering of shipborne depths;
- 2.
- Filter using a bandpass filter;
- 3.
- Derive the scale coefficients, denoted as a(x), between submarine topography and gravity anomaly in the inversion band;
- 4.
- Recover the bathymetry as Equation (3).
2.2. Bathymetry Inversion from DV
3. Data
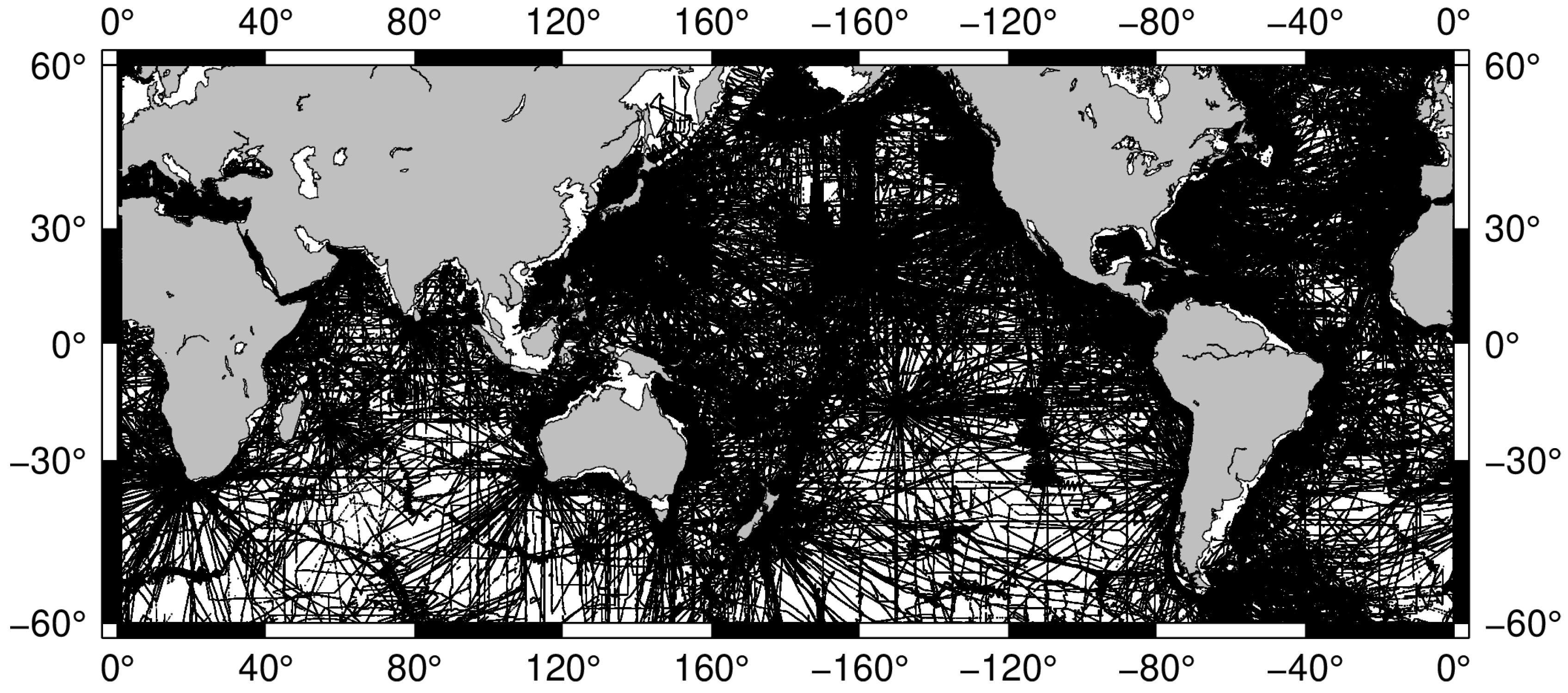
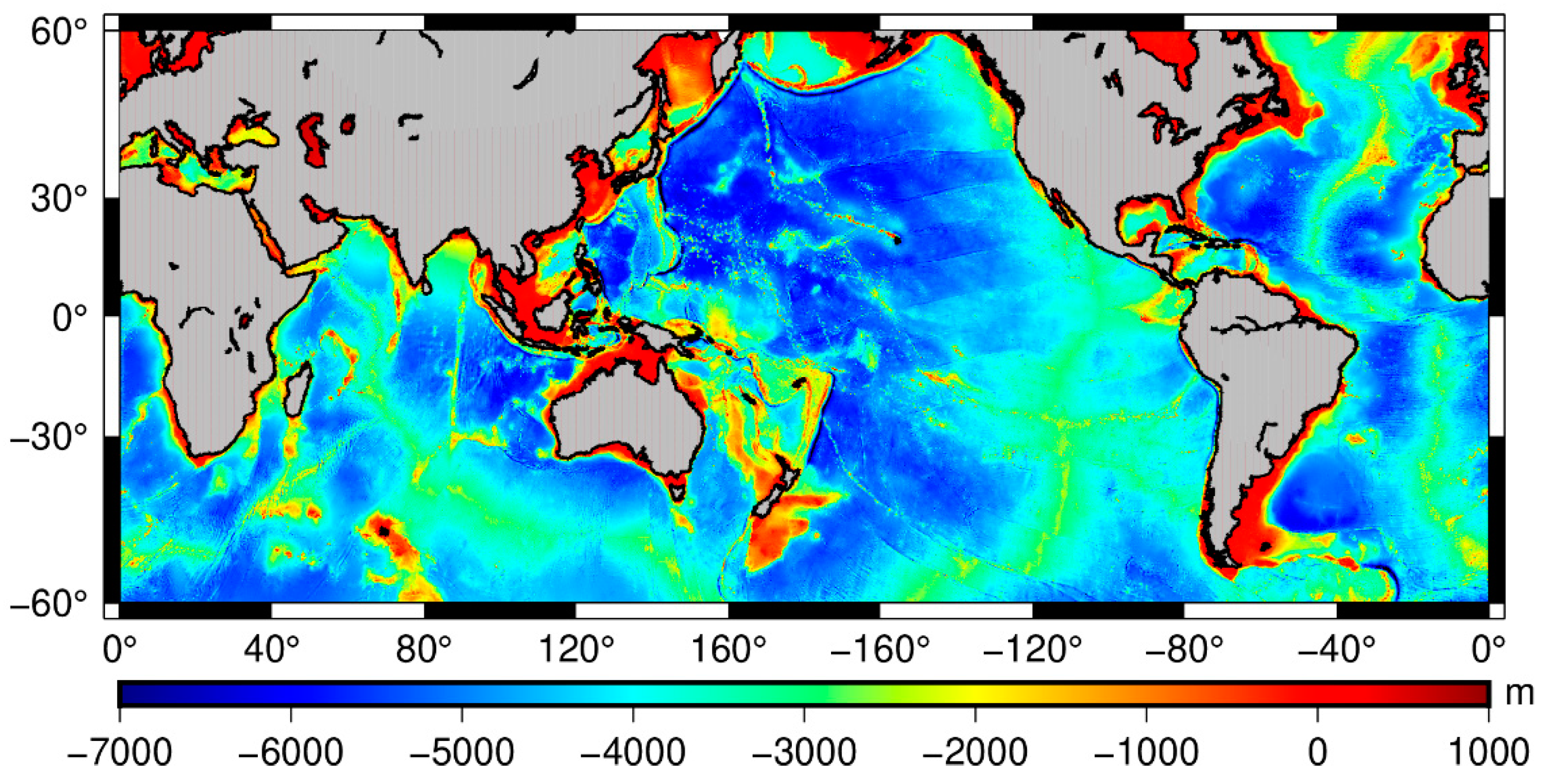
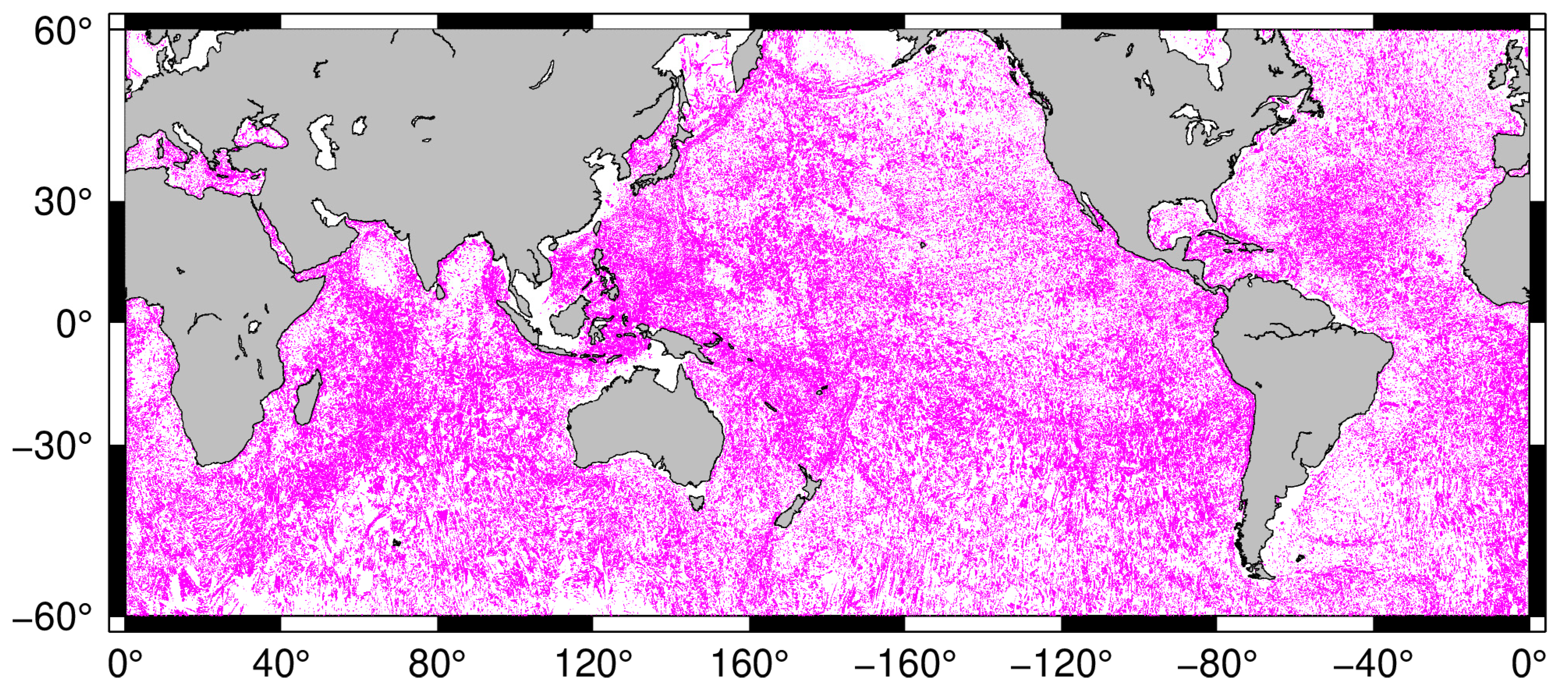
3.1. Shipborne Depth
3.2. Gravity Anomaly
3.3. Deflection of the Vertical
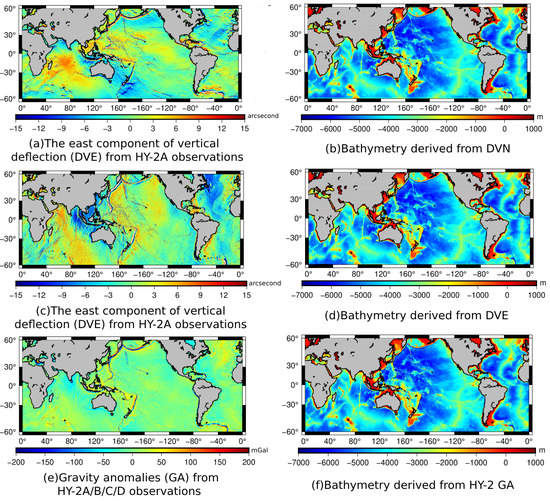
4. Results and Analysis
4.1. Results from DV
4.2. Results from GA
4.2.1. Precision Evaluation
4.2.2. Spatial Distribution of the Errors
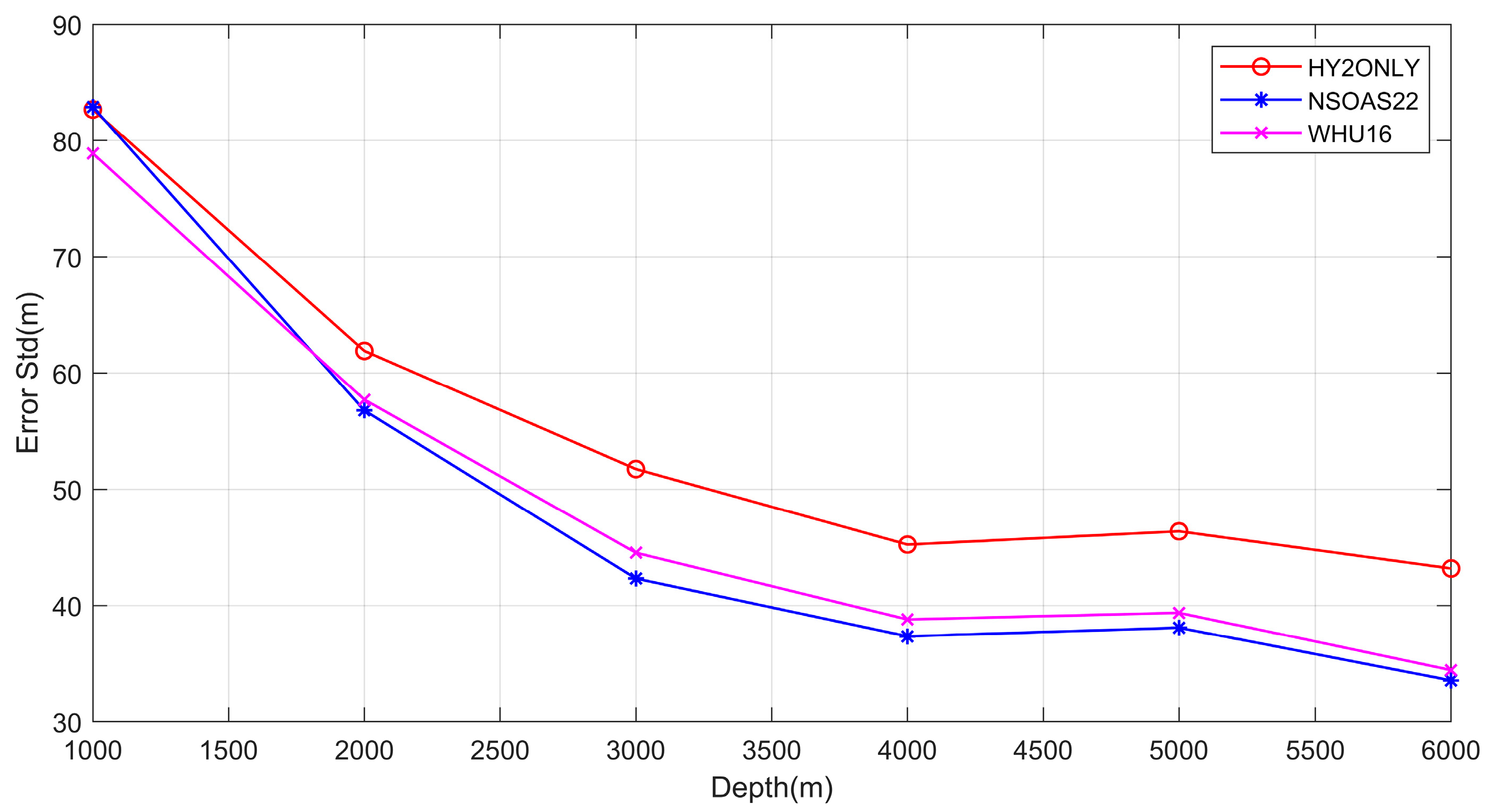
4.2.3. Analysis on Accuracy Variation with Water Depths
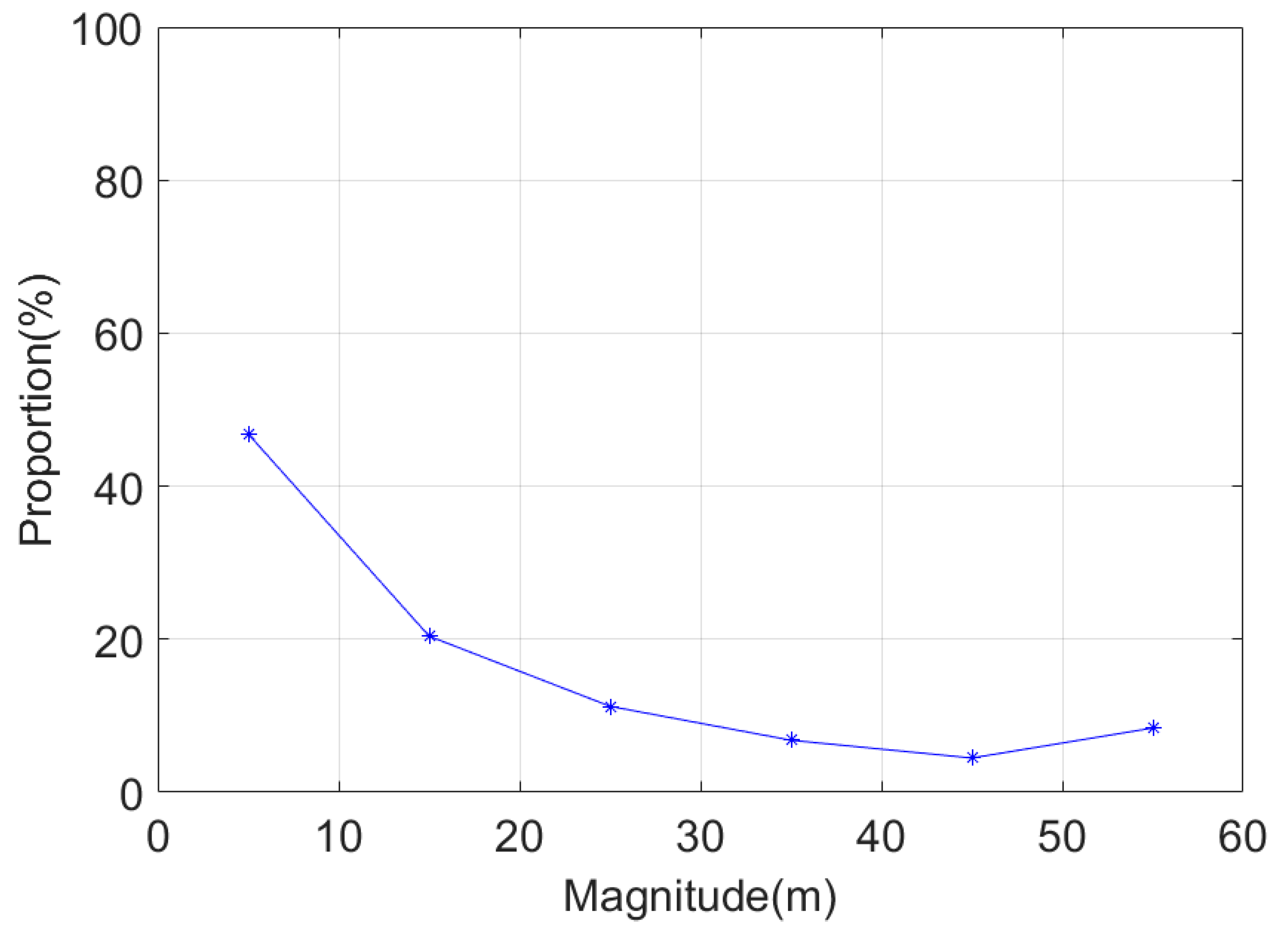
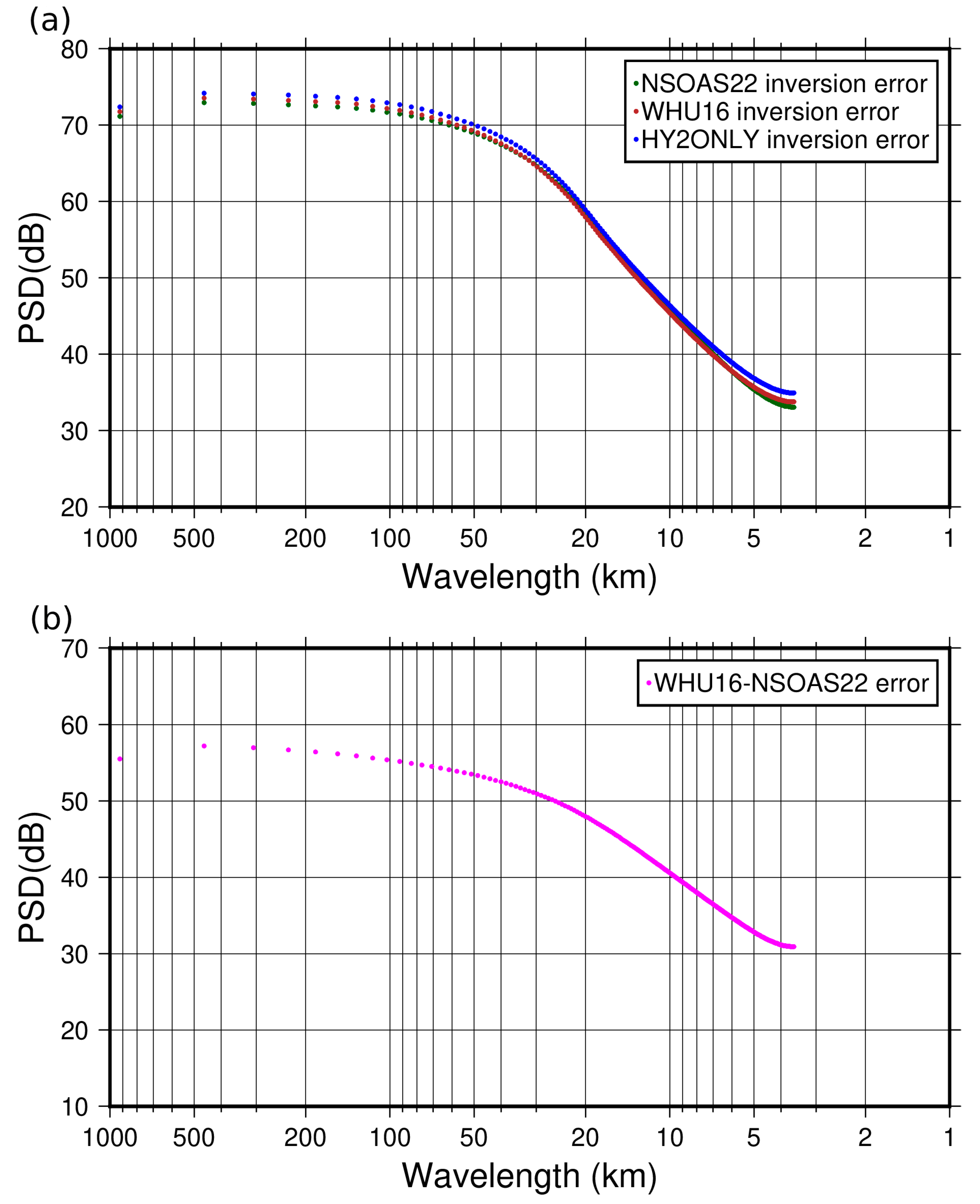
4.2.4. Accuracy Variation with Wavelength
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sandwell, D.T.; Smith, W.H.F.; Gille, S.; Jayne, S.; Soofi, K.; Coakley, B. Bathymetry from Space: White Paper in Support of a High-Resolution, Ocean Altimeter Mission; Scripps Institution of Oceanography: San Diego, CA, USA, 2001; pp. 1–54. [Google Scholar]
- Sandwell, D.T.; Smith, W.H.F. Marine gravity anomaly from Geosat and ERS 1 satellite altimetry. J. Geophys. Res. 1997, 102, 10039–10054. [Google Scholar] [CrossRef]
- Yang, J. Seafloor topography estimation from gravity gradients. Acta Geod. Cartogr. Sin. 2021, 50, 708. [Google Scholar] [CrossRef]
- Ouyang, M.; Sun, Z.; Zhai, Z.; Liu, X. Bathymetry Prediction Based on the Admittance Theory of Gravity Anomalies. Acta Geod. Cartogr. Sin. 2015, 44, 1092–1099. [Google Scholar] [CrossRef]
- Hwang, C. A bathymetric model for the south China Sea from altimetry and depth data. Mar. Geod. 1999, 22, 37–51. [Google Scholar] [CrossRef]
- Kim, J.W.; von Frese, R.R.B.; Lee, B.Y.; Roman, D.R.; Doh, S.-J. Altimetry-derived gravity predictions of bathymetry by the gravity-geologic method. Pure Appl. Geophys. 2011, 168, 815–826. [Google Scholar] [CrossRef]
- Hsiao, Y.S.; Hwang, C.; Cheng, Y.S.; Chen, L.C.; Hsu, H.J. High-resolution depth and coastline over major atolls of South China Sea from satellite altimetry and imagery. Remote Sens. Environ. 2016, 176, 69–83. [Google Scholar] [CrossRef]
- Yang, J.; Jekeli, C.; Liu, L. Seafoor topography estimation from gravity gradients using simulated annealing. J. Geophys. Res. Solid Earth 2018, 123, 6958–6975. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Meng, S.; Xing, Z.; Li, X.; Feng, J. Submarine topography model of South China Sea based on admittance function. Surv. Mapp. Sci. 2018, 43, 44–49. [Google Scholar] [CrossRef]
- Tozer, B.; Sandwell, D.T.; Smith, W.H.F.; Olson, C.; Beale, J.; Wessel, P. Global bathymetry and topography at 15 arc seconds: SRTM15+. Earth Space Sci. 2019, 6, 1847–1864. [Google Scholar] [CrossRef]
- Hu, M.; Zhang, S.; Jin, T.; Wen, H.; Chu, Y.; Jiang, W.; Li, J. A new global seafloor terrain model BAT_WHU2020. Acta Geod. Cartogr. Sin. 2020, 49, 939–954. [Google Scholar]
- Hu, M.; Jin, T.; Jiang, W.; Chu, Y.; Wen, H.; Li, J. Bathymetry Model in the Northwestern Pacific Ocean Predicted from Satellite Altimetric Vertical Gravity Gradient Anomalies and Ship-Board Depths. Mar. Geod. 2021, 45, 24–46. [Google Scholar] [CrossRef]
- Sui, X.; Zhang, R.; Wan, X.; Li, Y. Inversion and analysis of seafloor topography based on satellite altimeter data. Spacecr. Eng. 2017, 26, 130–136. [Google Scholar]
- Annan, R.F.; Wan, X. Recovering Bathymetry of the Gulf of Guinea Using Altimetry-Derived Gravity Field Products Combined via Convolutional Neural Network. Surv. Geophys. 2022, 43, 1541–1561. [Google Scholar] [CrossRef]
- Peng, H.; Lin, M.; Mu, B.; Zhou, W. Global statistical evaluation and quality analysis of HY-2A satellite radar altimeter data. Acta Oceanol. Sin. 2015, 37, 54–66. [Google Scholar]
- Zhu, C.; Guo, J.; Hwang, C.; Gao, J.; Yuan, J.; Liu, X. How HY-2A/GM altimeter performs in marine gravity derivation: Assessment in the South China Sea. Geophys. J. Int. 2019, 219, 1056–1064. [Google Scholar] [CrossRef]
- Wan, X.; Annan, R.F.; Jin, S.; Gong, X. Vertical Deflections and Gravity Disturbances Derived from HY-2A Data. Remote Sens. 2020, 12, 2287. [Google Scholar] [CrossRef]
- Ji, H.; Guo, J.; Zhu, C.; Yuan, J.; Liu, X.; Li, G. On Deflections of Vertical Determined From HY-2A/GM Altimetry Data in the Bay of Bengal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 12048–12060. [Google Scholar] [CrossRef]
- Zhang, S.; Zhou, R.; Jia, Y.; Jin, T.; Kong, X. Performance of HaiYang-2 altimetric data in marine gravity research and a new global marine gravity model NSOAS22. Remote Sens. 2022, 14, 4322. [Google Scholar] [CrossRef]
- Guo, J.; Luo, H.; Zhu, C.; Ji, H.; Li, G.; Liu, X. Accuracy comparison of marine gravity derived from HY-2A/GM and CryoSat-2 altimetry data: A case study in the Gulf of Mexico. Geophys. J. Int. 2022, 230, 1267–1279. [Google Scholar] [CrossRef]
- Wan, X.; Hao, R.; Jia, Y.; Wu, X.; Wang, Y.; Feng, L. Global marine gravity anomalies from multi-satellite altimeter data. Earth Planets Space 2022, 74, 165. [Google Scholar] [CrossRef]
- Wan, X.; Annan, R.F.; Wang, W. Assessment of HY-2A GM data by deriving the gravity field and bathymetry over the Gulf of Guinea. Earth Planets Space 2020, 72, 151. [Google Scholar] [CrossRef]
- Wan, X.; Ran, J.; Jin, S. Sensitivity analysis of gravity anomalies and vertical gravity gradient data for bathymetry inversion. Mar. Geophys. Res. 2019, 40, 87–96. [Google Scholar] [CrossRef]
- Xiang, X.; Wan, X.; Zhang, R.; Li, Y.; Sui, X.; Wang, W. Bathymetry Inversion with the Gravity-Geologic Method: A Study of Long-Wavelength Gravity Modeling Based on Adaptive Mesh. Mar. Geod. 2017, 40, 329–340. [Google Scholar] [CrossRef]
- Parker, R.L. 1972, The rapid calculation of potential anomalies. J. Geophys. R. 1972, 31, 447–455. [Google Scholar]
- Hu, M.; Li, J.; Li, H.; Xing, L. Bathymetry Predicted from Vertical Gravity Gradient Anomalies and Ship Soundings. Geod. Geodyn. 2014, 5, 41–46. [Google Scholar] [CrossRef]
- Hu, M.; Li, J.; Li, H.; Shen, C.; Jin, T.; Xing, L. Predicting Global Seafloor Topography Using Multi-Source Data. Mar. Geod. 2015, 38, 176–189. [Google Scholar] [CrossRef]
- Smith, W.H.F.; Sandwell, D.T. Bathymetric prediction from dense satellite altimetry and sparse shipboard bathymetry. J. Geophys. Res. 1994, 99, 21803–21824. [Google Scholar] [CrossRef]
- Wan, X.; Liu, B.; Sui, X.; Annan, R.F.; Hao, R.; Min, Y. Bathymetry inversion using the deflection of the vertical: A case study in South China Sea. Geod. Geodyn. 2022, 13, 492–502. [Google Scholar] [CrossRef]
- Marks, K.M.; Smith, W.H.F. Radially symmetric coherence between satellite gravity and multibeam bathymetry grids. Mar. Geophys. Res. 2012, 33, 223–227. [Google Scholar] [CrossRef]
- Hu, M.; Li, J.; Xing, L. Inversion of global seafloor topographic model from vertical gravity gradient anomalies. J. Surv. Mapp. 2014, 43, 558–565, +574. [Google Scholar] [CrossRef]
- Fan, D.; Li, S.; Meng, S.; Xing, Z.; Feng, J.; Zhang, C. Inversion of seafloor topography in the Philippine Sea area using combined multi-source gravity data. J. Surv. Mapp. 2018, 47, 1307–1315. [Google Scholar]
- Fan, D.; Li, S.; Meng, S.; Xing, Z.; Zhang, C.; Feng, J. Comparison and analysis on seafloor topography inversion methods with different isostatic compensation models. J. Chin. Inert. Technol. 2019, 27, 51–59. [Google Scholar]
- Fan, D.; Li, S.; Ouyang, Y.; Meng, S.; Chen, C.; Xing, Z.; Zhang, C. Least squares collocation inversion method considering the nonlinear term of seabed topography. J. Surv. Mapp. 2021, 50, 953–971. [Google Scholar]
- Fan, D.; Li, S.; Meng, S.; Xing, Z.; Zhang, C.; Feng, J.; Qu, Z. Influence Analysis of High-order Seafloor Topography on Sea Surface Gravity Information. Geomat. Inf. Sci. Wuhan Univ. 2021, 46, 1328–1335. [Google Scholar] [CrossRef]


| Term | Min (m) | Max (m) | Mean (m) | STD (m) | Removal Ratio |
|---|---|---|---|---|---|
| DOV_N2021BAT | −525.94 | 536.15 | 5.900 | 128.47 | 6.00% |
| DOV_E2021BAT | −568.96 | 580.49 | 5.62 | 130.27 | 6.09% |
| Term | Min (m) | Max (m) | Mean (m) | Std (m) | Removal Ratio |
|---|---|---|---|---|---|
| HY2ONLY_BAT | −2233.15 | 2513.65 | 2.62 | 142.41 | 0 |
| NSOAS22_BAT | −2284.91 | 2032.97 | 2.16 | 137.73 | 0 |
| WHU16_BAT | −3777.87 | 2976.51 | 5.77 | 154.20 | 0 |
| Term | Min (m) | Max (m) | Mean (m) | Std (m) | Removal Ratio |
|---|---|---|---|---|---|
| HY2ONLY_BAT | −297.24 | 305.74 | 5.22 | 82.93 | 5.16% |
| NSOAS22_BAT | −280.17 | 287.42 | 4.57 | 76.61 | 5.33% |
| WHU16_BAT | −296.49 | 305.32 | 4.99 | 79.37 | 5.16% |
| Term | Min (m) | Max (m) | Mean (m) | Std (m) | Removal Ratio |
|---|---|---|---|---|---|
| HY2ONLY_BAT | −411.25 | 436.97 | 12.93 | 135.76 | 4.27% |
| NSOAS22_BAT | −382.94 | 407.54 | 12.35 | 125.59 | 4.60% |
| WHU16_BAT | −385.64 | 410.71 | 12.52 | 126.20 | 4.71% |
| Term | Min (m) | Max (m) | Mean (m) | Std (m) | Removal Ratio |
|---|---|---|---|---|---|
| NSOA22_BAT-SIO | −394.15 | 428.25 | 17.00 | 122.21 | 3.85% |
| DTU21BAT-SIO | −265.58 | 275.16 | 4.11 | 79.61 | 3.83% |
| Term | Min (m) | Max (m) | Mean (m) | STD (m) | Removal Ratio (%) | |
|---|---|---|---|---|---|---|
| Without considering non-linear effect | Region A | −477.47 | 369.43 | 14.193 | 59.714 | 0 |
| Region B | −966.27 | 967.26 | 25.16 | 124.41 | 0.01% | |
| Region C | −993.93 | 965.60 | 8.00 | 80.15 | 0.02% | |
| Considering non-linear effect | Region A | −485.584 | 371.667 | 14.598 | 59.664 | 0 |
| Region B | −977.79 | 961.52 | 28.06 | 122.72 | 0.01% | |
| Region C | −995.31 | 981.17 | 9.50 | 79.27 | 0.02% | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wan, X.; Wang, H.; Jia, Y.; Ma, W. Performance of Haiyang-2 Derived Gravity Field Products in Bathymetry Inversion. Remote Sens. 2023, 15, 32. https://doi.org/10.3390/rs15010032
Wan X, Wang H, Jia Y, Ma W. Performance of Haiyang-2 Derived Gravity Field Products in Bathymetry Inversion. Remote Sensing. 2023; 15(1):32. https://doi.org/10.3390/rs15010032
Chicago/Turabian StyleWan, Xiaoyun, Huaibing Wang, Yongjun Jia, and Wenjie Ma. 2023. "Performance of Haiyang-2 Derived Gravity Field Products in Bathymetry Inversion" Remote Sensing 15, no. 1: 32. https://doi.org/10.3390/rs15010032
APA StyleWan, X., Wang, H., Jia, Y., & Ma, W. (2023). Performance of Haiyang-2 Derived Gravity Field Products in Bathymetry Inversion. Remote Sensing, 15(1), 32. https://doi.org/10.3390/rs15010032