Abstract
The land surface temperature obtained from remote sensing was widely used in the simulation of permafrost mapping instead of air temperature with the rapid development of remote sensing technology. The land surface freezing and thawing index (LFI and LTI), which is commonly regarded as the ground surface freezing and thawing index (GFI and GTI), can produce certain errors in the simulation of permafrost distribution on the Qinghai–Tibet Plateau. This paper improved the accuracy of the thermal condition of the surface soil in the Qinghai–Tibet Engineering Corridor (QTEC) by calculating the LFI (or LTI) and N-factors. The environmental factors affecting the spatial distribution of the GFI and GTI were detected by the GeoDetector model. Finally, the multiple linear relationships between the GFI (or GTI) and the environmental factors were established. The results from 25 monitoring sites in the QTEC show that the Nf (ratio of GFI to LFI) is 1.088, and the Nt (ratio of GTI to LTI) is 0.554. The explanatory power of the interaction between elevation and latitude for the GFI and GTI is 79.3% and 85.6%, respectively. The multiple linear regression model with six explanatory variables established by GFI (or GTI) has good accuracy. This study can provide relatively accurate upper boundary conditions for the simulation of permafrost distribution in the QTEC region.
1. Introduction
With an average elevation of over 4000 m above sea level and a total surface area of 2.57 million km2, the Qinghai–Tibet Plateau (QTP) is the highest and largest plateau in the world [1]. Permafrost is a common geographical phenomenon in the QTP, defined as ground that remains frozen for two or more consecutive years [2]. Climatic records from QTP suggest that this region might be sensitive to global warming and might result in important environmental influences [3,4]. Studies of soil hydrothermal conditions in recent decades have found that permafrost has degraded significantly in the QTP [5,6,7]. The thermal state of permafrost is a very important component for researching the impact of climate warming in the QTP. The thawing of permafrost can have ecological impacts and may lead to instability of construction facilities in the Qinghai-Tibet Engineering Corridor (QTEC) [8,9]. Therefore, accurate mapping of permafrost distribution is essential to understanding the thermal condition of permafrost on the QTP and the engineering stability of the QTEC [10].
Several empirical and semi-physical models have been applied to permafrost mapping on the QTP. The distribution characteristics of permafrost on the QTP were simulated by using the surface frost number model based on the ground surface freezing–thawing index as input parameters [11]. The temperature at the top of the permafrost model (TTOP) has been successfully used in many permafrost areas with its low input parameters and taking into account the thermal conductivity of the soil [12,13,14,15].
The permafrost distribution of the QTP includes 1.06 × 106 km2 of permafrost, 1.46 × 106 km2 of seasonally frozen ground, and 0.03 × 106 km2 of unfrozen ground, which is simulated by the TTOP model from 2003 to 2012 [16]. The active layer thickness (ALT) is a characteristic of permafrost and has important impacts on the surface energy balance, hydrologic cycle, and carbon exchange between the atmosphere and the soil [17]. He Stefan equation links the land surface temperature (LST) to the freezing–thawing process of ice-containing soils, simplifying the depth calculation of soil freezing–thawing [18]. A better performance has been shown in simulations of ALT in permafrost regions using the Stefan equation [19,20].
The simulation of permafrost distribution should take the thermal condition of the ground surface as the upper boundary condition, but the ground surface temperature (GST) over the region is only available to deploy monitoring sites. Air temperature (Ta) has been considered in permafrost mapping due to its easier accessibility compared to soil temperature. In early studies, the air freezing index (AFI) and air thawing index (ATI) were generally corrected to the ground surface freezing index (GFI) and ground surface thawing index (GTI), using the N-factors, respectively [19,21,22]. With the development of remote sensing technology, high-resolution surface temperature data can be acquired by thermal infrared sensors. Now, MODIS and Landsat provide spatial and temporal surface temperature readings on a global scale and are widely used in permafrost mapping [23,24,25]. Due to the buffering effect of ground cover such as vegetation, snow, and leaves, there is a fundamental difference between Ta, LST, and GST, although they are closely related. Ta usually refers to the monitoring temperature 1–2 m above the ground. LST is assumed to be the skin temperature with most signal coming from the top canopy layer, which is also the monitored temperature after the de-clouding process of the remote-sensing data [26]. GST is usually considered to be the temperature in the shallow 0–10 cm of the soil layer [27,28]. Since the freezing–thawing index has the effect of amplifying the difference in daily average temperatures, using daily average temperatures away from the ground surface can cause errors in permafrost mapping. LST and GST have a high correlation, and extending the high-resolution LFI (or LTI) into GFI (or GTI) can reduce the error on the permafrost mapping.
Spatial heterogeneity refers to the uneven distribution of attributes across a region and is one of the main characteristics of geographical phenomena [29,30]. GeoDetector is a new statistical method which can detect spatial heterogeneity and reveal the driving factors by the q-value [31]. The GeoDetector is widely applied in various fields due to its advantages in geographical statistics [32,33,34,35]. The GeoDetector model can be used to study the driving factors of the freezing–thawing index in a relatively comprehensive way and explore the interaction between explanatory variables and the freezing–thawing index. This model is used to detect the spatial differentiation of GFI and GTI and calculate and analyze the impact of various factors on it, thus providing a basis for the further analysis of the soil thermal condition in the QTEC.
The objectives of this study were to (1) analyze the differences between LFI (or LTI) from remote sensing and GFI (or GTI) from in situ measurement in QTEC area; (2) quantify the relationships between GFI (or GTI) and environmental factors such as elevation, latitude, soil type, and vegetation by GeoDetector; and (3) improve the accuracy of GFI and GTI in the QTEC based on MODIS LST products by using the multiple linear regression model.
2. Materials and Methods
2.1. Study Area
The study area is located in the Central Qinghai–Tibet Plateau, bounded by latitude 29°–36°N and longitude 90°–95°E (Figure 1a). The QTEC extends from Golmud, Qinghai Province in the north, to Lhasa, Tibet Autonomous Regions in the south (about 63000 km2), which were the start and end points of several constructions (e.g., Qinghai–Tibet Highway, Qinghai–Tibet Railway, Gas Pipiline, and Electric Transmission) (Figure 1b). The QTEC experiences a continental climate with cold (to −30 °C) winters with blowing snow and warm (to +25 °C) summers, almost continuous windy conditions, and widely variable annual precipitation of 50 to about 400 mm [36]. The 25 monitoring sites, including natural hole and active layer monitoring points, are distributed in various terrain, including high-altitude mountains, high plains, and basins from north to south of the plateau [37]. The near-surface sediments are dominated by coarse-grained materials such as gravels and sands [10]. The mean annual air temperatures (MAATs) were commonly between −6.5 °C and −2.0 °C. Most parts of the QTEC were located above 4000 m a.s.l., interlacing distribution of mountains, valleys, and basins. Vegetation in the area changes obviously with elevation, dominated by alpine meadows and alpine steppes and sparse alpine vegetation [38]. The Normalized Difference Vegetation Index (NDVI) was calculated by the maximum-value composite procedure ranging from 0 to 0.9 in the whole area.

Figure 1.
Study area map: (a) map of permafrost on the Qinghai-Tibet Plateau cited from the permafrost map by Zou et al. [16]; (b) elevation map of Qinghai-Tibet Engineering Corridor based on 90 m DEM data.
2.2. Data Source
2.2.1. Reanalysis Datasets
Based on the analysis data retrieved from remote sensing, this study selected 10 types of data from remote-sensing datasets, namely soil moisture, LST, latitude, longitude, slope, aspect, elevation, NDVI, soil type, and snow duration days (SDD). The data of LST are using the Thermal and Reanalysis Integrating Moderate-Resolution Spatial-Seamless LST—Tibetan Plateau [39,40,41,42], which was reanalyzed by MODIS LST and GLDAS productions. This dataset displays high accuracy when compared with the measured data. The Daily 0.01° × 0.01° Land Surface Soil Moisture Dataset of the Qinghai–Tibet Plateau (2005, 2010, 2015, 2017, and 2018) was downloaded from National Tibetan Plateau Data Center [43,44,45]. This dataset was downscaled from Land Surface Soil Moisture Dataset of SMAP Time-Expanded Daily 0.25° × 0.25° over the Qinghai–Tibet Plateau Area. Vegetation NDVI data are derived from the Resources and Environmental Science Data Center of the Chinese Academy of Sciences [46]. Soil-type data were obtained from Harmonized World Soil Database v1.2 (HWSD), with a spatial resolution of 1 km [47]. The HWSD soil types are classified based on the Food and Agriculture Organization (FAO) of the United Nations soil classification system. There are ten soil types in this study area, including Arenosols, Anthrosols, Cambisols, Fluvisols, Gleysols, Gypsisols, Leptosols, Phaeozems, Regosols, and Solonchaks. SDD data were extracted from daily cloud-free MODIS NDSI and snow phenology dataset over High Mountain Asia (2000–2021) [48,49]. Details about the datasets can be seen in Table 1. The multi-year average data were calculated and clipped. The variables (including type variables) were resampled to 0.01°, using nearest neighbor interpolation. The spatial coordinates of all variables were unified into the geographic coordinate system WGS 1984.

Table 1.
Types of remote-sensing data and their sources.
2.2.2. Topographic Data and Site Selection
The Shuttle Radar Topographic Mission (SRTM) provided digital elevation model (DEM) data. The SRTM DEM data with a 90 m horizontal resolution were downloaded from Geospatial Data Cloud. Topographic data, i.e., slope, aspect, and elevation, were extracted from the DEM after resampling the DEM data to 0.01°. The coordinates of the centroid of the cell grid were used as the latitude and longitude of the grid.
One auto climate monitoring station was established for long-term monitoring, near the Beiluhe Observation and Research Station of Frozen Soil Engineering and Environment. The 5 cm depth daily GST from 2008 to 2020 was collected to verify the differences with LST. Ground surface temperatures (5 cm or 10 cm) of 16 natural holes were selected to calculate the GFI and GTI. Another 9 active layer-monitoring sites also selected from “a synthesis dataset of permafrost for the Qinghai-Xizang (Tibet) Plateau, China” [50,51,52,53]. Equipment damage caused by harsh environment leads to some data loss. The missing data are obtained by numerical interpolation of years before and after.
2.3. Methods
2.3.1. Freezing Index, Thawing Index, and N-Factors
Freezing index or thawing index can be calculated by air temperature and ground surface temperature. The thawing index is calculated as the sum of degree days above 0 °C over the year, and the freezing index as the sum of degree days below 0 °C from a full year:
where FI and TI are the annual freezing index and thawing index (°C·d), Ti is the daily air temperature or ground temperature (°C), and nf and nt are the lengths of freezing and thawing days. The LFI and LTI were calculated by LST. The GFI and GTI were calculated by GST.
Nf was the ratios between GFI and LFI. Nt was the ratios between GTI and LTI:
2.3.2. GeoDetector
Wang et al. established a GeoDetetor model based on spatial variance analysis [54]. It can detect the similarity of variables in the same area and the difference of variables between different areas. The GeoDetector model is divided into four components: the risk detector, the factor detector, the ecological detector, and the interactive detector. In this work, the factor detector and interactive detector were used. The factor detector measures the degree of spatial heterogeneity of a variable, Y, and the determinant power of an explanatory variable, X of Y; the interaction detector reveals whether the risk factors, X1 and X2 (and more X), have an interactive influence on a response variable, Y. The interaction types can be seen in Table 2.

Table 2.
Types of interaction relationships between the two factors.
The spatial consistency and heterogeneity of the dependent variable, X, and response variable, Y, can be measured by the q-value [0, 1] in the GeoDetector. The higher similarity between the X and Y patterns, the more sensitive X is to Y. As a result, the q-value is used to compare the similarity of X and Y. The following equation represents the q-statistic:
where N and σ2 stand for the number of units and the variance of Y in the entire study area, respectively. The study area is divided into L strata (h = 1, 2, 3, …, L) based on the characteristics of the explanatory variables or determinant factors (X). Nh and σh2 represent the number of sample units and the variance in Y within zone h, considering factor X, respectively. X should be stratified if it is a numerical variable, the number of strata, L, might be 2–10 or more, according to prior knowledge or a classification algorithm [31]. In this study, two response variables are included, namely GFI and GTI, and the dependent variable are soil moisture, longitude, latitude, slope, aspect, elevation, NDVI, soil type, and snow duration days.
Soil moisture, snow duration days, elevation, and NDVI were classified into 7 categories according to the natural-breaks method. Longitude, latitude, and slope were classified into 5 categories due to their narrow distribution in the QTEC. The aspect data were reclassified into five categories according to flat (−1), shady slope (0°~45° and 315°~360°), semi-shady slope (45°~135°), sunny slope (135°~225°), and semi- sunny slope (225°~315°).
2.3.3. Statistical Model
The purpose of multiple linear regression is to clarify whether there is a linear relationship between multiple variables and to be able to predict the distribution of the variables through the model. The equation established as follows:
In the formula, y is the GFI or GTI; x1, x2, …, xn are the explaining variables selected by the GeoDetector; β is the coefficient; and u is the constant.
3. Results
3.1. Statistical Analysis of Differences between GST and LST Obtained from Reanalyzed Dataset
The LST dataset contains two instantaneous temperatures at nighttime and daytime, which are the same as the AQUA MODIS transit time of the pixel (1:30 at noon and 1:30 in the morning), and these times are close to the actual times of the observed maximum air temperature and minimum air temperature. Thus, the daily average temperature can simply be calculated from the arithmetic average of the maximum and minimum values. To assess the differences of the MODIS LST product and GST in the QTEC, the LST data from this dataset were compared with GST measurements based on the Beiluhe weather station from 2008 to 2020 (Figure 2).
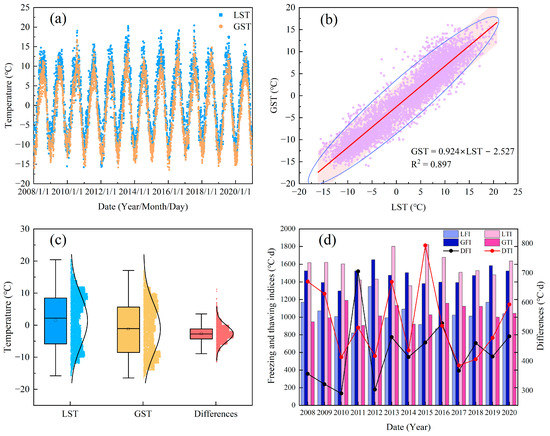
Figure 2.
Relationship and differences between land-surface and ground-surface thermal conditions: (a) temporal variation of LST and GST at the Beiluhe weather station from 2008 to 2020; (b) correlation analysis of LST and GST; (c) distribution and range of differences of LST and GST; (d) DFI = differences between GFI and LFI, and DTI = differences between GTI and LTI.
It is obvious that the LST and GST maintain a consistent trend of change during the study period and most LSTs are larger than GSTs (Figure 2a). The LST and GST satisfy the linear relation with high coefficient of determination (Figure 2b). The boxplot drawn from 13 years of data of LST and GST can clearly compare the difference of data distribution (Figure 2c). The LST has more positive temperature days, and the daily temperature exceeds 10 °C more frequently. In contrast, the GST accumulated more days with negative temperature, and its average temperature was negative, while that of the LST was positive. An average error of 2.6 °C in the daily mean temperature between the LST and GST is allowed because the temperature of a monitoring point often cannot represent its pixel information, especially when the spatial resolution is coarse. The errors between daily GST and LST can cause the differences between the GFI (or GTI) and LFI (or LTI). The GFI and LTI are greater than the LFI and GTI for all years (Figure 2d). The DFI varies from 290 to 705 °C·d, and the DTI varies from 385 to 793 °C·d. This difference will create uncertainty in the prediction of the thermal condition of the permafrost.
3.2. Obtain the N-Factors in the QTEC Based on Relationship between GFI (or GTI) and LFI (or LTI) from In Situ Measurements
The GFI and GTI are important input parameters in the model of permafrost distribution and thermal conditions. The accuracy of the GFI and GTI is a decisive factor in accessing the authentic condition of permafrost. Previous studies have found a good linear relationship between air temperature, LST, and GST, so their freezing–thawing index driven by temperature could have a certain relationship. Generally, the GFI and GTI can only be monitored at a single point by the temperature probe. It is hard to measure the whole area of the QTEC, so 25 ground-surface temperature-monitoring sites along the QTEC were used to obtain Nf and Nt. The GTI and GFI of QTEC were accessed depending on Nf and Nt, respectively.
Figure 3a,b show the multi-year average freezing and thawing index of ground surface and land surface of 25 sites in the QTEC and its differences. The GFI and LFI are relatively similar, with the freezing index of most sites exceeding 1000 °C·d. The maximum and minimum value of the in situ observed GFI occurs at site P17 2353 °C·d and Ch04 508 °C·d, respectively. The site with the maximum and minimum value of the LFI is 1814 °C d (P2) and 453 °C·d (CH04). The differences between the GFI and LFI range from 39 °C·d to 1428 °C·d, with an average of 334 °C·d. There is a linear relationship between the GFI and LFI (Figure 3c). The slope means that the Nf is approximately 1.088. The thawing index shows a great variation among the 25 sites. The overall LTI is above 1000 °C·d, with an average of 1500 °C·d, while the average of the GTI is 828 °C·d, and most are below 1000 °C·d. The differences between the GFI and LFI range from 240 °C·d (QT05) to 1246 °C·d (Ch04), with an average of 672 °C·d. Figure 3d shows that there is a correlation between the GTI and LTI of 25 sites and the Nt is approximately 0.554 on the QTEC.
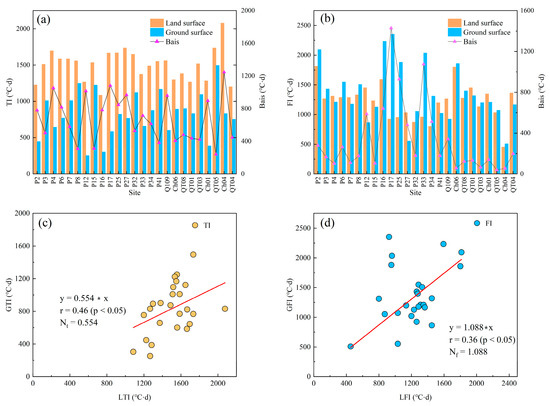
Figure 3.
N-factors analysis between the GFI (or GTI) and the LFI (or LTI) at 25 field sites: (a,c) differences between the GFI with the LFI and Nf, respectively; (b,d) differences between the GTI with the LTI and Nt, respectively. The Pearson correlation coefficient (r) was used to evaluate the correlation between the variables in (c,d).
The LFI and LTI obtained from remote-sensing technology were corrected to the GFI and GTI over QTEC through the Nf and Nt (Figure 4). The distribution of the GFI and GTI of QTEC is opposite. The areas near the north and south have lower elevation and flat terrain, resulting in a high GTI and low GFI. In contrast, the difference between the GFI and GTI in the central region of QTEC is insignificant, mostly in the range of 1000 to 2000 °C·d.
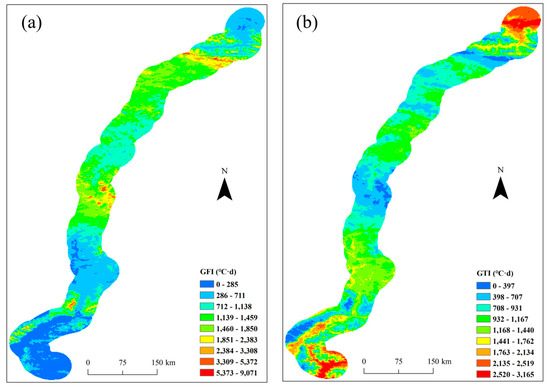
Figure 4.
GFI and GTI of QTEC: (a) GFI and (b) GTI.
3.3. Effect of Environmental Factors on GFI and GTI in the QTEC
The nine influencing factors selected for this study were classified according to the method presented in Section 2.3.2. The distribution diagram of various factors in QTEC was plotted (Figure 5). Except for the lower elevation at the north and south ends, the elevation of most areas exceeds 4000 m a.s.l (Figure 5a). The distribution pattern of snow duration days is closely related to the elevation, and the snow mainly occurs in the high mountains above 5000 m a.s.l (Figure 5b). Due to the intensive solar radiation on the plateau, stable snow cannot be formed in most areas. Figure 5c shows that the average annual soil moisture content in the QTEC regions varies from 7% to 17%, increasing gradually from north to south. Soil types in the QTEC are mainly Leptosols, accompanied by nine types (Figure 5d). Leptosols often contain large amounts of gravel and are approximately equally distributed among high mountain areas, deserts, and boreal regions, where soil formation is limited by severe climatic conditions. Soil types often represent various physicochemical properties of the soil. Soil types and vegetation can somewhat indicate the presence or absence of permafrost in permafrost regions. The vegetation conditions are closely related to shallow soil hydrothermal regime, and NDVI usually can reflect the vegetation growth. Understanding the distribution of vegetation in the study area through NDVI could help us obtain a general overview of soil moisture and heat conditions. The NDVI distribution of QTEC gradually increased from the beginning to the end of the Qinghai–Tibet Highway, with the NDVI increasing from below 0.2 in the north to above 0.6 in the south (Figure 5e). The slope, aspect, longitude, and latitude of the study areas were reclassified into five categories according to the optimal classification (Figure 5f–i). There is no significant difference in the number of shady and sunny slopes on the QTEC. The terrain is gently undulating, with slopes ranging from 0 ° to 27 °.
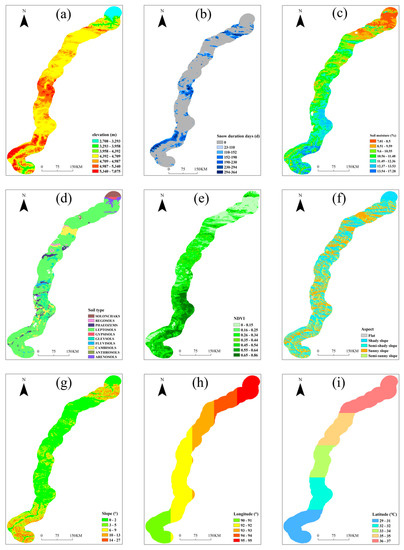
Figure 5.
Distribution of the 9 environmental factors in the QTEC after classification: (a) elevation, (b) snow duration days, (c) soil moisture, (d) soil type, (e) NDVI, (f) aspect, (g) slope, (h) longitude, and (i) latitude.
The GFI or GTI of QTEC was detected by the GeoDetector, along with nine environmental factors. The results of the factor detections show that the maximum q-values of GTI and GFI were 0.650 and 0.438 (Figure 6), corresponding to elevation and latitude, respectively. The influence of each factor on GFI and GTI (q-value) passed the significance test (p < 0.01). Altitude has the highest explanatory power for GTI, which is 0.650. The q-value of the soil type, snow cover days, and soil humidity exceeds 0.2, followed by longitude and latitude, which are 0.194 and 0.142, respectively (Figure 6a). In contrast, the impact of nine environmental factors on the spatial distribution of GFI in QTEC was quite different from that of GTI (Figure 6b). A total of 43.8% (q = 0.438) of the spatial variation in GFI was caused by latitude. Longitude can also explain the spatial change of GFI significantly (q = 0.321), followed by NDVI (q = 0.240), snow duration days (q = 0.236), and soil moisture (q = 0.219). Factor detection between the GFI (or GTI) and the explanatory variables selected in this study suggested that the same factor also had different explanatory power for the GFI and GTI. The spatial distribution of elevation is consistent with the GTI, and the temperature at lower elevation leads to a smaller GTI. However, the explanatory power of elevation on the spatial distribution of the GFI is low, which might be because the GST in the cold season is the combined effect of air temperature, snow cover, and vegetation cover. Some studies have shown that the insulation effect of vegetation on the soil surface layer is more significant in winter [55]. The soil type has more significant effects on the spatial distribution of GTI, but less on GFI. In contrast, NDVI was less significant for GTI but more significant for GFI. The explanatory powers of slope and aspect are both the lowest for GTI and GFI, thus indicating that the spatial variation of the freezing–thawing index of QTEC has little relationship with the slope and aspect.
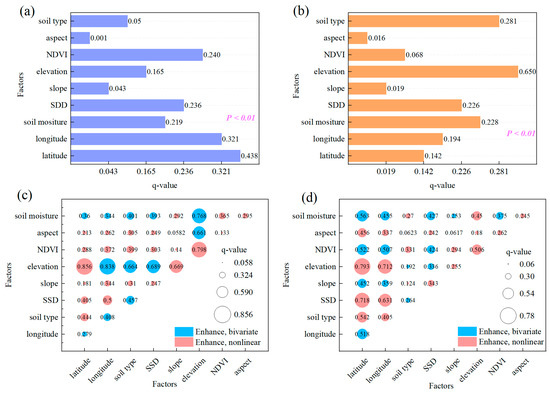
Figure 6.
Results of factor detector and interaction detector of GeoDetector in the QTEC: (a,c) factor detector results and interaction detector results for GFI, respectively; (b,d) factor detector results and interaction detector results for GTI, respectively.
The interaction of any two factors can improve their consistency with the spatial variation of GFI and GTI. The factor interaction module of the GeoDetector has a strong ability to detect spatial heterogeneity and can detect the effect of the interaction of two factors on the freezing–thawing index. As seen in Figure 6c,d, the interaction between any two influencing factors will lead to the improvement of the GFI and GTI. The interaction of factors contains two types. One type is the nonlinearly enhanced interaction, meaning that the q-value of the interaction is greater than the sum of the individual factors, indicating that their mutual enhancement is nonlinear. The other type is a bivariate enhancement interaction with a higher q-value than the q-value of the two univariate factors, but lower than their sum. The outcome of the factor interactions demonstrated that the two-factor nonlinear enhancement of elevation and latitude had the greatest explanatory power for GFI and GTI of 79.3% and 85.6%, respectively. This indicates that the annual heat accumulation in the shallow soil layer on QTEC is mainly a superposition of elevation and latitude. Compared with the other factors, the superposition of elevation and any factor explained more than 66% of the spatial distribution of the GTI (q > 0.66), containing nonlinear enhancement interaction and bivariate enhancement interaction (Figure 6c). Figure 6d confirmed the poor explanatory power of most of the factor interactions for the GFI. The interactions between elevation and latitude, elevation and longitude, SDD and latitude, and SDD and longitude are the four strongest explanatory powers for the freezing index (q > 0.6), which are nonlinear enhancement interactions. These results further illustrate that, in the single-factor analysis, elevation is the main factor affecting the spatial distribution of GTI, while the pattern of GFI is that multiple factors have a common level of influence.
3.4. Multi-Factors Quantitative Analysis of the GFI and GTI in the QTEC
To further investigate the quantitative relationship between environmental factors and the freezing–thawing indices of the ground surface, six factors with the strongest explanatory power (q > 0.1) for the spatial variation of GFI and GTI were selected in this study, respectively. The six factors are latitude, longitude, NDVI, SSD, soil moisture, elevation for GFI, and latitude, longitude, SSD, soil moisture, elevation, soil type for GTI. Since the soil type is a categorical variable containing data for ten different soils, the numbers 1~10 were assigned to the soil types. Multiple linear regression models were established for all pixel elements of QTEC. The explanatory power of the equation after the multi-factor regression was able to reach 88.8% of the variability of the GTI (Table 3), and the coefficients of each factor passed the significance test (p < 0.01). The values of the coefficients were all negative, indicating that there is a negative correlation between the GTI and the six factors.

Table 3.
Parameters of the multiple linear regression model constructed by GTI and explanatory variables.
The adjusted R2 of the regression model established by GFI and its influence factors is 0.797, indicating that this regression equation can explain almost 80% of the variation in GFI (Table 4). The longitude and NDVI showed a negative relationship with GFI, while all other factors were positively correlated with GFI.

Table 4.
Parameters of the multiple linear regression model constructed by GFI and explanatory variables.
To verify the applicability of the multiple linear regression equation, the multi-year average freezing–thawing indices of shallow soil (5 or 10 cm) from 25 field-monitored sites were used to compare the model results. Figure 7 shows the application of the multiple linear regression model to the 25 monitoring sites. It is clear that the GFI and GTI calculated by the regression equation and the measured values are consistent with each other in terms of trend. The predicted GFIs are generally smaller than the monitored values, while the predicted GTIs are larger than the monitored values. The equation-predicted GFI and GTI are correlated with the monitored values. The mean absolute error of the GTI is 236.09 °C·d, which is smaller than that of the GFI (327.19 °C·d), implying that the regression equation model has a higher accuracy in predicting GTI than GFI. The errors may only account for about 10%–20% of the freezing–thawing index of the site, which is also within a reasonable range.
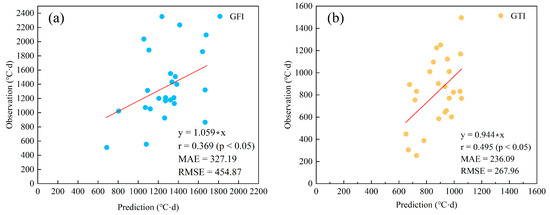
Figure 7.
Accuracy validation of multiple linear regression model at 25 field measurement sites: (a) GFI and (b) GTI. The Pearson correlation coefficient (r) was used to evaluate the correlation between the variables.
4. Discussion
4.1. Differences in the Thermal Condition of the Ground Surface and Land Surface
The relationships between the atmosphere, land surface, and ground surface are highly correlated and inextricably linked due to the intense interactions that occur between them in the presence of solar radiation. Studies have proved that there is a strong correlation between Ta and LST, and their correlation coefficient can even approach 1 [56]. Although Ta and LST are generally consistent, they have large and erratic errors with GST. Because of the insulating effects of the vegetation and snow, the daily GST and Ta are likely to be quite different [57]. Luo et al. studied the soil thermal conditions in the source areas of the Yangtze and Yellow rivers (SAYYR) on the QTP, showed that there was a good linear relationship between Ta with GST, and worked out a linear equation (GST = 0.72 × Ta + 1.63, R2 = 0.8477) [22]. This study verified the correlation between LST and GST at the Beiluhe weather station on the QTEC as GST = 0.924 × LST − 2.527, R2 = 0.897. Comparing the coefficients of the equations, the consistency between GST and LST is higher than that between Ta and GST, and the explanatory power of LST to GST is stronger.
GST is an indicator variable for the thermal condition of the upper boundary on permafrost, and the GFI and GTI calculated from it were widely used to indicate the occurrence of permafrost [14,58]. Figure 2 showed that, when the difference between the daily GST and LST reached 2.6 °C, the gap of their average GFI and GTI was 430 °C·d and 533 °C·d, respectively. Figure 8 shows the average freezing index and thawing index for 2020 and 2021 in the Beiluhe weather station. The values of LFI (or LTI) and GFI (or GTI) are closer than the AFI (or ATI). The difference between LFI and GFI is not significant due to the distribution of gravel and sparse vegetation on the soil surface in this station. Since Ta has the advantage of easy accessibility, Ta was corrected to the GST by the N-factors in permafrost mapping. In previous works on the N-factors, different values were available for different subsurface types [59,60]. Monitoring data in Northern Europe showed that the multi-year mean Nt and Nf were 1.6 and 0.6, respectively [12,61]. In this study, the N-factors were defined as the ratio between GST and LST, and the average Nt and Nf of the whole QTEC region were calculated as 0.554 and 1.088, respectively. Current research has focused on the N-factors between atmosphere and ground surface to obtain the regional GFI and GTI. There is a regional limitation of N-factors in this study. Due to the differences in surface conditions and scales, the N-factors are varied in different regions. Under natural ground conditions, vegetation and snow conditions can play a decisive role in the N-factors. The snow and vegetation covers are the two most important local factors influencing the difference between GST and the N-factors [19]. Relationships between N-factors and maximum snow depth were established in Southern Norway [62]. In most areas of the Qinghai–Tibet Plateau, continuous and stable snow cover cannot be formed. The thermal insulation function of snow cover causes the difference of N-factors between different areas. In the SAYYR of QTP, the Nt under dense vegetation is lower than 1, while it is higher than 1 at sites with sparse vegetation, and the Nf values are less than 1 at all sites [22]. In unnatural ground conditions, different constructions materials and different combinations can also lead to changes in surface heat fluxes [63,64]. This can complicate the local N-factors. The N-factors in this study work well throughout the large area of QTEC but have as yet unknown variability in localized areas and other permafrost zones. With the wide application of remote-sensing LST products, the N-factors between GST and LST are more conducive to obtaining accurate and high-resolution thermal status of soil upper boundary. The investigation of N-factors in the QTEC will help to improve the simulation accuracy of permafrost and soil thermal conditions.
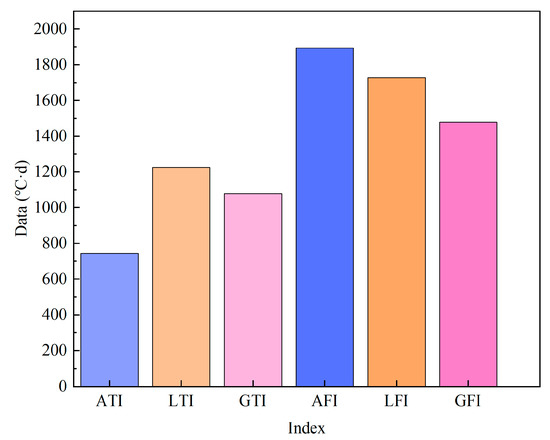
Figure 8.
Three types of freezing indexes and thawing indexes in the Beiluhe weather station from 2020 to 2022.
4.2. Analysis of Driving Factors Affecting Spatial Distribution of GFI and GTI in the QTEC
The essence of the distribution characteristics of GFI and GTI in the QETC is the variation of GST. The nine environmental factors that may affect the GST were selected to explore the heterogeneity of the spatial distribution of the GFI and GTI through GeoDetector. The results of the GeoDetector model indicate that elevation explains the variation in the distribution of the GTI better than other factors (q = 0.650). The difference is that latitude (q = 0.438) has the greatest explanatory power for the GFI, while elevation can only explain less changes in the GFI (q = 0.165). This is probably because the Qinghai–Tibet engineering facilities are mainly constructed in the relatively flat hinterland of the QTP, and elevation changes are not significant in most areas. In summer, the Ta contributes more heat to the GST variation due to the direct contact of the earth and atmosphere. The temperature differences generated by altitude create a high consistency in the spatial distribution of elevation and GTI. Conversely, erratic snow cover and violent winds in winter significantly weaken the effect of elevation on GST [16]. Overall, the snow cover is rare, thin (<3 cm), and has a short duration due to the strong solar radiation and wind in the vast interior and the Northern TP [65,66]. Latitude is an indicator of solar radiation intensity, which is the main explanation factor of GFI because it highlights the importance of radiation to GST in the cold season. The interaction detection from the two factors demonstrated that the GFI and GTI in the whole QTEC were mainly influenced by the interaction of elevation and latitude (q = 0.856 in GTI and q = 0.793 in GFI, respectively).
Multiple linear regression models between GFI (or GTI) and environmental factors were able to quantify the effects of explanatory variables on the GFI and GTI. The data from 25 monitoring sites showed a high correlation between predicted and observed values after calculation by the model. The slope of the trend line is closer to 1 than the correlation between land surface and ground surface shown in Figure 2. This indicates that the model basically satisfies the real thermal conditions of the ground surface. The mean absolute error (MAE) and root mean square error (RMSE) can reflect the deviation of the predicted GFI (or GTI) from the measured GFI (or GTI). If LFI and LTI are used directly instead of GFI and GTI without considering the difference between LST and GST, it will cause a large error especially for GTI (Table 5). The difference in thermal conditions between ground surface and land surface is inextricably linked to local environmental factors, and the model built by GFI (or GTI) and environmental factors can obviously reduce the simulation errors. These errors still exist because the monitoring sites are often not representative of the environmental conditions within 1 km of their location. More accurate GFI and GTI can be obtained by reducing the scale of pixels. The GFI and GTI obtained by remote sensing may cause some simulation errors if used directly as the upper boundary conditions of the heat-transfer model. The errors can be decreased after being corrected by using the N-factors and multiple linear regression models.

Table 5.
Errors of multiple linear regression models.
5. Conclusions
From this study, the following conclusions can be drawn:
- The freezing and thawing index can amplify the bias of thermal conditions between the ground and land surface. Although there is a high correlation between LST and GST, the error between LFI and GFI reaches 430 °C·d, and the difference between LTI and GTI is 533 °C·d. This will lead to errors in permafrost mapping. The Nf factor and Nt factor between GFI and LFI in the QTEC are approximately 1.088 (r = 0.36, p < 0.05) and 0.554 (r = 0.46, p < 0.05), respectively.
- The explanatory variables for the high consistency (q > 0.1) of the geographical distribution of the GFI and the GTI are different. The strongest explanatory power for the GFI is latitude (q = 0.438), followed by longitude, NDVI, snow duration days, soil moisture, and elevation. Elevation explains 65% of the spatial variation in GTI, followed by soil type, soil moisture, snow duration days, longitude, and latitude. Factor interaction detection indicates that the explanatory power of any two factors on the GFI and GTI is enhanced. The interaction of elevation and latitude have the highest explanatory power for both the GFI and GTI, with q-values of 0.793 and 0.856, respectively.
- Finally, the multiple linear regression equation established for the GFI (or GTI) and environmental factors performed well at the measured sites. The error of this equation is smaller than the error between the LFI (or LTI) and the GFI (or GTI). The N-factors method can greatly improve the accuracy of the ground surface freezing and thawing index.
Author Contributions
Conceptualization, S.M. and J.C.; methodology, J.Z.; software, Q.M.; validation, S.Z., T.D. and G.L.; formal analysis, X.H.; investigation, Q.M. and J.C.; resources, J.C., S.Z. and T.D.; data curation, G.L.; writing—original draft preparation, S.M.; writing—review and editing, J.Z. and J.C.; funding acquisition, J.C. and J.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Key Research and Development Program of China (2022YFF1302600), the State Key Laboratory of Frozen Soil Engineering Foundation (SKLFSE-ZY-19), and the State Key Laboratory of Frozen Soil Engineering Foundation (SKLFSE-ZQ-55).
Data Availability Statement
Not applicable.
Acknowledgments
The dataset of land surface temperature, soil moisture, and snow duration days was provided by the National Tibetan Plateau Data Center (http://data.tpdc.ac.cn (accessed on 10 November 2022)). The dataset of NDVI was provided by the Resources and Environmental Science Data Center of the Chinese Academy of Sciences (http://www.resdc.cn (accessed on 10 November 2022)). The dataset of SRTM DEM 90 m was provided by the Geospatial Data Cloud (http://www.gscloud.cn (accessed on 10 November 2022)). The authors thank Yan Zhang for his help with Figure 6.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Zhou, X.; Wang, F.; Fan, J.; Ochieng, R.M. Performance of solar chimney power plant in Qinghai-Tibet Plateau. Renew. Sustain. Energy Rev. 2010, 14, 2249–2255. [Google Scholar] [CrossRef]
- Çalışkan, O. Multi-Language Glossary of Permafrost and Related Ground-Ice Terms; National Snow and Ice Data Center: Boulder, CO, USA, 2017. [Google Scholar]
- Yao, T.; Guo, X.; Thompson, L.; Duan, K.; Wang, N.; Pu, J.; Xu, B.; Yang, X.; Sun, W. δ 18O record and temperature change over the past 100 years in ice cores on the Tibetan Plateau. Sci. China Ser. D 2006, 49, 1–9. [Google Scholar] [CrossRef]
- Yao, T.; Thompson, L.G.; Jiao, K.; Mosley-Thompson, E.; Yang, Z. Recent warming as recorded in the Qinghai-Tibetan cryosphere. Ann. Glaciol. 2017, 21, 196–200. [Google Scholar] [CrossRef]
- Li, R.; Zhao, L.; Ding, Y.; Wu, T.; Xiao, Y.; Du, E.; Liu, G.; Qiao, Y. Temporal and spatial variations of the active layer along the Qinghai-Tibet Highway in a permafrost region. Chin. Sci. Bull. 2012, 57, 4609–4616. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T. Recent permafrost warming on the Qinghai-Tibetan Plateau. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Wu, T.; Zhao, L.; Li, R.; Wang, Q.; Xie, C.; Pang, Q. Recent ground surface warming and its effects on permafrost on the central Qinghai-Tibet Plateau. Int. J. Climatol. 2013, 33, 920–930. [Google Scholar] [CrossRef]
- Cheng, G.; Wu, T. Responses of permafrost to climate change and their environmental significance, Qinghai-Tibet Plateau. J. Geophys. Res. 2007, 112. [Google Scholar] [CrossRef]
- Niu, F.; Luo, J.; Lin, Z.; Ma, W.; Lu, J. Development and thermal regime of a thaw slump in the Qinghai–Tibet plateau. Cold Reg. Sci. Technol. 2012, 83–84, 131–138. [Google Scholar] [CrossRef]
- Niu, F.; Yin, G.; Luo, J.; Lin, Z.; Liu, M. Permafrost Distribution along the Qinghai-Tibet Engineering Corridor, China Using High-Resolution Statistical Mapping and Modeling Integrated with Remote Sensing and GIS. Remote Sens. 2018, 10, 215. [Google Scholar] [CrossRef]
- Ran, Y.; Li, X.; Jin, R.; Guo, J. Remote Sensing of the Mean Annual Surface Temperature and Surface Frost Number for Mapping Permafrost in China. Arct. Antarct. Alp. Res. 2015, 47, 255–265. [Google Scholar] [CrossRef]
- Gisnås, K.; Etzelmüller, B.; Lussana, C.; Hjort, J.; Sannel, A.B.K.; Isaksen, K.; Westermann, S.; Kuhry, P.; Christiansen, H.H.; Frampton, A.; et al. Permafrost Map for Norway, Sweden and Finland. Permafr. Periglac. Process. 2017, 28, 359–378. [Google Scholar] [CrossRef]
- Juliussen, H.; Humlum, O. Towards a TTOP ground temperature model for mountainous terrain in central-eastern Norway. Permafr. Periglac. Process. 2007, 18, 161–184. [Google Scholar] [CrossRef]
- Obu, J.; Westermann, S.; Bartsch, A.; Berdnikov, N.; Christiansen, H.H.; Dashtseren, A.; Delaloye, R.; Elberling, B.; Etzelmüller, B.; Kholodov, A.; et al. Northern Hemisphere permafrost map based on TTOP modelling for 2000–2016 at 1 km2 scale. Earth-Sci. Rev. 2019, 193, 299–316. [Google Scholar] [CrossRef]
- Duchesne, C. Regional-Scale Permafrost Mapping Using the TTOP Ground Temperature Model. 2003. Available online: https://www.arlis.org/docs/vol1/ICOP/55700698/Pdf/Chapter_218.pdf (accessed on 25 April 2022).
- Zou, D.; Zhao, L.; Sheng, Y.; Chen, J.; Hu, G.; Wu, T.; Wu, J.; Xie, C.; Wu, X.; Pang, Q.; et al. A new map of permafrost distribution on the Tibetan Plateau. Cryosphere 2017, 11, 2527–2542. [Google Scholar] [CrossRef]
- Zhang, T. Spatial and temporal variability in active layer thickness over the Russian Arctic drainage basin. J. Geophys. Res. 2005, 110. [Google Scholar] [CrossRef]
- Riseborough, D.; Shiklomanov, N.; Etzelmüller, B.; Gruber, S.; Marchenko, S. Recent advances in permafrost modelling. Permafr. Periglac. Process. 2008, 19, 137–156. [Google Scholar] [CrossRef]
- Luo, D.; Liu, L.; Jin, H.; Wang, X.; Chen, F. Characteristics of ground surface temperature at Chalaping in the Source Area of the Yellow River, northeastern Tibetan Plateau. Agric. For. Meteorol. 2019, 281, 107819. [Google Scholar] [CrossRef]
- Peng, X.; Zhang, T.; Frauenfeld, O.W.; Du, R.; Wei, Q.; Liang, B. Soil freeze depth variability across Eurasia during 1850–2100. Clim. Chang. 2019, 158, 531–549. [Google Scholar] [CrossRef]
- Klene, A.E.; Nelson, F.E.; Shiklomanov, N.I.; Hinkel, K.M. The N-factor in Natural Landscapes: Variability of Air and Soil-Surface Temperatures, Kuparuk River Basin, Alaska, U.S.A. Arct. Antarct. Alp. Res. 2001, 33, 140–148. [Google Scholar] [CrossRef]
- Luo, D.; Jin, H.; Wu, Q.; Bense, V.F.; He, R.; Ma, Q.; Gao, S.; Jin, X.; Lu, L. Thermal regime of warm-dry permafrost in relation to ground surface temperature in the Source Areas of the Yangtze and Yellow rivers on the Qinghai-Tibet Plateau, SW China. Sci. Total Environ. 2018, 618, 1033–1045. [Google Scholar] [CrossRef]
- Hachem, S.; Allard, M.; Duguay, C. Using the MODIS land surface temperature product for mapping permafrost: An application to northern Québec and Labrador, Canada. Permafr. Periglac. Process. 2009, 20, 407–416. [Google Scholar] [CrossRef]
- Li, A.; Xia, C.; Bao, C.; Yin, G. Using MODIS Land Surface Temperatures for Permafrost Thermal Modeling in Beiluhe Basin on the Qinghai-Tibet Plateau. Sensors 2019, 19, 4200. [Google Scholar] [CrossRef] [PubMed]
- Ou, C.; LaRocque, A.; Leblon, B.; Zhang, Y.; Webster, K.; McLaughlin, J. Modelling and mapping permafrost at high spatial resolution using Landsat and Radarsat-2 images in Northern Ontario, Canada: Part 2—Regional mapping. Int. J. Remote Sens. 2016, 37, 2751–2779. [Google Scholar] [CrossRef]
- Bense, V.F.; Read, T.; Verhoef, A. Using distributed temperature sensing to monitor field scale dynamics of ground surface temperature and related substrate heat flux. Agric. For. Meteorol. 2016, 220, 207–215. [Google Scholar] [CrossRef]
- Liu, T. A summarization of formulas of calculating frozen or melted depth abroad (in Chinese). J. Glaciol. Geocryol. 1983, 5, 85–95. [Google Scholar]
- Luo, D.; Jin, H.; Marchenko, S.S.; Romanovsky, V.E. Difference between near-surface air, land surface and ground surface temperatures and their influences on the frozen ground on the Qinghai-Tibet Plateau. Geoderma 2018, 312, 74–85. [Google Scholar] [CrossRef]
- Anselin, L. Thirty years of spatial econometrics. Pap. Reg. Sci. 2010, 89, 3–25. [Google Scholar] [CrossRef]
- Fischer, M.; Wang, J. Spatial Data Analysis: Models, Methods and Techniques; Springer Science & Business Media: Cham, Switzerland, 2011. [Google Scholar]
- Wang, J.-F.; Zhang, T.-L.; Fu, B.-J. A measure of spatial stratified heterogeneity. Ecol. Indic. 2016, 67, 250–256. [Google Scholar] [CrossRef]
- Wang, W.; Samat, A.; Abuduwaili, J.; Ge, Y. Quantifying the influences of land surface parameters on LST variations based on GeoDetector model in Syr Darya Basin, Central Asia. J. Arid. Environ. 2021, 186, 104415. [Google Scholar] [CrossRef]
- Xu, L.; Du, H.; Zhang, X. Driving forces of carbon dioxide emissions in China’s cities: An empirical analysis based on the geodetector method. J. Clean. Prod. 2021, 287, 125169. [Google Scholar] [CrossRef]
- Yang, Y.; Yang, X.; He, M.; Christakos, G. Beyond mere pollution source identification: Determination of land covers emitting soil heavy metals by combining PCA/APCS, GeoDetector and GIS analysis. Catena 2020, 185, 104297. [Google Scholar] [CrossRef]
- Zhao, R.; Zhan, L.; Yao, M.; Yang, L. A geographically weighted regression model augmented by Geodetector analysis and principal component analysis for the spatial distribution of PM2.5. Sustain. Cities Soc. 2020, 56, 102106. [Google Scholar] [CrossRef]
- Jin, H.-j.; Yu, Q.-h.; Wang, S.-l.; Lü, L.-z. Changes in permafrost environments along the Qinghai–Tibet engineering corridor induced by anthropogenic activities and climate warming. Cold Reg. Sci. Technol. 2008, 53, 317–333. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, T.; Liu, Y. Thermal state of the active layer and permafrost along the Qinghai-Xizang (Tibet) Railway from 2006 to 2010. Cryosphere 2012, 6, 607–612. [Google Scholar] [CrossRef]
- Song, Y.; Jin, L.; Wang, H. Vegetation Changes along the Qinghai-Tibet Plateau Engineering Corridor Since 2000 Induced by Climate Change and Human Activities. Remote Sens. 2018, 10, 95. [Google Scholar] [CrossRef]
- Ji, Z.; Xiaodong, Z.; Wenbin, T.; Lirong, D.; Jin, M.; Xu, Z. Daily 1-km All-Weather Land Surface Temperature Dataset for Western China (TRIMS LST-TP; 2000–2021) V2; National Tibetan Plateau Data Center: Beijing, China, 2019; Available online: https://data.tpdc.ac.cn/home (accessed on 25 April 2022).
- Zhang, X.; Zhou, J.; Göttsche, F.M.; Zhan, W.; Liu, S.; Cao, R. A Method Based on Temporal Component Decomposition for Estimating 1-km All-Weather Land Surface Temperature by Merging Satellite Thermal Infrared and Passive Microwave Observations. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4670–4691. [Google Scholar] [CrossRef]
- Zhang, X.; Zhou, J.; Liang, S.; Wang, D. A practical reanalysis data and thermal infrared remote sensing data merging (RTM) method for reconstruction of a 1-km all-weather land surface temperature. Remote Sens. Environ. 2021, 260, 112437. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, X.; Zhan, W.; Gottsche, F.-M.; Liu, S.; Olesen, F.-S.; Hu, W.; Dai, F. A Thermal Sampling Depth Correction Method for Land Surface Temperature Estimation From Satellite Passive Microwave Observation Over Barren Land. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4743–4756. [Google Scholar] [CrossRef]
- Hu, Z.; Chai, L.; Crow, W.T.; Liu, S.; Zhu, Z.; Zhou, J.; Qu, Y.; Liu, J.; Yang, S.; Lu, Z. Applying a Wavelet Transform Technique to Optimize General Fitting Models for SM Analysis: A Case Study in Downscaling over the Qinghai–Tibet Plateau. Remote Sens. 2022, 14, 3063. [Google Scholar] [CrossRef]
- Qu, Y.; Zhu, Z.; Montzka, C.; Chai, L.; Liu, S.; Ge, Y.; Liu, J.; Lu, Z.; He, X.; Zheng, J.; et al. Inter-comparison of several soil moisture downscaling methods over the Qinghai-Tibet Plateau, China. J. Hydrol. 2021, 592, 125616. [Google Scholar] [CrossRef]
- Linna, C.; Zhongli, Z.; Shaomin, L. Daily 0.01° × 0.01° Land Surface Soil Moisture Dataset of the Qinghai-Tibet Plateau (2005, 2010, 2015, 2017a nd 2018) (SMHiRes, V1). 2020. Available online: https://data.tpdc.ac.cn/home (accessed on 25 April 2022).
- Xu, X. Spatial Distribution Dataset of Annual Normalized Difference Vegetation Index (NDVI) in China; 2018. Available online: https://www.resdc.cn/ (accessed on 1 April 2022).
- Nachtergaele, F.O.; Velthuizen, H.V.; Wiberg, D.; Batjes, N.H.; Dijkshoorn, J.A.; Engelen, V.W.P.v.; Fischer, G.; Jones, A.; Montanarela, L.; Petri, M.; et al. Harmonized World Soil Database (HWSD). 2014. Available online: https://www.fao.org/soils-portal/data-hub/soil-maps-and-databases/harmonized-world-soil-database-v12/en/ (accessed on 1 April 2022).
- Tang, Z.; Deng, G.; Hu, G.; Zhang, H.; Pan, H.; Sang, G. Satellite observed spatiotemporal variability of snow cover and snow phenology over high mountain Asia from 2002 to 2021. J. Hydrol. 2022, 613, 128438. [Google Scholar] [CrossRef]
- Tang, Z.; Deng, G. Daily Cloud-Free MODIS NDSI and Snow Phenology Dataset over High Mountain Asia (2000–2021); 2022. Available online: https://data.tpdc.ac.cn/en/data/70e403c0-0378-4034-9e7a-3b53b5a52126/ (accessed on 1 April 2022).
- Cheng, G.; Zhao, L.; Li, R. Characteristic, changes and impacts of permafrost on Qinghai-Tibet Plateau (In Chinese). Chin. Sci. Bull. 2019, 64, 2783–2795. [Google Scholar]
- Zhao, L.; Zou, D.; Hu, G.; Du, E.; Pang, Q.; Xiao, Y.; Li, R.; Sheng, Y.; Wu, X.; Sun, Z.; et al. Changing climate and the permafrost environment on the Qinghai–Tibet (Xizang) plateau. Permafr. Periglac. Process. 2020, 31, 396–405. [Google Scholar] [CrossRef]
- Zhao, L.; Zou, D.; Hu, G.; Wu, T.; Du, E.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A synthesis dataset of permafrost thermal state for the Qinghai–Tibet (Xizang) Plateau, China. Earth Syst. Sci. Data 2021, 13, 4207–4218. [Google Scholar] [CrossRef]
- Zhao, L.; Hu, G.; Zou, D.; Wu, T.; Du, E.; Liu, G.; Xiao, Y.; Li, R.; Pang, Q.; Qiao, Y.; et al. A synthesis Dataset of Permafrost for the Qinghai-Xizang (Tibet) Plateau, China (2002–2018); 2021. Available online: https://data.tpdc.ac.cn/en/data/789e838e-16ac-4539-bb7e-906217305a1d/ (accessed on 1 April 2022).
- Wang, J.F.; Li, X.H.; Christakos, G.; Liao, Y.L.; Zhang, T.; Gu, X.; Zheng, X.Y. Geographical Detectors-Based Health Risk Assessment and its Application in the Neural Tube Defects Study of the Heshun Region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Ma, S.; Yang, B.; Zhao, J.; Tan, C.; Chen, J.; Mei, Q.; Hou, X. Hydrothermal Dynamics of Seasonally Frozen Soil With Different Vegetation Coverage in the Tianshan Mountains. Front. Earth Sci. 2022, 9, 806309. [Google Scholar] [CrossRef]
- Hachem, S.; Duguay, C.R.; Allard, M. Comparison of MODIS-derived land surface temperatures with ground surface and air temperature measurements in continuous permafrost terrain. Cryosphere 2012, 6, 51–69. [Google Scholar] [CrossRef]
- Fisher, J.P.; Estop-Aragones, C.; Thierry, A.; Charman, D.J.; Wolfe, S.A.; Hartley, I.P.; Murton, J.B.; Williams, M.; Phoenix, G.K. The influence of vegetation and soil characteristics on active-layer thickness of permafrost soils in boreal forest. Glob. Chang. Biol. 2016, 22, 3127–3140. [Google Scholar] [CrossRef]
- Zorigt, M.; Myagmar, K.; Orkhonselenge, A.; van Beek, E.; Kwadijk, J.; Tsogtbayar, J.; Yamkhin, J.; Dechinlkhundev, D. Modeling permafrost distribution over the river basins of Mongolia using remote sensing and analytical approaches. Environ. Earth Sci. 2020, 79, 308. [Google Scholar] [CrossRef]
- Gisnås, K.; Etzelmüller, B.; Farbrot, H.; Schuler, T.V.; Westermann, S. CryoGRID 1.0: Permafrost Distribution in Norway estimated by a Spatial Numerical Model. Permafr. Periglac. Process. 2013, 24, 2–19. [Google Scholar] [CrossRef]
- Gisnås, K.; Westermann, S.; Schuler, T.V.; Litherland, T.; Isaksen, K.; Boike, J.; Etzelmüller, B. A statistical approach to represent small-scale variability of permafrost temperatures due to snow cover. Cryosphere 2014, 8, 2063–2074. [Google Scholar] [CrossRef]
- Sannel, A.B.K.; Hugelius, G.; Jansson, P.; Kuhry, P. Permafrost Warming in a Subarctic Peatland—Which Meteorological Controls are Most Important? Permafr. Periglac. Process. 2016, 27, 177–188. [Google Scholar] [CrossRef]
- Gisnås, K.; Westermann, S.; Schuler, T.V.; Melvold, K.; Etzelmüller, B. Small-scale variation of snow in a regional permafrost model. Cryosphere 2016, 10, 1201–1215. [Google Scholar] [CrossRef]
- Chen, L.; Lai, Y.; Fortier, D.; Harris, S.A. Impacts of snow cover on the pattern and velocity of air flow in air convection embankments of sub-Arctic regions. Renew. Energy 2022, 199, 1033–1046. [Google Scholar] [CrossRef]
- Chen, L.; Voss, C.I.; Fortier, D.; McKenzie, J.M. Surface energy balance of sub-Arctic roads with varying snow regimes and properties in permafrost regions. Permafr. Periglac. Process. 2021, 32, 681–701. [Google Scholar] [CrossRef]
- Che, T.; Li, X.; Jin, R.; Armstrong, R.; Zhang, T. Snow depth derived from passive microwave remote-sensing data in China. Ann. Glaciol. 2008, 49, 145–154. [Google Scholar] [CrossRef]
- Huang, X.; Deng, J.; Wang, W.; Feng, Q.; Liang, T. Impact of climate and elevation on snow cover using integrated remote sensing snow products in Tibetan Plateau. Remote Sens. Environ. 2017, 190, 274–288. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).