Improving Matching Efficiency and Out-of-domain Reliability of Underwater Gravity Matching Navigation Based on a Novel Soft-margin Local Semicircular-domain Re-searching Model
Abstract
:1. Introduction
2. Model Description
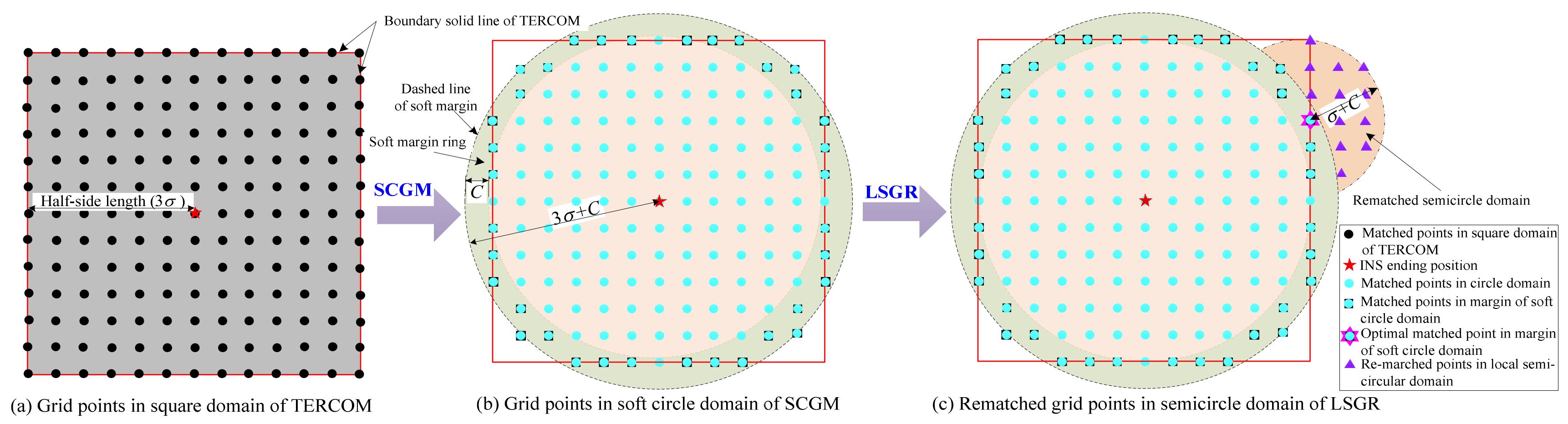
2.1. Matching Characteristic Analysis of the Canonical TERCOM Model
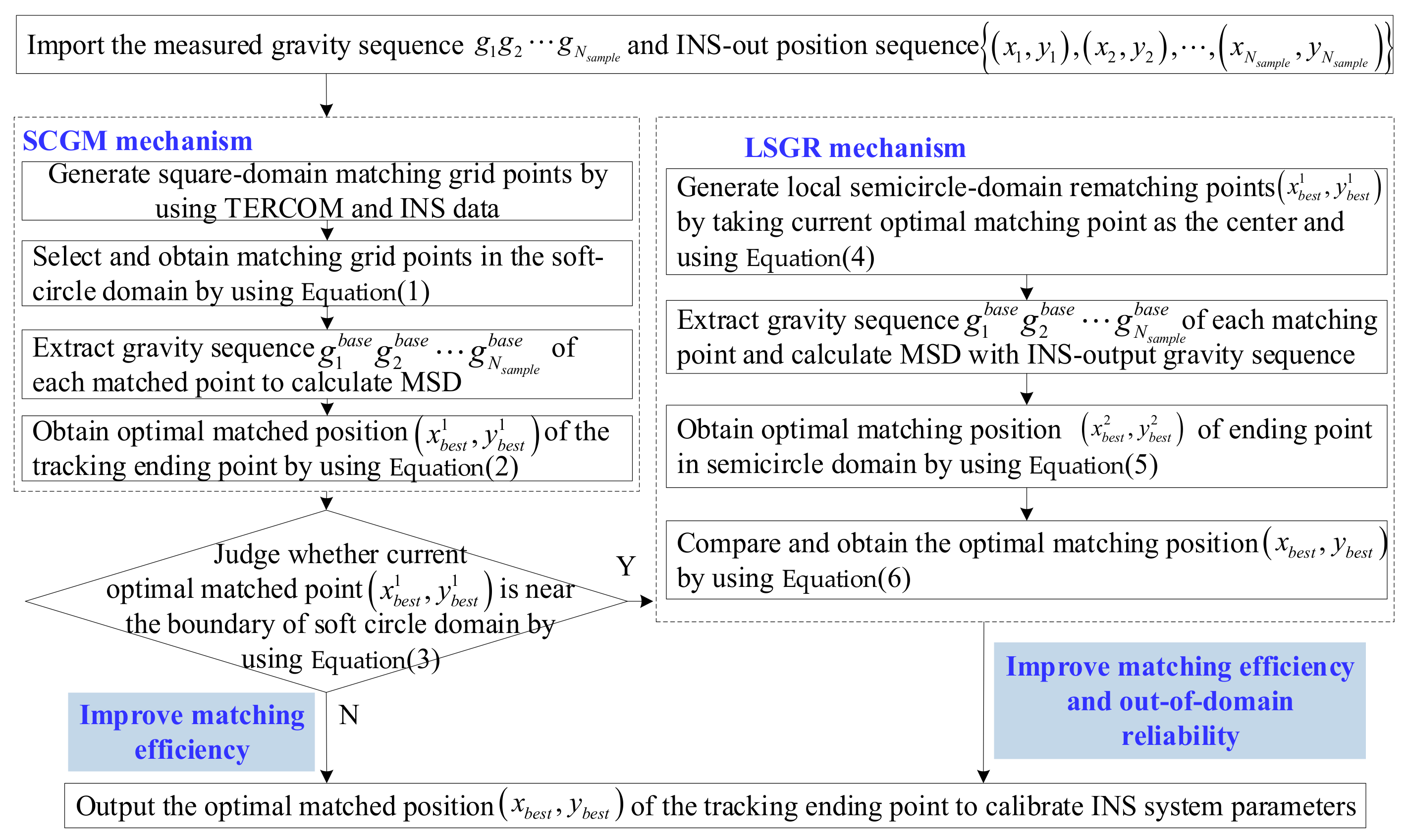
2.2. Soft-Margin Circular Grid Matching Mechanism (SCGM)
2.3. Local Semicircular Grid Re-Matching Mechanism (LSGR)
2.4. Implementation of the Proposed SLSR Model
3. Experimental Results and Discussions
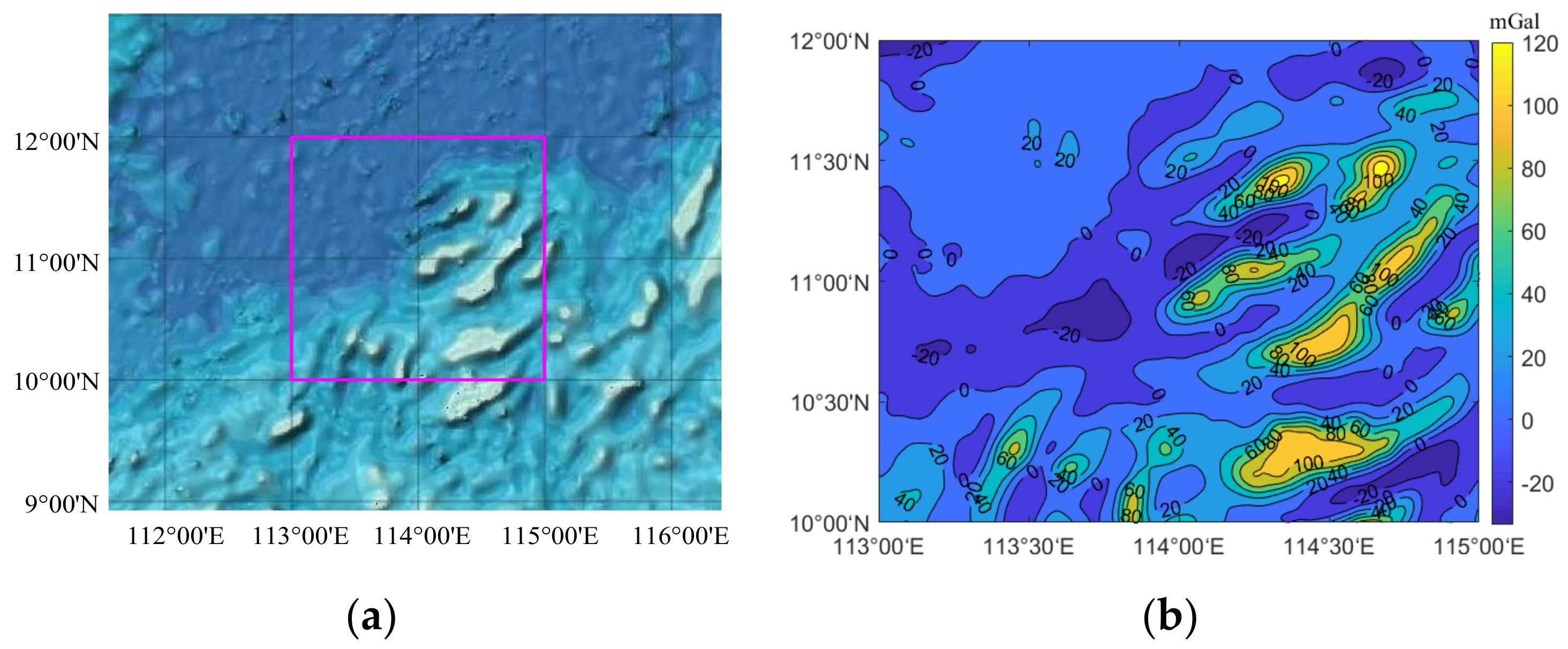
3.1. Data
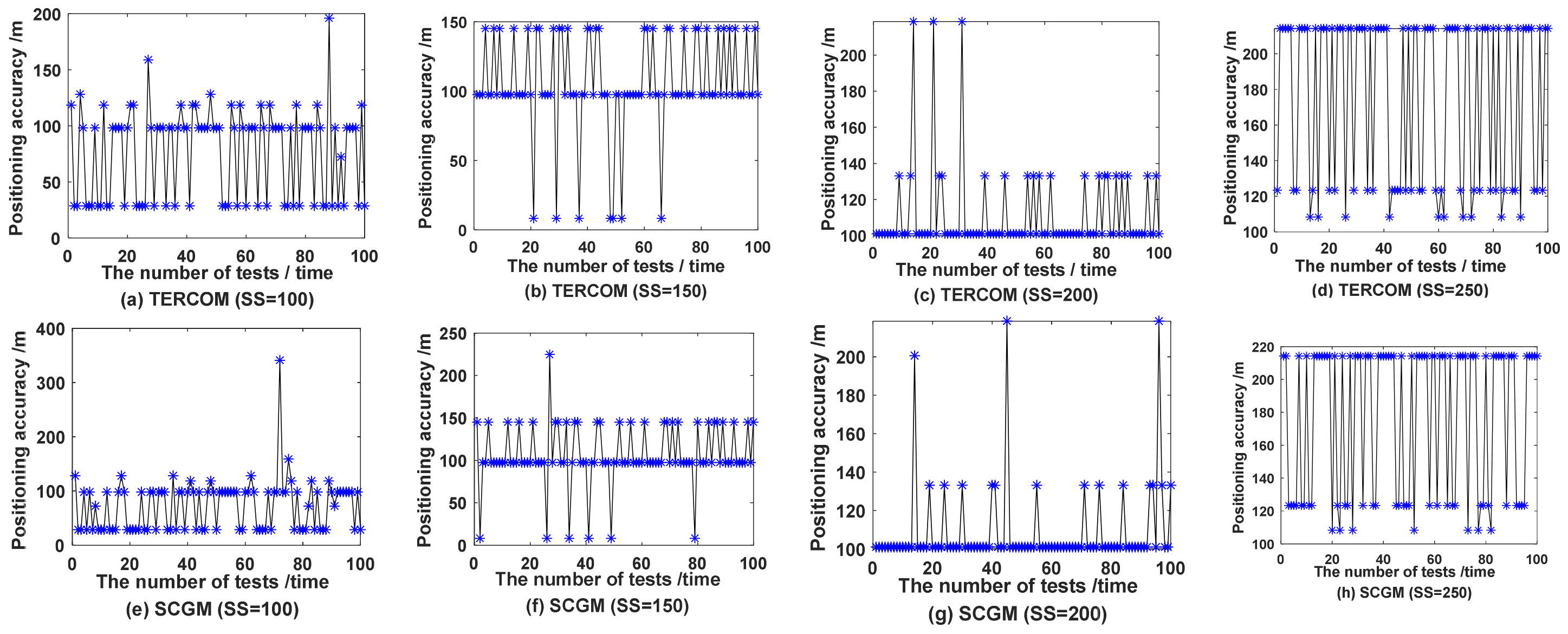
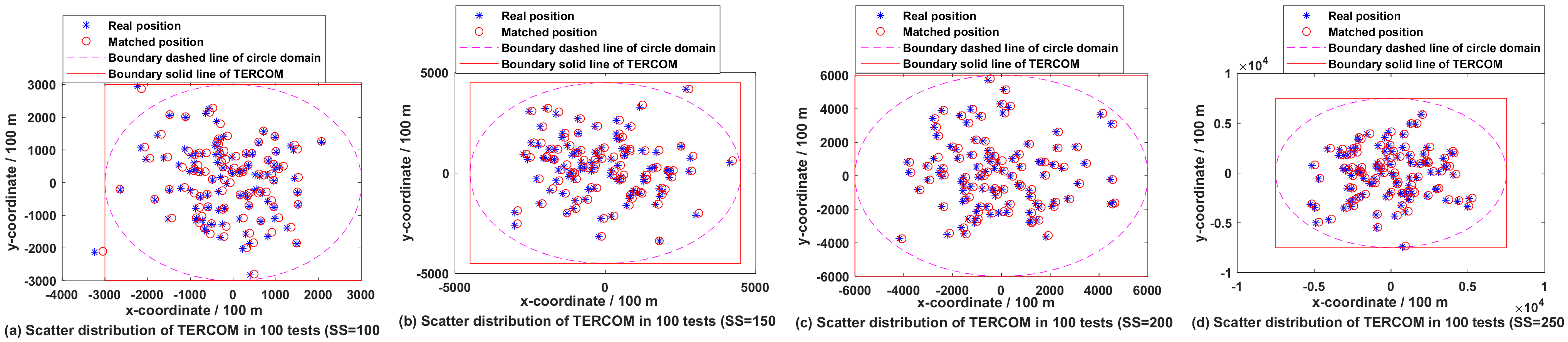
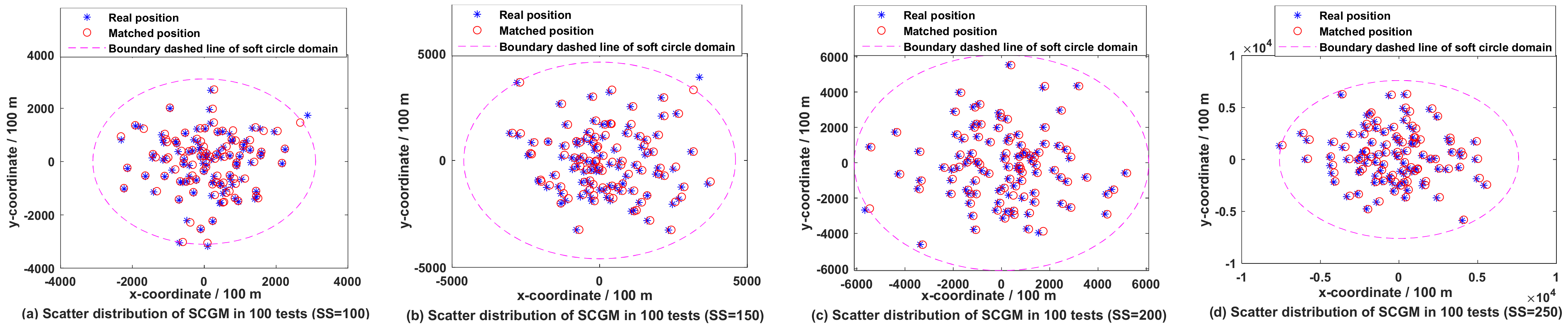
3.2. Analysis on Matching Efficiency of SLSR in Soft Circular Domain under Different Sampling Scales
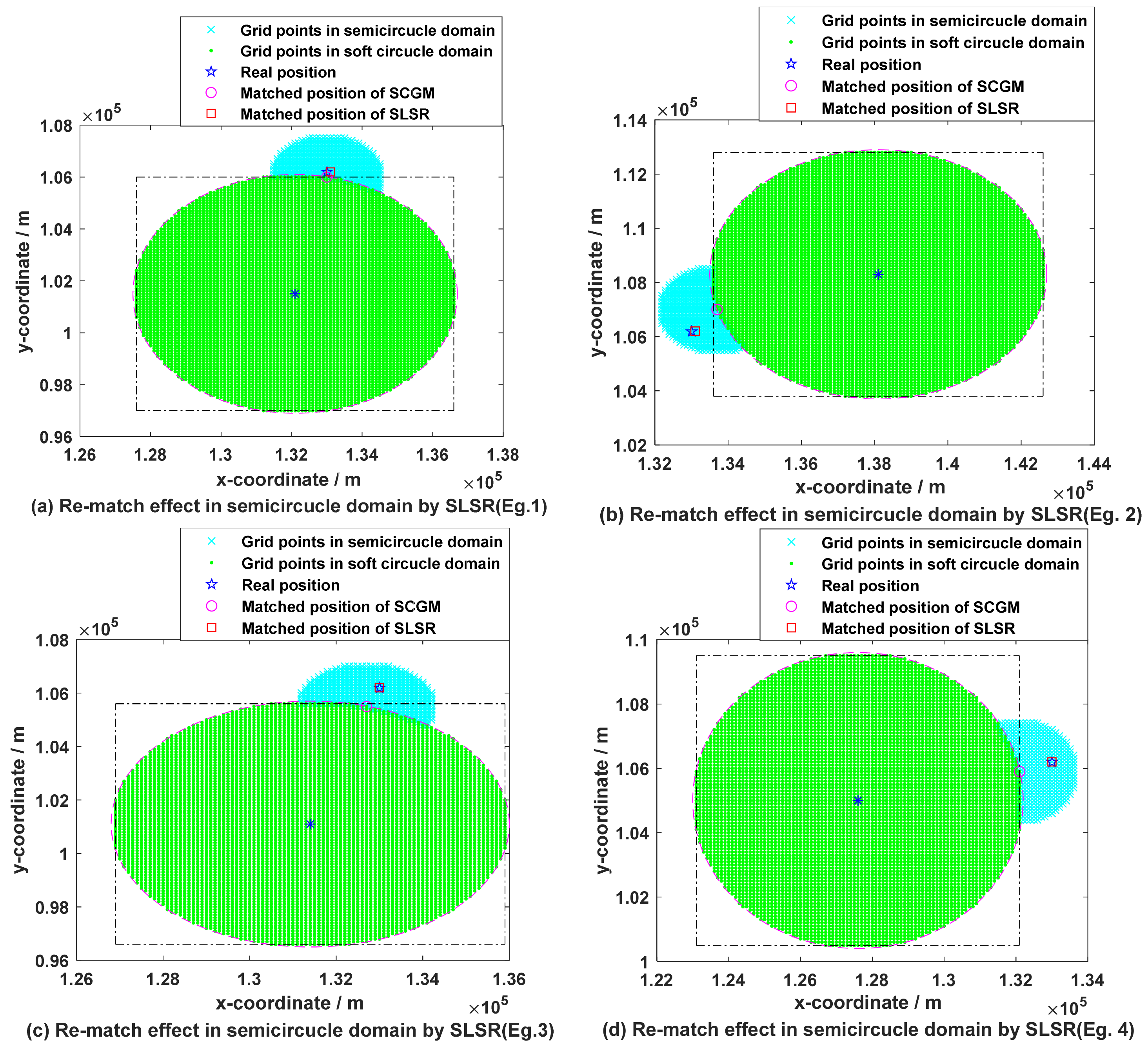
3.3. Analysis on the Out-of-Domain Matching Reliability of SLSR
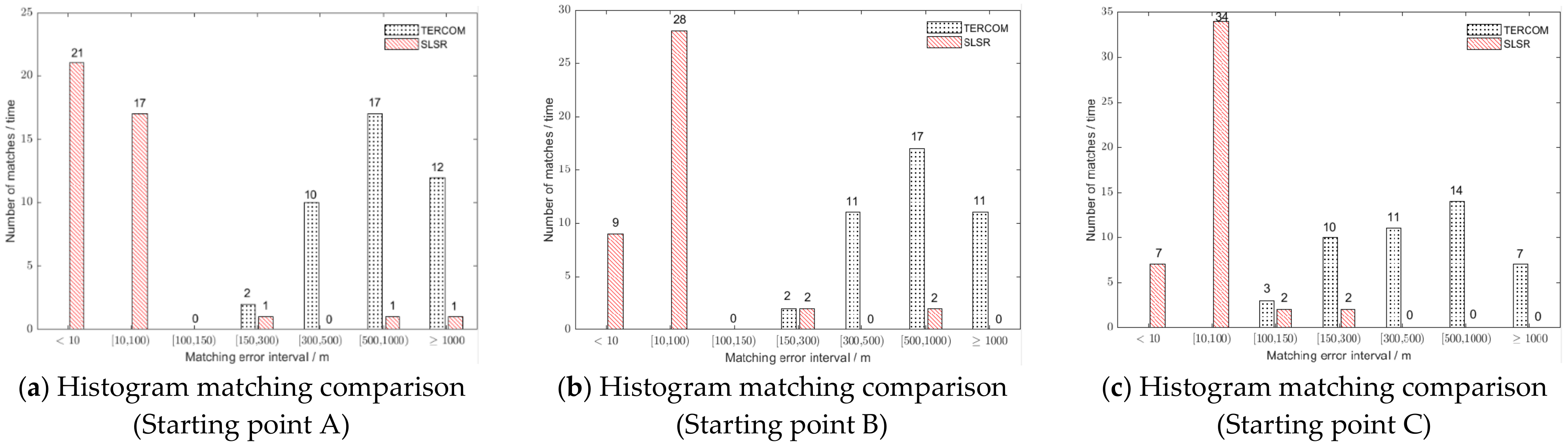
3.4. Analysis on Out-of-Domain Matching Efficiency and Reliability of SLSR under Different Tracking Starting Points
4. Conclusions
- (1)
- The establishment of a novel soft-margin local semicircular-domain re-searching method: Since the traditional TERCOM is inefficient in traversal search of fully matched points in the square grid domain, and it is difficult to locate the positions outside its square domain, the novel soft-margin local semicircular-domain re-searching method was proposed. The advantages of the proposed model are as follows: Based on the sum of the three-times INS cumulative error () and unit grid resolution as the boundary, the soft circular domain of matching grid points is constructed, and then these matching points in the soft circular domain are compared by following the optimal principle of matching index, so as to realize the high matching efficiency of the soft circular-domain grid matching mechanism for matching the optimal position. If the optimal matching position of the soft circular domain is located near its boundary, the semicircular domain of the local semicircular grid re-matching mechanism is generated around this optimal matching position and the re-matching comparison of these new matching points is performed, so as to improve the reliability of out-of-domain matching points.
- (2)
- The feasibility and effectiveness of the novel soft-margin local semicircular-domain re-searching model for improving the matching efficiency and out-of-domain reliability of underwater gravity navigation: The efficiency and out-of-domain reliability of underwater gravity matching navigation are closely related to the number of matched grid points and their coverage capacity for the out-of-domain real position of the underwater vehicle, respectively. To verify the effectiveness of the novel soft-margin local semicircular-domain re-searching model in improving the matching efficiency and out-of-domain matching reliability of underwater gravity navigation, the average matching time, the number of out-of-domain mismatches and the statistical results of matching accuracy were considered as the evaluation criteria for the performance of the matching algorithms. The re-matching experiments of different sampling scales and out-of-domain matching points were carried out to verify the high matching efficiency and good out-of-domain positioning reliability of the novel soft-margin local semicircular-domain re-searching model.
- (3)
- Verification of the improvement on the efficiency and out-of-domain matching reliability of underwater matching navigation: Under the same experimental conditions, the novel soft-margin local semicircular-domain re-searching model was tested by taking the parameter setting of this paper as an example. The test results show that the matching efficiency of the novel soft-margin local semicircular-domain re-searching model is 18% higher than that of the traditional TERCOM for three different tracking starting points. Compared with TERCOM, its number of out-of-domain mismatch points is decreased by 92.68%, 90.24% and 98.62%, respectively. Moreover, the average out-of-domain matching accuracy is increased to 91.79, 107.86 and 88.98 from 789.54, 742.61 and 544.66 of TERCOM; that is, the matching accuracy is improved by 88.37%, 85.48% and 83.66%, respectively. In summary, the novel soft-margin local semicircular-domain re-searching model can enhance the matching efficiency of underwater gravity matching navigation and effectively improve the positioning reliability of out-of-domain matched positions of underwater vehicles.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, S.; Zheng, W.; Li, Z.; Xu, A.; Zhu, H. Improving Matching Accuracy of Underwater Gravity Matching Navigation Based on Iterative Optimal Annulus Point Method with a Novel Grid Topology. Remote Sens. 2021, 13, 4616. [Google Scholar] [CrossRef]
- Huang, H.; Tang, J.; Liu, C.; Zhang, B.; Wang, B. Variational Bayesian-Based Filter for Inaccurate Input in Underwater Navigation. IEEE Trans. Veh. Technol. 2021, 70, 8441–8452. [Google Scholar] [CrossRef]
- Han, Y.; Wang, B.; Deng, Z.; Fu, M. A Matching Algorithm Based on the Nonlinear Filter and Similarity Transformation for Gravity-Aided Underwater Navigation. IEEE/ASME Trans. Mechatron. 2018, 23, 646–654. [Google Scholar] [CrossRef]
- Wang, B.; Zhu, J.; Ma, Z.; Deng, Z.; Fu, M. Improved Particle Filter-Based Matching Method with Gravity Sample Vector for Underwater Gravity-Aided Navigation. IEEE Trans. Ind. Electron. 2020, 68, 5206–5216. [Google Scholar] [CrossRef]
- Jeon, H.C.; Park, W.J.; Park, C.G. Grid Design for Efficient and Accurate Point Mass Filter-Based Terrain Referenced Navigation. IEEE Sens. J. 2017, 18, 1731–1738. [Google Scholar] [CrossRef]
- Lee, C.; Oh, J.; Hong, C.; Youn, J. Automated Generation of a Digital Elevation Model Over Steep Terrain in Antarctica From High-Resolution Satellite Imagery. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1186–1194. [Google Scholar] [CrossRef]
- Liu, H.; Wu, L.; Bao, L.; Li, Q.; Zhang, P.; Wang, Y. Gravity matching navigation algorithm based on multiscale search and Hadamard transformed difference. ISA Trans. 2021, in press. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Y.; Wang, M.; Wu, J.; Zhang, Y. A Computationally Efficient Outlier-Robust Cubature Kalman Filter for Underwater Gravity Matching Navigation. IEEE Trans. Instrum. Meas. 2022, 71, 8500418. [Google Scholar] [CrossRef]
- Park, J.; Park, Y.-G.; Park, C.G. Parameter Estimation of Radar Noise Model for Terrain Referenced Navigation Using a New EM Initialization Method. IEEE Trans. Aerosp. Electron. Syst. 2019, 56, 107–112. [Google Scholar] [CrossRef]
- Wang, B.; Yu, L.; Deng, Z.; Fu, M. A Particle Filter-Based Matching Algorithm with Gravity Sample Vector for Underwater Gravity Aided Navigation. IEEE/ASME Trans. Mechatron. 2016, 21, 1399–1408. [Google Scholar] [CrossRef]
- Golden, J.P. Terrain contour matching (TERCOM): A cruise missile guidance aid. In Image Processing for Missile Guidance; International Society for Optics and Photonics: Bellingham, WA, USA, 1980; Volume 238, pp. 10–18. [Google Scholar]
- Xiao, J.; Duan, X.; Qi, X.; Liu, Y. An Improved ICCP Matching Algorithm for use in an Interference Environment during Geomagnetic Navigation. J. Navig. 2020, 73, 56–74. [Google Scholar] [CrossRef]
- Wu, L.; Wang, H.; Chai, H.; Hsu, H.; Wang, Y. Research on the Relative Positions-Constrained Pattern Matching Method for Underwater Gravity-Aided Inertial Navigation. J. Navig. 2015, 68, 937–950. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Cheng, G.; Zhao, J. The study on the TERCOM mismatch diagnostic based on detecting the extreme value of similarity. In Proceedings of the 2011 Second International Conference on Mechanic Automation and Control Engineering, Hohhot, China, 15–17 July 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 4623–4626. [Google Scholar]
- Han, Y.; Wang, B.; Deng, Z.; Wang, S.; Fu, M. A Mismatch Diagnostic Method for TERCOM-Based Underwater Gravity-Aided Navigation. IEEE Sens. J. 2017, 17, 2880–2888. [Google Scholar] [CrossRef]
- Dai, T.; Miao, L.; Guo, Y. A Real-Time Mismatch Detection Method for Underwater Database-Referenced Navigation. Sensors 2019, 19, 307. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.; Tang, Y.-G.; Chen, C.-X.; Li, J.-X.; Chen, C.; Zhang, A.-Q.; Li, Y.-P.; Li, S. Terrain matching localization for hybrid underwater vehicle in the Challenger Deep of the Mariana Trench. Front. Inf. Technol. Electron. Eng. 2020, 21, 749–759. [Google Scholar] [CrossRef]
- Wang, C.; Wang, B.; Deng, Z.; Fu, M. A Delaunay Triangulation-Based Matching Area Selection Algorithm for Underwater Gravity-Aided Inertial Navigation. IEEE/ASME Trans. Mechatron. 2021, 26, 908–917. [Google Scholar] [CrossRef]
- Wang, R.; Chen, Y.; Li, Y.; Xu, P.; Shen, P. High-precision initialization and acceleration of particle filter convergence to improve the accuracy and stability of terrain aided navigation. ISA Trans. 2021, 110, 172–197. [Google Scholar]
- Yuan, G.; Zhang, H.; Yuan, K.; Tao, C. A Combinational Underwater Aided Navigation Algorithm Based on TERCOM/ICCP and Kalman Filter. In Proceedings of the 2011 Fourth International Joint Conference on Computational Sciences and Optimization, Kunming and Lijiang City, China, 15–19 April 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 952–955. [Google Scholar]
- Li, Z.; Zheng, W.; Wu, F.; Fang, J. Improving the matching efficiency of underwater gravity matching navigation based on a new hierarchical neighborhood threshold method. Chin. J. Geophys. 2019, 62, 2405–2416. (In Chinese) [Google Scholar]
- Li, Z.; Zheng, W.; Wu, F. Geodesic-Based Method for Improving Matching Efficiency of Underwater Terrain Matching Navigation. Sensors 2019, 19, 2709. [Google Scholar] [CrossRef] [Green Version]
- Zhao, L.; Gao, N.; Huang, B.; Wang, Q.; Zhou, J. A Novel Terrain-Aided Navigation Algorithm Combined with the TERCOM Algorithm and Particle Filter. IEEE Sens. J. 2014, 15, 1124–1131. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, T.; Shin, H.-S.; Wang, J.; Zhang, C. Geomagnetic Gradient-Assisted Evolutionary Algorithm for Long-Range Underwater Navigation. IEEE Trans. Instrum. Meas. 2020, 70, 2503212. [Google Scholar] [CrossRef]
- Dai, T.; Miao, L.; Shao, H. A robust underwater navigation method fusing data of gravity anomaly and magnetic anomaly. Int. J. Syst. Sci. 2019, 50, 679–693. [Google Scholar] [CrossRef]
- Salavasidis, G.; Munafo, A.; McPhail, S.D.; Harris, C.A.; Fenucci, D.; Pebody, M.; Rogers, E.; Phillips, A.B. Terrain-Aided Navigation with Coarse Maps—Toward an Arctic Crossing with an AUV. IEEE J. Ocean. Eng. 2021, 46, 1192–1212. [Google Scholar] [CrossRef]


| Parameter | Value (Unit) | Parameter | Value (Unit) |
|---|---|---|---|
| Accelerometer constant zero deviation | 10−3 m/s2 | Gyroscope drift | 0.01°/h |
| Heading (north by east) | 70° | Heading error | 0.05° |
| Speed | 10 m/s | Speed error | 0.04 m/s |
| Initial position error | 0 m | Gravity random noise | 1 mGal |
| Tracking sampling period | 20 s | Tracking sampling scale | - |
| SS | Alg. | /% | Mean/m | SD/m | Best/m | Worst/m | T/s |
|---|---|---|---|---|---|---|---|
| 100 | TERCOM | 98 | 77.20 | 39.76 | 28.62 | 196.10 | 2.48 × 10−2 |
| SCGM | 98 | 72.73 | 46.46 | 28.62 | 341.15 | 1.89 × 10−2 | |
| 150 | TERCOM | 70 | 105.53 | 34.42 | 8.30 | 145.12 | 5.06 × 10−2 |
| SCGM | 69 | 111.70 | 61.54 | 8.30 | 625.98 | 4.23 × 10−2 | |
| 200 | TERCOM | 97 | 110.63 | 22.87 | 101.00 | 218.56 | 1.23 × 10−1 |
| SCGM | 97 | 108.52 | 21.39 | 101.00 | 218.56 | 1.02 × 10−1 | |
| 250 | TERCOM | 40 | 176.35 | 46.76 | 108.33 | 214.19 | 2.63 × 10−1 |
| SCGM | 39 | 177.71 | 45.99 | 108.33 | 214.19 | 1.90 × 10−1 |
| Alg. | /% | Mean/m | SD/m | Best/m | Worst/M | T/s |
|---|---|---|---|---|---|---|
| TERCOM | 68.61 | 106.11 | 49.21 | 8.30 | 1170.50 | 4.95 × 10−2 |
| SCGM | 68.39 | 107.91 | 61.31 | 8.30 | 1843.95 | 4.10 × 10−2 |
| SLSR | 68.88 | 104.37 | 37.08 | 8.30 | 307.81 | 4.14 × 10−2 |
| Alg. | NOM/Time | Mean/m | SD/m | Best/m | Worst/m |
|---|---|---|---|---|---|
| TERCOM | 41 | 536.06 | 270.95 | 145.12 | 1170.50 |
| SCGM | 41 | 667.07 | 334.06 | 145.12 | 1843.95 |
| SLSR | 11 | 103.35 | 51.31 | 8.30 | 307.81 |
| Starting Point | Alg. | NOM/Time | Mean/m | SD/m | Best/m | Worst/m | T/s |
|---|---|---|---|---|---|---|---|
| A | TERCOM | 41 | 789.54 | 442.66 | 224.71 | 2194.02 | 4.97 × 10−2 |
| SLSR | 3 | 91.79 | 188.84 | 8.30 | 1076.81 | 4.06 × 10−2 | |
| B | TERCOM | 41 | 742.61 | 381.49 | 224.71 | 1857.80 | 4.86 × 10−2 |
| SLSR | 4 | 107.86 | 120.35 | 8.30 | 632.28 | 3.98 × 10−2 | |
| C | TERCOM | 45 | 544.66 | 370.07 | 145.12 | 1548.12 | 5.01 × 10−2 |
| SLSR | 2 | 88.98 | 40.93 | 8.30 | 197.31 | 4.07 × 10−2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, S.; Zheng, W.; Li, Z.; Zhu, H.; Xu, A. Improving Matching Efficiency and Out-of-domain Reliability of Underwater Gravity Matching Navigation Based on a Novel Soft-margin Local Semicircular-domain Re-searching Model. Remote Sens. 2022, 14, 2129. https://doi.org/10.3390/rs14092129
Zhao S, Zheng W, Li Z, Zhu H, Xu A. Improving Matching Efficiency and Out-of-domain Reliability of Underwater Gravity Matching Navigation Based on a Novel Soft-margin Local Semicircular-domain Re-searching Model. Remote Sensing. 2022; 14(9):2129. https://doi.org/10.3390/rs14092129
Chicago/Turabian StyleZhao, Shijie, Wei Zheng, Zhaowei Li, Huizhong Zhu, and Aigong Xu. 2022. "Improving Matching Efficiency and Out-of-domain Reliability of Underwater Gravity Matching Navigation Based on a Novel Soft-margin Local Semicircular-domain Re-searching Model" Remote Sensing 14, no. 9: 2129. https://doi.org/10.3390/rs14092129
APA StyleZhao, S., Zheng, W., Li, Z., Zhu, H., & Xu, A. (2022). Improving Matching Efficiency and Out-of-domain Reliability of Underwater Gravity Matching Navigation Based on a Novel Soft-margin Local Semicircular-domain Re-searching Model. Remote Sensing, 14(9), 2129. https://doi.org/10.3390/rs14092129






