Abstract
Forest height inversion with Polarimetric SAR Interferometry (PolInSAR) has become a research hotspot in the field of radar remote sensing. In this paper, we systematically studied a modified two-step, three-stage inversion simulating the L-band (L = 23 cm) full-polarization interferometric SAR data with an average forest height of 18 m using ESA PolSARpro-SIM software. We applied this method to E-SAR L-band single-baseline full PolInSAR data in 2003. In the first step, we modified the three-stage inversion algorithm based on phase diversity (PD)/maximum coherence difference (MCD) coherence optimization methods, corresponding to PD, MCD, respectively. In the second step, we introduced the coherence amplitude inversion term and modified the fixed weight to the variable of ε times the ground scattering ratio, which improved the accuracy of forest height inversion. The mean of forest height inversion by the HV method was the lowest (15.83 m) and the RMSE was the largest (4.80 m). The PD method was superior to the HV method with RMSE (4.60 m). The MCD method was slightly better than using the PD method with the smallest RMSE (4.43 m). After adding the coherence amplitude term, the RMSE was improved by 0.15 m, 0.14 m, and 0.08 m, respectively. The smallest RMSE was obtained by MCD, followed by the PD and HV methods. Although the robustness of the forest height inversion algorithm was reduced, the underestimation was improved and the RMSE was reduced. Due to the complexity of the real SAR E-SAR L-band single-baseline full PolInSAR data and the small sample sizes, the three-stage inversion methods based on coherent optimization were lower than the three-stage in-version method. After introducing the coherent magnitude term, the overestimation of the forest height was significantly weakened in HVWeight, PDweight, and MCDWeight, and PDWeight was optimal. The modified two-step, three-stage inversion algorithm had significant effects in alleviating forest height underestimation and overestimation, improving the accuracy of forest height inversion, and laying a foundation for the upcoming L-band SAR satellite generation, new SAR and LIDAR systems combined with RPAs (remotely piloted aircrafts)/UAVs (unmanned aerial vehicles) for small areas mapping initiatives, and promoting the depth and breadth of the SAR applications of the new SAR system.
1. Introduction
Forest height is an important biophysical parameter [1], and its spatial distribution is of great significance for forest resource management, forest biomass estimation, and regional and global carbon cycle research [2,3,4]. The measurement methods of forest height include ground survey, photogrammetry, Lidar, and so on. Since the measurement of large-scale forest height is difficult, it has not been well quantified [5]. Although forest ground survey data can also obtain forest heights, its application in large-scale research is limited due to the large amount of human and material resources, and the lack of observations in remote regions. Remote sensing is the most effective method for real-time forest inversion on a regional and global scale. Although LIDAR can achieve high accuracy, it is limited by the atmosphere, mist, and clouds, especially in areas with cloudy, rainy, foggy, and snowy weather. Moreover, the acquisition cost of LIDAR is too high to obtain information on the vertical structure of the forest, and there is no information on the horizontal structure of the forest. Optical remote sensing is not only influenced by clouds, fog, and snow, but also cannot penetrate the forest to the ground. Therefore, it is of great scientific significance to estimate forest height based on synthetic aperture radar (SAR), which combines the properties of both the real-time forest inversion at regional and global scales provided by remote sensing and the forest penetration to the ground by microwaves [6].
Among many forest height inversion methods widely used, Polarimetric SAR Interferometry (PolInSAR) combines the comprehensive advantages of interferometry and polarization information. PolInSAR is not only sensitive to the vegetation spatial distribution with SAR Interferometry (InSAR), but also has the property of Polarimetric SAR (PolSAR), which is sensitive to the shape and direction of the vegetation [7].
Cloude and Paphthanassious first proposed PolInSAR technology [8], and afterwards, formally proposed the concept and extended the random volume over ground (RVoG) [9] to the full PolInSAR, thus laying the foundation of forest height inversion with PolInSAR [10]. The applicability of the RVoG model for forest height inversion has been studied for cases of different forest density [11]. Due to the high computational complexity of the six-dimensional nonlinear parameter method [12], the PolInSAR forest height inversion was simplified to a three-stage method based on the RVOG model [13]. By reason of its simplicity and generality, the three-stage inversion algorithm has low calculation cost and been widely used. The three-stage inversion algorithm was validated in various activities at different frequencies and configurations [14,15,16,17]. Some literature has improved the three-stage algorithm by considering the effect of terrain or extinction coefficient successively, which ultimately improved the accuracy of forest height inversion [18,19].
However, the three-stage inversion algorithm accuracy is affected by the accuracy of the estimated topographic phase [20] and pure volume scattering complex coherence [21]. One of the main reasons is the irrational selection of polarized channels, resulting in the ineffective separation of ground and volume scattering phase centers. Therefore, several coherence optimization methods based on optimization theory [10,22,23,24,25,26] have emerged to solve this problem. Xie Q. et al. combine the three-stage inversion algorithm with the five effective separation phase centers generated by singular value decomposition (SVD) [10] and phase diversity (PD) [26] coherence optimization methods for forest height inversion, which improves the forest height accuracy [27]. Lavalle compared the max of phase with the max of magnitude over the coherence boundary and studied the dependence of L-band PolInSAR complex coherence on forest height inversion [28]. Fu W.X. et al. extend the three-stage algorithm and SVD [10] to the dual-polarized PolInSAR and, furthermore, propose a search method based on the RVoG model for solving pure volume scattering complex coherence on the fuzzy line segment, which has similar inverted forest height to full polarization [6]. Based on the RVoG model, Lin D.F. et al. have proposed a new method based on TSVD decomposition to directly estimate “pure” volume scattering complex coherence. Compared with the three-stage method, the RMSE of the inverted forest height is improved by 48.6% [29].
Aiming to reduce the underestimation of forest height, Cloude proposed a hybrid model combining interference coherence amplitude with the phase difference method [30,31,32]. Additionally, due to the underestimation of forest height by the estimating signal parameters by the use of the rotation invariance techniques (ESPRIT) method, the total least square ESPRIT (TLS-ESPRIT) method is combined with the coherence amplitude inversion method to improve the accuracy of forest height inversion [33,34]. Using a novel hybrid inversion algorithm based on covariance matrix decomposition, a forest vegetation parameter inversion experiment [35] was carried out on the L-band airborne data of the simulation and SIR-C/X-SAR system. Chen E.X. et al. verify and compare several available forest height inversion methods, such as the SINC, three stage SINC inversion (TSS), and phase and coherence inversion (PCI) methods, using E-SAR repeated orbits data and corresponding ground heights, besides analyzing the effect of SVD on the SINC method for forest height inversion [36]. Some scholars have estimated the forest height by combing the three stage inversion algorithm with coherence optimization [37,38]. Aghabalaei et al. demonstrated the capability for forest height estimation with the single-baseline L-band compact PolInSAR (C-PolInSAR) in the Remningstorp, southern Sweden [39]. They developed a novel four-stage algorithm with volumetric temporal decorrelation to improve the forest height estimation accuracy using the repeat-pass PolInSAR data of Gabon Lope Park acquired in the AfriSAR campaign of the German Aerospace Center (DLR) [40]. In recent years, some researchers have investigated the potential of forest height mapping with spotlight-mode data with TanDEM-X (TDM) combined with in situ measurements [41,42]. They aim to demonstrate the potential of space-borne PolInSAR datasets at the L-, C-, and X-band frequencies (ALOS-2/PALSAR-2, TerraSAR-X, and RadarSAT-2) for forest height estimation, with the RMSE of 5.4 m, 12.8 m, and 7.6 m, respectively [43]. Chen et al. have developed a new extended Fourier–Legendre series approach for combing Global Ecosystem Dynamics Investigation (GEDI) LiDAR waveforms with TanDEM-X data to improve forest height estimation [44]. Some papers use Tomographic SAR (TomoSAR) technology for forest 3D structure mapping [5,45,46].
In summary, although forest height inversion by single-baseline PolInSAR has been widely used at home and abroad with good precision, it still presents the phenomenon of underestimating and overestimating the forest height, to which there is no good solution yet. In this paper, without considering the influence of residual motion, baseline and coregistration error, topography, temporal, and signal-to-noise ratio (SNR) decorrelation sources, we used ESA PolSARproSIM software to simulate single-baseline PolInSAR data. Furthermore, we applied this method to E-SAR L-band single-baseline full PolInSAR data in 2003. The purpose of this paper was to alleviate alleviated the problem of the overestimation or underestimation of the three-stage inversion algorithm with the introduction of an automatic weight adjustment method, which was an improvement on the original three-stage method. First, for the problem of incomplete coherence separation in the three-stage inversion method, we introduced the PD/MCD method in coherence optimization. Then, for forest height underestimation and overestimation problems, we introduced the complex coherence amplitude inversion method and the ground scattering proportional variable to automatically select weight. We compared the performance of these methods of the forest height, laying the foundation for selecting the algorithm based on single-baseline PolInSAR forest height inversion and providing exploration to develop a better inversion method.
2. Study Data
Due to the difficulty in getting airborne SAR images in forested areas and data simulated by ESA PolSARproSIM software based on Maxwell’s wave propagation equation and scattering model without considering the influence of residual motion, baseline and coregistration error, topography, and temporal and signal-to-noise ratio (SNR) decorrelation sources [47], we thus used PolSARproSIM software to simulate the L-band (L = 23 cm) for single-baseline full-polarized PolInSAR data. The parameters were set as follows: the slopes of range and azimuth were both 0, regardless of topography; the radar platform height was 3000 m; the horizontal baseline was 10 m; the vertical baseline was 1 m; and the incidence angle was 45°. The center frequency was 1.3 GHz; the azimuth resolution was 1.5 m; the slant resolution was 1.0607 m; the forest type was coniferous; and the average forest height was 18 m. Since the product of the vertical wavenumber and the forest height is less than 2π, there is no ambiguous problem of forest height inversion [48]. Figure 1 presents the overall scenario of the study area, with the forest height of 18 m in height in the middle area and non-forest in the remaining areas. The tree height standard deviation would be under programmer control, and typically set to 5% of the mean value. The process of tree location map generation began by determining the number of trees in the scene, then initializing them in a regular pattern, and realizing their heights and global crown radii. The trees were subsequently “shuffled” around in random, collision-avoiding walks using Monte Carlo techniques, to reach a more realistic distribution of tree positions. The tree height would be drawn from a normal distribution. There were 137 trees in a stand of radius with 30 m, as shown in Figure 1. Although we could not get a clear value of RMSE from this information, we knew it had a low RMSE.

Figure 1.
Image of the simulate forest scene image. (a) Forest scene; (b) Power image of HV; (c) Pauli image.
3. Methods
3.1. RVoG Model
The RVoG model [9] considered vegetation as a common process of vegetation volume scatter decay and surface scatter. The vegetation layer was assumed to be an isotropic medium, so we used a single extinction coefficient to represent overall attenuation. The vegetation’s structural function decayed exponentially in the vertical direction.
The RVoG model was established by Treuhaft [9], and it was the theoretical basis of the forest height inversion algorithm. Regardless of other decoherence factors, only considering volume scattering coherence, we obtained the following explicit equation for the complex coherence [13]:
where is a three-component unitary complex vector defining the choice of polarization, is the ground phase center, is the ground-to-volume scattering ratio, which was only a function of polarization, and is pure volume complex coherence. Formula (2) is thus as follows
where is the mean wave extinction in the medium, is the scatter position, is forest height, was the mean angle of incidence, is the apparent angular separation of the baseline from the scattering point, is senor altitude, is vertical wavenumber, and is the vertical baseline.
is the ground ratio, which had a relation with :
G/G + V (ground/(ground + volume)) was also used to indicate the ground scattering ratio. Equation (1) represents a straight line in a complex plane passing through a point with a slope of .
When taking different extreme values of , were reached as follows:
where is the complex coherence corresponding to a pure volume scattering mechanism for the top forest canopy, and is the complex coherence corresponding to the surface scattering mechanisms near the ground surface under the forest canopy.
According to Formula (3), the formula for calculating the ground scattering ratio is as shown in (4):
in which , , and .
Figure 2 shows pure volume complex coherence changes with forest height and extinction in a complex plane according to the RVoG model. Figure 2 was used as a look-up table for the three-stage inversion algorithm described later, laying the basis for forest height estimation. When knowing pure volume scattering complex coherence, we can use this lookup table to inverse the forest height and extinction coefficient. Meanwhile, the estimation of pure volume scattering complex coherence was very important, so we introduced coherence optimization to make its estimation more accurate.
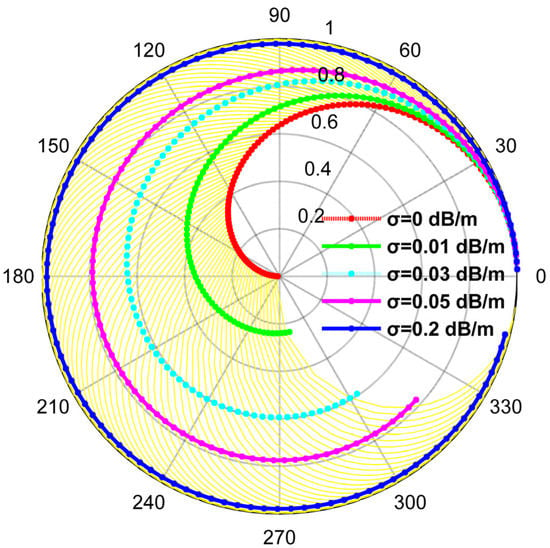
Figure 2.
Volume complex coherence changes with forest height and extinction at kz = 0.1154. Note: Calculate kz = 0.1154 and ha = 54.4470 m from the setting parameters. Different color curves corresponded to different extinction coefficients. With larger extinction or strong ground scattering, the pure volume complex coherence amplitude was prone to saturation (such as the blue curve), but the phase was not saturated. When the extinction coefficient was in the range of 0~2 dB/m (such as yellow curves), the pure volume complex coherence changed with forest height hv (0~ha m, step is 0.5 m). When the forest height was the same (any yellow curve) and pure volume complex coherence scattering amplitude was large, this was caused by surface scattering or the strong attenuation of vegetation. Complex coherence fell with increasing vegetation height, as a consequence of volume decorrelation.
3.2. Methods
In this paper, without considering baseline and coregistration error, topography, or temporal and signal-to-noise ratio (SNR) decorrelation sources, we introduced PD/MCD coherence optimization to solve for incomplete coherence separation in the three-stage inversion [13]. Additionally, we introduced complex coherence amplitude inversion [36] to solve the underestimation or overestimation problem and introduced the ground scatter ratio to automatically select the weight to improve the three-stage method. We compared and analyzed these methods combined with the topographic phase affecting forest height. A technical roadmap is shown in Figure 3.
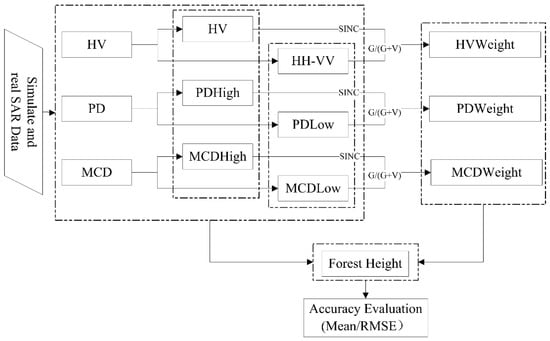
Figure 3.
Forest Height Inversion Technology Roadmap.
The symbol meanings are shown in Table 1. In addition, SINC: introduced the corresponding complex coherence amplitude inversion; G/(G + V): ground scatter ratio of the corresponding parameter estimation, namely . Weight: Based on three-stage inversion algorithm, it was further improved by introducing the corresponding complex coherence amplitude inversion and modified constant weight to the ε times of the ground scatter ratio. To correct the pure volume complex coherence, we projected it onto a coherence line to invert forest height.

Table 1.
Parameters corresponding to various methods.
The process of three-stage inversion [13] was as follows:
Stage 1: Least squares line fit: Least squares were used to linearly fit the real and imaginary components of the polarization interference complex coherence and found the best fit straight line within the complex unit circle.
Stage 2: Vegetation bias removal: The true topographic phase was estimated with the coherence ranking order algorithm and removed it.
Stage 3: Height and extinction estimation: According to Formula (2), a look-up table (LUT) was established, where pure volume coherence changed with forest height and extinction coefficient (Figure 2). According to the topographic phase estimated from stage 2, it was easy to determine the coherence farthest from it in observation data. By comparing with LUT, forest height and extinction can be obtained without additional iterative optimization algorithms.
The three-stage inversion method was based on the assumption that the ground-to-volume scatter ratio in one of the polarization channels is zero. To simplify the problem, it was generally assumed that the ground-to-volume scatter ratio in the HV channel was zero, i.e., the estimated pure volume coherence was obtained from the estimated HV channel coherence. In addition, since the estimated HV and HH-VV channel coherence did not reach the maximum separation, there were some errors in forest height inversion, so PD and MCD coherence optimization was introduced to invert forest height. Several studies had explained specific steps of PD and MCD coherence optimization [25,26]. However, even with coherence optimization, the volume phase center may lie anywhere between half-way and the top height layer. Hence, the true forest height will still be underestimated [31]. The retrieved forest height may be overestimated or underestimated depending on the selected vertical baseline. Therefore, at least a coherence amplitude correction term can be employed to partially compensate for this underestimate or overestimate problem [36]. Based on a hybrid method proposed by Cloude (such as Formula (5)) [31,32], this study compensated for the “compression” phenomenon of forest top height not considered in the three-stage method based on coherence optimization, and modified constant weight ε to a variable weight , as shown in Formula (6)
where is a weight.
The first term represents the forest height inversed by the three-stage method with PolSARpro, which affects the accuracy of the method according to the linear equations of different scattering fittings. The second term is the coherence amplitude correction term with PolSARpro, which was solved for the first term underestimation or overestimated problem, but only considering the pure volume scatter complex coherence. The second part affects the accuracy of the method according to the ε times of the ground scattering ratio of the SINC inversion method, where the ground scattering ratio is the performance of different scattering from the same vegetation/canopy or similar scattering from different types of vegetation, and the accuracy of the method is affected by volume scattering in the SINC inversion method. Therefore, we used the ground scatter ratio to modify it, and because the highest value of was approximately 0.8, we added an adjustment factor ε to modify it again with MATLAB. The general rule is that the RMSE between the retrieved forest heights of these two parts and the true stand average height is the smallest to invert the forest heights. Therefore, made the full expression as robust as possible to changes in the structure function. However, in practical applications, forest height inversion by single PolInSAR data required ideal baselines. The vertical baseline depended on the platform, target geometry, forest height, and forest vertical structure, and the length of the vertical baseline determined the sensitivity of the interferometric phase difference to different forest heights. The retrieved forest height may be overestimated or underestimated depending on the selected vertical baseline. The value of ε (−α~α, α = ) was obtained according to the minimum RMSE of forest height. Negative values of ε corresponded to overestimation, and positive values corresponded to underestimation. The flow chart is shown in Figure 4 with MATLAB software.
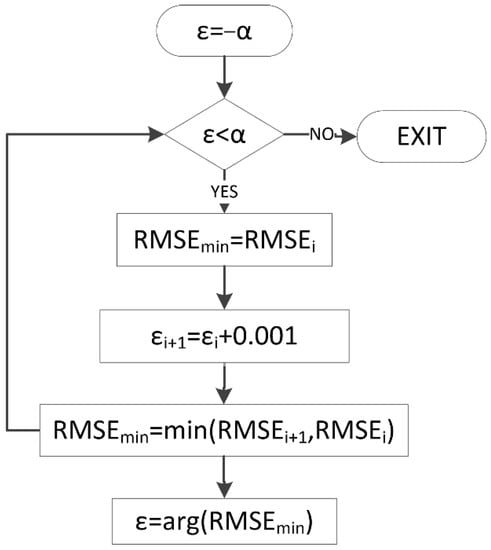
Figure 4.
Flow chart for automatically selecting ε.
In this paper, we improved the three-stage inversion method based on the PD/MCD coherence optimization method. The PD and MCD methods were compared with the three-stage inversion algorithm (HV method) to invert forest height. We further inverted the forest height according to Formula (6), and they were HVweight, PDweight, and MCDweight. To modify the pure volume scattering complex coherence, we projected it to the coherence line to invert the forest height. When using real data, we need to consider the impact of these errors and we cannot systematically evaluate this algorithm. The simulation data could be used to systematically evaluate the algorithm, laying the foundation for the future application of the airborne L-band SAR data to invert the forest height. However, if the decorrelation source was not considered, the result of the three-stage inversion algorithm for forest height inversion may be high, and therefore the Weight method was applicable with negative values of ε.
4. Experimental Results
4.1. Topographic Phase
Even if there was a slow terrain change, the coherence phase would change rapidly, so forest height inversion must take the topographic phase into account [20]. Figure 5 shows the ground scatter ratio. Figure 6 shows an image of the estimated topographic phase. Figure 7 present a profile at azimuth = 47 (yellow line in the Figure 1b) and the statistical histogram of the estimated topographic phase.
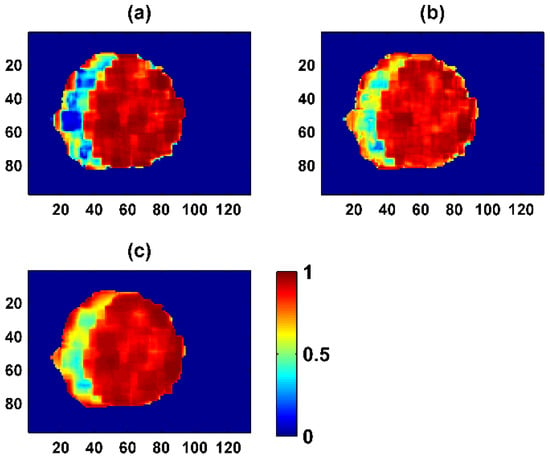
Figure 5.
Image of the estimated according to Formula (4), namely, the ground scatter ratio. (a) HV/HVWeight: calculated from complex of HH-VV and HV channel; (b) PD/PDWeight: calculated from a complex of Phase Diversity; (c) MCD/MCDWeight: calculated from complex of Maximum Coherence Difference.
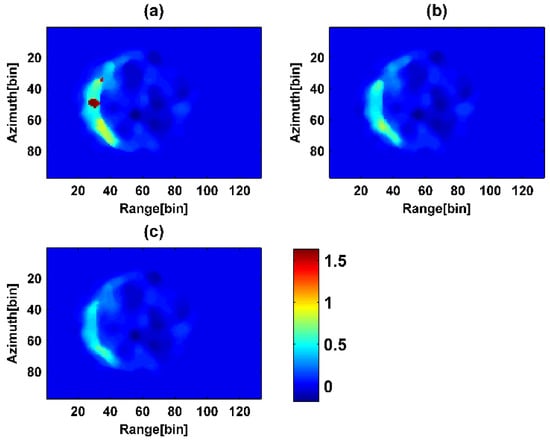
Figure 6.
Image of estimated topographic phase. (a) HV/HVWeight method; (b) PD/PDWeight method; (c) MCD/MCDWeight method.
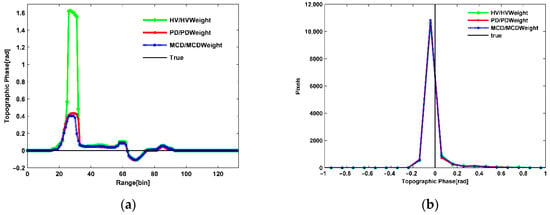
Figure 7.
Profile and statistical histogram of the estimated topographic phase. (a) Profile of the estimated topographic phase; (b) Statistical histogram of the estimated topographic phase.
It can be seen from Figure 5 that the overall ground scatter ratio trend was basically the same: small in the near direction and large in the far direction. After coherence optimization, the estimated ground scatter ratio improved. After PD and MCD coherence optimization, the ground scatter ratio was much better than the HV/HVWeight method, and the MCD/MCDWeight method was better than the PD/PDWeight method.
It can be seen from Figure 5 and Figure 6 that in the region with a small ground scattering ratio in Figure 5, the estimated topographic phase was obviously high, and the error was large. In Figure 6, the estimated topographic phases all had negative values, the HV/HVWeight method values were significantly higher, and the difference in topographic phase estimated by the PD/PDWeight and MCD/MCDWeight methods was small. The profile and the statistical histogram of the topographic phase in Figure 7 further illustrated it. As seen from the profile of Figure 7a, the overall trend of the four methods was basically the same, and the proximity to the topographic phase from small to large was MCD/MCDWeight, PD/PDWeight, and HV/HVWeight methods. The statistical histogram in Figure 7b shows that there was no significant difference between the three methods.
Since the true topographic phase was 0, it was easy to cause positive and negative cancellation, so we used the arithmetic mean of absolute values for quantitative analysis. Table 2 lists the mean of the absolute values and the RMSE of the estimated topographic phase. It can be seen that the HV/HVWeight method had the worst estimation and the largest error. The PD/PDWeight method was greatly improved compared with the HV/HVWeight method but was inferior to the MCD/MCDWeight method. The estimation of the MCD/MCDWeight method was optimal, and the error was minimal.

Table 2.
Estimation results of the topographic phase.
4.2. Forest Height
Figure 8 present an image of the inversed forest height, (A) the improved three-stage inversion algorithm based on coherence optimization, and (B) the forest height inversion after introducing the coherence amplitude. Figure 9 shows a profile at azimuth = 47 (yellow line in the Figure 1b) and the statistical histogram of the inversed forest height. Table 3 shows the image of inversed forest height inversion.
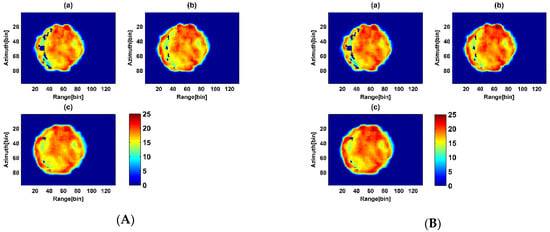
Figure 8.
Improved three-stage method for forest height inversion. (A) Three-stage method for forest height inversion based on coherence optimization (a) HV (b) PD (c) MCD (B) After introduction coherence amplitude for Forest height inversion (a) HVWeight (b) PDWeight (c) MCDWeight.
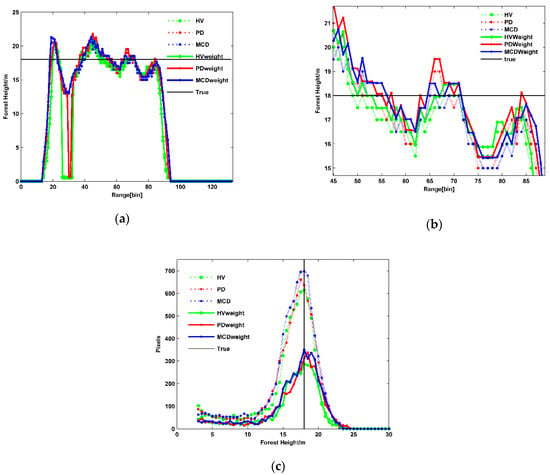
Figure 9.
Profile and statistical histogram of the inversed forest height. (a) Profile of the inversed forest height; (b) Enlargement image of Figure (a) in the range at 45~90; (c) Statistical histogram of the inversed forest height.

Table 3.
Results of forest height inversion.
In the area where the ground scatter ratio was small, the inversed forest height is low, and even there, the forest height cannot be inversed from Figure 5 and Figure 8. The HV method had the worst forest height inversion. After PD and MCD coherence optimization, the forest height inversion results were much better than the HV method, and the MCD method was better than the PD method. The decreasing order of missing values in different methods was as follows: HV, PD, MCD methods. The corresponding method in Figure 8B had the same trend as in Figure 8A.
The mean of forest height inversion by the HV method was the lowest (15.83 m) and the RMSE was the largest (4.80 m). The PD method maximized the separation of complex coherence phases representing canopy scattering and ground scattering, which making its mean (16.19 m) and its RMSE (4.60 m) superior to the HV method. The MCD method maximized the distance between canopy scattering and ground scattering complex coherence in the complex plane, its mean (16.19 m) was slightly better than using the PD method, and the RMSE was the smallest (4.43 m).
Figure 9b shows a profile of the inversed forest height enlargement image from Figure 9a in the range near 45~90. After adding ε times the ground scatter ratio as the weight, the forest height was equivalent to a proportionality increase. After adding the coherence amplitude term from Table 3, the mean of forest heights inversed by the HV, PD, and MCD methods were increased by 0.46 m, 0.57 m, and 0.52 m, respectively. The RMSE was improved by 0.15 m, 0.14 m, and 0.08 m, respectively, and the improvement of the HV method was obviously best, followed by the PD method. After adding the coherence amplitude inversion method from Figure 9c and Table 3, although the robustness of the forest height inversion algorithm was reduced, the underestimation was improved and the RMSE was reduced. Among these methods, the mean forest height inversion by the MCD method was the closest to the true value, followed by the PD and HV methods. The smallest RMSE was obtained by MCD, followed by the PD and HV methods. The MCD method made the coherence distance between the complex coherence maximum in the complex plane and obtained the accurate pure volume scatter coherence, such that the mean forest height inversion was the highest and its RMSE was the lowest. The PD method maximized the phase of complex coherence and obtained the accurate pure volume scatter coherence so that the mean and the RMSE of forest height inversion were lower than the MCD method. The mean of forest height inversion by the HV method was the largest difference from the true value, and its RMSE was the largest.
5. Discussion
The estimated topographic phase may be caused by the following aspects: (1) The ground scatter ratio: topographic phase was good and the error was large in the area where the ground scattering ratio was small. Combining Figure 5 and Figure 6, the estimated topographic phase error in Figure 6 was relatively large where the ground scattering ratio of Figure 5 was small. The estimated topographic phase error was significantly reduced where the ground scattering ratio of Figure 5 was large. (2) The difference of the complex coherence combination and sample number used to fit the coherence line: Among these methods, the coherence line was fitted according to the least squares method, in addition to jointly using a group of complex coherences, and the HV/HVWeight method also used B group complex coherences, the PD method with C group complex coherences. The MCD/MCDWeight method in addition used D group complex coherences. The sample number of HV/HVWeight/PD/PDWeight/MCD/MCDWeight methods was the same, and only the B/C/D group complex coherence was different. C/D was the complex coherence obtained after PD and MCD coherence optimization, respectively. PD coherence optimization maximized the phase center of complex coherence in the complex plane. MCD coherence optimization made the distance of complex coherence maximum in the complex plane. Figure 10 shows the complex coherence and the fitted coherence line used by these methods in a complex plane. The estimated topographic phase in Figure 10a from small to large was: MCD/MCDWeight, PD/PDWeight, and HV/HVWeight. Squares of different colors represented different complex coherences in Figure 10. Straight lines of different colors were coherence lines fitted by different methods according to corresponding complex coherences. (a) When the azimuth was 70 and the range was 40 in the image, various coherence lines were fit by different methods. The intersection of the coherence line fit by the MCD/MCDWeight method and the complex unit circle (the point close to the x real axis), i.e., the topographic phase, was closest to the real topographic phase, followed by PD/PDWeight and HV/HVWeight. (b) When the azimuth was 51 and the range was 44 in the image, because the distance between the complex coherence representing ground and volume scattering was enough large, and the distance in the normal coherence line direction was small, coherence lines fitted by these methods were the same, and the intersections with the unit circle were also the same, i.e., the topographic phases were the same. It could be seen that when the sample number of complex coherence was the same, the coherence line fit by the PD/PDWeight method was more accurate than the HV/HVWeight method. The PD/PDWeight method was lower than the MCD/MCDWeight method because it was considered complex coherence amplitude information. In Figure 10b, the estimated topographic phase is the same, and it can be seen that the greater the distance between volume and ground complex coherence in the complex plane, and the smaller the distance in the coherence line normal direction, the higher the accuracy of the topographic phase. The topographic phase was not affected by complex coherence when the direction of the complex coherence line and its normal reached a certain value, even without coherence optimization, the same topographic phase could be obtained. (3) The different selection of points closest to the ground phase: the HV/HVWeight/PD/PDWeight/MCD/MCDWeight methods select complex coherence closest to the ground phase, respectively. MCDLow was optimal, followed by PDLow and HH-VV.
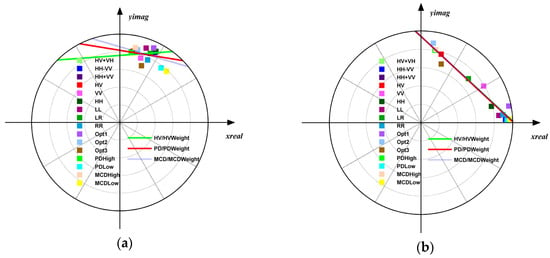
Figure 10.
Comparison of complex coherence and fitted coherence straight lines in a complex plane. (a) azimuth = 70 range = 40; (b) azimuth = 51 range = 44.
Without using coherence optimization, the topographic phase estimated by HV/HVWeight method was the worst. PD coherence optimization maximized the difference between coherence phase centers in the complex plane. Compared with the HV/HVWeight method, the topographic phase estimation accuracy was greatly improved. The MCD coherence optimization maximized the complex coherence distance in the complex plane, comprehensively considering phase and amplitude information. The obtained complex coherence MCDLow representing ground scattering was better than PD coherence optimization, and closer to the real ground phase. The topographic phase estimated by the MCD/MCDWeight method was optimal and closest to the true topographic phase. When applied to real SAR data with lots of field data, we can acquire the same conclusion as the simulation data. However, when the sample sizes were small, there may be some differences from this simulation conclusion. Therefore, in order to obtain higher accuracy, it was necessary to carry out a variety of optimization methods in single-baseline L-band PolInSAR technology with real SAR data.
With analyzing the effect of the estimated topographic phase on the forest height, we compared three-stage inversion methods based on coherence optimization. The HV method selected HV channel complex coherence as the canopy scattering complex coherence, and its phase center may be located at any position between half-way and the top forest height [31,32]. The estimated topographic phase was the highest, and the forest height inversion had the largest error. Due to the observed propagation error of the topographic phase, and the selection of channel as forest canopy scattering complex coherence, with the lowest forest height mean and largest error, the HV method estimated topographic phase accuracy performed worse. The PD method maximized the complex coherence phase center of canopy and ground scattering, which made it more accurate than the coherence line fitted using the HV and HH-VV channel complex coherence used by the HV method. Therefore, the mean of topographic phase absolute value was better than the HV method, and pure volume scatter complex coherence (PDHigh) was more accurate than the HV complex coherence. The mean forest height was increased by 0.33 m compared with the HV method, whereas the RMSE increased by 0.2 m. The MCD method made the distance between complex coherence of canopy and ground scattering maximum in the complex plane. The topographic phase and forest height were very similar to the PD method. However, overall, the MCD method, while comprehensively considering the coherence amplitude and phase, had a better forest height inversion than the PD method, as well as the smallest RMSE. The result estimated by the MCD method obtained the optimal topographic phase and more accurate pure volume coherence. Therefore, forest inversion based on the lookup table was also more accurate, and the mean of the inversed forest height was closest to the true value. Compared with the HV method, the forest height inversion underestimation was improved after coherence optimization, and the RMSE was reduced [27,36]. The PD method was based on phase information, which improved forest height inversion to some extent. The MCD method was based on coherence amplitude and phase, which was better than the PD method.
Figure 11 shows the relationship between the weighted forest height statistical indicator (MEAN/RMSE/SD) and ε. Compared with the three-stage inversion algorithm based on coherence optimization, after introducing the coherence amplitude term and modifying fixed weights to weight variables, the mean of forest height increased while the RMSE decreased [36]. As the ε increases, the average bias of the forest height increased first and then decreased, but the final reduced value was greater than the original, and the minimum value was near 0.1~0.2. The RMSE of forest height decreased first and then increased and finally decreased with the ε increased, with a minimum value near 0.1. After introducing the coherence amplitude inversion term, the standard deviation of forest height increased, i.e., the algorithm robustness was no better than the three-stage inversion method. We selected the ε corresponding to the RMSE minimum value with comprehensive consideration.
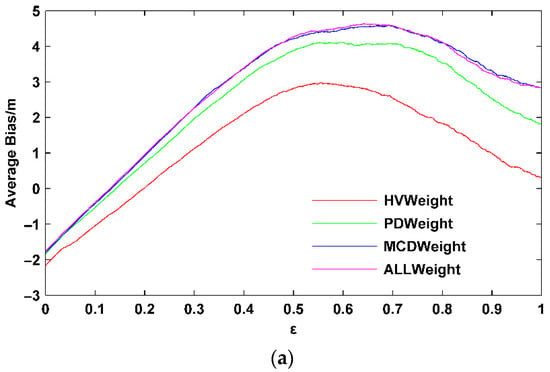
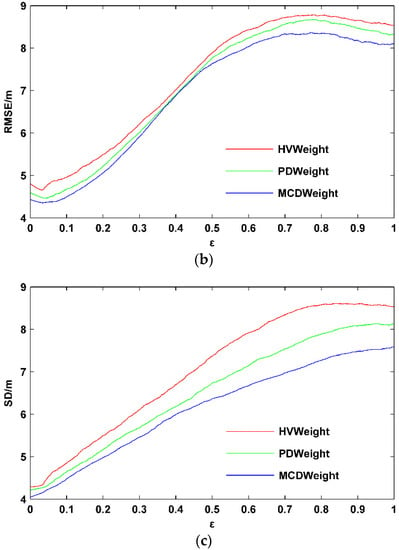
Figure 11.
Forest height statistical indicator changes with the ε. (a) Average bias; (b) RMSE; (c) Standard deviation.
Compared with the HV method, the underestimation of forest height inversion was improved after coherence optimization, and the RMSE was reduced [27,36]. The PD method was based on phase information, which improved forest height inversion to some extent. The MCD method was based on coherence amplitude and phase, which was better than the PD method. After introducing the coherence amplitude term and modifying fixed weights to weight variables, the corresponding method (weight) was the same as the overall trend of the three-stage inversion algorithm based on coherence optimization.
Considering time and signal-to-noise ratio decorrelation, this study could invest forest height from the airborne L-band single-baseline full polarization SAR data in the flat terrain. When applied to real data, the inverted forest height was combined with the average height of the forest stand to minimize its RMSE to automatically select an appropriate ε. The smaller the RMSE, the higher the accuracy of the corresponding method. At the same time, a y = x straight line equation could be fitted between the inverted forest height and the measured forest stand height. The closer the fitted straight line equation was to y = x, the more accurate the corresponding inversion method was.
The accuracy of the algorithm was related to the system parameters of the aircraft and the structural parameters of the forest (forest density, height), etc. Since only some parameters could be fixed to analyze the relative error of the RVoG model inversion of forest height, an uncertainty could not be given for quantifying all involved parameters. Due to the most influential factor being the vertical wave number kz of the forest, the forest height relative error changed with the forest height and vertical wavenumber kz when the time decorrelation was 0.8, and extinction coefficient was fixed at 0, 0.1, and 0.5 dB/m, respectively. Given the values of hv, σ and kz, the vegetation pure volume coherence γv (hv, σ, kz) was calculated according to Formula (2) for L-band data. Given a fixed time decorrelation intensity γt, γo = γv (hv, σ, kz) γt was then calculated. For each generated γo sample, the forest height hvi was inverted by the three-stage method within the 2π ambiguity elevation, and the relative error of forest height was analyzed. The relative error of forest height was |hvi − hv|/hv × 100%. Figure 12 shows the forest height relative error changes with the forest height and vertical wavenumber kz under three extinction coefficient levels (0.0, 0.1, and 0.5 dB/m) at γt = 0.8, respectively.
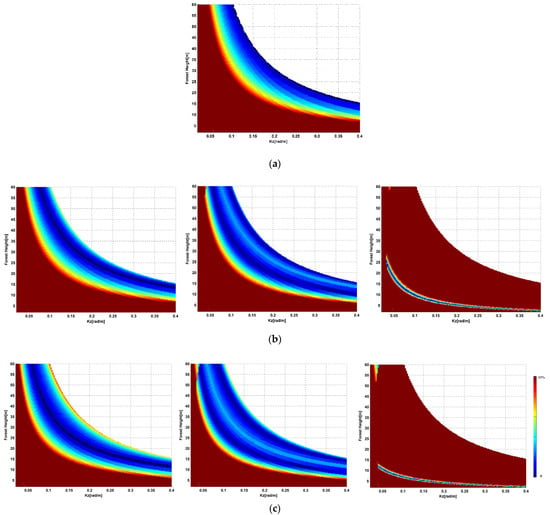
Figure 12.
When the time decorrelation was 0.8, and extinction coefficient was fixed at 0, 0.1, 0.5 dB/m, respectively, the forest height relative error changed with the forest height and vertical wavenumber kz. (a) σ = 0 dB/m; (b) σ = 0.1 dB/m left: = 0 middle: = 0.04 right: = 0.5; (c) σ = 0.5 dB/m left: = 0 middle: = 0.04 right: = 0.5.
It was shown that for a given vertical wavenumber kz, the inversion performance of forest height was the best only in a certain height range. The forest height relative error was larger in places with low forest height, and it decreased with increasing forest height (Figure 12).
The simulation results showed that in order to achieve 10% accuracy in the forest height range from 8 m to 60 m, various baselines (vertical wavenumber kz) had to be required, and the number of baselines required depended on the extinction coefficient. Among all extinction coefficient levels, the forest height ranged from 8 m to 60 m, and the three baselines were sufficient to make the forest height relative error better than 10% (on the left of Figure 12). For example, if the forest height ranged from 8 m to 40 m, the three baselines were sufficient to make the forest height relative error better than 10% at σ = 0.1 dB/m (on the left of Figure 12b), and only the two baselines were sufficient at σ = 0.5 dB/m (on the left of Figure 12c). After introducing the overestimation and underestimation terms (on the middle and right of Figure 12b,c), the accuracy of forest height inversion could be improved by selecting the appropriate weight coefficient , and even higher forest height inversion accuracy could be obtained by using one baseline (on the middle and right of Figure 12b,c). An uncertainty model that quantifies all involved parameters will be the subject of future work.
ALOS-2 with an enhanced PALSAR instrument launched in 2014, where ALOS left in 2011, and will build L-band SAR data for monitoring the global environment. However, ALOS-2 has a strong temporal decoherence effect, leading the coherence in the forest to be too low to make the forest height estimation with POLInSAR impossible. The upcoming TanDEM-L with spaceborne monostatic and bistatic SAR imagery solved the problem of time decoherence very well. We therefore expected that our results would be valuable for a wide range of future research topics, including all future airborne and spaceborne SAR with the upcoming low frequencies forest missions, ALOS-4, NISAR (NASA-ISRO Synthetic Aperture Radar), and Tandem-L (all L-band), as well as BIOMASS. An unprecedented combination of sensors will be seen in the next few years, e.g., BIOMASS links to the Global Ecosystem Dynamics Investigation (GEDI) and NISAR missions will be particularly important for measuring forest structure parameter, such as forest height and biomass. The in-situ data for GEDI, BIOMASS, and NISAR collaborated by the ESA-NASA, will further help to achieve more forest height inversion performance. Meanwhile, LIDAR data with a relatively fine scale and accurate map of forest height and biomass represents an important complement to in situ, airborne data. In situ data, when combined with LIDAR and GEDI data, will allow forest height inversion on canopy structure and even biomass with POLInSAR to be estimated. This study is expected to mitigate the overestimation and underestimation problem of forest height inversion for the upcoming L-band SAR satellite generation, new SAR and LIDAR systems combined with RPAs (Remotely Piloted Aircrafts)/UAVs (Unmanned Aerial Vehicles) for small areas mapping initiatives, and to promote the depth and breadth of SAR applications of the new SAR system.
6. Real SAR Data
The SAR data in the Traunstein were the E-SAR L-band single-baseline full PolInSAR data obtained by the German Aerospace Center (DLR) in 2003. The study area was a plantation forest, and the terrain was relatively flat with only some small slopes. The altitude of the aircraft was about 3000 m, the space baseline was about 5 m, the time baseline was 20 min, and the central incidence angle was 45°. The range resolution was 1.5 m, and the azimuth resolution was 3 m with four looks. The data were precisely registered, and flat phase and effective wavenumbers were provided.
The computational effort was 2~3 times that required of the original three-stage inversion method. The time of the SINC function inversion method was similar to that of the three-stage method, in which the time for the automatic weight selection method with one forest stand was about 45.70 s. Finally, the three weight methods with one forest stand with Matlab software for calculation took about 3.04 s.
The measured data and ground-truth data concerning the stand height of the sample plot are shown in Figure 13. The forest height images obtained by the three-stage inversion methods are shown in Figure 13A, and the three-stage methods introducing the coherent magnitude term are shown in Figure 13B. The ground-truth data used in the study mainly included the boundaries of eight stands and the average height of dominant trees, which were obtained by the Munich Forest Harvest Scientific Committee through field surveys, as shown in Figure 13Ad and 13Bd. Table 4 shows the RMSE of various methods for the corresponding eight forest stands with real data. The result showed that coherent optimization methods may also not achieve the best accuracy. After the modified two-step, three-stage inversion algorithm is carried out, the RMSE can always be minimized, and the number of the minimum RMSE obtained by the PD coherent optimization method is greater. In order to obtain a better RMSE, it was necessary to use coherent optimization methods. was the response to forest stand structure, because the scattering mechanisms were different for different forest stands and different forest heights. The approach performed well in the case of different plant densities and different plant height variability with simulation forest relative error and real forest stands. The fitting equations between the forest height estimated by six methods and the stand height of the plot are shown in Table 5. Unlike the simulated data, the three-stage inversion method overestimated the forest height, which may be caused by the vertical baseline of the data. Simulation data showed that the three-stage method would underestimate forest height, but in practical applications, forest height could produce overestimation and underestimation owing to the length of the vertical baseline determined by the sensitivity of the interferometric phase difference to different forest heights. Forest height inversion by PolInSAR data requires ideal baselines. Due to the complexity of the real SAR data and the small sample sizes, the three-stage inversion method based on coherent optimization was lower than the three-stage inversion method. After introducing the coherent magnitude term, the overestimation of the forest height was significantly weakened in HVWeight, PDweight, and MCDWeight, and PDWeight was optimal. Compared with the original three-stage method, the inversion accuracy of simulated data increased by up to 9.38%, and 59.85% with real data at most.
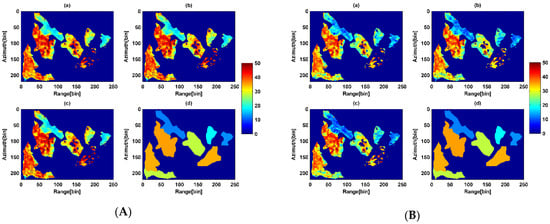
Figure 13.
Improved three-stage method for forest height inversion of ESA PolInSAR data. (A) Three-stage method for forest height inversion based on coherence optimization (a) HV (b) PD (c) MCD (d) The average stand forest height of field measurement (B) Introduction of coherence amplitude for Forest height inversion (a) HVWeight (b) PDWeight (c) MCDWeight (d) The average stand forest height of field measurement.

Table 4.
The RMSE of various methods for the corresponding 8 forest stands with real data.

Table 5.
The fitting equation between the retrieved forest height and the field measurement stand forest height.
7. Conclusions
Compared with the forest height inversion accuracy with the simulation and real SAR data, it was necessary to use coherent optimization methods to obtain a better RMSE for the forest height inversion using single-baseline L-band PolInSAR data. Using ε times the ground scattering ratio as the weight alleviates the underestimation and overestimation phenomena of the forest height estimation and reduces the RMSE to some extent, but the robustness of the forest height inversion is reduced due to the introduction of the coherence amplitude term.
This study can invest forest height from the airborne L-band single-baseline full polarization SAR data in the flat terrain. Since this study only simulates coniferous forests with a forest height of 18 m and a forest density of 500, and applies and validates these methods with small real data, other scholars can apply these methods with more airborne L-band SAR data to better explain the applicability and limitations of these methods.
Due to the inherent characteristics of SAR images, shadows, overlays, and top-to-bottom overlaps may occur with large terrain fluctuations. Single-baseline PolInSAR cannot solve these problems temporarily. Therefore, this study mainly considers areas with flat terrain, not taking the terrain into account. This study does not consider the effect of slope on forest height inversion, and mainly focuses on solving the problem of the overestimation and underestimation of forest height inversion by the three-stage method through a modified two-step, three-stage inversion algorithm. When the slope of the terrain is not very high, the R-RVoG model can be used to invert the forest height. In the case of a higher slope, the multi-baselines TomoSAR method can be used to invert the forest height more accurately, which is what we want to do in the near future.
Author Contributions
J.Z. conceived the idea, designed and performed the experiments, produced the results, and drafted the manuscript. W.F. contributed to discuss with the idea and results, and revision of the article. Y.Z., L.H., Y.Y. and X.M. contributed to the discussion of the results and revision of the article. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Natural Science Foundation of China (contract no. 31971654, 41725003), the Civil Aerospace Technology Advance Research Project (contract no. D040114), and the National Natural Science Foundation of China (contract no. 42101067).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Woodhouse, I.H. Predicting backscatter-biomass and height-biomass trends using a macroecology model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 871–877. [Google Scholar] [CrossRef]
- Houghton, R.A.; Hall, F.; Goetz, S.J. Importance of biomass in the global carbon cycle. J. Geophys. Res. 2015, 114, 1–13. [Google Scholar] [CrossRef]
- Wright, S.J. Tropical forests in a changing environment. Trends Ecol. Evol. 2005, 20, 553–560. [Google Scholar] [CrossRef] [PubMed]
- Pan, Y.; Birdsey, R.A.; Fang, J.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A large and persistent carbon sink in the world’s forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [Green Version]
- Minh, D.H.T.; Le Toan, T.; Rocca, F.; Tebaldini, S.; Villard, L.; Rejou-Mechain, M.; Phillips, O.L.; Feldpausch, T.R.; Dubois-Fernandez, P.; Scipal, K.; et al. SAR tomography for the retrieval of forest biomass and height: Cross-validation at two tropical forest sites in French Guiana. Remote Sens. Environ. 2016, 175, 138–147. [Google Scholar] [CrossRef] [Green Version]
- Fu, W.X.; Guo, H.D.; Li, X.W.; Tian, B.S.; Sun, Z.C. Extended Three-Stage Polarimetric SAR Interferometry Algorithm by Dual-Polarization Data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2792–2802. [Google Scholar]
- Sagues, L.; Lopez-Sanchez, J.M.; Fortuny, J.; Fabregas, X. Polarimetric radar interferometry for improved mine detection and surface clutter rejection. IEEE Trans. Geosci. Remote Sens. 2001, 39, 1271–1278. [Google Scholar] [CrossRef]
- Cloude, S.; Papathanassiou, K. Polarimetric optimisation in radar interferometry. Electron. Lett. 1997, 33, 1176–1178. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; Zyl, J.J. Vegetation characteristics and underlying topography from interferometric radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Cloude, S.R.; Papathanassiou, K.P. Polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 1998, 36, 1551–1565. [Google Scholar] [CrossRef]
- Wang, C.C.; Wang, L.; Fu, H.Q.; Xie, Q.H.; Zhu, J.J. The Impact of Forest Density on Forest Height Inversion Modeling from Polarimetric InSAR Data. Remote Sens. 2016, 8, 291. [Google Scholar] [CrossRef] [Green Version]
- Papathanassiou, K.P.; Cloude, S.R. Single-baseline polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 2352–2363. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R.; Papathanassiou, K.P. Three-stage inversion process for polarimetric SAR interferometry. IEE Proc-Radar Sonar Navig. 2003, 150, 125–134. [Google Scholar] [CrossRef] [Green Version]
- Ballester-Berman, J.D.; Lopez-Sanchez, J.M.; Fortuny-Guasch, J. Retrieval of biophysical parameters of agricultural crops using polarimetric SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 683–694. [Google Scholar] [CrossRef]
- Praks, J.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I.; Hallikainen, M. Height estimation of boreal forest: Interferometric model-based inversion at L- and X-band versus HUTSCAT profiling scatterometer. IEEE Geosci. Remote Sens. Lett. 2007, 4, 466–470. [Google Scholar] [CrossRef]
- Garestier, F.; Dubois-Fernandez, P.C.; Champion, I. Forest Height Inversion Using High-Resolution P-Band Pol-InSAR Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 3544–3559. [Google Scholar] [CrossRef]
- Lee, S.K.; Kugler, F.; Papathanassiou, K.P.; Hajnsek, I. Quantifying Temporal Decorrelation over Boreal Forest at L- and P-band. In Proceedings of the European Conference on Synthetic Aperture Radar, Friedrichshafen, Germany, 2–5 June 2008; pp. 1–4. [Google Scholar]
- Zhang, Q.; Liu, T.D.; Ding, Z.G.; Zeng, T.; Long, T. A Modified Three-Stage Inversion Algorithm Based on R-RVoG Model for Pol-InSAR Data. Remote Sens. 2016, 8, 861. [Google Scholar] [CrossRef] [Green Version]
- Managhebi, T.; Maghsoudi, Y.; Zoej, M.J.V. An Improved Three-Stage Inversion Algorithm in Forest Height Estimation Using Single-Baseline Polarimetric SAR Interferometry Data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 887–891. [Google Scholar] [CrossRef]
- Bai, L.; Hong, W.; Cao, F. Estimation error of topographic phase based on RVoG model using POLinSAR data. In Proceedings of the Progress in Electromagnetics Research Symposium (PIERS ONLINE), Nantes, France, 13–17 July 1998; pp. 306–310. [Google Scholar]
- Hashjin, S.S.; Khazai, S.; Sadeghi, A. A Method to Select Coherence Window Size for forest height estimation using PolInSAR Data. In Proceedings of the ISPRS, Tehran, Iran, 5–8 October 2013; pp. 505–508. [Google Scholar]
- Neumann, M.; Ferro-Famil, L.; Reigber, A. Multibaseline polarimetric SAR interferometry coherence optimization. IEEE Geosci. Remote Sens. Lett. 2008, 5, 93–97. [Google Scholar] [CrossRef]
- Colin, E.; Titin-Schnaider, C.; Tabbara, W. An interferometric coherence optimization method in radar polarimetry for high-resolution imagery. IEEE Trans. Geosci. Remote Sens. 2006, 44, 167–175. [Google Scholar] [CrossRef]
- Gomezdans, J.L.; Quegan, S. Constraining Coherence Optimisation in Polarimetric Interferometry of Layered Targets. In Proceedings of the POLinSAR 2005 Workshop ESRIN, Frascati, Italy, 17–21 January 2005; pp. 1–6. [Google Scholar]
- Flynn, T.; Tabb, M.; Carande, R. Coherence region shape extraction for vegetation parameter estimation in polarimetric SAR interferometry. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Toronto, ON, Canada, 24–28 June 2002; pp. 2596–2598. [Google Scholar]
- Tabb, M.; Orrey, J.; Flynn, T.; Carande, R. Phase diversity: A decomposition for vegetation parameter estimation using polarimetric SAR interferometry. In Proceedings of the Fourth European Synthetic Aperture RADAR Conference, Cologne, Germany, 4–6 June 2002; pp. 721–724. [Google Scholar]
- Xie, Q.; Zhu, J.; Wang, C.; Fu, H. Boreal forest height inversion using E-SAR PolInSAR data based coherence optimization methods and three-stage algorithm. In Proceedings of the International Workshop on Earth Observation and Remote Sensing Applications, Changsha, China, 11–14 June 2014; pp. 145–150. [Google Scholar]
- Lavalle, M.; Solimini, D.; Pottier, E.; Desnos, Y.L. Comparison of models of POLINSAR coherence for forest height retrieval using POLINSAR simulated data. Matrix 2008, 54, 2792–2802. [Google Scholar]
- Lin, D.F.; Zhu, J.J.; Fu, H.Q.; Xie, Q.H.; Zhang, B. A TSVD-Based Method for Forest Height Inversion from Single-Baseline PolInSAR Data. Appl. Sci. 2017, 7, 435. [Google Scholar] [CrossRef] [Green Version]
- Cloude, S.R. Polarization coherence tomography. Radio Sci. 2006, 41, 1–27. [Google Scholar] [CrossRef]
- Cloude, S.R. POL-InSAR training course. In Proceedings of the Advance Training Course on Land Remote Sensing, Scotland, UK, January 2008; pp. 1–44. [Google Scholar]
- Cloude, S.R. Polarisation Applications in Remote Sensing; Oxford University Press Inc.: New York, NY, USA, 2010. [Google Scholar]
- Minh, N.P.; Wang, C.; Zou, B.; Nguyen, Q.T.; Le, V.N. Forest Height Extraction from PolInSAR Image Using a Hybrid Method. Int. J. Signal Process. Image Process. Pattern Recognit. 2014, 7, 257–274. [Google Scholar] [CrossRef]
- Minh, N.P.; Zou, B.; Lu, D. Accuracy improvement method of forest height estimation for PolInSARImage. In Proceedings of the International Conference on Audio, Language and Image Processing, Shanghai, China, 16–18 July 2012; pp. 594–598. [Google Scholar]
- Minh, N.P.; Zou, B. A Novel Algorithm for Forest Height Estimation from PolInSAR Image. Int. J. Signal Process. Image Process. Pattern Recognit. 2013, 6, 15–32. [Google Scholar]
- Chen, E.X. Comparison of Methods to Derive Forest Height from Polarimetric SAR Interferometry. In Proceedings of the Proc Dragon, Beijing, China, 21–25 April 2008; pp. 1–9. [Google Scholar]
- Managhebi, T.Y.; Maghsoudi; Zoej, M.J.V. A volume optimization method to improve the three-stage inversion Algorithm for Forest Height Estimation Using PolInSAR Data. IEEE Geosci. Remote Sens. Lett. 2018, 15, 1214–1218. [Google Scholar] [CrossRef]
- Huu, C.T.; Minh, N.P.; Xuan, M.T.; Le, V.N.; Dang, C.H.; Nghia, P.M. An improved volume coherence optimization method for forest height estimation using PolInSAR images. In Proceedings of the 2019 3rd International Conference on Recent Advances in Signal Processing, Telecommunications & Computing (SigTelCom), Hanoi, Vietnam, 21–22 March 2019. [Google Scholar]
- Aghabalaei, A.; Ebadi, H.; Maghsoudi, Y. Forest height estimation by means of compact PolInSAR data. Remote Sens. Appl. Soc. Environ. 2021, 23, 100552. [Google Scholar] [CrossRef]
- Xing, C.; Zhang, T.; Wang, H.M.; Zeng, L.; Yin, J.; Yang, Y. A novel four-stage method for vegetation height estimation with repeat-pass PolInSAR data via temporal decorrelation adaptive estimation and distance transformation. Remote Sens. 2021, 13, 213. [Google Scholar] [CrossRef]
- Soja, M.J.; Karlson, M.; Bayala, J.; Bazié, H.R.; Sanou, J.; Tankoano, B.; Eriksson, L.E.B.; Reese, H.; Ostwald, M.; Ulander, L.M.H. Mapping tree height in Burkina Faso Parklands with TanDEM-X. Remote Sens. 2021, 13, 2747. [Google Scholar] [CrossRef]
- Lei, Y.; Treuhaft, R.; Gonçalves, F. Automated estimation of forest height and underlying topography over a Brazilian tropical forest with single-baseline single-polarization TanDEM-X SAR interferometry. Remote Sens. Environ. 2021, 252, 112132. [Google Scholar] [CrossRef]
- Khati, U.; Singh, G.; Kumar, S. Potential of space-borne PolInSAR for forest canopy height estimation over India—A case study using fully polarimetric L-, C-, and X-band SAR data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 2406–2416. [Google Scholar] [CrossRef]
- Chen, H.; Cloude, S.R.; White, J.C. Using GEDI Waveforms for improved TanDEM-X forest height mapping: A combined SINC + Legendre approach. Remote Sens. 2021, 13, 2882. [Google Scholar] [CrossRef]
- Lavalle, M.; Simard, M.; Solimini, D.; Pottier, E. Height-dependent temporal decorrelation for POLINSAR and TOMOSAR forestry applications. in Synthetic Aperture Radar (EUSAR). In Proceedings of the 2010 8th European Conference on VDE, Aachen, Germany, 7–10 June 2010. [Google Scholar]
- Pardini, M.; Cazcarra-Bes, V.; Papathanassiou, K.P. TomoSAR mapping of 3D forest structure: Contributions of L-band configurations. Remote Sens. 2021, 13, 2255. [Google Scholar] [CrossRef]
- Lucas, R.M.; Lee, A.C.; Williams, M.L. Enhanced Simulation of Radar Backscatter from Forests Using LiDAR and Optical Data. IEEE Trans. Geosci. Remote Sens. 2006, 44, 2736–2754. [Google Scholar] [CrossRef]
- Shi, L. Vegetation Height und Underlying Ground Altitude Estimation Based on Multi-Baseline POLINSAR Images. Ph.D. Thesis, Wuhan University, Wuhan, China, 2013. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).