Remote Sensing and Meteorological Data Fusion in Predicting Bushfire Severity: A Case Study from Victoria, Australia
Abstract
:1. Introduction
- What are the most important meteorological variables and their relative influence on bushfire severity prediction?
- What is the predictive performance capability of the different ensemble machine learning models?
- What management and policy recommendations can be synthesised from the research outcomes and transformed to community wellbeing?
- This is the first work to our knowledge that has performed a thorough analysis of 62 meteorological parameters (including humidity, temperature, and wind in multiple vertical isobar levels) of high spatial resolution and temporal frequency to quantify the relative influence of variables in bushfire severity prediction.
- A comparative assessment of predictive performances of widely used machine learning models on handling complex, high-dimensional, multicollinear meteorological data.
- Improve understanding of bushfire-severity-influencing variables that help formulate better bushfire management and suppression strategies.
2. Materials and Methods
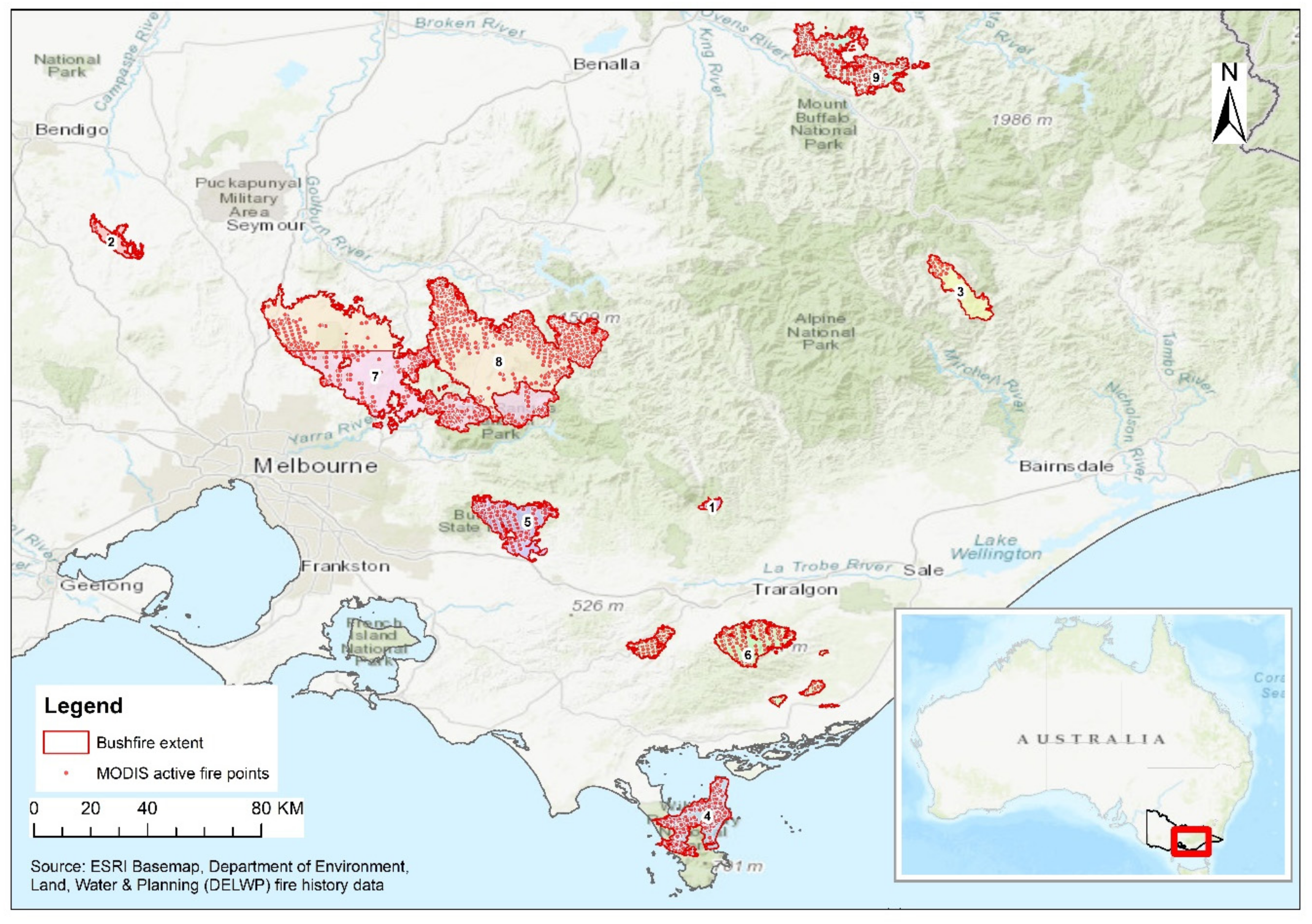
2.1. Study Area
2.2. Fire Data
2.3. Meteorological Data
2.3.1. Meteorological Data Extraction
2.3.2. Temporal Frequency
2.4. Target Variable–Bushfire Burn Severity
2.4.1. Approach to Multiscale Data Integration
2.4.2. Remote Sensing Data
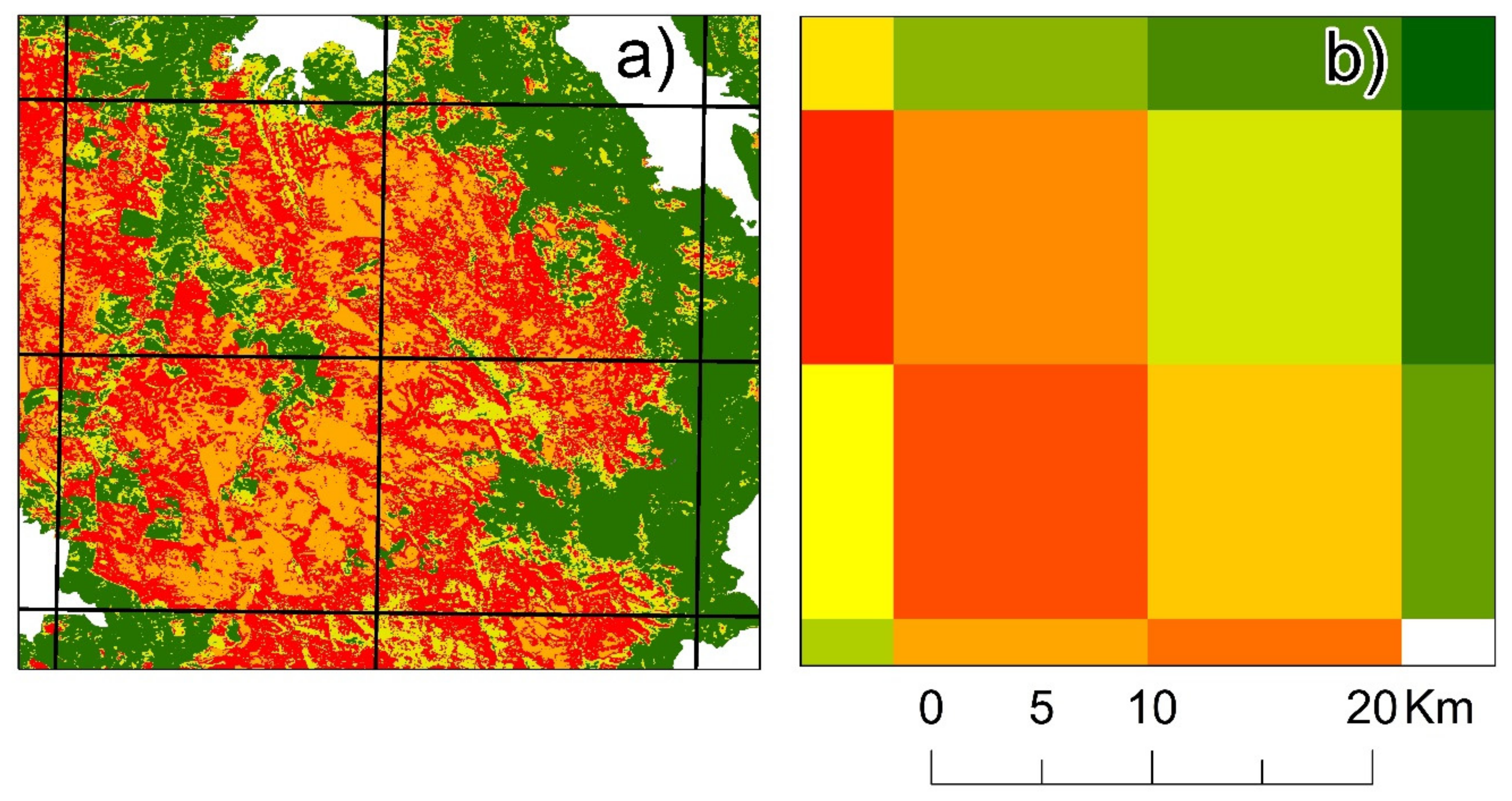
2.4.3. Bushfire Severity Classification
2.4.4. Bushfire Severity Accuracy Assessment
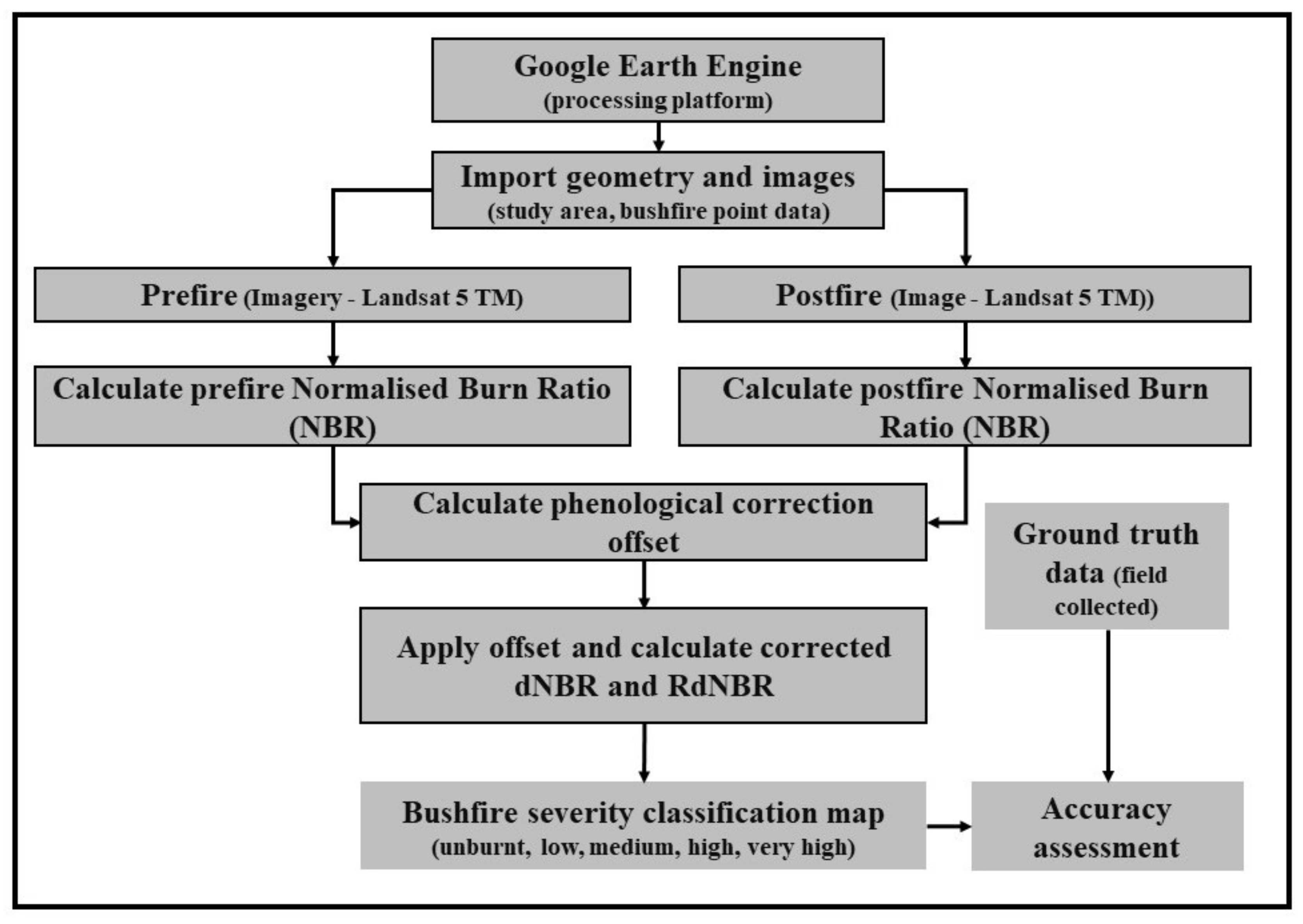
2.4.5. Processing Platform—Google Earth Engine
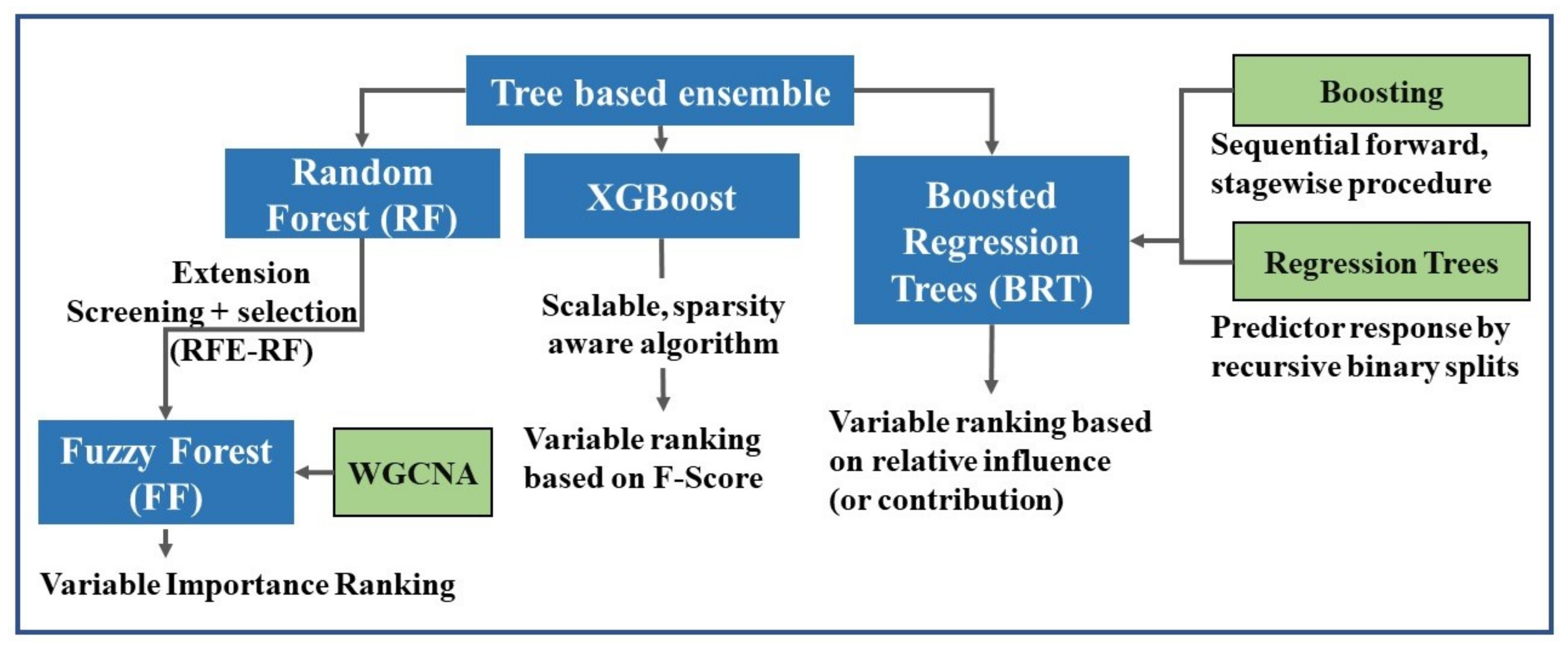
2.5. Methods for Variable Selection
2.5.1. Multicollinearity Test
2.5.2. Variable Selection Models
2.5.3. Accuracy Assessment Methods
2.6. Method Implementation
3. Results
3.1. Multicollinearity Analysis
3.2. Target Variable
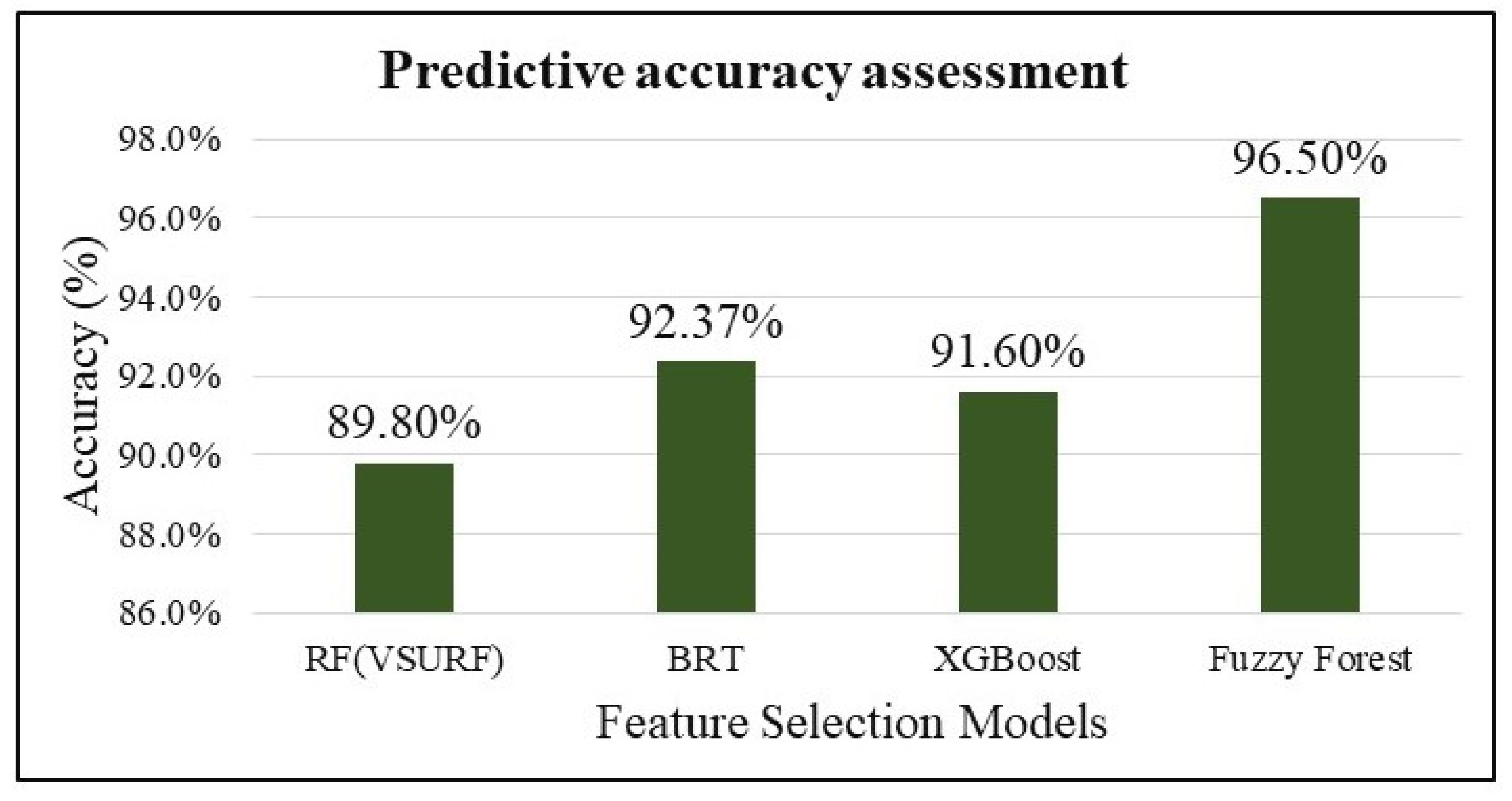
3.3. Predictive Assessment of Feature-Selection Models
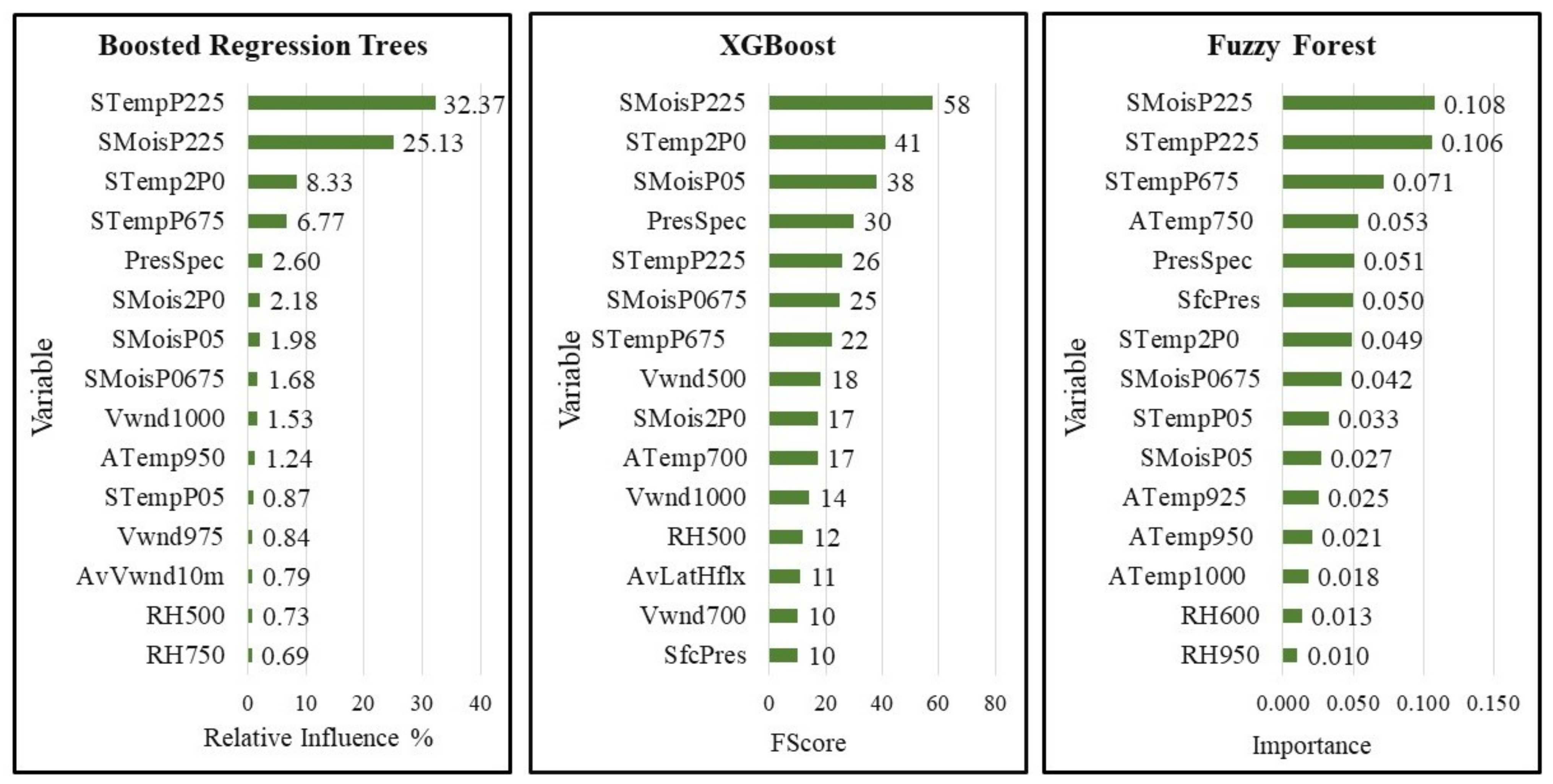
3.4. Variable Ranking
4. Discussion
4.1. Performance of Variable Selection Models
4.2. Relative Influence of Meteorological Variables on Bushfire Severity
4.3. Management and Policy Outlook
4.4. Limitations
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sharples, J.J.; Cary, G.J.; Fox-hughes, P.; Mooney, S.; Evans, J.P.; Fletcher, M.; Fromm, M.; Grierson, P.F.; Mcrae, R.; Baker, P. Natural Hazards in Australia: Extreme Bushfire. Clim. Change 2016, 139, 85–99. [Google Scholar] [CrossRef]
- Bowman, D.M.J.S.; Williamson, G.J.; Gibson, R.K.; Bradstock, R.A.; Keenan, R.J. The Severity and Extent of the Australia 2019–20 Eucalyptus Forest Fires Are Not the Legacy of Forest Management. Nat. Ecol. Evol. 2019, 5, 1003–1010. [Google Scholar] [CrossRef] [PubMed]
- Turco, M.; Rosa-Cánovas, J.J.; Bedia, J.; Jerez, S.; Montávez, J.P.; Llasat, M.C.; Provenzale, A. Exacerbated Fires in Mediterranean Europe Due to Anthropogenic Warming Projected with Non-Stationary Climate-Fire Models. Nat. Commun. 2018, 9, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Burke, M.; Driscoll, A.; Heft-Neal, S.; Xue, J.; Burney, J.; Wara, M. The Changing Risk and Burden of Wildfire in the United States. Proc. Natl. Acad. Sci. USA 2021, 118, e2011048118. [Google Scholar] [CrossRef] [PubMed]
- Bowman, D.M.J.S.; Balch, J.K.; Artaxo, P.; Bond, W.J.; Carlson, J.M.; Cochrane, M.A.; Antonio, C.M.D.; Defries, R.S.; Doyle, J.C.; Harrison, S.P.; et al. Fire in the Earth System. Science 2009, 324, 481–485. [Google Scholar] [CrossRef] [PubMed]
- Dutta, R.; Das, A.; Aryal, J. Big Data Integration Shows Australian Bush-Fire Frequency Is Increasing Significantly. R. Soc. Open Sci. 2016, 3, 150241. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Dutta, R.; Aryal, J.; Das, A.; Kirkpatrick, J.B. Deep Cognitive Imaging Systems Enable Estimation of Continental-Scale Fire Incidence from Climate Data. Sci. Rep. 2013, 3, 03188. [Google Scholar] [CrossRef] [Green Version]
- Prior, T.; Eriksen, C. Wildfire Preparedness, Community Cohesion and Social-Ecological Systems. Glob. Environ. Change 2013, 23, 1575–1586. [Google Scholar] [CrossRef] [Green Version]
- Linnenluecke, M.K.; Stathakis, A.; Griffiths, A. Firm Relocation as Adaptive Response to Climate Change and Weather Extremes. Glob. Environ. Change 2011, 21, 123–133. [Google Scholar] [CrossRef]
- Halgamuge, M.N.; Daminda, E.; Nirmalathas, A. Best Optimizer Selection for Predicting Bushfire Occurrences Using Deep Learning. Nat. Hazards 2020, 103, 845–860. [Google Scholar] [CrossRef]
- Shi, G.; Yan, H.; Zhang, W.; Dodson, J.; Heijnis, H.; Burrows, M. Rapid Warming Has Resulted in More Wildfires in Northeastern Australia. Sci. Total Environ. 2021, 771, 144888. [Google Scholar] [CrossRef]
- Beale, J.; Jones, W. Preventing and Reducing Bushfire Arson in Australia: A Review of What Is Known. Fire Technol. 2011, 47, 507–518. [Google Scholar] [CrossRef]
- Mcaneney, J.; Chen, K.; Pitman, A. 100-Years of Australian Bushfire Property Losses: Is the Risk Significant and Is It Increasing? J. Environ. Manag. 2009, 90, 2819–2822. [Google Scholar] [CrossRef]
- Godfree, R.C.; Knerr, N.; Encinas-viso, F.; Albrecht, D.; Bush, D.; Cargill, D.C.; Clements, M.; Gueidan, C.; Guja, L.K.; Harwood, T.; et al. Implications of the 2019–2020 Megafires for the Biogeography and Conservation of Australian Vegetation. Nat. Commun. 2020, 12, 1–13. [Google Scholar] [CrossRef]
- Tosic, I.; Mladjan, D.; Gavrilov, M.B.; Zivanović, S.; Radaković, M.G.; Putniković, S.; Petrović, P.; Mistridzelović, I.K.; Marković, S.B. Potential Influence of Meteorological Variables on Forest Fire Risk in Serbia during the Period 2000–2017. Open Geosci. 2019, 11, 414–425. [Google Scholar] [CrossRef] [Green Version]
- Santika, T.; Budiharta, S.; Law, E.A.; Dennis, R.A.; Dohong, A.; Struebig, M.J.; Medrilzam; Gunawan, H.; Meijaard, E.; Wilson, K.A. Interannual Climate Variation, Land Type and Village Livelihood Effects on Fires in Kalimantan, Indonesia. Glob. Environ. Change 2020, 64, 102129. [Google Scholar] [CrossRef]
- Bradstock, R.A. A Biogeographic Model of Fire Regimes in Australia: Current and Future Implications. Glob. Ecol. Biogeogr. 2010, 19, 145–158. [Google Scholar] [CrossRef]
- Oldenborgh, G.J.V.; Krikken, F.; Lewis, S.; Leach, N.J.; Lehner, F.; Saunders, K.R.; Van Weele, M.; Haustein, K.; Li, S.; Wallom, D.; et al. Attribution of the Australian Bushfire Risk to Anthropogenic Climate Change. Nat. Hazards Earth Syst. Sci. 2021, 21, 941–960. [Google Scholar] [CrossRef]
- Sharples, J.J. An Overview of Mountain Meteorological Effects Relevant to Fire Behaviour and Bushfire Risk. Int. J. Wildl. Fire 2009, 18, 737–754. [Google Scholar] [CrossRef]
- Sanderson, B.M.; Fisher, R.A. A Fiery Wake-up Call for Climate Science. Nat. Clim. Change 2020, 10, 175–177. [Google Scholar] [CrossRef]
- Argañaraz, J.P.; Gavier Pizarro, G.; Zak, M.; Landi, M.A.; Bellis, L.M. Human and Biophysical Drivers of Fires in Semiarid Chaco Mountains of Central Argentina. Sci. Total Environ. 2015, 520, 1–12. [Google Scholar] [CrossRef]
- Rasilla, D.F.; García-Codron, J.C.; Carracedo, V.; Diego, C. Circulation Patterns, Wildfire Risk and Wildfire Occurrence at Continental Spain. Phys. Chem. Earth 2010, 35, 553–560. [Google Scholar] [CrossRef]
- Ma, W.; Feng, Z.; Cheng, Z.; Chen, S.; Wang, F. Identifying Forest Fire Driving Factors and Related Impacts in China Using Random Forest Algorithm. Forests 2020, 11, 507. [Google Scholar] [CrossRef]
- Liang, H.; Zhang, M.; Wang, H. A Neural Network Model for Wildfire Scale Prediction Using Meteorological Factors. IEEE Access 2019, 7, 176746–176755. [Google Scholar] [CrossRef]
- Jenkins, M.E.; Bedward, M.; Price, O.; Bradstock, R.A. Modelling Bushfire Fuel Hazard Using Biophysical Parameters. Forests 2020, 11, 925. [Google Scholar] [CrossRef]
- Guo, F.; Su, Z.; Wang, G.; Sun, L.; Tigabu, M.; Yang, X.; Hu, H. Understanding Fire Drivers and Relative Impacts in Different Chinese Forest Ecosystems. Sci. Total Environ. 2017, 605–606, 411–425. [Google Scholar] [CrossRef]
- Su, Z.; Hu, H.; Wang, G.; Ma, Y.; Yang, X.; Guo, F. Using GIS and Random Forests to Identify Fire Drivers in a Forest City, Yichun, China. Geomat. Nat. Hazards Risk 2018, 9, 1207–1229. [Google Scholar] [CrossRef] [Green Version]
- Blanchi, R.; Leonard, J.; Haynes, K.; Opie, K.; James, M.; Oliveira, F.D. de Environmental Circumstances Surrounding Bushfire Fatalities in Australia 1901-2011. Environ. Sci. Policy 2014, 37, 192–203. [Google Scholar] [CrossRef] [Green Version]
- Nolan, R.H.; Boer, M.M.; Collins, L.; Resco de Dios, V.; Clarke, H.; Jenkins, M.; Kenny, B.; Bradstock, R.A. Causes and Consequences of Eastern Australia’s 2019–20 Season of Mega-Fires. Glob. Change Biol. 2020, 26, 1039–1041. [Google Scholar] [CrossRef] [Green Version]
- Dowdy, A.J.; Mills, G.A.; Finkele, K.; De Groot, W. Australian Fire Weather as Represented by the McArthur Forest Fire Danger Index and the Canadian Forest Fire Weather Index; Centre for Australian Weather and Climate Research: Melbourne, Austrialia, 2009. [Google Scholar]
- Bradstock, R.A.; Auld, T.D. Soil Temperatures During Experimental Bushfires in Relation to Fire Intensity: Consequences for Legume Germination and Fire Management in South-Eastern Australia. J. Appl. Ecol. 1995, 32, 76. [Google Scholar] [CrossRef]
- Storey, M.A.; Bedward, M.; Price, O.F.; Bradstock, R.A.; Sharples, J.J. Derivation of a Bayesian Fire Spread Model Using Large-Scale Wildfire Observations. Environ. Model. Softw. 2021, 144, 105127. [Google Scholar] [CrossRef]
- Knight, I.K.; Sullivan, A.L. A Semi-Transparent Model of Bushfire Flames to Predict Radiant Heat Flux. Int. J. Wildl. Fire 2004, 13, 201–207. [Google Scholar] [CrossRef]
- Potter, B.E. Atmospheric Interactions with Wildland Fire Behaviour I. Basic Surface Interactions, Vertical Profiles and Synoptic Structures. Int. J. Wildl. Fire 2012, 21, 779–801. [Google Scholar] [CrossRef]
- Taylor, J.; Webb, R. Meteorological Aspects of the January 2003 South-Eastern Australia Bushfire Outbreak. Aust. For. 2005, 68, 94–103. [Google Scholar] [CrossRef]
- Guo, H.; Wang, L.; Liang, D. Big Earth Data from Space: A New Engine for Earth Science. Sci. Bull. 2016, 61, 505–513. [Google Scholar] [CrossRef]
- Olden, J.D.; Lawler, J.J.; Poff, N.L. Machine Learning Methods Without Tears: A Primer for Ecologists. Q. Rev. Biol. 2008, 83, 171–193. [Google Scholar] [CrossRef] [Green Version]
- Sharma, A.; Dey, S. A Comparative Sudy of Feature Selection and Machine Learning Techniques for Sentiment Analysis. In Proceedings of the 2012 ACM Research in Applied Computation Symposium, San Antoino, TX, USA, 23–26 October 2012; pp. 1–7. [Google Scholar]
- Hosseini, F.S.; Choubin, B.; Mosavi, A.; Nabipour, N.; Shamshirband, S.; Darabi, H.; Haghighi, A.T. Flash-Flood Hazard Assessment Using Ensembles and Bayesian-Based Machine Learning Models: Application of the Simulated Annealing Feature Selection Method. Sci. Total Environ. 2020, 711, 135161. [Google Scholar] [CrossRef]
- Masmoudi, S.; Elghazel, H.; Taieb, D.; Yazar, O.; Kallel, A. A Machine-Learning Framework for Predicting Multiple Air Pollutants’ Concentrations via Multi-Target Regression and Feature Selection. Sci. Total Environ. 2020, 715, 136991. [Google Scholar] [CrossRef]
- Guan, D.; Yuan, W.; Lee, Y.K.; Najeebullah, K.; Rasel, M.K. A Review of Ensemble Learning Based Feature Selection. IETE Tech. Rev. 2014, 31, 190–198. [Google Scholar] [CrossRef]
- He, Q.; Jiang, Z.; Wang, M.; Liu, K. Landslide and Wildfire Susceptibility Assessment in Southeast Asia Using Ensemble Machine Learning Methods. Remote Sens. 2021, 13, 1572. [Google Scholar] [CrossRef]
- Polikar, R. Ensemble Machine Learning; Springer: Boston, MA, USA, 2012; ISBN 9781441993250. [Google Scholar]
- Fan, J.; Yue, W.; Wu, L.; Zhang, F.; Cai, H.; Wang, X.; Lu, X.; Xiang, Y. Evaluation of SVM, ELM and Four Tree-Based Ensemble Models for Predicting Daily Reference Evapotranspiration Using Limited Meteorological Data in Different Climates of China. Agric. For. Meteorol. 2018, 263, 225–241. [Google Scholar] [CrossRef]
- Elith, J.; Leathwick, J.R.; Hastie, T. A Working Guide to Boosted Regression Trees. J. Anim. Ecol. 2008, 77, 802–813. [Google Scholar] [CrossRef]
- Genuer, R.; Poggi, J.; Tuleau-malot, C.; Genuer, R.; Poggi, J.; Variable, C.T.; Forests, R.; Genuer, R.; Poggi, J.; Tuleau-malot, C. Variable Selection Using Random Forests. Pattern Recognit. Lett. 2010, 31, 2225–2236. [Google Scholar] [CrossRef] [Green Version]
- Cruz, M.G.; Sullivan, A.L.; Gould, J.S.; Sims, N.C.; Bannister, A.J.; Hollis, J.J.; Hurley, R.J. Anatomy of a Catastrophic Wildfire: The Black Saturday Kilmore East Fire in Victoria, Australia. For. Ecol. Manag. 2012, 284, 269–285. [Google Scholar] [CrossRef]
- Whittaker, J.; Haynes, K.; Handmer, J.; Mclennan, J. Community Safety during the 2009 Australian ‘Black Saturday’ Bushfires: An Analysis of Household Preparedness and Response. Int. J. Wildl. Fire 2013, 22, 841–849. [Google Scholar] [CrossRef] [Green Version]
- Cai, W.; Cowan, T.; Raupach, M. Positive Indian Ocean Dipole Events Precondition Southeast Australia Bushfires. Geophys. Res. Lett. 2009, 36, 039902. [Google Scholar] [CrossRef]
- Kala, J.; Evans, J.P.; Pitman, A.J. Influence of Antecedent Soil Moisture Conditions on the Synoptic Meteorology of the Black Saturday Bushfire Event in Southeast Australia. Q. J. R. Meteorol. Soc. 2015, 141, 3118–3129. [Google Scholar] [CrossRef] [Green Version]
- Ashton, D.H. The Environment and Plant Ecology of the Hume Range, Central Victoria. Proc. R. Soc. Vic. 2000, 112, 185–272. [Google Scholar]
- Peterson, D.; Wang, J.; Ichoku, C.; Hyer, E.; Ambrosia, V. A Sub-Pixel-Based Calculation of Fire Radiative Power from MODIS Observations: 1. Algorithm Development and Initial Assessment. Remote Sens. Environ. 2013, 129, 262–279. [Google Scholar] [CrossRef]
- Justice, C.O.; Giglio, L.; Korontzi, S.; Owens, J.; Morisette, J.T.; Roy, D.; Descloitres, J.; Alleaume, S.; Petitcolin, F.; Kaufman, Y. The MODIS Fire Products. Remote Sens. Environ. 2002, 83, 244–262. [Google Scholar] [CrossRef]
- Zhang, Y.; Lim, S.; Sharples, J.J. Modelling Spatial Patterns of Wildfire Occurrence in South-Eastern Australia. Geomat. Nat. Hazards Risk 2016, 7, 1800–1815. [Google Scholar] [CrossRef] [Green Version]
- Laurent, P.; Mouillot, F.; Yue, C.; Ciais, P.; Moreno, M.V.; Nogueira, J.M.P. Data Descriptor: FRY, a Global Database of Fire Patch Functional Traits Derived from Space-Borne Burned Area Products. Sci. Data 2018, 5, 132. [Google Scholar] [CrossRef] [Green Version]
- Briones-Herrera, C.I.; Vega-Nieva, D.J.; Monjarás-Vega, N.A.; Briseño-Reyes, J.; López-Serrano, P.M.; Corral-Rivas, J.J.; Alvarado-Celestino, E.; Arellano-Pérez, S.; álvarez-González, J.G.; Ruiz-González, A.D.; et al. Near Real-Time Automated Early Mapping of the Perimeter of Large Forest Fires from the Aggregation of VIIRS and MODIS Active Fires in Mexico. Remote Sens. 2020, 12, 2061. [Google Scholar] [CrossRef]
- Bureau of Meteorology Atmospheric High-Resolution Regional Reanalysis for Australia. Available online: http://www.bom.gov.au/research/projects/reanalysis/ (accessed on 6 January 2022).
- Su, C.H.; Eizenberg, N.; Steinle, P.; Jakob, D.; Fox-Hughes, P.; White, C.J.; Rennie, S.; Franklin, C.; Dharssi, I.; Zhu, H. BARRA v1.0: The Bureau of Meteorology Atmospheric High-Resolution Regional Reanalysis for Australia. Geosci. Model Dev. 2019, 12, 2049–2068. [Google Scholar] [CrossRef] [Green Version]
- Rew, R.; Davis, G. NetCDF: An Interface for Scientific Data Access. IEEE Comput. Graph. Appl. 1990, 10, 76–82. [Google Scholar] [CrossRef]
- Fernandez-Manso, A.; Quintano, C.; Roberts, D.A. Burn Severity Analysis in Mediterranean Forests Using Maximum Entropy Model Trained with EO-1 Hyperion and LiDAR Data. ISPRS J. Photogramm. Remote Sens. 2019, 155, 102–118. [Google Scholar] [CrossRef]
- Key, C.H.; Benson, N.C. Landscape Assessment (LA): Sampling and Analysis Methods. In FIREMON: Fire Effects Monitoring and Inventory System; Lutes, D.C., Keane, R.E., Caratti, C.H., Key, N.C., Sutherland, S., Eds.; Rocky Mountain Research Station, USDA Forest Service: Fort Collins, CO, USA, 2006; pp. LA-1–LA-55. [Google Scholar]
- Pelletier, F.; Eskelson, B.N.I.; Monleon, V.J.; Tseng, Y.C. Using Landsat Imagery to Assess Burn Severity of National Forest Inventory Plots. Remote Sens. 2021, 13, 1935. [Google Scholar] [CrossRef]
- Keeley, J.E. Fire Intensity, Fire Severity and Burn Severity: A Brief Review and Suggested Usage. Int. J. Wildl. Fire 2009, 18, 116–126. [Google Scholar] [CrossRef]
- Miller, J.D.; Knapp, E.E.; Key, C.H.; Skinner, C.N.; Isbell, C.J.; Creasy, R.M.; Sherlock, J.W. Calibration and Validation of the Relative Differenced Normalized Burn Ratio (RdNBR) to Three Measures of Fire Severity in the Sierra Nevada and Klamath Mountains, California, USA. Remote Sens. Environ. 2009, 113, 645–656. [Google Scholar] [CrossRef]
- Parks, S.A.; Dillon, G.K.; Miller, C. A New Metric for Quantifying Burn Severity: The Relativized Burn Ratio. Remote Sens. 2014, 6, 1827–1844. [Google Scholar] [CrossRef] [Green Version]
- Tran, B.N.; Tanase, M.A.; Bennett, L.T.; Aponte, C. Evaluation of Spectral Indices for Assessing Fire Severity in Australian Temperate Forests. Remote Sens. 2018, 10, 1680. [Google Scholar] [CrossRef] [Green Version]
- Cansler, C.A.; McKenzie, D. How Robust Are Burn Severity Indices When Applied in a New Region? Evaluation of Alternate Field-Based and Remote-Sensing Methods. Remote Sens. 2012, 4, 456–483. [Google Scholar] [CrossRef] [Green Version]
- Roy, D.P.; Boschetti, L.; Trigg, S.N. Remote Sensing of Fire Severity: Assessing the Performance of the Normalized Burn Ratio. IEEE Geosci. Remote Sens. Lett. 2006, 3, 112–116. [Google Scholar] [CrossRef] [Green Version]
- Martini, L.; Faes, L.; Picco, L.; Iroumé, A.; Lingua, E.; Garbarino, M.; Cavalli, M. Assessing the Effect of Fire Severity on Sediment Connectivity in Central Chile. Sci. Total Environ. 2020, 728, 139006. [Google Scholar] [CrossRef]
- Miller, J.D.; Thode, A.E. Quantifying Burn Severity in a Heterogeneous Landscape with a Relative Version of the Delta Normalized Burn Ratio (DNBR). Remote Sens. Environ. 2007, 109, 66–80. [Google Scholar] [CrossRef]
- Holsinger, L.M.; Parks, S.A.; Saperstein, L.B.; Loehman, R.A.; Whitman, E. Improved Fire Severity Mapping in the North American Boreal Forest Using a Hybrid Composite Method. Remote Sens. Ecol. Conserv. 2021, 112, 1–14. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, J.; Gao, F.; Liu, Y.; Schaaf, C.; Friedl, M.; Yu, Y.; Jayavelu, S.; Gray, J.; Liu, L.; et al. Exploration of Scaling Effects on Coarse Resolution Land Surface Phenology. Remote Sens. Environ. 2017, 190, 318–330. [Google Scholar] [CrossRef] [Green Version]
- Peng, D.; Wu, C.; Zhang, X.; Yu, L.; Huete, A.R.; Wang, F.; Luo, S.; Liu, X.; Zhang, H. Scaling up Spring Phenology Derived from Remote Sensing Images. Agric. For. Meteorol. 2018, 256–257, 207–219. [Google Scholar] [CrossRef]
- Parks, S.A.; Holsinger, L.M.; Voss, M.A.; Loehman, R.A.; Robinson, N.P. Mean Composite Fire Severity Metrics Computed with Google Earth Engine Offer Improved Accuracy and Expanded Mapping Potential. Remote Sens. 2018, 10, 879. [Google Scholar] [CrossRef] [Green Version]
- Parks, S.A.; Dobrowski, S.Z.; Panunto, M.H. What Drives Low-Severity Fire in the Southwestern USA? Forests 2018, 9, 165. [Google Scholar] [CrossRef] [Green Version]
- Cai, L.; Wang, M. Is the RdNBR a Better Estimator of Wildfire Burn Severity than the DNBR? A Discussion and Case Study in Southeast China. Geocarto Int. 2020, 1–15. [Google Scholar] [CrossRef]
- DELWP Fire Severity 2009 Ground Control Plot Locations. Available online: https://discover.data.vic.gov.au/dataset/fire-severity-2009-ground-control-plot-locations (accessed on 8 January 2022).
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-Scale Geospatial Analysis for Everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine Applications since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef] [Green Version]
- Bui, D.T.; Tsangaratos, P.; Ngo, P.T.T.; Pham, T.D.; Pham, B.T. Flash Flood Susceptibility Modeling Using an Optimized Fuzzy Rule Based Feature Selection Technique and Tree Based Ensemble Methods. Sci. Total Environ. 2019, 668, 1038–1054. [Google Scholar] [CrossRef]
- Midi, H.; Sarkar, S.K.; Rana, S. Collinearity Diagnostics of Binary Logistic Regression Model. J. Interdiscip. Math. 2010, 13, 253–267. [Google Scholar] [CrossRef]
- Eskandari, S.; Amiri, M.; Sãdhasivam, N.; Pourghasemi, H.R. Comparison of New Individual and Hybrid Machine Learning Algorithms for Modeling and Mapping Fire Hazard: A Supplementary Analysis of Fire Hazard in Different Counties of Golestan Province in Iran. Nat. Hazards 2020, 104, 305–327. [Google Scholar] [CrossRef]
- Michael, Y.; Helman, D.; Glickman, O.; Gabay, D.; Brenner, S.; Lensky, I.M. Forecasting Fire Risk with Machine Learning and Dynamic Information Derived from Satellite Vegetation Index Time-Series. Sci. Total Environ. 2021, 764, 142844. [Google Scholar] [CrossRef] [PubMed]
- Heikkinen, R.K.; Luoto, M.; Araujo, M.B.; Virkkala, R.; Thuiller, W.; Sykes, M.T. Methods and Uncertainties in Bioclimatic Envelope Modelling under Climate Change. Prog. Phys. Geogr. 2006, 30, 751–777. [Google Scholar] [CrossRef] [Green Version]
- Oliveira, S.; Oehler, F.; San-Miguel-Ayanz, J.; Camia, A.; Pereira, J.M.C. Modeling Spatial Patterns of Fire Occurrence in Mediterranean Europe Using Multiple Regression and Random Forest. For. Ecol. Manage. 2012, 275, 117–129. [Google Scholar] [CrossRef]
- Ozigis, M.S.; Kaduk, J.D.; Jarvis, C.H.; da Conceição Bispo, P.; Balzter, H. Detection of Oil Pollution Impacts on Vegetation Using Multifrequency SAR, Multispectral Images with Fuzzy Forest and Random Forest Methods. Environ. Pollut. 2020, 256, 113360. [Google Scholar] [CrossRef]
- Saha, S.; Arabameri, A.; Saha, A.; Blaschke, T.; Ngo, P.T.T.; Nhu, V.H.; Band, S.S. Prediction of Landslide Susceptibility in Rudraprayag, India Using Novel Ensemble of Conditional Probability and Boosted Regression Tree-Based on Cross-Validation Method. Sci. Total Environ. 2021, 764, 142928. [Google Scholar] [CrossRef]
- Asadikia, A.; Rajabifard, A.; Kalantari, M. Systematic Prioritisation of SDGs: Machine Learning Approach. World Dev. 2021, 140, 105269. [Google Scholar] [CrossRef]
- Jain, P.; Coogan, S.C.P.; Subramanian, S.G.; Crowley, M.; Taylor, S.; Flannigan, M.D. A Review of Machine Learning Applications in Wildfire Science and Management. Environ. Rev. 2020, 28, 478–505. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar]
- Conn, D.; Ngun, T.; Li, G.; Ramirez, C.M. Fuzzy Forests: Extending Random Forest Feature Selection for Correlated, High-Dimensional Data. J. Stat. Softw. 2019, 91, 1–25. [Google Scholar] [CrossRef]
- Mitchell, R.; Frank, E. Accelerating the XGBoost Algorithm Using GPU Computing. PeerJ Comput. Sci. 2017, 3, e127. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Degenhardt, F.; Seifert, S.; Szymczak, S. Evaluation of Variable Selection Methods for Random Forests and Omics Data Sets. Brief. Bioinform. 2019, 20, 492–503. [Google Scholar] [CrossRef] [Green Version]
- Friedman, J.H.; Meulman, J.J. Multiple Additive Regression Trees with Application in Epidemiology. Stat. Med. 2003, 22, 1365–1381. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms; Springer: Amsterdam, The Netherlands, 2021; Volume 54, ISBN 0123456789. [Google Scholar]
- Ramirez, C.M.; Abrajano, M.A.; Alvarez, R.M. Using Machine Learning to Uncover Hidden Heterogeneities in Survey Data. Sci. Rep. 2019, 9, 16061. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Zhou, D.; Qiu, W.; Shi, Y.; Yang, J.J.; Chen, S.; Wang, Q.; Pan, H. Application of Weighted Gene Co-Expression Network Analysis for Data from Paired Design. Sci. Rep. 2018, 8, 622. [Google Scholar] [CrossRef] [Green Version]
- Jung, Y. Multiple Predicting K-Fold Cross-Validation for Model Selection. J. Nonparametr. Stat. 2018, 30, 197–215. [Google Scholar] [CrossRef]
- Murtaugh, P.A. Performance of Several Variable-Selection Methods Applied to Real Ecological Data. Ecol. Lett. 2009, 12, 1061–1068. [Google Scholar] [CrossRef]
- Lafayette, L.; Sauter, G.; Vu, L.; Meade, B. Spartan Performance and Flexibility: An HPC-Cloud Chimera. In Proceedings of the OpenStack Summit, Barcelona, Spain, 27 October 2016. [Google Scholar]
- Zhang, T.; Han, L.; Chen, W.; Shahabi, H. Hybrid Integration Approach of Entropy with Logistic Regression and Support Vector Machine for Landslide Susceptibility Modeling. Entropy 2018, 20, 884. [Google Scholar] [CrossRef] [Green Version]
- Hong, H.; Liu, J.; Zhu, A.X. Modeling Landslide Susceptibility Using LogitBoost Alternating Decision Trees and Forest by Penalizing Attributes with the Bagging Ensemble. Sci. Total Environ. 2020, 718, 137231. [Google Scholar] [CrossRef]
- Guyon, I.; Elisseeff, A. An Introduction to Variable and Feature Selection. J. Mach. Learn. Res. 2003, 3, 1157–1182. [Google Scholar] [CrossRef]
- Langfelder, P.; Horvath, S. WGCNA: An R Package for Weighted Correlation Network Analysis. BMC Bioinform. 2008, 9, 559. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.; Wei, W.; Chen, L.; Chen, W.; Wang, J. Response of Temporal Variation of Soil Moisture to Vegetation Restoration in Semi-Arid Loess Plateau, China. Catena 2014, 115, 123–133. [Google Scholar] [CrossRef]
- Boisramé, G.; Thompson, S.; Stephens, S. Hydrologic Responses to Restored Wildfire Regimes Revealed by Soil Moisture-Vegetation Relationships. Adv. Water Resour. 2018, 112, 124–146. [Google Scholar] [CrossRef]
- Ambadan, J.T.; Oja, M.; Gedalof, Z.; Berg, A.A. Satellite-Observed Soil Moisture As an Indicator of Wildfire Risk. Remote Sens. 2020, 12, 1543. [Google Scholar] [CrossRef]
- Vinodkumar; Dharssi, I. Evaluation and Calibration of a High-Resolution Soil Moisture Product for Wildfire Prediction and Management. Agric. For. Meteorol. 2019, 264, 27–39. [Google Scholar] [CrossRef]
- Jia, S.; Kim, S.H.; Nghiem, S.V.; Kafatos, M.C. Live Fuel Moisture Estimation Using SMAP Soil Moisture and MODIS Vegetation Indices in Southern California, USA. In Proceedings of the 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 6126–6129. [Google Scholar] [CrossRef]
- Wright, B.R.; Clarke, P.J. Relationships between Soil Temperatures and Properties of Fire in Feathertop Spinifex (Triodia Schinzii (Henrard) Lazarides) Sandridge Desert in Central Australia. Rangel. J. 2008, 30, 317–325. [Google Scholar] [CrossRef]
- Hirschi, M.; Seneviratne, S.I.; Alexandrov, V.; Boberg, F.; Boroneant, C.; Christensen, O.B.; Formayer, H.; Orlowsky, B.; Stepanek, P. Observational Evidence for Soil-Moisture Impact on Hot Extremes in Southeastern Europe. Nat. Geosci. 2011, 4, 17–21. [Google Scholar] [CrossRef]
- Alexander, L. Climate Science: Extreme Heat Rooted in Dry Soils. Nat. Geosci. 2011, 4, 12–13. [Google Scholar] [CrossRef]
- Miralles, D.G.; Teuling, A.J.; Van Heerwaarden, C.C.; De Arellano, J.V.G. Mega-Heatwave Temperatures Due to Combined Soil Desiccation and Atmospheric Heat Accumulation. Nat. Geosci. 2014, 7, 345–349. [Google Scholar] [CrossRef]
- Sharples, J.J.; McRae, R.H.D.; Weber, R.O. Wind Characteristics over Complex Terrain with Implications for Bushfire Risk Management. Environ. Model. Softw. 2010, 25, 1099–1120. [Google Scholar] [CrossRef]
- Davies, L.; Reeder, M.J.; Lane, T.P. A Climatology of Atmospheric Pressure Jumps over Southeastern Australia. Q. J. R. Meteorol. Soc. 2017, 143, 439–449. [Google Scholar] [CrossRef] [Green Version]
- Beer, T. The Interaction of Wind and Fire. Bound. Layer Meteorol. 1991, 54, 287–308. [Google Scholar] [CrossRef]
- Andrews, P.L.; Cruz, M.G.; Rothermel, R.C. Examination of the Wind Speed Limit Function in the Rothermel Surface Fire Spread Model. Int. J. Wildl. Fire 2013, 22, 959–969. [Google Scholar] [CrossRef]
- Cruz, M.G.; Alexander, M.E.; Wakimoto, R.H. Development and Testing of Models for Predicting Crown Fire Rate of Spread in Conifer Forest Stands. Can. J. For. Res. 2005, 35, 1626–1639. [Google Scholar] [CrossRef]
- Miller, C.; Hilton, J.; Sullivan, A.; Prakash, M. SPARK—A Bushfire Spread Prediction Tool. IFIP Adv. Inf. Commun. Technol. 2015, 448, 262–271. [Google Scholar] [CrossRef] [Green Version]
- Tolhurst, K.; Shields, B.; Chong, D. Phoenix: Development and application of a bushfire risk management tool. Aust. J. Emerg. Manag. 2008, 23, 47–54. [Google Scholar]
- Kochanski, A.; Jenkins, M.A.; Sun, R.; Krueger, S.; Abedi, S.; Charney, J. The Importance of Low-Level Environmental Vertical Wind Shear to Wildfire Propagation: Proof of Concept. J. Geophys. Res. Atmos. 2013, 118, 8238–8252. [Google Scholar] [CrossRef]
- Bedia, J.; Herrera, S.; Gutiérrez, J.M.; Zavala, G.; Urbieta, I.R.; Moreno, J.M. Sensitivity of Fire Weather Index to Different Reanalysis Products in the Iberian Peninsula. Nat. Hazards Earth Syst. Sci. 2012, 12, 699–708. [Google Scholar] [CrossRef] [Green Version]
- Beer, T.; Gill, A.M.; Moore, P.H. Australian Bushfire Danger under Changing Climatic Regimes; CSIRO Publishing: Clayton, Australia, 1988. [Google Scholar]
- Deb, P.; Moradkhani, H.; Abbaszadeh, P.; Kiem, A.S.; Engström, J.; Keellings, D.; Sharma, A. Causes of the Widespread 2019–2020 Australian Bushfire Season. Earth Futur. 2020, 8, 1671. [Google Scholar] [CrossRef]
- Dowdy, A.J.; Mills, G.A.; Finkele, K.; de Groot, W. Index Sensitivity Analysis Applied to the Canadian Forest Fire Weather Index and the McArthur Forest Fire Danger Index. Meteorol. Appl. 2010, 17, 298–312. [Google Scholar] [CrossRef]
- Stephenson, A.G.; Shaby, B.A.; Reich, B.J.; Sullivan, A.L. Estimating Spatially Varying Severity Thresholds of a Forest Fire Danger Rating System Using Max-Stable Extreme-Event Modeling. Am. Meteorol. Soc. 2015, 54, 395–407. [Google Scholar] [CrossRef] [Green Version]
- Harris, S.; Anderson, W.; Kilinc, M.; Fogarty, L. The Relationship between Fire Behaviour Measures and Community Loss: An Exploratory Analysis for Developing a Bushfire Severity Scale. Nat. Hazards 2012, 63, 391–415. [Google Scholar] [CrossRef] [Green Version]
- Jefferson, U.; Carmenta, R.; Daeli, W.; Phelps, J. Characterising Policy Responses to Complex Socio-Ecological Problems: 60 Fire Management Interventions in Indonesian Peatlands. Glob. Environ. Change 2020, 60, 102027. [Google Scholar] [CrossRef]
- Schwartz, N.B.; Uriarte, M.; Gutiérrez-Vélez, V.H.; Baethgen, W.; DeFries, R.; Fernandes, K.; Pinedo-Vasquez, M.A. Climate, Landowner Residency, and Land Cover Predict Local Scale Fire Activity in the Western Amazon. Glob. Environ. Change 2015, 31, 144–153. [Google Scholar] [CrossRef]
- Simon, G.L.; Dooling, S. Flame and Fortune in California: The Material and Political Dimensions of Vulnerability. Glob. Environ. Change 2013, 23, 1410–1423. [Google Scholar] [CrossRef]
- Ghorbanzadeh, O.; Blaschke, T.; Gholamnia, K.; Aryal, J. Forest Fire Susceptibility and Risk Mapping Using Social/Infrastructural Vulnerability and Environmental Variables. Fire 2019, 2, 50. [Google Scholar] [CrossRef] [Green Version]
- Hamilton, M.; Fischer, A.P.; Ager, A. A Social-Ecological Network Approach for Understanding Wildfire Risk Governance. Glob. Environ. Change 2019, 54, 113–123. [Google Scholar] [CrossRef]
- Cattau, M.E.; Harrison, M.E.; Shinyo, I.; Tungau, S.; Uriarte, M.; DeFries, R. Sources of Anthropogenic Fire Ignitions on the Peat-Swamp Landscape in Kalimantan, Indonesia. Glob. Environ. Change 2016, 39, 205–219. [Google Scholar] [CrossRef]
- Tibbits, A.; Whittaker, J. Stay and Defend or Leave Early: Policy Problems and Experiences during the 2003 Victorian Bushfires Stay and Defend or Leave Early: Policy Problems and Experiences during the 2003 Victorian Bushfires. Environ. Hazards 2011, 7, 7891. [Google Scholar] [CrossRef]
- Blanchi, R.; Lucas, C.; Leonard, J.; Finkele, K. Meteorological Conditions and Wildfire-Related House Loss in Australia. Int. J. Wildl. Fire 2010, 19, 914–926. [Google Scholar] [CrossRef] [Green Version]
- Kc, U.; Aryal, J.; Hilton, J.; Garg, S. A Surrogate Model for Rapidly Assessing the Size of a Wildfire over Time. Fire 2021, 4, 20. [Google Scholar] [CrossRef]
- Yin, C.; Xing, M.; Yebra, M. Relationships between Burn Severity and Environmental Drivers in the Temperate Coniferous Forest of Northern China. Remote Sens. 2021, 13, 5127. [Google Scholar] [CrossRef]
| Variable | Parameter | Data name | Level | Unit |
|---|---|---|---|---|
| Humidity | 6-hourly average of hourly mean atmospheric specific humidity | AvQsair | S | Kg kg−1 |
| 6-hourly average of instantaneous 10 min specific humidity | QsairScrn | S | Kg kg−1 | |
| 6-hourly average of hourly instantaneous relative humidity | RelHumPrs | M | % | |
| 6-hourly average of instantaneous specific humidity at the end of the hourly timestep | SpecHum | S | Kg kg−1 | |
| Moisture | 6-hourly average of hourly instantaneous soil moisture | SoilMois | D | Kg m−2 |
| Precipitation | Total precipitation amount at the surface | AccPrcp | S | Kg m−2 |
| Pressure | 6-hourly average of hourly mean air pressure | AvMslp | S | Pa |
| 6-hourly average of instantaneous 10 min air pressure | MslpSpec | S | Pa | |
| 6-hourly average of instantaneous 10 min air pressure at 20 m height | PresSpec | S | Pa | |
| Surface pressure at the end of the timestep | SfcPres | S | Pa | |
| Temperature | 6-hourly average of hourly instantaneous air temperature (multi-levels) | AirTemp | M | Kelvin |
| 6-hourly average of hourly maximum temperature | MaxTemp | S | Kelvin | |
| 6-hourly average of hourly minimum temperature | MinTemp | S | Kelvin | |
| 6-hourly average of instantaneous 10 min surface temperature (topsoil layer) at the end of the timestep | SfcTemp | S | Kelvin | |
| 6-hourly average of hourly instantaneous soil temperature (multidepth) | SoilTemp | D | Kelvin | |
| 6-hourly average of instantaneous 10 min temperature at 1.5 m | TempScrn | S | Kelvin | |
| Surface Flux | 6-hourly average of hourly mean surface upward latent heat flux | AvLatHflx | S | Wm−2 |
| 6-hourly average of hourly mean surface upward sensible heat flux | AvSenHflx | S | Wm−2 | |
| 6-hourly average of hourly instantaneous surface upward total moisture flux | AvSfc | S | kg m−2 s−1 | |
| Wind | 6-hourly average of hourly mean of wind U component at 10 m | AvUwnd10 m | S | ms−1 |
| 6-hourly average of hourly mean of wind V component at 10 m | AvVwnd10 m | S | ms−1 | |
| 6-hourly average of hourly mean of wind speed of gust at 10 m | WndGst10 m | S | ms−1 | |
| 6-hourly average of instantaneous 10 min U component of wind at 10 m | Uwnd10 m | S | ms−1 | |
| Upward air velocity (multilevel) | VwndPrs | M | ms−1 | |
| 6-hourly average of instantaneous 10 min V component of wind at 10 m | Vwnd10 m | S | ms−1 | |
| 6-hourly average of instantaneous 10 min wind speed of gust at 10 m | Wgust10 m | S | ms−1 |
| Fire Event | Fire Ignition Date | Acquisition Date (Prefire) | Acquisition Date (Postfire) |
|---|---|---|---|
| 1 | 7/02/2009 | 4/10/2008 | 23/10/2009 |
| 2 | 7/02/2009 | 3/11/2008 | 8/10/2010 |
| 3 | 6/02/2009 | 4/10/2008 | 23/10/2009 |
| 4 | 8/02/2009 | 4/10/2008 | 8/11/2009 |
| 5 | 4/02/2009 | 13/01/2008 | 1/12/2009 |
| 6 | 29/01/2009 | 4/10/2008 | 8/11/2009 |
| 7 | 7/02/2009 | 13/01/2008 | 1/12/2009 |
| 8 | 7/02/2009 | 13/01/2008 | 1/12/2009 |
| 9 | 7/02/2009 | 27/10/2008 | 30/10/2009 |
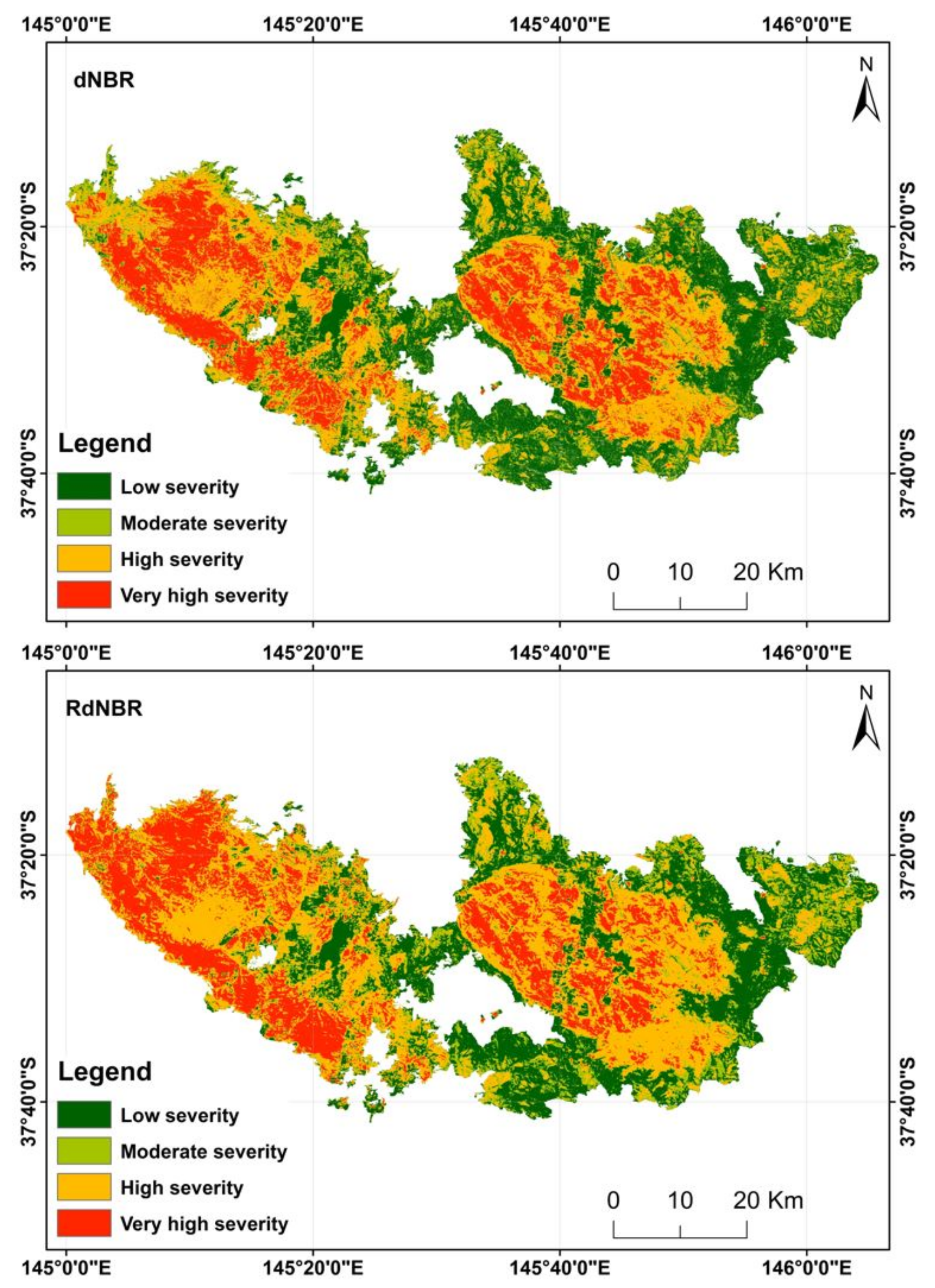
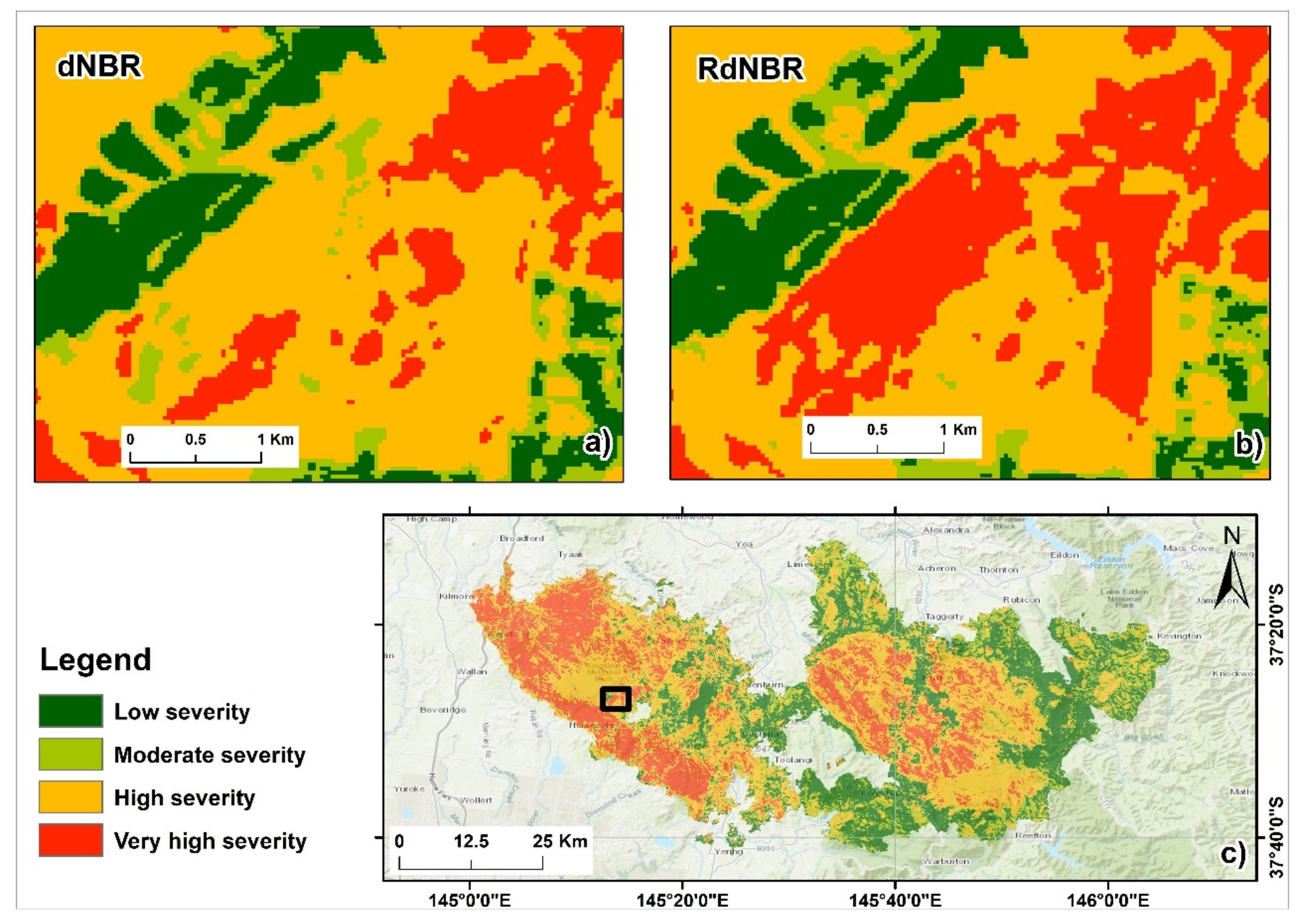
| Severity Category | Class Value (dNBR) | Class Value (RdNBR) |
|---|---|---|
| Unburnt | <100 | <0.1 |
| Low | 100–150 | 0.1–1.5 |
| Moderate | 150–250 | 1.5–2.5 |
| High | 250–350 | 2.5–3.5 |
| Very high | ≥350 | ≥3.5 |
| Class (dNBR) | Very High | High | Moderate | Low | Total | User Accuracy | Kappa |
| Very High | 135 | 26 | 0 | 0 | 161 | 0.839 | |
| High | 14 | 208 | 2 | 4 | 228 | 0.912 | |
| Moderate | 0 | 1 | 35 | 22 | 58 | 0.603 | |
| Low | 0 | 1 | 13 | 159 | 173 | 0.919 | |
| Total | 149 | 236 | 50 | 185 | 620 | 0.000 | |
| Producer Accuracy | 0.906 | 0.881 | 0.700 | 0.859 | 0.000 | 0.866 | |
| Kappa | 0.811 | ||||||
| Class (RdNBR) | Very High | High | Moderate | Low | Total | User Accuracy | Kappa |
| Very High | 132 | 14 | 0 | 0 | 146 | 0.904 | |
| High | 17 | 220 | 2 | 3 | 242 | 0.909 | |
| Moderate | 0 | 1 | 44 | 19 | 64 | 0.688 | |
| Low | 0 | 1 | 4 | 163 | 168 | 0.970 | |
| Total | 149 | 236 | 50 | 185 | 620 | 0.000 | |
| Producer Accuracy | 0.886 | 0.932 | 0.880 | 0.881 | 0.000 | 0.902 | |
| Kappa | 0.861 |
| Rank | RF (VSURF) | Boosted Regression Trees | Fuzzy Forest | XGBoost | |||
|---|---|---|---|---|---|---|---|
| Variable | Variable | Relative Influence | Variable | Importance | Variable | F Score | |
| 1 | STempP225 | STempP225 | 32.37 | SMoisP225 | 0.108 | SMoisP225 | 58 |
| 2 | SMoisP225 | SMoisP225 | 25.13 | STempP225 | 0.106 | STemp2P0 | 41 |
| 3 | STempP675 | STemp2P0 | 8.33 | STempP675 | 0.071 | SMoisP05 | 38 |
| 4 | SMois2P0 | STempP675 | 6.77 | ATemp750 | 0.053 | PresSpec | 30 |
| 5 | STemp2P0 | PresSpec | 2.60 | PresSpec | 0.051 | STempP225 | 26 |
| 6 | ATemp700 | SMois2P0 | 2.18 | SfcPres | 0.050 | SMoisP0675 | 25 |
| 7 | SfcPres | SMoisP05 | 1.98 | STemp2P0 | 0.049 | STempP675 | 22 |
| 8 | PresSpec | SMoisP0675 | 1.68 | SMoisP0675 | 0.042 | Vwnd500 | 18 |
| 9 | SMoisP0675 | Vwnd1000 | 1.53 | STempP05 | 0.033 | ATemp700 | 17 |
| 10 | ATemp750 | ATemp950 | 1.24 | SMoisP05 | 0.027 | SMois2P0 | 17 |
| 11 | ATemp950 | STempP05 | 0.87 | ATemp925 | 0.025 | Vwnd1000 | 14 |
| 12 | STempP05 | Vwnd975 | 0.84 | ATemp950 | 0.021 | RH500 | 12 |
| 13 | SMoisP05 | AvVwnd10m | 0.79 | ATemp1000 | 0.018 | AvLatHflx | 11 |
| 14 | RH700 | RH500 | 0.73 | RH600 | 0.013 | SfcPres | 10 |
| 15 | Vwnd1000 | RH750 | 0.69 | RH950 | 0.010 | Vwnd700 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, S.K.; Aryal, J.; Rajabifard, A. Remote Sensing and Meteorological Data Fusion in Predicting Bushfire Severity: A Case Study from Victoria, Australia. Remote Sens. 2022, 14, 1645. https://doi.org/10.3390/rs14071645
Sharma SK, Aryal J, Rajabifard A. Remote Sensing and Meteorological Data Fusion in Predicting Bushfire Severity: A Case Study from Victoria, Australia. Remote Sensing. 2022; 14(7):1645. https://doi.org/10.3390/rs14071645
Chicago/Turabian StyleSharma, Saroj Kumar, Jagannath Aryal, and Abbas Rajabifard. 2022. "Remote Sensing and Meteorological Data Fusion in Predicting Bushfire Severity: A Case Study from Victoria, Australia" Remote Sensing 14, no. 7: 1645. https://doi.org/10.3390/rs14071645
APA StyleSharma, S. K., Aryal, J., & Rajabifard, A. (2022). Remote Sensing and Meteorological Data Fusion in Predicting Bushfire Severity: A Case Study from Victoria, Australia. Remote Sensing, 14(7), 1645. https://doi.org/10.3390/rs14071645









