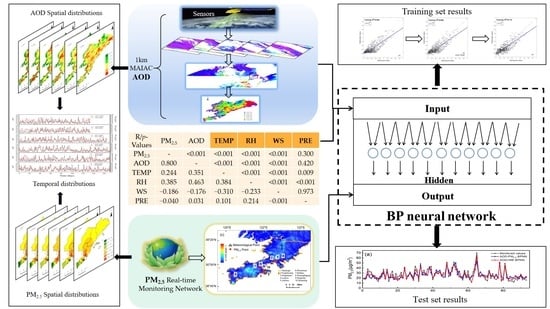
An Estimation Method for PM2.5 Based on Aerosol Optical Depth Obtained from Remote Sensing Image Processing and Meteorological Factors
Abstract
:1. Introduction
2. Materials and Methods
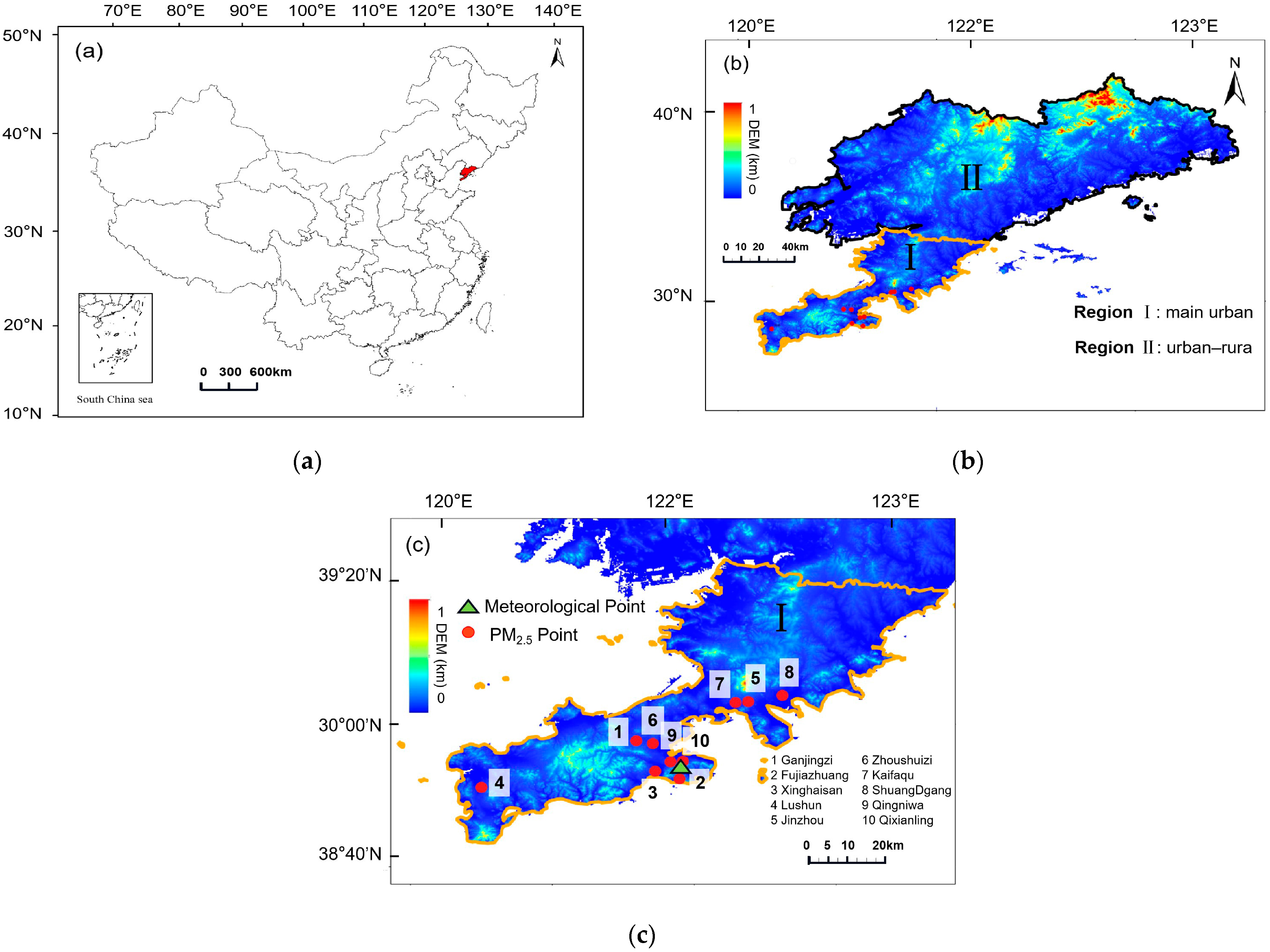
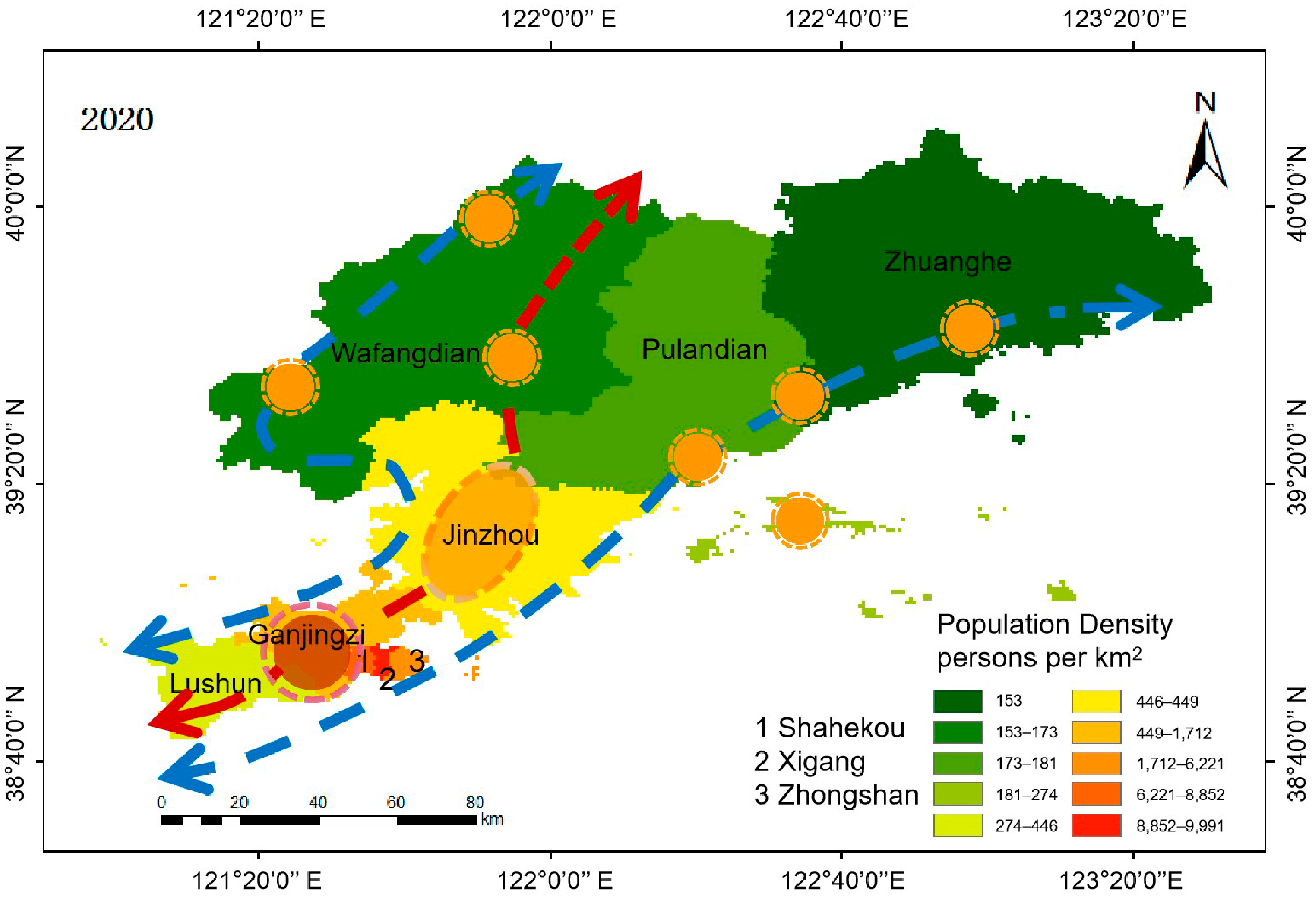
2.1. Study Area
2.2. Data Sources
2.2.1. PM2.5
2.2.2. AOD
2.2.3. Meteorological Factors
2.3. Methods
2.3.1. Data Preprocessing
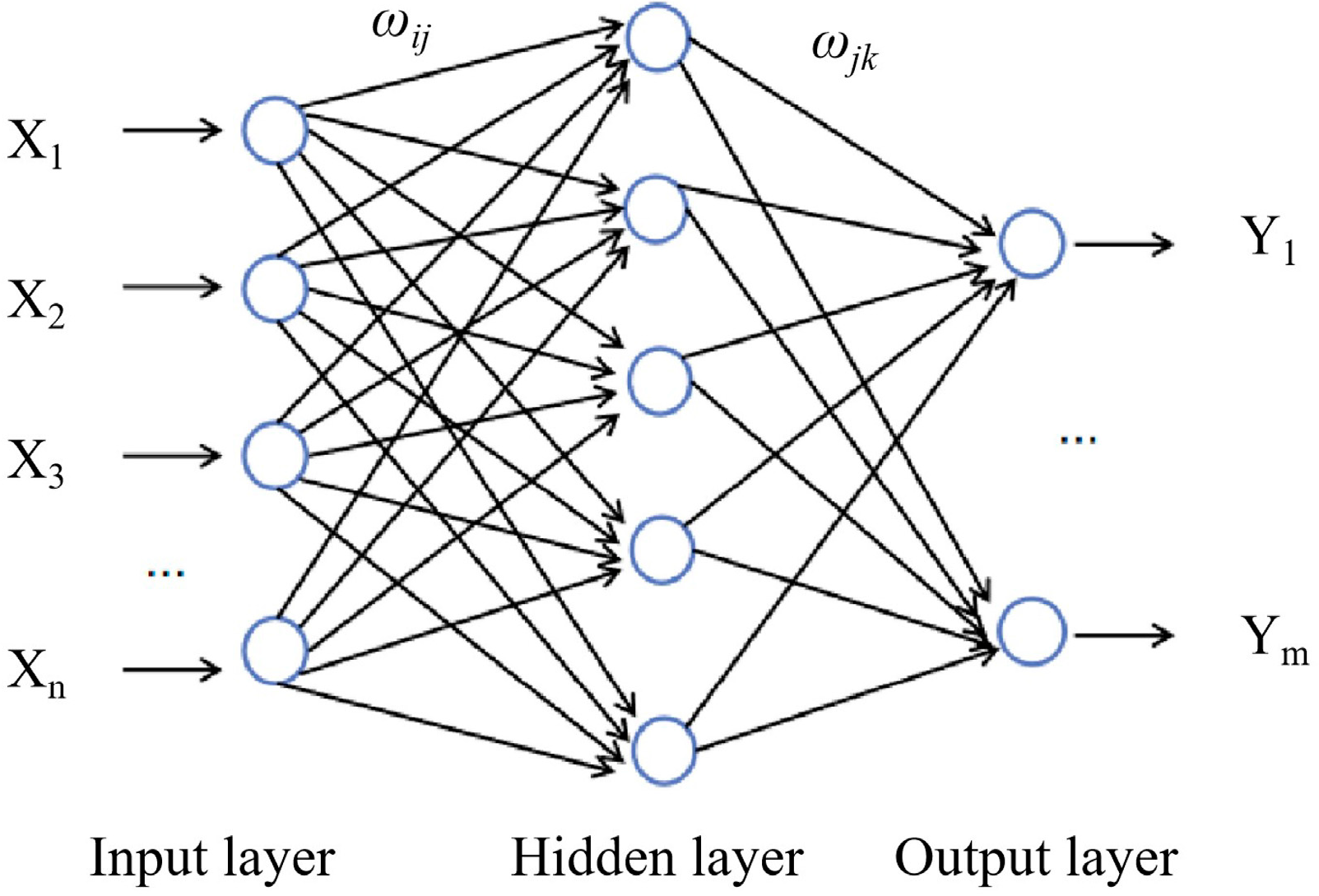
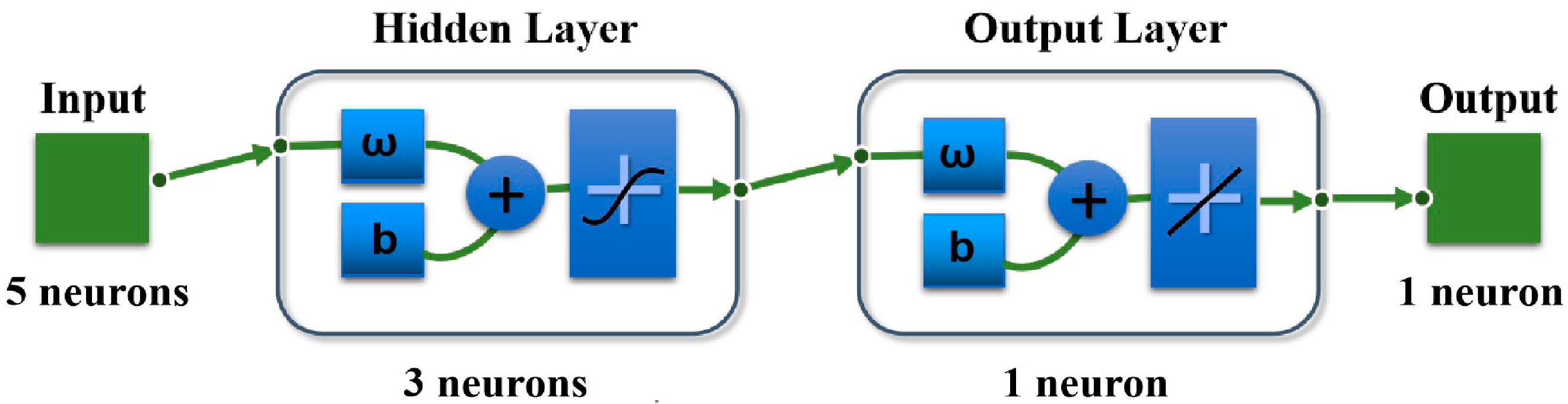
2.3.2. Establishment of BPNN
2.3.3. Model Comparison
2.3.4. Correlation Evaluation Indexes
3. Results and Discussion
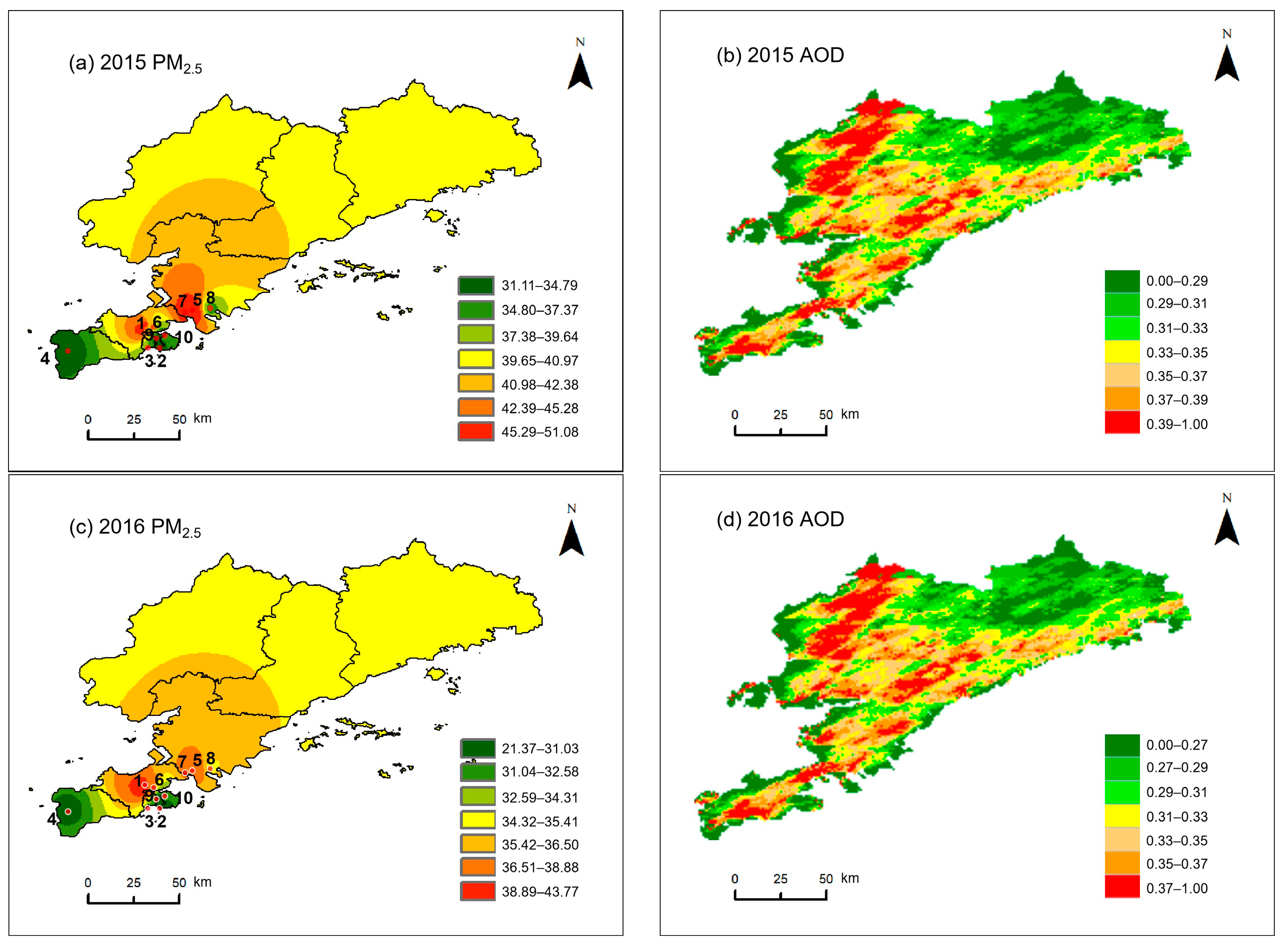
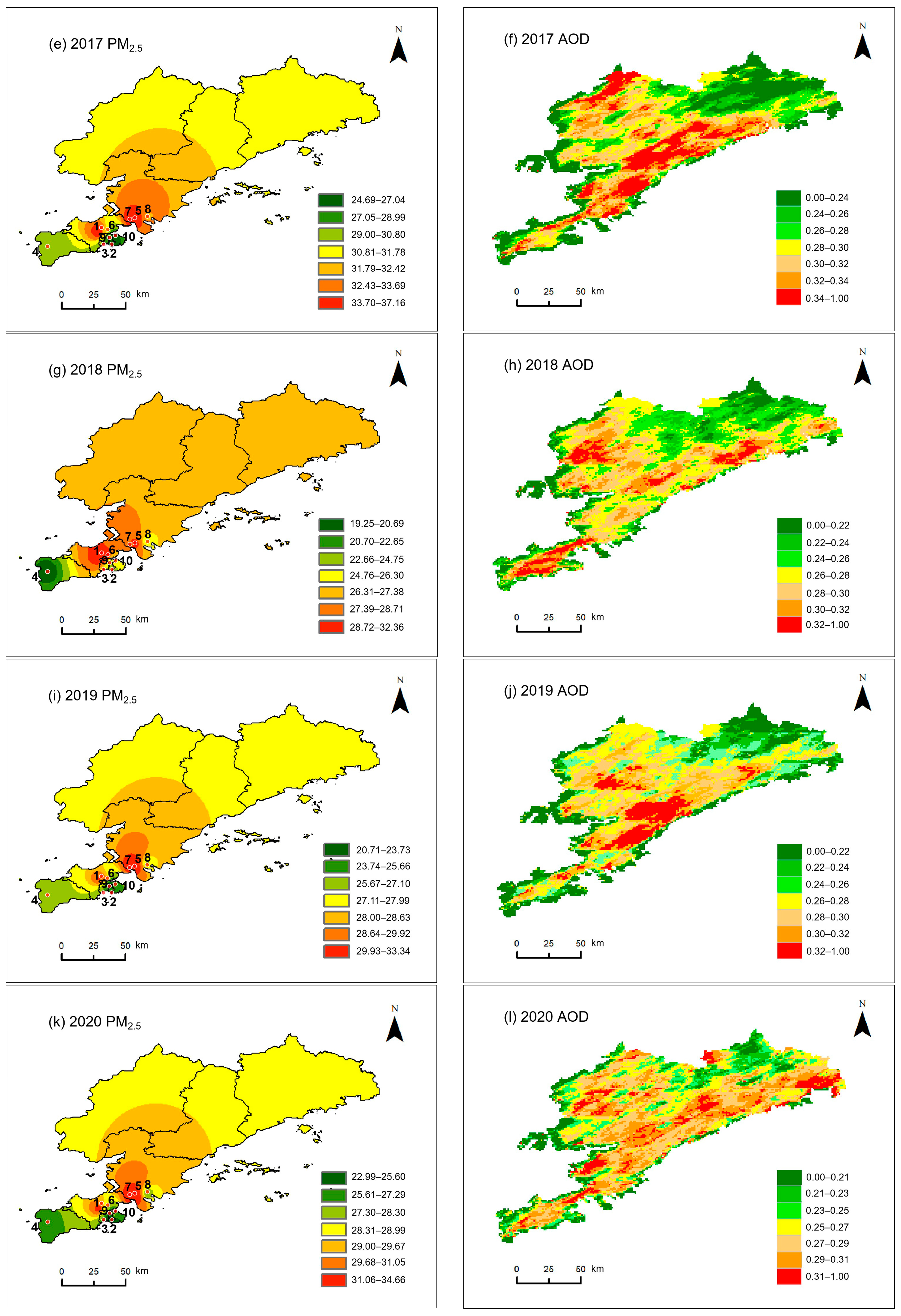
3.1. Temporal Distributions of AOD and PM2.5
3.2. Spatial Distributions of AOD and PM2.5
3.3. BPNN
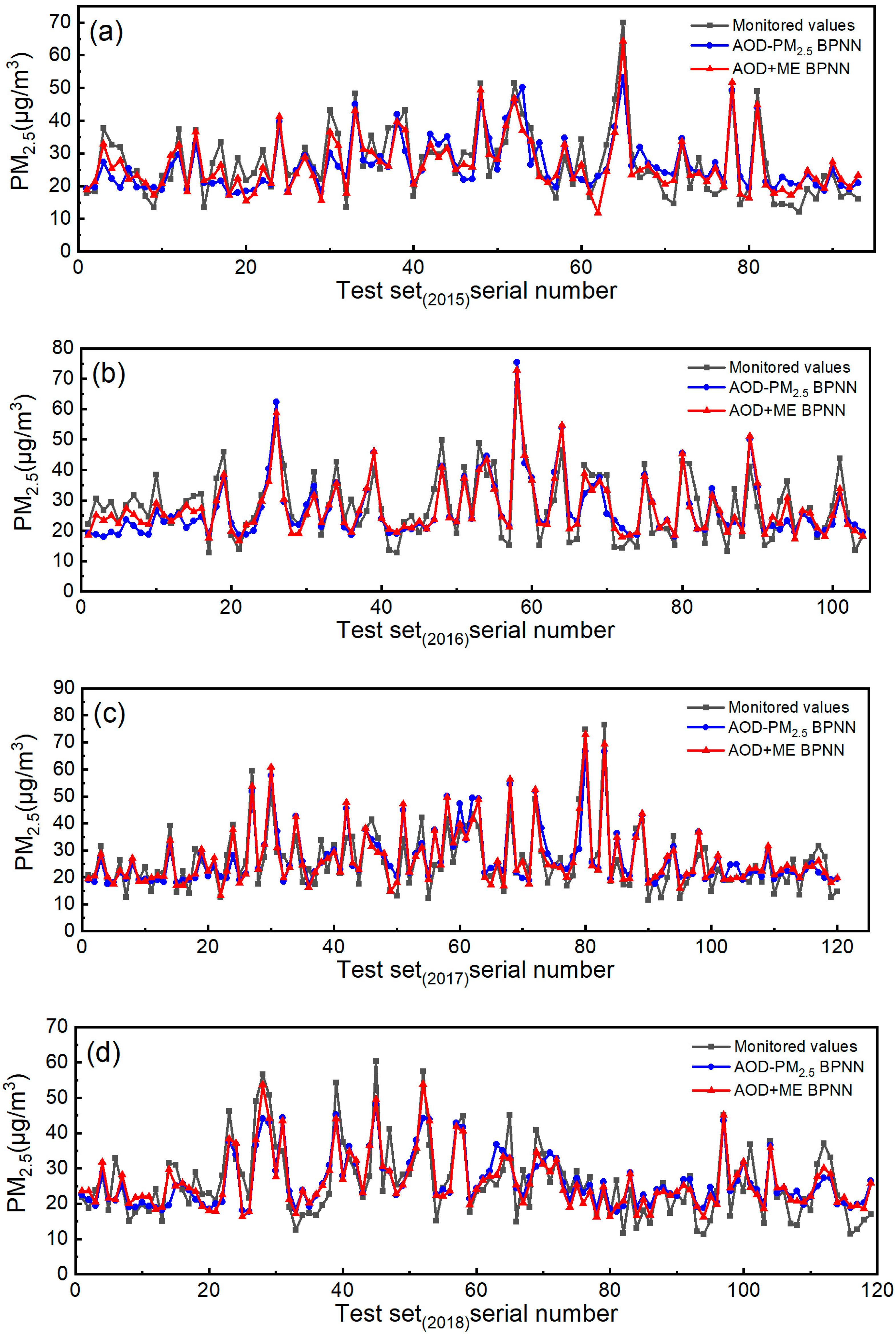
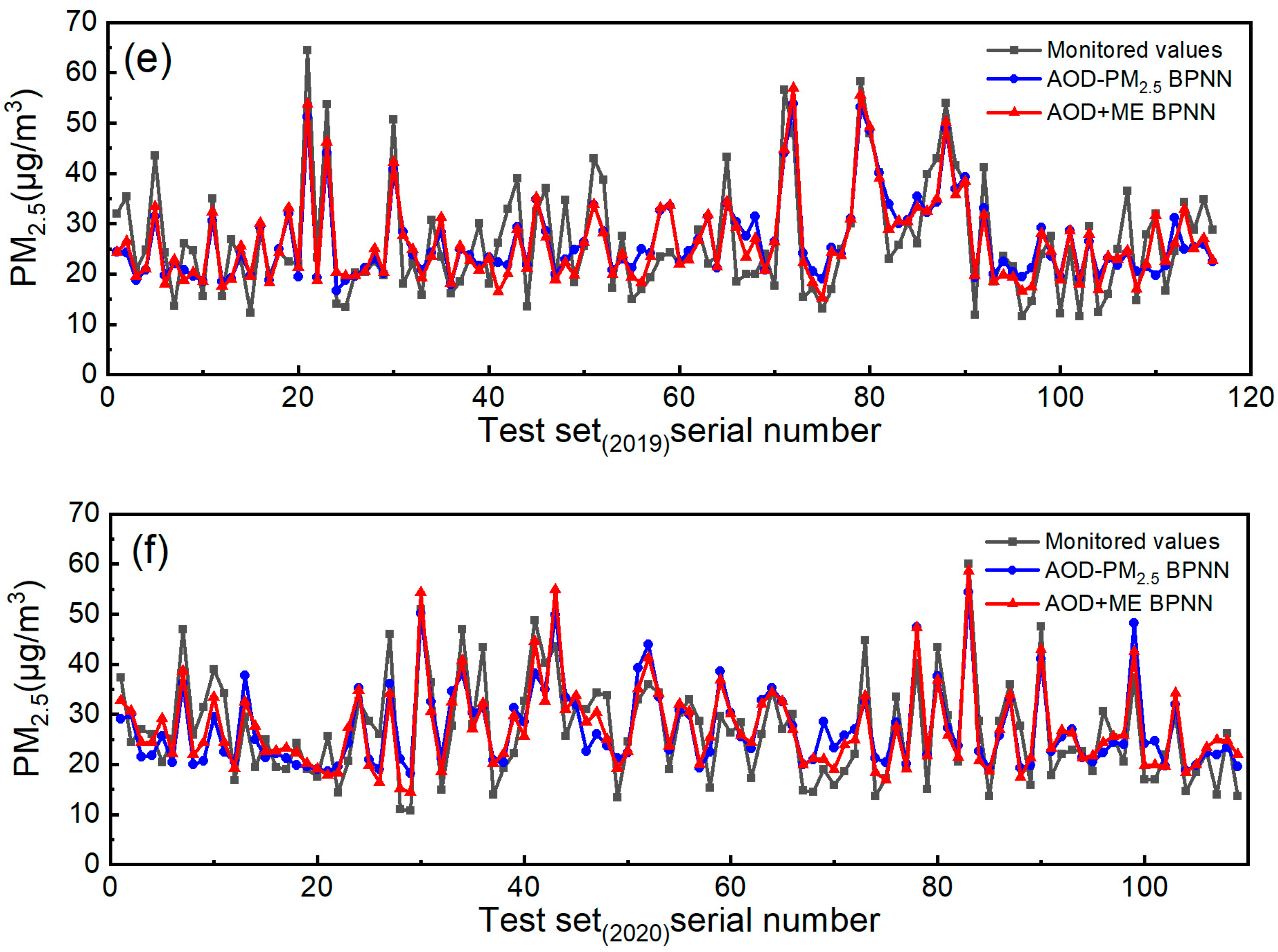
3.4. Comparison of BPNN with Regression Analysis and SVR
3.5. Discussion
3.5.1. Research Findings
3.5.2. Limitations
- (1)
- Here, the limited number of ground measurement points impeded the analysis of the spatiotemporal correlations between AOD and PM2.5.
- (2)
- Seasonal differences in AOD and PM2.5 were not incorporated into the establishment of BPNN.
- (3)
- The BPNN model can be used to estimate the trend of interannual PM2.5 and needs to be improved for estimating the daily extreme value of PM2.5 in the future.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Pope, C.A., III. Lung Cancer, Cardiopulmonary Mortality, and Long-term Exposure to Fine Particulate Air Pollution. JAMA 2002, 287, 1132. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, Y.M.; Huang, B.; He, Q.Q.; Chen, B.; Wei, J.; Mahmood, R. Dynamic assessment of PM2.5 exposure and health risk using remote sensing and geo-spatial big data. Environ. Pollut. 2019, 253, 288–296. [Google Scholar] [CrossRef] [PubMed]
- Lim, C.C.; Hayes, R.B.; Ahn, J.; Shao, Y.; Silverman, D.T.; Jones, R.R.; Garcia, C.; Thurston, G.D. Association between long-term exposure to ambient air pollution and diabetes mortality in the US. Environ. Res. 2018, 165, 330–336. [Google Scholar] [CrossRef]
- Liu, M.; Tang, W.; Zhang, Y.; Wang, Y.; Kangzhuo, B.; Li, Y.; Liu, X.; Xu, S.; Ao, L.; Wang, Q.; et al. Urban-rural differences in the association between long-term exposure to ambient air pollution and obesity in China. Environ. Res. 2021, 201, 111597. [Google Scholar] [CrossRef]
- Liu, Y.P.; Wu, J.G.; Yu, D.Y.; Hao, R.F. Understanding the Patterns and Drivers of Air Pollution on Multiple Time Scales: The Case of Northern China. Environ. Manag. 2018, 61, 1048–1061. [Google Scholar] [CrossRef]
- Liu, J.J.; Weng, F.Z.; Li, Z.Q.; Cribb, M.C. Hourly PM2.5 Estimates from a Geostationary Satellite Based on an Ensemble Learning Algorithm and Their Spatiotemporal Patterns over Central East China. Remote Sens. 2019, 11, 2120. [Google Scholar] [CrossRef] [Green Version]
- Li, L.F. A Robust Deep Learning Approach for Spatiotemporal Estimation of Satellite AOD and PM2.5. Remote Sens. 2020, 12, 264. [Google Scholar] [CrossRef] [Green Version]
- Han, X.; Cui, X.; Ding, L.; Li, Z. Establishment of PM2.5 Prediction Model Based on Maiac AOD Data of High Resolution Remote Sensing Images. Int. J. Pattern Recognit. 2019, 33, 1954009. [Google Scholar] [CrossRef]
- Fu, D.; Song, Z.; Zhang, X.; Wu, Y.; Duan, M.; Pu, W.; Ma, Z.; Quan, W.; Zhou, H.; Che, H.; et al. Similarities and Differences in the Temporal Variability of PM2.5 and AOD between Urban and Rural Stations in Beijing. Remote Sens. 2020, 12, 1193. [Google Scholar] [CrossRef] [Green Version]
- Xue, W.H.; Zhang, J.; Zhong, C.; Ji, D.Y.; Huang, W. Satellite-derived spatiotemporal PM2.5 concentrations and variations from 2006 to 2017 in China. Sci. Total Environ. 2020, 712, 77–144. [Google Scholar] [CrossRef]
- Wei, J.; Peng, Y.R.; Mahmood, R.; Sun, L.; Guo, J.P. Intercomparison in spatial distributions and temporal trends derived from multi-source satellite aerosol products. Atmos. Chem. Phys. 2019, 19, 7183–7207. [Google Scholar] [CrossRef] [Green Version]
- Levy, R.C.; Mattoo, S.; Munchak, L.A.; Remer, L.A.; Sayer, A.M.; Patadia, F.; Hsu, N.C. The Collection 6 MODIS aerosol products over land and ocean. Atmos. Meas. Tech. 2013, 6, 2989–3034. [Google Scholar] [CrossRef] [Green Version]
- Hsu, N.C.; Jeong, M.-J.; Bettenhausen, C.; Sayer, A.M.; Hansell, R.; Seftor, C.S.; Huang, J.; Tsay, S.-C. Enhanced Deep Blue aerosol retrieval algorithm: The second generation. J. Geophys. Res. Atmos. 2013, 118, 9296–9315. [Google Scholar] [CrossRef]
- Nabavi, S.O.; Haimberger, L.; Abbasi, E. Assessing PM2.5 concentrations in Tehran, Iran, from space using MAIAC, deep blue, and dark target AOD and machine learning algorithms. Atmos. Pollut. Res. 2019, 10, 889–903. [Google Scholar] [CrossRef]
- Fu, H.C.; Sun, Y.L.; Chen, L.; Zhang, H.; Gao, S. Temporal and spatial distribution characteristics of PM2.5 and PM10 in Xinjiang region in 2016 based on AOD data and GWR model. Acta Sci. Circumstantiae 2020, 40, 27–35. [Google Scholar]
- Ahmad, M.; Alam, K.; Tariq, S.; Anwar, S.; Mansha, M. Estimating fine particulate concentration using a combined approach of linear regression and artificial neural network. Atmos. Environ. 2019, 219, 117050. [Google Scholar] [CrossRef]
- Shen, X.; Bilal, M.; Qiu, Z.; Sun, D.; Wang, S.; Zhu, W. Validation of MODIS C6 Dark Target Aerosol Products at 3 km and 10 km Spatial Resolutions over the China Seas and the Eastern Indian Ocean. Remote Sens. 2018, 10, 573. [Google Scholar] [CrossRef] [Green Version]
- Bilal, M.; Nichol, J.; Spak, S. A New Approach for Estimation of Fine Particulate Concentrations Using Satellite Aerosol Optical Depth and Binning of Meteorological Variables. Aerosol. Air Qual. Res. 2017, 11, 356–367. [Google Scholar] [CrossRef] [Green Version]
- Zhang, J.; Xin, J.; Zhang, W.; Wang, S.; Wang, L.; Xie, W.; Xiao, G.; Pan, H.; Kong, L. Validation of MODIS C6 AOD products retrieved by the Dark Target method in the Beijing–Tianjin–Hebei urban agglomeration, China. Adv. Atmos. Sci. 2017, 34, 993–1002. [Google Scholar] [CrossRef]
- Xie, G.Q.; Wang, M.; Pan, J.; Zhu, Y. Spatio-temporal variations and trends of MODIS C6.1 Dark Target and Deep Blue merged aerosol optical depth over China during 2000–2017. Atmos. Environ. 2019, 214, 46–76. [Google Scholar] [CrossRef]
- Jethva, H.; Torres, O.; Yoshida, Y. Accuracy assessment of MODIS land aerosol optical thickness algorithms using AERONET measurements over North America. Atmos. Meas. Tech. 2019, 12, 4291–4307. [Google Scholar] [CrossRef] [Green Version]
- Li, Z.B.; Wang, N.; Zhang, Z.L.; Wang, T.T.; Tao, J.H.; Wang, P.; Ma, S.L.; Xu, B.B.; Fan, M. Validation and analyzation of MODIS aerosol optical depth products over China. China Environ. Sci. 2020, 40, 4190–4204. [Google Scholar] [CrossRef]
- Just, A.; De Carli, M.; Shtein, A.; Dorman, M.; Lyapustin, A.; Kloog, I. Correcting Measurement Error in Satellite Aerosol Optical Depth with Machine Learning for Modeling PM2.5 in the Northeastern USA. Remote Sens. 2018, 10, 803. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, Y.; Ho, H.C.; Wong, M.S.; Deng, C.; Shi, Y.; Chan, T.C.; Knudby, A. Evaluation of machine learning techniques with multiple remote sensing datasets in estimating monthly concentrations of ground-level PM2.5. Environ. Pollut. 2018, 242, 1417–1426. [Google Scholar] [CrossRef]
- Murray, N.L.; Holmes, H.A.; Liu, Y.; Chang, H.H. A Bayesian ensemble approach to combine PM2.5 estimates from statistical models using satellite imagery and numerical model simulation. Environ. Res. 2019, 178, 108601. [Google Scholar] [CrossRef] [PubMed]
- Pu, Q.; Yoo, E.H. Ground PM2.5 prediction using imputed MAIAC AOD with uncertainty quantification. Environ. Pollut. 2021, 274, 74–82. [Google Scholar] [CrossRef] [PubMed]
- Perez, P.; Menares, C.; Ramírez, C. PM2.5 forecasting in Coyhaique, the most polluted city in the Americas. Urban Clim. 2020, 32, 100608. [Google Scholar] [CrossRef]
- Zhai, L.; Zou, B.; Fang, X.; Luo, Y.Q.; Wan, N.; Li, S.; Robert, T. Land Use Regression Modeling of PM2.5 Concentrations at Optimized Spatial Scales. J. Atmos. 2016, 8, 1. [Google Scholar] [CrossRef] [Green Version]
- Tessum, C.W.; Paolella, D.A.; Chambliss, S.E.; Apte, J.S.; Hill, J.D.; Marshall, J.D. PM2.5 polluters disproportionately and systemically affect people of color in the United States. Sci. Adv. 2021, 7, eabf4491. [Google Scholar] [CrossRef]
- Luo, Y.; Liu, S.; Che, L.; Yu, Y. Analysis of temporal spatial distribution characteristics of PM2.5 pollution and the influential meteorological factors using Big Data in Harbin, China. J. Air Waste Manag. Assoc. 2021, 71, 964–973. [Google Scholar] [CrossRef]
- Li, J.; Carlson, B.E.; Lacis, A.A. How well do satellite AOD observations represent the spatial and temporal variability of PM2.5 concentration for the United States. Atmos. Environ. 2015, 102, 260–273. [Google Scholar] [CrossRef]
- Liu, Y. Mapping annual mean ground-level PM2.5 concentrations using Multiangle Imaging Spectroradiometer aerosol optical thickness over the contiguous United States. J. Geophys. Res. 2004, 109, 206–215. [Google Scholar] [CrossRef]
- Wang, J. Intercomparison between satellite-derived aerosol optical thickness and PM2.5 mass: Implications for air quality studies. Geophys. Res. Lett. 2003, 30, 2095. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.; Huang, B.; Li, S.; Lin, Y. Estimation and Analysis of the Nighttime PM2.5 Concentration Based on LJ1-01 Images: A Case Study in the Pearl River Delta Urban Agglomeration of China. Remote Sens. 2021, 13, 3405. [Google Scholar] [CrossRef]
- Zheng, Y.X.; Zhang, Q.; Liu, Y.; Geng, G.; He, K. Estimating ground-level PM2.5 concentrations over three megalopolises in China using satellite-derived aerosol optical depth measurements. Atmos. Environ. 2015, 124, 232–242. [Google Scholar] [CrossRef]
- Ma, Z.W.; Hu, X.F.; Huang, L.; Bi, J.; Liu, Y. Estimating ground-level PM2.5 in China using satellite remote sensing. Environ. Sci. Technol. 2014, 48, 7436–7444. [Google Scholar] [CrossRef]
- Bai, Y.; Wu, L.X.; Qin, K.; Zhang, Y.F.; Shen, Y.Y.; Zhou, Y.A. A Geographically and Temporally Weighted Regression Model for Ground-Level PM2.5 Estimation from Satellite-Derived 500 m Resolution AOD. Remote Sens. 2016, 8, 262. [Google Scholar] [CrossRef] [Green Version]
- Zhu, S.; Lian, X.; Wei, L.; Che, J.; Shen, X.; Yang, L.; Qiu, X.; Liu, X.; Gao, W.; Ren, X.; et al. PM2.5 forecasting using SVR with PSOGSA algorithm based on CEEMD, GRNN and GCA considering meteorological factors. Atmos. Environ. 2018, 183, 20–32. [Google Scholar] [CrossRef]
- Goulier, L.; Paas, B.; Ehrnsperger, L.; Klemm, O. Modelling of Urban Air Pollutant Concentrations with Artificial Neural Networks Using Novel Input Variables. Int. J. Env. Res. Public Health 2020, 17, 2025. [Google Scholar] [CrossRef] [Green Version]
- Wei, J.; Li, Z.; Peng, Y.; Sun, L. MODIS Collection 6.1 aerosol optical depth products over land and ocean: Validation and comparison. Atmos. Environ. 2018, 201, 428–440. [Google Scholar] [CrossRef]
- Gupta, P.; Christopher, S. Particulate matter air quality assessment using integrated surface, satellite, and meteorological products: 2. A neural network approach. J. Geophys. Res. 2009, 114, 1497. [Google Scholar] [CrossRef]
- Guo, J.P.; Wu, Y.R.; Zhang, X.Y.; Li, X.W. Estimation of MODIS aerosol optical thickness product under the framework of BP network PM_(2.5) in Eastern China. Environ. Sci. 2013, 34, 817–825. [Google Scholar] [CrossRef]
- Ni, X.L.; Cao, C.X.; Zhou, Y.K.; Cui, X.H.; Ramesh, P.S. Spatio-Temporal Pattern Estimation of PM2.5 in Beijing-Tianjin-Hebei Region Based on MODIS AOD and Meteorological Data Using the Back Propagation Neural Network. Atmosphere 2018, 9, 105. [Google Scholar] [CrossRef] [Green Version]
- Pan, J.; Cao, X. Integration Particle Swarm Algorithm and its Application in Neural Network. Appl. Mech. Mater. 2014, 543–547, 2133–2136. [Google Scholar] [CrossRef]
- Cai, Y.; Shao, Y. The relationship between PM2.5 value in Jinan the quantity of patients in the outpatient departmrnt of sensitive diseases. Mod. Chin. Dr. 2015, 53, 114–117. [Google Scholar]
- Gu, J.L.; Tang, H.S.; Liu, M.; Geng, Y.; Yu, Y.; Tao, T. Correlation Analysis between the Concentration of Atmospheric Pollutant and Aerosol Optical Depth in Dalian City. Sci. Geogr. Sin. 2019, 39, 516–523. [Google Scholar] [CrossRef]
- Lyapustin, A.; Wang, Y.; Korkin, S.; Huang, D. MODIS collection 6 MAIAC algorithm. Atmos. Meas. Tech. 2018, 11, 5741–5765. [Google Scholar] [CrossRef] [Green Version]
- Jiao, L.; Zhang, B.; Xu, G.; Zhao, S. Spatio-temporal variability of correlation between aerosol optical depth and PM2.5 concentration. J. Arid Land Resour. Environ. 2016, 30, 34–39. [Google Scholar]
- Jin, Y.N.; Yang, X.C.; Yan, X.; Zhao, W.J. MAIAC AOD and PM2.5 mass concentration characteristics and correlation analysis in Beijing-Tianjin-Hebei and surrounding areas. Environ. Sci. 2020, 42, 2604–2615. [Google Scholar] [CrossRef]
- Lü, X.; Lu, T.; Kibert, C.J.; Viljanen, M. Modeling and forecasting energy consumption for heterogeneous buildings using a physical-statistical approach. Appl. Energy 2015, 144, 261–275. [Google Scholar] [CrossRef]
- Shih, J.H.; Fay, M.P. Pearson’s chi-square test and rank correlation inferences for clustered data. Biometrics 2017, 73, 822–834. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.G. Prediction algorithm of PM2.5 mass concentration based on adaptive BP neural network. Computing 2018, 100, 825–838. [Google Scholar] [CrossRef]
- Wang, M.; Zou, B.; Guo, Y.; He, J.Q. Spatial prediction of urban PM2.5 concentration based on BP artificial neural network. Environ. Pollut. Prev. 2013, 35, 63–66+70. [Google Scholar] [CrossRef]
- Hecht-Nielsen, R. Kolmogorov’s mapping neural network existence theorem. In Proceedings of the International Conference on Neural Networks, Washington, DC, USA, 3–6 June 1996; IEEE Press: New York, NY, USA, 1987; 3, pp. 11–14. [Google Scholar]
- Guo, L.J.; Wang, H.X.; Meng, Q.H.; Qiu, Y.N. Modified algorithm for mobile robot SLAM based on particle fiter. Computer Eng. Appl. 2007, 43, 26–29. [Google Scholar]
- Wang, R.; Xu, H.; Li, B.; Feng, Y. Research on Method of Determining Hidden Layer Nodes in BP Neural Network. Comput. Technol. Develop. 2018, 28, 31–35. [Google Scholar]
- Masood, A.; Ahmad, K. A model for particulate matter (PM2.5) prediction for Delhi based on machine learning approaches. Proc. Comput. Sci. 2020, 167, 2101–2110. [Google Scholar] [CrossRef]
- Ma, S.; Cao, W.; Jiang, S.; Hu, J.; Lei, X.; Xiong, X. Design and implementation of SVM OTPC searching based on Shared Dot Product Matrix. Integration 2020, 71, 30–37. [Google Scholar] [CrossRef]
- Jaseena, K.U.; Binsu, C.K. A Wavelet-based hybrid multi-step Wind Speed Forecasting model using LSTM and SVR. Wind Eng. 2021, 45, 1123–1144. [Google Scholar] [CrossRef]
- Zhang, Z.Z.; Lin, Z.R. LIBSVM: Support Vector Machine Library. ACM Intell. Syst. Technol. Trans. 2011, 2, 1–27. Available online: http://www.csie.ntu.edu.tw/~cjlin/libsvm (accessed on 10 January 2022).
- Wang, H.L. Empirical Study on the Sales Forecast Accuracy and the Completion Rate of Orders in Clothing Industry; Shanghai Jiaotong University: Shanghai, China, 2016. [Google Scholar]
- Liu, H.; Gao, X.M.; Xie, Z.Y.; Li, T.T.; Zhang, W.J. Spatio-temporal characteristics of aerosol optical depth over Beijing-Tianjin-Hebei-Shanxi-Shandong region during 2000–2013. Acta Sci. Circumstantiae 2015, 35, 1506–1511. [Google Scholar]
- Hu, X.F.; Waller, L.A.; Al-Hamdan, M.Z.; Crosson, W.L.; Estes, M.G.; Estes, S.M.; Quattrochi, D.A.; Sarnat, J.A.; Liu, Y. Estimating ground-level PM2.5 concentrations in the southeastern U.S. using geographically weighted regression. Environ. Res. 2013, 121, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Wang, W.; Mao, F.Y.; Du, L.; Pan, Z.X.; Gong, W.; Fang, S.H. Deriving Hourly PM2.5 Concentrations from Himawari-8 AODs over Beijing–Tianjin–Hebei in China. Remote Sens. 2017, 9, 858. [Google Scholar] [CrossRef] [Green Version]
- He, Q.Q.; Huang, B. Satellite-based mapping of daily high-resolution ground PM2.5 in China via space-time regression modeling. Remote Sens. Environ. 2018, 206, 72–83. [Google Scholar] [CrossRef]
- Wei, J.; Li, Z.Q.; Lyapustin, A.; Sun, L.; Peng, Y.R.; Xue, W.H.; Su, T.N.; Cribb, M. Reconstructing 1-km-resolution high-quality PM2.5 data records from 2000 to 2018 in China: Spatiotemporal variations and policy implications. Remote Sens. Environ. 2021, 252, 112136. [Google Scholar] [CrossRef]
- Gogikar, P.; Tripathy, M.R.; Rajagopal, M.; Paul, K.K.; Tyagi, B. PM2.5 estimation using multiple linear regression approach over industrial and non-industrial stations of India. J. Ambient Intell. Humaniz. Comput. 2020, 12, 2975–2991. [Google Scholar] [CrossRef]
- Ma, X.; Wang, J.; Yu, F.; Jia, H.; Hu, Y. Can MODIS AOD be employed to derive PM2.5 in Beijing-Tianjin-Hebei over China. Atmos Res. 2016, 181, 250–256. [Google Scholar] [CrossRef]
- Zeng, Q.L.; Chen, L.F.; Zhu, H.; Wang, Z.F.; Wang, X.H.; Zhang, L.; Gu, T.Y.; Zhu, G.Y.; Yang Zhang, A. Satellite-Based Estimation of Hourly PM2.5 Concentrations Using a Vertical-Humidity Correction Method from Himawari-AOD in Hebei. Sensors 2018, 18, 3456. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.Y.; Jia, H.L. Particulate matter and gaseous pollutions in three megacities over China: Situation and implication. Atmos. Environ. 2016, 140, 476–494. [Google Scholar] [CrossRef]





| R/p-Values | PM2.5 | AOD | TEMP | RH | WS | PRE |
|---|---|---|---|---|---|---|
| PM2.5 | - | <0.001 | <0.001 | <0.001 | <0.001 | 0.300 |
| AOD | 0.800 | - | <0.001 | <0.001 | <0.001 | 0.420 |
| TEMP | 0.244 | 0.351 | - | <0.001 | <0.001 | 0.009 |
| RH | 0.385 | 0.463 | 0.384 | - | <0.001 | <0.001 |
| WS | −0.186 | −0.176 | −0.310 | −0.233 | - | 0.973 |
| PRE | −0.040 | 0.031 | 0.101 | 0.214 | −0.001 | - |
| Variable | Min | Max | Avg | SD |
|---|---|---|---|---|
| PM2.5 (μg/m3) | 10.750 | 76.493 | 26.808 | 10.862 |
| AOD | 0.025 | 1.776 | 0.289 | 0.249 |
| TEMP (°C) | −11.500 | 32.300 | 10.235 | 10.533 |
| RH (%) | 93.000 | 16.000 | 50.739 | 15.248 |
| WS (m/s) | 3.038 | 8.600 | 3.038 | 1.269 |
| PRE (mm) | 0.000 | 22.600 | 0.291 | 1.766 |
| Data Set | Training Set (Year) | Test Set (Year) |
|---|---|---|
| 1 | a (2016, 2017, 2018, 2019, 2020) | 2015 |
| 2 | b (2015, 2017, 2018, 2019, 2020) | 2016 |
| 3 | c (2015, 2016, 2018, 2019, 2020) | 2017 |
| 4 | d (2015, 2016, 2017, 2019, 2020) | 2018 |
| 5 | e (2015, 2016, 2017, 2018, 2020) | 2019 |
| 6 | f (2015, 2016, 2017, 2018, 2019) | 2020 |
| Hidden Layer Activation Function | Output Layer Activation Function | Training Function | Target Error | Number of Iterations | Learning Rate |
|---|---|---|---|---|---|
| tansig | purelin | trainlm | 10−5 | 3000 | 0.1 |
| Hidden Layer Neurons | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| RMSEa | 10.64 | 6.41 | 6.42 | 11.66 | 11.18 | 58.40 | 13.59 | 33.73 | 12.03 | 10.34 | 13.71 |
| RMSEb | 6.44 | 6.45 | 6.48 | 7.50 | 6.76 | 6.83 | 6.80 | 6.96 | 7.18 | 7.23 | 7.97 |
| RMSEc | 6.48 | 6.77 | 6.82 | 7.32 | 10.07 | 8.25 | 7.43 | 10.87 | 14.66 | 13.42 | 12.48 |
| RMSEd | 6.47 | 15.74 | 10.48 | 44.45 | 44.40 | 11.42 | 10.77 | 26.51 | 10.57 | 21.53 | 18.61 |
| RMSEe | 6.39 | 6.37 | 6.50 | 10.06 | 6.80 | 6.46 | 6.47 | 6.83 | 8.08 | 8.58 | 6.82 |
| RMSEf | 6.49 | 6.95 | 6.67 | 61.71 | 52.15 | 36.39 | 38.52 | 53.71 | 32.86 | 32.26 | 18.18 |
| Input Variable | Test Set (Year) | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| 2015 | 2016 | 2017 | |||||||
| R2 | RMSE | Acc | R2 | RMSE | Acc | R2 | RMSE | Acc | |
| AOD | 0.640 | 6.66 | 80.7% | 0.656 | 6.56 | 81.4% | 0.723 | 6.27 | 82.9% |
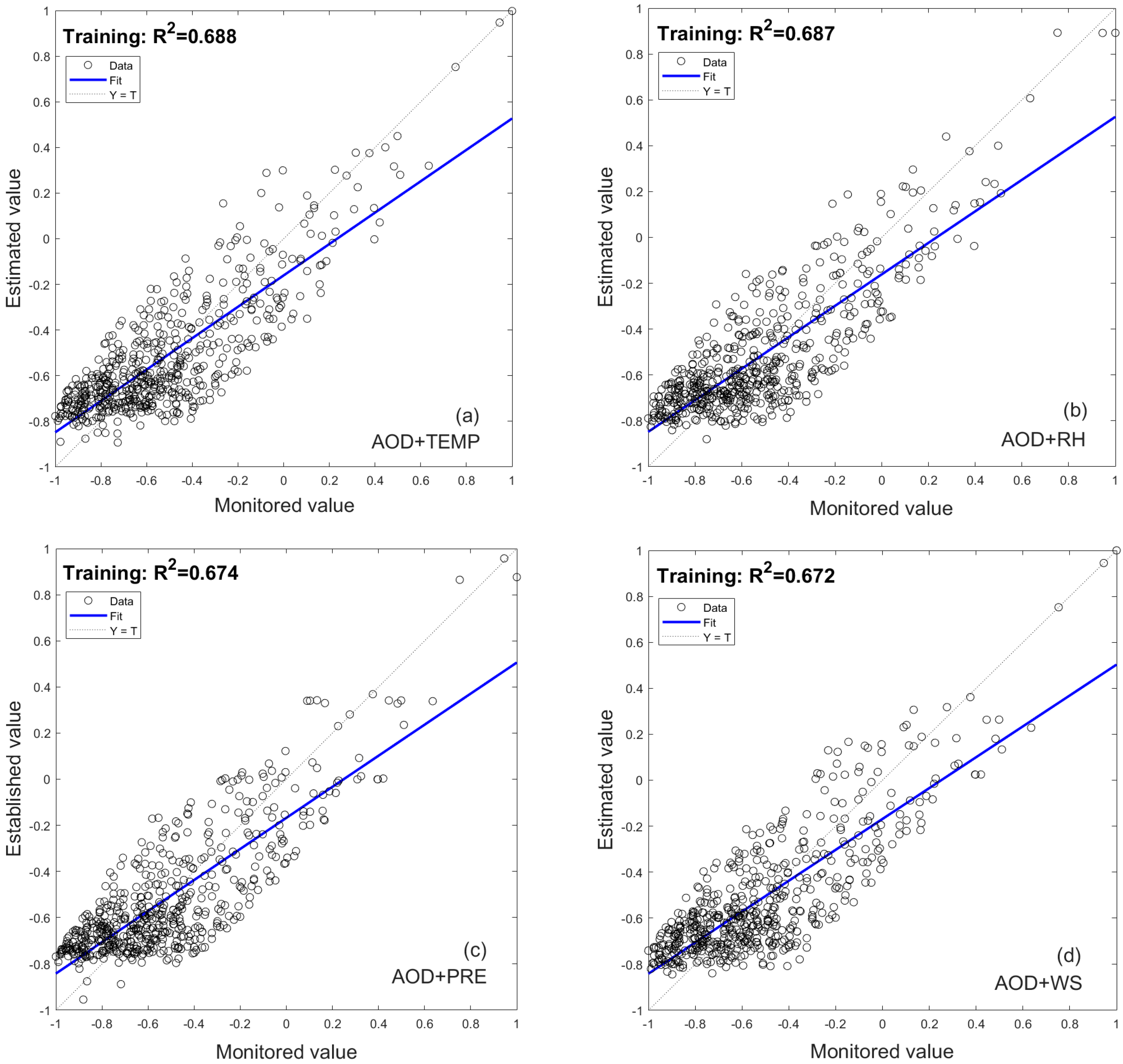
| AOD + TEMP | 0.661 | 6.47 | 82.0% | 0.672 | 6.48 | 82.0% | 0.731 | 6.23 | 83.2% |
| AOD + RH | 0.656 | 6.58 | 81.9% | 0.661 | 6.50 | 81.2% | 0.729 | 6.23 | 83.1% |
| AOD + PRE | 0.648 | 6.60 | 81.8% | 0.658 | 6.55 | 81.9% | 0.719 | 6.25 | 83.0% |
| AOD + WS | 0.645 | 6.65 | 81.7% | 0.658 | 6.62 | 81.8% | 0.711 | 6.26 | 82.9% |
| AOD + All Features | 0.676 | 6.45 | 82.2% | 0.691 | 6.34 | 82.7% | 0.752 | 6.23 | 83.4% |
| Input Variable | Test Set (Year) | ||||||||
| 2018 | 2019 | 2020 | |||||||
| R2 | RMSE | Acc | R2 | RMSE | Acc | R2 | RMSE | Acc | |
| AOD | 0.656 | 6.33 | 82.0% | 0.640 | 6.81 | 79.9% | 0.640 | 6.34 | 81.9% |
| AOD + TEMP | 0.679 | 6.29 | 82.7% | 0.671 | 6.74 | 80.4% | 0.661 | 6.20 | 82.6% |
| AOD + RH | 0.672 | 6.31 | 82.5% | 0.654 | 6.77 | 80.1% | 0.651 | 6.22 | 82.6% |
| AOD + PRE | 0.671 | 6.33 | 82.2% | 0.643 | 6.78 | 80.0% | 0.653 | 6.31 | 82.3% |
| AOD + WS | 0.667 | 6.33 | 82.2% | 0.642 | 6.80 | 79.9% | 0.650 | 6.34 | 82.0% |
| AOD + All Features | 0.677 | 6.30 | 82.8% | 0.686 | 6.54 | 82.0% | 0.663 | 6.32 | 82.4% |
| Model | Model Parameter | Model Expression | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Hidden Neurons | C | g | R2 | RMSE/μg/m3 | RMSE SD/μg/m3 | Acc | Time | ||
| BPNN | 2 | - | - | 0.723 | 6.35 | 0.26 | 82.4% | 2″00 | - |
| SVR | - | 4 | 0.06 | 0.672 | 6.37 | 0.27 | 82.2% | 13″12 | - |
| LR | - | - | - | 0.656 | 6.42 | 0.22 | 82.0% | - | PM2.5 = 34.28AOD + 17.00 |
| NLR | - | - | - | 0.672 | 6.37 | 0.23 | 82.2% | - | PM2.5 = 14.87 + 47.09AOD − 14.16AOD2 + 3.15AOD3 |
| MLR | - | - | - | 0.689 | 6.20 | 0.26 | 83.4% | - | PM2.5 = 0.80AOD + 0.07TEMP + 0.04RH − 0.05WS − 0.06PRE |
| Meteorological factors–SVR | - | 2 | 1 | 0.689 | 6.25 | 0.28 | 83.3% | 11″29 | - |
| Meteorological factors–BPNN | 2 | - | - | 0.757 | 6.11 | 0.26 | 84.4% | 2″00 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gu, J.; Wang, Y.; Ma, J.; Lu, Y.; Wang, S.; Li, X. An Estimation Method for PM2.5 Based on Aerosol Optical Depth Obtained from Remote Sensing Image Processing and Meteorological Factors. Remote Sens. 2022, 14, 1617. https://doi.org/10.3390/rs14071617
Gu J, Wang Y, Ma J, Lu Y, Wang S, Li X. An Estimation Method for PM2.5 Based on Aerosol Optical Depth Obtained from Remote Sensing Image Processing and Meteorological Factors. Remote Sensing. 2022; 14(7):1617. https://doi.org/10.3390/rs14071617
Chicago/Turabian StyleGu, Jilin, Yiwei Wang, Ji Ma, Yaoqi Lu, Shaohua Wang, and Xueming Li. 2022. "An Estimation Method for PM2.5 Based on Aerosol Optical Depth Obtained from Remote Sensing Image Processing and Meteorological Factors" Remote Sensing 14, no. 7: 1617. https://doi.org/10.3390/rs14071617
APA StyleGu, J., Wang, Y., Ma, J., Lu, Y., Wang, S., & Li, X. (2022). An Estimation Method for PM2.5 Based on Aerosol Optical Depth Obtained from Remote Sensing Image Processing and Meteorological Factors. Remote Sensing, 14(7), 1617. https://doi.org/10.3390/rs14071617