Las2DoD: Change Detection Based on Digital Elevation Models Derived from Dense Point Clouds with Spatially Varied Uncertainty
Abstract
:1. Introduction
2. Theory Background and Methodology
2.1. Error Propagation in DoD
2.2. Las2DoD
3. Case Study
3.1. Study Area and Datasets
3.2. Change Detection Methods
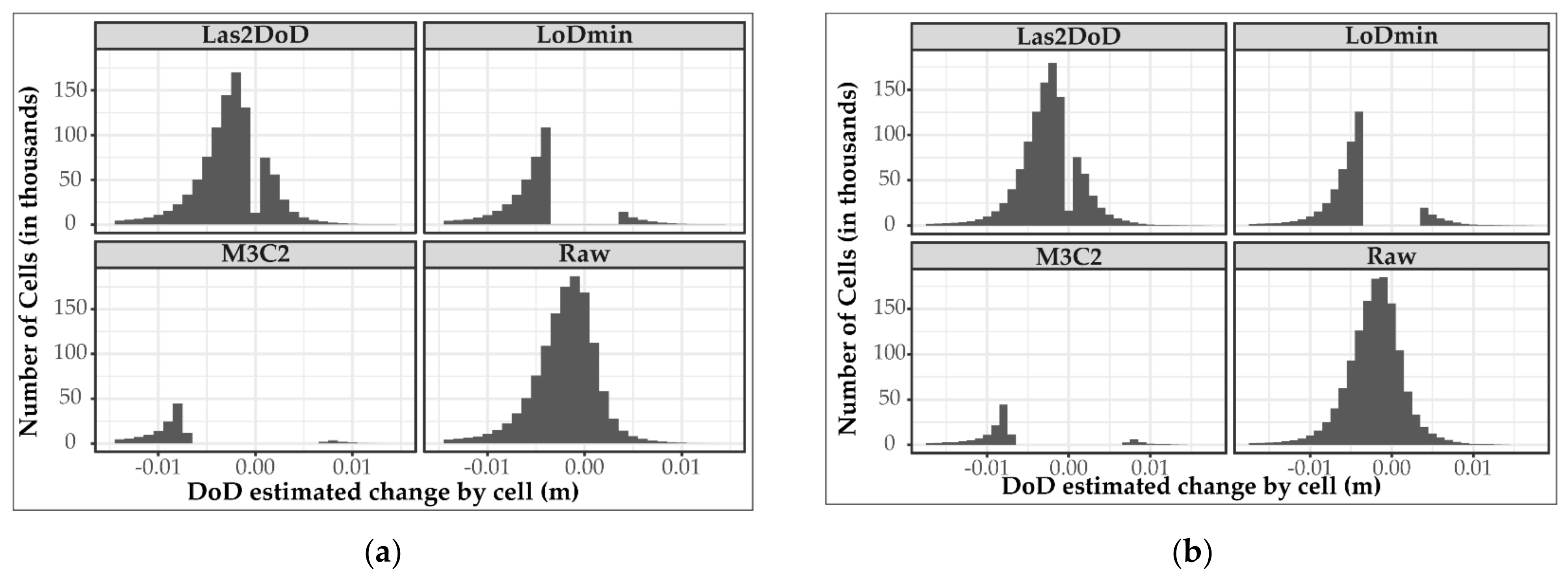
3.3. Results
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lefsky, M.A.; Cohen, W.B.; Parker, G.G.; Harding, D.J. Lidar Remote Sensing for Ecosystem StudiesLidar, an Emerging Remote Sensing Technology That Directly Measures the Three-Dimensional Distribution of Plant Canopies, Can Accurately Estimate Vegetation Structural Attributes and Should Be of Particular Interest to Forest, Landscape, and Global Ecologists. BioScience 2002, 52, 19–30. [Google Scholar] [CrossRef]
- Tarolli, P. High-Resolution Topography for Understanding Earth Surface Processes: Opportunities and Challenges. Geomorphology 2014, 216, 295–312. [Google Scholar] [CrossRef]
- Tarolli, P.; Dalla Fontana, G. Hillslope-to-Valley Transition Morphology: New Opportunities from High Resolution DTMs. Geomorphology 2009, 113, 47–56. [Google Scholar] [CrossRef]
- Slatton, K.C.; Carter, W.E.; Shrestha, R.L.; Dietrich, W. Airborne Laser Swath Mapping: Achieving the Resolution and Accuracy Required for Geosurficial Research. Geophys. Res. Lett. 2007, 34, L23S10. [Google Scholar] [CrossRef]
- Perroy, R.L.; Bookhagen, B.; Asner, G.P.; Chadwick, O.A. Comparison of Gully Erosion Estimates Using Airborne and Ground-Based LiDAR on Santa Cruz Island, California. Geomorphology 2010, 118, 288–300. [Google Scholar] [CrossRef]
- Höfle, B.; Griesbaum, L.; Forbriger, M. GIS-Based Detection of Gullies in Terrestrial LiDAR Data of the Cerro Llamoca Peatland (Peru). Remote Sens. 2013, 5, 5851–5870. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; McNelis, J.J.; Washington-Allen, R.A. Quantifying Short-Term Erosion and Deposition in an Active Gully Using Terrestrial Laser Scanning: A Case Study From West Tennessee, USA. Front. Earth Sci. 2020, 8, 14. [Google Scholar] [CrossRef]
- Goodwin, N.R.; Armston, J.D.; Muir, J.; Stiller, I. Monitoring Gully Change: A Comparison of Airborne and Terrestrial Laser Scanning Using a Case Study from Aratula, Queensland. Geomorphology 2017, 282, 195–208. [Google Scholar] [CrossRef]
- Rengers, F.K.; Tucker, G.E. The Evolution of Gully Headcut Morphology: A Case Study Using Terrestrial Laser Scanning and Hydrological Monitoring. Earth Surf. Process. Landf. 2015, 40, 1304–1317. [Google Scholar] [CrossRef]
- Eltner, A.; Baumgart, P. Accuracy Constraints of Terrestrial Lidar Data for Soil Erosion Measurement: Application to a Mediterranean Field Plot. Geomorphology 2015, 245, 243–254. [Google Scholar] [CrossRef]
- Lu, X.; Li, Y.; Washington-Allen, R.A.; Li, Y.; Li, H.; Hu, Q. The Effect of Grid Size on the Quantification of Erosion, Deposition, and Rill Network. Int. Soil Water Conserv. Res. 2017, 5, 241–251. [Google Scholar] [CrossRef]
- Lu, X.; Li, Y.; Washington-Allen, R.A.; Li, Y. Structural and Sedimentological Connectivity on a Rilled Hillslope. Sci. Total Environ. 2019, 655, 1479–1494. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lu, X.; Washington-Allen, R.A.; Li, Y. Microtopographic Controls on Erosion and Deposition of a Rilled Hillslope in Eastern Tennessee, USA. Remote Sens. 2022, 14, 1315. [Google Scholar] [CrossRef]
- Day, S.S.; Gran, K.B.; Belmont, P.; Wawrzyniec, T. Measuring Bluff Erosion Part 1: Terrestrial Laser Scanning Methods for Change Detection. Earth Surf. Process. Landf. 2013, 38, 1055–1067. [Google Scholar] [CrossRef]
- Vericat, D.; Smith, M.W.; Brasington, J. Patterns of Topographic Change in Sub-Humid Badlands Determined by High Resolution Multi-Temporal Topographic Surveys. CATENA 2014, 120, 164–176. [Google Scholar] [CrossRef]
- Schürch, P.; Densmore, A.L.; Rosser, N.J.; Lim, M.; McArdell, B.W. Detection of Surface Change in Complex Topography Using Terrestrial Laser Scanning: Application to the Illgraben Debris-Flow Channel. Earth Surf. Process. Landf. 2011, 36, 1847–1859. [Google Scholar] [CrossRef]
- Cândido, B.M.; Quinton, J.N.; James, M.R.; Silva, M.L.N.; de Carvalho, T.S.; de Lima, W.; Beniaich, A.; Eltner, A. High-Resolution Monitoring of Diffuse (Sheet or Interrill) Erosion Using Structure-from-Motion. Geoderma 2020, 375, 114477. [Google Scholar] [CrossRef]
- Bolkas, D.; Naberezny, B.; Jacobson, M.G. Comparison of SUAS Photogrammetry and TLS for Detecting Changes in Soil Surface Elevations Following Deep Tillage. J. Surv. Eng. 2021, 147, 04021001. [Google Scholar] [CrossRef]
- Meijer, A.D.; Heitman, J.L.; White, J.G.; Austin, R.E. Measuring Erosion in Long-Term Tillage Plots Using Ground-Based Lidar. Soil Tillage Res. 2013, 126, 1–10. [Google Scholar] [CrossRef]
- Turunen, M.; Turtola, E.; Vaaja, M.T.; Hyväluoma, J.; Koivusalo, H. Terrestrial Laser Scanning Data Combined with 3D Hydrological Modeling Decipher the Role of Tillage in Field Water Balance and Runoff Generation. CATENA 2020, 187, 104363. [Google Scholar] [CrossRef]
- Westoby, M.J.; Brasington, J.; Glasser, N.F.; Hambrey, M.J.; Reynolds, J.M. ‘Structure-from-Motion’ Photogrammetry: A Low-Cost, Effective Tool for Geoscience Applications. Geomorphology 2012, 179, 300–314. [Google Scholar] [CrossRef] [Green Version]
- James, M.R.; Robson, S. Straightforward Reconstruction of 3D Surfaces and Topography with a Camera: Accuracy and Geoscience Application. J. Geophys. Res. Earth Surf. 2012, 117, 03017. [Google Scholar] [CrossRef] [Green Version]
- Prosdocimi, M.; Calligaro, S.; Sofia, G.; Dalla Fontana, G.; Tarolli, P. Bank Erosion in Agricultural Drainage Networks: New Challenges from Structure-from-Motion Photogrammetry for Post-Event Analysis. Earth Surf. Process. Landf. 2015, 40, 1891–1906. [Google Scholar] [CrossRef]
- Meinen, B.U.; Robinson, D.T. Where Did the Soil Go? Quantifying One Year of Soil Erosion on a Steep Tile-Drained Agricultural Field. Sci. Total Environ. 2020, 729, 138320. [Google Scholar] [CrossRef]
- Kaiser, A.; Erhardt, A.; Eltner, A. Addressing Uncertainties in Interpreting Soil Surface Changes by Multitemporal High-Resolution Topography Data across Scales. Land Degrad. Dev. 2018, 29, 2264–2277. [Google Scholar] [CrossRef]
- Neugirg, F.; Stark, M.; Kaiser, A.; Vlacilova, M.; Della Seta, M.; Vergari, F.; Schmidt, J.; Becht, M.; Haas, F. Erosion Processes in Calanchi in the Upper Orcia Valley, Southern Tuscany, Italy Based on Multitemporal High-Resolution Terrestrial LiDAR and UAV Surveys. Geomorphology 2016, 269, 8–22. [Google Scholar] [CrossRef]
- Whitehead, K.; Moorman, B.J.; Hugenholtz, C.H. Brief Communication: Low-Cost, on-Demand Aerial Photogrammetry for Glaciological Measurement. Cryosphere 2013, 7, 1879. [Google Scholar] [CrossRef] [Green Version]
- Cook, K.L. An Evaluation of the Effectiveness of Low-Cost UAVs and Structure from Motion for Geomorphic Change Detection. Geomorphology 2017, 278, 195–208. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D.; Roux, M.; Marc, R.; Thibault, G. Change Detection on Point Cloud Data Acquired with a Ground Laser Scanner. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2005, 36, W19. [Google Scholar]
- Nourbakhshbeidokhti, S.; Kinoshita, A.; Chin, A.; Florsheim, J. A Workflow to Estimate Topographic and Volumetric Changes and Errors in Channel Sedimentation after Disturbance. Remote Sens. 2019, 11, 586. [Google Scholar] [CrossRef] [Green Version]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D Comparison of Complex Topography with Terrestrial Laser Scanner: Application to the Rangitikei Canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef] [Green Version]
- Williams, R. DEMs of Difference. Geomorphol. Tech. 2012, 2, 1–17. [Google Scholar]
- Wheaton, J.M.; Brasington, J.; Darby, S.E.; Sear, D.A. Accounting for uncertainty in DEMs from repeat topographic surveys: Improved sediment budgets. Earth Surf. Process. Landf. 2010, 35, 136–156. [Google Scholar] [CrossRef]
- Brasington, J.; Rumsby, B.T.; McVey, R.A. Monitoring and modelling morphological change in a braided gravel-bed river using high resolution GPS-based survey. Earth Surf. Process. Landf. 2000, 25, 973–990. [Google Scholar] [CrossRef]
- Wheaton, J.M. Uncertainty in Morphological Sediment Budgeting of Rivers. Ph.D. Thesis, University of Southampton, Southampton, UK, 2008. [Google Scholar]
- Blasone, G.; Cavalli, M.; Marchi, L.; Cazorzi, F. Monitoring Sediment Source Areas in a Debris-Flow Catchment Using Terrestrial Laser Scanning. CATENA 2014, 123, 23–36. [Google Scholar] [CrossRef]
- Croke, J.; Todd, P.; Thompson, C.; Watson, F.; Denham, R.; Khanal, G. The Use of Multi Temporal LiDAR to Assess Basin-Scale Erosion and Deposition Following the Catastrophic January 2011 Lockyer Flood, SE Queensland, Australia. Geomorphology 2013, 184, 111–126. [Google Scholar] [CrossRef]
- James, L.A.; Hodgson, M.E.; Ghoshal, S.; Latiolais, M.M. Geomorphic Change Detection Using Historic Maps and DEM Differencing: The Temporal Dimension of Geospatial Analysis. Geomorphology 2012, 137, 181–198. [Google Scholar] [CrossRef]
- Brasington, J.; Langham, J.; Rumsby, B. Methodological Sensitivity of Morphometric Estimates of Coarse Fluvial Sediment Transport. Geomorphology 2003, 53, 299–316. [Google Scholar] [CrossRef]
- Lane, S.N.; Westaway, R.M.; Hicks, D.M. Estimation of erosion and deposition volumes in a large, gravel-bed, braided river using synoptic remote sensing. Earth Surf. Process. Landf. 2003, 28, 249–271. [Google Scholar] [CrossRef]
- Welch, B.L. The Generalization of `Student’s’ Problem When Several Different Population Variances Are Involved. Biometrika 1947, 34, 28–35. [Google Scholar] [CrossRef]
- Bonilla, C.A.; Kroll, D.G.; Norman, J.M.; Yoder, D.C. Instrumentation for Measuring Runoff, Sediment, and Chemical Losses from Agricultural Fields. J. Environ. Qual. 2006, 35, 216–223. [Google Scholar] [CrossRef] [Green Version]
- Hoomehr, S.; Schwartz, J.S.; Yoder, D.C.; Drumm, E.C.; Wright, W. Curve Numbers for Low-Compaction Steep-Sloped Reclaimed Mine Lands in the Southern Appalachians. J. Hydrol. Eng. 2013, 18, 1627–1638. [Google Scholar] [CrossRef]
- Seo, Y.; Lee, J.; Hart, W.E.; Denton, H.P.; Yoder, D.C.; Essington, M.E.; Perfect, E. SEDIMENT LOSS AND NUTRIENT RUNOFF FROM THREE FERTILIZER APPLICATION METHODS. Trans. ASAE 2005, 48, 2155–2162. [Google Scholar] [CrossRef]
- Yoder, D.C.; Cope, T.L.; Wills, J.B.; Denton, H.P. No-till Transplanting of Vegetables and Tobacco to Reduce Erosion and Nutrient Surface Runoff. J. Soil Water Conserv. 2005, 60, 68–73. [Google Scholar]
- Pinson, W.T.; Yoder, D.C.; Buchanan, J.R.; Wright, W.C.; Wilkerson, J.B. Design and evaluation of an improved flow divider for sampling runoff plots. Appl. Eng. Agric. 2004, 20, 433. [Google Scholar] [CrossRef]
- Fan, L.; Smethurst, J.A.; Atkinson, P.M.; Powrie, W. Error in Target-Based Georeferencing and Registration in Terrestrial Laser Scanning. Comput. Geosci. 2015, 83, 54–64. [Google Scholar] [CrossRef] [Green Version]
- Barneveld, R.J.; Seeger, M.; Maalen-Johansen, I. Assessment of Terrestrial Laser Scanning Technology for Obtaining High-Resolution DEMs of Soils: TLS FOR HIGH-RESOLUTION DEMS. Earth Surf. Process. Landf. 2013, 38, 90–94. [Google Scholar] [CrossRef]
- Randrup, T.; Lichter, J. Measuring Soil Compaction on Construction Sites: A Review of Surface Nuclear Gauges and Penetrometers. J. Arboric. 2001, 27, 109–117. [Google Scholar] [CrossRef]
- Rousseva, S.S.; Ahuja, L.R.; Heathman, G.C. Use of a Surface Gamma-Neutron Gauge for in Situ Measurement of Changes in Bulk Density of the Tilled Zone. Soil Tillage Res. 1988, 12, 235–251. [Google Scholar] [CrossRef]
- Govers, G.; Poesen, J. Assessment of the Interrill and Rill Contributions to Total Soil Loss from an Upland Field Plot. Geomorphology 1988, 1, 343–354. [Google Scholar] [CrossRef]
- Yang, R.; Meng, X.; Yao, Y.; Chen, B.Y.; You, Y.; Xiang, Z. An Analytical Approach to Evaluate Point Cloud Registration Error Utilizing Targets. ISPRS J. Photogramm. Remote Sens. 2018, 143, 48–56. [Google Scholar] [CrossRef]



| Method | Area of Significant Change (m2) | Percentage of Surface Represented (%) | Volume Added (m3) | Volume Removed (m3) | Total Volume Change (m3) | Estimated Mass Change (kg) 1 | Estimated Mass Change/Measured Sediment Delivery 2 |
|---|---|---|---|---|---|---|---|
| Las2DoD | 101.65 | 79.5 | 0.05 | 0.34 | −0.30 | −369 | 0.90 |
| M3C2 | 16.48 | 12.9 | 0.01 | 0.2 | −0.19 | −237 | 0.58 |
| 39.74 | 31.1 | 0.02 | 0.25 | −0.23 | −287.5 | 0.70 |
| Method | Area of Significant Change (m2) | Percentage of Surface Represented (%) | Volume Added (m3) | Volume Removed (m3) | Total Volume Change (m3) | Estimated Mass Change (kg) 1 | Estimated Mass Change/Measured Sediment Delivery 2 |
|---|---|---|---|---|---|---|---|
| Las2DoD | 112.36 | 83.7 | 0.06 | 0.36 | −0.30 | −416 | 0.63 |
| M3C2 | 14.68 | 10.9 | 0.02 | 0.16 | −0.14 | −198 | 0.30 |
| 46.07 | 34.3 | 0.03 | 0.26 | −0.23 | −320 | 0.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bailey, G.; Li, Y.; McKinney, N.; Yoder, D.; Wright, W.; Washington-Allen, R. Las2DoD: Change Detection Based on Digital Elevation Models Derived from Dense Point Clouds with Spatially Varied Uncertainty. Remote Sens. 2022, 14, 1537. https://doi.org/10.3390/rs14071537
Bailey G, Li Y, McKinney N, Yoder D, Wright W, Washington-Allen R. Las2DoD: Change Detection Based on Digital Elevation Models Derived from Dense Point Clouds with Spatially Varied Uncertainty. Remote Sensing. 2022; 14(7):1537. https://doi.org/10.3390/rs14071537
Chicago/Turabian StyleBailey, Gene, Yingkui Li, Nathan McKinney, Daniel Yoder, Wesley Wright, and Robert Washington-Allen. 2022. "Las2DoD: Change Detection Based on Digital Elevation Models Derived from Dense Point Clouds with Spatially Varied Uncertainty" Remote Sensing 14, no. 7: 1537. https://doi.org/10.3390/rs14071537
APA StyleBailey, G., Li, Y., McKinney, N., Yoder, D., Wright, W., & Washington-Allen, R. (2022). Las2DoD: Change Detection Based on Digital Elevation Models Derived from Dense Point Clouds with Spatially Varied Uncertainty. Remote Sensing, 14(7), 1537. https://doi.org/10.3390/rs14071537






