Simulation and Analysis of Electromagnetic Scattering from Anisotropic Plasma-Coated Electrically Large and Complex Targets

Abstract

An efficient physical optics (PO) calculation method is proposed for the electromagnetic (EM) scattering of electrically large targets coated with magnetized plasma characterized by asymmetric tensor dielectric parameters. The outer surface of the arbitrarily shaped target is discretized into triangular elements. According to the principle of tangent plane approximation and by using the plane wave spectrum expansion method, the scattered field from one triangular element is derived as a double integral in the spectral domain. To obtain the solution in the spatial domain, the saddle point method is used to asymptotically calculate the integral. Then, the equivalent surface currents (ESCs) are constructed by calculating the surface field at the outer surface of the planar model, from which the PO solution is derived by using the Stratton–Chu integral. Moreover, to interpret the field propagation process in the plasma layer quantitatively, the total scattered field of the coated planar model is decomposed into the superposition of different mode field components. It is observed that the scattered fields demonstrate an inherent cross-polarization phenomenon due to the nonreciprocal constitutive relation of the plasma, which is a distinct feature and is different from the general anisotropic medium whose dielectric parameters can be diagonalized. The effectiveness of the proposed method is verified by numerical results. Furthermore, the proposed algorithm consumes less calculation time and memory as compared to commercial full solvers.

1. Introduction

As we all know, plasma is the fourth state of matter formed by gas ionization. Since the first discovery [1], due to the unique propagation characteristics of EM waves in plasma [2,3,4,5,6], it has attracted great attention in many fields such as target stealth technology represented by scatterer radar cross-section (RCS) control, and radiation system design represented by an antenna or a radome [7,8,9,10]. The research on the propagation effects of ultra-high frequency EM waves and microwaves in plasma can be roughly divided into two categories. The first type is the impact of the plasma sheath on EM wave propagation during spacecraft reentry into the atmosphere. When high-speed aircraft reenter the atmosphere, a plasma sheath with a complex structure will be produced on the surface of the reentry body and the surrounding space. The sheath with different parameters has different effects on the absorption, refraction, and reflection of the incident EM wave. When the attenuation of EM wave power is serious, it will cause signal interruption; that is, the so-called “black barrier” problem. It will also seriously affect radar detection and identification of reentry targets. The other is to generate plasma with controllable parameters through artificial means, including high-voltage ionization, isotope injection, etc. The research community has great expectations for the development and application of artificial manufacturing plasma technology. This paper is mainly based on the expected research on the high-frequency theoretical calculation method of EM wave scattering of plasma-coated targets.

In the existing research on the theoretical calculation method of EM scattering for plasma-coated targets, most of the plasma objects with complex flow field properties are simplified into non-flow field plasma layers, and the simplified plasma coating target is closer to the artificially manufactured plasma layer coating model. The research on the theoretical calculation method of EM scattering of plasma-coated targets can be roughly divided into three categories. One is the rigorous analytical method research carried out on the scattering of ideal-shape target models, such as plasma-coated cylinders and spheres [11,12,13]; The second category is the study of numerical calculation methods for EM scattering of plasma-coated targets with finite electric size and arbitrary shapes [14,15,16,17,18], and also includes research on numerical calculation method improvement or acceleration [19,20,21]. However, as the frequency of EM waves increases and the complexity of plasma material parameters increases, numerical calculation methods are facing a sharp increase in calculation time and memory requirements. The third category is the study of high-frequency calculation methods represented by the physical optics (PO) method [22,23,24,25,26,27]. Reference [22] calculated the monostatic RCS of the electrically large target simulated by the non-uniform rational B-spline (NURBS) surface covered by non-uniform and non-magnetized plasma. Yu [23] analyzed the scattering characteristics of hypervelocity models with shooting and bouncing rays (SBR). Liu [24] investigated the multi-band scattering characteristics of a blunt cone with a nonuniform plasma shroud by using the physical optics (PO) method. It should also be pointed out that the plasma model used in the above-mentioned high-frequency calculation method is not magnetized, and most models only use scalar media parameters to characterize plasma, instead of using an asymmetric tensor to characterize the plasma medium attributes. The propagation of EM waves by magnetized plasma usually shows anisotropic characteristics, and its dielectric parameters should be in the form of an asymmetric tensor [28,29] to characterize its non-reciprocal constitutive relationship. Only in this way can the inherent cross-polarization scattering phenomenon of magnetized plasma be reflected, which is similar to the cross-polarization scattering characteristics of the “surface” anisotropic medium. The asymmetric off-diagonal elements in the dielectric parameter tensor of plasma indicate that its constitutive relationship is more special than that of general anisotropic media, which makes the propagation process and mechanism of EM waves in the plasma layer more complicated. In our previous research, Yao [30,31] proposed an EM scattering estimation method for targets coated with anisotropic uniaxial and biaxial media based on the spectral domain method. In Yao’s method, the dielectric tensor of anisotropic media can still be diagonalized, and its scattering model is simpler than that of plasma coating.

Aiming at the targets coated with magnetized plasma characterized by asymmetric tensor dielectric parameters, this paper proposes an efficient and accurate physical optics algorithm based on a spectral-domain asymptotic calculation to achieve high-frequency scattering prediction of plasma-coated electrically large targets. The inherent cross-polarization scattering phenomenon of plasma is demonstrated in the research, and the mechanism of high-frequency scattering of EM waves propagating in the plasma layer is interpreted by analyzing different mode fields. The complex target surface of arbitrary shape is discretized into many triangular facets. Once the ESCs on the surface of the coating facet are obtained, the total scattering field can be obtained by superposing the corresponding integral formula. According to the tangent plane approximation principle of physical optics, the surface field of a coated facet is approximated as that of the infinite coated plane at the tangent plane. Therefore, firstly, it is necessary to solve the scattering field of the plasma-coated infinite PEC plate. In this paper, the spectral domain combined with saddle point evaluation (SDM-SPE) is applied to obtain the spectral-domain asymptotic solution of the scattering field of an infinite plasma-coated slab. To reveal the field propagation mechanism in the plasma layer, the total scattering field of the coated slab is further decomposed into the superposition of different mode field components, and the formation process of each mode field is quantitatively analyzed. The amplitude and phase of the main mode field and their effects on the total scattering field are discussed. Finally, the monostatic RCSs of canonical or complex targets coated with anisotropic plasmas are calculated. Compared with the numerical full-wave method, the proposed algorithm is more efficient and more suitable for the calculation of the scattering field of electrically large complex coated targets.

The remainder of this paper is organized as follows. In the second section, the plane spectral expansion method is first used to obtain the strict spectral-domain solution for the scattering of an infinite plasma-coated plate by plasma. Furthermore, the scattering total field is decomposed into the superposition of the secondary scattering fields of different modes, and the field components of each mode and the transmission relationship between them are solved. Section 3 constructs the physical optics algorithm for the EM scattering of complex targets coated with magnetized plasma. Numerical examples are given to illustrate the effectiveness of the proposed method in Section 4, and the scattering characteristics of anisotropic plasma-coated planar models and complex targets are discussed and analyzed. Section 5 gives the conclusion.

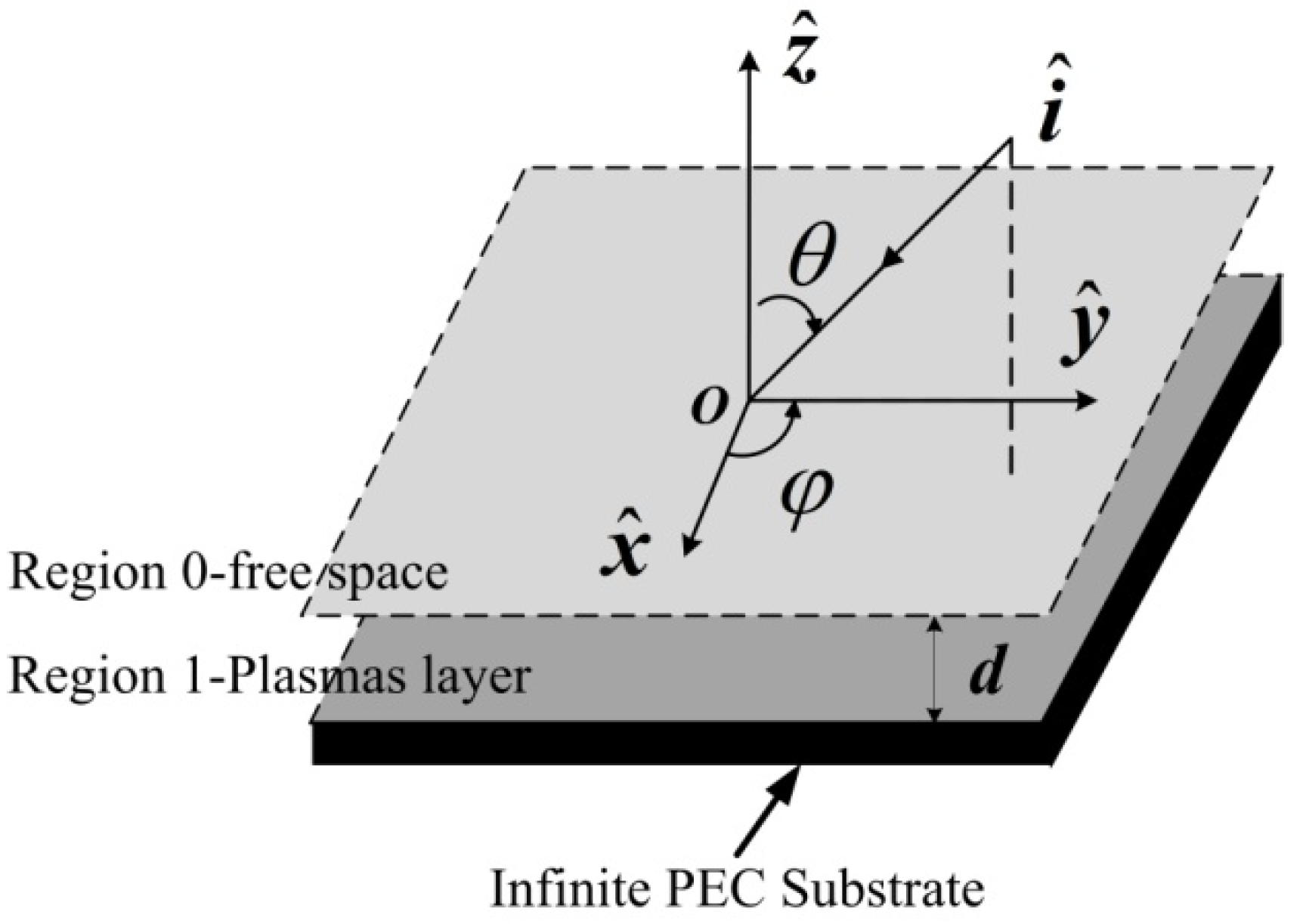
2. The Scattered Fields for An Infinite Plasma-Coated PEC Slab

In this section, we will study the exact spectral-domain solution of the scattering problem of an infinite PEC plate coated with anisotropic plasma. Firstly, the expression of the plane wave spectrum in anisotropic plasma is derived, then the total field in the spectral-domain of the infinite coated plate is obtained by strict boundary condition constraints, and the ray field solution of the spatial EM field is obtained by using the saddle point method. Finally, to analyze the propagation mechanism of the EM wave inside and outside the plasma layer, we decompose the total scattering field into the superposition of secondary scattering fields of different modes and solve the respective mode fields and the transmission relations between them.

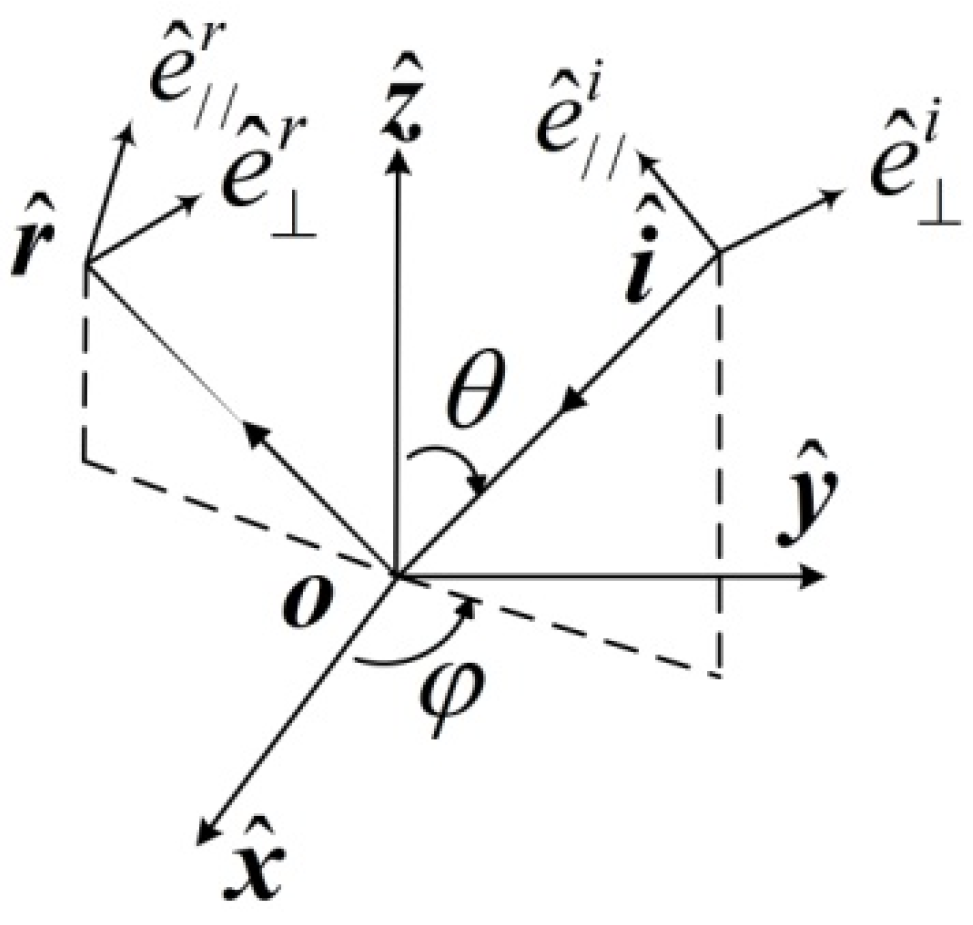
2.1. The Plane Wave Spectrum Representation of the Field in the Plasmas

The Maxwell equation in the anisotropic magnetized plasmas can be expressed as

$$\nabla \times \stackrel{\rightharpoonup }{E}=-j\omega {\mu }_0\stackrel{\rightharpoonup }{H},\nabla \times \stackrel{\rightharpoonup }{H}=j\omega {\epsilon }_0\overline{\overline{\epsilon }}\cdot \stackrel{\rightharpoonup }{E},\nabla \cdot \left(\overline{\overline{\epsilon }}\cdot \stackrel{\rightharpoonup }{E}\right)=0,\nabla \cdot \stackrel{\rightharpoonup }{H}=0.$$

(1)

The permittivity and permeability tensors of the plasma layer are characterized by two matrices:

$$\overline{\overline{\epsilon }}={\epsilon }_0\left[\begin{array}{ccc}{\epsilon }_1& {\epsilon }_2& 0\\ -{\epsilon }_2& {\epsilon }_1& 0\\ 0& 0& {\epsilon }_3\end{array}\right],\overline{\overline{\mu }}={\mu }_0\stackrel{=}{I}$$

(2)

Here, ${\epsilon }_1,{\epsilon }_2$, and ${\epsilon }_3$ are the complex function of electron plasma frequency, wave frequency, electron-neutral collision frequency, and electron cyclotron frequency. Their exact expressions are present in the previously published literature [32].

The Fourier expansions of the EM fields $\stackrel{\rightharpoonup }{E}\left(\stackrel{\rightharpoonup }{r}\right),{\eta }_0\stackrel{\rightharpoonup }{H}\left(\stackrel{\rightharpoonup }{r}\right)$ in Equation (1) are defined as

$$\left[\begin{array}{c}\stackrel{\rightharpoonup }{E}\left(\overrightarrow{r}\right)\\ {\eta }_0\stackrel{\rightharpoonup }{H}\left(\overrightarrow{r}\right)\end{array}\right]={\displaystyle \iint \left[\begin{array}{c}\widetilde{\stackrel{\rightharpoonup }{E}}\left(k_x,k_y\right)\\ {\eta }_0\widetilde{\stackrel{\rightharpoonup }{H}}\left(k_x,k_y\right)\end{array}\right]e^{-j\overrightarrow{k}\cdot \overrightarrow{r}}d{k}_{x}d{k}_y}$$

(3)

where $\stackrel{\rightharpoonup }{r}=\left(x,y,z\right)$, $\stackrel{\rightharpoonup }{k}=-k_x\widehat{x}-k_y\widehat{y}-k_z\widehat{z}$. From Equation (1), the formulas of each partial wave $\widetilde{\stackrel{\rightharpoonup }{E}},{\eta }_0\widetilde{\stackrel{\rightharpoonup }{H}}$ in Equation (3) satisfy

$$\stackrel{\rightharpoonup }{k}\times \widetilde{\stackrel{\rightharpoonup }{E}}=k_0\left({\eta }_0\widetilde{\stackrel{\rightharpoonup }{H}}\right),\stackrel{\rightharpoonup }{k}\times \left({\eta }_0\widetilde{\stackrel{\rightharpoonup }{H}}\right)=-k_0\left(\overline{\overline{\epsilon }}\cdot \widetilde{\stackrel{\rightharpoonup }{E}}\right),\stackrel{\rightharpoonup }{k}\cdot \left(\overline{\overline{\epsilon }}\cdot \widetilde{\stackrel{\rightharpoonup }{E}}\right)=0,\stackrel{\rightharpoonup }{k}\cdot \left({\eta }_0\widetilde{\stackrel{\rightharpoonup }{H}}\right)=0.$$

(4)

It can be derived by Equation (4) that

$$\left(\stackrel{\rightharpoonup }{k}\cdot \widetilde{\stackrel{\rightharpoonup }{E}}\right)\stackrel{\rightharpoonup }{k}-\left(k^2\stackrel{=}{I}-k_0^2\overline{\overline{\epsilon }}\right)\cdot \widetilde{\stackrel{\rightharpoonup }{E}}=0.$$

(5)

The existence of $\widetilde{\stackrel{\rightharpoonup }{E}}$ in Equation (5) can derive

$$\begin{array}{l}\hspace{1em}{\epsilon }_3{k}_z^4+[({\epsilon }_1+{\epsilon }_3)(k_x^2+k_y^2)-2k_0^2{\epsilon }_1{\epsilon }_3]k_z^2\\ +(k_x^2+k_y^2-k_0^2{\epsilon }_3)[{\epsilon }_1(k_x^2+k_y^2)-k_0^2{\epsilon }_1^2]+k_0^2{\epsilon }_2^2\left(k_0^2{\epsilon }_3-k_x^2-k_y^2\right)=0\end{array}$$

(6)

where $k^2=k_x^2+k_y^2+k_z^2$. If $k_x,k_y$ are determined, Equation (6) has four roots $\pm k_{Iz}$ and $\pm k_{IIz}$; that is,

$$\begin{array}{l}\hspace{1em}\hspace{1em}\hspace{1em}{k}_{Iz}=\sqrt{\alpha +\beta },k_{IIz}=\sqrt{\alpha -\beta }\\ \alpha =(2k_0^2{\epsilon }_1{\epsilon }_3-({\epsilon }_1+{\epsilon }_3)(k_x^2+k_y^2))/(2{\epsilon }_3),\\ \beta =-\sqrt{{({\epsilon }_1-{\epsilon }_3)}^2{(k_x^2+k_y^2)}^2-4{\epsilon }_3{k}_0^2{\epsilon }_2^2\left(k_0^2{\epsilon }_3-(k_x^2+k_y^2)\right)}/(2{\epsilon }_3).\end{array}$$

(7)

Thereby type I and II waves propagate in different directions ${\overrightarrow{k}}_{I,II}=-k_x\widehat{x}-k_y\widehat{y}-k_{I,IIz}\widehat{z}$. Substitution of ${\overrightarrow{k}}_I$ or ${\overrightarrow{k}}_{II}$ into Equation (4) leads to

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_I=\left(\frac{A_I}{k_{Iz}}\widehat{x}+\frac{B_I}{k_{Iz}}\widehat{y}+\widehat{z}\right)\zeta ,\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_I=\left(\frac{1}{k_0}\left(B_I-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_I\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{Iz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right)\zeta \end{array}$$

(8)

or

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_{II}=\left(\frac{A_{II}}{k_{IIz}}+\frac{B_{II}}{k_{IIz}}\widehat{y}+\widehat{z}\right)\xi ,\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{II}=\left(\frac{1}{k_0}\left(B_{II}-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_{II}\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{IIz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right)\xi \end{array}$$

(9)

where

$$\begin{array}{l}{A}_{I,II}=\left(k_{I,II}^2-k_0^2\right)\frac{k_x\left(k_{I,II}^2-k_0^2{\epsilon }_1\right)+k_0^2{\epsilon }_2{k}_y}{\left({\left(k_{I,II}^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)},\\ B_{I,II}=\left(k_{I,II}^2-k_0^2{\epsilon }_3\right)\frac{k_y\left(k_{I,II}^2-k_0^2{\epsilon }_1\right)-k_0^2{\epsilon }_2{k}_x}{\left({\left(k_{I,II}^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\end{array}$$

(10)

Equations (8) and (9) represent the type I and II waves in plasmas, and the parameters $\zeta ,\xi$ determine their complex amplitudes. Especially, type I and II waves with $k_x=k_y=0$ propagate along $\pm \widehat{z}$ axes, which are

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_I=\left(\frac{k_0^2{\epsilon }_1-k_{Iz}^2}{k_0^2{\epsilon }_2}\widehat{x}+\widehat{y}\right)\zeta ,{\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_I=\left(\frac{k_{Iz}}{k_0}\widehat{x}-\frac{k_{Iz}}{k_0}\frac{k_0^2{\epsilon }_1-k_{Iz}^2}{k_0^2{\epsilon }_2}\widehat{y}\right)\zeta \\ {\widetilde{\stackrel{\rightharpoonup }{E}}}_{II}=\left(\frac{k_0^2{\epsilon }_1-k_{IIz}^2}{k_0^2{\epsilon }_2}\widehat{x}+\widehat{y}\right)\xi ,{\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{II}=\left(\frac{k_{IIz}}{k_0}\widehat{x}-\frac{k_{IIz}}{k_0}\frac{k_0^2{\epsilon }_1-k_{IIz}^2}{k_0^2{\epsilon }_2}\widehat{y}\right)\xi \end{array}$$

(11)

2.2. The Total Scattered Fields in the Spectral Domain

Consider the planarly stratified model depicted in Figure 1, which shows an infinite PEC plate coated with a homogenous plasma layer whose thickness is $d$. This is divided into two distinct regions; namely, Region 0 for outer free space and Region 1 for the inner anisotropic plasma layer. A set of Cartesian axes $oxyz$ is adopted, with $+\widehat{z}$ an axis normal to the surface of the plasma layer extending from the bottom interface ($z=-d$) to the top interface ($z=0$).

The Fourier expansions of the EM fields $\stackrel{\rightharpoonup }{E}\left(\stackrel{\rightharpoonup }{r}\right),{\eta }_0\stackrel{\rightharpoonup }{H}\left(\stackrel{\rightharpoonup }{r}\right)$ in region 0 (air) and region 1 (plasmas layer) are

$$\left[\begin{array}{c}{\stackrel{\rightharpoonup }{E}}_{0,1}\left(\stackrel{\rightharpoonup }{r}\right)\\ {\eta }_0{\stackrel{\rightharpoonup }{H}}_{0,1}\left(\stackrel{\rightharpoonup }{r}\right)\end{array}\right]={\displaystyle \iint \left[\begin{array}{c}{\widetilde{\stackrel{\rightharpoonup }{E}}}_{0,1}\left(k_x,k_y,z\right)\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{0,1}\left(k_x,k_y,z\right)\end{array}\right]e^{j{k}_{x}x}{e}^{j{k}_{y}y}d{k}_{x}d{k}_y}$$

(12)

where $\stackrel{\rightharpoonup }{r}=x\widehat{x}+y\widehat{y}+z\widehat{z}$, $k_x,k_y$ are the eigenvalues, and the subscripts 0, 1 denote the fields in the air and the plasma layers, respectively. Equation (12) indicates that the arbitrary EM fields can be expanded as plane waves with different eigenvalues $k_x,k_y$ in the spectral domain.

Taking the case of $k_x\cdot k_y\ne 0$, the EM fields in region 1 (plasma layer) can be written as

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_1\left(k_x,k_y,z\right)=\\ \left(\frac{A_I}{k_{Iz}}\widehat{x}+\frac{B_I}{k_{Iz}}\widehat{y}+\widehat{z}\right){\zeta }_1^{+}{e}^{j{k}_{Iz}z}+\left(\frac{A_{II}}{k_{IIz}}+\frac{B_{II}}{k_{IIz}}\widehat{y}+\widehat{z}\right){\xi }_1^{+}{e}^{j{k}_{IIz}z}\\ +\left(\frac{A_I}{k_{Iz}}\widehat{x}-\frac{B_I}{k_{Iz}}\widehat{y}+\widehat{z}\right){\zeta }_1^{-}{e}^{-j{k}_{Iz}z}+\left(\frac{A_{II}}{k_{IIz}}-\frac{B_{II}}{k_{IIz}}\widehat{y}+\widehat{z}\right){\xi }_1^{-}{e}^{-j{k}_{IIz}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_1\left(k_x,k_y,z\right)=\\ \left(\frac{1}{k_0}\left(B_I-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_I\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{Iz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\zeta }_1^{+}{e}^{j{k}_{Iz}z}\\ +\left(\frac{1}{k_0}\left(B_{II}-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_{II}\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{IIz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\xi }_1^{+}{e}^{j{k}_{IIz}z}\\ +\left(\frac{1}{k_0}\left(B_I-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_I\right)\widehat{y}-\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{Iz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\zeta }_1^{-}{e}^{-j{k}_{Iz}z}\\ +\left(\frac{1}{k_0}\left(B_{II}-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_{II}\right)\widehat{y}-\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{IIz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\xi }_1^{-}{e}^{-j{k}_{IIz}z}\end{array}$$

(13)

Similarly, the EM fields in region 0 (air) can be represented as

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_0\left(k_x,k_y,z\right)=\\ \left(\frac{-k_x{k}_{0z}}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_y{k}_{0z}}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\zeta }_0^{+}{e}^{j{k}_{0z}z}+\left(\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\xi }_0^{+}{e}^{j{k}_{0z}z}\\ +\left(\frac{k_x{k}_{0z}}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{-k_y{k}_{0z}}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\zeta }_0^{-}{e}^{-j{k}_{0z}z}+\left(\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\xi }_0^{-}{e}^{-j{k}_{0z}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_0\left(k_x,k_y,z\right)=\\ \left(-\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}+\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\zeta }_0^{+}{e}^{j{k}_{0z}z}+\left(-\frac{k_{0z}{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{x}+\frac{-k_{0z}{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\xi }_0^{+}{e}^{j{k}_{0z}z}\\ +\left(-\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}+\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\zeta }_0^{-}{e}^{-j{k}_{0z}z}+\left(-\frac{-k_{0z}{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{x}+\frac{k_{0z}{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\xi }_0^{-}{e}^{-j{k}_{0z}z}\\ (2)\mathrm{where}{k}_{0z}=\sqrt{k_0^2-k_x^2-k_y^2}.\end{array}$$

(14)

In Equations (13) and (14), the subscripts $+,-$ indicate the partial EM waves propagating along $-\widehat{z}$ and $+\widehat{z}$, respectively. Thereby, the components of the incident and scattered electric fields in Equation (14) (that is, ${\tilde{E}}_0^i,{\tilde{E}}_0^s$) are extracted as

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_0^i=\left[\left(\frac{-k_x{k}_z}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_y{k}_z}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\zeta }_0^{+}+\left(\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\xi }_0^{+}\right]e^{j{k}_{0z}z}\\ {\widetilde{\stackrel{\rightharpoonup }{E}}}_0^s=\left[\left(\frac{k_x{k}_z}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{-k_y{k}_z}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\zeta }_0^{-}+\left(\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\xi }_0^{-}\right]e^{-j{k}_{0z}z}\end{array}$$

(15)

where ${\zeta }_0^{-},{\xi }_0^{-}$ determine the complex amplitudes of the scattered fields, which are requested in our investigation. Meanwhile, ${\zeta }_0^{+},{\xi }_0^{+}$ correspond to the incident fields.

The boundary conditions at the top and bottom interfaces of the plasma slab can be derived as

$$\begin{array}{l}\widehat{z}\times \left({\widetilde{\stackrel{\rightharpoonup }{E}}}_0\left(k_x,k_y,0\right)-{\widetilde{\stackrel{\rightharpoonup }{E}}}_1\left(k_x,k_y,0\right)\right)=0,\\ \widehat{z}\times \left({\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_0\left(k_x,k_y,0\right)-{\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_1\left(k_x,k_y,0\right)\right)=0,\\ \widehat{z}\times {\widetilde{\stackrel{\rightharpoonup }{E}}}_1\left(k_x,k_y,-d\right)=0.\end{array}$$

(16)

Substituting Equations (13) and (14) into Equation (16), the requested ${\zeta }_0^{-},{\xi }_0^{-}$ are represented in terms of ${\zeta }_0^{+},{\xi }_0^{+}$ by suppressing ${\zeta }_1^{\pm },{\xi }_1^{\pm }$; that is

$$\left[\begin{array}{l}{\zeta }_0^{-}\\ {\xi }_0^{-}\end{array}\right]=\left[\begin{array}{cc}\frac{u_1{u}_8-u_4{u}_5}{u_4{u}_6-u_2{u}_8}& \frac{u_3{u}_8-u_4{u}_7}{u_4{u}_6-u_2{u}_8}\\ \frac{u_2{u}_5-u_1{u}_6}{u_4{u}_6-u_2{u}_8}& \frac{u_2{u}_7-u_3{u}_6}{u_4{u}_6-u_2{u}_8}\end{array}\right]\cdot \left[\begin{array}{l}{\zeta }_0^{+}\\ {\xi }_0^{+}\end{array}\right]$$

(17)

where the formulas of $u_i\left(i=1~4\right)$ are

$$\begin{array}{l}\gamma =-1+\frac{\left({\left(k_{II}^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}{\left(k_{II}^2-k_I^2\right)\left(k_{II}^2-k_0^2{\epsilon }_3\right)}-\frac{\left({\left(k_I^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}{\left(k_{II}^2-k_I^2\right)\left(k_I^2-k_0^2{\epsilon }_3\right)}\\ u_1=\frac{k_0^2{\epsilon }_2}{\left(k_{II}^2-k_0^2{\epsilon }_1\right)}\left(1+\frac{k_{0z}}{k_0}\frac{k_{Iz}\left(1+e^{-2j{k}_{Iz}d}\right)}{k_0\left(1-e^{-2j{k}_{Iz}d}\right)}\gamma \right),u_2=-u_1+2\frac{k_0^2{\epsilon }_2}{\left(k_{II}^2-k_0^2{\epsilon }_1\right)}\\ u_3=\frac{k_{Iz}\left(1+e^{-2j{k}_{Iz}d}\right)}{k_0\left(1-e^{-2j{k}_{Iz}d}\right)}\gamma -\frac{k_0{\epsilon }_3{k}_{0z}}{\left(k_{II}^2-k_0^2{\epsilon }_3-k_{IIz}^2\right)},u_4=u_3+2\frac{k_0{\epsilon }_3{k}_{0z}}{\left(k_{II}^2-k_0^2{\epsilon }_3-k_{IIz}^2\right)}\end{array}$$

(18)

When $k_x=k_y=0$, it can be obtained by a similar derivation:

$$\begin{array}{l}{u}_1=\left(1-\frac{k_{Iz}}{k_0}\frac{\left(1+e^{-2j{k}_{Iz}d}\right)}{\left(1-e^{-2j{k}_{Iz}d}\right)}\right),u_2=u_1-2\\ u_3=\frac{k_{IIz}^2-k_0^2{\epsilon }_1}{k_0^2{\epsilon }_2}\left(1-\frac{k_{Iz}}{k_0}\frac{\left(1+e^{-2j{k}_{Iz}d}\right)}{\left(1-e^{-2j{k}_{Iz}d}\right)}\right),u_4=u_3+2\frac{k_0^2{\epsilon }_1-k_{IIz}^2}{k_0^2{\epsilon }_2}\end{array}$$

(19)

The expression form of $u_i\left(i=5~8\right)$ is the same as that of $u_i\left(i=1~4\right)$, only the following substitutions are needed: $k_I\leftrightarrow k_{II},k_{Iz}\leftrightarrow k_{IIz}$. So far, the scattered electric field in the spectral domain in Equation (15) can be established. The corresponding total spatial scattering field can be obtained by the following spectral-domain integration:

$$\begin{array}{l}{\stackrel{\rightharpoonup }{E}}_0^s\left(\stackrel{\rightharpoonup }{r}\right)={\displaystyle \iint {\widetilde{\stackrel{\rightharpoonup }{E}}}_0^s\left(k_x,k_y\right)e^{j{k}_{x}x}{e}^{j{k}_{y}y}{e}^{-j\sqrt{k_0^2-k_x^2-k_y^2}z}d{k}_{x}d{k}_y}.\\ \hspace{1em}\hspace{1em}\hspace{0.17em}={\displaystyle \iint \left(\begin{array}{l}\left(\frac{k_x{k}_z}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{-k_y{k}_z}{\left(k_x^2+k_y^2\right)}\widehat{y}+\widehat{z}\right){\zeta }_0^{-}\\ +\left(\frac{k_0{k}_y}{\left(k_x^2+k_y^2\right)}\widehat{x}-\frac{k_0{k}_x}{\left(k_x^2+k_y^2\right)}\widehat{y}\right){\xi }_0^{-}\end{array}\right)e^{j{k}_{x}x}{e}^{j{k}_{y}y}{e}^{-j\sqrt{k_0^2-k_x^2-k_y^2}z}d{k}_{x}d{k}_y}\end{array}$$

(20)

The saddle-point method is used to approximate the above double integral in Equation (19), and a high-efficiency spatial ray field calculation formula can be obtained, which is particularly suitable for the calculation of a fully propagating EM field. The saddle point can be obtained by derivation as

$${\theta }_s={\theta }_r,{\phi }_s={\phi }_r\pm \pi \left(0\le {\phi }_r<\pi :+,\hspace{0.17em}\pi \le {\phi }_r<2\pi :-\right)$$

(21)

where ${\theta }_r,{\phi }_r$ are the angles of the field point. Equation (20) indicates that the saddle point represents the specular reflection point of the field point by the surface of the infinite coated plate. Thereby, the scattered field asymptotically derived by the saddle point evaluation can be reasonably regarded as the reflected field.

After setting the incident angle, the eigenvalue of the plane wave spectrum corresponding to the saddle point is

$$k_{sx}=k_0\sin \theta \cos \phi ,\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{k}_{sy}=k_0\sin \theta \sin \phi$$

(22)

Therefore, the total scattered electric field of the coated plate in the spatial domain (that is, Equation (20)) can be written as

$${\stackrel{\rightharpoonup }{E}}_0^s\left(\stackrel{\rightharpoonup }{r}\right)\approx -2\pi j{k}_0{\widetilde{\stackrel{\rightharpoonup }{E}}}_0^s\left(k_{sx},k_{sy}\right)\cos \theta e^{-j{k}_{0}r}/r$$

(23)

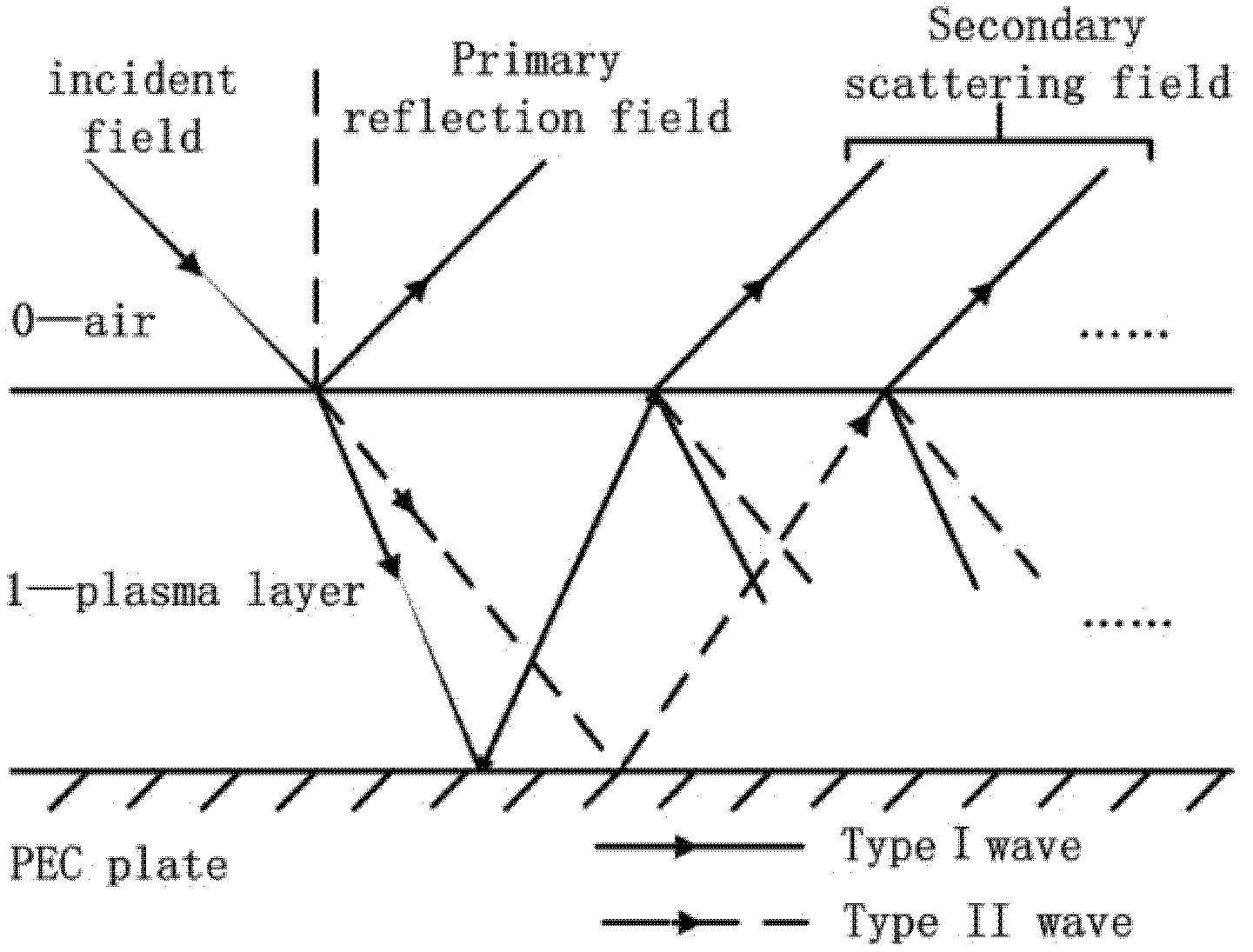
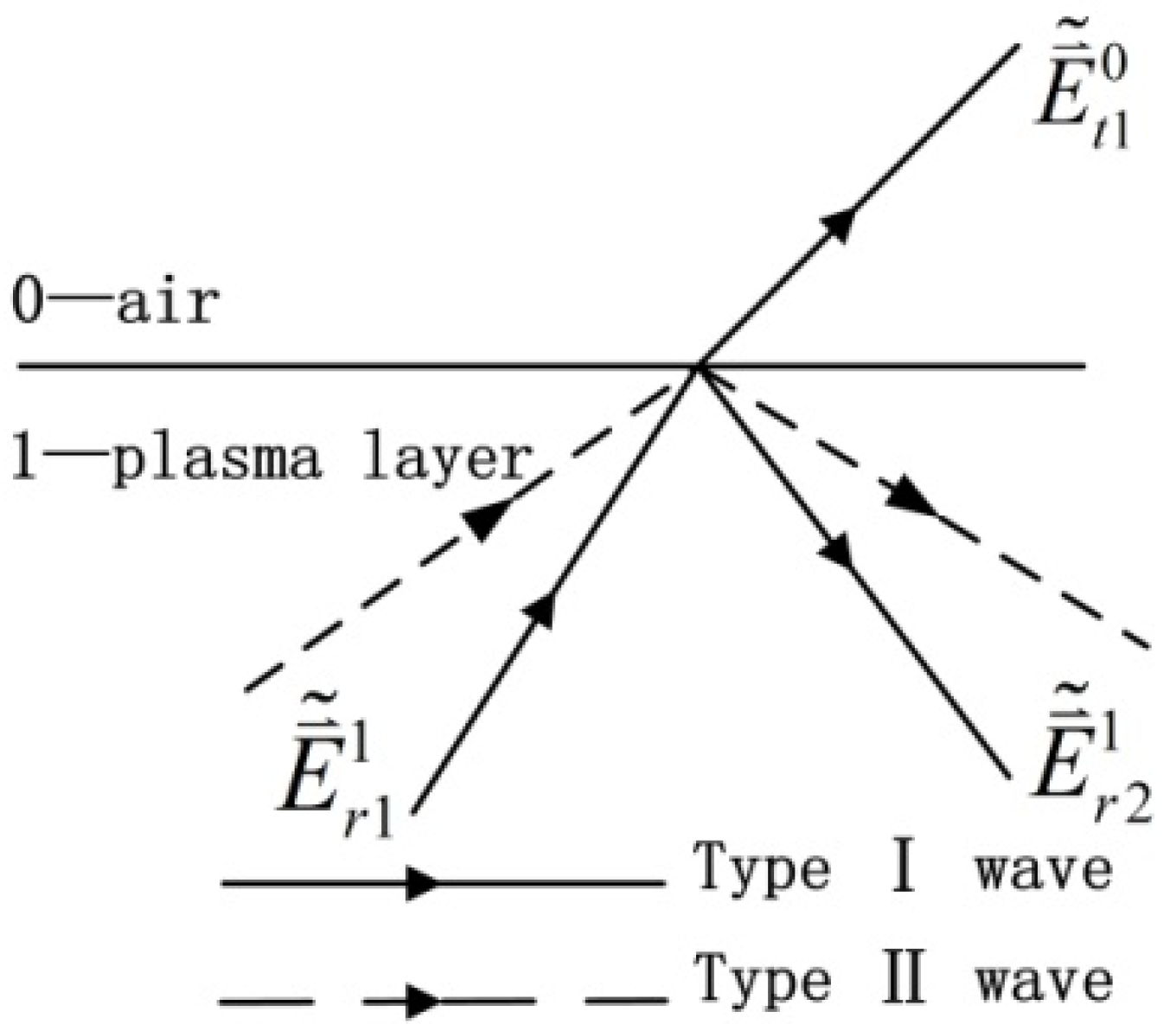
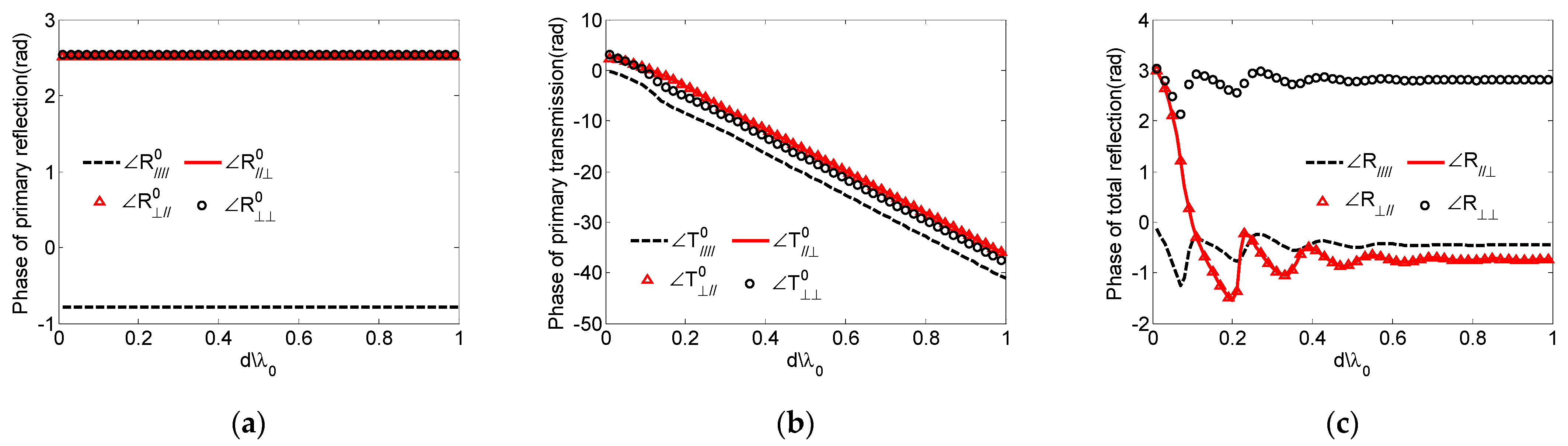
2.3. Propagation Analysis of Each Secondary Scattered Field

In the previous section, the strict spectral-domain solution of scattering from the anisotropic plasma-coated plane has been obtained, but the results cannot directly describe the physical process of the EM wave first penetrating the plasma, then multiple reflections in the layer and finally penetrating. In this section, we will use quantitative mathematical analysis to reveal the physical images of the propagation process of EM waves in each mode corresponding to different ray paths inside and outside the plasma layer. In this section, we will use quantitative mathematical analysis to reveal the physical images of the propagation process of EM waves in each mode corresponding to different ray paths inside and outside the plasma layer. The propagation process of EM waves incident on the plasma dielectric layer is shown in Figure 2. The total field on the upper surface of the dielectric layer includes the incident field, the primary reflection field formed by the incident wave on the upper surface of the plasma, and the superposition of each secondary scattering field transmitted to the dielectric layer, reflected in the layer and then transmitted to the air.

To deduce the field of the EM wave transmitted into the air through n reflections in the plasma layer, a series of coefficient matrices are introduced on each interface to establish the correlation between the EM wave in each mode and the incident wave, as shown in Figure 3. The specific correspondence is as follows:

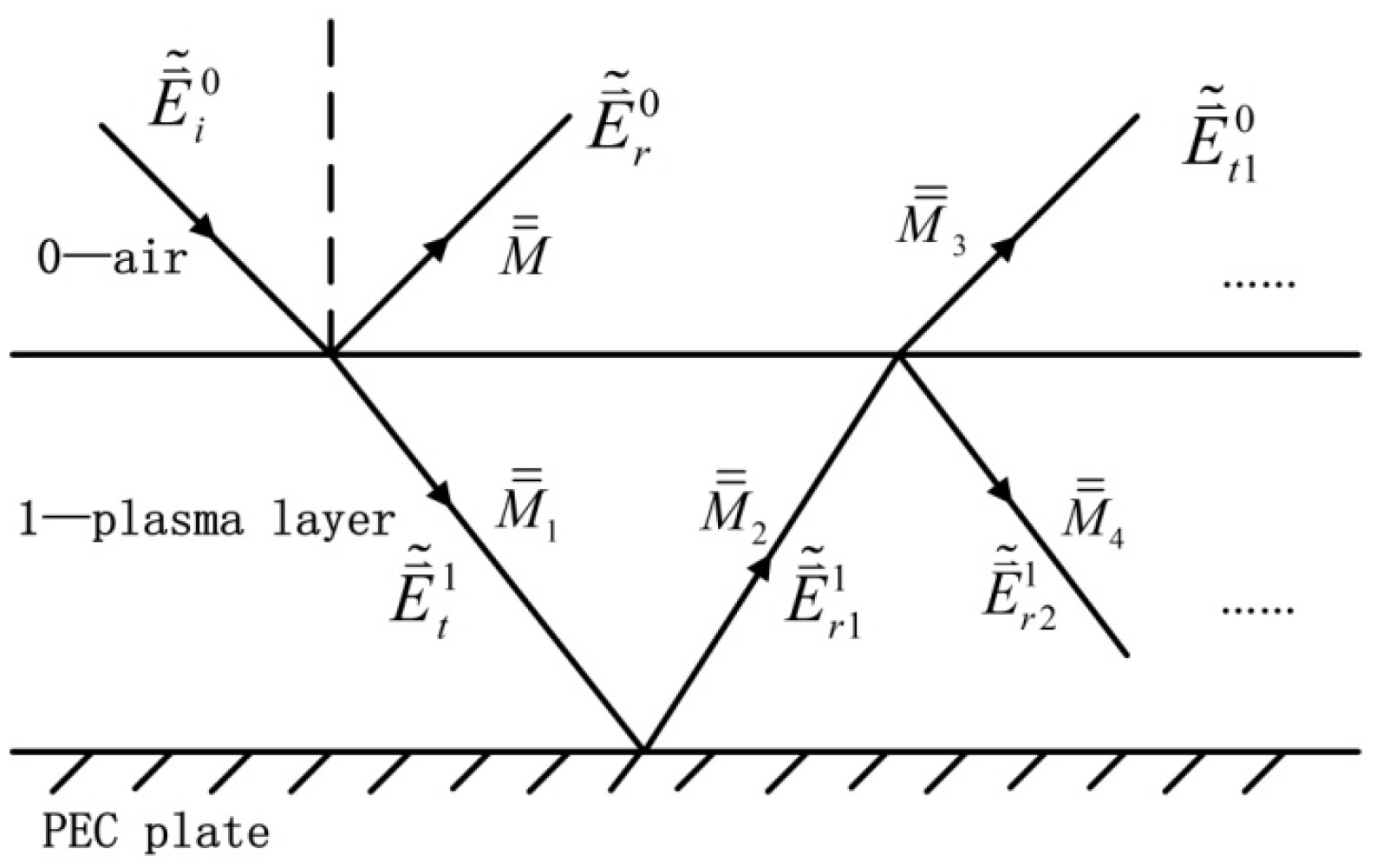
• ${\widetilde{\stackrel{\rightharpoonup }{E}}}_r^0$ is the primary reflection field of the EM wave incident on the surface of the plasma, $\stackrel{=}{M}$ is the corresponding reflection matrix;
• ${\widetilde{\stackrel{\rightharpoonup }{E}}}_t^1$ is the initial transmission field of the EM wave incident into the plasma layer, ${\stackrel{=}{M}}_1$ is the corresponding transmission matrix;
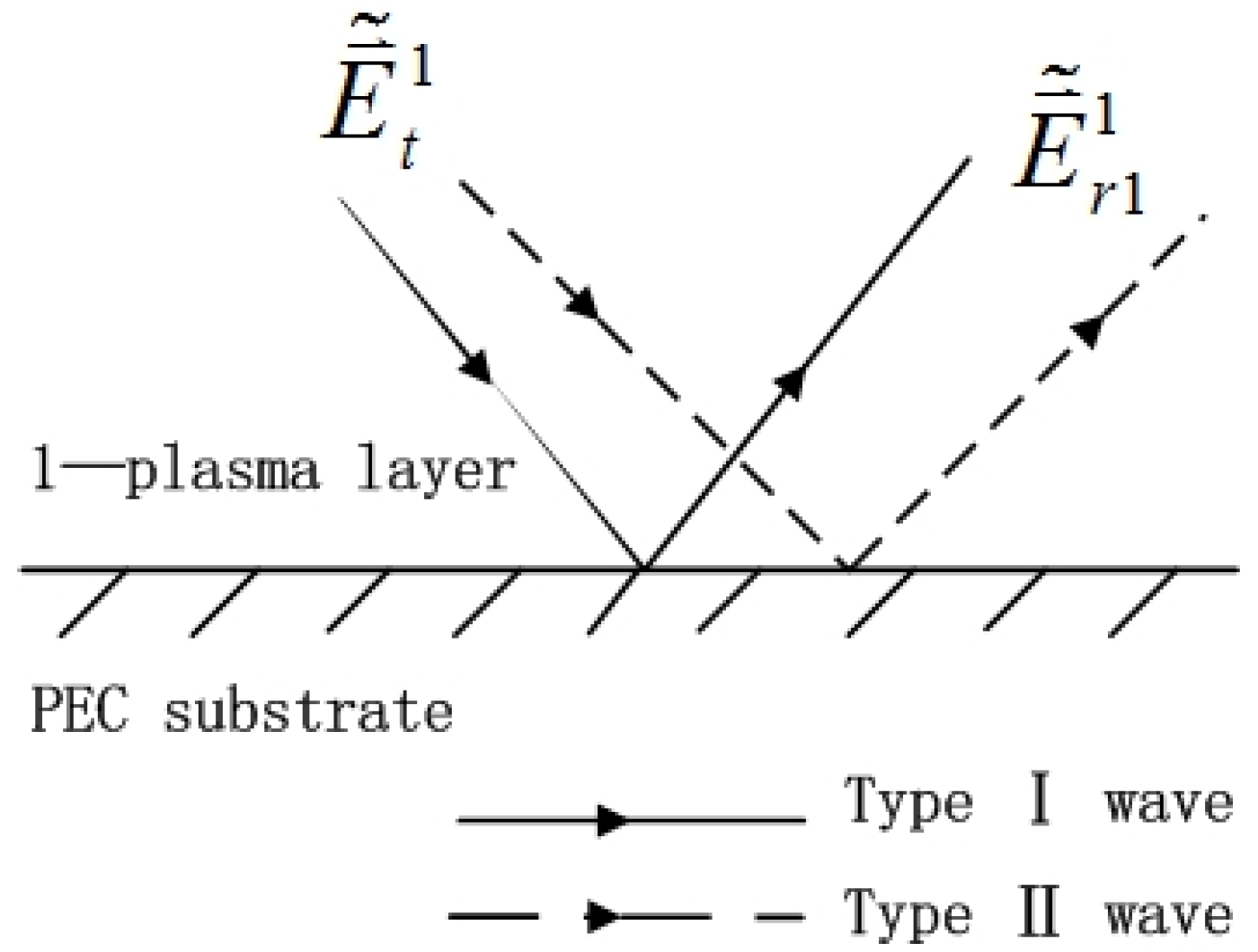
• ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$ is the reflected field after the initial transmission field is incident on the bottom PEC boundary, ${\stackrel{=}{M}}_2$ is the reflection matrix formed by ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$ and ${\widetilde{\stackrel{\rightharpoonup }{E}}}_t^1$;
• ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{t1}^0$ is the transmission field transmitted into the air after one reflection in the layer, ${\stackrel{=}{M}}_3$ is the transmission matrix formed by ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{t1}^0$ and ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$;
• ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r2}^1$ is the reflection field that is reflected back to the medium on the upper surface after one reflection in the layer, ${\stackrel{=}{M}}_4$ is the reflection matrix formed by ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r2}^1$ and ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$;

The above-mentioned fields and the corresponding coefficient matrix are derived below;

• The first reflection on the outer surface

When the EM wave is incident on the plasma layer and acts on the upper surface, as shown in Figure 4, the primary reflected wave does not enter the layer, and the problem can degenerate to a half-space problem: the upper half-space is air with incident field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_i^0$ and primary reflection field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_r^0$; the lower half-space is an anisotropic plasma layer with only the initial transmission field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_t^1$.

In region 0, there are downward incident waves and upward primary reflected fields. The corresponding expressions of the EM field in a spectral domain are as follows:

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_i^0=\frac{1}{t}\left[\left(-k_x{k}_{0z}\widehat{x}-k_y{k}_{0z}\widehat{y}+t\widehat{z}\right){\zeta }_i^{0+}+\left(k_0{k}_y{\eta }_0\widehat{x}-k_0{k}_x{\eta }_0\widehat{y}\right){\xi }_i^{0+}\right]e^{j{k}_{0z}z}\\ {\widetilde{\stackrel{\rightharpoonup }{E}}}_r^0=\frac{1}{t}\left(k_x{k}_{0z}\widehat{x}+k_y{k}_{0z}\widehat{y}+t\widehat{z}\right){\zeta }_r^{0-}{e}^{-j{k}_{0z}z}+\frac{1}{t}\left(k_0{k}_y\widehat{x}-k_0{k}_x\widehat{y}\right){\xi }_r^{0-}{e}^{-j{k}_{0z}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_i^0=\frac{1}{t}\left[\left(-k_0{k}_y\widehat{x}+k_0{k}_x\widehat{y}\right){\zeta }_i^{0+}+\left(-k_{0z}{k}_x\widehat{x}-k_{0z}{k}_y\widehat{y}+t\widehat{z}\right){\xi }_i^{0+}\right]e^{j{k}_{0z}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_r^0=\frac{1}{t}\left(-k_0{k}_y\widehat{x}+k_0{k}_x\widehat{y}\right){\zeta }_r^{0-}{e}^{-j{k}_{0z}z}+\frac{1}{t}\left(k_{0z}{k}_x\widehat{x}+k_{0z}{k}_y\widehat{y}+t\widehat{z}\right){\xi }_r^{0-}{e}^{-j{k}_{0z}z}\end{array}$$

(24)

where $t=k_x^2+k_y^2$. In region 1, there is only a downward initial transmission field, and its expression in the spectral domain can be written as

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_t^1\left(k_x,k_y,z\right)=\left(\frac{A_I}{k_{Iz}}\widehat{x}+\frac{B_I}{k_{Iz}}\widehat{y}+\widehat{z}\right){\zeta }_t^{1+}{e}^{j{k}_{Iz}z}\hspace{0.17em}+\left(\frac{A_{II}}{k_{IIz}}\widehat{x}+\frac{B_{II}}{k_{IIz}}\widehat{y}+\widehat{z}\right){\xi }_t^{1+}{e}^{j{k}_{IIz}z},\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_t^1\left(k_x,k_y,z\right)=\\ \left(\frac{1}{k_0}\left(B_I-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_I\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{Iz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\zeta }_t^{1+}{e}^{j{k}_{Iz}z}\\ +\left(\frac{1}{k_0}\left(B_{II}-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_{II}\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{IIz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\xi }_t^{1+}{e}^{j{k}_{IIz}z}\end{array}$$

(25)

The boundary conditions at the interfaces of the plasma layer can be derived as

$$\begin{array}{l}\widehat{z}\times ({\widetilde{\stackrel{\rightharpoonup }{E}}}_0(k_x,k_y,0)-{\widetilde{\stackrel{\rightharpoonup }{E}}}_1(k_x,k_y,0))=0\\ \widehat{z}\times ({\stackrel{\rightharpoonup }{H}}_0(k_x,k_y,0)-{\widetilde{\stackrel{\rightharpoonup }{H}}}_1(k_x,k_y,0))=0\end{array}$$

(26)

It can be solved by Equation (26)

$$\left[\begin{array}{c}{\zeta }_r^{0-}\\ {\xi }_r^{0-}\end{array}\right]=\stackrel{=}{M}\cdot \left[\begin{array}{c}{\zeta }_i^{0+}\\ {\xi }_i^{0+}\end{array}\right],\hspace{0.17em}\left[\begin{array}{c}{\zeta }_t^{1+}\\ {\xi }_t^{1+}\end{array}\right]={\stackrel{=}{M}}_1\cdot \left[\begin{array}{c}{\zeta }_i^{0+}\\ {\xi }_i^{0+}\end{array}\right]$$

(27)

where

$$\begin{array}{l}\stackrel{=}{M}={\left[\begin{array}{cc}\left(k_{0z}{k}_{Iz}+k_0{k}_0\chi \right)d& k_0\left[k_{0z}\chi t-\left(k_{Iz}+k_{0z}\chi \right)b\right]\\ \left(k_{0z}{k}_{IIz}+k_0{k}_0\chi \right)c& k_0\left[k_{0z}\chi t-\left(k_{IIz}+k_{0z}\chi \right)a\right]\end{array}\right]}^{-1}\\ \hspace{1em}\hspace{1em}·\left[\begin{array}{cc}\left(k_{0z}{k}_{Iz}-k_0{k}_0\chi \right)d& k_0\left[k_{0z}\chi t+\left(k_{Iz}-k_{0z}\chi \right)b\right]\\ \left(k_{0z}{k}_{IIz}-k_0{k}_0\chi \right)c& k_0\left[k_{0z}\chi t+\left(k_{IIz}-k_{0z}\chi \right)a\right]\end{array}\right]\\ {\stackrel{=}{M}}_1={\left[\begin{array}{cc}-\frac{a}{2k_{0z}{k}_{Iz}}-\frac{\left(a-t\right)}{2k_0{k}_0}& -\frac{b}{2k_{0z}{k}_{IIz}}-\frac{\left(b-t\right)}{2k_0{k}_0}\\ \frac{c}{2k_0}\left(\frac{1}{k_{Iz}}+\frac{1}{k_{0z}}\right)& \frac{d}{2k_0}\left(\frac{1}{k_{IIz}}+\frac{1}{k_{0z}}\right)\end{array}\right]}^{-1}\end{array}$$

(28)

where

$$\begin{array}{l}\chi =\frac{\left(k_I^2-k_0^2{\epsilon }_3\right)\left(k_{II}^2-k_0^2{\epsilon }_3\right)}{k_0^2{\epsilon }_2{k}_0^2{\epsilon }_2},t=k_x^2+k_y^2\\ a=\frac{t\left(k_I^2-k_0^2{\epsilon }_3\right)\left(k_I^2-k_0^2{\epsilon }_1\right)}{\left({\left(k_I^2-k_0^2{\epsilon }_1\right)}^2+k_0^2{\epsilon }_2{k}_0^2{\epsilon }_2\right)},b=\frac{t\left(k_{II}^2-k_0^2{\epsilon }_3\right)\left(k_{II}^2-k_0^2{\epsilon }_1\right)}{\left({\left(k_{II}^2-k_0^2{\epsilon }_1\right)}^2+k_0^2{\epsilon }_2{k}_0^2{\epsilon }_2\right)}\\ c=\frac{k_0^2{\epsilon }_{2}t\left(k_I^2-k_0^2{\epsilon }_3\right)}{\left({\left(k_I^2-k_0^2{\epsilon }_1\right)}^2+k_0^2{\epsilon }_2{k}_0^2{\epsilon }_2\right)},d=\frac{k_0^2{\epsilon }_{2}t\left(k_{II}^2-k_0^2{\epsilon }_3\right)}{\left({\left(k_{II}^2-k_0^2{\epsilon }_1\right)}^2+k_0^2{\epsilon }_2{k}_0^2{\epsilon }_2\right)}\end{array}$$

(29)

2.

The reflection of the substrate in the plasma layer

The original model can be simplified to the model of an anisotropic plasma half-space on the PEC substrate, as shown in Figure 5. At this time, there is the initial transmission field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_t^1$ and its reflection field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$ in the anisotropic half-space after the incidence on the PEC substrate; that is

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_1\left(k_x,k_y,z\right)={\widetilde{\stackrel{\rightharpoonup }{E}}}_t^1\left(k_x,k_y\right)+{\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1\left(k_x,k_y\right),\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_1\left(k_x,k_y,z\right)={\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_t^1\left(k_x,k_y\right)+{\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{r1}^1\left(k_x,k_y\right)\end{array}$$

(30)

The reflected field on the PEC substrate is

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1\left(k_x,k_y,z\right)=\left(-\frac{A_I}{k_{Iz}}\widehat{x}-\frac{B_I}{k_{Iz}}\widehat{y}+\widehat{z}\right){\zeta }_{r1}^{1-}{e}^{-j{k}_{Iz}z}+\left(-\frac{A_{II}}{k_{IIz}}\widehat{x}-\frac{B_{II}}{k_{IIz}}\widehat{y}+\widehat{z}\right){\xi }_{r1}^{1-}{e}^{-j{k}_{IIz}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{r1}^1\left(k_x,k_y\right)=\\ \left(\frac{1}{k_0}\left(B_I-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_I\right)\widehat{y}-\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{Iz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\zeta }_{r1}^{1-}{e}^{-j{k}_{Iz}z}\\ +\left(\frac{1}{k_0}\left(B_{II}-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_{II}\right)\widehat{y}-\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{IIz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\xi }_{r1}^{1-}{e}^{-j{k}_{IIz}z}\end{array}$$

(31)

The boundary condition at the PEC substrate is

$$\widehat{z}\times {\stackrel{\rightharpoonup }{E}}_1(k_x,k_y,-d)=0$$

(32)

Similarly, it can be solved by Equation (32)

$$\left[\begin{array}{l}{\zeta }_{r1}^{1-}\\ {\xi }_{r1}^{1-}\end{array}\right]={\stackrel{=}{M}}_2·\left[\begin{array}{c}{\zeta }_t^{1+}\\ {\xi }_t^{1+}\end{array}\right]=\left[\begin{array}{cc}{e}^{-2j{k}_{Iz}d}& 0\\ 0& e^{-2j{k}_{IIz}d}\end{array}\right]·\left[\begin{array}{c}{\zeta }_t^{1+}\\ {\xi }_t^{1+}\end{array}\right]$$

(33)

3.

Transmission from the plasma layer to the upper half-space

As shown in Figure 6, the upper half-space is air, and only the transmission field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{t1}^0$ travels from the layer to the air. The lower half-space is an anisotropic plasma layer, with ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$ and its reflected field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r2}^1$ reflected on the upper surface of the plasma.

In the plasma half-space, there are ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1$ and its reflection field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{r2}^1$ after reflection on the upper surface of the plasma; that is

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_1\left(k_x,k_y,z\right)={\widetilde{\stackrel{\rightharpoonup }{E}}}_{r1}^1\left(k_x,k_y\right)+{\widetilde{\stackrel{\rightharpoonup }{E}}}_{r2}^1\left(k_x,k_y\right),\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_1\left(k_x,k_y,z\right)={\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{r1}^1\left(k_x,k_y\right)+{\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{r2}^1\left(k_x,k_y\right)\end{array}$$

(34)

where

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_{r2}^1\left(k_x,k_y,z\right)=\left(\frac{A_I}{k_{Iz}}\widehat{x}+\frac{B_I}{k_{Iz}}\widehat{y}+\widehat{z}\right){\zeta }_{r2}^{1+}{e}^{j{k}_{Iz}z}+\left(\frac{A_{II}}{k_{IIz}}\widehat{x}+\frac{B_{II}}{k_{IIz}}\widehat{y}+\widehat{z}\right){\xi }_{r2}^{1+}{e}^{j{k}_{IIz}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{r2}^1\left(k_x,k_y\right)=\\ \left(\frac{1}{k_0}\left(B_I-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_I\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{Iz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\zeta }_{r2}^{1+}{e}^{j{k}_{Iz}z}\\ +\left(\frac{1}{k_0}\left(B_{II}-k_y\right)\widehat{x}+\frac{1}{k_0}\left(k_x-A_{II}\right)\widehat{y}+\frac{k_0{\epsilon }_2(k_x^2+k_y^2)\left(k^2-k_0^2{\epsilon }_3\right)}{k_{IIz}\left({\left(k^2-k_0^2{\epsilon }_1\right)}^2+k_0^4{\epsilon }_2^2\right)}\widehat{z}\right){\xi }_{r2}^{1+}{e}^{j{k}_{IIz}z}\end{array}$$

(35)

In the upper half-space, the transmitted field ${\widetilde{\stackrel{\rightharpoonup }{E}}}_{t1}^0$ that first penetrates the air after one reflection in the layer can be written as:

$$\begin{array}{l}{\widetilde{\stackrel{\rightharpoonup }{E}}}_{t1}^0=\frac{1}{t}\left(k_x{k}_{0z}\widehat{x}+k_y{k}_{0z}\widehat{y}+t\widehat{z}\right){\zeta }_{t1}^{0-}{e}^{-j{k}_{0z}z}+\frac{1}{t}\left(k_0{k}_y\widehat{x}-k_0{k}_x\widehat{y}\right){\xi }_{t1}^{0-}{e}^{-j{k}_{0z}z}\\ {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_{t1}^0=\frac{1}{t}\left(-k_0{k}_y\widehat{x}+k_0{k}_x\widehat{y}\right){\zeta }_{t1}^{0-}{e}^{-j{k}_{0z}z}+\frac{1}{t}\left(k_{0z}{k}_x\widehat{x}+k_{0z}{k}_y\widehat{y}+t\widehat{z}\right){\xi }_{t1}^{0-}{e}^{-j{k}_{0z}z}\end{array}$$

(36)

The boundary conditions at the interfaces of the plasma layer can be derived as

$$\begin{array}{l}\widehat{z}\times ({\widetilde{\stackrel{\rightharpoonup }{E}}}_1(k_x,k_y,0)-{\widetilde{\stackrel{\rightharpoonup }{E}}}_0(k_x,k_y,0))=0\\ \widehat{z}\times ({\stackrel{\rightharpoonup }{H}}_1(k_x,k_y,0)-{\widetilde{\stackrel{\rightharpoonup }{H}}}_0(k_x,k_y,0))=0\end{array}$$

(37)

It can be derived by Equation (37) that

$$\left[\begin{array}{l}{\zeta }_{t1}^{0-}\\ {\xi }_{t1}^{0-}\end{array}\right]={\stackrel{=}{M}}_3·\left[\begin{array}{l}{\zeta }_{r1}^{1-}\\ {\xi }_{r1}^{1-}\end{array}\right],\left[\begin{array}{l}{\zeta }_{r2}^{1+}\\ {\xi }_{r2}^{1+}\end{array}\right]={\stackrel{=}{M}}_4·\left[\begin{array}{l}{\zeta }_{r1}^{1-}\\ {\xi }_{r1}^{1-}\end{array}\right]$$

(38)

where

$$\begin{array}{l}{\stackrel{=}{M}}_3={\left[\begin{array}{cc}\frac{k_{0z}{k}_{Iz}d}{2tm}-\frac{k_0^{2}d}{2t\left(c-d-m\right)}& -\frac{k_0{k}_{Iz}b}{2tm}-\frac{k_0{k}_{0z}\left(t-b\right)}{2t\left(c-d-m\right)}\\ \frac{-k_{0z}{k}_{IIz}c}{2tm}+\frac{k_0^{2}c}{2t\left(c-d-m\right)}& \frac{k_0{k}_{IIz}a}{2tm}+\frac{k_0{k}_{0z}\left(t-a\right)}{2t\left(c-d-m\right)}\end{array}\right]}^{-1}\\ {\stackrel{=}{M}}_4={\left[\begin{array}{cc}\frac{c}{k_0}\left(\frac{1}{k_{Iz}}+\frac{1}{k_{0z}}\right)& \frac{d}{k_0}\left(\frac{1}{k_{IIz}}+\frac{1}{k_{0z}}\right)\\ \frac{\left(a-t\right)}{k_0^2}+\frac{a}{k_{0z}{k}_{Iz}}& \frac{\left(b-t\right)}{k_0^2}+\frac{b}{k_{0z}{k}_{IIz}}\end{array}\right]}^{-1}·\left[\begin{array}{cc}\frac{c}{k_0}\left(\frac{1}{k_{Iz}}-\frac{1}{k_{0z}}\right)& \frac{d}{k_0}\left(\frac{1}{k_{IIz}}-\frac{1}{k_{0z}}\right)\\ \frac{-\left(a-t\right)}{k_0^2}-\frac{a}{k_{0z}{k}_{Iz}}& \frac{-\left(b-t\right)}{k_0^2}-\frac{b}{k_{0z}{k}_{IIz}}\end{array}\right]\end{array}$$

(39)

where $m=\left(A_I{B}_{II}-A_{II}{B}_I\right)$. Then, the coefficient matrix of the EM wave transmitted into the air after one reflection in the layer can be written as

$$\left[\begin{array}{l}{\zeta }_{t1}^{0-}\\ {\xi }_{t1}^{0-}\end{array}\right]={\stackrel{=}{M}}_3·{\stackrel{=}{M}}_2·{\stackrel{=}{M}}_1·\left[\begin{array}{l}{\zeta }_i^{0+}\\ {\xi }_i^{0+}\end{array}\right]$$

(40)

Using the expression of the transmission matrix, the coefficient matrix of an EM wave reflected n times in the layer and then transmitted to the air is

$$\left[\begin{array}{l}{\zeta }_{tn}^{0-}\\ {\xi }_{tn}^{0-}\end{array}\right]={\stackrel{=}{M}}_3·{\left({\stackrel{=}{M}}_2·{\stackrel{=}{M}}_4\right)}^{n-1}·{\stackrel{=}{M}}_2·{\stackrel{=}{M}}_1·\left[\begin{array}{l}{\zeta }_i^{0+}\\ {\xi }_i^{0+}\end{array}\right]$$

(41)

Then, the field transmitted into the air after n refractions in the layer can be expressed as

$${\widetilde{\stackrel{\rightharpoonup }{E}}}_{tn}^0=\stackrel{=}{P}·{\stackrel{=}{M}}_3·{\left({\stackrel{=}{M}}_2·{\stackrel{=}{M}}_4\right)}^{n-1}·{\stackrel{=}{M}}_2·{\stackrel{=}{M}}_1{e}^{-j{k}_{0z}z}$$

(42)

where $\stackrel{=}{P}=\frac{1}{k_x^2+k_y^2}\left[\begin{array}{cc}{k}_x{k}_{0z}& k_0{k}_y\\ \begin{array}{l}{k}_y{k}_{0z}\\ k_x^2+k_y^2\end{array}& \begin{array}{l}-k_0{k}_x\\ -1\end{array}\end{array}\right]$.

Each secondary scattered field constitutes a proportional series, and the total secondary scattered field can be obtained by superimposing all the secondary scattered fields:

$$sum{\widetilde{\stackrel{\rightharpoonup }{E}}}_{tn}^0=\stackrel{=}{P}·{\stackrel{=}{M}}_3·{\displaystyle \sum _{n=1}^{\infty }{\left({\stackrel{=}{M}}_2·{\stackrel{=}{M}}_4\right)}^{n-1}}·{\stackrel{=}{M}}_2·{\stackrel{=}{M}}_1{e}^{-j{k}_{0z}z}$$

(43)

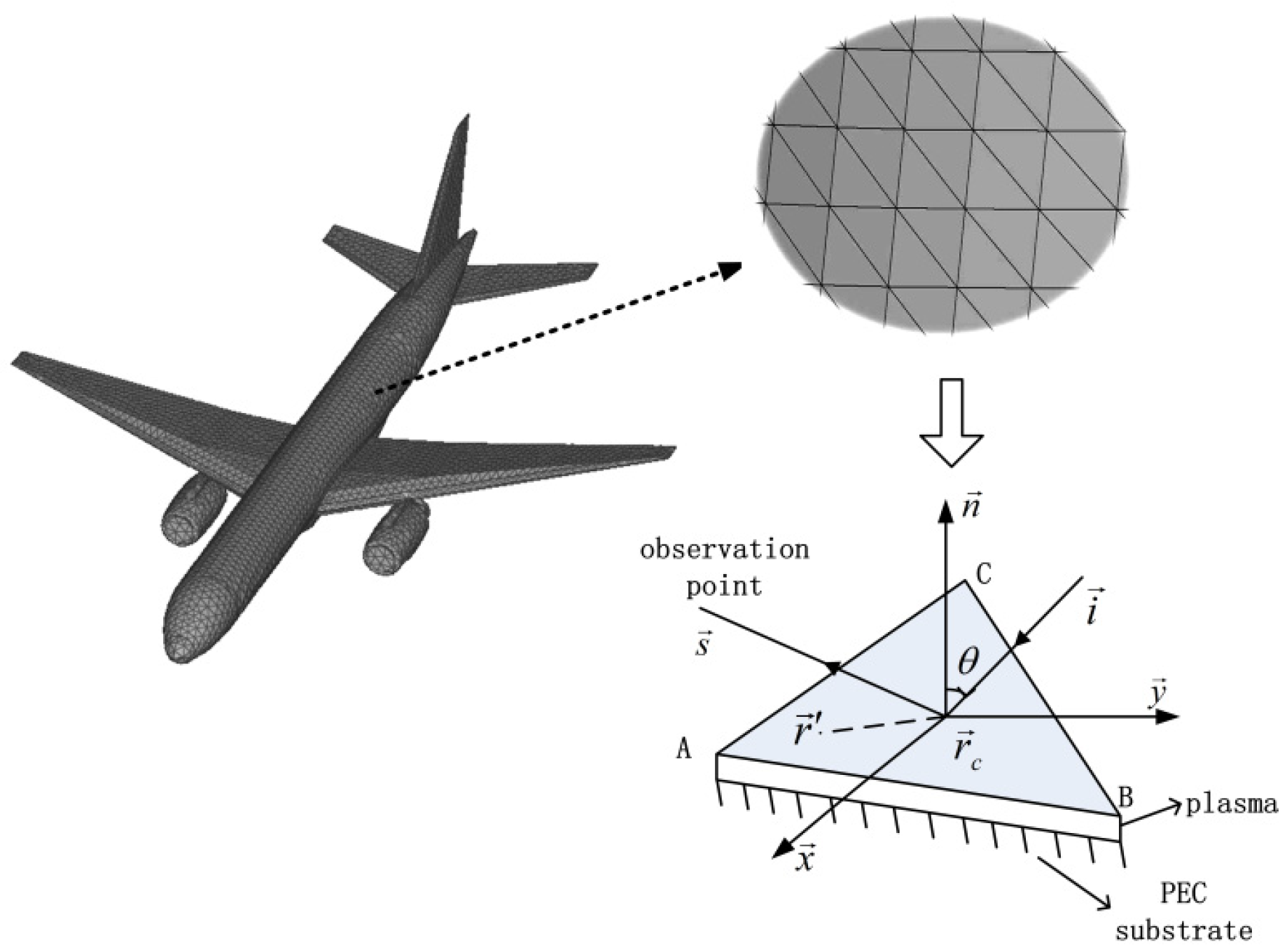
3. Physical Optical Solution of Electrically Large Plasma-Coated Targets

When estimating the scattering field of a complex target, flat elements are usually used to discretize the target surface. The physical optics algorithm discretizes the target surface into many flat triangular facets, calculates the scattering field of each illuminated flat triangular facet, and finally superimposes it to obtain the total scattering field of the target [33]. Figure 7 shows the discrete flat triangular facets on the outer surface of a coated aircraft. According to the principle of tangent plane approximation, it is considered that the surface EM field of the triangular facet has the same characteristics as the EM field on the infinite plane tangent to the surface at the incident point. Therefore, as long as the surface EM field of the plasma-coated infinite plate is obtained, the physical optics algorithm for the EM scattering of the plasma-coated target can be constructed.

3.1. Surface EM Field of an Infinite Plasma-Coated PEC Slab

As shown in Figure 8, assuming the incident angle and the scattering angle are, respectively, $\left({\theta }_i,{\phi }_i\right)$, $\left({\theta }_r,{\phi }_r\right)$, then the incident direction and the reflection direction are $\overrightarrow{i},\overrightarrow{r}$.

$${\widehat{e}}_{\perp }^i=\frac{\widehat{i}\times \widehat{z}}{\left|\widehat{i}\times \widehat{z}\right|},{\widehat{e}}_{//}^i=\frac{{\widehat{e}}_{\perp }^i\times \widehat{i}}{\left|{\widehat{e}}_{\perp }^i\times \widehat{i}\right|},{\widehat{e}}_{\perp }^r=\frac{\widehat{r}\times \widehat{z}}{\left|\widehat{r}\times \widehat{z}\right|},{\widehat{e}}_{//}^r=\frac{{\widehat{e}}_{\perp }^r\times \widehat{i}}{\left|{\widehat{e}}_{\perp }^r\times \widehat{i}\right|}.$$

(44)

From the previous section, after the saddle point of the total scattered field is calculated, the wave vector corresponding to the saddle point is ${\stackrel{\rightharpoonup }{k}}_s=-k_{sx}\widehat{x}-k_{sy}\widehat{y}-k_{sz}\widehat{z}$.

For the surface EM field at $z=0$, there are

$$\begin{array}{l}{\stackrel{\rightharpoonup }{E}}_0\left(z=0\right)=\frac{1}{{\left(2\pi \right)}^2}{\displaystyle \iint {\tilde{\overrightarrow{E}}}_0\left(z=0\right)\delta \left({\overrightarrow{k}}_{\rho }-{\overrightarrow{k}}_{s\rho }\right)e^{j{k}_{x}x}{e}^{j{k}_{y}y}d{k}_{x}d{k}_y}\\ {\eta }_0{\stackrel{\rightharpoonup }{H}}_0\left(z=0\right)=\frac{1}{{\left(2\pi \right)}^2}{\displaystyle \iint {\eta }_0{\widetilde{\stackrel{\rightharpoonup }{H}}}_0\left(z=0\right)\delta \left({\overrightarrow{k}}_{\rho }-{\overrightarrow{k}}_{s\rho }\right)e^{j{k}_{x}x}{e}^{j{k}_{y}y}d{k}_{x}d{k}_y}\end{array}$$

(45)

where ${\overrightarrow{k}}_{\rho }=k_x\widehat{x}+k_y\widehat{y},{\overrightarrow{k}}_{s\rho }=k_{sx}\widehat{x}+k_{sy}\widehat{y}$. Substituting Equations (15) and (44) into Equation (45), we can arrive at

$$\begin{array}{l}{\stackrel{\rightharpoonup }{E}}_0\left(z=0\right)=\frac{1}{{\left(2\pi \right)}^2\sin {\theta }_i}\left[\left({\zeta }_0^{+}{\widehat{e}}_{//}^i-{\xi }_0^{+}{\widehat{e}}_{\perp }^i\right)+\left({\zeta }_0^{-}{\widehat{e}}_{//}^r-{\xi }_0^{-}{\widehat{e}}_{\perp }^r\right)\right]e^{j{k}_{sx}x}{e}^{j{k}_{sy}y}\\ {\eta }_0{\stackrel{\rightharpoonup }{H}}_0\left(z=0\right)=\frac{1}{{\left(2\pi \right)}^2\sin {\theta }_i}\left[\left({\zeta }_0^{+}{\widehat{e}}_{\perp }^i+{\xi }_0^{+}{\widehat{e}}_{//}^i\right)+\left({\zeta }_0^{-}{\widehat{e}}_{\perp }^r+{\xi }_0^{-}{\widehat{e}}_{//}^r\right)\right]e^{j{k}_{sx}x}{e}^{j{k}_{sy}y}\end{array}$$

(46)

Assuming $E_{//}^i=\frac{{\zeta }_0^{+}}{{\left(2\pi \right)}^2\sin {\theta }_i},E_{\perp }^i=-\frac{{\xi }_0^{+}}{{\left(2\pi \right)}^2\sin {\theta }_i},E_{//}^r=\frac{{\zeta }_0^{-}}{{\left(2\pi \right)}^2\sin {\theta }_r},E_{\perp }^r=-\frac{{\xi }_0^{-}}{{\left(2\pi \right)}^2\sin {\theta }_r}$ Equation (46) becomes

$$\begin{array}{l}{\stackrel{\rightharpoonup }{E}}_0\left(z=0\right)=\left[\left({\widehat{e}}_{//}^i{E}_{//}^i+{\widehat{e}}_{\perp }^i{E}_{\perp }^i\right)+\left(E_{//}^r{\widehat{e}}_{//}^r+E_{\perp }^r{\widehat{e}}_{\perp }^r\right)\right]e^{-j\cdot k_0\cdot \overrightarrow{r}}\\ {\eta }_0{\stackrel{\rightharpoonup }{H}}_0\left(z=0\right)=\left[\left(E_{//}^i{\widehat{e}}_{\perp }^i-E_{\perp }^i{\widehat{e}}_{//}^i\right)+\left(E_{//}^r{\widehat{e}}_{\perp }^r-E_{\perp }^r{\widehat{e}}_{//}^r\right)\right]e^{-j\cdot k_0\cdot \overrightarrow{r}}\end{array}$$

(47)

The incident and reflected electric fields ${\stackrel{\rightharpoonup }{E}}_0^i,\hspace{0.17em}{\stackrel{\rightharpoonup }{E}}_0^s$ and their corresponding magnetic fields ${\stackrel{\rightharpoonup }{H}}_0^i,\hspace{0.17em}{\stackrel{\rightharpoonup }{H}}_0^s$ at the origin o are written as

$$\begin{array}{l}{\stackrel{\rightharpoonup }{E}}_0^i\left(\overrightarrow{0}\right)={\widehat{e}}_{//}^i{E}_{//}^i+{\widehat{e}}_{\perp }^i{E}_{\perp }^i,{\eta }_0{\stackrel{\rightharpoonup }{H}}_0^i\left(\overrightarrow{0}\right)=\overrightarrow{i}\times {\stackrel{\rightharpoonup }{E}}_0^i\left(\overrightarrow{0}\right)\\ {\stackrel{\rightharpoonup }{E}}_0^r\left(\overrightarrow{0}\right)=E_{//}^r{\widehat{e}}_{//}^r+E_{\perp }^r{\widehat{e}}_{\perp }^r,{\eta }_0{\stackrel{\rightharpoonup }{H}}_0^r\left(\overrightarrow{0}\right)=\overrightarrow{r}\times {\stackrel{\rightharpoonup }{E}}_0^s\left(\overrightarrow{0}\right)\end{array}$$

(48)

where $\stackrel{\rightharpoonup }{0}$ is the vector of the origin o. Assuming $R_{////},R_{//\perp },R_{\perp //},R_{\perp \perp }$ are the coefficients of the reflection matrix $\overline{\overline{R}}$, which are defined as

$$\left[\begin{array}{l}{E}_{//}^r\\ E_{\perp }^r\end{array}\right]=\stackrel{=}{R}·\left[\begin{array}{l}{E}_{//}^i\\ E_{\perp }^i\end{array}\right],\stackrel{=}{R}=\left[\begin{array}{l}{R}_{////}\hspace{1em}{R}_{//\perp }\\ R_{\perp //}\hspace{1em}{R}_{\perp \perp }\end{array}\right]$$

(49)

we can arrive at

$$\begin{array}{l}{R}_{////}=\frac{u_1{u}_8-u_4{u}_5}{u_4{u}_6-u_2{u}_8}|{}_{k_x=k_{sx},\hspace{0.17em}{k}_y=\hspace{0.17em}{k}_{sy}},R_{//\perp }=-\frac{u_3{u}_8-u_4{u}_7}{u_4{u}_6-u_2{u}_8}|{}_{k_x=k_{sx},\hspace{0.17em}{k}_y=\hspace{0.17em}{k}_{sy}}\\ R_{\perp //}=-\frac{u_2{u}_5-u_1{u}_6}{u_4{u}_6-u_2{u}_8}|{}_{k_x=k_{sx},\hspace{0.17em}{k}_y=\hspace{0.17em}{k}_{sy}},R_{\perp \perp }=\frac{u_2{u}_7-u_3{u}_6}{u_4{u}_6-u_2{u}_8}|{}_{k_x=k_{sx},\hspace{0.17em}{k}_y=\hspace{0.17em}{k}_{sy}}\end{array}$$

(50)

where the subscript $k_x=k_{sx},k_y=k_{sy}$ denoting the eigenvalues $k_x,k_y$ of $u_i\left(i=1~8\right)$ in Equation (50) are replaced by $k_{sx},k_{sy}$ respectively. Replacing the vector $\overrightarrow{0}$ in Equation (48) with the vector $\overrightarrow{r_c}$ from the origin to the center of each triangular facet, the surface EM field at the center $\overrightarrow{r_c}$ of each triangular facet can be obtained as

$$\stackrel{\rightharpoonup }{E}\left(\overrightarrow{r_c}\right)=\left({\stackrel{\rightharpoonup }{E}}_0^i\left(\overrightarrow{r_c}\right)+{\stackrel{\rightharpoonup }{E}}_0^r\left(\overrightarrow{r_c}\right)\right)e^{-j{k}_0\overrightarrow{i}\cdot \overrightarrow{r_c}},{\eta }_0\stackrel{\rightharpoonup }{H}\left(\overrightarrow{r_c}\right)=\overrightarrow{r}\times \stackrel{\rightharpoonup }{E}\left(\overrightarrow{r_c}\right)$$

(51)

3.2. PO Solution of Plasma-Coated Targets

The equivalent EM current at the center $\overrightarrow{r_c}$ of each triangular facet is

$${\stackrel{\rightharpoonup }{J}}_s\left(\overrightarrow{r_c}\right)=\widehat{n}\times {\eta }_0{\stackrel{\rightharpoonup }{H}}_0\left(\overrightarrow{r_c}\right),{\stackrel{\rightharpoonup }{J}}_{ms}\left(\overrightarrow{r_c}\right)={\stackrel{\rightharpoonup }{E}}_0\left(\overrightarrow{r_c}\right)\times \widehat{n}$$

(52)

According to the Stratton–Chu formula and the far-field approximation condition, the scattered field contributed by the triangular facet can be obtained as

$${\overrightarrow{E}}_0^s=\frac{j{k}_0{e}^{-j{k}_0\left(\overrightarrow{s}-\widehat{i}\cdot {\overrightarrow{r}}_c\right)}}{4\pi r}\left[\overrightarrow{s}\times {\overrightarrow{J}}_{ms}\left({\overrightarrow{r}}_c\right)+{\eta }_0\overrightarrow{s}\times \overrightarrow{s}\times {\overrightarrow{J}}_s\left({\overrightarrow{r}}_c\right)\right]\cdot {\displaystyle {\iint }_s{e}^{-j{k}_0{\overrightarrow{r}}^{\prime }\cdot (\widehat{i}-\overrightarrow{s})}}d{s}^{\prime }$$

(53)

where $\stackrel{\rightharpoonup }{s}$ is the vector corresponding to the field point. Using the Gordon integration method [34], the PO scattering electric field of the facet ABC can be derived as

$$\begin{array}{l}{\stackrel{\rightharpoonup }{E}}^s\left(\stackrel{\rightharpoonup }{s}\right)=\frac{j{k}_0{e}^{-j{k}_{0}s}}{4\pi s}\left[{\eta }_0\widehat{s}\times \widehat{s}\times {\stackrel{\rightharpoonup }{J}}_s\left({\stackrel{\rightharpoonup }{r}}_c\right)+\widehat{s}\times {\stackrel{\rightharpoonup }{J}}_{ms}\left({\stackrel{\rightharpoonup }{r}}_c\right)\right]\frac{e^{-j{k}_0{\stackrel{\rightharpoonup }{r}}_c\cdot \left(\widehat{i}-\widehat{s}-\stackrel{\rightharpoonup }{w}\right)}}{{\left|\stackrel{\rightharpoonup }{w}\right|}^2}\\ \hspace{1em}\hspace{1em}\hspace{1em}{\displaystyle \sum _{n=1}^3\left({\stackrel{\rightharpoonup }{w}}^{\ast }\cdot \left({\stackrel{\rightharpoonup }{r}}_{n+1}-{\stackrel{\rightharpoonup }{r}}_n\right)\right)e^{-j{k}_0\stackrel{\rightharpoonup }{w}\cdot \frac{{\stackrel{\rightharpoonup }{r}}_{n+1}+{\stackrel{\rightharpoonup }{r}}_n}{2}}\frac{\sin k_0\stackrel{\rightharpoonup }{w}\cdot \frac{{\stackrel{\rightharpoonup }{r}}_{n+1}-{\stackrel{\rightharpoonup }{r}}_n}{2}}{k_0\stackrel{\rightharpoonup }{w}\cdot \frac{{\stackrel{\rightharpoonup }{r}}_{n+1}-{\stackrel{\rightharpoonup }{r}}_n}{2}}}\end{array}$$

(54)

where $\stackrel{\rightharpoonup }{w}=\left(\widehat{i}-\widehat{s}\right)-\left(\left(\widehat{i}-\widehat{s}\right)\cdot \widehat{n}\right)\widehat{n},{\stackrel{\rightharpoonup }{w}}^{\ast }=\stackrel{\rightharpoonup }{w}\times \widehat{n}$, ${\overrightarrow{r}}_1,{\overrightarrow{r}}_2,{\overrightarrow{r}}_3$ are the direction vectors of the three vertices of the triangular facet. When the incident direction is perpendicular to the facet, namely $\widehat{i}=-\widehat{n}=-\widehat{s}$, Equation (54) will be invalid, and the scattered electric field can be written as

$${\stackrel{\rightharpoonup }{E}}^s\left(\stackrel{\rightharpoonup }{s}\right)=\frac{j{k}_0{e}^{-j{k}_{0}s}A}{4\pi s}\left[{\eta }_0\widehat{s}\times \widehat{s}\times {\stackrel{\rightharpoonup }{J}}_s\left({\stackrel{\rightharpoonup }{r}}_c\right)+\widehat{s}\times {\stackrel{\rightharpoonup }{J}}_{ms}\left({\stackrel{\rightharpoonup }{r}}_c\right)\right]$$

(55)

where A is the area of the facet ABC.

At a certain incident angle, when $N$ triangular facets on the surface of a complex target are illuminated by the incident wave, the scattering field of each facet is ${\stackrel{\rightharpoonup }{E}}_n^s\left(\stackrel{\rightharpoonup }{s}\right)$, and the scattering field of the entire target under a high-frequency approximation is

$${\stackrel{\rightharpoonup }{E}}^s\left(\stackrel{\rightharpoonup }{s}\right)={\displaystyle \sum _{n=1}^N{\stackrel{\rightharpoonup }{E}}_n^s}\left(\stackrel{\rightharpoonup }{s}\right)$$

(56)

4. Numerical Simulations and Discussion

Firstly, by comparing the reflection coefficient of the plasma-coated infinite plate obtained by the method in this paper with the results in the literature, the correctness of this method is verified, and the scattering characteristics of a plasma that is different from an ordinary uniaxial dielectric coating are analyzed. Then, the scattering characteristics of plasma coating are explored from the following two aspects.

Scattering characteristics of plasma-coated infinite PEC plate: the variation of the amplitude and phase of the scattered total field and the different mode fields after decomposition are investigated in detail when the parameters such as incident angle and coating thickness change.

Scattering characteristics of plasma-coated complex targets: the corresponding scattering characteristics of typical shapes and complex targets under different polarization incidences and different dielectric coatings are investigated, and their scattering contributions are analyzed.

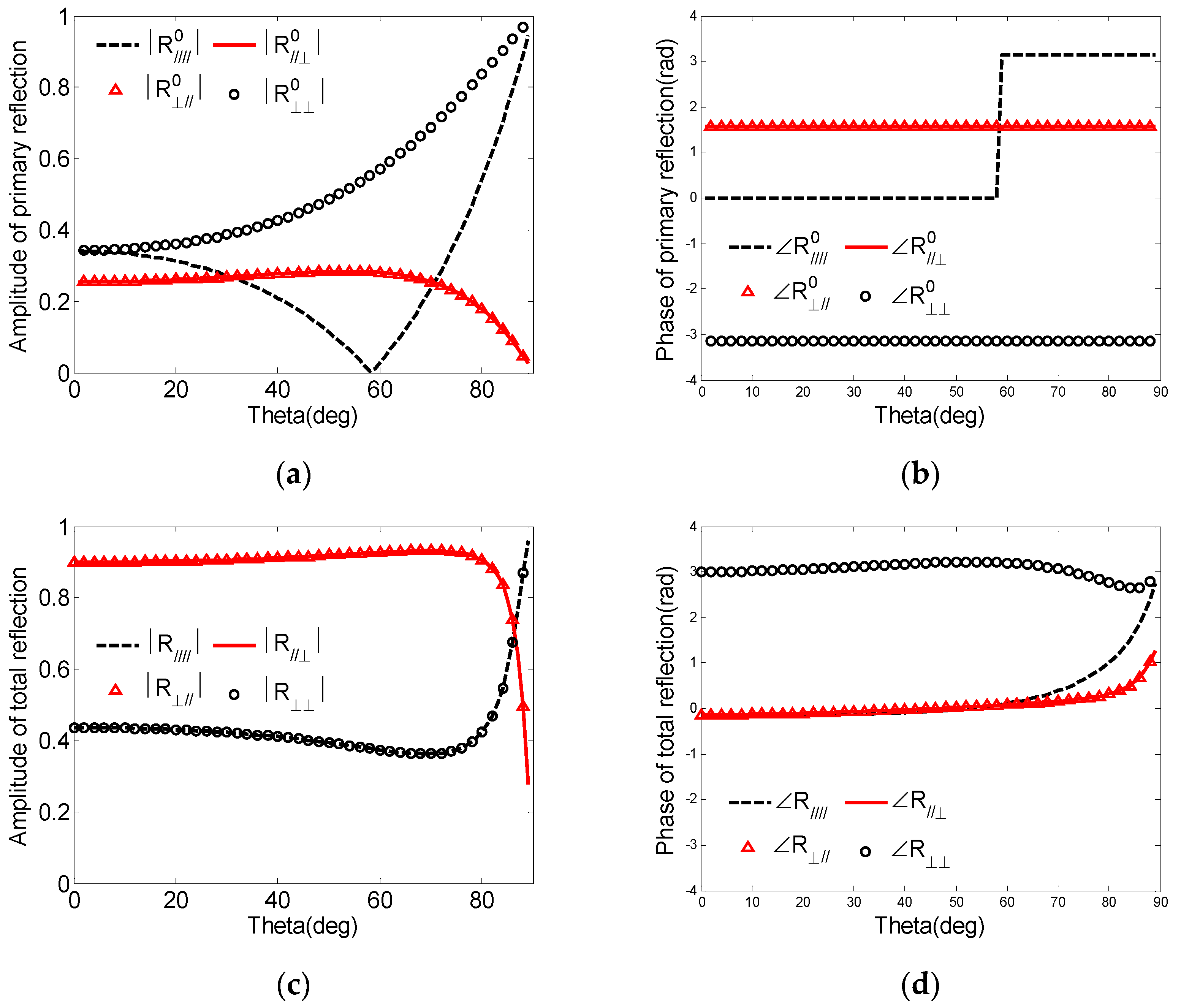
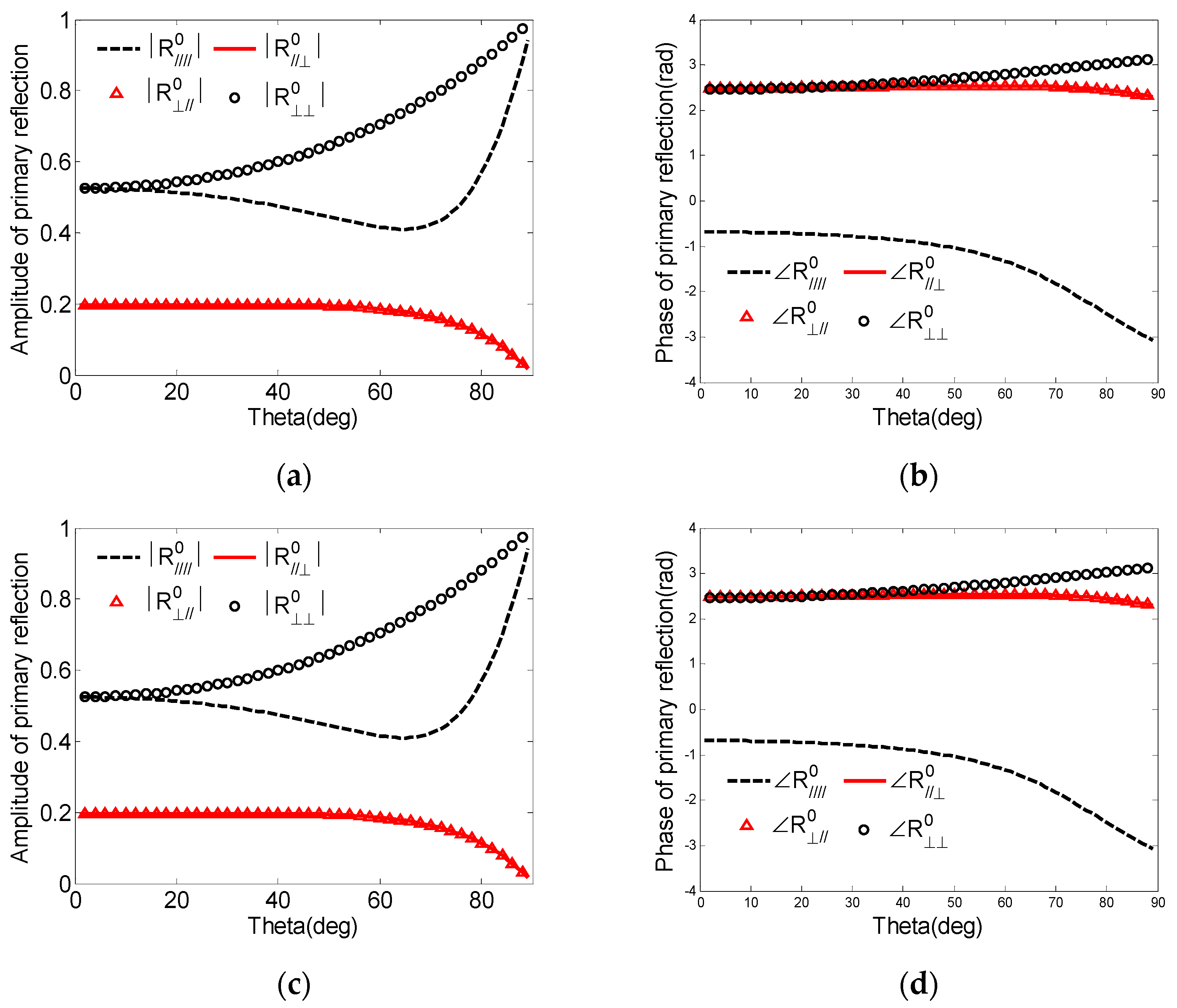
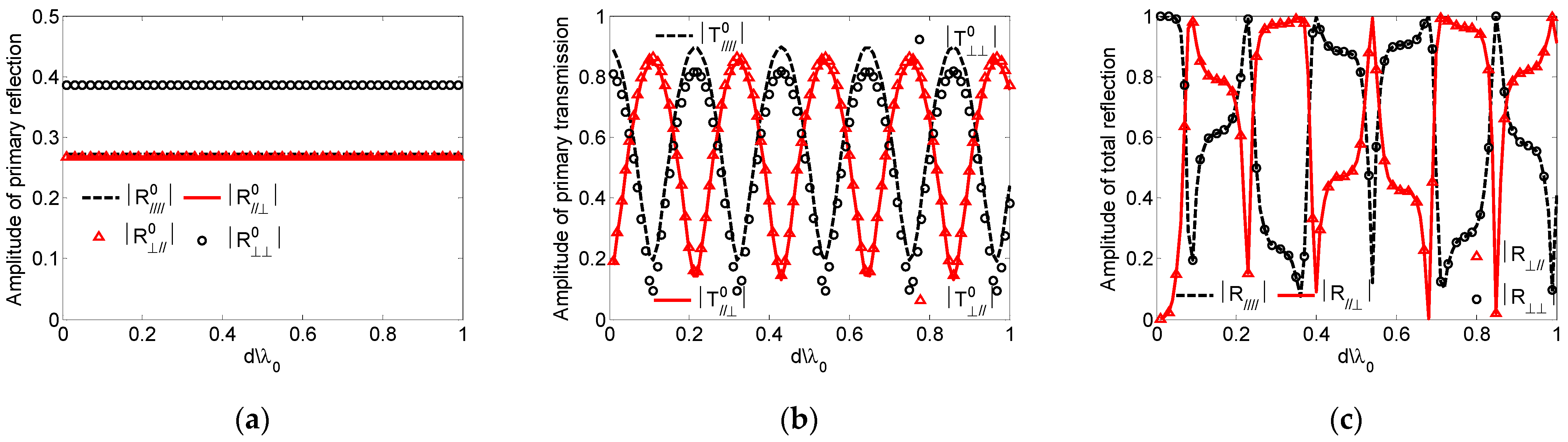
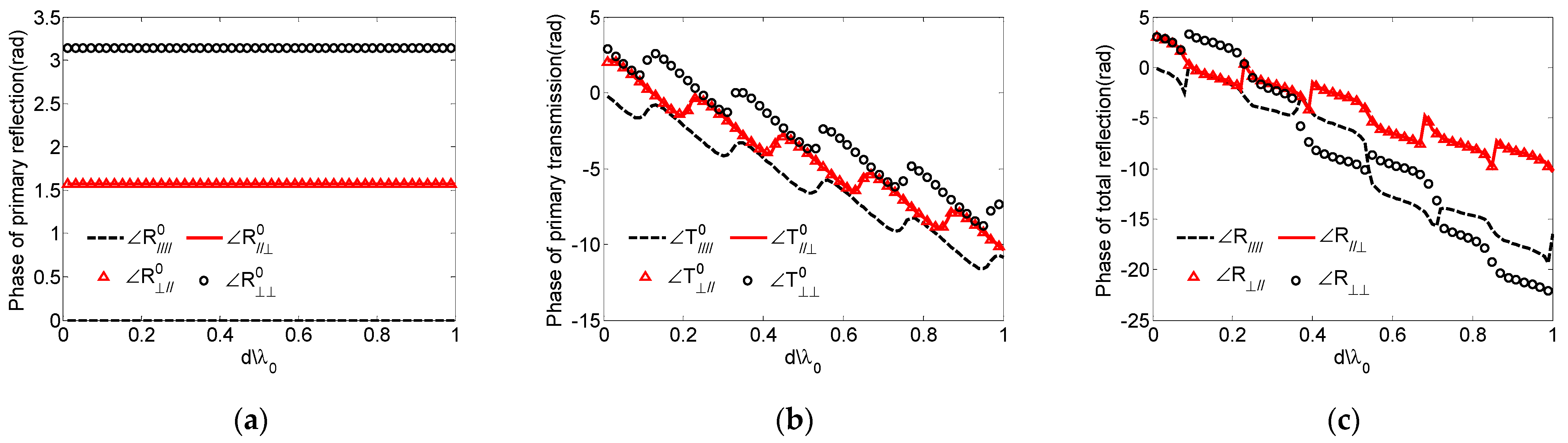
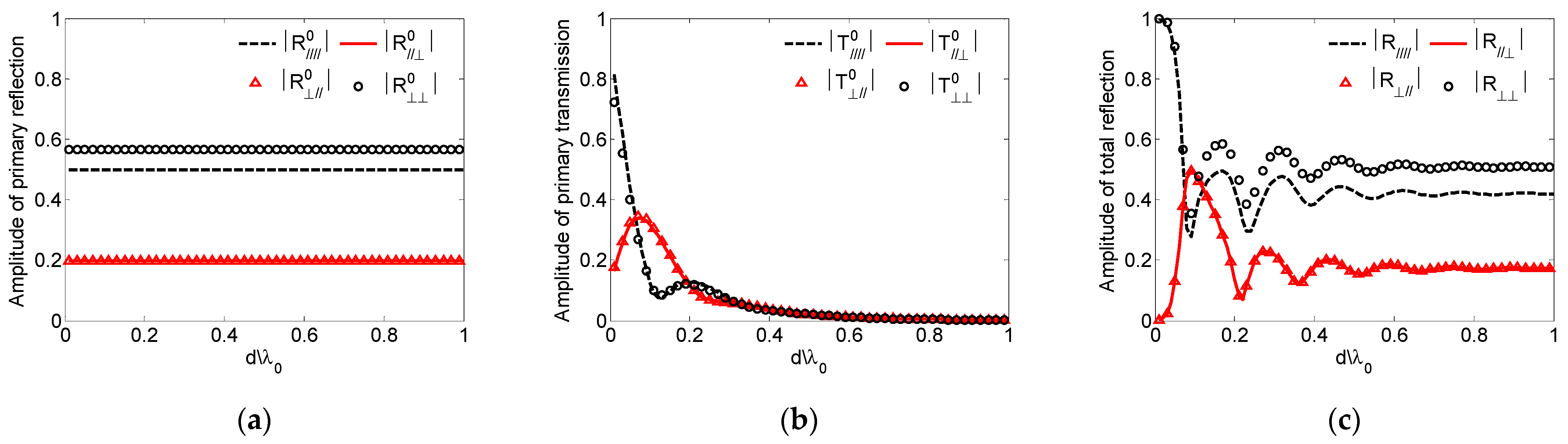
4.1. Validation and Analysis

To verify the correctness of the asymptotic solution of the spectral domain in this paper, we first calculated the reflection coefficient of the plasma-coated infinite PEC plate and compared the result with the result calculated by the numerical difference algorithm in the literature [35]. The plasma relative permittivity tensor elements are, respectively, ${\epsilon }_1=6-3j,{\epsilon }_2=-5j,{\epsilon }_3=4-0.7j$, and the incident angle is $\phi ={40}^{\circ }$. Figure 9 shows the reflection coefficient of the plasma-coated infinite PEC plate when the incident angle $\theta$ and coating thickness $d$ change. Excellent agreements are obtained between the results from the two methods. Therefore, the asymptotic solution of the scattered field obtained by the spectral domain method is reasonable and reliable.

To further study the scattering characteristics of plasma and general anisotropic media, the reflection coefficients of two different uniaxial medium coatings will be calculated by using the method of reference [35], and the results are compared with those of a plasma coating. The general anisotropic uniaxial dielectric tensor is a symmetric matrix, which can be converted into a diagonal matrix by rotating the coordinate axis. Taking the following two uniaxial media, the diagonalized dielectric tensors at $\phi =0^{\circ }$ are

$${\overline{\overline{\epsilon }}}_{uniaxial1}={\epsilon }_0\left[\begin{array}{ccc}10-2j& 0& 0\\ 0& 10-2j& 0\\ 0& 0& 3-4j\end{array}\right],{\overline{\overline{\epsilon }}}_{uniaxial2}={\epsilon }_0\left[\begin{array}{ccc}10-2j& 0& 0\\ 0& 3-4j& 0\\ 0& 0& 3-4j\end{array}\right]$$

With the rotation of the angle $\phi$, the dielectric tensor matrix of the uniaxial medium 1 will not change showing surface isotropy, while the dielectric tensors of uniaxial medium 2 are symmetric matrices at $\phi \ne 0^{\circ }$ with off-diagonal elements; for example, at $\phi ={45}^{\circ }$, the dielectric tensor is

$${\overline{\overline{\epsilon }}}_{uniaxial2}={\epsilon }_0\left[\begin{array}{ccc}6.5-3j& -3.5-j& 0\\ -3.5-j& 6.5-3j& 0\\ 0& 0& 3-4j\end{array}\right]$$

The most remarkable characteristic of plasma is that its dielectric tensor matrix is asymmetric, and there are always opposite off-diagonal elements. Take the plasma dielectric tensor as

$${\overline{\overline{\epsilon }}}_{plasma}={\epsilon }_0\left[\begin{array}{ccc}10-2j& -5j& 0\\ 5j& 10-2j& 0\\ 0& 0& 3-4j\end{array}\right]$$

Figure 10 shows the reflection coefficients when the above plasma and uniaxial media are coated separately, and the reflection coefficients with uniaxial media coated are obtained by Titchener’s method. The coating thickness is $d=0.1\lambda$.

In Figure 10a, the scattering of the plasma-coated infinite plate is independent of the angle $\phi$ and cross-polarization always exists. In Figure 10b, the dielectric tensors of the two uniaxial media are diagonal matrices at $\phi =0^{\circ }$, and no cross-polarization is generated. In Figure 10c, the dielectric tensor of the uniaxial medium 2 is an off-diagonal matrix with off-diagonal elements at $\phi ={45}^{\circ }$, and the phenomenon of cross-polarization has appeared. The unique dielectric tensor form of plasma makes it different from general anisotropic media and it has inherent cross-polarization scattering characteristics.

4.2. The Scattering Characteristics and Analysis of a Plasma-Coated Infinite PEC Plate

According to the analysis in Section 2, the total spectral scattered field can be decomposed into the primary reflection field on the upper surface and the secondary scattering fields transmitted from the plasma layer. In this section, the numerical curves of the primary reflection ${\stackrel{=}{R}}^0$ on the upper surface and the initial transmission ${\stackrel{=}{T}}^0$ after one reflection in the layer are given, and their relationship with the total scattering $\stackrel{=}{R}$ is compared and analyzed to explore the contribution of different modes of EM waves to the scattering.

Firstly, the reflection coefficients when the incident angle $\theta$ changes are investigated. Figure 11 and Figure 12, respectively, show the reflection coefficient of lossless and lossy plasma coating varying with the incident angle. The relative permittivity tensor elements of the lossless and lossy plasma, respectively, are ${\epsilon }_1=6,{\epsilon }_2=-5j,{\epsilon }_3=4$ and ${\epsilon }_1=6-3j,{\epsilon }_2=-5j,{\epsilon }_3=4-0.7j$; the incident angle is $\phi ={40}^{\circ }$; and the coating thickness is $d=0.1\lambda$. It can be seen from Figure 11 that when the lossless plasma is coated, the two main polarization components of the primary reflection ${\stackrel{=}{R}}^0$ are not equal, while the two main polarization components of the total reflection $\stackrel{=}{R}$ are equal. In Figure 12, when the coating plasma is lossy, the two main polarization components of ${\stackrel{=}{R}}^0$ are not equal, and the two main polarization components of $\stackrel{=}{R}$ are also not equal. Comparing Figure 11 and Figure 12, it can also be found that lossless coating produces stronger cross-polarization than that caused by lossy coating.

Then, the reflection and transmission of mode fields when the coating thickness $d$ changes are investigated. The relative permittivity tensor elements of the lossless and lossy plasma, respectively, are ${\epsilon }_1=6,{\epsilon }_2=-5j,{\epsilon }_3=4$ and ${\epsilon }_1=6-3j,{\epsilon }_2=-5j,{\epsilon }_3=4-0.7j$, and the incident angle is $\theta ={30}^{\circ },\phi ={30}^{\circ }$.

Figure 13 and Figure 14, respectively, show the amplitude and phase of different mode fields varying with coating thickness $d$ in the case of lossless plasma coating. It can be seen that each component of the primary reflection ${\stackrel{=}{R}}^0$ is independent of the coating thickness. The amplitude of each component of the initial transmission ${\stackrel{=}{T}}^0$ after one reflection in the layer changes periodically with the coating thickness, and the phase lags continuously with the increase in the thickness. The amplitude of final total reflection $\stackrel{=}{R}$ also tends to “Periodicity” with the coating thickness, and the phase lags further with the multiple reflections of waves in the layer.

Figure 15 and Figure 16, respectively, show the amplitude and phase of different mode fields varying with coating thickness $d$ in the case of lossy plasma coating. At this time, the components of the primary reflection ${\stackrel{=}{R}}^0$ are also independent of the thickness of the coating layer. The amplitude of each component of the initial transmission ${\stackrel{=}{T}}^0$ after one reflection in the layer is already very small, and the amplitude of final total reflection $\stackrel{=}{R}$ tends to converge with the increase in thickness. This is because when the thickness of the coated lossy plasma layer increases to a certain value, the PEC substrate does not reflect the waves in the anisotropic layer, which is a half-space problem. At this time, the EM wave is completely absorbed in the plasma layer, and the total field will mainly come from the contribution of the primary reflection on the upper surface.

From Figure 13, Figure 14, Figure 15 and Figure 16, it can be seen that the scattering characteristics of the two coated slabs are completely different. For lossless coating, strong cross-polarization scattering is generated, and the amplitudes of the two main polarization components are equal. However, in the case of lossy plasma coating, the two main polarization components are quite different, and the layer has a strong wave-absorbing ability.

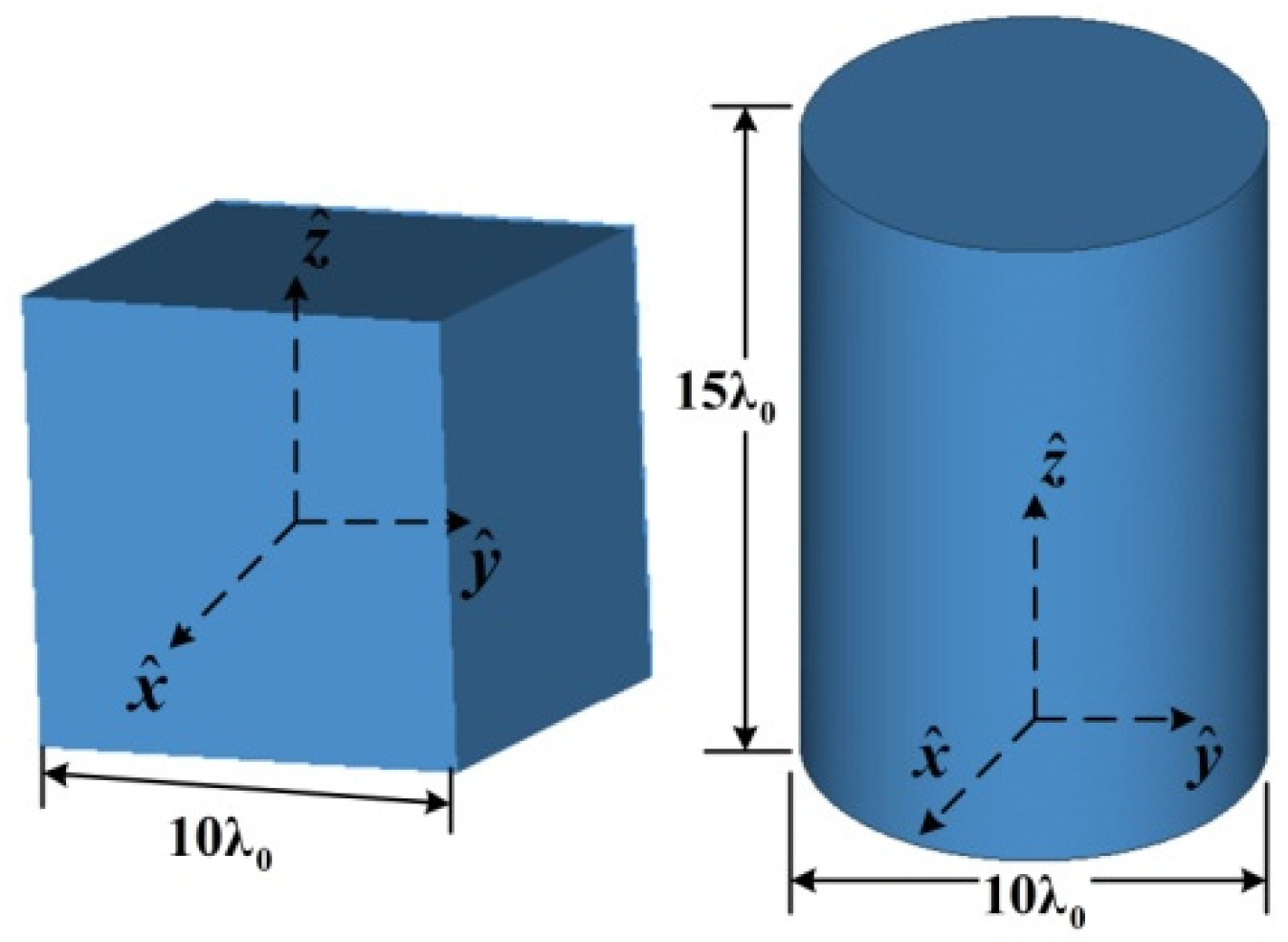
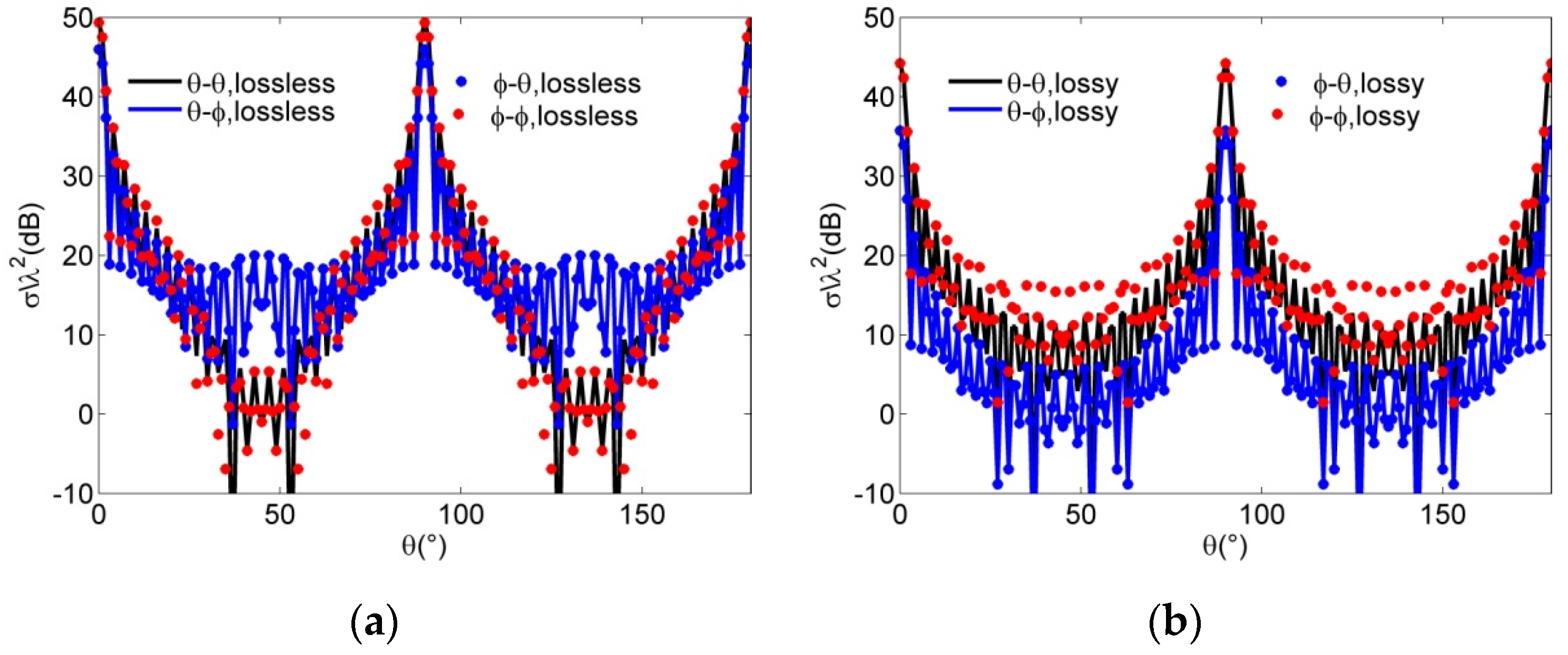
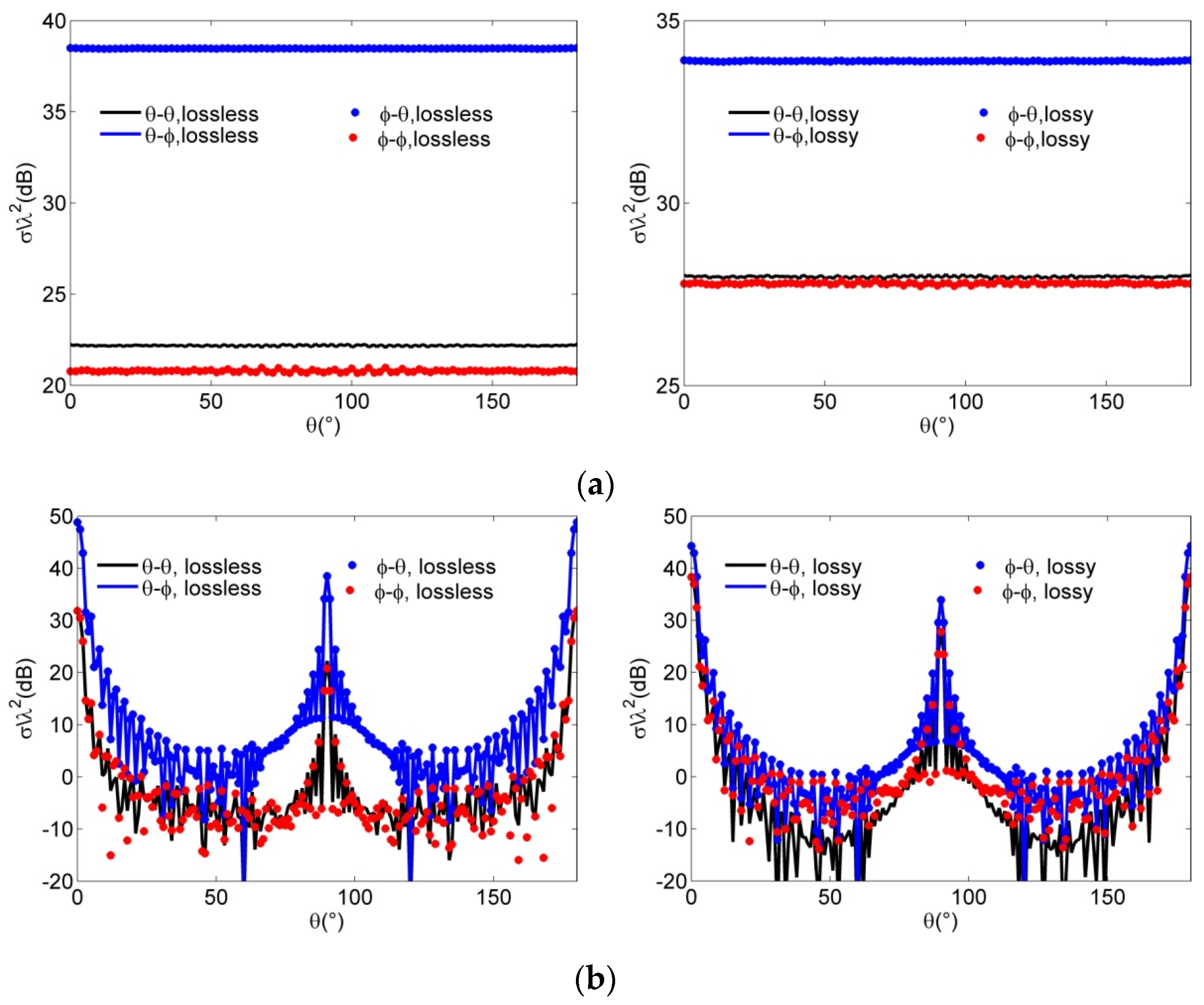
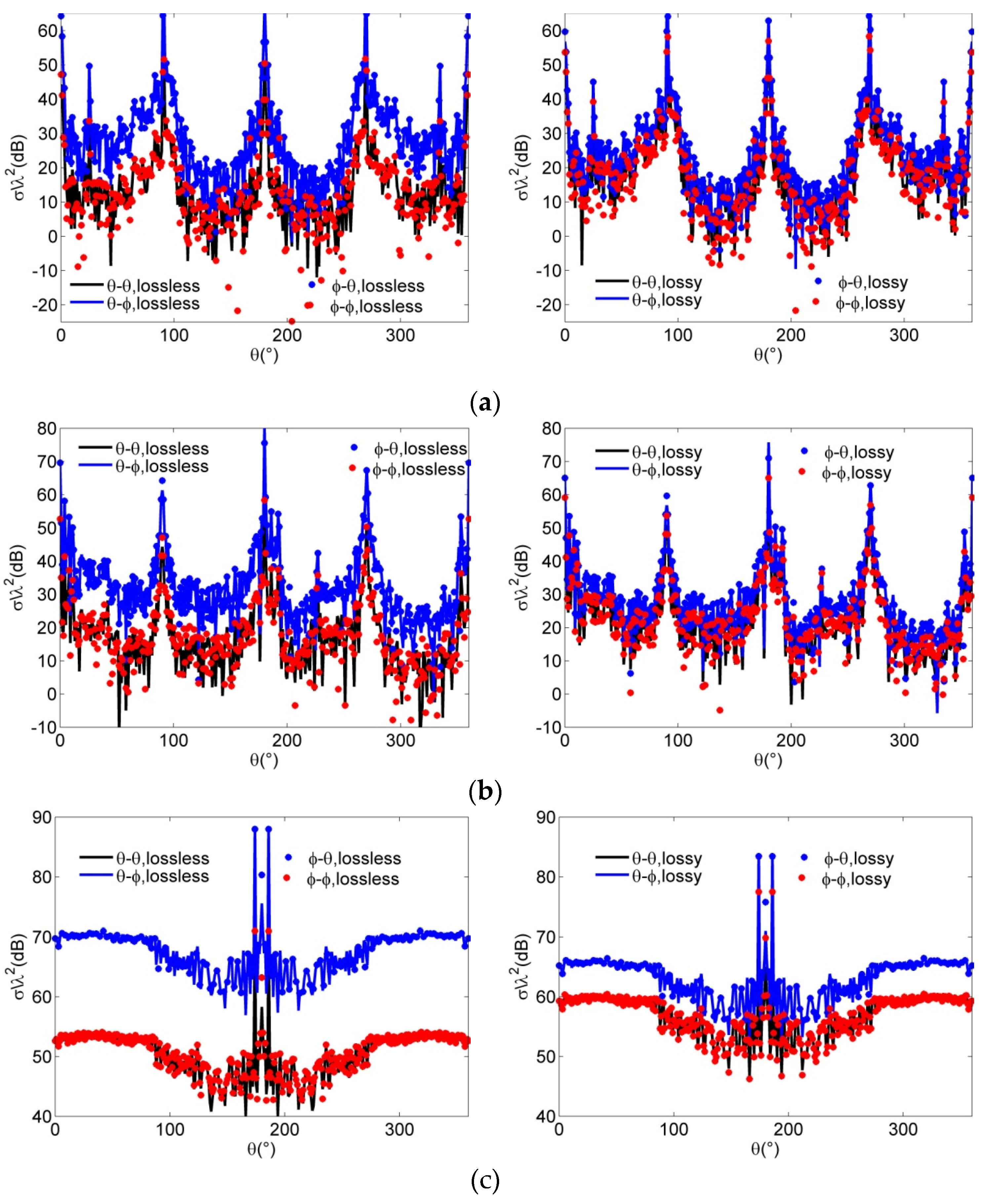
4.3. Scattering Characteristics and Analysis of Plasma-Coated Complex Targets

Because it is difficult to find the reference results of scattering from electrically large and complex targets coated with anisotropic plasma in the existing literature, and the commercial software HFSS can calculate the scattering of coated plates, the RCS of anisotropic plasma-coated plates has been calculated by this method and compared with the numerical algorithm of HFSS. Figure 17 shows the monostatic RCS of the rectangular coated plate obtained through this method and HFSS. It can be seen from the figure that the results obtained by the two methods are in good agreement in the range close to normal incidence. When the deviation from normal incidence is large, there is a certain gap between the results obtained by this method and the numerical algorithm. This is because the calculation error of the physical optics algorithm will increase when it deviates greatly from the specular reflection direction.

Table 1. The CPU time and required memory of Figure 17.

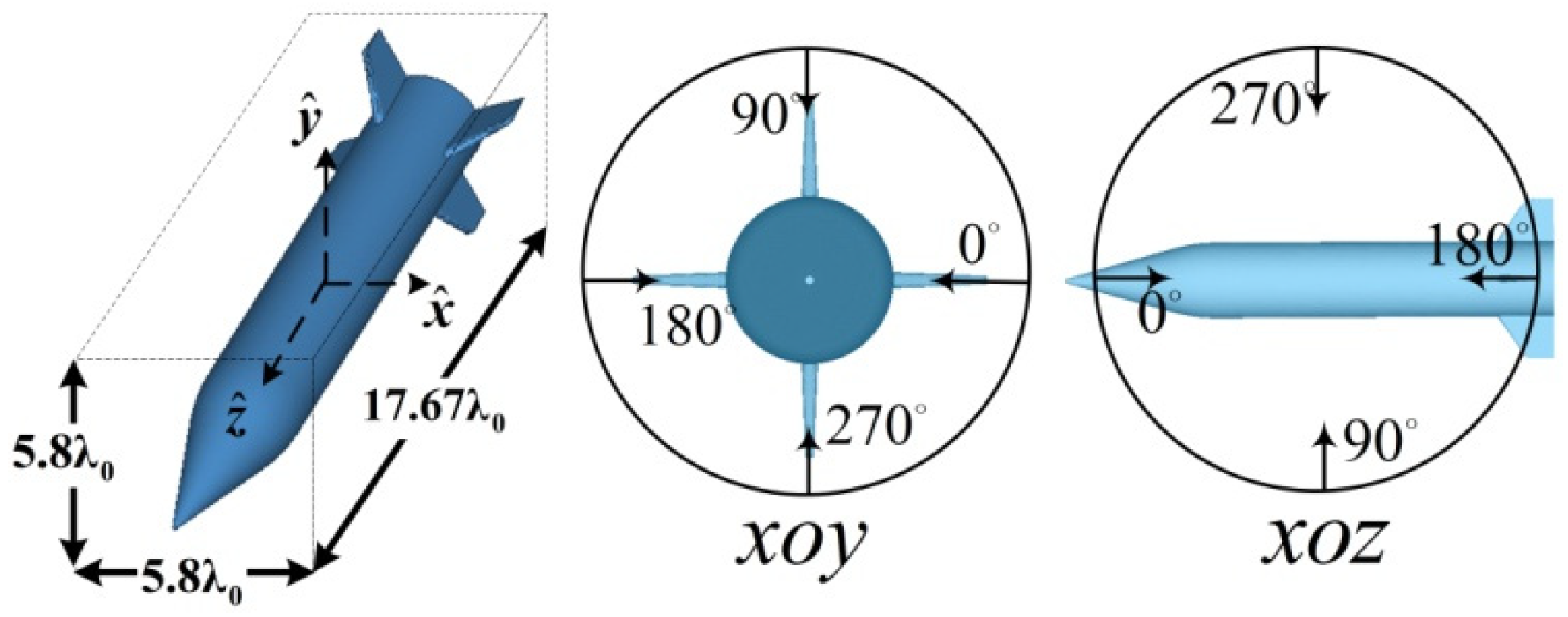
Method	The Proposed Method	HFSS
CPU time	6.17 s	308 s
Required memory	30.79 MB	6.26 GB

lists the time consumed and memory required for the two methods. Obviously, compared with the numerical algorithm, the proposed method requires very little time and memory and is more suitable for the scattering calculation of electrically large and complex targets.

The following will use the spectral domain combined with the physical optics algorithm proposed in this paper to investigate the scattering characteristics of plasma-coated typical bodies and complex targets. These targets include a cube, cylinder, missile, and airplane. In our calculation, the coating thickness is $d=0.1\lambda$.

The first object is a plasma-coated cube as shown in Figure 18. Figure 19 presents the monostatic RCSs of the cube coated with lossless and lossy plasma. It can be seen that the lossless plasma coating produces strong cross-polarization scattering, which is much larger than co-polarization scattering. When the lossy plasma coating is used, the cross-polarization scattering is weakened and the co-polarization scattering is enhanced. This means that the anisotropic plasma with off-diagonal dielectric parameters changes the spatial field distribution. This feature can also be seen in the scattering results of other dielectric parameters and other targets in our article.

The second target is a coated cylinder as shown in Figure 18. Figure 20 presents the monostatic RCSs of the coated cylinder in the $xoy$ and $xoz$ observation planes. It is observed that strong cross-polarization scattering occurs in both lossy and lossless plasma coating cases. In the roll-plane $\left(xoy\right)$, the co-polarization $\left(\theta \theta ,\phi \phi \right)$ RCSs by lossless plasma coating are different but almost equal by lossy plasma coating. In the meridian plane $\left(xoz\right)$ of the cylinder, the situation is the opposite: the co-polarization $\left(\theta \theta ,\phi \phi \right)$ RCSs by lossless plasma coating are very close but obviously different by lossy plasma coating.

The third example is the coated missile, whose model and observation planes are shown in Figure 21. Figure 22 presents the monostatic RCSs of the coated missile in the $xoz$ and $xoy$ observation planes. Again, strong cross-polarization scattering occurs in both coating cases. The missile’s body is a body of revolution with axis $\widehat{z}$ like a cylinder, so it has similar scattering characteristics. In the roll-plane $\left(xoy\right)$, the co-polarization $\left(\theta \theta ,\phi \phi \right)$ RCSs by lossless plasma coating are quite different, but very close by lossy plasma coating. In the meridian plane $\left(xoz\right)$, the situation is the opposite: the co-polarization $\left(\theta \theta ,\phi \phi \right)$ RCSs by lossless plasma coating are very close but different from lossy plasma coating.

The last example is the coated aircraft shown in Figure 23. Figure 24 shows the monostatic RCSs of the coated aircraft in the three observation planes. Again, compared with the lossless plasma coating, the cross-polarization RCSs decrease while the co-polarization RCSs increase by the lossy plasma coating, and this is especially obvious on the roll-plane $\left(yoz\right)$. Moreover, for both lossless and lossy plasma coatings, the co-polarization $\left(\theta \theta ,\phi \phi \right)$ RCSs are relatively close. This shows that the scattering mechanism of the coated aircraft is more complicated than the previous simple bodies.

5. Conclusions

A high-frequency algorithm for EM scattering from electrically large and complex targets coated with anisotropic plasma was proposed based on the spectral domain method. Compared with numerical algorithms, the proposed method is effective and has higher computational efficiency. Finally, the high-frequency scattering of plasma-coated electrically large complex targets was estimated and analyzed for the first time, and the RCS of plasma-coated canonical targets and complex targets were given. The numerical results show the inherent cross-polarization scattering phenomenon of magnetized plasma. Its complex interaction with EM waves significantly changes the scattering characteristics of coated targets. Note that the plasma coating studied in this paper is homogeneous, and the method extended to non-uniform plasma coating will be more applicable. Besides, in target stealth design, coating materials at a specific location is usually easier to achieve, and this demand is easy to meet through a little improvement in this method. The scattering characteristics of targets under different plasma parameters can be further explored by this method, so as to provide guidance for engineering applications. In summary, the research results of this paper have important theoretical research value and the engineering application potential in the areas of radar detection and recognition and target stealth design.