DA-IMRN: Dual-Attention-Guided Interactive Multi-Scale Residual Network for Hyperspectral Image Classification
Abstract
:1. Introduction
- We propose a dual-attention-guided interactive feature learning strategy, including the spatial and channel attention module (SCAM) as well as the spectral attention module (SAM). We interpret the problem of assigning label to each pixel as the pixel-to-pixel classification task, rather than the traditional patch-wise classification. The proposed network interactively extracts joint spectral-spatial information and performs feature fusion to enhance the classification performance. By adjusting the weights of feature maps from three different dimensions, the bidirectional attention can guide feature extraction effectively.
- We introduce a multi-scale spectral/spatial residual block (MSRB) for classification. It uses different kernel sizes at the convolutional layer to extract the features corresponding to multiple receptive fields, and provides abundant information for pixel-level classification.
- We evaluate the proposed modules and report their performance over three popular benchmark datasets. Extensive experimental results demonstrate that the proposed DA-IMRN outperforms state-of-the-art HSI classification methods. The related codes are publicly available at the following website: https://github.com/usefulbbs/DA-IMRN (accessed on 21 January 2021).
2. Methodology
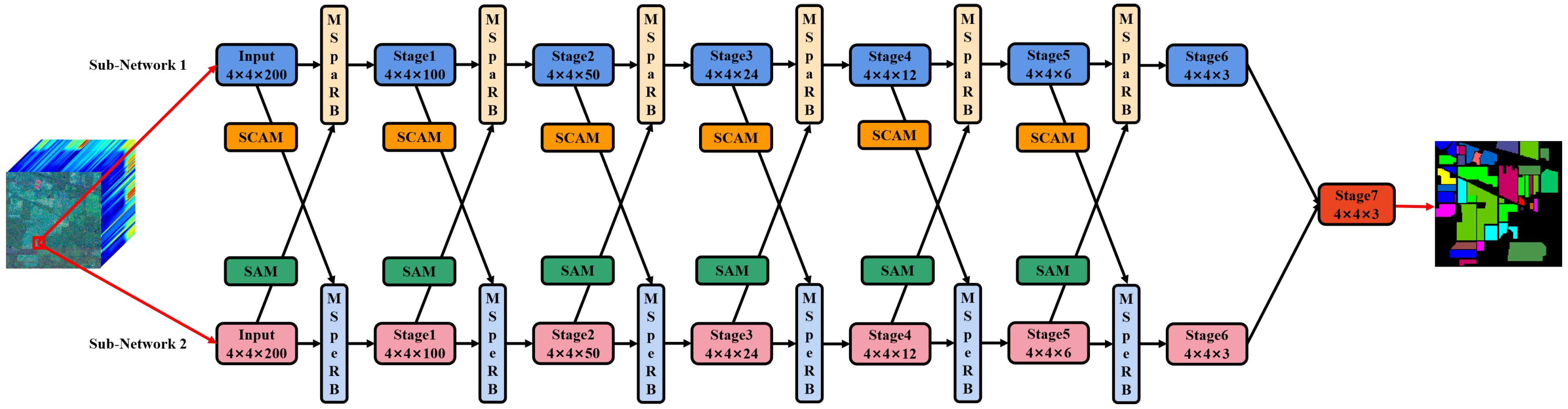
2.1. Proposed Framework
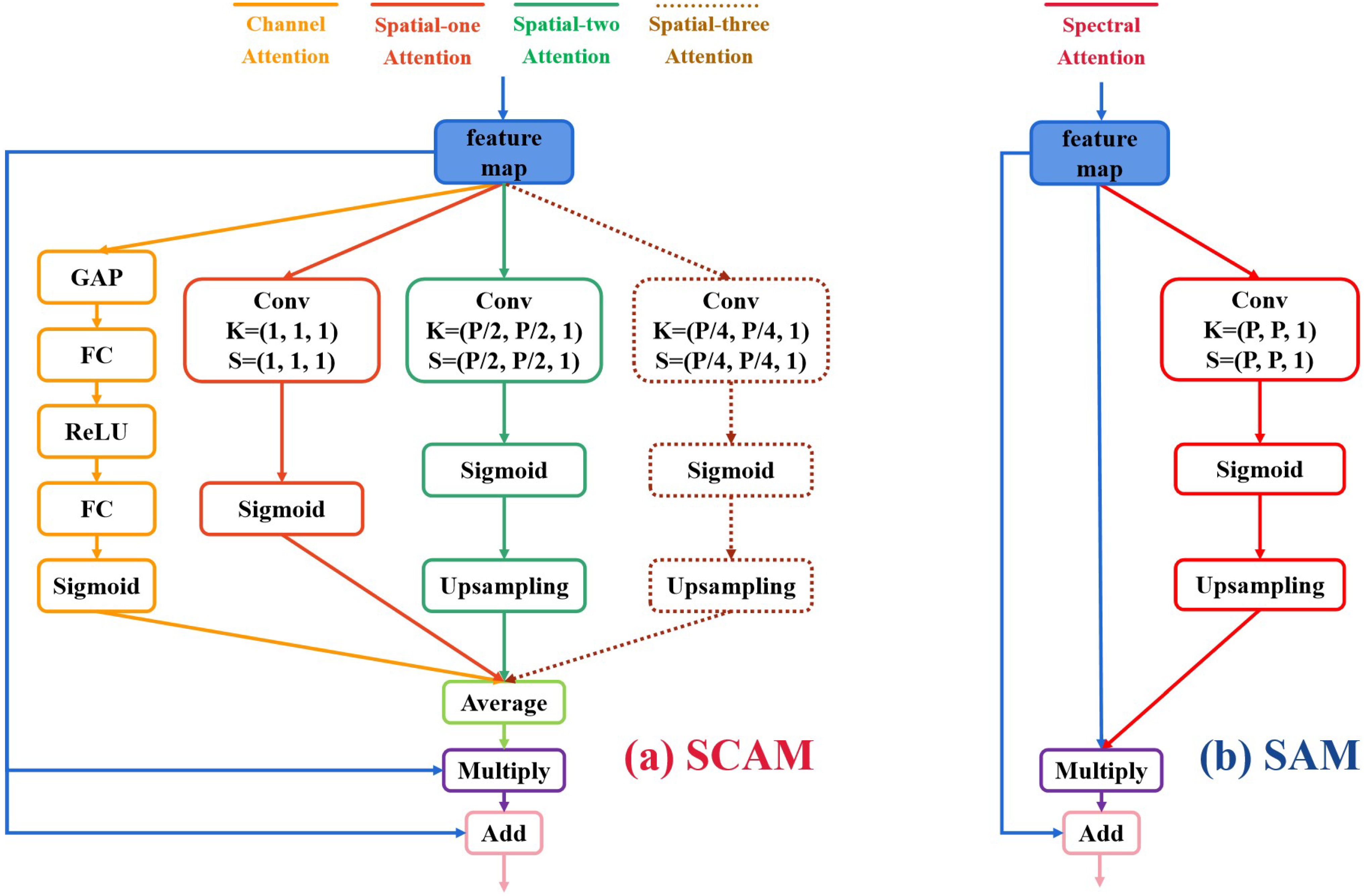
2.2. Dual-Attention Mechanism
2.2.1. Spatial-Wise & Channel-Wise Attention Module
2.2.2. Spectral-Wise Attention Module
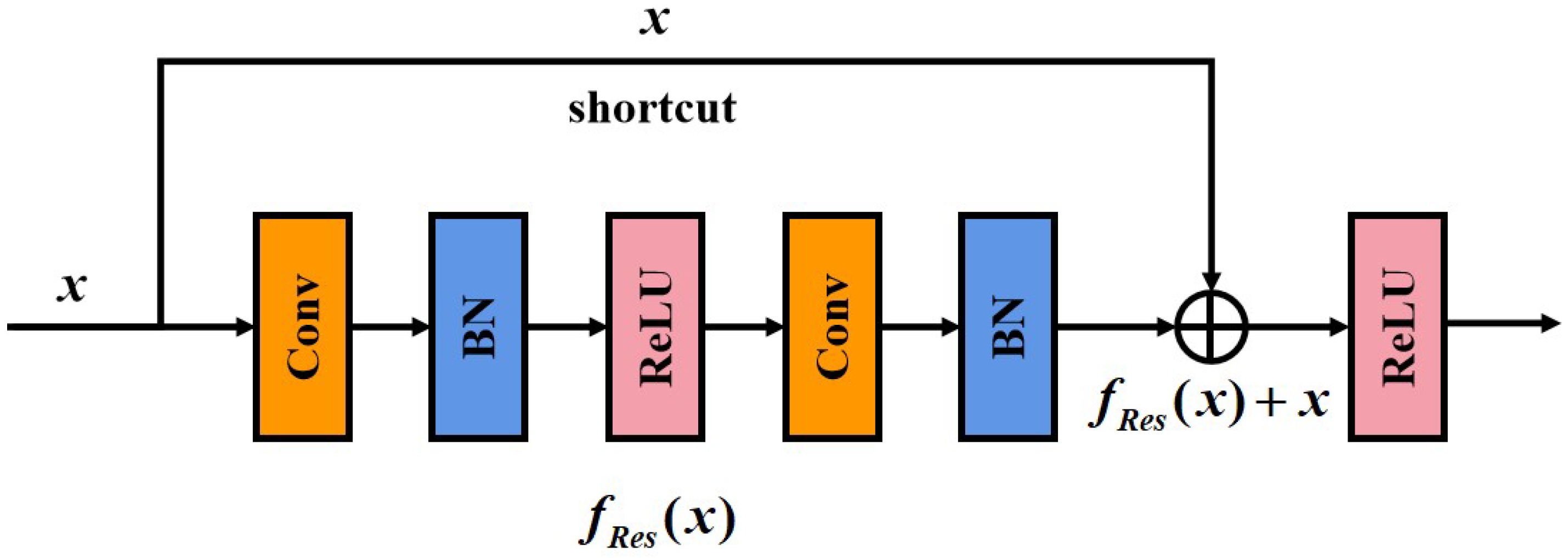
2.3. Multi-Scale Residual Block (MSRB)
2.3.1. Residual Learning
2.3.2. Multi-Scale Spectral/Spatial Residual Block
3. Experiment Result and Analysis
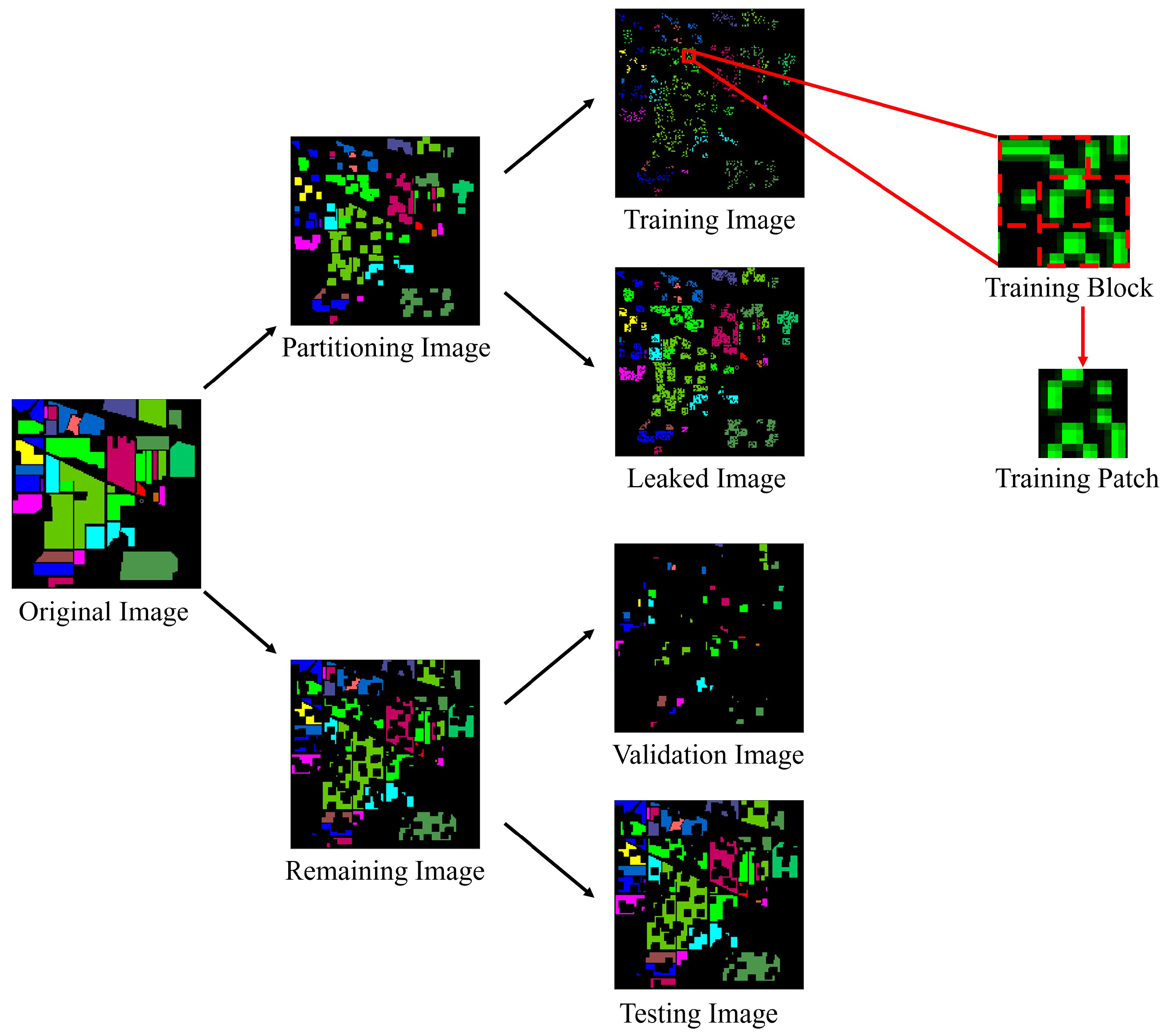
3.1. Dataset Partition
3.2. Dataset Description
3.3. Evaluation Matrices
3.4. Parameter Setting and Network Configuration
4. Experimental Result
4.1. Classification Result on Salinas Valley
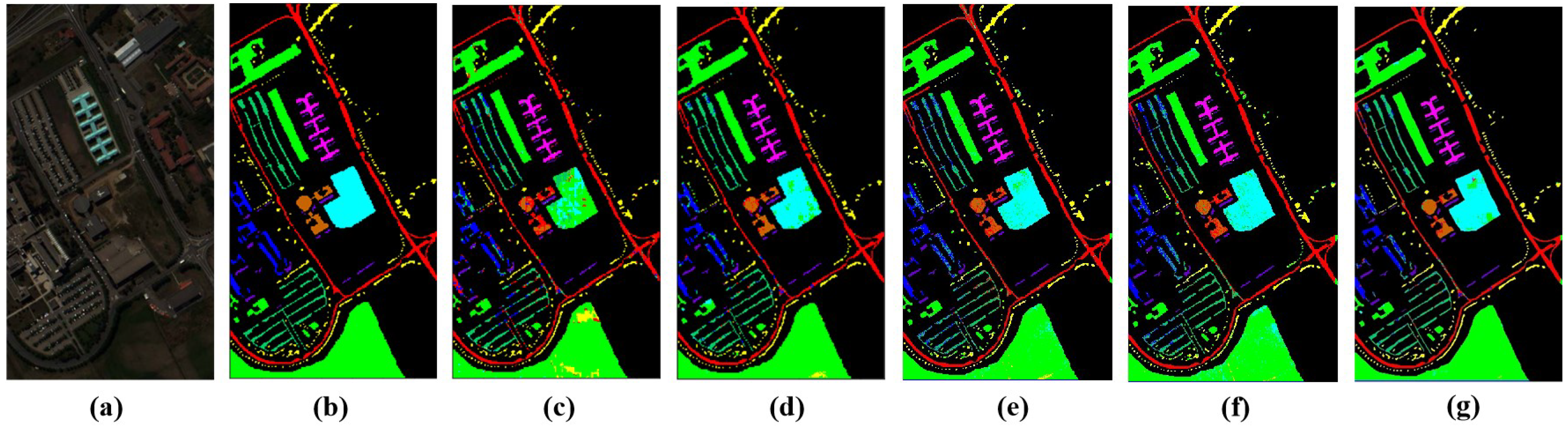
4.2. Classification Result on Pavia University
4.3. Classification Result on Indian Pines
5. Analysis and Discussion
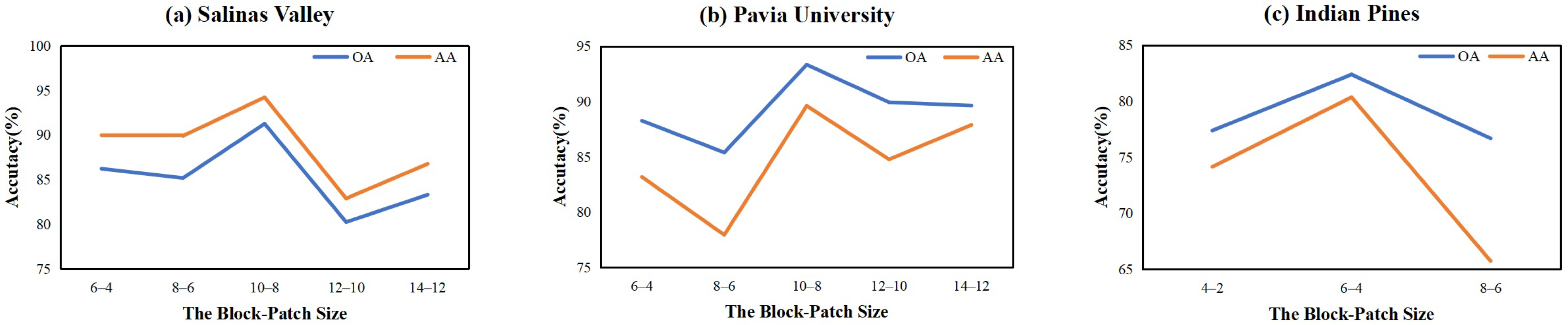
5.1. Effect of Block-Patch Size
5.2. Impact of the Attention-Guided Feature Learning
5.3. Impact of the Multi-Scale Spectral/Spatial Residual Block
5.4. Impact of the Numbers of Labeled Pixels for Training
5.5. Impact of Different Information Fusion Strategies
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhong, Z.; Li, J.; Luo, Z.; Chapman, M. Spectral–spatial residual network for hyperspectral image classification: A 3-D deep learning framework. IEEE Trans. Geosci. Remote Sens. 2017, 56, 847–858. [Google Scholar] [CrossRef]
- Van Ruitenbeek, F.; van der Werff, H.; Bakker, W.; van der Meer, F.; Hein, K. Measuring rock microstructure in hyperspectral mineral maps. Remote Sens. Environ. 2019, 220, 94–109. [Google Scholar] [CrossRef]
- Jiang, X.; Liu, W.; Zhang, Y.; Liu, J.; Li, S.; Lin, J. Spectral–Spatial Hyperspectral Image Classification Using Dual-Channel Capsule Networks. IEEE Geosci. Remote Sens. Lett. 2020, 18, 1094–1098. [Google Scholar] [CrossRef]
- Nalepa, J.; Myller, M.; Kawulok, M. Validating hyperspectral image segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 16, 1264–1268. [Google Scholar] [CrossRef] [Green Version]
- Nalepa, J.; Myller, M.; Kawulok, M. Training-and test-time data augmentation for hyperspectral image segmentation. IEEE Geosci. Remote Sens. Lett. 2019, 17, 292–296. [Google Scholar] [CrossRef]
- Bi, H.; Xu, F.; Wei, Z.; Xue, Y.; Xu, Z. An active deep learning approach for minimally supervised PolSAR image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9378–9395. [Google Scholar] [CrossRef]
- Zhao, G.; Wang, X.; Kong, Y.; Cheng, Y. Spectral-Spatial Joint Classification of Hyperspectral Image Based on Broad Learning System. Remote Sens. 2021, 13, 583. [Google Scholar] [CrossRef]
- Li, S.; Song, W.; Fang, L.; Chen, Y.; Ghamisi, P.; Benediktsson, J.A. Deep learning for hyperspectral image classification: An overview. IEEE Trans. Geosci. Remote Sens. 2019, 57, 6690–6709. [Google Scholar] [CrossRef] [Green Version]
- Fang, B.; Li, Y.; Zhang, H.; Chan, J.C.W. Hyperspectral images classification based on dense convolutional networks with spectral-wise attention mechanism. Remote Sens. 2019, 11, 159. [Google Scholar] [CrossRef] [Green Version]
- Xing, Z.; Zhou, M.; Castrodad, A.; Sapiro, G.; Carin, L. Dictionary learning for noisy and incomplete hyperspectral images. SIAM J. Imaging Sci. 2012, 5, 33–56. [Google Scholar] [CrossRef]
- Zhang, Y.; Cao, G.; Li, X.; Wang, B. Cascaded random forest for hyperspectral image classification. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 1082–1094. [Google Scholar] [CrossRef]
- Jain, D.K.; Dubey, S.B.; Choubey, R.K.; Sinhal, A.; Arjaria, S.K.; Jain, A.; Wang, H. An approach for hyperspectral image classification by optimizing SVM using self organizing map. J. Comput. Sci. 2018, 25, 252–259. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, C.; Su, W.; Yue, A. A Study of the optimal scale texture analysis for remote sensing image classification. Remote Sens. Land Resour. 2008, 4, 14–17. [Google Scholar]
- He, L.; Li, J.; Plaza, A.; Li, Y. Discriminative low-rank Gabor filtering for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2016, 55, 1381–1395. [Google Scholar] [CrossRef]
- Kang, X.; Li, S.; Benediktsson, J.A. Spectral–spatial hyperspectral image classification with edge-preserving filtering. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2666–2677. [Google Scholar]
- Liao, J.; Wang, L.; Hao, S. Hyperspectral image classification based on adaptive optimisation of morphological profile and spatial correlation information. Int. J. Remote Sens. 2018, 39, 9159–9180. [Google Scholar] [CrossRef]
- Li, J.; Marpu, P.R.; Plaza, A.; Bioucas-Dias, J.M.; Benediktsson, J.A. Generalized composite kernel framework for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2013, 51, 4816–4829. [Google Scholar] [CrossRef]
- Fang, X.; Gao, T.; Zou, L.; Ling, Z. Bidirectional Attention for Text-Dependent Speaker Verification. Sensors 2020, 20, 6784. [Google Scholar]
- Gu, Y.; Wang, Y.; Li, Y. A survey on deep learning-driven remote sensing image scene understanding: Scene classification, scene retrieval and scene-guided object detection. Appl. Sci. 2019, 9, 2110. [Google Scholar] [CrossRef] [Green Version]
- Lei, M.; Rao, Z.; Wang, H.; Chen, Y.; Zou, L.; Yu, H. Maceral groups analysis of coal based on semantic segmentation of photomicrographs via the improved U-net. Fuel 2021, 294, 120475. [Google Scholar] [CrossRef]
- Lei, M.; Li, J.; Li, M.; Zou, L.; Yu, H. An Improved UNet++ Model for Congestive Heart Failure Diagnosis Using Short-Term RR Intervals. Diagnostics 2021, 11, 534. [Google Scholar] [CrossRef] [PubMed]
- Xi, J.X.; Ye, Y.L.; Qinghua, H.; Li, L.X. Tolerating Data Missing in Breast Cancer Diagnosis from Clinical Ultrasound Reports via Knowledge Graph Inference. In Proceedings of the 27rd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Virtual Event, Singapore, 14–18 August 2021. [Google Scholar]
- Chen, Y.; Lin, Z.; Zhao, X.; Wang, G.; Gu, Y. Deep learning-based classification of hyperspectral data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 2094–2107. [Google Scholar] [CrossRef]
- Tao, C.; Pan, H.; Li, Y.; Zou, Z. Unsupervised spectral–spatial feature learning with stacked sparse autoencoder for hyperspectral imagery classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 2438–2442. [Google Scholar]
- Ma, X.; Wang, H.; Geng, J. Spectral–spatial classification of hyperspectral image based on deep auto-encoder. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4073–4085. [Google Scholar] [CrossRef]
- Chen, Y.; Zhao, X.; Jia, X. Spectral–spatial classification of hyperspectral data based on deep belief network. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2381–2392. [Google Scholar] [CrossRef]
- Yue, J.; Zhao, W.; Mao, S.; Liu, H. Spectral–spatial classification of hyperspectral images using deep convolutional neural networks. Remote Sens. Lett. 2015, 6, 468–477. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–spatial classification of hyperspectral imagery with 3D convolutional neural network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Ma, N.; Ming, Y.; Wang, Q.; Xia, J. Classification of hyperspectral imagery with a 3D convolutional neural network and JM distance. Adv. Space Res. 2019, 64, 886–899. [Google Scholar] [CrossRef]
- Ma, W.; Yang, Q.; Wu, Y.; Zhao, W.; Zhang, X. Double-branch multi-attention mechanism network for hyperspectral image classification. Remote Sens. 2019, 11, 1307. [Google Scholar] [CrossRef] [Green Version]
- Zou, L.; Zhu, X.; Wu, C.; Liu, Y.; Qu, L. Spectral–spatial exploration for hyperspectral image classification via the fusion of fully convolutional networks. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2020, 13, 659–674. [Google Scholar] [CrossRef]
- Wang, D.; Du, B.; Zhang, L.; Xu, Y. Adaptive Spectral–Spatial Multiscale Contextual Feature Extraction for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2020, 59, 2461–2477. [Google Scholar] [CrossRef]
- Shi, H.; Cao, G.; Ge, Z.; Zhang, Y.; Fu, P. Double-Branch Network with Pyramidal Convolution and Iterative Attention for Hyperspectral Image Classification. Remote Sens. 2021, 13, 1403. [Google Scholar] [CrossRef]
- Qu, L.; Zhu, X.; Zheng, J.; Zou, L. Triple-Attention-Based Parallel Network for Hyperspectral Image Classification. Remote Sens. 2021, 13, 324. [Google Scholar] [CrossRef]
- Wu, F.; Chen, F.; Jing, X.Y.; Hu, C.H.; Ge, Q.; Ji, Y. Dynamic attention network for semantic segmentation. Neurocomputing 2020, 384, 182–191. [Google Scholar] [CrossRef]
- Ragab, M.; Chen, Z.; Wu, M.; Kwoh, C.K.; Yan, R.; Li, X. Attention-based sequence to sequence model for machine remaining useful life prediction. Neurocomputing 2021, 466, 58–68. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, Y.; Xu, Y.; Yang, Y.; Luo, X.; Miao, C. Heterogeneous star graph attention network for product attributes prediction. Adv. Eng. Informatics 2022, 51, 101447. [Google Scholar] [CrossRef]
- Long, Y.; Wu, M.; Liu, Y.; Zheng, J.; Kwoh, C.K.; Luo, J.; Li, X. Graph contextualized attention network for predicting synthetic lethality in human cancers. Bioinformatics 2021, 37, 2432–2440. [Google Scholar] [CrossRef]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3146–3154. [Google Scholar]
- Qu, L.; Wu, C.; Zou, L. 3D Dense Separated Convolution Module for Volumetric Medical Image Analysis. Appl. Sci. 2020, 10, 485. [Google Scholar] [CrossRef] [Green Version]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Paoletti, M.E.; Haut, J.M.; Fernandez-Beltran, R.; Plaza, J.; Plaza, A.J.; Pla, F. Deep pyramidal residual networks for spectral–spatial hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2018, 57, 740–754. [Google Scholar] [CrossRef]
- Bing, L.; Xuchu, Y.; Pengqiang, Z.; Xiong, T. Deep 3D convolutional network combined with spatial-spectral features for hyperspectral image classification. Acta Geod. Cartogr. Sin. 2019, 48, 53. [Google Scholar]
- Xu, Q.; Xiao, Y.; Wang, D.; Luo, B. CSA-MSO3DCNN: Multiscale octave 3D CNN with channel and spatial attention for hyperspectral image classification. Remote Sens. 2020, 12, 188. [Google Scholar] [CrossRef] [Green Version]
- Mohan, A.; Venkatesan, M. HybridCNN based hyperspectral image classification using multiscale spatiospectral features. Infrared Phys. Technol. 2020, 108, 103326. [Google Scholar] [CrossRef]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-spatial attention networks for hyperspectral image classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef] [Green Version]
- Lin, T.Y.; Goyal, P.; Girshick, R.; He, K.; Dollár, P. Focal loss for dense object detection. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 2980–2988. [Google Scholar]
- Chen, Y.; Zhu, K.; Zhu, L.; He, X.; Ghamisi, P.; Benediktsson, J.A. Automatic design of convolutional neural network for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 7048–7066. [Google Scholar] [CrossRef]





| Stage | Input | Stage1 | Stage2 | Stage3 | |
| Sub-Network1: | |||||
| Kernel Size | |||||
| Feature Size | |||||
| Sub-Network2: | |||||
| Kernel Size | |||||
| Feature Size | |||||
| Stage | Stage4 | Stage5 | Stage6 | Stage7 | |
| Sub-Network1: | / | / | |||
| Kernel Size | / | / | |||
| / | / | ||||
| Feature Size | |||||
| Sub-Network2: | / | / | |||
| Kernel Size | / | / | |||
| / | / | ||||
| Feature Size | |||||
| Backbone Structure | Pixels for Training over SV/PU/IP Datasets (%) | |
|---|---|---|
| VHIS | 1D-CNN | 8.91%/6.31%/19.00% |
| DA-VHIS | 1D-CNN + Data augmentation methods | 8.91%/6.31%/19.00% |
| AutoCNN | 1D-AutoCNN | 5.91%/4.20%/25.20% |
| SS3FCN | 1D-FCN + 3D-FCN | 3.76%/6.64%/11.02% |
| TAP-Net | Parallel network + Triple-attention mechanism | 3.73%/6.36%/11.59% |
| DA-IMRN | Multi-scale residual network + Interactive attention-guided feature learning | 3.73%/6.31%/11.59% |
| Class | Method | |||||||
|---|---|---|---|---|---|---|---|---|
| VHIS | DA-VHIS | AutoCNN | SS3FCN | TAP-Net | DA-IMRN (sub-net1) | DA-IMRN (sub-net2) | DA-IMRN | |
| C1 | 85.91 | 96.36 | 96.75 | 92.36 | ||||
| C2 | 73.88 | 94.71 | 99.26 | 92.58 | ||||
| C3 | 33.72 | 49.95 | 79.46 | 66.35 | ||||
| C4 | 65.92 | 79.62 | 99.09 | 98.13 | ||||
| C5 | 46.42 | 64.30 | 97.21 | 95.63 | ||||
| C6 | 79.63 | 79.89 | 99.68 | 99.30 | ||||
| C7 | 73.59 | 79.62 | 99.35 | 99.43 | ||||
| C8 | 72.16 | 74.54 | 75.82 | 69.72 | ||||
| C9 | 71.87 | 96.10 | 99.05 | 99.67 | ||||
| C10 | 73.11 | 87.28 | 87.54 | 84.07 | ||||
| C11 | 72.51 | 73.08 | 89.15 | 85.31 | ||||
| C12 | 71.06 | 98.25 | 96.99 | 97.98 | ||||
| C13 | 75.80 | 97.67 | 98.36 | 98.45 | ||||
| C14 | 72.04 | 88.07 | 90.61 | 87.32 | ||||
| C15 | 45.03 | 62.92 | 63.47 | 52.31 | ||||
| C16 | 22.54 | 45.39 | 89.26 | 59.97 | ||||
| OA | 64.20 | 77.52 | 87.15 | 81.32 | 91.26 ± 0.89 | |||
| AA | 64.70 | 79.24 | 91.32 | 86.13 | 94.22 ± 0.90 | |||
| Kappa | / | 0.749 | 0.857 | / | 0.885 ± 0.03 | |||
| Class | Method | |||||||
|---|---|---|---|---|---|---|---|---|
| VHIS | DA-VHIS | AutoCNN | SS3FCN | TAP-Net | DA-IMRN (sub-net1) | DA-IMRN (sub-net2) | DA-IMRN | |
| C1 | 93.40 | 93.42 | 83.40 | 97.48 | ||||
| C2 | 86.20 | 86.52 | 93.32 | 90.86 | ||||
| C3 | 47.58 | 46.88 | 61.52 | 58.75 | ||||
| C4 | 86.89 | 92.21 | 78.86 | 84.81 | ||||
| C5 | 59.81 | 59.74 | 98.25 | 94.82 | ||||
| C6 | 27.14 | 27.68 | 73.34 | 23.59 | ||||
| C7 | 0 | 0 | 64.56 | 61.61 | ||||
| C8 | 78.46 | 78.32 | 76.86 | 88.84 | ||||
| C9 | 79.27 | 79.60 | 97.69 | 88.68 | ||||
| OA | 73.26 | 73.84 | 84.63 | 79.89 | 93.33 ± 1.00 | |||
| AA | 62.08 | 62.71 | 80.87 | 76.60 | 89.61 ± 1.12 | |||
| Kappa | / | 0.631 | 0.800 | / | 0.923 ± 0.02 | |||
| Class | Method | |||||||
|---|---|---|---|---|---|---|---|---|
| VHIS | DA-VHIS | AutoCNN | SS3FCN | TAP-Net | DA-IMRN (sub-net1) | DA-IMRN (sub-net2) | DA-IMRN | |
| C1 | 17.68 | 15.89 | 19.58 | 40.4 | ||||
| C2 | 56.89 | 70.41 | 60.16 | 77.89 | ||||
| C3 | 51.55 | 61.44 | 44.12 | 60.74 | ||||
| C4 | 36.27 | 42.28 | 25.35 | 11.8 | ||||
| C5 | 69.02 | 73.02 | 77.80 | 67.5 | ||||
| C6 | 92.35 | 92.13 | 90.99 | 91.95 | ||||
| C7 | 0 | 0 | 35.63 | 20.14 | ||||
| C8 | 86.95 | 86.44 | 95.87 | 81.71 | ||||
| C9 | 19.55 | 21.28 | 5.31 | 31.67 | ||||
| C10 | 60.05 | 67.47 | 55.93 | 78.15 | ||||
| C11 | 74.05 | 65.24 | 68.73 | 69.32 | ||||
| C12 | 43.71 | 49.56 | 36.96 | 40.81 | ||||
| C13 | 94.15 | 96.01 | 87.33 | 93.43 | ||||
| C14 | 91.18 | 92.68 | 84.90 | 91.77 | ||||
| C15 | 43.39 | 52.79 | 39.02 | 37.93 | ||||
| C16 | 45.04 | 44.78 | 48.02 | 75.19 | ||||
| OA | 67.11 | 65.97 | 65.35 | 71.47 | 82.38 ± 2.04 | |||
| AA | 55.11 | 54.06 | 54.73 | 60.65 | 80.35 ± 2.69 | |||
| Kappa | / | 0.653 | 0.600 | / | 0.791 ± 0.02 | |||
| Salinas Valley | Pavia University | Indian Pines | ||||
|---|---|---|---|---|---|---|
| OA | AA | OA | AA | OA | AA | |
| DA-IMRN (- -) | ||||||
| DA-IMRN (single SCAM) | ||||||
| DA-IMRN (single SAM) | ||||||
| DA-IMRN | ||||||
| DA-IMRN (Single SCAM) | DA-IMRN (Single SAM) | DA-IMRN | |
|---|---|---|---|
| DA-IMRN (- -) | |||
| DA-IMRN (single SCAM) | 0.234 | 0.002 | |
| DA-IMRN (single SAM) | 0.014 |
| Salinas Valley | Pavia University | Indian Pines | ||||
|---|---|---|---|---|---|---|
| OA | AA | OA | AA | OA | AA | |
| DA-IMRN (- -) | ||||||
| DA-IMRN (single MSpaRB) | ||||||
| DA-IMRN (single MSpeRB) | ||||||
| DA-IMRN | ||||||
| DA-IMRN (Single MSpaRB) | DA-IMRN (Single MSpeRB) | DA-IMRN | |
|---|---|---|---|
| DA-IMRN (- -) | |||
| DA-IMRN (single MSpaRB) | 0.692 | 0.017 | |
| DA-IMRN (single MSpeRB) | 0.011 |
| Training Pixels | 2949.7 | 2701.4 | 2554.8 | 2318.8 | 2136 |
| Ratio (%) | 6.89% | 6.31% | 5.97% | 5.42% | 4.99% |
| OA (%) | |||||
| AA (%) | |||||
| Kappa |
| SV | PU | IP | ||||
|---|---|---|---|---|---|---|
| Feature Fusion | Decision Fusion | Feature Fusion | Decision Fusion | Feature Fusion | Decision Fusion | |
| OA (%) | ||||||
| AA (%) | ||||||
| Kappa | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zou, L.; Zhang, Z.; Du, H.; Lei, M.; Xue, Y.; Wang, Z.J. DA-IMRN: Dual-Attention-Guided Interactive Multi-Scale Residual Network for Hyperspectral Image Classification. Remote Sens. 2022, 14, 530. https://doi.org/10.3390/rs14030530
Zou L, Zhang Z, Du H, Lei M, Xue Y, Wang ZJ. DA-IMRN: Dual-Attention-Guided Interactive Multi-Scale Residual Network for Hyperspectral Image Classification. Remote Sensing. 2022; 14(3):530. https://doi.org/10.3390/rs14030530
Chicago/Turabian StyleZou, Liang, Zhifan Zhang, Haijia Du, Meng Lei, Yong Xue, and Z. Jane Wang. 2022. "DA-IMRN: Dual-Attention-Guided Interactive Multi-Scale Residual Network for Hyperspectral Image Classification" Remote Sensing 14, no. 3: 530. https://doi.org/10.3390/rs14030530
APA StyleZou, L., Zhang, Z., Du, H., Lei, M., Xue, Y., & Wang, Z. J. (2022). DA-IMRN: Dual-Attention-Guided Interactive Multi-Scale Residual Network for Hyperspectral Image Classification. Remote Sensing, 14(3), 530. https://doi.org/10.3390/rs14030530









