Orthogonal Set of Indicators for the Assessment of Flexible Pavement Stiffness from Deflection Monitoring: Theoretical Formalism and Numerical Study
Abstract
:1. Introduction
1.1. Use of Deflection Measurements
1.2. Recall of the Various Means for Conducting Deflection Measurements
2. Construction of Indicators to Assess the Individual Stiffness of Pavement Layers
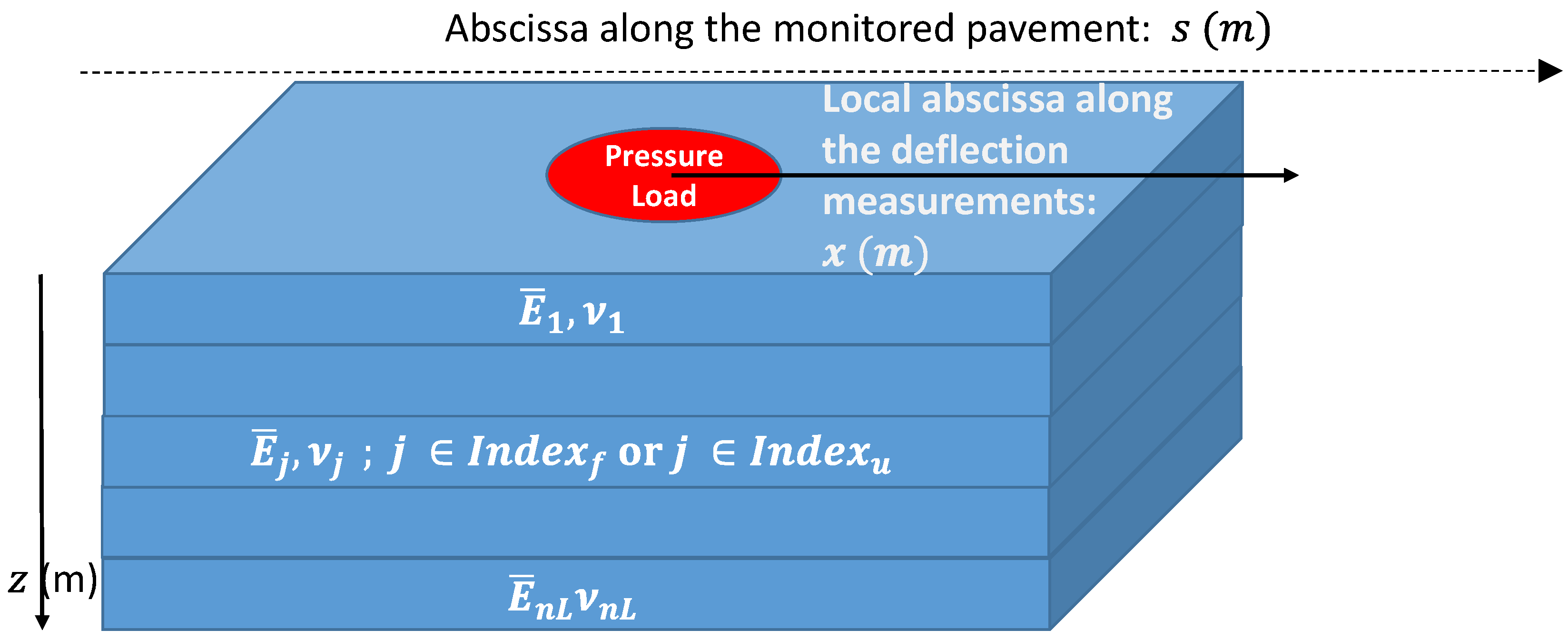
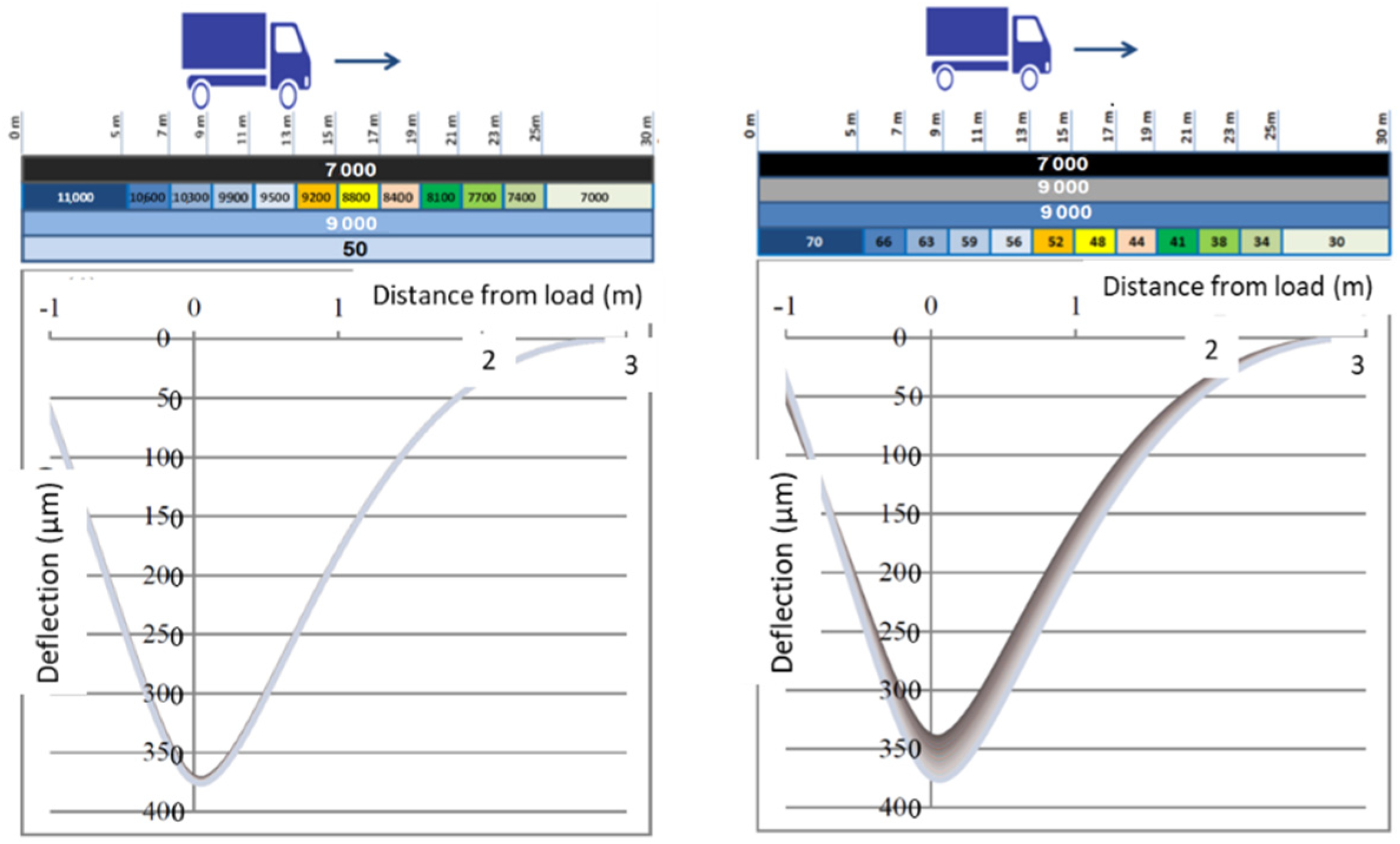
2.1. Pavement Model for the Determination of Indicators
2.2. Proposed Indicators and Constraints for Their Determination
- = “Weighting functions” (or distributions) defined on
- = linear form for functions from to , defined as either:
- o
- ,in the case of (quasi) continuous measurements, with being the characteristic function of the interval
- o
- Or: in the case of discrete measurements
- (= in the discrete case) = scalar product of functions defined on and related to the norm assumed to be finite: in the discrete case)
- Indicator maximizes the sensitivity of the deflection measurements to the stiffness of layer # (condition #1).
- Indicator is “weakly” sensitive to the stiffness of the other layers # for (condition #2). The best case would be for indicators to be independent of the stiffness of the other layers # (orthogonal indicator).
- The functions are imposed to have a finite norm , in avoiding infinite values for (condition #3).
- The values that is the magnitude of functions are chosen to give a direct physical meaning to the indicators (condition #4).
2.3. Determination of the Weighting Functions
2.4. Variations of Indicators along a Given Route
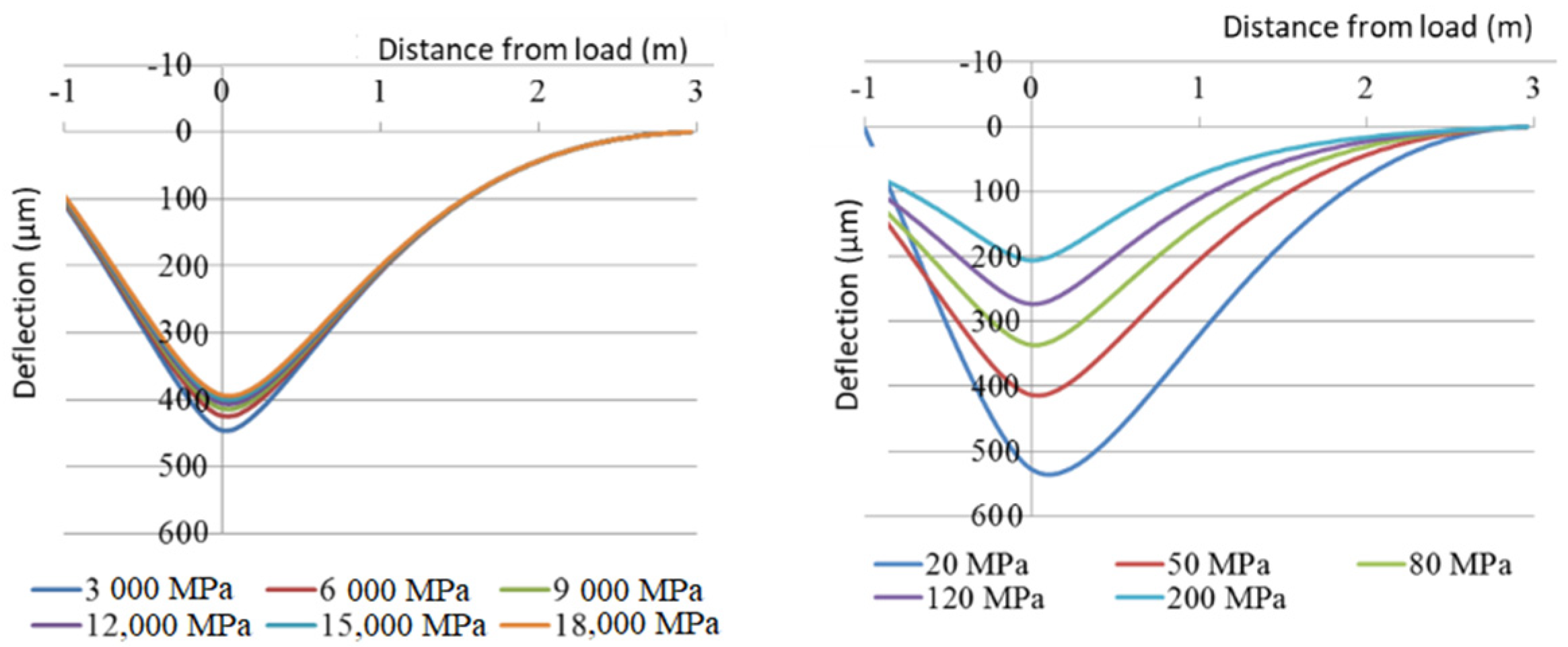
3. Numerical Applications of the Method (Theoretical Examples)
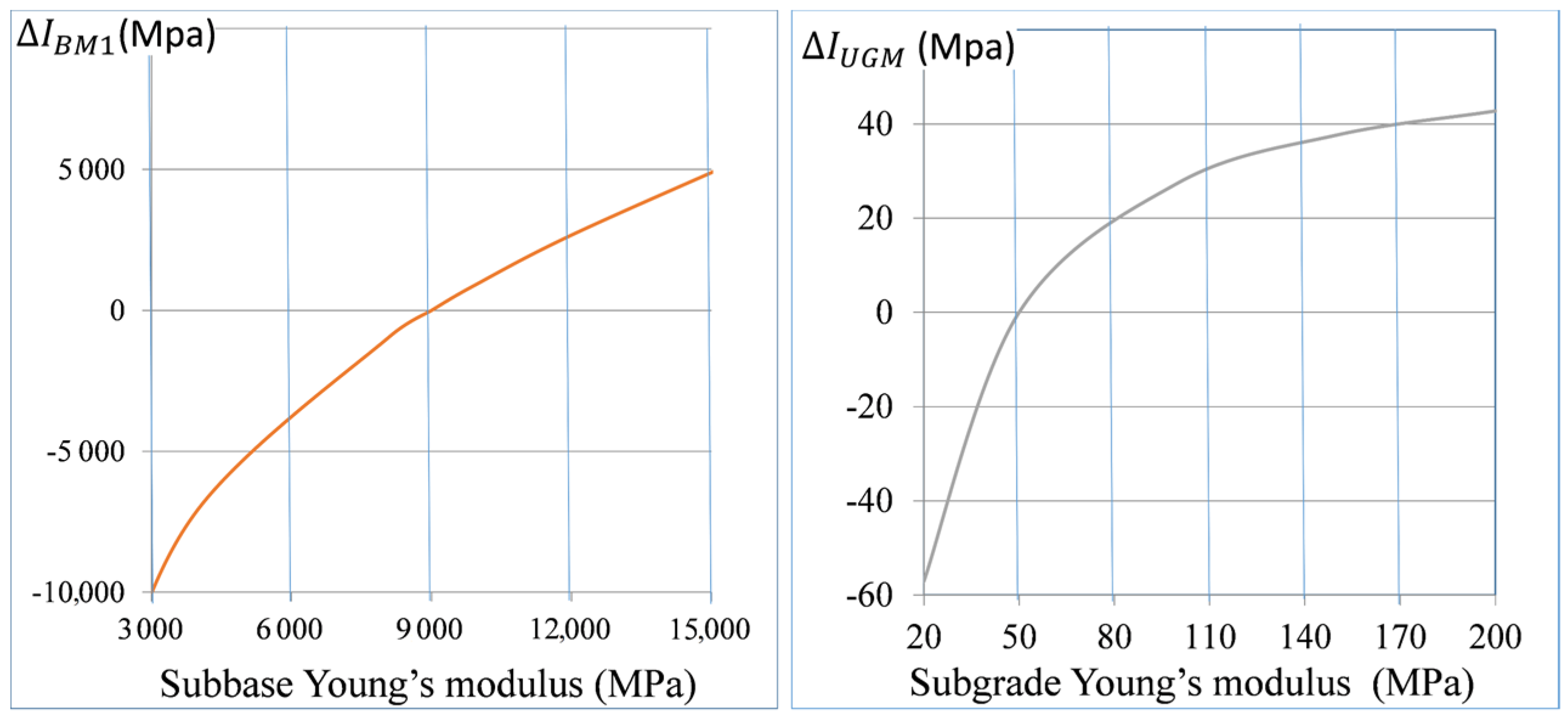
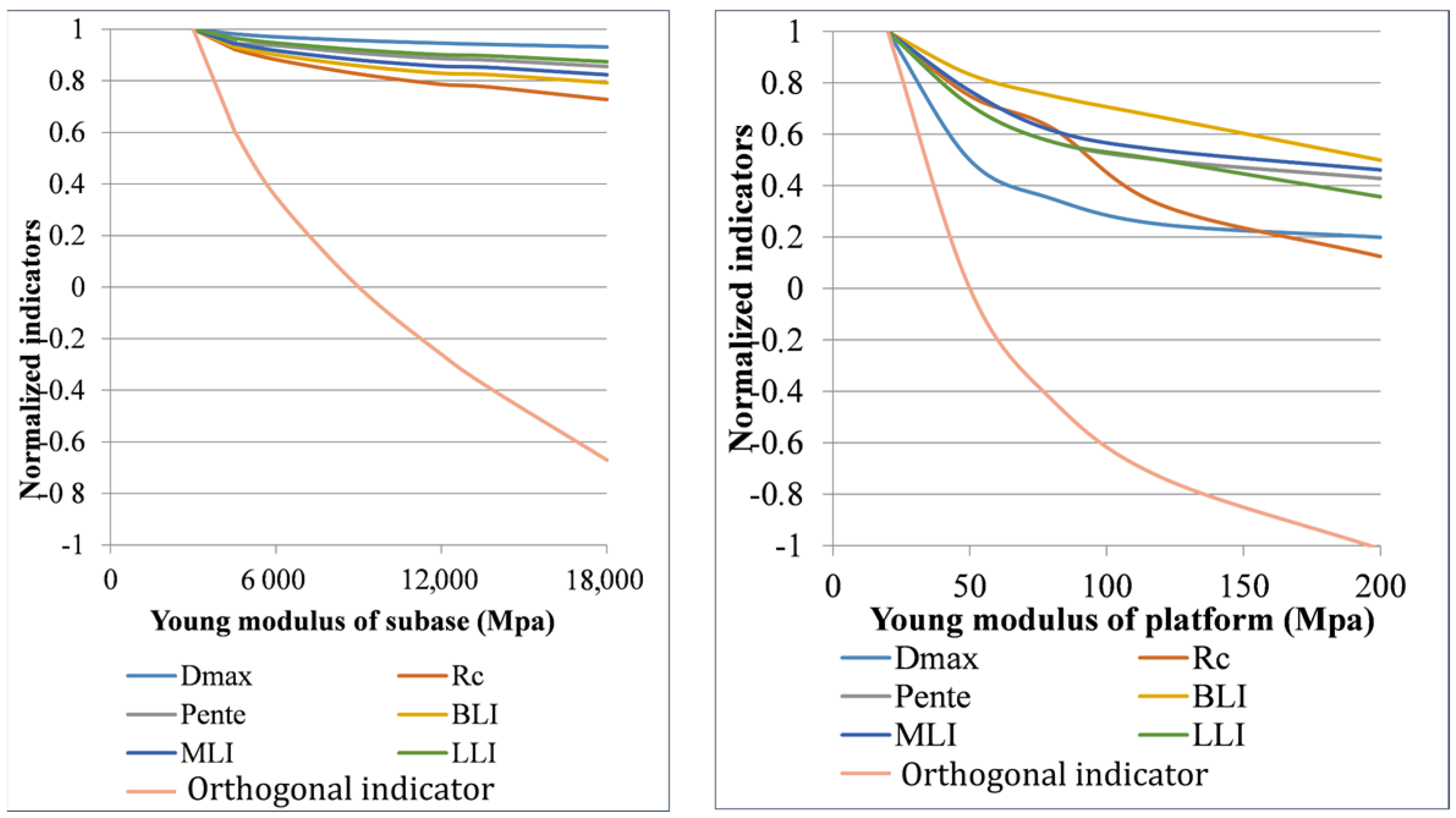
- Variations in the Young’s modulus of the upper base layer between 3000 and 18,000 MPa.
- Variations in the Young’s modulus of the subgrade layer between 20 and 200 MPa.
3.1. Local Variations of E-Moduli (Theoretical Application Example)
3.2. Sensitivity of the Indicators to Measurement Errors
4. Possible Extensions to the Method
4.1. Model with Interface Shear Stiffness
4.2. Visco-Dynamic Models for FWD or HWD Measurements
4.3. Application to Structural Health Monitoring with Embedded Sensors
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Sensitivity of the Optimized Indicators to Deflection Measurement Uncertainties
| Weighting Function | Configuration with 2 Geophones Position of Geophones (cm) | Norm of Indicators | ||||||
|---|---|---|---|---|---|---|---|---|
| G1 | G2 | |||||||
| 0 | 30 | |||||||
| Weighting coefficients | ||||||||
| −550 | 566 | 789 | ||||||
| Weighting coefficients | ||||||||
| 0.1568 | −0.2946 | 0.33 | ||||||
| Weighting function | Configuration with 7 geophones Position of geophones (cm) | Norm of indicators | ||||||
| G1 | G2 | G3 | G4 | G5 | G6 | G7 | ||
| 0 | 20 | 30 | 45 | 60 | 90 | 120 | ||
| Weighting coefficients | ||||||||
| −249 | −88 | −17 | 49 | 95 | 145 | 159 | 357 | |
| Weighting coefficients | ||||||||
| 0.0438 | 0.0010 | −0.0176 | −0.0345 | −0.0457 | −0.0567 | −0.0578 | 0.11 | |
References
- PIARC. Technical Committee B.4 Freight Transport, Truck-Traffic on Highways for Sustainable, Safer and Higher Energy Efficient Freight Transport, PIARC Ref. 2019R23EN, ISBN 978-2-84060-553-9. Available online: https://www.piarc.org/en/order-library/31308-en-Truck-Traffic on Highways for Sustainable, Safer and Higher Energy Efficient Freight Transport (accessed on 2 December 2021).
- Wright, D.; Baltazart, V.; Elsworth, N.; Hamrouche, R.; Karup, J.; Antunes, M.L.; McRobbie, S.; Merecos, V.; Saarenketo, T. D4.3 Monitoring Structural and Surface Conditions, Tomorrow’s Road Infrastructure Monitoring and Management (TRIMM), FP7 Project 285119. October 2014. Available online: https://cordis.europa.eu/docs/results/285/285119/final1-trimm-d5-3-finalreport2014-to-print.pdf (accessed on 2 December 2021).
- PIARC. PIARC Working Group D.2.3—Road Monitoring Techniques. PIARC Ref. 2019R14EN, ISBN 978-84060-530-0. Available online: https://www.piarc.org/en/order-library/30891-en-State of the Art in Monitoring Road Condition and Road/Vehicle Interaction (accessed on 2 December 2021).
- Autret, P. Utilisation du produit Rd pour l’auscultation des chaussées à couche de base traitées. Bull. Liaisons Lab. Ponts Chausséees 1969, 42, 67–80. [Google Scholar]
- Horak, E.; Emery, S. Evaluation of airport pavements with FWD deflection bowl parameter benchmarking methodology. In Proceedings of the 2nd European Airport Pavement Workshop, Amsterdam, The Netherlands, 13–14 May 2009; pp. 13–14. [Google Scholar]
- Ullidtz, P. Pavement Analysis; ELSEVIER: New York, NY, USA, 1987. [Google Scholar]
- Le Boursicaud, V. New Uses of Deflection Bowls Measurements to Characterize the Structural Conditions of Pavements. Ph.D. Thesis, Ecole Centrale de Nantes, Nantes University, Nantes, France, 8 November 2018. [Google Scholar]
- Burmister, D.M. The theory of stresses and displacements in layered systems and applications of the design of airport runways. Proc. Highw. Res. Board 1943, 23, 126–148. [Google Scholar]
- Corte, J.-F. French Design Manual for Pavement Structures, Guide Techniques, LCPC Editor, ISBN 2-7208-7070-6. May 1997. Available online: https://trid.trb.org/view/484504 (accessed on 2 December 2021).
- COST 336. Use of Falling Weight Deflectometers in Pavement Evaluation. Final Report of the 1996 COST Action 336. 1999. Available online: https://cordis.europa.eu/docs/publications/3182/31828341-6_en.pdf (accessed on 2 December 2021).
- Roussel, J.M.; Sauzéat, C.; Di Benedetto, H.; Broutin, M. Numerical simulation of falling/heavy weight deflectometer test considering linear viscoelastic behaviour in bituminous layers and inertia effects. Road Mater. Pavement Des. 2019, 20 (Suppl. S1), S64–S78. [Google Scholar] [CrossRef]
- Geem, C.; Le Parc, J.-F. 20 years of experience with the Curviameter at the BRRC—An overview. In Proceedings of the Workshop on the Curviameter: Interpretation and Exploitation of Measurements, Brussels, Belgium, 21–22 January 2015. [Google Scholar]
- Lepert, P.; Aussedat, G.; Simonin, J.-M. Evaluation du curviamètre MT 15. Bull. Lab. Ponts Chaussées 1997, 209, 3–12. [Google Scholar]
- De Boissoudy, A.; Gramsammer, J.; Keryell, P.; Paillard, M. Appareils d’auscultation. Le déflectographe 04. Bull. Liaison Lab. Ponts Chaussées 1984, 129, 81–98. [Google Scholar]
- Simonin, J.-M.; Geffard, J.-L.; Hornych, P. Performance of Deflection Measurement Equipment and Data. In Proceedings of the International Symposium Non-Destructive Testing in Civil. Engineering (NDT-CE), Berlin, Germany, 15–17 September 2015. [Google Scholar]
- Simonin, J.-M.; Riouall, A. Evaluation des déflectographes. Bull. Lab. Ponts Chaussées 1997, 208, 39–47. [Google Scholar]
- Elseifi, M.; Abdel-Khalek, A.M.; Dasari, K. Implementation of Rolling Wheel Deflectometer (RWD) in PMS; Louisiana Transportation Research Center: Baton Rouge, LA, USA, 2012. [Google Scholar]
- Baltzer, S.; Pratt, D.; Weligamage, J.; Adamsen, J.; Hildebrand, G. Continuous bearing capacity profile of 18,000 km Australian road network in 5 months. In Proceedings of the Dans: 24th ARRB Conference, Melbourne, Australia, 12–15 October 2010. [Google Scholar]
- Rada, G.R.; Nazarian, S. The State-of-the-Technology of Moving Pavement Deflection Testing; Final Rep. FHWA-DTFH61-08-D-00025; U.S. Dept of Transportation: Washington, DC, USA, 2011. [Google Scholar]
- Jansen, D. TSD Evaluation in Germany, Berlin. In Proceedings of the International Symposium Non-Destructive Testing in Civil Engineering (NDT-CE), Berlin, Germany, 15–17 September 2015. [Google Scholar]
- Man, J.; Yan, K.; Miao, Y.; Liu, Y.; Yang, X.; Diab, A.; You, L. 3D Spectral element model with a space-decoupling technique for the response of transversely isotropic pavements to moving vehicular loading. Road Mater. Pavement Des. 2021, 22, 1–25. [Google Scholar] [CrossRef]


| Index | Definition | Comments | References |
|---|---|---|---|
| D0: Maximum Deflection | D0 = Dmax | Affected by all layers | [2,3,4,5,6,7,10,11,12,13,14,15,16] |
| Di: Deflections | Deflection measurement recorded by sensor #i or at “i” millimeters from the center of the plate | [5,6,7,10,11] | |
| RoC: Radius of Curvature | Second derivative of the deflection basin at the maximum deflection Calculation method depending on the device | Sensitive to both the base layer and interface | [4,7,12,13] |
| Rd: | D0 | Sensitive to platform variations for flexible pavements | [4,7] |
| BLI: Base Layer Index or SCI: Surface Curvature Index | BLI = D0 − D300 | More sensitive to surface layers | [10,11] |
| MLI: Middle Layer Index or BDI: Base Damage Index | MLI = D300 − D600 | More sensitive to base layers | [10,11] |
| LLI: Lower Layer Index or BCI: Base Damage Index | LLI = D900 − D600 | More sensitive to both base and foundation layers | [10,11] |
| Material Type | Thickness (m) | Reference Structure Young’s Modulus (MPa) | Variations (MPa) |
|---|---|---|---|
| BBSG | 0.06 | 7000 | |
| BM1 | 0.08 | 9000 | 3000 to 18,000 |
| BM2 | 0.08 | 9000 | |
| UGM | 6 | 50 | 20 to 200 |
| Rigid bedrock | Infinite | 55,000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simonin, J.-M.; Piau, J.-M.; Le-Boursicault, V.; Freitas, M. Orthogonal Set of Indicators for the Assessment of Flexible Pavement Stiffness from Deflection Monitoring: Theoretical Formalism and Numerical Study. Remote Sens. 2022, 14, 500. https://doi.org/10.3390/rs14030500
Simonin J-M, Piau J-M, Le-Boursicault V, Freitas M. Orthogonal Set of Indicators for the Assessment of Flexible Pavement Stiffness from Deflection Monitoring: Theoretical Formalism and Numerical Study. Remote Sensing. 2022; 14(3):500. https://doi.org/10.3390/rs14030500
Chicago/Turabian StyleSimonin, Jean-Michel, Jean-Michel Piau, Vinciane Le-Boursicault, and Murilo Freitas. 2022. "Orthogonal Set of Indicators for the Assessment of Flexible Pavement Stiffness from Deflection Monitoring: Theoretical Formalism and Numerical Study" Remote Sensing 14, no. 3: 500. https://doi.org/10.3390/rs14030500
APA StyleSimonin, J.-M., Piau, J.-M., Le-Boursicault, V., & Freitas, M. (2022). Orthogonal Set of Indicators for the Assessment of Flexible Pavement Stiffness from Deflection Monitoring: Theoretical Formalism and Numerical Study. Remote Sensing, 14(3), 500. https://doi.org/10.3390/rs14030500






