A Preliminary Numerical Study to Compare the Physical Method and Machine Learning Methods Applied to GPR Data for Underground Utility Network Characterization
Abstract
1. Introduction
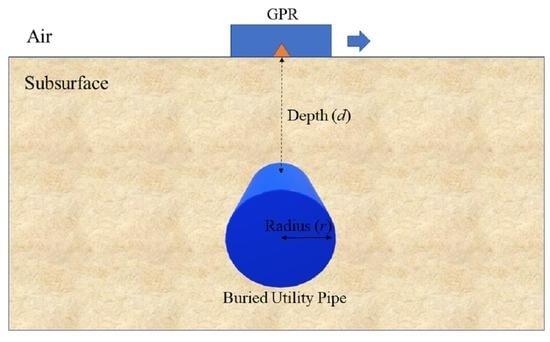
2. Estimation Methods
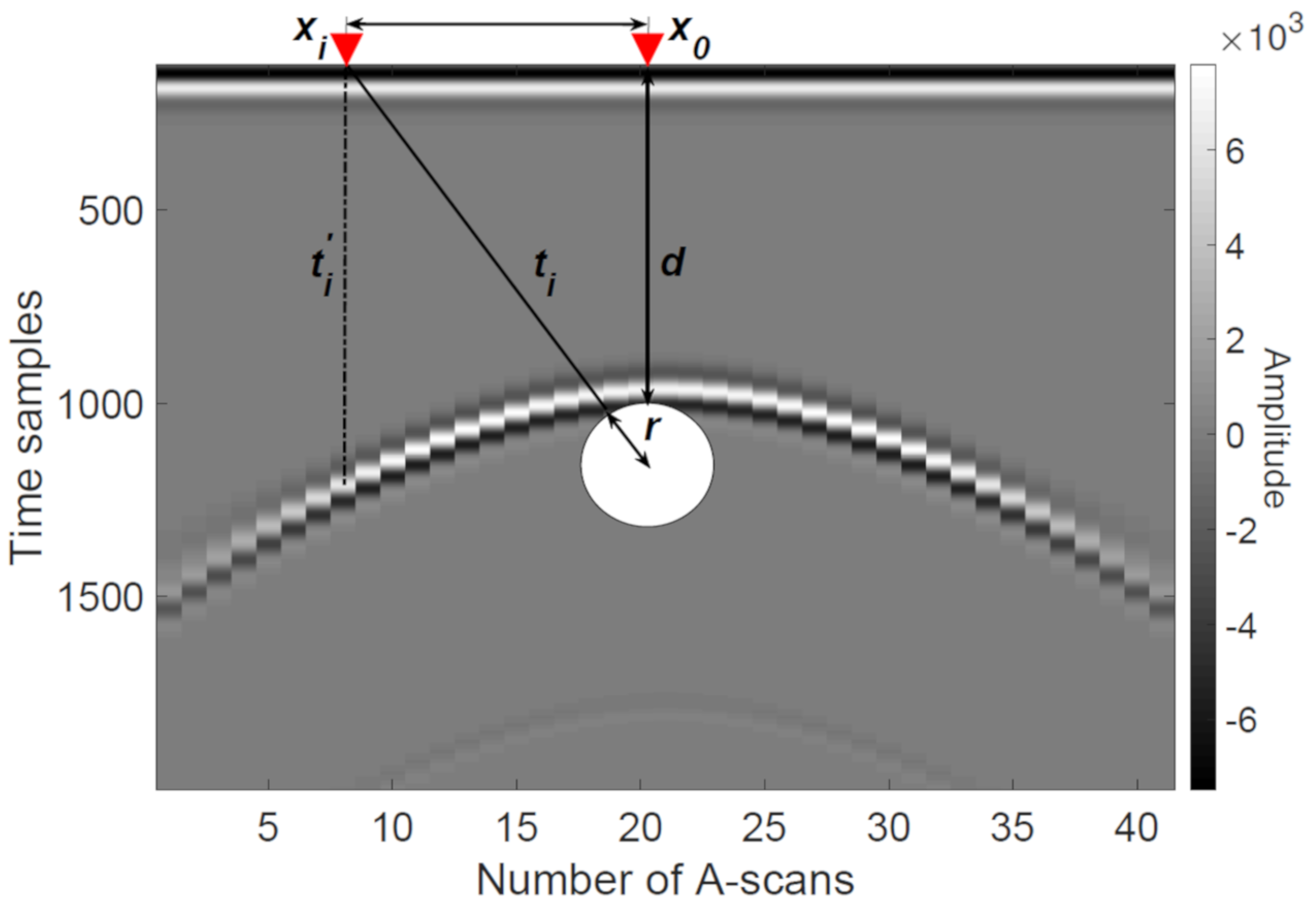
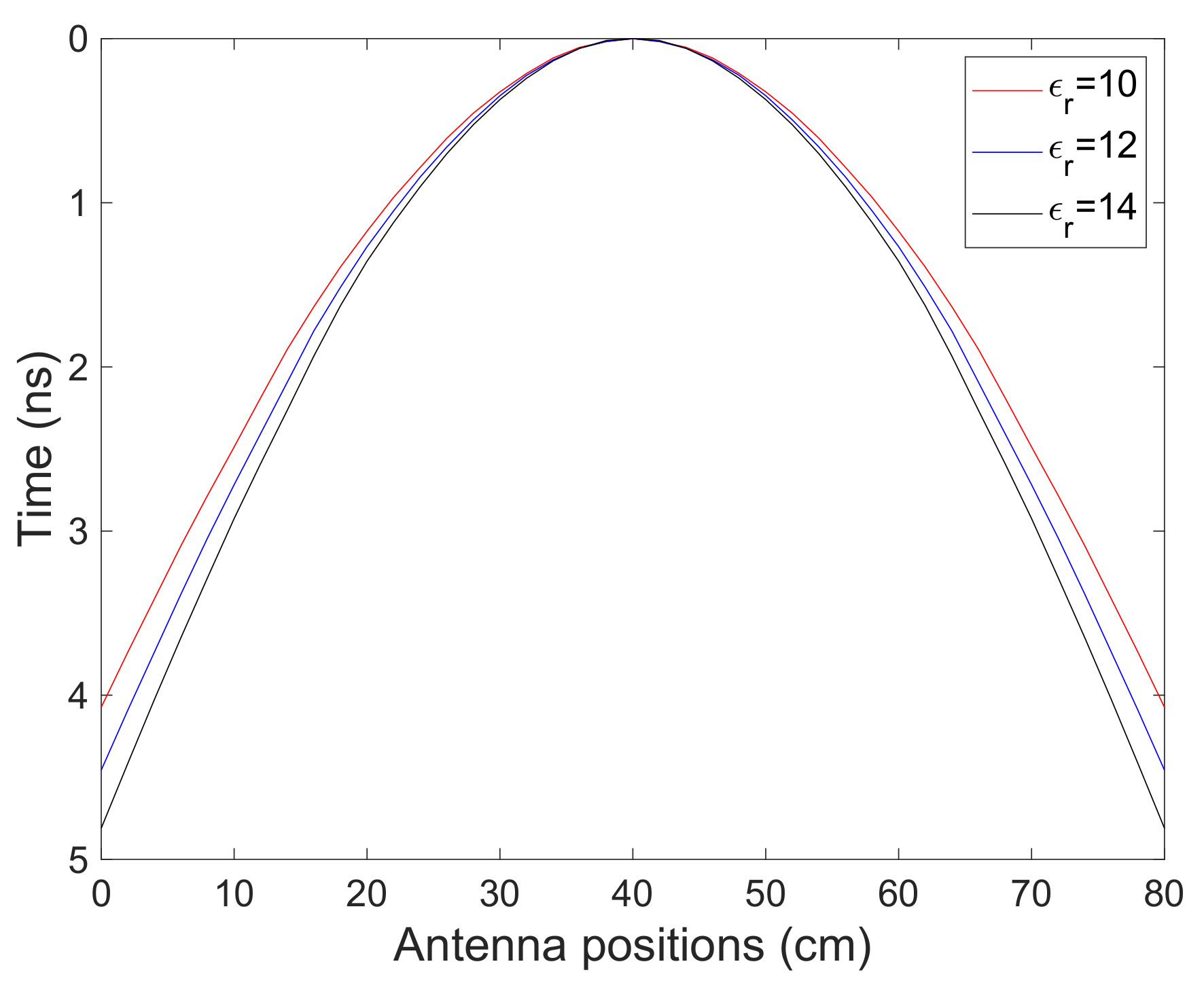
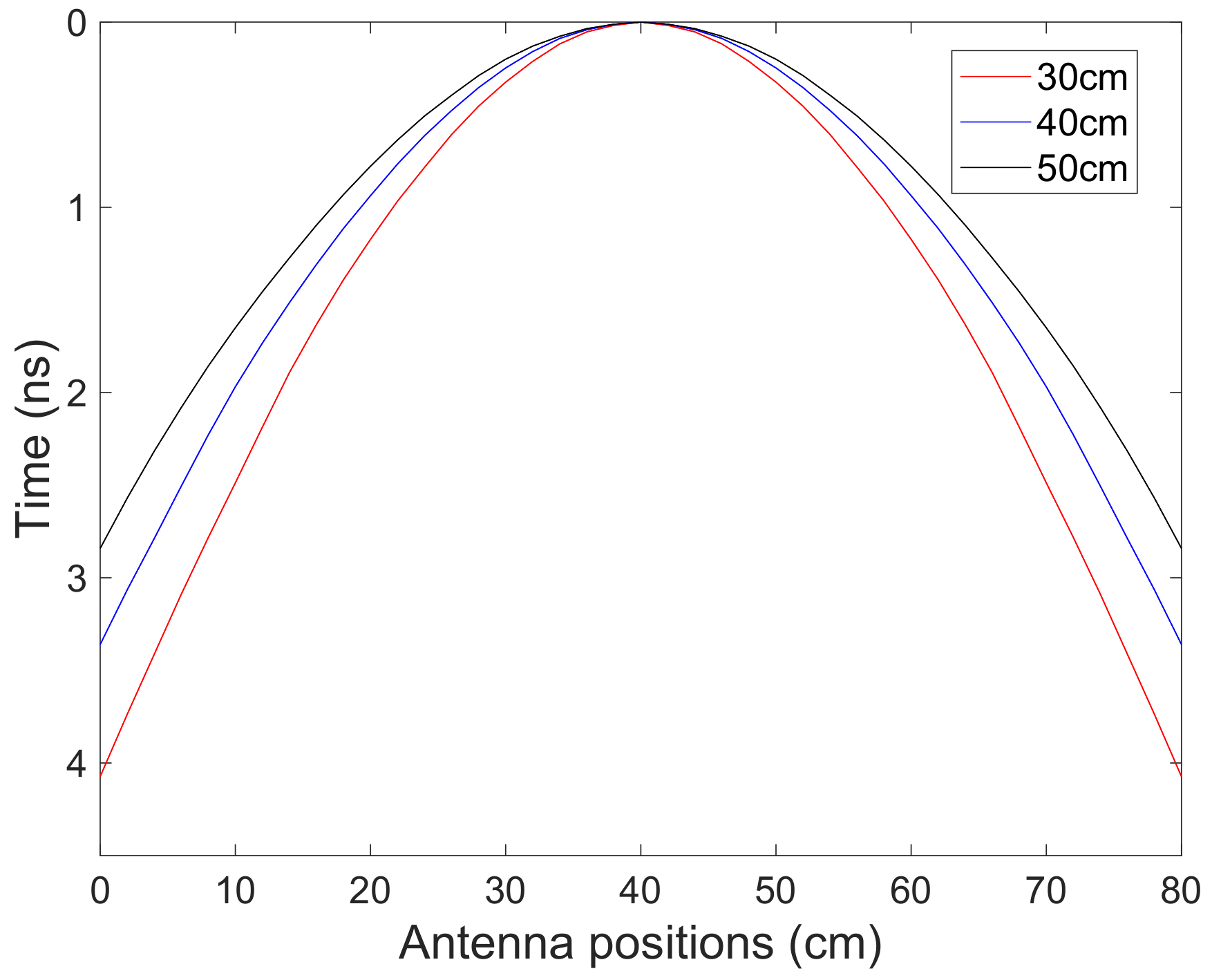
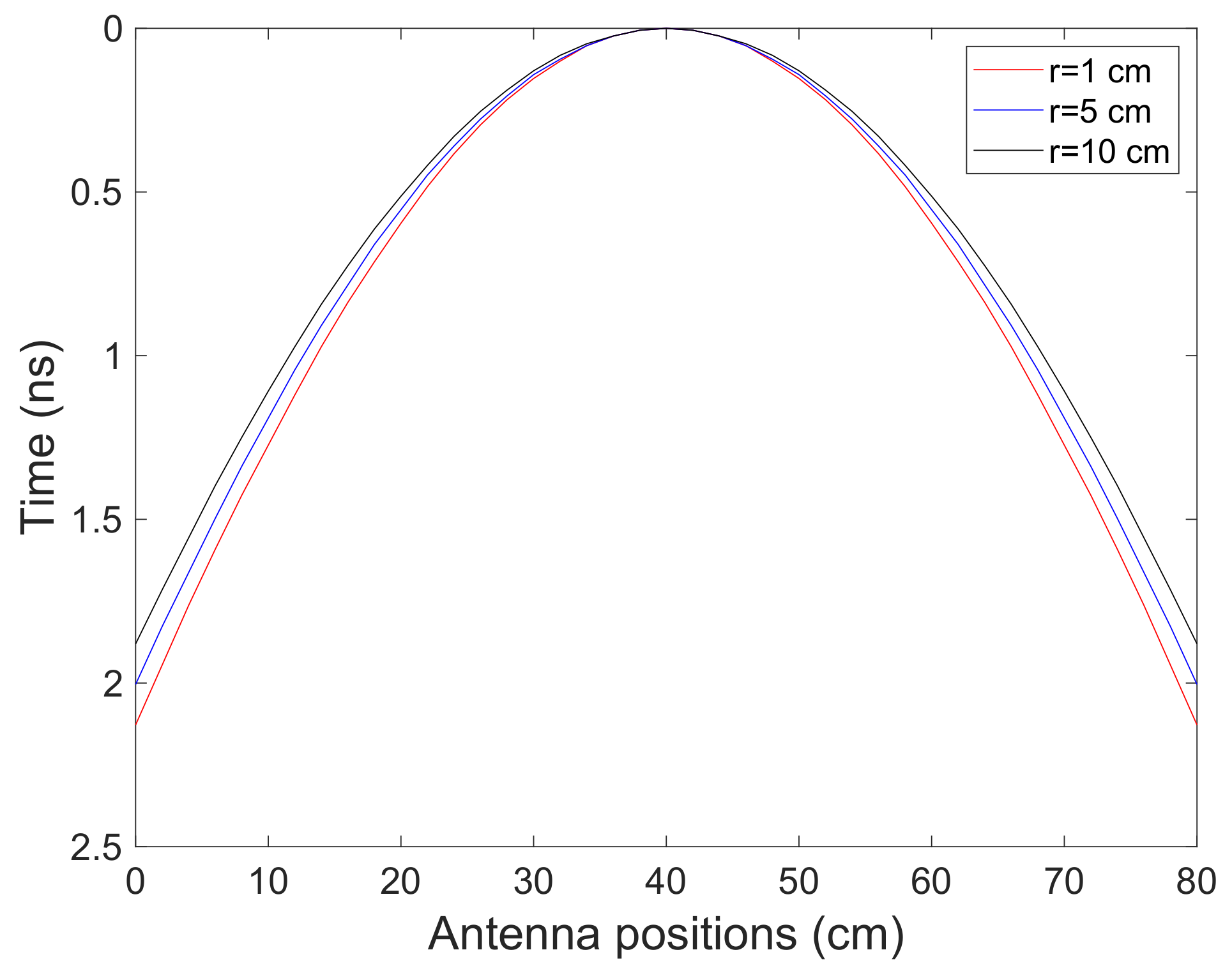
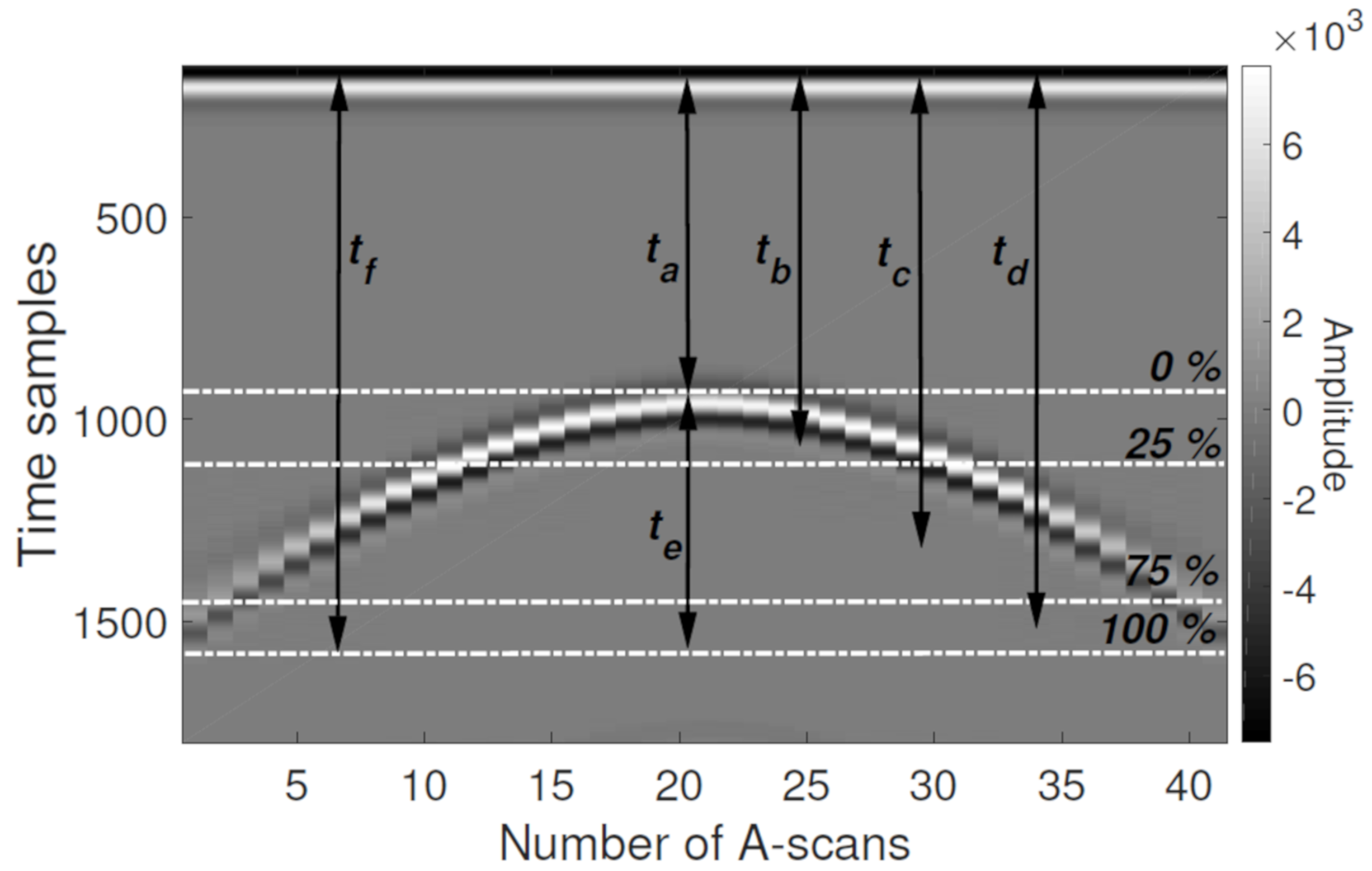
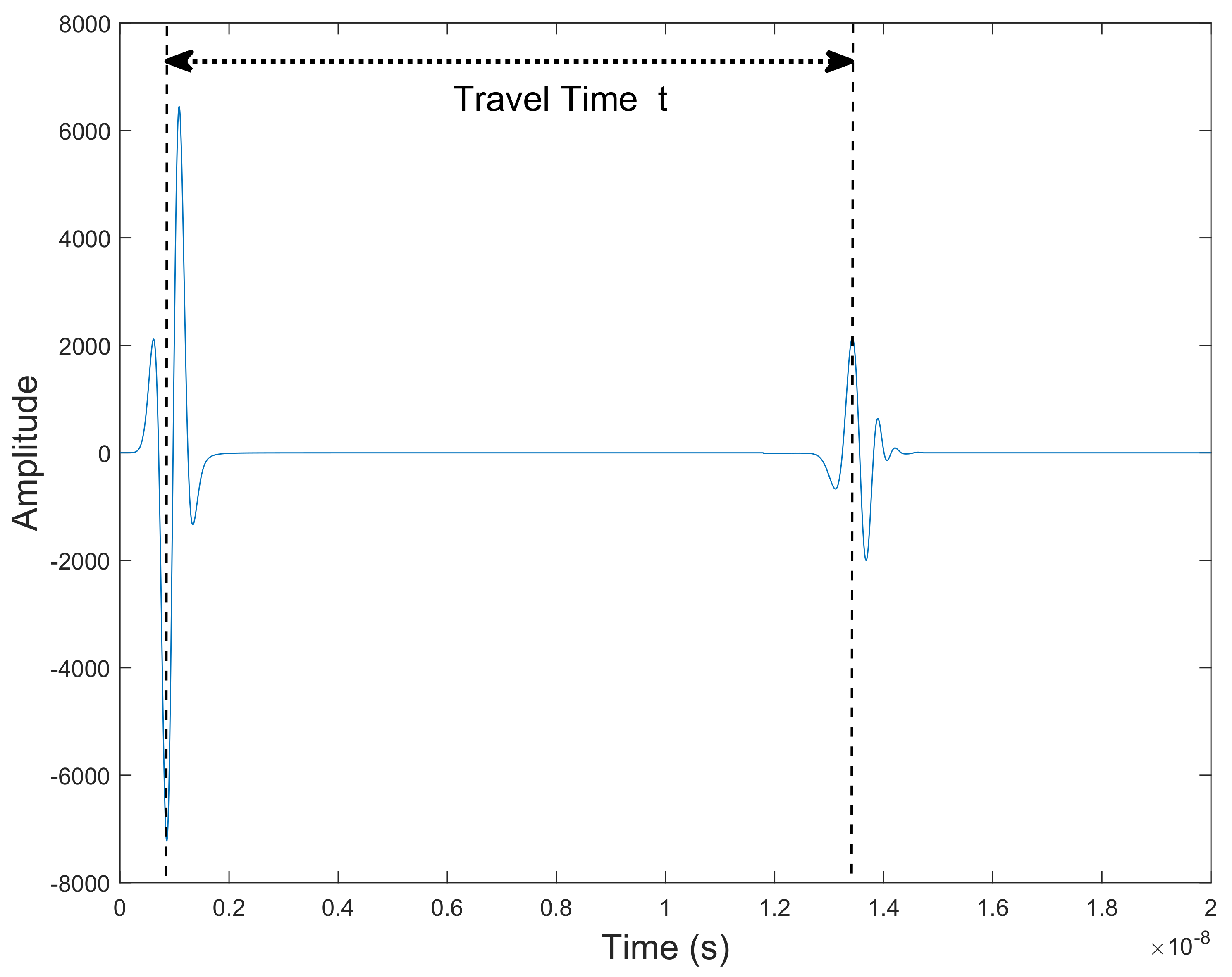
2.1. Ray-Based Method
2.2. Machine Learning Methods: SVM and SVR
Formulation
2.3. SVM Implementation
2.3.1. Feature Selection
2.3.2. Training, Validation and Testing
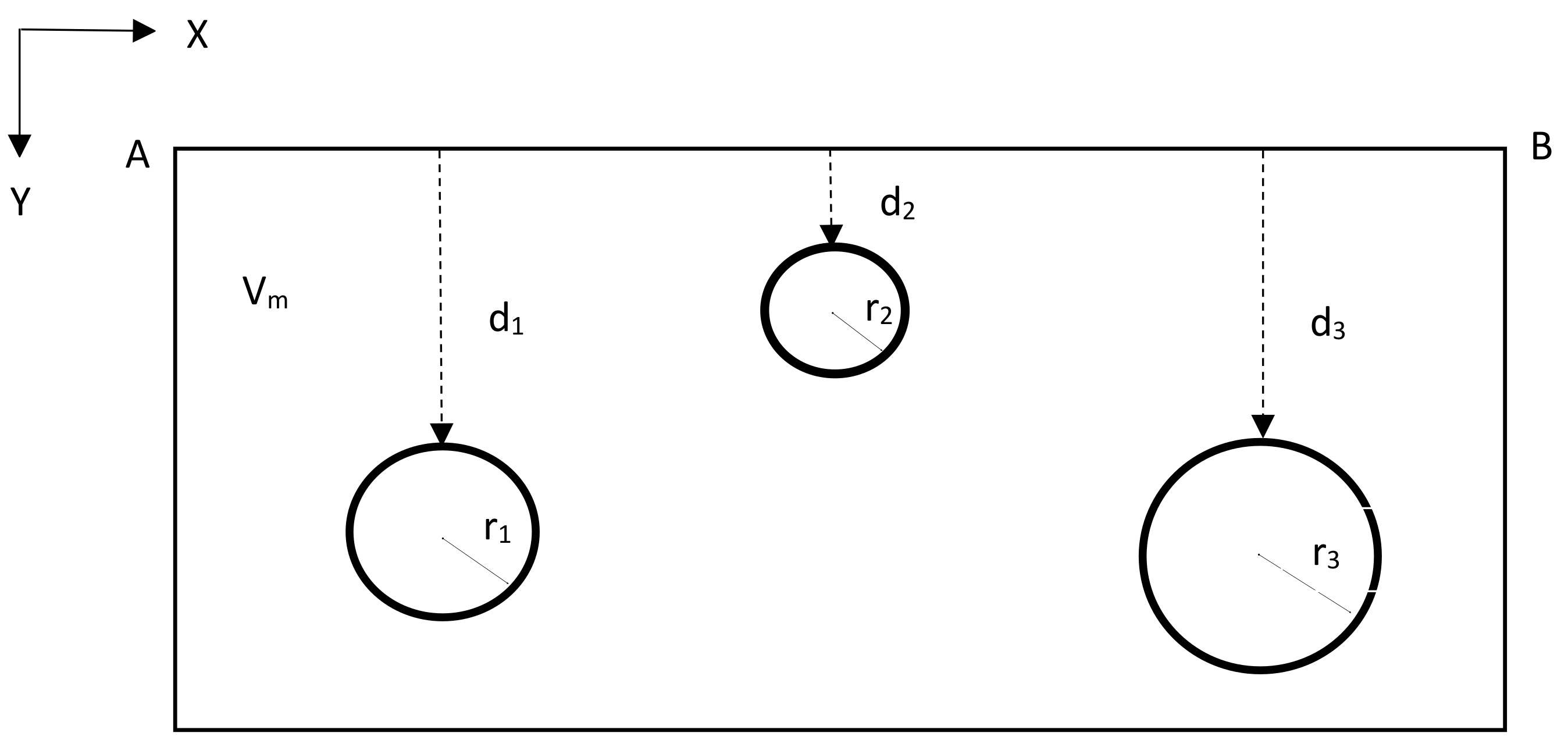
3. Database Generation
4. Results
5. Discussion
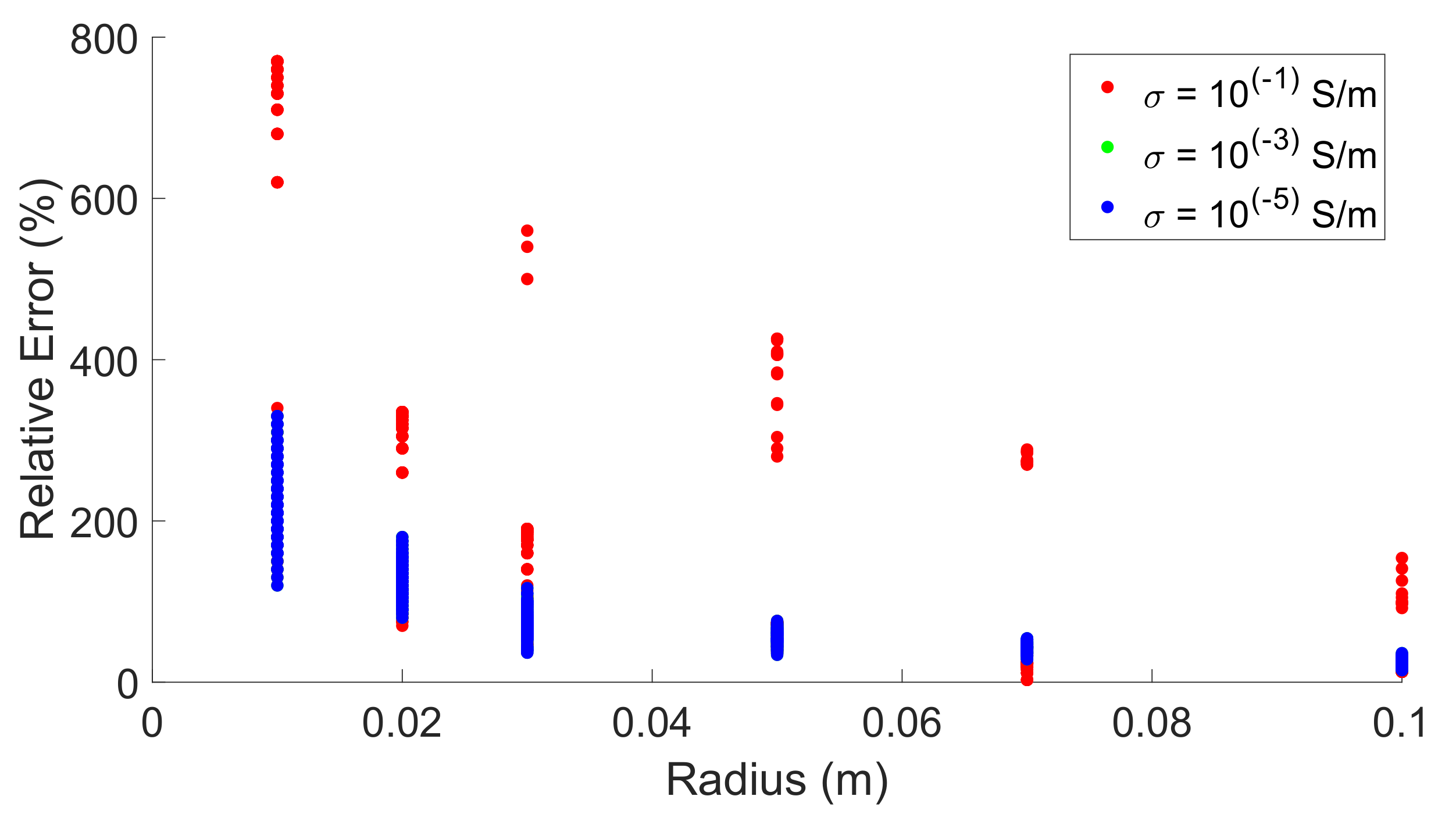
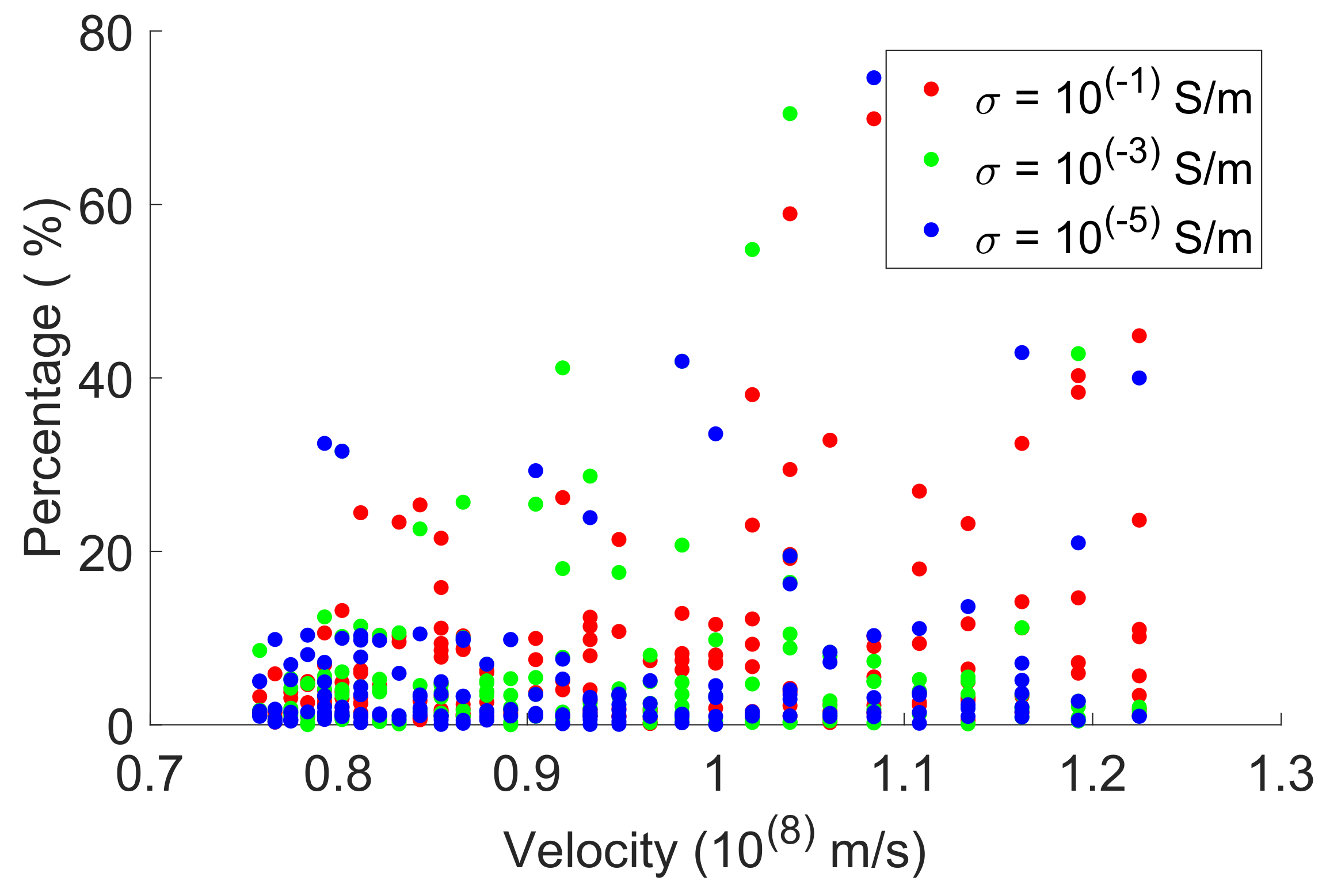
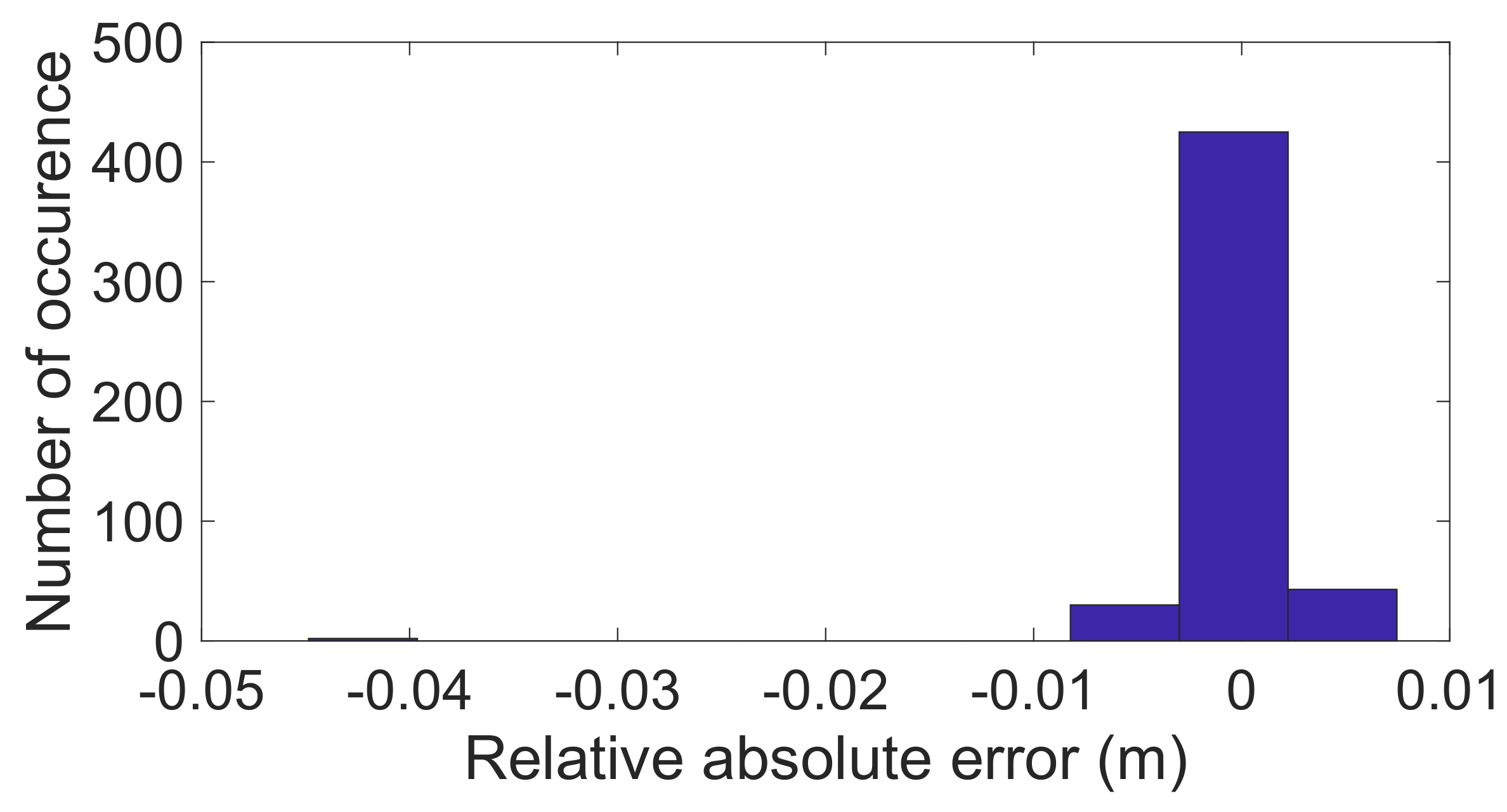
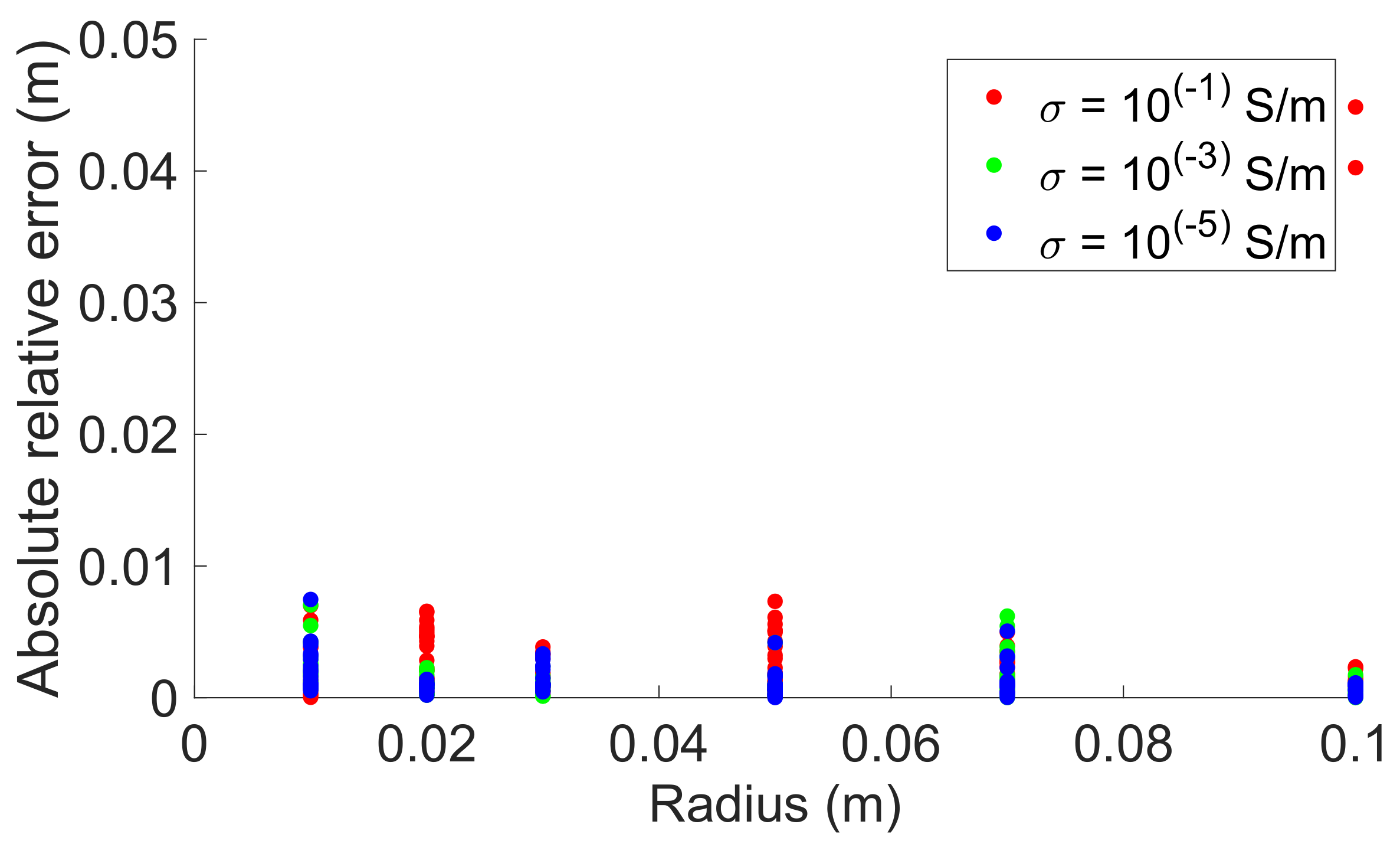
5.1. Ray-Based Method
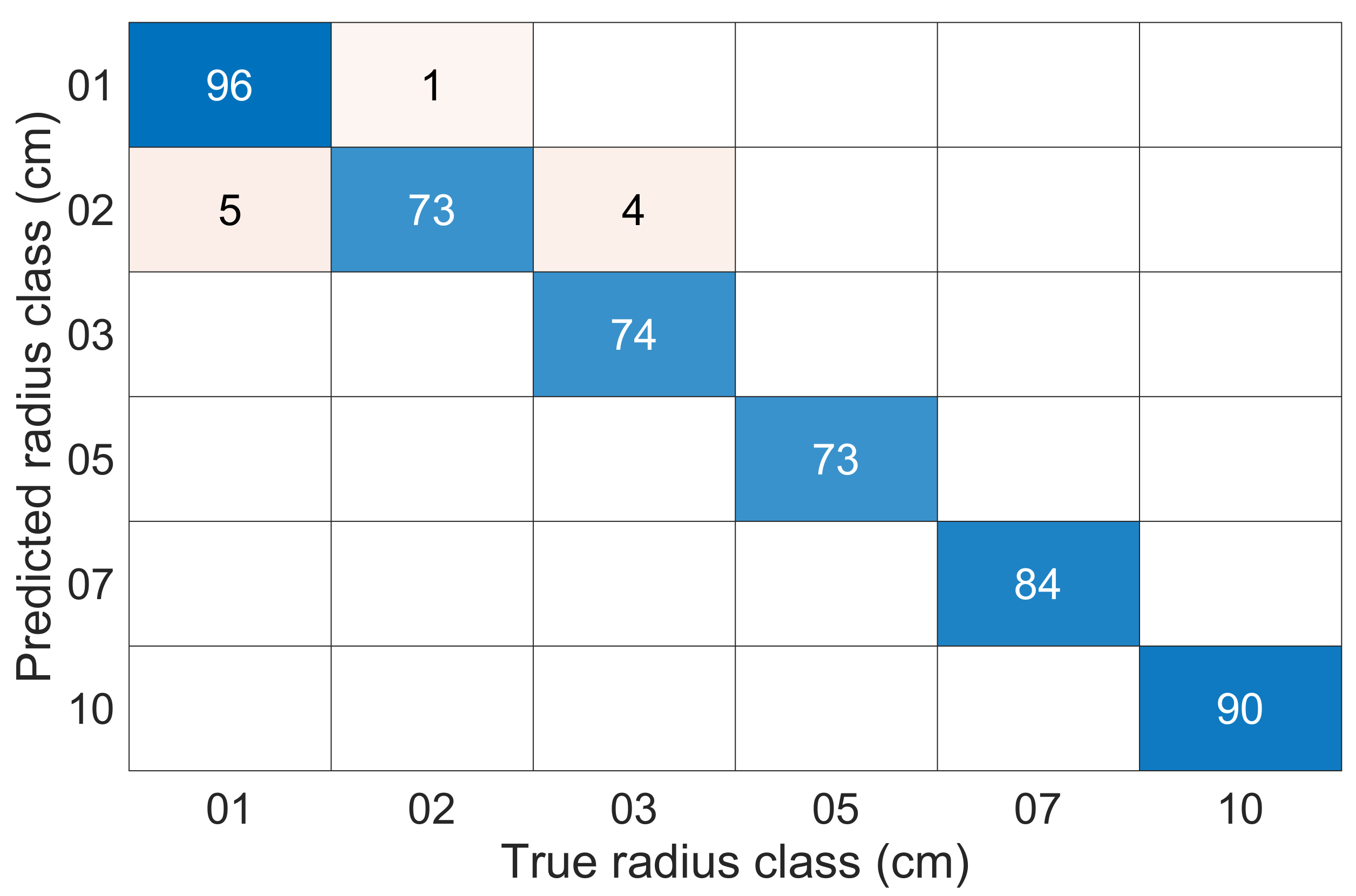
5.2. SVM
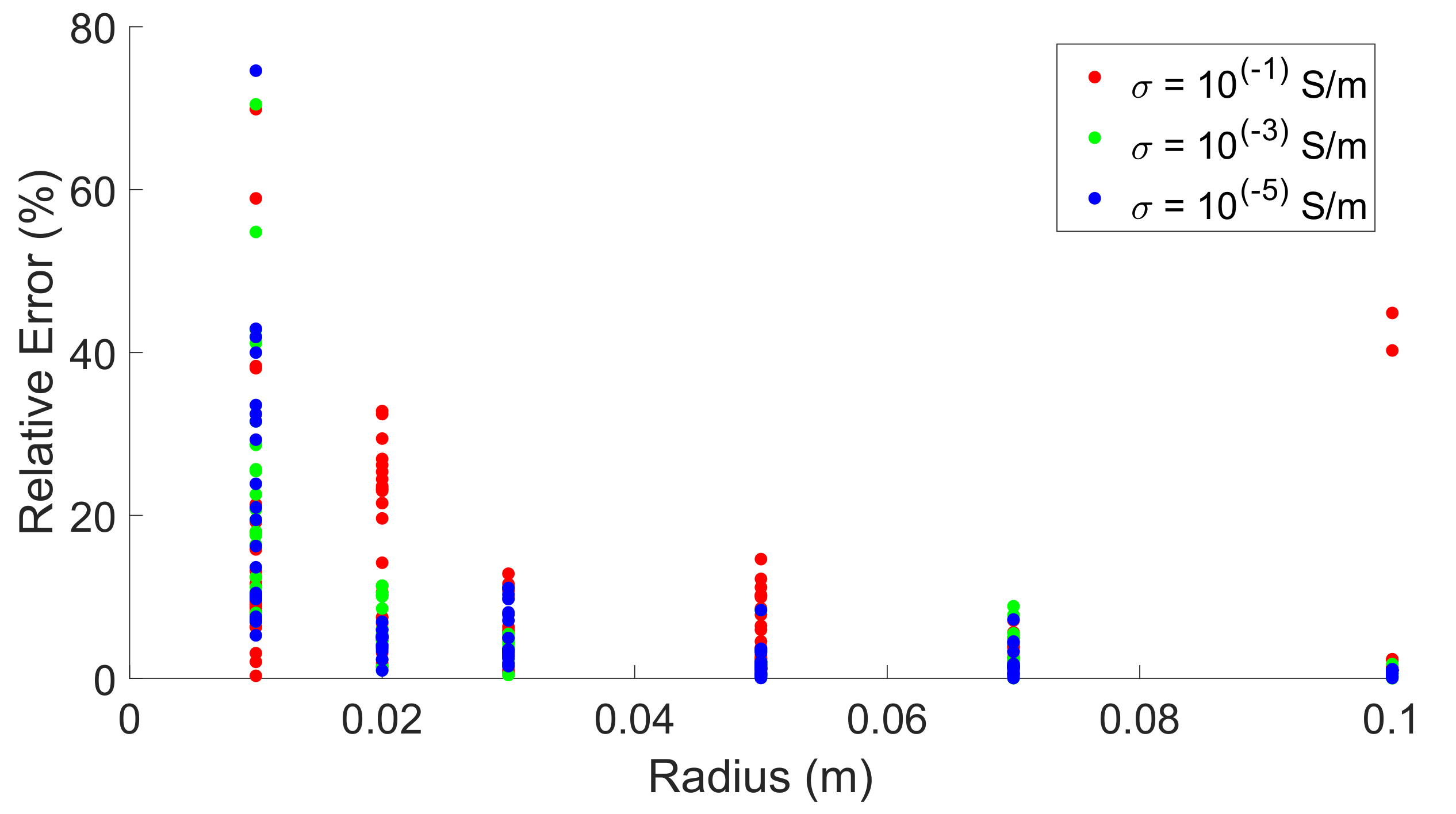
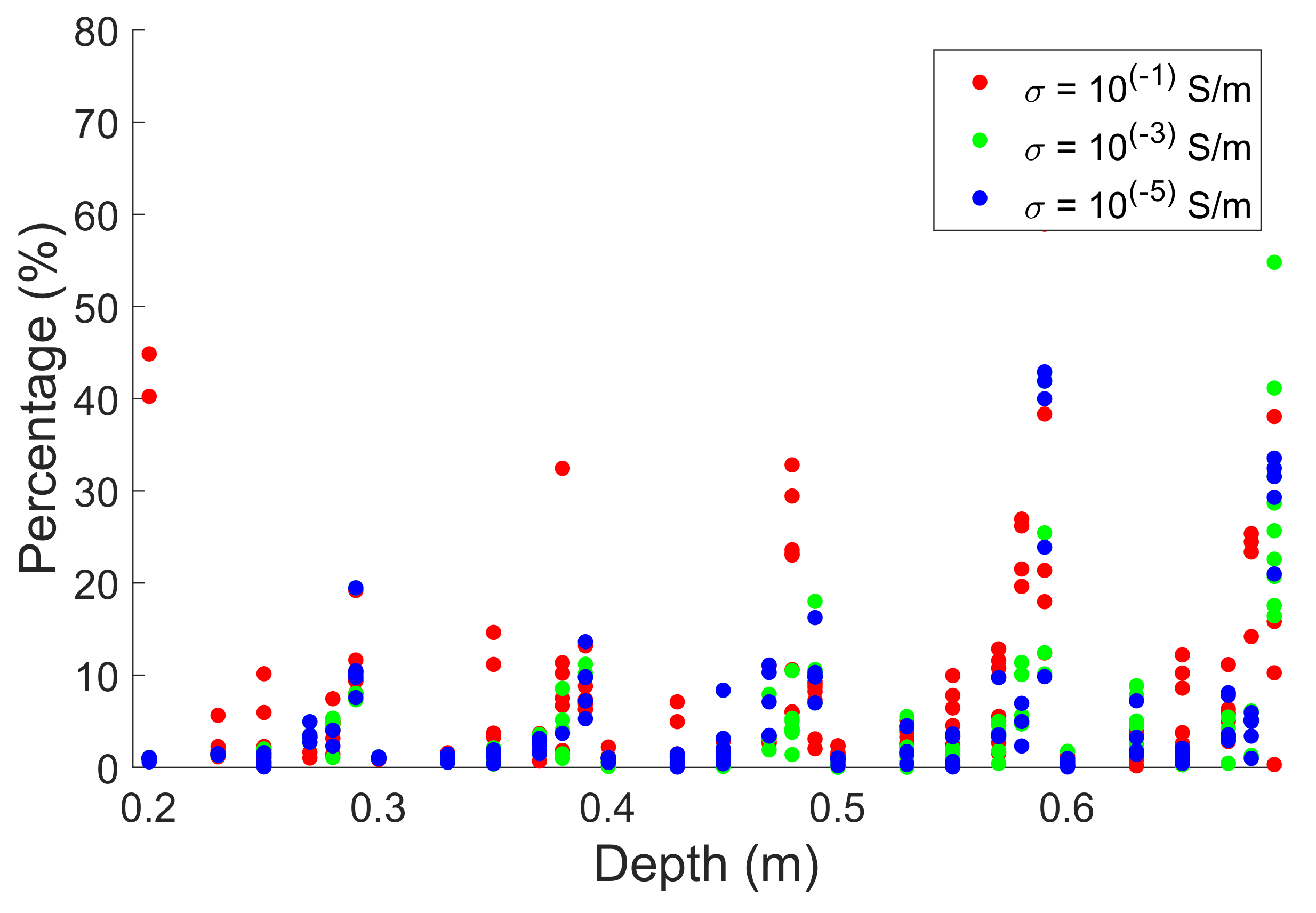
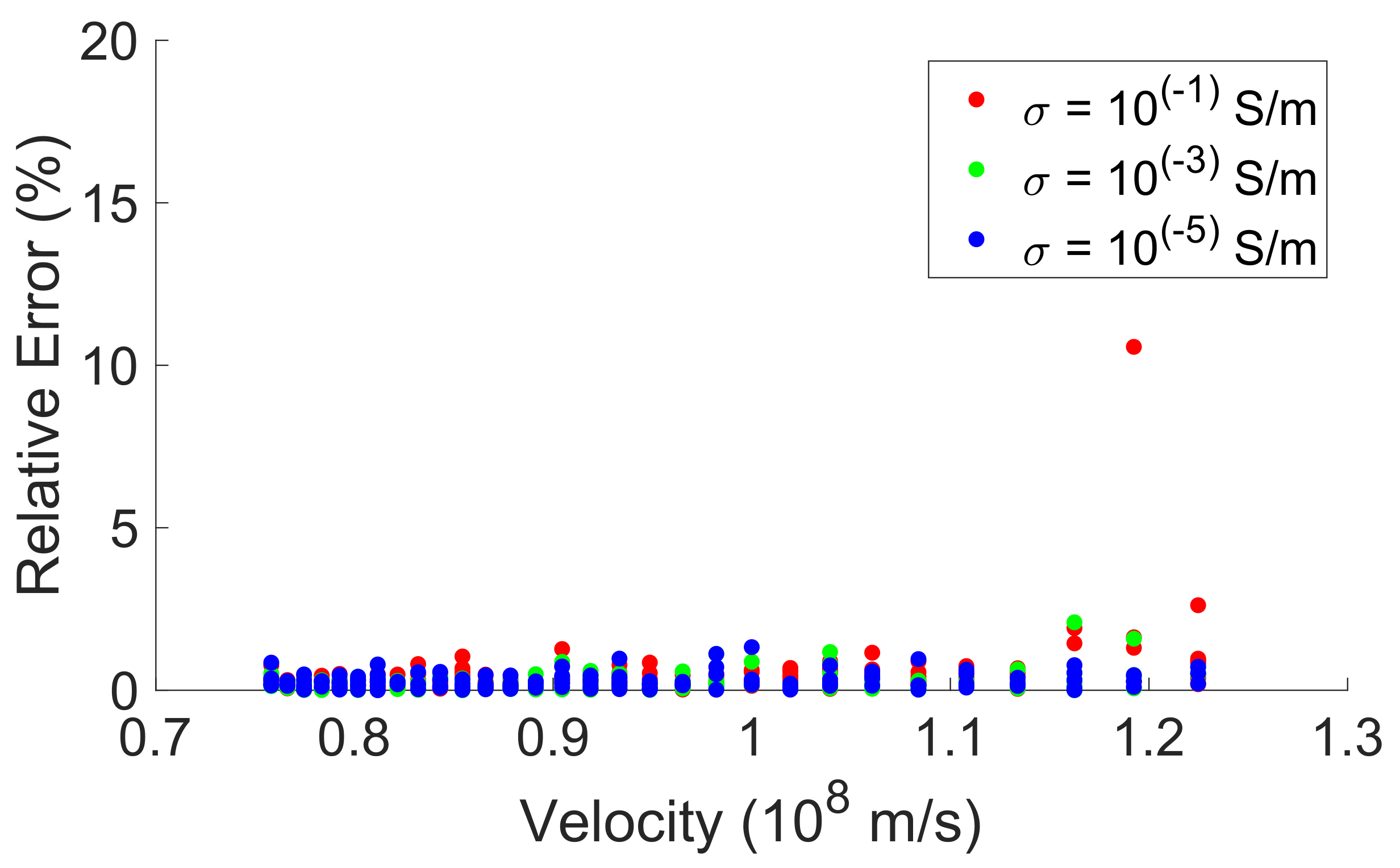
5.3. SVR
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lai, W.W.; Dérobert, X.; Annan, P. A review of Ground Penetrating Radar application in civil engineering: A 30-year journey from Locating and Testing to Imaging and Diagnosis. NDT & E Int. 2018, 96, 58–78. [Google Scholar] [CrossRef]
- Pajewski, L.; Benedetto, A.; Derobert, X.; Giannopoulos, A.; Loizos, A.; Manacorda, G.; Marciniak, M.; Plati, C.; Schettini, G.; Trinks, I. Applications of Ground Penetrating Radar in civil engineering—COST action TU1208. In Proceedings of the 2013 7th International Workshop on Advanced Ground Penetrating Radar, Nantes, France, 2–5 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1–6. [Google Scholar]
- Liu, T.; Klotzsche, A.; Pondkule, M.; Vereecken, H.; Su, Y.; van der Kruk, J. Radius estimation of subsurface cylindrical objects from ground-penetrating-radar data using full-waveform inversion. Geophysics 2018, 83, H43–H54. [Google Scholar] [CrossRef]
- Mechbal, Z.; Khamlichi, A. Sensitivity of the inverse problem solution related to detection of rebars buried in concrete by using GPR scanning. In MATEC Web of Conferences; EDP Sciences: Les Ulis, France, 2018; Volume 191, p. 00010. [Google Scholar] [CrossRef][Green Version]
- Windsor, C.; Capineri, L.; Falorni, P. The Estimation of Buried Pipe Diameters by Generalized Hough Transform of Radar Data. In Proceedings of the Proceedings Progress in Electromagnetics Research Symposium (PIERS), Hangzhou, China, 22–26 August 2005; Volume 1, pp. 345–349. [Google Scholar]
- Muniappan, N.; Rao, E.P.; Hebsur, A.V.; Venkatachalam, G. Radius estimation of buried cylindrical objects using GPR—A case study. In Proceedings of the 2012 14th International Conference on Ground Penetrating Radar (GPR), Shanghai, China, 4–8 June 2012; pp. 789–794. [Google Scholar] [CrossRef]
- Ihamouten, A.; Le Bastard, C.; Xavier, D.; Bosc, F.; Villain, G. Using machine learning algorithms to link volumetric water content to complex dielectric permittivity in a wide (33–2000 MHz) frequency band for hydraulic concretes. Near Surf. Geophys. 2016, 14, 527–536. [Google Scholar] [CrossRef]
- Le Bastard, C.; Baltazart, V.; Dérobert, X.; Wang, Y. Support Vector Regression method applied to thin pavement thickness estimation by GPR. In Proceedings of the 2012 14th International Conference on Ground Penetrating Radar (GPR), Shanghai, China, 4–8 June 2012; pp. 349–353. [Google Scholar] [CrossRef]
- Todkar, S.S.; Le Bastard, C.; Baltazart, V.; Ihamouten, A.; Dérobert, X. Performance assessment of SVM-based classification techniques for the detection of artificial debondings within pavement structures from stepped-frequency A-scan radar data. NDT & E Int. 2019, 107, 102128. [Google Scholar] [CrossRef]
- Terrasse, G.; Nicolas, J.; Trouvé, E.; Drouet, É. Application of the Curvelet Transform for Clutter and Noise Removal in GPR Data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 4280–4294. [Google Scholar] [CrossRef]
- Terrasse, G.; Nicolas, J.; Trouvé, E.; Drouet, E. Sparse decomposition of the GPR useful signal from hyperbola dictionary. In Proceedings of the 2016 24th European Signal Processing Conference (EUSIPCO), Budapest, Hungary, 29 August–2 September 2016; pp. 2400–2404. [Google Scholar] [CrossRef]
- Kaur, P.; Dana, K.J.; Romero, F.A.; Gucunski, N. Automated GPR Rebar Analysis for Robotic Bridge Deck Evaluation. IEEE Trans. Cybern. 2016, 46, 2265–2276. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Zheng, Z. Fast Extraction of Hyperbolic Signatures in GPR. In Proceedings of the 2007 International Conference on Microwave and Millimeter Wave Technology, Guilin, China, 19–21 April 2007; pp. 1–3. [Google Scholar] [CrossRef]
- Dolgiy, A.; Dolgiy, A.; Zolotarev, V. GPR Estimation for Diameter of Buried Pipes. In Near Surface 2005, Proceedings of the 11th European Meeting of Environmental and Engineering Geophysics, Palermo, Italy, 4–7 September 2005; European Association of Geoscientists & Engineers: Houten, The Netherlands, 2005; Volume cp-13-00175. [Google Scholar] [CrossRef]
- Ristic, A.V.; Petrovacki, D.; Govedarica, M. A new method to simultaneously estimate the radius of a cylindrical object and the wave propagation velocity from GPR data. Comput. Geosci. 2009, 35, 1620–1630. [Google Scholar] [CrossRef]
- Borgioli, G.; Capineri, L.; Falorni, P.; Matucci, S.; Windsor, C.G. The Detection of Buried Pipes from Time-of-Flight Radar Data. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2254–2266. [Google Scholar] [CrossRef]
- Warren, C.; Giannopoulos, A.; Giannakis, I. gprMax: Open source software to simulate electromagnetic wave propagation for Ground Penetrating Radar. Comput. Phys. Commun. 2016, 209, 163–170. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]


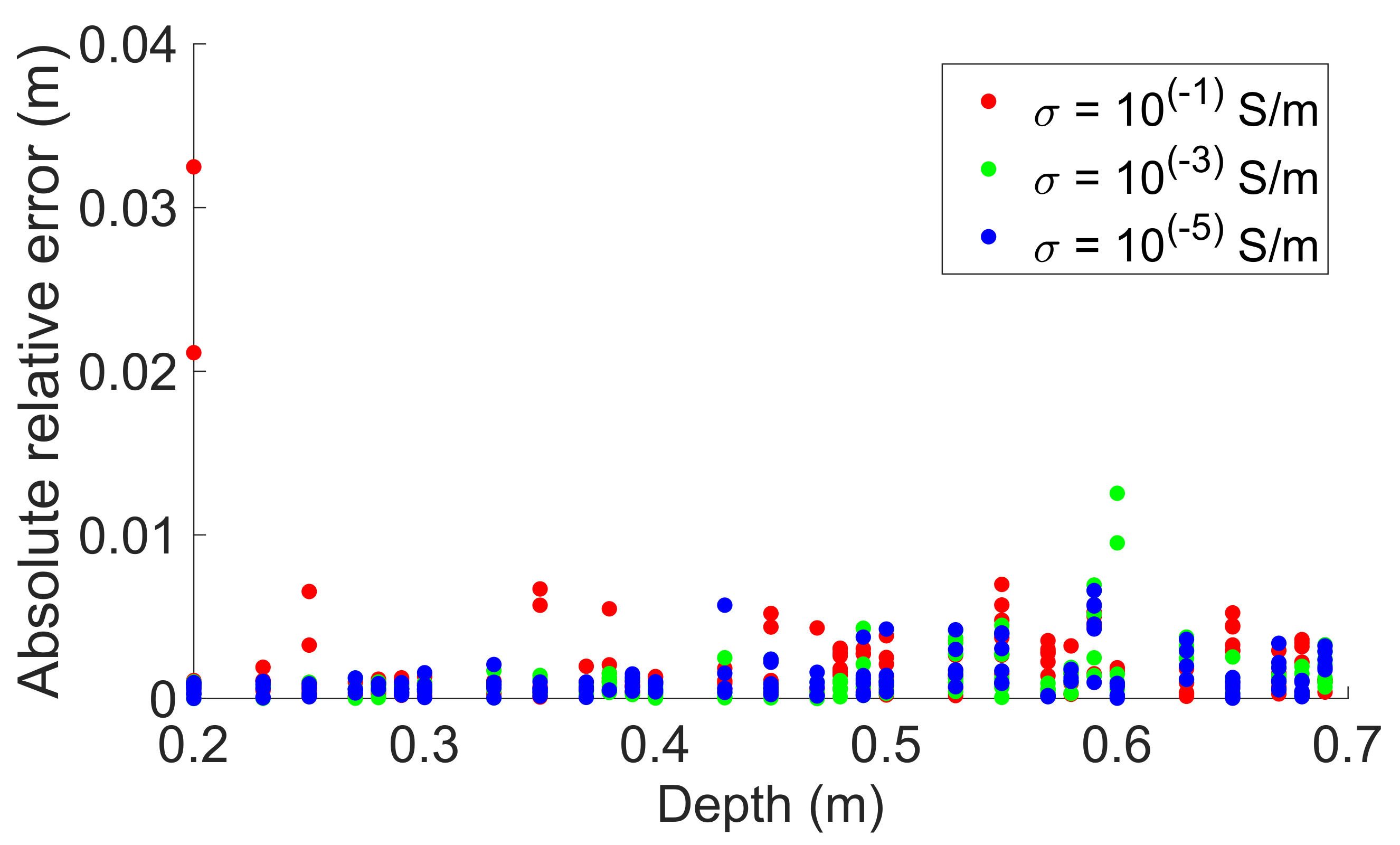

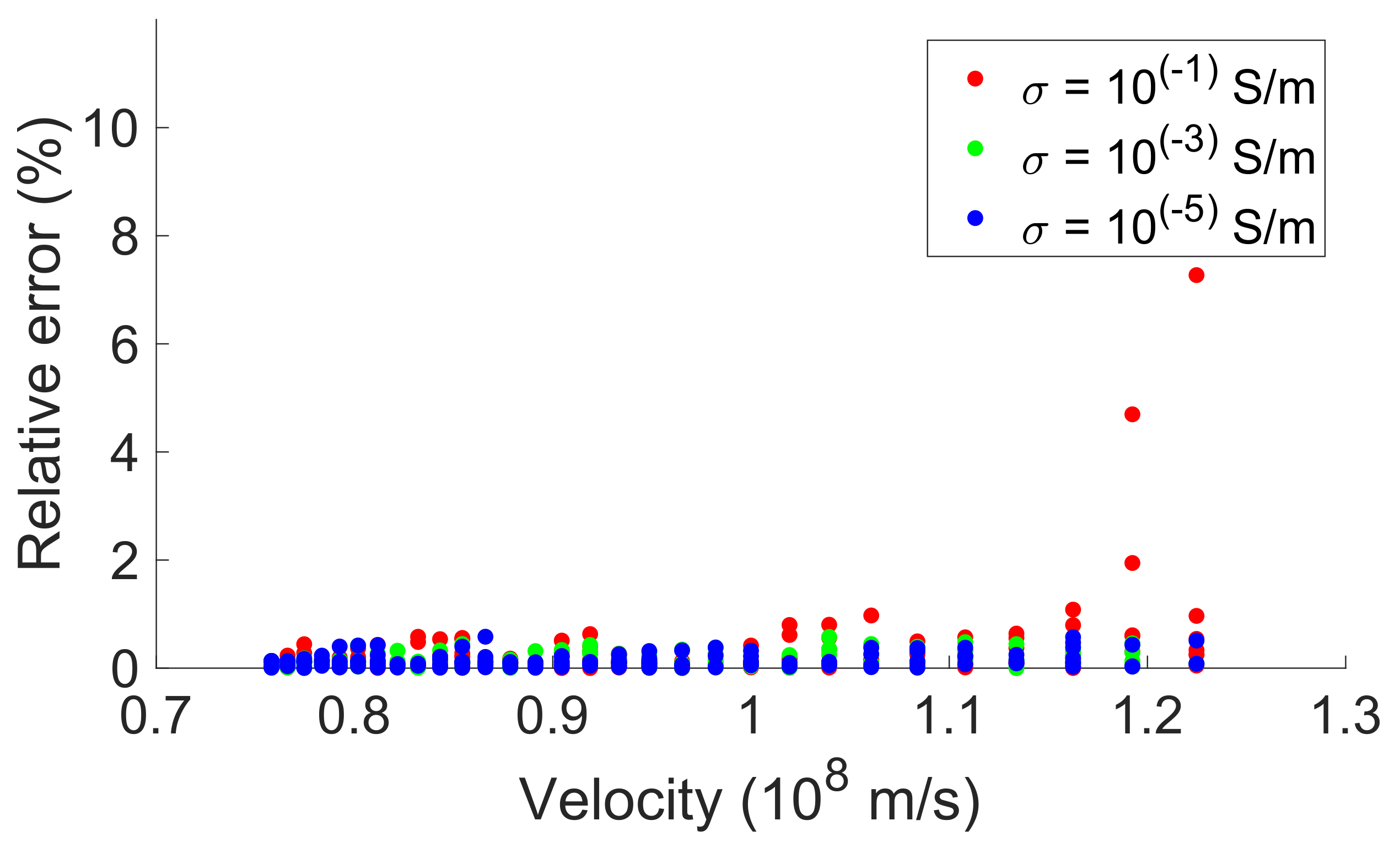
| Method | % | % | % | |||
|---|---|---|---|---|---|---|
| Mean | Mean | Mean | ||||
| Ray-based concurrent | 260% | 464% | 25.1% | 65% | 11.3% | 22% |
| Ray-based fixed velocity | 120% | 353% | - | - | - | - |
| Regression (SVR) | 6.3% | 26.5% | 0.39% | 1% | 0.22% | 0.5% |
| Classification (SVM) | 2% (10/500) | 0% (0/500) | 1% (5/500) | |||
| Conductivity () | % | % | % | |||
|---|---|---|---|---|---|---|
| Mean | Mean | Mean | ||||
| 1 × 10−5 S m−1 | 5.3% | 26.04% | 0.25% | 0.74% | 0.12% | 0.39% |
| 1 × 10−3 S m−1 | 5.9% | 25.5% | 0.26% | 0.75% | 0.14% | 0.42% |
| 1 × 10−1 S m−1 | 7.7% | 28.4% | 0.52% | 1.1% | 0.32% | 0.79% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jaufer, R.M.; Ihamouten, A.; Goyat, Y.; Todkar, S.S.; Guilbert, D.; Assaf, A.; Dérobert, X. A Preliminary Numerical Study to Compare the Physical Method and Machine Learning Methods Applied to GPR Data for Underground Utility Network Characterization. Remote Sens. 2022, 14, 1047. https://doi.org/10.3390/rs14041047
Jaufer RM, Ihamouten A, Goyat Y, Todkar SS, Guilbert D, Assaf A, Dérobert X. A Preliminary Numerical Study to Compare the Physical Method and Machine Learning Methods Applied to GPR Data for Underground Utility Network Characterization. Remote Sensing. 2022; 14(4):1047. https://doi.org/10.3390/rs14041047
Chicago/Turabian StyleJaufer, Rakeeb Mohamed, Amine Ihamouten, Yann Goyat, Shreedhar Savant Todkar, David Guilbert, Ali Assaf, and Xavier Dérobert. 2022. "A Preliminary Numerical Study to Compare the Physical Method and Machine Learning Methods Applied to GPR Data for Underground Utility Network Characterization" Remote Sensing 14, no. 4: 1047. https://doi.org/10.3390/rs14041047
APA StyleJaufer, R. M., Ihamouten, A., Goyat, Y., Todkar, S. S., Guilbert, D., Assaf, A., & Dérobert, X. (2022). A Preliminary Numerical Study to Compare the Physical Method and Machine Learning Methods Applied to GPR Data for Underground Utility Network Characterization. Remote Sensing, 14(4), 1047. https://doi.org/10.3390/rs14041047