Exploiting the Combined GRACE/GRACE-FO Solutions to Determine Gravimetric Excitations of Polar Motion
Abstract
1. Introduction
2. Data and Methodology
2.1. Reference Geodetic Residual Time Series
2.2. Gravimetric Excitation Series from GRACE and GRACE-FO Solutions
- CSR RL06 (for both GRACE and GRACE-FO period)—provided by the Center for Space Research, Austin, USA, abbreviated here as CSR;
- JPL RL06 (for both GRACE and GRACE-FO period)—provided by the Jet Propulsion Laboratory, Pasadena, USA, abbreviated here as JPL;
- GFZ RL06 (for both GRACE and GRACE-FO period)—provided by GeoForschungsZentrum, Potsdam, Germany, abbreviated here as GFZ;
- ITSG-Grace2018 (for GRACE period) and ITSG-Grace_op (for the GRACE-FO period)—provided by the Institute of Geodesy at Graz University of Technology, Graz, Austria, abbreviated here as ITSG;
- CNES/GRGS RL05 (for both GRACE and GRACE-FO period)—provided by the Centre National d’Etudes Spatiales/Groupe de Recherche de Géodésie Spatiale, Toulouse, France, abbreviated here as CNES;
- AIUB RL02 (for GRACE period) and AIUB-GRACE-FO_op (for the GRACE-FO period)—provided by the Astronomical Institute University Bern, Bern, Switzerland, abbreviated here as AIUB;
- LUH-Grace2018 (for GRACE period) and LUH-GRACE-FO-2020 (for the GRACE-FO period)—provided by Leibniz Universität Hannover, Hannover, Germany, abbreviated here as LUH.
2.3. The Generalized TCH Method
2.4. A Combined GRACE/GRACE-FO-Based Excitation Time Series
- COMB1: a combination of data from CNES, COST-G, ITSG, JPL, and CSR;
- COMB2: a combination of data from CNES, ITSG, JPL, and CSR;
- COMB3: a combination of data from CNES, ITSG, JPL, CSR, and GFZ;
- COMB4: a combination of data from CNES, JPL, CSR, LUH, AIUB.
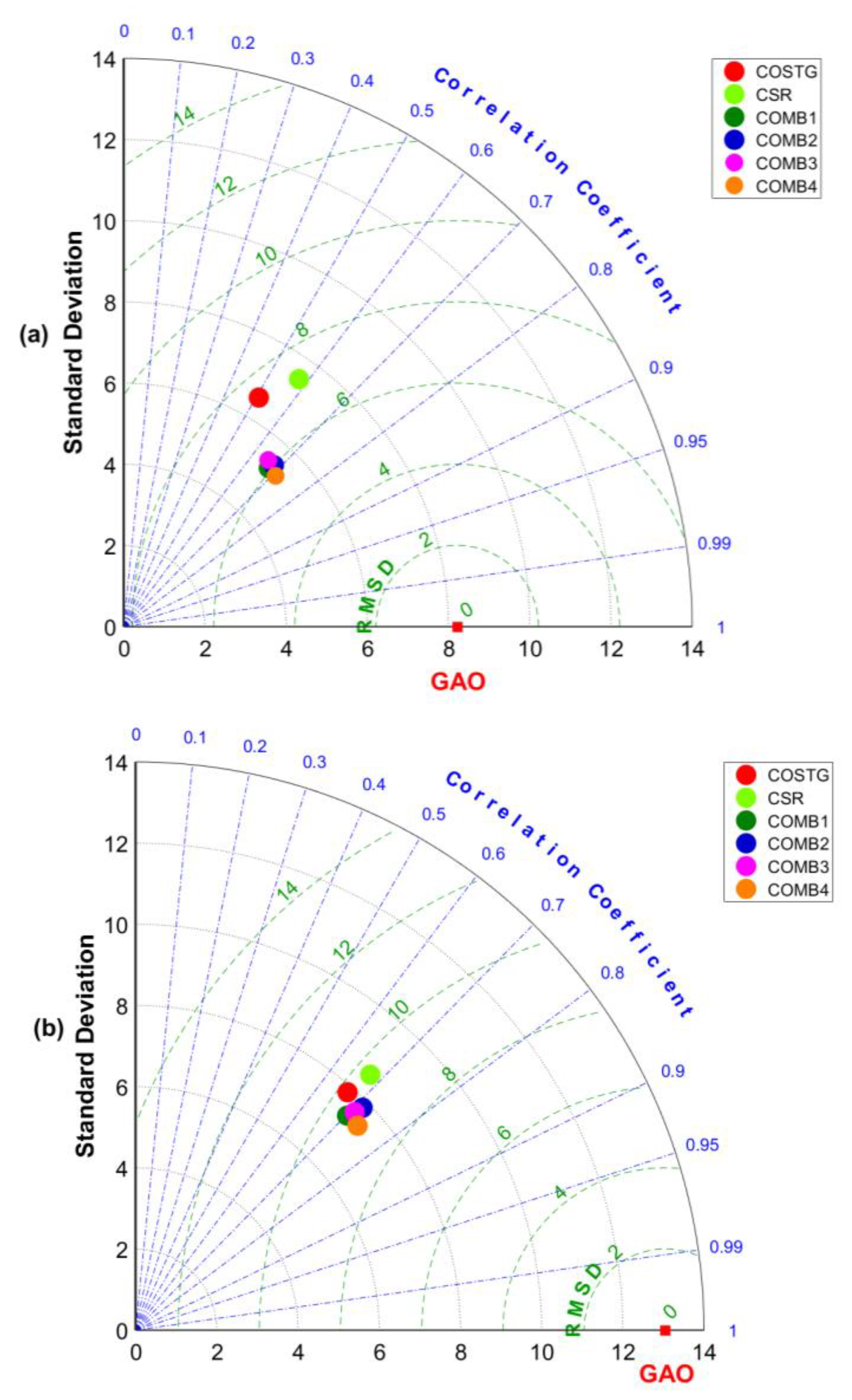
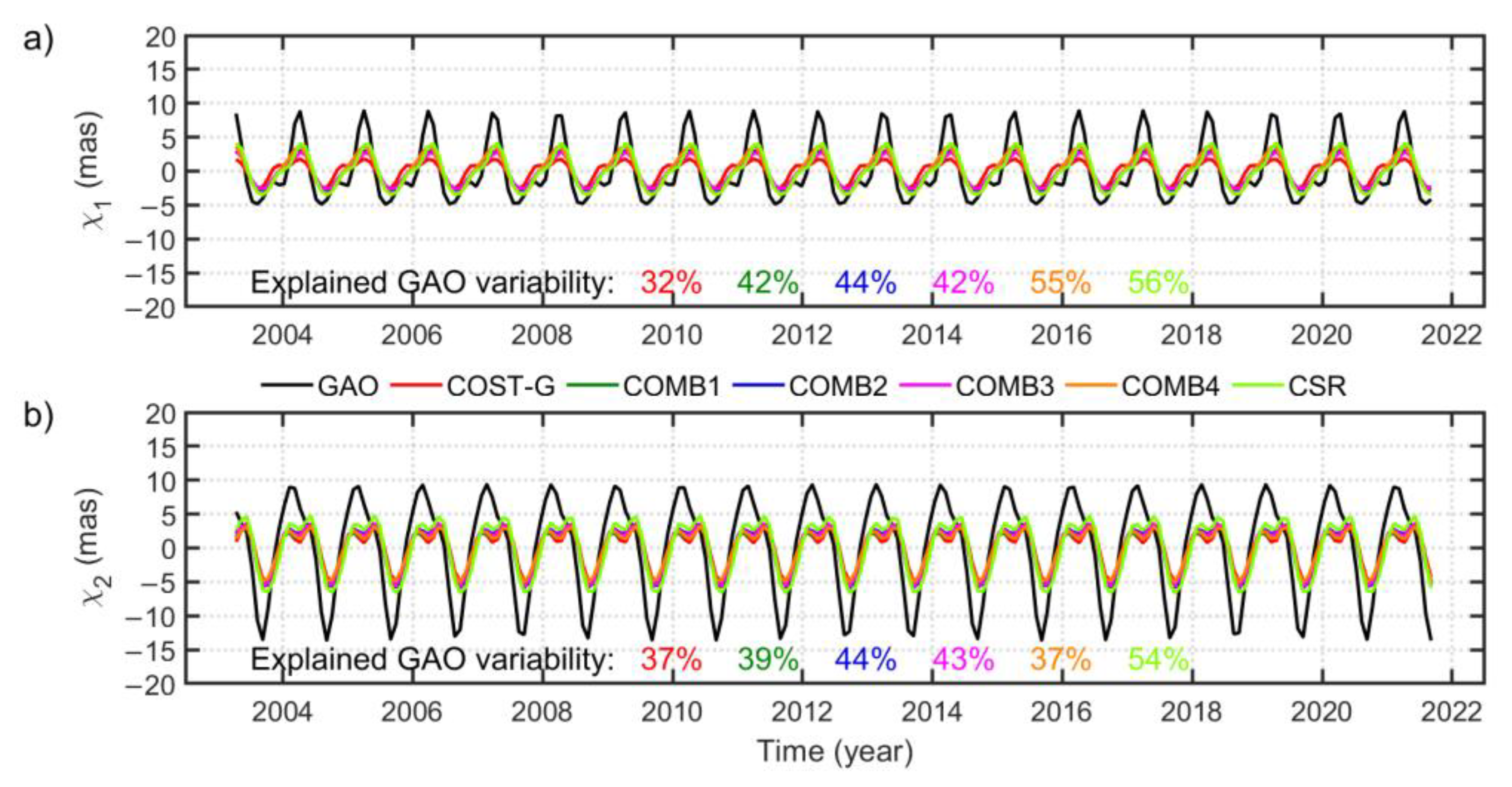
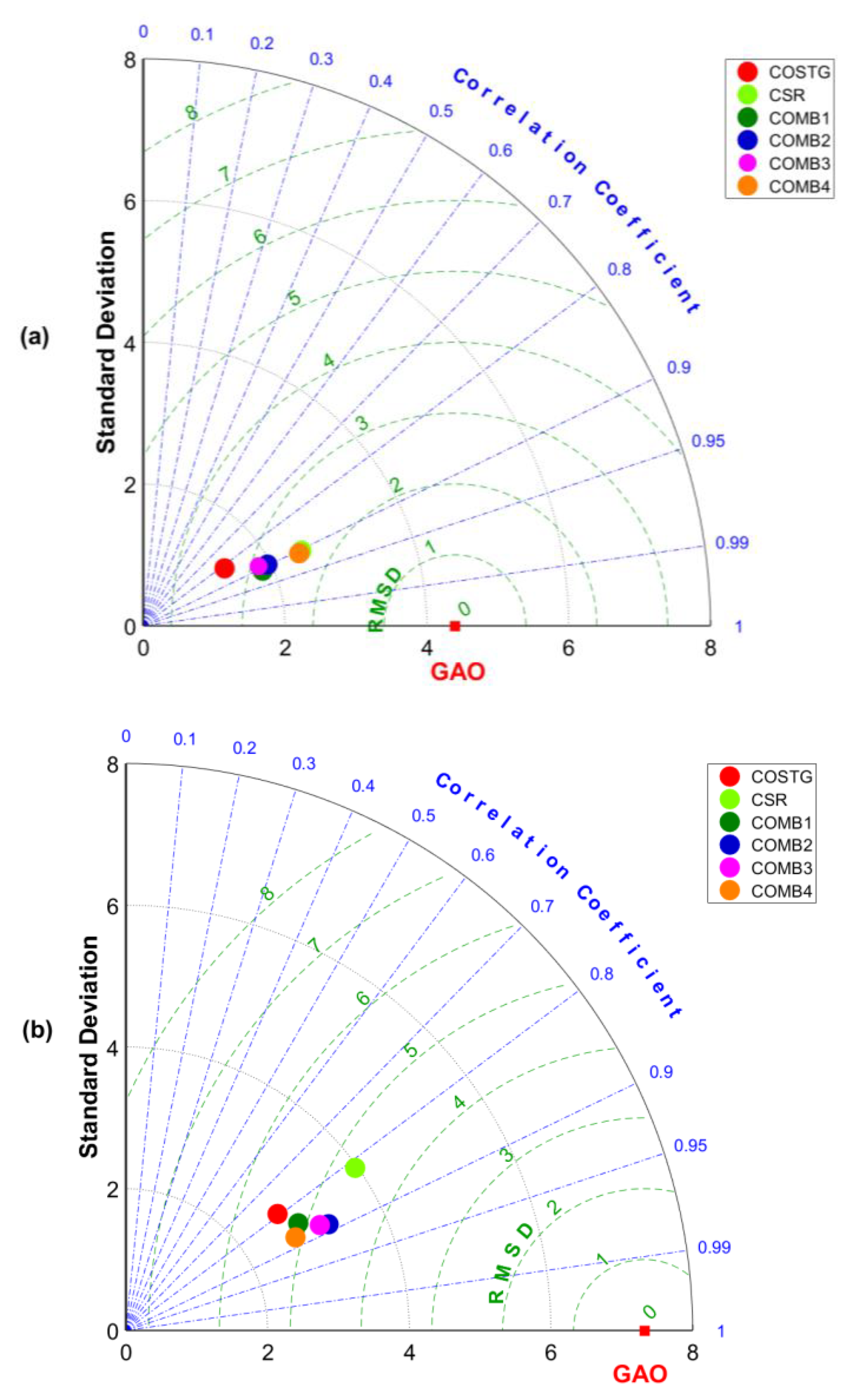
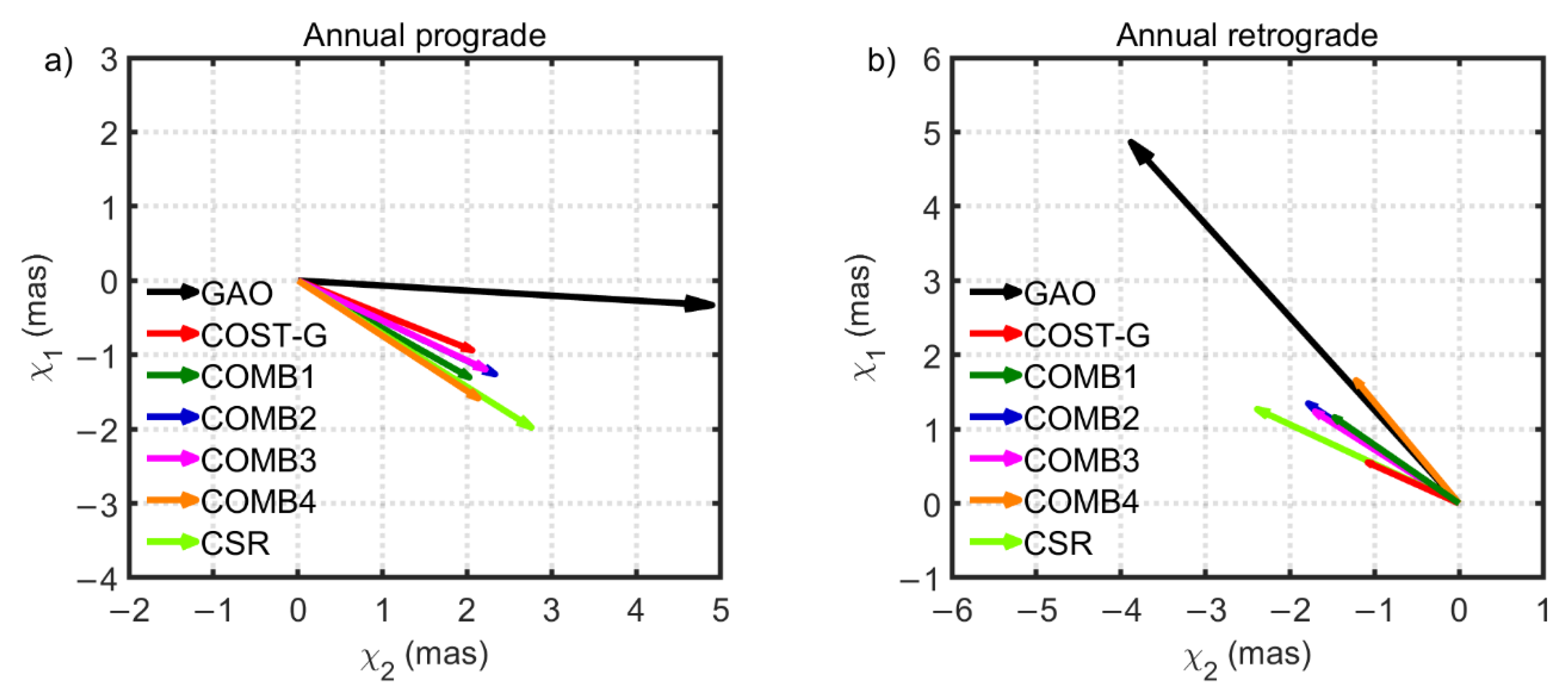
3. Results
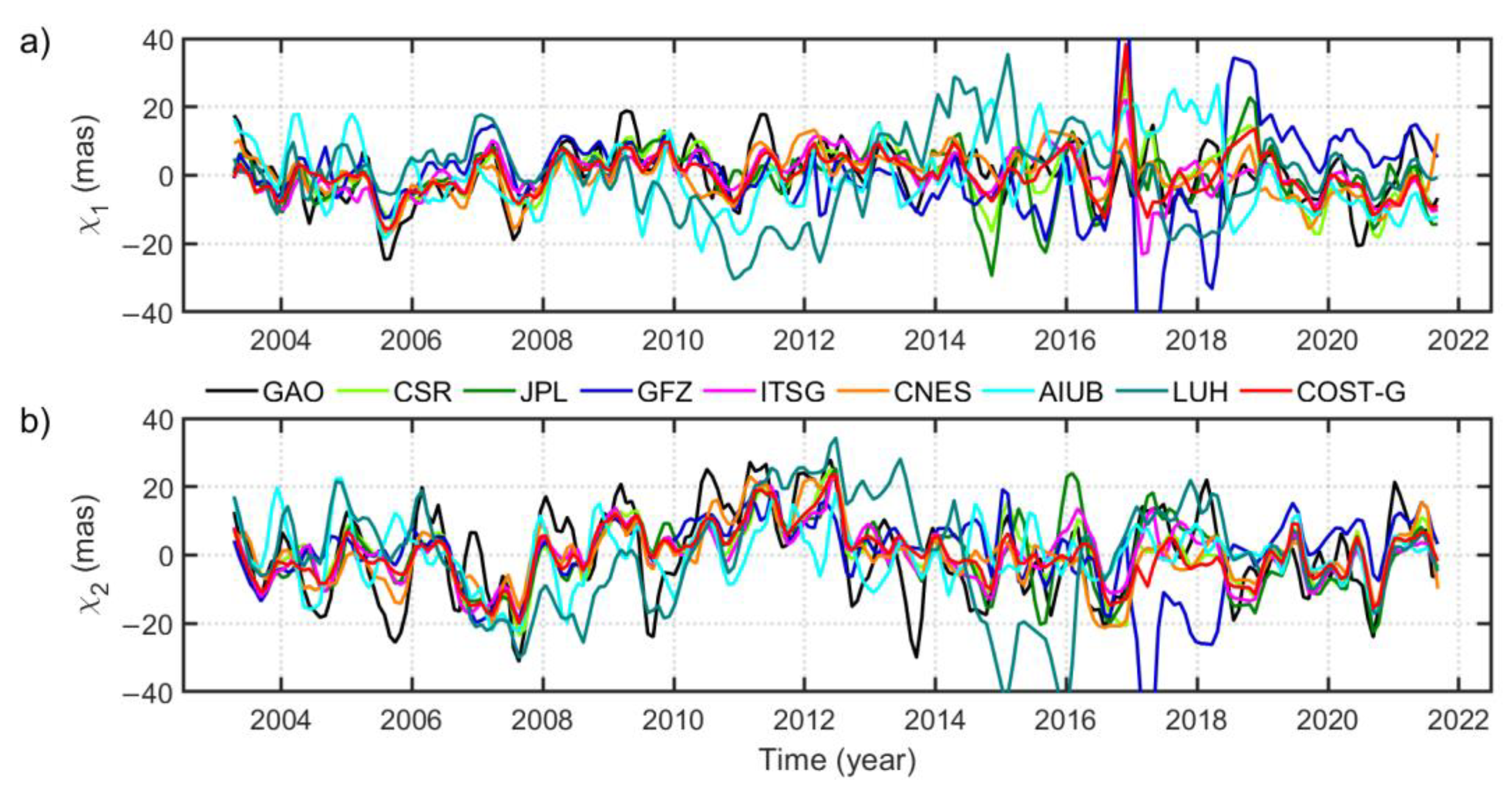
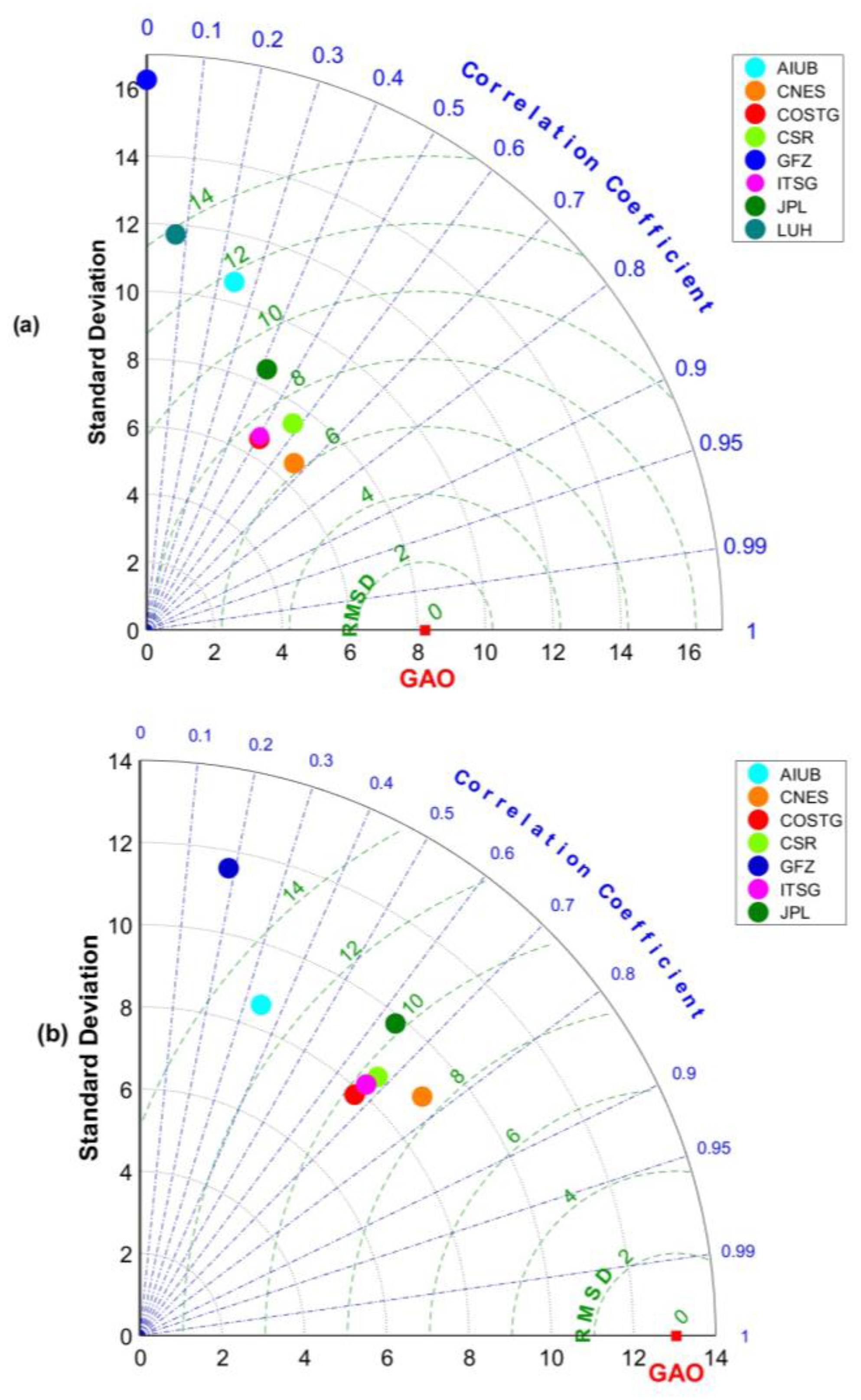
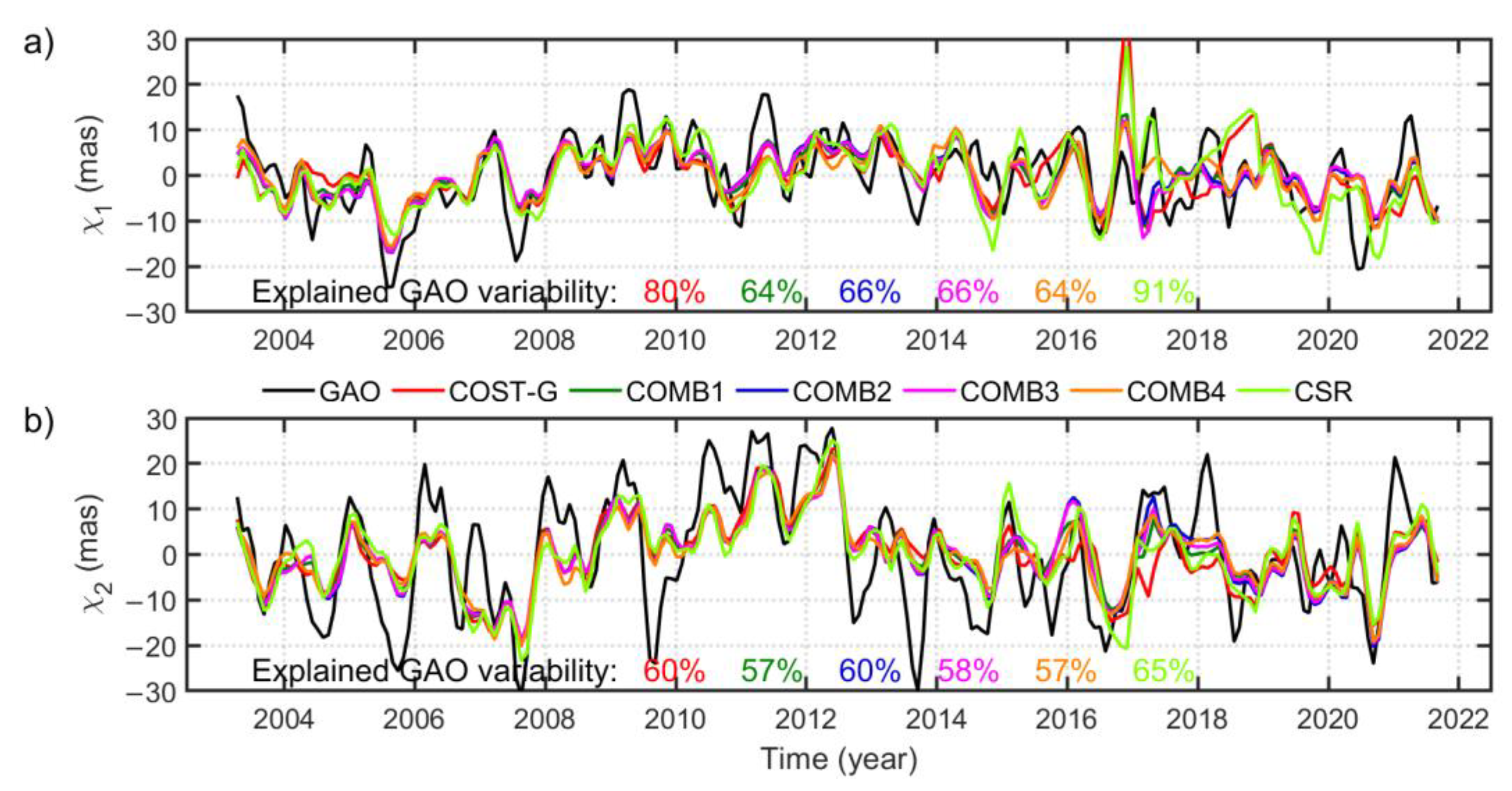
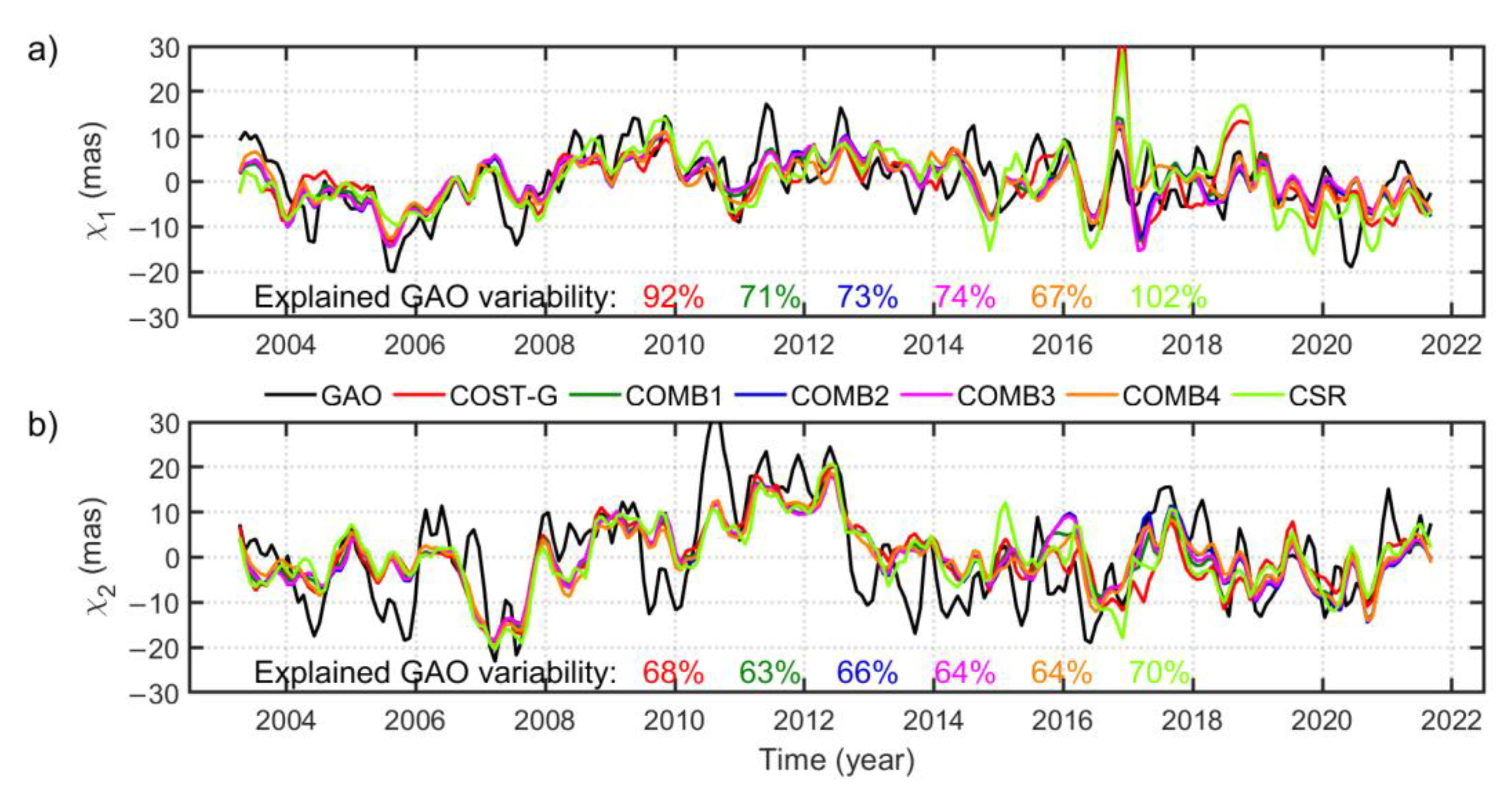
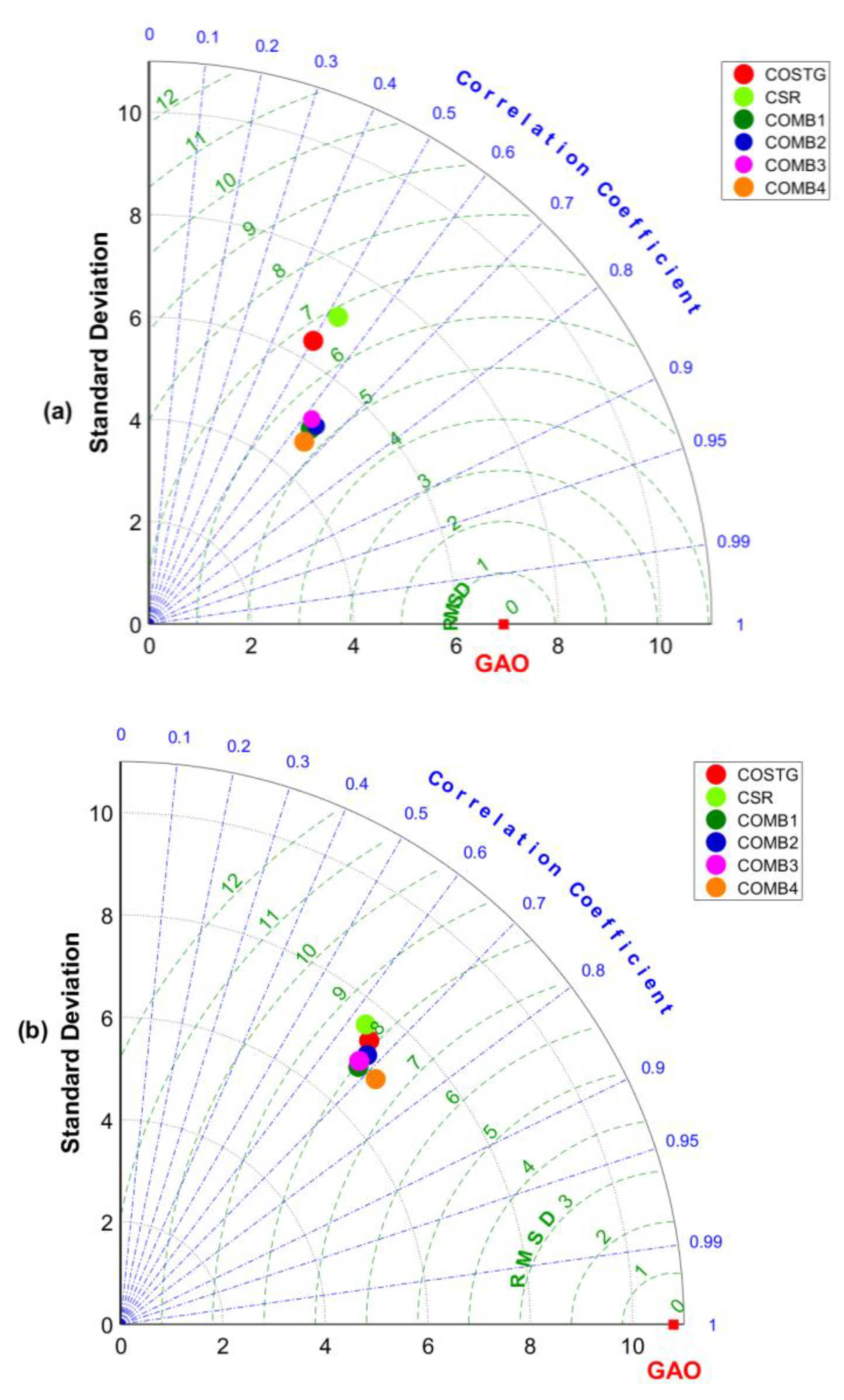
3.1. Overall Time Series
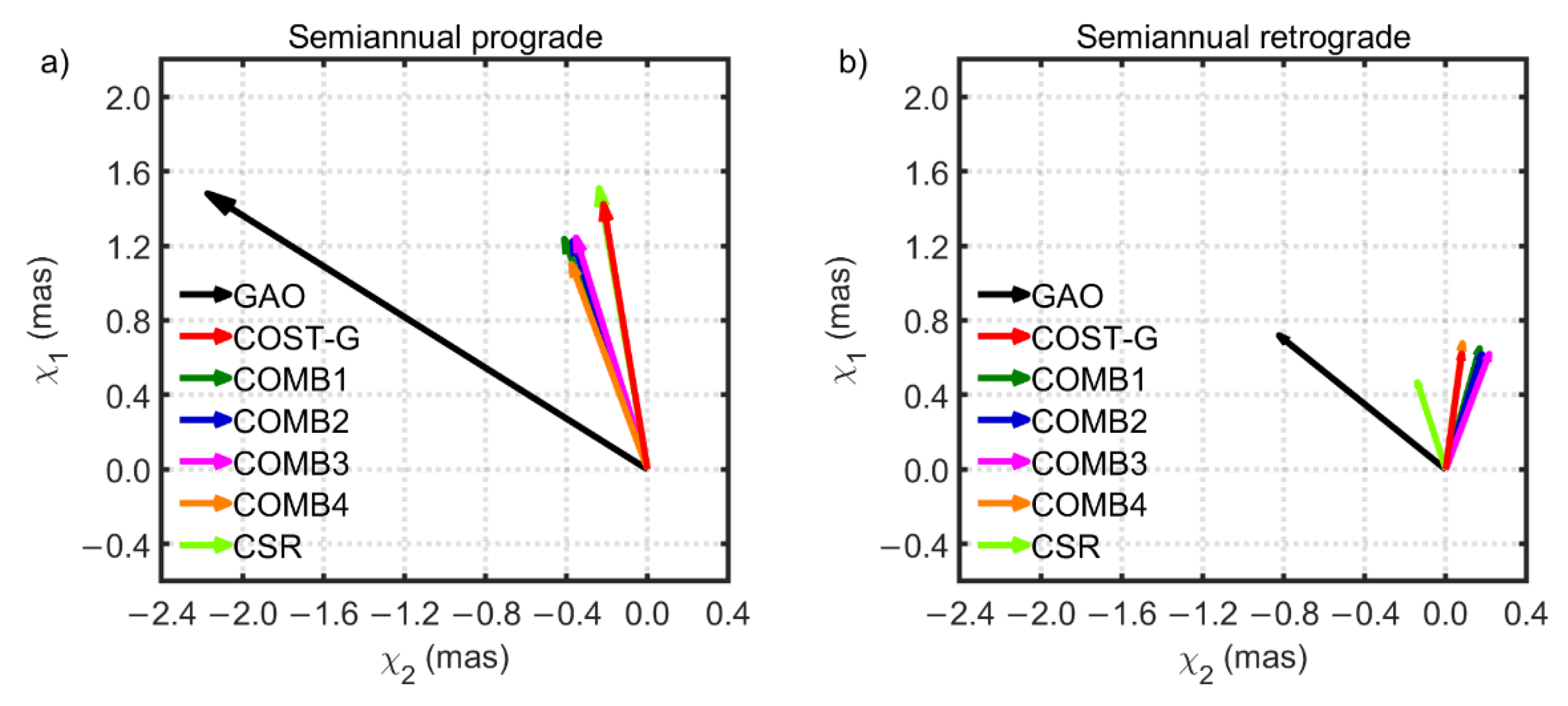
3.2. Seasonal Variations
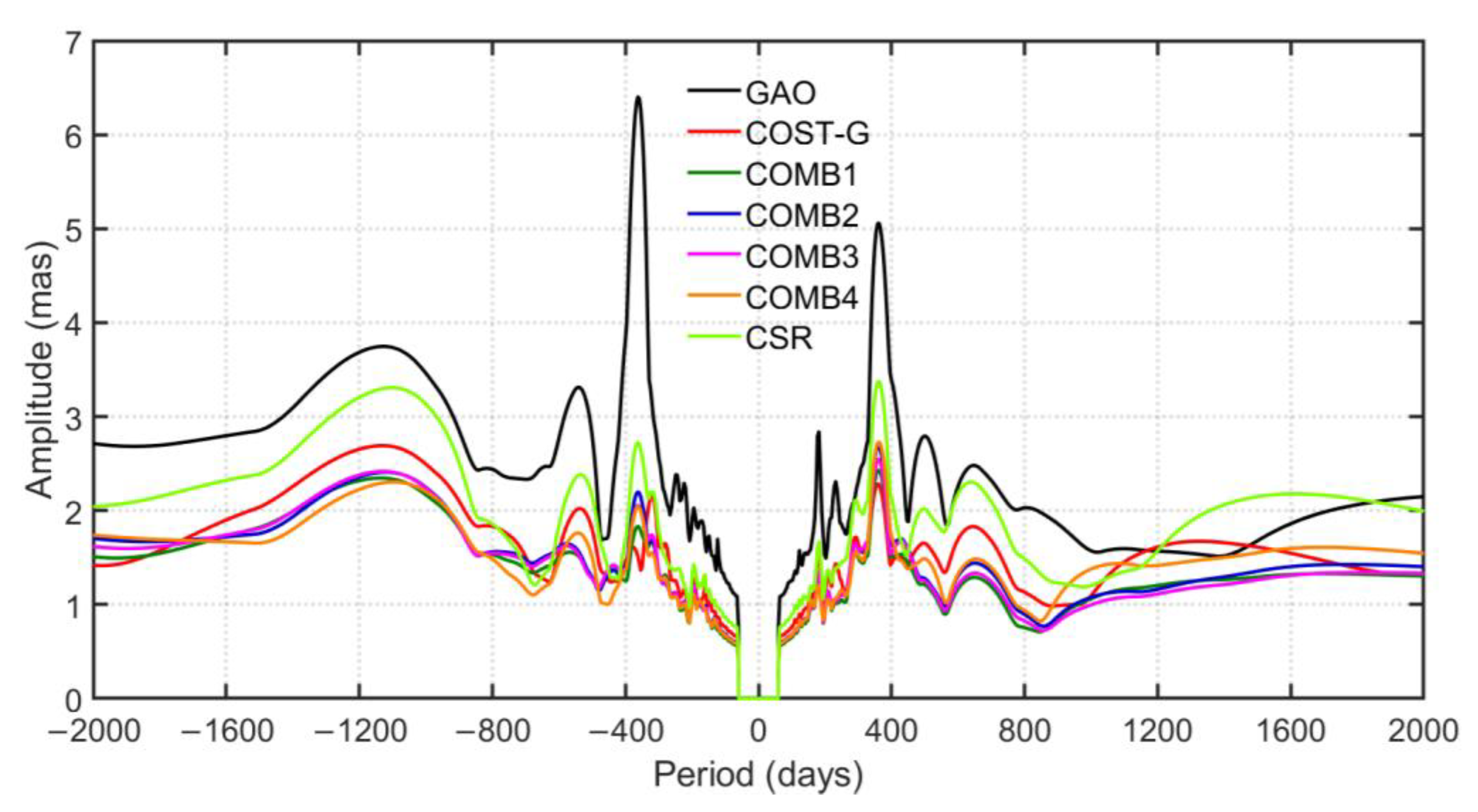
3.3. Nonseasonal Variations
4. Discussion and Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barnes, R.T.H.; Hide, R.; White, A.; Wilson, C.A. Atmospheric angular momentum fluctuations, length-of-day changes and polar motion. Proc. R. Soc. A 1983, 387, 31–73. [Google Scholar] [CrossRef]
- Lambeck, K. The Earth’s Variable Rotation: Geophysical Causes and Consequences (Cambridge Monographs on Mechanics); Cambridge University Press: Cambridge, UK, 1980. [Google Scholar] [CrossRef]
- Adhikari, S.; Ivins, E.R. Climate-driven polar motion: 2003–2015. Sci. Adv. 2016, 2, e1501693. [Google Scholar] [CrossRef] [PubMed]
- Brzeziński, A.; Ponte, R.M.; Ali, A.H. Non-tidal oceanic excitation of nutation and diurnal/semi-diurnal polar motion revisited. J. Geophys. Res. Solid Earth 2004, 109, 1–14. [Google Scholar] [CrossRef]
- Brzeziński, A.; Nastula, J.; Kołaczek, B. Seasonal excitation of polar motion estimated from recent geophysical models and observations. J. Geodyn. 2009, 48, 235–240. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R.; Grötzsch, A.; Brzeziński, A.; Thomas, M. Seasonal polar motion excitation from numerical models of atmosphere, ocean, and continental hydrosphere. J. Geophys. Res. Solid Earth 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Göttl, F.; Schmidt, M.; Seitz, F. Mass-related excitation of polar motion: An assessment of the new RL06 GRACE gravity field models. Earth Planets Space 2018, 70, 195. [Google Scholar] [CrossRef]
- Gross, R.S.; Fukumori, I.; Menemenlis, D. Atmospheric and oceanic excitation of the Earth’s wobbles during 1980–2000. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Gross, R.S.; Fukumori, I.; Menemenlis, D.; Gegout, P. Atmospheric and oceanic excitation of length-of-day variations during 1980–2000. J. Geophys. Res. Solid Earth 2004, 109, B01406. [Google Scholar] [CrossRef]
- Jin, S.; Chambers, D.P.; Tapley, B.D. Hydrological and oceanic effects on polar motion from GRACE and models. J. Geophys. Res. Solid Earth 2010, 115, 1–11. [Google Scholar] [CrossRef]
- Nastula, J.; Wińska, M.; Śliwińska, J.; Salstein, D. Hydrological signals in polar motion excitation—Evidence after fifteen years of the GRACE mission. J. Geodyn. 2019, 124, 119–132. [Google Scholar] [CrossRef]
- Seoane, L.; Biancale, R.; Gambis, D. Agreement between Earth’s rotation and mass displacement as detected by GRACE. J. Geodyn. 2012, 62, 49–55. [Google Scholar] [CrossRef]
- Kornfeld, R.P.; Arnold, B.W.; Gross, M.A.; Dahya, N.T.; Klipstein, W.M. GRACE-FO: The Gravity Recovery and Climate Experiment Follow-On Mission. J. Spacecr. Rocket. 2019, 56, 931–951. [Google Scholar] [CrossRef]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31, L09607. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R. Low degree gravity changes from GRACE, earth rotation, geophysical models and satellite laser ranging. J. Geophys. Res. Solid Earth 2008, 113, 1–9. [Google Scholar] [CrossRef]
- Cheng, M.; Ries, J.C.; Tapley, B.D. Variations of the Earth’s figure axis from Satellite Laser Ranging and GRACE. J. Geophys. Res. Solid Earth 2011, 116, 1–14. [Google Scholar] [CrossRef]
- Nastula, J.; Pasnicka, M.; Kolaczek, B. Comparison of the geophysical excitations of polar motion from the period 1980.0–2007.0. Acta Geophys. 2011, 59, 561–577. [Google Scholar] [CrossRef]
- Nastula, J.; Śliwińska, J. Prograde and retrograde terms of gravimetric polar motion excitation estimates from the GRACE monthly gravity field models. Remote Sens. 2020, 12, 138. [Google Scholar] [CrossRef]
- Seoane, L.; Nastula, J.; Bizouard, C.; Gambis, D. The use of gravimetric data from GRACE mission in the understanding of polar motion variations. Geophys. J. Int. 2009, 178, 614–622. [Google Scholar] [CrossRef]
- Śliwińska, J.; Nastula, J.; Dobslaw, H.; Dill, R. Evaluating gravimetric polar motion excitation estimates from the RL06 GRACE monthly-mean gravity field models. Remote Sens. 2020, 12, 930. [Google Scholar] [CrossRef]
- Meyrath, T.; van Dam, T. A comparison of interannual hydrological polar motion excitation from GRACE and geodetic observations. J. Geodyn. 2016, 99, 1–9. [Google Scholar] [CrossRef]
- Śliwińska, J.; Wińska, M.; Nastula, J. Preliminary estimation and validation of polar motion excitation from different types of the grace and grace follow-on missions data. Remote Sens. 2020, 12, 3490. [Google Scholar] [CrossRef]
- Śliwińska, J.; Nastula, J.; Wińska, M. Evaluation of hydrological and cryospheric angular momentum estimates based on GRACE, GRACE-FO and SLR data for their contributions to polar motion excitation. Earth Planets Space 2021, 73, 71. [Google Scholar] [CrossRef]
- Śliwińska, J.; Wińska, M.; Nastula, J. Validation of GRACE and GRACE-FO Mascon Data for the Study of Polar Motion Excitation. Remote Sens. 2021, 13, 1152. [Google Scholar] [CrossRef]
- Nastula, J.; Ponte, R.M.; Salstein, D.A. Comparison of polar motion excitation series derived from GRACE and from analyses of geophysical fluids. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Seoane, L.; Nastula, J.; Bizouard, C.; Gambis, D. Hydrological excitation of polar motion derived from GRACE gravity field solutions. Int. J. Geophys. 2011, 2011, 174396. [Google Scholar] [CrossRef]
- Śliwińska, J.; Wińska, M.; Nastula, J. Terrestrial water storage variations and their effect on polar motion. Acta Geophys. 2019, 67, 17–39. [Google Scholar] [CrossRef]
- Wińska, M.; Nastula, J.; Kołaczek, B. Assessment of the global and regional land hydrosphere and its impact on the balance of the geophysical excitation function of polar motion. Acta Geophys. 2016, 64, 270–292. [Google Scholar] [CrossRef]
- Wińska, M.; Nastula, J.; Salstein, D.A. Hydrological excitation of polar motion by different variables from the GLDAS model. J. Geod. 2017, 91, 1461–1473. [Google Scholar] [CrossRef]
- Jean, Y.; Meyer, U.; Jäggi, A. Combination of GRACE monthly gravity field solutions from different processing strategies. J. Geod. 2018, 92, 1313–1328. [Google Scholar] [CrossRef]
- Meyer, U.; Jean, Y.; Kvas, A.; Dahle, C.; Lemoine, J.M.; Jäggi, A. Combination of GRACE monthly gravity fields on the normal equation level. J. Geod. 2019, 93, 1645–1658. [Google Scholar] [CrossRef]
- Jäggi, A.; Meyer, U.; Lasser, M.; Jenny, B.; Lopez, T.; Flechtner, F.; Dahle, C.; Förste, C.; Mayer-Gürr, T.; Kvas, A.; et al. International Combination Service for Time-Variable Gravity Fields (COST-G). Int. Assoc. Geod. Symp. 2019, 152, 57–65. [Google Scholar] [CrossRef]
- Encarnacao, J.; Visser, P.; Jaeggi, A.; Bezdek, A.; Mayer-Gürr, T.; Shum, C.K.; Arnold, D.; Doornbos, E.; Elmer, M.; Guo, J.; et al. Multi-Approach Gravity Field Models from Swarm GPS Data; GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Lemoine, J.-M.; Biancale, R.; Reinquin, F.; Bourgogne, S.; Gégout, P. CNES/GRGS RL04 Earth Gravity Field Models, from GRACE and SLR Data; GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Meyer, U.; Sosnica, K.; Arnold, D.; Dahle, C.; Thaller, D.; Dach, R.; Jäggi, A. SLR, GRACE and Swarm Gravity Field Determination and Combination. Remote Sens. 2019, 11, 956. [Google Scholar] [CrossRef]
- Weigelt, M. Time Series of Monthly Combined HLSST and SLR Gravity Field Models to Bridge the Gap between GRACE and GRACE-FO: QuantumFrontiers_HLSST_SLR_COMB2019s; GFZ Data Services: Potsdam, Germany, 2019. [Google Scholar] [CrossRef]
- Sasgen, I.; Martinec, Z.; Fleming, K. Wiener optimal combination and evaluation of the Gravity Recovery and Climate Experiment (GRACE) gravity fields over Antarctica. J. Geophys. Res. Solid Earth 2007, 112, B04401. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Bruinsma, S. Ensemble prediction and intercomparison analysis of GRACE time-variable gravity field models. Geophys. Res. Lett. 2014, 41, 1389–1397. [Google Scholar] [CrossRef]
- Śliwińska, J.; Birylo, M.; Rzepecka, Z.; Nastula, J. Analysis of groundwater and total water storage changes in Poland using GRACE observations, in-situ data, and various assimilation and climate models. Remote Sens. 2019, 11, 2949. [Google Scholar] [CrossRef]
- Premoli, A.; Tavella, P. A revisited three-cornered hat method for estimating frequency standard instability. IEEE Trans. Instrum. Meas. 1993, 42, 7–13. [Google Scholar] [CrossRef]
- Koot, L.; de Viron, O.; Dehant, V. Atmospheric angular momentum time-series: Characterization of their internal noise and creation of a combined series. J. Geod. 2006, 79, 663–674. [Google Scholar] [CrossRef]
- Quinn, K.J.; Ponte, R.M.; Heimbach, P.; Fukumori, I.; Campin, J.-M. Ocean angular momentum from a recent global state estimate, with assessment of uncertainties. Geophys. J. Int. 2019, 216, 584–597. [Google Scholar] [CrossRef]
- Vernotte, F.; Addouche, M.; Delporte, M.; Brunet, M. The three cornered hat method: An attempt to identify some clock correlations. In Proceedings of the 2004 IEEE International Frequency Control Symposium and Exposition, Montreal, QC, Canada, 23–27 August 2004; pp. 482–488. [Google Scholar] [CrossRef]
- O’Carroll, A.G.; Eyre, J.R.; Saunders, R.W. Three-way error analysis between AATSR, AMSR-E, and in situ sea surface temperature observations. J. Atmos. Ocean. Technol. 2008, 25, 1197–1207. [Google Scholar] [CrossRef]
- Sjoberg, J.P.; Anthes, R.A.; Rieckh, T. The Three-Cornered Hat Method for Estimating Error Variances of Three or More Atmospheric Datasets. Part I: Overview and Evaluation. J. Atmos. Ocean. Technol. 2021, 38, 555–572. [Google Scholar] [CrossRef]
- Roebeling, R.A.; Wolters EL, A.; Meirink, J.F.; Leijnse, H. Triple collocation of summer precipitation retrievals from SEVIRI over Europe with gridded rain gauge and weather radar data. J. Hydrometeor. 2012, 13, 1552–1566. [Google Scholar] [CrossRef]
- Nastula, J.; Śliwińska, J.; Kur, T.; Wińska, M.; Partyka, A. Preliminary study on hydrological angular momentum determined from CMIP6 historical simulations. Earth Planets Space 2022, 74, 84. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Zhou, Y.H. Seasonal excitation of polar motion. J. Geodyn. 2012, 62, 8–15. [Google Scholar] [CrossRef]
- Wińska, M.; Śliwińska, J. Assessing hydrological signal in polar motion from observations and geophysical models. Stud Geophys Geod 2019, 63, 95–117. [Google Scholar] [CrossRef]
- Naito, I.; Zhou, Y.H.; Sugi, M.; Kawamura, R.; Sato, N. Three-dimensional atmospheric angular momentum simulated by the Japan Meteorological Agency model for the period of 1955–1994. J. Meteorol. Soc. Jpn. Ser. II 2000, 78, 111–122. [Google Scholar] [CrossRef][Green Version]
- Zhou, Y.H.; Chen, J.L.; Liao, X.H.; Wilson, C.R. Oceanic excitations on polar motion: A cross comparison among models. Geophys. J. Int. 2005, 162, 390–398. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.; Ray, J.; Cheng, M. Improved Geophysical Excitations Constrained by Polar Motion Observations and GRACE/SLR Time-Dependent Gravity. Geod. Geodyn. 2017, 8, 377–388. [Google Scholar] [CrossRef]
- Bizouard, C. Geophysical Modelling of the Polar Motion; De Gruyter: Berlin, Germany; Boston, MA, USA, 2020. [Google Scholar] [CrossRef]
- Bizouard, C.; Lambert, S.; Gattano, C.; Becker, O.; Richard, J.-Y. The IERS EOP 14C04 solution for Earth orientation parameters consistent with ITRF 2014. J. Geod. 2019, 93, 621–633. [Google Scholar] [CrossRef]
- Gross, R. Theory of Earth Rotation Variations. In VIII Hotine-Marussi Symposium on Mathematical Geodesy; Sneeuw, N., Novák, P., Crespi, M., Sansò, F., Eds.; Springer: Cham, Switzerland, 2015. [Google Scholar] [CrossRef]
- Wilson, C.R.; Vicente, R.O. Maximum likelihood estimates of polar motion parameters. In Variations in Earth Rotation; McCarthy, D.D., Carter, W.E., Eds.; AGU Geophysical Monograph Series; Wiley: Washington, DC, USA, 1990; Volume 59, pp. 151–155. [Google Scholar]
- Nastula, J.; Gross, R. Chandler wobble parameters from SLR and GRACE. J. Geophys. Res. Solid Earth 2015, 120, 4474–4483. [Google Scholar] [CrossRef]
- Available online: https://hpiers.obspm.fr/eop-pc/index.php?index=excitactive&lang=en (accessed on 1 July 2022).
- Dill, R.; Dobslaw, H.; Hellmers, H.; Kehm, A.; Bloßfeld, M.; Thomas, M.; Seitz, F.; Thaller, D.; Hugentobler, U.; Schönemann, E. Evaluating processing choices for the geodetic estimation of Earth orientation parameters with numerical models of global geophysical fluids. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020025. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R. Effective Angular Momentum Functions From Earth System Modelling at GeoForschungsZentrum in Potsdam; Technical Report, Revision 1.0; GFZ: Potsdam, Germany, 2018; Available online: ftp://ig2-dmz.gfz-potsdam.de/EAM/ESMGFZ_EAM_Product_Description_Document.pdf (accessed on 1 July 2022).
- Yu, N.; Ray, J.; Li, J.; Chen, G.; Chao, N.; Chen, W. Intraseasonal variations in atmospheric and oceanic excitation of length-of-day. Earth Space Sci. 2021, 8, e2020EA001563. [Google Scholar] [CrossRef]
- Jungclaus, J.H.; Fischer, N.; Haak, H.; Lohmann, K.; Marotzke, J.; Matei, D.; Mikolajewicz, U.; Notz, D.; von Storch, J.S. Characteristics of the ocean simulations in MPIOM, the ocean component of the MPI-Earth system model. J. Adv. Model. Earth Syst. 2013, 5, 422–446. [Google Scholar] [CrossRef]
- Dill, R.; Dobslaw, H. Seasonal variations in global mean sea level and consequences on the excitation of length-of-day changes. Geophys. J. Int. 2019, 218, 801–816. [Google Scholar] [CrossRef]
- Chen, W.; Shen, W. New estimates of the inertia tensor and rotation of the triaxial nonrigid Earth. J. Geophys. Res. 2010, 115, B12419. [Google Scholar] [CrossRef]
- Box, G.E.P.; Jenkins, G.M.; Reinsel, G.C.; Ljung, G.M. Time Series Analysis: Forecasting and Control, 5th ed.; John Wiley and Sons Inc.: Hoboken, NJ, USA, 2016; ISBN 978-1-118-67502-1. [Google Scholar]
- Koch, I.; Flury, J.; Naeimi, M.; Shabanloui, A. LUH-GRACE2018: A New Time Series of Monthly Gravity Field Solutions from GRACE. In International Association of Geodesy Symposia; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar] [CrossRef]
- Meyer, U.; Jäggi, A.; Jean, Y.; Beutler, G. AIUB-RL02: An improved time-series of monthly gravity fields from GRACE data. Geophys. J. Int. 2016, 205, 1196–1207. [Google Scholar] [CrossRef]
- Dahle, C.; Murböck, M.; Flechtner, F.; Dobslaw, H.; Michalak, G.; Neumayer, K.H.; Abrykosov, O.; Reinhold, A.; König, R.; Sulzbach, R.; et al. The GFZ GRACE RL06 monthly gravity field time series: Processing details and quality assessment. Remote Sens. 2019, 11, 2116. [Google Scholar] [CrossRef]
- Taylor, K.E. Summarizing multiple aspects of model performance in a single diagram. J. Geophys. Res. 2001, 106, 7183–7192. [Google Scholar] [CrossRef]
- Gray, J.E.; Allan, D.W. A method for estimating the frequency stability of an individual oscillator. In Proceedings of the 28th Annual Symposium on Frequency Control, Atlantic City, NJ, USA, 29–31 May 1974; pp. 243–246. [Google Scholar] [CrossRef]
- Chin, T.; Gross, R.; Dickey, J. Multi-reference evaluation of uncertainty in earth orientation parameter measurements. J. Geod. 2005, 79, 24–32. [Google Scholar] [CrossRef]
- Ferreira, V.G.; Montecino, H.D.C.; Yakubu, C.I.; Heck, B. Uncertainties of the Gravity Recovery and Climate Experiment time-variable gravity-field solutions based on three-cornered hat method. J. Appl. Rem. Sens. 2016, 10, 015015. [Google Scholar] [CrossRef]
- Grubbs, F.E. On Estimating Precision of Measuring Instruments and Product Variability. J. Am. Stat. Assoc. 1948, 43, 243–264. [Google Scholar] [CrossRef]
- Torcaso, F.; Ekstrom, C.R.; Burt, E.; Matsaki, D. Estimating Frequency Stability and Cross-Correlations. In Proceedings of the 30th Annual Precise Time and Time Interval Systems and Applications Meeting, Reston, VA, USA, 1–3 December 1998; pp. 69–82. [Google Scholar]
| COMB1 Weights | COMB2 Weights | COMB3 Weights | COMB4 Weights | |||||
|---|---|---|---|---|---|---|---|---|
| χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | χ1 | χ2 | |
| CNES | 0.131 | 0.127 | 0.204 | 0.213 | 0.196 | 0.202 | 0.276 | 0.285 |
| COST-G | 0.358 | 0.404 | × | × | × | × | × | × |
| ITSG | 0.284 | 0.175 | 0.344 | 0.463 | 0.330 | 0.440 | × | × |
| JPL | 0.221 | 0.276 | 0.442 | 0.294 | 0.424 | 0.280 | 0.399 | 0.383 |
| CSR | 0.006 | 0.018 | 0.010 | 0.030 | 0.009 | 0.028 | 0.200 | 0.148 |
| GFZ | × | × | × | × | 0.041 | 0.050 | × | × |
| LUH | × | × | × | × | × | × | 0.059 | 0.062 |
| AIUB | × | × | × | × | × | × | 0.066 | 0.122 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Śliwińska, J.; Wińska, M.; Nastula, J. Exploiting the Combined GRACE/GRACE-FO Solutions to Determine Gravimetric Excitations of Polar Motion. Remote Sens. 2022, 14, 6292. https://doi.org/10.3390/rs14246292
Śliwińska J, Wińska M, Nastula J. Exploiting the Combined GRACE/GRACE-FO Solutions to Determine Gravimetric Excitations of Polar Motion. Remote Sensing. 2022; 14(24):6292. https://doi.org/10.3390/rs14246292
Chicago/Turabian StyleŚliwińska, Justyna, Małgorzata Wińska, and Jolanta Nastula. 2022. "Exploiting the Combined GRACE/GRACE-FO Solutions to Determine Gravimetric Excitations of Polar Motion" Remote Sensing 14, no. 24: 6292. https://doi.org/10.3390/rs14246292
APA StyleŚliwińska, J., Wińska, M., & Nastula, J. (2022). Exploiting the Combined GRACE/GRACE-FO Solutions to Determine Gravimetric Excitations of Polar Motion. Remote Sensing, 14(24), 6292. https://doi.org/10.3390/rs14246292









