Societal Applications of HF Skywave Radar
Abstract
1. Introduction
2. HF Skywave Radar in a Nutshell
Spatial Coverage and Resolution
- represents the selected waveform;
- represents the transmitting complex, including amplifiers and antennas;
- represents propagation from the transmitter to the first scattering zone;
- represents all scattering processes in the j-th scattering zone;
- represents propagation from the j-th scattering zone to the (j + 1)-th zone;
- denotes the number of scattering zones that the signal visits on a specific route from
- the transmitter to the receiver;
- denotes the number of external noise sources or jammers;
- represents propagation from the i-th noise source to its first scattering zone;
- denotes the number of scattering zones that the l-th noise emission visits on a specific route from its source to the receiver;
- denote the maximum number of zones visited by signal and external noise,
- respectively;
- represents the receiving complex, including antennas and receivers;
- represents internal noise;represents the signal delivered to the processing stage.
3. Skywave Radar Observables
3.1. The Role of Parametric Models of the Environment
3.2. Radio Wave Scattering from the Ocean Surface
3.2.1. First-Order Theory
3.2.2. Second-Order Theory
3.3. Remote Sensing of the Ocean Surface with HF Radar
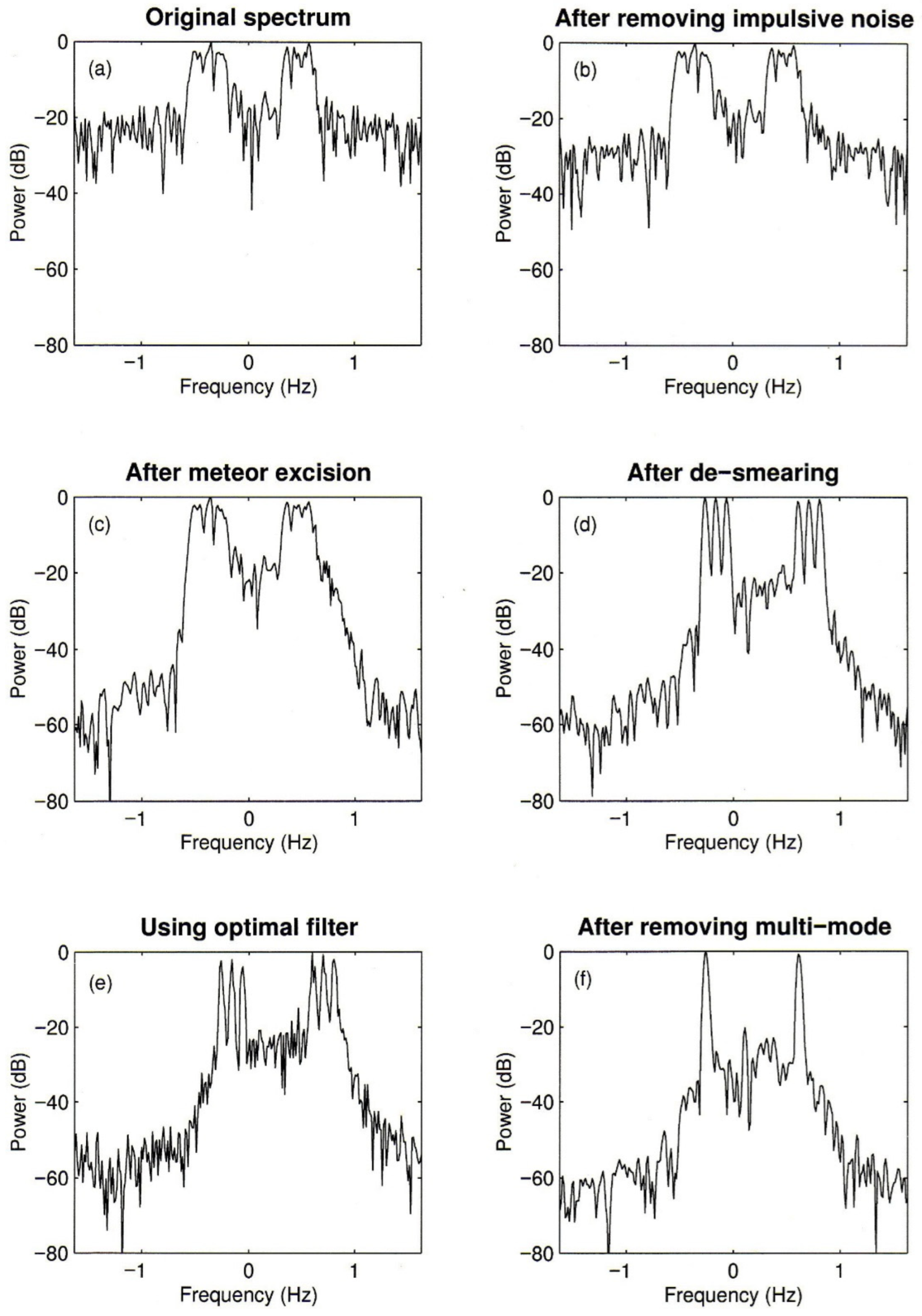
3.4. Dealing with Imperfect Data
4. Assessment of Societal Utility
4.1. Historical Assessments
4.2. Contemporary Assessment
4.2.1. Shipping
4.2.2. Fishing
4.2.3. Military
4.2.4. Offshore Oil and Gas Industries
4.2.5. Science
4.2.6. Deep Sea Mining
4.2.7. Search and Rescue
4.2.8. Coastal Damage, Cyclone, and Tsunami Warning
4.2.9. Recreation
4.2.10. People Smuggling and Illegal Immigration
4.2.11. Intrusion of Foreign Fishing Vessels
4.2.12. Offshore Wind Farms
4.2.13. Sovereignty Violation
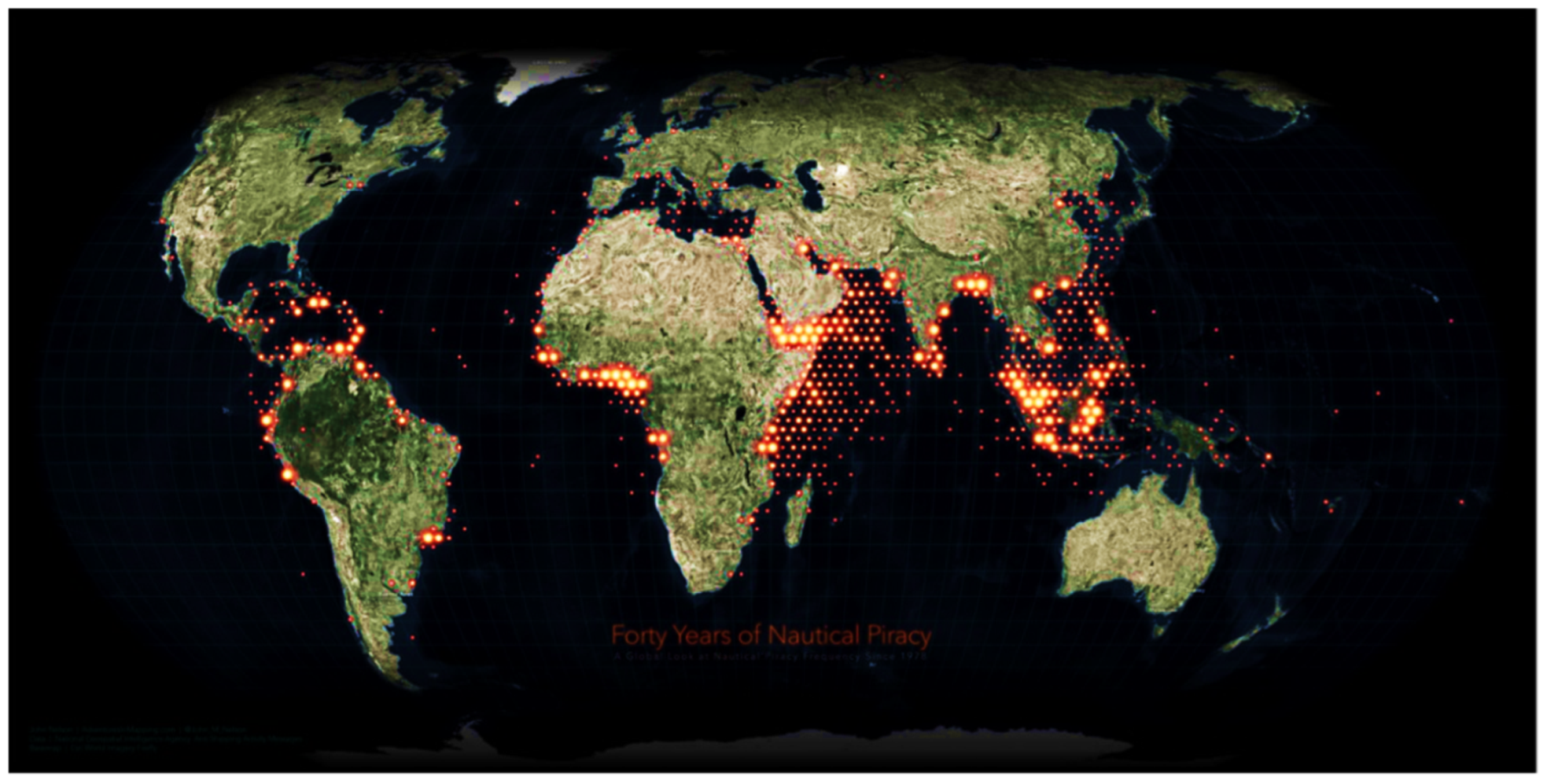
4.2.14. Piracy and Sanction-Breaking
4.2.15. Oil Spill Detection and Tracking
5. Conclusions
Funding
Conflicts of Interest
References
- Barrick, D.E. Remote sensing of sea state by radar. In Remote Sensing of the Troposphere; Derr, V.E., Ed.; NOAA/Environmental Research Laboratories: Boulder, CO, USA, 1972; pp. 12.1–12.6. [Google Scholar]
- Long, A.E.; Trizna, D.E. Measurements and Preliminary Interpretation of HF Radar Doppler Spectra from the Sea Echo of an Atlantic Storm; NRL Report 7456; Naval Research Laboratory: Washington, DC, USA, 1972. [Google Scholar]
- Long, A.E.; Trizna, D.B. Mapping of North Atlantic winds by HF radar sea backscatter interpretation. IEEE Trans. Antennas Propag. 1973, AP-21, 680–685. [Google Scholar] [CrossRef]
- Anderson, S.J. Over-the Horizon Radar Meteorology; Weapons Research Establishment Technical Report WRE-TR-1752 (A); Defence Science and Technology Group: Adelaide, Australia, 1977. [Google Scholar]
- Washburn, T.W.; Sweeney, L.E.; Barnum, J.R.; Zavoli, W.B. Development of HF skywave radar for remote sensing applications. In AGARD Special Topics in HF Propagation; SEE N80-19372 10-32; Advisory Group for Aerospace Research and Development: Neuilly-Sur-Seine, France, 1979. [Google Scholar]
- Anderson, S.J. Bistatic and Stereoscopic Configurations for HF Radar. Remote Sens. 2020, 12, 689. [Google Scholar] [CrossRef]
- Croft, T.A. Sky-Wave Backscatter: A Means for Observing our Environment at Great Distances. Rev. Geophys. Space Phys. 1972, 10, 73–155. [Google Scholar] [CrossRef]
- CODAR. Available online: https://codar.com (accessed on 15 November 2022).
- Available online: https://apollo.nvu.vsc.edu/classes/remote/lecture_notes/satellite/history/tiros.html#:~:text=Satellites%20with%20meteorological%20instrumentation%20were,this%20satellite%20was%2079%20days (accessed on 12 November 2022).
- Shutler, J.D.; Quartly, G.D.; Donlon, C.J.; Sathyendranath, S.; Platt, T.; Chapron, B.; Johannessen, J.A.; Girard-Ardhuin, F.; Nightingale, P.D.; Woolf, D.K.; et al. Progress in satellite remote sensing for studying physical processes at the ocean surface and its borders with the atmosphere and sea ice. Prog. Phys. Geogr. 2016, 40, 215–246. [Google Scholar] [CrossRef]
- Georges, T.M.; Maresca, J.W., Jr. Report on the Skywave Sea-State-Radar Workshop Held in Rockville, Maryland, 20–22 May 1981; NOAA Technical Memorandum ERL WPL-81; NOAA: Washington, DC, USA, 1981. [Google Scholar]
- Georges, T.M.; Maresca, J.W., Jr. Opportunities for New Ocean-Remote-Sensing Services Using Skywave Radar. In Proceedings of the IEEE Digest for 1981 International Geoscience and Remote Sensing Symposium, Washington, DC, USA, 8–10 June 1981; pp. 1395–1400. [Google Scholar]
- Anderson, S.J. Remote sensing applications of HF skywave radar: The Australian experience. Turk. J. Electr. Eng. Comput. Sci. 2010, 18, 339–372. [Google Scholar] [CrossRef]
- Headrick, J.M.; Anderson, S.J. HF Over-the-Horizon Radar. In Radar Handbook, 3rd ed.; Chapter 20; Merrill Skolnik; McGraw-Hill: New York, NY, USA, 2008. [Google Scholar]
- Anderson, S.J. Limitations to the extraction of information from multihop skywave radar signals. In Proceedings of the IEEE International Conference on Radar, Adelaide, Australia, 3–5 September 2003. [Google Scholar]
- Anderson, S.J. The Doppler structure of diffusely-scattered multi-hop skywave radar echoes. In Proceedings of the IEEE International Conference on Radar, Toulouse, France, 10–23 October 2004. [Google Scholar]
- Walsh, J.; Gill, E. An analysis of the scattering of high-frequency electromagnetic radiation from rough surfaces with application to pulse radar operating in backscatter mode. Radio Sci. 2000, 35, 1337–1359. [Google Scholar] [CrossRef]
- Anderson, S.J. Multiple scattering of HF surface waves: Implications for radar design and sea clutter interpretation. IET Radar Sonar Navig. 2010, 4, 195–208. [Google Scholar] [CrossRef]
- Anderson, S.J. Estimation and removal of multiple scattering contributions to HF surface wave radar echoes. In Proceedings of the IET Radar Conference, Hangzhou, China, 14–16 October 2015. [Google Scholar]
- Anderson, S.J. The Challenge of Signal Processing for HF Over-the-Horizon Radar. In Proceedings of the Workshop on Signal Processing and Applications, WOSPA’93, Queensland University of Technology, Brisbane, Australia, 13–15 December 1993. [Google Scholar]
- Anderson, S.J. OTH Radar Phenomenology: Signal Interpretation and Target Characterization at HF. IEEE Aerosp. Electron Syst. Mag. 2017, 32, 4–16. [Google Scholar] [CrossRef]
- Abramovich, Y.I.; Gorokhov, A.Y.; Mikhaylyukov, V.N.; Malyavin, I.P. Exterior noise adaptive rejection for OTH radar implementations. In Proceedings of the ICASSP ’94, IEEE International Conference on Acoustics, Speech and Signal Processing, Adelaide, Australia, 19–22 April 1994; pp. 105–108. [Google Scholar]
- Abramovich, Y.I.; Anderson, S.J.; Gorokhov, A.Y.; Spencer, N.K. Stochastic constraints method in nonstationary hot clutter cancellation, Part I: Fundamentals and supervised training applications. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 1271–1292. [Google Scholar] [CrossRef]
- Abramovich, Y.I.; Anderson, S.J.; Spencer, N.K. Stochastic-constraints method in nonstationary hot clutter cancellation, Part II: Unsupervised training applications. IEEE Trans. Aerosp. Electron. Syst. 2000, 36, 132–149. [Google Scholar] [CrossRef]
- Abramovich, Y.I.; Anderson, S.J.; Gorokhov, A.Y.; Spencer, N.K. Stochastically constrained spatial and spatio-temporal adaptive processing for nonstationary hot-clutter cancellation; Chapter 17. In Applications of Space-Time Adaptive Processing; Klemm, R.K., Ed.; IEEE: New York, NY, USA, 2004; pp. 603–697. [Google Scholar]
- Jannsen, P.A.E.M. On some consequences of the canonical transformation in the Hamiltonian theory of water waves. J. Fluid Mech. 2009, 637, 1–44. [Google Scholar] [CrossRef]
- Anderson, S.J.; Anderson, W.C. Bistatic scattering from the ocean surface and its application to remote sensing of seastate. In Proceedings of the 1987 IEEE APS International Symposium, Blacksburg, VA, USA, 15–19 June 1987. [Google Scholar]
- Stewart, R.H.; Joy, J.W. HF radio measurements of surface currents. Deep-Sea Res. 1974, 21, 1039–1049. [Google Scholar] [CrossRef]
- Skop, R.A. An approximate dispersion relation for wave-current interactions. J. Waterw. Port Coast. Ocean Eng. 1987, 113, 187–195. [Google Scholar] [CrossRef]
- Kirby, J.T.; Chen, T.M. Surface waves on vertically sheared flows: Approximate dispersion relations. J. Geophys. Res. 1989, 94, 1013–1027. [Google Scholar] [CrossRef]
- Ha, E.C. Remote sensing of Ocean Surface Current and Current Shear by HF Backscatter Radar. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1979. Technical Report D415-1. [Google Scholar]
- Teague, C. Multifrequency HF radar observations of currents and current shears. J. Ocean. Eng. 1986, 11, 258–269. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Teague, C.C.; Onstott, R.G.; Daida, J.M.; Hansen, P.M.; Fernandez, D.; Schnepf, N.; Fischer, K. Observations of near-surface ocean currents at varying depths using a new multifrequency HF radar. In Proceedings of the IEEE International Geoscience and Remote Sensing Symposium, Singapore, 3–8 August 1997. [Google Scholar]
- Broche, P.; de Maistre, J.C.; Forget, P. Mesure par radar decametrique coherent des courants superficiels engenders par le vent. Oceanol. Acta 1983, 6, 43–53. [Google Scholar]
- Anderson, S.J. The HF radar signatures of surface gravity wave spectra on shear flows. In Proceedings of the Australian Institute of Physics Congress, Adelaide, Australia, 11–16 December 2022. [Google Scholar]
- Kenyon, K.E. Stokes drift for random gravity waves. J. Geophys. Res. 1969, 74, 6991–6994. [Google Scholar] [CrossRef]
- Punzmann, H.; Francois, N.; Xia, H.; Falkovich, G.; Shats, M. Generation and reversal of surface flows by propagating waves. Nat. Phys. 2014, 10, 658. [Google Scholar] [CrossRef]
- Rohrs, J.; Christensen, K.H. Drift in the uppermost part of the ocean. Geophys. Res. Lett. 2015, 42, 10–349. [Google Scholar] [CrossRef]
- Ardhuin, F.; Marie, L.; Rascle, N.; Forget, P.; Roland, A. Observation and estimation of Lagrangian, Stokes and Eulerian Currents Induced by Wind and Waves at the Sea Surface. J. Phys. Oceanogr. 2009, 39, 2820–2838. [Google Scholar] [CrossRef]
- Bye, J.A.T.; Wolff, J.-O.; Lettmann, K.A. A note on ocean surface drift with applications to surface velocities measured with HF radar. J. Oceanogr. 2017, 73, 491–502. [Google Scholar] [CrossRef]
- Van den Bremer, T.S.; Breivik, Ø. Stokes Drift. Philos. Trans. R. Soc. 2017, A376, 20170104. [Google Scholar] [CrossRef] [PubMed]
- Van der Mheen, M.; Pattiaratchi, C.; Cosoli, S.; Wandres, M. Depth-dependent Correction for Wind-driven Drift Current in Particle Tracking Applications. Front. Mar. Sci. 2020, 7, 305. [Google Scholar] [CrossRef]
- Tamtare, T.; Dumont, D.; Chavanne, C. The Stokes drift in ocean surface drift prediction. J. Oper. Oceanogr. 2021, 15, 156–168. [Google Scholar] [CrossRef]
- Wright, J.W. The wind drift and wave breaking. J. Phys. Oceanogr. 1976, 6, 402–405. [Google Scholar] [CrossRef]
- Lipa, B.; Nyden, B.; Barrick, D.E.; Kohut, J. HF radar sea-echo from shallow water. Sensors 2008, 8, 4611–4635. [Google Scholar] [CrossRef] [PubMed]
- Anderson, S.J. Symbiosis of remote sensing and ocean surveillance missions of HF skywave radar. In Ocean Remote Sensing Technologies: High Frequency, Marine and GNSS-Based Radar; Huang, W., Gill, E.W., Eds.; SciTech Publishing: London, UK, 2022. [Google Scholar]
- Anderson, S.J. Channel characterization for polarimetric HF skywave radar. In Proceedings of the IEEE Radar Conference, Washington, DC, USA, 2–6 May 2016. [Google Scholar] [CrossRef]
- Anderson, S.J. Prospects for tsunami detection and characterisation with HF skywave radar. In Proceedings of the 2008 International Conference on Radar, Adelaide, Australia, 2–5 September 2008; pp. 639–645. [Google Scholar] [CrossRef]
- Anderson, S.J. HF skywave radar performance in the tsunami detection and measurement role. In The Tsunami Threat—Research and Technology; Morner, N.-A., Ed.; IntechOpen: London, UK, 2011. [Google Scholar] [CrossRef][Green Version]
- Occhipinti, G.; Dorey, P.; Farges, T.; Lognonné, P. Nostradamus: The radar that wanted to be a seismometer. Geophys. Res. Lett. 2010, 37, L18104. [Google Scholar] [CrossRef]
- Coisson, P.; Occhipinti, G.; Lognonne, P.; Molinie, J.-P.; Rolland, L.M. Tsunami signature in the ionosphere: A simulation of OTH radar observations. Radio Sci. 2011, 46, RS0D20. [Google Scholar] [CrossRef]
- Lipa, B. Derivation of directional ocean-wave spectra by integral inversion of second-order radar echoes. Radio Sci. 1977, 12, 425–434. [Google Scholar] [CrossRef]
- Trizna, D.B.; Headrick, J.M.; Bogle, R.W.; Moore, J.C. Directional sea spectrum determination using HF Doppler radar techniques. IEEE Trans. Antennas Propag. 1977, AP-25, 4–11. [Google Scholar] [CrossRef]
- Lipa, B. Inversion of second-order radar echoes from the sea. J. Geophys. Res. Ocean. 1978, 83, 959–962. [Google Scholar] [CrossRef]
- Anderson, S.J. The Extraction of Wind and Sea State Parameters from HF Skywave Radar Echoes; IREECON-83; IREECON International Digest: Sydney, Australia, 1983; pp. 654–656. [Google Scholar]
- Wyatt, L.R. A relaxation method for integral inversion applied to HF radar measurement of the ocean wave directional spectrum. Int. J. Remote Sens. 1990, 11, 1481–1494. [Google Scholar] [CrossRef]
- Howell, R.; Walsh, J. Measurement of ocean wave spectra using narrow beam HF radar. IEEE J. Ocean. Eng. 1993, 18, 296–305. [Google Scholar] [CrossRef]
- Hisaki, Y. Nonlinear inversion of the integral equation to estimate ocean wave spectra from HF radar. Radio Sci. 1996, 31, 25–39. [Google Scholar] [CrossRef]
- Barrick, D.E. The ocean waveheight nondirectional spectrum from inversion of the HF sea-echo Doppler spectrum. Remote Sens. Environ. 1977, 6, 201–227. [Google Scholar] [CrossRef]
- Barrick, D.E. Extraction of wave parameters from measured HF radar sea-echo Doppler spectra. Radio Sci. 1980, 12, 415–424. [Google Scholar] [CrossRef]
- Maresca, J.W.; Georges, T.M. Measuring rms waveheight and the scalar ocean wave spectrum with HF skywave radar. J. Geophys. Res. 1980, C-85, 2759–2771. [Google Scholar] [CrossRef]
- Barrick, D.E. Status of HF radars for wave-height directional spectral measurements. In Proceedings of the Symposium and Workshop on Wave-Measurement Technology, Washington, DC, USA, 22–24 April 1981; National Academy Press: Washington DC, USA, 1982; pp. 112–117. [Google Scholar]
- Weber, B.L.; Barrick, D.E. On the nonlinear theory for gravity waves on the ocean’s surface. Part I: Derivations. J. Physical. Oceanogr. 1977, 7, 3–10. [Google Scholar] [CrossRef]
- Barrick, D.E.; Weber, B.L. On the nonlinear theory for gravity waves on the ocean’s surface. Part II: Interpretation and applications. J. Phys. Oceanogr. 1977, 7, 11–21. [Google Scholar] [CrossRef]
- Creamer, D.B.; Henyey, F.; Schult, R.; Wright, J. Improved linear representation of ocean surface waves. J. Fluid Mech. 1989, 205, 135–161. [Google Scholar] [CrossRef]
- Wright, J.; Creamer, D.B. Improved linear representation of surface waves. Part 2. Slowly varying bottoms and currents. J. Fluid Mech. 1994, 261, 65–74. [Google Scholar] [CrossRef]
- Mao, Y.; Heron, M.L. The influence of fetch on the response of surface currents to wind studied by HF ocean surface radar. J. Phys. Oceanogr. 2008, 38, 1107–1121. [Google Scholar] [CrossRef][Green Version]
- Anderson, S.J.; Mahoney, A.R.; Zollo, A.O. Applications of Higher-Order Statistical Signal Processing to Radar, Chapter 13. In Higher-Order Statistical Signal Processing; Boashash, B., Powers, E.J., Zoubir, A.M., Eds.; Longman Australia and Halstead Press: Sydney, Australia, 1995; pp. 405–446. [Google Scholar]
- Anderson, S.J.; Mahoney, A.R.; Zollo, A.O. Diagnosis of Corrupted Skywave Radar Signals using Higher-Order Spectrum Analysis. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, ICASSP’93, Minneapolis, MN, USA, 27–30 April 1993. [Google Scholar]
- Jannsen, P.A.E.M. The Wave Model: May 1995. ECMRF Meteorological Training Course Lecture Series. 2003. Available online: https://www.ecmwf.int/sites/default/files/elibrary/2002/16951-wave-model.pdf (accessed on 2 September 2022).
- Anderson, S.J.; Abramovich, Y.I.; Skinner, A.I. Robust mapping of tropical cyclone wave fields using HF skywave radar. In Proceedings of the IEE Conference Publication 490, Proceedings of RADAR 2002, Edinburgh, UK, 15–17 October 2002; pp. 47–50. [Google Scholar]
- Stewart, R.H.; Barnum, J.R. Radio measurements of ocean winds at long ranges: An evaluation. Radio Sci. 1975, 10, 853–857. [Google Scholar] [CrossRef]
- Maresca, J.W., Jr.; Barnum, J.R. Measurement of oceanic wind speed from HF sea scatter by skywave radar. IEEE Trans. Antennas Propag. 1977, AP-25, 132–136. [Google Scholar] [CrossRef]
- Barnum, J.R.; Maresca, J.W.; Serebreny, S.M. High-resolution mapping of oceanic wind fields with skywave radar. IEEE Trans. Antennas Propag. 1977, 2, 128–132. [Google Scholar] [CrossRef]
- Parent, J.; Gaffard, C. Detection of meteorological fronts over the North Sea with Valensole skywave radar. IEEE J. Ocean. Eng. 1986, OE-11, 174–179. [Google Scholar] [CrossRef]
- Keenan, T.D.; Anderson, S.J. Some examples of surface wind field analysis based on JINDALEE skywave radar data. Aust. Meteorol. Mag. 1987, 35, 153–161. [Google Scholar]
- Young, G.S.; Harlan, J.A.; Georges, T.M. Application of over-the-horizon radar observations to synoptic and mesoanalysis over the Atlantic. Weather Forecast. 1997, 12, 44–55. [Google Scholar] [CrossRef]
- Anderson, S.J. On the sensitivity of HFSWR wave height and directional wave spectrum estimation to non-stationarity of forcing winds. In Proceedings of the IUGG General Assembly, IAPSO Session, Melbourne, Australia, 2 July 2011. [Google Scholar]
- Georges, T.M.; Harlan, J.A.; Leben, R.; Lematta, R.A. A test of ocean surface current mapping with over-the-horizon radar. IEEE Trans. Geosci. Remote Sens. 1998, 36, 101–110. [Google Scholar] [CrossRef]
- Trizna, D.B. Mapping ocean currents using over-the-horizon radar. Int. J. Remote Sens. 1982, 3, 295–309. [Google Scholar] [CrossRef]
- Georges, T.M.; Harlan, J.A. The first large-scale map of ocean surface currents made with dual over-the-horizon radars. In Proceedings of the OCEANS 96, MTS/IEEE Conference, Fort Lauderdale, FL, USA, 23–26 September 1996. [Google Scholar] [CrossRef]
- Georges, T.M.; Harlan, J.A.; Lee, T.N.; Leben, R. Observations of the Florida Current with two over-the-horizon radars. Radio Sci. 1998, 33, 1227–1240. [Google Scholar] [CrossRef]
- Anderson, S.J.; Buchan, S. HF radar detection of internal waves in the ocean. In Proceedings of the IEEE International Radar Conference, Lille, France, 13–17 October 2014. [Google Scholar]
- Anderson, S.J. HF radar signatures of ocean surface geometry and dynamics arising from localized disturbances. In Proceedings of the 2015 IEEE US Radar Conference, Arlington, VI, USA, 10–15 May 2015. [Google Scholar]
- Anderson, S.J. Monitoring the marginal ice zone with HF radar. In Proceedings of the IEEE US International Radar Conference, Seattle, WA, USA, 8–12 May 2017. [Google Scholar]
- Anderson, S.J. Remote Sensing of the Polar Ice Zones with HF Radar. Remote Sens. 2021, 13, 4398. [Google Scholar] [CrossRef]
- Anderson, S.J. HF radar signatures of rain-modified ocean surfaces. In Proceedings of the Asia-Pacific Microwave Conference, Adelaide, Australia, 11–13 August 1992. [Google Scholar]
- Anderson, S.J. Rainfall Detection. U.S. Patent 5,438,334, 1 August 1995. [Google Scholar]
- Anderson, S.J. Sensitivity of HF Radar Signatures of Ship Wakes to Hull Geometry Parameters. In Proceedings of the 21st Australasian Fluid Mechanics Conference, Adelaide, Australia, 10 December 2018. [Google Scholar]
- Anderson, S.J. HF radar signatures of ship and submarine wakes. J. Eng. 2019, 21, 7512–7520. [Google Scholar] [CrossRef]
- Anderson, S.J. HF Radar Scattering from a Sea Surface Perturbed by Multiple Ship Wakes. In Proceedings of the 2019 International Conference on Electromagnetics in Advanced Applications (ICEAA), Granada, Spain, 9–13 September 2019; pp. 0087–0089. [Google Scholar] [CrossRef]
- Anderson, S.J. Prospects for submarine detection with HF over-the-horizon radar. In Proceedings of the 6th Submarine Science, Technology and Engineering Conference, Adelaide, Australia, 8–10 November 2021. [Google Scholar]
- Anderson, S.J. HF radar detection and tracking of oil spills in the marine environment. In Proceedings of the IEEE International Geophysics and Remote Sensing Symposium, IGARSS’97, Singapore, 3 August 1997. [Google Scholar]
- Parent, J.; Bourdillon, A. Enhancement of remote sensing capability of HF skywave radar by correcting the signal for frequency modulations. In Proceedings of the Fourth International Conference on HF Radio Systems and Techniques, London, UK, 11–14 April 1988. [Google Scholar]
- Parent, J.; Bourdillon, A. A method to correct HF skywave backscattered signals for ionospheric frequency modulation. IEEE Trans. Antennas Propag. 1988, 36, 127–135. [Google Scholar] [CrossRef]
- Bourdillon, A.; Delloue, J.; Parent, J. Effects of geomagnetic pulsations on the Doppler shift of HF backscatter radar echoes. Radio Sci. 1989, 24, 183–195. [Google Scholar] [CrossRef]
- Anderson, S.J.; Abramovich, Y.I. A unified approach to detection, classification and correction of ionospheric distortion in HF skywave radar systems. Radio Sci. 1998, 33, 1055–1067. [Google Scholar] [CrossRef]
- Anderson, S.J. Adaptive Remote Sensing with HF Skywave Radar. IEE Proc. F 1992, 139, 182–192. [Google Scholar] [CrossRef]
- Anderson, S.J. Oceanographic and Meteorological Data. U.S. Patent 5,469,168, 21 November 1995. [Google Scholar]
- Earl, G.F.; Ward, B.D. The frequency management system of the Jindalee over-the-horizon backscatter HF radar. Radio Sci. 1987, 22, 275–291. [Google Scholar] [CrossRef]
- Rhodes, R.S.; Chadwick, R.B. Economic Appraisal of Real-Time Synoptic Sea-State Measurements by Over-the-Horizon Radar; NOAA Technical Report EREL 299-WPL 32; Environmental Research Laboratories: Boulder, CO, USA, 1974. [Google Scholar]
- Anderson, S.J. Remote sensing with the JINDALEE skywave radar. IEEE J. Ocean Eng. 1986, OE-11, 158–163. [Google Scholar] [CrossRef]
- Keenan, T.D.; Parker, P.R. National Significance of Meteorological Data Derived from the Jindalee Operational Radar Network; Working Paper; Australian Bureau of Meteorology Research Centre, Australian Government Bureau of Meteorology: Melbourne, Australia, 1992. [Google Scholar]
- Greenwald, R.A. History of the Super Dual Auroral Radar Network (SuperDARN)-I: Pre-SuperDARN developments in high frequency radar technology for ionospheric research and selected scientific results. Hist. Geo-Space Sci. 2021, 12, 77–93. [Google Scholar] [CrossRef]
- Baker, J.B.H. The Super Dual Auroral Radar Network (SuperDARN). Available online: http://vt.superdarn.org/tiki-index.php?page=sd_tutorial (accessed on 25 October 2021).
- Greenwood, R.; Schultz, E.; Parkinson, M.; Neudegg, D. Evaluation of the TIGER SuperDARN Over-The-Horizon Radar Systems for Providing Remotely Sensed Marine and Oceanographic Data Over the Southern Ocean; Technical Report No. 045; Australian Government, Bureau of Meteorology, Centre for Australian Weather and Climate Research: Melbourne, VIC, Australia, 2011. [Google Scholar]
- Available online: https://www.marinetraffic.com/en/ais/home/ (accessed on 12 November 2022).
- Available online: https://public.wmo.int/en/our-mandate/what-we-do/observations (accessed on 12 November 2022).
- Interim Report of Committee on Large Container Ship Safety; Ministry of Land, Infrastructure, Transport and Tourism, Government of Japan: Tokyo, Japan, December 2013.
- Young, I.; Babanin, A.V.; Zieger, S. The decay rate of ocean swell observed by altimeter. J. Phys. Oceanogr. 2013, 43, 2322–2333. [Google Scholar] [CrossRef]
- Lucas, C.; Soares, C.G. On the modelling of swell spectra. Ocean Eng. 2015, 108, 749–759. [Google Scholar] [CrossRef]
- Lipa, B.J.; Barrick, D.E.; Maresca, J.W. HF radar measurements of long ocean waves. J. Geophys. Res. 1981, 86, 4089–4102. [Google Scholar] [CrossRef]
- Available online: https://www.bloomberg.com/news/articles/2021-04-26/shipping-containers-plunge-overboard-as-supply-race-raises-risks (accessed on 12 November 2022).
- Bloomberg, L.P. Huge Spike in Shipping Containers Lost at Sea. Available online: https://gcaptain.com/shipping-containers-lost-at-sea/ (accessed on 1 January 2022).
- Ocean Container Losses Topple Annual Average in 2 Months. American Shipper. Available online: https://www.freightwaves.com/news/ocean-container-losses-topple-annual-average-in-2-months (accessed on 12 November 2022).
- Blenkey, N. IMO Moves on Container Losses at Sea. Marine Log, May 18, 2021. Available online: https://www.marinelog.com/legal-safety/safety-and-security/imo-moves-on-container-losses-at-sea/ (accessed on 12 November 2022).
- Anderson, S.J. A novel technique for measuring the surface wave Green’s function in the open sea, with applications to HFSWR. In Proceedings of the URSI General Assembly, Rome, Italy, 24 August–4 September 2021. [Google Scholar]
- Rousseau, Y.; Watson, R.A.; Blanchard, J.L.; Fulton, E.A. Evolution of global fishing fleets and the response of fished resources. Proc. Natl. Acad. Sci. USA 2018, 116, 12238–12243. [Google Scholar] [CrossRef]
- Morris, M.Y.; Roemmich, D.H.; Mayers, G.; Weisberg, R. Upper ocean heat and freshwater advection in the western Pacific Ocean. J. Geophys. Res. 1998, 103, 13023–13039. [Google Scholar] [CrossRef][Green Version]
- Figure Courtesy of Dr David Griffin, CSIRO, Australia. Data Was Sourced from Australia’s Integrated Marine Observing System (IMOS)—IMOS Is Enabled by the National Collaborative Research Infrastructure Strategy (NCRIS). It Is Operated by a Consortium of Institutions as an Unincorporated Joint Venture, with the University of Tasmania as Lead Agent. Available online: https://www.education.gov.au/ncris (accessed on 12 November 2022).
- Bagaglini, L.; Falco, P.; Zambianchi, E. Eddy detection in HF radar-derived surface currents in the Gulf of Naples. Remote Sens. 2019, 12, 97. [Google Scholar] [CrossRef]
- Roarty, H.; Cook, T.; Hazard, L.; George, D.; Harlan, J.; Cosoli, S.; Wyatt, L.; Alvarez Fanjul, E.; Terrill, E.; Otero, M.; et al. The Global High Frequency Radar Network. Front. Mar. Sci. Front. Media 2019, 6, 164. [Google Scholar] [CrossRef]
- Anderson, S.J.; Darces, M.; Helier, M.; Payet, N. Accelerated convergence of genetic algorithms for application to real-time problems. In Proceedings of the 4th International Symposium on Inverse Problems, Design and Optimization, Albi, France, 26–28 June 2013. [Google Scholar]
- Available online: https://www.maritimemanual.com/types-of-fishing-vessels (accessed on 12 November 2022).
- Klocker, A.; Abernathey, R. Global patterns of mesoscale eddy properties and diffusivities. J. Phys. Oceanogr. 2014, 44, 1030–1046. [Google Scholar] [CrossRef]
- Chelton, D.B.; Schlax, M.G.; Samuelson, R.M. Global observations of nonlinear mesoscale eddies. Prog. Oceanogr. 2011, 91, 167–216. [Google Scholar] [CrossRef]
- Rohrs, J.; Christensen, H.K.; Vikebø, F.; Sundby, S.; Saetra, Ø.; Brostrom, G. Wave-induced transport and vertical mixing of pelagic eggs and larvae. Limnol. Oceanogr. 2014, 59, 1213–1227. [Google Scholar] [CrossRef]
- Williams, R.G. Ocean eddies and plankton blooms. Nat. Geosci. 2011, 4, 739–740. [Google Scholar] [CrossRef]
- Gode, O.R.; Samuelsen, A.; Macaulay, G.J.; Patel, R.; Hjollo, S.S.; Horne, J.; Kaartvedt, S.; Johannessen, J.A. Mesoscale eddies are oases for higher trophic marine life. PLoS ONE 2012, 7, e30161. [Google Scholar] [CrossRef] [PubMed]
- Penna, A.D.; Gaube, P. Mesoscale eddies structure mesopelagic communities. Front. Mar. Sci. 2020, 7, 454. [Google Scholar] [CrossRef]
- Schmid, M.S.; Cowen, R.K.; Robinson, K.; Luo, J.Y.; Briseno-Avena, C.; Sponaugle, S. Prey and predator overlap at the edge of a mesoscale eddy: Fine-scale, in-situ distributions to inform our understanding of oceanographic processes. Sci. Rep. 2020, 10, 921. [Google Scholar] [CrossRef]
- Chang, Y.-L.; Miyazawa, Y.; Béguer-Pon, M. The dynamical impact of mesoscale eddies on migration of Japanese eel larvae. PLoS ONE 2017, 12, e0172501. [Google Scholar] [CrossRef]
- Suthers, I. Cited in CSIROscope, 3 June 2015. Available online: https://blog.csiro.au/expedition-to-study-ocean-eddies/ (accessed on 12 November 2022).
- Wang, X.; Wang, H.; Liu, D.; Wang, W. The prediction of oceanic mesoscale eddy properties and propagation trajectories based on machine learning. Water 2020, 12, 2521. [Google Scholar] [CrossRef]
- Available online: https://globalfishingwatch.org/research/global-footprint-of-fisheries/ (accessed on 12 November 2022).
- Kurup, N.V.; Shi, S. Study of nonlinear internal waves and impact on offshore drilling units. In Proceedings of the ASME 30th International Conference on Ocean, Offshore and Arctic Engineering, Rotterdam, The Netherlands, 19–24 June 2011. [Google Scholar] [CrossRef]
- Hein, J.R.; Mizell, K.; Koschinsky, A.; Conrad, T.A. Deep-ocean mineral deposits as a source of critical metals for high- and green-technology applications: Comparison with land-based resources. Ore Geol. Rev. 2013, 51, 1–14. [Google Scholar] [CrossRef]
- Sharma, R. Approach towards Deep-Sea Mining: Current Status and Future Prospects. In Perspectives on Deep-Sea Mining; Sustainability, Technology, Environmental Policy and Management; Springer: Cham, Switzerland, 2022. [Google Scholar]
- Miller, K.A.; Thompson, K.F.; Johnston, P.; Santillo, D. An overviews of seabed mining including the current state of development, environmental impacts, and knowledge gaps. Front. Mar. Sci. 2018, 4, 418. [Google Scholar] [CrossRef]
- Sharma, R. (Ed.) Environmental Issues of Deep Sea Mining: Impacts, Consequences and Policy Perspectives; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-12696-4 (eBook). [Google Scholar] [CrossRef]
- Fukushima, T.; Tsune, A.; Sugishima, H. Comprehensive Understanding of Seafloor Disturbance and Environmental Impact Scenarios. In Perspectives on Deep-Sea Mining; Sustainability, Technology, Environmental Policy and Management; Springer: Cham, Switzerland, 2020; pp. 313–337. [Google Scholar] [CrossRef]
- Available online: https://www.isa.org.jm/ (accessed on 12 November 2022).
- International Union for the Conservation of Nature, Deep-sea mining, Issues Brief May 2022. Available online: https://www.iucn.org/resources/issues-brief/deep-sea-mining (accessed on 18 September 2022).
- Hylton, W.S. History’s Largest Mining Operation Is About to Begin. The Atlantic, January–February 2020 Issue. Available online: https://www.theatlantic.com/magazine/archive/2020/01/20000-feet-under-the-sea/603040/ (accessed on 12 November 2022).
- Deep-sea Mining. US Govt. Accountability Office Science & Tech Spotlight, 15 December 2021, GAO-22-105507. Available online: https://www.gao.gov/products/gao-22-105507 (accessed on 3 February 2022).
- Helmons, R.; de Wit, L.; de Stigter, H.; Spearman, J. Dispersion of benthic plumes in deep-sea mining: What lessons can be learned from dredging? Front. Earth Sci. 2022, 10, 868701. [Google Scholar] [CrossRef]
- Marshall, W.F.; Barnum, J.R. Measurement of Sea Scatter and Buoy Tracks at Long Ranges by High-Resolution OTH-B Radar; Stanford Research Institute Technical Report 1; Stanford Research Institute: Stanford, CA, USA, 1975. [Google Scholar]
- Li, L.; Wu, X.; Yan, S.; Long, C.; Liu, B.; Shen, Z. Drifter trajectory tracking experiment and analysis with multi-frequency HFSWR in the East China Sea. Wuhan Univ. J. Nat. Sci. 2011, 16, 541–547. [Google Scholar] [CrossRef]
- Kumar, N.; Cahl, D.L.; Crosby, S.C.; Voulgaris, G. Bulk versus spectral wave parameters: Implications on Stokes drift estimates, regional wave modelling, and HF radars applications. J. Phys. Oceanogr. 2017, 47, 1413–1431. [Google Scholar] [CrossRef]
- Breivik, O.; Janssen, P.A.E.M.; Bidlot, J.-R. Approximate Stokes Drift Profiles in Deep Water; European Centre for Medium-Range Weather Forecasting Technical Memorandum 716; ECMWF: Reading, UK, 2013. [Google Scholar]
- Dagestad, K.-F.; Rohrs, J. Prediction of ocean surface trajectories using satellite derived vs. modeled ocean currents. Remote Sens. Environ. 2019, 223, 130–142. [Google Scholar] [CrossRef]
- Christensen, K.H.; Breivik, O.; Dagestad, K.-F.; Rohrs, J.; Ward, B. Short-term predictions of oceanic drift. Oceanography 2018, 31, 59–67. [Google Scholar] [CrossRef]
- Breivik, O.; Allen, A.A.; Maisondieu, C.; Olagnon, M. Advances in search and rescue at sea. Ocean Dyn. 2013, 63, 83–88. [Google Scholar] [CrossRef]
- Van Sebille, E.; Aliani, S.; Law, K.L.; Maximenko, N.; Alsina, J.M.; Bagaev, A.; Bergmann, M.; Chapron, B.; Chubarenko, I.; Cózar, A.; et al. The physical oceanography of the transport of floating marine debris. Environ. Res. Lett. 2020, 15, 023003. [Google Scholar] [CrossRef]
- Available online: https://www.nasa.gov/mission_pages/hurricanes/features/hurricane_brew.html (accessed on 12 November 2022).
- Maresca, J.W., Jr.; Carlson, C.T. Tracking and Monitoring Hurricanes by HF Skywave Radar Over the Gulf of Mexico; Technical Report 1, Contract F49620-76-C-0023; SRI International: Menlo Park, CA, USA, 1977. [Google Scholar]
- Anderson, S.J. The remote sensing of tropical meteorological and oceanographic phenomena by over-the-horizon radar. In Proceedings of the 1st International Conference on Tropical Cyclones, Perth, Australia, 24 December 1979. [Google Scholar]
- Maresca, J.W., Jr.; Carlson, C.T. Comment on "Longshore currents on the fringe of hurricane Anita" by Ned P. Smith. J. Geophys. Res. 1980, 85, 1640–1641. [Google Scholar] [CrossRef]
- Maresca, J.W.; Carlson, C.T. High-frequency skywave radar measurements of Hurricane Anita. Science 1989, 209, 1189–1196. [Google Scholar] [CrossRef] [PubMed]
- Georges, T.M.; Harlan, J.A.; Meyer, L.R.; Peer, R.G. Tracking Hurricane Claudette with the U.S. Air Force OTH-B Radar; NOAA Technical memorandum ERL WPL-219; NOAA: Washington, DC, USA, 1992. [Google Scholar]
- Anderson, S.J. (Physics Department, University of Adelaide, Adelaide 5005, Australia). Unpublished work. 2019. [Google Scholar]
- Possner, A.; Caldeira, K. Geophysical potential for wind energy over the open oceans. Proc. Natl. Acad. Sci. USA 2017, 114, 11338–11343. [Google Scholar] [CrossRef]
- Available online: https://www.visualcapitalist.com/map-visualizing-40-years-of-nautical-piracy/ (accessed on 12 November 2022).
- ITOPF. Oil Tanker Spill Statistics 2021. Available online: https://www.itopf.org/knowledge-resources/data-statistics/statistics/ (accessed on 12 November 2022).
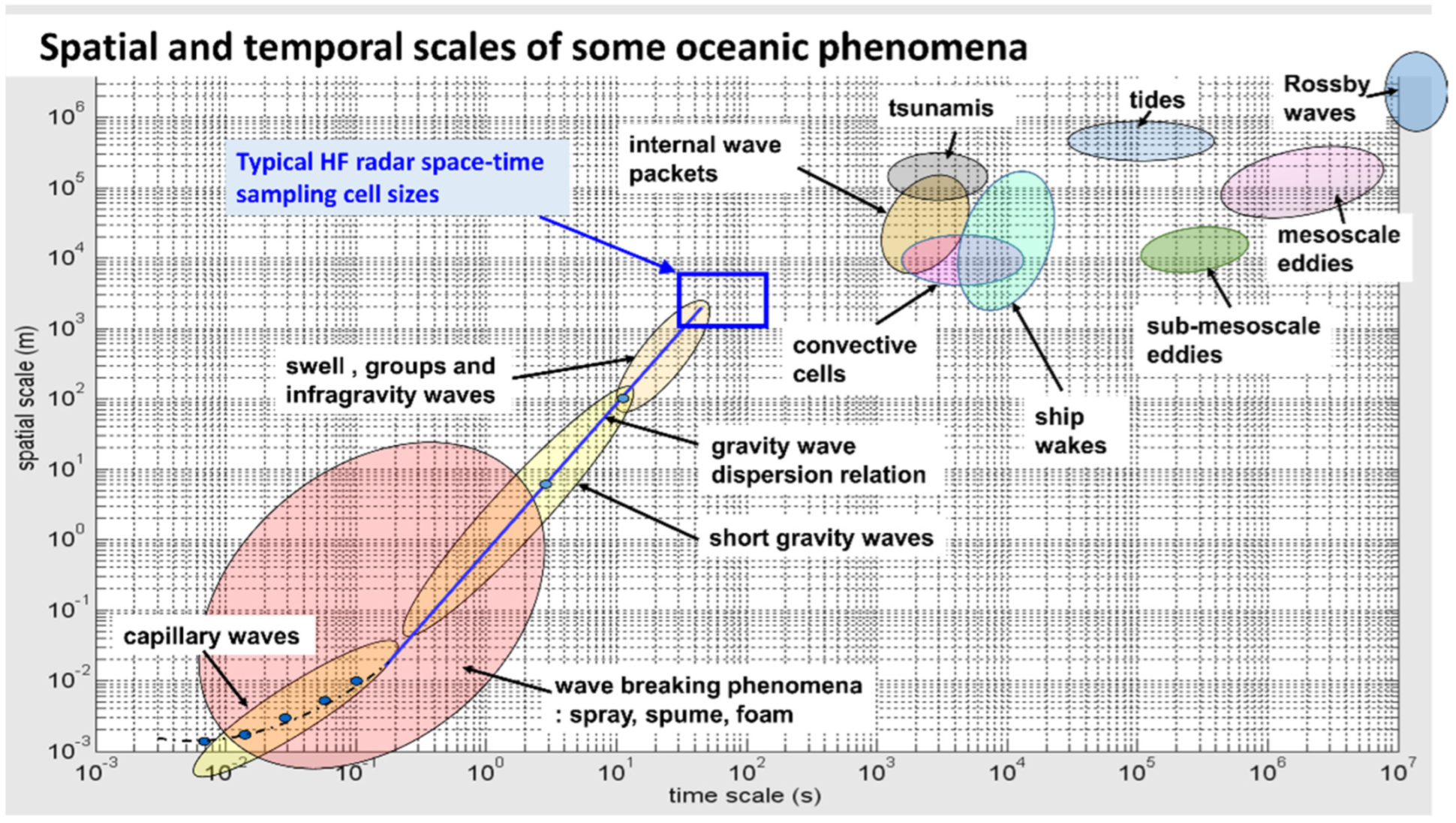
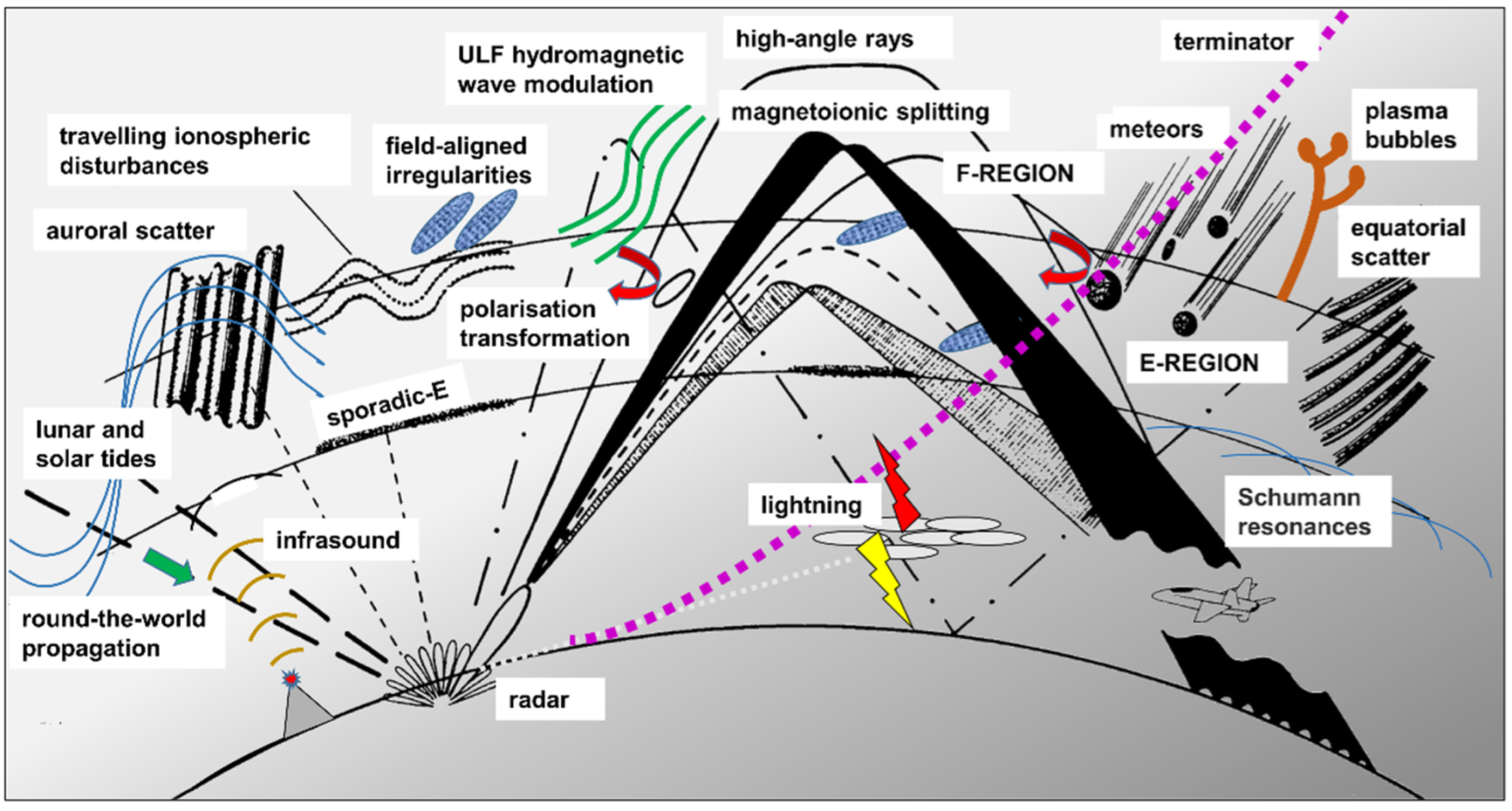
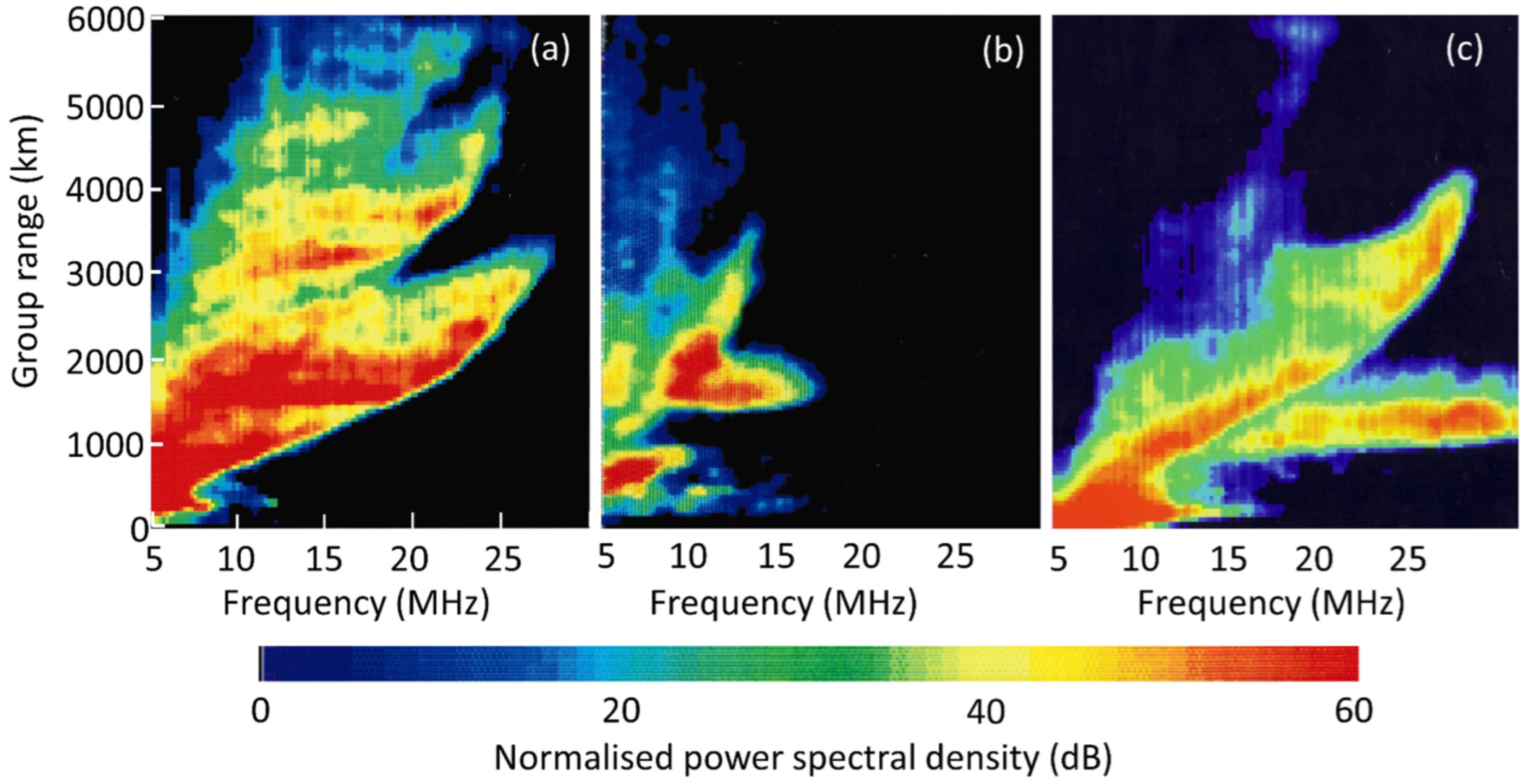
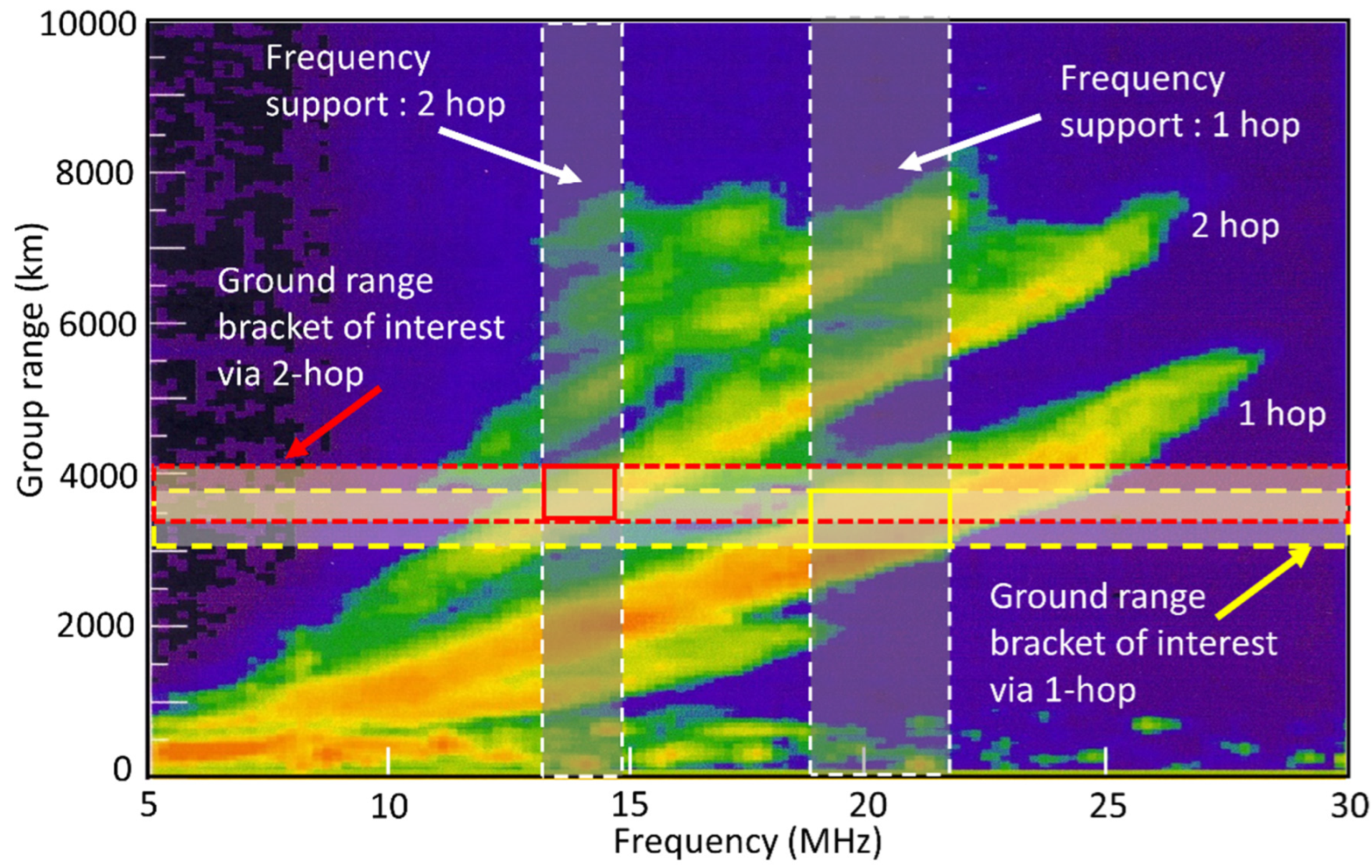

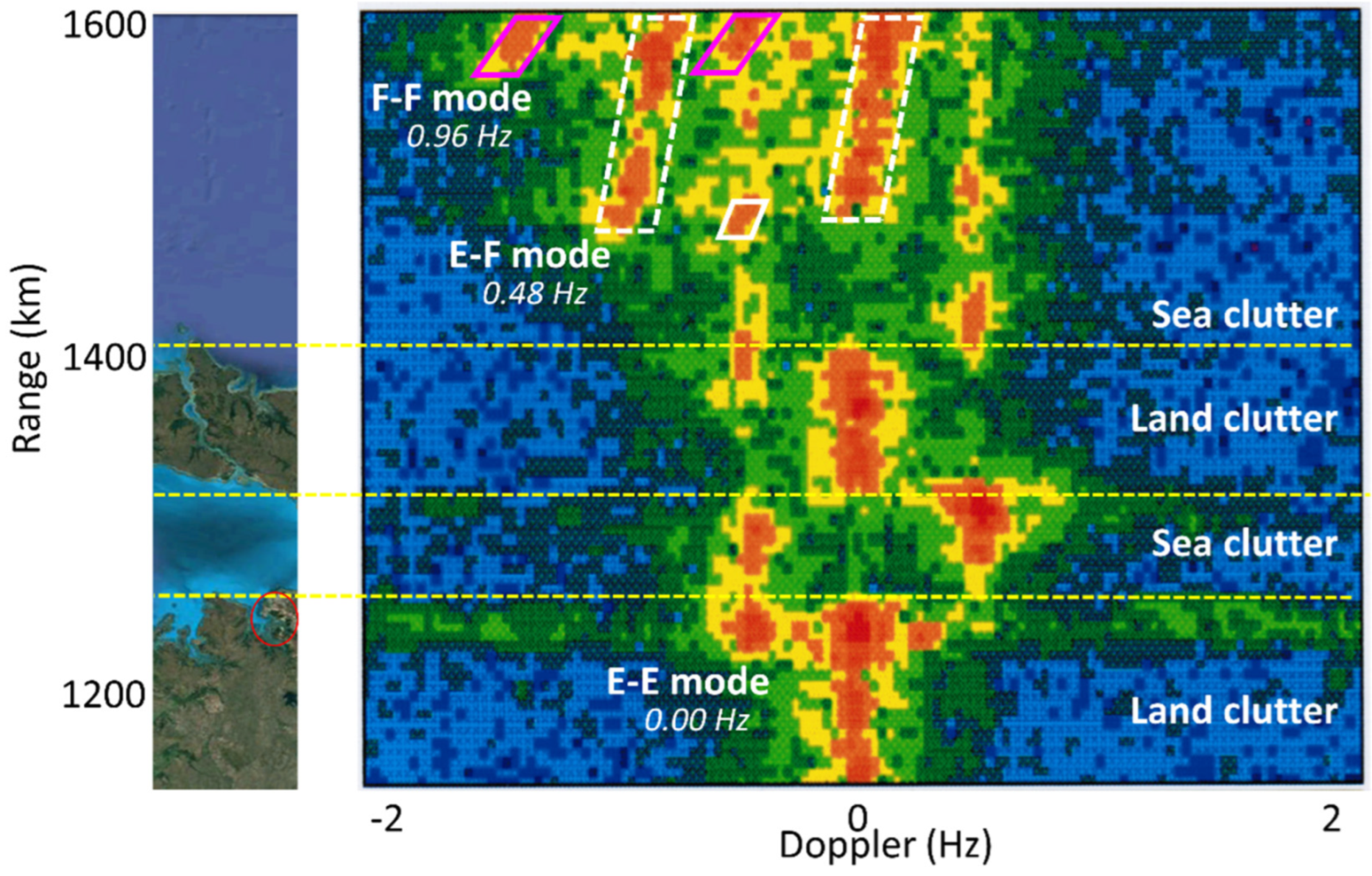
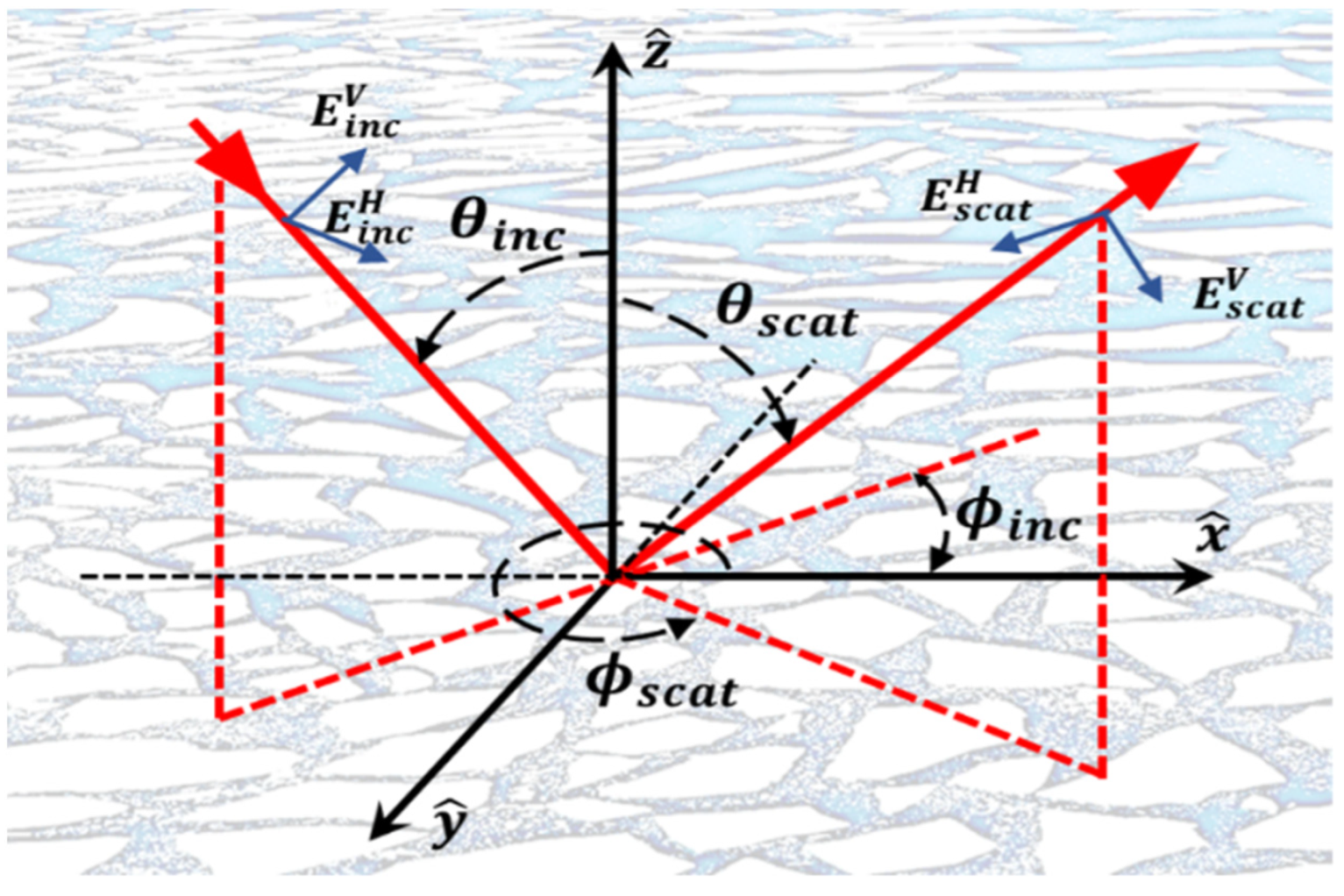
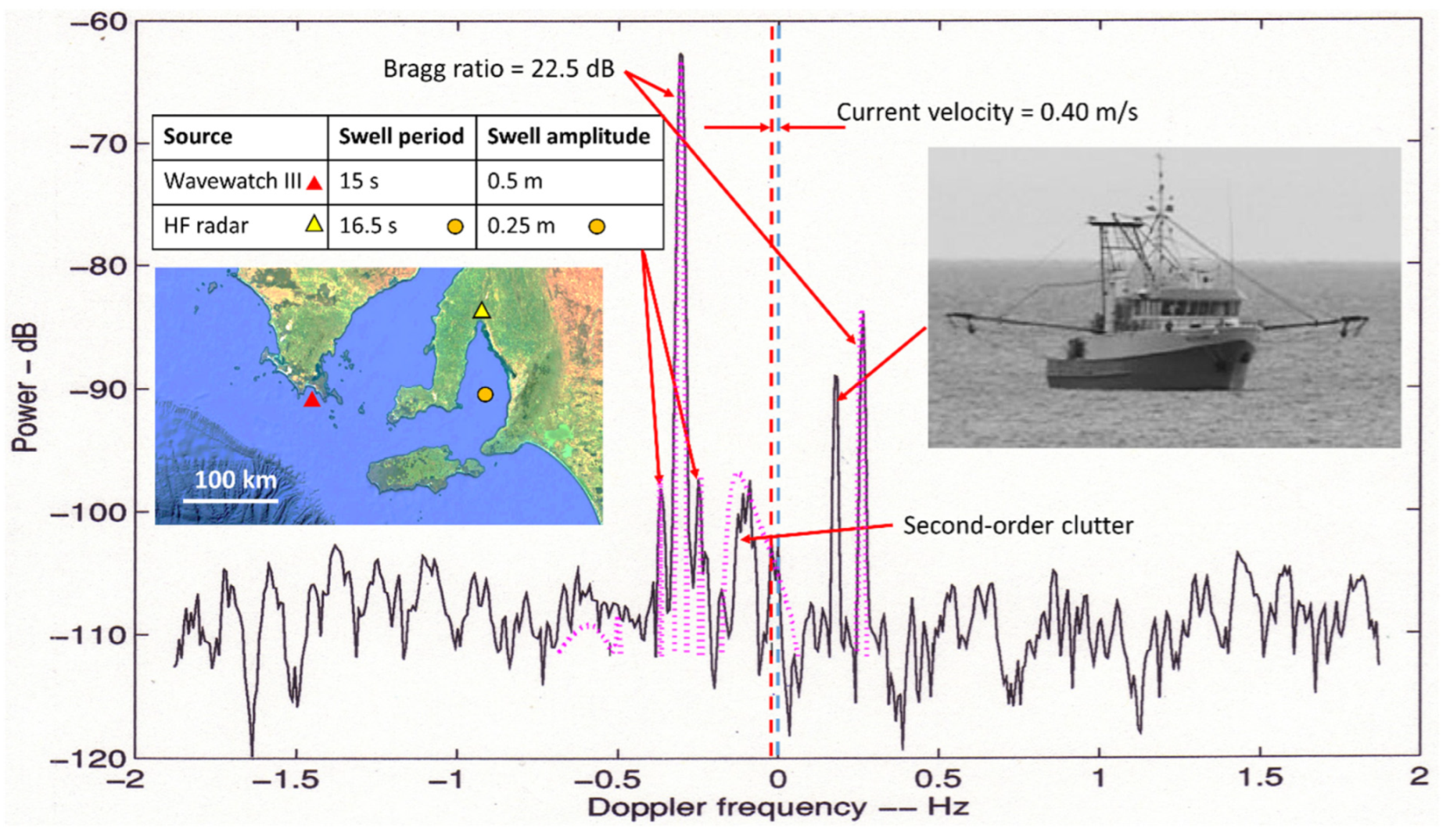

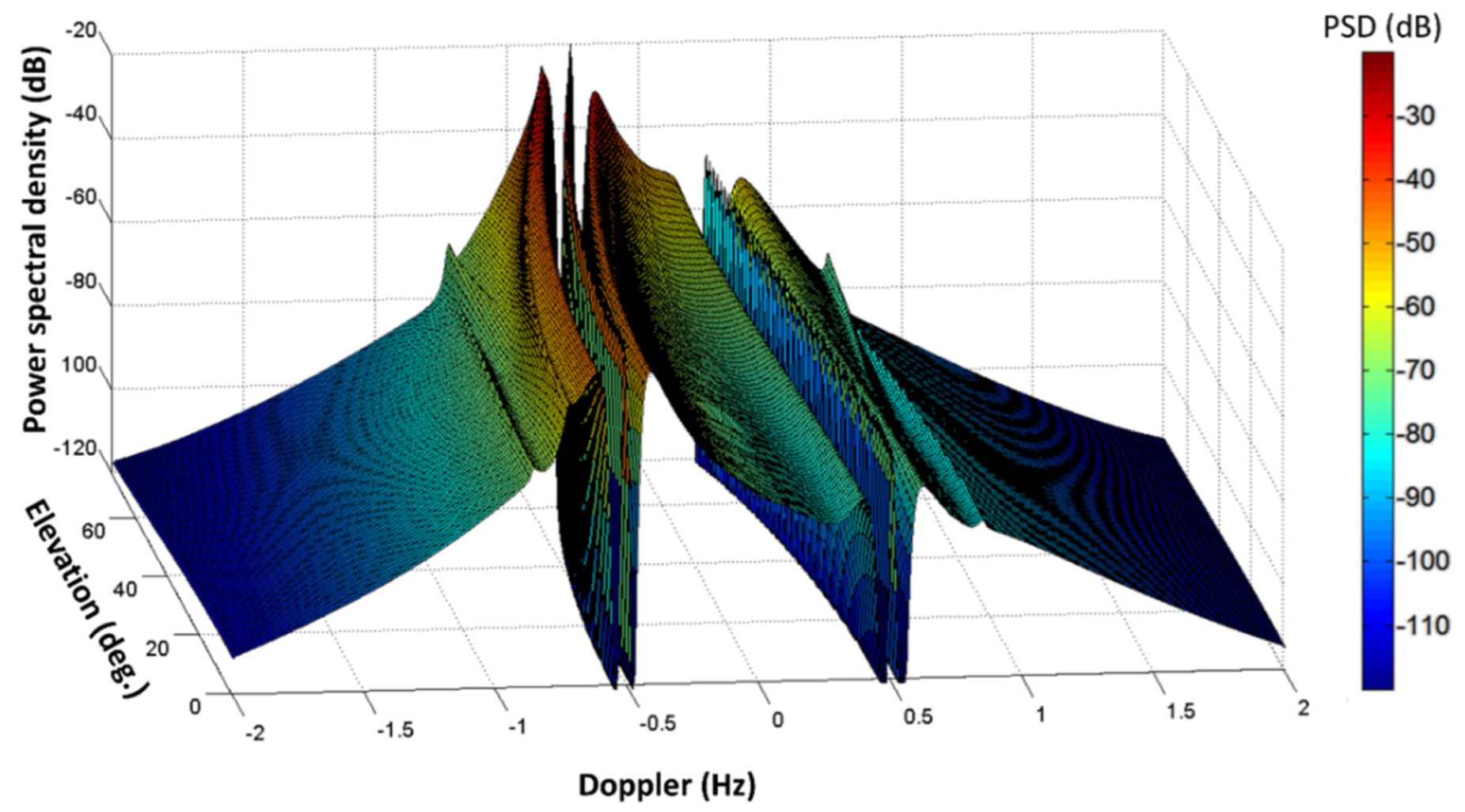
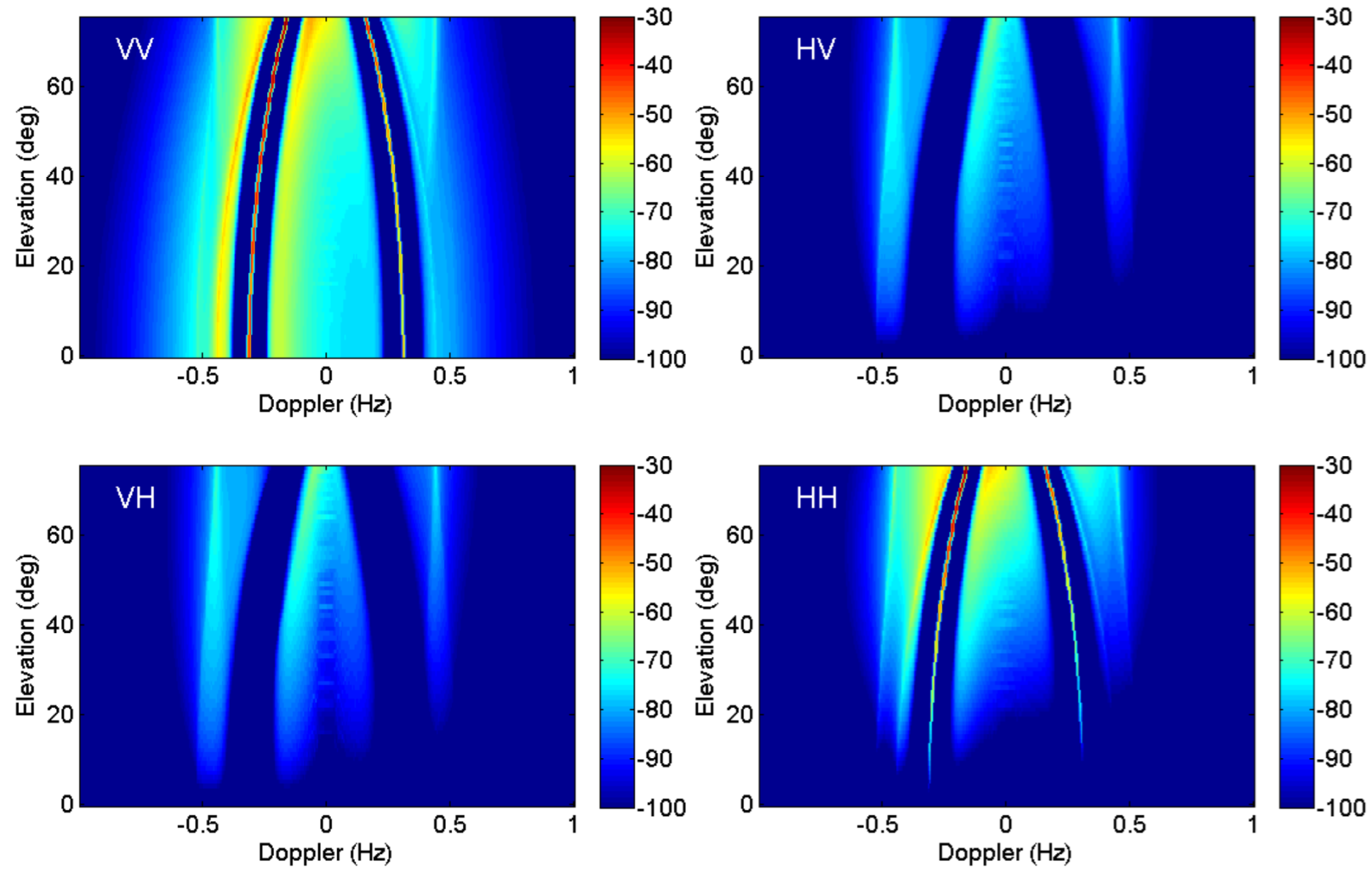
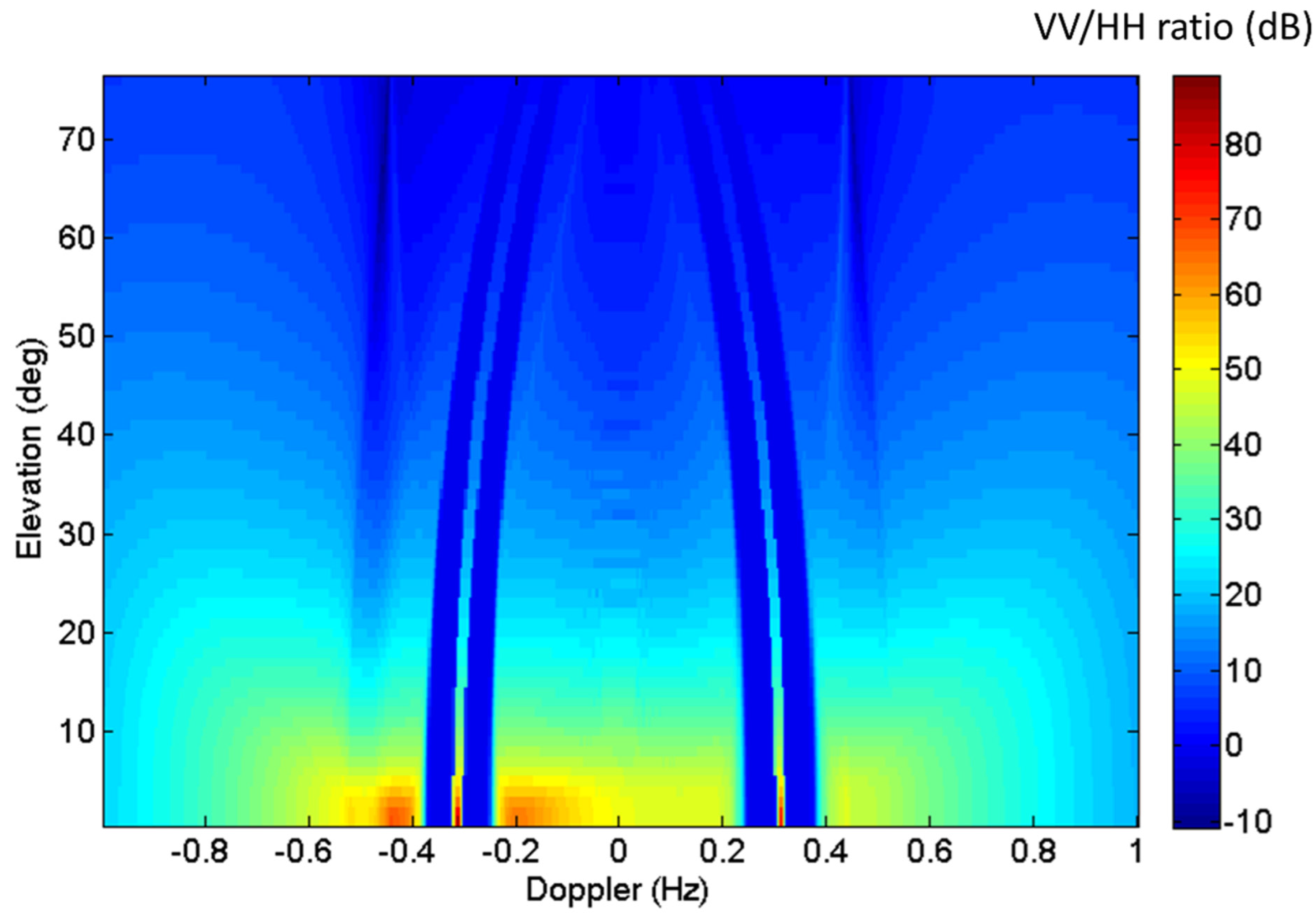
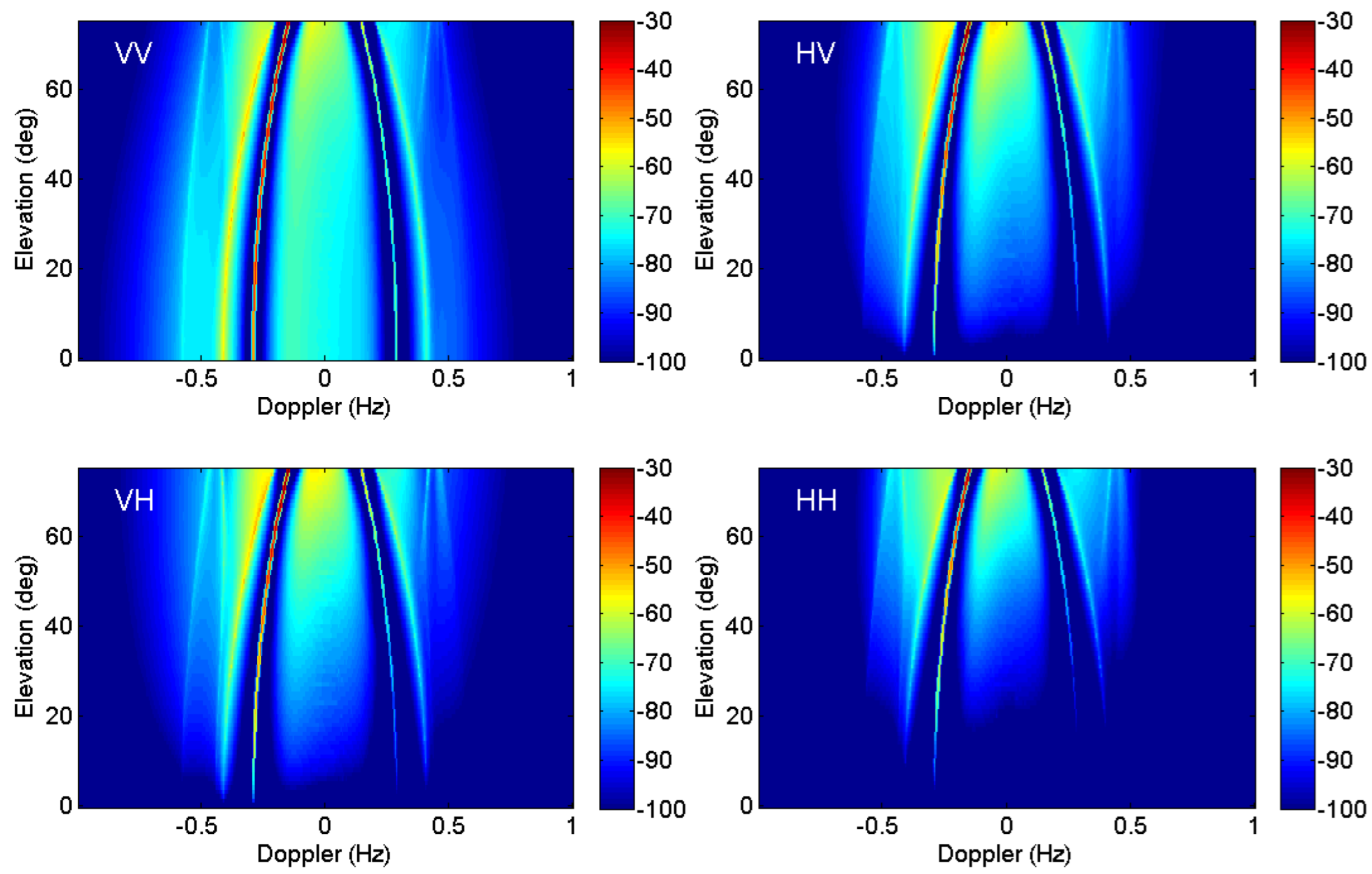
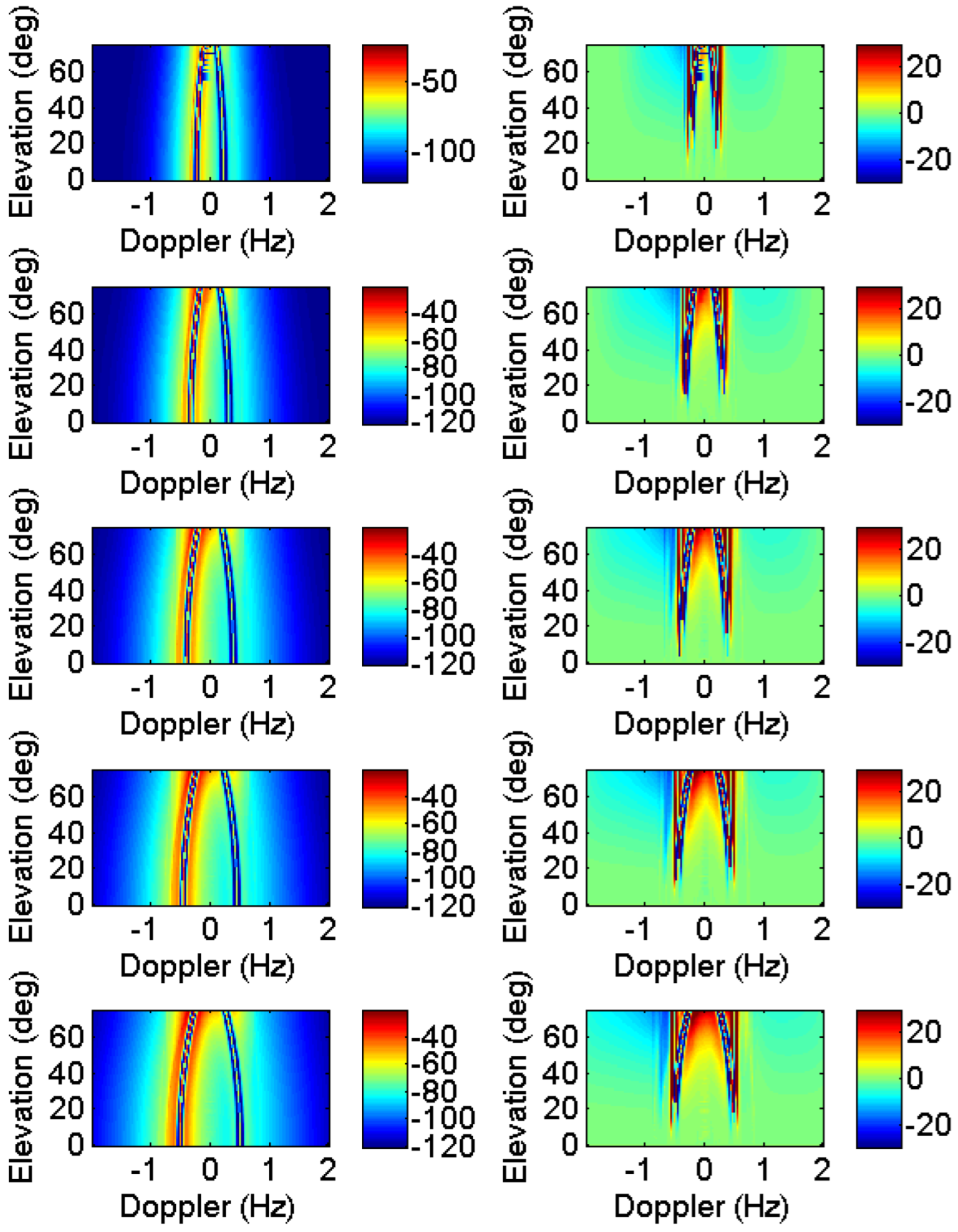
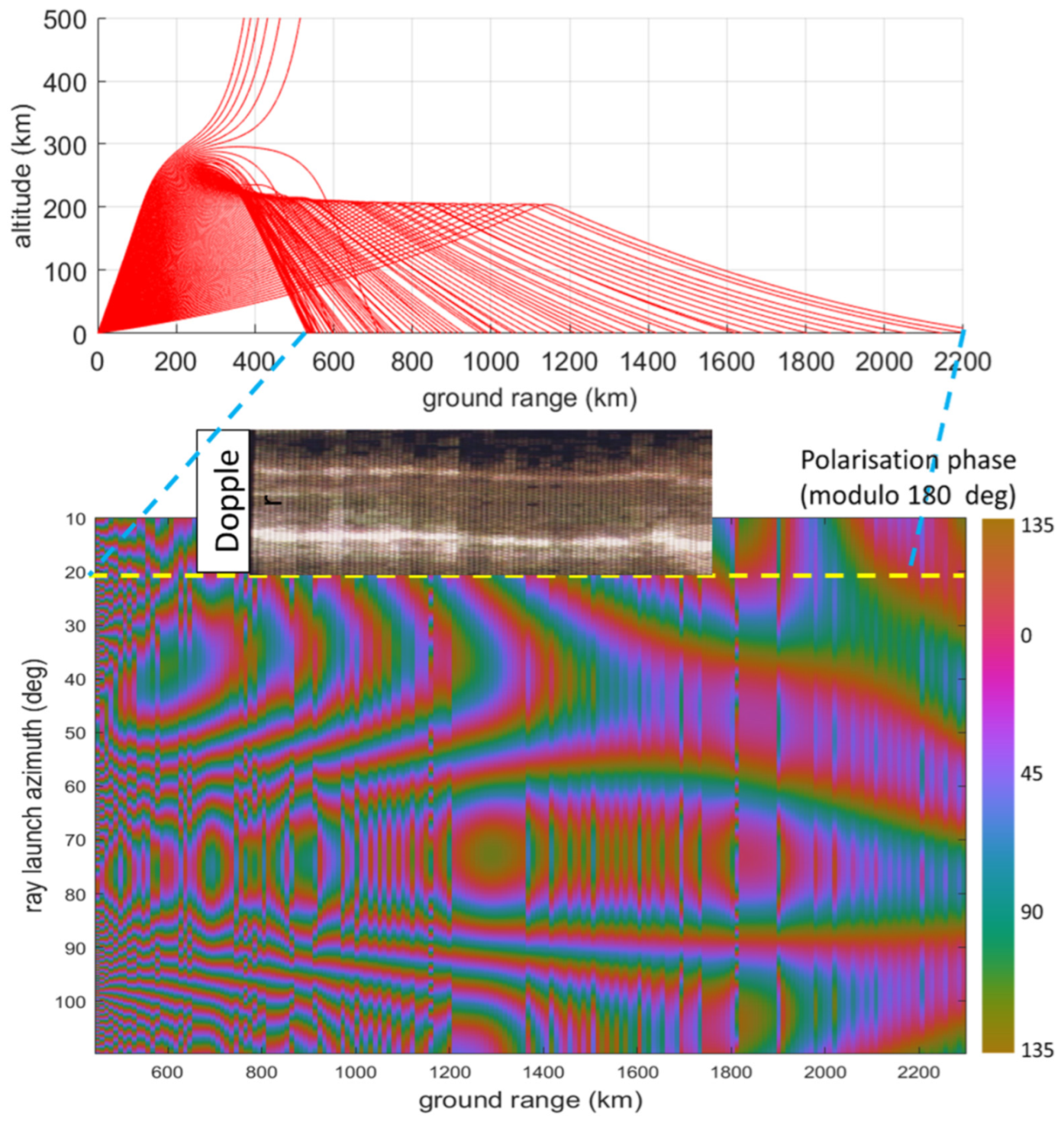


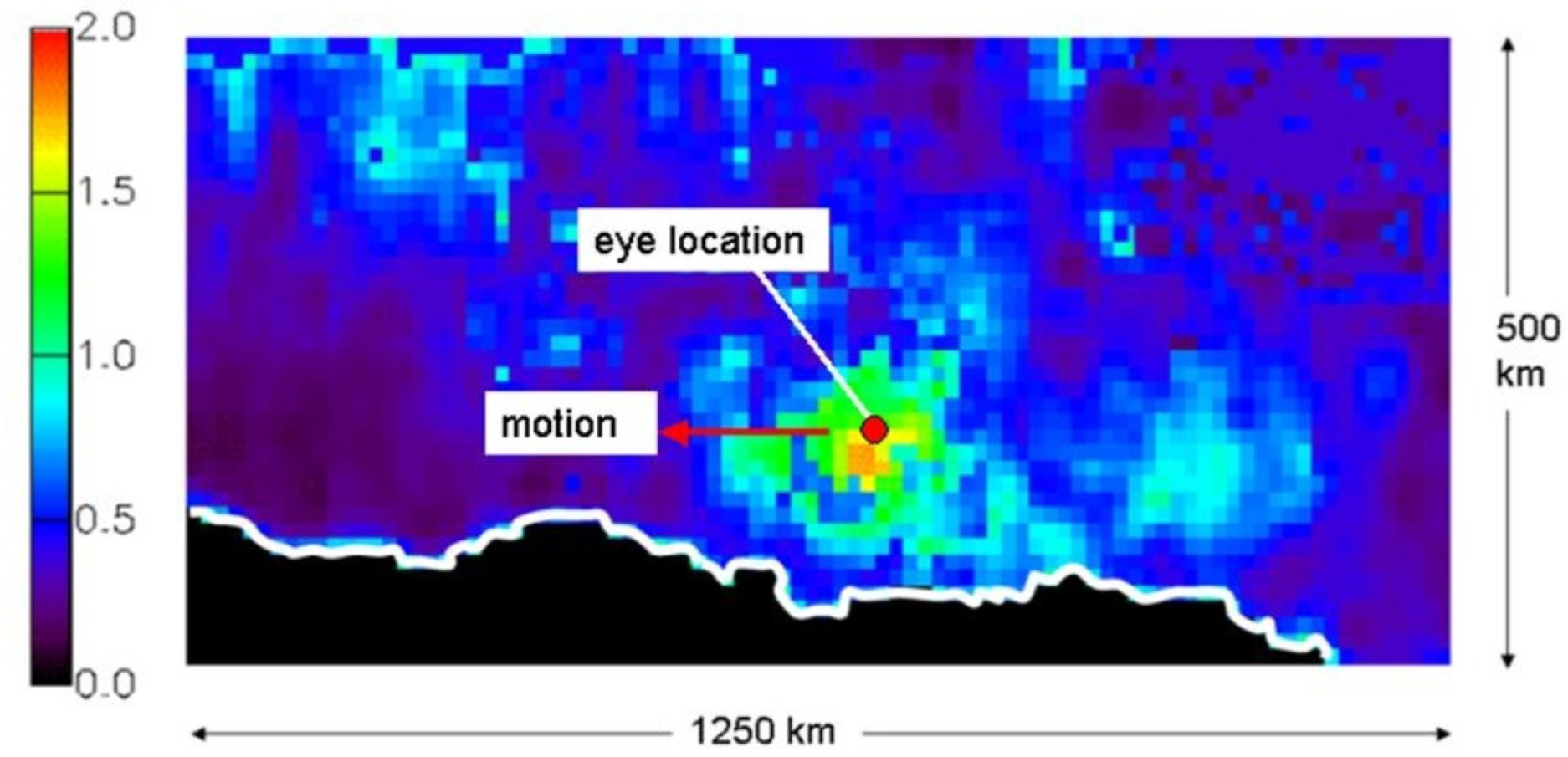
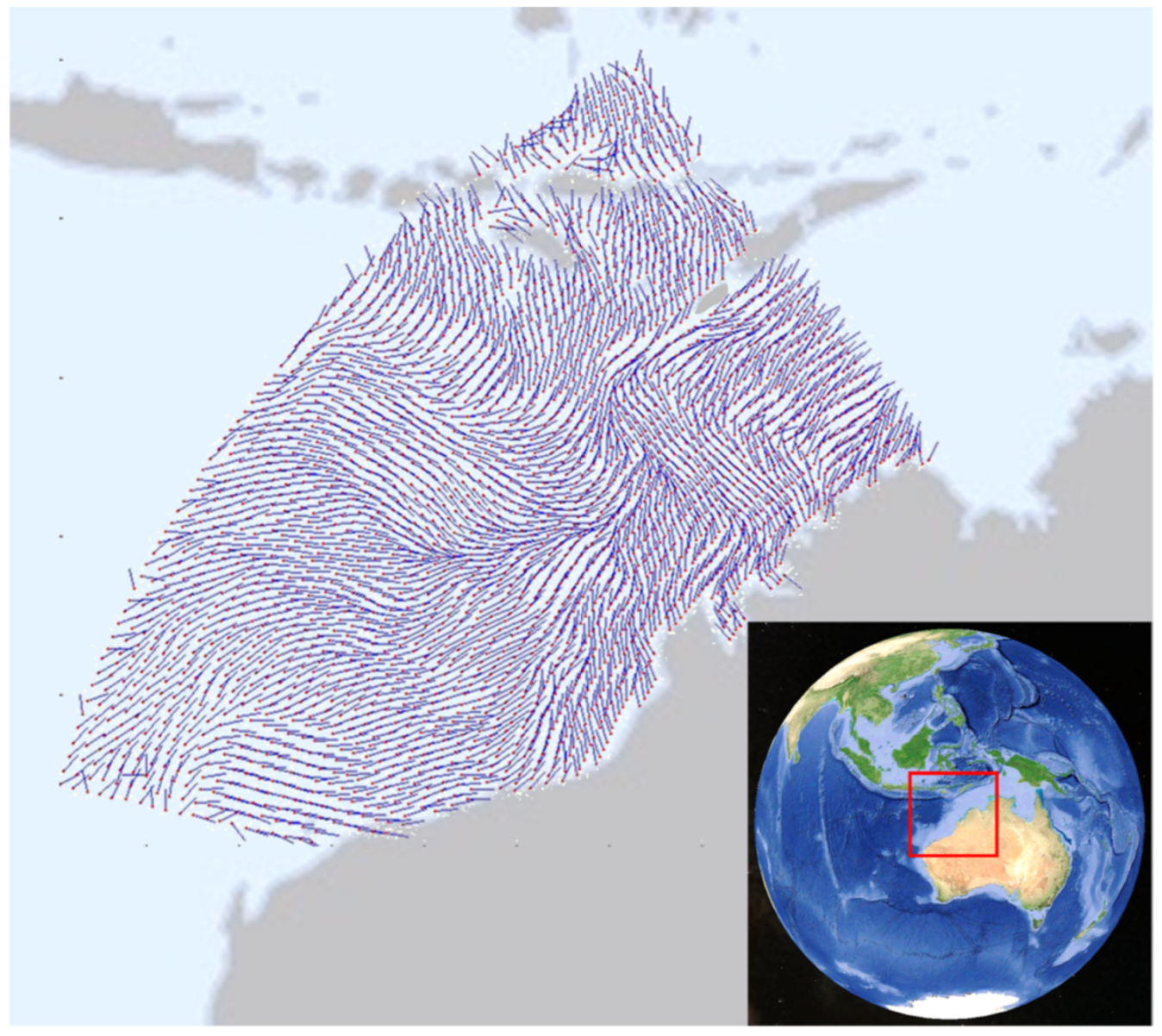
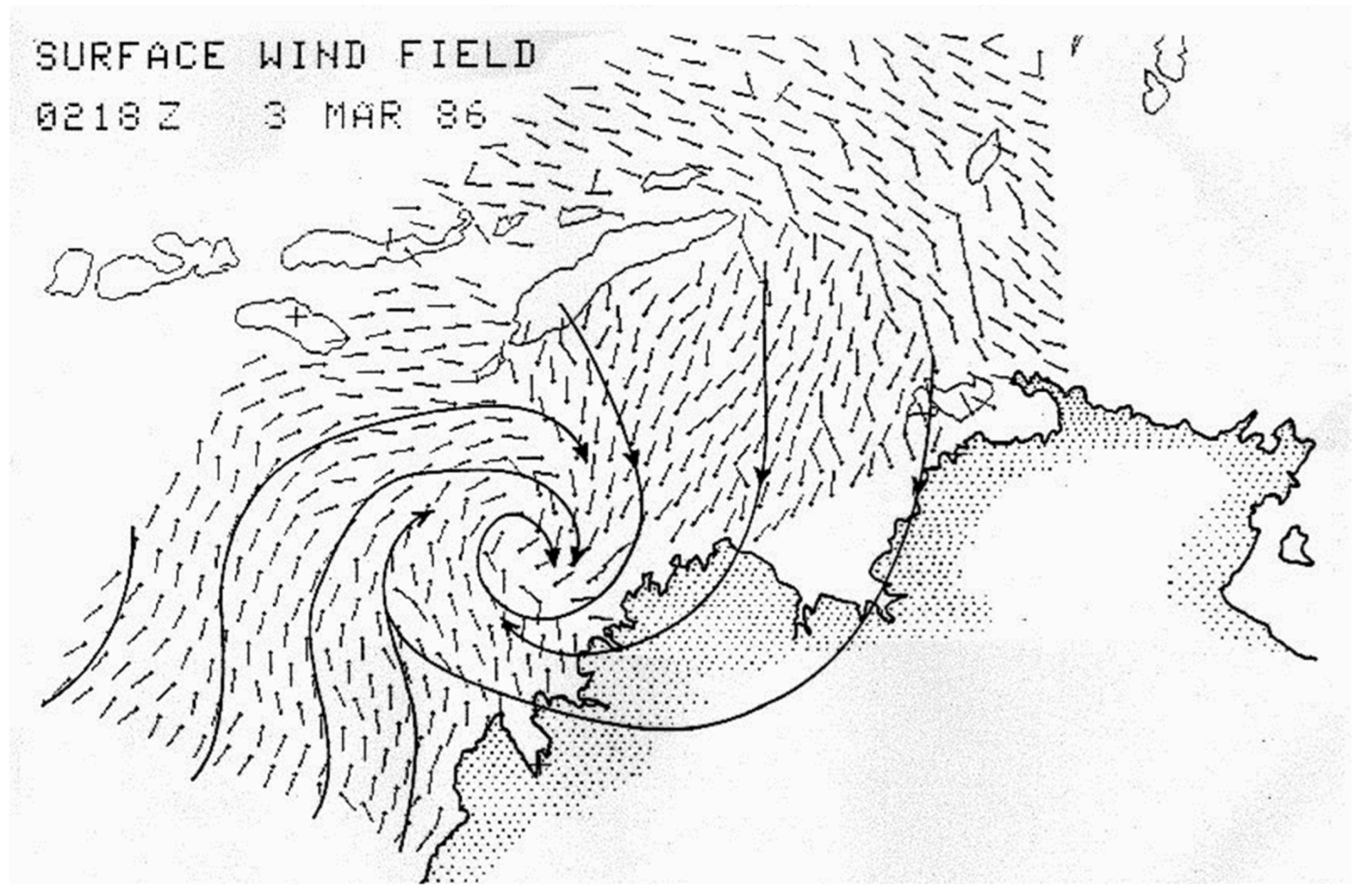


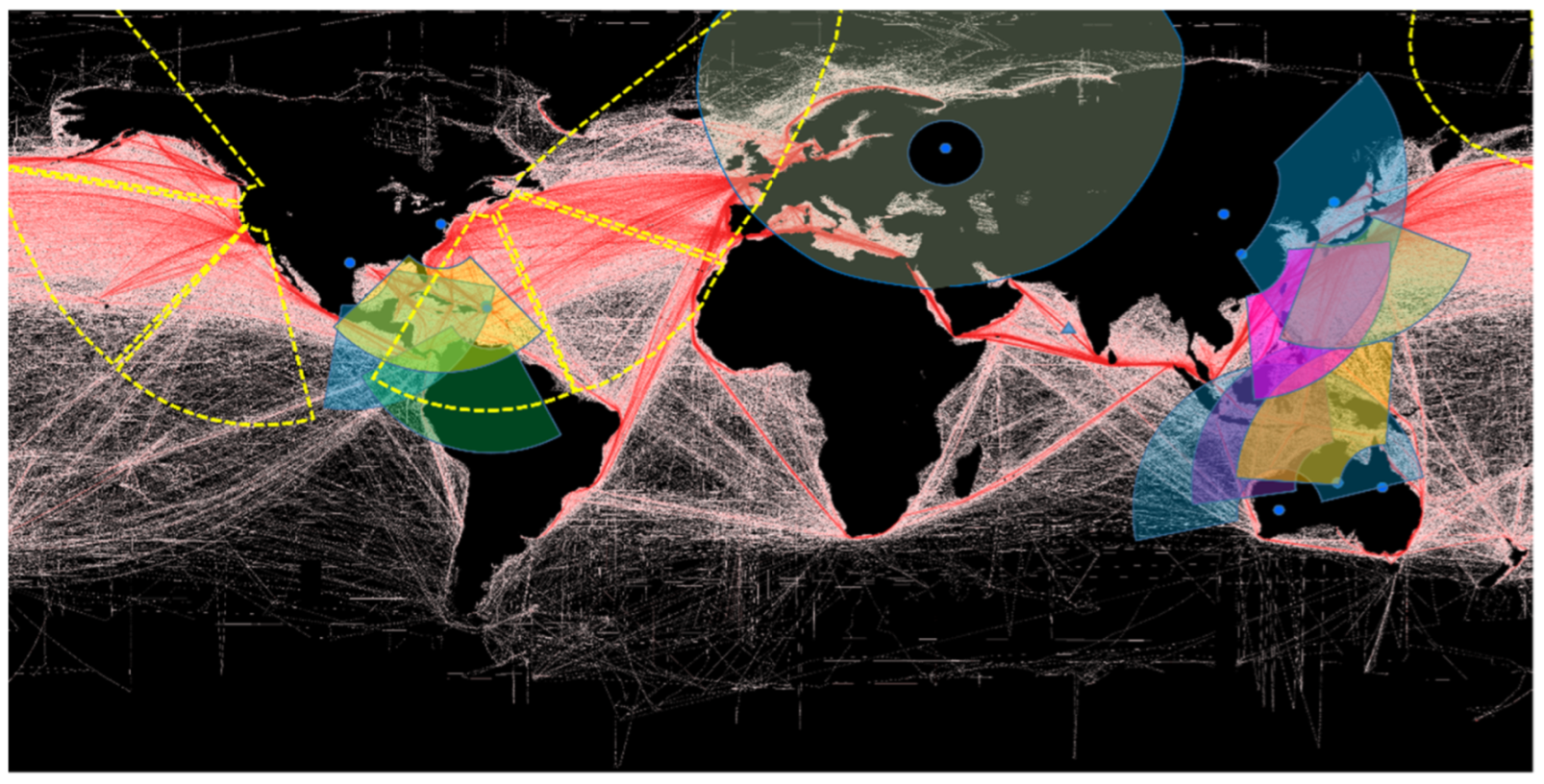
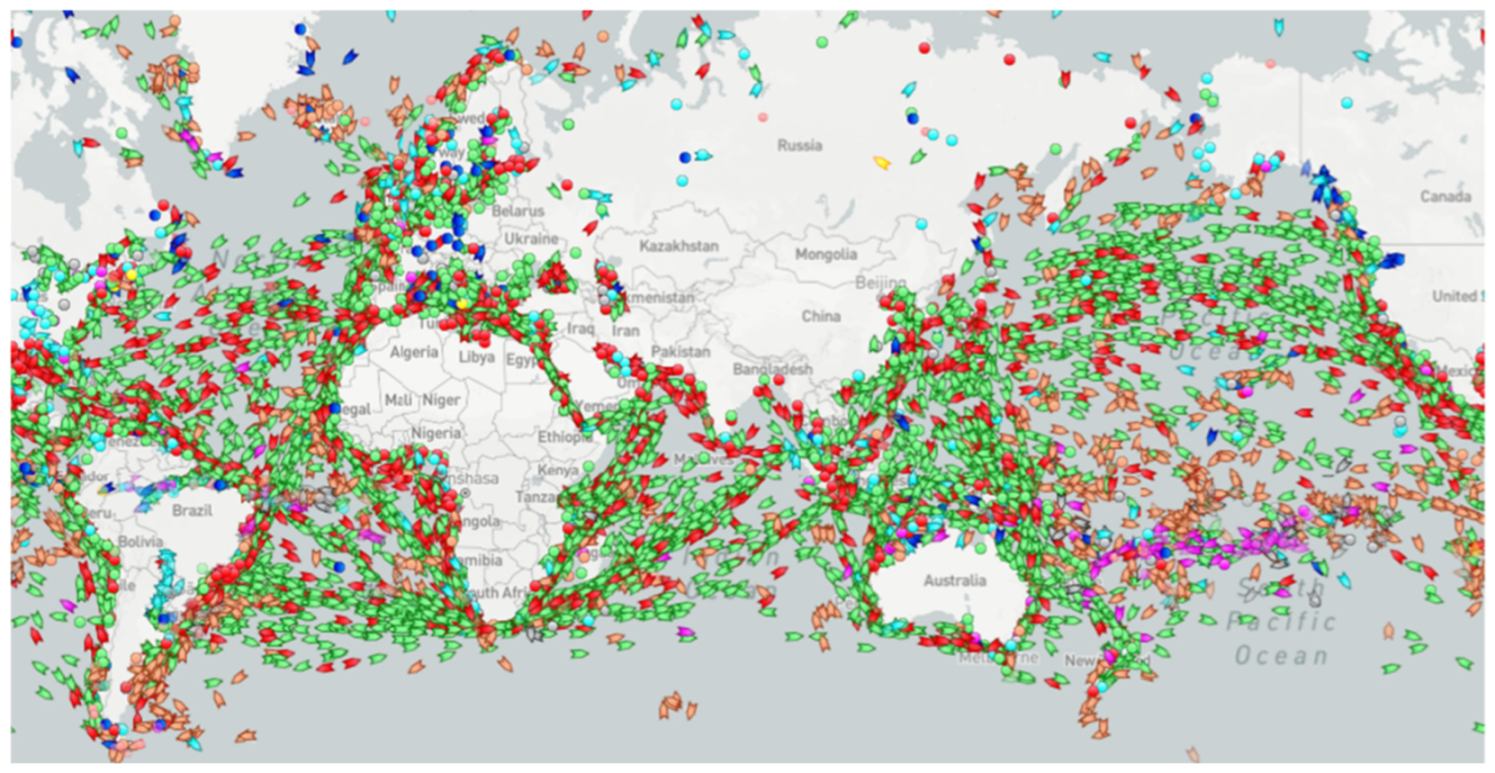
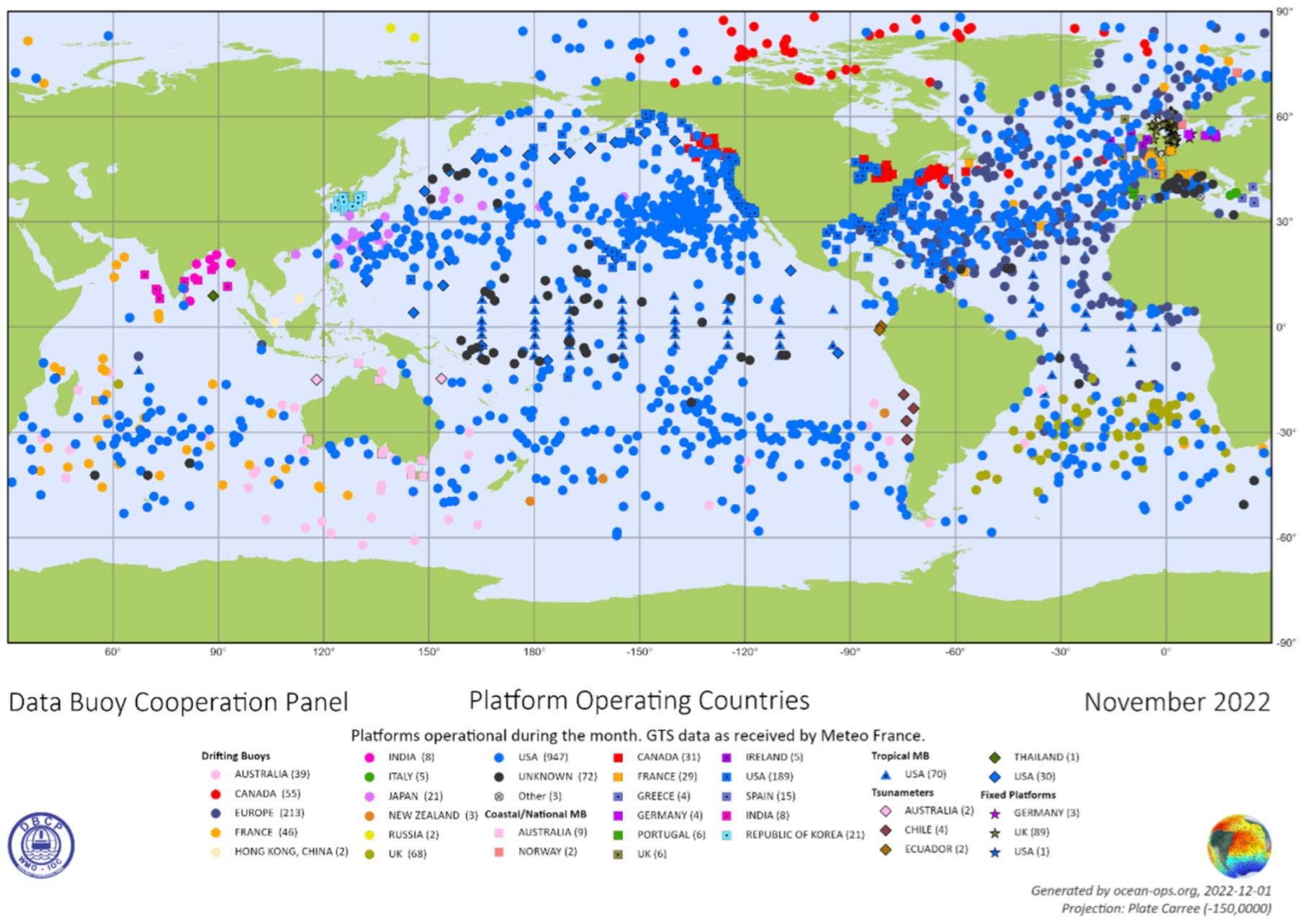





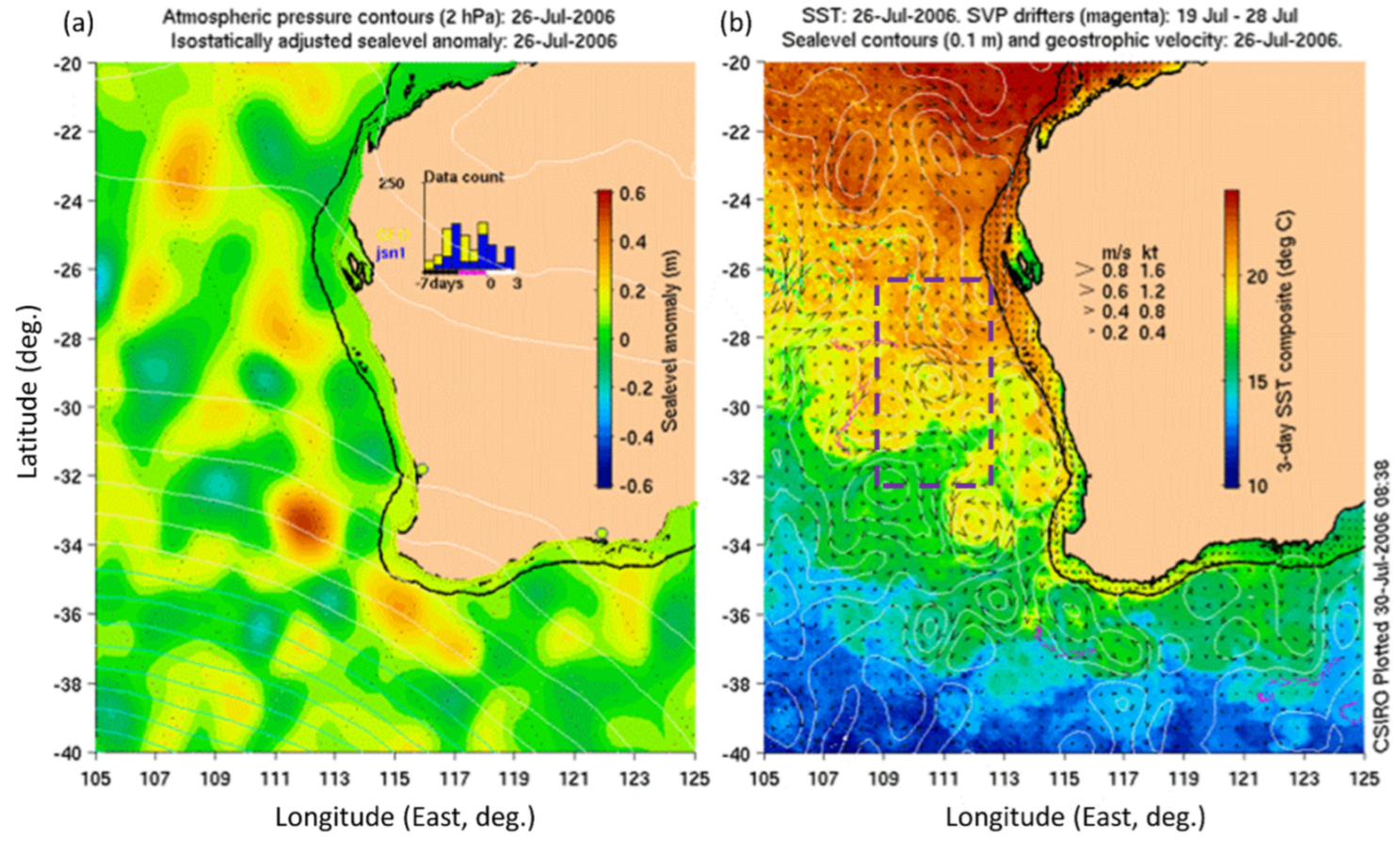


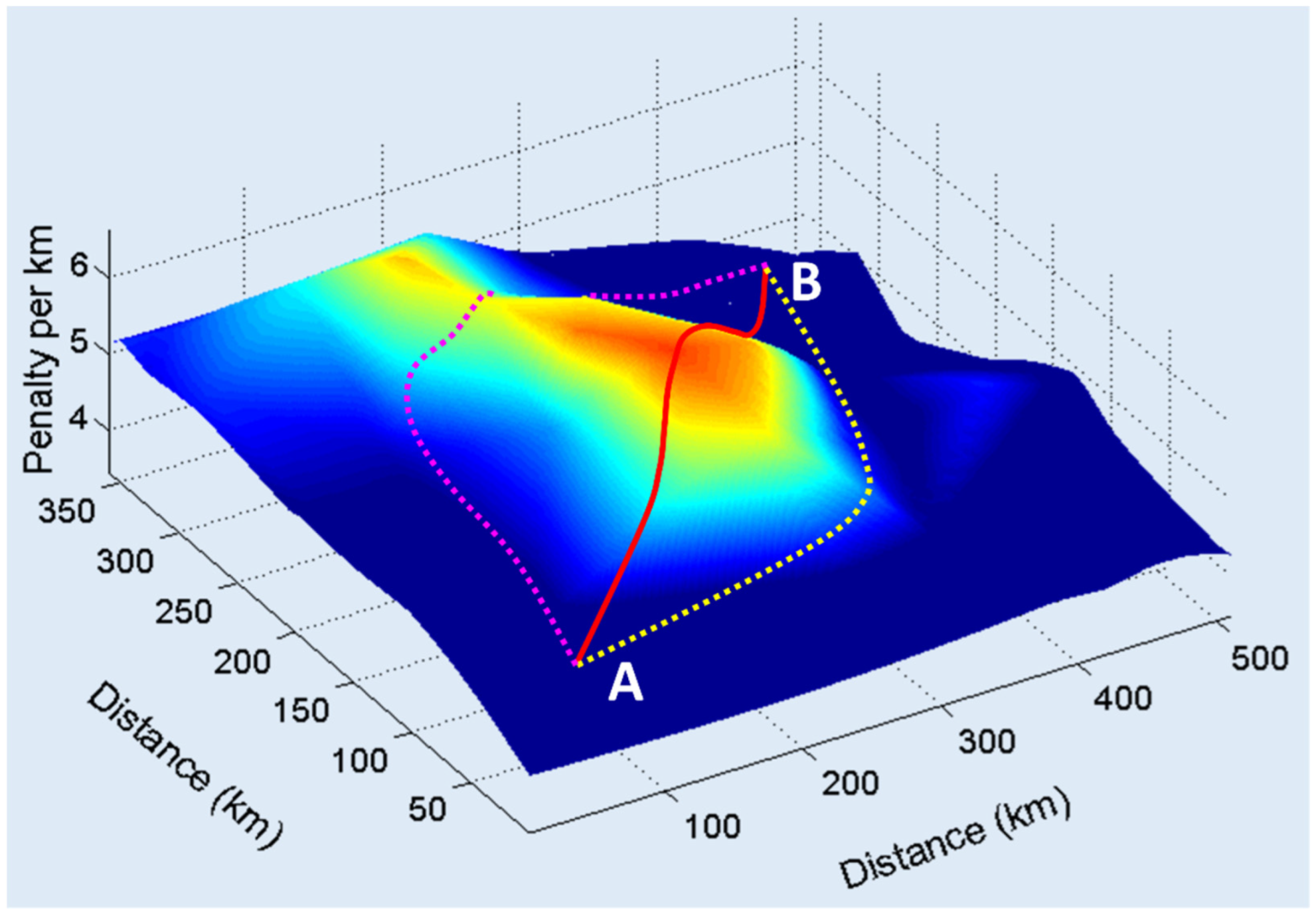
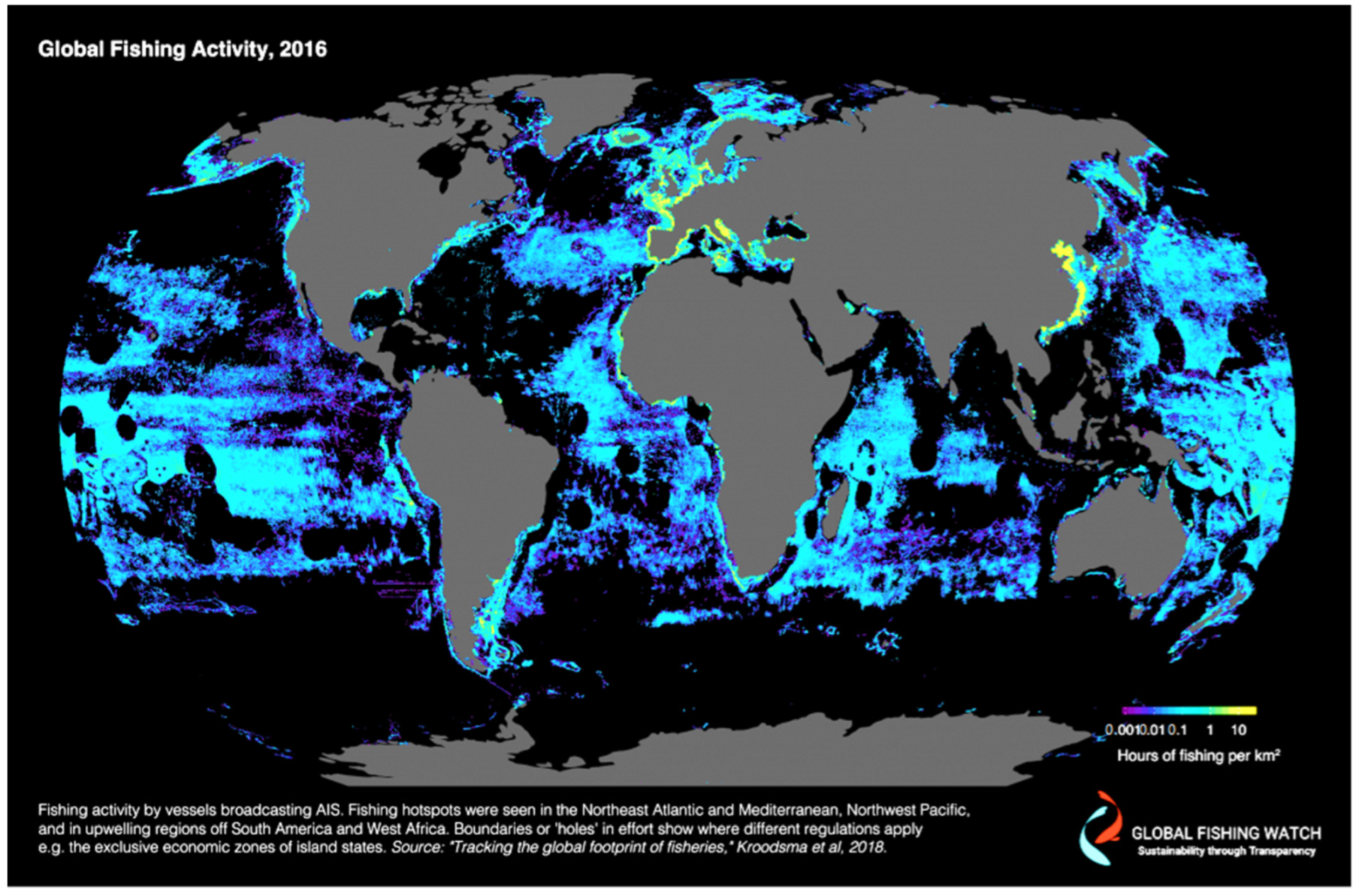



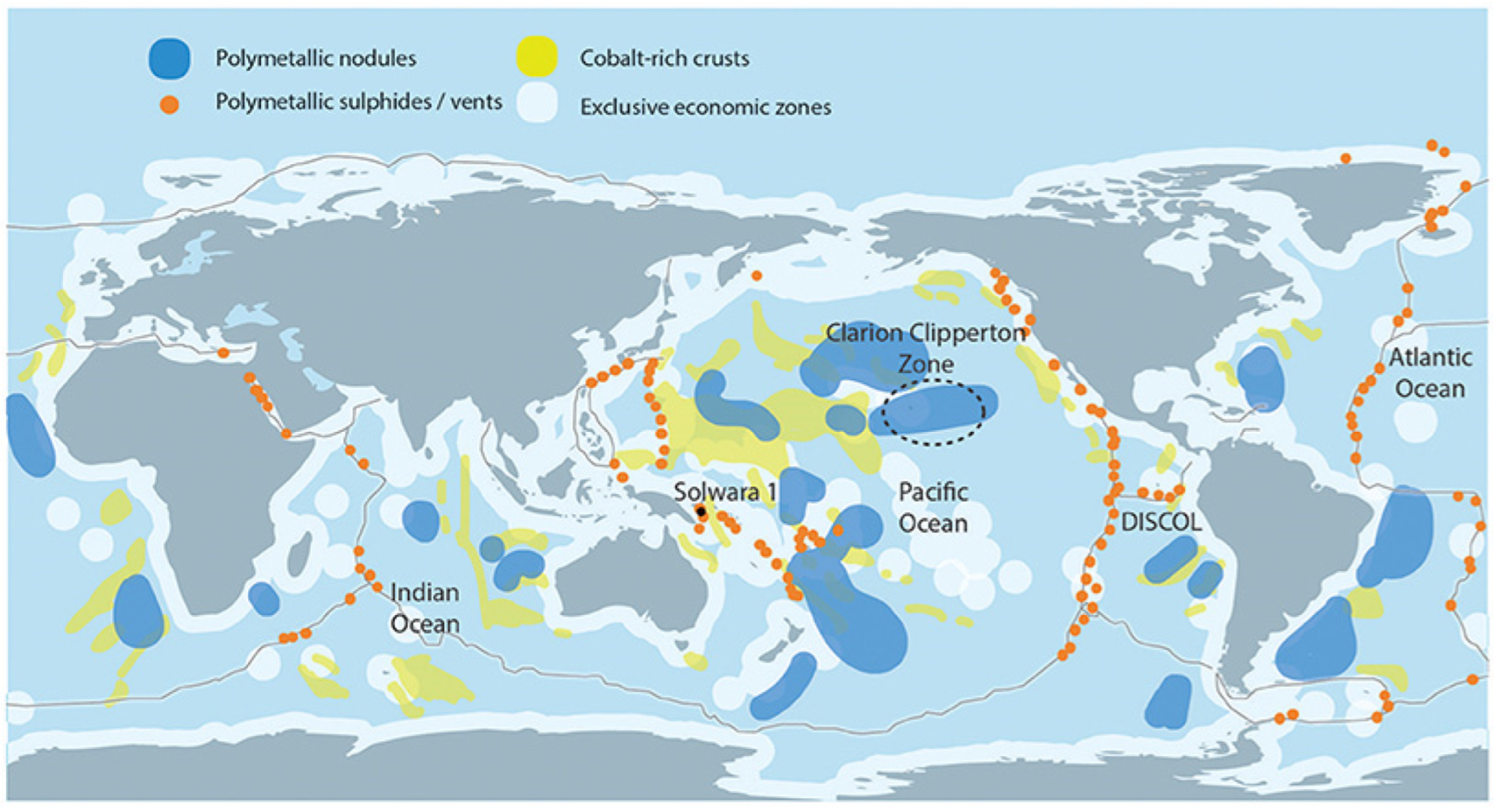


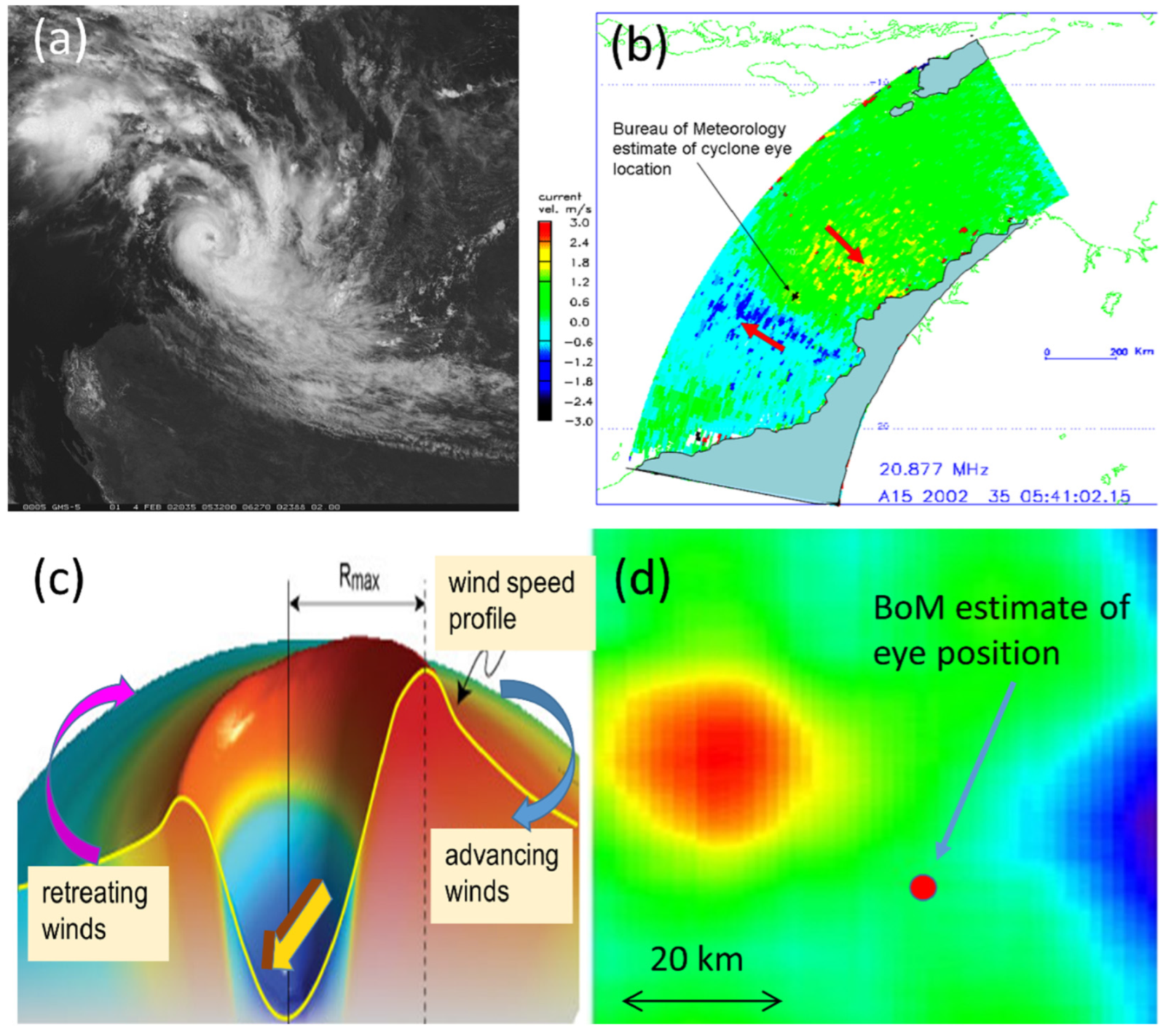

| Prospective Observable | Physical Mechanism for HF Radar Signature | Seen | Ref. |
|---|---|---|---|
| Internal waves | modulation of the gravity wave field by converging and diverging flows | Y | [83] |
| Convective cells | wave components generated by high wind stress combined with rain-induced damping | Y | [84] |
| Sea ice | wave dynamics changed as dispersion relation depends on ice type and thickness | Y | [85,86] |
| Rainfall | gravity waves damped by increased kinematic viscosity in the impacted surface layer | N | [87,88] |
| Ship wakes | additional spectral components superimposed on the ambient wave spectrum | Y | [89,90,91,92] |
| Mesoscale eddies | spiral current advection of surface gravity waves—cyclonic or anti-cyclonic | Y | - |
| Surfactants | short gravity waves damped by Marangoni damping and changed wind stress | N | [93] |
| Wave-train disintegration and recovery | Benjamin-Feir modulational instability and Fermi-Pasta-Ulam recurrence | Y | [20,46] |
| Tsunamis | currents, infrasonic waves perturbing the ionosphere, wind-wave coupling, magnetics | Y | [48,49,50,51] |
| Use (U.S.) | 1970 Expenditures (est.) $M | Most Needed Sea State Parameters |
|---|---|---|
| Shipping | 5000 | Wave height, direction, period, swell |
| Fishing | 600 | Wave height, current |
| Military | ? | All |
| Petroleum | 2500 | Wave height, current, direction |
| Science | 600 | All |
| Mining | 50 | Wave height |
| Rescue | 580 | Wave height, direction |
| Coastal damage | 500 | Wave height, direction, current |
| Recreation | 5300 | Wave height, swell, direction |
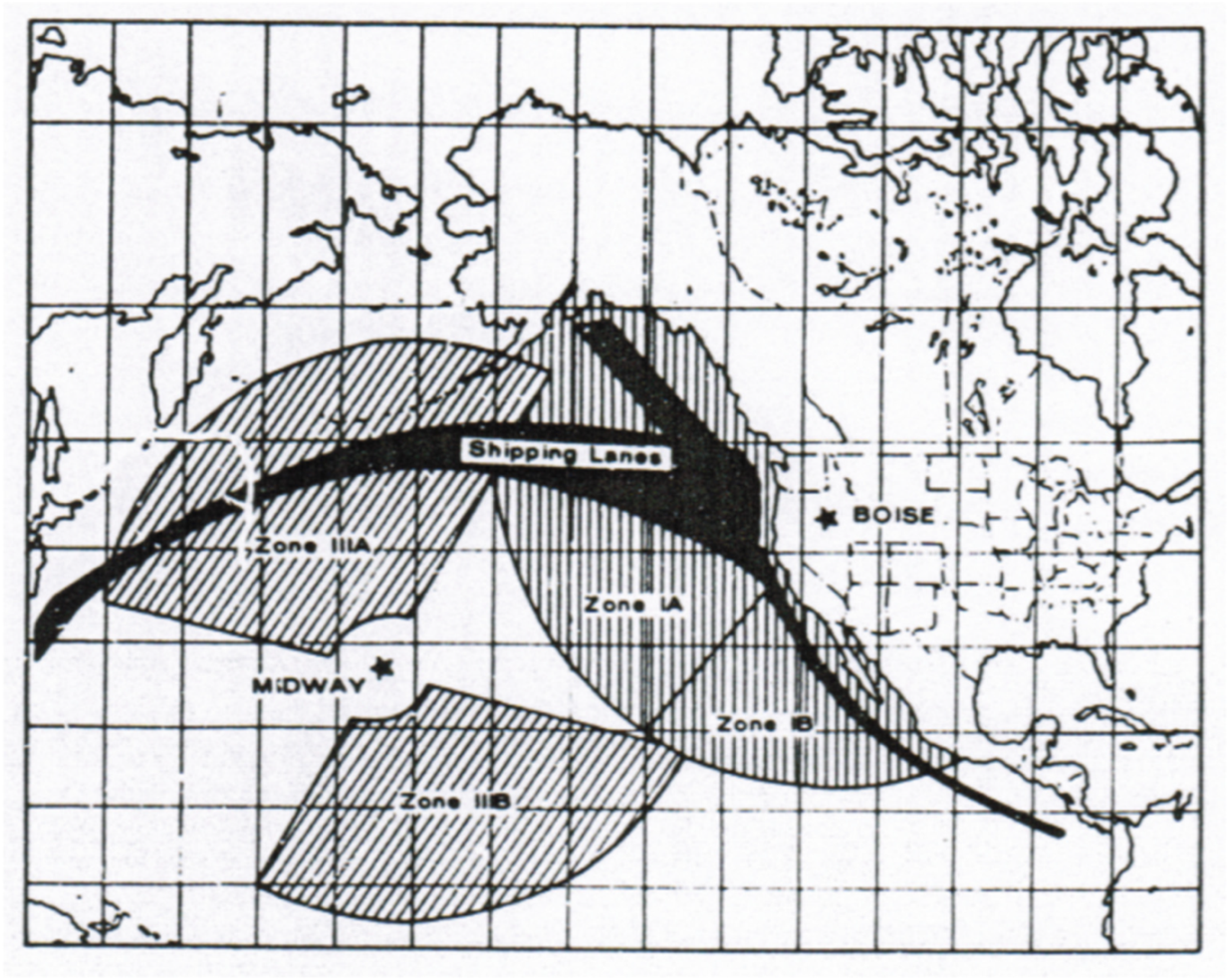
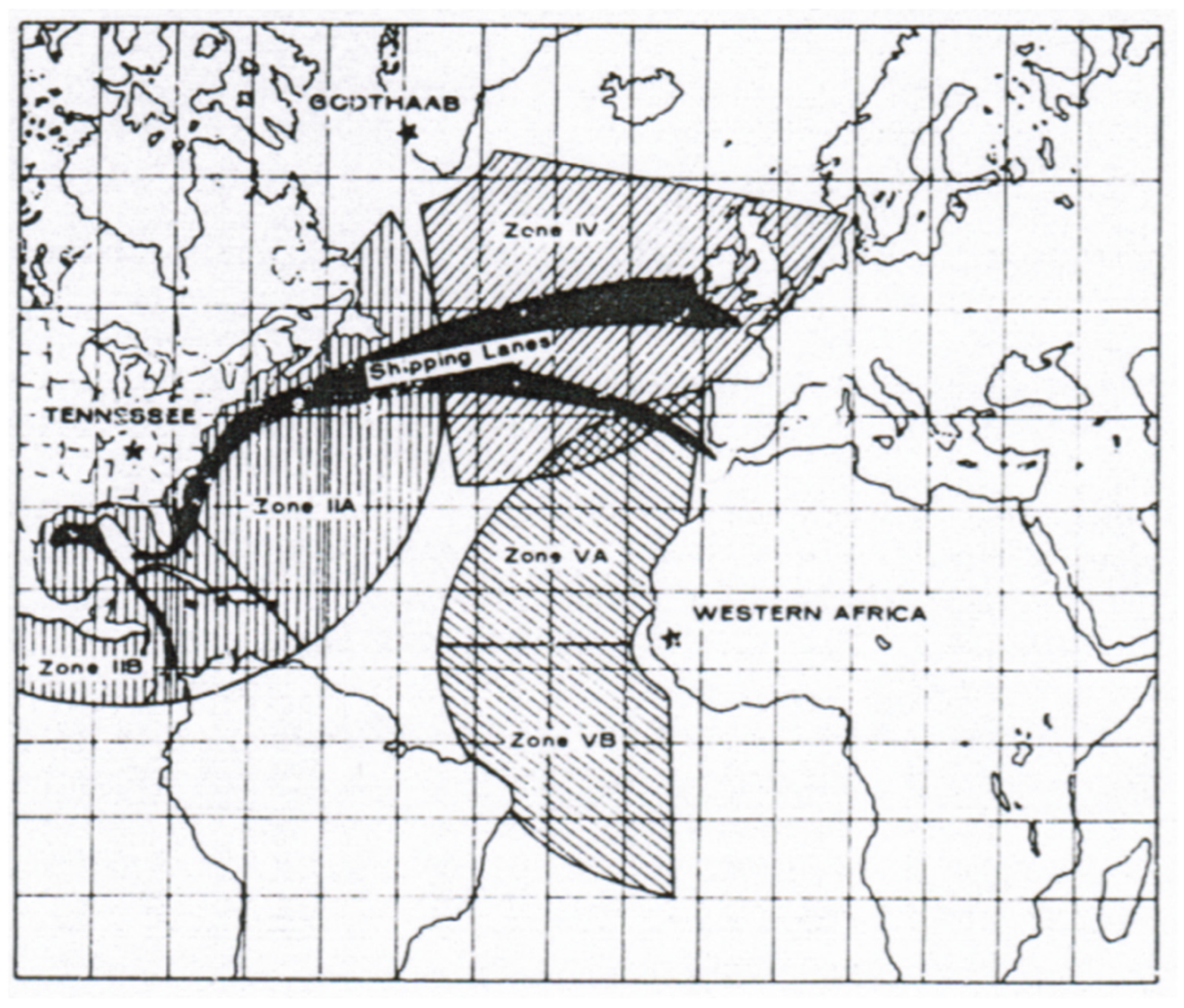
| U.S. User | Site I (Idaho) | Site II (Kentucky) | Site III (Midway) | Site IV (Greenland) | Site V (Africa) | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Min. | Max. | Min. | Max. | Min. | Max. | Min. | Max. | Min. | Max. | |
| Shipping | 12 | 15 | 24 | 30 | 24 | 24 | 24 | 24 | n/a | |
| Fishing | 2 | 3 | 3 | 3 | 1 | 1 | n/a | n/a | ||
| Military | 4 | 8 | 4 | 8 | 4 | 8 | 4 | 4 | 3 | 4 |
| Petroleum | 5 | 7 | 5 | 7 | 1 | 1 | n/a | n/a | ||
| Science | 1 | 2 | 1 | 3 | 1 | 2 | 1 | 1 | 1 | 2 |
| Mining | n/a | n/a | n/a | n/a | n/a | |||||
| Rescue | n/a | n/a | n/a | n/a | n/a | |||||
| Coastal damage | 1 | 1 | 3 | 3 | n/a | n/a | n/a | |||
| Recreation | 2 | 2 | 6 | 6 | n/a | n/a | n/a | |||
| TOTAL BENEFIT | 27 | 38 | 46 | 62 | 31 | 36 | 29 | 29 | 4 | 6 |
| Construction cost | 2 | 6 | 2 | 6 | 2 | 4 | 2 | 4 | 2 | 6 |
| Operation cost | 0.6 | 1.2 | 0.6 | 1.2 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 1.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Anderson, S. Societal Applications of HF Skywave Radar. Remote Sens. 2022, 14, 6287. https://doi.org/10.3390/rs14246287
Anderson S. Societal Applications of HF Skywave Radar. Remote Sensing. 2022; 14(24):6287. https://doi.org/10.3390/rs14246287
Chicago/Turabian StyleAnderson, Stuart. 2022. "Societal Applications of HF Skywave Radar" Remote Sensing 14, no. 24: 6287. https://doi.org/10.3390/rs14246287
APA StyleAnderson, S. (2022). Societal Applications of HF Skywave Radar. Remote Sensing, 14(24), 6287. https://doi.org/10.3390/rs14246287





